GHz laser-free time-resolved transmission electron microscopy: A stroboscopic high-duty-cycle method

Abstract

A device and a method for producing ultrashort electron pulses with GHz repetition rates via pulsing an input direct current (dc) electron beam are provided. The device and the method are based on an electromagnetic-mechanical pulser (EMMP) that consists of a series of transverse deflecting cavities and magnetic quadrupoles. The EMMP modulates and chops the incoming dc electron beam and converts it into pico- and sub-pico-second electron pulse sequences (pulse trains) at >1 GHz repetition rates, as well as controllably manipulates the resulting pulses. Ultimately, it leads to negligible electron pulse phase-space degradation compared to the incoming dc beam parameters. The temporal pulse length and repetition rate for the EMMP can be continuously tunable over wide ranges.

Applying the EMMP to a transmission electron microscope (TEM) with any dc electron source (e.g. thermionic, Schottky, or field-emission source), a GHz stroboscopic high-duty-cycle TEM can be realized. Unlike in many recent developments in time-resolved TEM that rely on a sample pumping laser paired with a laser launching electrons from a photocathode to probe the sample, there is no laser in the presented experimental set-up. This is expected to be a significant relief for electron microscopists who are not familiar with laser systems. The EMMP and the sample are externally driven by a radiofrequency (RF) source synchronized through a delay line. With no laser pumping the sample, the problem of the pump laser induced residual heating/damaging the sample is eliminated. As many RF-driven processes can be cycled indefinitely, sampling rates of 1–50 GHz become accessible. Such a GHz stroboscopic TEM would open up a new paradigm for in situ and in operando experiments to study samples externally driven electromagnetically. Complementary to the lower (MHz) repetition rates experiments enabled by laser photocathode TEM, new experiments in the multi-GHz regime will be enabled by the proposed RF design. Because TEM is also a platform for various analytical methods, there are infinite application opportunities in energy and electronics to resolve charge (electronic and ionic) transport, and magnetic, plasmonic and excitonic dynamics in advanced functional materials. In addition, because the beam duty-cycle can be as high as ~10⁻¹ (or 10%), detection can be accomplished by commercially available de-tectors.

In this article, we report an optimal design of the EMMP. The optimal design was found using an analytical generalized matrix approach in the thin lens approximation along with detailed beam dynamics taking actual realistic dc beam parameters in a TEM operating at 200 keV.

1. Introduction

The past 10 years has seen enormous advancement in time-resolved transmission electron microscopes (TEMs), driven largely by advances in pulsed laser systems. Time-resolved ultrafast TEM (UTEM) [1] and dynamic TEM (DTEM) [2] are steadily establishing new measurement capabilities to observe, understand and control solid or soft materials at the most basic level under equilibrium, far-from-equilibrium, extreme, or in situ and in operando conditions. In a broader context, UTEM and DTEM are electron methods to probe structural dynamics. Even though electrons interact with matter 10⁵ times more strongly than photons (electrons are ~10⁵ stronger in scattering power than photons), ultrafast science instrumentation is currently dominated by synchrotron x-ray and x-ray free electron laser facilities, as well as by the use of rare and highly customized high harmonic generation laser microscopes. Since electron- and photon-based tools are fundamentally different, a comparison can be drawn using a combined resolution metric called space-time resolution (STR, spatial resolution times temporal resolution) – in both classes STR can be ≤10⁻²⁰ m · s. Nevertheless, there are two other parameters that are important: the sampling rate (repetition rate) and beam duty cycle of the electron or photon pulse sequences. In the modern technological era, many breakthroughs rely on understanding how advanced nanoscopic materials or devices operate at rates approaching or exceeding 1 GHz. For example, spintronics exploit ferromagnetic resonance in magnetic materials which occurs in the GHz regime [3]. Understanding how magnetic eigenmodes and magnons interact with real material, defects, and interfaces is a major impendent to the advancement of spintronics. Another example is MEMS/NEMS, which exploit mechanical oscillation of micro-/nano-structures in the MHz and GHz [4]. In operando measurements of mechanical properties of these structures will lead to breakthroughs for smaller and faster devices. These examples illustrate the need for adequate instrumentation. At the moment, none of the aforementioned techniques/tools is able to provide GHz-scale sampling rates.

Factors limiting sampling rates at light sources are complex, and even if they are solved, limited beam time allocations will still limit ubiquity of x-ray GHz methods. In contrast, UTEM and ultrafast electron diffraction [5] approaches can be developed at the scale of single principal investigators, and in this case the barrier to GHz sampling arises from the inherent limitations of driving processes with a pump laser. UTEM is a stroboscopic pump-probe method in which data are repeatedly collected over extended periods of time and thermal load from the pump laser must be handled so a process under study stays reversible [6]. Therefore, even though lasers with higher repetition rates are available, UTEM systems typically operate at much less than 0.1 GHz, and sometimes even at ~0.1 MHz, depending on the experiment. In contrast to most laser-driven processes, many processes driven electrically/magnetically or both can be cycled indefinitely at GHz frequencies, one example being switching in a semiconductor device. This class of problems, characterized by electrical stimulus and lack of an extended cool-down time, is largely distinct from the class of problems typically studied in laser-based UTEM systems. Thus a purely electrical approach to pump/probe electron microscopy can complement existing laser-based approaches by reaching much higher repetition rates in the study of processes that can be so driven. Higher repetition rates have an immediate advantage in terms of the amount of time required to accumulate a measured signal because of the potential for much higher duty cycles and thus much higher time-averaged probe current.

As an alternative to the laser-photocathode combination method of producing electron pulses, blanking of a direct current (dc) electron beam can produce periodic electron pulse sequences with a flexible temporal structure that can be perfectly synchronized with the clock signal driving a high-frequency nanoscale device (be it a transistor, a plasmonic laser diode, a nano-electromechanical system, a spin-transfer torque memory, or any other device). The basic principle of such stroboscopic TEM is presented in Fig. 1. A small part of the RF signal to the dc beam pulsing device is diverted to the sample through a phase-locked delay line. Similar to UTEM, issues like heating can be anticipated, but even so, essential difference here is that near- in operando examination of devices or device structures is feasible, since their realistic operation is itself electromagnetically driven and long thermal cool-down can be avoided. More specifically, the stroboscopic TEM would reveal the inner workings of such devices in unprecedented ways, by bringing all of the high-resolution imaging, analytical, nanoscale diffraction (including strain measurements), and other capabilities (such as holographic imaging of electric fields or spectroscopic imaging of plasmonic fields combined with tomography, making it truly 4D) of a modern TEM down to the time scale of the device’s normal operation. In the method being proposed, the pulsed laser system is eliminated, which significantly reduces system complexity and enhances the ease of use. These are important factors to consider when studying already highly-complicated systems for high-technology applications.

Fig. 1.

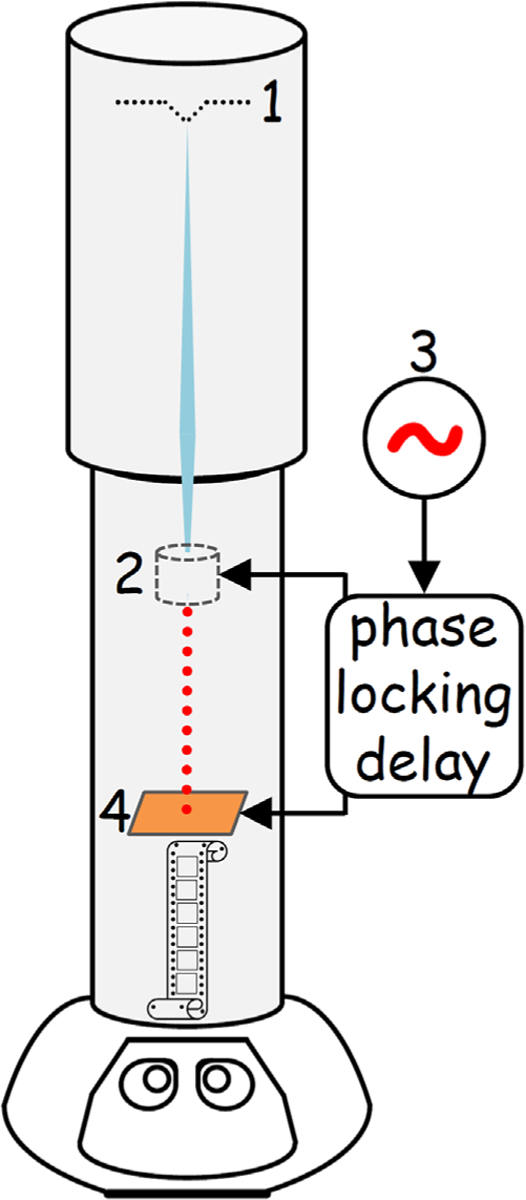
Basic principle of the stroboscopic laser-free high-duty cycle TEM: 1 is the electron dc source; 2 is a dc beam pulsing device; 3 is an RF source; 4 is the sample.

The first prototypes of time-resolved electron microscopes operating in a stroboscopic regime via blanking the dc beam were dates back to the 1960s. Those were scanning electron microscopes (SEM) used to image electron current propagation in novel (for that time) semiconductor devices such as MOSFETs [7] and Gunn-effect devices [8]. The achievable sampling rates were driven by progress in semiconductor technology – from MHz in 1968 [7] to GHz in 1978 [8]. Thus, by early 1980s stroboscopic SEMs looking into processes with temporal resolution as low as 10 ps were widely prototyped. While ns-pulses at MHz repetition rates were easy to generate using a standard deflecting plate system [7], ps-pulses at GHz repetition rates required development of new strategies, which included a specialty meander traveling-wave line [9], specialty fast capacitors [10], and an RF pillbox cavity with a deflecting mode operating at 1 GHz applied for practical use in electron microscopy for the first time [8]. The aforementioned examples made use of SEMs with lateral resolution <~1 μm. While imaging with spatial resolution between 1Å and 1 nm is routine in a modern TEM, recent interest in time-resolved and pump-probe experiments sets much more challenging requirements for electron microscopy: additional temporal resolution between 10 ns and <100 fs is now expected on top of the same spatial resolution range. None of the existing time-resolved microscopes have simultaneously achieved all three of the following parameters: (1) continuously tunable pulse duration between ~100 fs and ~100 ps; (2) continuously tunable rates of repetition from ~0.1 GHz to ~50 GHz; (3) phase-space fidelity of electron pulses so that processes at nanometer length scales and below can be resolved. By continuously tunable we mean that these parameters can be adjusted smoothly throughout their defined ranges, with no gaps.

In this paper, we describe a design of a compact, versatile, drop-in dc beam pulsing device for medium electron energies (~100 keV) to enable laser-free GHz stroboscopic TEM. The final design was chosen from a number of candidates based on the results of analytical geometrical optics approximation and detailed beam dynamics calculations. The solution is such that when the dc beam pulsing device is ON, only electrons matching the strobe frequency are allowed access to the sample and the TEM operates in the GHz stroboscopic mode. When the dc beam pulsing device is OFF, the TEM operates in its conventional mode.

2. Approaches and methods: basic design of the dc beam pulsing device

To pulse the dc beam, mechanical or electromagnetic approaches can be used. Both mechanical shaping and/or electromagnetic manipulations of electron pulsed beams are common in the field of particle accelerators. They are used to tailor electron beam properties and for electron beam diagnostics, including emittance exchange experiments [11], phase-space imaging [12], energy-chirp compensation [13] and accelerator-based radiation sources [14,15]. Particularly, electromagnetic RF cavities are gaining more applications in time-resolved electron microscopes/beam-lines being utilized as electron RF guns [16] and electron pulse compressors [6,17,18]. Following previous reports on designing a combined electromagnetic-mechanical pulser (dubbed as EMMP) operated at GHz rates [8,19], the core component consists of a transverse deflecting cavity (TDC) and a chopping collimating aperture (CCA). A concept of this device is shown in Fig. 2. A vacuum TDC, externally driven by an RF source, operated in TM110 mode at f₀=10 GHz (corresponding to a TDC diameter of 39 mm) and a CCA are used to form ultrahigh repetition rate pulse sequences (the repetition rate here is 20 GHz because pulses are produced by cutting both sides, leading and trailing, of the sinusoid). At the fixed fundamental TDC frequency of 10 GHz, the pulse length can be continuously changed between 100 fs and 10 ps by varying the CCA diameter and/or RF power in the cavity. The exact range of duty cycle depends on the ratio of the diameters of the TDC (determining f₀) and the CCA, and the power fed by the RF source into the TDC. For the TM110 mode in a pillbox, a general relation between all the parameters involved is described as

$$P\propto B^2=\frac{r\times m_e}{d\times e\times \Delta t},$$ (1)

where P and B are power and magnetic component of the electromagnetic field in the TDC, respectively; m_e and e are the electron mass and charge, respectively; r is the radius of the CCA; d is the free-drifting distance between the TDC and the CCA; and Δt is the electron pulse length. This leads to duty cycles of up to 2 × 10⁻¹ (or 20%). One important note: the RF pillbox cavity technology is downwards compatible to sampling rate (or strobe rate) in the MHz by replacing vacuum in the TDC with a high permittivity dielectric. The general relation linking the TDC diameter (D), the fundamental TDC frequency (f₀) and the permittivity (ε) is $D~\frac{1}{f_0\times \sqrt{\epsilon }}$. With a high permittivity ferroelectric, the TDC can be continuously tunable too in a specific frequency range. We present the case where the TDC is operated at fundamental frequency of 10 GHz (20 GHz strobe) in this study because such a sampling rate can satisfy a multitude of ultrafast experiments (e.g. nanoscale magnetic dynamics). At the same time, this example illustrates the challenges in preserving remarkable quality of the unmodified dc beam like the original energy spread. Lower sampling rates at longer pulse lengths will always have more benign effects on the pulsed electron beam.

Fig. 2.

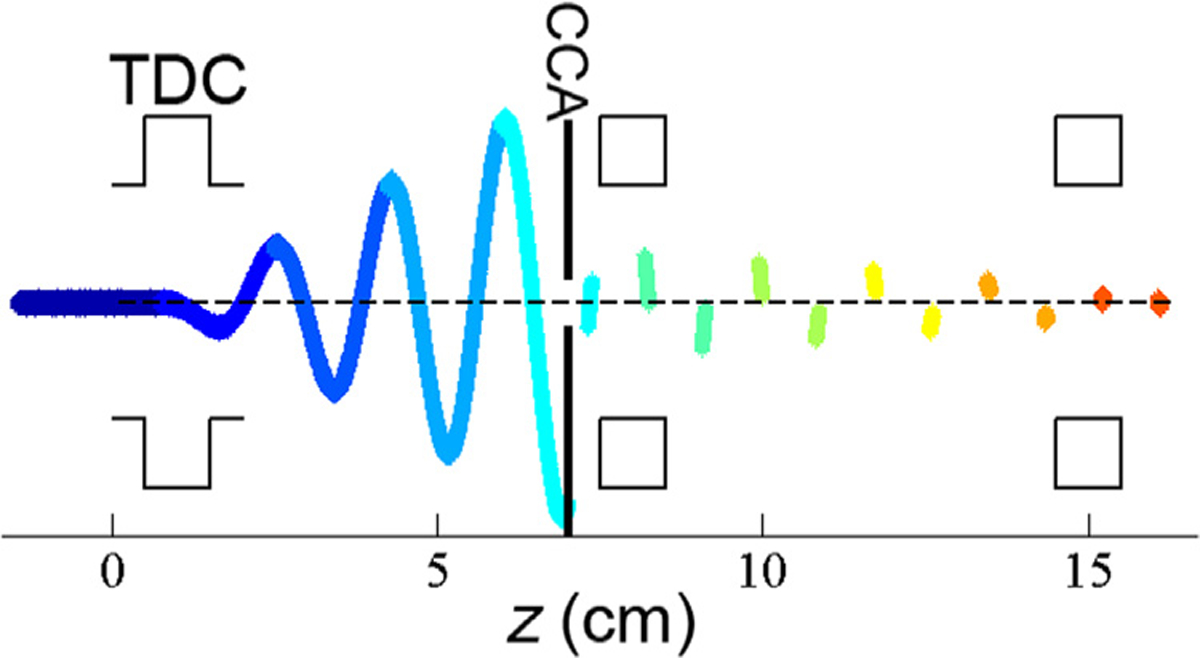
General concept of the compact electromagnetic-mechanical pulser (EMMP) for pulsing dc electron beams and manipulating electron pulses in the phase space. (The z-scale is approximate, and color coding is arbitrary.) Additional elements (shown here as generic squares representing either two TDCs or a magnetic quadrupole and a second TDC) after the CCA compensate for the introduced transverse momentum, resulting in a beam with very nearly the same transverse phase space profile as in normal operation by the time it exits the EMMP at the right-hand side of the diagram.

The incoming longitudinal electron dc beam traveling along the z-axis (Fig. 2), blue straight segment originating before z=0 cm) picks up a transverse sinusoidal momentum by the electromagnetic (EM) field in the TDC. Since the EM field oscillates with the radial frequency f₀, the modulation force depends on the time at which electrons arrive in the TDC. The amplitude of the sinusoid grows as the modulated beam propagates. The CCA is placed on axis to chop the beam and converts it into a pulse train. As mentioned in earlier publications on the stroboscopic pulsers/choppers, different scenarios of spatial deterioration of the electron beam were observed [8,19]. Indeed, using the concept in Fig. 2 the beam would expand in the transverse (beam diameter growth) and longitudinal (temporal coherence deterioration) directions after drifting a certain distance. While this was not an issue for imaging on the micron scale, much more rigorous schemes must be considered in order to ensure beam spatial and energy co-herence necessary for TEM spectroscopy, diffraction and imaging. Thus, additional optical elements are required downstream of the CCA to mitigate the effects produced by the first TDC. These additional elements are represented as blank squares in Fig. 2, which will be determined in Sections 3 and 4.

3. Generalized matrix calculations

Since the final goal is integration with a TEM, the EMMP should be as compact as possible. This not only places an upper limit on the number of optical elements, but also makes it desirable to minimize the number of necessary adjustments to tune the EMMP. To come up with the best miniature design for removing the post-TDC distortions of the resulting electron pulses, we use a generalized matrix approach. In this approach, optical elements are described by matrices. Matrix components depend on the actual geometry of the EMMP, and the strength of various effects on electron dynamics in the phase space can be predicted and evaluated. The matrix methodology relies on three basic assumptions: (1) electron optics elements are approximated as thin lenses; (2) it considers a single particle/electron; (3) only linear matrix transformations are considered. All three assumptions are intertwined. When combined, they establish the basis for the geometrical optics framework in which the problem is solved. This idealized framework provides a good first-order model for rapid progress in the design, to be followed up with full ray-trace calculations including space charge effects to determine the effects of aberrations and undesired couplings on the electron phase space.

An initial and a final state of an electron at input and at the output of the EMMP are linked in the momentum-coordinate phase space via a beam transport matrix as follows

$$\left(\begin{array}{l}{x}_f\hfill \\ x_f^{\prime }\hfill \\ y_f\hfill \\ y_f^{\prime }\hfill \\ z_f\hfill \\ \frac{\Delta p_f}{p_0}\hfill \end{array}\right)=\left(\begin{array}{llllll}{R}_{11}\hfill & R_{12}\hfill & R_{13}\hfill & R_{14}\hfill & R_{15}\hfill & R_{16}\hfill \\ R_{21}\hfill & R_{22}\hfill & R_{23}\hfill & R_{24}\hfill & R_{25}\hfill & R_{26}\hfill \\ R_{31}\hfill & R_{32}\hfill & R_{33}\hfill & R_{34}\hfill & R_{35}\hfill & R_{36}\hfill \\ R_{41}\hfill & R_{42}\hfill & R_{43}\hfill & R_{44}\hfill & R_{45}\hfill & R_{46}\hfill \\ R_{51}\hfill & R_{52}\hfill & R_{53}\hfill & R_{54}\hfill & R_{55}\hfill & R_{56}\hfill \\ R_{61}\hfill & R_{62}\hfill & R_{63}\hfill & R_{64}\hfill & R_{65}\hfill & R_{66}\hfill \end{array}\right)\left(\begin{array}{l}{x}_i\hfill \\ x_i^{\prime }\hfill \\ y_i\hfill \\ y_i^{\prime }\hfill \\ z_i\hfill \\ \frac{\Delta p_i}{p_0}\hfill \end{array}\right),$$ (2)

where x is the relative horizontal beam position, x′ is the horizontal divergence, y is the relative vertical beam position, y′ is the vertical divergence, z is the relative longitudinal position (principal optical axis of the TEM) or time, and $\frac{\Delta p}{p_0}$ is the relative longitudinal momentum.

In Eq. 2, the matrix R(6 × 6) is called the transport matrix. It is a result of multiplication of all matrices describing every single component of an EMMP design; this includes the drifting matrix describing empty gaps/pipes between hardware components. The perfect case is when the matrix R has only diagonal elements: it means an electron beam transformation took place, yet cross-correlations, described by off-diagonal elements resulting in pulse size change in transverse and longitudinal directions and energy spread, are absent. A number of combinations and designs were analyzed, and the main conclusion was that at least 3 active elements must be present to minimize off-diagonal elements. While the first element is always a TDC, second and third elements are shown as blank squares in Fig. 2, and should be determined from the matrix analysis. It was found that best results can be anticipated when combinations of TDCs and/or magnetic quadrupoles (MQs) are used, provided such combinations are also most compact and simple from the operational point of view. Two most attractive designs are illustrated in Fig. 3.

Fig. 3.

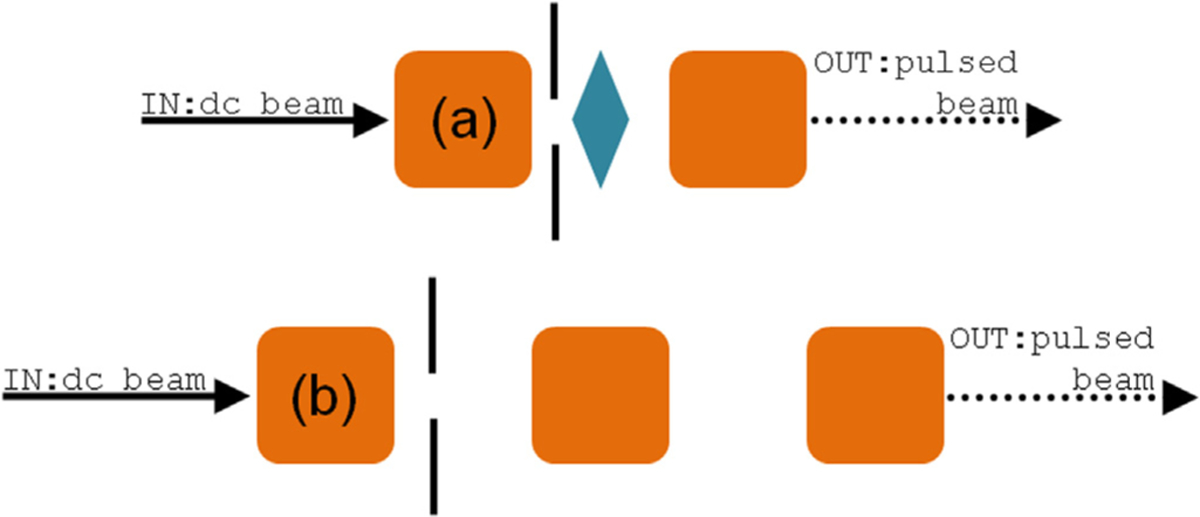
Two main EMMP designs for further considerations based on the matrix analysis (not to scale). The orange square is the TDC, and the cyan diamond is the MQ. Design (a) is abbreviated as TDC+MQ+TDC and design (b) is abbreviated as 3TDC.

Thus, the resulting matrix R(6 × 6) is the product of 5-fold multiplication of 3 key matrices related to the EMMP designs in Fig. 3. Free drift beam pipe of length d (empty space between either optical component in the EMMP) [measured in meters] is described by the following matrix

$$\left(\begin{array}{llllll}1\hfill & d\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & d\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & \frac{d}{{\gamma }^2}\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\right),$$ (3)

where γ is the Lorentz factor. Its value depends on the electron energy. The magnetic quadrupole with a focal length f [measured in meters] is described as

$$\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ \frac{1}{f}& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& -\frac{1}{f}& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right).$$ (4)

The TDC has a matrix

$$\left(\begin{array}{llllll}1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill & k\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ k\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\right),$$ (5)

where k is the transverse momentum acquired by an electron in the TDC, and it can be measured in reciprocal meters or eV. In what follows, k will be referred to as kick. Resulting transport matrices for the designs, sketched in Fig. 3, were optimized in order to zero as many off-diagonal elements as possible. For this calculation, the following dc beam input parameters were considered: (1) beam energy (E₀) 200 keV; (2) energy spread (ΔE) 0.5 eV; (3) emittance 1.5 nm × rad which was a product of a beam diameter of 10 μm and a divergence angle of 0.15 mrad; these values are also typical for various accelerator applications. The TDC+MQ+TDC design (Fig. 3a) has a transport matrix

$$\left(\begin{array}{cccccc}-\frac{d_2}{d_1}& 0& 0& 0& 0& 0\\ -\frac{\left({\gamma }^2-d_1^2{k}_1^2\right)\left(d_1+d_2\right)}{d_1{d}_2{\gamma }^2}& -\frac{d_1}{d_2}& 0& 0& 0& \frac{d_1{k}_1\left(d_1+d_2\right)}{d_2{\gamma }^2}\\ 0& 0& 2+\frac{d_2}{d_1}& 2\left(d_1+d_2\right)& 0& 0\\ 0& 0& \frac{d_1+d_2}{d_1{d}_2}& 2+\frac{d_1}{d_2}& 0& 0\\ \frac{k_1\left(d_1+d_2\right)}{{\gamma }^2}& 0& 0& 0& 1& \frac{d_1+d_2}{{\gamma }^2}\\ 0& 0& 0& 0& 0& 1\end{array}\right),$$ (6)

where d₁ and d₂ are the drift distances between the first TDC and the MQ, and between the MQ and the second TDC respectively; k₁ is the kick strength of the first deflecting cavity. The focal length of the MQ is $f=-\frac{d_1{d}_2}{d_1+d_2}$, and the kick strength of the second deflecting cavity is $k_2=\frac{d_1}{d_2}{k}_1$. For the 3TDC (Fig. 3b) design, the R-matrix is

$$\left(\begin{array}{cccccc}1-\frac{d_1\left(d_1+d_2\right)k_1^2}{{\gamma }^2}& d_1+d_2& 0& 0& 0& -\frac{d_1\left(d_1+d_2\right)k_1}{{\gamma }^2}\\ -\frac{d_1\left(d_1+d_2\right)k_1^2}{d_2{\gamma }^2}& 1+\frac{d_1^2\left(d_1+d_2\right)k_1^2}{d_2\left(d_1\left(d_1+d_2\right)k_1^2-{\gamma }^2\right)}& 0& 0& 0& -\frac{d_1^2{\left(d_1+d_2\right)}^2{k}_1^3}{d_2\left(d_1^2{k}_1^2+d_1{d}_2{k}_1^2-{\gamma }^2\right)}\\ 0& 0& 1& d_1+d_2& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& -\frac{d_1\left(d_1+d_2\right)k_1}{{\gamma }^2}& 0& 0& 1-\frac{d_1\left(d_1+d_2\right)k_1^2}{{\gamma }^2}& \frac{d_1+d_2}{{\gamma }^2}\\ 0& -\frac{d_1^2{\left(d_1+d_2\right)}^2{k}_1^3}{d_2\left(d_1^2{k}_1^2+d_1{d}_2{k}_1^2-{\gamma }^2\right)}& 0& 0& -\frac{d_1\left(d_1+d_2\right)k_1^2}{d_2}& 1+\frac{d_1^2\left(d_1+d_2\right)k_1^2}{d_2\left(d_1\left(d_1+d_2\right)k_1^2-{\gamma }^2\right)}\end{array}\right)$$ (7)

where $k_2=-\frac{d_1+d_2}{d_2}{k}_1$ and $k_3={\gamma }^2\frac{d_1}{d_2\left({\gamma }^2-d_1\left(d_1+d_2\right)k_1^2\right)}{k}_1$ are found as optimal for the overall system design, i.e. maximum off-diagonal elements are zeros.

While the matrix methodology is widely used in high energy physics (electron beam energy range ~10 MeV), it is challenging to apply it to the medium energy electron beams (~100 keV) found in TEMs due primarily to the Lorentz factor. Many off-diagonal elements in the transport matrices (Eqs. (6) and (7)) are proportional to $\frac{1}{{\gamma }^2}$ So for a 10 MeV beam where γ≈20, the off-diagonal elements become negligibly small. This is certainly not the case for a 100 keV beam where γ≈1. From the matrices, it is seen that in transverse directions both designs may lead to satisfactory results such that sufficient spatial coherence in the beam is conserved upon EMMP installation. The main problem here is the matrix term R₆₅ which is responsible for energy spread growth. In this idealized geometrical optics framework, R₆₅ is zero for the TDC+MQ+TDC design, but is finite for the 3TDC design. That is, in the 3TDC case, the additional energy spread at E₀=200 keV is higher than 1 eV on top of the default/intrinsic energy spread of 0.5 eV.

4. Beam dynamics simulations

Matrix calculations provided a good starting point for the actual EMMP design. In the 3TDC case, it is seen that the energy spread is proportional to the kick value to the second power, $k_1^2$. Since the resulting electron pulse length is controlled by both k₁ and the CCA radius, to achieve a short pulse we must either have a large kick or a small aperture. Therefore, to reduce energy spread for a given pulse size, we should choose a CCA radius as small as reasonably possible, because it reduces the kick. At the same time, if the beam radius is larger than the CCA radius the EMMP will not be able deliver effective chopping at the CCA no matter how strong the kick is. Thus, the radius of the incoming dc beam produces a limitation for the EMMP in terms of the relation between the CCA radius and the kick strength, and consequently a limitation for minimal extrinsic/induced energy spread achievable upon pulsing. Beam dynamics calculations were carried out to compare transverse and longitudinal phase spaces between the input dc beam and the output pulsed beam. Using the geometry and beam radius), we conducted our simulation in the soft focusing regime meaning that an input dc beam radius was 3 μm and an angle of convergence was 0.1 mrad, resulting in beam emittance 0.3 nm × rad. Changing the beam emittance between the default TEM mode and the soft focusing regime can be achieved by inserting a custom condenser lens (C0) similar to one described in Ref. [20], thus allowing a large fraction of the current emitted from the gun to be collected, collimated, and aligned into the pulser with a small convergence angle. Total dc current at C0 of ×100 nA is feasible in this alignment. The soft focusing is illustrated in Fig. 4. Dotted red lines represent a way the dc beam should propagate and converge through the EMMP when it is OFF. Using C0 to create a soft crossover at the CCA plane allows optimal modulation and chopping upon turning the EMMP ON. Normal TEM operation with a low-emittance dc beam is obtained by turning off both C0 and the pulser components.

Fig. 4.

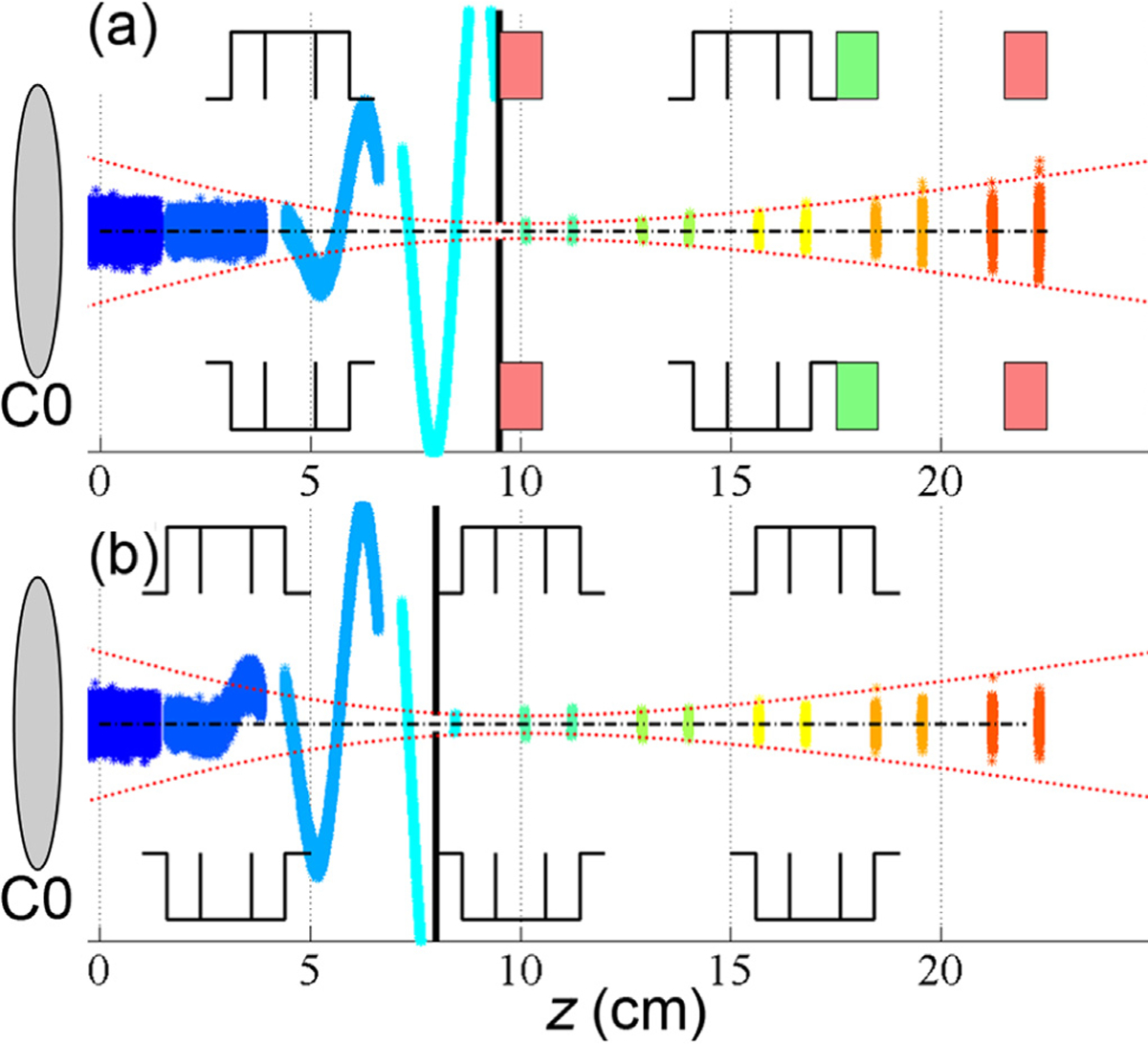
Two key designs identified by the matrix calculations and tested through beam dynamics. (a) TDC+MQ+TDC design; (b) 3TDC design. Red Dotted lines represent beam waist in the middle of the second active EMMP element, i.e. MQ (a) and TDC (b) – not to scale. The central black dash-dotted line is the symmetry (optic) axis.

In terms of the device placement, a combined section containing C0 and EMMP should be inserted after the ultrahigh vacuum gun chamber but before the condenser lens section. This means operation and maintenance under the moderate column vacuum conditions which (1) completely circumvents the need to disturb the electron source and (2) preserves the factory packaging and design of the condenser system. After reviewing microscope ray-diagrams, we found this was the best location for preserving all the available imaging and diffraction modalities. First, we emphasize that there is no change in dc beam propagation before the condenser lens system. Since beam phase-space manipulations to achieve different imaging modes in a TEM column take place at or below the condensers, by inserting the device between the gun and the condenser lenses, the problem is reduced to preserving the transverse and longitudinal phase spaces as the dc beam converts into a pulse train passing through the EMMP. Based on the soft focusing parameters, an input file representing the incoming dc beam was built using the code PARMELA [21,22]. Input dc parameters and geometry used in the calculations are summarized in Table 1 and Fig. 4, respectively. Particle tracking through the EMMP in the longitudinal and transverse phase spaces was performed by a custom-developed MATLAB [22] code. Resulting parameters are compiled in Table 1. While both designs deliver nearly perfect conservation of the transverse phase space (ε_x, ε_y), energy spread becomes a major parameter for design considerations. In TDC+MQ+TDC design, an induced energy spread as low as 0.25 eV was achieved. Given a typical intrinsic energy spread in a TEM of 0.5 eV, the total value is 0.56 eV for a 10 ps pulse. As it was first suggested by Eq. (6), the TDC+MQ+TDC configuration (Figs. 3a and 4a) is chosen for further hardware development based on this analysis. Such an energy resolution will allow pulsed electron energy-loss spectroscopy in TEM.

Table 1.

Key design quantities (kick and CCA radius), and values characterizing the transverse and longitudinal phase spaces of the pulsed beam at the output of the EMMP with the two basic designs (3TDC and TDC+MQ+TDC) considered.

EMMP design	Pulse length (ps)	Kick (keV)	Aperture radius (μm)	εx (nm × rad)	εy (nm × rad)	Energy spread (eV)
INPUT	-	-	-	0.3	0.3	-
TDC+MQ+TDC	1	1.25	5	0.24	0.39	0.81
		1.88	7.5	0.31	0.40	1.38
		2.50	10	0.38	0.43	2.23
		5.00	20	0.41	0.43	9.7
	10	0.25	10	0.36	0.40	0.25
		0.50	20	0.38	0.39	1.01
3TDC	1	2.5	10	0.34	0.42	28.4
		5	20	0.38	0.39	118
	10	0.5	20	0.38	0.43	12.5

At this point, the two MQs placed right after the second TDC are to stigmate the output pulses. Upon modifications, we expect that stigmation correction can be performed using the default optics in the TEM, and these MQs can be excluded from the design. In the TDC+MQ+TDC design, the MQ can be assembled with electro- or permanent magnets. Making use of a permanent magnet MQ would simplify the overall EMMP implementation. Taking it one step further, let us consider dc beam behavior when the EMMP is OFF. Fig. 5 illustrates the root-mean-square (rms) transverse beam size, i.e. beam envelop in two transverse directions, with the EMMP ON (solid red and blue lines) and OFF (dotted red and blue lines). The state OFF means that only the TDCs are OFF, and the MQs are permanent magnets, i.e. ON all the time. It is seen that envelop and divergence after the aperture, especially at the outlet of the EMMP, are nearly identical. This result suggests that to return back to default TEM imaging mode with dc beam, in the TDC+MQ+TDC environment with the permanent magnets the RF source can be simply turned OFF such that TDCs become additional free drift space. If compact electromagnetic quadrupoles are in use, they can be either turned OFF such that the whole EMMP becomes a drift pipe and the dc beam is adjusted via C0, or the electromagnets are additionally used to steer and focus the dc beam, or they stay ON at the nominal values such that the situation in Fig. 5 takes place.

Fig. 5.

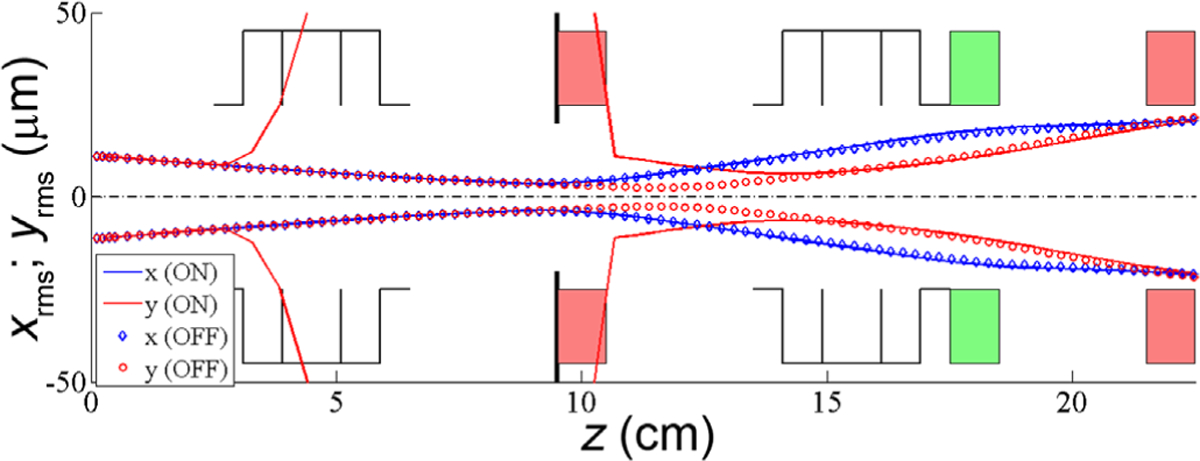
Beam envelop with the EMMP ON (solid lines) and OFF (dotted lines) – not to scale. Apparent discontinuity in the red solid curve is the result of RF modulation of the dc beam. The central black dash-dotted line is the symmetry (optic) axis.

5. Conclusions

To summarize, a novel time-resolved GHz stroboscopic concept for transmission electron microscopy is proposed. Such concept is laser-free and is aimed at resolving sub-nanosecond processes in advanced magnetic, electronic, ionic and photonic materials under actual operation conditions. A sample is given a GHz excitation with a radiofrequency source which is phase-locked through a delay line to a pulser, which converts a standard dc beam in a TEM into pulse trains being driven by the same radiofrequency source. In the family of time-resolved electron probe methods, the laser-free/electromagnetically-driven GHz stroboscopic concept fulfills a different temporal landscape that is complementary to the existing commercial solutions. We used an analytical matrix algorithm and beam dynamics simulations to identify and rationalize a de-pulser for a 200 keV electron beam sign-of-choice for a compact TEM columns. Table 2 summarizes key compatible with performance parameters anticipated in the proposed GHz stroboscopic TEM.

Table 2.

Summary of parameters considered in the paper.

Initial beam energy	200 keV
Intrinsic energy spread	0.5 eV
Dc beam current at gun exit	~100 nA
Operation mode	Stroboscopic
Laser	Not required
Pulse length	1 ps	10 ps
Sampling rate at specimen	20 GHz	20 GHz
Duty cycle	2 × 10−2 (2%)	2 × 10−1 (20%)
Number of electrons per cycle	~1	~10
Rms emittance	≤0.4 nm × rad	≤0.4 nm × rad
Extrinsic rms energy spread	0.81 eV	0.25 eV
Total energy spread $\sqrt{\left({\text{intrinsic}}^2+{\text{ induced}}^2\right)}$	0.95 eV	0.56 eV
Total relative energy spread	4.75 × 10−6	2.80 × 10−6
STR at 1 nm spatial resolution	<10−21 m s	<10−20 m s