Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2024 Jul 1.
Published in final edited form as: J Physiol. 2023 Apr 25;601(13):2733–2749. doi: 10.1113/JP284244

Graft–host coupling changes can lead to engraftment arrhythmia: a computational study

Chelsea E Gibbs 1, Silvia Marchianó 2,3,4, Kelly Zhang 1, Xiulan Yang 2,3,4, Charles E Murry 1,2,3,4,5, Patrick M Boyle 1,2,4
PMCID: PMC10901678  NIHMSID: NIHMS1966318  PMID: 37014103

Abstract

After myocardial infarction (MI), a significant portion of heart muscle is replaced with scar tissue, progressively leading to heart failure. Human pluripotent stem cell-derived cardiomyocytes (hPSC-CM) offer a promising option for improving cardiac function after MI. However, hPSC-CM transplantation can lead to engraftment arrhythmia (EA). EA is a transient phenomenon arising shortly after transplantation then spontaneously resolving after a few weeks. The underlying mechanism of EA is unknown. We hypothesize that EA may be explained partially by time-varying, spatially heterogeneous, graft–host electrical coupling. Here, we created computational slice models derived from histological images that reflect different configuration of grafts in the infarcted ventricle. We ran simulations with varying degrees of connection imposed upon the graft–host perimeter to assess how heterogeneous electrical coupling affected EA with non-conductive scar, slow-conducting scar and scar replaced by host myocardium. We also quantified the effect of variation in intrinsic graft conductivity. Susceptibility to EA initially increased and subsequently decreased with increasing graft–host coupling, suggesting the waxing and waning of EA is regulated by progressive increases in graft–host coupling. Different spatial distributions of graft, host and scar yielded markedly different susceptibility curves. Computationally replacing non-conductive scar with host myocardium or slow-conducting scar, and increasing intrinsic graft conductivity both demonstrated potential means to blunt EA vulnerability. These data show how graft location, especially relative to scar, along with its dynamic electrical coupling to host, can influence EA burden; moreover, they offer a rational base for further studies aimed to define the optimal delivery of hPSC-CM injection.

Keywords: Arrhythmia, computer modelling, hPSC-CM

Graphical Abstract

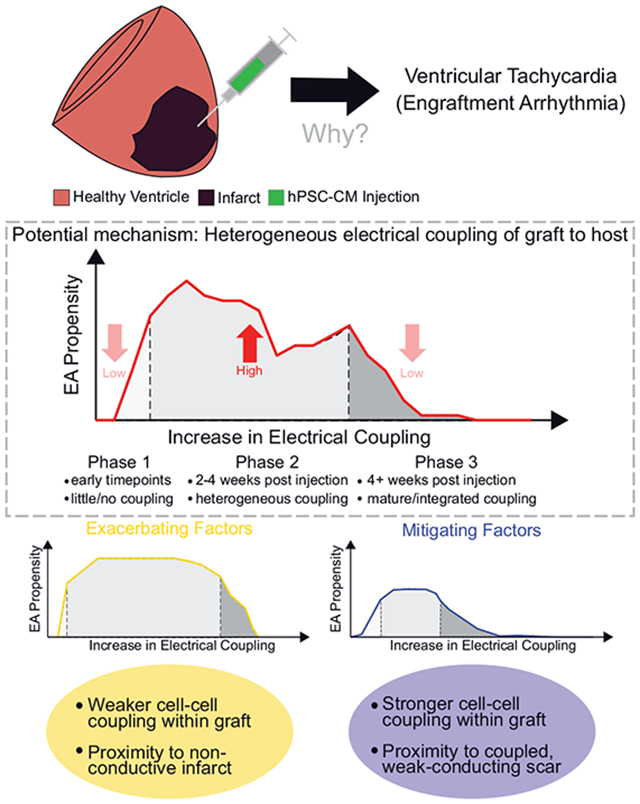
graphic file with name nihms-1966318-f0001.jpg

Engraftment arrhythmias (EA) following hPSC-CM injection can be explained in part by spatially and temporally heterogeneous graft to host electrical coupling. EA propensity can be exacerbated by weak intra-graft cell–cell coupling or by graft proximity to non-conductive infarct; conversely, it can be mitigated by graft proximity to weak-conducting scar or by strong intra-graft cell–cell coupling.

Introduction

Myocardial infarction (MI) is a global health burden and the leading cause of death worldwide (GBD 2019 Diseases and Injuries Collaborators, 2020). The regenerative capacity of the human heart decreases soon after birth (Bergmann et al., 2009; Laflamme & Murry, 2011), and muscle tissue lost after MI is replaced by non-contractile scar tissue (Richardson et al., 2015; Rog-Zielinska et al., 2016; Prabhu & Frangogiannis, 2016). This leads to detrimental structural remodelling and heart failure (HF), which is common following MI (Velagaleti et al., 2008; Ezekowitz et al., 2009; Gerber et al., 2016; GBD 2019 Diseases and Injuries Collaborators, 2020). Current HF treatment options focus on symptom management and delaying disease progression, but these strategies fail to solve the underlying issue of damaged myocardium, namely replacement of functional myocardium with fibrosis (Bahit et al., 2018). Heart transplantation remains the ultimate option, but this procedure is limited by the number of donor hearts available (Colvin et al., 2022). Thus, there is a pressing need for regenerative-based cardiac therapies (Eschenhagen et al., 2017; Bertero & Murry, 2018).

Human pluripotent stem cell-derived cardiomyocytes (hPSC-CM) represent a promising candidate for cardiac regenerative cell-based therapies. Pre-clinical studies have shown that hPSC-CM limited adverse remodelling of the heart while also improving ventricular function (Laflamme et al., 2005; Caspi et al., 2007; Eschenhagen et al., 2017; Bertero & Murry, 2018; Dhahri et al., 2022). However, after transplantation in large animal models (e.g. pigs and non-human primates (NHP)), this therapeutic approach leads to transitory but serious cardiac arrhythmias, defined as engraftment arrhythmia (EA) (Chong et al., 2014; Shiba et al., 2016; Liu et al., 2018; Romagnuolo et al., 2019; Nakamura et al., 2021). Electrical mapping studies suggest EA is focal in nature, with ectopic excitations originating at the sites of hPSC-CM implantation (Liu et al., 2018; Romagnuolo et al., 2019; Filice et al., 2020; Nakamura et al., 2021). This notion agrees with the immature profile of hPSC-CMs that, like embryonic cardiomyocytes, exhibit automaticity (i.e. the ability to spontaneously depolarize and generate action potentials) (Peinkofer et al., 2016; Guo & Pu, 2020; Karbassi et al., 2020). EA burden becomes detectable as graft starts to electromechanically couple with host cells (within ~1 week), and it peaks to occupy >50–75% of the day, around 2-weeks post-treatment. These arrhythmias persist for multiple weeks while the burden progressively wanes before resolving (Liu et al., 2018; Romagnuolo et al., 2019). It is still mechanistically unclear, however, how spontaneous excitations in a relatively small number of transplanted hPSC-CMs can serve as a rapid-firing bioelectrical source that elicits propagating responses in the dense, well-coupled current sink of host myocardium. Previous studies have shown that expression of the proteins mediating mechanical and electrical coupling between host myocardium and grafts, such as N-cadherin and connexin43, are progressively upregulated and localized to nascent intercalated disks with maturation. In turn, maturation is accelerated after in vivo transplantation, compared to in vitro culture (Lundy et al., 2013; Kadota et al., 2017; Karbassi et al., 2020); however, how this upregulation in proteins is related to EA propensity remains poorly understood.

Computational cardiology has emerged as a useful tool to gain mechanistic insights into arrhythmia initiation and perpetuation at various spatial scales (Moreno et al., 2011; Boyle, Franceschi et al., 2019; Fassina et al., 2022). Cell-, tissue- and organ-scale computational models have helped in understanding arrhythmias in ways difficult to achieve through traditional experimental or clinical techniques (Arevalo et al., 2016; Trayanova et al., 2017; Boyle, Zghaib et al., 2019). Prior computational modelling work suggests re-entrant mechanisms may play a role in EA onset (Yu et al., 2019; Yu, Liang, Weinberg et al. 2022), but those studies assumed a continuum of graft–host electrical coupling and were unable to recapitulate the key observation from pre-clinical animal studies that EA is focal in nature. The development of histology-based computational tools that can reconcile this apparent contradiction will lead to a better understanding of EA and may lead to new strategies for mitigating side effects in cell-based heart regeneration therapies.

In this study, we created computational models from 2D-histological images of engrafted hPSC-CMs to better represent the spatial distribution of graft, host and scar tissue. Simulations were conducted in these models to assess how heterogeneous graft–host electrical coupling affects EA propensity. Specifically, we examined the role played by spatiotemporal evolution of coupling along boundaries between hPSC-CM and host myocardium regions. We hypothesized that temporal dynamics of EA in pre-clinical studies (i.e. delayed onset post-engraftment, eventual resolution) can be explained partially by the formation of graft–host electrical connections in a gradual, spatially heterogeneous manner. To model this, we used ventricular slice models derived from histological images (Liu et al., 2018), and stochastically modified graft–host coupling patterns to comprehensively test thousands of plausible combinations. In each configuration, EA propensity, intended as the possibility of graft–host ectopic excitation, was evaluated during its evolution: from the time of hPSC-CM injection to fully integrated grafts. Finally, we examined how the presence or absence of scar tissue modified graft arrhythmogenicity in the same ventricular slice models.

Methods

Ethical approval

The histology images used in this study were derived from infarcted macaque hearts that came from a previous study (Liu et al., 2018). All procedures and protocols used for the animals in that study complied with the NIH Guidelines for the Care and Use of Laboratory Animals and the Animal Welfare Act. Ethical approval was obtained from the University of Washington Animal Care and Use Committee. Animals are housed in the primate centre facility of the University of Washington Department of Comparative Medicine and monitored by University of Washington’s staff veterinarians. All activities involving animals are reviewed and approved by the University of Washington’s Institutional Animal Care and Use Committee (IACUC, protocol number 448602).

Histology-based slice models

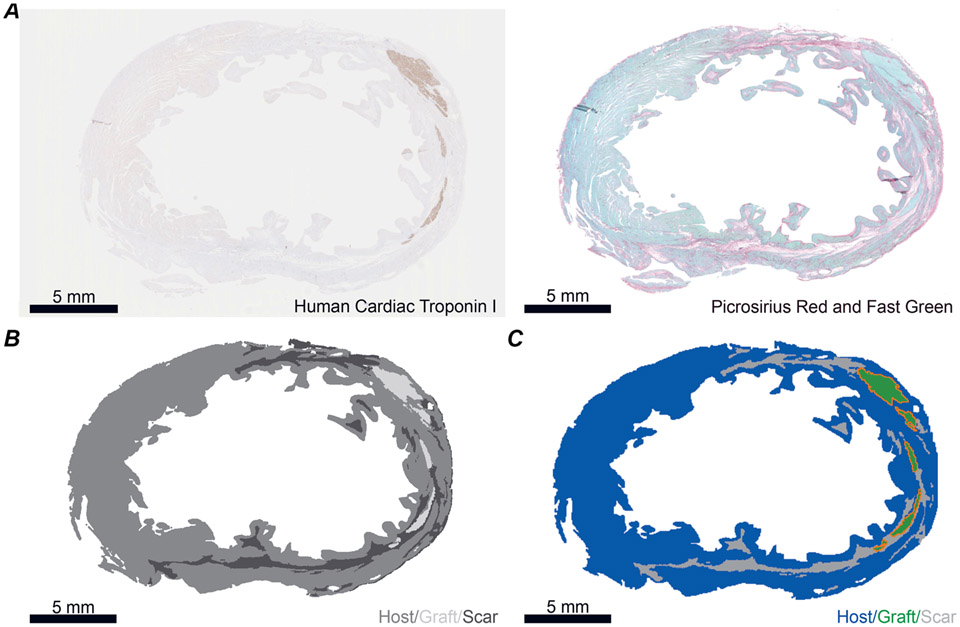
Five unique histology images from post-MI ventricles of two macaque NHPs 3 months following hPSC-CM injection were used to reconstruct two-dimensional slice models (Liu et al., 2018). Models 1–2 came from one NHP; models 3–5 came from a second animal. The histology approach has been described previously (Liu et al., 2018). Briefly: human cardiac troponin I staining was used to visualize hPSC-CM graft; picrosirius red and fast green stains were used to delineate regions of collagen (i.e. infarct or scar, red) and healthy myocardium (green), respectively (Fig. 1A). Images for each stain were aligned in imaging software (GNU Image Manipulation Program) and colour thresholding was used to create four bins (graft, scar, myocardium, non-cardiac) (Fig. 1B). Thresholded images were loaded into 3D modelling software (Blender). Using the thresholded images as a reference, slice models were constructed using triangles with an edge length of ~50 μm. Each region (graft, host and scar) was assigned to its respective vertex groups. Finally, the points interconnected by region-labelled triangles were exported, then converted to a format compatible with our finite element modelling software (Fig. 1C). The number of nodes and triangular finite elements for each model are shown in Table 1.

Figure 1. Deriving slice models from histological images of post-MI macaque ventricles.

Figure 1.

Open in a new tab

A, example histology images used to generate slice model. Left: human cardiac troponin I stained for graft. Right: Fast Green stained for myocardium and Picrosirius Red stained for collagen (i.e. scar). B, example thresholded image. Areas that are within the tissue boundary but are delineated as neither scar nor graft are deemed host myocardium. C, example slice model with grafts outlined in orange. All scale bars: 5 mm.

Table 1.

Finite element mesh properties for models used in this study

Number of nodes Number of elements
Model 1 52,446 103,523
Model 2 80,419 158,908
Model 3 67,061 131,027
Model 4 52,823 103,135
Model 5 47,193 92,475
Open in a new tab

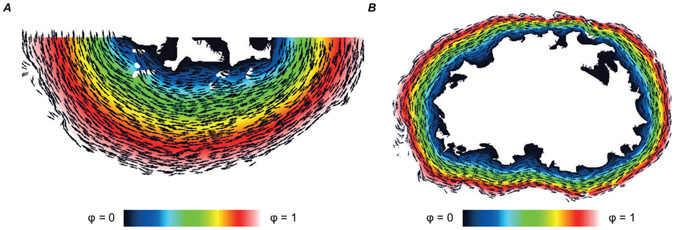
Myocardial fibres are helically wound within the ventricular wall, with fibre axes ranging from −60° at the endocardium to +60° at the epicardium relative to the transverse short axis. Histological sections here were taken after sectioning the heart in the transverse plane, from the apex to the base; this poses a substantial challenge in reconstructing the orientation of the fibres from histological images (Papadacci et al., 2017; Williams et al., 2020). For this reason, we used a mathematical approximation to represent idealized fibrous structure for each slice model used in this study. Our guiding assumption was that fibres should be tangential to the surface at the epicardial and endocardial walls and vary smoothly in between. First, we solved the Laplacian equation (F = ∇2ϕ = 0) with Dirichlet boundary conditions imposed at the endocardium (ϕ = 0) and epicardium (ϕ = 1). Second, we calculated the gradient of this field (∇F) to produce a map of radial vectors on each triangle in the model domain. Finally, we rotated these element-wise vectors 90° in-plane to produce the field approximating myocardial fibre orientations (see examples in Fig. 2A and B).

Figure 2. Illustration of the process used to map myocardial fibre orientations into each model.

Figure 2.

Open in a new tab

Vectors (black arrows) show fibre orientations calculated using the Laplacian-based approach (see text). Colour map shows the solution to the Laplacian problem with boundary conditions imposed on the endocardial (ϕ = 0) and epicardial (ϕ = 1) surfaces. A, Model 1; B, Model 3.

HPSC-CM differentiation and characterization by RTqPCR

RUES2, a human embryonic stem cell (hESC) line, was differentiated into CMs (hESC-CMs) through small molecules that modulate the Wnt pathway: briefly, hESCs are treated with CHIR99021 (Wnt agonist) to initiate direct differentiation and the Wnt antagonist WNTC59 to induce the cardiomyocyte state after mesoderm formation (Palpant et al., 2017). Fourteen days after the induction of cardiac differentiation, RNA from hESC-CMs was harvested using RNAeasy Mini kit (Qiagen, Germantown, MD, USA) according to manufacturer’s instructions. RNA was then retro-transcribed using M-MLV RT kit (Thermo Fisher Scientific, Waltham, MA, USA), and RT-qPCR was performed with SYBR Select Master Mix (Thermo Fisher Scientific). Reactions were run on a CFX384 Real-Time System (Bio-Rad Laboratories, Hercules, CA, USA), and data were analysed using the ΔΔCt method using HPRT1 (hypoxanthine-guanine phosphoribosyl transferase 1) as the housekeeping gene. Primers were designed using PrimerBlast and confirmed to amplify a single product. Primer sequences (5′ → 3′): HPRT1 (forward: TGACACTGGCAAAACAATGCA, reverse: GGTCCTTTTCACCAGCAAGCT); KCNJ2 (forward: GTGCGAACCAACCGCTACA, reverse: CCAGCGAAT GTCCACACAC); HCN4 (forward: GATCCTCAG CCTCTTACGCC, reverse: CCCCAGGAGTTGTTCAC CAT); SLC8A1 (forward: AGACCTGGCTTCCCACTT TG, reverse: TGGCAAATGTGTCTGGCACT).

Modelling of varied graft–host coupling

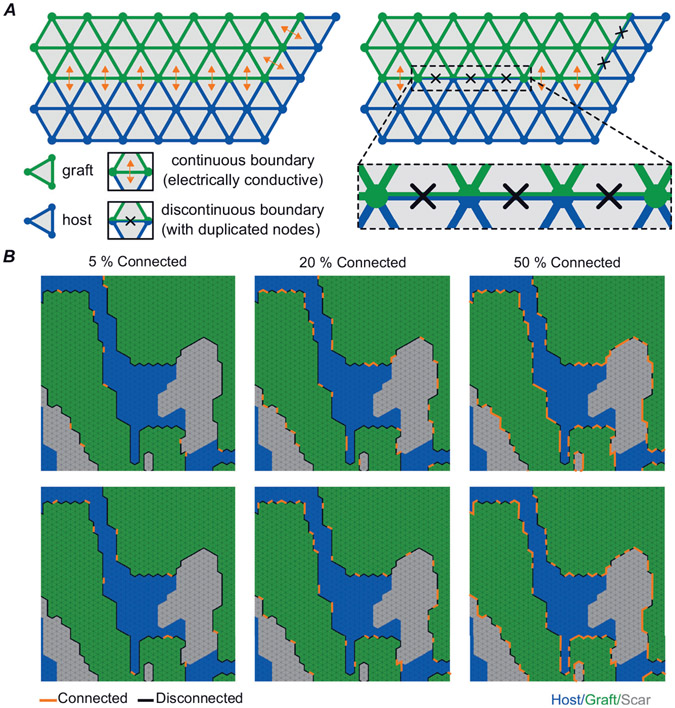
We modelled differences in graft–host coupling using a discontinuous finite element method (Costa et al., 2016). From the starting point of a continuous boundary that uniformly allows passage of electrical current between graft and surrounding tissue, a subset of edges shared between graft and host finite elements (triangles) is identified for disconnection. For this part of the boundary, finite element edges and nodes are duplicated such that current flux between the adjacent triangles is no longer possible (Fig. 3A). Since the timing and spatial pattern with which graft–host coupling evolves during engraftment is not well understood, we used a stochastic approach to examine a wide variety of potential electrical coupling configurations. In each model, for 24 distinct values of graft–host connectedness level (pc) – 2.5% to 60% in steps of 2.5% – we used random edge selection to generate 40 unique variants in which exactly that proportion of boundaries were disconnected (see examples in Fig. 3B). pc values above 60% were never tested since graft–host excitation was never observed in that parameter range. The pc constraint was imposed on a graft-by-graft basis (i.e. in a model with several distinct ‘islands’ of graft, the same proportion of boundary was modelled as electrically conductive in each of them).

Figure 3. Schematic representation of how graft–host coupling was varied.

Figure 3.

Open in a new tab

A, schematic illustration of continuous vs. discontinuous finite element modelling. B, two example permutations each are shown for pc levels of 5%, 20% and 50% connected. Each image has regions of graft (green), host (blue) and scar (grey) labelled. Edges of graft connected to surrounding tissue are shown with orange lines and edges that are disconnected are shown with black lines.

Cell- and tissue-scale electrophysiological modelling

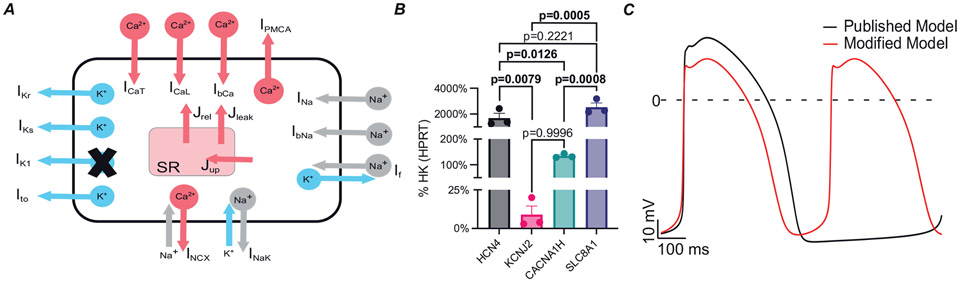
In graft tissue regions, we used an existing model of hPSC-CM membrane kinetics (Kernik et al., 2019) with two modifications (Fig. 4A). These modifications were motivated by several experimental observations. First, EA originates from graft and cause heart rates much faster (>5 Hz) than the intrinsic rate of the Kernik model (1.1 Hz) or published experimental in vitro data (Koivumäki et al., 2018; Liu et al., 2018; Romagnuolo et al., 2019). Second, early stage hPSC-CMs, similar to those used in transplanted hearts, have a less negative minimum diastolic potential (MDP; between −68 and −57 mV) (Lundy et al., 2013; Karbassi et al., 2020) compared to the Kernik model (MDP = −75.826 mV). Lastly, our in vitro hPSC-CMs, analysed by real-time quantitative PCR (RTqPCR), showed low expression of KCNJ2 (the gene encoding Kir2.1, corresponding to the inward rectifier potassium channel (IK1); Fig. 4B), compared to HCN4, CACNA1H (encoding Cav3.2) and SLC8A1 (encoding NCX1). All three of these channels are involved in action potential formation in immature cardiomyocytes (Li et al., 2013; Peinkofer et al., 2016; Karbassi et al., 2020). This observation is consistent with prior work showing that the inward rectifier potassium channel (IK1) is barely detectable in immature cardiomyocytes, like hPSC-CMs (Ivashchenko et al., 2013; Karbassi et al., 2020). Accordingly, we removed IK1 from the model and doubled the conductance associated with the HCN4-mediated ‘funny’ current (If). The latter change was motivated by the fact that If is among the most important drivers of pacemaker activity and controls the diastolic membrane potential, together with IK1 (Verkerk et al., 2009; Kim et al., 2015; Sun et al., 2017). These two changes led to a markedly faster spontaneous beating rate (~1.9 Hz), but the effect on MDP was less dramatic (−72.096 mV; Fig. 4C). We modelled membrane kinetics of host myocardium using the human ventricular ionic model of Ten Tusscher & Panfilov (2006) since there is no published model of NHP cardiomyocyte electrophysiology. For ease of reproducibility, all cell-scale initial conditions were identical to those used in the published version of the Kernik model.

Figure 4. Modifications made to published hPSC-CM model.

Figure 4.

Open in a new tab

A, schematic representation showing modifications made to ionic model. IK1 was blocked and If was doubled. B, RTqPCR analysis of wild-type hPSC-CMs at day 14 after differentiation. Data shown as means (SD) of 3 independent biological replicates. HK, housekeeping gene. Statistical differences are reported by one-way ANOVA with Šidák’s correction. Bolded P-values denote statistical significance. C, action potential traces of published model (black) compared to modified model (red). The spontaneous beating rate of modified model showed an increased beating rate of 1.9 Hz compared to 1.1 Hz in the published model.

At the tissue scale, a finite-element approximation of the monodomain formulation was used to govern the propagation of electrical activity (Vigmond et al., 2009; Rocha et al., 2011). Partial differential equations were solved to describe electrical current flow in the myocardium; ordinary differential and algebraic equations were solved to represent membrane kinetics (as described in the preceding section) at each finite-element node. This approach has been used in many other studies examining cardiac arrhythmia mechanisms (Balaban et al., 2020; Bifulco et al., 2021; Ochs et al., 2021; O’Hara et al., 2022). As in prior work (Arevalo et al., 2016), conductivity tensor values in the longitudinal and transverse directions with respect to fibre orientation were set to σL = 0.255 S/m and σT = 0.0775 S/m, respectively. hPSC-CM graft islands were modelled with isotropic conductivity (i.e. no difference between longitudinal and transverse directions). Since intra-graft conduction velocity in hPSC-CM islands remains poorly characterized but is presumed to be slower than in the longitudinal direction in host myocardium (Dhahri et al., 2022), we assigned a baseline conductivity value identical to σT (i.e. σhPSC-CM = 0.0775 S/m). We ran additional simulations with this parameter adjusted by 4×, 2×, ½× or ¼× to examine a range of plausible conditions. Scar was modelled either as a non-conductive insulator (Prakosa et al., 2018) or as slow-conducting passive tissue (i.e. pure electrical sink) (Connolly & Bishop, 2016; Fassina et al., 2022). To avoid spurious scar-to-host excitations from electrotonic current, we set the resting potential of slow-conducting scar to match that of the human ventricular ionic model (−85.8 mV) (Ten Tusscher & Panfilov, 2006). Additionally, we sought to explore how the absence of infarct might influence EA propensity. In these cases, cell- and tissue-scale electrophysiological properties of regions previously tagged as ‘scar’ were indistinguishable from host myocardium. In all simulations, no external pacing was applied. To summarize each model’s EA susceptibility, we extracted metrics from graphs of EA incidence as a function of coupling: area under the curve (AUC) to quantify EA burden, and window of vulnerability (WOV) to reflect the range of pc values within which EA occurred.

Identifying earliest activation sites

For each simulation resulting in graft-initiated host excitation, we identified the earliest activation sites that led to full-blown propagating wavefronts in the host myocardium. To do this, we identified the time at which activation occurred distal to the graft and worked backward to identify the origin. This approach avoided incorrect identification of false positive breakthrough sites where spontaneous activity in the graft caused subthreshold depolarization in coupled host tissue.

Computational resources

This work was facilitated through the use of advanced computational, storage and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. Simulations of bioelectrical activity were conducted using openCARP (Plank et al., 2021) and the resulting data were visualized using the meshalyzer tool by Dr Edward J. Vigmond; both of the latter are freely available for non-commercial reuse (see: http://opencarp.org/).

Statistics

For the in vitro experiment (RTqPCR Fig. 4B), the number of biological replicates is intended as independent batches of hPSC-CM differentiation. For multiple group comparison, one-way ANOVA with Šidák correction was used as statistical analysis. Difference was considered statistically significant when P < 0.05.

Results

Arrhythmogenic propensity as a function of graft–host coupling

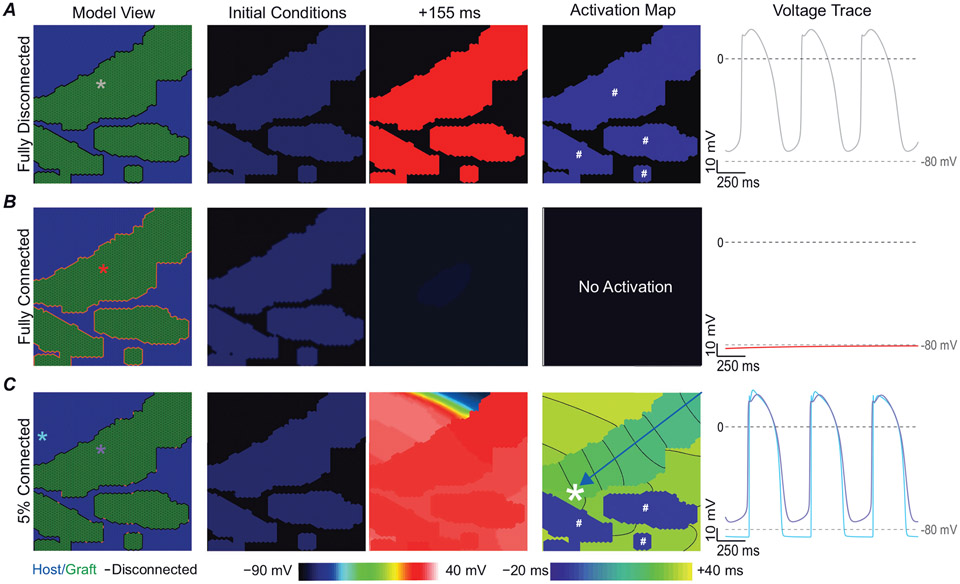
We first wanted to understand graft behaviour in the context of full isolation from (connectedness level (pc) = 0% connected) or full coupling (pc = 100%) with the surrounding myocardium. When fully decoupled, isolated grafts beat spontaneously but never initiated a response in the host (Fig. 5A). When grafts were fully connected to surrounding tissue, spontaneous depolarization was suppressed due to dissipation of excitatory current in the well-coupled electrical sink of surrounding myocardium (Spector, 2013). As shown in Fig. 5B, the tissue quickly returned to a quiescent state. We then tested many intermediate configurations of partial graft coupling that created a milieu in which graft-initiated host excitation occurred. Figure 5C shows an illustrative example where a pc = 5% gave rise to conditions favourable to graft-initiated host excitation. For the example shown, the leading pacemaker site was in the upper right-hand corner of the large graft, and the resulting wavefront followed the path indicated by the blue arrow before breaking through into host myocardium (white asterisk).

Figure 5. Fully coupled graft–host myocardium does not facilitate any graft-initiated host excitation.

Figure 5.

Open in a new tab

A, fully isolated grafts beat spontaneously in isolation. B, grafts fully coupled to host myocardium, showed impaired propagation due to dissipation of spontaneous depolarization originating from graft into surrounding myocardium. C, when graft is 5% coupled to host myocardium graft-initiated host excitation occurs (white asterisk). Column 1 shows the labelled model with coloured asterisks denote the location of voltage traces shown in column 5. Column 2 shows voltage initial conditions. Column 3 shows the voltage at +155 ms. Column 4 shows the activation map. Grafts that spontaneously excite in isolation before the lead pacemaker graft are denoted by the white # symbol. Blue arrow highlights wavefront path. Voltage traces are shown starting at t = 500 ms to highlight the equilibrium conditions after the initial conditions have resolved.

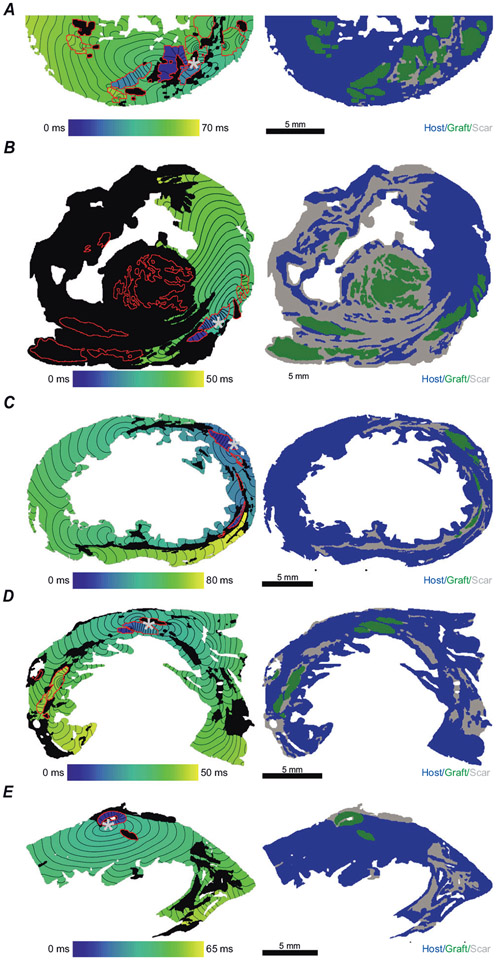
Next, we examined the relationship between EA propensity and graft–host connectedness (i.e. pc) in all five of our slice models. For this set of stimulations, the baseline graft conductivity value was kept at σhPsc-CM = 1× (see Methods). Characteristics of each model can be found in Table 2. The total area of each model ranged from 1.0 to 1.7 cm2. Models 1 and 2 contained a total graft area of ~0.27 cm2 but the amount of scar in Model 2 was ~12× greater. Models 3–5 had roughly the same graft size and amount of scar. Figure 6 shows a representative activation map for each model at 10% pc for a case inwhich graft-initiated host excitation occurred (Fig. 6, column 1). In Fig. 6A, two grafts undergo spontaneous excitation but only the graft denoted with a grey asterisk successfully excited the host. The wavefront then propagated clockwise exciting both host and non-refractory grafts. In Fig. 6B, most grafts were isolated in scar thus making only grafts in the lower right corner capable of graft-initiated host excitation. In Fig. 6C, two of the four grafts underwent spontaneous excitation, but the uppermost graft is where graft-initiated host excitation was first to occur. Similarly to Fig. 6B and C, in Fig. 6D two grafts underwent spontaneous excitation but only one led to host excitation. In Fig. 6E, only the graft at the upper left was large enough to successfully excite the host.

Table 2.

Computational slice model characteristics

Total graft area (cm2) Total scar area (cm2) Graft-scar perimeter (cm) Total area of model (cm2)
Model 1 0.2675 0.0661 2.2367 1.1150
Model 2 0.2664 0.7866 10.9174 1.7629
Model 3 0.0477 0.1550 0.7910 1.4536
Model 4 0.0691 0.1686 0.9079 1.1442
Model 5 0.0344 0.1598 0.6759 1.0259
Open in a new tab

Figure 6. In all models at 10% connected at least one permutation had graft-initiated host excitation.

Figure 6.

Open in a new tab

A-E, models 1–5. The left panel shows an example activation map at 10% connected. The grey asterisks denote site of graft-initiated host excitation. The right panel shows the geometry of the mesh labelled with graft (green), host (blue) and non-conductive scar (grey). All scale bars: 5 mm.

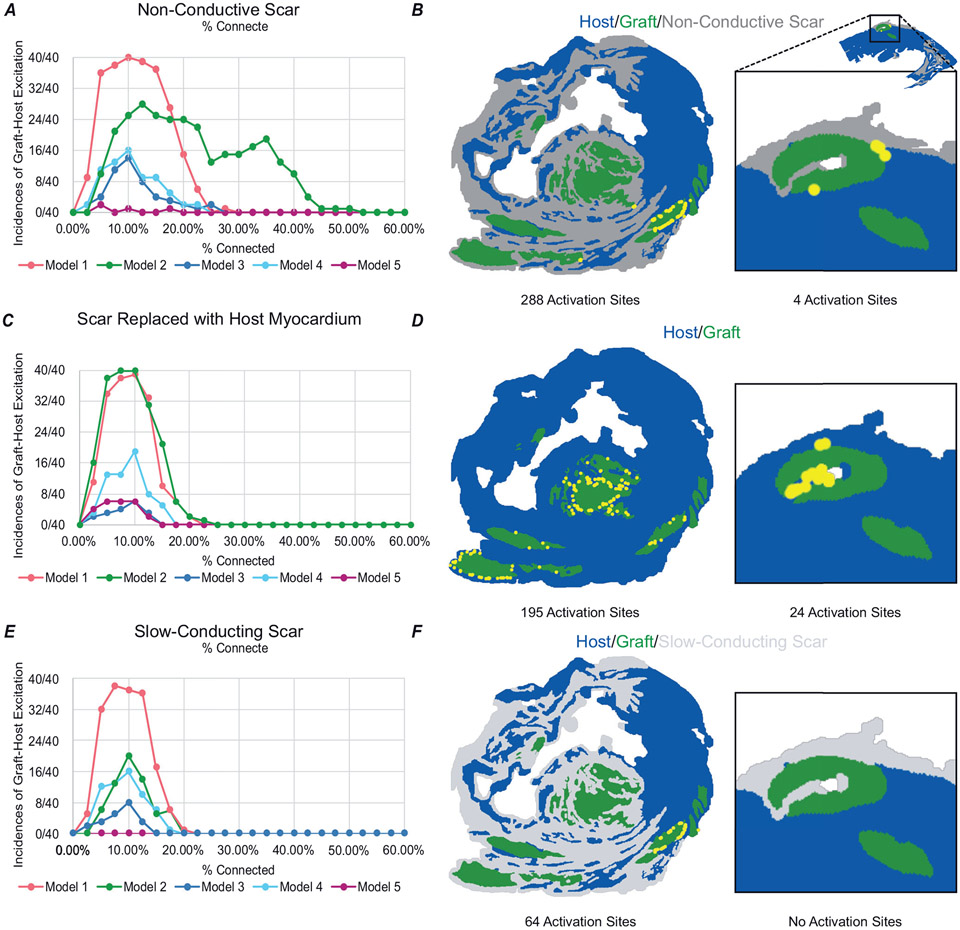
Analysis of all simulations revealed a consistent trend. As pc increased from very low (i.e. near-complete graft insulation from host) to intermediate values, there was an initial increase in the likelihood of ectopic graft-initiated host excitation. Then, with further increase in pc (i.e. towards full electrical integration of graft), the propensity for these excitations was attenuated and eventually ceased altogether. We observed this inverted paraboloid-shaped relationship in all five models examined (Fig. 7A). In four out of five models, the peak incidence of graft-initiated host excitation was at a pc value of 10–12.5%. At these coupling levels, the proportion of stochastically generated coupling permutations that led to ectopic excitation ranged from ~40% to 100% (in the case of Model 1). The WOV to graft-initiated host excitation ranged from 0% to 25% in most of these cases. An exception was Model 2, in which ectopic excitations were observed at higher coupling rates up to ~40%. In Model 5, very few permutations resulted in graft-initiated host excitation and peak incidence was at pc = 5%. Overall, the relationship to graft–host electric coupling was highly dependent on model geometry.

Figure 7. Engraftment arrhythmia is dynamically determined by graft–host connectedness.

Figure 7.

Open in a new tab

A-C, incidence of graft-initiated host excitation across all pc levels for all five models, (A) with non-conductive scar, (B) scar replaced by host myocardium, and (C) slow-conducting scar. D, Model 2 at 1 × σ with non-conductive scar had 288 activation sites localized to a few grafts and Model 5 had 4 activation sites. E, when scar was replaced with host myocardium at 1 × σ, Model 2 had only 195 activation sites in more widespread locations whereas Model 5 had an increase to 24 activation sites. F, when non-conductive scar was replaced by slow-conducting scar, Model 2 had only 64 activation sites and Model 5 had none.

Effects of scar

It remains unclear how the presence of non-conductive scar affects EA propensity. Does it create restricted channels with arrhythmogenic potential, does it isolate spontaneous excitations by preventing them from reaching host myocardium, or some complex combination of the two? For this reason, we sought to examine the effects of scar on EA propensity. We first replaced scar with healthy myocardium and repeated our experiments as described above. For each model, we still observed an inverted paraboloid shape in the EA relationship; however, the incidence of EA decreased and WOV was shortened to 0–20% in most cases (Fig. 7B). To further illustrate this point, Model 2 was an interesting case to consider because several large grafts were isolated by scar. For simulations in this model across all tested pc values, we observed 288 activation sites (Fig. 7C); most of these sites were located around a single medium-sized graft (lower-right corner of image). When identical simulations were re-run with infarcted tissue replaced by host myocardium, the total number of graft-initiated host excitations decreased to 195 (Fig. 7D). The only exception to this trend was Model 5, in which replacement of scar with host myocardium increased the number of graft–host excitations. This occurred because removing non-conductive scar left narrow clefts of host myocardium in close proximity to graft, creating conditions that favoured initiation of excitation (see right-most panels of Fig. 7B and D).

To further understand the range of possible infarct–graft interactions, we conducted additional simulations in which scar was modelled as slow-conducting passive tissue instead of non-conductive insulator. Under these conditions, scar behaved as a pure electrical sink absorbing spontaneously generated current from graft that could have otherwise initiated excitation elsewhere in host myocardium. This reduced the number of graft-initiated host excitations in all five models, to levels that were even lower than in simulations where scar was removed altogether (Fig. 7E and F).

Modulation of intrinsic cell–cell coupling within the graft and EA propensity

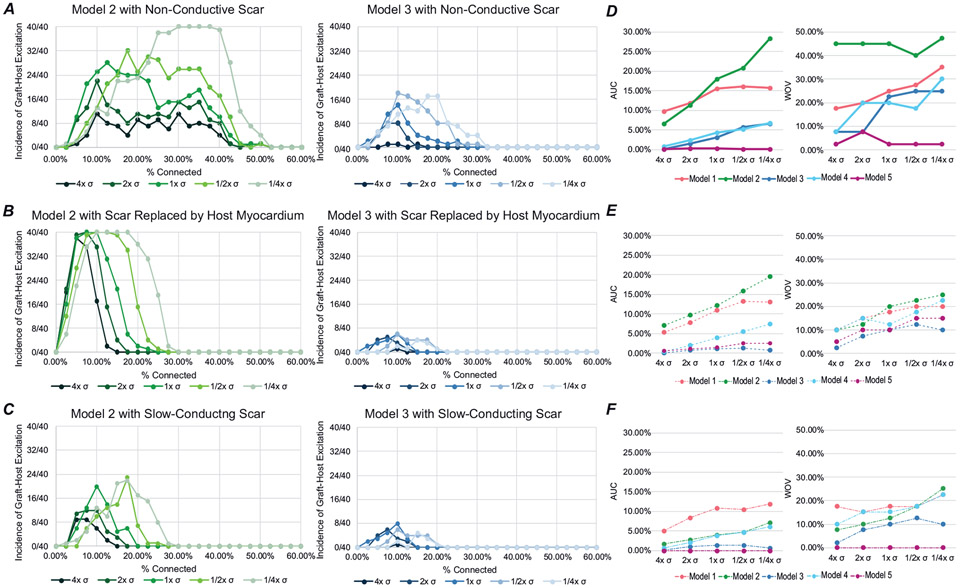
Next, we explored how changes in σhPSC-CM affected EA propensity with non-conductive scar, scar replaced by host myocardium and slow-conducting scar. For all cases with modified σhPSC-CM, EA propensity vs. pc relationships retained the characteristic inverted paraboloid shape. Figure 8A shows the effect of σhPSC-CM modifications in two representative examples with non-conductive scar. In Model 2, we observed an increase in graft-initiated host excitation at low conductivities, with a dramatic increase at ¼× σhpsc-CM compared to ½× σhpsc-CM. In Model 3, we also observed an increase in graft-initiated host excitation but the change between ¼× σhPSC-CM and ½× σhPSC-CM was not as pronounced. In the same representative examples with scar replaced by host myocardium, we observed similar trends. In Model 2, we observed an increase in graft-initiated host excitation at low conductivities relative to 1× σhPSC-CM, but the WOV was shortened from 2.5–55% to 2.5–30%. In Model 3, we still saw an increase in the incidence of graft-initiated host excitation as we decreased conductivity; however, the overall incidence was flattened when compared to non-conductive scar (Fig. 8B). We also observed that as we increase σhPSC-CM, we saw a reduction in the overall prevalence of EA as quantified by AUC and WOV across all models tested for graft conductivities (Fig. 8D and E). Finally, when scar was modelled as slow conducting instead of non-conductive, we saw a similar trend towards reduction in EA prevalence. In both representative models shown, we observed a decrease in graft-initiated host excitation compared to non-conductive scar at all σhPSC-CM values (Fig. 8C). The AUC and WOV values across all models were also reduced and abbreviated (Fig. 8F). Overall, these findings support the idea that low intrinsic cell–cell coupling in graft strongly favours the incidence of EA.

Figure 8. Increase in conductivity within the graft and the absence of scar decreases the instances of graft-initiated host excitation in most models.

Figure 8.

Open in a new tab

A–C, incidence of graft-initiated host excitation with scar at pc = 0–60% for all conductivities tested for Model 2 (green) and Model 3 (blue) with non-conductive scar (A), with scar replaced by host myocardium (B), and slow-conducting scar (C). D–F, the AUC and WOV for all models with non-conductive scar (D), with scar replaced by host myocardium (E), and slow-conducting scar (F).

Discussion

In this study, we present a novel computational approach to assess spatiotemporally heterogeneous electrical coupling between graft and host cells in anatomically realistic 2D slice models of remuscularized post-MI macaque ventricles. Our simulations were designed to show how spontaneous excitations of engrafted hPSC-CMs could serve as a source that elicits propagating responses in host myocardium. In all five of our models, we showed (1) varied graft–host coupling creates a milieu conducive to graft-initiated host excitation, (2) in most cases the replacement of scar with host myocardium reduces but does not abolish EA, and (3) increasing intrinsic graft conductivity decreases EA propensity. To our knowledge, this is the first study to computationally investigate focal sources of EA at the tissue scale when the true location and shape of grafts are known.

In our study, we first showed that varying the percentage of graft connected to surrounding tissue could result in graft-initiated host excitation (Figs 5-7). For each model, the relationship between EA propensity and the extent of graft–host coupling had an inverted paraboloid shape ranging from pc = 2.5% to 50%, but the exact dimensions of that shape varied from model to model. Inter-model variability in these characteristics could arise from numerous factors, including differences in MI location and size, the number of cells engrafted in the heart of each animal, details of cardiac anatomy, and locations of the slices with respect to injection sites. This phenomenon observed in simulations is reminiscent of a distinct observation from in vivo studies, namely the variability in timing of the wax and wane of EA from animal to animal (Liu et al., 2018; Romagnuolo et al., 2019; Nakamura et al., 2021). While we do not know the exact evolution of coupling or whether this phenomenon progresses linearly over time, our results provide a promising starting point to further explore how focal EA mechanisms might depend on graft–host electrical coupling in a broad sense. In vivo hPSC-CM transplantation led to a progressive increase of adherens and gap junction proteins, which suggests that electromechanical coupling might be spatiotemporally regulated (Kadota et al., 2017). This is also consistent with our findings which show that increasing graft conductivity decreases graft-initiated host excitation (and vice versa, see Fig. 8).

Finally, we gained more insights into the relationship between scar and graft excitation in the context of EA. In particular, when scar was replaced with host myocardium, graft-initiated host excitation still occurred but was reduced in all but one model. When non-conductive scar was replaced by slow-conducting scar, graft-initiated host excitation was reduced in all models since it created a pure electrotonic sink, effectively increasing the amount of spontaneously generated current that was ‘squandered’ instead of depolarizing host cells (Figs 7 and 8). Overall, these data suggest that non-conductive scar has a pronounced effect on EA propensity due to changes it creates in source–sink equilibrium. Interestingly, Model 5 showed an increase in EA when scar was replaced by host myocardium. In our simulations of Model 5 with non-conductive scar, there were very few locations at which graft-initiated host excitation could escape: this is because the largest graft region was mostly encased in scar. In Model 5 when non-conductive scar was replaced by slow-conducting scar, no graft–host excitations were observed. Upon the replacement of scar with host myocardium, that graft had more locations where excitation of coupled host myocardium could occur. Moreover, proximity to the non-conductive boundary of the model (i.e. the edge of the heart itself) created a favourable source–sink relationship in the thin strip of host myocardium (akin to a Purkinje fibre or an electrically insulated tissue region within a protected isthmus). Although further investigation into the location and consequences of scar relative to graft is needed, these data showed that in some situations the presence of scar could be protective in the context of EA. Finally, on the subject of whether scar should ideally be modelled as non-conductive insulator, weakly conductive passive electrical sink, or some combination of the two, we note that recent studies have shown that non-myocytes can electrically conduct and couple with myocytes (Quinn et al., 2016; Hulsmans et al., 2017; Dhanjal et al., 2017), but it remains unclear if this connection between hPSC-CMs and non-myocytes occurs after transplantation and contributes to EA. In the absence of definitive evidence, we feel that inclusion of both model variants is a prudent approach.

Previous computational work in this area devised a multiscale framework to simulate stem cell-based repair technology in patient-specific models of human hearts post-MI (Yu et al., 2019). This study was designed to investigate both focal and re-entrant mechanisms. Consistent with our findings, it found that graft-initiated host excitation was constrained by the source–sink mismatch, with the likelihood of ectopic propagation highly dependent on proximity to scar and the theoretical spatial pattern of engrafted cells (in this case represented using a stochastic approximation). Another study created a new biophysically detailed computational model to further assess focal EA mechanisms (Yu, Liang, Weinberg et al. 2022). Like our work, that study examined the consequences of different graft conductivities and found that ectopic beat propagation was reduced by increased coupling or interface area between graft and host. However, the observed ectopic beats never exceed the intrinsic automaticity rate of ~96 bpm. This might be due to the use of a guinea pig ventricular myocyte model to simulate the graft (Luo & Rudy, 1991), with automaticity induced by the addition of a constant depolarizing current. Due to this slow graft-induced focal beating rate, the authors again concluded that a re-entrant driver mechanism is more likely to contribute to fast EA. Additional studies have tried to look at EA in the context of remuscularization via an hPSC-CM patch (Yu, Liang, Franceschi et al., 2022; Fassina et al., 2022); however, multiple experimental studies have demonstrated that no electrical coupling occurs in cardiac patches, due to scar-induced insulation of the graft–host border (Gerbin et al., 2015; Jackman et al., 2018). We believe that this is the key to understanding why prior work undervalued the potential importance of focal EA drivers.

Our study has some notable limitations. When modelling variable graft coupling, we chose to stochastically generate different versions of our models, each having a fixed proportion of random graft edges connected to the surrounding tissue. Contemporary understanding from hPSC-CMs suggests that connexin-43 co-localizes at the cell membrane in clusters (Sottas et al., 2018) and is circumferentially distributed up to 3 months following engraftment (Liu et al., 2018). Our stochastic approach is plausible and recapitulates this distribution, but it is possible that functional gap junctions would form only along boundaries confluent with fibres, not along laminar boundaries due to shear forces during myocardial contraction.

We also chose to exclude electrophysiological changes that graft myocytes undergo during maturation (e.g. cells become electrically quiescent due to increased IK1 expression and downregulation of If and ICaT). The rationale for this decision was to deliberately explore models in which variables like pC were the only differences, ruling out other potential confounding factors like changes due to intrinsic cell-scale maturity. Moreover, the exact changes in electrophysiological properties of engrafted cells over time are not yet fully characterized in vitro, so it would be hard to properly calibrate models attempting to probe their importance to EA at this time.

We used 2D slice models derived from histology images, which allowed us to include exact locations of scar, graft and host myocardium. Creation of 3D models from histology images was not an option in this study due to the inter-slice spacing of 3 mm, which would have led to a staircase effect in the z-direction due to much coarser resolution compared to the x–y plane. While it might be possible to create 3D models using other imaging techniques, such as magnetic resonance imaging (MRI), graft locations would need to be synthetically generated since contrast agents have not yet been developed to differentiate graft from healthy myocardium in border zone tissue (Liu et al., 2018). A related limitation is that in our models we do not modify the underlying ionic currents in host myocardium directly adjacent to scar, as in many prior computational studies (Arevalo et al., 2016; Prakosa et al., 2018). However, our models do have a high-resolution representation of the patchy intermingling of myocardium and infarct in these areas, with a resolution greater than what could be observed using MRI.

Finally, since the framework described in this study explored a carefully chosen but narrow question about how spatial properties of graft–host interface may contribute to EA propensity, some important factors remain unexplored. For instance, additional investigations will be needed to clarify the relationship between EA propensity and the spatial conformation of graft/host/scar areas. Moreover, since we did not apply any external pacing to our model, it is unclear if the types of focal sources observed in our simulations could overdrive sinus rhythm. We also note that the MDP in our cell-scale model is slightly lower than values reported in general experimental data (Karbassi et al., 2020), and this might affect the dynamics of impulse propagation. We found that the adjustments made to the cell-scale model were the farthest we could push the resting potential towards a more depolarized level without deranging other action potential properties (upstroke velocity, action potential duration, beating rate, etc.).

In conclusion, our study presented a new way to model hPSC-CM injection with an emphasis on focal mechanisms. We found that varied graft coupling allowed for the waxing and waning of EA to be captured in our simulations. This work also allowed us to elucidate the role of scar tissue in the onset of EA and how this can change due to source–sink mismatch. While we may not yet have elucidated the true mechanism of EA, these data can be used in the future to pinpoint areas that are less arrhythmogenic for targeted delivery of hPSC-CM therapy.

Supplementary Material

Statistical summary, as published with article
Peer review history, as published with article

Key points.

  • Human pluripotent stem cell-derived cardiomyocytes (hPSC-CM) hold great cardiac regenerative potential but can also cause engraftment arrhythmias (EA).

  • Spatiotemporal evolution in the pattern of electrical coupling between injected hPSC-CMs and surrounding host myocardium may explain the dynamics of EA observed in large animal models.

  • We conducted simulations in histology-derived 2D slice computational models to assess the effects of heterogeneous graft–host electrical coupling on EA propensity, with or without scar tissue.

  • Our findings suggest spatiotemporally heterogeneous graft–host coupling can create an electrophysiological milieu that favours graft-initiated host excitation, a surrogate metric of EA susceptibility. Removing scar from our models reduced but did not abolish the propensity for this phenomenon. Conversely, reduced intra-graft electrical connectedness increased the incidence of graft-initiated host excitation.

  • The computational framework created for this study can be used to generate new hypotheses, targeted delivery of hPSC-CMs.

Funding

These studies were supported by the UW Medicine Heart Regeneration Program, the Washington Research Foundation, a gift from Mike and Lynn Garvey, and a sponsored research agreement from Sana Biotechnology (all Seattle, WA, USA). This work also was supported in part by NIH grants R01HL158667 (to P.M.B), R01HL128368, R01HL146868 and R01HL148081 (to C.E.M.), as well as a grant from the Foundation Leducq Transatlantic Network of Excellence (Boston, MA, USA; to C.E.M.). S.M. was supported in part by a fellowship from the UW Institute for Stem Cell and Regenerative Medicine. C.E.G. was supported by a National Science Foundation Graduate Research Fellowship under Grant No. DGE-2140004.

Biography

graphic file with name nihms-1966318-b0002.gif

Chelsea Gibbs is currently a PhD student in the Bioengineering Department at the University of Washington. She obtained her Honours BS in Biomedical Engineering from the University of Utah. The focus of her PhD has been using computational modelling to better understand mechanisms of engraftment arrhythmia following cardiac injection of human pluripotent stem cell-derived cardiomyocytes. In the future, she aims to expand upon the framework presented in this study to help experimentalists and clinicians discover new ways to prevent engraftment arrhythmia and improve the safety of cardiac regenerative therapy.

Footnotes

Competing interests

The laboratories of C.E.M. and P.M.B. previously received funding from Sana Biotechnology as part of a sponsored research agreement to conduct research on engraftment arrhythmia mechanisms. C.E.M. was an employee of Sana Biotechnology while some of this work was performed and is an equity holder in Sana.

Supporting information

Additional supporting information can be found online in the Supporting Information section at the end of the HTML view of the article. Supporting information files available:

Data availability statement

Where possible, raw numerical data underlying figures are available via dryad: https://doi.org/10.5061/dryad.63xsj3v75. Source files for representative examples of all simulations conducted in this study, which can be re-run or modified using publicly available software tools, can be found via the same permanent link as above.

References

  1. Arevalo HJ, Vadakkumpadan F, Guallar E, Jebb A, Malamas P, Wu KC, & Trayanova NA (2016). Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nature Communications, 7(1), 11437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bahit MC, Kochar A, & Granger CB (2018). Post-myocardial infarction heart failure. JACC Heart Failure, 6(3), 179–186. [DOI] [PubMed] [Google Scholar]
  3. Balaban G, Costa CM, Porter B, Halliday B, Rinaldi CA, Prasad S, Plank G, Ismail TF, & Bishop MJ (2020). 3D electrophysiological modeling of interstitial fibrosis networks and their role in ventricular arrhythmias in Non-ischemic cardiomyopathy IEEE Transactions on Bio-Medical Engineering, 67(11), 3125–3133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bergmann O, Bhardwaj RD, Bernard S, Zdunek S, Barnabé-Heider F, Walsh S, Zupicich J, Alkass K, Buchholz BA, Druid H, Jovinge S, & Frisén J (2009). Evidence for cardiomyocyte renewal in humans. Science, 324(5923), 98–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bertero A, & Murry CE (2018). Hallmarks of cardiac regeneration. Nature Reviews Cardiology, 15(10), 579–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bifulco SF, Scott GD, Sarairah S, Birjandian Z, Roney CH, Niederer SA, Mahnkopf C, Kuhnlein P, Mitlacher M, Tirschwell D, Longstreth W, Akoum N, & Boyle PM (2021). Computational modeling identifies embolic stroke of undetermined source patients with potential arrhythmic substrate. eLife, 10, e64213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Boyle PM, Franceschi WH, Constantin M, Hawks C, Desplantez T, Trayanova NA, & Vigmond EJ (2019). New insights on the cardiac safety factor: Unraveling the relationship between conduction velocity and robustness of propagation. Journal of Molecular and Cellular Cardiology, 128, 117–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Boyle PM, Zghaib T, Zahid S, Ali RL, Deng D, Franceschi WH, Hakim JB, Murphy MJ, Prakosa A, Zimmerman SL, Ashikaga H, Marine JE, Kolandaivelu A, Nazarian S, Spragg DD, Calkins H, & Trayanova NA (2019). Computationally guided personalized targeted ablation of persistent atrial fibrillation. Nature Biomedical Engineering, 3(11), 870–879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Caspi O, Huber I, Kehat I, Habib M, Arbel G, Gepstein A, Yankelson L, Aronson D, Beyar R, & Gepstein L (2007). Transplantation of human embryonic stem Cell–derived cardiomyocytes improves myocardial performance in infarcted rat hearts. Journal of the American College of Cardiology, 50(19), 1884–1893. [DOI] [PubMed] [Google Scholar]
  10. Chong JJH, Yang X, Don CW, Minami E, Liu YW, Weyers JJ, Mahoney WM, Van Biber B, Cook SM, Palpant NJ, Gantz JA, Fugate JA, Muskheli V, Gough GM, Vogel KW, Astley CA, Hotchkiss CE, Baldessari A, Pabon L, … Murry CE (2014). Human embryonic-stem-cell-derived cardiomyocytes regenerate non-human primate hearts. Nature, 510(7504), 273–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Colvin M, Smith JM, Ahn Y, Skeans MA, Messick E, Bradbrook K, Gauntt K, Israni AK, Snyder JJ, & Kasiske BL (2022). OPTN/SRTR 2020 annual data report: Heart. American Journal of Transplantation, 22(2), 350–437. [DOI] [PubMed] [Google Scholar]
  12. Connolly AJ, & Bishop MJ (2016). Computational representations of myocardial infarct scars and implications for arrhythmogenesis. Clinical Medicine Insights Cardiology, 10(s1), CMCS39708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Costa CM, Silva PAA, & Santos RWD (2016). Mind the Gap: A semicontinuum model for discrete electrical propagation in cardiac tissue. IEEE Transactions on Bio-Medical Engineering, 63(4), 765–774. [DOI] [PubMed] [Google Scholar]
  14. Dhahri W, Sadikov Valdman T, Wilkinson D, Pereira E, Ceylan E, Andharia N, Qiang B, Masoudpour H, Wulkan F, Quesnel E, Jiang W, Funakoshi S, Mazine A, Gomez-Garcia MJ, Latifi N, Jiang Y, Huszti E, Simmons CA, Keller G, & Laflamme MA (2022). In vitro matured human pluripotent stem Cell-derived cardiomyocytes form grafts with enhanced structure and function in injured hearts. Circulation, 145(18), 1412–1426. [DOI] [PubMed] [Google Scholar]
  15. Dhanjal TS, Lellouche N, Von RCJ, Abehsira G, Edwards DH, Jean-Luc D-R, Moschonas K, Teiger E, Williams AJ, & George CH (2017). Massive accumulation of myofibroblasts in the critical isthmus is associated with ventricular tachycardia inducibility in Post-infarct swine heart. JACC Clinical Electrophysiology, 3(7), 703–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Eschenhagen T, Bolli R, Braun T, Field LJ, Fleischmann BK, Frisén J, Giacca M, Hare JM, Houser S, Lee RT, Marbán E, Martin JF, Molkentin JD, Murry CE, Riley PR, Ruiz-Lozano P, Sadek HA, Sussman MA, & Hill JA (2017). Cardiomyocyte regeneration: A consensus statement. Circulation, 136(7), 680–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Ezekowitz JA, Kaul P, Bakal JA, Armstrong PW, Welsh RC, & McAlister FA (2009). Declining In-hospital mortality and increasing heart failure incidence in elderly patients with first myocardial infarction. Journal of the American College of Cardiology, 53(1), 13–20. [DOI] [PubMed] [Google Scholar]
  18. Fassina D, Costa CM, Longobardi S, Karabelas E, Plank G, Harding SE, & Niederer SA (2022). Modelling the interaction between stem cells derived cardiomyocytes patches and host myocardium to aid non-arrhythmic engineered heart tissue design ed. McCulloch AD. PLoS Computational Biology, 18(4), e1010030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Filice D, Dhahri W, Solan JL, Lampe PD, Steele E, Milani N, Van Biber B, Zhu W-Z, Valdman TS, Romagnuolo R, Otero-Cruz JD, Hauch KD, Kay MW, Sarvazyan N, & Laflamme MA (2020). Optical mapping of human embryonic stem cell-derived cardiomyocyte graft electrical activity in injured hearts. Stem Cell Research and Therapy, 11(1), 417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. GBD 2019 Diseases and Injuries Collaborators. (2020). Global burden of 369 diseases and injuries in 204 countries and territories, 1990–2019: A systematic analysis for the Global Burden of Disease Study 2019. The Lancet, 396(10258), 1204–1222. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gerber Y, Weston SA, Enriquez-Sarano M, Berardi C, Chamberlain AM, Manemann SM, Jiang R, Dunlay SM, & Roger VL (2016). Mortality associated with heart failure after myocardial infarction: A contemporary community perspective. Circulation Heart Failure, 9(1), e002460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gerbin KA, Yang X, Murry CE, & Coulombe KLK (2015). Enhanced electrical integration of engineered human myocardium via Intramyocardial versus epicardial delivery in infarcted rat hearts. PLoS ONE, 10(7), e0131446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Guo Y, & Pu WT (2020). Cardiomyocyte maturation: New phase in development. Circulation Research, 126(8), 1086–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hulsmans M, Clauss S, Xiao L, Aguirre AD, King KR, Hanley A, Hucker WJ, Wülfers EM, Seemann G, Courties G, Iwamoto Y, Sun Y, Savol AJ, Sager HB, Lavine KJ, Fishbein GA, Capen DE, Da Silva N, Miquerol L, … Nahrendorf M (2017). Macrophages facilitate electrical conduction in the heart. Cell, 169(3), 510–522.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ivashchenko CY, Pipes GC, Lozinskaya IM, Lin Z, Xiaoping X, Needle S, Grygielko ET, Hu E, Toomey JR, Lepore JJ, & Willette RN (2013). Human-induced pluripotent stem cell-derived cardiomyocytes exhibit temporal changes in phenotype. American Journal of Physiology - Heart and Circulatory Physiology, 305(6), H913–H922. [DOI] [PubMed] [Google Scholar]
  26. Jackman CP, Ganapathi AM, Asfour H, Qian Y, Allen BW, Li Y, & Bursac N (2018). Engineered cardiac tissue patch maintains structural and electrical properties after epicardial implantation. Biomaterials, 159, 48–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kadota S, Pabon L, Reinecke H, & Murry CE (2017). In vivo maturation of human induced pluripotent stem Cell-derived cardiomyocytes in neonatal and adult rat hearts. Stem Cell Reports, 8(2), 278–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Karbassi E, Fenix A, Marchiano S, Muraoka N, Nakamura K, Yang X, & Murry CE (2020). Cardiomyocyte maturation: Advances in knowledge and implications for regenerative medicine. Nature Reviews Cardiology, 17(6), 341–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kernik DC, Morotti S, Wu HD, Garg P, Duff HJ, Kurokawa J, Jalife J, Wu JC, Grandi E, & Clancy CE (2019). A computational model of induced pluripotent stem-cell derived cardiomyocytes incorporating experimental variability from multiple data sources. The Journal of Physiology, 597(17), 4533–4564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kim JJ, Yang L, Lin B, Zhu X, Sun B, Kaplan AD, Bett GCL, Rasmusson RL, London B, & Salama G (2015). Mechanism of automaticity in cardiomyocytes derived from human induced pluripotent stem cells. Journal of Molecular and Cellular Cardiology, 81, 81–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Koivumäki JT, Naumenko N, Tuomainen T, Takalo J, Oksanen M, Puttonen KA, Lehtonen Š, Kuusisto J, Laakso M, Koistinaho J, & Tavi P (2018). Structural immaturity of human iPSC-derived cardiomyocytes: In silico investigation of effects on function and disease modeling. Frontiers in Physiology, 9(14), 80. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Laflamme MA, Gold J, Xu C, Hassanipour M, Rosler E, Police S, Muskheli V, & Murry CE (2005). Formation of human myocardium in the rat heart from human embryonic stem cells. American Journal of Pathology, 167(3), 663–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Laflamme MA, & Murry CE (2011). Heart regeneration. Nature, 473(7347), 326–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Li S, Chen G, & Li RA (2013). Calcium signalling of human pluripotent stem cell-derived cardiomyocytes. The Journal of Physiology, 591(21), 5279–5290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Liu YW, Chen B, Yang X, Fugate JA, Kalucki FA, Futakuchi-Tsuchida A, Couture L, Vogel KW, Astley CA, Baldessari A, Ogle J, Don CW, Steinberg ZL, Seslar SP, Tuck SA, Tsuchida H, Naumova AV, Dupras SK, Lyu MS, … Murry CE (2018). Human embryonic stem cell-derived cardiomyocytes restore function in infarcted hearts of non-human primates. Nature Biotechnology, 36(7), 597–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Lundy SD, Zhu W-Z, Regnier M, & Laflamme MA (2013). Structural and functional maturation of cardiomyocytes derived from human pluripotent stem cells. Stem Cells and Development, 22(14), 1991–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Luo CH, & Rudy Y (1991). A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circulation Research, 68(6), 1501–1526. [DOI] [PubMed] [Google Scholar]
  38. Moreno JD, Zhu ZI, Yang P-C, Bankston JR, Jeng M-T, Kang C, Wang L, Bayer JD, Christini DJ, Trayanova NA, Ripplinger CM, Kass RS, & Clancy CE (2011). A computational model to predict the effects of Class I Anti-arrhythmic drugs on ventricular rhythms. Science Translational Medicine, 3(98), 98ra83. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nakamura K, Neidig LE, Yang X, Weber GJ, El-Nachef D, Tsuchida H, Dupras S, Kalucki FA, Jayabalu A, Futakuchi-Tsuchida A, Nakamura DS, Marchianò S, Bertero A, Robinson MR, Cain K, Whittington D, Tian R, Reinecke H, Pabon L, … Murry CE (2021). Pharmacologic therapy for engraftment arrhythmia induced by transplantation of human cardiomyocytes. Stem Cell Reports, 16(10), 2473–2487. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Ochs AR, Karathanos TV, Trayanova NA, & Boyle PM (2021). Optogenetic stimulation using anion channelrhodopsin (GtACR1) facilitates termination of reentrant arrhythmias with low light energy requirements: A computational study. Frontiers in Physiology, 12, 718622. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. OHara RP, Binka E, Prakosa A, Zimmerman SL, Cartoski MJ, Abraham MR, Lu D-Y, Boyle PM, & Trayanova NA (2022). Personalized computational heart models with T1-mapped fibrotic remodeling predict sudden death risk in patients with hypertrophic cardiomyopathy. eLife, 11, e73325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Palpant NJ, Pabon L, Friedman CE, Roberts M, Hadland B, Zaunbrecher RJ, Bernstein I, Zheng Y, & Murry CE (2017). Generating high-purity cardiac and endothelial derivatives from patterned mesoderm using human pluripotent stem cells. Nature Protocols, 12(1), 15–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Papadacci C, Finel V, Provost J, Villemain O, Bruneval P, Gennisson J-L, Tanter M, Fink M, & Pernot M (2017). Imaging the dynamics of cardiac fiber orientation in vivo using 3D Ultrasound Backscatter Tensor Imaging. Scientific Reports, 7(1), 830. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Peinkofer G, Burkert K, Urban K, Krausgrill B, Hescheler J, Saric T, & Halbach M (2016). From early embryonic to adult stage: Comparative study of action potentials of native and pluripotent stem Cell-derived cardiomyocytes. Stem Cells and Development, 25(19), 1397–1406. [DOI] [PubMed] [Google Scholar]
  45. Plank G, Loewe A, Neic A, Augustin C, Huang Y-L, Gsell MAF, Karabelas E, Nothstein M, Prassl AJ, Sánchez J, Seemann G, & Vigmond EJ (2021). The openCARP simulation environment for cardiac electrophysiology. Computer Methods and Programs in Biomedicine, 208, 106223. [DOI] [PubMed] [Google Scholar]
  46. Prabhu SD, & Frangogiannis NG (2016). The biological basis for cardiac repair after myocardial infarction: From inflammation to fibrosis. Circulation Research, 119(1), 91–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Prakosa A, Arevalo HJ, Deng D, Boyle PM, Nikolov PP, Ashikaga H, Blauer JJE, Ghafoori E, Park CJ, Blake RC, Han FT, MacLeod RS, Halperin HR, Callans DJ, Ranjan R, Chrispin J, Nazarian S, & Trayanova NA (2018). Personalized virtual-heart technology for guiding the ablation of infarct-related ventricular tachycardia. Nature Biomedical Engineering, 2(10), 732–740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Quinn TA, Camelliti P, Rog-Zielinska EA, Siedlecka U, Poggioli T, O’Toole ET, Knöpfel T, & Kohl P (2016). Electrotonic coupling of excitable and nonexcitable cells in the heart revealed by optogenetics. Pnas, 113(51), 14852–14857. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Richardson WJ, Clarke SA, Alexander Quinn T, & Holmes JW (2015). Physiological implications of myocardial scar structure. Comprehensive Physiology, 5(4), 1877–1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Rocha BM, Kickinger F, Prassl AJ, Haase G, Vigmond EJ, Weber dos Santos R, Zaglmayr S, & Plank G (2011). A macro Finite-element formulation for cardiac electrophysiology simulations using hybrid unstructured grids. IEEE Transactions on Bio-Medical Engineering, 58(4), 1055–1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Rog-Zielinska EA, Norris RA, Kohl P, & Markwald R (2016). The Living scar - cardiac fibroblasts and the injured heart. Trends in Molecular Medicine, 22(2), 99–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Romagnuolo R, Masoudpour H, Porta-Sánchez A, Qiang B, Barry J, Laskary A, Qi X, Massé S, Magtibay K, Kawajiri H, Wu J, Valdman Sadikov T, Rothberg J, Panchalingam KM, Titus E, Li RK, Zandstra PW, Wright GA, Nanthakumar K, … Laflamme MA (2019). Human embryonic stem Cell-derived cardiomyocytes regenerate the infarcted pig heart but induce ventricular tachyarrhythmias. Stem Cell Reports, 12(5), 967–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Shiba Y, Gomibuchi T, Seto T, Wada Y, Ichimura H, Tanaka Y, Ogasawara T, Okada K, Shiba N, Sakamoto K, Ido D, Shiina T, Ohkura M, Nakai J, Uno N, Kazuki Y, Oshimura M, Minami I, & Ikeda U (2016). Allogeneic transplantation of iPS cell-derived cardiomyocytes regenerates primate hearts. Nature, 538(7625), 388–391. [DOI] [PubMed] [Google Scholar]
  54. Sottas V, Wahl C-MM, Trache MC, Bartolf-Kopp M, Cambridge S, Hecker M, & Ullrich ND (2018). Improving electrical properties of iPSC-cardiomyocytes by enhancing Cx43 expression. Journal of Molecular and Cellular Cardiology, 120, 31–41. [DOI] [PubMed] [Google Scholar]
  55. Spector P (2013). Principles of cardiac electric propagation and their implications for re-entrant arrhythmias. Circulation: Arrhythmia and Electrophysiology, 6(3), 655–661. [DOI] [PubMed] [Google Scholar]
  56. Sun Y, Timofeyev V, Dennis A, Bektik E, Wan X, Laurita KR, Deschênes I, Li RA, & Fu J-D (2017). A singular role of IK1 promoting the development of cardiac automaticity during cardiomyocyte differentiation by IK1-Induced activation of pacemaker current. Stem Cell Reviews and Reports, 13(5), 631–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Ten Tusscher K, & Panfilov AV (2006). Alternans and spiral breakup in a human ventricular tissue model. American Journal of Physiology - Heart and Circulatory Physiology, 291(3), H1088–H1100. [DOI] [PubMed] [Google Scholar]
  58. Trayanova NA, Pashakhanloo F, Wu KC, & Halperin HR (2017). Imaging-based simulations for predicting sudden death and guiding ventricular tachycardia ablation. Circulation: Arrhythmia and Electrophysiology, 10(7), e004743. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Velagaleti RS, Pencina MJ, Murabito JM, Wang TJ, Parikh NI, D’Agostino RB, Levy D, Kannel WB, & Vasan RS (2008). Long-term trends in the incidence of heart failure after myocardial infarction. Circulation, 118(20), 2057–2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Verkerk AO, van Ginneken ACG, & Wilders R (2009). Pacemaker activity of the human sinoatrial node: Role of the hyperpolarization-activated current, If. International Journal of Cardiology, 132(3), 318–336. [DOI] [PubMed] [Google Scholar]
  61. Vigmond E, Vadakkumpadan F, Gurev V, Arevalo H, Deo M, Plank G, & Trayanova N (2009). Towards predictive modelling of the electrophysiology of the heart: Predictive modelling of cardiac electrophysiology. Experimental Physiology, 94(5), 563–577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Williams NP, Rhodehamel M, Yan C, Smith AST, Jiao A, Murry CE, Scatena M, & Kim D-H (2020). Engineering anisotropic 3D tubular tissues with flexible thermoresponsive nanofabricated substrates. Biomaterials, 240, 119856. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Yu JK, Franceschi W, Huang Q, Pashakhanloo F, Boyle PM, & Trayanova NA (2019). A comprehensive, multiscale framework for evaluation of arrhythmias arising from cell therapy in the whole post-myocardial infarcted heart. Scientific Reports, 9(1), 9238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Yu JK, Liang JA, Franceschi WH, Huang Q, Pashakhanloo F, Sung E, Boyle PM, & Trayanova NA (2022). Assessment of arrhythmia mechanism and burden of the infarcted ventricles following remuscularization with pluripotent stem cell-derived cardiomyocyte patches using patient-derived models. Cardiovascular Research, 118(5), 1247–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Yu JK, Liang JA, Weinberg SH, & Trayanova NA (2022). Computational modeling of aberrant electrical activity following remuscularization with intra-myocardially injected pluripotent stem cell-derived cardiomyocytes. Journal of Molecular and Cellular Cardiology, 162, 97–109. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Statistical summary, as published with article
NIHMS1966318-supplement-Statistical_summary__as_published_with_article.pdf (179.2KB, pdf)
Peer review history, as published with article
NIHMS1966318-supplement-Peer_review_history__as_published_with_article.pdf (346.5KB, pdf)

Data Availability Statement

Where possible, raw numerical data underlying figures are available via dryad: https://doi.org/10.5061/dryad.63xsj3v75. Source files for representative examples of all simulations conducted in this study, which can be re-run or modified using publicly available software tools, can be found via the same permanent link as above.

RESOURCES