Abstract
Diffusion tensor imaging (DTI) consistently detects increased mean diffusivity and decreased fractional anisotropy with advancing age in regions of primarily single white matter (WM) fiber populations, but findings have been inconsistent in regions of more complex fiber architecture. Given that DTI remains more common for characterizing aging WM than advanced diffusion MRI models due to DTI’s simplicity, robustness, and efficiency, it is critical to strive to maximize the information extracted from DTI across the entire WM. The present study uses an orthogonal diffusion tensor decomposition based on the 3 eigenvalue moments (mean diffusivity, norm of anisotropy, and mode of anisotropy), yielding clear voxelwise degeneration patterns across the WM, including regions of complex fiber architecture. This indicates that the previous challenges of DTI in these regions were due to the choice of tensor decomposition rather than the DTI model itself. This study therefore presents a revised view of DTI of aging WM and indicates how age-related degeneration in complex fiber architecture can manifest in forms other than decreased fractional anisotropy.
Keywords: Diffusion tensor imaging, Normal adult aging, White matter, Complex fiber architecture, Tensor decomposition
1. Introduction
The cognitive decline that accompanies normal adult aging is associated with alterations in white matter (WM) microstructure, which can be classified into cellular and extracellular changes. Cellular changes include degeneration of WM fibers, including Wallerian degeneration and axonal death, as well as degradation, splitting, and ballooning of myelin sheaths (Peters, 2002). Extracellular changes include enlargement of interstitial and perivascular spaces, increased neuroinflammation and blood-brain-barrier breakdown (Maclullich et al., 2004; Meier-Ruge et al., 1992; Sonntag et al., 2011; Sparkman and Johnson, 2008). Accordingly, in vivo characterization of WM microstructure is highly relevant for monitoring age-related changes and distinguishing normal versus pathological aging. The method of choice in this regard has been diffusion tensor imaging (DTI), which models the microscopic diffusion of water molecules as a second-order symmetric positive-definite tensor that can be decomposed into scalar invariant metrics (Basser et al., 1994). The trivial decomposition is a spectral decomposition into 3 orthogonal eigenvalues that describe the magnitude of diffusion along each of the 3 dimensions. Since the early days of DTI, however, metrics derived from the eigenvalues that holistically describe the size and shape of the tensor have been acknowledged as a useful alternative to assessing the directional diffusivities individually (Pierpaoli and Basser, 1996). DTI studies most commonly use the metrics mean diffusivity (MD), a measure of the size of the tensor, and fractional anisotropy of diffusion (FA), a measure of the shape of the tensor.
Studies of healthy WM have consistently reported the trend of increased MD and decreased FA with advancing age, most pronounced in association tracts (superior longitudinal fasciculus, arcuate fasciculus, fronto-occipital fasciculus, inferior longitudinal fasciculus, and uncinate fasciculus) and genu of the corpus callosum, whereas less pronounced in the corticospinal tract and the splenium of the corpus callosum. These trends of increased MD and decreased FA with advancing age are typically interpreted as an overall decline in WM microstructural integrity with advancing age (Cox et al., 2016; Lebel et al., 2012; Madden et al., 2012; Sullivan and Pfefferbaum, 2006).
Voxelwise analyses have become a common procedure for DTI studies as they allow for visualization of trends spatially across the WM. The standard approach is tract-based spatial statistics (TBSS), which measures variation in DTI metrics across subjects per voxel of a standardized WM skeleton (Smith et al., 2006). This allows for simultaneous assessment of DTI trends in the lateral WM, which consists of short association fibers connecting adjacent cortical areas, and the medial WM, which consists of more compact tracts, including the corpus callosum (medial-lateral), projection tracts (superior-inferior), and association tracts (anterior-posterior) (Catani and de Schotten, 2012). However, virtually all voxels of the WM skeleton contain more than one distinct fiber orientation (Jbabdi et al., 2010). While short association fibers in lateral voxels form primarily single fiber bundles, medial voxels contain more complex fiber architecture, particularly in the corona radiata and internal capsule. Here, the primary fibers stem from projection tracts, notably the corticospinal tract, and secondary crossing fibers stem from association tracts. The conflation of multiple fiber tracts within voxels may be even further exaggerated by imperfect cross-subject registration and skeletonization during TBSS preprocessing (Bach et al., 2014). In the corona radiata and internal capsule, FA has been shown to exhibit weak sensitivity to age, and recent TBSS studies with larger samples have found sporadic increases in FA with age (de Groot et al., 2016; Miller et al., 2016). Increases in FA are often detected in these regions among patients with Alzheimer’s disease relative to healthy controls, interpreted as selective degeneration of the secondary association fibers, which would result in increased anisotropy along the primary direction (Doan et al., 2017; Douaud et al., 2011; Mito et al., 2018; Teipel et al., 2014). It has been suggested that increases in FA in normal adult aging also reflect selective degeneration that occurs to a lesser extent than in neurodegenerative disease (Chad et al., 2018; de Groot et al., 2016). This indicates that in the presence of complex fiber architecture, WM degeneration does not always manifest itself as decreased FA, and increased FA may serve as a proxy of selective degeneration of secondary fibers crossing the primary tract. That said increased FA in normal aging is rarely detected across the corona radiata and internal capsule despite selective degeneration of association fibers being expected throughout these regions. This is presumably due to this increased anisotropy resulting from selective degeneration being conflated with increased isotropic diffusion in aging resulting from the extracellular processes mentioned earlier, which would explain the low sensitivity of FA to age in these complex regions.
It is often maintained that DTI is inherently limited in regions of complex fiber architecture and alternative advanced diffusion MRI methods are necessary. For example, a two-compartment free-water DTI model has been used to model the increased diffusivity with age into a separate free water compartment, such that the tissue compartment exhibited clear and consistent positive age associations of tissue FA throughout the corona radiata and internal capsule (Chad et al., 2018). Neurite orientation dispersion and density imaging has been used to find negative age associations of fiber orientation dispersion in these regions (Miller et al., 2016). Constrained spherical deconvolution has been used to explicitly model a fiber orientation distribution function in patients with Alzheimer’s disease to demonstrate selective degeneration in these regions relative to the controls (Mito et al., 2018). Nevertheless, DTI remains the most commonly used diffusion MRI approach in practice due to its simplicity, robustness (DTI does not rely on assumptions about the tissue like advanced models), efficiency (applicability to any rapid single-shell acquisition, which remains the most common clinical approach), and availability (abundance of legacy single-shell data). Therefore, rather than relying on advanced diffusion models, it is crucial to maximize the information that can be extracted from the DTI model for illuminating age-related degeneration in regions of complex fiber architecture.
As mentioned, a key challenge of decomposing the tensor into FA in the corona radiata and internal capsule is that increased anisotropy in aging (resulting from selective degeneration) is conflated with the increased isotropic portion of MD in aging (resulting from extracellular processes), thereby limiting the sensitivity of FA to age in these regions. In other words, while FA describes the shape of the tensor, the measure is normalized by the size of the tensor, and hence FA and MD are not orthogonal. It is therefore worthwhile to explore a set of size and shape measures that provide a fully orthogonal decomposition of the diffusion tensor (Ennis and Kindlmann, 2006). Here, we choose an alternative orthogonal decomposition based on the eigenvalue moments: MD, norm of anisotropy (NA), and mode of anisotropy (MO). Visualization of how MD, NA, and MO reflect tensor size and shape is displayed in Supplementary Figures 1 and 2. Briefly, while MD remains a measure for the size of the tensor, NA is a shape measure directly based on the variance of the eigenvalues and thus irrespective of alterations in MD (i.e., irrespective of alterations in isotropic diffusion). Degeneration of primarily single-tract regions would manifest as decreased NA, whereas selective degeneration of secondary crossing tracts would manifest as increased NA. MO is another shape measure that corresponds with the skewness of the eigenvalues and hence whether the anisotropy is linear (MO = 1), as in a “stick” shaped tensor, or planar (MO = −1), as in a “pancake” shaped tensor. Because WM usually has positive values of MO, decreases and increases in anisotropy are typically interpreted as decreases and increases in linearity. The use of MO allows us to verify that decreased anisotropy in aging is indeed decreased linear anisotropy, consistent with reduced microstructural integrity, and that increased anisotropy in aging is indeed increased linear anisotropy, consistent with selective degeneration of secondary fibers.
Given the aforementioned issues of sensitivity and interpretability of DTI findings in aging, and also given the ongoing popularity of DTI while advanced diffusion MRI techniques often remain unfeasible, this study aims to push the boundaries of a conventional TBSS-style DTI analysis. The purpose of this study is to determine if the orthogonal diffusion tensor decomposition based on the eigenvalue moments can allow DTI to provide insight into age-related degeneration across the WM, including regions of complex fiber architecture. In conjunction with our DTI analysis, we additionally use a crossing fiber model to test the hypothesis that age-related differences in tensor shape in these regions correspond to differences in the relative proportions of crossing fiber tracts. Accordingly, rather than interpreting the diffusion tensor as representing a single fiber tract as encouraged by the conventional FA decomposition, the orthogonal decomposition is used while bearing in mind that degeneration in the presence of complex fiber architecture does not necessarily manifest as decreased anisotropy.
2. Methods
2.1. Study participants
All participants of the present study were participants of the UK Biobank initiative. The UK Biobank (ukbiobank.ac.uk) recruited 500,000 participants aged 40–69 across the United Kingdom between 2006 and 2010, and has since embarked on a plan to image 100,000 of these participants. The UK Biobank received ethical approval under Research Ethics Committee reference number 16/NW/0274 and all participants provided written consent.
The present study was conducted as a component of UK Biobank Application 40922. At the time of application in 2018, 22,427 participants aged 44–80 years had been imaged. Participants were excluded from our study if they reported a neurological, psychological, or psychiatric disorder, neurological injury, or history of stroke. Participants were then divided up into 7 age categories of [46–50, 51–55, 56–60, 61–65, 66–70, 71–75, 76–80] years, and 50 male and 50 female participants were randomly selected from each of the 7 age categories. The final sample thus consisted of 700 participants aged 46–80 years (50% male, 50% female).
2.2. Diffusion MRI data
Detailed information about MRI data and processing from the UK Biobank can be found in the study by Alfaro-Almagro et al. (2018). In brief, diffusion MRI data were acquired on a Siemens Skyra 3T system with 5 b = 0, 50 b = 1000s/mm2 and 50 b = 2000s/mm2 volumes (100 distinct directions) at TR = 3.6s, TE = 92 ms, matrix size = 104 × 104 × 72 with (2 mm)3 resolution, 6/8 partial Fourier, 3x multislice acceleration and no in-plane acceleration. An additional 3 b = 0 volumes were acquired with a reversed phase encoding. The data were corrected for eddy-current and susceptibility-related distortions via EDDY (Andersson and Sotiropoulos, 2016) and TOPUP (Andersson et al., 2003), respectively.
2.3. Diffusion tensor imaging
The diffusion tensor was computed voxelwise by fitting diffusion MRI signal from the b = 0 and b = 1000s/mm2 shells to the DTI model (implemented in FSL’s DTIFIT as per the UK Biobank preprocessing pipeline). was decomposed into
| (1) |
Where
| (2) |
in which I is the identity matrix such that is an isotropic tensor based on the first moment of the eigenvalues (MD is defined in Eq. 5); and
| (3) |
is the residual anisotropy, based on the second moment of the eigenvalues. FA, the conventional DTI metric for tensor shape, is defined by the ratio between and , where is the Frobenius norm (square root of the sum of the squares of tensor elements):
| (4) |
Eq. (4) demonstrates that FA depends on both the first (MD) and second () moment of the eigenvalues of . Therefore, for example, any increase in isotropic diffusivity (i.e., affecting MD but not ) will cause FA to decrease (Supplementary Fig. 1B). This is further discussed in Appendix A.
For the present study, rather than merely describing the tensor with its 3 orthogonal eigenvalues the size and shape of the tensor are described by further deriving 3 orthogonal scalar invariants from the decomposition of Eq. 1 which is based on the first, second, and third moments of tensor eigenvalues: MD, NA, and MO (Ennis and Kindlmann, 2006):
| (5) |
| (6) |
| (7) |
where MD is a measure of the overall diffusivity, NA is a measure of anisotropy without confounding any changes in diffusivity, and MO is a measure of whether the anisotropy is linear (indicative of a single fiber tract) or planar (indicative of, for instance, crossing or fanning fiber tracts). For this study, MD and MO are output directly from DTIFIT, whereas NA is computed via Eq. 6 from the eigenvalue decomposition output by DTIFIT. The relationship between these 3 metrics and the moments of the eigenvalue distribution is shown in Table 1.
Table 1.
Decomposing the tensor into invariant scalars based on the first 3 moments of the eigenvalue distribution
| Raw moment | Central moment | Standardized moment | |
|---|---|---|---|
|
| |||
| First | “Mean” | 0 | 0 |
| Second | “Variance” | 1 | |
| Third | MO “Skewness” | ||
∥ is Frobenius norm (i.e., matrix extension of the L2 norm), whereas is the matrix extension of the L3 norm. D is the diffusion tensor being assessed; , the anisotropic portion of D, is defined in Eq. 3. In this study, the 3 orthogonal metrics chosen are (“mean diffusivity”), (“norm of anisotropy”), and MO (“mode of anisotropy”), based on the first raw, second central and third standardized moment, respectively. The first raw and second central moment are also the first 2 cumulants, and the third standardized moment is the third standardized cumulant.
Note that in the study by Ennis and Kindlmann (2006), MO is erroneously described as (i.e., the subtraction of MD from each eigenvalue is omitted). The scaling factor is used to normalize values of MO to lie between −1 and 1.
2.4. Explicit crossing-fiber modeling
The use of the aforementioned basis for tensor shape is motivated by the presence of complex fiber architecture, but none of the orthogonal DTI metrics are actually specific to crossing fibers. To aid in biological interpretation, the orientation of fiber bundles underlying the tensor is explicitly modeled via BEDPOSTX (Bayesian estimation of diffusion parameters obtained using sampling techniques) (Jbabdi et al., 2012), available in FSL and implemented as part of the UK Biobank processing pipeline. This approach uses Markov Chain Monte Carlo sampling from all shells of diffusion MRI data (i.e., both b = 1000s/mm2 and b = 2000s/mm2) to estimate the posterior mean fractional voxel occupancy of 3 tracts, that is, the proportion of the primary, secondary, and tertiary tract per voxel, occupying fractions f1, f2, and f3 of the voxel, respectively.
2.5. Statistical analysi
This study is designed to emulate a standard DTI study of WM aging, but using alternative tensor decomposition. FSL’s TBSS (Smith et al., 2006) was used with default parameters to obtain a WM skeleton based on the 700-subject sample registered to MNI152 space (182 × 218 × 182). For voxelwise analysis, a significant correlation of metric with age was defined by p < 0.05 with correction for multiple comparisons (clusterwise controlling familywise error rate with 500 permutations) as per FSL’s randomize (Winkler et al., 2014). Age-related difference in metric per year (effect size), defined as the slope of the regression line of metric versus age, was calculated in each voxel using a general linear model (mri_glmfit) as implemented in FreeSurfer (Fischl, 2012), and displayed only for statistically significant associations. To control for potential sex differences in aging trajectories (Kodiweera et al., 2016), the linear model was fit separately for males and females and the 2 regression line slopes were averaged (i.e., mri_glmfit controlled for sex). Screenshots were taken for the figures of this article at MNI coordinate (116, 130, 91).
3. Results
Fig. 1 displays significant associations of MD and FA with age across the 700-subject sample from the UK Biobank. Positive associations of MD with age are widespread across the WM skeleton, most notably in the genu and body of the corpus callosum, the anterior and posterior corona radiata, and parts of the anterior limb of internal capsule (Fig. 1A). Negative associations of FA with age are also widespread across the WM skeleton, particularly in the genu of the corpus callosum, anterior corona radiata and posterior thalamic radiations (Fig. 1B). Conversely, select regions of the WM skeleton also display positive associations of FA with age in the superior and posterior corona radiata, as well as small portions of the posterior and retrolenticular limbs of the internal capsule. There are also numerous areas exhibiting no significant association of FA with age, mostly in the corona radiata, as well as the posterior most section of the anterior limb of the internal capsule (shown in the coronal slice; Fig. 1B).
Fig. 1.
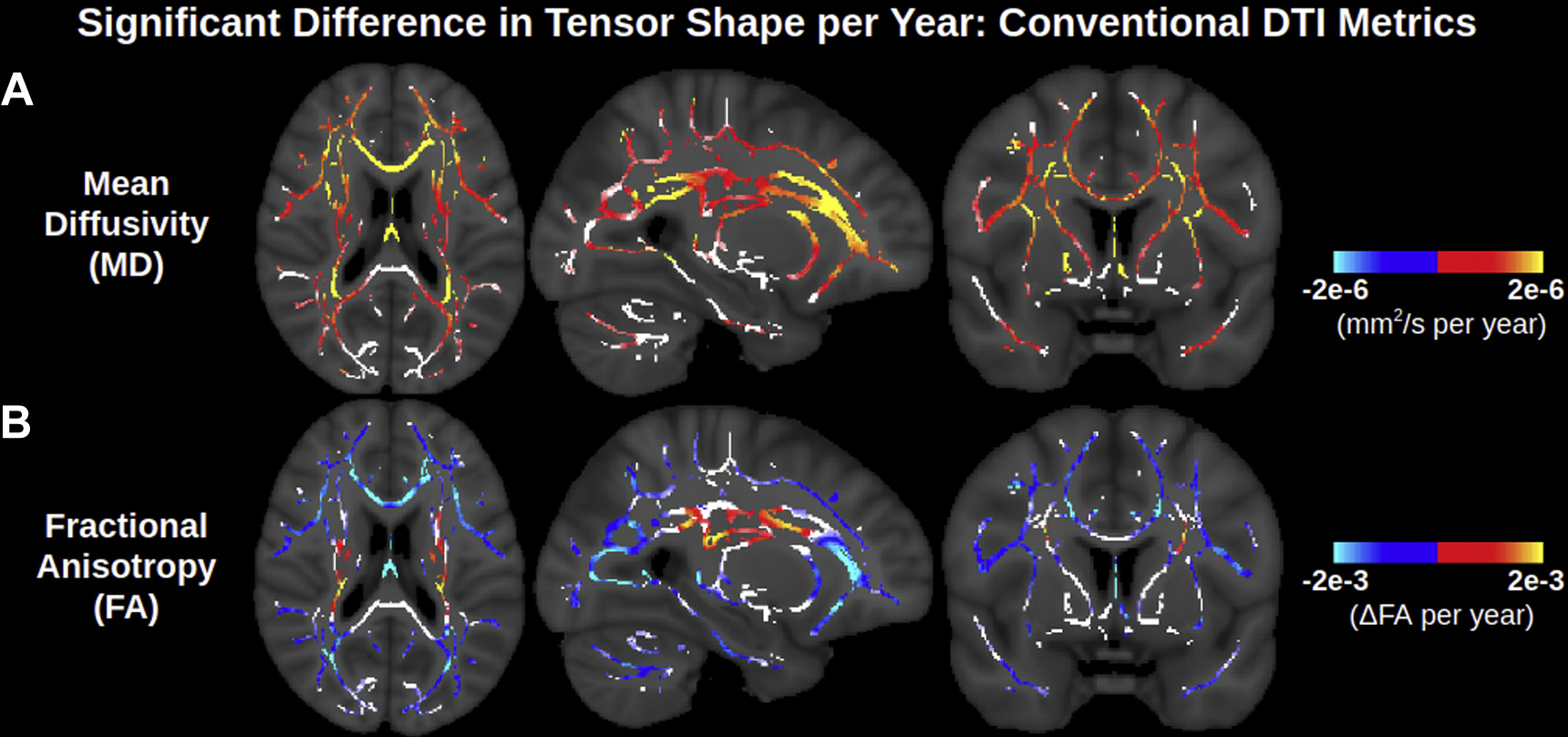
Widespread significant associations of conventional DTI metrics (MD and FA) with age across the WM skeleton. Age associations are largely positive for MD and negative for FA, although certain medial WM regions have no or positive age associations of FA. Note that the contrast is the difference in metric per year derived from a linear regression and displayed only in voxels with significant correlations with age. Voxels of the WM skeleton without significant correlations with age are displayed in white. Abbreviations: DTI, diffusion tensor imaging; MD, mean diffusivity; FA, fractional anisotropy; WM, white matter.
Fig. 2 displays significant age associations of the 3 eigenvalues, resulting from the trivial orthogonal tensor decomposition. Positive associations of all 3 eigenvalues are ubiquitous across the WM skeleton and exhibit much overlap, indicative of widespread positive associations of isotropic diffusion with age. Fig. 2A represents the primary eigenvalue (axial diffusivity), which exhibits positive age associations in much of the anterior and superior WM, negative age associations in some of the posterior and inferior WM, and no significant associations with age in other (primarily lateral) regions. The positive associations of the primary eigenvalue with age are most pronounced in the corona radiata, internal capsule and genu of the corpus callosum. The secondary (Fig. 2B) and tertiary (Fig. 2C) eigenvalues exhibit significant positive associations with age in many of the regions that the primary eigenvalue does not, consistent with decreasing anisotropy in aging. That said, it is notable that whereas the tertiary eigenvalue is positively associated with age throughout the WM skeleton, the secondary eigenvalue does not exhibit significant associations with age through much of the corona radiata and internal capsule, and even exhibits some negative associations with age in these regions. In such regions without positive age associations of the secondary eigenvalue, the magnitude of age-related increases in the tertiary eigenvalue is smaller than those in the primary eigenvalue, whereas in the remainder of the WM skeleton, the magnitudes of age-related increases in the tertiary eigenvalue (and secondary eigenvalue) are larger than that of the primary eigenvalue.
Fig. 2.
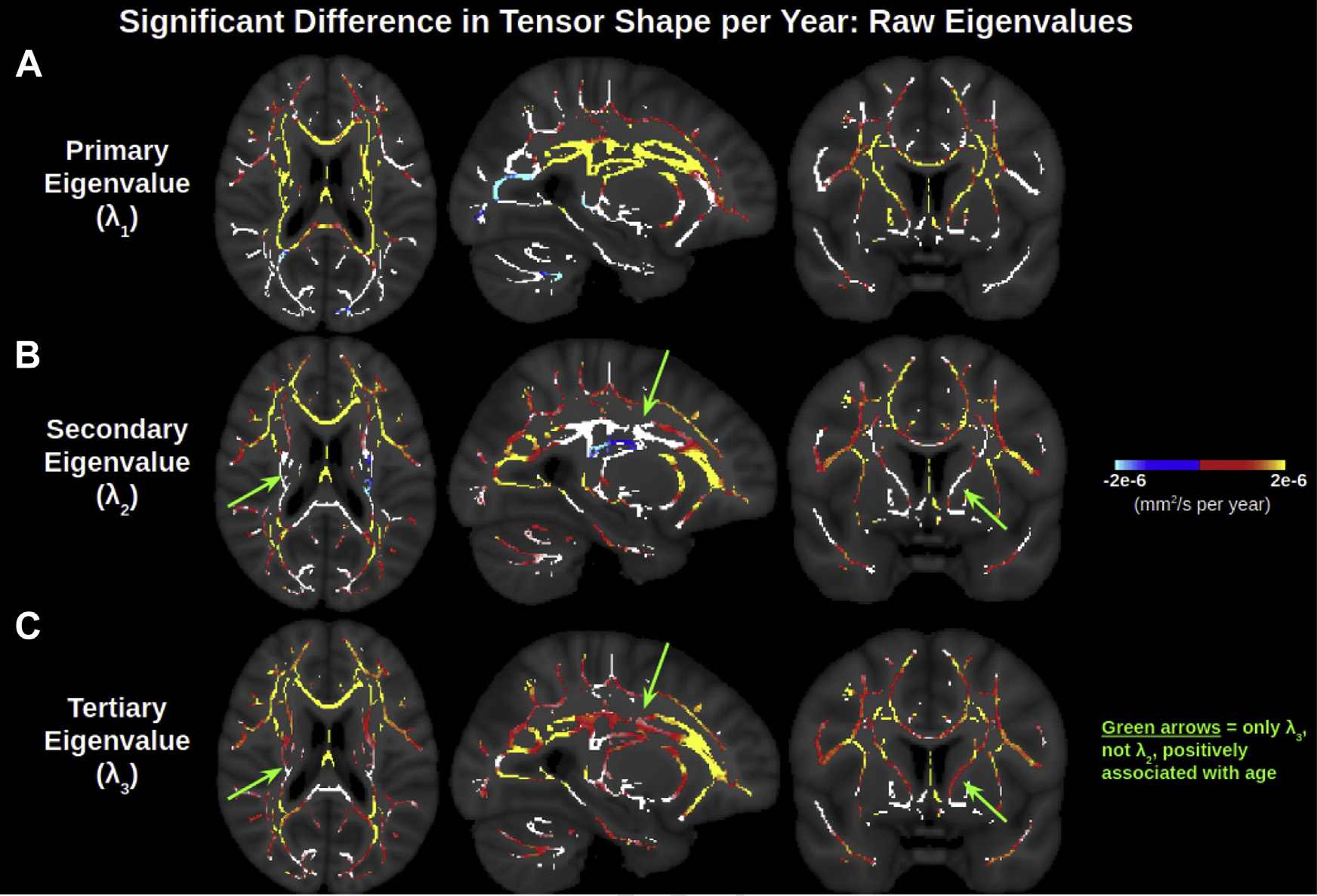
Widespread significant associations of the 3 orthogonal eigenvalues of the diffusion tensor with age across the WM skeleton. The effect size of positive age associations of the primary eigenvalue is smaller than those of the secondary and tertiary eigenvalue in lateral WM regions, and larger than those of the secondary and tertiary eigenvalue in medial WM regions. In these medial WM regions, the effect size of the positive age associations of the secondary eigenvalue is smaller than of the tertiary eigenvalue, and the secondary eigenvalue also displays insignificant or negative age associations in certain parts of the medial WM. Note that the contrast is the effect size of metric per year derived from a linear regression and displayed only in voxels with significant correlations with age. Voxels of the WM skeleton without significant correlations with age are displayed in white. Abbreviations: WM, white matter.
To provide a more holistic representation of tensor shape (and thus aid in biological intuition/comprehensibility), age associations of 3 orthogonal metrics based on the 3 moments of the eigenvalues are displayed in Fig. 3. Fig. 3B shows that the NA is negatively associated with age across the lateral WM, as is FA. However, NA displays many more positive associations with age across the WM skeleton than does FA, notably throughout the corona radiata, internal capsule, and corpus callosum. Regions where NA displays positive associations with age, whereas FA does not, include the anterior limb of the internal capsule and the splenium of the corpus callosum, as well as parts of certain regions where FA is negatively associated with age, such as the body of the corpus callosum. Accordingly, as shown in Fig. 4, the relative age-related decline in NA is smaller than that in FA across voxels exhibiting positive age associations of MD, further reiterating higher isotropic diffusivity with advancing age (i.e., increase in all 3 eigenvalues with advancing age, as shown in Fig. 2, and further interpreted in Appendix A). Fig. 3C shows that MO is also associated with age across the WM skeleton. Most MO associations with age are negative (i.e., the decreasing anisotropy is decreasing linear anisotropy—i.e., the tensor is less linear and less anisotropic with advancing age—as opposed to decreasing planar anisotropy), and the affected voxels largely overlap with those exhibiting negative age associations of NA. Other regions of the WM skeleton exhibit positive age associations of MO (i.e., increasingly linear with advancing age), largely overlapping with regions where NA exhibits positive age associations. A summary of these results are displayed in Table 2, and corresponding scatter plots of trends and their co-efficients of determination are displayed in Supplementary Fig. 3.
Fig. 3.
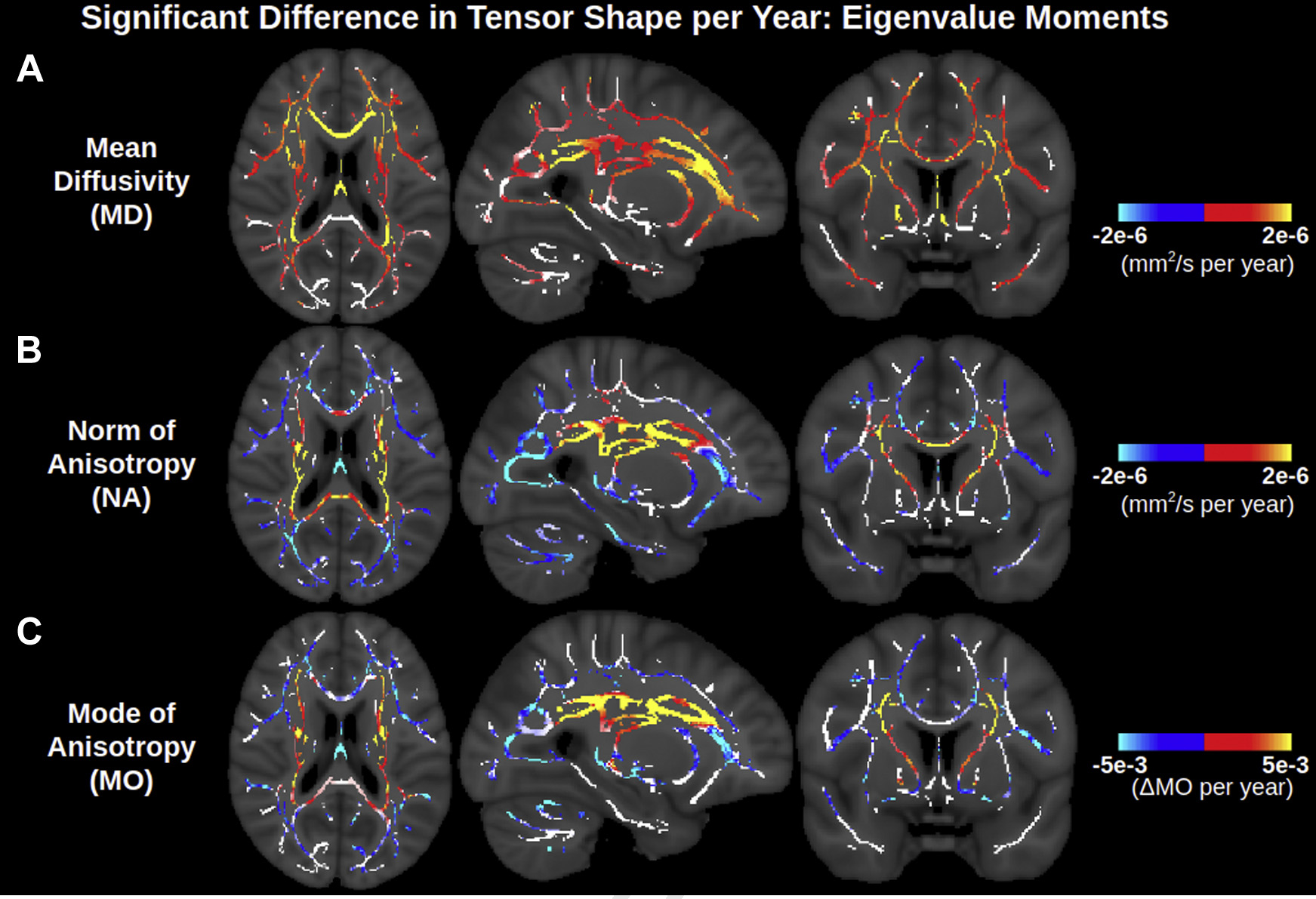
Widespread significant associations of orthogonal DTI metrics based on eigenvalue moments with age across the WM skeleton. NA exhibits more positive age associations than FA (Fig. 1), and these positive age associations of NA largely overlap with positive age associations of MO. MD maps are repeated from Fig. 1 for ease of visualization. Note that the contrast is the effect size of metric per year derived from a linear regression and displayed only in voxels with significant correlations with age. Voxels of the WM skeleton without significant correlations with age are displayed in white. Abbreviations: DTI, diffusion tensor imaging; MD, mean diffusivity; MO, mode of anisotropy; FA, fractional anisotropy; WM, white matter.
Fig. 4.
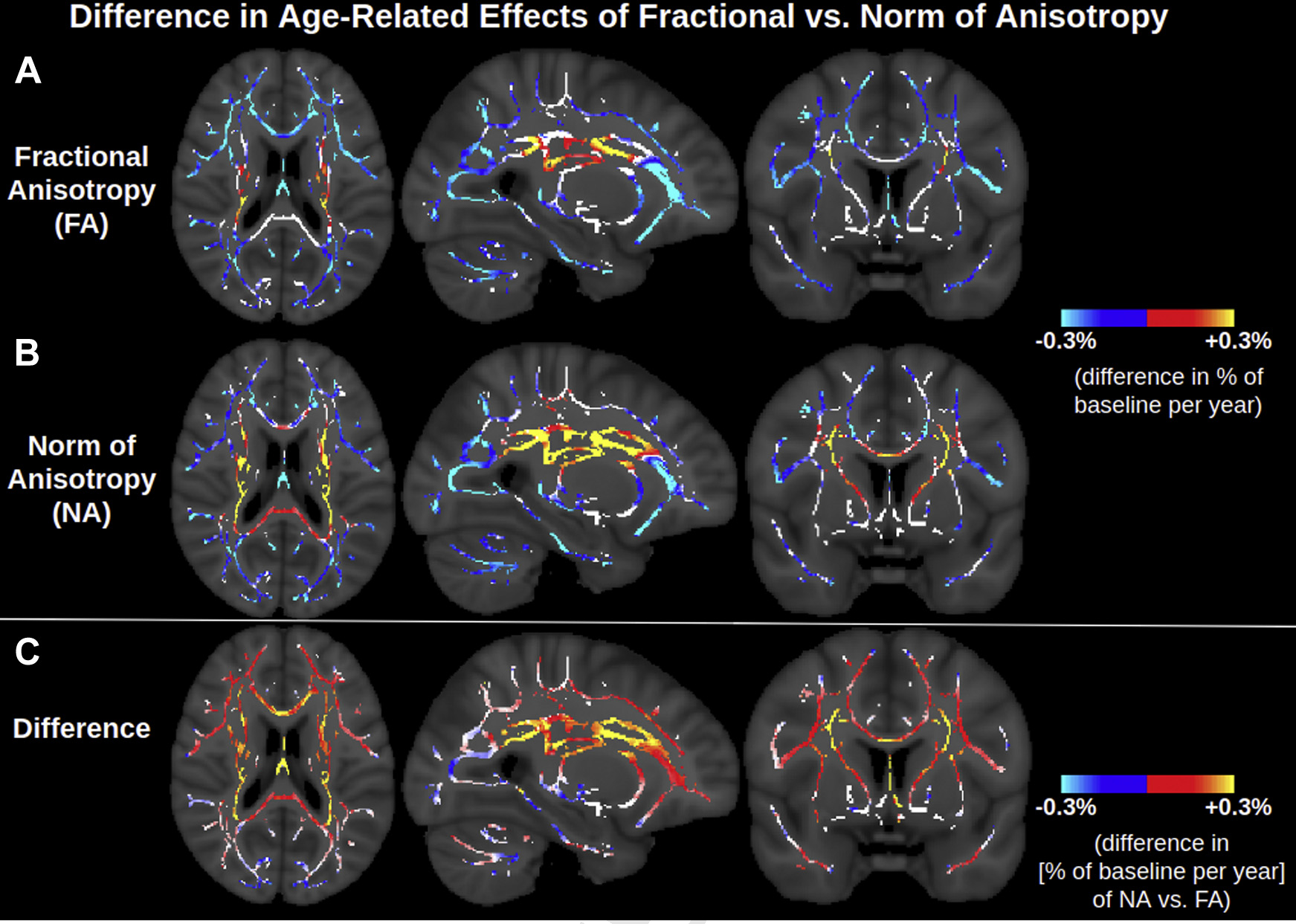
Difference in age-related effect of fractional anisotropy versus norm of anisotropy. Units are the slope of the regression line divided by the baseline of each metric, where “baseline” is defined as the average of the metric in the voxel for participants aged 46–50 years. The red-yellow in c indicates voxels where FA decreases with age faster than NA, that is, voxels exhibiting higher isotropic diffusivity with advancing age. The blue in c indicates regions where isotropic diffusivity is unassociated with age, and thus NA decreases with age slightly faster than FA, as described mathematically in Appendix A. Abbreviations: FA, fractional anisotropy; NA, norm of anisotropy. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Table 2.
Summary of results
| Trend with age | Regions | Interpretation |
|---|---|---|
|
| ||
| Conventional view | ||
| Increased MD | Association fibers; anterior corpus callosum | Decreased integrity of primarily single fiber bundles |
| Decreased FA | ||
| Increased MD | Projection fibers crossing secondary association fibers | FA = unsuitable metric |
| Inconsistent FA | ||
| Revised view | ||
| Increased MD | Association fibers; Genu of corpus callosum | Decreased integrity of primarily single fiber bundles |
| Decreased NA | ||
| Decreased MO | ||
| Increased MD | Projection fibers crossing secondary association | Selective degeneration of secondary crossing fibers |
| Increased NA | fibers; Splenium of corpus callosum | |
| Increased MO | ||
| Increased MD | Body of corpus callosum | Dual degeneration of primary fibers and secondary crossing fibers |
| Increased NA | ||
| Decreaseda MO | ||
Key: MD, mean diffusivity; MO, mode of anisotropy; FA, fractional anisotropy; NA, norm of anisotropy.
Refers to decreased or no significant age associations of MO.
To help interpret this positive age association of linear anisotropy (positive age associations of both NA and MO), BEDPOSTX was used to explicitly model the underlying fiber architecture by estimating the fractional voxel signal occupancy of the primary and secondary tracts. Fig. 5 displays that in medial WM regions (corona radiata, internal capsule, and corpus callosum), the fractional voxel occupancy of the secondary tract decreases with age faster than that of the primary tract (i.e., the ratio secondary:primary tract is negatively associated with age, consistent with a “selective degeneration” scenario). This selective degeneration largely overlaps with regions displaying positive associations of both NA and MO with age, with the exception of the corpus callosum. In the corpus callosum, BEDPOSTX models the primary tract as mediallateral (presumably callosal fibers) and the secondary tract as anterior-posterior (presumably the cingulum). Negative age associations of NA and MO are found in the genu of the corpus callosum, positive age associations of NA and MO are found in the splenium of the corpus callosum, and negative age associations of MO alongside positive age associations of NA are found in the body of the corpus callosum (Fig. 6). BEDPOSTX indicates faster age-related decline of the secondary tract than the primary tract throughout the corpus callosum, but this only corresponds to the “selective degeneration” pattern of positive age associations of NA and MO in the splenium. The situation in the genu and body differs from the selective degeneration in the corona radiata and internal capsule in that (1) there are less crossings in the corpus callosum than the corona radiata and internal capsule in general, and (2) the proportion of the primary tract in the corpus callosum still exhibits negative age associations, unlike in the corona radiata and internal capsule, which only display negative age associations for the proportion of the secondary tract.
Fig. 5.
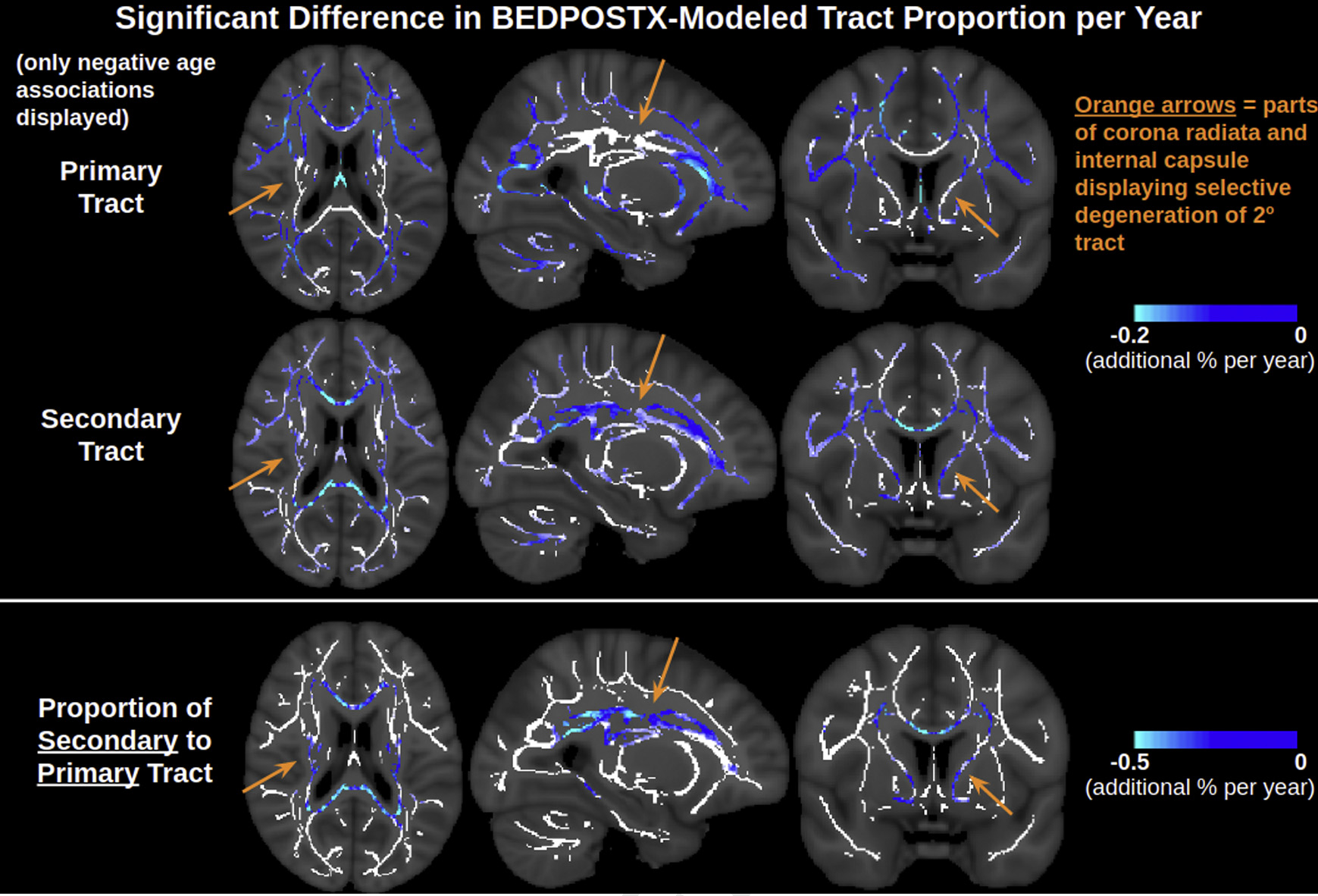
BEDPOSTX indicates that the proportion of the secondary tract decreases with advancing age faster than the primary tract in the corona radiata, internal capsule and corpus callosum. In much of the corona radiata and internal capsule specifically, only the proportion of the secondary tract, but not primary tract, is negatively associated with age. Note that the contrast is the effect size of metric per year derived from a linear regression and displayed only in voxels with significant negative correlations with age. Voxels of the WM skeleton without significant negative correlations with age are displayed in white. Abbreviations: WM, white matter.
Fig. 6.
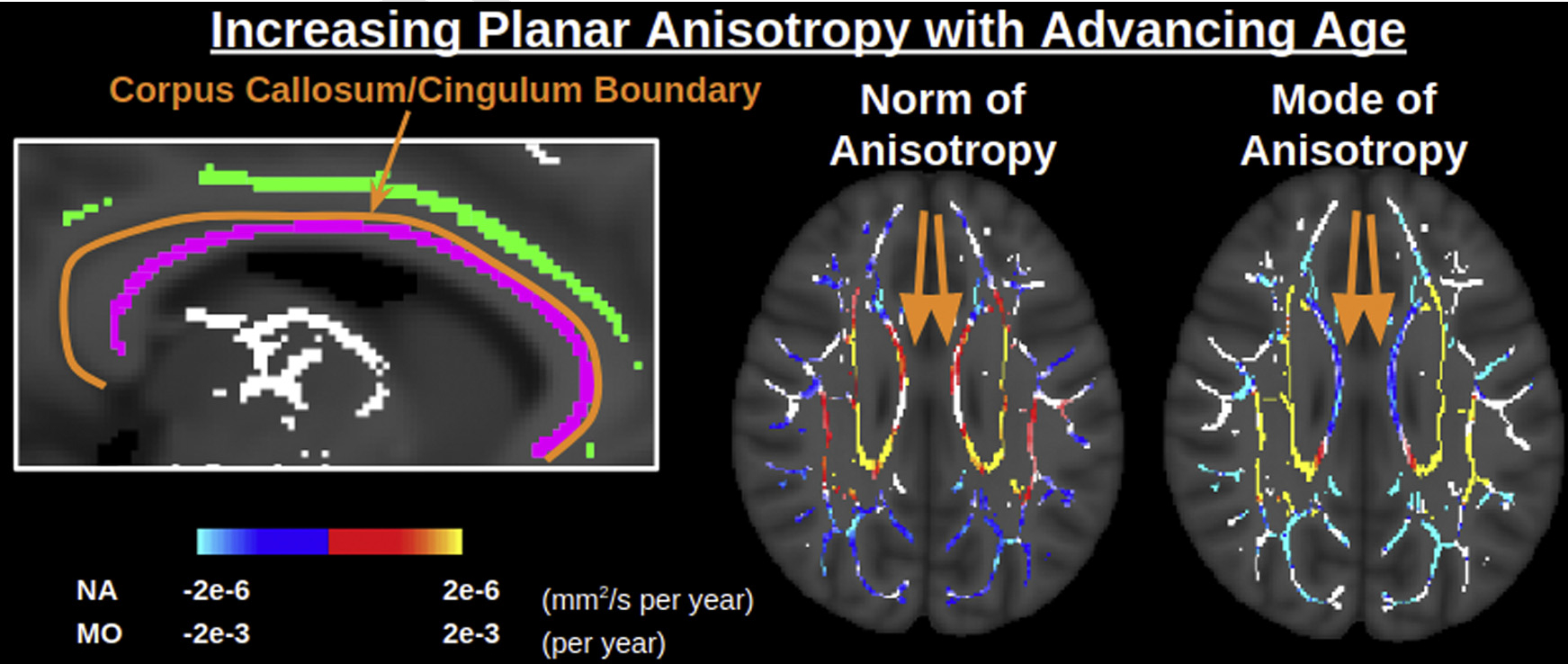
Interpreting positive associations of planar anisotropy with age in the body of the corpus callosum. The body of the corpus callosum (callosum skeleton outlined in purple) is located directly by the border with the cingulum (cingulum skeleton outlined in green), which can presumably lead partial volume effects within the TBSS skeleton. Here the norm of anisotropy (norm) is positively associated with age, whereas the mode of anisotropy (mode) is negatively associated with age, consistent with alterations in more than one tract in aging (e.g., Supplementary Figure 2c). Abbreviations: TBSS, tract-based spatial statistics. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
4. Discussion
This study presents a revised view of voxelwise (TBSS) DTI trends in aging WM by using an orthogonal tensor decomposition based on the 3 eigenvalue moments, yielding clear degeneration patterns across the WM. This includes regions of complex fiber architecture which exhibited limited age associations of FA. Specifically, while FA demonstrates low sensitivity to age in the corona radiata and internal capsule, this study found that NA and MO are consistently sensitive to age throughout these regions, indicating that the previous challenges of DTI in these regions were due to the choice of decomposition rather than the DTI model itself. Therefore, if an advanced diffusion MRI technique is not feasible, the conventional DTI model can still be used to gain insight into crossing fiber regions by using the orthogonal tensor decomposition, bearing in mind that the complex fiber architecture of WM tissue means that degeneration does not always manifest itself as decreases in tensor anisotropy.
FA has become a popular measure of tensor anisotropy due to its proven sensitivity to tissue processes, at least in the lateral WM, where each voxel is more likely to represent a single fiber population. In the case of aging, decreased FA in a single fiber population could reflect both a change in the shape of the tensor, that is, less anisotropic diffusion resulting from processes such as myelin breakdown and overall reduced microstructural integrity, and change in the size of the tensor, that is, increase isotropy, resulting from extracellular processes such as atrophy, enlarged interstitial space and increased inflammation. The high sensitivity of FA to age detected in single fiber regions, including a decline of FA by about 3% per decade, has already been established in the literature (Grieve et al., 2007). In regions of selective degeneration of secondary fibers, however, the 2 processes—increase in NA and increase in MD—effectively compete with one another, likely explaining the low sensitivity of FA to age in these regions. Accordingly, because the isotropic component does not contribute to changes in NA, in the lateral WM, NA exhibits a smaller magnitude of normalized age-related decreases than does FA, and in regions of complex fiber architecture, NA exhibits more positive age associations than does FA. Therefore, NA is ostensibly a more specific measure of microstructural tissue anisotropy in aging (e.g., myelin compactness) than FA, and its use holds particular promise in the presence of partial voluming between WM tissue and cerebrospinal fluid or edema. These findings agree with our previous work, which found that if positive age associations of MD in aging are allocated to a separate free water compartment, then age associations of FA of the tissue compartment are highly similar to those of NA found in the present study (Chad et al., 2018). In other words, the present study reached analogous findings to the two-compartment free water model by using the conventional DTI model: MD instead of free water and NA instead of free-water eliminated (tissue) FA.
By using a third metric, MO, we further tested the hypothesis that decreases and increases in anisotropy in aging represent decreases and increases in linear anisotropy, under the assumption that age-related changes of WM anisotropy are related to the linear structure of WM fibers. Positive and negative age associations of MO indeed largely overlapped with positive and negative age associations of NA, respectively, supporting the interpretation of decreased NA in aging as reduced microstructural integrity and increased NA in aging as selective degeneration of secondary crossing fibers. The notable exception is the body of the corpus callosum, in which positive age associations of NA overlapped spatially with negative age associations of MO (i.e., the corpus callosum displayed positive age associations of planar anisotropy). This implies increased diffusivity in both the primary and secondary directions and is consistent with degeneration of both callosal fibers and partial-volumed cingulum fibers in aging, which may be exaggerated by imperfect registration and skeletonization during TBSS preprocessing (Bach et al., 2014). Such a finding suggests that alterations in crossing fibers with age have a profound effect on the diffusion tensor in TBSS analyses of the corpus callosum and goes undetected in the conventional DTI framework without the use of the orthogonal decomposition, and likely interpreted erroneously. Hence, attaining a complete representation of tensor shape with 3 orthogonal metrics, rather than stopping short at MD and FA, provides insight into age-related tensor changes that muddle conventional interpretations.
To support the interpretation of DTI in the presence of complex fiber architecture, alterations in crossing fibers in aging were further assessed using BEDPOSTX given the pertinence of selective degeneration for understanding the WM aging process. Our previous work had also used BEDPOSTX to suggest selective degeneration of crossing fibers in the corona radiata and internal capsule, but the study was limited in its use of a single low b-value of 700s/mm2 (Chad et al., 2018), adding value to the current replication. The present study used a multishell approach with b = 1000s/mm2 and 2000s/mm2, which is expected to reduce uncertainty in resolving crossing fibers (Jbabdi et al., 2012). The finding that the secondary tract modeled by BEDPOSTX exhibits greater age-related decline in these regions than the primary tract in the corona radiata and internal capsule supports the hypothesis that selective degeneration of secondary crossing fibers underlies positive associations of both NA and MO (and FA) with age. Based on the tract orientations identified by BEDPOSTX, this effect is presumably the selective degeneration of long association fibers (superior longitudinal fasciculus, arcuate fasciculus, fronto-occipital fasciculus, inferior longitudinal fasciculus), all of which are thought to be relevant for cognitive aging, while the corticospinal tract remains relatively intact. The same effect was detected in the splenium of the corpus callosum, presumably reflecting selective degeneration of any minor fibers crossing the primary callosal fibers. Future microscopy work comparing tracts in aging is critical for validating the interpretation of selective degeneration—to date, the only known microscopic evidence supporting this interpretation is that the g-ratio (ratio of the inner and outer diameters of a myelinated axon) of the corticospinal tract has been found to be unassociated with age in rats (Xie et al., 2014). Moreover, because BEDPOSTX is insufficient for being able to fully capture the extent of alterations in complex fiber architecture in aging due to its limited three-stick model (and hence may not be able to perfectly distinguish isotropic diffusion from 3 or more crossing tracts in the presence of noise), further investigating selective degeneration using advanced tractography approaches such as constrained spherical deconvolution (Raffelt et al., 2017) is part of our future work.
Given the alterations in complex fiber architecture in aging deduced by this study, it would of course be ideal, if feasible, to use more sophisticated tissue modeling approaches than DTI, as the diffusion tensor is not specific to any single fiber tract. Nor does DTI reflect any single tissue process, as it can reflect all of axonal membranes, density, dispersion, myelination, and diameter (Beaulieu, 2002). However, given that diffusion MRI studies of aging (as well as other neuroscience and clinical domains) continue to most commonly apply DTI, it is nevertheless worthwhile to maximize the information extracted from the tensor, especially if only legacy data are available for a population of interest. Clearly, using three orthogonal metrics cannot increase the specificity of the tensor to the underlying microstructure, and cannot lead to discernment of multiple tissue compartments or fiber populations, as is the goal of more sophisticated methods. However, it does allow for a complete representation of tensor shape to at least be available to aid in interpretation. We note that any orthogonal triplet can accomplish a complete representation of tensor shape. The 3 eigenvalues (Fig. 2) collectively provide the same information as the 3 eigenvalue moments (Fig. 3), but the latter provide a more holistic representation of tensor shape and thus convey more visually conspicuous trends. We also note that the full trivariate decomposition is necessary to provide a complete representation of tensor shape. If the secondary and tertiary eigenvalues are averaged to form “radial diffusivity”, the information in Fig. 2 that demonstrates how selective degeneration manifests markedly different age associations of the secondary and tertiary eigenvalues gets lost. Of course, it may still be of interest to use FA rather than metrics described by the eigenvalue moments. FA’s conflation of isotropic and anisotropic diffusion make it very sensitive to age in single fiber bundles, where both processes collectively contribute to decreased FA with advancing age, and FA is also useful for skeletonization in TBSS because it helps ensure that a voxel contaminated with a significant amount of non-WM is not included in the skeleton. As shown in Supplementary Fig. 4, an orthogonal triplet may be chosen that includes FA as a means to still extract maximal information from the diffusion tensor (Ennis and Kindlmann, 2006). That being said, because FA conflates isotropic and anisotropic diffusion, caution should be taken when interpreting the metric in the presence of complex tissue microstructure.
For this first investigation into the effect of orthogonal tensor decomposition, we chose to emulate a standard TBSS analysis to provide a fair comparison with established DTI studies of aging. Evidently, TBSS suffers from limitations in itself, which include dependency of cross-subject registration to the target template (which is an MNI152 template in this and most other studies). This can lead to misalignments between subjects with anatomical differences that occur, for example, during neurodegeneration (Keihaninejad et al., 2012). To help identify whether such issues substantially affected our findings, we additionally conducted voxelwise analyses without TBSS skeletonization (Supplementary Fig. 5). Negative age associations of FA are indeed exaggerated in the direct vicinity of the ventricles, indicating issues with cross-registration amid ventricular enlargement in aging, but these issues do not seem to be present in the deep WM, reiterating the purpose of skeletonization. While skeletonization may collapse multiple fiber tracts atop each other, the effects of complex fiber architecture identified in our study do not seem to have been artificially driven by skeletonization because positive age associations of FA (and corresponding stronger positive age associations of NA) occur even without skeletonization. In any case, while the present study was designed to address issues of complex fiber architecture that were identified in established TBSS studies, important extensions of this work include using a study-specific template, or to go beyond TBSS to average over regions of interest or tracts.
As a limitation in terms of the statistical analysis, we note that all associations with age in this study were modeled as linear correlations. DTI metrics across the life span, from development to old age, can be better modeled by a quadratic or Poisson function (Lebel et al., 2012; Peters et al., 2014). When only investigating adult aging, however, the relationship of DTI metrics with age can be approximated as linear associations (Sullivan and Pfefferbaum, 2006), and linear correlations are the simplest first step for demonstrating the effect of the orthogonal tensor decomposition. Nonetheless, as larger sample sizes are becoming increasingly available, nonlinearities of diffusion MRI metrics in adult aging can be more easily detected, as was recently shown using 3513 participants of the UK Biobank (Cox et al., 2016). Our inspection of the data used in the current study, based on a 700-subject subsample of UK Biobank participants, did not suggest significant nonlinearities (Supplementary Fig. 3), but future work should explore more complex models of age-associations of the 3 orthogonal DTI metrics, which can also include explicit modeling of sex differences.
5. Conclusion
The orthogonal diffusion tensor decomposition based on the 3 eigenvalue moments enables clear identification of degeneration patterns voxelwise across the WM, including regions of complex fiber architecture where FA exhibits low sensitivity to age. Therefore, given the ongoing ubiquity of DTI, this study demonstrates the utility of taking a few moments to fully decompose the tensor.
Supplementary Material
Acknowledgements
This research has been conducted using the UK Biobank Resource under Application Number 40922. The authors thank Lydia Sun and Amy Lin for their assistance with downloading and performing quality control on the UK Biobank data, respectively, and Drs. Cheryl Grady and David Salat for useful discussions on the manuscript. Jordan Chad was funded by the Natural Sciences and Engineering Research Council (NSERC) of Canada (Doctoral Post-graduate Scholarship). Dr. Ofer Pasternak was funded by National Institutes of Health (NIH) grant R01AG042512. Dr. Jean Chen was funded by NSERC Discovery Grant RGPIN #418443, the Canadian Institutes of Health Research (CIHR) Foundation Grant FRN #148398, and the Sandra Rotman Foundation.
Footnotes
Disclosure statement
The authors declare no actual or potential conflict of interest.
CRediT authorship contribution statement
Jordan A. Chad: Conceptualization, Investigation, Writing - review & editing. Ofer Pasternak: Conceptualization, Supervision, Writing - review & editing. J. Jean Chen: Conceptualization, Supervision, Writing - review & editing.
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.neurobiolaging.2020.12.020.
References
- Alfaro-Almagro F, Jenkinson M, Bangerter NK, Andersson JLR, Griffanti L, Douaud G, Sotiropoulos SN, Jbabdi S, Hernandez-Fernandez M, Vallee E, Vidaurre D, Webster M, McCarthy P, Rorden C, Daducci A, Alexander DC, Zhang H, Dragonu I, Matthews PM, Miller KL, Smith SM, 2018. Image processing and Quality Control for the first 10,000 brain imaging datasets from UK Biobank. Neuroimage 166, 400–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Skare S, Ashburner J, 2003. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20, 870–888. [DOI] [PubMed] [Google Scholar]
- Andersson JLR, Sotiropoulos SN, 2016. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bach M, Laun FB, Leemans A, Tax CMW, Biessels GJ, Stieltjes B, MaierHein KH, 2014. Methodological considerations on tract-based spatial statistics (TBSS). Neuroimage 100, 358–369. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D, 1994. MR diffusion tensor spectroscopy and imaging. Biophys. J. 66, 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu C, 2002. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR Biomed. 15, 435–455. [DOI] [PubMed] [Google Scholar]
- Catani M, de Schotten MT, 2012. Atlas of Human Brain Connections. OUP, Oxford. [Google Scholar]
- Chad JA, Pasternak O, Salat DH, Chen JJ, 2018. Re-examining age-related differences in white matter microstructure with free-water corrected diffusion tensor imaging. Neurobiol. Aging 71, 161–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox SR, Ritchie SJ, Tucker-Drob EM, Liewald DC, Hagenaars SP, Davies G, Wardlaw JM, Gale CR, Bastin ME, Deary IJ, 2016. Ageing and brain white matter structure in 3,513 UK Biobank participants. Nat. Commun. 7, 13629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Groot M, Cremers LGM, Ikram MA, Hofman A, Krestin GP, van der Lugt A, Niessen WJ, Vernooij MW, 2016. White matter degeneration with aging: longitudinal diffusion MR imaging analysis. Radiology 279, 532–541. [DOI] [PubMed] [Google Scholar]
- Doan NT, Engvig A, Persson K, Alnæs D, Kaufmann T, Rokicki J, CórdovaPalomera A, Moberget T, Brækhus A, Barca ML, Engedal K, Andreassen OA, Selbæk G, Westlye LT, 2017. Dissociable diffusion MRI patterns of white matter microstructure and connectivity in Alzheimer’s disease spectrum. Sci. Rep. 7, 45131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douaud G, Jbabdi S, Behrens TEJ, Menke RA, Gass A, Monsch AU, Rao A, Whitcher B, Kindlmann G, Matthews PM, Smith S, 2011. DTI measures in crossing-fibre areas: increased diffusion anisotropy reveals early white matter alteration in MCI and mild Alzheimer’s disease. Neuroimage 55, 880–890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ennis DB, Kindlmann G, 2006. Orthogonal tensor invariants and the analysis of diffusion tensor magnetic resonance images. Magn. Reson. Med. 55, 136–146. [DOI] [PubMed] [Google Scholar]
- Fischl B, 2012. Freesurfer. Neuroimage 62, 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grieve SM, Williams LM, Paul RH, Clark CR, Gordon E, 2007. Cognitive aging, executive function, and fractional anisotropy: a diffusion tensor MR imaging study. AJNR Am. J. Neuroradiol. 28, 226–235. [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S, Behrens TEJ, Smith SM, 2010. Crossing fibres in tract-based spatial statistics. Neuroimage 49, 249–256. [DOI] [PubMed] [Google Scholar]
- Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TEJ, 2012. Modelbased analysis of multishell diffusion MR data for tractography: how to get over fitting problems. Magn. Reson. Med. 68, 1846–1855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keihaninejad S, Ryan NS, Malone IB, Modat M, Cash D, Ridgway GR, Zhang H, Fox NC, Ourselin S, 2012. The importance of group-wise registration in tract based spatial statistics study of neurodegeneration: a simulation study in Alzheimer’s disease. PLoS One 7, e45996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kodiweera C, Alexander AL, Harezlak J, McAllister TW, Wu Y-C, 2016. Age effects and sex differences in human brain white matter of young to middle-aged adults: a DTI, NODDI, and q-space study. Neuroimage 128, 180–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebel C, Gee M, Camicioli R,Wieler M, Martin W, Beaulieu C, 2012. Diffusion tensor imaging ofwhitematter tract evolution over the lifespan. Neuroimage 60, 340–352. [DOI] [PubMed] [Google Scholar]
- Maclullich AMJ, Wardlaw JM, Ferguson KJ, Starr JM, Seckl JR, Deary IJ, 2004. Enlarged perivascular spaces are associated with cognitive function in healthy elderly men. J. Neurol. Neurosurg. Psychiatry 75, 1519–1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madden DJ, Bennett IJ, Burzynska A, Potter GG, Chen N-K, Song AW, 2012. Diffusion tensor imaging of cerebral white matter integrity in cognitive aging. Biochim. Biophys. Acta 1822, 386–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier-Ruge W, Ulrich J, Brühlmann M, Meier E, 1992. Age-related white matter atrophy in the human brain. Ann. N. Y. Acad. Sci. 673, 260–269. [DOI] [PubMed] [Google Scholar]
- Miller KL, Alfaro-Almagro F, Bangerter NK, Thomas DL, Yacoub E, Xu J, Bartsch AJ, Jbabdi S, Sotiropoulos SN, Andersson JLR, Griffanti L, Douaud G, Okell TW, Weale P, Dragonu I, Garratt S, Hudson S, Collins R, Jenkinson M, Matthews PM, Smith SM, 2016. Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nat. Neurosci. 19, 1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mito R, Raffelt D, Dhollander T, Vaughan DN, Tournier J-D, Salvado O, Brodtmann A, Rowe CC, Villemagne VL, Connelly A, 2018. Fibre-specific white matter reductions in Alzheimer’s disease and mild cognitive impairment. Brain. [DOI] [PubMed] [Google Scholar]
- Peters A, 2002. The effects of normal aging on myelin and nerve fibers: a review. J. Neurocytol. 31, 581–593. [DOI] [PubMed] [Google Scholar]
- Peters BD, Ikuta T, DeRosse P, John M, Burdick KE, Gruner P, Prendergast DM, Szeszko PR, Malhotra AK, 2014. Age-related differences in white matter tract microstructure are associated with cognitive performance from childhood to adulthood. Biol. Psychiatry 75, 248–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierpaoli C, Basser PJ, 1996. Toward a quantitative assessment of diffusion anisotropy. Magn. Reson. Med. 36, 893–906. [DOI] [PubMed] [Google Scholar]
- Raffelt DA, Tournier J-D, Smith RE, Vaughan DN, Jackson G, Ridgway GR, Connelly A, 2017. Investigating white matter fibre density and morphology using fixel-based analysis. Neuroimage 144, 58–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, Watkins KE, Ciccarelli O, Cader MZ, Matthews PM, Behrens TEJ, 2006. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage 31, 1487–1505. [DOI] [PubMed] [Google Scholar]
- Sonntag WE, Eckman DM, Ingraham J, Riddle DR, 2011. Regulation of cerebrovascular aging. In: Riddle DR (Ed.), Brain Aging: Models, Methods, and Mechanisms. CRC Press/Taylor & Francis, Boca Raton (FL. [Google Scholar]
- Sparkman NL, Johnson RW, 2008. Neuroinflammation associated with aging sensitizes the brain to the effects of infection or stress. Neuro-immunomodulation 15, 323–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan EV, Pfefferbaum A, 2006. Diffusion tensor imaging and aging. Neurosci. Biobehav. Rev. 30, 749–761. [DOI] [PubMed] [Google Scholar]
- Teipel SJ, Grothe MJ, Filippi M, Fellgiebel A, Dyrba M, Frisoni GB, Meindl T, Bokde ALW, Hampel H, Klöppel S, Hauenstein K, EDSD study group, 2014. Fractional anisotropy changes in Alzheimer’s disease depend on the underlying fiber tract architecture: a multiparametric DTI study using joint independent component analysis. J. Alzheimers. Dis. 41, 69–83. [DOI] [PubMed] [Google Scholar]
- Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE, 2014. Permutation inference for the general linear model. Neuroimage 92, 381–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie F, Liang P, Fu H, Zhang J-C, Chen J, 2014. Effects of normal aging on myelin sheath ultrastructures in the somatic sensorimotor system of rats. Mol. Med. Rep. 10, 459–466. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


