Application of physics-based flow models in cardiovascular medicine: Current practices and challenges

Abstract

Personalized physics-based flow models are becoming increasingly important in cardiovascular medicine. They are a powerful complement to traditional methods of clinical decision-making and offer a wealth of physiological information beyond conventional anatomic viewing using medical imaging data. These models have been used to identify key hemodynamic biomarkers, such as pressure gradient and wall shear stress, which are associated with determining the functional severity of cardiovascular diseases. Importantly, simulation-driven diagnostics can help researchers understand the complex interplay between geometric and fluid dynamic parameters, which can ultimately improve patient outcomes and treatment planning. The possibility to compute and predict diagnostic variables and hemodynamics biomarkers can therefore play a pivotal role in reducing adverse treatment outcomes and accelerate development of novel strategies for cardiovascular disease management.

I. INTRODUCTION

The last several decades have witnessed lifestyle modification and evidence-based interventions to decrease the burden of cardiovascular diseases (CVDs). Despite the success of these approaches, CVDs continue to place a large burden on the healthcare system. At present, there are 92.1 million adults in the United States suffering from some form of CVD. Therefore, CVDs continue to dominate healthcare costs and are projected to surpass 1 trillion dollars by 2035, according to the American Heart Association.^1–4 The methods for diagnosis and prevention of CVDs remain largely elusive due to the broad heterogeneity in patient profiles and clinical outcomes, which thereby necessitate deeper phenotyping of patient physiology. This gap has paved the way for personalized cardiovascular computational modeling approaches in basic and clinical cardiovascular research and practice.⁵ Such models are designed to incorporate the unique anatomy and physiology of a patient used to define model parameters, predict patient outcomes, and devise optimal treatment strategies. The initial studies incorporating blood flow simulations to derive pressure loss across an arterial vessel go back 40 years;⁶ however, due to the tremendous increase in computational power and recent developments in medical imaging there has been an exponential increase in physics-based flow models to understand the development and progression of CVDs.^7–12 In this review, we discuss the theory and application of personalized, physics-based models of cardiovascular dynamics.

The pursuit and clinical acceptance of physics-based models in cardiovascular medicine have been accelerated in part by the work found in Refs. 13–19. The underlying reason for clinical acceptance is the potential wealth of information provided by physiological flow data, in addition to the anatomic detail provided by the medical diagnostic imaging data. Patient physiology provides a powerful complement to clinical decision-making and helps to uncover the complex relationship between patient anatomy and outcome. This complex relationship has been established by several clinical studies that have demonstrated that anatomy by itself does not reveal the underlying pathophysiological mechanisms.^20–22 The evidence of this complexity was demonstrated by a sub-study of the Clinical Outcomes Utilizing Revascularization and Aggressive Drug Evaluation trial, where patients with similar lesion anatomy ( $>70\%$ stenosis—narrowing in the vessel) exhibited conflicting outcomes, such that 32% had severe ischemia and 40% had mild-to-no ischemia.^11,21 Therefore, physiology-guided interventions have been the cornerstone of modern cardiology practice. However, interventional procedures are generally invasive and expensive, which has inhibited the wide-scale use of such approaches.^11,23 Avoidance of an invasive procedure not only reduces patient discomfort but also lowers the procedural cost and saves physician time. These reasons have inspired development of physics-based models being used as a fundamental tool in cardiovascular research, justifying the efforts being made to integrate such computational methods into routine cardiovascular practice. There have been a vast number of physics-based principles of electromechanics, solid mechanics, and fluid dynamics that are being applied to study the cardiac electrophysiology, cellular mechanics, and cardiovascular dynamics. However, in this review we restrict our discussion to macroscopic (>1 mm) flow models of the cardiovascular system, and for electrophysiology and cellular mechanics, refer interested readers to the works of Roberts et al.,²⁴ Niederer et al.,²⁵ and Trayanova et al.²⁶

Physics-based models hold significant appeal because they can be used to create a physiological road map for physicians directly from diagnostic imaging data. They advance the concept of evidence-based medicine to precision medicine by tailoring interventional procedures to each individual patient instead of designing procedures for a general patient population. However, current cardiology practice lies between this continuum of personalization and generalization.^27,28 Personalization of cardiovascular models is attained by integrating patient-specific imaging data and patient clinical record data as input parameters to physics-based flow models (Fig. 1). Physics-based flow models are based on well-established governing equations of mass and momentum conservation with appropriate initial and boundary conditions. As such, there are several medical imaging modalities and physics-based models that can be used for developing computational framework to study cardiovascular flows. We will discuss both these aspects in Sec. II. Furthermore, in Sec. III, we will discuss the application of cardiovascular models in different CVDs for transforming clinical cardiology and cardiovascular research. We will then detail challenges and limitations of existing modeling approaches in Sec. IV, specifically focusing on model parameterization, accuracy, and robustness.

FIG. 1.

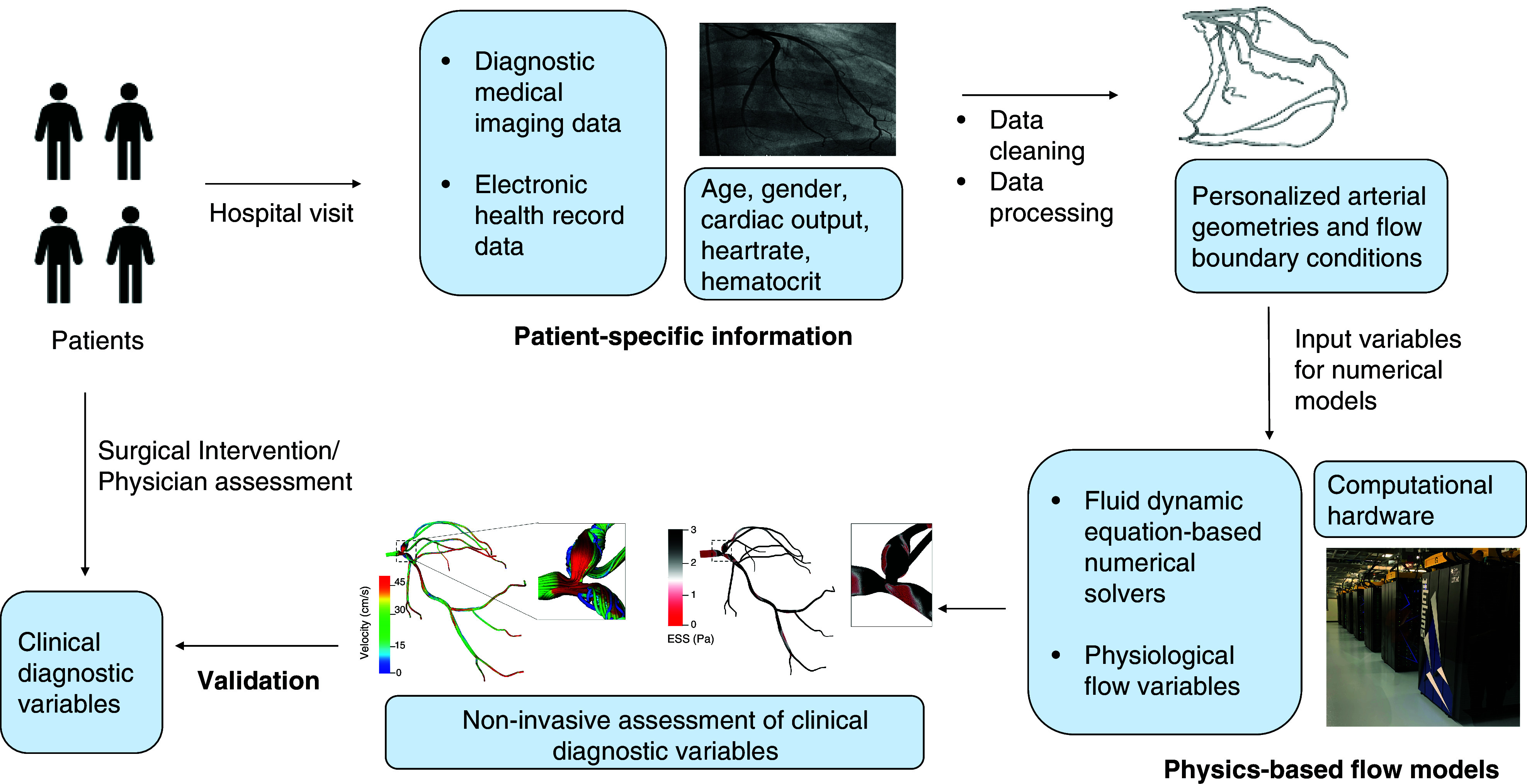
Overview of cardiovascular modeling workflow. The process involves collecting patient information, medical imaging data, and clinical records, which are then processed to reconstruct patient-specific three-dimensional geometries and derive personalized boundary and initial conditions. Subsequently, this information is used as input to numerical solvers, which then solve using mathematical equations of physics-based models using state-of-art computer hardware. Such a computational framework results in patient-specific physiological flow information, which can be used for model validation against clinical measurements.

II. CURRENT METHODS FOR PATIENT-SPECIFIC MODELING

In this section, we will cover three key areas that together make up the necessary framework required for developing cardiovascular flow models: (1) medical imaging modalities commonly used for arterial reconstruction, (2) computational methods for performing cardiovascular simulations, and (3) importance of initial and boundary conditions (Fig. 2).

FIG. 2.

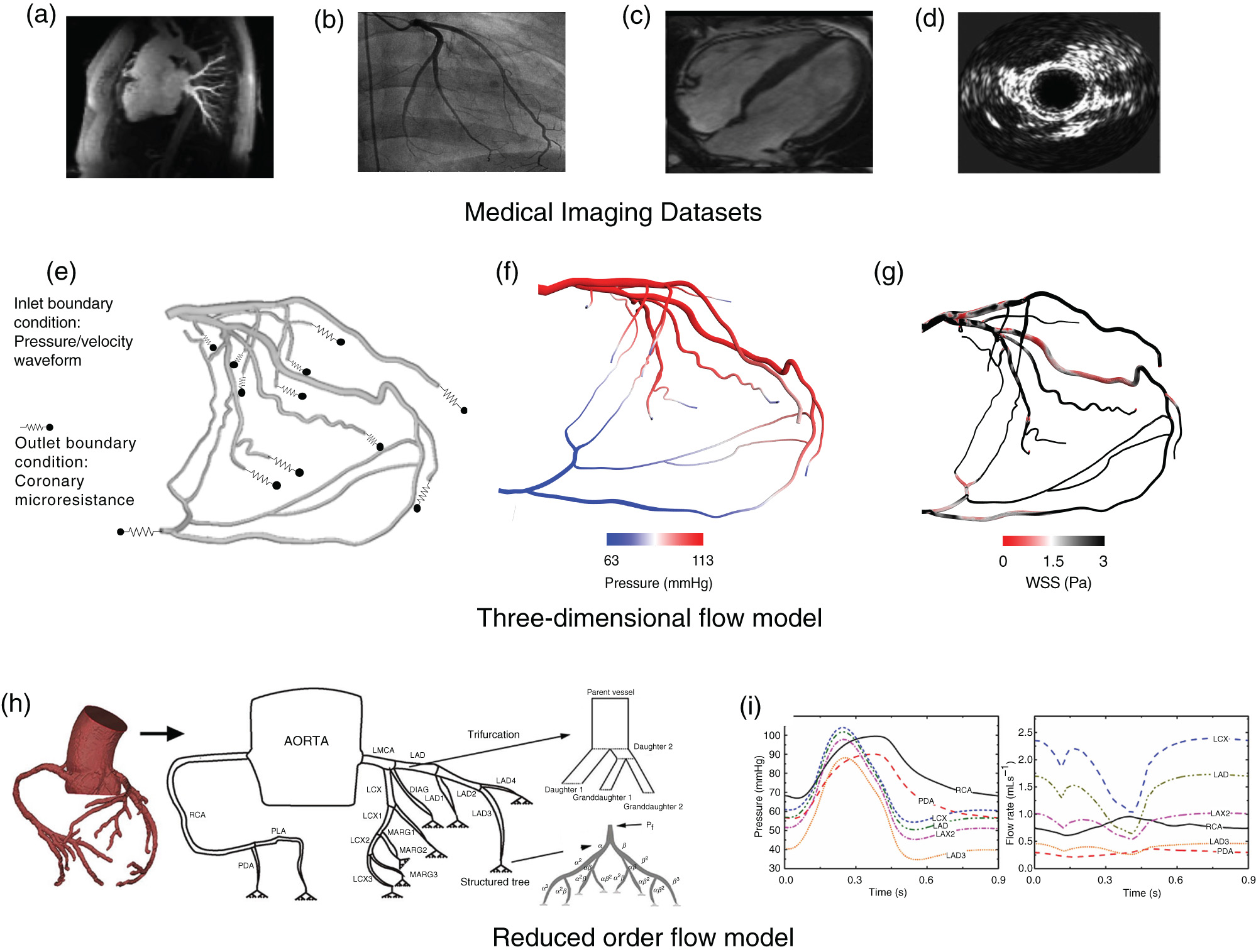
Framework for physics-based models to simulate cardiovascular flows. Top panel (a–d) depicts different medical imaging modalities commonly used in cardiovascular flow models. (a) Computed tomography angiography. (b) Coronary angiography. (c) Magnetic resonance imaging. (d) Intravascular ultrasound. Middle panel [(e)–(g)] depicts three-dimensional (3D) computational fluid dynamic model. (e) Initial conditions applied to a patient-derived 3D left coronary artery geometry. (f) 3D output data: pressure field. (g) 3D output data: wall shear stress (WSS). [(h) and (i)] depicts reduced-order flow model. (h) 3D coronary model reduced to one-dimensional coronary tree model with trifurcation and terminal branches modeled using a structured tree with feedback pressure. (i) Output data: pressure and flow rate for different coronary vessels. Panels (b) and (c) reproduced from H. Baccouche, T. Beck, M. Maunz, P. Fogarassy, and M. Beyer, Journal of Cardiovascular Magnetic Resonance 11(1), 1–4 (2009).²³⁷ Copyright 2009 Authors, licensed under a Creative Commons Attribution (CC BY) license. Panel (d) reproduced from Y. Rim, D. D. McPherson, and H. Kim, Biomedical Engineering Online 12(1), 115 (2013).²⁹ Copyright 2013 Authors, licensed under a Creative Commons Attribution (CC BY) license. Panels (h) and (i) reproduced from Z. Duanmu, W. Chen, H. Gao, X. Yang, X. Luo, and N. A. Hill, Frontiers in Physiology 10, 853 (2019).³⁰ Copyright 2019 Authors, licensed under a Creative Commons Attribution (CC BY) license.

A. Medical imaging modalities for patient-specific model reconstructions

An important driver for cardiovascular flow simulations is the medical imaging data. Advancements in the field of medical imaging have been attributed to underpin the paradigm shift that is being witnessed with respect to the increasing adoption of mechanistic descriptions of arterial hemodynamics. Furthermore, innovative extension of established diagnostic imaging techniques, such as magnetic resonance imaging (MRI), coronary angiography (CA), and computed tomography angiography (CTA), have enabled integration with numerical flow models and helped gain insight into cardiovascular biophysics that was previously unavailable [Figs. 2(a)–2(d)]. Synergistic overlap between clinical imaging techniques (CTA, MRI) and mathematical modeling (numerical solvers) has allowed researchers to interrogate arterial physiology in novel ways.^31–33

Generally, after the acquisition of medical imaging data from various diagnostic techniques, the data is processed using image segmentation software. Different regions of interest consisting of a particular anatomic feature are identified along the full stack of image data, which is followed by mesh discretization, voxel reconstruction, and three-dimensional (3D) volume rendering to create a patient-specific 3D geometry.^33,34 This process of anatomic reconstruction can be performed using various open source and commercial software packages.⁷ Since geometric reconstruction is generally the first step of computational modeling, it is also imperative to validate the accuracy of reconstructed patient geometries with experts in the respective field. As such, operator-based variations in segmentation and reconstruction can be seldom avoided and remain inherent; however, double-blinded experiments, automated segmentation approaches, and uncertainty quantification can help determine the exact nature of influence on simulation results.^35,36 In addition to the variance and validation of medical image reconstruction, two important considerations are the ease and speed of the software.³³ To this end, deep learning (DL) algorithms are gaining significant traction for medical image analysis and segmentation.^37–40 Since image segmentation is a fundamental application of machine learning (ML), improving the time needed to segment by automating the reconstruction process and alleviating user-specific judgment bias can increase the accuracy and availability of patient-specific segmentation.^37–40

With the availability of imaging data from different diagnostic techniques, there are a range of cardiovascular flow modeling studies that have used different model reconstructions derived from various imaging modalities (Table I). CTA has been a forerunner in driving cardiovascular modeling due to several important features including: non-invasiveness, high spatial-temporal resolution, perfusion assessment, and characterization of plaque development.^31,41,42 CTA-based computational methods are an excellent demonstration of an end-to-end non-invasive pipeline for diagnostic assessment of arterial physiology.^11,43–46

TABLE I.

Physics-based flow model in cardiovascular diseases. (Abbreviations listed below.^a)

Computational Framework	General Topic of Study	Reference
Imaging modality; CFD model
IVUS, CA, CT; NS	Association between wall thickness and ESS promotes atherosclerosis and can lead to ACS in vivo coronary models	19,47
IVUS and OCT; LBM	Understand the impact of the anatomy of coronary lesions on FFR using QCA and IVUS	48
IVUS, CA; NS	PROSPECT study: Predict non-culprit MACEs using plaque characteristic and low ESS	49
CTA; NS, FEA	Studying adverse conditions during TAVR	50,51
CTA, FSI (Simvascular)	CAA hemodynamics in anomalous aortic origin of the right coronary artery	52, 53
CTA; NS	Validate on-site algorithm for CCTA-FFR against invasive FFR	13–15, 43 ,54
CTA; LBM	Evaluated the diagnostic accuracy of LBM based flow solver for CT-FFR	46
CTA; NS (COMSOL)	Using simple boundary conditions to validate CCTA-FFR with invasive FFR	44
CTA; NS (Ansys Fluent)	Predictive parameters (f: viscous friction and s: expansion loss) without hyperemic conditions using idealized models and patient-specific models for initial validation and clinical validation	55
CTA; NS	Accuracy and consistency of CCTA-FFR compared to QCA-FFR in patients with stenoses in the left coronary artery relative to invasive FFR	45
CA, 3D QCA; NS	Simple boundary conditions for virtual hemodynamic assessment of coronary arteries using routine angiogram data	18
CA, 3D QCA with TIMI; NS (Fluent)	Efficient computer model to compute non-invasive FFR and determine the functional significance of intermediate lesions in obstructed coronary arteries	17
CA, VH-IVUS; NS	Examine the difference between physiology and anatomy derived from IVUS and CA	56
CA, OCT, CT; LBM, NS	Study the impact of anatomy on TAWSS and volumetric flow in coronary arteries	57–59
OCT, CA, NS and FSI	Determine the difference between the FSI and the CFD-based model in calculating local hemodynamic parameters	60, 61
OCT; NS (Ansys Fluent)	Identify vulnerable plaques using frequency-domain OCT-based ESS assessment	62
OCT; NS	Validate OCT-based noninvasive FFR against invasive FFR for intermediate lesions (40%–70% lesions)	63
MRI; NS, FSI	Biomechanics in bicuspid aortic valve	64
MRI; NS	Study hemodynamic conditions to understand aneurysm thrombosis in Kawasaki disease	65
MRI; NS	Compare CFD-derived hemodynamics from MRI and CT for realistic coronary geometries	66
4D MRI; NS	Application of blood flow imaging in predictive cardiovascular medicine	67
PC-MRI; NS	Coupled application of PC-MRI and fluid-physics model to study blood flow	68
Imaging Modality; Reduced-order model
CCTA; 1D–0D	Feasibility of using reduced-order models compared to 3D CFD methods: accuracy and computational time	69
IVUS, CCTA; 1D, 3D	Validate 1D models against 3D models in hyperemic conditions and established when properly tuned, the 1D model provides an exact match to 3D models for diagnosis	70
Idealized reconstructions; 2D, 3D	Compare 2D, semi-3D, and 3D models for FFR computation to study the influence of model order using parameterized arterial geometries	71
CCTA; 1D–0D, 3D rigid	Benchmark study comparing the diagnostic performance of four different reduced-order models and 3D CFD model	72
Open source 3D geometry; 1D multifidelity parameter inference	Predictive probabilistic model: Uncertainty quantification and Bayesian optimization for a 1D model to compute FFR in coronary artery disease	73
IVUS, CCTA; 1D–0D	Impact of flow parameters on fractional flow reserve prediction	74
Medical imaging data; 0D, 1D, 3D	Uncertainty quantification in cardiovascular hemodynamics using multilevel-multifidelity computational approaches	75
CA; LPM	Clinical assessment for the adoption of fast FFR approaches using routine angiogram data	12, 23, 76
CT; LPM	Derived FFR and compared LPM to 3D CFD data	77
CT; LPM	Accuracy of on-site CT-based FFR assessment relative to CT alone	78
Imaging modality; Machine learning approach
MRI, CT; NN	NN-based cardiovascular framework to reduce manual segmentation	79
Synthetic database CT; NN	Validate a ML model against conventional physics-based approaches	80
CT; NN	Multi-center trial to compare ML with CFD based FFR	81
CT-based virtual and real patient imaging data; Feed-forward NN	Compare three ML models of varying complexity for FFR calculation	72
Automatic Image Analysis	Interpretation of chest roentgenograms, ecetrocardiographs, angiograms, CT data and echocardiographic parameters	82–86
CT, NN	ML-based DOE study to understand the effect of physiological conditions on patient hemodynamics	87
Multilayer perceptron neural network and Gaussian conditional random fields	Calculating pro-atherogenic factors such as WSS and TAWSS to reduce computational time	88, 89
Multi-objective optimization	Optimal stent design to minimize adverse flow conditions and stent failure	90

^a Abbreviations—ACS: acute coronary syndrome; MACEs: major adverse cardiac events; FFR: fractional flow reserve; LPM: lumped parameter model; CT: computed tomography; CA: coronary angiography; CCTA: computed coronary tomography angiography; 3D QCA: three-dimensional quantitative coronary angiography; OCT: optical coherence tomography; IVUS: intravascular ultrasound; VH-IVUS: virtual histology intravascular ultrasound; MRI: magnetic resonance imaging; LBM: lattice Boltzmann method; 0D: zero dimensional; FSI: fluid-structure interaction; ML-machine learning; CFD: computational fluid dynamics; NN: neural network; 1D: one-dimensional; 2D: two-dimensional; WSS: wall shear stress; TAWSS: time-averaged wall shear stress; TIMI: thrombolysis in myocardial infarction; CAA: coronary artery anomaly; TAVR: trans aortic valve replacement.

Beyond arterial physiology, CTA also enables development of personalized ventricular models for treatment planning procedures.⁹¹

MRI is regarded as the “one-stop-shop”⁹² for the diagnostic assessment of cardiac physiology, it can provide information ranging from anatomy, perfusion, and tissue properties.^31,92 As a result, many cardiovascular studies have employed 3D geometries derived from MRI.^66–68 Additionally, phase-contrast MRI (PC-MRI) or four-dimensional (4D) MRI can provide information about flow velocity, which can be used for in vivo validation and setting initial conditions in cardiovascular simulations.^67,68,93 However, long acquisition time over several cardiac cycles, electrocardiogram gating, and risks to patients with implanted devices can affect the image resolution and the quality of flow information derived from MRI.^31,94

CA is the current gold standard for the assessment and diagnosis of coronary arteries, vessels that supply blood to the heart.^95,96 More than 1.2 million catheterizations are performed each year in the United States.⁹⁵ CA also has a higher temporal and spatial resolution than CTA.⁹⁶ Similar to CTA, 3D reconstructions from CA can be derived using commercial software packages (QFR, Angio XA 3D software, Medis Medical Imaging System bv, the Netherlands; AngioPlus, Pulse Medical Imaging Technology, Shanghai, China; CAAS Workstation, Pie Medical Imaging, Maastricht, the Netherlands) or complex mathematical reconstruction algorithms.^10,97,98 Advancements in CA with adoption of 3D quantitative CA (3D QCA) and rotational coronary angiography (RoCA) have furthermore made CA amenable for arterial reconstruction.^{17,18,97,99–101} However, when both the aorta and coronary arteries are the vascular region of interest, other imaging modalities such as CTA or cardiac magnetic resonance (CMR) are more commonly used. Additionally, when just the coronary arteries are segmented using CA, the inlet boundary conditions, e.g., coronary flow velocity may require the need of clinical techniques, such as Doppler velocity calculation, or a literature-derived rather than patient-specific boundary condition. In contrast, CTA can be used to directly estimate coronary blood flow using transluminal attenuation flow encoding.¹⁰²

Intravascular ultrasound (IVUS) and optical coherence tomography (OCT) are also common imaging modalities that have been employed in computational cardiology.^{47,48,56,62,63,103,104,240} IVUS has been used for reliably detecting plaque compositions, but due to the low spatial resolution (150 μm), it cannot provide a detailed anatomic view of stented vessel segments and micro-calcification.^105,106 OCT overcomes these limitations by using light waves instead of mechanical waves (employed in IVUS) and can accurately detect plaque formation and atherosclerosis in vessel segments at very high resolutions (15 μm).^107–109 However, OCT suffers from poor signal penetration and therefore cannot be used for visualizing entire arterial wall.^107–109 Recently, IVUS-OCT based multimodality approaches are being proposed for calculating patient-specific coronary cap thickness and stress/strain calculations with greater accuracy.^110,111

With several state-of-art medical imaging modalities, we note that the choice of imaging technique used for geometric reconstruction depends on the research question being interrogated by a specific study, physical scale of the anatomic feature being investigated, and the availability of the data. As such, for characterization of plaque microstructures, OCT is a suitable choice, whereas for vessel segments, such as coronary arteries, CA and CTA and would be more appropriate.¹⁰⁷ Due to the wider availability of CA data, CA can be the imaging technique of choice to conduct large-scale retrospective population-based studies.⁹⁵ MRI and CTA can be useful for understanding the whole anatomy of the heart, major vessels, ventricle function, and aortic diseases.^109,112 Finally, PC-MRI or 4D MRI can be used for direct evaluation of hemodynamics by determining the velocity field in all directions of the gradient magnetic field.^109,112

B. Computational methods for cardiovascular simulations

Medical imaging data provides anatomic information, but does not reveal the underlying patient physiology. Anatomy-physiology relationships are complex and to gain insight into the physiological landscape flow metrics, such as pressure and velocity, are needed. Numerical models can be used to compute these metrics using cardiovascular form-function relationships.^11,41,113 Such relationships can be mathematically defined using governing equations of fluid dynamics applied to the anatomic information attained in the form of 3D patient-specific geometries.^11,41,113 As such, one of the initial implementations of such a relationship is Murray's law, which establishes the mathematical relationship between vessel size and flow $Q\propto d^k$, where Q is the flow rate through a blood vessel, d is its diameter, and k is a constant. This relationship is further exemplified by Poiseuille's equation, which relates vessel flow rate, Q; vessel diameter, d; fluid viscosity, μ; and wall shear stress (WSS), τ_w, with the following equation:¹¹

$$Q=\frac{\pi }{32\mu }{\tau }_w{d}^3.$$ (1)

WSS can be computed as

$${\tau }_w=\frac{r\Delta p}{2\ell },$$ (2)

where r is radius of the vessel, $\ell$ is the length of the vessel, and $\Delta P$ is pressure gradient.¹¹⁴

Another important relationship is that of pressure, p, and flow rate, Q, to determine the resistance, R, of flow,¹¹⁵

$$p=QR.$$ (3)

The physiological behavior of arterial vessels in the cardiovascular system can be recovered through the application of these equations [Eqs. (1) and (2)]. For example, the inverse relationship between Q and R implies that vessels with smaller diameters offer larger resistances to flow. The physiological flow variables of pressure and velocity can be derived from solving the 3D Navier-Stokes (NS) equations, which are the governing equations of fluid dynamics. The NS equations account for conservation of mass and momentum [Eq. (4)],

$$\begin{array}{c}\nabla ·\mathit{v}=0,\\ \rho \frac{D\mathit{v}}{Dt}=-\nabla P+\mu {\nabla }^2\mathit{v}+f.\end{array}$$ (4)

In these equations, $v$ is velocity, ρ is density, μ is viscosity, pressure is P, and f is the force term.

It is important to note the powerful nature of NS equations, which can be applied to a range of fluid dynamic applications ranging from aerodynamic to biological flows. The NS equations are non-linear partial differential equations that cannot be analytically solved for a realistic complex patient-specific geometry. Therefore, numerical methods are needed to solve the NS equations and these collectively form the specialist field of mathematics and physics, commonly called computational fluid dynamics (CFD). Besides pressure and velocity, additional flow variables, WSS, oscillatory shear index (OSI), and vorticity can also be derived from 3D CFD solvers [Figs. 2(e)–2(i)]. OSI characterizes whether the WSS vector is aligned with the time-averaged wall sheer stress (TAWSS) vector during the phase of a cardiac cycle, and vorticity is the magnitude of the curl of the velocity vector.^116–118 Generally, incompressible NS equations are solved for hemodynamic simulations.^9,41 Table I lists different cardiovascular studies that use CFD solvers based on the NS equations. In these studies, a common assumption in cardiovascular flow simulation is that the blood is modeled as Newtonian fluid.^41,58,99 This assumption is valid for larger arteries, such as the aorta and coronary arteries; however, in smaller vessels the shear rates necessitate a non-Newtonian description.^7,119 An alternate to traditional numerical discretization schemes for NS solvers, such as finite difference and finite volume methods, is the lattice Boltzmann method (LBM)^{114,120–123} LBM is becoming increasingly popular, as it can handle complex geometries and scales efficiently on parallel architectures due to the low communication to computation ratio.^{46,48,124–127} Instead of solving directly for velocity and pressure, in the LBM, fluid is described by a particle distribution function $f_i(x,t)$, which represents the density of particles at grid point, x, and time, t, traveling with discrete velocity, ${\mathit{c}}_{\mathit{i}}$,

$$f_i(\mathit{x}+{\mathit{c}}_{\mathit{i}},t+1)-f_i(\mathit{x},t)=-\Omega (f_i(\mathit{x},t)-f_i^{eq}(\mathit{x},t)).$$ (5)

$f_i^{eq}$ denotes that equilibrium distribution function, and Ω denotes the collision operator.^114,128 The left-hand side of Eq. (5) is the non-local streaming step where particles propagate to their nearest neighbors, and the right-hand side of Eq. (5) is the local collision step, which is non-linear and where particles relax to their equilibrium state based on the local equilibrium distribution rule.¹¹⁴

The non-linearity and complexity of solving the NS equations in 3D using either finite difference or the LBM schemes pose extraordinary computational demands, and typically to meet those demands, high performance computing (HPC) and modern computer hardware are required. As an alternative, researchers have also investigated the use of reduced-order blood flow models, which simplify the spatial dimensions of the underlying governing equations [(Figs. 2(j) and 2(k)].^129,130 Table I lists several studies that rely on reduced-order models. One-dimensional (1D) model and 0-dimensional [0D or lumped parameter models (LPM)] are commonly used in cardiovascular studies.^{12,23,69–74,76} Similar to NS equations, the governing equations for 1D blood flow consist of conservation of mass [Eq. (6)] and momentum [Eq. (7)], and are derived by integrating the 3D Newtonian and incompressible NS equations over a cross-sectional area,^131–134

$$\frac{\partial A}{\partial t}+\frac{\partial Q}{\partial x}=0,$$ (6)

$$\frac{\partial Q}{\partial t}+\frac{\partial }{\partial x}\left(\alpha \frac{Q^2}{A}\right)+\frac{A}{\rho }\frac{\partial P}{\partial x}=-C_f\frac{Q}{A}.$$ (7)

In Eqs. (6) and (7), A is the cross-sectional area, Q is the flow rate, P is the pressure, and ρ is the density of blood. The term $C_f=$ represents friction with dynamic viscosity, ν, and α represents the velocity profile.^131–134 Finally, to establish the relationship between P and A, Eq. (8) is commonly used,^135,136

$$P=P_{\mathit{ext}}+\beta (\sqrt{A}-\sqrt{A_0}),\hspace{1em}\beta =\frac{\sqrt{\pi }Eh}{(1-{\eta }^2)A_0}.$$ (8)

Here, P_ext is the external pressure on the blood vessels, A₀ is the cross-sectional area of the segment when $P=P_{\mathit{ext}}$, β is a vessel stiffness parameter determined by elastic modulus, E; vessel wall thickness, h; and Poisson's ratio, η.^135,136

Similar to 1D models, LPMs (or 0D models) are also used to perform patient-specific cardiovascular simulations.^12,23,70 The essential difference between 1D and 0D models is the limiting assumption in 0D models that wave propagation is not incorporated, which is an important component of cardiovascular flows.¹³⁷ Several works have extensively compared reduced-order models (1D models or 0D models) and traditional 3D CFD approaches.^70,137–140 1D models capture pressure and flow wave propagation along the axial direction.¹³⁶ 0D models treat the arterial network as an electrical circuit and the vessel segments as resistors.²³ This reduction in spatial dimensions lowers the degrees of freedom significantly, enabling fast computation in minutes on a single computer core.^{9,132,133,138} However, the dimensional reduction also results in loss of important hemodynamics flow variables such as WSS, velocity profile, vorticity, and OSI.^116–118 Therefore, there exists a trade-off between the use of 3D models and reduced-order models. As such, to capture local flow features and high-fidelity physics, 3D models would be more suitable, although they come with significant computational cost.^116,124

Alongside an increased use of 3D CFD models and reduced-order models, machine-learning approaches, specifically deep-learning (DL) algorithms, are gaining traction within cardiovascular medicine.^{72,79,81–86} Broadly, the application of ML algorithms can be described in three domains: (1) image-based interpretation/segmentation, (2) electronic health record (EHR) data using natural language processing (NLPs), and (3) predicting flow features. We discussed ML application for image-based interpretation/segmentation in Sec. II B. Due to the diverse literature on the application of ML methods, such as use of NLPs in clinical notes and EHR data, the interested reader is referred to some recent reviews.^141–143 In this review, we focus on studies relying on ML algorithms to predict physiological flow variables that have been traditionally derived from 3D CFD solvers and play an important role in the progression of cardiovascular disease.

Trans-stenotic pressure gradient, WSS, and OSI are examples of flow variables being predicted. A recent CFD study combined machine learning and design of experiment methodologies to investigate the effect of physiological conditions (such as flow rate and hematocrit) on patient hemodynamics.⁸⁷ Another study with the goal to reduce computational time needed for performing 3D CFD simulations used multilayer perceptron and Gaussian conditional random fields to calculate pro-atherogenic factors, such as WSS and TAWSS.^88,90 Furthermore, few works have applied ML-based multi-objective optimization in treatment planning of CVDs, for example, to determine optimal stent design [a stent is an expandable tube-like structure used for treating a stenosed (narrowed) vessel] that can minimize adverse flow conditions and stent failure.⁹⁰ ML methods, such as neural networks, have also been applied to compute global hemodynamic-based diagnostic metrics, such as trans-stenotic pressure gradient, using synthetic datasets and validated on real patient imaging datasets.^72,80,81 Such studies underscore that there is an expanding body of literature in ML applied to cardiovascular flow modeling. While these techniques require further refinement and validation by conducting large prospective and retrospective clinical evaluations, they show promising results for a future role in accelerating CVD modeling research.

C. The importance of boundary conditions

Computational simulations of the entire human cardiovascular network is time-intensive and poses formidable computational demand. To address this challenge, simulations are performed only on specific regions of the cardiovascular system such as, aorta, carotid, or coronary arteries.^93,144–146 As the human cardiovascular system is a closed loop system, the effect of excluded portions of the cardiovascular network can be modeled by applying appropriate boundary conditions (BC) at the open boundaries: inlets and outlets.^93,144,145 Accurate application of BC is important to precisely model the cardiovascular network outside of the simulated domain, therefore, BC bridge the global vascular circulation with the local 3D domain.^147,148 Furthermore, the choice of BC has a direct impact on how accurately in vivo hemodynamics can be captured by CFD models because local fluid dynamic conditions are determined based on conditions upstream and downstream of the simulated 3D domain.^41,57,58,145 Several studies have demonstrated the importance of realistic BCs by evaluating quantitative differences in the flow parameters and velocity fields.^145,149,150

In cardiovascular simulations, boundary conditions at the vascular walls are generally implemented with the no-slip or zero-velocity boundary conditions.^11,144,145 However, the choice for open boundaries (inlet and outlet) is not trivial.^93,144,149 Several works have investigated the role of different inlet and outlet BC in cardiovascular flow models.^149–151 Generally, inlet boundary conditions are prescribed by using a pressure or flow waveform in pulsatile simulations, or fixed velocity or pressure measurements for steady flow simulations.¹⁴⁹ If the waveform is directly applied at the inlet of a vessel segment, such an implementation is called open loop configuration, and with this implementation the effects of global circulation cannot be recovered.¹⁴⁴

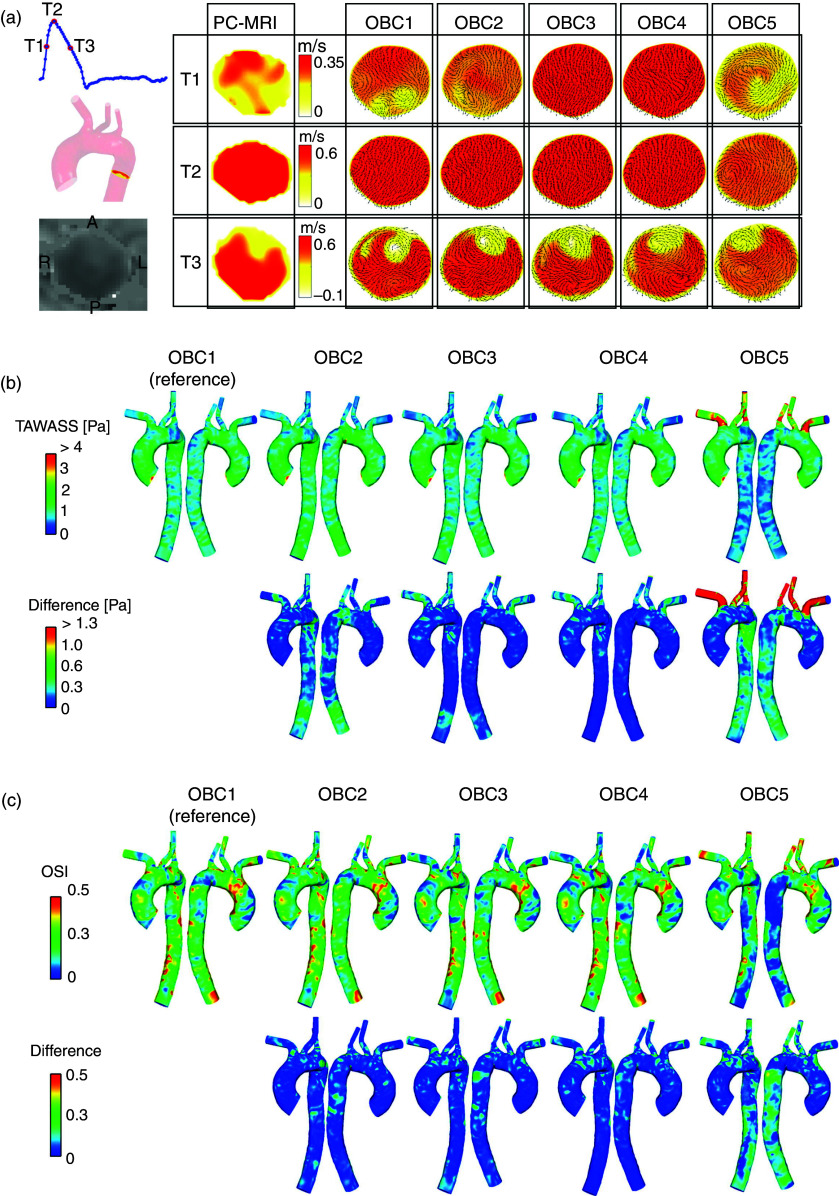
In the case of outlet BCs, several choices exist. Zero-traction or zero-pressure BC have the simplest numerical implementation and can be applied at the boundaries. However, they cannot capture physiologic levels of pressure and are therefore not amenable for patient-specific cardiovascular simulations.¹⁴⁴ A more sophisticated approach for outlet BC is using the Windkessel circuit, which connects the 3D NS simulation domain to LPM. The LPM can be explained as an electrical circuit such that the pressure can be modeled with resistors, vessel deformation with capacitors, and inertial flow using inductors.¹⁴⁶ A Windkessel circuit is comprised of two resistors and a capacitor, which correspond to proximal and distal pressure drop and distal vessel compliance, respectively.¹⁴⁵ A study by Pirola et al.⁹³ compared five different implementations of boundary conditions, including Windkessel and pressure BC, in aortic circulation. This study evaluated the differences in flow distributions and WSS arising from five different outlet BC (OBC) types compared to PC-MRI data for aortic flow (Fig. 3). The five different OBCs were implemented as follows: Windkessel model at ascending and descending aorta (OBC 1), Windkessel model at ascending aorta and flow waveform at descending aorta (OBC 2), flow waveform at ascending aorta and pressure waveform at descending aorta (OBC 3), flow waveform at ascending aorta and zero pressure at descending aorta (OBC 4), and zero pressure at ascending aorta and descending aorta (OBC 5). The findings of this study suggested that the Windkessel model was in good agreement with in vivo PC-MRI flow data and recovered physiological pressure waveforms. On the other hand, zero-pressure outlet BCs should generally be avoided in cardiovascular flow models if the goal is to predict physiologically relevant flow and pressure features, reinforcing the need for careful examination of BCs.^93,144

FIG. 3.

Suitability of boundary conditions in aortic flow. (a) Comparing axial velocity along the descending aorta using phase contrast magnetic resonance imaging (represented by the slice location in the aorta) data. Comparisons were made at different point of the cardiac cycle: T1—mid-systolic (T1, top row), T2—peak systole (T2, middle row), and T3—mid-systolic deceleration (T3, bottom row). (b) Top panel—Time-averaged wall shear stress (TAWSS) results obtained with the five sets of outlet boundary conditions (OBCs). Bottom panel—local absolute differences in TAWSS compared to results obtained with OBC1. (c) Top panel—Oscillatory shear index (OSI) results obtained with the five sets of OBCs. Bottom panel—local absolute differences in OSI compared to results obtained with OBC1. Panels (a), (b), and (c) reproduced with permission from Pirola et al., J. Biomech 60, 15–21 (2017). Copyright 2017 Elsevier.

III. TRANSLATING PHYSIOLOGICAL FLOW DATA INTO CLINICAL READOUTS

Personalized computational models can be used as a complementary tool to improve the understanding of complex biomechanical behaviors in several cardiovascular diseases. Modeling approaches described in Sec. II B can compute intravascular hemodynamic forces at spatiotemporal resolutions that have been intractable for even modern day clinical diagnostic methodologies.⁹

These investigations are of paramount importance to push the boundaries of cardiovascular research and drive novel insights into disease pathologies and treatment planning because the remodeling of the vascular system is inherently regulated by mechanical loads and hemodynamic forces.⁷ One such important metric is WSS, which is a pro-atherogenic risk factor that has been demonstrated to play a role in stent thrombosis and restenosis.^116,152,153 Deriving WSS clinically can be difficult and invasive without specialized imaging techniques.¹⁵⁴

3D CFD models can compute spatial maps of WSS across the arterial geometry reconstructed from patient images.^{56,57,153,155} In addition, physical quantities that are routinely used in clinics, such as pressure and volumetric flow fields, can also be computed from CFD models.^57,59,76 For deriving WSS there do not exist direct clinical techniques such as invasive pressure wire, which underscores the importance to validate such flow-based models. Typically, the accuracy of CFD applications is established by comparing results to flow simulations where analytic results, such as Womersley and Dean flows can be computed using the incompressible NS equations. Such analytical comparisons are unfeasible for vascular geometries because flow through these structures needs to be resolved through complex narrow branches. Therefore, it is important for studies reporting WSS in vascular geometries to validate either using in vitro experiments or 4D MRI measurements.

Validated CFD models of the cardiovascular system have established the direct influence of hemodynamic forces on the development of atherosclerosis and disease progression.^153,156 Several clinical trials demonstrate the usefulness of physics-based modeling approaches for understanding and improving diagnosis and treatment of several different types of CVDs (Table II). In Secs. III A–III C, we will discuss the application of computational models spanning from development of new devices to routine clinical decision-making in different cardiovascular disease areas, specifically coronary disease, aortic diseases, and congenital heart diseases.

TABLE II.

Clinical trials based on cardiovascular flow models in aortic diseases, congenital heart diseases, and coronary artery diseases. (Abbreviations and sources listed below.^a)

Conditions	Study Title	Interventions
Coronary Artery Disease	HeartFlowNXT - HeartFlow Analysis of Coronary Blood Flow Using Coronary CT Angiography	Procedure: ICA (Invasive Coronary Angiography); Procedure: FFR (Fractional Flow Reserve); Procedure: cCTA (coronary computed tomography angiography); Other: FFRct Analysis (Fractional Flow Reserve Computed Tomography)
Coronary Artery Stenosis	Validation of Stenosis Assessment by Coronary Artery Computed Tomography Against Invasive Measurements of Fractional Flow Reserve in Patients With Significant Coronary Artery Stenoses	Procedure: FFR, IVUS, VH, or combination of the three
Abdominal Aortic Aneurysm	Development of Novel Imaging Markers Predicting the Progression of Abdominal Aortic Aneurysm Using 3D Computed Tomography
Abdominal Aortic Aneurysm	Measurement of Maximum Diameter of Native Abdominal Aortic Aneurysm by Angio-CT	Other: Angio-CT
Aortic Aneurysm	Patient Specific Biomechanical Modeling of Abdominal Aortic Aneurysm to Improve Aortic Endovascular Repair	Other: Biomechanical computer program
Endograft Implantation to Repair Abdominal Aortic Aneurysm	Contrast Enhanced Ultrasound vs Computed Tomographic Angiography in the Detection of Endoleaks Following AAA Repair	Procedure: Contrast Enhanced Ultrasound (Contrast Agent: OptisonTM)
Abdominal Aortic Aneurysms	Validation of Fenestrations Positioning by Numerical Simulation	Other: numerical simulation
Aortic Aneurysm, Abdominal	Enhanced Guidance for Endovascular Repair of Abdominal Aortic Aneurysm	Other: Validation of the new elastic registration software; Other: Validation of the new rigid registration software
Aortic Arch Aneurysm	Simulation of Stent-graft Deployment in Aortic Arch Aneurysms	Other: Collection of data
Acute Coronary Syndrome, Plaque, Atherosclerotic	Prediction of Vulnerable Plaque Using Coronary CT Angiography and Computational Fluid Dynamic in Acute Coronary Syndrome
Acute Coronary Syndrome, Myocardial Infarction, Plaque, Atherosclerotic, Rupture, Spontaneous	Exploring the Mechanism of Plaque Rupture in Acute Coronary Syndrome Using Coronary CT Angiography and Computational Fluid Dynamic	Diagnostic Test: Coronary CT angiography
Acute Myocardial Infarction, Unstable Angina	Exploring the Mechanism of Plaque Rupture in Acute Coronary Syndrome Using Coronary CT Angiography and Computational Fluid Dynamics II (EMERALD II) Study	Procedure: Computed Tomographic Angiography
Coronary Stenosis, Acute Coronary Syndrome, Acute Myocardial Infarction	Coronary Plaque Geometry and Acute Coronary Syndromes	Diagnostic Test: CCTA
Myocardial Infarction, Acute Coronary Syndrome,	The Supplementary Role of Non-invasive Imaging to Routine Clinical Practice in Suspected Non-ST-elevation Myocardial Infarction	Other: Cardiovascular Magnetic Resonance Imaging; Other: Computed Tomography Angiography
Coronary Artery Disease, Acute Coronary Syndrome, Acute Myocardial Infarction	The Value of CT-FFR Compared to CCTA or CCTA and Stress MPI in Low to Intermediate Risk ED Patients With Toshiba CT-FFR	Device: Toshiba CT-FFR
Coronary Disease	Prospective Evaluation of Myocardial Perfusion Computed Tomography Trial	Device: computed tomography perfusion guided treatment; Device: Fractional flow reserve guided treatment
Coronary Artery Disease	CT Coronary Angiography and Computational Fluid Dynamics	Device: CT coronary angiography and computational fluid dynamics
Coronary Artery Disease	Stress Testing Compared to Coronary Computed Tomographic Angiography in Patients With Suspected Coronary Artery Disease	Other: Stress MPI SPECT; Other: Coronary CTA
Coronary Artery Disease	Determination of Fractional Flow Reserve by Anatomic Computed Tomographic Angiography	Device: FFR
Coronary Disease	Diagnostic Accuracy of CT-FFR Compared to Invasive Coronary Angiography With Fractional Flow Reserve	Diagnostic Test: CT-FFR; Diagnostic Test: Stress echocardiography
Cardiovascular Diseases	Computed Tomography Coronary Angiography for the Prevention of Myocardial Infarction (The SCOT-HEART 2 Trial)	Diagnostic Test: Computed tomography coronary angiography; Other: ASSIGN Score
Congenital Heart Disease; Atherosclerosis; Myocardial Ischemia	Cardiovascular Disease Screening	Device: Toshiba Aquilion ONE CT; Device: Swiemens MRI scanner
Cardiovascular Abnormalities	Heartflow (AFFECTS)	Procedure: FFRct and SPECT
Multivessel Coronary Artery Disease	A Multicentre, Pilot Study to Evaluate the Safety and the Feasibility of Planning and Execution of Surgical Revascularization in Patients With Complex Coronary Artery Disease, Based Solely on MSCT Imaging Utilizing GE Healthcare Revolution CT and HeartFlow FFRCT	Radiation: Multi-sliced computed tomography (MSCT)
Coronary Artery Disease; Atherosclerosis	Determination of Instantaneous Wave-Free Ratio by Computed Tomography	Device: PressureWireTM Certus (St. Jude Medical Systems, Sweden)
Atherosclerosis; Coronary Artery Disease; Acute Coronary Syndrome	Imaging and Biomarkers of Atherosclerosis in Patients With Stable or Unstable Coronary Artery Disease	Device: Coronary intervention using IVUS-VH & FDG PET-MDCT
Aortic Valve Stenosis; Coronary Artery Disease	Evaluation of Fractional Flow Reserve Calculated by Computed Tomography Coronary Angiography in Patients Undergoing TAVR	Device: iFR / FFR measurement
Coronary Artery Disease	Augmented-Reality CTA Plus Angiography vs Angiography Alone for Guiding PCI in Coronary Lesions - Randomized Study	Procedure: Angiographic guided PCI; Procedure: Augmented-Reality CTA guided PCI
Coronary Artery Disease; Coronary Atherosclerosis; Stress Testing	CT-FIRST: Cardiac Computed Tomography Versus Stress Imaging for Initial Risk Stratification	Procedure: Cardiac CT Angiography; Procedure: Stress Imaging Test (Stress Myocardial Perfusion Study or Stress Echocardiogram)
Coronary Artery Disease	Ultra-high-resolution CT vs Conventional Angiography for Detecting Coronary Heart Disease	Diagnostic Test: CT angiography; Diagnostic Test: Invasive coronary angiography
Coronary Artery Disease	Virtual Coronary Physiology: An Angiogram Is All You Need	Procedure: Percutaneous Coronary Intervention
Coronary Artery Disease	One-Dimensional Mathematical Model-Based Automated Assessment of Fractional Flow Reserve	Device: FFR
Coronary Artery Stenosis	Validation of Stenosis Assessment by Coronary Artery Computed Tomography Against Invasive Measurements of Fractional Flow Reserve in Patients With Significant Coronary Artery Stenoses	Procedure: FFR, IVUS, VH, or combination of the three
Coronary Occlusion	Validation of Quantitative Flow Ratio (QFR) - Derived Virtual Angioplasty	Diagnostic Test: Quantitative Flow Ratio (QFR) measurement
Non ST Elevation Myocardial Infarction	Non-invasive and Invasive Plaque Characterisation	Device: Imaging
ST Segment Elevation Myocardial Infarction	Early Assessment of QFR in STEMI-II	Diagnostic Test: Computation of quantitative flow ratio
Coronary Stenosis	Comparison of Optical Coherence Tomography-derived Minimal Lumen Area, Invasive Fractional Flow Reserve and FFRCT	Diagnostic Test: OCT, FFR, CTA and FFRCT
Coronary Artery Disease	The Computed Tomography-derived Fractional Flow Reserve STAT Trial	Diagnostic Test: CTFFR-Guided Group Management; Diagnostic Test: SOC Group Management
Aortic Aneurysm, Abdominal	Follow-up of Endovascular Aneurysm Treatment - The FEAT Trial	Procedure: Computed Tomography Angiography; Procedure: Magnetic Resonance Angiography
Pulmonary Embolism; Coronary Artery Disease; Aortic Aneurysm	Computed Tomography Dose Reduction Using Sequential or Fast Pitch Spiral Technique
Aortic Aneurysm	Dynamic Computed Tomography Angiography (CTA) Follow-up for EndoVascular Aortic Replacement (EVAR)
Aortic Diseases; Thoracic Aortic Aneurysm; Aortic Dissection	Biomechanical Reappraisal of Planning for Thoracic Endovascular Aortic Repair	Diagnostic Test: TEVAR patients
Endovascular Repair of Abdominal Aortic Aneurysm	Computed Tomography Scan Versus Color Duplex Ultrasound for Surveillance of Endovascular Repair of Abdominal Aortic Aneurysm. A Prospective Multicenter Study	Procedure: Computed tomography scan versus color duplex ultrasound
Endovascular Abdominal Aortic Aneurysm Repair	Contrast Ultrasound in the Surveillance of Endovascular Abdominal Aortic Aneurysm Repair
Congenital Heart Disease; Pulmonary Hypertension	Integrated Computational Modeling of Right Heart Mechanics and Blood Flow Dynamics in Congenital Heart Disease	Procedure: Cardiac Magnetic Resonance - MRI; Other: Cardiopulmonary Exercise Test; Other: Blood Sampling for all participants
Pulmonary Hypertension; Congenital Heart Disease; Pediatric Congenital Heart Disease	Image-based Multi-scale Modeling Framework of the Cardiopulmonary System: Longitudinal Calibration and Assessment of Therapies in Pediatric Pulmonary Hypertension	Procedure: cardiac catheterization; Radiation: Cardiac MRI
Coronary Disease	Prospective Evaluation of Myocardial Perfusion Computed Tomography Trial	Device: computed tomography perfusion guided treatment; Device: Fractional flow reserve guided treatment
Coronary Artery Disease	Computed Tomography as the First-Choice Diagnostics in High Pre-Test Probability of Coronary Artery Disease	Other: Cardiac CT as the first diagnostic modality in suspected CAD; Other: Invasive coronary angiography as indicated by the guidelines
Aortic Aneurysm	Evaluation of Aortic Aneurysms With Focus on Wall Stress and Wall Rupture Risk	Other: CT-acquisition
Thoracic Aortic Aneurysm	The Cardiovascular Remodeling Following Endovascular Aortic Repair (CORE) Study	Other: TEVAR; Other: Non-TEVAR medical treatment
Abdominal Aortic Aneurysm	Control Post Endovascular Treatment of Aortic Aneurisms Through Magnetic Resonance and Ultrasound (SAFEVAR)	Radiation: CT with contrast agent; Diagnostic Test: MR without contrast agent; Diagnostic Test: Color-Doppler Ultrasound; Other: Questionnaire
Radiation Burn; Aortic Aneurysm, Abdominal	Evaluation of 3D Rotational Angiography After EVAR	Radiation: 3D rotational angiography (3DRA)
Aortic Valve Stenosis	Added Value of Patient-specific Computer Simulation in Transcatheter Aortic Valve Implantation (TAVI)	Other: Computer simulation
Cardiovascular Modeling; Aortic Coarctation; Aortic Valve Disease; Cardiovascular MRI	Proof of Concept of Model Based Cardiovascular Prediction	Procedure: Surgery or Treatment by Heart Catheter
Cardiac Ischemia; Coronary Artery Disease; Coronary Stenosis	Radiographic Imaging Validation and Evaluation for Angio iFR (ReVEAL iFR)	Diagnostic Test: iFR
Hypotension and Shock	Physiological Validation of Current Machine Learning Models for Hemodynamic Instability in Humans	Other: Assigned Interventions
Coronary Microvascular Disease; Artificial Intelligence; Cardiovascular Diseases; Heart Failure	Artificial Intelligence With Deep Learning on Coronary Microvascular Disease
Hypotension and Shock	Measurement of Hemodynamic Responses to Lower Body Negative Pressure	Other: Lower body negative pressure
Coronary Heart Disease; Coronary Artery Diseases	Machine Learning Based CT Angiography Derived FFR: A Multi-center, Registry
Atherosclerosis	Hemodynamic Change of Coronary Atherosclerotic Plaque After Evolocumab Treatment
Coronary Artery Disease	Can We Predict Coronary Resistance By Eye Examination ? (COREYE)	Other: OCTA (angiography by tomography in optical coherence)
Coronary Disease	International Post PCI FFR Registry	Device: Percutaneous coronary intervention
Atherosclerosis, Coronary	Fluid-dynamics in Bifurcation PCI	Procedure: Coronary angiography and optical coherence tomography
Coronary Stenosis	Validation of a Predictive Model of Coronary Fractional Flow Reserve in Patients With Intermediate Coronary Stenosis	Diagnostic Test: Fractional Flow Reserve
Aortic Valve Stenosis; Heart Valve Diseases	Assessments of Thrombus Formation in TAVI
Coronary Artery Disease	Improvement Assessment of Coronary Flow Dysfunction Using Fundamental Fluid Dynamics	Procedure: Cardiac PET, Coronary catheterization
Coronary Artery Disease	Non-invasive Fractional Flow Reserve CT (FFRCT) Scan for the Study of Coronary Vaso-motion
Coronary Artery Disease	Effect of FFRCT-angio in Functional Diagnosis of Coronary Artery Stenosis	Diagnostic Test: FFRCT-angio
Angina Pectoris; Coronary Stenosis	Evaluation of the Correlation Between the Coronary Stenosis Degree With FFRCT and the Grade of Stable Angina Pectoris	Radiation: Computed tomographic angiography of coronary artery
Coronary Artery Disease	The PLATFORM Study: Prospective Longitudinal Trial of FFRct: Outcome and Resource Impacts
Coronary Artery Disease	FFRangio Accuracy vs Standard FFR	Device: FFRangio
Multi Vessel Coronary Artery Disease	Angiogram Based Fractional Flow Reserve in Patients With Multi-Vessel Disease	Device: FFRangio
Left Main Coronary Artery Disease; Coronary Arteriosclerosis	Registry on Left Main Coronary Artery Bifurcation Percutaneous Intervention	Procedure: PCI on left main
Acute Coronary Syndrome	FFR-CT to Detect the Absence of Hemodynamically Significant Lesions in Patients With High-risk Acute Coronary Syndrome	Diagnostic Test: FFR-CT; Diagnostic Test: FFRangioTM
Coronary Stenosis	The Sensitivity and Specificity of CardioSimFFRct Analysis Software on Coronary Artery Stenosis	Diagnostic Test: FFR and FFRCT
Coronary Vessel Anomalies	Physiologic Evaluation of Anomalous Right Coronary Artery Stenosis	Procedure: revascularization

^a Abbreviations—FFR: fractional flow reserve; CT: computed tomography; ICA: invasive coronary angiography; STEMI: ST elevation myocardial infarction; 3DRA: three-dimensional rotational angiography; iFR: instantaneous wave free ratio; AR: augmented reality; TAVI: transcatheter aortic valve replacement; PET: positron emission tomography; SPECT: single photon emission computed tomography; OCT: optical coherence tomography; IVUS: intravascular ultrasound; TEVAR: thoracic endovascular aortic repair; FDG: fluorodeoxyglucose; MDCT: multi-detector computed tomography; SOC: standard of care; PCI: percutaneous coronary intervention; VH: virtual histology. From http://www.clinicaltrials.gov accessed November 14, 2020.

A. Coronary artery disease and physiology

Coronary artery diseases account for 45% of overall deaths due to CVDs. Accurately diagnosing the severity of coronary disease generally requires an invasive procedure. Computational models can minimize the need for invasive instrumentation by deriving intravascular physiology non-invasively; such approaches are gaining increasing acceptance in interventional cardiology. A notable example is fractional flow reserve (FFR), which has emerged as the gold standard for the assessment of coronary artery physiology and is widely employed to determine ischemia-causing lesions.¹⁵⁷

FFR is an invasive procedure where a physician uses a pressure-guided wire to measure the ratio of mean distal pressure in the coronary artery (P_d) to the mean aortic pressure (P_a) during the period of maximum hyperemia. Hyperemia is induced using intravenous administration of pharmacological agents that cause vasodilation. However, the accessibility and the high procedural costs of FFR have restricted its wide-scale utilization and have paved the way for computational methods that can non-invasively derive FFR (Table I). In addition to traditional 3D CFD solvers (NS- and LBM-based), both reduced-order models and ML-based approaches have extended computation of FFR with clinical accuracy (Table I).

Several clinical trials have been conducted to assess the accuracy of non-invasive FFR using either CTA, CA, or IVUS-OCT imaging data (Table II). These trials have successfully resulted in two medical software packages approved by the US Food and Drug Administration (FDA): FFR_CTA¹¹ (FFR derived from computed tomography, HeartFlow, Inc., Redwood City, California, USA) and FFR_angio¹² (FFR derived from coronary angiography, CathWorks, Ltd., Kfar-Saba, Israel). FFR_CTA relies on solving 3D NS equations whereas FFR_angio uses LPM for computing pressure gradient across the stenoses in order to derive FFR.^12,41 The accuracy of both technologies FFR_CTA and FFR_angio is high at 87% and 92%, respectively, on a per-vessel basis.^12,158

Another FDA-approved software, CardioInsight (Medtronic), is a non-invasive electrocardiograph software that creates 3D multi-chamber cardiac mapping and accurately identifies premature ventricular dysfunction.^159,160 Such FDA-approved technologies have led to significantly increased clinical adoption of non-invasive patient-specific assessment in routine practice of cardiology. Apart from hyperemic pressure ratios, other non-invasive diagnostic metrics are being researched that are either flow-based or resting pressure-based. Common examples of such metrics are volumetric-flow based, quantitative flow ratio and resting pressure-based, and instantaneous wave free ratio, which are also being clinically evaluated^161,162

An overarching goal of diagnostic metrics is to clinically determine the impaired blood-flow carrying capacity of coronary arteries in the presence of stenosis.¹⁶³ Diagnostic assessment is followed by treatment procedures such as percutaneous coronary interventions (PCI), which help restore coronary flow through revascularization of a stenosis.¹⁶⁴ Despite the success of PCI, complications such as in-stent restenosis (ISR) and stent thrombosis (ST) are common in patients and thereby compromise the benefits of interventional procedures¹¹⁶ ISR and ST present multifactorial etiology and cannot be explained by the type of stenosis or stent used in PCI.¹⁶⁵ The development of ISR and ST is driven by the arterial remodeling processes that are activated due to the alterations in local hemodynamic forces, particularly low WSS.^7,116,153 Evidence from in vitro and in vivo experimental and clinical studies increasingly suggests that flow disturbances, reversal of flow, and low WSS affect development and progression of atherosclerosis,^166,167 and contribute toward stenting complications, such as ISR and ST.^{153,168–172} Importantly, these studies help establish that beyond diagnostic assessment, CFD studies that map underlying hemodynamic risk factors, such as WSS, play a crucial role in identifying coronary artery disease patients who present highest risk of post-PCI complications.

B. Congenital heart diseases and aortic diseases

Congenital heart diseases (CHD) are those related to the structural abnormality of the heart or functionally significant great vessels of the heart.¹⁷³ Some common CHDs that have been computationally investigated are hypoplastic left heart syndrome (HLHS), Tetralogy of Fallot (ToF), and Coarctation of the aorta (CoA).^34,174–181

HLHS is surgically treated using series of procedures: Norwood, Glenn or hemi-Fontan, and the complete Fontan procedures.^34,182 The goal of these consecutive surgical procedures is to create a direct connection between the systemic venous and pulmonary arterial circulations. While establishing such a connection allows surgeons to bypass the non-functional ventricle, it creates distinct anatomies of the ventricle that suffer from different energy losses and uneven blood distribution.^34,182 To study such disturbed flow patterns and their associated outcomes, CFD models are a powerful tool that can be used to pre-operatively determine and predict underlying hemodynamics.^{174–177,183,184} CFD allows visualization of flow patterns across different stages of HLHS surgeries, specifically in the regions of systemic-to-pulmonary shunt because in this region, flow is initially complex and at later procedural stages becomes less pulsatile with uniform pressure fields.¹⁸²

Per-patient assessment in HLHS treatment is important because shunt geometry and shunt flow varies significantly among the patient population.^182,238 CFD simulations provide detailed flow metrics that hold immense clinical relevance. For example, pressure fields are used as a surrogate for oxygenation, and velocity fields are indicative of physical properties, such as systemic and end-organ oxygen delivery.¹⁷⁷ Another useful hemodynamic variable is WSS, which is associated with thrombosis—a fatal complication in the aortopulmonary shunt. WSS can be used for guiding shunt modifications that reduce the risk of thrombosis.^185,186 Similarly, energy loss is an important clinical consideration in HLHS patients because circulation is provided by a single ventricle. Minimizing energy loss improves Fontan circulation and therefore CFD can be used to determine specific Fontan configurations which result in minimum energy loss.^183,187

Apart from CFD, reduced-order models have also been used to ascertain hemodynamics in shunt for Norwood procedures.^188,189 This work used a closed loop lumped parameter model (LPM). The shunt was modeled as a non-linear resistor with varying diameter and flow rate. The LPM approach enables modeling interactions with the remainder of the circulatory system. Furthermore, combining the benefits of reduced-order models and 3D models, multiscale approaches are being used to model shunt hemodynamics, pulmonary and coronary perfusion, and ventricular performance.^188,189

Another commonly investigated CHD is Tetralogy of Fallot (ToF), which is characterized by distinct features such as ventricular septal defect, right ventricular outflow tract obstruction, and right ventricular hypertrophy.¹⁷⁸ A CFD study used WSS to understand the effect of shunt configuration and shunt geometry design on local hemodynamics, and suggested that a direct shunt improves hemodynamic conditions rather than the central oblique or right pulmonary artery shunts.¹⁷⁹

Coarctation of the aorta (CoA) is a CHD characterized by a narrowing of the aorta and constitutes 8%–11% of the total congenital defects in the United States.¹ Revascularization using stents is a common surgical treatment option; however, CoA patients suffer from severe long-term outcomes, reduced life-expectancy, and morbidities such as hypertension, stroke, and aneurysm formation.^190,191 A pioneering study suggested that morbidities in the CoA patients could be explained based on the disturbed hemodynamic conditions.¹⁹² Important considerations apart from physiological boundary conditions need to be taken into account for accurately modeling CoA.^180,181 For example, it is important to take compliance and tissue properties into account because in CoA patients there is a disruption with respect to the aorta storing blood during systole and delivering it to the rest of the body during diastole.^115,193

Studies using patient-specific CFD models based on physiological boundary conditions revealed that hemodynamic variables TAWSS and OSI for CoA patients were significantly higher compared to control patients and validated against invasively measured peak pressure gradients.^180,181 Another study compared surgical treatments for CoA patients and suggested that there exists preferential anatomic locations where surgical correction can result in worsened WSS.¹⁸⁰ Such non-invasive CFD-based investigation can aid clinicians to determine hemodynamic changes resulting from different surgical options for a treated patient.

Hemodynamic forces also play a crucial role in the progression of aortic dissection: a condition that results in blood to flow through the inner and middle walls creating a true lumen (TL) and false lumen (FL) due to a tear in the inner aortic wall.^194,195 While aortic dissection is not a congenital disease, it is the most common acute aortic syndrome.¹⁹⁴ CFD enables capturing the hemodynamic field in the TL and FL.^195–197 Several works suggest that marked pressure and flow differences exist between the TL and FL, and the hemodynamic fields differ based on the location of tear, vessel distensibility, and anatomical structure.^195–197 Quantitative assessment of hemodynamic patterns can help identify patients who are at a risk of developing aneurysm and thrombosis post endovascular aortic repair.¹⁹⁸ Overall, there is an increasing application of patient-specific physics-based models to aid clinical decision-making for patients with aortic dissection.

C. Designing and optimizing medical devices and treatment

Generally, treatment outcomes are affected by the interaction between the medical device and the biomechanics at the implantation site.²⁰⁰ These interactions are further complicated by the dynamic physiological conditions, unique 3D anatomy, and mechanics of the device. It is therefore important to consider the characteristics of the medical device and its influence on biomechanics. To this end, physics-based flow simulations offer tremendous opportunities to model the impact of device implantation on a per-patient basis and predict the long-term effect of the device on the body.^9,200 Moreover, planning individualized treatment options can be challenging using in vivo animal models or in a clinical setting due to the associated time, cost, and inevitable population variability.²⁰¹ However, personalized flow models using CFD and patient-specific anatomy derived from medical imaging data (Sec. II) are a cost-effective and suitable option since they enable quantitative biomechanical evaluations across diseased vascular segments. Such evaluations can be invaluable for predicting treatment outcome since hemodynamic alterations have been shown to play a key role in the progression of adverse treatment outcomes, such as ISR and ST (Sec. III).^{116,153,202–204}

CFD methods have contributed to rapid device prototyping, reducing human risk and cutting down in vitro and in vivo experimental costs, and have led to a major shift in treatment and management of CVDs.^9,205 Several studies have demonstrated the potential of in silico models to optimize device design commonly used in the treatment of cardiovascular diseases.^{153,202–204,206–212} CFD simulations have played a central role in coronary artery disease treatment using PCI with the overarching goal to refine stent design and deployment strategy, and have guided clinicians toward identifying suitable implantation sites.^{153,202–204,212} Specifically, studies have emphasized the assessment of hemodynamic properties within the stented lesion to determine the biomechanical response, as WSS alterations have been related to in-stent restenosis.^{116,153,202,203} Flexible stents that conform to natural vessel shape improves WSS patterns due to a reduced radius of curvature and increased Dean number within the stented region, while rigid stents (inflexible) result in vast spatiotemporal WSS variations along the curved coronary arterial regions, which are common sites of restenosis (Fig. 4).¹⁹⁹ Furthermore, CFD simulations have been used to test the pre-clinical efficacy of stent, with respect to design features such as strut thickness, vessel surface area coverage, and radial force, on blood flow disturbances and thrombogenicity.^170,213

FIG. 4.

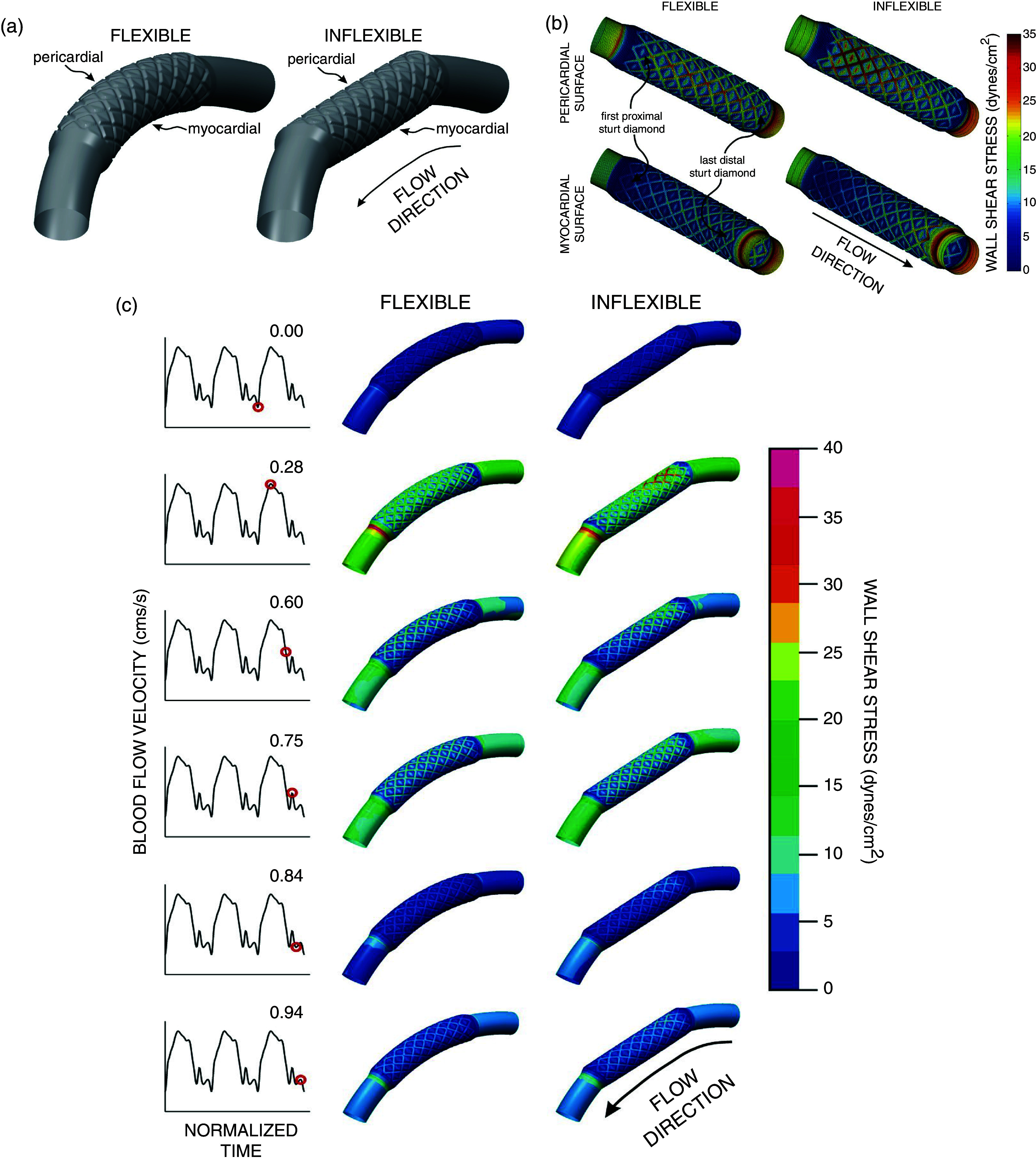
Example of CFD study for optimizing stent design and features for implanting in the case of coronary artery disease. (a) Depicting flexible and inflexible stents. Three-dimensional vessel reconstructions implanted with 12-mm stents that conform to the vessel (flexible, left) or result in vessel straightening (inflexible, right). The 3D vessel is an idealized curved coronary artery model. The diagram also depicts the pericardial and myocardial regions. Following vessel and stent dimensions were used by the study: 8 axial and circumferential repeating strut sections with stent-to-artery diameter ratio of 1.2, thickness equals 0.096 mm, and the width equals 0.197 mm. (b) Spatial distributions of WSS along the pericardial (top panel) and myocardial (bottom panel) luminal regions. Simulations results depicted for maximum blood flow velocity for flexible and inflexible stents implanted in an idealized curved coronary artery vessel. (c) Time-dependent alterations in spatial wall shear stress throughout the period of the entire cardiac cycle flexible and inflexible stents implanted in an idealized curved coronary artery vessel. Reproduced with permission from J. F. LaDisa, Jr., L. E. Olson, H. A. Douglas, D. C. Warltier, J. R. Kersten, and P. S. Pagel, Biomedical Engineering Online 5(1), 1–11 (2006).¹⁹⁹ Copyright 2006 Authors, licensed under a Creative Commons Attribution (CC BY) license.

Design of mechanical heart valves and ventricular assist devices (VADs) are other important areas where CFD simulations have been used to gain insight in the thrombogenic biological response.^206–211 To this end, studies have focused on modeling valve dynamics, closure mechanism, and upstream and downstream blood flow separation.^206–208 CFD studies in conjunction with experimental approaches have investigated continuous flow VADs to determine optimal thromboresistance and VAD implantation sites.^209–211 Extending CFD application to virtual treatment planning generally involves implanting a device, such as an annuloplasty ring, into the 3D model of patients with ischemic mitral regurgitation.²¹⁴ High resolution visualization of CFD simulation results enables non-invasive characterization of cardiac function and mechanical reliability of the device under different physical condition.²¹⁴ Such studies establish the role of CFD models to deliver objective, per-patient assessment on a wide scale and are particularly lucrative for international regulatory agencies due to their potential to reduce prototyping and clinical studies prior to in vivo implantation. This is exemplified by the various initiatives that have been undertaken by the European Commission and the US FDA. The European commission started the Virtual Physiological Human (http://www.vph-institute.org/), and the US FDA introduced the Device Innovation Consortium. The broad objective of such projects is assessment, evaluation, and standardization of non-invasive computational approaches to improve the quality and performance of medical devices.^205,215

IV. CHALLENGES AND LIMITATIONS

Sections II and III discuss the emerging applications of physics-based flow models in clinical cardiology and basic cardiovascular research, such that these methods constitute an actively evolving field. Despite the tremendous developments in computational resources, medical imaging technology, and numerical solvers, there are several questions that still remain unanswered to demonstrate usefulness of physics-based models for improved diagnosis and treatment of CVDs. These questions can best be categorized under the following three headings: (1) uncertainty quantification and model parameterization to determine the model robustness, (2) model verification and validation for clinical use, and (3) computational complexity and time-to-solution minimization. The first topic outlines the limitations of computational frameworks related to uncertainty and optimization algorithms in image segmentation, geometric reconstruction, and modeling approaches. The second addresses the need for robustly validated and realistic models that can enable seamless integration in routine clinical cardiology practice. Finally, the third topic is related to the real-time diagnostic assessment using non-invasive computational approaches.

A. Uncertainty quantification and model parameterization to determine the model robustness

Uncertainty quantification (UQ) is a mathematical concept to determine the uncertainty of physical models due to noisy data, theoretical limitations of the numerical model, and reliability of computations, approximations, and algorithms.²¹⁶ UQ can be particularly important for cardiovascular flow models because of the variations in the anatomical and physiological parameters that are used as inputs to the model and thus have profound effects on the overall simulation results.²¹⁷ In patient-specific models, anatomical variations can arise from medical image segmentation while physiological parameter uncertainties can come from inherently variable clinical record measurements such as heart rate.^35,218 Image segmentation and input parameter variability have been examined by recent works that highlighted large changes in the segmented lumen regions and inlet boundary conditions.^219,220 To illustrate this notion, two modeling challenges were used by these studies: the 2015 International Aneurysm CFD Challenge and the Multiple Aneurysms AnaTomy CHallenge (MATCH) 2018 study.^219,220 These studies illustrated marked inter-team variability with respect to image segmentation and reconstructed 3D geometry, and thus lack consensus on severity of hemodynamic metrics associated with disease progression.^219,220 Authors also noted that apart from segmentation variability, only a few teams were able to accurately segment the geometry and took several hours longer than other teams.²¹⁹

Another interesting study was performed UQ by changing the stenosis severity by ±1 image voxel and flow rates by ±10% to model operator uncertainty.²²¹ Authors reported uncertainty in pressure drop as high as 20 mmHg.²²¹ Furthermore, non-invasive computation of clinical diagnostic metrics, for example FFR, also requires sensitivity analysis and UQ.^218,222 As performing parameter sweeps for 3D CFD simulations can become computationally prohibitive, authors in this study used a reduced-order model and varied eight input parameters and reported uncertainty to be dominated by the peripheral resistance, whereas the more obvious culprit, stenosis severity, had modest influence.²²² Contrary, to the findings of this study, another UQ study using 3D CFD models showed stenosis severity and stenoses length had the strongest impact on non-invasive FFR computation.²²³

Such conflicting findings from different works suggest that UQ should be performed for any given modeling framework to assess the driving features that have maximum influence on computational results. Model parameterization requires in depth knowledge of physiological features that may affect circulation but cannot be directly measured, such as microcirculatory resistance.²²⁴ Therefore, further understanding of the relative importance of physiological parameters is required to determine which are most influential and which can be assumed or averaged.²²⁴ Given the importance of UQ in cardiovascular flow models and the time-intensive nature of these studies, multilevel and multifidelity techniques are being incorporated in UQ workflows instead of traditional high-fidelity models or single-fidelity Monte Carlo estimators.⁷⁵ Alternately, ML-based methods may also be attractive to estimate geometric and parameter variability and assimilate the distribution of variability for cardiovascular flow models.^79,82

B. Model verification and validation for clinical use

Successful clinical translation of cardiovascular flow models requires closer association between engineers and clinicians for embedding computational models in routine clinical practice. This level of acceptance requires standardization, scrutiny, and model credibility evaluation.²¹⁵ Instilling confidence in predictive capability of computational simulations has been at the forefront of FDA's Critical Path Initiative for CFD via verification and validation of these methods.²²⁵ Model verification tests the accuracy of the numerical solutions of the governing equations, and model validation determines whether the simulation results accurately represent the real-world application.²²⁶ Verification thus involves numerical tests of mesh discretization, accuracy, stability, and spatial and temporal convergence.²²⁶ On the other hand, in vitro and in vivo data has been generally accepted as the standard for the validation of cardiovascular flow models.³⁵ Clinical trials on non-invasive hemodynamic characterization (Table II) have demonstrated the accuracy of their models by comparing with invasive measurements and reporting the diagnostic accuracy, sensitivity, specificity, and positive and negative predictive values.^11,12,81 A prime example here is non-invasive FFR computation, where studies using either 3D CFD, reduced-order, or ML-based approaches report the accuracy of their frameworks through a comparison to invasively measured FFR data.^11,12,81

Comparison with invasive diagnostic measurements distills the simulation predictions to the expected biological response but does not necessarily validate the complete flow field. To achieve that, studies have relied on in vitro particle imaging velocity (PIV) experiments and used PIV as the reference standard against which CFD velocity predictions must be validated.^{155,227–229} Another approach for validating computational models is using pulse wave velocity measurements and velocity data from 4D MRI, which enable characterizing in vivo velocity flow field and vessel wall stiffness.^93,230 Overall, such validation methodologies allow researchers to truly test the biological and physiological (biophysical) attributes of physics-based flow models, diminish skepticism in prediction capabilities of simulations, and lay the necessary groundwork for successful clinical translation.

C. Computational complexity and time-to-solution minimization

Real-time non-invasive diagnostic assessment is one of the important clinical goals for cardiovascular flow models. However, 3D numerical simulations are computationally intensive and have long execution times due to complex geometries, pulsatile flow, and physiological boundary conditions. Therefore, there is always a need for faster computations. To meet the computational demand, the availability and advancement in parallel processing and graphic processing units (GPUs) is very timely because fluid dynamics algorithms can be parallelized and are ripe for such computing advancements.^{11,124,126,231} While increasing computational power and efficient parallelization reduces the time-to-solution by several orders of magnitude, it requires computational resources that may not be easily available in routine clinical practice.

There has been a growing interest in reduced-order models and machine learning approaches to compute global hemodynamic-based diagnostic metrics that were traditionally computed using 3D NS solvers.^{12,23,80,81,100} A study proposed a simpler mathematical implementation based on LPM to compute FFR without the need for complex pulsatile CFD simulations.¹⁰⁰ This study in direct comparison to a 3D CFD model demonstrated that the execution time reduced from >36 h to <4 min without compromising the accuracy of computed FFR.¹⁰⁰ Similar results have been reported by other studies using 1D and LPM models.^70,137–140 Hence, reduced-order models are attractive for computing global hemodynamic quantities such as pressure gradient and volumetric flow rate.

However, it is important to note that 3D CFD models allow us to capture fine flow details for biological processes that benefit from underlying knowledge of detailed local hemodynamics. While global hemodynamic-based quantities, such as FFR, are helpful for diagnostic purposes, it is the local hemodynamic-based quantities that enable researchers and clinicians to gain valuable insight into the underlying complex relationship between hemodynamics and cardiovascular disease progression.^116,165 Using 3D CFD flow models, local hemodynamic risk-factors, such as WSS and OSI, can be accurately and non-invasively computed.^{153,166,167,239} These metrics have been shown to play a role in understanding and predicting progression of coronary artery disease, post-PCI complications, and congenital heart disease (as discussed in Sec. III). Thus, unified models that combine the benefits of high-fidelity physics from 3D CFD and computational efficiency from reduced-order models could significantly advance cardiovascular flow models.^232–234 In such coupled (1D-3D or 0D-1D-3D) models at the connection interface, each domain informs the other domain.^232–234 Researchers are, therefore, developing multiscale cardiovascular flow models (1D-3D or 0D-1D-3D) with the potential of real-time flow assessment and fine physiological detail.^75,235,236

AUTHORS' CONTRIBUTIONS

All authors contributed equally to this manuscript. All authors reviewed the final manuscript.

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.