Stability and robustness properties of bioelectric networks: A computational approach

Abstract

Morphogenesis during development and regeneration requires cells to communicate and cooperate toward the construction of complex anatomical structures. One important set of mechanisms for coordinating growth and form occurs via developmental bioelectricity—the dynamics of cellular networks driving changes of resting membrane potential which interface with transcriptional and biomechanical downstream cascades. While many molecular details have been elucidated about the instructive processes mediated by ion channel-dependent signaling outside of the nervous system, future advances in regenerative medicine and bioengineering require the understanding of tissue, organ, or whole body-level properties. A key aspect of bioelectric networks is their robustness, which can drive correct, invariant patterning cues despite changing cell number and anatomical configuration of the underlying tissue network. Here, we computationally analyze the minimal models of bioelectric networks and use the example of the regenerating planarian flatworm, to reveal important system-level aspects of bioelectrically derived patterns. These analyses promote an understanding of the robustness of circuits controlling regeneration and suggest design properties that can be exploited for synthetic bioengineering.

INTRODUCTION

A remarkable aspect of living systems is the ability to restore complex structure and function despite drastic perturbations (Bely and Nyberg, 2010; Maden, 2018; and Stocum and Cameron, 2011). Unlike embryogenesis, which always begins in the same way, regeneration requires the organism to restore its morphology despite injury that can occur in different positions (Harris, 2018; Pezzulo and Levin, 2016). Closely related are examples of dramatic remodeling, such as those occurring during metamorphosis (Pinet and McLaughlin, 2019), which impart invariant anatomical endpoints on a diverse set of starting conditions (Pinet et al., 2019; Thompson, 2021; and Vandenberg et al., 2012).

Alongside familiar biochemical gradients and gene-regulatory networks (GRNs), the coordination of cell activity toward specific functional anatomies is also guided by the information processed by bioelectric networks (Bates, 2015; Harris, 2021; and Levin, 2021). All cells, not just neurons, produce resting potentials across their cell surface (V_mem) and communicate those potentials to neighboring cells via electric synapses known as gap junctions (GJs) (Levin et al., 2017; Levin and Martyniuk, 2018). Because the channels and gap junctions can themselves be voltage-sensitive, this system enables complex transition rules and non-obvious dynamics, such as feedback loops, memory, pattern recognition, and computation (Cervera et al., 2018a; 2018b; 2019a; 2019b; 2020a; Law and Levin, 2015; Manicka and Levin, 2019; and Pietak and Levin, 2016; 2017).

Endogenous voltage gradients have been implicated in the control of eye (Pai et al., 2012), wing (Dahal et al., 2017; George et al., 2019), skin (Jiang et al., 2021), fin (Daane et al., 2018; Lanni et al., 2019; and Perathoner et al., 2014), brain (Pai et al., 2015a; Pai et al., 2015b), and craniofacial (Adams et al., 2016; Vandenberg et al., 2011) development, inducing patterning modules during embryogenesis (Levin, 2021; Sullivan et al., 2016) and regeneration (Adams et al., 2007; Tseng et al., 2010). They also regulate the polarity of the anterior–posterior, left-right, and dorso-ventral axes (Beane et al., 2011; Levin et al., 2002; and Stern, 1982) as well as size determination of heads, wings, and tails in a range of model systems (Belus et al., 2018; Daane et al., 2018; Lanni et al., 2019; and Perathoner et al., 2014). Bioelectric control mechanisms are highly conserved, being also implicated in stem cell biology (Hinard et al., 2008; Konig et al., 2004; 2006; Lobikin et al., 2015; and Sundelacruz et al., 2008) and cancer (Chernet and Levin, 2013; Lang and Stournaras, 2014; Levin, 2021c; and Prevarskaya et al., 2018), and functioning in systems ranging from bacterial biofilm dynamics to human birth defects induced by channelopathies (Martinez-Corral et al., 2019; Prindle et al., 2015; Srivastava et al., 2021; and Yang et al., 2020). In addition to their endogenous functions, they are beginning to be used in synthetic biology applications to build artificial bioelectric tissues with many biomedical and soft robotics applications (Cheney et al., 2014; McNamara et al., 2016; 2018; 2019; 2020).

An important direction in the biomedical applications of bioelectricity is the control of differentiation, in cell types, such as mesenchymal stem cells (Pai et al., 2016; Sundelacruz et al., 2008; 2013; 2015; 2019) and cardiomyocytes (Lan et al., 2014), and of wound healing (Forrester et al., 2007; Zhao et al., 2006; 2012; 2020). Beyond simple cellular phenotypes, computational modeling has begun to enable the inference of ion channel stimulation strategies to repair complex phenotypes, such as cancer normalization (Chernet et al., 2014; Chernet and Levin, 2014; and Chernet et al., 2016) and repair of brain defects due to genetic mutations (Pai et al., 2015b) or teratogenic chemicals (Pai et al., 2018; 2020). All of these strategies require an understanding of how the bioelectric circuit will respond to change. A key aspect of bioelectric networks' computations in morphogenesis is robustness and stability to perturbation of the tissue substrate. While these properties have been explored in chemical (e.g., reaction-diffusion) signaling modes (Kondo and Miura, 2010; Landge et al., 2020), they are only now beginning to be probed in bioelectric signaling (Brodsky, 2018; Brodsky and Levin, 2018; and Pietak and Levin 2016; 2017; 2018). Here, we use the planarian regeneration model as a context in which to develop a new computational analysis and testable model of bioelectric circuit resilience.

Planaria are champions of regeneration, able to restore a perfect little worm from any fragment (Lobo et al., 2012, Saló et al., 2009, and Sheiman and Kreshchenko, 2015). This is in effect a kind of homeostatic process in which growth and remodeling occur to implement a specific invariant anatomy and cease when that pattern is complete (Owlarn and Bartscherer, 2016). In order to do this, a piece of an adult worm has to contain the information describing the correct final state and implement it in a much smaller overall tissue context (Beane et al., 2013; Oviedo et al., 2003; Pellettieri, 2019; and Thommen et al., 2019). While recent work has made significant progress on the molecular networks necessary for the production of the required cell types from stem cells (Fincher et al., 2018; Owlarn and Bartscherer, 2016), many questions still remain about the processes that allow tissue to determine the correct number, location, and size of structures like the head.

One crucial aspect is non-local signaling. A single bisecting cut results in cells on one side of the cut making a head, while cells on the other side of the cut make a tail (Levin et al., 2019). These cells have radically different morphogenetic fates and yet were direct neighbors before the bisection. Thus, anatomical fate cannot be determined purely from a local position of the regeneration blastemal—instead, cells need to coordinate with other components of the fragment to determine which direction is anterior, whether a head already exists, etc. Work over the last decade suggests that such communication is mediated by gap junctions (Nogi and Levin, 2005; Oviedo et al., 2010) as well as by ventral nerve cord (VNC) (Pietak et al., 2019). Moreover, the head–tail decisions are now known to involve a bioelectric circuit—a pattern of resting potentials that acts in the first few hours after the cut to determine anatomical layout of the resulting animal, including the production of normal worms, no-head worms, or bipolar 2-head heteromorphoses (Beane et al., 2011; Durant et al., 2019; and Emmons-Bell et al., 2019). While a number of models for this phenomenon have been suggested (Cervera et al., 2020b; De et al., 2016; Pietak and Levin, 2017; and Stuckemann et al., 2017), important aspects of the data remain unexplained. How does the bioelectric circuit that determines head–tail identity re-scale to operate in fragments after amputation?

There are several candidates for the long-range signaling required to explain planaria axial regenerative scaling:

• •Reaction-diffusion (Turing, 1952), where two morphogens (an activator and an inhibitor) both diffuse and react with each other, resulting in a wide range of potential patterns.
• •Electrodiffusion (Pietak and Levin, 2017), where a charged morphogen drifts to one end of an organism under the influence of an electric field and then diffuses back.
• •VNC transport (Pietak et al., 2019), where a morphogen moves from one end of the planarian ventral nerve cord (VNC) to the other via axonal transport and then diffuses back.

Whichever one or more of these is correct, it must operate robustly. For example, planaria can regrow from very small segments. Whichever physical system long-range signaling uses, it must operate equally well at both small and large body sizes. Pietak et al. have shown (Pietak and Levin, 2018; Pietak et al., 2019) that both electrodiffusion and VNC transport work on both large and small worm fragments.

The reaction-diffusion mechanism proposed by (Turing, 1952) successfully explains many aspects of morphogenesis in various organisms (e.g., Pietak and Levin, 2018; Raspopovic et al. 2014). However, the patterning outcomes of reaction-diffusion mechanisms are strongly dependent on system size; as such, they are unlikely to produce consistent results across the wide range of planarian-fragment sizes that can regenerate (Pietak and Levin, 2018). Fortunately, Werner et al. (2015) described an extension of reaction-diffusion that does scale. All three potential mechanisms can thus be made to work for both small and large fragments. However, while robustness across the size of worm fragments is necessary, it is not sufficient.

The evolutionary mandate for biological processes to be robust is not limited to robustness across organism size. Arkin (McAdams and Arkin, 1999) summarized arguments that robustness at the molecular level, while necessary, is difficult to achieve. Many protein species have only tens to a few hundred molecules per cell. If a parent cell has only, e.g., 50 molecules, mitosis will statistically result in 6% of the daughters receiving 18 or fewer molecules rather than the expected 25. Thus, protein count alone may not always be a robust means of storing morphological state. Furthermore (McAdams and Arkin, 1999), reaction rates are not only stochastic due to the low number of DNA and RNA molecules, but as always are highly temperature dependent.

Morphogenesis (to say nothing of the many other biological processes involved in life) is nonetheless typically quite robust. Alon (2019, Chap. 7–12) details numerous mechanisms that have evolved to overcome these issues. Among them are the use of exact adaptation in bacterial chemotaxis (Alon, 2019, Chap. 9; Barkai and Leibler, 1997) and the use of self-enhanced morphogen degradation for robust morphogen-concentration detection (Alon, 2019, Chap. 12; Eldar et al., 2002).

Thus, the question: can electrodiffusion, VNC transport and reaction–diffusion be robust across parameter drift? We focus on electrodiffusion, and try to determine whether it can be robust enough to be a feasible candidate for planarian long-range signaling. Can it work reliably even as its parameters naturally drift? What requirements must its parameters satisfy, and can a single set of parameters work correctly as a small planarian fragment regrows?

RESULTS

Overview of the electrodiffusion hypothesis and our model of it

Pietak (Pietak and Levin, 2017; 2018) has described the electrodiffusion hypothesis in detail. We summarize it briefly here and explain the important parameters that we will explore for robustness.

At the heart of the model is a charged morphogen M. We will assume for simplicity that M always has a negative charge; positive would work equally well if the appropriate pathways were altered. Planaria are typically hyperpolarized (i.e., quite negative V_mem) at their tail and depolarized (i.e., less negative or slightly positive V_mem) at their head (Beane et al., 2011; Durant et al., 2017). The resulting head-to-tail electrical field creates an electrical force on the morphogen, thus creating a drift flux that moves M toward the head. With concentrations higher at the head, diffusion then tends to move M back toward the tail. At some point, the drift and diffusion fluxes balance, resulting in a steady-state profile with [M] (the concentration of M) gradually rising as we get closer to the planarian head.

The balance of drift and diffusion is quite like the standard formulation of a cell voltage in the Nernst equation (Nelson et al., 2004, Chap. 4). We make the situation more complex by assuming long-range communication through gap junctions (GJs), with most cells directly connected to their nearest neighbor(s). We follow the assumption that the cells have very small electric fields and thus nearly constant [M] within any single cell, with gradients of [M] occurring at the GJs (Pietak and Levin, 2016).

While this describes how an existing electrical field can create a morphogen profile, it does not explain the formation and expansion of an electrical field as a small fragment regrows. A small worm fragment would naturally have a small head-to-tail voltage difference ΔV_mem, producing a small head-to-tail gradient of [M], but how does this become a much larger ΔV_mem as the fragment regenerates?

One answer is that the electrodiffusion hypothesis adds positive feedback. For example, ligand-sensitive sodium ion channels at the head (tail) might increase (decrease) their conductance at higher [M]. Since Na has a positive V^Nernst, this would (Nelson et al., 2004, Chap. 11) result in increasing(decreasing) V_mem at the head(tail). This cycle would then ideally cascade upon itself, amplifying the original small gradient.

The basic electrodiffusion hypothesis may have various forms. It may work with other ion channels in addition to (or instead of) Na. It may add a gene-regulatory network (GRN); e.g., M may be a transcription factor or ligand that triggers a pathway that eventually (rather than directly) gates an ion channel.

The version that we use in this paper has [M] directly gating K channels. M inhibits these channels, thus creating overall positive feedback. Specifically, with the head depolarized, the resulting voltage difference creates a concentration gradient with higher [M] near the head. This closes K ion channels at the head, which (since K has a negative V^Nernst) further depolarizes the head cells.

The worm parameters in our model are as follows:

• •num_cells: the number of cells in the worm from head to tail.
• •k_M and N: the model parameters for the ligand concentration [M] to inhibit a K ion channel in the standard Hill model $\frac{1}{1+{\left(\frac{\left[M\right]}{k_M}\right)}^N}$.
• •GJ_scale: we assume that every two adjacent cells are connected by a GJ. This parameter gives the cross-sectional area of that GJ. It is a unitless scale factor, relative to a typical area. In our simple model, the GJs are ungated.
• •Z_M: the valence of the morphogen ion M. As noted, we assume M to be negatively charged for simplicity.
• •τ_gd: we assume that the morphogen M decays with a rate proportional to its concentration. For simplicity, we assume that M is created at a constant rate in each cell; thus $\frac{d\left[M\right]}{dt}=k_{\mathit{Gen}}+k_{\mathit{Dec}}\left[M\right].$ This leads to an exponential decay to the steady-state value ${\left[M\right]}_{SS}=\frac{k_{\mathit{Gen}}}{k_{\mathit{Dec}}},$ with the time constant k_Dec. We denote this generation-decay time constant as τ_gd (and note that it is simply equal to k_Dec).

If GJs are too conductive, the worm short-circuits

Each cell has its own positive-feedback system. If the cells were isolated (without GJs), then each single cell could maintain its own V_mem, independent of all other cells, and swing to either fully hyperpolarized or depolarized. However, the GJs form low-resistance paths connecting cells, forcing the neighboring cells to have nearly the same V_mem. As we make GJ_scale larger, different cells have their V_mem forced closer together and the V_mem gradient across the worm thus shrinks.

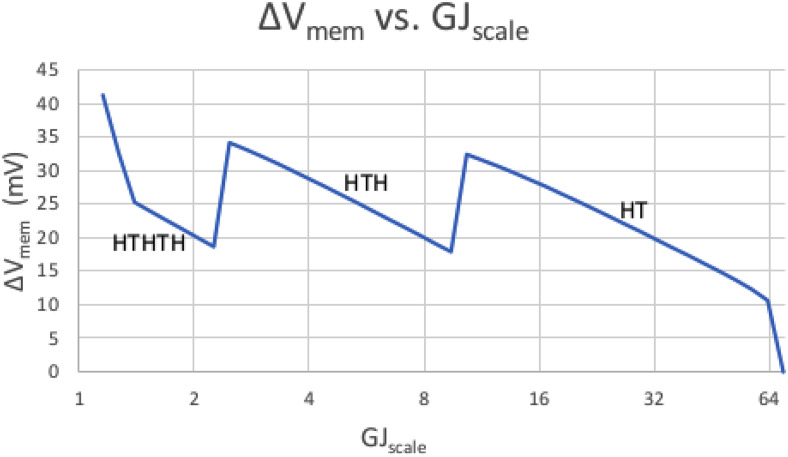
Figure 1 shows the shape and magnitude of a worm's V_mem pattern as we sweep GJ_scale higher. Focus on the right side of the graph, from roughly GJ_scale = 10 and higher, labeled as HT. We see that as GJ_scale rises, the resultant ΔV_mem (i.e., the difference between the highest and lowest value of V_mem anywhere in the worm) falls. The rightmost graph point shows ΔV_mem finally collapsing to near 0 as the worm short-circuits when GJ_scale approaches 70.

FIG. 1.

The effect of GJ_scale on ΔV_mem. The x axis represents GJ_scale (i.e., the density of GJs relative to an arbitrary reference); the y axis is ΔV_mem (the difference between the highest and lowest V_mem anywhere in the worm). Each portion of the graph is also labeled with the worm's overall pattern of heads and tails, as read from the peaks and valleys of V_mem distribution across the worm. The right side of the graph shows ΔV_mem forced to near zero when GJs are too dense. As we move to the left, the lessening GJ conductivity allows the formation of more and more voltage islands and allows V_mem to swing high and low more and more times (where, e.g., HTH would represent a V_mem peak at each end with a valley in the middle).

This is in accordance with basic circuit theory. As described by Pietak and Levin (Pietak and Levin, 2016), there is very little voltage drop across any cell; the voltage drop is largely across the GJs. Larger values of GJ_scale imply lower GJ resistance; Ohm's Law says that V = IR (Nilsson and Riedel, 2019), and a lower R thus implies a lower voltage drop V across each GJ and across the worm as a whole.

If GJs are not conductive enough, then local islands replace global communication

Again, each cell has its own local positive-feedback system. If all cells were isolated (GJ_scale = 0), each cell could independently arrive at its own decision to be a head or tail (i.e., a V_mem peak or valley). We could then see V_mem patterns representative of, e.g., HTHTHTHT rather than forming one head and one tail. In fact, external drugs, such as octanol, which block GJs and thus increase GJ resistance, can cause exactly this effect.

See Fig. 1 again. This time, focus on the portion of the graph to the left of GJ_scale = 10. We see the worm transitioning from a WT worm (i.e., HT) to two-headed (i.e., HTH) as GJ_scale < 10. We further see a transition from HTH to HTHTH at roughly GJ_scale = 2.7. As GJ_scale gets lower and lower (i.e., as GJ density drops), we have more and more voltage islands, allowing more and more switches between hyperpolarized and depolarized V_mem.

Again, this is in accordance with basic circuit theory. A high enough GJ resistance allows almost every cell to operate independently and to be its own voltage island. A somewhat lower GJ resistance lowers the possible ΔV_mem between adjacent cells enough that only a few head-to-tail swings are possible over the worm's length. A still lower GJ resistance encourages proper gradients, with only one head and one tail. Still lower, as noted above, short-circuits the worm.

Just-right GJ density requires allometric scaling

GJ_scale must be large enough to prevent island formation and small enough to avoid short-circuiting ΔV_mem, thus leaving only a range of robust values, but how wide is this range, and does it vary as the worm increases in length during regeneration?

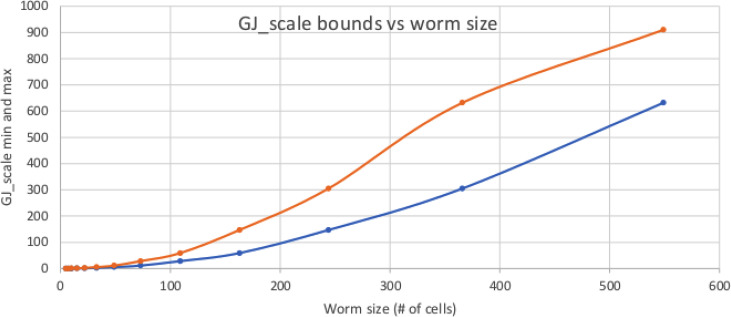
Figure 2 shows that as the worm grows, GJ_scale must become correspondingly larger. Intuitively, a larger worm has more physical distance between head and tail, but robust electrical communication over longer distances requires “thicker” wires, which essentially means that GJ_scale must get larger so as to keep a low-resistance communication path as the worm grows.

FIG. 2.

Acceptable values of GJ_scale for different worm sizes. As a worm grows, the distance from head to tail grows; maintaining global communication thus requires high GJ density. The upper (orange) curve is the upper limit on GJ density for a worm of a given size before ΔV_mem collapses. The lower (blue) curve is the lowest GJ density before multiple islands form, allowing a HTH worm to be stable.

Electrodiffusion can only create a gradient if loop gain is greater than unity

For a small worm fragment to regenerate, its initial small head-to-tail gradient of [M] must expand. In principle, regrowing a full worm from a small fragment sounds easy:

• 1.A fully grown worm may have, e.g., [M] = 0.1 at the tail and 1.9 at the head. Our small worm segment taken from the middle of the worm may have, e.g., [M] = 0.9 at its rear-facing end and [M] = 1.0 at its forward-facing end. We then define its Δ[M] = 1.0 − 0.9 = 0.1.
• 2.The slightly higher [M] in front, working through the Hill model of the K⁺ ion channel, then leads to lower turn-on of K⁺ channels at the front than at the rear of the worm.
• 3.Since V^Nernst of K⁺ < 0, this results in V_mem being more positive at the front than at the rear of the worm. We define ΔV_mem as the maximal difference between the V_mem of the cell with the highest V_mem and the cell with the lowest V_mem (which, in a WT worm, is typically between the head and tail cells).
• 4.The ΔV_mem attracts more M to the front, and the cycle loops back to step 2, quickly resulting in ΔV_mem becoming large.

Simple as this sounds, it does not always work. Simulations show that some parameter choices instead result in the initial small gradient quickly collapsing to near zero. Why do some parameter sets succeed better than others at regenerating a full gradient?

A simple concept called loop gain largely explains these results. Assume we start with an initial head-to-tail concentration gradient Δ[M]⁰. The combination of electrodiffusion and ion-channel gain (steps 2–4) results in a new gradient Δ[M]¹. We define the ratio $L\equiv \frac{\Delta {\left[M\right]}^1}{\Delta {\left[M\right]}^0}$ as the loop gain.

Intuitively, parameter choices that result in L > 1 allow small initial gradient differences to expand and eventually become large, while L < 1 means that any initial gradient difference contracts. Thus, loop gain is an excellent predictor of regenerative ability.

Two parameters largely determine loop gain

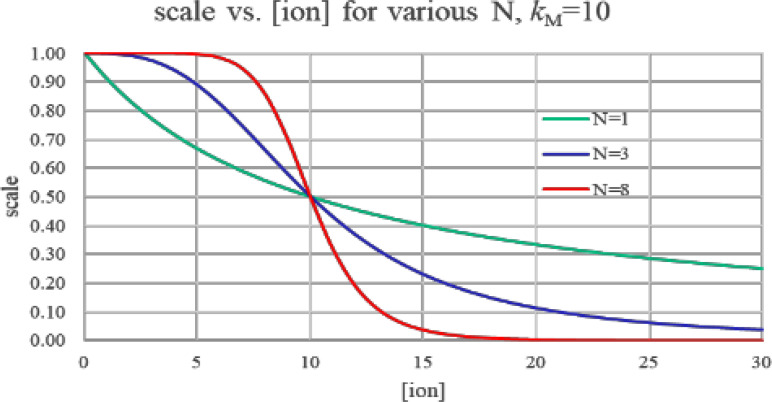
Which of our model parameters determines loop gain? Two of them have the most effect. First, large values of N (i.e., high Hill-model cooperativity) increase gain (Fig. 3). An existing Δ[M]⁰, working through a large N, creates a larger difference in ion-channel turn-on at the head vs tail, which then causes a larger ΔV_mem¹; i.e., step 2 above has higher gain.

FIG. 3.

Hill-model inhibition scale vs input ligand concentration. Gain (i.e., the slope of the curve) is reasonably uniform for the N = 1 curve (no cooperativily). For N = 8, gain is quite high at the knee of the curve (in this figure, at [ion] = 10), but extremely low as we move further away from there. A worm built with N = 8 would thus only reestablish a gradient for worm fragments from near the worm's center.

Second, high Z_M (the valence of our morphogen ion) also increases the loop gain. An existing ΔV_mem⁰ creates an electric field that segregates our charged morphogen M; the field exerts a force on M that is directly proportional to Z_M (Nelson et al., 2004), amplifying step 4.

Table I collects results from the simulation of over 1700 worms with various parameter sets. The worms had a Hill-model N of either 2, 5, or 8; and Z_M of −1, −2, −3, or −4. The number in each cell of Table I shows the number of worms with that parameter pair that succeeded in maintaining a gradient (i.e., for that N and Z_M value, the number of working combinations of parameters other than N and Z_M). The results show that gain—be it from a large N or from a large Z_M—was the key factor in maintaining a gradient.

TABLE I.

Number of parameter choices that maintain an existing gradient vs N, Z_M.

	ZM = −1	ZM = −2	ZM = −3	ZM = −4
N = 2	0	12	21	23
N = 5	25	37	44	51
N = 8	27	42	46	48

Increasing loop gain via cooperative binding is not robust

Hill-model gain does not come for free. Increasing the Hill-model N increases gain at the knee of the curve, but diminishes gain elsewhere. In Fig. 3, the red N = 8 curve is very steep (i.e., high gain) at a ligand concentration near its k_M, but quite flat (low gain) elsewhere. The Y axis of Fig. 3 is Hill-model gain, which in our model is equal to the fraction of K⁺ gates that are on. With N = 8, any values of [M] that are less than 5 or greater than 20 have close to zero gain, since nearly all ion channels are already on (for [M] < 5) or off (for [M] > 20).

If, for example, an entire whole worm's [M] ranged from 0.1 at the tail to 1.9 at the head, then if we cut it into nine fragments the rearmost fragment would have [M] ranging from 0.1 to 0.3, the frontmost fragment from 1.7 to 1.9, and the middle fragment from 0.9 to 1.1. If, for example, the model had k_M = 1, then with N = 8 the middle fragment would have $\frac{1}{1+{\left(\frac{.9}{1.0}\right)}^8}\approx 70\%$ of K⁺ channels on at its rear, and $\frac{1}{1+{\left(\frac{1.1}{1.0}\right)}^8}\approx 32\%$ on at its front. This large difference would likely amplify itself quickly.

However, the rearmost fragment would have $\frac{1}{1+{\left(\frac{.1}{1.0}\right)}^8}\approx 99.999999\%$ of K⁺ channels on at its rear, and $\frac{1}{1+{\left(\frac{.3}{1.0}\right)}^8}\approx 99.993\%$ on at its front. This would quickly shrink any existing ΔV_mem.

So worms with high N do a very good job of regrowing segments whose range of [M] spans their k_M, but a bad job of regrowing other segments. The best worms at regrowing equally well from all segments are those with low cooperativity (i.e., low N); their nearly flat response means that they do not have any glaring areas of low gain.

To show this, we have modified our planaria model from Table I so that, in addition to checking whether a planarian can sustain an initial entire gradient from [M] = 0 at the tail to [M] = 2 at the head, it also checks regeneration of 20 fragments. For example, a tail fragment would have its [M] range from 0 to 0.1; a mid-body fragment would have [M] range from 0.9 to 1.0. Table II shows the number of worm-parameter choices that result not only in the worm maintaining an initial full gradient, but also regeneration from all of its 20 fragments.

TABLE II.

Number of parameter choices producing robust fragment regrowth vs N.

	N = 2	N = 5	N = 8
5 cells	6	6	0
30 cells	6	6	1
100 cells	5	3	1

We see that while increased Hill-model cooperativity was quite effective at maintaining a full [M] = 0–2 gradient (Table I), it is quite ineffective at regrowing small fragments robustly. Note, though, that the N = 8 column is not populated by all zeros—there are some parameter choices that seemingly make N = 8 robust. But how? By taking advantage of dynamics.

Two time constants model electrodiffusion dynamics

Loop gain is a static concept. However, the differential equations of electrodiffusion physics involve time. Our electrodiffusion model has two important time constants. First, τ_spread, driven by drift and diffusion velocities, describes how quickly M can move along the worm and create a gradient.

Step 4 of our loop-gain sequence above describes how the head-to-tail ΔV_mem attracts more M to the front, creating a new [M] profile. If the ΔV_mem remains fixed long enough, electrodiffusion will eventually reach its new resulting [M] profile. τ_spread describes how quickly that process occurs.

Second, the generation/decay process has a time constant τ_gd for how quickly the morphogen M reaches a steady-state [M]_ss where generation and decay balance. Molecules do not last forever; they are sooner or later transformed via chemical reactions or other degradation. As noted above, we assume that M is created at a constant rate k_Gen moles/second in each cell and decays with rate τ_gd[M] mole/second; thus $\frac{d\left[M\right]}{dt}=k_{\text{Gen}}+{\tau }_{GD}\left[M\right].$ This leads to an exponential decay to the steady-state value ${\left[M\right]}_{SS}=\frac{k_G}{k_{\text{Dec}}},$ with the time constant τ_gd.

If generation and decay are too fast, they overwhelm electrodiffusion

If τ_gd ≪ τ_spread, then generation and decay will bring every cell to the steady-state [M]_ss much faster than electrodiffusion can redistribute M. In this case, all cells are forced by generation/decay to the same [M]_ss, any existing gradient collapses and electrodiffusion fails.

Even if loop gain is greater than unity—and statically electrodiffusion should be successful—the dynamics will not work. Generation and decay remove any gradient faster than electrodiffusion can amplify it.

Table III shows the number of worm-parameter choices that resulted in the creation of a gradient for various values of τ_gd. At τ_gd = 1 (the fastest generation and decay rate), no gradient can be maintained, no matter what the other parameters are or how much loop gain is present. At τ_gd = 10 (i.e., still quite fast), a small number of parameter sets can now regrow a worm—mostly those with slightly higher values of GJ_scale, allowing diffusion and drift currents to pass through the worm more quickly.

TABLE III.

Number of parameter choices producing robust fragment regrowth vs τ_gd.

	τgd = 1	τgd = 10	τgd = 100	τgd = 1000
5 cells	0	4	35	61
30 cells	0	5	64	77
100 cells	0	7	61	62

Generation and decay can be too slow—or just right

If τ_spread ≪ τ_gd, then generation and decay happen too slowly to substantially affect the establishment of a gradient. Our static loop-gain analysis, which ignored generation and decay, roughly made this assumption. Again, it concluded that for large Hill-model N, a worm fragment will only regrow a large gradient if the small fragment's initial range of [M] spans k_M.

However, we noted that the N = 8 column of Table II did have two successful parameter sets. In fact, they are due to the “Goldilocks” case of τ_gd ≈ τ_spread—i.e., the two time constants matching each other “just right.” Specifically, generation and decay pull all cells to [M]_ss at roughly the same rate as electrodiffusion spreads M. In this case, head, tail, and belly slice all regenerate identically well; the beauty of two processes works in synchrony. It does not matter how big either time constant is, but only that they are roughly equal.

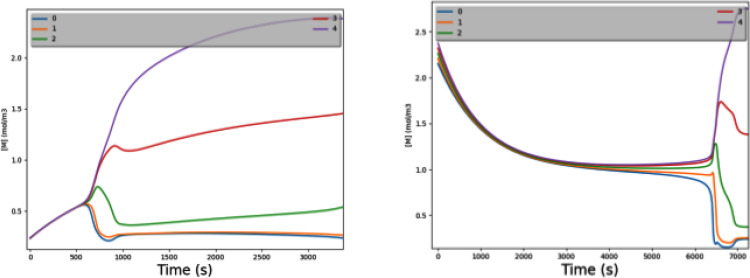
Figure 4 shows [M] varying over time during regrowth of worm fragments from near the tail [Fig. 4(a)] and head [Fig. 4(b)]. Both graphs represent the same parameter set that has τ_gd ≈ τ_spread. The tail fragment starts with all cells having very low [M] but still having a gradient; Δ[M] is small but nonzero. The generation/decay process naturally follows an exponential-decay trend toward [M]_ss (which is 1.0 in this example). The low initial [M] is far from the knee of the Hill-model curve, resulting in an initially low loop gain. However, before Δ[M] can fully collapse, generation/decay takes the fragment close enough to the knee that loop gain grows above 1. At that point, Δ[M] explodes to a large-scale gradient.

FIG. 4.

Regrowing a morphogen gradient with τ_gd ≈ τ_spread. This shows the rate of generation/decay being well balanced with that of electrodiffusion. The graph shows [M] vs time; each of the five worm cells is a separate curve in the graph. (a) A fragment from near the tail of a 5-cell worm has all 5 cells starting with very low [M]. Generation/decay raises them all toward [M]_ss (which is 1.0 in this example). As all cells rise toward [M]_ss, they barely maintain their very small Δ[M]. As they all approach [M] = k_M (0.8 in this example; the knee of the Hill model), the loop gain rises sharply and a substantial gradient quickly forms. (b) Exactly like (a), but now a fragment from near the head of a 5-cell worm; it starts with all cells having a high [M] (but with a small Δ[M] still existing). As generation/decay lowers them all toward [M]_ss, they eventually approach the knee of the Hill-model curve and generate a substantial gradient. If generation/decay is too slow, this process does not occur in time to affect cellular differentiation. If generation/decay is too fast, the small initial Δ[M] collapses before we reach the knee.

Figure 4(b) shows a similar process, but for a fragment from near the head of the worm. This time, the cells start with a high initial [M]. They slowly decay toward [M]_ss; again, when concentrations approach the knee of the Hill-model curve, the loop gain climbs over 1 and we explosively generate a gradient.

This serendipitous process can only occur if generation/decay is not too slow (which would prevent the fragment from reaching the knee of the curve before the low loop gain collapsed the initial gradient) and not too fast (in which case the cells would be quickly forced to [M]_ss). Can such a process work robustly when real-world generation rates can vary widely?

Matching τ_gd and τ_spread cannot be done robustly

To test this, we altered our simulations again. We started as before, simulating a wide range of parameter choices on 5-cell worms, and defining a successful parameter set as one that successfully regenerated at least 18 of 20 fragments. For each such parameter set, we then tried varying GJ_scale and τ_gd over wider and wider ranges until the worm was no longer successful. Table IV shows the results, ordered by the acceptable range of τ_gd:

TABLE IV.

Robustness to variation in GJ_scale and τ_gd.

N	qM	GJscale range	τgd range
2	−3	0.058–30 (5.2×)	65–6200 (95×)
2	−4	0.069–0.3 (4.3×)	65–5200 (79×)
2	−2	0.04–0.17 (4.3×)	190–13 000 (66×)
5	−1	0.034–0.17 (5.2×)	94–5200 (55×)
2	−3	0.1–0.21 (2.1×)	70–1300 (18×)
2	−3	0.058–0.21 (3.6×)	160–3000 (18×)
2	−4	0.069–0.21 (3×)	190–3600 (18×)
⋯	⋯	⋯	⋯
8	−2	0.1–0.1 (1×)	830–1000 (1.2×)

The widest range of τ_gd (i.e., the most robust worm) occurs when we achieve our gain at N = 2, as expected. The first (and in fact only) worm that successfully regenerates at N = 8 does so for only a very narrow range of GJ_scale and τ_gd; it is not robust to parameter variation.

DISCUSSION AND CONCLUSIONS

We have demonstrated that, within the predictions of our model, electrodiffusion can indeed be robust—but only for certain classes of parameter sets. Specifically, we must have sufficient loop gain, but we cannot achieve it with high Hill-model cooperativity. When we made the Hill-model N too high, we found that while a full worm could maintain a gradient easily, small fragments did not regenerate robustly. In other words, regeneration was not robust for all 20 fragment locations across worm sizes from 5 to 100 cells.

On the other hand, creating loop gain by combining a low or moderate cooperativity with a higher-valence morphogen worked quite well across the range of fragment locations and worm sizes. We did not need an extremely high valence; −2 or −3 worked well enough.

The morphogen is not only constrained with respect to valence, but also to physical size—since we are proposing that it pass through GJs, it must be small enough to do so. Furthermore, while GJs are selective to the size and valence of molecules passing through them, this selectivity can be quite complex (Harris, 2007); all of which constrains the choice of acceptable morphogens. Suitable candidates have been implicated in other systems including calcium, other ions, serotonin, and other small signaling molecules (Esser et al., 2006; Fukumoto et al., 2005; Harks et al., 2003; Krysko et al., 2005; Schumacher et al., 2012; and Zhang and Levin, 2009).

We found that while in principle a high cooperativity could be made to work by matching time constants to each other (τ_gd ≈ τ_spread), this could not be done robustly. Generation rates, in particular, are quite physically variable, and we found that making high cooperativity work across a range of fragment locations unfortunately requires unrealistically tight parameter tolerances.

We showed that robustness across fragment sizes required an allometric change in GJ_scale across worm size. Is this reasonable? While experimental testing of GJ density variation is not technically feasible, allometric scaling across a wide range of biological parameters has, of course, been long accepted (Schmidt-Nielsen, 1984).

Similar arguments to ours have been made for the atrioventricular (AV) node in the mammalian heart. The AV node consists of a large number of independent bioelectrical oscillator cells. Each cell would intrinsically oscillate at its own frequency; however, they interconnect to each other via GJs and hence all entrain to a single frequency, which ultimately determines the mammalian heart rate. Keener (Keener and Sneyd, 2009, Vol. 2) argues that too much GJ conduction prevents oscillations (much as we have shown that a high GJ_scale short-circuits worms), and also that not enough GJ conduction prevents entrainment (resulting in many uncoupled oscillators).

Cardiac GJs have a very short half-life (Falk et al., 2014); clearly there must be a mechanism to regulate the cardiac GJ_scale. However, we are not aware of any efforts to measure whether cardiac GJ density varies with organism size.

We have not, of course, explored all possible models of planarian electrodiffusion. One might easily consider using a GRN to insert gain stages (i.e., buffers and/or inverters) between the morphogen and the K⁺ ion channels. However, it seems unlikely that this would have any substantial effect. Step 2 of our loop-gain discussion was that the slightly higher [M] in front, working through the Hill model of the K⁺ ion channel, leads to the lower turn-on of K⁺ channels at the front than at the rear of the worm. No matter what GRN we use, it must still map from the existing [M] gradient to the fraction of K⁺ channels that are open, and that fraction must be between 0 and 1. Thus, just as we saw with high cooperativity, adding gain for some fragment locations must necessarily subtract gain for others.

On the other hand, it seems reasonable that altering our model, e.g., by using, Na⁺ channels in addition to K⁺ channels, would be quite effective. It essentially adds more gain to loop-gain's step 3; with roughly twice the number of ion channels in play, a given [M] gradient can result in a substantially higher ΔV_mem, resulting in higher loop gain.

In summary, we have found that it is possible to implement electrodiffusion robustly, and that the most effective way to do so is by using a higher-valence morphogen combined with allometric scaling of GJ density.

These results make several predictions for experimental verification. First, with respect to planaria:

• •Our morphogen will likely be a molecule with valence higher than 1. A good candidate could be serotonin, with a +2 valence and which is a morphogen in other electrically controlled systems. Indeed, serotonin has already been found to be an electrophoretically redistributed morphogen in other patterning systems, such as frog and chick embryos (Adams et al., 2006; Blackiston et al., 2015; Esser et al., 2006; and Fukumoto et al., 2005).
• •GJ density will scale allometrically with worm length.
• •Reactions involved with ligand-controlled ion channels will have a low cooperativity.

Second, beyond the understanding of existing model systems, our model makes suggestions for the design of synthetic morphology. Recent work in organoids and computer-designed organisms (Kriegman et al., 2020; Levin and Martinez Arias, 2019) offers the opportunity to use the knowledge of signaling dynamics to implement regenerative, self-patterning capacities in bioengineered systems by taking advantage of bioelectric circuits.

We should also note the limitations of our work. First, showing that electrodiffusion can be robust is not the same as providing direct experimental evidence that electrodiffusion is used in planaria. As mentioned above, axonal transport (Pietak et al., 2019) and reaction-diffusion (Turing, 1953) are also viable candidates for creating an anterior–posterior morphogen gradient, as are combinations of all three types of mechanisms.

Furthermore, we live in a three-dimensional world and thus need morphogen gradients along multiple axes; it is completely plausible that different mechanisms are used to produce different gradients, with a global mechanism needed to coordinate them that is still not understood. No matter which method creates the initial head-to-tail morphogen gradients, GRNs will be required to create the proteins needed for physical cell development, and in doing so are likely to create their own local morphogen gradients (Reddien, 2018), all of which must work together in as-yet-poorly understood ways.

Finally, planaria are the champions of regeneration; while it seems reasonable to expect many aspects of regeneration to be conserved across other organisms (Bely and Nyberg, 2010; Maden, 2018), the details may not be. In particular, bioelectric signaling has now been implicated in numerous model systems including plants, zebrafish, frog, mouse, and human (reviewed in Bates, 2015; Harris, 2021; and Levin, 2021), but many specifics remain to be worked out with respect to how the bioelectric circuits function in different patterning contexts across taxa.

Future work

In silico evolutionary algorithms have been (Kriegman et al., 2020) used to design synthetic organisms called “Xenobots” that exhibit locomotion. The researchers found that the designs predicted by computer simulation to move quickly only performed well in vivo when they incorporated robustness into their evolutionary fitness function. We predict that in order to build an Xenobot-like organism that uses electrodiffusion for global communication, one would have to use a robust parameter set similar to ours. It should be possible to build such an organism using ligand-controlled ion channels and GJs; the ion channels could be directly controlled by a morphogen (e.g., serotonin) (Wu et al., 2015) or via an intermediate GRN. We would need a mechanism of controlling the ion-channel and GJ densities.

Experimental technique cannot currently measure GJ density. However, one could still support our prediction of allometric GJ scaling with in silico simulation of the human heart. It would seem that cardiac sinoatrial cells would require similar allometric GJ scaling in order for them to entrain each other and produce a single coherent heartbeat. Since human-heart ion-channel and GJ models are more detailed than their planarian equivalents, that would arguably be a better proof of concept than our simulations.

While we arrived at robust planarian parameter sets by using large-scale simulations of myriad parameter choices, the robustness (like all biological traits) is an evolved property. It would thus be useful to show that an evolutionary algorithm with a suitable fitness function (e.g., one that gives points for robustness) could evolve to produce results similar to those we found.

We have focused on electrodiffusion and ignored the axonal-transport hypothesis. However, if axonal transport is to be a viable hypothesis, it too must be robust. While Pietak (2019) argued that axonal transport itself is robust, they did not show that their proposed GRN is equally robust. Future work should evaluate that.

DATA AVAILABILITY

The data that support the findings of this study are openly available in Gitlab at https://gitlab.com/grodstein/bitsey (Grodstein, 2018).