Microfluidic techniques for mechanical measurements of biological samples

Abstract

The use of microfluidics to make mechanical property measurements is increasingly common. Fabrication of microfluidic devices has enabled various types of flow control and sensor integration at micrometer length scales to interrogate biological materials. For rheological measurements of biofluids, the small length scales are well suited to reach high rates, and measurements can be made on droplet-sized samples. The control of flow fields, constrictions, and external fields can be used in microfluidics to make mechanical measurements of individual bioparticle properties, often at high sampling rates for high-throughput measurements. Microfluidics also enables the measurement of bio-surfaces, such as the elasticity and permeability properties of layers of cells cultured in microfluidic devices. Recent progress on these topics is reviewed, and future directions are discussed.

I. INTRODUCTION

Measurements of biological systems were one of the original motivations for the development of microfluidic technologies.¹ These early "lab-on-a-chip" devices primarily focused on microreactors or for molecular analyses such as high-throughput DNA sequencing. The methodologies used in the fabrication and design of these devices have been adopted by many different fields for manipulating flow at micrometer length scales for a wide variety of purposes. The measurement of mechanical properties of biological material has been a particular area for a proliferation of new measurement techniques not feasible with macroscale instrumentation.

For instance, the use of microfluidics for rheological characterization has been of interest to characterize high shear rate viscosity, extensional flow behaviors, while requiring small sample sizes.² Microfluidics is also frequently combined with microscopy imaging to characterize the dynamic behavior of suspended bio-particles.³ The application of these techniques is often well-suited for biological applications where many biofluids are suspensions with viscoelastic properties and sample volumes are often limited.⁴

The measurement of individual cell properties has been a long-standing purpose for microfluidics.^5–8 The ultimate goal of many of these technologies is to produce platforms for testing medical treatments by comparing normal cell properties to cells in diseased states and then after treatment. Methods developed for manipulation and characterization of individual cells have also been increasingly used for assisted reproductive technologies, many of which require measurements of biomechanical properties.^9–11 The controlled flow environment in microfluidics has also lead to new methods for studying the development of biofilms and developing mitigation technologies for biofouling.¹²

The small length scales used in microfluidic channel flows are a natural fit for in vitro models for studying the microcirculatory system, such as red blood cell (RBC) behavior and endothelium properties.¹³ Other examples of devices that mimic physiological systems, often referred to as "organ-on-a-chip" technologies, are produced by culturing cells in microfluidic chambers with applied flow.¹⁴ The flow in these devices is needed for transport of nutrients and waste products as well as applying stress, which is important for the function of many biological components. The response of cells to applied stress in microfluidics is increasingly used for mechanobiology research, which aims to understand the responses of biological systems to applied mechanical stress.^15–19 The mechanical properties of cells and tissues are important aspects for cell functions. For instance, the application of stress to cells during culturing and the measurement of mechanical properties can both be accomplished through design and flow controls of microfluidic devices.

This review focuses on microfluidic techniques recently developed for making mechanical property measurements of biological materials. The emphasis is on the measurement of mechanical properties and mass transport, such as viscosity, elastic modulus, and permeability, of biological samples. Techniques that are intended for biological samples, but demonstrated with synthetic systems are highlighted as well. First, the use of microfluidic rheometers for the measurement of properties such as shear viscosity, extensional viscosity, and relaxation time are reviewed. The development of robust devices intended for high shear rates and point-of-care deployment are focused on due to their applications in pharmaceutical industry and medical testing. Section II focuses on the measurement of mechanical properties of soft biological particles, such as cells and vesicles. Various approaches are discussed including methods for deforming particles by flow stress, geometric confinement, and externally applied fields. Devices specifically intended for measuring mechanical properties of bacteria and forces exerted by nematodes are highlighted. Section III focuses on measurements of the properties of cell layers. This includes the response of biofilms to flow stress and the elasticity and permeability of cell layers, such as endothelial cells, in both planar and 3D geometries. In conclusion, challenges and future directions for biomechanical measurements in microfluidics are discussed. A summary of the types of devices, their working principles, main applications, and commonly studied samples covered in this review are shown in Table I.

TABLE I.

Summary of the device types, their working principle, main applications, and samples of interest covered in this review.

	Device type	Principle	Main applications	Common samples
Viscoelastic fluids	Microelectromechanical (MEMS) viscometers	Resonator characteristics are used to measure viscosity and density.	Microliter volumes for single shear rate point-of-care measurements	Blood, saliva
	Capillary viscometers	Capillary pressure-driven flow through microchannels or paper and measured flow is used to determine viscosity relative to reference	Small volume requirements and point-of-care applications	Blood, saliva
	Shear viscosity rheometers	Shear viscosity as a function of shear rate is determined using relationship between pressure drop and flow rate	Measurement of both Newtonian and non-Newtonian fluids often at high shear rates with $\mu \mathrm{l}$ to ml volumes	Blood, protein solutions
	On-chip particle tracking rheology	Relate diffusion of dispersed particles to material creep compliance	Measurements of viscoelastic properties during phase transitions without applied deformation	Hydrogels, protein solutions
	Extensional rheometers	Measure resistance to fluid due to the extensional components of microchannel flows	Extensional viscosity measurement of non-Newtonian fluids at high rates with small volumes	Saliva, synovial fluid
Biological particles	Constrictions (flow deformation)	Measure modulus due to extensional flow stress in a fluidic constriction	Rapid measurement of modulus for flow cytometry	Red blood cells, DNA, actin
	Cross-slot	Deformation from extensional flow in center of cross-slot is related to viscoelastic properties	Measurements of large strains, time-dependent deformation, and manipulation of individual cells	Red blood cells, cancer cells, DNA, vesicles
	Constrictions (confinement)	Particles are forced into narrow constrictions and resistance to applied force is used to determine viscoelastic properties	Large deformation, multiplexed, and high-throughput measurements	Red blood cells, cancer cells
	Electrical and optical	Electrical and optical fields generate stress on particles to induce deformation that is related to mechanical properties	Manipulation of particles, tunable stress, and cyclic loading for fatigue measurements	Red blood cells, vesicles
	Filament shape specific	Elongated cells are trapped in chambers and flow stress produces bending	Observation of the change in properties under different growth conditions	Escherichia coli
	Cell forces	Deformation of soft micropillars with known properties are used to measure forces exerted by organisms	Measure forces under different environmental conditions and organism mutations	Caenorhabditis elegans
Cell layers	Biofilms	Measurements of the structure, growth, and internal flow of biofilms provide viscoelastic properties and critical shear stress	Testing impact of various chemical and stress conditions on growth and mechanical properties	Bacterial biofilms
	Planar cell layers	The deformation of membranes with cultured cells is used to measure elastic modulus. Flow through cell layers on permeable membranes is used to measure permeability	Measures the effect of environment, including media type and flow stress, and exposure to drugs	Epithelial and endothelial cells
	3D geometries	Cell layers or tissues are cultured in cylindrical or suspended geometries to observe their deformation and/or mass transport across them	The elasticity and permeability of cell layers exposed to flow conditions mimicking physiological environment	Collagen, endothelial cells

II. MICROFLUIDIC RHEOLOGY OF BIOLOGICAL FLUIDS

Rheometry measures the viscoelastic properties of complex fluids under the flow. The mechanical properties of many biological and biocompatible materials are crucial for proper biological function. For instance, high concentration of biologic drug formulations can vary significantly in viscosity, which can affect injectability and processing. The stability of these high concentration formulations is also an important factor for therapeutic efficacy, where change in solution state and the loss of efficacy manifest as a change in rheological properties. Changes in the mechanical properties of biological fluids, such as blood and saliva, can also be indicators of disease. See previous reviews of microfluidic viscometers and rheometers for discussion on a range of device designs and applications.^2,20

Biological fluids are also often high in value and available in small quantities, which has motivated the development of microfluidic rheometers that use smaller volumes than traditional rheologic techniques. Small form factor microfluidic devices are particularly well-suited for biological fluids that rapidly change properties outside of the physiological conditions, such as blood, which necessitates the point-of-care measurement. The rheology of blood is a challenge due to the complexity of the suspension and donor to donor variation. See a recent review by Beris et al. for more details on blood rheology.²¹ One particular challenge for blood rheology measurements is the rapid coagulation of RBCs, which occurs after collection and can have a significant effect on viscosity. Typically stabilization agents are added to the blood immediately after collection, but the measurement is best performed soon after collection. The deploy ability of a microfluidic device provides the possibility for screening through blood property measurements. See a review by Kang and Lee on the in vitro and ex vivo measurement of blood properties using microfluidics for more details.²²

In this section, advancements in microfluidic viscometers and rheometers are discussed. Here, viscometers are referred to as devices that measure viscosity at a single shear rate, while rheometers measure it at multiple shear rates. The integration of rheometric measurements based on particle tracking into microfluidic devices is discussed. Finally, the methods for measuring extensional viscosity of complex fluids are discussed.

A. Microfluidic MEMS viscometers

Many methods exist for measuring fluid viscosity where viscosity is independent of the shear rate, i.e., Newtonian fluids, or only one shear rate is of interest, such as the 0 s⁻¹ shear rate limit. The advantage of many viscometers is that they often require very small sample sizes on the order of (10 to 100) µL. Measurements can also be made without the application of flow but with other sensors integrated into microelectronic mechanical systems (MEMS). For more details on microfluidic viscometers, see a recent review by Puneeth et al.²³ Another recent review from Singh et al. focuses on MEMS-based viscometers.²⁴ Here, we highlight approaches related to biological fluids.

A popular approach for measuring fluid viscosity and density uses the resonant characteristics of MEMS resonators.^27,28 This approach is well-suited for biological fluids and point-of-care applications because it requires small volumes and can be incorporated into established electronic sensing technologies. Improvements to the designs for the MEMS sensors have focused on increasing sensitivity and reducing complexity and cost.

For example, a MEMS resonator was developed by Cakman et al. to measure the viscosity of samples as small as 150 µL.²⁹ The device worked by actuating Ni cantilevers using a magnetic field and their response, measured using a phase lock loop control circuit, and detected changes by the reflection of a laser off the cantilever. A model to relate the phase change to the viscosity was calibrated with glycerol solutions. The device capabilities were demonstrated with viscosity measurements in the range of (1 to 14) mPa s and tested on various bovine serum albumin (BSA) solutions and blood plasma.³⁰ The cantilever technique was later incorporated into a device with multiple channels and mounted on a temperature control stage, and the required sample size was decreased to 10 µL.³¹ Solutions with different viscosities and densities were used to calibrate the device. The samples were combined with different coagulation activators used in clinical settings, and the coagulation is measured by the viscosity over time to distinguish between normal and abnormal samples. The device was further developed to measure both density and viscosity using multiple cantilevers with different dimensions.³²

The use of cantilever resonators for measuring blood coagulation was pursued by Padovani et al. with the motivation to reduce issues with adsorption onto the cantilevers and analyze the rate of RBC aggregation in addition to the density and viscosity measurements.³³ A calibration process using glycerol-water mixtures was used to determine density and viscosity measurements. Various surface functionalization on the cantilevers were evaluated by measuring the mass adsorption using thrombin and fibrinogen protein solutions, and a polyethylene-glycol (PEG) surface coating was determined to be the most effective at reducing adsorption. The sensitivity of the device was used to measure human plasma coagulation kinetics through the change in viscosity. The device was used in another study to measure coagulation kinetics in response to various activated coagulation tests used in clinical settings.³⁴

Similar to the cantilever design, magnetically actuated microposts were used by Judith et al. to measure the viscoelasticity of blood clots.³⁵ The microposts were fabricated from polydimethylsiloxane (PDMS) with a magnetic nickel shell on top of the posts. The microposts were actuated by an oscillatory magnetic field, and the response was observed through microscopy and a photodiode detector. The device was used to measure the stiffness of blood clots over time and after a sequence of dilutions. Modeling of the micropost response was developed to include hydrodynamic interactions of the actuated microposts to measure viscosity.²⁶ Measurements of the viscosity of sucrose and corn syrup solutions were compared to reference measurements, and the capability for measuring biofluids such as mucus, synovial fluid, and blood was discussed.

Rather than using posts or cantilevers, a MEMS resonating microplate design was developed by Manzaneque et al. that works by sensing the response of the resonator to an applied actuation.³⁶ A model was developed to describe the relationship between the oscillations, the density, and viscosity of the fluid surrounding the plate. The device was tested on a set of fluids in the (1 to 10) mPa s range and showed good agreement with reference measurements. Another film-based design by Ahumada et al. used a quartz crystal microbalance (QCM) to measure viscosity of hyaluronic acid (HA) as a method for detecting arthritis.³⁷ The quartz crystal resonator works by stimulation with an alternating current (AC) voltage that vibrates the crystal at a resonant frequency. By conducting a frequency sweep near the resonant frequency, the response of the crystal to the fluid surrounding liquid can be related to the viscoelastic properties of the fluid. A sample holder that used about 50 µL of solution was connected to an Arduino card for applying and analyzing the electrical signals. The results were compared to reference measurements, and an error between 9 % and 56 % was determined for different HA solution concentrations.

The QCM approach was later used by Yao et al. to measure blood coagulation by tracking the dissipation factor measured by the sensor and related the changes to blood viscoelasticity.³⁸ The testing portion of the device was integrated with electronics to connect to a smartphone for analysis. The results showed high correlation with coagulation times made from reference measurements. A different approach for measuring the aggregation kinetics of blood was taken by Chen et al. using a film bulk acoustic resonator (FBAR), a MEMS sensor that works at gigahertz frequencies and has higher sensitivities than other MEMS sensors, see Fig. 1(a).²⁵ The viscosity was measured through a calibration procedure with glycerol–water solutions. Microliter-scale drops were placed on the sensor surface, and the change in viscosity over time is used to determine the coagulation response to various additives. For instance, the effect of added heparin to blood samples was studied to measure the effect of the concentration on coagulation. A different surface-based device by Chen et al. measured changes in the viscoelastic properties of blood during coagulation using a surface acoustic wave sensor (SAW).³⁹ The device was designed to be disposable and used 1 µL of sample. The shift in the maximum frequency of the SAW was used to determine the change in viscosity over time. The large frequency shift with viscosity changes produced more sensitivity compared to other resonator-based measurements. Coagulation kinetics of blood samples are measured and compared to standard thromboelastography measurements.

FIG. 1.

(a) A film bulk acoustic resonator using a ZnO film designed by Chen et al. for blood viscosity measurements.²⁵ Reproduced with permission from Chen et al., Sensors 17, 1015 (2017). Copyright 2017 authors, licensed under a Creative Commons Attribution (CC BY) License. (b) Magnetically actuated flexible microposts were used by Judith et al. to measure the viscosity through hydrodynamic interactions.²⁶ Reproduced with permission from Judith et al., PLoS One 13, e0200345 (2018). Copyright 2018 authors, licensed under a Creative Commons Attribution (CC BY) License.

The deformation of materials that can be excited by resonators in microfluidic device has also been used as viscometers. For example, a magnetoelastic material that resonates in an AC magnetic field was incorporating into a microfluidic device by Chen et al.⁴⁰ The resonance spectra of the sensor were measured to calibrate the device for different glycerol–water solutions in the range of (1 to 1420) mPa s. The device was used to measure plasma solutions in the range of (1 to 3) mPa s with uncertainty around 1 $\%$. A membrane transducer made from silicon nitride was used by Oliva et al. to measure density and viscosity of polymerizing F-actin solutions placed in a 1 µL microwell.⁴¹ The setup consisted of excitation and detection lasers, which were used to excite the membrane resonator through photothermal actuation and then measure the response from a separate detection laser optical path. The glycerol–water calibration approach was used to extract the density and viscosity from the eigenfrequency and quality factor. One main advantage of the membrane resonator is the rapid measurement time, about 3 min for each sample, which could be further reduced using faster readout systems.

A different approach using suspended magnetic particles as resonators was demonstrated by Wu et al.⁴² The paramagnetic particles were actuated by a mixed high and low frequency signal. A detection coil was used to measure the phase lag, determined by a voltage drop, between the particles response and the applied field. The phase lag was used to determine the viscosity by calibration with various glycerol–water mixtures over the range of (1 to 1000) mPa s. The technique was used to measure the viscosity of serum samples in the range of (1 to 8) mPa s.

An indirect approach for viscosity measurement was developed by Zarrin et al. through relating changes in dielectric properties to viscosity of saliva of patients with Chronic Obstructive Pulmonary Disease (COPD).⁴³ The saliva in COPD patients was approximately 10 % more viscous due to a lower water content, which was measured by a decrease in electrical conductivity compared to healthy controls. The measurement is challenging due to the small changes in conductivity and viscosity, but the simplicity of the measurement makes it advantageous for point-of-care measurements.

B. Capillary driven viscometers and rheometers

Capillary driven flows are well-suited for microfluidic viscometry because microfluidic geometries easily generate sufficient force to drive flow. One main advantage of the technique is that flow can be produced without the need for syringe pumps or pneumatics. They also often require small amounts of sample. Capillary driven viscometers generally fall under two categories, either using small microchannels or paper based devices.

An example of a small volume capillary driven flow method for measuring fluid viscosity was developed by Srivastava et al.⁴⁴ A reference fluid was used to calibrate the capillary pressure and then the velocity of the meniscus was used to determine the viscosity relative to the calibration fluid viscosity. The approach could measure fluid viscosities in the range of (1 to 5) mPa s and was used to measure blood plasma samples while using less than 1 µL of sample. Further development integrated electronic sensing, rather than optical methods, to determine the velocity of the meniscus.⁴⁵ The same capillary driven flow method was used to measure non-Newtonian fluids by tracking the variation in velocity over time as the sample loads into the device.⁴⁶ Recently, the capillary driven flow concept was used by Lee et al. to measure the viscosity of zebrafish blood at high shear rates, see Fig. 2(d).⁴⁷ The device required a sample of 3 µL and was calibrated using water. The viscosity of the zebrafish blood was shown to be Newtonian in the shear rate range of approximately ( ${10}^3$ to ${10}^4$) s⁻¹. The viscosity as a function of hematocrit levels was measured in both adult and embryonic zebrafish. Another recent method by Puneeth et al. used a fused deposition fabrication to make devices from polycaprolactone and used meniscus tracking to measure capillary driven flow rate.⁴⁸ The device integrates into a single-board computer with an integrated camera, and image processing is automated to determine the flow rate by tracking the change in position of the liquid meniscus in the microfluidic channel.

FIG. 2.

(a) A paper based device developed by Li et al. for measuring the coagulation of blood by related the travel time of the fluid front to the viscosity. The device was later tested as a point-of-care diagnostic device by Hegener et al.^49,50,52 Reproduced from Li et al., Biomicrofluidics 12, 014110 (2018) with the permission of AIP Publishing LLC. (b) A paper based device by Jang et al. used two paper strips for faster capillary driven flow to measure fluid viscosity without requiring a separate surface tension measurement.⁵⁵ Reproduced with permission from Jang et al., Sens. Actuators, B 319, 128240 (2020). Copyright 2020 Elsevier B.V. (c) A paper-based device developed by Kang et al. uses the color of two mixed streams to measure the relative flow rates of the stream and determine viscosity.⁵⁶ Reproduced with permission from Kang et al., Anal. Chem. 91, 4868 (2019). Copyright 2019 American Chemical Society. (d) A capillary-driven flow device designed by Lee et al. was used to measure zebrafish blood viscosity by tracking the interface velocity.⁴⁷ Reproduced with permission from Lee et al., Sci. Rep. 7, 1980 (2017). Copyright 2017 authors, licensed under a Creative Commons Attribution (CC BY) License.

Paper based devices are often useful as disposable point-of-care devices. A paper based device by Li et al. was designed to measure the coagulation of blood through changes in viscosity, see Fig. 2(a).⁴⁹ The device consists of three sections, a sample pad for sample collection, analytical membrane where the blood interface is tracked and wicking pad for continuous capillary force. The transport of both plasma and RBCs was both tracked on the membrane portion of the device. The travel time is related to the viscosity using reference values from glycerin–water solutions. The effect of CaCl₂ on clotting was studied by measuring the travel distance at a fixed time for different concentrations of CaCl₂. The device was used by Hegener et al. to obtain clinical results for blood coagulation measurements using 30 µL of whole blood.⁵⁰ In this device, the travel distance was shown to vary with both hematocrit level and international normalized ratio (INR), a measure of prothrombin (blood clotting) time. The devices were designed to provide rapid and low-cost measurement to determine if a patient was within a normal range or if further tests were needed. A calibration method was developed to correct for the effect of the hematocrit level and improved the measurement of INR.⁵¹ The device was also demonstrated for measurements of blood clotting in animal blood.⁵² The effect of hematocrit on the lateral flow velocity was exploited by Frantz et al. by using a smartphone to automate tracking of the RBC front.⁵³ Hematocrit levels between 28 % and 45 $\%$ were measured within about (1 to 3) $\%$ difference from the nominal values after about 20 s.

A device to measure biofluid viscosity was developed by Rayaprolu et al. by using the transit time between two marks on a paper strip.⁵⁴ The sample viscosity was determined relative to the viscosity of water by comparing the sample's transit time and density relative to water results. The measured viscosity with the addition of either glycerol or sucrose was shown to have high correlation with measurements with an Ostwald viscometer between 1 mPa s and 40 mPa s. The device used less than 20 µL and the total time required was between 20 s and 1000 s, about four times faster than using the Ostwald viscometer. The device was used to measure the viscosity of saliva, protein solutions, and dextran solutions.

A different type of paper device was developed by Jang et al., based on a theoretical analysis by Shaumburg and Berli, that had a gap between two paper strips such that capillary driven flow would be increased compared to flow through paper, see Fig. 2(b).^55,57 The effect of the gap dimension on the rate of meniscus travel was studied, and a maximum rate was observed for a 195 µm gap. One feature of the two layer design was the liquid was drawn up in the gap in the early flow stage but later only within the paper. The equilibrium height of the liquid in the gap and curve fitting of the meniscus velocity was used to determine the viscosity and diffusivity of the solution. Only one calibration parameter was required, the effective radius, but that parameter only depended on the device geometry. The device was validated by comparing PEG solutions and artificial saliva with reference measurements. Measurement errors less than 4 $\%$ were shown for samples with viscosity in the range of (1 to 6) mPa s.

Another paper based viscometer used a "colorimetric" method by coflowing two fluids of two colors together into a T-junction, see Fig. 2(c).⁵⁶ The reference fluid was dyed blue, and the sample fluid was dyed yellow. The color in the main channel was then used to measure the relative flow rates of the two fluids, which is inversely related to the relative viscosities. The device was constructed from multiple paper layers to create a loading, mixing, and measurement portions of the device. The viscosity can be determined by a single image, rather than a video, which makes measurement by a mobile phone simpler. Various biofluids such as blood plasma and bovine-serum-albumin solution were tested and compared to reference measurements within a few percent. While this method does not measure multiple shear rates, the device used as little as 20 µL of sample.

C. Shear viscosity measurements and capillary rheometers

Microfluidic rheology is often designed for high shear rate measurements due to the small channel dimensions.⁵⁸ A common microfluidic measurement is to determine the shear viscosity. The velocity gradient at the wall, defined as $\dot{\gamma }=\partial v_x/\partial y$, is used to determine the viscous resistance, $\eta ={\sigma }_{xy}/\dot{\gamma }$, where ${\sigma }_{xy}$ is the $x-y$ shear stress component of the stress tensor. For Newtonian fluids, the viscosity is independent of shear rate and the viscosity at the wall of a rectangular channel is determined by the ratio of wall shear stress, ${\sigma }_w$, to the wall shear rate, $\gamma$, using the equations,

$$\begin{array}{c}\dot{\gamma }=\frac{6Q}{w{h}^2},\hspace{1em}{\sigma }_w={\sigma }_{xy}=\frac{\Delta \mathit{Pwh}}{2L(w+h)},\hspace{1em}\eta =\frac{{\sigma }_w}{\dot{\gamma }},\hfill \end{array}$$ (1)

where Q is the flow rate and h is the channel height and w is the channel width. Flow is generated either by applying a known flow rate from a syringe pump and measuring the pressure drop along the channel or by applying a known pressure drop and measuring the flow rate. Additional analysis is needed to measure the non-Newtonian viscosity, see Pipe and McKinley for details.⁵⁹

For pressure driven flow microfluidic rheometers, limitations include the range of pressure regulators and the maximum pressure a device can withstand before deforming or bursting. The accuracy and operating range of flow sensors is another limitation. For syringe pump driven flow, which typically has a wide operating range, the accuracy of pressure or stress sensors are often the limiting factor. The accuracy of the channel dimensions, particularly the channel height or radius, is important since the viscosity scales as $\eta \sim h^{-3}$ for rectangular channels. Wall slip can also lead to error in the measurement of viscosity in microfluidics. The effects of wall slip can be investigated by changing channel dimensions or through particle tracking methods.⁶⁰

For biological fluids, many of the technological improvements in shear viscosity measurement have focused on novel shear stress measurements and flow rate measurements using meniscus tracking to limit sample volume. A small volume microfluidic rheometer using pressure driven flow was developed by Hudson et al. that used a drawn glass capillary to measure the viscosity of protein solutions.⁶¹ Using water as a working fluid, water was brought in contact with the sample in a reservoir and then through pneumatic controls the sample liquid was drawn up into the microcapillary section. A calibrated flow sensor in-line with the water tubing measured the flow rate. The viscosity was calculated using by accounting for the resistances of the various flow components and determining the pressure drop associated with the microcapillary section. The device was used to measure the viscosity of protein solutions at different concentrations and temperature. The advantage of the approach was the ability to measure up to three decades in shear rate using a single capillary setup between 10 s⁻¹ to over ${10}^5$ s⁻¹. The small volume rheometer was used by Dharmaraj et al. to measure the viscosity of lysozyme solutions at different concentrations and temperatures.⁶² Non-Newtonian behavior was observed and the structural relaxation time was related to the relaxation time determined by dynamic light scattering as a function of temperature.

Another method well-suited for flow rate measurements but without using a working fluid is meniscus tracking. The velocity of the meniscus can be converted to flow rate through multiplication with the cross sectional area of the channel.⁶³ This method was adapted by Solomon et al. to track the meniscus through a PDMS channels using a phone camera, see Fig. 3(b).⁶⁴ The device was used to measure viscosity over about two decades in the shear rate for a given fluid within the range of (10 to 10⁴) s⁻¹. A straight channel geometry allowed for multiple channels to be fabricated in parallel on the same chip and "multiplexed" measurements of different samples was performed. The viscosity of shear-thinning biocompatible polymer solutions and bovine serum albumin (BSA) protein solutions was measured using the device.

FIG. 3.

(a) A "smart" pipette designed by Oh et al. with an air chamber to deliver pneumatic pressure to microcapillary channels in a 3D-printed microfluidic for viscosity measurement at different flow rates.⁶⁷ Reproduced with permission from S. Oh and S. Choi, Micromachines 9, 314 (2018). Copyright 2018 Authors, licensed under a Creative Commons Attribution (CC BY) License. (b) A meniscus method for viscosity measurements by Solomon et al. to measure flow rate through a microchannel using a smartphone camera.⁶⁴ Reproduced with permission from Solomon et al., Rheol. Acta 55, 727 (2016). Copyright 2016 Springer-Verlag Berlin Heidelberg. (c) A microfluidic rheometer fabricated by Mendez-Mora et al. with gold electrodes across a microfluidic channel used to track the fluid meniscus for flow rate measurements.⁶⁵ Reproduced with permission from Méndez-Mora et al., Micromachines 12, 726 (2021). Copyright 2021 authors, licensed under a Creative Commons Attribution (CC BY) License. (d) A small volume rheometer designed by Salipante et al. uses real-time mesniscus tracking using a linear image sensor and a pneumatic valve to reversibly drive flow through a microcapillary.⁶⁶ Reproduced with permission from Salipante et al., Rheol. Acta 61, 309 (2022). Copyright 2022. This is a U.S. government work and not under copyright protection in the U.S.; foreign copyright protection may apply.

Another example of a small volume rheometer using interface tracking was designed by Mendez-Mora et al. as a point-of-care device, see Fig. 3(c).⁶⁵ Channels in PDMS were bonded to a glass substrate with gold electrodes along a surface. The change in electrical signals of the electrode array was used to track the fluid meniscus. A portable pneumatic pressure pump was used for point-of-care purposes. The device was validated with reference fluids and then used to measure blood samples at different hematocrit levels as a function of shear rate. The volume of fluid used in the experiments was 0.5 mL, but the interface tracking approach can use less than 0.1 mL of volume with different device geometries.

A device that utilized the interface tracking approach was recently developed by Salipante et al. for small volume high shear rate measurements.⁶⁶ The device used pneumatically driven flow through a silica microcapillary connected to larger glass capillary where the meniscus is tracked with a linear image sensor, see Fig. 3(d). A pneumatic valve is used to switch the direction of the applied pressure and automatic controls were used to sample multiple transits at different applied pressures. The viscosity over the range of approximately (1 to 1000) mPa was measured between 10 s⁻¹ and 10⁵ s⁻¹ shear rate range using a single capillary device. A minimum volume of approximately 50 µL was demonstrated.

A slightly different approach based on interface tracking was taken by Oh and Choi for a “smart" pipette rheometer, see Fig. 3(a).⁶⁷ The device used an air chamber as a pressure buffer to deliver the same pneumatic pressure to different microcapillary channels in a 3D-printed microfluidic device. The compressed air volume was used to calculate the pressure relative to atmosphere, which eliminated the need for either a syringe pump or a pressure controller. The displacement of fluid volume by the air was small relative chamber size, which limited the change in applied pressure during operation. The flow rates are determined by tracking the transit of the meniscus using a phone camera in each of the fluidic chambers. The viscosity at different shear rates can be obtained by changing the resistance of the microcapillaries, which is performed by changing the capillary geometry. Glycerol and xanthan gum solutions, examples of Newtonian and non-Newtonian fluids respectively with comparable viscosity to blood, were used to test the device in the shear rate range of about (10 to 100) s⁻¹.

Rather than track a meniscus inside a channel, a design by Tammaro et al. measured flow rate by tracking the free surface of the liquid as it exits a microcapillary.⁶⁸ Multiple microcapillaries machined in stainless steel are used for measurements at different shear rates. The assembled parts integrated temperature control, pressure sensors, inlets for gas and sample, and a window for observing the sample outlet. The multiple microcapillaries resulted in a wide shear rate range of about (0.01 to ${10}^3$) s⁻¹ for high viscosity polymer melts. The volume requirements for polymer melts was shown to be about 10 ml, and the device geometry could be modified for measurements of biofluids with lower viscosities.

A different type of interface tracking based methods was recently developed by Shih et al. using a centrifugal platform to deform the interface of the sample liquid.⁶⁹ The deflection angle of the meniscus is obtained visually or through image analysis. A theoretical model was developed to describe the relationship between interface deformation and the sample viscosity. The device was shown to use approximately 25 µL of samples and was designed for portability and ease of operation.

These examples of microfluidic rheometers utilized pneumatic controls and interface tracking for shear viscosity measurements over wider range of shear rates than previously demonstrated and using microliter-scale volumes. Future developments of this technology have multiple directions. For instance, point-of-care measurements require reducing the need for extensive lab equipment while maintaining accuracy. Further reducing the required fluid volume to less than 100 µL is particular important for pharmaceutical applications where early stage manufacture of samples is expensive and viscosity is important for therapeutic efficacy. Improvements to device robustness and scalability are required for both small volume and point-of-care applications, particularly for the commercial development of these types of rheometers.

Another method for measuring shear viscosity involves tracking the position of an interface between two co-flowing streams in a rectangular microchannel. The method was developed by Galambos and Forster and was later extended to measure complex fluids by Guillot et al.^70,71 Sample fluid was flowed through one inlet port while a reference fluid was flowed through the other, creating an interface between the two fluids in the main channel. The position of the interface and relative flow rates of the two fluids were used to determine the viscosity contrast, which was used to determine the unknown viscosity of the sample. The device was used to measure the shear thinning behavior of various fluids in the range of (10 to 1000) s⁻¹ and compared to reference measurements. Using a slightly different coaxial flow approach, Lan et al. measured viscosity by tracking the diameter of the co-flowing stream.⁷² Similar to the rectangular geometry, the flow rate of the two streams, the viscosity of the reference fluid, and the measured stream diameter was used to determine the sample viscosity.

The co-flow method was used by Kang et al. to study the non-Newtonian properties of blood by using an array of channels downstream of a Y-junction to determine the relative viscosity from the relative flow rates and the number of downstream channels occupied by each fluid.⁷³ The device was validated by comparing viscosity measurements of the shear-thinning behavior of blood to rotational rheometry. Further developments based on the co-flowing approach have focused on measuring blood viscoelasticity by tracking both steady and transient flow. This was performed by Jun Kang and Lee using a device where sample transfers through a bridging channel, an analogue to a Wheatstone-bridge, to a second channel flowing a reference fluid, see Fig. 4(a).^74,75 The steady flow in the bridge channel was used to determine the viscosity, while the time for the bridge channel flow to change after a change in sample flow was used to determine a characteristic elastic timescale. The device was used to measure blood properties with different hematocrit levels, temperature treatments, and shear history. The device was capable of measuring non-Newtonian flow between about 100 s⁻¹ and 1000 s⁻¹ by changing the flow rates and compared the change in viscosity of blood in plasma and buffer solution. While this method used high precision syringe pumps and high speed cameras, the approach was useful for modifying the blood constituents through mixing before being flowed into the channel. This was tested by adding dextran and glutaraldehyde to the blood and measuring the effect of the concentration of these additives on blood properties.⁷⁶ A study by Yeom et al. used the device to simultaneously measure platelet adhesion and blood viscosity in samples with different hematocrit levels and was able to measure changes over time.⁷⁷

FIG. 4.

(a) A co-flowing device made continuous measurement of blood viscosity by tracking the position of the interface between the sample and reference fluid.⁷⁷ Reproduced with permission from Yeom et al., Sci. Rep. 6, 24994 (2016). Copyright 2016Authors, licensed under a Creative Commons Attribution (CC BY) License. (b) A co-flowing device by Kim et al. used a smartphone camera to track the interface position to determined the viscosity of blood and plasma samples.⁸⁰ Reproduced with permission from Kim et al., Opt. Lasers Eng. 104, 237 (2018). Copyright 2018 Elsevier Ltd. (c) A suspended micro-membrane with folded beams by Liu et al. measured viscosity by relating deflection of the membrane to the fluid stress.⁸¹ Reproduced with permission from Liu et al., Micromachines 11, 934 (2020). Copyright 2020 authors, licensed under a Creative Commons Attribution (CC BY) License. (d) A co-flowing viscometer by Mehri et al. tracked aggregation of RBC at different flow rates.⁸² Reproduced with permission from Mehri et al., PLoS ONE 13, 7 (2018). Copyright 2018 authors, licensed under a Creative Commons Attribution (CC BY) License.

The device was altered to create an array of outlet channels where the number filled with the sample fluid was used to determine the position of the reference-sample interface.⁷⁸ A theoretical model based on the circuit approach was developed to calculate the viscosity from the flow rates and fluidic resistances of the channels. The viscosity of rat blood at different hematocrit levels was measured with this method. Recently, the change of blood properties over time was measured by tracking the aggregation of RBCs in a closed loop microfluidic channel.⁷⁹ The same liquid is continuously flowed using a peristaltic pump through the parallel flow device where the blood viscosity and RBC aggregation is measured periodically. The effect of hematocrit and dextran over long durations and on-off cycles was investigated. One potential application cited for this work is for extracorporeal bypass loops, a similar closed loop systems, that would not require periodic collection for off-line analysis.

A recent method for measuring viscosity using the co-flowing approach in a single channel was developed by Kim et al. using imaging from a smartphone camera, see Fig. 4(b).⁸⁰ The device was constructed with a 3 mm wide channel so that the interface between two optically distinct fluids can be tracked using a low-magnification camera. Experiments with phosphate buffer solutions were used to determine a relationship between the position of the interface and the pressure ratio. The approach was used to measure the viscosity of blood and plasma in the range of approximately (40 to 5000) s⁻¹.

A different approach using the co-flowing method was taken by Mehri et al. to study RBC aggregation at low shear rates.⁸² A dual-camera setup was used to perform microparticle image velocimetry to determine shear rates and a high speed camera to measure RBC aggregate size, see Fig. 4(d). The viscosity measurements showed shear-thinning behavior in the range of (5 to 50) s⁻¹. The shear-thinning was related to the average aggregate size, which was observed to decrease with increasing shear rate. The device demonstrated connections between blood microstructure and viscosity by utilizing particle tracking to perform microfluidic rheometry at low shear rates.

A droplet-based method for measuring blood viscosity was demonstrated in the study by Mena et al. by relating the size of blood droplets formed at a T-junction to the relative viscosity of the surrounding fluid.⁸³ The device was used to measure the change in viscosity over time of swine blood as an indicator of coagulation. The effect of coagulant activators and inhibitors were tested and compared to thromboelastography (TEG), the clinical method for testing coagulation. The change in viscosity was shown to have a more rapid response than the measurements of clots with TEG. The device was demonstrated to operate at different shear rates, making it capable of measuring shear rate dependent behavior.

A commercial instrument (Formulaction) utilizes the co-flowing method in a single channel rheometry measurements. The flow rate can be adjusted to reach a range of shear rates, typically (10² to 10⁵) s⁻¹. The device was used by Sepulveda et al. to measure the viscosity xanthan gum solutions in combination with rotation rheometry over a range of shear rates from ( ${10}^{-3}$ to ${10}^5$) s⁻¹. The effect of adding whey protein isolate to the viscosity of the xanthum gum solutions was also investigated.⁸⁴ The rheometer was used to measure the viscosity of HA solutions, used as artificial tears, in comparison with the viscosity of natural tears.⁸⁵ The results showed both natural and artificial tears were shear-thinning and a low molecular weight HA based formulation most closely matched the natural tears.

Methods for making shear viscosity measurements with a fixed flow rate from syringe pumps often rely on pressure sensors integrated into microfluidic channels. Advancement in materials and fabrication methods also provide opportunities for improved pressure sensors. For instance, liquid metal filled into a pressure sensing channel with a thin film of PDMS between the sensing and fluidic channel was used by Jung et al.⁸⁶ The change in electric resistance through the liquid metal channel was calibrated to the applied pressure from the sample liquid channel. The device was shown to measure viscosity of fluids similar to blood viscosity over a range of shear rates from about (30 to 1000) s⁻¹. A different type of pressure sensor was developed by Doshi and Thostenson using nanotube-based piezoresistive sensors. The thin film was less than a micrometer thick and had a sensing range between 10 kPa and 50 MPa, which makes these types of sensors appealing for integration into microfluidic rheometers.⁸⁷

In contrast to measuring pressure, a method for measuring shear stress was demonstrated by Mustafa et al. that used the deflection of PDMS micropillars.⁸⁸ The nonlinear relationship between viscosity, shear rate, and the deflection of the micropillar was used to create a calibration curve based on reference fluids. The deflection of the pillars was then used to measure both Newtonian and non-Newtonian fluids with viscosity similar to blood over a range of shear rates about (60 to 400) s⁻¹. A different deflection-based technique was used by Liu et al. to measure viscosity by tracking the deformation of a suspended micro membrane as a function of flow rate, see Fig. 4(c).⁸¹ The membrane was made from SU-8 epoxy and consisted of a plate connected by folded cantilever beams to the surrounding film. The membrane was surrounded by PDMS layers that made up the microfluidic channel. The spring constant of the beam was determined by the geometry and elasticity of the beams. The viscosity was determined through a relationship including this spring constant and the other geometric parameters of the channel and membrane. The device capabilities were demonstrated by measuring bovine blood samples at different hematocrit levels.

A commercial microfluidic rheometer (mVROC) with pressure sensors integrated into microfluidic channels has frequently been used for high shear rate measurements of protein solution viscosity. A syringe pump drive flow through the device and the range of shear rates can be adjusted by using channels with different heights. The device has typically been used to measure the constant viscosity plateau present in protein solutions at high shear rates and in combination with rheometry measurements better suited for lower shear rate.^89–100 The rheometer has also been used to measure shear-thinning behavior in protein solutions.^101–103 Other studies have used the device to determine the intrinsic viscosity of marine oligosaccharides and polyelectrolyte matrices.^104,105

D. On-chip particle tracking based methods

Particle tracking methods are useful for rheological characterization without applying large deformations to the material, making them well-suited for many biological materials. An established method called passive microrheology uses the tracks of diffusive microparticles to make measurements in viscoelastic fluids. The method utilizes the relationship between the mean squared displacement of the particle, $⟨\Delta r^2(\tau )⟩$, to the creep compliance, $J(\tau )$ of the suspending material by the generalized Stokes–Einstein relation,

$$\begin{array}{c}⟨\Delta r^2(\tau )⟩=\frac{k_{B}T}{\pi a}J(\tau )\hfill \end{array},$$ (2)

where $\tau$ is the lag time, $k_{B}T$ is thermal energy, and a is the particle radius.^106,107 While this method is accurate and uses very small material quantities, measurements using microscopes can be labor intensive and low throughput. The measured viscosity can be accurate as long as the particles remain dispersed, which can be a problem for some systems that introduce attractive interactions. For example, dissolved proteins can produce attractive depletion interaction between the particles, so that they aggregate. Recent efforts have used microfluidic approaches to improve throughput and control the microenvironment to observe phase changes through changes in pH or temperature.¹⁰⁸

A high-throughput approach developed by Schultz and Furst used a T-junction drop generator to adjust drop composition through changes in relative flow rates of the fluid components.¹⁰⁹ The flow was stopped and particles included in the fluids were tracked to make microrheology measurements. This approach can measure changes in viscosity with fluid of different composition as well as measure gelation processes in hydrogels.¹¹⁰ A recent device by Yang et al. used traps in microfluidic channels to capture concentrated droplets of protein solutions for microrheology characterization.¹¹¹ The water in the drops slowly partitioned into the surrounding mineral oil, increasing the concentration of the protein filled droplets. Microrheology measurements over time were then used to characterize the change in viscosity with concentration.

Another high-throughput microrheology method developed by Josephson et al. measured protein solutions in multiple channels on a single temperature controlled microfluidic device.¹¹² The device was fabricated using a microfluidic stickers technique, which used a PDMS mold to imprint channels in a UV curable resin to make thin sheets that were then sealed between glass and a polyethylene substrate. The device was mounted in a temperature control stage mounted onto a microscope for particle tracking. Combined with bulk rheology, the temperature dependence on the viscosity provided a calculation of the apparent activation as a function of concentration and indicated when protein-protein interactions begin to dominate the activation energy.

A device by Wehrman et al. utilized microfluidic techniques to control the concentration of components in a fluid chamber, which induced a gel to sol transition that was measured by microrheology, see Fig. 5(a).^113,114 The device created a fluid exchange through vertical channels separating materials of different density that can be driven by gravity or through suction into the other chamber. The effect of pH on covalently adaptable hydrogels was studied, which have a wide variety of applications including cell culturing, tissue regeneration, and drug delivery due to their ability to change properties with external stimuli.¹¹⁵ The microfluidic device was also used to probe the change in structure as a function of time after a change in pH, similar to what would occur in the gastrointestinal (GI) tract. A sequence of different pH conditions based on the expected pH and duration in the GI tract was developed.¹¹⁶ The device was used to measure gel properties and kinetic transitions through repeated gelation and degradation cycles induced by pH changes.¹¹⁷

FIG. 5.

(a) A multilayer microfluidic device by Wehrman et al. to control release of components into a chambers where phase transitions between gel and sol transition are measured with microrheology tracking¹¹⁴ Reproduced with permission from Wehrman et al., J. Rheol. 62, 437 (2018). Copyright 2018 The Society of Rheology. (b) Mean-squared-displacement measurements from microparticle tracking by Wehrman et al. in covalently adaptable hydrogels during phase changes.¹¹³ Reproduced with permission from Wehrman et al., Lab Chip 17, 2085–2094 (2017). Copyright 2017 Royal Society of Chemistry.

Particle tracking methods have also been integrated with microfluidics to study cell properties. The effects of pressure on the intracellular environment of E. coli cells was studied by Yu et al. using a multilayer microfluidic device combined with particle tracking methods.¹¹⁸ The device was used to compress the cells by pressurizing an upper channel and deforming the PDMS membrane separating the channel with E. coli. The mean squared displacement (MSD) from microparticle tracking of cytoplasmic particles and DNA loci with and without compression were compared. The rate of change of the MSD with lag-time was used to show changes in subdiffusive behavior, an indication of a viscoelastic medium. The results showed a decrease in the diffusivity and more subdiffusive behavior when pressure was applied.

Microrheology is often used in combination with other microfluidic techniques for thorough characterization of material properties. An example of a multimodal characterization study was performed by Del Giudice et al. on hydroxyethyl cellulose using various techniques including microrheology, bulk rheology, microfluidic rheology.¹¹⁹ Microfluidic rheology was used for high shear rate viscosity measurements and included with bulk rheology to measure viscosity over a range of ( ${10}^{-1}$ to ${10}^4$) s⁻¹. A technique for determining the longest relaxation time by tracking the cross stream motion of the microparticles in a microfluidic channel.¹²⁰ The microfluidic technique is well-suited for shorter relaxation times and characterized the relaxation time at low collagen concentrations while higher concentrations were measured using bulk rheology, dynamic light scattering, and optical tweezers.

E. Extensional viscosity on a chip

The composition of many biological fluids, especially fluids containing biopolymers, results in a high resistance to extensional flow. Often this is an important characteristic for the biological function of the fluids. For instance, saliva has a high extensional viscosity relative to shear viscosity due to the composition of high molecular weight mucin molecules.^121,122 Extensional viscosity is the resistance to the stretching of a fluid element by the strain rate, $\dot{\epsilon }=\partial v_x/\partial x$, where $v_x$ is the velocity in the flow direction. The extensional viscosity is therefore defined by the stress due this stretching flow, defined by ${\eta }_E=({\tau }_{xx}-{\tau }_{y}y)/\dot{\epsilon }$, where ${\tau }_{x}x$ and ${\tau }_{y}y$ are the normal components of the stress tensor.^123,124 Many flows in biological systems are mixed, containing both shear and extension components. If the extensional viscosity changes significantly with extension rate, the flow behavior can be altered.

Extensional viscosity measurements are commonly performed using a capillary breakup extensional rheometer (CABER) device. The device works by pulling apart two posts with the sample fluid bridging the posts. The breakup of the liquid capillary thread connecting the two posts is tracked with a high speed camera. The thinning and breakup of the capillary thread is predominantly an extensional flow field and, therefore, the dynamics are sensitive to the extensional viscosity. The CABER approach was integrated into microfluidics by Nelson and Kavehpour, but instead of mechanical actuation, electrowetting was used to retract fluid between two electrodes.¹²⁵ The capillary thinning analysis was tracked similarly from a high speed camera. The use of electric fields was shown not to influence the measured rheology. The device is well-suited for biological samples since it requires microliter scale sample volumes.

Most microfluidic devices designed to measure extensional viscosity do so by creating geometries where large portions of the fluid experience extensional flow. The resistance to flow can then be related the extensional viscosity similarly to how flow rate and pressure drop are used to measure shear viscosity described in Sec. II C. One main difficulty in using microfluidic channels for extensional viscosity measurements is that the flow at the wall is dominated by shear, making the overall fluid flow field a mixture of both extensional and shear components. One method for creating a large region of extensional flow is a cross-slot geometry, a perpendicular intersection of two straight channels. Haward et al. used oscillatory flow in a cross-slot to measure extensional viscosity of saliva by subtracting off the pressure drop due to shear in the microchannel.¹²¹ The remaining pressure drop and the geometry of the channels were then used to calculate the extensional viscosity microliter volumes. The rheology of saliva before and after centrifugation is compared to separate large mucin proteins. The results shows that non-Newtonian behavior remained even after centrifugation. The device was also used with birefringence measurements, a method of relating the change in optical properties of the fluid to the alignment and stretching of molecules, which was used to estimate the relaxation time of mucin and measure its birefringence. A subsequent study by Haward et al. used a cross-slot geometry with a shape optimized with computational fluid dynamics (CFD) for measuring extensional viscosity, see Fig. 6(b).¹²⁶ The device was used to measure the extensional viscosity of hyaluronic acid solutions, a main component in synovial (joint) fluid. The Trouton ratio, the ratio of extensional viscosity to shear viscosity, was measured as a function of Weissenberg number, which compares the magnitude of elastic stress to viscous stress in a viscoelastic fluid.

FIG. 6.

(a) A two-channel device by Kim et al. with a differential pressure sensor to measure the extra pressure drop from a converging channel used to measure extensional viscosity.¹²⁹ Reproduced with permission from S. G. Kim and H. S. Lee, Macromolecules 52, 9585 (2019). Copyright 2019 American Chemical Society. (b) An optimized cross-slot device by Haward et al. to create a larger region of extensional flow for extensional rheology measurements.¹²⁶ Reproduced from Haward et al., Biomicrofluidics 7, 044108 (2013) with the permission of AIP Publishing LLC. (c) A microfluidic flow focusing device by Metaxas et al. used to measure extensional rheology by tracking the thinning of the fluid filament.¹³⁰ Reproduced with permission from Metaxas et al., Phys. Rev. Fluids 5, 113302 (2020). Copyright 2020 American Physical Society.

Recent work for optimizing extensional flows in the cross-slot geometry was performed by Zografos et al. using CFDsimulations.¹²⁷ The optimization process updated the geometry based on CFD simulation results for both Newtonian and viscoelastic fluids to create a homogeneous extensional flow region in the device. The CFD results were also used to investigate theoretical limits of operation based on viscoelastic and inertial instabilities. A subsequent paper investigated a commercial microfluidic extensional rheometer using CFD simulations of non-Newtonian viscoelastic fluids.¹²⁸ The results showed that the flow field through a contraction-expansion geometry is dominated by shear flow. They also analyzed how it changed with flow rate for non-Newtonian fluids compared to Newtonian fluids and the effect of normal stresses on the extensional viscosity measurement. The authors argued for improvements to the geometry based on optimization method modification of the geometry based on whether the fluid is Newtonian or non-Newtonian.

The concept of subtracting the stress contribution from shear flow in a contraction flow was developed by Lee and Muller and later implemented by Kim and Lee.^129,131,132 The microfluidic device consisted of two channels, one with a constriction and another with a straight channel with length that provided the same resistance due to shear, see Fig. 6(a). A differential pressure sensor between the two channels at the inlet provided the pressure drop due to the extensional flow. The microfluidic extensional rheometer was used to measure the average normal stress and extensional viscosity of polyethylene oxide (PEO) solutions over an extension rate between 1 s⁻¹ and 1000 s⁻¹ using different constriction geometries. The extensional relaxation time determined using the rheometer agreed with reference measurements from other CABER measurements. Another constriction-based device was used by Suteria et al. to measure extensional viscosity.¹³³ Meniscus tracking using a phone camera was used to determine the flow rate. The pressure drop due to the shear viscosity was determined by 3D CFD simulations of the flow field. The experimental 3D flow field was measured using in-line holographic particle tracking to determine velocity gradients for shear and extension, which confirmed the need for the pressure drop correction calculated using CFD. Particle tracking was also used to assess when instabilities occur, which can produce an additional pressure drop leading to errors. Extensional viscosities of polymer solutions were tested and agree with previous microfluidic extensional rheometers and dripping on a substrate measurements.

An example of a fluid used in medical applications where extensional viscosity characterization is important for function is methylcellulose, often used as a biocompatible rheological modifier used for applications such as cell culture media, artificial tears, and saliva.¹³⁴ Recent measurements of methylcellulose have used a microfluidic contraction–expansion geometry to measure extensional viscosity as a function of strain rate for different salt conditions.¹³⁵ As discussed above, the shear viscosity was measured in a straight channel and the corresponding pressure drop from these measurements were used to determine the pressure drop due to the extensional flow in the contraction-expansion channel. The results of the measurements showed thinning in the extensional viscosity, which was attributed to the loss of entanglements between the molecules as they align with the flow. The effect of salt on the extensional viscosity was observed to be largest at low strain rates (below $\stackrel{·}{\epsilon }\approx$ 100 s⁻¹) with more salt resulting in higher extensional viscosity. The contraction-expansion geometry was used by Lin et al. for characterizing the extensional viscosity of a particle-loaded biocompatible sprayable gel.¹³⁶ The fluid was composed of polyethylene particles embedded in a solution of associating polysaccharides, xanthan, and konjac glucomannan. The extensional viscosity was needed to determined appropriate values of yield stress and spray ability. Here, the shear-thinning shear viscosity of the fluid was fit with a power-law curve to calculate the pressure drop contribution. The results showed strain-thinning for the polysaccharide solutions and the extensional viscosity could be adjusted through the addition of salt that modifies the molecular interactions. The results were contrasted with PEO solutions, which exhibited extensional thickening, demonstrating that these solutions were well-suited for spraying applications.

A different method is based on flow-focusing tracks the thinning of a liquid filament downstream of a microfluidic junction. This method was used by Steinhaus et al., and Arratia et al. to measure extensional rheology of polymer solutions.^137,138 The method was subsequently employed by Juarez and Arratia to measure the effect of DNA molecular weight and concentration on extensional rheology.¹²² More recently, Metaxas et al. used this method to measure methylcellulose solution properties.¹³⁰ The sample fluid was surrounded by an immiscible continuous phase of 50 mPa s silicone oil, and the diameter of methylcellulose stream thins after the junction with the surrounding oil, see Fig. 6(c). Images were recorded on a microscope using a high speed camera and analyzed to measure the thinning of the filament diameter as a function of time. Similar to analysis used with CABER, the rate of thinning was used to determine the extensional viscosity while also considering the contribution of the viscosity of the surrounding oil. The extensional viscosity for different salt concentrations was determined from the early time thinning behavior where the extensional flow dominates the dynamics.

Microfluidic extensional viscometers are increasingly being used to characterized biofluid and fluids used in medical applications. The inherent challenge in these devices is reducing uncertainties from the shear flow components of the flow. Developments in optimizing geometries enhance the pressure drop from extensional flow compared to shear flow and therefore improve the accuracy of these measurements. While there are a few examples of point-of-care extensional rheometer devices, the principles used toward deployment of microfluidic shear rheometers can also be applied to future deployment of microfluidic extensional rheometers.

III. ELASTICITY OF SOFT BIOLOGICAL PARTICLES

Many soft biological materials are characterized as viscoelastic solids that exhibit both nonlinear and time-dependent response to loading, see a recent review by Efremov et al. for more details.¹³⁹ Many of these materials constitute biological cells or lipid vesicle membranes or may compose bulk materials such as collagen. Methods for measuring mechanical properties of individual cells in microfluidics are typically done by imposing deformation through applied flow or a geometric constriction. First these methods are reviewed, specifically flow through a constriction, flow in a cross-slot geometry, and confinement through capillary constrictions. Alternative methods by integrating electrical or optical forces are discussed, followed by approaches for mechanical measurements on filament shaped systems. Finally, measurements of forces generated by cells are discussed.

A. Deformation through flow constrictions

Extensional flow is useful for mechanical measurements on cells, particles, and molecules because the applied flow stress can be related to the measured strain. Similar to Sec. II E, the difficulty in microfluidic channel flows is creating either homogeneous regions of strain or flow trajectories of cells where the extensional flow stress is well described. A microfluidics-based method to quantify mechanical properties of deformable objects through a constriction was developed by Cabral and Hudson using fluid drops to determine interfacial tension.¹⁴⁰ Similar approaches were used to study the dynamics of adenosine triphosphate release from RBCs due to the hydrodynamic stress as the cells flow through a constriction.¹⁴¹

More recent work has focused on the properties of cells, which are stiffer than drops and therefore require higher strain rates to deform. Improvement in high speed camera technology, notably complementary metal-oxide semiconductor (CMOS) cameras, enabled Otto et al. to develop a real-time deformability cytometry method capable of measured deformation of 100 cells/s.¹⁴² The cytometry technique was able to identify different cell populations by analyzing size vs deformability. In contrast to other cytometry techniques, deformability is appealing because it is label free and therefore can be combined with other cytometry techniques. This approach was extended to produce dynamic real-time measurements by simultaneously characterizing size and shape of cells passing through the constriction.¹⁴³ The recorded cell shapes were analyzed by fitting the shapes to models that considered the balance between hydrodynamic stresses on cell surface and elastic stresses of the cell. Various models for the cells, including an elastic sphere, and elastic shell, were used to determine values for Young's modulus and surface tension. The quantitative method was compared to atomic force microscopy (AFM) measurements and for agar particles with known stiffness.

Cells can adopt non-ellipsoidal shapes in flow contractions due to complex viscoelastic dynamics. An approach for analyzing the cell shape based on Fourier analysis was taken by Fregin et al. for the analysis of the time-dependent shape, see Fig. 7(a).¹⁴⁴ The measurement of Young's modulus was obtained using the modeling from Mietke et al. and the time dependent information was used to determined viscosity from a viscoelastic Kelvin–Voigt model. The method was shown to precisely discriminate between cell components based on their rate of deformation, including different types of leukocytes. A high-throughput shape analysis of RBCs through a channel was used to investigate the different types of flow behaviors such as tumbling, tank-treading, or adopting a parachute shape.¹⁴⁵ A mix of behaviors was observed within a sample and the probability of each behavior for different flow conditions was measured. Through comparisons between simulations and experiments, the variability in the shear elasticity was analyzed to explain variations in flow states observed in experiments. The study showed how characterization of variability inherent to RBCs can provide a framework for detection of diseased states. A different approach based on the flow of cells through a constriction was demonstrated by Dannhauser et al. using non-Newtonian polymer solutions as the suspending fluid.¹⁴⁶ By tuning the polymer concentration and flow rate the viscoelastic forces on the cells could be tuned. The method was used to determine the phenotype breast cell lines that differ in mechanical properties by flow observing different flow behavior.

FIG. 7.

(a) The time-dependent shape deformation and shear stress used of cells flowed through a constriction by Fregin et al for high-throughput cytometry to measure viscoelastic properties.¹⁴⁴ Reproduced with permission from Fregin et al., Nat. Commun. 10, 415 (2019). Copyright 2019 Authors, licensed under a Creative Commons Attribution (CC BY) License. (b) A microfluidic nozzle by Rubio et al. formed by melt-shaping a glass capillary used to measure elastic properties of RBCs by tracking deformation in the nozzle.¹⁵³ Reproduced with permission from Rubio et al., Polymers 14, 2784 (2022). Copyright 2022 Authors, licensed under a Creative Commons Attribution (CC BY) License. (c) An optimized constriction geometry developed by Liu et al. to create a region of uniform extension used for measurements of DNA and actin filaments under extension.¹⁵¹ Reproduced with permission from Liu et al., Soft Matter 16, 9844–9856 (2020). Copyright 2020 Royal Society of Chemistry.

The extensional flow in contractions can also be used to measure properties of DNA molecules. For instance, Hirano et al. tracked fluorescently labeled DNA strands elongated by the flow through a constriction.¹⁴⁷ The change in length observed was compared against the difference in flow velocity between the two ends of the DNA. The nonlinear elastic behavior of the DNA strand was then analyzed compared by stretch against strain rate.

While abrupt contractions provide strong extensional forces, the extension rate changes rapidly along the path lines that particles and cells follow. The extension rate can be adjusted by changing the geometry of the entrance.¹⁴⁸ For instance, Faghih and Sharp used a hyperbolic shaped contraction with a constant extension rate along the channel centerline for studying the deformation of RBCs.¹⁴⁹ The stress on the cells was modified by changing the flow rate and viscosity of the suspending solution and compared to measured aspect ratio. The deformation under shear flow was observed to be lower than the extensional flow at comparable stress due to the different flow kinematics. The deformation was compared to previous work using rabbit blood cells and significant discrepancies were observed, which demonstrated that animal models are not always well-suited for extrapolating to human cells. A hyperbolic contraction was also used by Faustino et al. to compare the RBC deformability between patients with end-stage kidney disease and samples from healthy individuals as controls.¹⁵⁰ The samples from the diseased patients were shown to have less deformability than the samples from the control group and the deformability decreased further for patients with diabetes. The study demonstrated that the method may lead to new diagnostic tools and blood pathologies.

While the constant strain rate along the centerline of a hyperbolic contraction is theoretically well-suited for deformation measurements, the implementation in a microfluidic channel can lead to deviations from the constant strain rate due to finite size effects. To overcome this limitation, a microfluidic device was designed using CFD optimization methods to create a large region of uniform strain rate, see Fig. 7(c).¹⁵¹ The millimeter scale length of device necessitated tracking particles on a microscope with a motorized stage to capture the deformation of bio-particles. The strain rate was verified using particle tracking velocimetry and then the measured extension of DNA and actin filaments was used to characterize their elastic properties.¹⁵²

The mix of extensional and shear flow that exists for most particle trajectories through constriction geometries was studied by Piergiovanni et al. using CFD to determine the flow field experience by leukemia particles.¹⁵⁴ Different types of flow behaviors were evaluated by analyzing trajectories with different mixes of extensional and shear flow. The study showed that CFD simulations can be used to evaluate viscoelastic properties of cells and also provide a process for evaluating whether a microfluidic geometry produces a flow type that can differentiate cell lines based on viscoelastic properties.

Most studies using microfluidic constrictions are made from PDMS. While these devices are well-suited for research, the difficulty of mass production, limited ability to withstand high pressures, and a lack of general robustness make them ill-suited for commercialized devices. To address these limitations, Rubio et al. developed a microfluidic nozzle created by melt-shaping a glass capillary in a capillary puller, see Fig. 7(b).^153,155 The nozzle was submerged in glycerol to reduce the distortion effects of the curved glass surface for optical imaging. The flow was characterized by comparing CFD simulations with particle tracking velocimetry. This resulted in identification of a region with small variations in strain rate where the most accurate deformation measurements could be made. The nozzle device was used to measure the deformation of two RBC populations in the near constant strain rate region, one healthy and another treated with glutaraldehyde to increase rigidity. The difference in deformation between the two populations was studied in nozzles of different size and shapes. The relative simplicity of fabrication and robust glass construction makes it attractive for scaling up production, cleaning, and clinical applications.

The use of constrictions in microfluidics is a useful technique for observing differences in cell properties by deformation and flow behavior in the channels. Access to CFD simulations has enabled more detailed analysis of the flow field in these microfluidic geometries. Connections to measuring material properties is difficult due to the complex flow fields the particles experience in the entrances. Work toward optimizing geometries to create large regions of constant strain-rates provide opportunities for more accurate measurement of viscoelastic properties of cells. The development of more robust microfluidic fabrication techniques will also promote high-throughput and automated measurements for clinical applications.

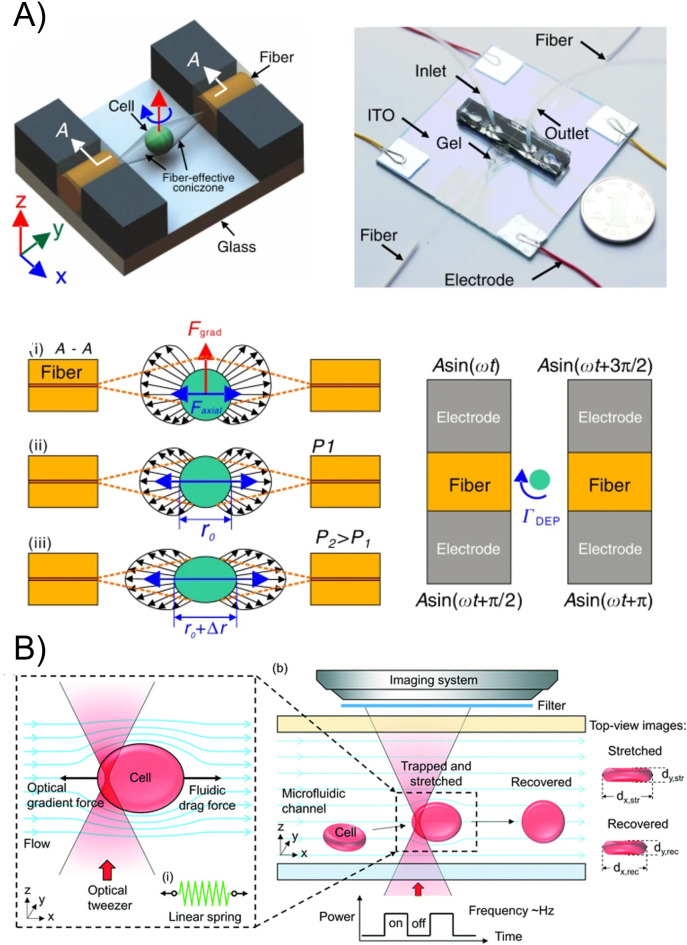
B. Cross-slot devices

The cross-slot geometry is a common microfluidic design for generating extensional flow. Microfluidic cross-slots and four-roll mill designs have been used commonly as rheological tools.^156–158 These devices have also been used for characterizing deformable particles, such as the dynamics of giant vesicles in flow.^159,160 One challenge with using a cross-slot for mechanical measurements of cells and other bio-particles is controlling the flow field experienced by the particle. Some approaches, such as that used by Marie et al., have used confining channels to trap DNA and then apply extensional flow to measure properties of the DNA¹⁶¹ More recent approaches have developed real-time feedback over the flow to maintain the position and deformation, or have used CFD to model the flow experienced by the particles.

For instance, the flow field in a cross-slot channel was analyzed using CFD simulations by Guillou et al. to determine the strain rate experienced by a cell and identified the region within 95% of the maximum strain rate.¹⁶² A viscoelastic model based on the deformation of an elastic sphere with a time-dependent stiffness was used to determine material properties. Microgel particles were used to validate the approach by comparing the measured shear modulus to other measurement techniques, including micropipette aspiration and osmotic de-swelling. The methodology was used to measure the shear modulus and fluidity parameter of fibroblasts treated with different drugs that affect the cell's cytoskeleton properties. The results showed the drugs affected the measured shear modulus without significant alteration of the fluidity parameter. The analytical model provided quantitative measurements at small deformations and changes to the suspending fluid provided an approach for altering applied stress without significantly changing flow rates. The higher flow rate regime was recently explored by Armistead et al. to characterize the transition to nonlinear deformation of different types of circulating cancer cells, including leukemia and colorectal cancer cells, see Fig. 8(a).¹⁶³ The time-dependent deformation was characterized by fitting the exponential growth and decay of the deformation and the shear modulus was determined by fitting a Kelvin–Voigt model. The approach demonstrated measurements using a different elastic model as well as the limits of elastic deformation, above which the cells experienced irreversible damage and did not return to their original shape.

FIG. 8.

(a) A cross-slot geometry used by Armistead et al. to measure the nonlinear viscoelastic deformation and failure points for different types of circulating cancer cells.¹⁶³ Reproduced with permission from Armistead et al., Biophys. J. 116, 1127–1135 (2019). Copyright 2019 Authors, licensed under a Creative Commons Attribution (CC BY) License. (b) A Stokes trap used by Kumar et al. to trap and control extensional flow to induce large asymmetric dumbbell shape deformation of vesicle.¹⁶⁴ Reproduced with permission from D. Kumar and C. M. Schroeder, Langmuir 37, 13976–13984 (2021). Copyright 2021 American Chemical Society.

One difficulty with the deformation of bio-particles in a cross-slot is controlling the duration the particle stays in the center region of the junction where extensional flow is dominant. Small deviations from the centerline of the flow will lead the particle to be swept to the outlet channels. A method for real-time control of the flow field in cross-slot geometry, called a Stokes trap, was designed by Shenoy et al. to address these challenges.¹⁶⁵ The flow at the intersection was controlled by pressure regulators on each of the inlets and outlets that rapidly adjust the relative flow through each channel to maintain the position of tracked object in the center of the cross-slot, see Fig. 8(b). This approach was used to observe deformation of a giant lipid vesicle held in the cross-slot while the flow strength was adjusted. Dahl et al. used the Stokes trap to study the non-equilibrium configuration of vesicles under straining flow.¹⁶⁶ The transitions between single domain shapes at equilibrium and weak flows to a dumbbell shapes, a shape with two domains connected with a tether, in strong flows. These behaviors were investigated as a function of flow strength and reduced volume, a measure of surface area to internal volume.¹⁶⁷ The approach enabled careful measurement of the transitions between either symmetric or asymmetric dumbbell shapes and the dependence of shape transitions on membrane properties and viscosity contrast.¹⁶⁴

The high speed pneumatic controls utilized in the Stokes trap have allowed for time-dependent oscillatory flows capable of investigating the nonlinear shape dynamics of vesicles.¹⁶⁸ The different dynamical regimes of the vesicle shapes were categorized, including behaviors described as pulsating, reorienting, and symmetrical. The transition between the different dynamical states depended on the applied flow frequency and theoretical modeling of the vesicle shape was used to determine the viscous and membrane timescales of the vesicle. Through model comparisons, the measurements gave information about how membrane properties such as bending modulus and tension affect the transition. The dynamical response of the vesicles was used to calculate how such microstructural transitions can affect the rheology of particle suspensions, which can be built upon further for cells such as RBCs.

C. Capillary constriction based on confinement

In contrast to constrictions where the channels are larger than the particles and flow stresses drive deformation, constrictions that are narrower than the particle diameter provide geometric confinement. These approaches often mimic the environment cells experience while flowing through capillaries in the microcirculation system. The advantage for using geometric confinement is a well-defined deformation can be imposed by the channel walls. Property measurements can be determined based on passage time through the constriction or by measuring the additional pressure drop created by the confined particle. The similarity to physiological systems also provides a method for studying changes to cells that result from the imposed stress. The microfluidic approach was pioneered by Shelby et al. by observing malaria infected RBCs and how the various disease stages affected flow through microconstrictions due to changes in the cell properties.¹⁶⁹ Recent advances using the approach have focused on high-throughput methods and relating the transit behavior to viscoelastic cell properties.¹⁷⁰

One example of a high-throughput method for measuring cell properties using capillary constrictions was by Lange et al.¹⁷¹ They tracked the transit time of cells through a parallel array of microconstrictions with a high speed camera, see Fig. 9(a). They measured entry times as a function of pressure and used a model that related the entry time to the cell elasticity and fluidity, a parameter describing whether the cell response was viscous or elastic. The effect of various drugs on the elastic modulus and fluidity of leukemia cells was studied based on over 2000 cell measurements for each drug. The relationship between the elasticity and fluidity is analyzed, providing a method for estimating cell properties based on one parameter. Differentiation between different cell types can be difficult with these methods. This difficulty often arises from various sources of bias and uncertainty, such as strain stiffening effects and time between harvesting and measurements. Control over these effects was demonstrated to improve the reliability of the measurement method.¹⁷² Improvements to speed and reliability of high-throughput confinement based measurements by Davidson et al. used automated image analysis based on micropipette aspiration techniques.¹⁷³ The viscoelastic properties of cell nuclei were tested for cells with and without a nuclear envelope protein. The results show a significant change in the viscoelastic properties of the nuclei of the different cell types.

FIG. 9.

(a) The transit time of cells through a parallel array of microconstrictions used by Lange et al. for high-throughput measurements of cell viscoelastic properties.¹⁷¹ Reproduced with permission from Lange et al., Biophys. J. 109, 26–34 (2015). Copyright 2015 Biophysical Society. (b) The protrusion length of the cell into the microconstriction combined with the measured pressure drop was used by Chen et al. to measure the viscoelastic properties of cells.¹⁷⁴ Reproduced with permission from Chen et al., Methods X 8, 101247 (2021). Copyright 2021 Authors, licensed under a Creative Commons Attribution (CC BY) License. (c) Automated image analysis method by Nyberg et al. to perform shape analysis on leukemia cells driven through a microcontrictions is used to measure viscoelastic properties of the cells.¹⁷⁵ Reproduced with permission from Lange et al., Biophys. J. 112, 1472–1480 (2017). Copyright 2017 Biophysical Society.

A different approach by Guo et al. used constrictions to determine the pressure required to push through an RBC. The critical pressure and cell size was used to determine the cortical tension using Laplace's law, which describes the resistance to deformation by the membrane tension.¹⁷⁶ The approach was used to observe variation in cortical tension over multiple days and discriminate between healthy and unhealthy RBCs from different donors. While little change in tension was observed over time, the tension was shown to increase with addition of glutaraldehyde.

A similar pressure-based method was developed by Hu et al. to study elastic properties of cancer cells by measuring their deformation in a tapered confining constriction.¹⁷⁷ Using the penetration depth of the cell in the tapered channel and the cell diameter, the forces on the cell can be calculated, which gives a measurement of Young's modulus. The theoretical description was further developed to consider large cell deformations.¹⁷⁸ The large deformation theory characterized the change in elastic modulus in the narrow constrictions and led to an improved ability to discriminate between the elasticity of cancerous and non-cancerous cells. While limited to about approximately 10 cell/min, the approach measured both small and large deformation and could be scaled to higher throughput. A similar approach used by Xu et al. to measure the shear modulus of the protein microgel particles trapped by trapping them in an array of constrictions.¹⁷⁹ The steady state shape of the particles in each of the channels was measured as a function of flow rate. Numerical simulations were used to determined the pressure drop on each of the particle-filled channels. The measured deformation and calculated applied pressure drop were used to measure the shear modulus of 10 trapped particles in a single cycle.

A computational approach was used by Lykov et al. to relate the measured deformation trapped in microfluidic constrictions to the material properties of cell components.¹⁸⁰ Breast epithelial cells studied in experiments were simulated using dissipative particle dynamics, which describes the interaction between model particles to describe the viscoelastic response of the cell membrane, cytoskeleton, and nucleus. The parameters for the model were calibrated using data from micropipette aspiration measurements. By adjusting the parameters that described the cell components, the authors were able to match the velocity of the cells through different sized microfluidic constrictions. The detailed description of the cell showed that the cytoskeleton affects the cell stiffness most significantly, while a smaller impact from the cell nuclei was observed.

A method developed by Nyberg et al. used pressure-driven flow to pass leukemia cells through a constriction while automated image analysis tracked the shape during transit, see Fig. 9(c).¹⁷⁵ The tracked shape was used to determine the strain based on the change in circularity of the cell. The setup was shown to acquire measurements at the rate in the range of approximately ${10}^3$– ${10}^4$ cells/min, depending on the applied pressure. The effects of the cell size to pore size ratio were explored, and a ratio of approximately 2 was found to limit the strain stiffening response of the cells. A power-law model was found to describe the cell transit behavior. Using this, they obtained measurements of apparent elastic modulus and fluidity based on over 500 measurements with different drug treatments. The results also demonstrated that the large variation in properties between individual cells necessitated large sample sizes to characterize the distribution of properties. A method developed by Chen et al. used both the transit time and excess pressure to determine cell elasticity using a differential pressure sensor, see Fig. 9(b).¹⁸¹ The protrusion length of the cell into the constriction in combination with the pressure drop measurement was used in a power-law model to describe the viscoelastic behavior.¹⁷⁴ Similar to previous studies, this gives an elastic stiffness modulus and fluidity coefficient. The device was used to measure two cell types, K562 and endothelial cells, which differed in elastic modulus but had similar fluidity. The measured values were consistent with previous measurements, but faster than AFM or micropipette aspiration techniques. The device was shown to measure up to 3 cells/min, but the measurement speed depended on the measurement values because higher stiffness cells experienced longer transit times.

Another elasticity method based on the penetration depth of cells in a constriction was developed by Ren et al. using arrays of constrictions.¹⁸² The device was used to measure elasticity of cells and calcium-alginate hydrogel microbeads by measuring size and deformation while under pressure by using large deformation elasticity theory. The device was able to distinguish elastic moduli in the range of (3 to 8) kPa and was able to distinguish differences of about 1 kPa. The device demonstrated a high-throughput capability based on a penetration depth method that could produce elasticity-based classification of normal and cancerous cells.

A comparison of different flowing microfluidic methods for single cell mechanical properties was performed by Urbanska et al.¹⁸³ They compared three flow through methods discussed above, passage of a cell through a narrow constriction cell, flow through a constricted channel larger than the cell, and extensional flow from a cross-slot. The constriction based methods were similar in applied stress magnitude, but differed in strain rate. The extensional flow produced much larger strain rates and was shown to produce greater response from cell components other than the actin cytoskeleton. The effect of osmotic pressure on the deformation and the osmotic shock induced by deformation were also assessed.

Another confinement based approach to probe cell mechanics use devices with actuated components similar to a large scale compression testing. One example developed by Sugiura et al. used a piezoelectric actuated beam as probes to compress the cell that was positioned in front of the probe via a microfluidic channel.¹⁸⁴ A second piezeoelectric probe measured the force transmitted across the cell. The displacement of the probe sensor is imaged on a microscope and an interference pattern called moiré fringe was generate by patterns in the device to obtain sub-optical resolution of around 40 nm. Measurements of kidney cells demonstrated that the device resulted in two times the sensitivity of previous measurements. Another type of actuated microfluidic device developed by Shorr et al. used deformable PDMS channel walls actuated by adjacent pressurized chambers.¹⁸⁵ The deformation and compression of embryos was investigated using numerical simulations to determine optimal channel dimensions including wall thickness and rigidity. While the main purpose of the device was to test the response of gene expression in embryos under mechanical compression, the device was used to measure the Young's modulus of the embryos using numerical simulations. The device also monitored viscoelastic creep resulting in changes in embryo shape over a duration of hours under compression.

D. Electrical and optical methods for mechanical measurements

Electric fields are often used for manipulation of biological particles in microfluidic because electrodes can be integrated onto channel surfaces to produce forces on particles in combination with flow. A well-established method for particle manipulation involves electric field gradients to create a dielectrophoretic force on polarizable objects. The strength of the force depends on mismatch in dielectric properties between the bioparticle and the suspending medium. Dielectrophoresis (DEP) for cell manipulation is a long-standing field of research, with significant amount of work focused on sorting based on differences in DEP force.^186–188

Recent use of DEP forces have included mechanical property measurements of cells and other bio-particles in microfluidic devices. For instance, a device by Du et al. used arrays of electrodes with posts that trapped and stretched RBCs at the end of the post by DEP force to measure mechanical cell properties.¹⁸⁹ The DEP stretching force on the cells was calculated from numerical simulations of the electric field which used literature values for the system's electric properties. The force could be modified by changing the frequency of the AC electric field. The shear modulus calculated for both healthy and RBCs infected with malaria parasites was found to be similar to previously measured values using optical tweezers. Although high-throughput capabilities were not implemented, the device was well-suited for parallel measures because the design could trap cells with a density of about 700 cells/mm². A different electrode design was used by Zhang et al. to produced DEP stresses on cells between two parallel electrodes on a glass substrate.¹⁹⁰ A PDMS microfluidic channel was placed over the electrodes and leukemia cells were flowed between the electrodes. Numerical simulations were also used to determine the DEP stress and a Maxwell viscoelastic linear solid model was used to describe the cell's response. The modeling produced a calculated elastic modulus and viscosity for leukemia cells with and without drug treatment. A decrease in stiffness with drug treatment was observed.

An increase in the throughput of cell mechanical measurements using DEP was devised by Yang et al.¹⁹¹ The device used 14 capture ports for trapping cells and positioned electrodes on either side of the ports to apply a DEP for trapping and stretching the cells, see Fig. 10(b). Obstacles were placed in the main channel to deflect cells toward the ports for better capture efficiency. The flow was reversed to release cells from the ports and repeated with new cells. Automated image analysis resulted in a measurement rate of approximately ten cells per minute and the device was used to measure Young's modulus of various cell populations using more than 600 measurements per cell type.

FIG. 10.

(a) Electrodes in a microfluidic channel by Qiang et al. produced dielectrophoretic force on cells to measured viscoelastic properties of the cells under cyclical loading.¹⁹² Reproduced with permission from Qiang et al., Acta Biomater. 57, 352–362 (2017). Copyright 2017 Acta Materialia Inc. (b) A device by Yang et al. used to periodically trap and deform multiple cells using dielectrophoretic force for high-throughput viscoelastic measurements.¹⁹¹ Reproduced with permission from Yang et al., iScience 25, 104275 (2022). Copyright 2022 Authors, licensed under a Creative Commons Attribution (CC BY) License.

Electric fields also allow easy cycling of stresses for fatigue measurements. For example, cyclical measurements on RBCs were performed by Qiang et al. using DEP stress created by interdigitated electrodes on glass under a PDMS microfluidic channel, see Fig. 10(a).¹⁹² The large area of the interdigitated electrodes made trapping multiple cells possible. For cyclical loading, square pulses of DEP forcing were applied and the time-dependent behavior was compared to a Kelvin–Voigt solid model. A decrease in the observed maximum strain for the same loading was observed over time, which lead to an observed increase in the elastic modulus that was attributed to mechanical degradation. An increase in measured viscosity was also observed over time, which was indicated an increase in intracellular hemoglobin concentration due to cell dehydration. While not examined in this study, the technique could be used to investigate the change in cellular electrical properties over time, which may affect the interpretation of the change in observed strain.

For investigations requiring cyclical loading for fatigue measurements and parallel measurements, DEP offers advantages compared to other methods. The approach is well-suited for high-throughput measurements which can be automated by image processing algorithms. Improvements to electrode design and characterization through numerical methods will improve the accuracy of the technique. Additionally, characterization of the electrical properties and whether they change with DEP stress will also improve the accuracy of measurements.

A different electric field approach called electrodeformation uses uniform electric fields to deform particles. Differences in electrical properties inside and outside of shell particles produce electric stresses at the interface. Electrodeformation experiments are typically performed in chambers where bio-particles sediment and the ones that are between electrodes can be interrogated with electric fields.¹⁹³ The electrodeformation as a function of field strength, frequency, and in response to pulses has been used to measure membrane properties of vesicles.^194,195 Recent advances in the technique have measured the interfacial viscosity of vesicles through transient electrodeformation of giant unilamellar vesicles.¹⁹⁶ The method measured the change in vesicle shape immediately after a uniform alternating current electric field is applied and when the field is turned off. The bending rigidity and tension of the membrane was measured from measurements of the membrane fluctuations at equilibrium. Using image processing of multiple vesicles in a field of view allowed for parallel measurements. The approach was used to measure the membrane viscosity for a range of different compositions of lipid vesicles or biocompatible polymer vesicles. Integration into a chamber where cells are created and can be trapped or flow stopped for analyzes, similar to approaches taken by Paterson et al. could lead to increased throughput.¹⁹⁷

Optical stress methods are another set of techniques that avoid flow stresses or geometric confinement. The use of optical beams to stretch cells, a method developed by Guck et al., has been widely used on microscope stages with nonfocused laser beams.¹⁹⁸ Integration of optical waveguides into microfluidics has produced the capability of measuring cell elastic properties in microfluidic channels.^199–201 For example, a dual-beam optical stretcher in a microfluidic devices was demonstrated by Delabre et al. to stretch vesicles flowed through a channel.²⁰² Optical fibers were aligned pointing at each other across a glass capillary and mounted on a slide as shown by Lincoln et al.²⁰³ A theoretical model was developed to describe the deformation of vesicles under the applied stress of the optical trap. The microfluidic integrated setup was also compared to an open setup placed on a glass slide. One challenge using optical stretching is the heat generated by the optical source. In this case, heating from a long wavelength stretcher was used to probe the effect of temperature on vesicle deformation while a shorter wavelength laser showed less heating effects. Similar to electrodeformation measurements, the bending rigidity, membrane tension, and stretching modulus were determined base on the stretching response of the vesicle. The measured values for bending rigidity were lower than that of previous measurements, which was attributed to the description of shape in the model used or the high osmolarity used in the experiments.

The use of optical forces was combined by Yang et al. with acoustic forcing to measure the acoustic compressibility of two human breast cancer lines.²⁰⁴ The device was fabricated from glass to include waveguides perpendicular to the channel for optical stretching and the device was mounted on a piezo transducer. The trajectories of cells driven by acoustic forces were used to determine the acoustic compressibility by using an equation describing the balance of viscous drag force and acoustic forcing, which depends on acoustic compressibility. The two measures of deformation did not correlate strongly, indicating that the cellular components respond to the optical stretching differently than the acoustic forcing.

A different multimodal approach was taken by Huang et al. by combining DEP based electrorotation and an optical stretcher in a single device to relate electrical and mechanical property measurements of different cell types, see Fig. 11(a).²⁰⁵ The optical fibers were designed to trap cells passing through the channel and then apply a step stress in optical stretching force. The time-dependent viscoelastic response was used to measure the shear modulus, viscosity, and relaxation time of the cells. These measurements were combined with measurements of membrane capacitance and cytoplasm electrical conductivity to compare normal and cancerous cell lines.

FIG. 11.

(a) Two optical fibers are fabricated in a microfluidic channel by Huang et al. to deform cells passing through using optical stretching.²⁰⁵ Reproduced with permission from Huang et al., Microsyst. Nanoeng. 6, 57 (2020). Copyright 2020 Authors, licensed under a Creative Commons Attribution (CC BY) License. (b) An optical tweezer used by Yao et al. temporarily traps flowing RBCs and the stretch induced by the flow past the pinned cell is used to measure cell stiffness.²⁰⁶ Reproduced with permission from Yao et al., Lab Chip 20, 601–613 (2020). Copyright 2020 Authors, licensed under a Creative Commons Attribution (CC BY) License.

A different approach using optical stress to measure bio-particle properties was taken by Yao et al.²⁰⁶ The method used an optical tweezer in a flowing microfluidic channel to temporarily trap RBCs and then measured the cell deformation induced by the flow stress on the pinned cell, see Fig. 11(b). The force on the cell was calculated by the drag force on a circular disk shape and an elastic spring constant was used to relate the observed deformation to the applied force. The device was used to measure the change in cell stiffness with the addition of glutaraldehyde to RBC suspensions. The combination of flow and optical trapping offers the advantages of both methods, namely, the non-contact nature of optical trapping and the continuous supply of cells in a flow cell, with a rate of about 1 cell/s.

E. Filament deformation methods

The cylindrical shapes of certain cell types such as E. coli have required in particular, designed approaches for measuring mechanical properties in microfluidics. An example of this was a device designed by Caspi to enable mechanical measurements of E. coli bacteria in the same device in which they are grown.²⁰⁷ A pattern of chambers on the side of a main channel acted as growth channels for the bacteria. The growth channels were shaped such that part of the cylindrical bacteria are trapped in the chamber while the rest of the bacteria was exposed to the main channel flow. The deformation of bacterial cells under flow was used to determine the flexural rigidity of the bacteria and compare growing and non-growing cells. An elastic response was observed for non-growing cells while a plastic-elastic response was observed for growing cells, which resulted in the cells not fully returning to their initial configuration. A different approach developed by Amir et al. used pressure driven flow pulses to make periodic rigidity measurements during the bacteria growth.²⁰⁸ A model based on the compressive and tensile stress inherent to filament bending was used to understand the plastic deformation through inhibiting or promote cell wall insertions. The modeling produced a quantitative measure of the magnitude of “snap-back,” determined by the angle after deformation, that described the plastic response. The prediction relied on parameters of cell properties, including the Young's modulus, cell radius, turgor pressure, and cell wall thickness. The theory was validated with various strains of bacteria. The approach was subsequently used by Rojas et al. to study the properties of the outer membrane by introducing chemical agents that disrupt the lipopolysaccharides in the outer membrane and produced a decrease in bending rigidity.²⁰⁹ A different approach for studying the plasticity of bacteria was performed by Wong et al. by growing bacteria in microchambers with features that confined the bacteria into a circular shape.²¹⁰ The cells were subsequently transferred to chambers without confinement and a return to straight shape was observed over time. The shape recovery was modeled by relating the growth of the cell and elastic parameters to the rate of straightening.

Jahnke et al. demonstrated a different approach for deforming E. coli using microfluidic flows by adhering the bacteria to a glass surface with physiosorbed RNAse B.²¹¹ The shear force on the bacteria was modified by including alginate in the flowing solution to increase the fluid viscosity. The effect of shear rate on the growth was studied by tracking the end to end length as a function contour length, therefore characterizing the flow conditions required for alignment with the flow. The binding affinity was characterized as a function of flow rate by the half-life of bound time after flow was applied. Additional investigations of the surface forces were performed by measuring the detachment force with AFM and analyzing the stress on model filament with CFD.

A combined approach using tapered microfluidic constrictions and fluorescent molecule tracking was used to study the effect of applied stress on bacterial properties.²¹² The pressure was adjusted on either side of an array of constriction channels to measure the effect of total pressure and pressure drop across the bacteria. Single molecule tracking of a fluorescent membrane protein was used to determine the diffusion constants of the protein in the cell under different loading. The results showed that shear stress from a pressure differential produced more disassembled proteins but the diffusion constant of the disassembled protein decreased with pressure differential, suggesting a change in the membrane fluidity. The control of stress through microfluidic controls provided independent measurement of pressure drop across the cell and absolute pressure, which combined with single molecule tracking could identify changes in the cell properties under stress.

F. Cell force measurements

In contrast to the previous measurements where biological particles were deformed by external actuation, microfluidic devices have been used to measure forces exerted by organisms such as C. elegans and cardiac tissues. For instance, Aung et al. used particle tracking methods to measure the contractile stresses generated by cardiac microtissues.²¹³ The cells were encapsulated in a methacrylated gelatin surrounded by layer of polyacrylamide hydrogel with embedded fluorescent particles on either side. With the measured elastic properties of the polyacrylamide hydrogel, the contractile stresses generated by the cardiac cells could be measured from the displacements of the particles in the gel layer. The time periodic contraction stress of the cell was quantified by tracking the peak stress. When the cell were exposed to the drug epinephrine the amplitude and frequency of the contraction cycle increased. The approach demonstrates a method for measuring tracking stresses generated by cells in a 3D environment and for further study of cardiac cells in vitro.

A platform for muscle force measurements of C. elegans was developed by Rahman et al. by tracking the deflection of an array of pillars during locomotion, see Fig. 12(b).²¹⁴ The device consisted of an array of cylindrical PDMS pillars with variable spacing and diameter, and was designed to measure the range of forces exerted by the C. elegans under different degrees of confinement. An automated image processing algorithm was developed to track the displacement of pillars in contact with the nematode. The maximum force exerted was determined by sampling multiple worms and determining the maximal force at 95% cumulative probability of the population. This measure was used to study the behavior of worms in different confinement and in different modes of locomotion. A scaling relationship from a biomechanical model found that the force was approximately proportional to the cube of the worm body diameter. The relationship was shown in experiments to be a good approximation for populations of different mutants and at different ages. The device was used by Hewitt et al. to assess the validity of two different mutants as models for muscular dystrophy studies.²¹⁵ The response of the different mutants was measured under exposure to drugs known to treat muscular dystrophy. Another recent study by Ellwood et al. used the device as part of an assessment of treatments based on hydrogen sulfide supplementation by comparing the strength of the nematodes with and without treatment.²¹⁶ The device was also used by Lesanpezeshki et al. to study the physiology of muscle cells measuring the force of mutants with different genetic modifications affecting proteins that are components of muscle structure.²¹⁷

FIG. 12.

(a) Two arrays of pillars in a microfluidic device by Sofela et al. measures the forces exerted by the trapped C. elegans by tracking large deformation of pillars.²¹⁸ Reproduced with permission from Sofela et al., PLoS One 16, e0246496 (2021). Copyright 2021 authors, licensed under a Creative Commons Attribution (CC BY) License. (b) An array of pillars used by Rahman et al. to measure the C. elegans forces by tracking the deflection of pillars during locomotion.²¹⁴ Reproduced with permission from Rahman et al., Lab Chip 18, 2187–2201 (2018). Copyright 2018 Royal Society of Chemistry.

A different device design based on the deflection of pillars was developed by Sofela et al. to measure the forces exerted by C. elegans.²¹⁹ The device used a constriction where the head of the C. elegans was trapped. The deflection of an array of deformable pillars located along the length of the unconstrained body was tracked to determine the forces exerted by the nematode, see Fig. 12(a). Due to the large deformation of the pillars, numerical analysis of the beam deflection was used to determined the thrashing force of the nematode. The force was analyzed at different positions along the body at different stages of development. The fixed position of the nematode allowed for the force from the same portion of the nematode to be assessed under different conditions. The effect of glucose concentration during culturing was studied to mimic glucose concentrations in patients with type II diabetes. In addition to a control C. elegans strain, two diabetic model C. elegans strains were used to measure the effect of glucose and a diabetes treatment on the thrashing force. The throughput was increased by designing a device with eight force measuring channels where measurements could be performed simultaneously. The device was used in a subsequent study to measure the forces exerted by mutant C. elegans strains that modeled neurodegenerative and neuromuscular diseases such as muscular dystrophy, ALS, and Parkinson's disease.²¹⁸ They compared the disease mutants to the control strain without drugs, then compared each disease mutant with and without drugs.

IV. MEASUREMENTS OF CELL LAYERS

The mechanical properties of cell layers are important for many biological functions, and the response to applied stress is important for many mechanotransduction processes. For more detail on mechanobiology of endothelial cell layers, see a recent review by Dessalles et al.²²⁰ The barrier created by cell layers must also be sufficiently robust to experience deformation without damage while maintaining barrier functions. Therefore, many measurements of cell layers include both elasticity and permeability. Integration of cell layers into microfluidic devices is challenging because it often requires culturing cells in the microfluidic device. Once the cell layer is established, the effect of shear stress from flow on layer properties can be investigated, for instance observing the growth and viscoelastic characteristics of biofilms. Multilayer planar devices have also been used to measure the permeability of cell layers by tracking the flow of solutes from one channel to another across a cell layer. Improved fabrication techniques have enabled non-planar geometries, where cells are cultured on cylindrical channel walls or on supported pillars and enabled measurements of elasticity and permeability in conditions that mimic the vascular environment.

A. Biofilm property measurements

The flow environment in microfluidics is particularly useful for studying bacterial films due to the ability to control fluid stresses and chemical composition to make long duration experiments feasible. Initial measurements on the elasticity of biofilms tracked the deformation of the film surface (see Stoodley et al.) or rolling behavior under flow (see Rupp et al.).^221,222 More recent methods for the characterization of biofilm mechanical properties have combined flow cells with local probe techniques. For instance, Mosier et al. used a microfluidic device with a detachable top that could be removed at the end of a culturing phase to perform AFM measurements.²²³ The flow stress on the film was calculated using CFD and the growth of the film was monitored with fluorescence imaging. AFM measurements were conducted at different locations in the chamber to measure spatial variations in elasticity. The study established a method that could produce a dynamic environment with different flow conditions and related its effects on biofilm mechanics.

More recently, a method for measuring biofilm properties under the flow was developed by Paquet-Mercier et al. by tracking the transport of segmented domains in the biofilm, see Fig. 13(a).²²⁴ The growth and movement of portions of the biofilm were tracked by defining regions with different optical density in transmission microscopy images. The height of the biofilm was estimated by a calibration method comparing the optical density to the biofilm height. A two-phase viscous flow model was developed to use the film height and velocity to solve for the viscosity of the biofilm. The results showed a rapid thickening during experiments that were conducted over 70 h. While the height of the film over time did not vary much with changes in salt concentration, the maximum viscosity varied over orders of magnitude between ${10}^{-1}$ and ${10}^5$ Pa s. The increase in salt concentration also led to a more rapid thickening transition to occur.

FIG. 13.

(a) Transmission microscopy is used by Paquet-Mercier et al. to track structures imaged in biofilms to measure the film viscosity under flow over time. A rapid increase in viscosity was observed at different times depending on salt concentration.²²⁴ Reproduced with permission from Paquet-Mercier et al., Lab Chip 16, 4710–4717 (2016). Copyright 2016 Royal Society of Chemistry. (b) The onset of sloughing events is measured by Greener et al. using optical density measurements to determined the biofilm height and probe yielding behavior of the biofilms under different conditions.²²⁵ Reproduced from Greener et al., Biomicrofluidics 10, 064107 (2016) with the permission of AIP Publishing LLC.

A slightly different approach was taken by Greener et al. by tracking the height and average speed of the biofilm adhered to the sides of a low-aspect ratio channel.²²⁶ The measurements were used in a segmented model of the flow in the channel to measure the change in viscosity of the biofilms over time. The approach was used to study the effect of nutrient conditions on viscosity, which had the largest effect at early times, but the difference between nutrient conditions decrease over time. Another study by Greener et al. used the optical density method to track the structure of the biofilm under flow over time, see Fig. 13(b).²²⁵ Two parallel channels were observed as the biofilms grew, with one exposed to magnesium ions and the other acting as a control. The onset and characteristics of sloughing events, release of large portions of the biofilm, were tracked. The measured shape of the biofilm was used in CFD analysis to determine the shear stress just before the onset of sloughing. The critical shear stress increased for the film exposed to magnesium ions and the failure mode resembled a visco-plastic failure. The approach demonstrated a method for probing yielding behavior of the biofilms and culturing under different conditions.

B. Planar cell layers

The integration of soft layers suitable for culturing cells into microfluidic channels has enabled interrogation of cells using various microfluidic techniques.²²⁷ For example, particle tracking methods can measure deformation and adjusting channel dimensions and flow rate can change the applied pressure and shear stress on the cell layers. Integrated sensors and deformable components are also able to measure the response of the cell layers. The permeability can also be measured by tracking solutes across cell layers supported by membranes.

A technique that uses the deformation of an elastic layer due to fluid shear stress at the surface of a microfluidic channel, first developed for synthetic soft materials, was applied on a layer of endothelial cells by Galie et al.²²⁸ The device was constructed by curing hydrogel-based substrates of different stiffness to mimic healthy and diseased vascular conditions and then covered with a PDMS gasket with step features to create channels of different height. The wall shear stress on the substrate was calculated with numerical simulations, and particle tracking velocimetry was used to validate the comparison between experiment and simulation. The response of the cell layer structure to flow was observed in the channel, and then the elastic modulus of the cell layer was measured using AFM after the gasket was removed. The results showed an increase in elastic modulus of the cell layer with applied shear stress. Stiffer substrates resulting in a higher cell layer modulus and the difference between the modulus measured without shear stress on different substrates decreased with applied shear.

The approach of culturing cells on a soft substrate in a microfluidic channel was used by Suki et al. to perform measurements of the elasticity of the cell layer through applied shear stress.²²⁹ The layer's linear elasticity was measured by tracking the displacement of particles on the layer surface under flow and through numerical simulations the displacement was related to the layer stiffness. The technique was applied to measure endothelial and vascular smooth muscle cells. The effect of blebbistatin was shown to decrease the modulus of endothelial cells, leading to the conclusion that disruption of the actin-myosin network decreases stress transmission. Because the approach used the applied flow stress to measure elastic modulus, the influence on stress on the modulus can be directly measured as well as the spatial distribution of elastic response.

Another particle-based approach developed by Nguyen et al. used acoustic forces to actuate particles on the cell layer, see Fig. 14(b).²³⁰ The approach used acoustic force spectroscopy, a method for applying oscillatory force with a piezoelectric element, to transmit acoustic waves and then the particle position is tracked with microscopy. The acoustic forces on the particle were calibrated by tracking the translation of particles in water and used theory for a sphere translation near a wall to determine the force as a function of height. The spatial variation in the pressure field was also accounted for by performing the calibration on particles dispersed on the channel surface. The technique was used to measure the storage and loss modulus of the cell layer as a function of frequency. The results were compared to viscoelastic models, and a Kelvin–Voigt model was determined to be the best fit. While the use of acoustic force required significant calibration, the study showed that the approach can be used in a closed microfluidic device and multiple measurements over a wide area can be performed simultaneously using numerous probes.

FIG. 14.

(a) A multilayer device by Frost et al. cultured epithelial and endothelial cells on either side to measured permeability by tracking fluorophore transport across the membrane to model the lung-blood barrier.²³⁵ Reproduced with permission from Frost et al., Micromachines 10, 533 (2019). Copyright 2019 authors, licensed under a Creative Commons Attribution (CC BY) License. (b) An method by Nguyen et al. actuated particles embedded on a cell layer by acoustic force as a probe of the viscoelastic properties of the cell layer. The particle oscillations are tracked using microscopy and create a spatial information about the cell layer properties.²³⁰ Reproduced with permission from Nguyen et al., Lab Chip 21, 1929–1947 (2021). Copyright 2021 Authors licensed under a Creative Commons Attribution (CC BY) License. (c) Electrochemical sensors are integrated into a device by Wong et al. to measure the transport of electroactive tracers across a cell layer to measure permeability.²³⁷ Reproduced with permission from Wong et al., Biosens. Bioelectron. 147, 111757 (2020). Copyright 2019 Elsevier B.V.

A different approach was taken for measuring the in-plane elasticity of a cell layer by culturing cells on top of a deformable PDMS membrane actuated by applied pressure.²³¹ The strain on the applied layer is measured by a Wheatstone bridge circuit mounted on the PDMS membrane that detects changes in resistance with deformation. Calibration of the change in resistance without cells provided a relationship between the measured voltage change and the applied pressure The change in the strain response of the membrane with the cell layer on top was then used to determine elasticity using theory for the deflection of a composite beam under applied pressure. The device was used to measure the elasticity of human fetal lung fibroblast cells cultured in the device and the effect of transforming growth factor on elasticity. The measured in-plane elasticity was in the mPa range and an fivefold increase was measured with cells treated with the growth factor. The measurements were compared to AFM measurements, which were in the kPa range. The large difference in measured values was attributed to AFM probing local properties of softer materials in the out-of-plane direction while the in-plane measurements probe the various networks of cytoskeleton components.

The approach was developed further to measure anisotropic elastic properties of endothelial cells by altering the direction of circuit pattern of the strain sensing resistors.²³² Thus, the in-plane elasticity could be measured parallel and perpendicular to the flow direction and the effect of physiological flow stress, about 1.2 Pa, on the structure of the cell layer and its elasticity. The results showed that under flow, the cells developed an anisotropic shape with the major axis of the cells oriented with the flow direction. The elasticity of the cell layer increased overall after exposure to shear flow, and the parallel direction was about 70% higher than the transverse direction.

A critical barrier function of cell layers is regulating flow across the layer. For instance, the transfer of oxygen and nutrients to tissue surrounding the microcirculatory system. The measurement of cell layer permeability is important for developing in vitro methods for studying the change in permeability to diseased conditions or drug treatments. Permeability measurements traditionally use the flow measured across a membrane suspending the cell layer called a transwell insert.²³³

Cell layer permeability measurements in a microfluidic device were made by Sato et al. using a multilayer device to measure transport across blood and lymphatic endothelial cells.²³⁴ A lower and upper channel were separated by a porous polyethylene terephthalate (PET) membrane with micrometer sized pores. The contribution of the PET layer to the hydrodynamic resistance was quantified by measuring permeability coefficient without cells present. The PET layer was coated with fibronectin and then blood and lymphatic endothelial cells were cultured on either side of the membrane. The permeability coefficient was determined by measuring the concentration of different sized fluorescently labeled molecules to the outlet channel as function of time after being introduced to inlet channel. The effect of flow on permeability was measured as function of time by applying pulsing and continuous flow, which reduced permeability compared to static conditions. The microfluidic setup also enabled observations on the effects of drugs on the permeability. For instance, the change in permeability with the addition of histidine and snake venom were tested, both lead to an increase in permeability.

The multilayer device approach was utilized by Frost et al. to model the lung-blood barrier by culturing epithelial and endothelial cells on either side of a membrane separating two channels, see Fig. 14(a).²³⁵ The effect of flow on the permeability was studied by tracking the concentration of fluorophore that passed through the cell layers from the upper channel where fluorophores are suspended in the flowing solution. The effect of shear stress on transport was assessed by comparing a normalized permeability with measurements using transwells. The effect of shear stress from the flow was shown to enhance transport more significantly for intermediate sized molecules, while the change was not as significant for the smallest and largest molecules measured. The results demonstrated how mimicking the physiological environment through mechanical stress can affect permeability of cell layers.

A different approach for measuring the transport of solutes across cell layers was taken by Wong and Simmons, through the use of electrochemical sensors rather than fluorescence intensity.²³⁶ A similar multilayer microfluidic device was constructed with a porous membrane separating top and bottom channels where a layer of endothelial cells was cultured, see Fig. 14(c). The electrodes for chemical sensing were patterned on the glass layer in the lower channel and square wave voltammetry was used for chemical sensing. Different types of electroactive tracers were injected into the upper channel and the concentration tracked over time in the bottom channel. The use of electrochemical sensors has the potential for higher throughput and automated long duration sampling compared to fluorescence since imaging is not needed.²³⁷

A recent millimeter-scale fluidic model system was developed by Doryab et al. to model lung fibrosis.²³⁸ The device cultured epithelial and endothelial cells with fibroblasts on a deformable membrane where liquid can be removed from one side of the chamber to create air–liquid cell layer interface. Real-time measurement of tissue stiffness during incubation was made by tracking the displaced air volume to calculate the membrane displacement from an applied pressure differential. Once the liquid was removed from the top chamber, membrane permeability was measured to assess the transport of aerosolized particles of various size into the air chamber. The response of the cell layer to aerosolized drug treatments was then made by measuring the layer's compliance from the displaced volume vs pressure along with microscope to observe changes in the cell layer structure. The approach improved on previous device designs by co-culturing multiple cells and combining real-time noninvasive mechanical measurements during culturing to detect fibrosis.

C. 3D geometry devices

Three-dimensional devices with cylindrical channels coated with cells are increasingly common for measuring properties of cell layers. The biomimetic geometry was designed as an in vitro mimic of the microvasculature, particularly for studying endothelial cells. The approach was conceived by Weinber and Bell and later used by Neumann et al. using smooth muscle cells.^239,240 The approach was developed further by Chrobak et al. to measure permeability of endothelial cell layers by tracking the passage of fluorescently labeled molecules through the cell layer.²⁴¹ The devices consisted of a PDMS chamber mounted on glass with a center chamber filled with collagen. A horizontally inserted needle was inserted through the device and when the collagen solidified the needle was removed to create a cylindrical channel. Liquid ports on either size of the center chamber delivered fluid containing cells to the cylindrical channel. The effects of gelling temperature and collagen concentration were studied to determine optimal conditions for culturing of endothelial cells.

Recently, similar devices made with the needle extraction method have been used to measure permeability of cell layers in cylindrical channels. The effect of pericyte cells on the permeability of endothelial cells was studied by Alimperti et al. by comparing devices that were seeded with different ratios of pericyte to endothelial cells.²⁴² The results showed a decrease in permeability with an increase in the relative concentration of the pericyte cells, which demonstrated the importance of the pericyte cells in the barrier function of the endothelial cells. The permeability was then measured after the addition of drugs that induced inflammatory conditions followed by drugs that were intended to restore the barrier function. The methodology demonstrated how cell functions and responses to various drugs can be tested in vitro by permeability measurements.

Similar to the approach for applying shear stress in planar cell layers, shear stress has been applied to the 3D vascular model devices by applying flow. Perez-Rodriguez et al. observed the effect of shear stress on permeability by culturing endothelial cells in static or flow conditions by placing the device on an oscillatory rocker during culturing, see Fig. 15(a).²⁴³ The results showed a significant decrease in the permeability of the cell layer when cultured under flow. The device was used without cells to measure the hydraulic permeability of the collagen gel layer under hydrostatic pressure. The method tracked the displacement of a photobleached spot in FITC dextran filled collagen in an applied pressure gradient using a fluorescence recovery after photobleaching (FRAP) setup. A higher hydraulic permeability was measured for the lower concentration collagen and decreased as a function of pressure. The results were compared to measurements of cell permeability for the two collagen concentrations studied. The lower collagen concentration resulted in lower permeability and fewer extravasated cells into the surrounding collagen. They concluded that the lower concentration resulted in greater cell layer integrity even though extravasated cells would encounter more resistance.

FIG. 15.

(a) The hydraulic permeability of a 3D vascular device by Perez-Rodriguez et al. layer under applied hydrostatic pressure by tracking the transport of fluorescent molecules out of channel. A decrease in the permeability is observed in vessels where flow is applied during culturing.²⁴³ Reproduced from Pérez-Rodríguez et al., Biomicrofluidics 15, 054102 (2021) with the permission of AIP Publishing LLC. (b) A microfluidic device by Chen et al. with patches of collagen suspended between micropillars that are used to measure contractile stress and stiffness of microclots formed by adhered platelets.²⁴⁴ Reproduced with permission from Chen et al., Nat. Commun. 10, 2051 (2019). Copyright 2019 authors, licensed under a Creative Commons Attribution (CC BY) License.

The effect of flow stress on an endothelial cell layer in a 3D microvessel-on-chip device was studied by Dessalles et al. for a wide range of different flow magnitudes and device conditions, see Fig. 16(c).²⁴⁷ Flow was applied using a pressure-driven hydrostatic reservoir for low flow rates or a syringe pump flow for higher flow rates. A 120 $\mu$m diameter channel with a length to diameter ratio of 100 was used. The long channel length resulted in a change in flow rate in the streamwise direction due to flow out of the channel through cell layer. Particle tracking velocimetry at different stream-wise positions was used to determine the change in flow rate. The results were compared to a fluidic circuit model to determine the hydraulic resistance of the channel flow and the porous flow through the cell layer and collagen gel. The applied pressure was controlled by adjusting the length of tubing downstream of the chamber. The strain was measured by tracking the channel diameter using brightfield microscopy and the circularity of the cross section was verified using optical coherence tomography. The stress–strain relationship was studied for a number of different device conditions, including changing the total downstream hydraulic resistance, size of the surrounding gel, and the collagen gel concentration. The behavior under oscillatory flow delivered from the syringe pump was also analyzed and the strain response of the channel was measured as a function of channel length and frequency up to frequencies of 3 Hz. The device and measurement methodology demonstrated physiological levels of stress and flow in a 3D microvessels-on-a-chip platforms for mechanobiology studies.

FIG. 16.

(a) A 3D microvessel-on-chip device by Salipante et al. was pressurized using pneumatic controls to measure elasticity and permeability of the cell layer.²⁴⁵ Reproduced with permission from Salipante et al., Soft Matter 18, 117–125 (2022). Copyright 2022, This is a U.S. Government work and not under copyright protection in the U.S.; foreign copyright protection may apply. (b) A bifurcating stream device by Akbari et al. measured the effect of flow stress on endothelial cell layer permeability studied by tracking fluorescent molecules transport into an extracellular matrix at different locations in the bifurcation.²⁴⁶ Reproduced with permission from Akbari et al., Lab Chip 18, 1084–1093 (2018). Copyright 2018 Royal Society of Chemistry. (c) A 3D microvessel-on-chip device by Dessalles et al. studied the effect of flow stress on a for a wide range of different flow magnitudes and device conditions.²⁴⁷ Reproduced with permission from Dessalles et al., Biofabrication 14, 015003 (2022). Copyright 2022 authors licensed under a Creative Commons Attribution (CC BY) License.

An approach based on pressurization of a 3D microvessel was used by Salipante et al. to measure the permeability and nonlinear elasticity of an endothelial cell layer, see Fig. 16(a).²⁴⁵ A pneumatic controller capable of applying pressures in the range of (0 to 300) Pa was used to pressurize both ends of the vessel. The pneumatic controller was used to ramp the pressure up and down while simultaneous measurements of the vessel diameter were performed using phase contrast imaging. A linear elastic response was observed in the range of approximately 0–50 Pa applied pressure while a nonlinear strain hardening response was observed at higher pressures. A Gent nonlinear elastic model was used to characterize the response, which provided values for the shear elastic modulus and a maximum strain parameter. The flow resistance of the cell layer was measured as a function of applied pressure by determining the flow out of the vessel from the rate of change of fluorescence intensity. The local stress was also measured by tracking the fluorescent stained nuclei of the cells on a confocal microscope. The local deformation between neighboring cells was calculated and compared to fluorescent particles that were flowed through the vessel and became trapped in the collagen, indicating the location of pores in the cell layer. The largest deformations were shown to occur in the regions where particles breached the vessel.

Improvements to 3D printing technologies have made more complex microfluidic geometries possible. A device by Costa et al. was made by 3D printing a template from arteries reconstructed from computed tomography angiograph scans.²⁴⁸ PDMS devices were then made from the template and endothelial cells were cultured on the walls. Blood with fluorescently stained platelets was flowed through the device to compare the amount of platelet aggregation. Two different geometries were compared, one from a stenotic artery and another from a healthy artery. They observed an increase in aggregation in the device reconstructed from the stenotic artery. The ability to replicate physiological vascular environments opens up further opportunities for studying the effect of stress and flow geometries on mechanical response of cells.

Recently, the mechanics of clotting have been investigated by Chen et al. by creating a microfluidic device with patches of collagen suspended on micropillars and a flexible membrane in a channel where platelets are introduced, see Fig. 15(b).²⁴⁴ The contractile force resulting from platelet adhesion on the collagen microtissue was measured by the deflection of the micropillars. Mechanical stretching of the flexible membrane was used to measure the stiffness of the microtissue before and after platelet adhesion. The contractile force and tissue stiffness were also measured as a function of shear rate in the channel. The device was used to study the effect of various treatments that either promote or inhibit platelet adhesion and measure resulting change in the mechanical properties of the model clot. A different method for measuring clotting dynamics was developed by Jain et al. by measuring the relative pressure drop over time of syringe driven flow through an array of channels with repeated 60^° corners designed to mimic stenosed arterioles.²⁴⁹ An exponential fit to the increase in the relative pressure drop was used to determine a characteristic clotting time. The clotting time was then compared for different concentrations of heparin, an anticoagulant, as well as shear gradients by changing the flow rate. The device was used to assess coagulation and anticoagulation therapies through an extracorporeal circuit in a live pig.

A different microfluidic model vessel approach was developed by Akbari et al.²⁴⁶ A bifurcation was made using PDMS fabrication [see Fig. 16(b)] and the inner part of the bifurcation was filled with a collagen gel while the surrounding parts were seeded with endothelial cells. Transport across the cell layer was measured in locations at the bifurcation point and along the sides of the branched vessel. The hydraulic conductivity across the cell layers in the different positions was measured under static and flow conditions by tracking fluorescence transport. The hydraulic conductivity initially increased after 1 h of exposure to flow but decreased after 6 h of exposure to a value below that of static conditions. The bifurcation method demonstrated a method for studying cell layer permeability under different flow stress conditions due to the geometry of the design and enabled long duration measurements.

V. CONCLUSION

Microfluidic tools are increasingly being used for mechanical property measurements of biological materials. The need for high-throughput measurements, in vitro microenvironments that better mimic physiological systems, and point-of-care measurements are some of the applications that utilize microfluidic-based technologies.

Advancements in microfluidic rheology have focused on a number of different measurement needs where microscale flows are advantageous. One is small-volume measurements for high value samples such as pharmaceutical solutions in testing phases. The use of interface tracking to determine flow rate in a pressure driven flow device has been the primary method for minimizing volume below 100 $\mu$l. Microrheology using particle tracking in small chambers has also been developed to measure rheology of small samples and carry out concentration and temperature assays through mixing and device controls. The use of phone based cameras and low-cost sensors are examples of steps toward deployment outside of a laboratory setting. Another step is applying controlled flow without the use of expensive pressure controllers or syringe pumps. Wider use of these devices also requires development using low cost, robust, and cleanable materials. Simplification of device operation and data analysis is also required for use by operators not in particularly trained in microfluidic devices.

The development of microfluidic-based rheometric measurements beyond shear viscosity is also of growing interest. The use of multiple channels and controlled extensional flow in channel contractions or in cross-slot flows provide measurements of extensional viscosity of non-Newtonian fluids. The optimization of device design through numerical simulations has been shown to be a promising method for improving these rheological measurements and for expanding capabilities to measure other rheological parameters, such as relaxation time or normal stresses. The optical access available in most microfluidic devices has provided structural characterization of biological suspensions, such as blood or saliva, using other simultaneous measurements such as microscopy. Improvements to sensor integration for other measurement modalities are likely to improve measurements of other rheological properties.

Mechanical measurements of suspended bio-particles in microfluidics had significant attention and advancements in recent years. One main motivation is to increase throughput for cytometry techniques based on mechanical properties. This is particularly important for biological cells where physical properties can inherently have large variances in a population. Therefore, large sample sizes are necessary for properly quantifying property differences between different cell populations. As with extensional flows in microfluidic rheometers, channel designs have been improved through numerical simulations to create regions of near ideal extensional flow. The continued improvement in channel design, imaging tools, and analysis of the flow stress and viscoelastic response will provide more accurate and faster measurement of bioparticle properties.

The use of confining channels has increasingly been used in microfluidics for mechanical characterization of bio-particles. The techniques produce measurements similar to micropipette tensiometry, but microfluidic approaches have improved throughput by creating multiple constrictions and by monitoring the transit times through pores. Through careful control of the constriction geometry, these methods have proven to be successful at distinguishing properties of different cell populations. Continued improvements to device robustness, processing of images, and modeling will improve the applicability of these methods.

Other fields, electrical and optical, create stress on bio-particles and can be incorporated into microfluidic devices. Using electric field gradients to create DEP forces is commonly used to create deformation by imposing electric stress. Similar to flow field optimization, the design of electrodes has been aided by numerical simulations to better characterize the stress on the bio-particles. While there are fewer examples using optical forces to measure mechanical properties in microfluidics, the advancements of optical tweezer integration into devices for cell measurements provides a foundation for combining optical forces with flow for high-throughput measurements.

The mechanical measurement of nonspherical biological systems, such as bacteria and nematodes, is also of increasing interest due to the biological relevance of E. coli and C. elegans. Deformation by flow of bacteria in channels provides new methods for measuring mechanical properties during and after growth. Developing measurements of model organisms used for medical research has shown promise by providing assays for diseases that affect mechanical properties. Measuring the forces exerted by nematodes is a clear example of this progress.

The measurement of mechanical properties of cell layers has made significant progress due to improvements in culturing of cell layers in microfluidic devices. It has been possible to probe cell layers by the application of channel flow and the effects of flow during culturing can also be explored. For the purpose of studying biofilms, integration of cell culturing within the devices has enabled both viscoelastic measurements of cell layers and breakdown of the layers under different conditions. Culturing cell layers, such as endothelial cells, either on 2D surfaces or in 3D scaffolds in collagen has created new approaches for measuring cell layer properties such as permeability and elasticity in vitro.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

Paul Francis Salipante: Conceptualization (lead); Visualization (equal); Writing – original draft (lead); Writing – review & editing (lead).

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.