Self-organization of whole-gene expression through coordinated chromatin structural transition

Abstract

The human DNA molecule is a 2–m-long polymer collapsed into the micrometer space of the cell nucleus. This simple consideration rules out any “Maxwell demon”-like explanation of regulation in which a single regulatory molecule (e.g., a transcription factor) finds autonomously its way to the particular target gene whose expression must be repressed or enhanced. A gene-by-gene regulation is still more contrasting with the physical reality when in the presence of cell state transitions involving the contemporary expression change of thousands of genes. This state of affair asks for a statistical mechanics inspired approach where specificity arises from a selective unfolding of chromatin driving the rewiring of gene expression pattern. The arising of “expression waves” marking state transitions related to chromatin structural reorganization through self-organized critical control of whole-genome expression will be described in the present paper. We adopt as a model system the gene expression time course of a cancer cell (MCF-7) population exposed to an efficient stimulus causing a state transition in comparison with an ineffective stimulus. The obtained results will be put into the perspective of biological adaptive systems living on the edge of chaos.

I. INTRODUCTION

To elucidate the mechanism by which an integrated genome system guides cell-fate change is a fundamental challenge in current bioscience. This mechanism acts through the complex spatiotemporal self-organization of the genome involving on/off switching of thousands of functionally unique heterogeneous genes in a remarkably cooperative manner (MacArthur et al., 2009 and Chang et al., 2006). However, there are two main fundamental physical difficulties in achieving such a large-scale coordinated control on a gene-by-gene basis. The first one is the lack of a sufficient number of regulatory molecules in a cell to reach a stable thermodynamic state (i.e., breakdown of the mass action law). The low copy number of specific gene mRNAs provokes stochastic noise (Ferreiro et al., 2011), thereby inducing a substantial instability of genetic product concentrations falsifying any gene-by-gene feedback control hypothesis (Raser and O'Shea, 2005 and Yoshikawa and Yoshikawa, 2002).

The second one derives from the huge linear dimension of human DNA molecule (around 2 m) with respect to cell nucleus that makes chromatin very far from a Turing-like string freely accessible by regulatory molecules at the single-gene level.

This extreme compression generates a stunning complex organized structure of chromatin at different orders of magnitude (Cremer et al., 2004). There is much evidence of the existence of cell type-specific chromatin folding organization (Mayer et al., 2005) as well as of transcription dependent local changes in chromatin organization (Bohn et al., 2010). In this work, we explore the consequences on transcription dynamics of considering chromatin remodeling as the main material basis of gene expression regulation.

Our recent studies (Tsuchiya et al., 2010; 2014; 2015; 2016; 2020; and Giuliani et al., 2018) demonstrated that self-organized criticality (SOC) is a physically motivated candidate for massive, coordinated gene expression regulation. The basic issues of genome expression control by SOC are as follows:

• Self-organized critical control (SOC) of whole expression: Whole-genome expression is dynamically self-organized through the emergence of a critical point (CP) at both the cell-population and single-cell levels;

• The ON-OFF switch of the CP state occurs through change in critical transition on its singular behaviors. The CP represents a specific set of critical genes, which has an activated (ON) or deactivated (OFF) state. It is to be noted that this ON-OFF state does not indicate a simple binary state, but admits different state levels. Furthermore, this set of critical genes induces a change in genome attractor (GA: center of mass of genome expression).

• In OFF state of the CP, the stochastic perturbations propagate locally but when a peculiar effective disturbance activates the CP, the perturbation can spread over the entire system in a highly cooperative manner.

• In ON state of the CP, the system approaches its critical point and global behavior emerges in a self-organized manner. In such a way, it is possible that an autonomous critical-control genomic system (genome-engine) develops through the formation of dominant cyclic flux between critical states.

• (1)Coherent perturbation on the genome-engine through the change in the CP drives cell-fate decision and, thus, the CP acts as the center of cell-fate change.

On a more general ground, SOC is consistent with the location of genome expression on the “edge of chaos” (Huang et al., 2009), which can be summarized as a state, in which continuous adjustments of gene expression levels around an “ideal” (attractor) cell-kind specific gene expression profile happens in response to continuous (albeit relatively minor) microenvironment perturbations.

In addition to the purely qualitative resemblance of a paradigm like SOC that implies a “critical equilibrium state” characterized by continuous fluctuations around a native configuration in response to the system adjustments to the tiny and unpredictable microenvironment perturbations, the possibility to operationally use the SOC model in this present case stems from some modifications with respect to the original model. As aptly stressed in Sanchez and Newman (2015) in a completely different field of investigation (plasma physics), SOC cannot be considered as a classical physical theory giving rise to exact quantitative predictions: “Predictions can indeed be made within the SOC framework, but they have to do with trends, probabilities, and scaling, not with specific values of transport coefficients or fluxes. SOC is more a collection of concepts and ideas that helps to assess the relative importance of the couplings between the different elements that interact within a system.” According to this line of thinking, we introduced a crucial difference with respect to classical SOC (Bak et al., 1987), namely, the presence of three internal states (super-, near-, and sub-critical states) that we define on the sole basis of temporal variation of gene expression normalized for their average expression. This rules out the problem pointed in Sanchez and Newman (2015) with respect to mean profiles and fluctuation equivalence of scale. This modification allowed us to state the concept of genome-engine (not present in classical SOC) and consequently to show how critical transition occurs through dynamic interactions (expression flux) among co-existing critical states (Tsuchiya et al., 2016). Moreover, the impossibility to get a strictly quantitative theory in biology prompted us to check the relevance of our SOC-like model by means of its consistency with a purely data-driven statistical approach such as principal component analysis.

As expected, the presence of a cell-kind specific gene expression profile allows for a dramatic reduction of dimensionality of phase space that collapses into very few (two or three) principal components accounting for the whole-gene expression variation. Notably, a main principal component accounts for almost totality of between gene variation (first principal component, PC1, corresponding to the Sanchez and Newman mean profile); this component is the image in light of the presence of a cell-kind specific expression profile. In addition to PC1, there are a few minor components accounting for the motions (fluctuation modes) orthogonal to the first component.

As we will see in the following, different gene component scores allow to characterize their roles in SOC in terms of critical states.

While such a model can predict many observed features of biological regulation at both single cell and population levels, it still lacks a foundation in terms of molecular mechanisms involved.

In this paper, we give a proof for both local character of the fine-tuning regulation along the chromosome and evidence of SOC critical states at the single-gene expression level. Both issues point to chromatin flexibility around its cell-kind specific organization as the main driver of gene expression regulation at large. The present work deals with this proof and redounds around three main issues:

• (I)To give a proof-of-concept of the existence of a relation between the spatial proximity of genes along the chromosome and their co-regulation.
• (II)To investigate the presence of specific genes (“hot spots”) organizing the fluctuations around the “cell-kind specific ideal expression value” (“attractor”) and their role in genome expression self-organization.
• (III)The correlation in time between cell-state transition and the chromatin dynamics as made evident by chromatin reorganization in terms of folding/unfolding of chromatin knots (Krigerts et al., 2021).

II. SETTING THE SCENE

A. The biological case

The biological case studied in this work comes from Saeki et al. (2009) and has optimal characteristics to highlight the essential of biological regulation. Actually, it allowed us to recognize the SOC-based gene expression regulation reported in previous papers (Tsuchiya et al., 2020).

The dataset collects gene expression data relative to the same cell-kind (MCF-7 a breast tumor immortalized cell line) observed for 18 time points after the administration of two different stimuli: epidermal growth factor (EGF) and heregulin (HRG). EGF-stimulated cells proliferate without any sign of cell differentiation, whereas HRG stimulation induces cell differentiation (Nagashima et al., 2007). Notably, while EGF does not provoke a critical transition in MCF-7 cells, HRG does (Tsuchiya et al., 2014).

This allows for a direct comparison between the two EGF and HRG conditions to single out what discriminates the two situations in the presence of a fully controlled and homogenous system (same cell-kind, observed time points, and microarray system).

In this model, terminal differentiation is evident in terms of a clear phenotype change after a week or more of treatment, but this late manifestation needs very early changes in gene expression (on the order of 15–30 min after the first administration) that we will investigate in this review.

The effects on the gene expression follow the nuclear transport of EGFR (epidermal growth factor receptor) induced by HRG; the same phenomenon is elicited by EGF (epidermal growth factor), but at odds with HRG, EGF administration does not end-up with any relevant phenotypic change.

The initial “wave of change” dissipates after 30 min (the system goes back to its initial equilibrium gene expression profile), but its “memory” remains for around 1–1.5 h by the action of FOS, a proto-oncogene of retroviral origin playing a key role in both tumorigenesis and tumor suppression. FOS down-regulates the MAPK/ERK pathway (a cascade of subsequent protein activation that communicate signals from membrane receptors to cell nucleus causing tumor growth). The ERK activation is abated by 3 h; after this time, the system is committed to leave the neoplastic fate to enter the path ending up in a terminally differentiated state (production of fat) evident after one week (Krigerts et al., 2021). Even in this case, the erasure of the initial-state sandpile critical behavior (criticality) occurs after 3 h as in the case of gene expression (see Fig. 4, Tsuchiya et al., 2020a).

In this paper, we concentrate on the very early phase of the above process starting from around 15 min after drug administration and ending at 30 min; in other words, we are describing a transient that perturbs for a short period the “business-as-usual” life of the system that, after a while, recovers its pristine gene expression profile. The duration and intensity of this transient are crucial for the subsequent commitment of the system toward a phenotypic phase transition. This situation is very favorable for our aims, because it allows to neatly separate a rapid response asking for an almost immediate global rewiring of a gene expression pattern from a long-lasting continuous process ending up into the effective phenotypic change. In other words, we can exactly locate in time the phenomenon of interest (early response) so as to compare the responses to HRG and EGF administration that we know in advance to have very different consequences on the long timescale.

The rapid response is analyzed in depth in terms of the gene expression dynamics in the studies by Tsuchiya et al. (2010), (2014), (2015), and (2016) recently, the structural counterpart of the same phenomenon came into light in the study by Krigerts et al. (2021). The centromere of chromosomes is rich of the so-called “satellite repeats”—very repetitive DNA sequences that are condensed as heterochromatin. This pericentromeric heterochromatin is traditionally considered to comprise a repressive environment in the nucleus. These regions are visible as “knots” by microscopy and are called PADs (pericentromeric associated domains); the greater the PADs size and number, the lower the transcription activity. By experimentally tethering an active locus to chromocenters (Wijchers et al., 2015), the authors established a causal role of peri-centromere proximity in the transcriptional repression of associated loci. The same experimental setting adopted for genome expression (identical time points, same MCF-7 cell line) of SOC studies (Tsuchiya et al. 2010; 2014; 2015; and 2016) was replicated in Krigerts et al. (2021) in terms of chromatin microscopic image analysis focusing on the dynamics PADs.

The correspondence in the time between PADs and gene expression dynamics is the most cogent proof of the material basis of the proposed gene expression regulation model.

B. General considerations and data analysis strategy

The common experience of any scientist working with transcriptome microarrays is the near-to-unity correlation between the gene expression profiles of independent samples coming from the same cell-type (Tsuchiya et al., 2016).

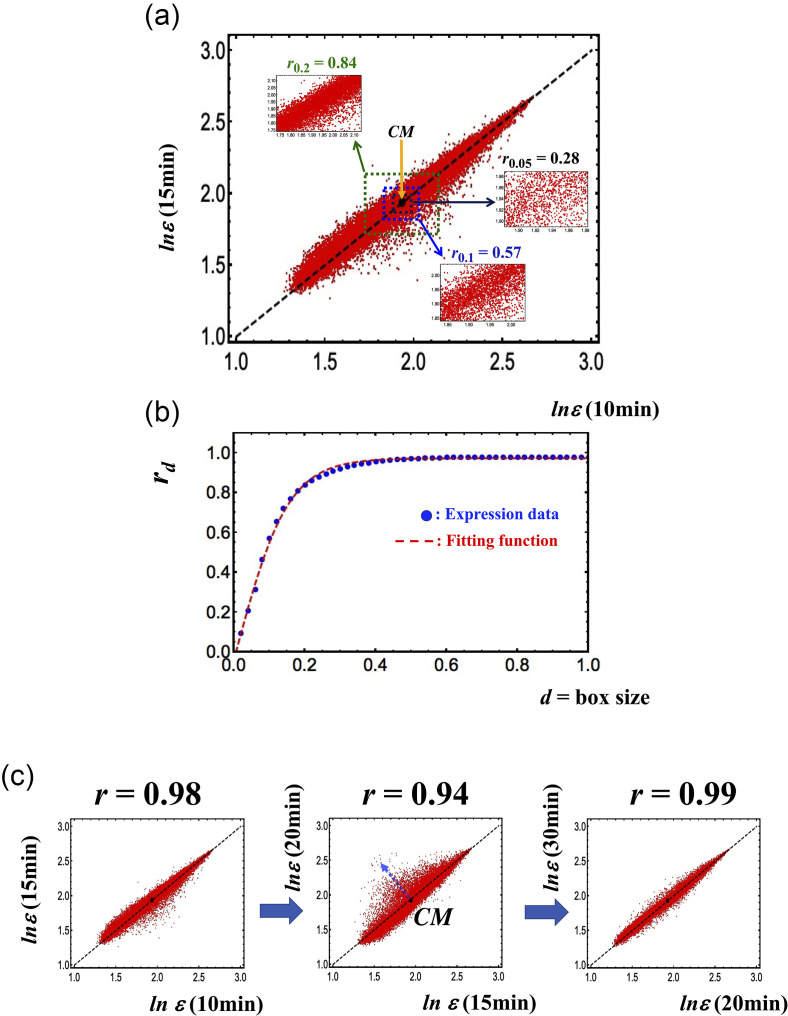
Figure 1(a) refers to MCF-7 cell line and clarifies this point: the axes refer to two independent MCF-7 samples whose single-gene expression values are the points of the graph (around 23 000, expression values in logarithm units), and the d-value corresponds to the range (box size) of variation, inside which the correlation (Pearson coefficient, r) is computed. The correlation computed overall is near to unity (r = 0.98) and declines at the decreasing range of variation.

FIG. 1.

Transition from a stochastic to a genome-wide attractor profile. (a) Pearson's correlation between two independent samples (10 min vs 15 min) of MCF-7 (axes of the plot) in terms of expression levels of around 23 000 mRNAs (vector points). (b) Profiles correlation r_d vs d (box size); see the tangent hyperbolic function as signature of transition from a stochastic to a genome-wide attractor profile. (c) The Pearson's correlation between the gene expressions profiles at different time points reveals the occurrence of critical transition at 15–20 min around the CM (back solid dot) corresponding to a decrease in Pearson r and visually to an increase in the scattering of points from the identity line. A tipping point in terms of the critical transition exists at 15 min (see more in Fig. 5). This stems from the (coil-globule) critical transition at the CP, where the CP corresponds to the CM when expression is ordered by the normalized root mean square fluctuation (nrmsf).

Figure 1(b) shows the reaching of a plateau correlation at d = 0.45. This remark outlines how the correlation values are tightly dependent on the observation scale. The scale dependence of the correlation is instrumental to keep alive both the functionality of the tissue (the specialized physiological function asks for an almost invariant ideal pattern of gene expression) and the flexibility required to adapt to changing microenvironment, tuning the specific gene expressions at the small scale. This fine-tuning does not alter the global profile invariance and corresponds to the scattering of the points around the identity line [y = x line in Fig. 1(a)]. The dispersion across the identity line corresponds to the equilibrium around a definite physiological (tissue dependent) state that, as expected in SOC, corresponds to a “critical dynamically stable state” encompassing continuous fluctuations around the cell-kind specific profile.

Figure 1(c) reports the increase in scattering orthogonal to identity line near the tipping point (central panel).

The near-to-unity correlation between the independent samples of the same cell-kind tells us that the main driver of gene expression is the protection of cell physiological identity. Humans have approximately 400 cell-kinds (Vickaryous and Hall, 2006); each one corresponds to a global stable expression pattern out of the infinite number of patterns possibly stemming from around 25 000 genes each potentially varying across four orders of magnitude.

The very low number of allowed stable expression profiles is the image in light of the limited number of stable chromatin global organization patterns, each corresponding to a cell-kind attractor of transcription dynamics. In the following, we will further elaborate about the resemblance between “cell-kind specific gene expression profile” and the notion of attractor. Here, it is sufficient to refer to Figs. 1 and 2 of Tsuchiya et al. (2016) that show the loss of near-to-unity correlation when two different cell types are compared (Fig. 1) and the converging of streamlines toward the identity line (cell-kind ideal profile) (Fig. 2; Tsuchiya et al., 2016). This stream plot suggests the presence of a basin of attraction around the average profile.

The fluctuation around the ideal expression profile generates very robust oscillations encompassing the entire genome. These oscillations reflect the apparent conundrum of “sandpile” SOC regulation in which the attractor state is a critical state characterized by “small avalanches” functional to the stability of gene expression profile when exposed to continuous small environmental perturbations (adding grains to the sandpile = continuously changing microenvironment) (Bak et al., 1987 and Bak and Chen, 1991).

As aptly stressed in Marr et al. (2016), “Pearson's principal component analysis (PCA) identifies genes that vary the most within the profiled population of cells and linearly projects the high-dimensional data into a lower dimensional space.” Consequently, we do expect PCA is able to discriminate genes mostly varying in time as those with higher absolute score values as for motion across the ideal profile (PC2, PC3) components. Genes with near zero value of PC2 and PC3 are the ones less affected by fluctuation corresponding to the core of the sandpile (and consequently to the most invariant ones). These genes correspond (in SOC terms) to the CM (center of mass) of the system (genome attractor: GA) and are put in motion only when the transition is activated by a domino effect summing up the small avalanches thus ending up into an effective perturbation.

If the system stays in the very center of the attractor (corresponding to the identity line of Fig. 1), with no fluctuation, we observe a maximal correlation between the variables because each time profile is identical to all the others. This implies that all the variance of the system lays along the ideal line ordering the genes from the less to the more expressed. We call this ideal line “cell-kind attractor”; this line corresponds to the first principal component (PC1) of gene expression in time. Consistent to what depicted in Fig. 1, PC1 (see Sec. III) explains more than 90% of total variance.

We can factorize the total variance (how diverse the values in the matrix having genes as statistical units and different times expression profiles as variables are) in terms of “Between Genes Variance” and “Within Gene Variance,”

$$\text{Total}\hspace{0.17em}\text{Variance}=\text{Between}\hspace{0.17em}\text{Genes}\hspace{0.17em}\text{Variance}+\text{Within}\hspace{0.17em}\text{Genes}\hspace{0.17em}\text{Variance}.$$ (1)

The normalized root mean square fluctuation (nrmsf), the parameter that we used in previous works (Tsuchiya et al., 2014; 2015; and 2016) to group the genes in different critical states, has to do with the second term of (1): it comes from the variance in time internal to each gene (i.e., each gene has a specific nrmsf value). In other terms, the between variance is relative to variability along the columns and reflects the different average expression values of the genes, and the within variance is relative to variability along the rows and reflects the variability in time of each gene.

When in the presence of a dominant first component (size component, Jolicoeur and Mosimann, 1960), the fluctuations around the attractor are accounted for minor components (from second onward) that, by construction, are orthogonal to each other and to the main order parameter (PC1). Near a tipping point, the second term of (1) becomes increasingly important: some genes deviate more than usual from their ideal expression level along direction(s) orthogonal to PC1 (we discovered two main directions of this motion: PC2 and PC3, see Results). This provokes a decrease in between profiles correlation especially evident in “high motion” (supercritical in SOC terminology) genes (profile correlation going from 0.98 to 0.75 for supercritical state, see Fig. 4 in Tsuchiya et al. (2015).

In PCA terms, the expression value E(i), for each gene i, across the 18 time points can be reconstructed as a linear combination of the component scores as

$$\mathrm{E}\left(\mathrm{i}\right)=\mathrm{a}\cdot \left(\text{PC}1\left(\mathrm{i}\right)\right)+\mathrm{b}\cdot \left(\text{PC}2\left(\mathrm{i}\right)\right)+\mathrm{c}\cdot \left(\text{PC}3\left(\mathrm{i}\right)\right)+\cdots .$$ (2)

Equation (2) is intended on the entire set of 18 components but, if we stop the weighted sum at the first three components, thanks to the very strong correlation structure of the system, we can reconstruct the actual expression value with 99% of accuracy (see Sec. III).

PC2 and PC3 are coordinated “waves of fluctuation” spanning the entire genome, and we will see in the following that they account for the collective gene expression oscillations responsible for SOC.

In the same vein, we expect that, in the case of a real transition (HRG), the relative importance of fluctuation (PC2 and PC3) modes should be greater with respect to the no transition (EGF) case.

Going back to Eq. (2) is evident how each gene expression value (E(i)) derives from the weighted summation over the contribution of all the intervening components. This implies that at the critical point, when the fluctuation components (PC2, PC3), in the HRG case, dramatically increase their relative contribution (see Sec. III), CM genes whose expression is normally only dependent on PC1 show a relevant contribution from PC2 and PC3. This provokes a drastic displacement of these genes from the identity line [central plot of panel (c), Fig. 1]. We call this displacement as “avalanche” corresponding to the participation of CM in the fluctuation modes. The term avalanche, derived from SOC sandpile model, indicates the transmission of motion to previously invariant genes. The term avalanche is further justified by the strictly local character of gene co-regulation described in the RQA chapter (see Sec. III). In other words, the nearby “hot spots” scattered all over the chromosome transmit their motion to the low nrmsf genes constituting the CM.

C. Structural constrains implies a local character of gene co-regulation

In our formalization, the raw data matrix has genes (n = 22035) as statistical units (rows) and the expression profiles at different times as variables (18 columns). The location of each gene along the corresponding chromosome is perfectly known, and this implies that we can exactly measure the along chromosome distance of different genes, while the eventual between genes proximities generated by 3D chromatin folding are out of reach of the analysis. In any case, the within chromosome gene contacts are largely more common than the between chromosome ones (Tan et al., 2018).

If the chromatin structure is the main driver of gene co-regulation, we do expect that the correlation of the fluctuations around their average expression of two A and B genes will negatively scale with their spatial distance.

On a statistical point of view, any effort in demonstrating the existence of a relation between spatial proximity of genes along the chromosome and their co-regulation must eliminate the “batch effect” caused by the huge between genes differences in the average expression (PC1).

This makes mandatory to approach the problem by preliminary normalization of the single-gene expressions. This row-by-row (genes are the rows of the original matrix, and time points are the columns) normalization was faced by the transforming expression values to z-scores by the formula

$$\mathrm{Z}\left(\text{ij}\right)=\hspace{0.17em}\left[\mathrm{X}\left(\text{iJ}\right)-\mathrm{m}\left(\mathrm{i}\right)\right]/\sigma \left(\mathrm{i}\right),$$ (3)

where X(ij) is the expression value of gene i, at time j (t_j), and m(i) and σ(i) are the average and standard deviation, respectively, of X(i) across all the times.

After this transformation, we posit that two A(X(i = A, j)) and B(X(i =B, j)) genes are co-regulated (at a specific time j) if they have similar z-scores. In other words, two A and B genes are co-regulated if they have approximately the same normalized difference with respect to their respective cell-kind ideal expression value.

The series of normalized expression values of genes along the chromosome is mathematically equivalent to a discrete time-series whose values are the single-gene z-scores sampled along chromosome location (gene1, gene2, and gene3 according to the relative order along the chromosome). This allows approaching the problem of the link between the gene co-regulation and spatial position on chromosome by means of signal analysis methods. To this aim, we adopted the recurrence quantification analysis (RQA) paradigm.

Recurrence quantification analysis (RQA) is a nonlinear technique, originally developed by Eckmann et al. (1992) as a purely graphical method and then made quantitative by Webber and Zbilut (1994). It was successfully applied to different fields ranging from physiology (Zimatore, et al., 2020a and 2020b), molecular dynamics (Manetti et al., 1999), acoustics (Zimatore et al., 2017), and economics (Orlando and Zimatore, 2020). The concept of recurrence is straightforward: for any ordered series (time or spatial), a recurrence is simply a value that comes back (almost) identical in different sections of the series. This makes RQA immediately applicable to biopolymers like DNA (Pizzi et al., 2001) and proteins (Giuliani et al., 2002) where the order of monomers (nucleotides, amino-acid residues, gene expression values as in our case) along the sequence is isomorphic to a time series sampled at discrete equally spaced intervals. Recurrences are the most basic of relations shaping a given system, since they are strictly local and independent of any mathematical assumption regarding the system itself. Furthermore, it is worth stressing that the calculation of recurrences, unlike other methods, such as Fourier, Wigner–Ville, or wavelets, requires no transformation of the data and does not require a minimum length of the series.

RQA works on the embedding matrix (EM) of an original linear time series. EM is a n-dimensional matrix generated by shifting the original series of a fixed lag. The rows of the embedding matrix (EM) correspond to subsequent windows of length k (embedding dimension) along the sequence. RQA is based on the computation of the Euclidean distance matrix (DM) between the rows (epochs) of the EM, looking for epochs close to each other (recurrences).

The concept of a recurrence can be expressed as follows: given a reference point, X0, and a ball (Br) of radius r, a point X is said to recur (with reference to X0) if

$$\text{Br}\left(\mathrm{X}0\right)=\left\{\mathrm{X}:|\mathrm{X}-\mathrm{X}0|\right\}\hspace{0.17em}\le \mathbf{r}.$$ (4)

In the case of a time series of a system occupying in different times different positions along a trajectory in a suitable state space, the recurrences correspond to the time points where the system passes nearby to already visited states. In our case, in which the elements are single-gene expressions, time corresponds to the location of genes along the chromosome and the recurrences are patches, with a length equal to the embedding dimension, sharing their expression profile with other patches along the chromosome. The number and relative positions of recurrences are expressed by recurrence plots (RP) that are symmetrical N_*N arrays in which a point is placed at (i, j) whenever a point Xi on the trajectory is close to another point Xj. The closeness between Xi and Xj is expressed by calculating the Euclidian distance between these two normed vectors. The two points are scored as recurrent if their Euclidian distance is lower than the pre-defined fixed radius r. This procedure allows for the construction of the recurrence plot (RP) corresponding to the distance matrix between the different epochs (rows of the embedding matrix, patches made of k genes in our case). In order to get an RP, the distance matrix is filtered, by the action of the radius, to a binary 0/1 matrix having a 1 (dot) for distances falling below the radius and a 0 for distances greater than radius.

Because the graphical representations may be difficult to evaluate, Webber and Zbilut (1994) developed several strategies to quantify the features of such plots. Hence, the quantification of RPs leads to the generation of some global descriptors, but in our case we only rely on the most basic one, i.e., the number of recurrences computed at increasing length epochs corresponding to the increasing distances along the chromosome.

In our case, the original series consists of the subsequent standardized gene expression values along the chromosome at each time point. Each chromosome was separately analyzed obtaining practically identical results for all the chromosomes at any time point. The chosen embedding dimension was set to 3, and the radius was set to 60% of mean distance. The number of recurrent gene pairs (REC) was then plotted in the function of the along chromosome distance between the recurrent (co-regulated) couple.

D. A Short physics/biology translation help

The last paragraph of this section is a sort of “disclaimer” about the (largely unescapable) terminological confusion of a research work located at the very edge between physics and biology. Each specific discipline attaches to the same term a slightly different meaning; the de novo introduction of new terms for research on the edge between different disciplines is clearly unfeasible, so we prefer to overtly declare the possible ambiguities linked to the use of crucial terms frequently encountered in the paper:

• (1)Attractor: We used this word in both a general “a preferred configuration the system tends to” and a more specific “a stable (albeit critical) state actively maintained by system fluctuation” sense. The first case is more familiar to the biologist: it simply describes the evidence that each cell-kind has a typical profile of gene expression spanning the entire genome. The most straightforward biological analogy is the existence of a protein native structure that remains recognizable along the (small) fluctuations due to thermal motion. In this sense, all the different genes participate of the same attractor whose strength is evident by the fact that the by far major part of system variance is accounted by PC1. The identification of average expression profile as an attractor, in life sciences, is totally intuitive (albeit largely qualitative) redounding on the time-honored concept of homeostasis, i.e., the tendency, shared by all physiological process, to go back to the original status after a perturbation (Goldstein, 2019).

  The second, more physically oriented, use of the word “Attractor” we make in this work has to do with the (modified) SOC model we adopted. In this case, the term refers to the contemporary presence of three (“super-critical,” “near-critical,” and “sub-critical”) expression states that tend to the “critical state” (attractor). In this frame, the attractor has a main “core” corresponding to the center of mass genes and a periphery corresponding to the most fluctuating (in the following hot spots) genes.

  These two different notions are mutually consistent; in the following, we will demonstrate that the center of mass genes are those with an overwhelming contribution of PC1 (near zero value for PC2 and PC3 “fluctuating” components).

  On a more theoretical ground, we can derive the concept of attractor from the seminal Lagrange definition of stability that as reported in Nikolov et al. (2007) “If, in some arbitrary position of a given system, the potential energy V has a minimum, then this position is the system's equilibrium state, which is stable.” Equilibrium states can serve as attractors of the dynamical systems, i.e., all trajectories in their neighborhood can be asymptotically attracted toward the equilibrium state (Nikolov et al., 2007).

  The idea of dynamical stability was mathematically defined and made operative by the Russian mathematician Aleksandr Lyapunov in 1892 (Lyapunov, 1966). In general, attractors are irreducible attracting sets and in view of Lyapunov stability, equilibrium states can serve as attractors of the dynamical systems (Nikolov et al., 2007). In the case of Biology, things are fuzzier due to both the huge dimensionality of the studied systems and the lack of a strictly formal definition of the dynamics. This implies the shift toward “structural stability” that can be equated to the concept of “robustness” and to the physiological principle of homeostasis.

  While physics allows for a formal a priori approach in terms of explicit equations (and consequently an immediate check of the congruence between theoretical a priori prediction and experimental results), biology, due to the lack of any formal a priori theory, does not allow for such a direct approach. This implies that the recognition of structural stability (and as a consequence the definition of a given equilibrium state as an attractor) can be only verified a posteriori by a statistical approach, i.e., by the observation of the “coming back” of the systems at hand to a condition very similar (phenotypically equivalent) to the initial point after a perturbation. In the case at hand, the statistical metrics adopted for judging of states quasi-identity is the Pearson correlation coefficient between gene expression profiles at different times. As a matter of fact, 30 min after the occurrence of the examined perturbation, the correlation coefficient between actual and initial state goes back to a near unity value (see Figs. 1 and 5).

  All in all, we can use Lyapunov stability as “general concept” but with the caveat of the impossibility to get a rigorous mathematical definition and only relying on the statistical evidence.

• (2)Ideal: The attribute ideal has no implications of value; it is only used (like frequently happens in biomedical literature) to identify a “paradigmatic” or “exemplar” configuration. In this case, the “ideal cell-kind profile” corresponds to what we called “attractor” in the generic sense (see above paragraph). Each gene has an Ideal (cell-kind specific) expression value that corresponds to its mean value across the 18 time points.
• (3)Motion: PCA corresponds to the “eigenvalue/eigenvector” decomposition of classical dynamics. This means that the displacement from an average value can be equated to the motion of a material point. The variance of a probability distribution is analogous to the moment of inertia (classical mechanics term) of a corresponding mass distribution along a line, with respect to rotation about its center of mass. The fact that PCA solution maximizes the “explained variance” of a multivariate dataset by the projection of the original dataset into a new space spanned by a minimal number of independent axes corresponds to say that PCA solution maximizes the moment of inertia. Here, we use “variance explained” and “entity of motion” in an interchangeable way as usual in statistical literature (Husson et al., 2011).
• (4)Tipping point: The term “tipping point” is becoming popular in the biological applications of dynamics for indicating the reaching of a situation preceding a transition that can be detected by statistical parameters linked to changes of correlation and variance properties of the system at hand (Ma et al., 2020; Gorban et al., 2021; and Scheffer et al., 2012). We adopted this term for its general statistical character not necessarily linked to a specific transition behavior.
• (5)Critical point (CP): Our findings of SOC does not correspond to a phase transition in the overall expression from one critical state to another (i.e., sub-critical to super-critical genome state transition), describing the genome approaching to a critical point (CP). Instead, the whole-genome expression is dynamically self-organized through the emergence of a CP (ensemble of critical genes), with the co-existence of three distinct response domains (critical states). The properties of the CP, such as sandpile critical and scaling-divergent behaviors, were described in detail in our previous paper (refer to Fig. 4 in Tsuchiya et al., 2016). Note that our approach on genome expression is based on the mean field (ensemble average). The state change in the CP induces a change in the GA, which derives the cell-fate guiding genome avalanche in the system.

FIG. 5.

ON-OFF switch of critical point (CP). (a) The dynamics of gene expression profile correlation between adjacent time points. At the tipping point (15–20 min), there is a decay in correlation. (b) Probability density functions (PDFs) of whole expression in HRG response is estimated in the space nrmsf (x-axis) vs natural-log of fold change in expression (y-axis). The combined PDFs plot of adjacent time points shows the ON-OFF switch of the CP: ON at 10–15 min and OFF at 15–20 min. where the CP corresponds to the peak of probability density (red area). (c) Same as panel (b) for EGF response. The panels (b) and (c) reveal that, while in HRG response, a big avalanche in genome expression occur, only local fluctuations are evident in EGF response.

III. RESULTS

A. Spatial proximity of genes and co-regulation

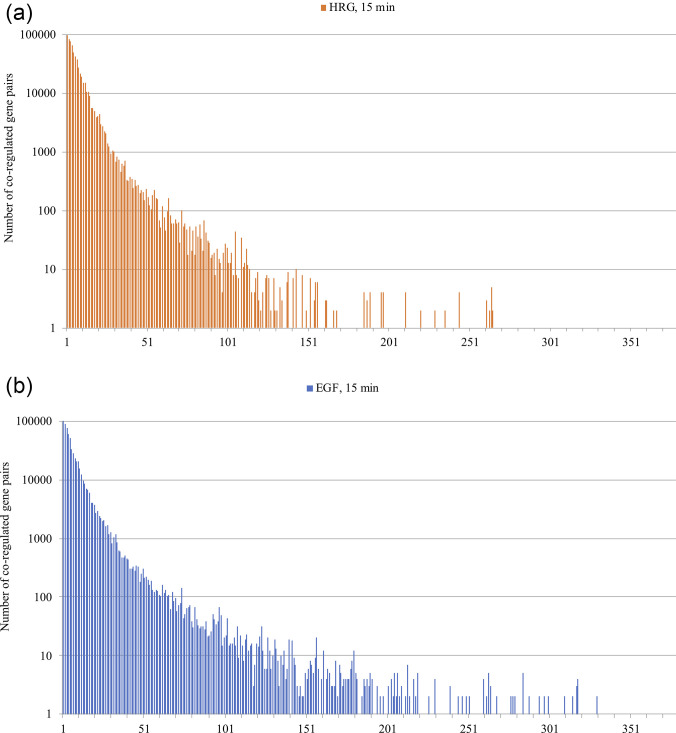
The mono-dimensional series corresponding to the normalized expression values of the genes ordered along their position on relative chromosomes was analyzed by means of the recurrence quantification analysis (RQA). In this work, we relied on the amount of recurrence (REC) descriptor that was expressed in terms of the spectrum of recurrence distribution at different separation along the sequence (RQI): the y corresponds to the number of recurrences scored between genes located at a distance x (expressed as number of gene pairs with a normalized expression value difference below the threshold).

The recurrence spectra (each recurrent event corresponds to a pair of co-regulated genes) shows a very robust exponential decay of co-regulation with an increased spacing of gene pairs along the chromosome. This behavior is consistent with the effect of local structural chromatin features (folding status, flexibility) on gene co-regulation. Figure 2 reports the recurrence spectrum [(radius = 60% of mean difference, see Eq. (4)] along chromosomes for both HRG and EGF conditions. The x axis corresponds to the distance between AB recurrent pairs in terms of number of genes between A and B loci, while the y axis corresponds to the number of recurrent pairs (co-regulated gene couples). The same pattern holds for all the time points, conditions, and chromosomes.

FIG. 2.

Recurrence spectrum along the chromosome 1. The graphs are relative to HRG (top) and EGF (bottom) conditions as for time 15 min and chromosome 1. The y axis corresponds to the number of recurrences (number of co-regulated gene pairs). The x axis corresponds to the spacing of recurrent couples along the chromosome. The spacing is expressed in terms of number of genes between the recurrent pairs. The exponential decay of co-regulation entity with the increasing between genes spacing is identical for different times of observation, different chromosomes, and for the two EGF and HRG conditions. The local character of fine co-regulation around cell-kind specific value is the same for all the experiments.

Figure 2 demonstrates that transition and no-transition conditions do not imply qualitatively different regulation mechanisms: the response to the two HRG and EGF stimuli happens through the same basic mechanism involving local chromatin folding status (exponential decay of recurrence at increasing linear distance along the chromosome). The differences between HRG and EGF conditions are only quantitative (and very subtle) as we will discover in the following.

These subtle differences were evident looking at the genes acting as hot spots (high absolute value of PC2, corresponding to the super-critical state of SOC, as we will see in the following) present in HRG but not in EGF. These HRG-specific genes were mostly related to the chromatin stability and remodeling and to the specific transcription factors.

In the case of HRG, the chromatin remodeling genes, SMARCA2 and SS18, have a prominent role with a PC2 score around 4 for both (component scores have zero mean and unit standard deviation; thus, a value of 4 identifies a point 4 standard deviations apart from the mean). Both SMARCA2 and SS18 pertain to the swi/snf family of proteins that are thought to regulate transcription of certain genes by altering the chromatin structure. Both these proteins are part of a large ATP-dependent chromatin-remodeling complex, which is required for transcriptional activation of genes normally repressed by chromatin condensed state.

As for HRG specific transcription factors, it is worth noting the elevated score (PC2 = −4.2, the negative sign pointing to a suppression of the gene expression) of c-FOS gene that perfectly fits with the known molecular mechanism of action of HRG (see paragraph 1.1).

The local character of co-regulation is consistent with the domino effect of SOC sandpile model, where each sliding grain of sand has a direct effect on the neighbor and the formation of big avalanches depending on the traveling of local perturbation by chaining single-step events. The occurrence of genome-wide global perturbation when in the presence of an exponential decay of co-regulation with linear distance suggests that the chaining of single steps follows first-order transitional behavior on chromatin (Yoshikawa et al., 1996; Yoshikawa and Yoshikawa, 2002; and Zinchenko et al., 2008). The dependence of co-regulation on the location on chromosome gives a proof-of-concept of main hypothesis at the basis of our previous works: gene expression fluctuations mirror chromatin flexibility. This is consistent with the observation that chromatin modifications can cause a cascade of events leading to promote or block gene expression (van der Knaap and Verrijzer, 2016): Post-translational modifications (PTMs) of chromatin play a major role in the activation or repression of gene transcription. These include acetylation, methylation, and phosphorylation of the histones and DNA methylation. Some of these chromatin modifications are involved in the maintenance of stable patterns of gene expression corresponding to the specific patterns of epigenetic regulation. In van der Knaap and Verrijzer (2016), the authors found that the stimulation of MCF-7 cells by HRG causes a large instability of gene expression and, consequently, the occurrence of post-translation processes of chromatin modifications (i.e., acetylation, methylation, and phosphorylation of the histones) in order to attain/maintain stable pattern of gene expression.

This same feedback leads to avalanche (or domino effect), and it is in accordance with the present review. The illusion could be that attaining the stability of gene expression is a different task than keeping functionality, but it should be noted that attaining stability (i.e., attaining attractor) means that the appropriate functionality has also been established in accordance with homeostasis principles.

B. Hot spots, critical point, and transition

Tables I and II reports the results of PCA as applied to EGF condition in terms of both eigenvalue distribution Table I) and component loadings (correlation coefficient between original variables and components Table II).

TABLE I.

Eigenvalues distribution (EGF).

Component	Eigenvalue	Explained variance (%)	Cumulative variance (%)
PC1	17.767	98.71	98.71
PC2	0.073	0.41	99.12
PC3	0.046	0.26	99.38
PC4	0.027	0.15	99.51
PC5	0.017	0.10	99.60

TABLE II.

Loading pattern (EGF).

Label	Time (min)	PC1	PC2	PC3
T0	0	0.985	0.018	0.121
T10	10	0.995	0.027	−0.069
T15	15	0.995	0.041	−0.059
T20	20	0.996	0.033	−0.050
T30	30	0.997	0.014	0.007
T45	45	0.994	−0.036	−0.053
T60	60	0.997	0.015	−0.009
T90	90	0.994	−0.087	−0.010
T2h	120	0.995	−0.082	0.004
T3h	180	0.995	−0.077	0.025
T4h	240	0.996	−0.071	0.009
T6h	360	0.994	−0.023	0.068
T8h	480	0.996	−0.014	0.005
T12h	720	0.995	0.032	−0.062
T24h	1440	0.993	0.084	0.005
T36h	2160	0.994	0.077	−0.035
T48h	2880	0.983	0.140	0.083
T72h	4320	0.990	−0.091	0.021

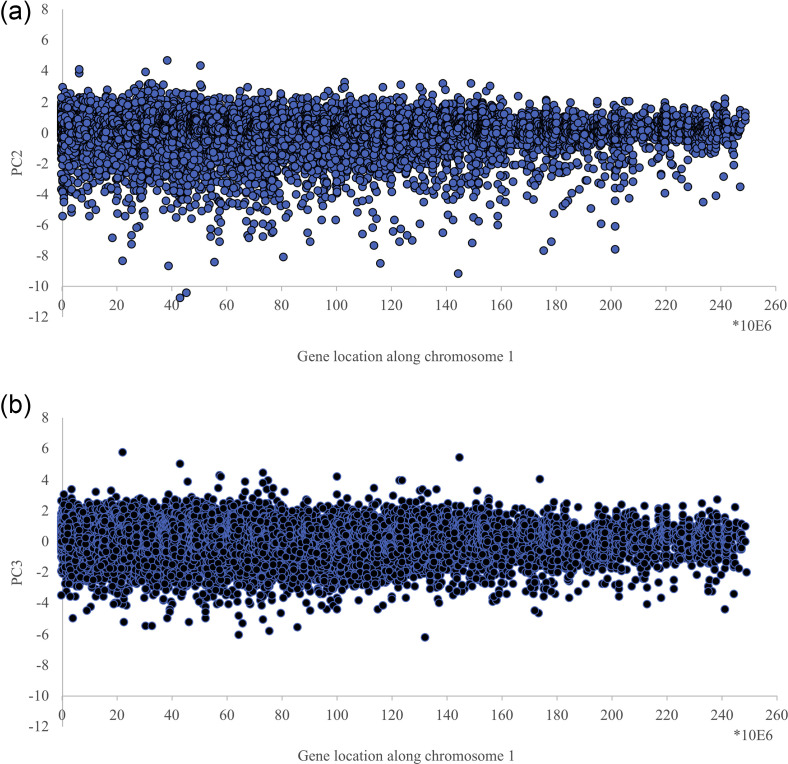
It is worth noting the cell-kind attractor component (PC1) accounts for around 99% of total variance while only two minor components (PC2, PC3) can be considered as bona fide signals. Figure 3 reports the distribution of PC2 and PC3 scores along the chromosome 1.

FIG. 3.

Distribution of PC2 and PC3 scores along chromosome 1. The x axis is the gene location along chromosome 1, while the y axis reports the correspondent PC2 (top panel) and PC3 (bottom panel) scores. The figure refers to chromosome 1 EGF at 15 min. but the same general pattern is identical across all the analyzed conditions.

From Fig. 3, the presence of “outliers” (PC scores > 4), genes whose expression is driven by the oscillatory PC2 and PC3 modes much more than others, is evident. These outliers are scattered all along the chromosome and can be considered as hot spots with respect to the gene expression variability: genes whose fluctuation around the “ideal value” (corresponding to their PC1 score) is very high. The peculiar relation of hot spots with their “cell-kind” specific expression value is depicted in Fig. 4.

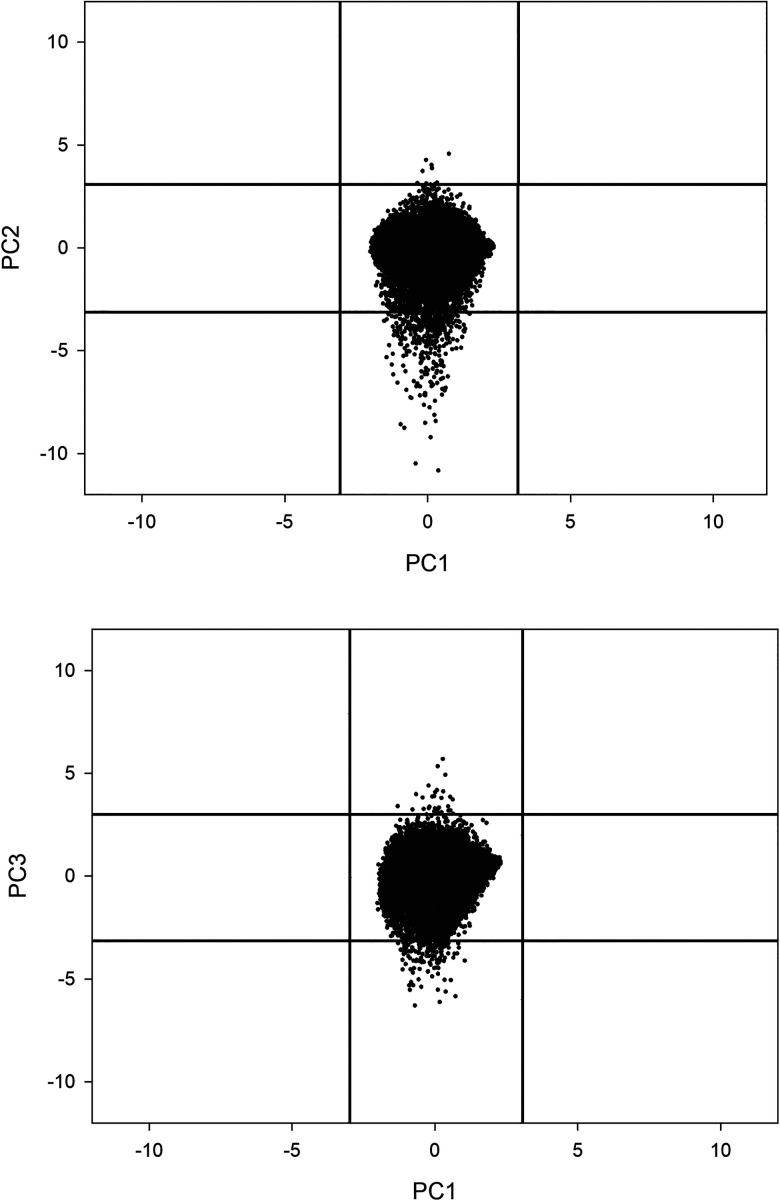
FIG. 4.

Distributional properties of fluctuations around cell-kind specific expression. The projection of the genes in the PC1-PC2 (top) and PC1-PC3 (bottom) spaces. Vertical and horizontal black lines correspond to the 3 standard deviation interval of PC1 and (PC2, PC3), respectively. Genes outside PC2 (or PC3) confidence intervals are the hot spots. All the components have by definition zero mean and unit standard deviation but while the variance of fluctuation modes (PC2, PC3) is driven by the outliers, the cell-kind attractor mode (PC1) has a continuous Gaussian distribution restricted into a much narrower variation range and no outliers.

Principal component scores have by construction zero mean and unit standard deviation on the whole set [see Eq. (4)]; thus, Fig. 4 tells us that attractor mode (PC1) scores variability is constrained into 3 standard deviation intervals (vertical black lines), while fluctuation modes (PC2 and PC3) variance is driven by gene expression values outside the 3 standard deviation interval (horizontal black lines).

This difference in the character of distribution of PC1 scores with respect to PC2 and PC3 is consistent with their different biological meaning. PC1 is the image in light of the cell-kind specific ideal expression profile corresponding to the global scale chromatin organization and thus is expected to give rise to a continuous expression value distribution. On the contrary, fluctuation modes (PC2 and PC3) are driven by discrete local variations in chromatin flexibility that in turn are expected to give rise to hot spots of extremely variant expression. Tables III and IV report the PCA solution for HRG condition.

TABLE III.

Eigenvalues distribution (HRG condition).

Component	Eigenvalue	Explained variance (%)	Cumulative variance (%)
PC1	17.63	97.95	97.95
PC2	0.129	0.72	98.67
PC3	0.065	0.36	99.04
PC4	0.040	0.22	99.26
PC5	0.031	0.17	99.43

TABLE IV.

Loading pattern (HRG condition).

Label	Time (min)	PC1	PC2	PC3
T0	0	0.984	0.046	−0.023
T10	10	0.983	0.150	0.034
T15	15	0.956	0.280	0.064
T20	20	0.992	−0.004	−0.089
T30	30	0.989	0.018	−0.128
T45	45	0.993	0.000	−0.076
T60	60	0.991	0.011	−0.106
T90	90	0.994	−0.025	−0.040
T2h	120	0.995	−0.020	−0.006
T3h	180	0.994	−0.022	0.017
T4h	240	0.992	−0.071	0.050
T6h	360	0.995	−0.046	0.038
T8h	480	0.994	−0.055	0.053
T12h	720	0.994	−0.042	0.040
T24h	1440	0.990	−0.083	0.060
T36h	2160	0.994	−0.044	0.034
T48h	2880	0.994	−0.047	0.039
T72h	4320	0.990	−0.035	0.040

Comparing Tables III and IV with Tables I and II, besides a general resemblance of the global results with a by far major first principal component and two minor fluctuation modes, it is worth noting that, as expected, HRG fluctuation components account for more variance with respect to EGF (PC2 goes from 0.41% to 0.72% of explained variance, PC3 goes from 0.26% to 0.36%). Still more important, the third time point (15 min) (third row values in bold), corresponding to the start of “early response,” is both the one less correlated with the ideal profile (loading on PC1 = 0.955) and the time point where the most important fluctuation component (PC2) has the by far more relevant influence (loading on PC2 = 0.28). This is consistent with the observation that time point 3 (15 min) shows a drastic decay in gene expression profiles correlation with respect to the initial time t = 0 condition (see Fig. 5) particularly evident in the supercritical state (most fluctuating genes).

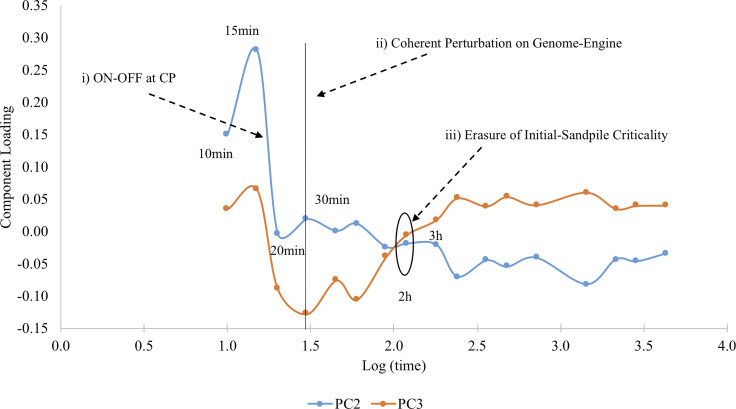
The oscillation in time of the two main regulatory components is evident in Fig. 6 reporting the loadings on PC2 and PC3 of the different time points. Loadings correspond to the relative importance of the two modes in determining the observed gene expression pattern at different times.

FIG. 6.

Temporal variation of regulatory modes (PC2, PC3) for HRG. PCA oscillation coincides with major SOC events: (i) The ON(15 min)–OFF(20 min) at the CP (change in the genome attractor) induces a genome-wide avalanche; ii) after 30 min, the coherent perturbation on the genome-engine occurs for the preparation of the cell-fate change; (iii) initial sandpile CP disappears after 3 h. suggesting the occurrence of the cell-fate change.

Going back to Eq. (1), we can easily appreciate how the oscillatory modes affect all the genes (with varying intensities); in fact, these modes are not only responsible for cell-fate transitions, but during “business as usual” periods, they adapt the gene expression levels to the continuous microenvironment fluctuations. The gene expression fluctuations in the normal conditions are instrumental to keep largely invariant the cell-kind ideal profile by a continuous adaptation to continuously changing microenvironment. This is exactly the essence of self-organized complexity: the system is kept in a constantly changing condition (corresponding to small avalanches in the sandpile model) around an ideal profile. Thus, PC2 and PC3 modes are the counterpart of the local regulation spread all along the genome that in normal conditions take care of contrasting the microenvironment changes. To shift from a purely narrative to a quantitative proof of the resemblance between SOC and PCA results, we will try to predict nrmsf (the ordering criterion of SOC) by means of single-gene component scores (Tables V and VI).

TABLE V.

EGF condition. Multiple regression model: nrmsf = 0.226 + 0.032 × PC1 – 0.068 × PC2 − 0.015 × PC3, F-value: 3988.39—Pearson r = 0.590 p < 0.0001. Inferential statistics (null hypothesis: regression coefficient = 0).

Component	t-value	p
PC1	45.74	<0.000 1
PC2	−97.05	<0.000 1
PC3	−21.31	<0.000 1

TABLE VI.

HRG condition. Multiple regression model: nrmsf = 0.283 + 0.055 × PC1 − 0.078 × PC2 − 0.057 × PC3, F-value: 4689.7—Pearson r = 0.620 p <0.0001, Inferential statistics (null hypothesis: regression coefficient = 0).

Component	t-value	p
PC1	58.24	<0.000 1
PC2	−83.29	<0.000 1
PC3	−61.29	<0.000 1

Tables VI and VII gives a clear proof-of-concept of our model: global gene expression modes allow to reconstruct a single-gene feature (normalized mean square fluctuation: nrmsf) computed over the entire 18 time points by only three regressors (PC1, PC2, and PC3). It is worth noting that minor components, explaining less than 1/1000 of PC1 variance, have an influence in the model (as expressed by t-values of the different regression coefficients) equal (or greater) than PC1. This is consistent with the fact that PC2 and PC3 correspond to free fluctuation of the system, while the motion along PC1 is much more constrained.

TABLE VII.

Sequence of events in cell-fate transition.

1.	A sufficiently strong external perturbationa provoking a large instability of current cell-kind attractor state that cannot be faced by “adaptive” chromatin remodeling.
2.	Setting the CP to ON by a consequent shift to swollen coil state. In this way, chromatin remodeling allows to activate a new set of genes leading to an activation of a new “preliminary” cell fate.
3.	Establishing a new preliminary cell-fate.
4.	Activation of a new preliminary cell-fate and occurrence of bifurcation as a result.
5.	Setting the CP to OFF shifting to compact globule state.
6.	The switch of coherent perturbation on the genome-engine.
7.	Gradual stabilization of a new cell-fate by positional chromatin remodeling with a gradual disappearance of bifurcation as a result.
8.	Attainment of a new cell-fate attractor.

^a In our case stimulation of MCF-7 cells by HRG).

The physical counterpart of this statistical evidence is that variation along PC1 corresponds to shift the “center of mass” (CM) of the system that can lead jumping off the attractor (transition). If this is the case, we expect that the genes with near zero values of PC2 and PC3 (and thus only affected by PC1, ideal profile mode) are exactly the “genome vehicle” (Tsuchiya et al., 2010), the genes that cause the critical behavior of the SOC regulated system.

This genome vehicle can be appreciated in (Tsuchiya et al. 2020): the CP (critical point) acts as the organizing center of SOC to induce the change in the genome attractor (see Fig. 3 in Tsuchiya et al. 2020) which represents a specific set of critical genes with an activated (ON) or deactivated (OFF) state (see Introduction). In HRG, the CP is ON at 15 min and then OFF at 20 min through the coil-globule transition at the CP. This ON-OFF switch of the CP state at 15–20min (refer to Fig. 4 in Tsuchiya et al. 2020); i.e., change in the genome attractor induces a big avalanche effect on genome expression [Fig. 5(b)]. It is important to compare EGF and HRG conditions, from here onward PC1, PC2, and PC3 of the EGF and HRG will be indicated as EGF1, EGF2, EGF3 and HRG1, HRG2, HRG3, respectively.

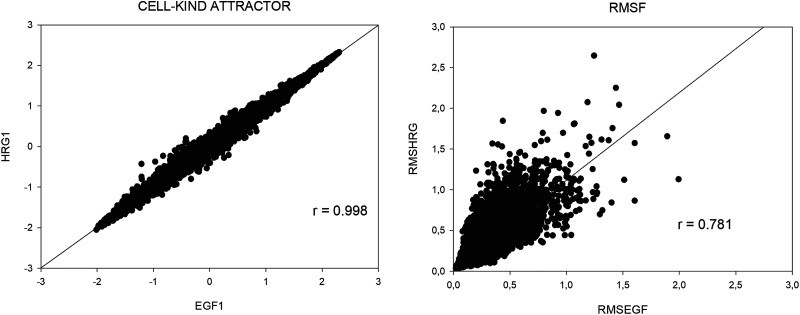
Both EGF and HRG mediated perturbations operate on the same cell-kind (MCF-7 cells), if our interpretation of the meaning of different components is correct, we should find a complete superposition between the first components PC1 of EGF and HRG (EGF1 and HRG1, respectively) given they refer to the same cell-kind ideal profile. That is exactly what we find with a near-to-unity correlation between EGF1 and HRG1 (left panel of Fig. 7).

FIG. 7.

EGF and HRG comparison. (a) Left panel has as axis the first component of the two conditions (HRG1 and EGF1, respectively). The near-to-unity correlation of HRG1 and EGF1 scores demonstrates that the first component corresponds to the cell-kind (shared by the two conditions). (b) Right panel shows the single-gene fluctuation in time (rmsf) correlates between the two EGF and HRG cases, pointing to the fact that “fluctuation entity” is an intrinsic property of each gene largely independent of the nature of the stimulus.

Shifting to nrmsf (entity of fluctuation in time of genes), the correlation between EGF (x axis) and HRG (y axis) scores a correlation coefficient r = 0.78 (right panel of Fig. 7). This relation is statistically very significant and implies that the two EGF and HRG stimuli impinge over a highly superimposable set of genes. The HRG and EGF comparison encompasses some useful tracks to understand the difference between a stimulus that is able to induce a transition (HRG) and one that is not (EGF). The first track is the observation that HRG nrmsf is (on average) greater than EGF one (0.28 vs 0.22) points to a greater applied energy in the transition case. Indeed, any detachment from ideal expression value can be considered as provoked by the need to dissipate an excess of energy, being the cell-kind attractor located in an energy minimum. The second track was suggested by the entrainment into a resonant peak of HRG2 and HRG3 depicted in Figs. 5 and 6, this resonant peak is absent in EGF case [see Fig. 5, panel (c)], this resonance drastically increases the applied energy on the genome.

These results are consistent with SOC analysis in that ON-OFF switch of the CP (i.e., provoking genome avalanche through change in the genome attractor) occurs at 15–20 min through transitional change in singular behaviors at the CP for HRG cell response, whereas the CP is at OFF state in EGF cell response (i.e., no genome avalanche).

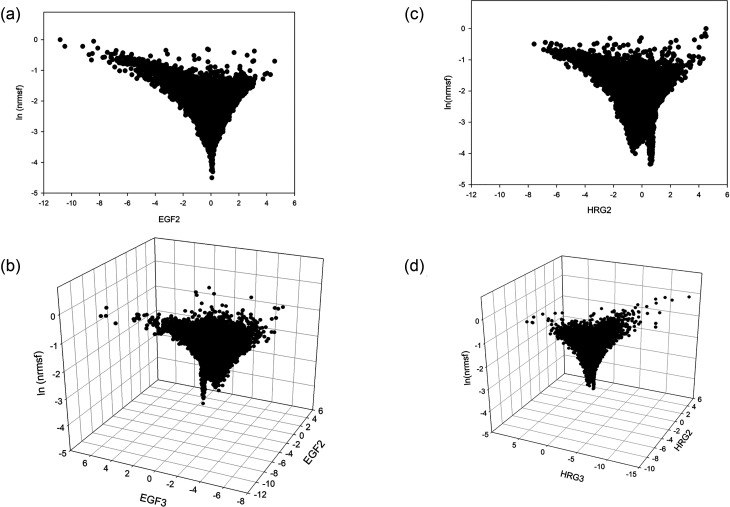
According to SOC, we do expect a value within −2.5 to −2.6 interval: singular behaviors of the CP: it occurs consistently around −2.58 for both HRG and EGF. The left panel of Fig. 8 reports the space spanned by EGF2 and log-normalized rmsf on the top and the 3D space with added EGF3 (bottom panel).

FIG. 8.

SOC critical parameter in terms of oscillating expression modes. Left panels (a) and (b): EGF, no transition case; right panels (c) and (d): HRG, transition case. The bottom of the funnel corresponds to the “core” of the attractor (CP, genes with very low fluctuations that consequently have near zero contribution of fluctuations modes (EGF2, EGF3) and (HRG2, HRG3), respectively.

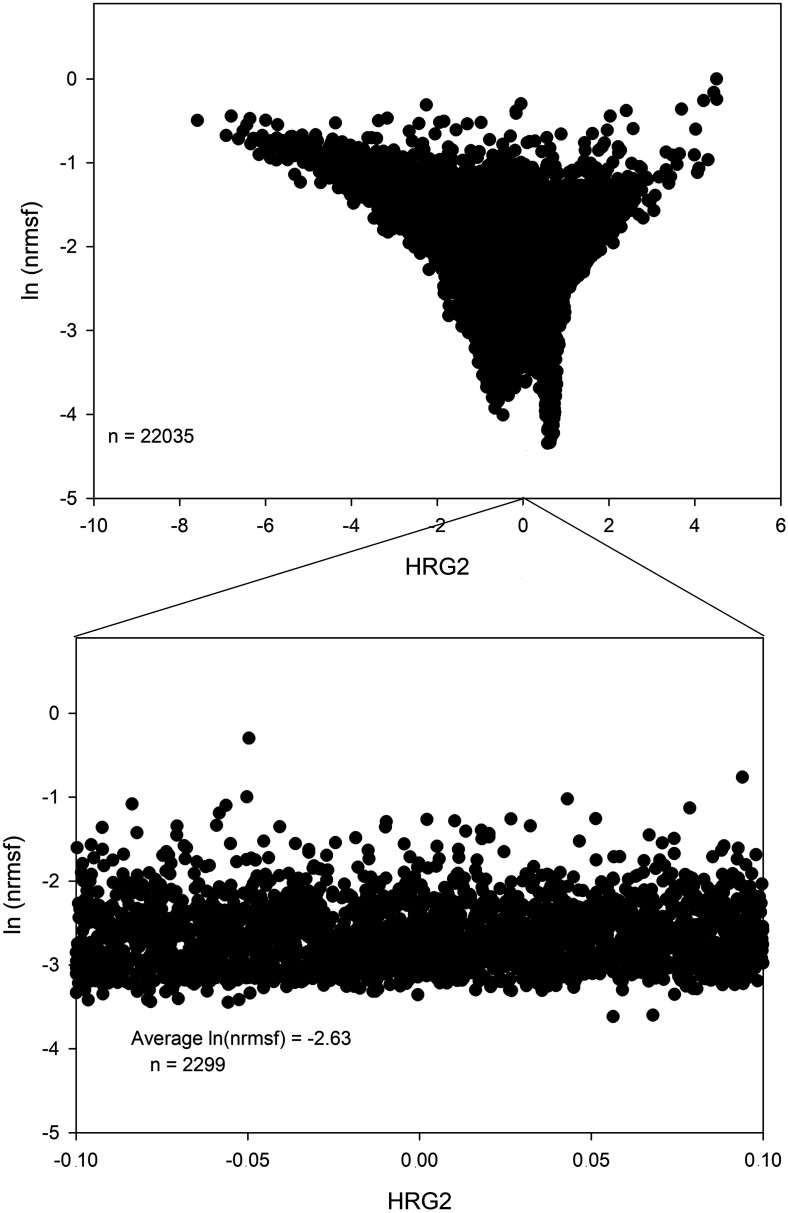
The right panel of Fig. 8 is relative to the HRG transition case, it is very similar to the EGF case (left panel) but with some subtle differences. The presence of a clear funnel landscape with a minimum of fluctuation (near zero PC2) mode at very low ln(nrmsf) is evident in both EGF and HRG cases. This is consistent with the fact that zero values of oscillating modes correspond to the “invariant core” (genome attractor) of cell-kind profile and suggests that the genome attractor genes [low values of ln(nrmsf)] correspond to those invariant (and thus zero valued as for oscillating modes). In EGF case (left panel Fig. 8), there is a uni-modal minimum exactly located at PC2score = 0 (minimum influence of PC2). On the contrary, in the case of HRG (top right panel of Fig. 8) the minimum of the main oscillating mode (HRG2) is split in a bimodal way around zero. In Fig. 5(b), the second peak in the HRG response has to do with the signature of ON-OFF transition of the CP. The CP shows a clear bimodal expression distribution reminiscent of the swollen coil (ON) and compact globule (OFF) DNA transition, corresponding to the inversion of the intra-chain phase segregation of the coil and globule states, see Fig. 4(b) in Tsuchiya et al. (2020). The main proof of the convergence between the theoretical (SOC) and bottom-up (PCA) approach is given by the possibility to estimate the SOC-theoretically predicted values of ln(nrmsf) by means of principal component scores (Fig. 9). Top panel of Fig. 9 reports the bimodal minimum of ln(nrmsf) for near 0 values of HRG2. Bottom panel is an inset focusing on HRG2 scores between −0.10 and +0.10. This range corresponds approximately to 1/10 of total number of genes; the average ln(nrmsf) of these genes is −2.63, which shows that the CP, ln(nrmsf) = −2.58, exists in the vicinity of the genome attractor, ln(nrmsf) = −2.63. Our recent study shows that synchronization of expression dynamics between the CP and genome attractor occurs at the critical transition in HRG response, whereas in EGF response, no such synchronization occurs (Fig. 10). This synchronization suggests how the change in the CP induces change in the genome attractor.

FIG. 9.

The core of cell-kind attractor corresponds to CP. The figure depicts, in the HRG transition case, the ability of second component (main oscillating mode) to exactly predict the theoretical value of CP in ln(nrmsf) terms. The top panel reports the bi-dimensional space spanned by HRG2 and ln(nrmsf) with the evidence of the bimodal negative peak corresponding to near zero values of HRG2. Bottom panel reports the estimation of ln(nrmsf) in terms of average over 2299 genes in the vicinity of zero HRG2 score (from −0.1 to 0.1 standard deviation units).

FIG. 10.

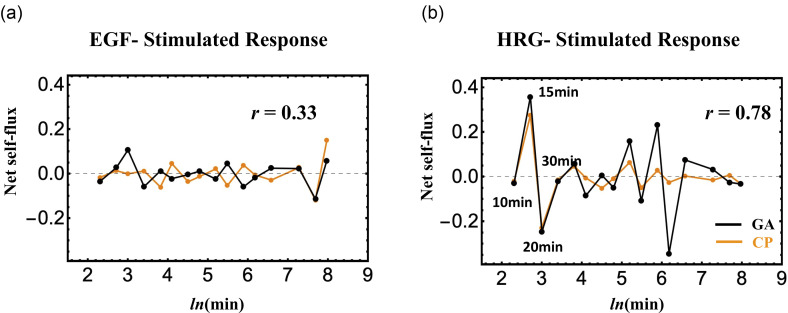
Net self-flux of the CP and GA (black solid line for the GA and orange for the CP). Left panel: ERG and right panel, HGF. The net self-flux is the difference between IN flux and OUT flu and describes the effective force on them.

Figure 10 represents the gene expression dynamics in terms of fluxes. This representation is consistent with the need of a force field corresponding to chromatin re-arrangements, but here we will only consider its phenomenological consequences in terms of gene expression fluctuations. A net self-flux represents the difference between the positive sign for incoming force (i.e., resulted in up-regulated expression) and the negative sign for outgoing force (down-regulated expression). The right panel of Fig. 10 reveals the occurrence of synchronization (Pearson correlation, r = 0.77) of (average) expression dynamics between the CP and GA in HRG response at the critical transition (10–20min; see the similar behavior in Fig. 6), whereas in EGF response, such a synchronization does not occur (antiphase behavior: r = 0.31) (left panel). GA results for both responses were multiplied by 10 times. This constitutes a further point of view on the difference between an effective (HRG) and a non-effective (EGF) stimulus besides their strict resemblance in terms of detailed molecular mechanism.

C. Folding–unfolding dynamics of chromatin goes hand in hand with gene expression

The initial hypothesis that the gene expression fluctuation in time (nrmsf) was the functional counterpart of chromatin flexibility was only indirectly proven by the RQA-base demonstration of the correlation between the co-regulation and spatial proximity along the chromosome (par. 2.1) and by the prevalence of chromatin remodeling genes in HRG-specific hot spots (par. 2.1 and 2.2). A more cogent proof of the fact that the material bases of whole-genome expression regulation are located at the level of folding–unfolding dynamics of chromatin comes from the recent (Krigerts et al., 2021) paper which exactly followed the same experimental scheme of gene expression studies in HRG-mediated transition (see par. 1.1). The authors found that control MCF-7 cells displayed a typical scale-free 1/f distribution of PADs size consistent with SOC regulation. Analogously to gene expression distribution, the PADs 1/f scaling is reminiscent of a continuous fusing/division dynamics of PADs corresponding to folding/unfolding of chromatin. This puts genome organization “on the edge of chaos,” making it possible to undergo transitions by global rewiring through self-organization. At 15–30 min, the authors observe such a transition with a dramatic shrinking of PADs (see Fig. 6 of Krigerts et al., 2021) together with an increase in euchromatin compartment (corresponding to an increased structural flexibility). The superposition between specific gene markers activation (FOS mediated ERK pathway), global gene expression fluctuation, and chromatin reorganization suggest a unitary picture in which the genome acts as an integrated dynamical system undergoing critical transitions that can be appreciated at different organization layers.

IV. DISCUSSION AND CONCLUSION

In this review, we validated the role of chromatin remodeling as the material basis of the self-organized critical control (SOC) of genome expression by means of the convergence between gene expression fluctuations and structural reorganization of peri-centromeric (PADs) nuclear regions. The specific location in time and repeatability of the studied transition make HRG-stimulated MCF-7 cells an almost ideal system to study the onset of massive gene expression regulation. The comparison between an effective (HRG) and a non-effective (EGF) perturbation allows us to go in depth into the subtle details of biological regulation. The necessary pre-requisite for genome expression regulation is its peculiar position on the edge of chaos, i.e., the presence of a “critical attractor state,” in which a specific stochastic perturbation can spread over the entire system through an autonomous critical-control genomic system (genome-engine in Tsuchiya et al., 2020). In EGF response, at odds with HRG, the critical attractor state remains as a sub-critical state. The critical point (CP), acting as the organizing center of the cell-fate, determines whether the genome resides in a super- or sub-critical state, in which the change in the CP induces the change in the GA going hand in hand with the genome-wide expression avalanche as resulted in the cell-fate changes. This resembles the classical SOC sandpile model (Bak et al., 1987 and Bak and Chen, 1991), where the grain-by-grain addition to the sandpile is the counterpart of critical attractor state characterized by small avalanches only affecting the periphery (here hot spots genes) of the system. When these small avalanches self-organize into huge avalanches, they involve the core of the system (here lowly fluctuation genes with near zero values of PC2 and PC3 modes), making a global restructuring of the system possible. RQA and PCA demonstrated this avalanche stems from coordinated activity of positional-based local chromatin interaction.

It is important to stress that RQA approach is forced to analyze only the spatial proximity of genes along the linear order of chromosomes that, while being the main driving factor of co-regulation is not the only one, being complemented by areas put aside by chromatin folding and “lineage-specific chromosomal topologies” (Rajapakse, 2009) and by the action of shared enhancers transcription hubs made of clusters of condensate polymerase II (Heist et al., 2019).

In this respect, it is worth noting the elevated number of chromatin remodeling genes having very elevated PC2 scores especially in HRG case (e.g., SMARCA2, SS18, TRRAP, SMC3, ATRX, FXR1) and transcription factors (e.g., c-FOS) known to act as “multiple sites” co-regulators. In our opinion, this can be considered as the “functional counterpart” of a systemic regulatory effect at the entire genome scale consistent with SOC model.

In chromatin remodeling perspective, we summarize in Table VII a cell-fate transition by a sequence of events in MCF-7 cell response.

It is worth reminding the modification we made on the classical SOC model by the introduction of three internal states of the system qualified by their super-, near- and, sub-critical states that were empirically confirmed by PCA; this allows for a further refinement of the above steps:

• (1)Establishing a new preliminary cell-fate: HRG activates the ErbB receptor with sustained extracellular signal regulated kinase (ERK) activity (Nagashima et al., 2007). This induces a sufficiently strong perturbation (mirrored by a peak of PC2 and PC3 explained variance) on the MCF-7 cell genome, i.e., setting the CP to ON by a consequent shift to swollen coil state before 15 min. The activation of the CP genes occurs through a purely positional basis of chromatin. This ON state of the CP leads to a new preliminary cell-fate accompanying with the bifurcation of the super-critical attractor at 15 min (Fig. 5).
• (2)Setting the CP to OFF shifting to compact globule state: A critical transition occurs at the CP from the swollen-coiled state to compact-globule state, which sets the CP from ON to the OFF state during 15–20min. This exactly concedes with the timing of the resonant mode of PC2 and PC3 (Figs. 5 and 6) at 10–20 min. This released energy ignites the local and positional chromatin to coherent first order transition on chromatin (genome-wide expression avalanche).
• (3)Switch of coherent perturbation on the genome-engine: The perturbation on the CP (the genome attractor) induces the switch of coherent perturbation on the genome-engine from suppression to enhancement of the dominant cyclic expression flux between super- and sub-critical state attractors. This coherent perturbation drives the cell-fate decision (Tsuchiya et al., 2020).
• (4)Stabilization of a new cell-fate: After 20 min, gradual stabilization (Figs. 5 and 6) of a new cell-fate occurs by positional chromatin remodeling, which is consistent with the SOC event that implies the apparent conundrum of a dynamically stable critical state.
• (5)Attainment of a new cell-fate attractor: After 3h, the initial-state criticality is erased (i.e., erasure of the memory of the initial-state CP (Tsuchiya et al., 2016), which indicates that the genome system attains a new cell-fate attractor (Figs. 5 and 6).
• (6)Sub-critical vs super-critical in the genomic state: In EGF-stimulated response, EGF-stimuli do not elicit the CP ON state and the perturbation is locally confined. Thus, the genome state (at cell-population level) of EGF-stimulated system, at odds with HRG condition, remains sub-critical (no cell-fate change).

The motion along PC2 and PC3 is orthogonal with respect to PC1 and thus does not affect the center of mass (CM) of the system (genome attractor: GA); on the contrary, their oscillating behavior in time allows for maintaining the system on its attractor profile on the edge of chaos dissipating external perturbations. This describes the basis of SOC sandpile model (Bak et al., 1987 and Bak and Chen, 1991), where the grain-by-grain addition to the sandpile is the counterpart of critical attractor state characterized by small avalanches only affecting the periphery (here hot spot genes) of the system. The situation is functionally analogous to what happens in molecular dynamics with the fluctuation of amino-acid residues keeping largely invariant the 3D structure of the system; it is not a case that proteins are SOC governed systems too (Phillips, 2009).

The unique property of SOC of being a critical attractor state (super-critical state) allows proteins to manage with thermal motion without losing their global 3D configuration while in the same time (thanks to CP-like amino-acid residues) responding with fast transition to allosteric stimuli.

The cell-type specific 3D chromatin conformation is the material counterpart of the cell-kind attractor that we observed in terms of the emerging of a first principal component (PC1) explaining the almost totality of between gene expression variance. This interpretation is supported by the results of Zhou et al. (2019). In Fig. 1 [panel (a)] of their paper, they report, for each chromosome, the Pearson correlation of chromatin interactions between different biological replicates: these correlations are extremely high and of the same order of magnitude of the correlation we observe in terms of gene expression. This is another confirmation of the structural re-organization of PADs we discussed in the present review and gives an indirect, albeit very cogent, proof of the onset of a “cell type” ideal profile of expression by a cell-type specific chromatin folding. Moreover, the authors refer to the same MCF-7 cell line we used as reference model and by means of a different stimulus (estrogen) identify in the “dynamic compartment” of the chromatin many of the genes that have a very high score (>4) in our PC2 and PC3 responsible for the response to the applied stimuli. This is a further proof of the chromatin organization/gene expression link: not only the “invariant global architecture” but also the “fluctuation dynamics” are consistent between the expression and structural viewpoints.

In Nurick et al. (2018), the authors face the link between the gene expression and chromatin structure at two different scales. The larger scale refers to the A/B compartments of the nucleus: A is gene-rich, transcriptionally active and located near the center of the nucleus, while B gene-poor heterochromatic and located in the nucleus periphery. A/B organization is largely cell-type specific; consequently, epigenetic differences among cell lines are mirrored by different A/B compartmentalization of the nucleus (Nurick et al., 2018). These results tell us that our “cell-kind ideal profile” can be immediately translated in terms of A/B compartmentalization. The more detailed scale at the “bottom” of A/B organization is relative to the so-called TADs (Topological Associating Domains). At odds with A/B configuration, TADs are largely cell-type independent (Nurick et al., 2018), and TADs play a crucial role in the regulation: bringing in close proximity the enhancers (E) and promoters (P) regions that are distant along the linear DNA sequence, they allow for common activation of distant regions. These E–P loops, a portion of which is cell-kind specific, mostly occur within TADs that can be considered as the bottom organization level of gene expression (Nurick et al., 2018). The authors propose a very intriguing model for keeping together the largely aspecific (TADs) and cell-kind specific (A/B organization) regulation levels by hypothesizing that chromatin organization at large (cell-kind specific) constraints the otherwise aspecific regulation influence of transcription factors (TFs) stemming from TAD level.

In Fig. 3 of Nurick et al. (2018) [panel (b)], the authors report a comparison between the A/B preference of a set of 48 transcription factors differentially expressed in different cell lines giving a proof-of-concept of the above model. We compared the list of the 48 TFs reported in the figure (relative to different cell lines and stimuli with respect to our model) and we found that 15 of these 48 TFs were present in our “main fluctuating component (PC2)” with a score > 4.This is a very significant superposition that supports the local cell type aspecific/global cell-type specific regulation model.

Having recognized a plausible material basis for our results, shifting to the kinetics phenomenological aspects, it is worth noting that the time-dependent behavior of the genomic DNA transition follows a kinetic equation that shows a cubic nonlinearity (Takagi and Yoshikawa, 1999). The cubic-type nonlinearity plays an essential role in the nervous system excitability (see, for example, the FitzHugh–Nagumo-type equation to show cubic nonlinearity for the fundamental characteristics nerve firing (FitzHugh, 1955 and Izhikevich and FitzHugh, 2006). Furthermore, SOC is at play in neuronal networks (Plenz and Niebur, 2014 and Shew et al., 2009), which indicates a non-trivial similarity between the coherent network of genomic DNA transitions and neural networks.

It is worth noting other authors stepped into very similar processes in many biological settings (for a review see Gorban et al., 2021); here, we will quote two paradigmatic cases:

• (1)A purely data-driven statistical approach based on the changes in correlation structure of the system was demonstrated to be of very effective in detecting the tipping point preceding cell-fate change. In Mojtahedi et al. (2016), the authors, analogously to our approach, detected the critical point of cell-fate transition by the decrease of correlation among gene expression profiles.
• (2)The destabilization of a previous homeostatic condition (erasure of previous critical states in the frame of SOC) seems to be a necessary pre-requisite of biological state transitions in Bizzarri et al. (2018). This pattern corresponds to what observed in the case of HRG stimulation we commented in this work, suggesting the presence of a shared mechanism possibly of great practical interest in both diagnosis and therapy.

On a methodological point of view, we tried and set some general principles for setting a sort of “conversion table” from physics to biology jargons. The analyzed case (that in principle can be generalized to the huge spectrum of bifurcation behavior in biology ranging from ecology to biochemistry) is, in our opinion, a sort of paradigm of the urgency of such a conversion table. In order to be considered as “satisfactory” by mainframe biologists, any explanation effort must include the reference to the involved molecular players and to their mutual interactions. On the other hand, any “reliable” physical approach encompasses a rigorous definition of the adopted theoretical model. The lack of a quantitative theory able to explain biological systems at the level of microscopic molecular agents and the contemporary need of integrative approaches for detecting general phenotypic features pushes toward the search of an “intermediate” approach. In our opinion, this intermediate approach can be obtained by the use of statistical techniques encompassing a specific physical perspective (here PCA) and by the use of known physical models adapting them to the specific biological reality (SOC), together with the link of the physics-derived concepts with their biological material counterparts (chromatin folding/unfolding, master genes known to be implied in the studied phenomenon).

Overall, we demonstrate the feasibility of a “biological statistical mechanics” spanning different organization layers of biological material that can push the research toward a more integrative and physically motivated view of biology.

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.