On Manifold Learning in Plato’s Cave: Remarks on Manifold Learning and Physical Phenomena

Abstract

Many techniques in machine learning attempt explicitly or implicitly to infer a low-dimensional manifold structure of an underlying physical phenomenon from measurements without an explicit model of the phenomenon or the measurement apparatus. This paper presents a cautionary tale regarding the discrepancy between the geometry of measurements and the geometry of the underlying phenomenon in a benign setting. The deformation in the metric illustrated in this paper is mathematically straightforward and unavoidable in the general case, and it is only one of several similar effects. While this is not always problematic, we provide an example of an arguably standard and harmless data processing procedure where this effect leads to an incorrect answer to a seemingly simple question. Although we focus on manifold learning, these issues apply broadly to dimensionality reduction and unsupervised learning.

I. Background

The abundance of data in many applications in recent years allows scientists to sidestep the need for parametric models and discover the structure of underlying phenomena directly from some form of intrinsic geometry in the measurements. Such concepts frequently appear in unsupervised learning, manifold learning, non-parametric statistics and, more broadly, machine learning. Often, a scientist may have in mind a concept of the “natural” geometry or parametrization of the phenomenon; in other cases, they may implicitly assume that only one such objective geometry exists even if they do not know what it is. This paper aims to illustrate the difference between the structure of observed data and some notion of natural or unique objective structure. To this end, we offer a concrete example with an obvious underlying natural geometry (up to symmetries) and demonstrate the existence of discrepancies between the data and the natural variables, even in this benign setting.

In our example, described more formally below, a simplified instance of a physical phenomenon is represented by a rigid 3D model of a horse on a spinning table. The measurement device is a fixed camera that takes images of the object. The orientation angles of the horse are distributed uniformly. Here, a natural variable is the angle at which the figure is oriented at the time of the measurement. A simple example of a scientific question is to find the mode of the distribution, which is intuitively the most prevalent orientation angle (we know that the correct answer is that the distribution is uniform and, therefore, we do not expect to find a clear mode). Since this is meant to be a simplified, intuitive version of a generic problem with no obvious underlying model, we consider generic algorithms and forgo in advance image analysis and computer vision methods that use of the special properties of images and the specific rotating motion of the object.

This benign task yields results that we find surprising yet predictable. The naive analysis discovers clear modes of the distribution, which are inconsistent with the true uniform distribution. In Appendix A3, we demonstrate that these modes are not invariant to the measurement modality.

In our discussion, we explain the reasons for the experiment’s results and refer the reader to existing work on special cases where the problem can be corrected. However, there is no method for correcting the problem in the general case. We conclude by pointing to where care should be taken in defining the problem and using the output in downstream tasks.

We emphasize that this paper aims to highlight an omission that we observe in the practical use of manifold-related machine learning algorithms in applications. The purpose of this paper is not to advocate against these methods but rather to suggest that care should be taken in stating and interpreting their output.

II. The problem

The mathematical setting of the experiment is simple: let $𝒳\subset {\mathbb{R}}^d$ and $𝒴\subset {\mathbb{R}}^D$ be two manifolds with $d\ll D$ and $f:𝒳\to 𝒴$ be a diffeomorphism. We refer to $𝒳$ and $𝒴$ as the phenomenon manifold and the measurement manifold respectively and to $f$ as the measurement function. In our simple experiment, the phenomenon manifold $𝒳$ is the one-dimensional torus representing the orientation of the horse with respect to a fixed frame of reference (independent of the camera), the measurement function $f$ outputs an image of the horse as captured by the camera, and the measurement manifold $𝒴$ is the manifold of images obtained by the camera. In particular, a sample $x\in 𝒳$ is the angle of the horse at a specific point in time, and the corresponding measurement $f\left(x\right)\in 𝒴$ is the image of the horse at the same point in time. In a typical setting, we are given a large set of measurements ${\left\{y_i\right\}}_{i=1}^n\subset 𝒴$ of a set of samples ${\left\{x_i\right\}}_{i=1}^n$ drawn from a distribution $𝒟$ on $𝒳$. Here, we take the distribution $𝒟$ of the orientation angles of the horse to be uniform, which would be unknown in an actual experiment. We only have access to the measurements ${\left\{y_i\right\}}_{i=1}^n$ (the images of the horse), which we assume to be noise-free for simplicity, and we are interested in uncovering the low-dimensional organization of the samples of angles ${\left\{x_i\right\}}_{i=1}^n$, for example, their empirical distribution on $𝒳$. The setting of this numerical experiment is illustrated in Figure 1. For simplicity and concreteness, we apply common techniques to answer a simple question: what is the most dominant physical state? We know that the ground truth answer is, in this case, that there is no dominant state; the data are generated with uniform distribution over the orientation angles of the horse.

Fig. 1:

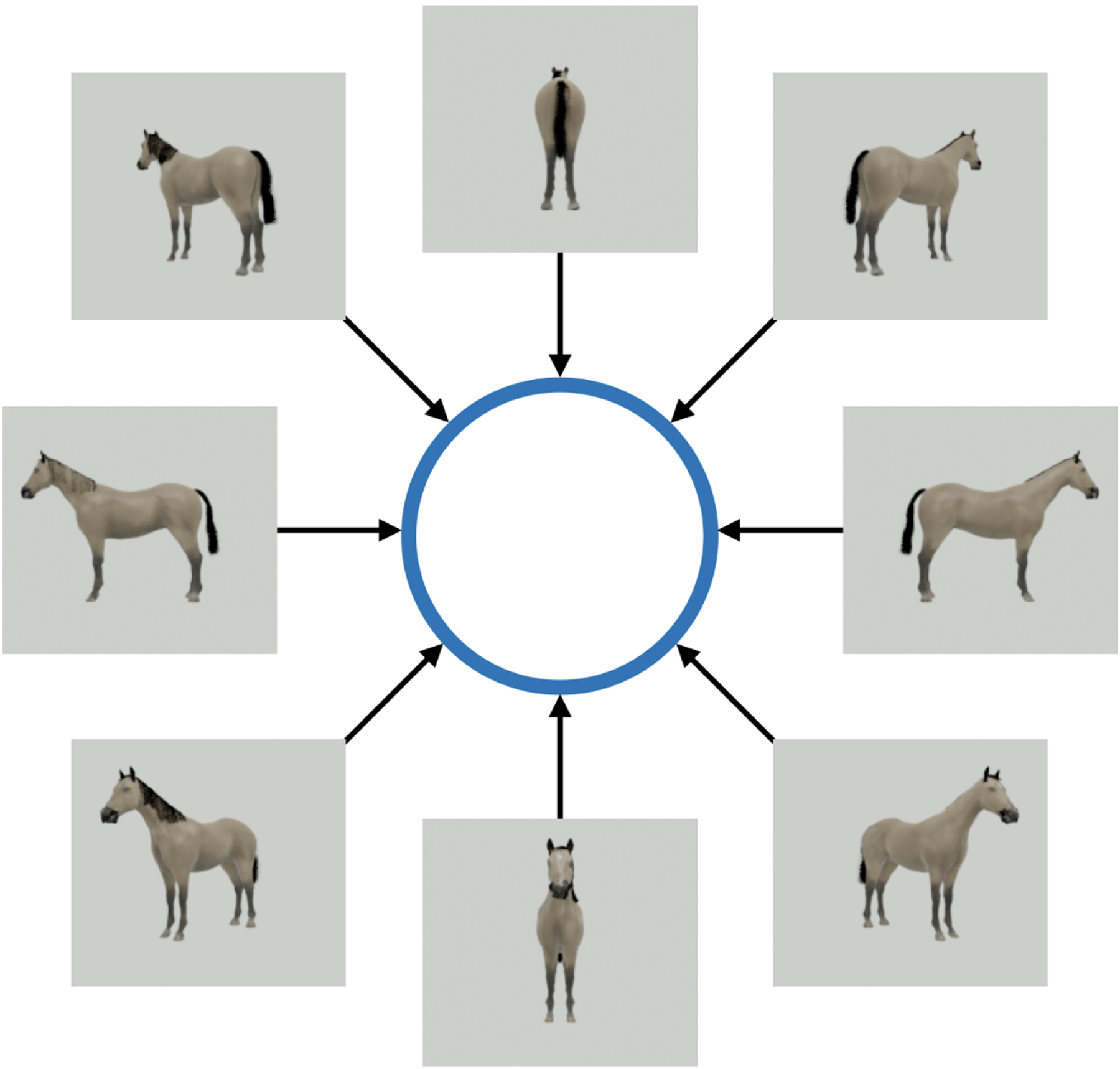
The phenomenon manifold $𝒳$ is a one-dimensional torus corresponding to the in-plane orientation angle of a rigid object rotating around the $z$-axis, and the measurement manifold $𝒴$ is the manifold of images of the object as captured by a camera at a fixed location.

We follow a common practice of assuming a low-dimensional structure and apply a manifold learning algorithm. This produces the map $\rho :𝒴\to Ƶ$, which yields a low-dimensional embedding of the measurements $\rho \left(y_i\right)\in Ƶ$ for $i=1,\dots ,n$ and $Ƶ\subset {\mathbb{R}}^s$ with $d\le s\ll D$. In our experimental setting, the low-dimensional assumption is clearly true: the orientation angles of the horse lie on the one-dimensional torus manifold, while the measurements are clearly high-dimensional (the number of pixels of each image). For simplicity, in our numerical experiment, we use the diffusion maps algorithm, whose theoretical properties are well understood [1, 2], and we retain only the first two diffusion coordinates, a standard practice in this simple case. The output we expect to see is an embedding of the one-dimensional torus in ${\mathbb{R}}^2$: a circle.

It is common in applications to apply a machine learning or manifold learning algorithm to the measurements ${\left\{y_i\right\}}_{i=1}^n$, and consider the low-dimensional embeddings ${\left\{\rho \left(y_i\right)\right\}}_{i=1}^n$ to be a proxy for the geometry of the actual samples ${\left\{x_i\right\}}_{i=1}^n$; the potential effects of the measurement function $f$ are omitted. The aim of this manuscript is to demonstrate that even in the most benign setting, the measurements distort the physical problem in a way that can impact a seemingly straightforward analysis.

Many algorithms for manifold learning and visualization have been developed over the years and have been found useful in applications. Often, these algorithms start with the pair-wise distances $∥y_i-y_j∥$ (in some norm), for $i,j=1,\dots ,n$, as a measure of (inverse) similarity, but diverge in their precise formulation of the problem. One of the notable departures from this approach is the use of the latent space estimated in the training of deep neural networks as the manifold embedding, with the variational autoencoder (VAE) [3] being one of a number of popular approaches.

The diffusion maps algorithm produces coordinates that are related to the geometry of the data through a diffusion operator on the data manifold. While there are technical nuances in the metric defined by diffusion maps (and other algorithms) and in retaining only two dimensions, this example is particularly benign, symmetric, and without boundary effects. Therefore, one expects the leading eigenvectors of the discretized diffusion operator to preserve the local geometry of the data (up to scaling). For a formal description of the diffusion maps algorithm and its properties, see [1, 2]. One of the appealing properties of the diffusion maps algorithm is that it is (asymptotically) invariant to the local density of the data and captures only its local geometry. This property and the algorithm’s explicit relationship to the geometry of the data made it a good choice for our experiments.

Indeed, a diffusion map of the points on $𝒳$ preserves the geometry and the uniform distribution (shown in Appendix A1). However, our measurement function is not necessarily an isometry (even up to scaling), and therefore, it distorts the geometry and the local pair-wise distances.

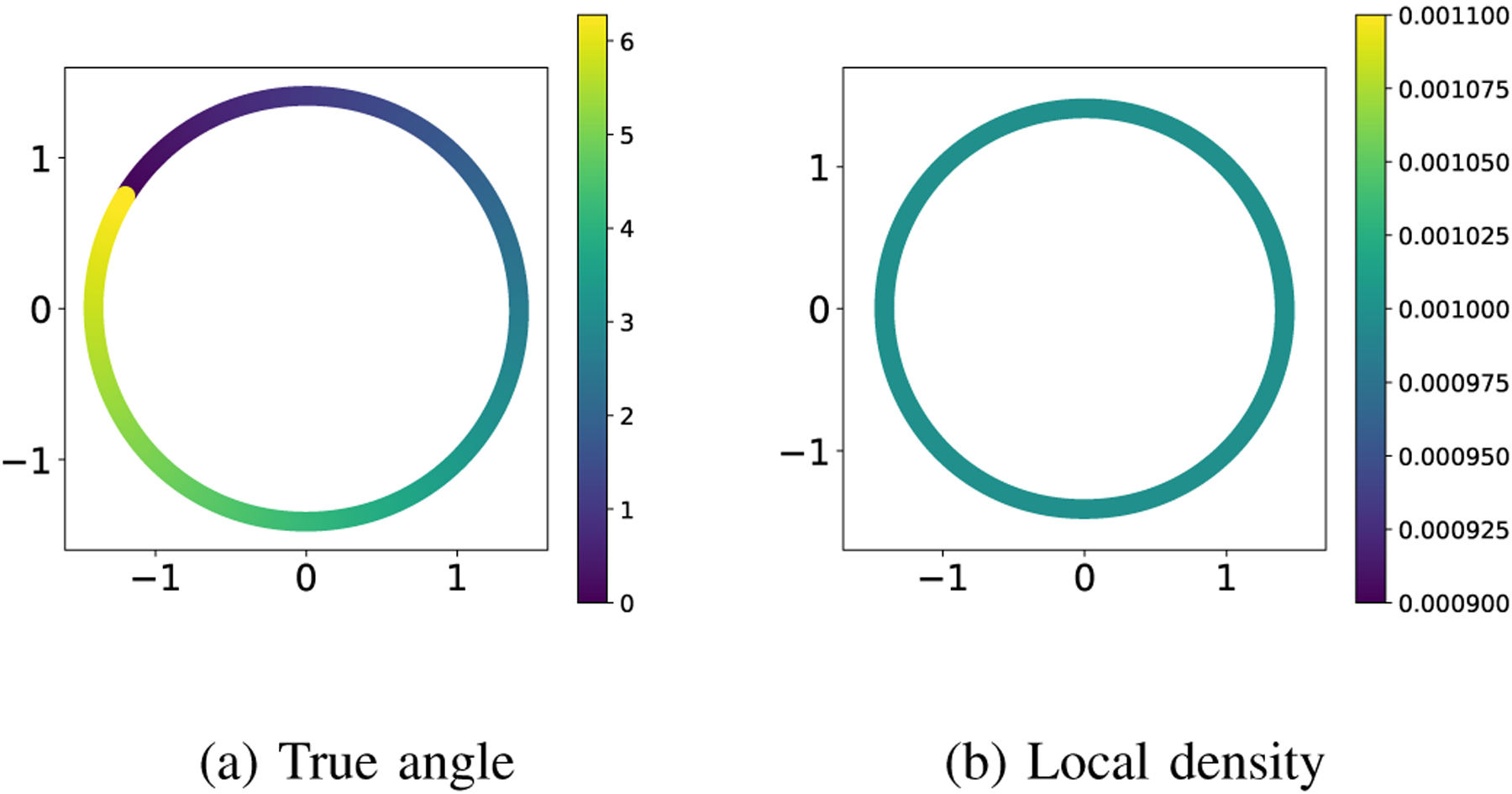
The low-dimensional embedding obtained by applying the diffusion maps algorithm to a dataset ${\left\{y_i\right\}}_{i=1}^n$ of size $n=1000$ and ambient dimension $D=108000$ (180 × 200 size images with 3 color channels) in our experimental setting¹ is shown in Figure 2. Both panels show a scatter plot using the first two embedding coordinates given by the diffusion maps algorithm. The points in panel (a) are colored according to the true angle $x_i$ for $i=1,\dots ,n$. Visually, it appears that the algorithm reveals the correct topology and it organizes the images correctly by their angle. It is compelling to say that the embedding is a good approximation of the angles (up to shift). However, taking a closer look at the distribution of the points in panel (b), we see that that their local density² has not been preserved on the embedding manifold $Ƶ$: while the distribution $𝒟$ of the points ${\left\{x_i\right\}}_{i=1}^n$ on $𝒳$ is uniform (by construction!), the distribution of the embedded points ${\left\{\rho \left(y_i\right)\right\}}_{i=1}^n$ on $Ƶ$ is not uniform. Moreover, the distribution of the embedded points has two clear modes, with no indication that they are an artifact of the analysis.

Fig. 2:

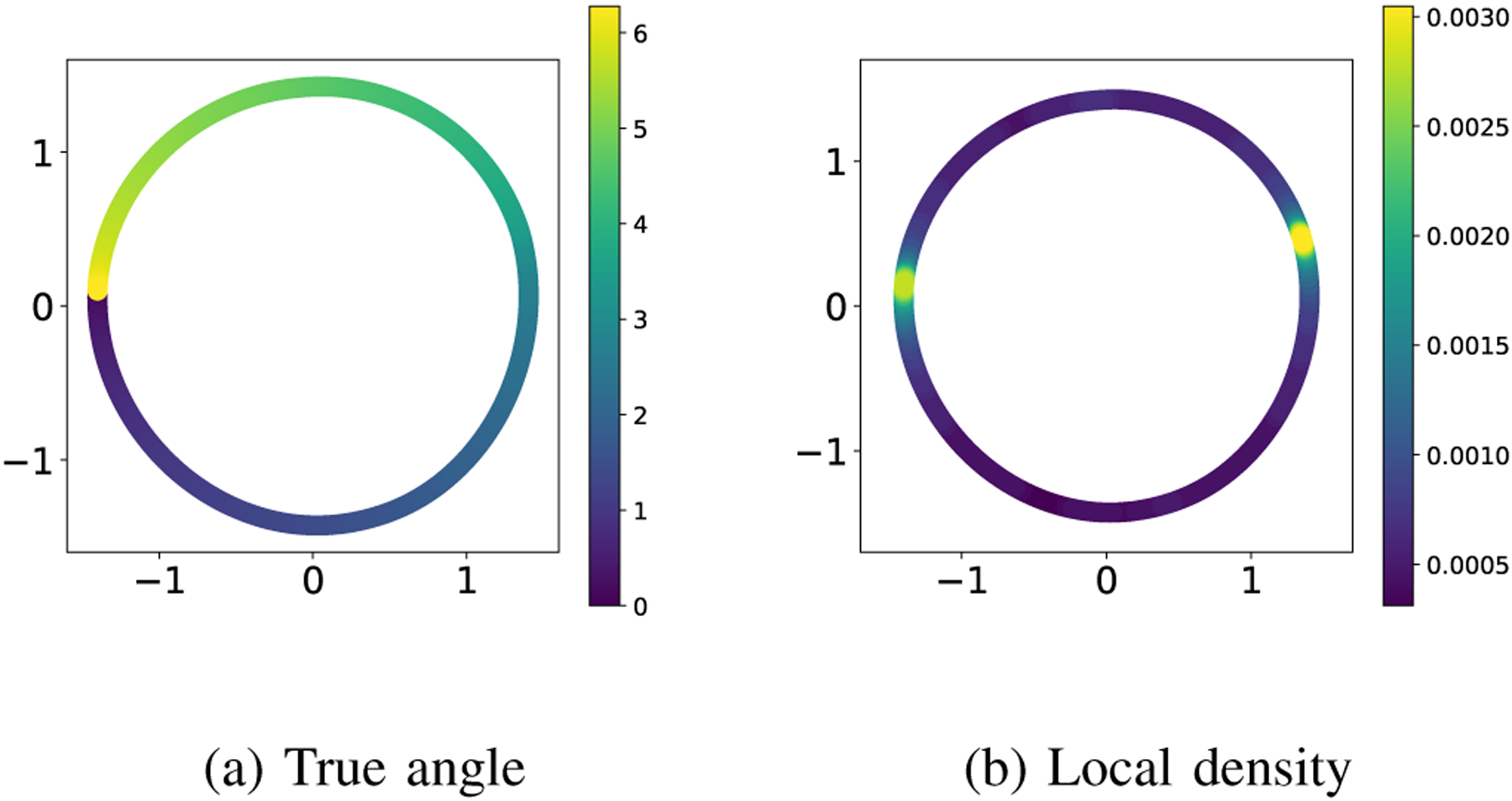
Low-dimensional embedding of the images of the spinning horse. The coloring is given by the true orientation angle of the horse in panel (a) and the local density of points $(r=0.05)$ in panel (b).

An additional experiment showing how the distribution of the embedded points varies when the viewing angle is changed is described in Appendix A3, and the specific implementation of the diffusion maps algorithm that we used in our experiments is presented in Appendix B.

III. Discussion

In the previous section, we empirically showed how the distribution of the points on the embedding manifold $Ƶ$ does not reflect the true distribution of the points on the phenomenon manifold $𝒳$: the distribution on $Ƶ$ has two distinct modes, while the distribution on $𝒳$ is uniform. To see that this is a metric-related issue, it is worth examining the modes of the distribution on $Ƶ$.

In Figure 3, we show measurements at a high and a low-density point on $Ƶ$. It is revealed that the high-density regions correspond to images where the three-dimensional object is perpendicular (or nearly perpendicular) to the viewing direction of the camera, while the low-density regions correspond to the object facing toward or away from the camera. This is because, according to our chosen metric on $𝒴$ (i.e., the Euclidean norm on the space of vectorized images), a small difference $\Delta x$ between two angles in $𝒳$ is not transformed to the same distance in different regions of $𝒳$: two images of the object facing the camera that differ by $\Delta x$ have a larger Euclidean distance than two images of the object facing sideways that are separated by the same angle. The metric based on the measurements alone does not account for the distortion introduced by the measurement function $f$ on the true metric on $𝒳$, namely the wrap-around distance on $[0,2\pi )$.

Fig. 3:

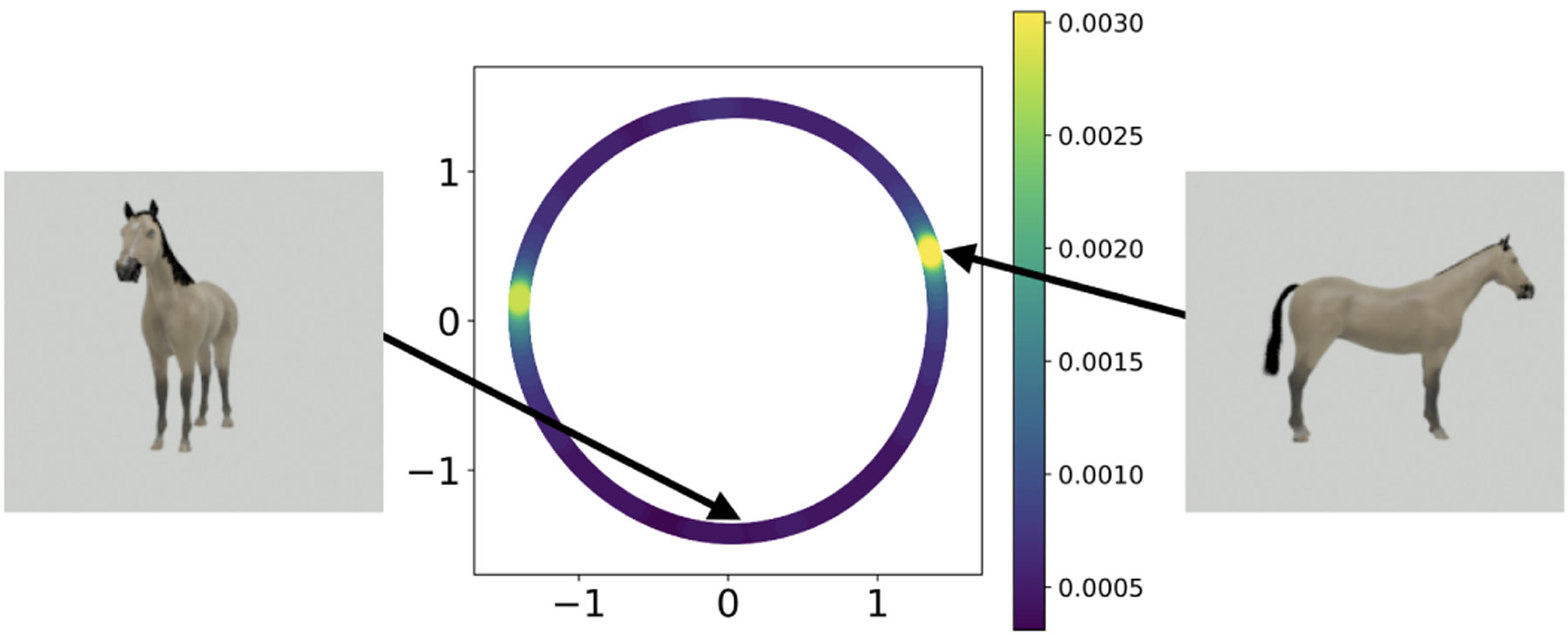
The low-dimensional embedding with example images corresponding to samples from the estimated distribution. The image to the left of the embedding plot is chosen to be at a low local density in the embedding, and the image to the right is chosen to be at the maximum density point.

The discrepancy between the metric on the phenomenon manifold, which is the metric we want to recover, and the arguably arbitrary metric produced by the measurement modality can be corrected in some special cases. For example, when bursts of measurements around each point on $𝒳$ are available, one can use the Jacobian of the measurement function to define metrics that are invariant to the measurement modality (see, for example, [4–8]). Such metrics might still not be the “desired” metrics we want to conceptualize, but they are “Platonic” in the sense that they are defined on the phenomenon manifold $𝒳$ and are invariant to the arbitrary measurement function. Other works such as [9–12] correct the metric distortion introduced by the embedding $\rho$ from the measurement manifold $𝒴$ to the embedded manifold $Ƶ$; these works do not correct the discrepancy between the measurements and the metric on the phenomenon manifold.

We emphasize that the problem illustrated here is not due to a failure of the diffusion maps or other algorithms; the algorithm performs as expected and characterizes the measurement manifold very well. However, the metric of this measured manifold is incompatible with the natural metric of in-plane rotation angles. As a result, we identify modes of the distribution in the measurement space, but these do not correspond to modes of the underlying distribution of angles.

We note that the problem discussed here is not unique to the diffusion maps algorithm or the setup we chose; in fact, other algorithms are not as well-understood as diffusion maps, and applications are rarely as simple as our illustrative example. Many modern algorithms add layers of complexity to the problem. For instance, deep learning approaches that generate latent variables, such as VAEs, are often combined with more standard manifold learning algorithms to obtain low-dimensional data representations. In [13, 14], the distortions introduced by popular algorithms like t-SNE and UMAP are analyzed in the context of single-cell genomics, although the focus is on the discrepancy between the high dimension of the measurement space and the very low dimension (2 or 3) of the embedding space, rather than on the choice of metric. While such algorithms provide valuable new insights into datasets, practitioners should be aware that the results they generate, even when they perform as intended, may have a subtle relation to the “Platonic” physical reality. These outputs should arguably mainly be used for visualization and confirmed by other means. Indeed some of the original work on popular non-linear dimensionality reduction algorithms defines them as tools for visualization [15, 16].

IV. Conclusions

This paper illustrates one of the discrepancies between the measured manifold and a perceived natural parametrization of the underlying phenomenon. In addition, Appendix A3 demonstrates how this discrepancy depends on the measurement modality and how the measured manifold is not invariant to measurements. The discrepancy presented here is by no means the only type of discrepancy; we defer the discussion of additional effects to future work. While the existence of this discrepancy is a natural consequence of various mathematical formulations of manifold learning problems (with the exception of special cases where the metric can be corrected), it is occasionally omitted, which may lead to incorrect and inconsistent answers to seemingly simple scientific questions. In the absence of a general solution to the problem, we suggest the following points to consider when using these methods.

• A good rule of thumb is that manifold learning and dimensionality reduction can provide (when they “work”) an embedding, but they may not provide the embedding (that we might have in mind). In fact, without a good definition of the desired embedding, the embedding is not unique.

• Sometimes, the effects can be controlled if there is knowledge of the structure of the measurement function (e.g., Lipschitz constant). However, nuances in definitions of the output of algorithms, the increased complexity of algorithms, and the practice of layering algorithms on top of each other may make it much more difficult to control such effects. In some special cases, additional measurements may allow one to reverse the effect [4–8].

• In many (but not all) applications, the inferred manifold may reveal enough about the topology of the problem, or the distortion in the metric might be sufficiently small to be a sufficiently good proxy for the geometry. What is “sufficiently good” may depend on the downstream task. For example, the low-dimensional manifold may be a starting point for an analysis by an expert, regression or careful clustering, suspected outliers detection, and even for identification of clear modes. It may not be as helpful for aligning data collected using different modalities (or even different algorithms applied to the same data) with different distortions (see Appendix A3), or for certain analyses of free energy associated with the distribution.

Appendix

A. Additional experiments

This appendix shows several plots and numerical experiments that further illustrate the discrepancy between the phenomenon manifold and the measurement manifold.

1). Manifold learning on the phenomenon manifold:

We have shown in the main text of the paper how applying a manifold learning algorithm to the points on $𝒴$ leads to modes in the data, while we know that the samples are uniformly distributed on the phenomenon manifold $𝒳$ (the orientation angles of the horse). In this section, we present the same manifold learning algorithm applied directly to the points in $𝒳$ (which are not available to us as measurements in our original problem setup) as a benchmark for comparison to the results in the main text, where we apply the algorithm to the measurements. In Figure 4, we ran the diffusion maps algorithm to the set of angles that generated the images, where we represented each angle by a complex number with the magnitude of one and the given angle, and we used the Euclidean distance between them as the distance on $𝒳$. As expected, the embedded points have constant local density (i.e., they are uniformly distributed).

Fig. 4:

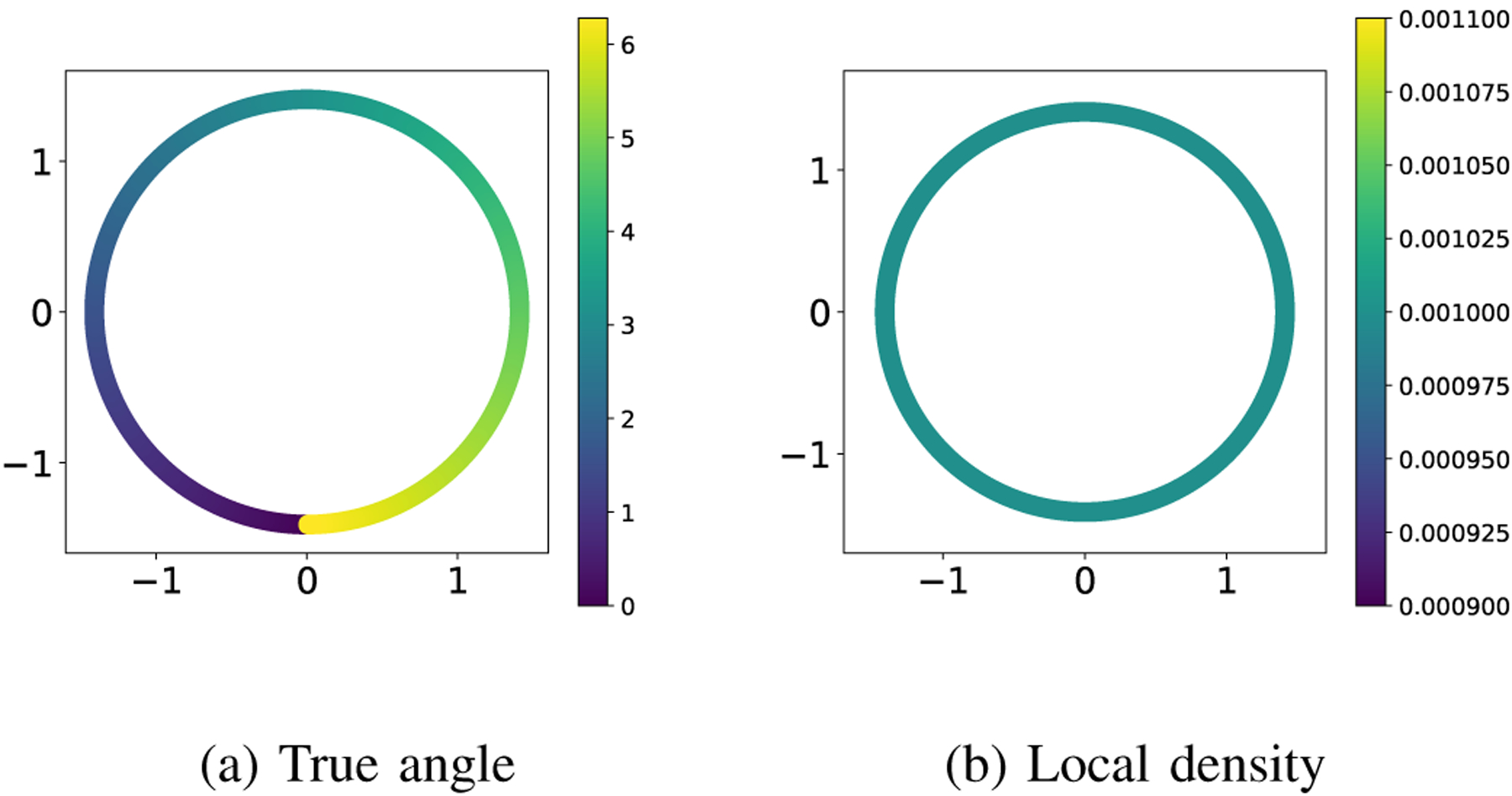
The embedding resulting from applying diffusion maps to the angles directly, represented as complex numbers of magnitude one. The coloring is given by the true angle in panel (a) and the local density with $r=0.05$ in panel (b).

2). Local density of the measured data points:

The central claim of this paper is that applying manifold learning to measured data without careful attention to the metric on $𝒴$ can lead to wrong conclusions about certain questions. The point where metric distortions due to the measurement function are introduced in the processing pipeline is when computing pair-wise distances between the points on $𝒴$. As a further check that this is indeed the case, in Figure 5 we show the local density of the images themselves (the points on $𝒴$): the coordinates of each image are its embedding coordinates (the same as in the main text), and the coloring is given by the local density of the images in panel (a) and the local density of the embeddings in panel (b). The radius $r$ of the ball used to approximate the local density in (a) was chosen so that the maximum value of the local density is approximately the same as the maximum value of the local density in (b). Figure 5 shows that the same modes seen in the embedding are also present in the measured data. The specific value may not be numerically identical due to subtleties in the definition of the embedding and the nature of the approximation. However, the same kind of effect is clearly visible.

Fig. 5:

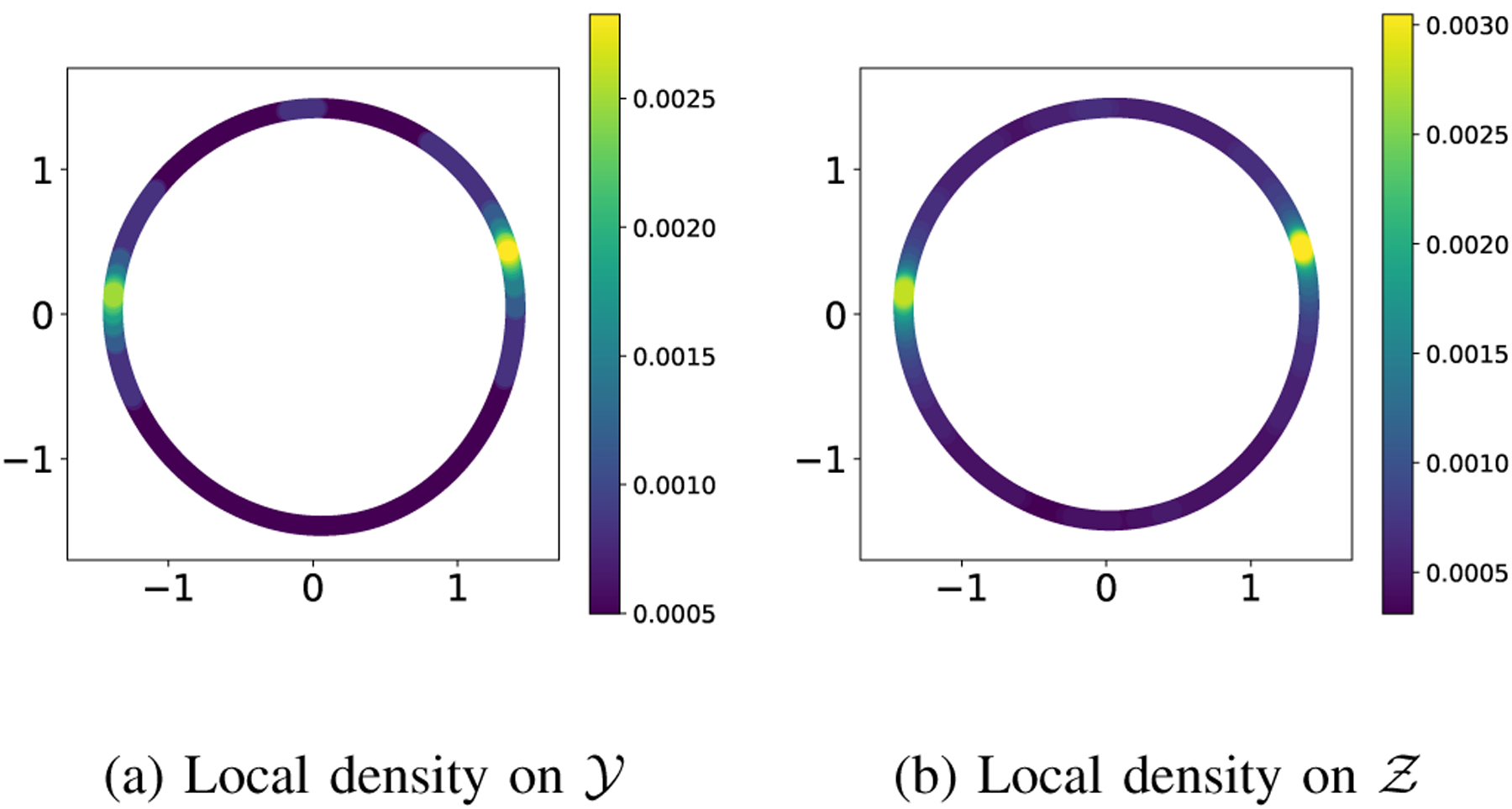
Local density of the points on $𝒴$ in (a) and on $Ƶ$ in (b). The coordinates of the points are given by the embedding in $Ƶ$ in both plots. The radius for computing the local density on $𝒴,r=9$, was chosen so that the maximum value of the density matches the maximum value of the density on $Ƶ$.

3). Two modalities and non-uniqueness:

To further illustrate the problem raised in this article, we now consider a slightly modified setup to demonstrate the non-uniqueness of the parametrization. Instead of one camera, we take photographs of the spinning rigid object using two different cameras placed at two distinct locations. We denote the two measurement functions by $f_1$ and $f_2$ and the two datasets by ${\left\{y_i^1\right\}}_{i=1}^n\subset {𝒴}_1$ and ${\left\{y_i^2\right\}}_{i=1}^n\subset {𝒴}_2$. The images $y_i^1$ and $y_i^2$ at index $i$ taken by the two cameras respectively correspond to the same ground truth point $x_i$. This setup is illustrated in Figure 6. The ambient dimension is $D=108000$, the number of images taken by each camera is $n=1000$, and the measurements are taken at equal time intervals, so the distribution of the data on the phenomenon manifold $𝒳$ is uniform.

Fig. 6:

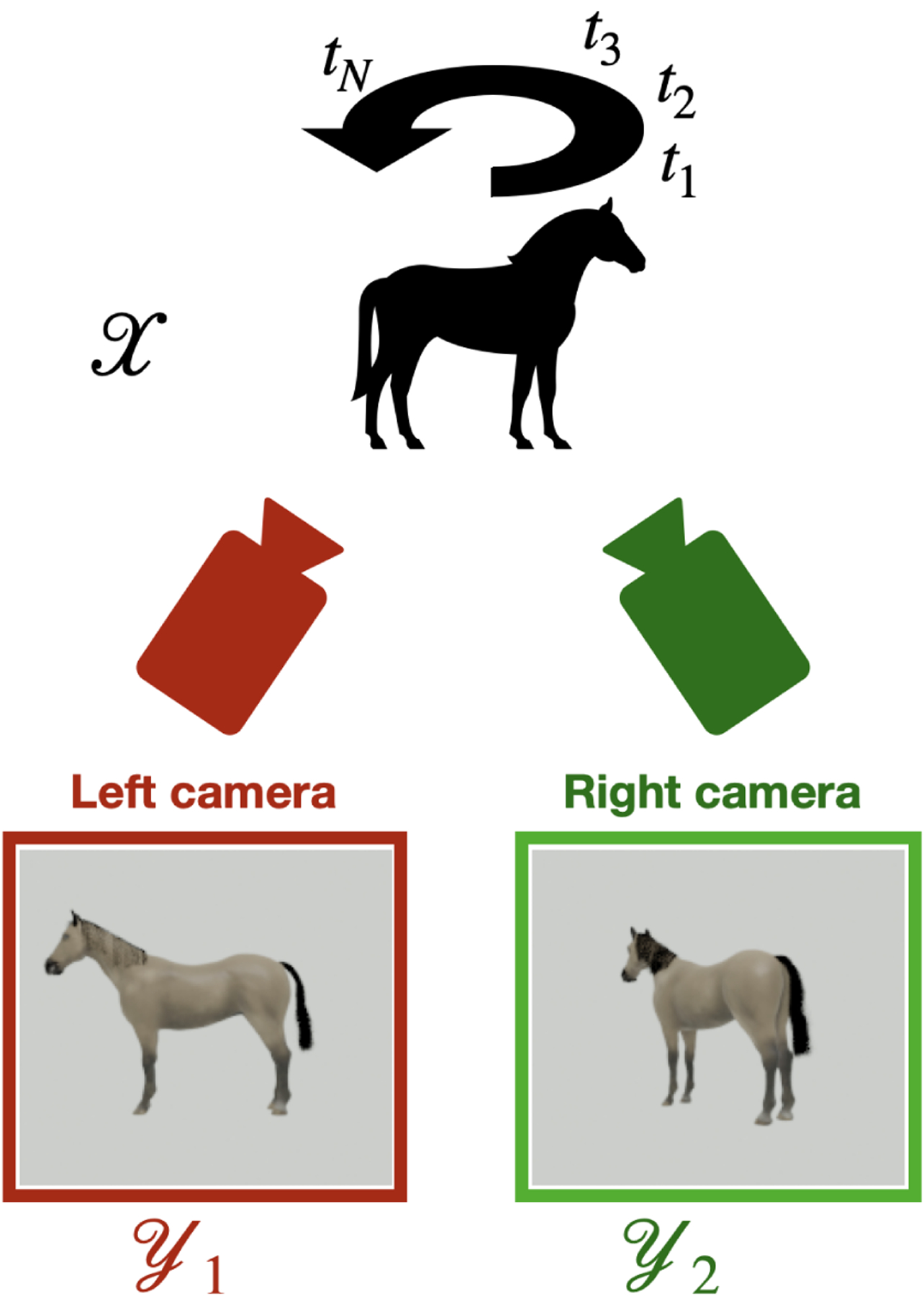
Setup of the numerical experiment with two measured datasets. Using two cameras at different locations, we collect two distinct sets of images on the measurement manifolds ${𝒴}_1$ and ${𝒴}_2$, respectively.

We apply the diffusion maps algorithm separately to each dataset, corresponding to samples from the two measurement manifolds ${𝒴}_1$ and ${𝒴}_2$. The resulting two-dimensional embeddings are shown in Figure 7: the left column shows the embedding ${\left\{{\rho }_1\left(y_i^1\right)\right\}}_{i=1}^n$ obtained from the measurements ${\left\{y_i^1\right\}}_{i=1}^n\subset {𝒴}_1$ and the right column shows the embedding ${\left\{{\rho }_2\left(y_i^2\right)\right\}}_{i=1}^n$ obtained from ${\left\{y_i^2\right\}}_{i=1}^n\subset {𝒴}_2$. In each panel, we show a scatter plot using the first two embedding coordinates given by the diffusion maps algorithm. We denote by ${Ƶ}_1$ and ${Ƶ}_2$ the resulting low-dimensional manifolds. Similarly to the one-camera experiment described in the main text, the one-dimensional torus topology of the orientation angles of the object is correctly identified (panels (a) and (b)). However, panels (c) and (d) show that the metric is distorted. In particular, the distributions of the images in both datasets are incorrectly shown to have two modes (we know that the true distribution is uniform). Moreover, the modes are not compatible: the mode observed in one camera does not correspond to the same true angles as those observed in the other camera. This can be seen in Figure 8, where images from high and low-density regions on ${Ƶ}_1$ correspond to seemingly arbitrary points on ${Ƶ}_2$, whose high and low-density regions correspond to different orientations on $𝒳$. This is, of course, not surprising, given that each camera takes the photographs from different directions and considering the symmetries in this problem.

Fig. 7:

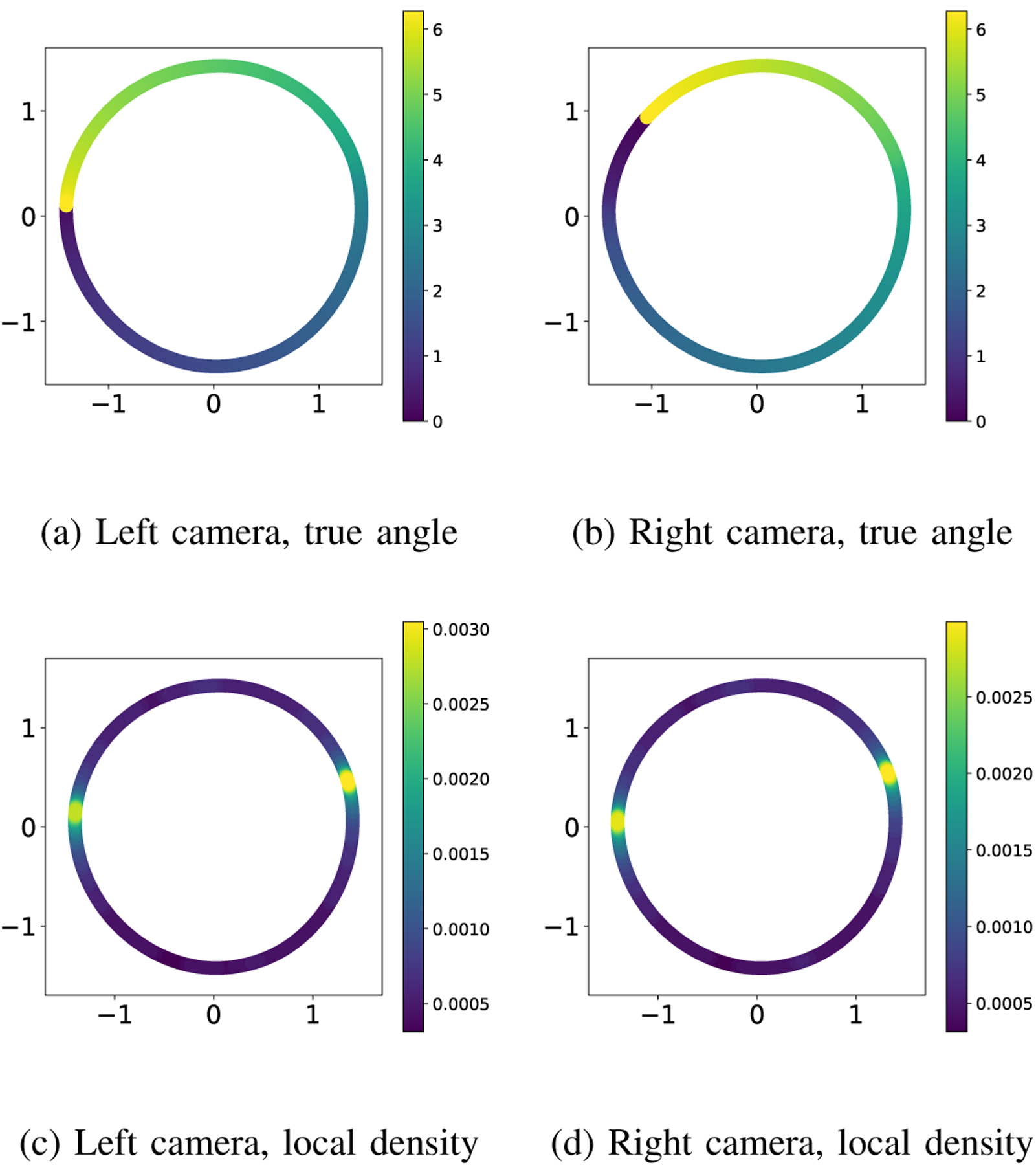
Embeddings obtained using images from the left camera (left column) and the right camera (right column). The coloring is given by the true angle in the top row and the local density of points $(r=0.05)$ in the bottom row.

Fig. 8:

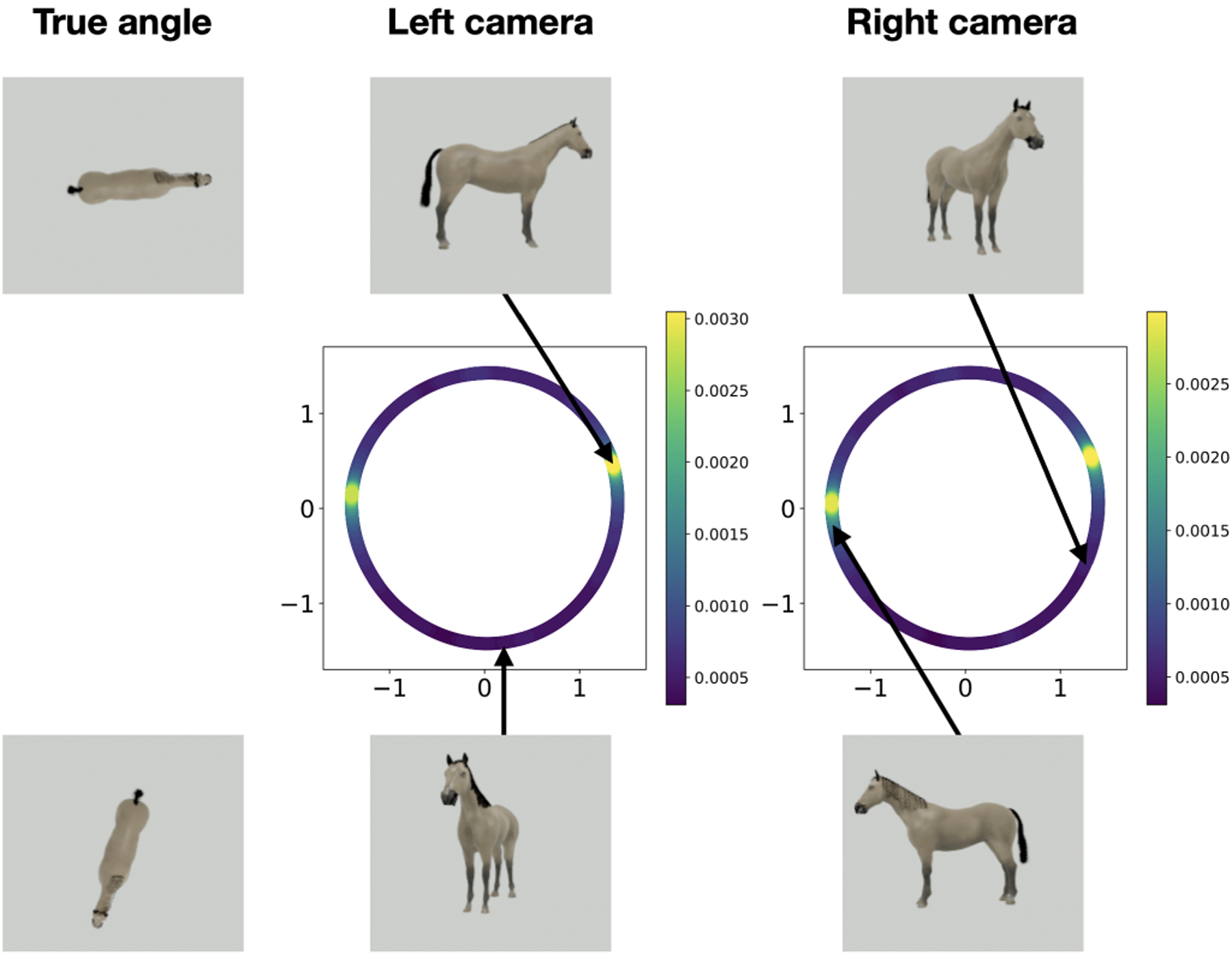
The embeddings with example images from the estimated distributions. The images in the top row correspond to a point in a high-density region of the left camera embedding, and the images in the bottom row correspond to a point in a low-density region of the left camera embedding. In each row of images, we show the top view of the object displaying the true orientation angle (left), the object as seen by the left camera (middle), and the object as seen by the right camera (right).

In this paper, we showed how attempts to solve a simple problem, such as identifying the dominant state of a system, can lead to incorrect answers when applying manifold learning to the measured data. While the experiment presented in the main text of the article shows that the answer we obtain can be incorrect in a non-obvious way, the two-camera experiment presented in this appendix demonstrates that different measurement modalities can produce different answers, with no way to compare the quality of the two answers objectively. More generally, this shows that the estimated measurement manifold is not unique and not invariant to the measurement modality.

This experiment corresponds to several relatively common real-life settings. One example is when multiple different algorithms are applied to the same data, perhaps with different processing pipelines. The processing pipelines are analogous to our different cameras and may not produce the same result.

Another real-life setting is when attempting to align measurements of an underlying phenomenon, acquired using two distinct modalities, calibrated differently and possibly taken on different days. This is the case, for example, when the data is collected in two separate batches, potentially in different laboratories. In this case, even if the two datasets are assumed to have the same distribution, batch effects are present due to potentially different experimental settings. Our experiments show that a rigid transformation cannot align embeddings obtained from such datasets.

4). Top view measurements:

In the previous experiment, we showed that different measurement functions lead to embeddings where the metric is distorted in different ways without knowing which one is more accurate. To further strengthen this argument, we show an example where the measurement function distorts the distances but preserves the local geometry. The images of the rotating horse are captured from the top, and the resulting embedding and density are shown in Figure 9. In practice, there is no way of knowing, only from the data, that we are in a case where the local geometry on $𝒳$ is preserved. This experiment and the one in Appendix A3 reinforce that the embedding we obtain depends heavily on how the measurements are taken and that the solution we expect to see is not objectively better than other possible solutions, given the data.

Fig. 9:

Low-dimensional embedding of the images of the spinning horse viewed from the top. The coloring is given by the true orientation angle of the horse in panel (a) and the local density of points $(r=0.05)$ in panel (b).

B. Diffusion maps

For completeness, we present the diffusion maps algorithm used throughout the article, as described in [1] and adapted in [17]. The phenomena discussed in this paper are not specific to diffusion maps. Broadly interpreted, these issues appear in many machine learning and manifold learning problems in one form or another, except for special cases where they can be corrected or “defined away.”