Abstract
Meiotic recombination is crucial for human genetic diversity and chromosome segregation accuracy. Understanding its variation across individuals and the processes by which it goes awry are long-standing goals in human genetics. Current approaches for inferring recombination landscapes rely either on population genetic patterns of linkage disequilibrium (LD)—capturing a time-averaged view—or on direct detection of crossovers in gametes or multigeneration pedigrees, which limits data set scale and availability. Here, we introduce an approach for inferring sex-specific recombination landscapes using data from preimplantation genetic testing for aneuploidy (PGT-A). This method relies on low-coverage (<0.05×) whole-genome sequencing of in vitro fertilized (IVF) embryo biopsies. To overcome the data sparsity, our method exploits its inherent relatedness structure, knowledge of haplotypes from external population reference panels, and the frequent occurrence of monosomies in embryos, whereby the remaining chromosome is phased by default. Extensive simulations show our method's high accuracy, even at coverages as low as 0.02×. Applying this method to PGT-A data from 18,967 embryos, we mapped 70,660 recombination events with ∼150 kbp resolution, replicating established sex-specific recombination patterns. We observed a reduced total length of the female genetic map in trisomies compared with disomies, as well as chromosome-specific alterations in crossover distributions. Based on haplotype configurations in pericentromeric regions, our data indicate chromosome-specific propensities for different mechanisms of meiotic error. Our results provide a comprehensive view of the role of aberrant meiotic recombination in the origins of human aneuploidies and offer a versatile tool for mapping crossovers in low-coverage sequencing data from multiple siblings.
Recombination between homologous chromosomes is a key source of human genetic diversity (Lynn et al. 2004; Peñalba and Wolf 2020). The crossovers that mediate such genetic exchanges during meiosis are also important for ensuring the accuracy of chromosome segregation (Lister et al. 2010; Webster and Schuh 2017). Notably, female meiosis initiates during fetal development, when homologs pair, acquire double-strand breaks, and establish crossovers that form physical linkages (chiasmata) to stabilize the chromosomes. Such chiasmata must then be maintained over decades-long meiotic arrest, until meiosis resumes at ovulation. Abnormal number and/or location of crossovers may predispose oocytes to gains or losses of whole chromosomes (aneuploidies), which are the leading cause of human pregnancy loss and congenital disorders (Hassold and Hunt 2001). Hypotheses about the role of recombination in aneuploidy formation largely originated from studies of model organisms (Lamb et al. 2005; Lister et al. 2010; Herbert et al. 2015). Meanwhile, the smaller number of studies in humans have primarily focused on the subset of trisomies that are compatible with in utero development (Zaragoza et al. 1994; Kong et al. 2004; Oliver et al. 2008; Middlebrooks et al. 2014), with less focus on the most common trisomies (Chr 15, Chr 16, and Chr 22) observed in oocytes and preimplantation embryos (although see Hassold et al. 1995; Robinson et al. 1998; Hall et al. 2007). To overcome this limitation, several previous studies have analyzed all products of meiosis (i.e., the first and second polar body, as well as a biopsy of the corresponding embryo) (Capalbo et al. 2013; Ottolini et al. 2015). Although insightful, such sampling is technically demanding, limiting sample sizes and, in turn, limiting power and resolution for comparing genetic maps.
Over the past decade, several studies on human embryos have been conducted within the framework of preimplantation genetic testing for monogenic disorders (PGT-M) using methods such as karyomapping (Handyside et al. 2010), siCHILD/haplarithmisis (Zamani Esteki et al. 2015), OnePGT (Masset et al. 2019), and GENType (De Witte et al. 2022), whereby parental DNA is assayed along with that of the embryos, and unaffected embryos are prioritized for transfer. These genome-wide haplotyping methods allow mapping of maternal and paternal crossovers along chromosomes. However, the number of patients that undergo PGT-M is small compared with the number of patients that undergo preimplantation genetic testing for aneuploidy (PGT-A), again limiting answers to broader questions about the crossover landscape. For example, a recent PGT-M study by Tšuiko et al. (2021) inferred the parental and mechanistic origin of chromosome abnormalities in 2706 embryos from PGT-M patients and found 269 trisomies in total. A similar PGT-M study of recombination by Ma et al. (2023) analyzed 1519 embryos and 353 autosomal aneuploidies.
Other current approaches for inferring the landscape of recombination rely either on population patterns of linkage disequilibrium (LD)—capturing a time-averaged view of historical recombination events—or on direct detection of crossovers based on genotyping of haploid gametes or multigeneration pedigrees (e.g., parent–offspring trios), again limiting the scale and availability of relevant data sets (Auton and McVean 2007; Halldorsson et al. 2019; Spence and Song 2019; Adrion et al. 2020). Moreover, most of these methods are designed for discovering recombination using data from normal, disomic chromosomes. Mapping meiotic crossovers in large samples of both normal and aneuploid embryos using a unified statistical framework would allow a robust test of the role of recombination in the genesis of aneuploidy.
To this end, we introduce a statistical approach tailored to sequencing data from PGT-A, which is based on low-coverage (<0.05× per homolog) whole-genome sequencing of biopsies from in vitro fertilized (IVF) embryos. We retrospectively apply our method to normal disomic chromosomes identified in existing low-coverage PGT-A data from 18,967 embryos and replicate features of sex-specific recombination maps that were previously described based on large prospective studies of living populations. We then extend our method to trisomies, testing the extent to which the landscape of recombination differs between normal and aneuploid chromosomes. Together, our study sheds light on the dual function of meiotic recombination in generating genetic diversity while ensuring fidelity of human meiosis.
Results
A method for inferring crossovers based on low-coverage sequencing data from multiple siblings
One general approach for discovering the genomic locations of meiotic recombination events is to compare genotype data from related individuals. Such data can be scanned to identify regions where haplotypes match (i.e., are identical by descent [IBD]). The boundaries of the matched haplotypes reflect the locations of meiotic crossovers in the history of the sample. The information gained by comparing haplotypes among relatives serves as the foundation for several different approaches for PGT-M (Handyside et al. 2010; Zamani Esteki et al. 2015; Masset et al. 2019). However, directly calling diploid genotypes from sequencing data requires a minimum coverage of 2× (to sample both alleles) and in practice requires coverage several fold higher to overcome technical challenges such as coverage variability, ambiguous alignments owing to repetitive sequences, and other sequencing and analytic artifacts. Because data from PGT-A typically fall well below these coverage requirements, they are generally assumed unsuitable for applications that demand genotypes, including the study of recombination landscapes in embryos. However, as exemplified by common methods such as genotype imputation (Marchini and Howie 2010), knowledge of patterns of LD from external population genetic reference panels may facilitate the extraction of meaningful signal from sparse, low-coverage data sets, including in the context of prenatal genetics (Liu et al. 2018; Ariad et al. 2021).
Building on this logic, we introduce a haplotype matching approach, named linkage disequilibrium-informed comparison of haplotypes among sibling embryos (LD-CHASE), tailored to DNA sequencing data from PGT-A. Most current implementations of PGT-A involve low-coverage high-throughput sequencing of trophectoderm biopsies from IVF embryos at day 5 or 6 postfertilization, with the goal of prioritizing chromosomally normal (i.e., euploid) embryos for transfer to improve IVF outcomes (Vermeesch et al. 2016). PGT-A offers a unique source of genomic data from large numbers of sibling samples, as each IVF cycle typically produces multiple embryos, and often multiple IVF cycles are necessary in infertility treatment.
Disomic chromosomes of any two sibling embryos will possess discrete genomic intervals with different counts of matching haplotypes, and transition points between these intervals reflect the locations of meiotic crossovers. The occurrence of monosomy (or uniparental isodisomy [isoUPD], isolated to individual chromosomes or genome-wide [GW-isoUPD]) among a set of sibling embryos greatly simplifies this comparison, as the remaining chromosome is phased by default, facilitating discovery of sex-specific crossovers (i.e., originating during gamete formation in one of the two parents). Here, we leverage the common occurrence of chromosome loss to reveal the sex-specific landscapes of meiotic crossovers among a large sample of IVF embryos.
Briefly, LD-CHASE uses sparse genotypes obtained from low-coverage sequencing data to identify the locations of meiotic crossovers (Fig. 1; Supplemental Fig. S1). At such coverages, direct comparison of haplotypes is not possible, as a small minority of the genome is covered by any sequencing reads, and positions of aligned reads from samples under comparison rarely overlap. We circumvent this challenge based on patterns of LD, whereby observations of a set of alleles from one sequencing read may provide indirect information about the probabilities of alleles at nearby, unobserved variant sites. This, in turn, informs the relative probability that a given pair of reads originated from identical homologous chromosomes versus from distinct homologous chromosomes, which we formalize using a likelihood framework (see Methods). Transitions between these matched and unmatched states indicate the locations of meiotic crossovers.
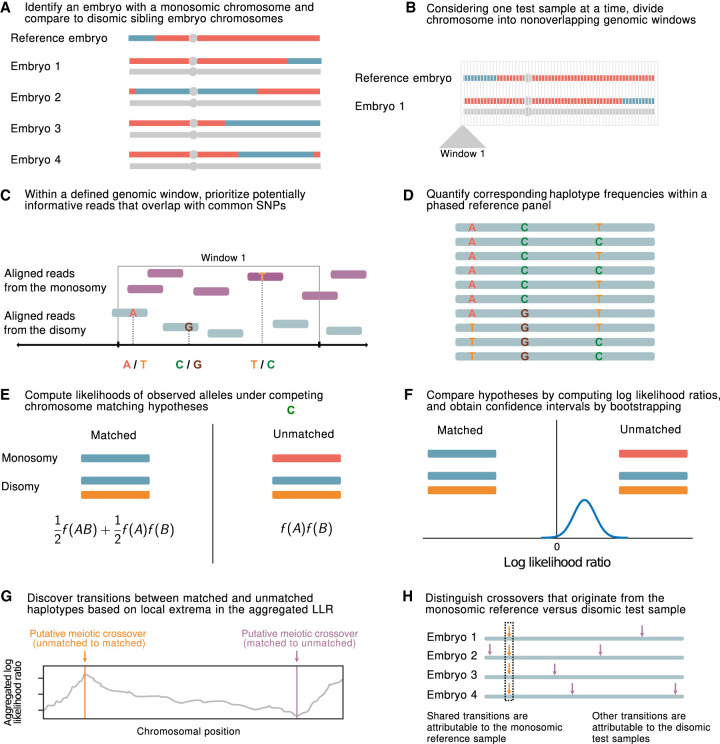
Figure 1.
A statistical approach for meiotic crossover discovery based on low-coverage sequencing data from preimplantation genetic testing. (A) Crossover detection is based on haplotype matching between a monosomic chromosome (which is phased by default) and the disomic chromosomes of sibling embryos from the same IVF case. (B) Analysis is conducted within nonoverlapping genomic windows on the scale of 10–100 kbp, defined by the length of typical human haplotypes. (C) Within each window, two to 18 reads are resampled, prioritizing potentially informative reads that overlap common polymorphisms in the population. (D) Frequencies and joint frequencies (i.e., haplotype frequencies) of these SNPs are quantified within an external phased genetic reference panel. (E) Based on these frequencies, the likelihoods of the observed reads are computed under both the matched- and unmatched-haplotype hypotheses. (F) The hypotheses are compared by computing a likelihood ratio, with variance estimated by bootstrapping. (G) Local extrema in the aggregated log-likelihood ratio indicate the locations of meiotic crossovers. (H) Putative crossovers observed in the majority of sibling embryos can be attributed to the monosomic reference chromosome, whereas the remaining crossovers are attributed to the test samples.
Evaluating method performance via simulation
To assess the performance of LD-CHASE, we simulated chromosomes from pairs of embryos consisting of a monosomy (i.e., reference sample) and disomy (i.e., test sample) that either shared a matching haplotype or were unrelated. A meiotic monosomy can occur owing to errors at several distinct stages of oogenesis (Supplemental Fig. S2). We generated these pairs by mixing phased chromosomes from the 1000 Genomes Project (The 1000 Genomes Project Consortium 2015), as described in the Methods. We focused our simulations on Chromosome 16, which is the chromosome most frequently affected by aneuploidy in preimplantation embryos, using a bin size of 2 Mbp and varying the sample ancestries across all superpopulations from the 1000 Genomes Project.
We allowed our classifier to assign bins as “matched,” “unmatched,” or “ambiguous” to denote uncertainty, and we used a balanced receiver operating characteristic (ROC) curve to evaluate performance (see Methods) (Fig. 2; Supplemental Fig. S3). Our results showed high sensitivity and specificity across all ancestries at a coverage of 0.05× per homolog (average area under the curve [AUC] of 0.989). As coverage was reduced to 0.025× and 0.013×, the AUC decreased by 0.014 and 0.053 on average, respectively, although performance was more or less affected in certain regions of the genome (Fig. 2). Notably, performance of the classifier is affected by the local density of SNPs and sequencing reads, as well as ancestry matching between the reference panel and the target samples (Supplemental Figs. S3, S4).
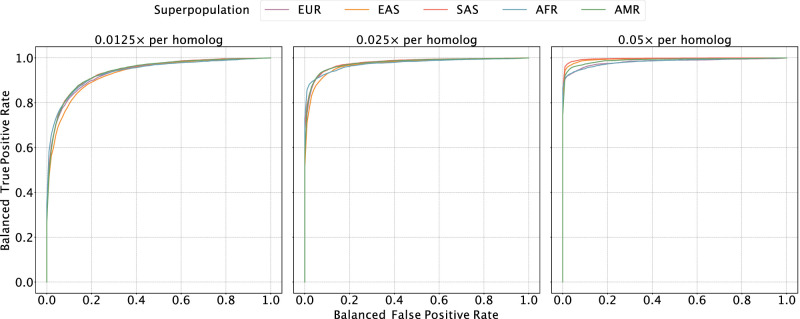
Figure 2.
Evaluating the sensitivity and specificity of meiotic crossover detection based on simulation. Using data from the 1000 Genomes Project, we simulated pairs of monosomy 16 and disomy 16, in which half of the pairs possessed matched haplotypes and the other half possessed unmatched haplotypes. Then we divided Chromosome 16 into 45 bins (of ∼2 Mbp) and calculated a balanced ROC curve (see Methods) for each bin, averaging over all the balanced ROC curves to obtain a mean balanced ROC curve. We repeated this procedure over a range of depths of coverage and across sets of samples from all superpopulations of the 1000 Genomes Project, abbreviated as follows: (AMR) admixed American, (AFR) African, (EAS) East Asian, (EUR) European, (SAS) South Asian.
Application to a large PGT-A data set
Encouraged by the performance of LD-CHASE on simulated data, we proceeded to apply it to a large data set from the CReATe Fertility Centre (Toronto, Canada). The data set consists of low-coverage sequencing data from 18,967 embryos from 2558 IVF patients, collected between April 2020 and August 2022. To select appropriate ancestry-matched reference panels, we first inferred the genetic similarity of each embryo to reference samples from the 1000 Genomes Project (The 1000 Genomes Project Consortium 2015) using LASER (see Methods) (Wang et al. 2014). The results reflect the diverse ancestry composition of the patient population, with 68.71% (13,104) of embryos showing the greatest genetic similarity to European reference samples, 6.76% (1290) of embryos showing the greatest genetic similarity to South Asian reference samples, 5.74% (1094) of embryos showing the greatest genetic similarity to East Asian reference samples, and the remaining embryos showing lower genetic similarity to reference samples, for example, owing to recent admixture (Supplemental Fig. S5).
Previous studies have shown that the vast majority of monosomies observed in blastocyst-stage embryos with PGT-A are of maternal meiotic origin, such that only the paternal chromosome remains (McCoy et al. 2015; Tšuiko et al. 2021). LD-CHASE uses such monosomies to map paternal crossovers in sibling disomic embryos. Meanwhile, haploidy or genome-wide uniparental isodisomy (GW-isoUPD) observed at the blastocyst stage nearly exclusively involves the sole presence of the maternal genome (McCoy et al. 2015; Sagi and Benvenisty 2017; Tšuiko et al. 2021), allowing us to map genome-wide maternal crossovers in sibling disomic embryos. LD-CHASE thus requires preliminary analysis to identify chromosome abnormalities based on signatures of altered depth of coverage and/or genotype observations.
To this end, the copy number of each autosome of each sample was inferred using WisecondorX (Raman et al. 2019) based on within-sample normalized depth of coverage. Across the entire data set, we identified 388,366 disomies, 3307 trisomies, 4294 monosomies, 332 segmental gains, and 685 segmental losses (Supplemental Fig. S6; Supplemental Table S1). The monosomic chromosomes traced to embryos obtained from 1506 (58.85%) unique patients, facilitating mapping of paternal crossovers among 30,645 disomic chromosomes of 12,348 total embryos. Because maternal meiotic monosomies observed in blastocyst-stage embryos are highly enriched for Chromosomes 15, 16, 21, and 22, the mapping of paternal crossovers was largely relegated to these chromosomes, with much lower resolution for the rest of the genome.
Importantly, methods such as WisecondorX compare coverage across chromosomes within a sample and may therefore fail to detect aneuploidies that simultaneously affect many chromosomes. In extreme cases such as triploidy and haploidy/GW-isoUPD, in which coverage is uniform across the genome despite the ploidy aberration, embryos may be erroneously classified as euploid. To overcome this limitation, we applied our published haplotype-aware method, LD-PGTA (Ariad et al. 2021), to reclassify all chromosomes that were initially identified as disomic by WisecondorX. LD-PGTA identified 155 (1.65%) samples as triploid and 395 (4.20%) samples as haploid/GW-isoUPD. Importantly, such haploid/GW-isoUPD embryos were distributed across 184 (7.19%) patients, facilitating mapping of genome-wide maternal crossovers among 40,015 disomic chromosomes of 1898 total embryos.
Sex-specific maps of crossovers on disomic chromosomes
Considering only chromosomes with informative genomic windows that covered at least 50% of their total length (see Methods), we identified 54,284 maternal crossovers across 27,026 chromosomes and 22,578 paternal crossovers across 21,050 chromosomes. An example of crossovers mapped in a single set of sibling embryos is provided in Figure 3, in which transitions from intervals that do not match (blue) and that do match (red) the reference monosomic chromosome indicate the locations of meiotic crossovers (purple lines; see Methods). The exception to this interpretation involves transitions that are shared across all (or nearly all) sibling embryos, which instead reflect crossovers attributable to the reference monosomic chromosome itself (orange dashed lines). The genome-wide distributions of crossovers on disomic chromosomes are provided in Supplemental Figures S7 and S8. We note that no crossovers are reported on the short arms of Chromosomes 13, 14, 15, 21, and 22 as their heterochromatic, highly repetitive nature makes them largely inaccessible to short-read-based analyses. Moreover, for the same reason, these chromosome arms are largely devoid of variation in the reference panel data upon which our method relies.
Figure 3.
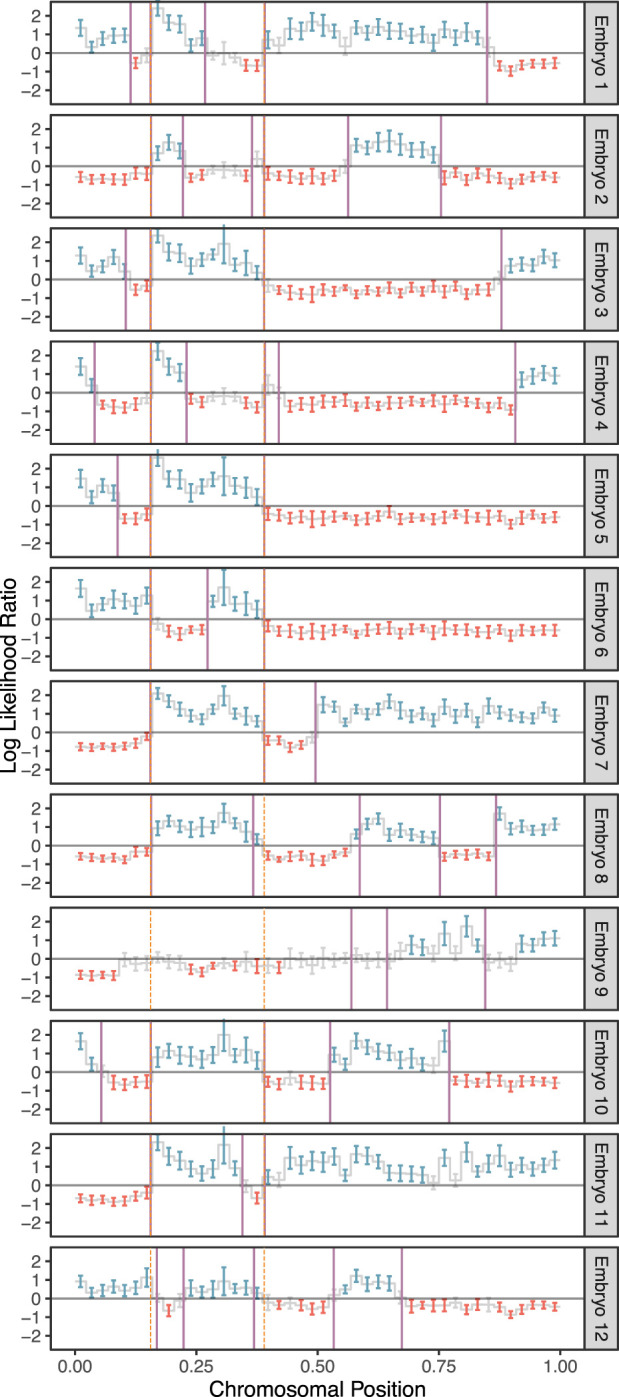
A representative example of crossover discovery based on haplotype matching among sibling IVF embryos. In this example, Chromosome 10 of each test embryo is compared with a single sibling reference embryo with monosomy of Chromosome 10. Evidence of haplotype nonmatching is indicated by positive log-likelihood ratios, whereas evidence of haplotype matching is indicated by negative log-likelihood ratios. Crossovers are identified as transitions from positive (blue) to negative (red) log-likelihood ratios or vice versa. Each point corresponds to a bin size of 3 Mbp and consists of a varying number of genomic windows. Error bars denote 95% confidence intervals. Crossovers attributed to the monosomic chromosome are indicated with dashed orange lines (defined as those observed in more than half of test samples), whereas crossovers attributed to the test samples themselves are indicated with purple lines.
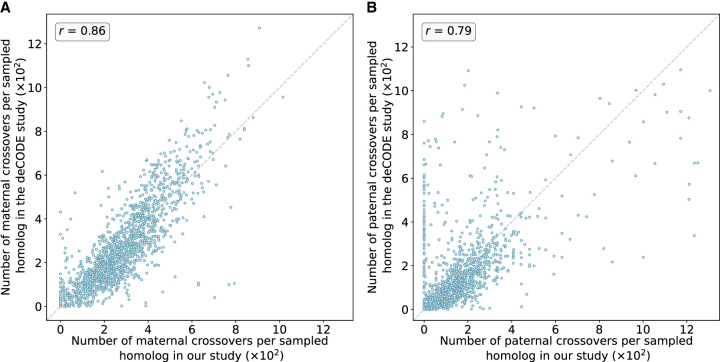
The crossover distributions were strongly correlated with sex-specific genetic maps published by deCODE, which were based on whole-genome sequencing of living parent–offspring trios (Halldorsson et al. 2019), in broad support of the accuracy of our method (Fig. 4). The observed correlation was particularly strong for putative maternal crossovers (r = 0.86) compared with putative paternal crossovers (r = 0.79). The smallest autosomal chromosomes are enriched for maternal meiotic aneuploidies and thus offer the greatest resolution for mapping paternal crossovers (for chromosome-specific correlations, see Supplemental Figs. S8–S10). It was evident from our analysis that LD-CHASE performed differently for maternal and paternal crossovers because monosomies have only half the coverage compared with haploidy and uniparental isodisomy (isoUPD). This difference in depth of coverage stems from a lower copy number relative to the baseline. Additionally, the frequency of monosomies varies among autosomes, with some being rare. The low frequencies reduce our resolution and result in recombination maps that are relatively less precise. Notably, we observed that the correlations significantly declined when comparing our inferred female map to the deCODE male map (r = 0.33) and vice versa (r = 0.75), supporting our assumptions about the parental origins of various chromosome abnormalities (Supplemental Figs. S11, S12).
Figure 4.
Number of maternal (A) and paternal (B) crossovers per sampled homolog in genomic bins compared between our study and published genetic maps from deCODE. Data from deCODE were obtained from Halldorsson et al. (2019). Crossovers were identified as transitions between regions of “matched” and “unmatched” haplotypes, in which each region included at least 15 genomic windows and a z-score of at least 1.96. Pearson correlation coefficients (r) between the deCODE map and our map across genomic bins are reported for each panel (for chromosome-specific comparison, see Supplemental Figs. S9, S10).
Chromosome-specific propensities for various mechanisms of trisomy formation
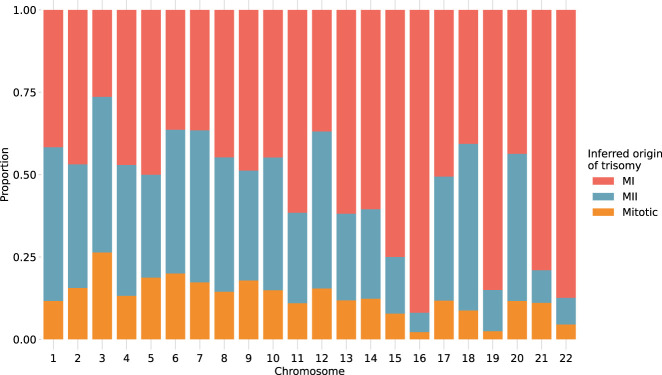
Previous studies have suggested that chromosomes may vary in their susceptibility to segregation errors occurring during meiosis I (MI), meiosis II (MII), and mitosis (Hassold et al. 1995; Lamb et al. 1996; Bugge et al. 1998, 2007; Robinson et al. 1998; Hall et al. 2007). MI and MII errors can be roughly identified based on tracts of distinct (i.e., “both parental homologs” [BPH]) or identical (i.e., “single parental homolog” [SPH]) haplotypes, respectively, inherited from a single parent in regions spanning the centromere. Meanwhile, patterns of SPH chromosome-wide indicate a potential mitotic origin of trisomy (or MII error without recombination). Although previous studies have noted that the attribution of centromere-spanning BPH and SPH patterns to MI and MII errors is imperfect owing to alternative mechanisms by which the signatures may originate (Chernus et al. 2021), our results support the hypothesis that chromosomes possess unique propensities for various forms of segregation error (χ2 [21, N = 1911] = 393.3, P = 2.3 × 10−70) (Fig. 5; Supplemental Table S2). The vast majority (>81%) of trisomies of Chromosomes 15, 16, 19, 21, and 22 showed haplotypic patterns consistent with errors in MI, whereas Chromosomes 11, 13, and 14 showed more modest excesses (∼70%) of MI errors (binomial test, Bonferroni-adjusted P < 0.05 for all noted chromosomes). Meanwhile, the remainder of chromosomes were characterized by a roughly equal number of MI and MII errors (36%–61%; binomial test, Bonferroni-adjusted P > 0.05 for all noted chromosomes).
Figure 5.
Stratification of trisomies by autosome and inferred source of error. Chromosome-wide patterns of SPH were designated as potentially mitotic in origin (yellow). Samples with tracts of BPH in regions surrounding the centromere were classified as putative MI errors (red), whereas tracts of BPH elsewhere on the chromosome were classified as putative MII errors (blue).
An altered landscape of crossovers among aneuploid versus disomic chromosomes
Abnormal number or location of meiotic crossovers between homologous chromosomes may predispose oocytes to aneuploidy, as shown by several previous studies (for review, see Hassold and Hunt 2021). Our published method, LD-PGTA (Ariad et al. 2021), facilitates the mapping of crossovers on trisomic chromosomes, which can then be compared to the crossover map for disomic chromosomes obtained via LD-CHASE. One caveat of this comparison is that LD-PGTA and LD-CHASE possess different sensitivities and specificities, which also vary along the genome, as evident from our simulation-based benchmarking analyses (Supplemental Figs. S3, S4, S13, S14). To ensure that the observed differences between the crossover distributions were not driven by these technical differences, we merged together monosomies and disomies to create artificial trisomies (see Methods) such that the disomies and trisomies could both be analyzed with LD-PGTA in a standardized manner. The number (r = 0.99) and genome-wide distribution (r = 0.90) of disomic crossovers inferred by LD-CHASE and LD-PGTA showed strong agreement, suggesting that the methods are robust to their technical differences and supporting the use of LD-CHASE in downstream comparisons between trisomies and disomies (see Supplemental Fig. S15).
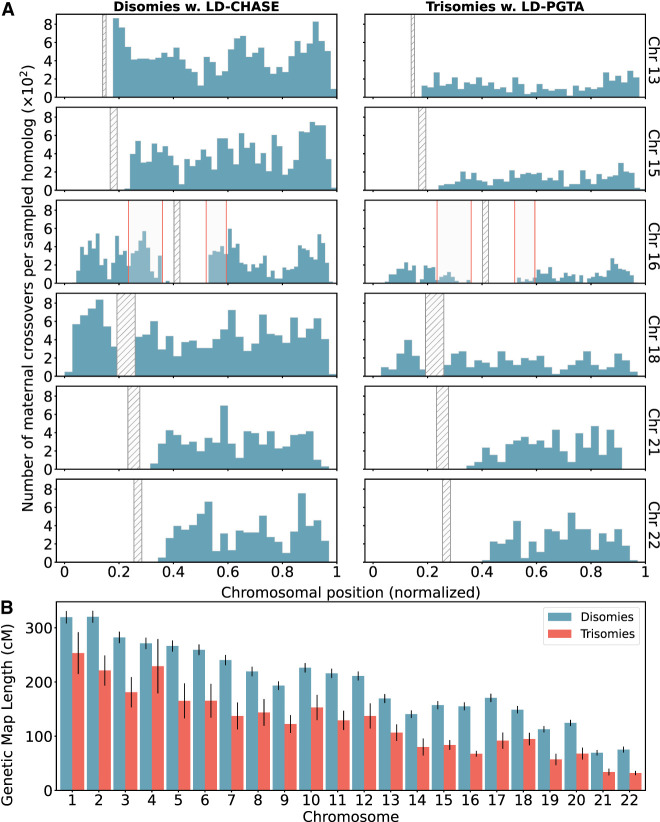
Across all chromosomes, these comparisons revealed a 35% depletion of crossovers for trisomies relative to disomies (Fig. 6). On a per-chromosome basis, the depletion was observed across all chromosomes but was largest for Chromosome 16 (54%) and smallest for Chromosome 4 (17%). Although these observations are consistent with the hypothesis that a reduced rate (or absence; i.e., “exchangeless homologs”) of recombination contributes to aneuploidy risk (Hassold and Hunt 2021; Hassold et al. 2021), we note that they may be partially driven by a failure of our method to detect crossovers on reciprocal recombinant chromosomes—a limitation that uniquely applies to trisomies but not disomies and affects nearly all previous genotype-based studies (see Discussion).
Figure 6.
Differences in number and location of inferred crossovers between disomic and trisomic samples. (A) Spatial distributions of inferred meiotic crossovers in disomies (left; mapped with LD-CHASE) and trisomies (right; mapped with LD-PGTA) across Chromosomes 13, 15, 16, 18, 21, and 22. Regions with qualitative differences are highlighted in light gray, whereas centromeres are indicated with diagonal shading. (B) Comparisons of female genetic map length for disomies (blue) versus trisomies (red) for each autosome. The observed rates of meiotic crossover were consistently lower for trisomies compared with disomies. Error bars denote 95% confidence intervals as estimated by bootstrapping.
In addition to these global differences in numbers of crossovers, several chromosome-specific alterations in the landscapes of crossovers were evident from our results (Fig. 6; Supplemental Figs. S16–S19). We used the Kolmogorov–Smirnov (KS) test to quantify differences in crossover landscapes, generating the null distribution by permutation (see Methods). Chromosomes 7, 14, and 16 showed significant differences in crossover landscapes between disomic and trisomic chromosomes (p-value <0.05; although note the small sample sizes for Chromosomes 7 and 14), whereas Chromosome 22 fell just above this threshold (p-value = 0.051) (Supplemental Table S3). Our observations reveal that on Chromosome 16, trisomies lacked a pair of hotspots in the vicinity of the centromere—one on each arm—broadly consistent with the previous observation that distal crossovers were enriched among a smaller sample of 62 cases of trisomy 16 (Hassold et al. 1995; Hassold and Hunt 2021). Meanwhile, trisomies of Chromosome 22 appeared relatively enriched for crossovers near the center of the q-arm. Results for less frequent trisomies are depicted in Supplemental Figures S16 through S19.
Discussion
Meiotic crossovers are necessary for ensuring accurate pairing and subsequent segregation of chromosomes following decades-long dictyate arrest in human females (Gray and Cohen 2016). Previous studies have shown chromosome-specific associations between patterns of recombination and various forms of meiotic aneuploidy (Hassold et al. 1995; Lamb et al. 1996; Bugge et al. 1998, 2007; Robinson et al. 1998; Hall et al. 2007). For example, early studies of trisomy 16 (the most common autosomal trisomy detected in human preimplantation embryos) suggested a depletion of recombination in pericentromeric regions relative to euploid control samples (Southern 1975; Saiki et al. 1985). However, the accuracy, genomic resolution, and statistical power of many such studies have been limited by the genetic assays they used (e.g., Southern blot, PCR, etc.), as well as the challenge of achieving large samples from living trisomic individuals or products of conception. Because of its inherent relatedness structure, PGT-A offers a natural source of retrospective data for crossover mapping, including both viable and nonviable embryos, but current implementations based on low-coverage whole-genome sequencing pose a technical challenge for recovering relevant genotype information.
To address this challenge, our haplotype-aware method (LD-CHASE) uses known LD structure from an external reference panel, as well as the frequent occurrence of monosomies (which are phased by default), to map crossovers based on comparisons of haplotypes among samples of sibling embryos. The resulting sex-specific maps of crossovers generated by our method were broadly consistent with those generated in previous prospective studies. The sex-specific nature of these patterns also supports our assumption that most monosomies observed in blastocyst-stage IVF embryos (of adequate morphology to be candidates for transfer and thus tested with PGT-A) originate during maternal meiosis, whereas most cases of haploidy/GW-isoUPD solely possess a maternally inherited set of chromosomes. The latter phenomenon may arise when sperm cells trigger egg activation but fail to fuse with the ovum, after which the maternal genome may duplicate to produce two identical complements (Xu et al. 2015). Our observations about the sex-specific origins of various forms of aneuploidy thus independently replicate previous studies that directly assayed parental genomes (McCoy et al. 2015; Tšuiko et al. 2021). Although we are eager to understand the differences in recombination maps of trisomies stemming from both MI and MII errors, the size of our data set limits such exploration. The most frequently observed trisomies are 15, 16, 19, 21, and 22, yet <25% are of MII origin. In the future, we intend to delve deeper using larger PGT-A data sets that include parental genomic data. Furthermore, the ability to produce sex-specific crossover maps from PGT-A data could pave the way for studies seeking to understand the genetic basis of recombination phenotypes and the implications of extreme deviations in these phenotypes for meiotic errors and potential infertility.
As a first step toward this goal, we investigated the association between crossover phenotypes and chromosome abnormalities observed in preimplantation embryos. Although broadly consistent with previous studies that used smaller samples or were restricted to living individuals with viable trisomies, our data provide unified views of these phenomena across all autosomes and support the hypothesis that the number and chromosome-specific locations of meiotic crossovers influence risk of aneuploidy. However, the observation that the length of the genetic map is shorter for trisomies versus disomies could be partially driven by the inability to detect crossovers on reciprocal chromosomes that derive from a single crossover event and were both transmitted to the oocyte to produce a trisomy. Future studies may use linked-read or long-read sequencing to achieve direct read-based phasing and overcome this limitation (Bansal 2019; Sun et al. 2019).
Despite the methodological advances we report here, crossover mapping from sequencing-based PGT-A data possesses several other technical limitations, including the modest resolution per sample (∼150 kbp). This limitation is driven by the combination of the low coverage (and thus sparsity) of the aligned reads (less than 0.05×), the low rates of heterozygosity of human genomes (less than 0.001), and the extent of LD in the reference panel (<1 Mb). Our benchmarking analyses additionally show that performance degrades with genetic distance between the test sample and reference panel owing to differences in allele frequencies and LD structure, similar to challenges encountered when transferring polygenic scores across populations (Wang et al. 2022). To overcome these sources of error, we aggregated signal across consecutive genomic windows, thereby increasing the classification accuracy at the cost of resolution. Even with such an approach, it is important to note that performance is not uniform across the genome, as regions near centromeres, telomeres, or other repetitive regions are enriched for false positives and negatives relative to the genomic background.
An additional potential caveat regards the possibility that ovarian stimulation or other aspects of IVF may alter the crossover landscape of IVF embryos compared with non-IVF embryos or live-born individuals. Although we cannot formally rule out this possibility, we consider it implausible because maternal crossovers are established during prophase I of meiosis, which begins during female fetal development. As such, the locations of crossovers are determined long before any IVF-related procedures are introduced. The observed differences in the crossover landscapes between IVF embryos and living individuals are therefore likely to be indirect, for example, driven by differences in viability of embryos with high versus low recombination rates owing to the relationship between recombination and aneuploidy. Although we expect this viability selection to apply to both IVF and naturally conceived embryos, this is an intriguing question for future investigation.
One promising future direction is the extension of our haplotype-aware approach to PGT-M, combining knowledge of population genetic patterns of LD in a reference panel with information from sibling embryos (or alternative data sources such as gametes) to infer transmission or nontransmission of pathogenic haplotypes from parents to offspring. Although potentially lowering costs and increasing efficiency, such an approach will require extensive validation and benchmarking to determine its feasibility and accuracy given the probabilistic nature of LD and the high stakes of PGT-M. In the meantime, LD-CHASE offers a flexible tool for mapping crossovers in low-coverage sequencing data from multiple sibling embryos, toward a better understanding of the factors that modulate the meiotic crossover landscape and the role of recombination in the origins of aneuploidies.
Methods
Prioritizing informative reads
Our method seeks to overcome the sparse nature of low-coverage sequencing data by leveraging LD structure of an ancestry-matched reference panel, consisting of phased haplotypes from high-coverage sequencing data. Measurements of LD require pairwise and higher-order comparisons and may thus grow intractable when applied to large genomic regions. To ensure computational efficiency, we developed a scoring algorithm to prioritize reads based on their potential information content, as determined by measuring haplotype diversity within a reference panel at sites that they overlap. We emphasize that the priority score of a read only depends on variation within the reference panel and not on the alleles that the read possesses. The score of a read is calculated as follows:
Given the ancestry composition of the target sample (e.g., 30% ancestry with genetic similarity to European reference samples and 70% ancestry with genetic similarity to East Asian reference samples), a suitable reference panel is chosen (see subsequent section “Assembling an ancestry-matched reference panel”).
Based on this reference panel, we list all biallelic SNPs that overlap with the read and their reference and alternative alleles.
Using the former list, we enumerate all the possible haplotypes. In a region that contains n biallelic SNPs, there are 2n possible haplotypes.
- The effective frequency of each haplotype is estimated from the reference panel as
where αi is the ancestry proportion from the ith population, and (e.g., α1 = 0.3 and α2 = 0.7). Moreover, is the joint frequency of the SNP alleles A, B, and C in the ith population. Here we assumed n = 3, but the formula is applicable to any n.(1) We increment the priority score of a read by one for every haplotype with a frequency between f0 and 1 − f0.
An example of scoring a read that overlaps with three SNPs appears in the Supplemental Methods. Our scoring metric is based on the principle that reads that overlap SNPs with intermediate allele frequencies should receive high priority, as the inclusion of such sites will increase our ability to discern between two haplotypes. In the simplest case, in which a read overlaps with only a single SNP, the score of the read would be two when the minor allele frequency (MAF) is at least f0 and otherwise would be zero. We note that all observed alleles from the same read are considered as originating from the same underlying molecule. Hence, our score metric reflects the number of common haplotypes existing in the population in the chromosomal region that overlaps with the read. For a reference panel on the scale of the 1000 Genomes Project (about 2500 unrelated individuals), 25%–45% of common SNPs have a nearest neighbor within 35 bp. Hence, even for short reads, it is beneficial to use a scoring metric that accounts for reads that span multiple SNPs.
Comparing haplotype matching hypotheses
By virtue of LD, observations of a set of alleles from one read may provide information about the probabilities of allelic states in another read that originated from the same DNA molecule (i.e., chromosome). In contrast, when comparing reads originating from distinct homologous chromosomes, allelic states observed in one read will be uninformative of allelic states observed in the other read. As two siblings are characterized by chromosomal regions with different counts of matched haplotypes, a change in the count along the chromosome indicates the position of a meiotic crossover, that is, an exchange of DNA segments between nonsister chromatids during prophase I of meiosis. Similarly, a pair of half-siblings allows us to contrast the crossovers in either the paternal or the maternal homologs. Extending this logic, we note that sequences from either a monosomic sibling-embryo, a sibling embryo with GW-isoUPD, or individual parental gametes would similarly allow us to isolate crossovers in embryo genomes that arose during oogenesis or spermatogenesis.
We consider two sibling embryos, one has a monosomy and the second is a healthy diploid, consisting of two copies of the genome: a maternal and a paternal copy. For a set of reads aligned to a defined genomic region, we compare the likelihoods of the observed alleles under two competing hypotheses:
The monosomic embryo and the healthy diploid have matched haplotypes, denoted as the matched-haplotype hypothesis.
The monosomic embryo and the healthy diploid have unmatched haplotypes, denoted as the unmatched-haplotype hypothesis.
A transition between regions with matched and unmatched haplotypes indicates the location of a meiotic crossover.
Our statistical models consider a situation in which one read is drawn from the monosomic chromosome and the second from the disomic chromosome of a sibling. The odds of two reads being drawn from identical versus distinct haplotypes differ under the matched- and unmatched-haplotype hypotheses. Specifically, for the matched-haplotype hypothesis, the odds are 1:1, and for the unmatched-haplotype hypothesis, the odds are 0:1. If a pair of reads is drawn from identical haplotypes, the probability of observing the two alleles is given by the joint frequency of these two alleles (i.e., the frequency of the haplotype that they define) in the reference panel. In contrast, if a pair of reads is drawn from distinct haplotypes, then the probability of observing the two alleles is simply the product of the frequencies of the two alleles in the reference panel:
| (2) |
| (3) |
where f(A) is the frequency of allele A, and f(A, B) is the joint frequency of alleles A and B in the population.
These statistical models can then be generalized to arbitrary admixture scenarios by a simple substitution. We assume that each distinct parental haplotype is drawn from an ancestral population with a probability equal to the ancestry proportion of the tested individual that is associated with that population. In accordance with the assumption, we replace each allele frequency distribution, f, by the combination . Here αi is the probability that the alleles originated from the ith population, fi is the allele frequency distribution for the ith population, and . For example, under this substitution, for admixture between two populations.
Likelihoods of the two hypotheses are compared by computing a log-likelihood ratio (LLR):
| (4) |
When a read overlaps with multiple SNPs, f(A) should be interpreted as the joint frequency of all SNP alleles that occur in read A (i.e., the frequency of haplotype A). Similarly, f(A, B) would denote the joint frequency of all SNP alleles occurring in reads A and B. The equations above were extended to consider up to six reads per window and homolog, as described in the later section “Generalization to an arbitrary number of reads.” Estimates of allele and haplotype frequencies from a reference panel do not depend on theoretical assumptions but rely on the idea that the sample is randomly drawn from a population with similar ancestry. One limitation, which we consider, is that reliable estimates of probabilities near zero or one require large reference panels, such as the 1000 Genomes Project (The 1000 Genomes Project Consortium 2015).
Determining optimal size of a genomic window
Because pairwise LD in human genomes decays on average to a quarter of its maximal value over physical distances of 100 kbp (The 1000 Genomes Project Consortium 2015), the length of the chromosomes is divided into genomic windows on a scale consistent with the length of typical human haplotypes (104–105 bp). Although one library consists of two homologs and the second consists of a single homolog, we would like to sample an even number of reads from each homolog. Thus, for each DNA sequence, we only consider the depth of coverage per homolog (i.e., we divide the coverage by the ploidy for the chromosome of each sample under consideration).
We require a minimal number of reads per genomic window and homolog, as determined by the sample with the lowest average depth of coverage. We then scan the chromosome in a sliding window, using a window size that adjusts according to the local depth of coverage of the two different sequenced samples. This adaptive sliding window approach possesses advantages over a fixed length window in that it (1) accounts for GC-poor and GC-rich regions of a genome, which tend to be sequenced at lower depths of coverage using Illumina platforms (Chen et al. 2013), and (2) accounts for varying densities of SNPs across the genome (The International SNP Map Working Group 2001).
The algorithm simultaneously scans aligned reads from the two samples in the forward direction of the reference genome and identifies informative reads (i.e., reads that reach the priority score threshold) from both samples within genomic windows. For each genomic window, the minimal number of required reads from the DNA sequence of the disomy is twice the minimal number from the monosomy. If (1) the distance between consecutive reads in one of the samples is >100 kbp or (2) a genomic window extends to 350 kbp and does not meet the minimal number of reads per homolog, the window is dismissed.
Quantifying uncertainty by bootstrapping
To quantify uncertainty in our likelihood estimates, we performed m out of n bootstrapping by iteratively resampling reads within each window (Chernick 2007). Resampling was performed without replacement to comply with the assumptions of the statistical models about the odds of drawing two reads from the same haplotype. Thus, in each iteration, only subsets of the available reads can be resampled. Specifically, within each genomic window, up to six reads per homolog with a priority score exceeding a defined threshold are randomly sampled with equal probabilities. The likelihood of the observed combination of SNP alleles under each competing hypothesis is then calculated, and the hypotheses are compared by computing a LLR. The sample mean and the unbiased sample variance (i.e., with Bessel's correction) of the LLR in each window are calculated by repeating this process using a bootstrapping approach,
| (5) |
| (6) |
where γs is the LLR for sth subsample of reads from the wth genomic window, and m is the number of subsamples. Because the number of terms in the statistical models grows exponentially, we subsample at most six reads per window and homolog. Moreover, accurate estimates of joint frequencies of many alleles require a very large reference panel. Given the rate of heterozygosity in human populations and the size of the 1000 Genomes Project data set, six reads per homolog is generally sufficient to capture one or more heterozygous SNPs that would inform our comparison of hypotheses.
Aggregating signal across consecutive windows
Even when sequences are generated according to one of the hypotheses, a fraction of genomic windows will emit alleles that do not support that hypothesis and may even provide modest support for an alternative hypothesis. This phenomenon is largely driven by the sparsity of the data, as well as the low rates of heterozygosity in human genomes, which together contribute to random noise. Another possible source of error is a local mismatch between the ancestry of the reference panel and the tested sequence. Moreover, technical errors such as spurious alignment and genotyping could contribute to poor results within certain genomic regions (e.g., near the centromeres). To overcome this noise, we binned LLRs across consecutive genomic windows, thereby reducing biases and increasing the classification accuracy at the cost of resolution. Specifically, we aggregated the mean LLRs of genomic windows within a larger bin,
| (7) |
where is the mean of the LLRs associated with the wth genomic window. In addition, using the Bienaymé formula, we calculated the variance of the aggregated LLRs,
| (8) |
where Var(γ(w)) is the variance of the LLRs associated with the wth window. For a sufficiently large bin, the confidence interval for the aggregated LLR is , where z = Φ−1(1 − α) is the z-score, Φ is the cumulative distribution function of the standard normal distribution, and C = 100(1 − 2α)% is the confidence level. The confidence level is chosen based on the desired sensitivity versus specificity. We normalized the aggregated LLRs by the number of genomic windows that compose each bin, . Thus, the variance of the mean LLR per window is . These normalized quantities can be compared across different regions of the genome, as long as the size of the genomic window is the same on average.
Simulating parental haplotypes and diploid offspring
Using a generative model, we simulated trios of a (1) parental chromosome, (2) diploid offspring with haplotypes matching the parental chromosome, and (3) an unrelated chromosome. This allows us to evaluate the classifier performance in each genomic window along the human genome. To this end, we constructed synthetic samples comprising combinations of phased haplotypes from the 1000 Genomes Project (The 1000 Genomes Project Consortium 2015). These phased haplotypes are extracted from variant call sets to effectively form a pool of haploid sequences.
We first consider nonadmixed offspring by drawing three effective haploid sequences from the same superpopulation. The first two haploid sequences are used to simulate the diploid offspring, whereas the first and third sequences are used to simulate the parental chromosome and the unrelated chromosome, respectively. We then simulate reads by selecting a random position along the chromosome from a uniform distribution to represent the midpoint of an aligned read with a given length. Based on the selected position, one out of the three haplotypes is drawn from a discrete distribution,
| (9) |
where, in general, the probability of haplotype h depends on the position of the read, x. When simulating a nonadmixed diploid offspring, the first haplotype is just as likely as the second haplotype (p2 = p1), and the third haplotype is absent (p3 = 0). Similarly, for the parental chromosome, p1 = 1 and p2 = p3 = 0, whereas for the unrelated chromosome, p3 = 1 and p1 = p2 = 0. Then, from the selected haplotype, h, a segment of length l that is centered at the selected chromosomal position, x, is added to simulated data, mimicking the process of short-read sequencing. This process of simulating sequencing data is repeated until the desired depth of coverage is attained.
To simulate an offspring descended from parents from distinct superpopulations (hereafter termed “recent admixed ancestry”), we draw two effective haploid sequences from different superpopulations of the 1000 Genomes Project. A third haploid sequence is then drawn from one of the two former pools to simulate the unrelated chromosome. Finally, we use the generative model with these three effective haploid sequences to simulate reads. A procedure for simulating diploid offspring under a scenario involving more distant admixture is discussed in the Supplemental Methods.
Evaluating model performance on simulated data
We developed a classification scheme to determine whether a bin supports one of two competing hypotheses. To this end, we performed m out of n bootstrapping by iteratively resampling reads within each window pairs and computed LLRs of competing statistical models, as described in the section “Quantifying uncertainty by bootstrapping.”
The confidence interval for the mean LLR is , and z is referred to as the z-score. Thus, we classify a bin as showing support for the matched-haplotype hypothesis when
| (10) |
and for the unmatched-haplotype hypothesis when
| (11) |
where the first (second) criterion is equivalent to requiring that the bounds of the confidence interval lie on the positive (negative) side of the number line. When a confidence interval crosses the origin of the number line, we classify the bin as ambiguous (for a diagram of these classes, see Supplemental Fig. S20).
For a given depth of coverage and read length, we simulate an equal number of sequences generated according to both hypotheses, as explained in the previous section. We define true positives (negatives) as simulations in which sequences generated under the “unmatched” (“matched”) haplotypes hypothesis are correctly classified. Based on these simulations, we generate balanced ROC curves for each bin (Ariad et al. 2021). The balanced true- and false-positive rates for a bin are defined as
| (12) |
| (13) |
where TPR, TNR, FPR, and FNR are the true-positive rate, true-negative rate, false-positive rate, and false-negative rate, respectively.
The “balanced ROC curve” is tailored for trinomial classification tasks. Here the three possible classes are “unmatched,” “matched,” and “ambiguous.” The ambiguous class contains all instances that do not fulfill the criteria in Equations 10 and 11 (i.e., instances in which the boundaries of the confidence interval span zero). This classification scheme allows us to optimize the classification of both “unmatched” and “matched” instances at the expense of leaving ambiguous instances. The advantage of this optimization is a reduction in the rate of spurious classification. To generate a balanced ROC curve for each genomic bin, we varied the z-score.
Generalization to an arbitrary number of reads
The model of the unmatched-haplotype hypothesis for nonadmixed samples and an arbitrary number of reads is based on the disomy model for nonadmixed samples that was derived for LD-PGTA (Ariad et al. 2021). More specifically, the “unmatched” statistical model for m + n reads is merely the joint frequency f(A1, A2, …, Am) multiplied by the disomy model of n-reads for nonadmixed samples. Here Ai are reads drawn from the monosomic reference sample, whereas Bi are reads drawn from the disomic test sample.
The model of the matched-haplotype hypothesis for nonadmixed samples and an arbitrary number of reads is based on the disomy model for recent admixture, which was previously introduced by Ariad et al. (2021). More specifically, modeling the matched-haplotype hypothesis for m + n reads can be accomplished by substituting effective joint frequency distributions in the disomy model of n-reads for recent admixture. The adjusted model involves two distributions, f(X) and g(X). The distribution f is derived from a reference panel of a population as before, whereas g is an effective distribution that is defined as g(X) ≡ f(A1, A2…, Am, X). The reads Ai with i = 1, 2, …, m are drawn only from the monosomic reference sample, whereas the rest of the reads are drawn from the disomic test sample. Also, each term in the linear model should take into account the presence of the reads A1, A2, …, Am, and thus, terms in the disomy model for recent admixture that involve only the distribution f should be multiplied by . Derivations and explicit statistical models for nonadmixed ancestry, recent admixture, and more distant admixture scenarios for m + 2, m + 3, and m + 4 reads can be found in the Supplemental Methods.
Identifying meiotic crossovers
To identify the locations of meiotic crossovers, we analyze the cumulative sums of LLRs from individual genomic windows as we move along the chromosome. Because we performed m out of n bootstrapping by iteratively resampling reads within each window and calculating LLRs, we define two quantities:
| (14) |
where we assume negligible LD between alleles in different genomic windows and, hence, according to the Bienaymé formula, . Local maxima of yn indicate potential transitions from “unmatched” to “matched” regions, whereas local minima of yn indicate potential transitions from “matched” to “unmatched” regions. Thus, a crossover occurred within the jth genomic window if there exists a region in which either or , and in addition,
| (15) |
| (16) |
where z is the threshold for calling a crossover, and δ is the minimal number of genomic windows in the region. In addition, we define a metric that describes the confidence in calling the jth crossover:
| (17) |
which fulfills κj ≥ zscore. When, based on the criteria above, two consecutive crossovers are identified as local maxima or minima of the accumulated LLR, yn, this implies that a crossover was skipped. Failure to detect a crossover occurs when the values of z and/or δ are too restrictive. Given two consecutive maxima in the ith and kth genomic windows, we identify the genomic window with a skipped minimum as
| (18) |
where this condition means that zscore of the “matched” and “unmatched” intervals are maximized simultaneously. In case of two consecutive minima, we replace the function with .
Assigning crossovers to reference versus test samples
Because we scan for crossovers by comparing sequences from two sibling embryos, assigning each crossover to a single embryo requires additional information. When sequencing data from three or more sibling embryos are available, we contrast the crossovers of sibling embryos with one common monosomic sibling (see Fig. 1). This, in turn, produces a repeated pattern in each sequence of crossovers that can be attributed to the common sibling (see Fig. 3). Once the repeated pattern is identified, we subtract it to recover the crossovers in the rest of the embryos.
More specifically, we consider a set of n + 1 sibling embryos, in which one embryo is used to contrast the crossovers in the rest of the sibling embryos. All crossovers are then combined to form a sorted list, and we scan the list for n sequential crossovers within a region of size l. For each cluster, we calculate the average position of the crossovers. The average position from each cluster is associated with the common sibling. Finally, the union of all the clusters is subtracted from each of the n sequences of crossovers, and remaining crossovers are traced back to the sibling embryos.
The sequencing quality may vary from one embryo to another, and some crossovers might not be identified. Hence, we adjust the algorithm to allow clusters with various sizes. After seeking all clusters of size n, we continue seeking clusters of the size n − 1. This process of seeking smaller clusters is repeated iteratively for cluster sizes greater than n/2. Another issue that may arise is that when the region size, l, is too large, two or more crossovers from the same embryo may overlap. In such cases, we only consider the crossover that is closest to the cluster mean.
Each crossover that is attributed to the common reference embryo is assigned two scores. The first score is the proportion of sibling embryos supporting the crossover: λi = ki/n, where ki and n are the size of cluster i and the number of contrasted embryos, respectively. The second score is the minimal confidence score in the ith cluster: , where κ was defined in the section titled “Identifying meiotic crossovers.”
Isolating sex-specific meiotic crossovers
Here we discuss the possibility of identifying sex-specific crossovers by matching haplotypes between natural occurring monosomies and genome-wide isodisomies (GW-isoUPD) in IVF embryos and disomic sibling embryos from the same IVF cycles. This in turn allows us to leverage the high volume of aneuploidies observed in IVF to obtain sex-specific distributions of crossovers. We also review how maternal crossovers in trisomies can be identified by scanning for transitions between tracts of two versus three unique homologs.
Paternal crossovers (i.e., crossovers originating from spermatogenesis) can be identified by focusing on IVF cycles that yielded at least one embryo with a monosomy of a given chromosome, as well as at least one embryo that is disomic for that chromosome. The vast majority of monosomies are of maternal meiotic origin, such that the remaining chromosome is of paternal origin. The opposite scenario, whereby a haploid ovum is fertilized by an nullisomic sperm cell, accounts for <10% of autosomal monosomies (Hassold and Hunt 2001; Rabinowitz et al. 2012; Kubicek et al. 2019). Moreover, when intracytoplasmic sperm injection (ICSI) is performed, sperm in vitro selection and capacitation may further reduce the rates of paternal-origin monosomies (Cayli et al. 2003; Jakab et al. 2005; Huszar et al. 2007; Sakkas et al. 2015). Conversely, maternal crossovers (i.e., crossovers originating from oogenesis) can be identified by focusing on IVF cycles that yielded at least one case of haploidy/genome-wide isodisomy (which are indistinguishable with sequencing-based PGT-A), as well as at least one sibling that is disomic for one or more chromosomes. Such cases of GW-isoUPD may originate from oocytes that commence cleavage and early embryonic development without fertilization (Sagi and Benvenisty 2017).
Aneuploidy (gain or loss of entire chromosomes) is the leading cause of IVF failure. We found that 351 (13.7%), 529 (20.7%), 332 (13.0%), and 470 (18.4%) of IVF cycles in the CReATe data set had at least one embryo with monosomy of Chromosome 15, 16, 21, or 22, respectively, as well as 7.3 disomic siblings on average (for the rest of the autosomes, see Supplemental Table S4). Thus, LD-CHASE can use these natural occurring monosomies to identify paternal crossovers along the chromosomes of sibling embryos. Similarly, we found that 201 (9.1%) of the IVF cycles in the CReATe data set had at least one haploid/GW-isoUPD embryo and an additional 7.8 euploid siblings on average (see Supplemental Table S5), offering good resolution for mapping maternal crossovers genome-wide.
Coverage-based discovery of chromosome abnormalities
We used WisecondorX to deduce the chromosomal copy numbers of each of the 20,160 embryos in the CReATe data set (Straver et al. 2014; Raman et al. 2019). To this end, we first created four sets of reference samples for read counts: (1) 9202 sequences were obtained from biopsies of four to six cells and consist of single reads of 75 bp, (2) 9818 sequences were obtained from biopsies of four to six cells and consist of paired-end reads of 75 bp, (3) 578 sequences were obtained from biopsies of four to five cells and consist of single reads of 75 bp, and (4) 562 sequences were obtained from biopsies of four to five cells and consist of paired-end reads of 75 bp. We used all the sequences in a category (e.g., sequences associated with four to five cells and single reads) as reference samples. This approach is effective as long as aneuploid chromosomes are rare and as long as the rate of chromosome loss and chromosome gain are sufficiently similar to balance out one another in large samples. The first assumption is justified based on previous PGT-A studies, which showed that the rate of aneuploidy per chromosome is <10% (including monosomy, trisomy, and mosaics) (Ariad et al. 2021). The second assumption is justified by noting that for each chromosome, the rate of trisomy should be similar to the rate of monosomy, as both are mainly caused by nondisjunction (Hassold and Hunt 2001). To assess the robustness of this approach, we compared the results obtained from WisecondorX with those generated by NxClinical, a diagnostic tool used by the CReATe Fertility Centre, for select chromosomes that showed copy number variations, as shown in Supplemental Figure S21. In addition, we applied WisecondorX to a separate published PGT-A data set from the Zouves Fertility Center consisting 8881 samples. The data set was previously analyzed using BlueFuse Multi, and we found that the inferred copy numbers were in strong agreement with the WisecondorX. The number of sequences that were analyzed successfully via WisecondorX was 20,114. The number of relevant sequences was further reduced to 18,967 after filtering sequences without a corresponding record in the metadata table or when the genetic ancestry could not be inferred.
Haplotype-aware discovery of ploidy abnormalities
Coverage-based approaches for inferring chromosome copy numbers, such as WisecondorX, are based on relative differences in the depth of coverage across chromosomes within samples. As such approaches assume that the baseline coverage corresponds to disomy, scenarios when many chromosomes are simultaneously affected, such as haploidy and triploidy, violate this assumption and may elude detection. To overcome this limitation, we applied our haplotype-aware method, LD-PGTA, to scan for the number of unique haplotypes along the genome (Ariad et al. 2021) and calculate chromosome-wide LLR comparing hypotheses of monosomy, disomy, and various forms of trisomy. When the LLR for at least 15 chromosomes supported a common aneuploidy hypothesis (monosomy or trisomy), the sample was classified as haploid/GW-isoUPD or triploid, respectively.
Assembling an ancestry-matched reference panel
Given the aforementioned importance of the ancestry of the reference panel, we used LASER v2.04 (Wang et al. 2014, 2015) to perform automated ancestry inference for each embryo sample from the low-coverage sequencing data. LASER applies principal component analysis (PCA) to genotypes of reference individuals with known ancestry. It then projects target samples onto the reference PCA space, using a Procrustes analysis to overcome the sparse nature of the data. We excluded markers with less than 0.01× depth of coverage and restricted analysis to the top 32 principal components, performing five replicate runs per sample.
Ancestry of each target sample was deduced using a k-nearest neighbors approach. Specifically, we identified the nearest 150 nearest neighbor reference samples to each target sample based on rectilinear distance. We then calculated the superpopulation ancestry composition of the 150 reference samples. When >95% of such samples derived from the same 1000 Genomes Project superpopulation, we used downstream statistical models designed for nonadmixed samples. In cases in which two superpopulations were represented in roughly equal proportions (maximal difference of 10%), we used downstream statistical models designed for recent admixture. For all other samples, we used downstream statistical models designed for more distant admixture scenarios. For this latter group, superpopulations represented at levels of ≥5% among the nearest neighbors to each target sample were used in the construction of reference panels.
Testing robustness versus LD-PGTA
One aspect of our study involved comparing the landscapes of meiotic crossovers between disomic and trisomic chromosomes, as inferred by LD-CHASE and LD-PGTA, respectively. This comparison poses a statistical challenge, as the two methods possess distinct sensitivities and specificities, which also vary across the genome and as a function of coverage of the respective samples. To validate our findings, we therefore sought to compare these landscapes under a single statistical framework by combining disomic samples with separate monosomic samples to produce artificial trisomies. Such artificial trisomies can be analyzed uniformly with LD-PGTA and compared with true trisomies analyzed with the same method, as well as with the more direct analysis of disomies with LD-CHASE.
In principle, such artificial trisomies can be produced by combining monosomies and disomies from the same IVF patients in ratios of 2:1, such that they can be analyzed with LD-PGTA. In practice, naive merging based on the genome-wide average depth of coverage yields poor results owing to the low complexity of DNA libraries from PGT-A, which results in sample-specific nonuniformity in coverage across the genome. To overcome this challenge, we merely replaced the statistical models of LD-CHASE with those of LD-PGTA, thereby controlling the ratio of reads from each sample on a local scale (i.e., genomic window) as opposed to a genome-wide scale. Thus, the construction of the genomic windows and the approach to sample reads from a genomic window are identical to LD-CHASE. However, the statistical models of LD-PGTA have no prior knowledge about the DNA sample from which a given read is drawn. Supplemental Figures S16 through S19 display the concordance in crossover distributions between disomic chromosomes as analyzed by both LD-CHASE and LD-PGTA.
The coverage of genomic windows
To further address the low complexity of DNA libraries prepared from few input cells, we introduced an additional metric that simultaneously captures both the depth of coverage and the complexity of the library. After we tile a chromosome with genomic windows, as described in the section “Determining optimal size of a genomic window,” we calculate the coverage of genomic windows for a given sample as
| (19) |
where lw is the length of the wth genomic window, L is the length of the chromosome, and thus 0 < C < 1. We then restricted our analysis to samples with C ≥ 0.5 (i.e., genomic windows covering at least half of the chromosome). For the subset of patients with multiple monosomic embryo samples (affecting the same chromosome) from which to choose, we selected the monosomy that yielded the highest value of C in order to maximize resolution for identifying meiotic crossovers.
Distinguishing trisomies originating from errors in MI and MII
Samples with tracts of BPH in regions surrounding the centromere were classified as putative MI errors, whereas tracts of BPH elsewhere on the chromosome were classified as putative MII errors. Ambiguous samples were also noted. Specifically, regions bounded by crossovers and emitting a z-score above 1.96 and below −1.96 were regarded as BPH and SPH regions, respectively, and otherwise were regarded as ambiguous. We defined a pericentromeric region as a region 20% of the chromosome length and centered on the centromere. However, for the acrocentric chromosomes, the pericentromeric region only includes the q-arm and is thus effectively reduced to 10% of the chromosome length. When at least 10% of the chromosome showed tracts of BPH, the trisomy was classified as a meiotic error. If it was not classified as a meiotic error and at least 50% of the chromosome showed tracts of SPH, the trisomy was classified as a mitotic error. Otherwise, it was classified as ambiguous. Cases that were classified as meiotic errors were further classified as follows: When at least 50% of the pericentromeric region reflected BPH, the trisomy was classified as a MI error. Moreover, if it was not classified as MI and at least 50% of the pericentromeric region reflected SPH, then the trisomy was classified as an MII error; otherwise, the case was classified as ambiguous. In this analysis, only trisomy cases with genomic windows that covered at least 50% of the chromosome length were taken into account.
To compare the frequency of MI versus MII error across chromosomes, we fit a binomial generalized linear model implemented with the “lme4” package (Bates et al. 2014), in which the response variable was defined as the counts of MI and MII errors per patient, the patient identifier was included as a random effect predictor variable (to account for nonindependence among sibling embryos), and the chromosome was included as a categorical predictor variable. We compared this full model to a reduced model without the chromosome predictor variable using analysis of deviance.
Comparing distributions of chromosomal crossover via empirical cumulative distribution functions and KS tests
Each chromosome in a given sample typically shows between one and three crossover events. Although the overall pool of crossovers shows a continuous spatial distribution along the genome, the underlying crossovers are largely independent events and thus can be treated as such in downstream statistical tests. To formulate our comparison of landscapes, we summarized each landscape as an empirical cumulative distribution function (eCDF), which traces the cumulative genetic map length as one moves from the beginning to the end of a given chromosome (i.e., a line plot comparing the physical map to the genetic map). One advantage of this approach is that it circumvents the need to bin the data and thus is bin size independent. We note that such summaries are common in the recombination literature, for example, Figure 4B of the work by Peñalba and Wolf (2020). We then applied the two-sample KS test to test whether two underlying one-dimensional probability distributions differ, computing the p-value by permutation. Although the KS test is nonparametric and makes no assumptions about the form of the distribution from which the data were drawn, permutations further ensure that the p-value calculation is based solely on the observed data without any reliance on asymptotic approximations. To calculate the p-value, we constructed a null hypothesis that posits the two empirical samples come from the same continuous distribution. This was achieved by evaluating all possible combinations of assignments of the combined data into two groups, each of the sizes of the two original samples, and computing the KS statistic for each combination. The p-value is then computed as the proportion of permutations that result in a KS statistic as extreme as, or more extreme than, the observed statistic.
Ethics approval and consent to participate
The Homewood Institutional Review Board of Johns Hopkins University determined that this work does not qualify as federally regulated human subjects research (HIRB00011705).
Data access
Software for implementing our method is available at GitHub (https://github.com/mccoy-lab/LD-CHASE). Tables with chromosome abnormalities and crossovers detected for each sample in the study are available in the same repository. Source code and data tables are also uploaded as Supplemental Materials.
Supplementary Material
Acknowledgments
We thank the staff of Advanced Research Computing at Johns Hopkins University. The research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R35GM133747. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Author contributions: S.M., M.M., S.C., R.A., and C.L. performed data collection and data curation; D.A. and R.C.M. contributed to experimental design and data interpretation; D.A. performed data analysis; and D.A. and R.C.M. wrote the paper, with input from S.M. All authors reviewed and approved the manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.278168.123.
Competing interest statement
D.A. and R.C.M. are coinventors of the LD-PGTA method. Johns Hopkins University has filed a patent application related to the work described here. The title of the patent is “Methods and related aspects for analyzing chromosome number status”. The U.S. Patent Application was filed on November 5, 2021, US18/035,811.
References
- The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526: 68–74. 10.1038/nature15393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adrion JR, Galloway JG, Kern AD. 2020. Predicting the landscape of recombination using deep learning. Mol Biol Evol 37: 1790–1808. 10.1093/molbev/msaa038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ariad D, Yan SM, Victor AR, Barnes FL, Zouves CG, Viotti M, McCoy RC. 2021. Haplotype-aware inference of human chromosome abnormalities. Proc Nat Acad Sci USA 118: e2109307118. 10.1073/pnas.2109307118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auton A, McVean G. 2007. Recombination rate estimation in the presence of hotspots. Genome Res 17: 1219–1227. 10.1101/gr.6386707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bansal V. 2019. Integrating read-based and population-based phasing for dense and accurate haplotyping of individual genomes. Bioinformatics 35: i242–i248. 10.1093/bioinformatics/btz329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D, Mächler M, Bolker B, Walker S. 2014. Fitting linear mixed-effects models using lme4. J Stat Softw 67: 1–48. 10.18637/jss.v067.i01 [DOI] [Google Scholar]
- Bugge M, Collins A, Petersen MB, Fisher J, Brandt C, Michael Hertz J, Tranebjærg L, de Lozier-Blanchet C, Nicolaides P, Brøndum-Nielsen K, et al. 1998. Non-disjunction of chromosome 18. Hum Mol Genet 7: 661–669. 10.1093/hmg/7.4.661 [DOI] [PubMed] [Google Scholar]
- Bugge M, Collins A, Hertz JM, Eiberg H, Lundsteen C, Brandt CA, Bak M, Hansen C, Delozier CD, Lespinasse J, et al. 2007. Non-disjunction of chromosome 13. Hum Mol Genet 16: 2004–2010. 10.1093/hmg/ddm148 [DOI] [PubMed] [Google Scholar]
- Capalbo A, Bono S, Spizzichino L, Biricik A, Baldi M, Colamaria S, Ubaldi FM, Rienzi L, Fiorentino F. 2013. Sequential comprehensive chromosome analysis on polar bodies, blastomeres and trophoblast: insights into female meiotic errors and chromosomal segregation in the preimplantation window of embryo development. Hum Reprod 28: 509–518. 10.1093/humrep/des394 [DOI] [PubMed] [Google Scholar]
- Cayli S, Jakab A, Ovari L, Delpiano E, Celik-Ozenci C, Sakkas D, Ward D, Huszar G. 2003. Biochemical markers of sperm function: male fertility and sperm selection for ICSI. Reprod Biomed Online 7: 462–468. 10.1016/S1472-6483(10)61891-3 [DOI] [PubMed] [Google Scholar]
- Chen YC, Liu T, Yu CH, Chiang T, Hwang C. 2013. Effects of GC bias in next-generation-sequencing data on de novo genome assembly. PLoS One 8: e62856. 10.1371/journal.pone.0062856 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernick MR. 2007. Bootstrap methods: a guide for practitioners and researchers, 2nd ed. John Wiley & Sons, Hoboken, NJ. [Google Scholar]
- Chernus JM, Sherman SL, Feingold E. 2021. Analyses stratified by maternal age and recombination further characterize genes associated with maternal nondisjunction of chromosome 21. Prenat Diagn 41: 591–609. 10.1002/pd.5919 [DOI] [PubMed] [Google Scholar]
- De Witte L, Raman L, Baetens M, De Koker A, Callewaert N, Symoens S, Tilleman K, Vanden Meerschaut F, Dheedene A, Menten B. 2022. GENType: all-in-one preimplantation genetic testing by pedigree haplotyping and copy number profiling suitable for third-party reproduction. Hum Reprod 37: 1678–1691. 10.1093/humrep/deac088 [DOI] [PubMed] [Google Scholar]
- Gray S, Cohen PE. 2016. Control of meiotic crossovers: from double-strand break formation to designation. Annu Rev Genet 50: 175–210. 10.1146/annurev-genet-120215-035111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall HE, Surti U, Hoffner L, Shirley S, Feingold E, Hassold T. 2007. The origin of trisomy 22: evidence for acrocentric chromosome-specific patterns of nondisjunction. Am J Med Genet A 143A: 2249–2255. 10.1002/ajmg.a.31918 [DOI] [PubMed] [Google Scholar]
- Halldorsson BV, Palsson G, Stefansson OA, Jonsson H, Hardarson MT, Eggertsson HP, Gunnarsson B, Oddsson A, Halldorsson GH, Zink F, et al. 2019. Characterizing mutagenic effects of recombination through a sequence-level genetic map. Science 363: eaau1043. 10.1126/science.aau1043 [DOI] [PubMed] [Google Scholar]
- Handyside AH, Harton GL, Mariani B, Thornhill AR, Affara N, Shaw MA, Griffin DK. 2010. Karyomapping: a universal method for genome wide analysis of genetic disease based on mapping crossovers between parental haplotypes. J Med Genet 47: 651–658. 10.1136/jmg.2009.069971 [DOI] [PubMed] [Google Scholar]
- Hassold T, Hunt P. 2001. To err (meiotically) is human: the genesis of human aneuploidy. Nat Rev Genet 2: 280–291. 10.1038/35066065 [DOI] [PubMed] [Google Scholar]
- Hassold TJ, Hunt PA. 2021. Missed connections: recombination and human aneuploidy. Prenat Diagn 41: 584–590. 10.1002/pd.5910 [DOI] [PubMed] [Google Scholar]
- Hassold T, Merrill M, Adkins K, Freeman S, Sherman S. 1995. Recombination and maternal age-dependent nondisjunction: molecular studies of trisomy 16. Am J Hum Genet 57: 867. [PMC free article] [PubMed] [Google Scholar]
- Hassold T, Maylor-Hagen H, Wood A, Gruhn J, Hoffmann E, Broman KW, Hunt P. 2021. Failure to recombine is a common feature of human oogenesis. Am J Hum Genet 108: 16–24. 10.1016/j.ajhg.2020.11.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herbert M, Kalleas D, Cooney D, Lamb M, Lister L. 2015. Meiosis and maternal aging: insights from aneuploid oocytes and trisomy births. Cold Spring Harb Perspect 7: a017970. 10.1101/cshperspect.a017970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huszar G, Jakab A, Sakkas D, Ozenci CC, Cayli S, Delpiano E, Ozkavukcu S. 2007. Fertility testing and ICSI sperm selection by hyaluronic acid binding: clinical and genetic aspects. Reprod Biomed Online 14: 650–663. 10.1016/S1472-6483(10)61060-7 [DOI] [PubMed] [Google Scholar]
- The International SNP Map Working Group. 2001. A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409: 928–933. 10.1038/35057149 [DOI] [PubMed] [Google Scholar]
- Jakab A, Sakkas D, Delpiano E, Cayli S, Kovanci E, Ward D, Ravelli A, Huszar G. 2005. Intracytoplasmic sperm injection: a novel selection method for sperm with normal frequency of chromosomal aneuploidies. Fertil Steril 84: 1665–1673. 10.1016/j.fertnstert.2005.05.068 [DOI] [PubMed] [Google Scholar]
- Kong A, Barnard J, Gudbjartsson DF, Thorleifsson G, Jonsdottir G, Sigurdardottir S, Richardsson B, Jonsdottir J, Thorgeirsson T, Frigge ML, et al. 2004. Recombination rate and reproductive success in humans. Nat Genet 36: 1203–1206. 10.1038/ng1445 [DOI] [PubMed] [Google Scholar]
- Kubicek D, Hornak M, Horak J, Navratil R, Tauwinklova G, Rubes J, Vesela K. 2019. Incidence and origin of meiotic whole and segmental chromosomal aneuploidies detected by karyomapping. Reprod Biomed Online 38: 330–339. 10.1016/j.rbmo.2018.11.023 [DOI] [PubMed] [Google Scholar]
- Lamb NE, Freeman SB, Savage-Austin A, Pettay D, Taft L, Hersey J, Gu Y, Shen J, Saker D, May KM, et al. 1996. Susceptible chiasmate configurations of chromosome 21 predispose to non–disjunction in both maternal meiosis I and meiosis II. Nat Genet 14: 400–405. 10.1038/ng1296-400 [DOI] [PubMed] [Google Scholar]
- Lamb N, Sherman S, Hassold T. 2005. Effect of meiotic recombination on the production of aneuploid gametes in humans. Cytogenet Genome Res 111: 250–255. 10.1159/000086896 [DOI] [PubMed] [Google Scholar]
- Lister LM, Kouznetsova A, Hyslop LA, Kalleas D, Pace SL, Barel JC, Nathan A, Floros V, Adelfalk C, Watanabe Y, et al. 2010. Age-related meiotic segregation errors in mammalian oocytes are preceded by depletion of cohesin and Sgo2. Curr Biol 20: 1511–1521. 10.1016/j.cub.2010.08.023 [DOI] [PubMed] [Google Scholar]
- Liu S, Huang S, Chen F, Zhao L, Yuan Y, Francis SS, Fang L, Li Z, Lin L, Liu R, et al. 2018. Genomic analyses from non-invasive prenatal testing reveal genetic associations, patterns of viral infections, and Chinese population history. Cell 175: 347–359.e14. 10.1016/j.cell.2018.08.016 [DOI] [PubMed] [Google Scholar]
- Lynn A, Ashley T, Hassold T. 2004. Variation in human meiotic recombination. Annu Rev Genomics Hum Genet 5: 317–349. 10.1146/annurev.genom.4.070802.110217 [DOI] [PubMed] [Google Scholar]
- Ma Y, Wang J, Li R, Ding C, Xu Y, Zhou C, Xu Y. 2023. Mapping of meiotic recombination in human preimplantation blastocysts. G3 Genes Genom Genet 13: jkad031. 10.1093/g3journal/jkad031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Howie B. 2010. Genotype imputation for genome-wide association studies. Nat Rev Genet 11: 499–511. 10.1038/nrg2796 [DOI] [PubMed] [Google Scholar]
- Masset H, Zamani Esteki M, Dimitriadou E, Dreesen J, Debrock S, Derhaag J, Derks K, Destouni A, Drüsedau M, Meekels J, et al. 2019. Multi-centre evaluation of a comprehensive preimplantation genetic test through haplotyping-by-sequencing. Hum Reprod 34: 1608–1619. 10.1093/humrep/dez106 [DOI] [PubMed] [Google Scholar]
- McCoy RC, Demko ZP, Ryan A, Banjevic M, Hill M, Sigurjonsson S, Rabinowitz M, Petrov DA. 2015. Evidence of selection against complex mitotic-origin aneuploidy during preimplantation development. PLoS Genet 11: e1005601. 10.1371/journal.pgen.1005601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks CD, Mukhopadhyay N, Tinker SW, Allen EG, Bean LJ, Begum F, Chowdhury R, Cheung V, Doheny K, Adams M, et al. 2014. Evidence for dysregulation of genome-wide recombination in oocytes with nondisjoined chromosomes 21. Hum Mol Genet 23: 408–417. 10.1093/hmg/ddt433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliver TR, Feingold E, Yu K, Cheung V, Tinker S, Yadav-Shah M, Masse N, Sherman SL. 2008. New insights into human nondisjunction of chromosome 21 in oocytes. PLoS Genet 4: e1000033. 10.1371/journal.pgen.1000033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottolini CS, Newnham LJ, Capalbo A, Natesan SA, Joshi HA, Cimadomo D, Griffin DK, Sage K, Summers MC, Thornhill AR, et al. 2015. Genome-wide maps of recombination and chromosome segregation in human oocytes and embryos show selection for maternal recombination rates. Nat Genet 47: 727–735. 10.1038/ng.3306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peñalba JV, Wolf JB. 2020. From molecules to populations: appreciating and estimating recombination rate variation. Nat Rev Genet 21: 476–492. 10.1038/s41576-020-0240-1 [DOI] [PubMed] [Google Scholar]
- Rabinowitz M, Ryan A, Gemelos G, Hill M, Baner J, Cinnioglu C, Banjevic M, Potter D, Petrov DA, Demko Z. 2012. Origins and rates of aneuploidy in human blastomeres. Fertil Steril 97: 395–401. 10.1016/j.fertnstert.2011.11.034 [DOI] [PubMed] [Google Scholar]
- Raman L, Dheedene A, De Smet M, Van Dorpe J, Menten B. 2019. WisecondorX: improved copy number detection for routine shallow whole-genome sequencing. Nucleic Acids Res 47: 1605–1614. 10.1093/nar/gky1263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson W, Kuchinka B, Bernasconi F, Petersen M, Schulze A, Brøndum-Nielsen K, Christian S, Ledbetter D, Schinzel A, Horsthemke B, et al. 1998. Maternal meiosis I non-disjunction of chromosome 15: dependence of the maternal age effect on level of recombination. Hum Mol Genet 7: 1011–1019. 10.1093/hmg/7.6.1011 [DOI] [PubMed] [Google Scholar]
- Sagi I, Benvenisty N. 2017. Haploidy in humans: an evolutionary and developmental perspective. Dev Cell 41: 581–589. 10.1016/j.devcel.2017.04.019 [DOI] [PubMed] [Google Scholar]
- Saiki RK, Scharf S, Faloona F, Mullis KB, Horn GT, Erlich HA, Arnheim N. 1985. Enzymatic amplification of β-globin genomic sequences and restriction site analysis for diagnosis of sickle cell anemia. Science 230: 1350–1354. 10.1126/science.2999980 [DOI] [PubMed] [Google Scholar]
- Sakkas D, Ramalingam M, Garrido N, Barratt CL. 2015. Sperm selection in natural conception: what can we learn from mother nature to improve assisted reproduction outcomes? Hum Reprod Update 21: 711–726. 10.1093/humupd/dmv042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Southern EM. 1975. Detection of specific sequences among DNA fragments separated by gel electrophoresis. J Mol Biol 98: 503–517. 10.1016/S0022-2836(75)80083-0 [DOI] [PubMed] [Google Scholar]
- Spence JP, Song YS. 2019. Inference and analysis of population-specific fine-scale recombination maps across 26 diverse human populations. Sci Adv 5: eaaw9206. 10.1126/sciadv.aaw9206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straver R, Sistermans EA, Holstege H, Visser A, Oudejans CB, Reinders MJ. 2014. WISECONDOR: detection of fetal aberrations from shallow sequencing maternal plasma based on a within-sample comparison scheme. Nucleic Acids Res 42: e31. 10.1093/nar/gkt992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H, Rowan BA, Flood PJ, Brandt R, Fuss J, Hancock AM, Michelmore RW, Huettel B, Schneeberger K. 2019. Linked-read sequencing of gametes allows efficient genome-wide analysis of meiotic recombination. Nat Commun 10: 4310. 10.1038/s41467-019-12209-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tšuiko O, Vanneste M, Melotte C, Ding J, Debrock S, Masset H, Peters M, Salumets A, De Leener A, Pirard C, et al. 2021. Haplotyping-based preimplantation genetic testing reveals parent-of-origin specific mechanisms of aneuploidy formation. NPJ Genom Med 6: 81. 10.1038/s41525-020-00165-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vermeesch JR, Voet T, Devriendt K. 2016. Prenatal and pre-implantation genetic diagnosis. Nat Rev Genet 17: 643–656. 10.1038/nrg.2016.97 [DOI] [PubMed] [Google Scholar]
- Wang C, Zhan X, Bragg-Gresham J, Kang HM, Stambolian D, Chew EY, Branham KE, Heckenlively J, Fulton R, Wilson RK, et al. 2014. Ancestry estimation and control of population stratification for sequence-based association studies. Nat Genet 46: 409–415. 10.1038/ng.2924 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Zhan X, Liang L, Abecasis GR, Lin X. 2015. Improved ancestry estimation for both genotyping and sequencing data using projection procrustes analysis and genotype imputation. Am J Hum Genet 96: 926–937. 10.1016/j.ajhg.2015.04.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Tsuo K, Kanai M, Neale BM, Martin AR. 2022. Challenges and opportunities for developing more generalizable polygenic risk scores. Ann Rev Biomed Data Sci 5: 293–320. 10.1146/annurev-biodatasci-111721-074830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster A, Schuh M. 2017. Mechanisms of aneuploidy in human eggs. Trends Cell Biol 27: 55–68. 10.1016/j.tcb.2016.09.002 [DOI] [PubMed] [Google Scholar]
- Xu J, Zhang M, Niu W, Yao G, Sun B, Bao X, Wang L, Du L, Sun Y. 2015. Genome-wide uniparental disomy screen in human discarded morphologically abnormal embryos. Sci Rep 5: 12302. 10.1038/srep12302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamani Esteki M, Dimitriadou E, Mateiu L, Melotte C, Van der Aa N, Kumar P, Das R, Theunis K, Cheng J, Legius E, et al. 2015. Concurrent whole-genome haplotyping and copy-number profiling of single cells. Am J Hum Genet 96: 894–912. 10.1016/j.ajhg.2015.04.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaragoza MV, Jacobs PA, James RS, Rogan P, Sherman S, Hassold T. 1994. Nondisjunction of human acrocentric chromosomes: studies of 432 trisomic fetuses and liveborns. Hum Genet 94: 411–417. 10.1007/BF00201603 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.