Data integration and inference of gene regulation using single-cell temporal multimodal data with scTIE

Abstract

Single-cell technologies offer unprecedented opportunities to dissect gene regulatory mechanisms in context-specific ways. Although there are computational methods for extracting gene regulatory relationships from scRNA-seq and scATAC-seq data, the data integration problem, essential for accurate cell type identification, has been mostly treated as a standalone challenge. Here we present scTIE, a unified method that integrates temporal multimodal data and infers regulatory relationships predictive of cellular state changes. scTIE uses an autoencoder to embed cells from all time points into a common space by using iterative optimal transport, followed by extracting interpretable information to predict cell trajectories. Using a variety of synthetic and real temporal multimodal data sets, we show scTIE achieves effective data integration while preserving more biological signals than existing methods, particularly in the presence of batch effects and noise. Furthermore, on the exemplar multiome data set we generated from differentiating mouse embryonic stem cells over time, we show scTIE captures regulatory elements highly predictive of cell transition probabilities, providing new potentials to understand the regulatory landscape driving developmental processes.

In eukaryotic cells, gene expressions are intricately regulated through complex interactions of transcription factors (TFs), various regulatory elements, and target genes. Deciphering the functions of gene regulatory networks (GRNs) in shaping cell identity and cell fate is one of the central quests in understanding the mapping from genomic blueprints to phenotypes. Over the past decades, much effort has been devoted to developing statistical and computational methods for inferring GRNs from tissue-level bulk data containing genome-wide profiling of gene expression, TF binding, and 3D chromatin structure. More recently, the advent of single-cell sequencing technologies has propelled the study of GRNs into a new era, in which context-specific regulation mechanisms can be investigated. Unlike global GRNs, which inherently aggregate gene interactions over all the biological conditions present in a given data set, context-specific GRNs are tailored to a particular biological setting. These specialized networks detail the regulatory interactions that occur in unique circumstances, such as within specific cell types, lineages, or tissues or under certain environmental conditions. Alongside new opportunities, the sparse and noisy nature of these single-cell data also brings new challenges to the statistical and computational analyses.

A growing number of methods have been developed to extract GRNs from data generated by assays of single-cell RNA sequencing (scRNA-seq) and single-cell transposase-accessible chromatin sequencing (scATAC-seq). Most of these methods infer the relationships between TFs and target genes by estimating their interactions with cis-regulatory elements (CREs) as an intermediate, using information including TF motif enrichment, marginal or conditional correlations between genes and CRE accessibility, and physical proximity between different elements (Duren et al. 2022; Jiang et al. 2022; Kartha et al. 2022; Tran et al. 2022; Zhang et al. 2022b). These methods typically work with multimodal data that provide joint profiling of scRNA-seq and scATAC-seq from the same cells, or unpaired data from a matched population of cells, possibly measured over a time course. However, they do not directly address the data integration problem accompanying such data, in which noise, sparsity, and batch effects can obscure identification of cell types and affect the downstream inference of context-specific GRNs. Furthermore, to compare how GRNs dynamically evolve in developmental data, features (e.g., genes, CREs) that are different between time points (or pseudotime points) are identified using differential expression (DE)/accessibility (DA) analyses. Although this captures marginal correlations, the features found are not necessarily predictive of the developmental changes.

On a separate front, an increasing number of computational methods have been proposed to perform data integration for single-cell multiomic data from unpaired measurements (Gong et al. 2021; Cao and Gao 2022; Lin et al. 2022; Zhang et al. 2022a). As more technologies capable of multimodal profiling start to emerge (Chen et al. 2019; Ma et al. 2020; Plongthongkum et al. 2021), integration methods designed for paired data (Argelaguet et al. 2020; Jin et al. 2020; Hao et al. 2021; Ashuach et al. 2023) have also attracted significant research interests. However, most of these integration methods do not directly address the immediate downstream problem of inferring GRNs; one exception is GLUE (Cao and Gao 2022), although the GRNs inferred there remain global and not context specific. One difficulty lies in the fact that most of these methods rely on finding a low-dimensional representation of the data sets across modalities and data batches, and how to extract interpretable biological signals from blackbox methods such as neural networks is a challenging problem. Neural networks offer a conceptual advantage over methods built on linear models, including cross-correlation analysis and nonnegative matrix factorization, as their superior representation power can capture complex nonlinear interactions in the feature space. However, this comes with the drawback that the relationships between the measured features (e.g., genes) and cellular phenotypes in trained models become more difficult to interpret. Although alternative architectures have been proposed involving linearizing part of the neural network (Svensson et al. 2020), a tradeoff remains between the network's representation power and interpretability.

Here, we propose scTIE, an autoencoder-based method for integrating multimodal profiling of scRNA-seq and scATAC-seq data over a time course and inferring context-specific GRNs. Unlike existing GRN inference methods that study cell type–specific or condition-specific GRNs, scTIE focuses on cellular state transitions and aims to infer GRNs that predict cellular changes along a developmental process. To the best of our knowledge, scTIE provides the first unified framework for the integration of temporal data and the inference of context-specific GRNs that predict cell fates. We achieve this through three main innovations in the architecture design of the autoencoder and the interpretation of a blackbox neural network method. First, scTIE uses iterative optimal transport (OT) fitting to align cells in similar states between different time points and estimate their transition probabilities. scTIE incorporates OT into the loss function of the autoencoder so that the alignment of cells is updated iteratively throughout training to achieve a desirable balance between time point alignment and cell type separation. This is in contrast to many widely used applications of OT in the trajectory inference of scRNA-seq data (Schiebinger et al. 2019; Forrow and Schiebinger 2021), in which most of the methods solve OT only once on suitably constructed cell distance matrices. Second, scTIE removes the need for selecting highly variable genes (HVGs) as input through a pair of coupled batchnorm layers to account for large variations in gene expression levels, making it more robust and generalizable. Third, scTIE provides the means to extract interpretable features from the common embedding space by linking the developmental trajectories of cell representations to their measured features (genes and peaks). We formulate a trajectory prediction problem using the estimated transition probabilities from OT and use gradient-based saliency mapping (Ciortan and Defrance 2021; Yang et al. 2021) to identify genes and peaks that are potentially driving the cellular state changes. Compared with most GRN inference methods, which focus on developing new ways to construct network relationships among features selected through DE/DA analysis, the main innovation of scTIE lies in selecting these informative features based on their ability to predict cellular changes.

To show the performance of scTIE on developmental data, we have chosen to focus on multimodal time course data, as this emerging form of data provides better opportunities to understand the key transcriptional regulatory activities driving a developmental process. To assess scTIE's integration performance against other existing methods, we constructed a variety of synthetic data sets using a mouse early organogenesis multiome data set. Furthermore, we generated an exemplar data set comprising paired scRNA-seq and scATAC-seq measurements from approximately 11,000 differentiating mouse embryonic stem cells (mESCs) over a time course. Using these data sets, our primary aim was to assess scTIE's ability to integrate multimodal developmental data for better cell type identification and to uncover key regulatory elements predictive of cell fate in a unified framework.

Results

Overview of scTIE

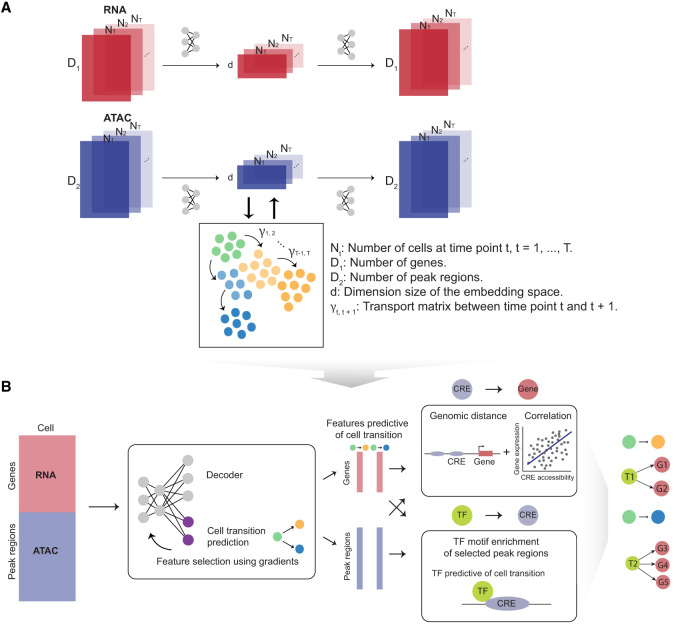
scTIE consists of two main steps. In the first step, scTIE uses modality-specific encoders and decoders to project high-dimensional input data from all time points into a lower-dimensional common embedding space and reconstruct them in the original space (Fig. 1A). Each encoder–decoder pair is designed to preserve the original information in the input data with minimal information loss, with appropriate loss functions to guide the integration process. For scATAC-seq, accessibility peaks are used as input without conversion to gene activity scores. The encoder and decoder for scRNA-seq use an additional pair of coupled batchnorm layers to handle heterogeneity in gene expression levels and achieve high-fidelity reconstruction of the signals without the need for selecting HVGs. Between consecutive time points, scTIE models cell trajectories using the principle of OT based on the current embeddings and computes an OT loss using the transport cost matrix. The OT loss is incorporated into the total loss function to update the embedded features, aligning cells by their estimated transition probabilities in the trajectories; the cost matrix itself is also updated iteratively throughout training. In addition to the OT loss, a modality alignment loss is used to ensure the projected feature vectors from the two modalities (RNA and ATAC) are close in distance for the same cell.

Figure 1.

Overview of scTIE, a unified framework for the integration of temporal data and the inference of context-specific GRNs that predict cell fates. The input of scTIE consists of the gene expression matrix of scRNA-seq and peak matrix of scATAC-seq from single-cell multiome data over a time course. scTIE consists of two main steps. (A) In the first step, each cell, represented by a pair of gene and peak vectors, is projected into a common embedding space by separate encoders and decoders. The two modalities and time points are aligned by appropriate loss functions, whereas the transition probability matrix between cells from consecutive time points is iteratively estimated. (B) In the second step, users have the ability to select specific subgroups of cells whose transitions are of interest, finetune the previously trained neural network, identify features that are predictive of transition probabilities, and construct the corresponding GRNs.

In the second step, scTIE finetunes the learned embeddings to build a supervised model for predicting cellular transition probabilities for user-selected subgroups of cells (Fig. 1B). Genes and peak regions highly predictive of the cellular transitions are selected by backpropagating the gradients, allowing us to construct GRNs responsible for developmental changes.

We show the advantages of scTIE on a number of synthetic and real data sets. On synthetic data sets constructed from a mouse early organogenesis multiome data set, our results reveal that scTIE can effectively align cells from different time points and mitigate batch effects, achieving an optimal balance between time alignment, modality alignment, and cell type separation. Furthermore, our analysis of an exemplar multiome data set from differentiating mESCs shows its superior capacity to capture biological signals from each modality and achieve better day alignment compared with other methods, resulting in the identification of distinct cell subpopulations. Finally, using developmental transitions from an anterior primitive streak as a case study, we show scTIE's ability to construct lineage-specific GRNs consisting of regulatory elements with a high predictive power of cell fate and identify key regulatory signals that would be missed by DE- or DA-based analysis.

scTIE outperforms existing methods in integrating temporal multimodal data

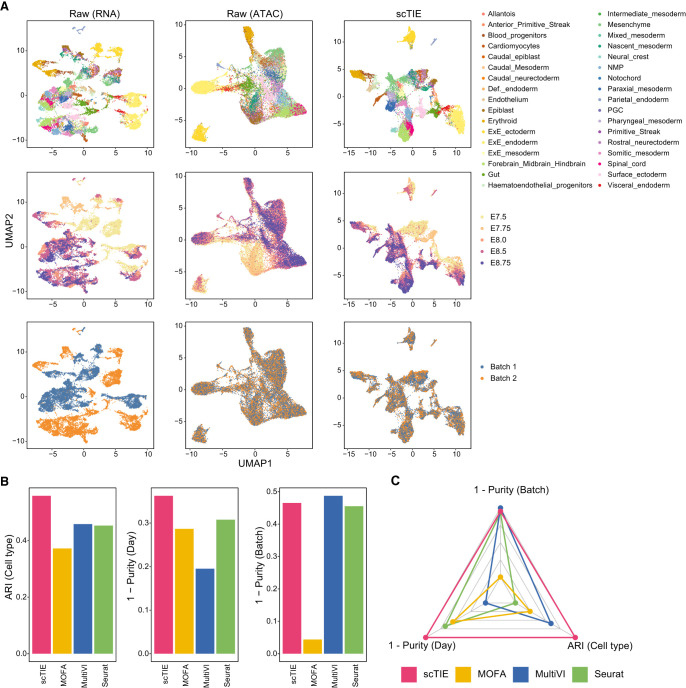
We first evaluated the data integration performance of scTIE against recent methods designed to integrate paired multimodal data, including Seurat (Hao et al. 2021), scAI (Jin et al. 2020), multiVI (Ashuach et al. 2023), and MOFA (Argelaguet et al. 2020). We generated four synthetic data sets by introducing batch effects and noise into a mouse early organogenesis multiome data set (Fig. 2A; Supplemental Figs. S1–S5; Argelaguet et al. 2022). As shown in the UMAP plots of the data with synthetic batch effects introduced in RNA and noise introduced in ATAC (Fig. 2A), scTIE effectively removed the batch effects while also better revealing the cell type signals.

Figure 2.

Performance benchmarking for integrating temporal multimodal data. (A) Joint visualization using UMAP of the synthetic data set with batch effect in RNA and noise in ATAC, colored by cell type annotations (top), sampling days (middle), and synthetic batch information (bottom). Each dot represents a cell in the embedding space. (B) Bar plots showing the evaluation metrics of different data integration methods, including ARI values for clustering with annotations (left), 1 − average purity scores of sampling days with the number of neighbors equal to 50 (middle), and 1 − average purity scores of the synthetic batch with the number of neighbors equal to 50 (right). Higher values indicate better agreement with annotations and mixing of batches/days. (C) Radar plot summarizing the three evaluation metrics shown in B, in which each line represents the performance of one method, and each axis represents an evaluation metric, starting from the minimum value of all methods. It is noted that scAI was not included in this benchmarking owing to its long computational time (>2 d).

Next, we compared the performance of these methods from three aspects quantitatively, namely, batch effect removal, time point alignment, and their ability to capture cell type signals (Fig. 2B,C). We quantify the quality of batch removal and time point alignment using purity scores, which calculate the proportion of cells from the same batch/sampling time among neighbors of given cells. A lower purity score indicates a better mixing of batch/time points. We measured the cell type preservation using the adjusted Rand index (ARI) with the cell type annotations provided in the original paper as the ground truth. An ideal embedding should mix well cells from different batches and different time points, while maintaining well-separated cell types. These three metrics are summarized in Figure 2C, in which scTIE encloses the largest area, thus outperforming the other methods in the overall performance (Supplemental Fig. S1). Furthermore, scTIE's superior performance is robust against the number of neighbors used in the purity score calculation (Supplemental Fig. S2). We observe similar trends across the other three synthetic scenarios, in which scTIE consistently exhibits better performance than the other methods (Supplemental Figs. S3–S5). Together, we show the superiority of scTIE in data integration, enabling better capture of biological signals through batch effect removal and time point alignment.

scTIE enables identification of cellular subpopulations via modality and time point alignment with robust performance

Encouraged by scTIE's performance in data integration, we next generated a temporal single-cell multimodal data set and leveraged scTIE for the integration of cells across time points and annotation of cell types. We performed single-cell multiome sequencing from mESCs treated with activin A/lithium chloride (LiCl) and measured on days 2, 4, and 6 using the 10x Genomics Chromium Single Cell Multiome platform. After quality-control filtering (Supplemental Fig. S6), we obtained high-quality measurements of RNA and ATAC from a total of 11,440 cells, with a median detection of 4130 genes expressed per cell and a median of 11,267 peaks detected per cell.

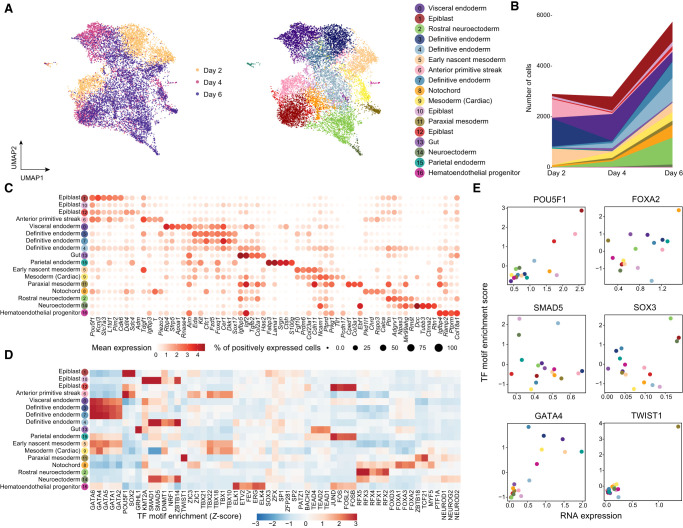
By clustering on the joint embeddings produced by scTIE, we identified 17 clusters with either distinct transcription or chromatin accessibility profiles that include cell types from all the three germ layers as well as from extraembryonic layers of embryonic development (Fig. 3A–C). We annotated these clusters based on the key markers identified in the two previous studies (Fig. 3C; Pijuan-Sala et al. 2019; Mittnenzweig et al. 2021) and confirmed them by label transfer using a public reference (Supplemental Fig. S7; Lin et al. 2020; Mittnenzweig et al. 2021). Further explorations of the motif enrichment of regions with DA in specific clusters highlight the cluster-specific TFs of the annotated cell types (Fig. 3D,E). Additionally, we quantitatively assessed the clustering results using evaluation metrics. Our findings show that compared with the existing methods, scTIE better preserves biological signals in each modality and achieves better alignment in days, further supporting our annotation of the cells using the integrated data from scTIE (Supplemental Figs. S8, S9). Furthermore, we performed the same training and clustering procedure on two pseudoreplicates constructed by randomly splitting the data into two halves, and showed the consistency of the cell type annotation results. The UMAP visualizations for these two subsets are mostly consistent, with an overall accuracy rate of 81% across cell types (Supplemental Figs. S10, S11).

Figure 3.

Integration and cell type identification of the mESC data set by scTIE. (A) Joint visualization of the mESC data set using UMAP, colored by sampling day and cell type annotations. Each dot represents a cell in the embedding space. (B) Cell type compositions per time point. (C) Dot plots of mean expression of RNA data. Rows represent cell types, and columns indicate each gene. The color scale represents the expression level, and the size indicates proportion of positively expressed cells. The five most significantly expressed genes for each cluster are included. (D) Heatmap of the TF motif enrichment (Z-scores) of ATAC data. Rows represent cell types, and columns indicate TFs. The five most significantly enriched TFs for each cluster are included. (E) Scatter plots of the mean RNA expression levels by clusters (x-axis) and the average TF motif enrichment scores of ATAC (y-axis) for the selected TFs. The dots are colored by the cell type annotations, with the color legend consistent with that in A.

Notably, scTIE identifies three distinct clusters of definitive endoderm (clusters 3, 4, and 7) (Supplemental Fig. S12A). We find that cluster 4 uniquely expresses several Wnt pathway direct targets (Vcan, Nrcam, and Ccnd2) and Wnt TF (LEF1) and has lower expressions in the Wnt inhibitor Dkk1 and some definitive endoderm markers (Hhex and Sox17) (Supplemental Fig. S12B). The activation of Wnt signaling of this group of cells could be linked to primordial lung specification progenitors (Ikonomou et al. 2020). Cluster 3 and cluster 7 have similar expression profiles to each other. Compared with cluster 3, we find cluster 7 with a majority of cells from day 6 has lower expressions in the Nodal signaling genes Nodal and Tdgf1 but has higher expressions in genes that negatively regulate the Nodal pathway (Cer1 and Lefty1) (Supplemental Fig. S12B).

An inspection of the epiblast subsets further shows that scTIE enables cellular subpopulation identification (Supplemental Fig. S13A). We find that one of the epiblast clusters (cluster 12) has up-regulation of genes related to hypoxia (Adm, Anxa2, Ddit4, and Gbe1), which could enhance the definitive endoderm differentiation, as suggested previously (Supplemental Fig. S13B; Pimton et al. 2015; Chu et al. 2016). In addition, we find that cluster 1 is enriched with anterior epiblast markers (Pou3f1, Enpp3, Pten, and Slc7a3), whereas cluster 10 highly expresses posterior epiblast markers (Lhx1, Ifitm1) (Supplemental Fig. S13B; Peng et al. 2016), with down-regulation of the TFs POU5F1 and SOX2 but up-regulation of the TFs FOXA1 and FOXA2 (Supplemental Fig. S13C).

Finally, we examine the stability of our results in both modality alignment and cluster identification, with respect to key tuning parameters in scTIE, including the weight of OT in the loss function, the number of nodes in hidden layer, and the updating frequency of OT. We find that the weight of the OT loss is an important parameter to reach a balance between the alignment of modalities and time points, with a larger weight resulting in a better alignment in time points but poorer performance in modality integration (Supplemental Figs. S14A,E, S15A). In this sense, the choice of this parameter can be guided by the performance in modality alignment, because the pairing information for all cells is known and serves as the ground truth. The two other tuning parameters have a small impact on our results (Supplemental Figs. S14B–D,F–H, S15B–D).

Together, we show that scTIE is able to capture distinct cellular subpopulations by preserving information from both epigenomic and transcriptomic profiles, while also aligning the cells from different time points.

scTIE embeddings capture interpretable biological features

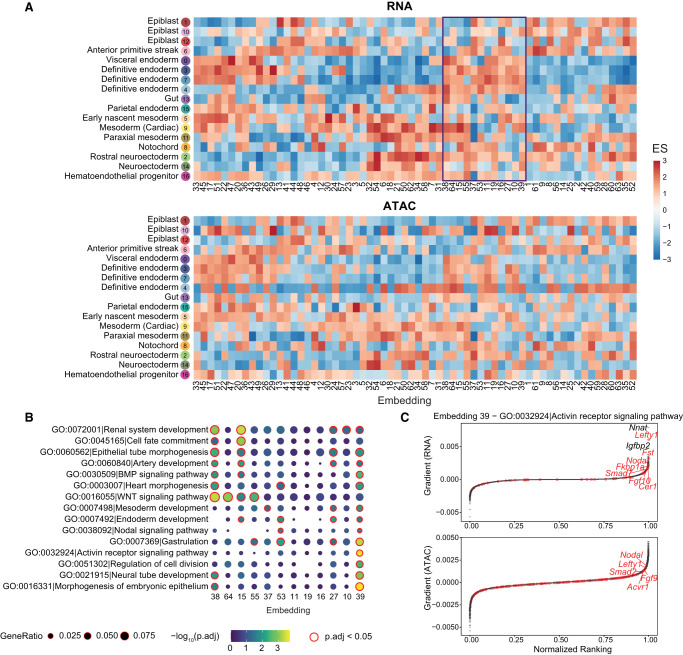
To interpret the embedding space projected by scTIE, we deconvoluted the latent representation by backpropagating the gradient of each dimension in the embedding layer with respect to gene and peak input, followed by ranking the features. We then computed the enrichment scores of the cell type marker list for the feature rankings of each embedding dimension (see Methods). We find that each dimension exhibits distinct patterns of enrichment of cell type markers, and at the same time, the cell types from the same lineage share similar enrichment patterns across the dimensions, indicating that scTIE captures diverse and biologically meaningful information from the data (Fig. 4A). We further observe that the enrichment results of RNA and ATAC share similar patterns, illustrating that scTIE is able to link the transcriptomic profiles with the chromatin accessibility through the common embeddings (Fig. 4A).

Figure 4.

Biological signals in the mESC data set captured by each embedding dimension of scTIE. (A) Enrichment scores of the gradient ranking in each embedding dimension using the RNA (top) and ATAC (bottom) marker list for each cell type. (B) Gene Ontology enrichment of selected pathways on the gradient ranking of a subset of embedding dimensions. (C) Gradient rankings for RNA (top) and ATAC (bottom) of embedding dimension 39, in which genes/peaks are ranked based on the gradient values. The labeled points are genes in the selected gene set (activin receptor signaling pathway).

The embedding gradients can be further interpreted in terms of known biological functions, based on their Gene Ontology (GO) enrichment. As illustrated in Figure 4B, we find that the embedding dimensions enriched with definitive endoderm cell type markers can be associated with different pathways. We observe that dimension 39 is uniquely enriched with activin receptor signaling, as confirmed by the top-ranking genes, including Lefty1, Fst, and Nodal from this pathway (Fig. 4C). Consistently, the nearest genes of the top-ranking peaks also include genes associated with the activin pathway, such as Nodal, Lefty1, and Fgf9. Because treatment by activin is a key component of our differentiation protocol (see Methods), it is comforting to see that the relevance of this pathway is captured by the fitted model. Together, we show that scTIE is able to project the two modalities into a joint embedding space that captures interpretable biological signals of the data.

Lastly, we find that the above results are robust to the choice of dimension size (i.e., number of nodes in the embedding layer). We trained scTIE and performed the same gradient calculations with the number of dimensions set to 32 and 96 (vs. the current choice of 64) and found qualitatively similar enrichment patterns (Supplemental Fig. S16). Selected embeddings also show enrichment of GO pathways related to the definitive endoderm development, similar to that in Figure 4B (Supplemental Fig. S17).

scTIE uncovers cell fate–specific regulatory networks

scTIE constructs lineage-defining GRNs by combining information across different dimensions of the embedding layer to predict the cell transition probabilities between time points. As a case study, we investigated the transitions of cells from an anterior primitive streak on earlier days into endoderm and mesoderm, as well as those remaining as an anterior primitive streak on later days. The primitive streak is a transient embryonic structure that marks bilateral symmetry, helps confer anterior–posterior spatial information during gastrulation, and initiates germ layer formation (Mikawa et al. 2004). A distinct group of cells located at anterior primitive streak, the node, forms the axial mesodermal structures and definitive endoderm cells (Hoodless et al. 2001).

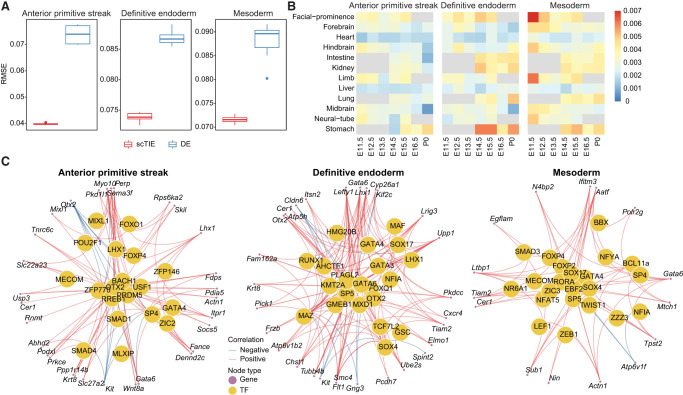
In each of the above three possible cell fates, we finetuned the trained embeddings using a prediction layer with weight regularization and back-propagated the gradients from the prediction layer to select the top 200 genes and 500 peak regions as the most predictive features of the lineage. Compared with the conventional approach that uses DE/DA analysis to select the top features, scTIE selects genes and peak regions with significantly better prediction performance (Fig. 5A). The superior prediction performance is consistent across a range of tuning parameters, including the regularization weights and the number of top features, evaluated via cross-validation (Supplemental Fig. S18). To show the benefit of jointly modeling RNA and ATAC data, we considered the alternative approach of only integrating the RNA data across the time points. Then, we used the same gradient approach to select the top genes for each of the three lineages and selected top peaks by physical proximity and correlation. The predictive power of these features decreased compared with joint modeling (Supplemental Fig. S19). Conceptually, we note that joint modeling allows us to train a separate autoencoder for the ATAC modality and back-propagate the gradients from the prediction layer to select the most informative peaks for predicting the transition probabilities. Thus, the framework of scTIE is capable of jointly finding the most predictive features in both modalities.

Figure 5.

Lineage-specific regulatory elements selected by scTIE and the corresponding GRNs. (A) Performance of top genes and peaks selected by each method in predicting cell fate probabilities. (B) Similarity of top gradient peaks with enhancers of 12 tissues at seven developmental stages from known enhancer databases. (C) GRN of three cell fates.

In addition, we assessed the stability of the gradient analysis through subsampling. For both the definitive endoderm and mesoderm lineages, we randomly subsampled 60% of the cells considered for each lineage analysis, finetuned the trained neural network, and calculated the feature gradients for RNA and ATAC the same way as we did for the full data. The correlations of gradients between the subsampling approach (averaged over 50 repetitions) and the full set show a high level of agreement across all genes and peaks used as input to scTIE (Supplemental Fig. S20).

To annotate the top peaks, we overlapped the selected peaks with the published enhancer database from 12 tissues of seven developmental stages from 11.5 d after conception until birth (Gorkin et al. 2020), quantified by the Jaccard index. We find that the top peaks associated with mesoderm transition potential are enriched with facial prominence and limb enhancers at E11.5, whereas endoderm transition–related peaks identified by scTIE show higher enrichment and distinct overlap with stomach enhancers at E14.5, E15.5, and P0 (Fig. 5B). In contrast, the peaks selected by DA analysis show enrichments in tissues that are much less specific to the predicted lineages of mesoderm or endoderm (Supplemental Fig. S21). Together, these results illustrate that scTIE is able to identify peaks that are specific to lineage transition.

The identification of genes and peaks that are predictive of cell transition further allows us to infer GRN for each of the lineages: anterior primitive streak, endoderm, and mesoderm (see Methods). In the GRN of the anterior primitive streak (Fig. 5C, left panel), we identified a few TFs that play key roles in jointly governing anterior mesendoderm and the node development (LHX1, OTX2, and SMAD4) (Chu et al. 2004; Costello et al. 2015), as well as a TF related to axial mesendoderm morphogenesis and patterning (MIXL1) (Hart et al. 2002). When focusing on the endoderm GRN (Fig. 5C, middle panel), we find that besides identifying TFs that are central regulators for the formation of definitive endoderm development (SOX17, GATA4, GATA6, and GSC) (Bossard and Zaret 1998; Kanai-Azuma et al. 2002; Li et al. 2011; Fisher et al. 2017; Heslop et al. 2021), scTIE also captures TFs that are associated with early mesendoderm differentiation (RUNX1) (VanOudenhove et al. 2016) and morphogenetic movement (LHX1) (Tam and Loebel 2007).

Lastly, we examined the mesoderm GRN (Fig. 5C, right panel), which identifies a few key TFs (HHEX, SOX17, SMAD3, ZIC3, TWIST1, and NFAT5) that are associated with mesoderm lineages. Notably, most of these TFs have insignificant P-values under DE analysis (Supplemental Table S1), illustrating that scTIE captures key regulatory signals in this lineage that would be missed otherwise. More specifically, the mesoderm GRN highlights TFs that are associated with cardiac development, such as ZIC3 in early mesodermal patterning (Jiang et al. 2013; Sutherland et al. 2013); HHEX, which is involved in mediating the SOX17 for cardiac mesoderm formation in mESCs (Liu et al. 2014); and NFAT5 for cardiomyogenic during mesodermal induction through regulating the canonical Wnt pathway (Adachi et al. 2012). We also identify TFs that are essential for mesoderm formation and patterning (SMAD3) (Dunn et al. 2004) and cranial mesoderm development (TWIST1) (Bildsoe et al. 2016).

Discussion

Although the rapidly increasing collection of single-cell multiomic data provides a wealth of information for examining context-specific regulatory mechanisms, accurate characterization of cell identities remains the first hurdle to be overcome in such tasks. scTIE provides a unified framework for the integration and joint modeling of temporal multimodal data and the subsequent visualization, cell type identification, and inference of key regulatory modules predictive of the developmental transitions of cells. Incorporating OT into the training of an autoencoder, scTIE alternates between updating the alignment of cells at different time points and using the current alignment for training the projections into the common embedding space, thus achieving a better balance between integrating time points and maintaining cell type–specific signals. As we have shown on the real and synthetic data sets, scTIE outperforms existing paired methods in terms of integration performance.

Different from existing integration methods that also use the notion of a common embedding space, scTIE directly exploits the information in this space produced by the nonlinear projections of a neural network, linking it to interpretable features such as genes and peak regions. scTIE extracts context-specific gene regulatory relationships through the identification of features that are predictive of cell transition probabilities, which quantify how likely a collection of cells on earlier days will transit to a certain cell state on later days, relative to other cells. These sets of cells can be flexibly defined, allowing users to investigate any cell transition process of interest. In addition to cell transition probabilities derived from OT, the current framework can also be adapted to select features that are predictive of other types of response variables, such as pseudotime and perturbation, which potentially enables the construction of differential GRN under continuous cell differentiation and in perturbed conditions.

scTIE is designed for temporal multimodal data, which is ideal for studying single-cell genomics in developmental trajectories. Paired measurements from the same cells remove the need for computational pairing, which can introduce errors into the downstream GRN analysis if cells of different cell types are paired, and the issue of cell type imbalance between different modalities. The integration of unpaired developmental data across multiple time points remains an open problem itself. For data sets taken from a matched population, a loss function performing global alignment between modalities, such as the one used by Zhang et al. (2022a), can be potentially incorporated into the training of scTIE. However, the problem is more challenging if cells are sampled at different time points or develop at a different rate across the modalities, and we will pursue this in future work.

Although a large number of methods exist for inferring pseudotime ordering of cells from a static snapshot of a developmental process, pseudotime inference assumes that a continuum of cellular states is observed at the sampled time and thus may not capture the entire transition process (Tritschler et al. 2019). An interesting extension would be combining pseudotime inference and experimental time points to create a finer temporal resolution. However, we note that this would also increase the computation time of scTIE, because iterative OT estimation is performed between consecutive time points; efficient and accurate OT algorithms remain an active area of research.

We have focused on scRNA-seq and scATAC-seq as common modalities from multimodal profiling technologies. Other modalities such as methylation and protein levels (Mimitou et al. 2021; Swanson et al. 2021; Wang et al. 2021) can be easily incorporated into scTIE through appropriate encoder–decoder pairs. Because transcriptional regulation involves interactions of protein complexes, histone modifications, and other microenvironmental factors, we expect the addition of such information will allow us to build a more accurate prediction model for cellular state changes. Furthermore, emerging single-cell perturbation assays (Rubin et al. 2019) can either be used to validate the top candidates found in our predictive model or be built into the neural network architecture as a prior knowledge graph (Cao and Gao 2022).

In summary, scTIE provides an integrative framework for analyzing temporal multimodal data, which is an emerging form of data we expect will become more readily available as interests in characterizing GRNs at single-cell resolution continue to rise. On real and synthetic developmental data sets, scTIE is shown to provide effective integration of cells from all time points and select key regulatory elements with superior performance in predicting cellular state changes. We envision that advances in single-cell technologies generating new forms of temporal data will enable us to further expand the functionalities of scTIE, paving the way toward a holistic understanding of cellular transitions and responses in development and disease.

Methods

Synthetic data construction

The 10x Genomics multiome data of mouse early organogenesis, along with its cell type annotation, were obtained from the NCBI Gene Expression Omnibus database (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE205117 (Argelaguet et al. 2022). The data set comprises 59,132 cells from a time course of mouse embryonic development, spanning five time points from E7.5 to E8.75.

To construct synthetic data that could be processed by most of the methods within their computational capacity, we subset the data to 24,188 cells by selecting only one sample at each time point. We filtered out genes expressed in <1% of cells and peaks expressed in <5% of cells, resulting in 15,754 genes and 81,108 peaks. To introduce noise and batch effects to the data, we used the downsampleReads() function in the DropletUtils R package (R Core Team 2022) to downsample the reads. We generated five synthetic scenarios: (1) subsample 10% for all cells in ATAC; (2) subsample 10% for all cells in ATAC and 50% for all cells in RNA; (3) subsample 50% for half of cells in RNA to create the synthetic batch effect in the data; (4) subsample 50% for half of cells in both RNA and ATAC to create the synthetic batch effect in the data; and (5) subsample 10% for all cells in ATAC, subsample 50% for half of the cells in RNA, and 25% for the other half of the cells.

mESC data generation

Cell culture

The mESC line R1 was obtained from ATCC. The cells were first expanded on an MEF feeder layer previously irradiated. Then, subculturing was performed on 0.1% bovine gelatin-coated tissue culture plates. The cells were propagated in mESC medium consisting of KnockOut DMEM supplemented with 15% KnockOut serum replacement, 100 µM nonessential amino acids, 0.5 mM beta- mercaptoethanol, 2 mM GlutaMax, and 100 U/mL penicillin–streptomycin with the addition of 1000 U/mL of LIF (ESGRO, Millipore).

Cell differentiation

mESCs were differentiated using the hanging drop method (Wang and Yang 2008). Trypsinized cells were suspended in chemically defined medium CDM (Li et al. 2011) to a concentration of 37,500 cells/mL. CDM consists of 75% Iscove's Modified Dulbecco's Medium (IMDM; Invitrogen), 25% Ham's F12 medium (Invitrogen), 1× N2 supplements (Invitrogen), 0.05% bovine serum albumin (BSA; Invitrogen), 2 mM GlutaMAX-I (Invitrogen), 0.5 mM ascorbic acid (Sigma-Aldrich), and 4.5 × 10⁴ M MTG (Sigma-Aldrich). Twenty-microliter drops (about 750 cells per drop) were then placed on the lid of a bacterial plate, and the lid was upside down. After 48-h incubation in a 37°C incubator with 5% CO₂, embryoid bodies (EBs) formed at the bottom of the drops were collected and placed in the well of a six-well ultralow attachment plate (Corning) with fresh CDM medium containing 50 ng/mL activin A (R&D Systems 338-AC-050/CF) and 2 mM LiCl (Sigma-Aldrich) for up to 6 d, with the medium being changed daily.

Single-cell multiome library

We followed 10x Genomics single-cell multiome library preparation protocol. The EBs were collected at days 2, 4, and 6 after activin A/LiCl treatment. For each time point, the cells were first treated with StemPro Accutase cell dissociation reagent (Thermo Fisher Scientific) for 10–15 min at 37°C with pipetting. Single-cell suspension was obtained by passing through a 37-µM cell strainer (Stemcell Technologies) twice. After measuring cell concentration, about 1 million cells were centrifuged at 300 rcf for 5 min. Nuclei were isolated by following the protocol provided by 10x Genomics (nuclei isolation for single-cell multiome ATAC + gene expression sequencing, CG00365, Rev A). The final nuclei concentration was adjusted to 3000 cell/µL in 1× nuclei buffer (10x Genomics). The sample was immediately submitted to Stanford Genomics Service Center (SGSC) for single-cell sorting using a 10x chromium controller (target cells: 5000 per replicate, total of two to three replicates per time point). The single-cell multiome library was generated using a chromium next GEM single-cell multiome ATAC + gene expression reagent bundle kit (10x Genomics, PN-1000283).

Data preprocessing

10x Genomics Cell Ranger arc v2.0.0 was used to process the raw FASTQ files for each multiome single-cell data set separately. The reference genome and transcriptome for alignment and annotation was version arc-mm10-2020-A-2.0.0. To integrate all filtered count matrices for scRNA-seq and scATAC-seq from different replicates and time points, the cellranger-arc aggr command was applied with the default depth normalization method.

Next, we performed quality control on the cell level. We removed cells based on the following criteria in scRNA-seq: (1) with the total number of UMI (nUMI) less than 6000 on day 2 and 3000 on day 4 and day 6; (2) with nUMI greater than 100,000; (3) with the number of genes less than 2000 on day 2, 1800 on day 4, and 1500 on day 6; and (4) mitochondrial reads >25%. We further removed cells based on the following criteria in scATAC-seq: (1) with fewer than 500 total ATAC fragments and (2) with less than 500 peaks detected. After quality control, we retained 11440 cells (day 2: 2896 cells; day 4: 2796 cells; and day 6: 5748 cells). We then performed the quality control on the feature level, removing the genes that are not expressed in any cells and the peaks that are expressed at least 5% of cells, resulting in 26,717 genes and 61,744 peaks as input in scTIE.

Architecture and training of scTIE

scTIE uses an autoencoder structure to project high-dimensional feature vectors (i.e., gene expression levels and accessibility peaks) from all time points into a lower-dimensional common embedding space and reconstruct the features in the original high-dimensional space. Each modality has its own encoder and decoder (Table 1). For RNA, the architecture has an additional pair of coupled batchnorm layers, in which the final reconstructed output uses the moving average µ and standard deviation σ stored in the first batchnorm layer of the encoder to perform rescaling. This accounts for the high variability in gene expression levels without the need for selecting HVGs and allows us to significantly improve the performance in reconstruction correlation, modality and day alignment, and clustering quality (Supplemental Fig. S22). The pairing between feature vectors from the same cell is enforced through a modality loss function minimizing their distance in the embedding space. An OT matrix is used to construct cell trajectories between each pair of consecutive time points. In contrast to existing methods using OT for trajectory inference, we integrate an OT loss into the autoencoder training process and estimate the OT matrix iteratively throughout. A larger weight on the OT loss leads to better alignment between days (Supplemental Fig. S15A).

Table 1.

Autoencoder architecture for RNA (left) and ATAC (right)

Encoder	Encoder
Batchnorm (267,17)	Batchnorm (61,744)
Linear (26,717, 1000)	Linear (61,744, 1000)
Batchnorm (1000)	Batchnorm (1000)
LeakyReLU (0.2)	LeakyReLU (0.2)
Linear (1000, 1000)	Linear (1000, 1000)
Batchnorm (1000)	Batchnorm (1000)
LeakyReLU (0.2)	LeakyReLU (0.2)
Linear (1000, 64)	Linear (1000, 64)
Decoder	Decoder
Linear (64, 500)	Linear (64, 500)
Batchnorm (500)	Batchnorm (500)
LeakyReLU (0.2)	LeakyReLU (0.2)
Linear (500, 1000)	Linear (500, 1000)
Batchnorm (1000)	Batchnorm (1000)
LeakyReLU (0.2)	LeakyReLU (0.2)
Linear (1000, 26,717)	Linear (1000, 61,744)
Batchnorm (26,717)
Multiply by σ and add µ

Let X^(t,s) denote the data matrix from time point t and modality s, where t = 1, …, T and s = 1, 2 for RNA and ATAC, respectively. Each time point t provides measurements for N_t cells; thus in this case, $X^{(t,1)}\in {\mathbb{R}}^{D_1\times N_t}$ with D₁ = number of genes and $X^{(t,2)}\in {\mathbb{R}}^{D_2\times N_t}$ with D₂ = number of peak regions. In each iteration, a mini-batch of data is sampled by taking equal-sized subsets of cells from each time point; that is, $\mathcal{B}={\{{\mathcal{B}}^{(t)}\}}_{t=1}^T$, where each subset ${\mathcal{B}}^{\left(t\right)}$ has B cells. Three loss functions are applied to the mini-batch.

1. Reconstruction loss. (f_s, g_s) represents the encoder–decoder pair for modality s. Compared with the architecture for ATAC, the RNA part has a pair of coupled batchnorm layers, starting with a batchnorm layer in the encoder to remove scale variations in genes and prevent the gradients from being dominated by a small number of highly expressed genes (Table 1). Let $x_i^{(t,1)}$ denote the gene expression vector from cell i at time t and ${\tilde{x}}_i^{(t,1)}$ denote the normalized output from the first batchnorm layer, then ${\tilde{x}}_i^{(t,1)}=(x_i^{(t,1)}-\mu )/\sigma$, where μ and σ are the moving average and standard deviation of the genes saved in the batchnorm layer throughout training. The reconstruction loss is applied to the normalized data and the output from the decoder, defined as

   $$L_{\mathrm{recon}}^{\left(1\right)}={\displaystyle \frac{1}{TB}\sum _{t=1}^T\sum _{i\in {\mathcal{B}}^{\left(t\right)}}{\parallel {\tilde{x}}_i^{(t,1)}-g_1(f_1(x_i^{(t,1)}))\parallel }_2^2.}$$

   For ATAC, the first layer in the encoder is a fully connected layer, and the reconstruction loss is computed on the input $x_i^{(t,2)}$ and output $g_2(f_2(x_i^{(t,2)}))$ as usual. The overall L_recon is the sum of $L_{\mathrm{recon}}^{\left(1\right)}$ and $L_{\mathrm{recon}}^{\left(2\right)}$.
2. OT loss. We leverage OT to effectively align cells from all time points in the embedding space. For notational convenience, we will suppress the dependence on modality s for now, with understanding that the following steps are performed for each modality. For any two adjacent time points t and t + 1, a transport cost matrix $C^{(t,t+1)}\in {\mathbb{R}}^{N_t\times N_{t+1}}$ can be computed using the current embeddings, where the (k, l)th entry is given by $C^{(t,t+1)}(k,l)=||f(x_k^{\left(t\right)})-f(x_l^{(t+1)})|{|}_2$ for the kth cell from t and the lth cell from t + 1. With the cost matrix, Waddington-OT (Schiebinger et al. 2019) is then used as the algorithm to estimate a transport matrix ${\gamma }^{(t,t+1)}\in R^{N_t\times N_{t+1}}$. Each row in γ^(t,t+1) sums to one, representing the transition probabilities of a cell in time step t to all the other cells in time step t + 1. Given T time steps, we need to maintain a total of T − 1 transport matrices throughout the autoencoder training process. For a given mini-batch $\mathcal{B}$ in each iteration, a submatrix version of C^(t,t+1) is computed using the rows and columns specified in $\mathcal{B}$ and is denoted by ${\tilde{C}}^{(t,t+1)}$. Similarly, a mini-batch version ${\tilde{\gamma }}^{(t,t+1)}$ of γ^(t,t+1) is calculated by taking the appropriate submatrix and rescaling the rows to unit sum. The batch-wise feature alignment loss (for each modality s) is defined as

   $$L_{\mathrm{ot}}={\displaystyle \frac{1}{T-1}\sum _{t=1}^T\left(\sum _{k=1}^B\sum _{l=1}^B({\tilde{C}}^{(t,t+1)}\odot {\tilde{\gamma }}^{(t,t+1)})(k,l)\right),}$$

   where $\odot$ is the Hadamard product. The final L_ot is the sum over modalities s.
3. Modality alignment loss. For each mini-batch, the modality alignment loss is simply defined as the L2 distance between feature vectors from the same cell in the embedding space, which is to be minimized:

   $$L_{\mathrm{modality}}={\displaystyle \frac{1}{TB}\sum _{t=1}^T\sum _{i\in {\mathcal{B}}^{\left(t\right)}}{\parallel f_1(x_i^{(t,1)})-f_2(x_i^{(t,2)})\parallel }_2^2.}$$

The total loss in each iteration is L = λ_reconL_recon + λ_otL_ot + L_modality, where the λ’s are tuning parameters controlling the relative weighting of the losses. For every K epochs, the transport matrices (for each modality s) ${\gamma }_s^{(t,t+1)},1\le i\le T-1$ are updated by computing OT on the current embedding features.

The functionalities of each loss function in L are as follows:

1. The reconstruction loss preserves the original data signals (i.e., distinct cell type signals) at each time point by encouraging the autoencoders to learn a low-dimensional embedding that can reproduce the data input.

2. The OT loss aligns embeddings between consecutive time points by calculating an alignment cost function derived from the estimated transition probabilities. To reduce the alignment cost, cell pairs with high transition probabilities should be near each other in the embedding space and vice versa. The transition probabilities and embeddings are iteratively refined. Additionally, the loss aids in mitigating batch effects, as OT can cross-align cells from different batches when mapping cells between consecutive time points. As we showed on the synthetic data with batch effects in both RNA and ATAC data (Supplementary Fig. S4), the pretraining stage (see Training Details section below), which only trains the RNA autoencoder using the OT loss and the reconstruction loss, already removes most of the batch effects in RNA data (Supplementary Fig. S23).

3. The modality alignment loss makes use of the pairing information between RNA and ATAC so that the final embeddings take into account signals in both modalities.

Training details

scTIE took a collection of peak matrices from scATAC-seq data and raw count matrices from scRNA-seq data from multiple time points as input. For ATAC, the peak matrices were transformed to binary matrices, where one represents any nonzero original values. For RNA, the raw count matrices were sized-factor-normalized and then log-transformed. For the overall multimodal training, we first pretrained the RNA autoencoder f₁, g₁ for 500 epochs (excluding L_modality). Then, we fixed the weights of the pretrained RNA model to train the ATAC model for 300 epochs with the overall loss L. Finally, the two models were jointly trained for 200 epochs using the full algorithm as detailed in Algorithm 1. The final joint embeddings were calculated by taking the averages of $f_1(x_i^{(t,1)})$ and $f_2(x_i^{(t,2)})$ for each cell i from time t, followed by computing the final γ^(t,t+1) from the joint embeddings. Throughout training, we used Adam as the optimizer with the learning rate set to 0.1, a batch size B = 256, and the tuning parameters λ_recon = 1, λ_ot = 0.1, and OT was updated every 10 epochs.

We note here that owing to the pretraining of the RNA autoencoder, the biological signals use by scTIE to produce the common embeddings were mostly driven by the RNA modality. However, complementary signals from scATAC-seq still play a role in generating the embeddings because the modality alignment loss is affected by both RNA and ATAC positions in the embedding space. Pretraining with RNA signals is essential for stable training of the neural network because (1) the RNA modality generally contains stronger signals for cell type identification and (2) the dimension of ATAC input (number of peaks) is much larger than that of the RNA modality (number of genes).

Algorithm 1. Multimodal OT autoencoder (two-modality case). —

Data matrices X^(t,s), training iterations M, batch size B, autoencoder f₁, g₁, f₂, g₂ with weights θ, learning rate α, loss weight tuning parameters λ_recon, λ_ot, OT update frequency K.

Initialize all ${\gamma }_s^{(t,t+1)}$ 1 ≤ t ≤ T−1 matrices with zero matrices.

 for iteration = 1, 2, …, M do

  Sample cells $\mathcal{B}-={\{{\mathcal{B}}^{\left(t\right)}\}}_{t=1}^T$, where each subset ℬ^(t) has B cells.

  Compute L_recon, L_ot, L_modality.

  Compute L = λ_reconL_recon + λ_otL_ot + L_modality.

  Perform gradient descent step on autoencoder weights θ ← θ−α∇_θ L.

  if M%K == 0 then

   Update ${\gamma }_s^{(t,t+1)}$, 1 ≤ t ≤ T − 1, s = 1, 2 using current embeddings.

  end if

 end for

Estimation of long-range transition probabilities

Long-range transition probabilities can be estimated by multiplying the transport matrices. For example, γ^(t,t+2) can be calculated as γ^(t,t+1)γ^(t+1,t+2). An alternative approach is to compute γ^(t,t+2) directly from OT. However, because OT interpolates between two observed data sets by finding the shortest path in the space of distributions, one has to implicitly assume that the cells do not change their expression or accessibility by large amounts over the two time points. It is generally recommended that long-range time-couplings are estimated by multiplying the gamma matrices (Schiebinger et al. 2019). On the mESC data set, these two ways of estimation give positively correlated results, with the mode of correlations lying around 0.6 (Supplemental Fig. S24).

Cell type annotation of mESC data

Cell clustering of scTIE

To identify the clusters on the common embedding of scTIE, we first constructed a shared nearest-neighbor graph using buildSNNGraph in R package scran (v 1.23.0) (Lun et al. 2016), with the number of nearest neighbors set as 15 with the weighted scheme set as Jaccard. Next we performed Leiden community detection (Traag et al. 2019) on the shared nearest graph with resolution at 1.8 and the number of iterations at 50, implemented in R package leidenAlg (v 1.0.3), resulting in 17 clusters in total.

Motif enrichment

We used Signac (Stuart et al. 2021) to calculate the overrepresented motif of each cluster based on the differential accessible peaks. The motif position frequency matrices are obtained from Cis-BP (Weirauch et al. 2014). We used limma-trend (Ritchie et al. 2015) to perform DA analysis between the cells in one cluster and the remaining cells, where the top 500 peaks of each cluster with a log-fold change greater than 0.1 and adjusted P-value less than 0.001 are selected. We then performed the motif enrichment analysis using FindMotifs to find motifs overrepresented in the selected set of peaks.

Benchmarking and evaluation metrics

Settings used in other methods

We benchmarked the performance of scTIE against four other methods designed for single-cell paired multimodal data integration: Seurat, scAI, MultiVI, and MOFA. We compared scTIE's performance in terms of visualization of the latent space, alignment of the days, and clustering in the latent space against these methods.

• Seurat. R package Seurat v4.1.0 (Hao et al. 2021) was used. We ran Seurat (WNN) using FindMultiModalNeighbors, with the reduction list input as the first 50 components of LSI reduced dimension of scATAC-seq (with the first dimension excluded) and 50 top PCs of scRNA-seq, with the other parameters set as default.

• scAI. R package scAI v1.0.0 (Jin et al. 2020) was used. We ran scAI using run_scAI by setting the rank of the inferred factor set as 64 and nrun = 5, with the other parameters set as default.

• MultiVI. Python package scvi v0.15.0 (Ashuach et al. 2023) was used. We ran MultiVI using MULTIVI by setting the fully_ paried = True, n_hidden = 256, and n_latent = 64, with the other parameters set as default. The model was then trained with max_epochs = 200.

• MOFA. R package MOFA2 v1.7.0 (Argelaguet et al. 2020) was used. We ran MOFA using run_mofa by setting the number of factors as 64, with the other parameters set as default.

Benchmarking of mESC data

Modality alignment

We used two metrics to measure scTIE's performance in the alignment of the two modalities, namely, FOSCTTM and paired data proportion.

• FOSCTTM. FOSCTTM refers to fraction of samples closer than true match, which was first introduced in MMD-MA (Liu et al. 2019) to quantify the alignment of multiomic data. To evaluate the modal alignment of scTIE using FOSCTTM, we first calculated the Euclidean distance between the ATAC embedding and RNA embedding. Then, for each modality we calculated one FOSCTTM score that summarizes the proportion of cells that are closer to the ground truth–matched cells based on the distance matrix. Finally, we summarized the FOSCTTM scores from the two modalities into one score by taking the average.

• Paired data proportion. Paired data proportion (used in Cobolt) (Gong et al. 2021) calculated the proportion of cells whose ground truth–matched cells are included within a certain number of neighbors, based on the Euclidean distance between the ATAC embedding and RNA embedding. We varied the number of neighbors from one to the total number of cells in the data.

Day alignment

We quantified the alignment of data sampled on different days using neighborhood purity using neighborPurity in R package bluster (v1.5.1), which calculated the proportion of cells from the same day among a certain number of neighbors, based on the UMAP coordinates generated from the common latent embeddings.

Comparison with single-modality clustering

We benchmarked clustering results from scTIE against other paired data integration methods by evaluating how similar the results are compared to clustering dimension-reduced scRNA-seq (PCA space) or scATAC-seq (LSI space) alone. On the latent space of each method or the dimension-reduced space from scRNA-seq or scATAC-seq, we performed Leiden clustering on the shared nearest-neighbor graphs constructed, with the same parameter settings as mentioned in the section Cell Clustering. Note that for Seurat, we performed Leiden clustering directly on the weighted nearest-neighbor graph it outputs. We used two metrics to quantify the results, adjusted Rand index (ARI) and silhouette coefficient:

• ARI. We computed the ARI scores of clustering results from each data integration method and clustering results from scRNA-seq or scATAC-seq alone.

• Silhouette coefficient. For each clustering result, we computed the silhouette coefficient based on the Euclidean distance calculated from the UMAP coordinates generated from the dimension-reduced scRNA-seq or scATAC-seq.

For both metrics, higher values indicate a method better captures the clustering information in a single modality.

Benchmarking of synthetic data

We benchmarked the data integration performance of scTIE with the other paired data integration methods in terms of three evaluation metrics: (1) ARI scores of the cell type annotation provided by the original study and the Leiden clustering results from each method, (2) neighborhood purity of days, and (3) neighborhood purity of batch for scenarios with synthetic batch effects.

Enrichment analysis for embedding dimensions

Upon completion of training, scTIE has projected the high-dimensional feature vectors (genes and peaks) into a 64-dimensional embedding space. Treating each dimension as a representation unit, for each cell type, we back-propagate the gradient of each unit with respect to gene and peak input to select features with the largest impact. More specifically, for each cell in cell type G, we pass its gene expression vector through the autoencoder to obtain its embedding vector y and compute ${\displaystyle \frac{\mathrm{\partial }{y}_j}{\mathrm{\partial }{x}_i}}$ for each dimension j and gene input node i. The gradients are averaged over all cells in G to obtain the mean gradient for each gene. We then take the variability of gene expression into account by multiplying each mean gradient by its corresponding gene standard deviation, so that the final gradients are equivalent to gradients after the first batchnorm layer. Finally, we rank the genes by their gradient values and calculate the enrichment scores of the top 200 genes from the DE analysis of cell type G, where the DE analysis is performed using limma-trend (Ritchie et al. 2015) between the cells in one cluster and the remaining cells. Similar steps are performed for the peaks, and the top 500 peaks are selected for enrichment score calculation.

We used fgsea function in the R package FGSEA (Korotkevich et al. 2021) to perform the gene set enrichment analysis (GSEA) on the pathways related to mESCs (as listed in Fig. 4B). Significant pathways are defined with an adjusted P-value of less than 0.05.

GRN inference

Selecting features with high predictive power

By building a prediction framework on the obtained transition probabilities, scTIE selects genes and peaks jointly with high predictive power for developmental outcomes. For the mESC data, we consider how a group of cells from earlier days, denoted as G₀, develops into two other groups, G₁ and G₂, on later days.

The transition probabilities are obtained from γ^(t,t+1) (t = 1, 2 in our data) so that each cell i in G₀ is associated with a probability vector (p_i1, p_i2) indicating its probabilities of becoming G₁ and G₂ (see section Cell Transition Probability Calculation). We finetune a one-layer classifier on the pretrained features in the embedding space of cells in G₀ to predict their transition probabilities. A simple linear classifier is sufficient to partition the cell feature space into G₁ and G₂ when the pretrained features are representative enough. Concretely, letting q be the linear classifier and $\mathcal{B}$ be a mini-batch of cells from G₀ of size B, we use a batch-wise KL divergence loss defined as

$$L_{kl}={\displaystyle \frac{1}{B}\sum _{j\in \mathcal{B}}{D}_{KL}(q(f(x_j))||P_j),}$$

where f is the trained encoder, P_j = (p_j1, p_j2). This loss enforces the classifier q to output transition probability distributions close to those in P_j’s. We also include the modality alignment loss L_modality, with weight default set as 0.1. The classifier is trained with Adam setting learning rate to 0.001, training epochs to 200, batch size to 256, and L1 regularization.

After training, gradients from the two classification nodes are back-propagated to each gene (or peak) input the same way as in computing embedding gradients. The gene gradients are then scaled by multiplying with the gene-wise standard deviations. A positive gradient for gene (or peak) j with respect to the node for G₁ means increasing the input feature value tends to increase the cells’ probabilities of becoming G₁, whereas a negative value indicates more contribution to G₂. The final feature ranking is based on the average gradients by repeating this procedure 20 times with different seeds.

Selection of G₀, G₁, G₂

As a case study in this paper, we focus on the transition of cells from the anterior primitive streak on day 2 and day 4 into endoderm and mesoderm, as well as that remaining as an anterior primitive streak on day 4 and day 6.

First, we considered the cells that are annotated as anterior primitive streak (cluster 6) on day 2 and day 4 as G₀. G₁ and G₂ are then selected from the cells on day 4 and day 6 that are more likely to be the descendants of G₀, as quantified by the descendant scores. The descendant scores are defined similarly as in WOT (Schiebinger et al. 2019). Recall γ^(t,t+1) is the N_t by N_t+1 transition probability matrix between time points t and t + 1; let $s_t\in R^{N_t}$ be the vector of descendant scores for all cells at time point t, and then we can calculate

$$s_{t+1}=s_t{\gamma }^{(t,t+1)},\mathrm{where}{s}_t(i)=\{\begin{array}{cc}{\displaystyle \frac{1}{|G_0|}}& \mathrm{if}\mathrm{cell}i\mathrm{is}\mathrm{in}{G}_0.\\ 0,& \mathrm{otherwise}.\end{array}$$

This formula can then be pushed forward again to calculate the descendant scores for the next time point t + 2, and so on. For all cells in G₀ at time point t (here t = 1 or 2), we calculated the descendant scores s_t+k of all cells at the later time point t + k, for k = 1, …, T − t. We then considered the cells with descendant scores greater than the median of all cells at a certain time point as the potential descendants, namely, cells with s_t+k(i) > median(s_t+k). Among these descendant cells, we selected three pairs of G₁ and G₂ corresponding to the three cell fates we have analyzed: G₁, which is annotated as (1) anterior primitive streak or (2) definitive endoderm or (3) mesoderm; for each selection of G₁, G₂ always represents the remaining descendant cells.

Cell transition probability calculation

For each cell i ∈ G₀ on day t, and G₁, G₂ on day k ∈ K, where K = {k:t < k ≤ T}, the transition probability vector $(p_{i1}^{\left(t\right)},p_{i2}^{\left(t\right)})$ is calculated as the following:

$$\begin{array}{c}{p}_{i1}^{(t,k)}=\sum _{y\in G_1}{\gamma }^{(t,k)}(i,y),\\ p_{i2}^{(t,k)}=\sum _{y\in G_2}{\gamma }^{(t,k)}(i,y),\\ p_{ij}^{(t,k)}={\displaystyle \frac{p_{ij}^{\left(t\right)}}{{\sum }_j{p}_{ij}^{\left(t\right)}},j=1,2,}\\ p_{ij}^{\left(t\right)}={\displaystyle \frac{1}{|K|}\sum _k{p}_{ij}^{(t,k)}.}\end{array}$$

(p_i1, p_i2) is then the concatenated vector of $(p_{i1}^{\left(t\right)},p_{i2}^{\left(t\right)})$.

Evaluation of cell transition probability prediction

To evaluate the predictive power of the selected features to the transition probability, we performed support vector machine (SVM) with radial kernel to predict the transition probability using days 2 and 4 anterior primitive streak gene expression of the top selected genes and peak matrix of the top selected peaks. The performance is quantified by root mean squared error (RMSE) from a 20 repeated fivefold cross-validations. We benchmarked the predictive power of the features selected by gradients with different regularization weights (0, 1, 10, 100), against the features selected by DE/DA analysis using limma-trend (Ritchie et al. 2015).

GRN construction

To construct the GRN for each cell fate (anterior primitive streak, definitive endoderm and mesoderm), we focus on the top 500 genes based on the gradient ranking. For each gene, we consider the open chromatin regions that are within 250 kb upstream of and downstream from its transcription start site (TSS), as well as ranked top 2000 according to the gradients as the distal candidate functional regions, which results in 396, 404, and 339 gene–peak pairs for the three cell fates, respectively. We next filtered the pairs based on the gene–peak correlation, calculated from the metacells. The metacells were constructed using the following strategies: We first randomly selected 100 cells from the anterior primitive streak cells on day 2. For each cell, we looked for its five nearest neighbors based on the Euclidean distances of the common embeddings and aggregated them as a metacell. Then, we calculated the Pearson's correlation of the gene–peak pairs for these 100 metacells. This procedure is repeated 20 times, and the gene–peak pairs with an absolute average correlation greater than 0.2 are retained (APS: 35; DE: 38; and MES: 17 pairs remained).

To link the peak region with the TF, we identified the enriched TF using matchMotifs function in R package motifmatchr of the peaks from the selected gene–peak pairs based on Cis-BP database (Weirauch et al. 2014). We only consider if the TFs are the top 500 genes. Finally, by linking the TF–region and peak–gene relationships, we construct the TF-GRNs that are associated cell fate probabilities.

In the alternative approach of only integrating RNA across time, we selected the peaks that are within 250 kb upstream of and downstream from the TSS of the top-ranking genes, with a Pearson's correlation greater than 0.2.

Data access

All raw and processed sequencing data generated in this study have been submitted to the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE223041. scTIE is available at GitHub (https://github.com/SydneyBioX/scTIE) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.