Abstract

Potassium ion channels are the structural basis for excitation transmission, heartbeat, and other biological processes. The selectivity filter is a critical structural component of potassium ion channels, whose structure is crucial to realizing their function. As biomolecules vibrate and rotate at frequencies in the terahertz band, potassium ion channels are sensitive to terahertz waves. Therefore, it is worthwhile to investigate how the terahertz wave influences the selectivity filter of the potassium channels. In this study, we investigate the structure of the selectivity filter of Kv1.2 potassium ion channels using molecular dynamics simulations. The effect of an electric field on the channel has been examined at four different resonant frequencies of the carbonyl group in SF: 36.75 37.06, 37.68, and 38.2 THz. As indicated by the results, 376GLY appears to be the critical residue in the selectivity filter of the Kv1.2 channel. Its dihedral angle torsion is detrimental to the channel structural stability and the transmembrane movement of potassium ions. 36.75 THz is the resonance frequency of the carbonyl group of 376GLY. Among all four frequencies explored, the applied terahertz electric field of this frequency has the most significant impact on the channel structure, negatively impacting the channel stability and reducing the ion permeability by 20.2% compared to the absence of fields. In this study, we simulate that terahertz waves in the mid-infrared frequency region can significantly alter the structure and function of potassium ion channels and that the effects of terahertz waves differ greatly based on frequency.
1. Introduction
Ion channels are an essential class of membrane proteins, which play a vital role in many physiological processes such as neural signal generation, transmission, and heart beating.1 Regulating ion channel function is considered a means of modulating physiological processes and treating channelopathy.2 Research over the past few decades has indicated that ion channels can be modulated by a variety of factors, such as temperature,3 pH,4,5 and electromagnetic fields.6−14 In the context of electromagnetic fields, the terahertz wave has emerged as a recent focal point of research and is regarded as a novel tool for biological modulation. It has been proved that living organisms are sensitive to terahertz waves, as biomolecules vibrate and rotate in the terahertz band.15,16 Therefore, terahertz is known as the light of life,17 and the development of terahertz technology has attracted the attention of many fields, such as physics, biology, and medicine.18−20 Researchers are dedicated to exploring which frequencies in future terahertz technology applications might aid in disease treatments and which frequencies might need to be avoided.
Liu and his colleagues demonstrated that the physical field of neural information should be high-frequency electromagnetic fields within the range of terahertz to infrared,21 with the most probable frequency range being 0.5–100 THz, referred to as generalized terahertz waves.18 In recent decades, the interaction of terahertz electromagnetic waves with organisms,10−13 cells,22−24 and molecules8,9,14,25−27 have been extensively studied. An important object among them is the ion channel due to their vital physiological roles previously mentioned. Many studies have proved that terahertz waves can modulate ion channel structure28 and function10−13 and have been proposed as an emerging method of neuromodulation and disease treatment. It has been demonstrated by Li et al. that a 42.55 THz electric field can resonate with the carboxyl group of the Cav1.2 selectivity filter, lowering the potential barrier for calcium ions to pass through the channel, increasing calcium ion flux, which may be used for synaptic stimulation.8 An electric field centered at 53.6 THz has been demonstrated to resonate with the carbonyl group in a selectivity filter of potassium ion channels, improving the permeability of potassium ion channels, as demonstrated by Liu et al. They have also shown experimentally that terahertz waves of this frequency can modify zebrafish excitability, indicating that neuromodulation could be possible using terahertz waves.10 A study by Tan et al. found that an electric field at 34.88 THz resonates with the carbonyl group in the potassium channel selectivity filter and improves the sensitivity of the cochlea in mice, suggesting possible applications for terahertz waves in the treatment of diseases.12 The work of Hu et al. demonstrated that a 0.1 THz electric field resonates with potassium ions in potassium ion channels and improves permeability, which is a novel method of regulating channel functions.14 Our previous study found that an electric field of 15 THz could resonate with water molecules, reducing both the frozen and relaxation durations of potassium ion transmembrane movement and enhancing permeability.29 In addition, some studies have investigated the terahertz effect of bionic artificial channels.30,31 These studies can improve our comprehension of the physical mechanisms governing the interaction between terahertz waves and channels. Many of these studies, however, have been conducted using simplified channel models, which may overlook the subtle structural details of the ion channel as a biological protein. Moreover, most of these studies reported that terahertz waves increased permeability. However, we believe that the effects of terahertz waves on ion channels should be multifaceted and deserve in-depth studies.
In the family of ion channels, the potassium ion channel was the first to be resolved and has the most experimental structures with important physiological implications.32 Moreover, extensive research has been conducted regarding the properties of this channel.33−37 In addition, the existing studies suggest that potassium ion channels are potential molecular targets for terahertz waves. Modulating potassium channel permeability as a means of modulating neural activity has been studied extensively.10−13 However, the research on the interaction mechanisms between terahertz waves and the internal structure of potassium ion channels is still not thorough enough.
Therefore, we investigated the terahertz effects of Kv1.2 potassium ion channels in greater depth. In addition, the research on Kv1.2 ion channels may be more generalizable than research based on KcsA channels derived from bacteria17 because the Kv1.2 channel is one of a class of voltage-gated ion channels widely expressed in mammals’ nervous system38,39 and is associated with a wide variety of neurological diseases, making it therapeutically targeted.2 The selectivity filter (SF) and its adjacent residues play a fundamental role in the proper function of potassium ion channels, thus attracting extensive research attention.40−43 SF has been found to function as an external gate in potassium ion channels.44,45 Hence, in this study, we focused on the structural analysis of the Kv1.2 channel’s selectivity filter (SF), exploring the response of different SF residues to terahertz waves and investigating their influence on its structural characteristics and functional properties.
In this study, an analysis of the SF structure of the Kv1.2 voltage-gated potassium ion channel was carried out using molecular dynamics simulations. In addition, simulations with the applied terahertz electric fields of 36.75 37.06, 37.65, and 38.2 THz were used to explore the effects of the carbonyl resonance of each site on the channel. It has been found that the dihedral angle orientation of the 376GLY residue, which constitutes the S2 site of the Kv1.2 potassium ion channel, has a significant effect on its structure and permeability; 36.75 THz is the resonance frequency of the carbonyl group of this residue. Applying a terahertz electric field at this frequency is unfavorable to the channel’s structural stability and permeability.
2. Methods
2.1. Simulation Model
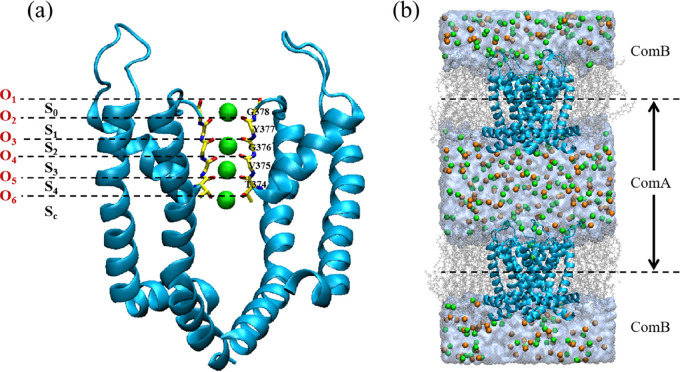
Kv1.2 voltage-gated potassium ion channel structure in an open and conductive state was obtained from Protein Data Bank entry 3LUT.46 Pore domains consisting of residues 312–421 were selected to provide a pathway for potassium to traverse the membrane, as shown in Figure 1a. The ion channel was embedded in a 9 × 9 nm POPC membrane with a natural solution environment of potassium chloride. The original model was constructed using the CHARMM-GUI Web site,47 and it consists of 178 POPC molecules, 12131 water molecules, 213 potassium ions, and 205 chloride ions. It forms a similar environment for the Kv1.2 channel to the literature48 and is identical to the model we used previously.29 Molecular graphics images were rendered by visual molecular dynamics (VMD).49
Figure 1.
Schematic diagram of the simulation model. (a) Pore domain of the Kv1.2 potassium channel and the initial potassium ion loading state in the selectivity filter (SF). For clarity, only two of the four protein subunits are shown in the New Cartoon. For the SF, the licorice modality is employed where S0–S4 and Sc represent six potassium ion sites. The six sites are composed of oxygen atoms O1–O6. O1–O5 are carbonyl oxygen atoms from the conserved sequence TVGYG in the potassium channel. O6 is the oxygen atom for the threonine side chain at the SF entrance; (b) Bilayer model. VDW spheres are used to represent ions, with green spheres representing potassium ions and orange spheres representing chloride ions. Water molecules are represented by blue QuickSurf, while membrane molecules are represented by silver lines. The membrane divides the system into two layers: ComA and ComB. As shown in the figure, the dotted line represents the position of the channel protein’s center of mass.
To use the computational electrophysiology (CompEL)50,51 method to induce a transmembrane potential, the original model was translated to a bilayer system. As illustrated in Figure 1b, the membrane divides the system into two parts: ComA and ComB. According to the CompEL code, the number of potassium and chloride ions in ComA and ComB can be adjusted to create a charge difference between the two sides of the membrane. Once the transmembrane movement of ions occurs, the CompEL code will exchange water molecules and ions in the two reservoirs to maintain the imbalance. Thus, the code can form a transmembrane potential on both sides of the membrane to provide a driving force to facilitate the transmembrane movement of potassium ions. A more detailed description of the computational electrophysiology method can be found in the literature.50,51
2.2. Simulation of Terahertz Electromagnetic Field
The molecular dynamics model size in this paper is [8.6 nm 8.6 nm 17.7 nm] on a nanoscale, and electromagnetic wavelength is on a microscale. In molecular dynamics simulations, we can disregard the wave characteristics of the terahertz electromagnetic fields, focusing solely on its field properties because terahertz waves have a significantly larger wavelength than the model’s dimensions. Furthermore, the ratio of the force applied by the magnetic field to that applied by the electric field on a charged particle is v/c, where v represents the particle’s velocity and c is the speed of light. Given that v ≪ c, the influence of the magnetic field can be neglected. These two approximate treatments of electromagnetic fields have been widely used in molecular dynamics simulation studies.8,9,14,27,31,52 In our simulations, an electric field of E = E0cos(ωt) was employed to simulate the influence of an electromagnetic field, where E0 represents the field strength and ω signifies its angular frequency. The strength of the electric field used in this study is 0.4 V/nm, which is on the same order of magnitude as the field strength used in other molecular dynamics simulation studies.8,27,52−56 According to English et al., an electric field of this magnitude is reasonable and necessary in molecular dynamics simulations,57 since the intermolecular localized electric field is usually on the order of V/nm.58−60 The frequencies we focus on in this paper are carbonyl vibrational frequencies in SF. This is because the carbonyl groups in SF are critical to the potassium ion channel function. ATR-FTIR spectroscopy experiments conducted by Furutani et al. have revealed that the SF of the potassium ion channel has abundant vibrational information at the terahertz frequency range.61,62 Applying an electric field of the frequency associated with their vibration will create a resonance, which may significantly impact the channel’s structure and functional properties. In order to obtain the vibrational power spectrum of SF carbonyl groups, their atomic velocities were recorded every 4 fs, and then the autocorrelation function was transformed by using a Fourier transform. According to the following formula, vibrational power spectra are calculated:
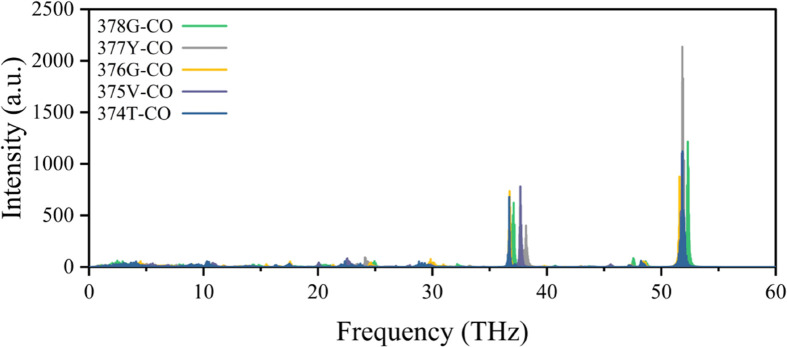
where c(t) refers to the autocorrelation function, v(t) refers to the atomic velocity, and ω refers to the vibrational frequency. The vibration power spectrum of each carbonyl is shown in Figure 2. As can be seen, each carbonyl group has its first main vibration peak around 51.8 THz. This frequency corresponds to the amide I vibration, which represents the stretching vibration of the carbonyl group.63 When an electric field is applied at this frequency, it is not easy to distinguish the effect of carbonyl resonance at each site. Further, at the second main peak around 35–40 THz, the carbonyl vibration frequencies of each site are separated. Furthermore, vibrations within this frequency range are known as amide III vibration, for the carbonyl group, primarily involving an in-plane bending motion.63 The excitations at this band will induce a structural change in C=O bending, which might affect the SF structure; therefore, we chose to study in this frequency range. The applied electric field frequency corresponds to the vibration peaks in this area, which are 36.75THz, 37.06THz, 37.68THz, and 38.2THz, corresponding to the wave numbers of 1225, 1235.3, 1256, and 1273.3 cm–1, respectively. The direction of the electric field is along the z-axis perpendicular to the membrane surface.
Figure 2.
Vibrational power spectra of the carbonyl group of the conserved residue TVGYG in SF. They correspond to the residue sequence numbers 374–378 in 3LUT, as shown in the figure. TVGY is the single-letter abbreviation for threonine, valine, glycine, and tyrosine, respectively.
2.3. Simulation Settings
All simulations were conducted using GROMACS software version 2019.4.64 CHARMM36m force field65 and CHARMM TIP3P66 water model were used due to their robustness and wide application in molecular dynamics studies of protein. An extended CHARMM-GUI equilibration protocol was followed before production simulation with a total duration of approximately 100 ns. During the relaxation simulation, restraints on the protein and lipid were gradually released. After that, the system was simulated in an NPT ensemble with no constraints imposed. Temperature and pressure were maintained at 310 K and 1 atm, respectively, using a V-rescale thermostat and a Parrinello–Rahman barostat. Particle mesh Ewald (PME) method was used to treat the long-range electrostatic force. Both electrostatic and van der Waals interactions were cut off at 1.2 nm. Under all conditions, a charge imbalance was maintained at 4e between the two sides of the membrane by using the CompEL method. The results of all analyses are averages of six repetitions of 400 ns simulations for each condition, unless otherwise stated.
It is essential to emphasize that we utilized a classical, nonpolarized molecular dynamics simulation method. While this method is efficient and widely employed in the study of terahertz biological effects,8−14,25,27,29−31 it does have its limitations. Notably, it lacks the capability to account for polarization, quantum effects, and other factors. The interaction of terahertz waves with biomolecules may not be fully described by the current method. Nevertheless, this method seems to be the most feasible to study the interactions between terahertz waves and biomolecules, at present, due to the high computational costs associated with complex methodologies such as polarized force fields and quantum computing, which are currently challenging to employ in the study of such extensive systems.8,56,67,68
3. Results and Discussion
3.1. Structure of Kv1.2 Channel Selectivity Filter
The SF structure of the Kv1.2 voltage-gated potassium ion channel is shown in Figure 1a, which consists of the conserved residue sequence of TVGYG. The carbonyl oxygen atoms of these five residues and the hydroxyl oxygen atoms of the 374THR residues constitute five sites: S0–S4. These oxygen atoms can bind tightly to potassium ions, providing a pathway for their transmembrane movement. Normally, the aperture of the SF is about 0.8 nm, and the distance between two adjacent sites is about 0.3 nm. When potassium ions pass through SF, there are charge and space conflicts with the atoms in SF, which cause structural fluctuations, and studies have shown that slight changes in the structure of these sites have a significant impact on the function of the potassium ion channel.40 The orientation change of the main-chain dihedral angle of residues in SF significantly affects its structure and is regarded as an external gating mechanism. Thus, first, we examined the distribution of the dihedral angle of the residue main chain in the SF.
3.1.1. Dihedral Angle Distribution in SF
According to Figure 3a, the main chains of residues 378GLY, 377TYR, 376GLY, and 375VAL constitute the S0, S1, S2, and S3 sites, respectively. The S4 site is formed by the main chain and side chain of 374THR. Therefore, the N-CA–C-O dihedral angles of 378GLY, 377TYR, 376GLY, 375VAL, and 374THR residues, as well as the N-CA-CB-OG1 dihedral angles of 374THR’s side chain, were analyzed to assess the stability of each site. In each residue, N represents the nitrogen atom in the amino group, CA represents the α carbon atom, and C and O represent the carbon and oxygen atoms in the carbonyl group. CB and OG1 represent the carbon and hydroxyl oxygen atoms, respectively, in the side chain of 374THR. The probability distribution for each dihedral angle value is shown in Figure 3b. Figure 3c–e illustrates the statistics of the number of flips or torsions in the four chains of each angle. Flip is defined as the dihedral angle deviating outside the major peak (i.e., the normal state) and bearing the opposite sign to that of the major peak, whereas torsion is defined as the dihedral angle deviating outside the major peak and sharing the same sign as the major peak.
Figure 3.
Distribution of dihedral angles in SF. (a) Schematic structure of SF of Kv1.2, where the green balls represent the five sites S0–S4. Licorice denotes SF; the small green balls represent the carbonyl carbon atoms (C) or the side-chain carbon atoms (CB) of 374THR; the red balls represent the carbonyl oxygen atoms (O) or the hydroxyl oxygen atoms (OG1) of 374THR; the gray balls represent the α carbon atoms (CA); and the blue balls represent the amido nitrogen atoms (N). (b) Distribution probability of each dihedral angle in SF. (c) Probability of the number of N-CA-CB-OG1 dihedral angles of the 374THR side chain flipped in four chains. (d) Probability of the number of N–CA–C–O dihedral angles of 376GLY torsion in four chains. (e) Probability of the combined state of the N–CA–C–O dihedral angle of 375VAL in four chains.
As shown in Figure 3b, there is no apparent flipping or torsion associated with the 374THR, 377TYR, and 378GLY. They fluctuate within a certain angular range and are relatively stable. In the case of the 374THR side chain, the N-CA-CB-OG1 dihedral angle has two peaks: 68 and −38°, which suggest that the dihedral angle may flip. Additionally, most of this dihedral angle has only one chain flip in four chains, as shown in Figure 3c. For 376GLY, the dihedral angle exhibits two peaks at −117 and −54°, indicating its potential for torsional motion. Moreover, torsion of one or four chains is more likely to occur, as shown in Figure 3d, and the torsion of two or three chains may be unstable. For 375VAL, the dihedral angle exhibits peaks at −125, 131, and 97°, suggesting that the dihedral angle can show both flip and torsion. Therefore, the 375VAL dihedral angle exhibits a more complex combinatorial state among the four chains, as shown in Figure 3e. Furthermore, 375VAL and 376GLY exhibit the highest proportion of abnormal (flip or torsion) dihedral angles. In previous simulation studies of potassium ion channels, these two dihedral angles were also observed to be torsion and flip frequently.40,69 Thus, we will analyze in more detail the effects of these two dihedral angle states on ion permeation events.
3.1.2. Correlation between Dihedral Angle Orientation and Ion Permeation Events
To investigate the effect of 375VAL and 376GLY dihedral angles on ion permeation events, we plotted residue dihedral angle-ion permeation event maps, as shown in Figure 4. The 400 ns trajectory is divided into 1 ns segments, where the x-axis represents the average dihedral angle over 1 ns, and the y-axis represents the number of permeation events within each segment. Figure 4a,b shows the correspondence between the dihedral angle of 375VAL/376GLY residues and ion permeation events, respectively. As can be seen, ion permeation events can occur over a wide range of 375VAL dihedral angles. However, permeation events are highly dependent on the state of the 376GLY dihedral angle and can occur only at dihedral angles −130 to −100°. Accordingly, we believe that the dihedral angle of 376GLY has a more significant influence on the channel permeability.
Figure 4.
Relationship between the dihedral angle states of 375VAL, 376GLY, and ion permeability events. md1–md6 denote six independent simulations. (a) Relationship between the 375VAL dihedral angle and ion permeation events. (b) Relationship between the 376GLY dihedral angle and ion permeability events.
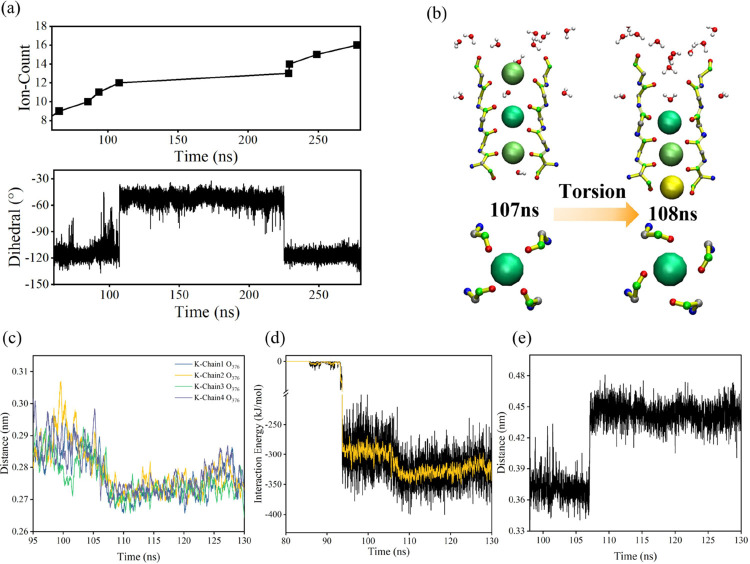
To demonstrate more clearly the relationship between the 376GLY dihedral angle and the channel permeability, we show a comparison of the ion flux with the change of the 376GLY dihedral angle over time in a single simulation, as shown in Figure 5a. A visual representation of the variation in the 376GLY dihedral angle is provided in Figure 5b. We can see that the ion flux ceases when the dihedral angle deviates from −117° and resumes when it recovers. Hence, why is the 376GLY dihedral angle torsion unfavorable for ion flux events? We attempt to provide an answer to this question.
Figure 5.
Effect of 376GLY dihedral angle torsion on ion transmembrane motion. (a) Evolution of the 376GLY dihedral angle and ion flux over time. (b) Schematic diagram of 376GLY dihedral angle torsion. (c) Effect of 376GLY dihedral angle torsion on the distance between the 376GLY carbonyl oxygen atom O376 and the potassium ion in the S2 site. (d) Effect of 376GLY dihedral angle torsion on the Coulomb potential energy between O376 and the potassium ion in the S2 site. (e) Effect of 376GLY dihedral angle torsion on the distance between the carbonyl oxygen atom O376 of 376GLY and the carbonyl oxygen atom of 377TYR.
When 376GLY is torsioned (at 108 ns), it seems clear from Figure 5c that the distance dK–O376, which represents the distance between the potassium ion in the S2 site and the carbonyl oxygen atom of 376GLY, decreases. Consequently, the Coulomb potential energy between the carbonyl oxygen atom of 376GLY and the potassium ion in S2 increases, as illustrated in Figure 5d. It means the affinity of the S2 site for the potassium ion is enhanced. Furthermore, as shown in Figure 5e, the distance between the atoms of O376 and the atom of O377 increases, making it more difficult for potassium ions to jump between the atoms of S0 and S2 sites.
Our analysis suggests that there is a significant correlation between 376GLY and ion permeation events. Additionally, Julio F. Cordero-Morales has highlighted the critical role of this residue in the KcsA channel as well.70 As TVGYG is a conserved sequence in potassium channels, we postulate that the pivotal role of this amino acid within the potassium ion channel may possess a universal character. Consequently, what accounts for the distinctiveness of this particular amino acid?
3.1.3. Crucial Role of 376GLY Residue in the Selectivity Filter
We posit that the pivotal role and distinctive status of 376GLY in the potassium channel can be attributed to several key factors.
First, in terms of the channel structure, the 376GLY residue is located in the central region of the SF. Its orientation change will be transmitted to other residues in the SF, which will have a significant effect on the structure. The aperture and the length of the sites, as the main structural features in the SF, are significantly influenced by the dihedral angle torsion of 376GLY, as indicated in Figure 6a,b. In addition, the structure is affected differently by different numbers of 376GLY dihedral angle torsions. SF structures suffer more damage from the simultaneous torsion of four chains. It can change the aperture by more than 7.6% and the site length by more than 23.5%.
Figure 6.
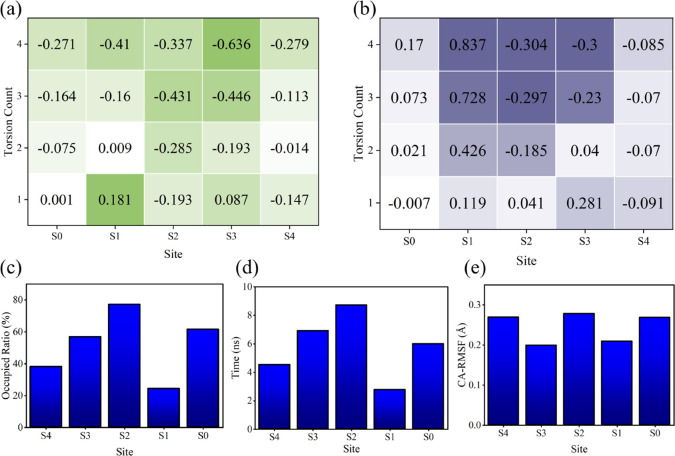
Critical role of 376GLY in Kv1.2 potassium ion channels. (a) Effect of different numbers of 376GLY dihedral angle torsions in the four chains on the SF pore diameter. For each site, the pore diameter is measured as the distance between the α carbon atoms of the residues forming the site in the two chains opposite each other. The figure displays the changes in the aperture under different numbers of torsions compared to the untorsioned state, with the unit in Ångströms (Å). The pore diameters of the S0–S4 sites in the untorsioned state are 9.15, 8.3, 8.2, 8.1, and 8.8 Å, respectively. (b) Effect of different numbers of 376GLY dihedral angle torsions in the four chains on the lengths of each SF site. Site length is defined as the distance between the upper and lower oxygen atoms corresponding to the site. The figure displays the changes in site length under different numbers of torsions compared to the untorsioned state, with the unit in Ångströms (Å). The lengths of sites S0–S4 in the untorsioned state are 4.32, 3.6, 3.4, 3.6, and 3.3 Å, respectively. (c) Probability of each site in the SF being occupied by a potassium ion. (d) Retention time of potassium ions at each site. (e) RMSF values of α carbon atoms of residues at each site.
Second, SF serves as a pathway for the transmembrane movement of potassium ions. The main chain of 376GLY constitutes the S2 site of this pathway, as shown in Figure 3. As can be seen in Figure 6c,d, the S2 site has the highest ion occupancy among all of the sites in the SF, and the ions oscillate for the longest time at this site. Therefore, the change at this site will significantly affect potassium ions’ transmembrane movement.
Finally, as depicted in Figure 6e, the RMSF of each residue’s Cα atom was employed to characterize its fluctuation behavior. Notably, 374THR, 376GLY, and 378GLY residues exhibit higher flexibility than others. Considering that 374THR and 378GLY directly interact with aqueous solutions, it is conceivable that 376GLY may be more sensitive to external influences such as the electromagnetic environment, which will be examined in this paper.
In conclusion, the various residues within the SF exert distinct influences on both the structural features and the permeation events. The 376GLY residue is one of the most important among them. Previous studies have shown that the carbonyl group in the SF of potassium ion channels can respond to an applied terahertz electric field and have an effect on the channel properties.10−12 This suggests that terahertz electric fields can modulate the functionality of potassium ion channels with the carbonyl group in the SF serving as a target for such modulation. Hence, our investigation will delve into the impact of electric fields with varying frequencies on the structure and function of the Kv1.2 channel’s selectivity filter. Specifically, we will explore the effects of electric fields applied at four distinct frequencies: 36.75, 37.06, 37.68, and 38.2 THz, which correspond to the four resonant frequencies of the carbonyl group within the selectivity filter.
3.2. Effect of Terahertz Electric Field on Kv1.2 Potassium Ion Channel
3.2.1. Effect of Terahertz Electric Field on the Channel Structure
To investigate the terahertz field’s impact on various segments of the channel, we divided the S5 and S6 helices into six distinct regions: the outer helix, turret, pore helix, selectivity filter, S6 loop, and inner helix, as depicted in Figure 7a. The mean and standard deviation of the RMSD were computed for distinct regions under varying terahertz electric field conditions, illustrated in Figure 7b. In the figure, the bar heights represent the average extent to which the channel structure deviates from its initial state under different conditions. The error bars on bars indicate the average fluctuation level of the structure. As can be seen, different frequencies of terahertz electric fields affect the channel structure differently and have varying effects on different regions. The mean of RMSD of the outer helix decreases under a terahertz field and the effects of different electric field frequencies are similar. Other regions, however, behave similarly. The turret, SF, S6 loop, and pore helix regions have the most significant deviation from the initial state and the most substantial fluctuations under the action of the 36.75 THz electric field, indicating that the electric field at this frequency is not conducive to the stabilization of the Kv1.2 structure. In contrast, the 37.06THz electric field stabilizes the structures in various regions. Electric fields applied at 38.2 and 37.68 THz induce structural damage of a similar nature, though with a lesser degree of severity compared to the 36.75 THz field. As can be seen, carbonyl resonances at different sites affect the channel structure differently. Moreover, there is a correlation between structural changes in various channel segments. This supports the conclusion drawn by Céline Boiteux’s research:45 there exists a complex conformational network within the channel, where changes in the SF can be transmitted to other structural elements, such as inner helices, and vice versa.
Figure 7.
Effect of a terahertz electric field on the structure of the Kv1.2 potassium ion channel. (a) Kv1.2 potassium ion channel structure, with orange representing the outer helix, light purple representing the turret, gray representing the pore helix, yellow representing the selectivity filter, dark green representing the S6 loop, and blue representing the inner helix. It should be noted that the S4–S5 linker is included within the outer helix for convenience in our analysis. (b) Effect of terahertz fields on the structure of various regions of the channel. The height of the bars represents the average value of RMSD from six simulations, indicating the average extent of deviation of the channel structure from its initial state. The error bars on the bars illustrate the average standard deviation of the RMSD from six simulations, indicating the average fluctuation level of structures.
Since SF constitutes a critical component of the Kv1.2 potassium channel, we examined in depth how terahertz electric fields interact with it at different frequencies. According to Figure 8a–d, different frequencies of terahertz electric fields have different effects on the anomalous ratio of the dihedral angle, RMSF values of residues, aperture, and site length. It is evident that the impact of a terahertz electric field is more pronounced on the upper half of the SF compared to the lower half. Other studies have found greater stability in the lower half of the potassium channel SF71 as well. We attribute this phenomenon to the higher probability of potassium ions occupying the lower part of the SF, which contributes to the structural stability. Moreover, the effects of different frequencies of the electric field on the SF structure vary significantly. An electric field with a frequency of 36.75 THz exerts the most significant impact on the SF structure, leading to the highest percentage of anomalies in the dihedral angle. This effect is particularly pronounced in the upper segment of the SF, notably at positions 376GLY, 377TYR, and 378GLY. The electric field at this frequency causes significant distortions in the upper region of the SF and increases the number of fluctuations of the sites. This indicates that the 36.75 THz electric field is detrimental to the stability of the SF and may impair its functionality. The reason for this may be that 36.75 THz is the vibration frequency of the key residue 376GLY carbonyl, as shown in Figure 2. Therefore, SF exhibits a higher sensitivity to the electric field at this particular frequency, resulting in a more pronounced effect on its structure. This is because the 36.75 THz electric field alters the bending state of the 376GLY carbonyl, making it more prone to a torsional state compared with that when no external field is applied. As evident from the analysis in Figure 6, this is unfavorable for the stability of the SF structure. Consequently, the electric field at this frequency induces a more pronounced deformation in the channel. Carbonyl vibration frequencies of residues 375VAL and 377TYR, located close to the 376GLY residue, are 38.2 and 37.68 THz, respectively. At these two frequencies, the SF also demonstrates sensitivity to electric fields, and there are noticeable structural changes; however, the magnitude of the effect is less pronounced compared to the impact observed at 36.75 THz. The effects of the electric field at these two frequencies on the various regions of the channel are approximate, as shown in Figure 7b. However, there is a more pronounced difference in the effects on the various sites in the SF. This suggests that the SF internal structure may be more sensitive to electric fields. Additionally, channel stability improves significantly when an electric field at 37.06 THz is applied. We hypothesize that the resonance of the 378GLY carbonyl at the SF exit with the 37.06 THz electric field may contribute to its increased capacity for coordinating potassium ions. As a result, as shown in Figure 9a, the S0 site can be more effective at stabilizing potassium ions under this electric field. It has been shown by Wojciech Kopec’s study that S0 loss of potassium ions is detrimental to SF stabilization,72 which is a plausible explanation for the increased channel stability caused by this electric field.
Figure 8.
Effect of a terahertz electric field on the structure of the Kv1.2 selectivity filter. (a) Effect of terahertz electric fields on the ratio of dihedral angle anomalies at each site of the SF. (b) Effect of terahertz electric fields on the RMSF of each residue α carbon atom in SF. (c) Effect of terahertz electric fields on the SF aperture. For each site, the pore diameter is measured as the distance between the α carbon atoms of the residues forming the site in the two chains opposite each other. The figure illustrates changes in the average aperture when subjected to a terahertz electric field, in comparison to the scenario without an applied field. In the absence of an applied field, the average apertures at S4–S0 sites measure as follows: 9.1, 8.3, 8.1, 8.1, and 8.8 Å. (d) Effect of the terahertz electric fields on the length of SF sites. The figure illustrates changes in the average site length when subjected to a terahertz electric field in comparison with the scenario without an applied field. In the absence of an applied field, the average length of S4–S0 sites measured as follows: 3.3, 3.6, 3.3, 3.7, and 4.3 Å.
Figure 9.
Terahertz electric field effects on potassium ion transmembrane movement. (a) Potassium ion occupancy probability at each site. (b) Water molecule occupancy probability at each site. (c) Probability of the simultaneous presence of two or three potassium ions in SF. (d) Ion flux within 2.4 μs.
3.2.2. Effect of Terahertz Electric Field on the Potassium Ion Movement within the SF
The SF of Kv1.2 is a pathway for potassium ions to achieve transmembrane movement; therefore, its structure alterations will impact the distribution of potassium ions within the SF. Based on Figure 9, when exposed to a 36.75 THz electric field, there was a reduction in potassium ion occupancy at S1 and S0 sites within the SF, an increase in water molecule occupancy at these sites, and the state of three potassium ions existing simultaneously in SF decreased. On the contrary, the 37.06 THz electric field reduces the water molecule occupancy and increases the potassium ion occupancy at the S1 and S0 sites, and the state in which three potassium ions occupy SF simultaneously is significantly increased. It is thought that this is due to the 37.06 THz electric field improving the stability of the SF structure, so that it is able to accommodate more potassium ions. Conversely, at 36.75 THz, the SF structure deviates further from its normal state, leading to a diminished capacity for potassium ion accommodation. At 37.68 and 38.2 THz electric fields, the average number of potassium ions in the SF is similar, slightly lower than that in the absence of an external field. However, there are significant differences in their distribution across the sites. This implies that the effect of terahertz electric fields of different frequencies on the channel is highly specific.
Permeability is one of the most important functional characteristics of potassium ion channels. The comparison of channel permeability under different electric field effects was conducted based on the cumulative potassium ion flux through the channel within 2.4 μs. In Figure 9 d, it is evident that the permeability of the Kv1.2 potassium ion channel was reduced by 20.2% with an electric field of 36.75 THz, while it was increased by 12.8% with an electric field of 37.06 THz. In Figures 5 and 6, we show that the torsion of the 376GLY main-chain dihedral angle hinders the transmembrane movement of potassium ions, resulting in a distorted potassium-depleted state at the S1 and S0 sites. Furthermore, the state of deformation and nonoccupancy of the S1 and S0 sites is generally considered to be associated with the inactivation of potassium ion channels, which impairs their permeability.34,69,71 Therefore, from the previous analysis of the structure and the distribution state of potassium ions, it makes sense that an electric field of 36.75 and 37.06 THz would have the effect on permeability described above. Unexpectedly, despite the similarities in the structural impact of electric fields at 37.68 and 38.2 THz on potassium ion channels, their effects on permeability are, in fact, contrasting. The permeability was reduced by 12.8% when the electric field was 37.68 THz, while it increased by 11.7% when it was 38.2 THz. This indicates that even subtle changes in the SF structure are sufficient to lead to alterations in its functionality.
4. Conclusions
The selectivity filter represents a pivotal structure within potassium ion channels, and its configuration plays a fundamental role in facilitating the transmembrane passage of potassium ions. In this paper, molecular dynamics simulations were conducted to examine the structure of the selectivity filter of the Kv1.2 voltage-gated potassium ion channel as well as the effects of terahertz electric fields of different frequencies on the channel properties. We investigated four frequencies in this paper, which correspond to the vibration frequencies of carbonyls in SF, namely 36.75 37.06, 37.68, and 38.2 THz. It was concluded that the dihedral angle orientation of 376GLY in the SF of the Kv1.2 channel is critical to the stability of the SF structure and the transmembrane movement of potassium ions in the channel. Moreover, the residue was sensitive to an electric field of 36.75 THz, as this frequency corresponded to the resonance frequency of the carbonyl group in this amino acid. The 36.75 THz electric field makes the 376GLY main-chain dihedral angle more prone to a torsional state compared with that when no external field is applied, resulting in an 18.7% increase in anomalies of the 376GLY dihedral angle. This is considered detrimental to the stability and permeability of the channel, thereby leading to a 20.2% decrease in ion permeability. In contrast, the 37.06 THz electric field significantly enhances the capability of the S0 site to accommodate potassium ions, thereby promoting channel stability, and resulting in a remarkable 12.8% increase in ion permeability. Both the 37.68 and 38.2 THz electric fields induce structural perturbations in the channel, albeit with slight variations in their effects. As a result, they have opposite effects on permeability, with the former reducing ion permeability by 12.8% and the latter increasing it by 11.7%. This suggests that slight differences in the structural properties of SF are sufficient to alter the function of potassium channels.
This study indicates that terahertz electric fields are extremely complex in their interaction with biomolecules, and their effect on ion channels has a significant frequency specificity. The terahertz electric field can have a dual impact: it can enhance the ion channel functionality, serving as a potential therapeutic approach for ion channel-related diseases. However, it can also disrupt the channel structure and function, which may be detrimental to biological systems. Hence, it is highly desirable to conduct further investigations into the mechanisms of interaction between terahertz fields and biomolecules. In addition, this study also offers novel insights for the design and manipulation of nanodevices inspired by biological channels: the applied terahertz electric field may serve as a novel modulation method for improving their flexibility and functionality.
Acknowledgments
This work was financially supported by the Fundamental Research Funds for the Central Universities (No. xzy022023057). The authors acknowledge the powerful computing resources and the technical support provided by the HPC Platform, Xi’an Jiaotong University.
The authors declare no competing financial interest.
References
- Hille B.Ion Channels of Excitable Membranes; Sinauer Associates: Sunderland, Massachusetts U.S.A., 2001. [Google Scholar]
- Wulff H.; Castle N. A.; Pardo L. A. Voltage-Gated Potassium Channels as Therapeutic Targets. Nat. Rev. Drug Discovery 2009, 8, 982–1001. 10.1038/nrd2983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X.; Jiang Y.; Rommelfanger N. J.; Yang F.; Zhou Q.; Yin R.; Liu J.; Cai S.; Ren W.; Shin A.; et al. Tether-Free Photothermal Deep-Brain Stimulation in Freely Behaving Mice via Wide-Field Illumination in the Near-Infrared-II Window. Nat. Biomed. Eng. 2022, 6, 754–770. 10.1038/s41551-022-00862-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giudici A. M.; Renart M. L.; Díaz-García C.; Morales A.; Poveda J. A.; González-Ros J. M. Accessibility of Cations to the Selectivity Filter of KcsA in the Inactivated State: An Equilibrium Binding Study. Int. J. Mol. Sci. 2019, 20, 689. 10.3390/ijms20030689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakrapani S.; Cordero-Morales J. F.; Perozo E. A Quantitative Description of KcsA Gating I: Macroscopic Currents. J. Gen. Physiol. 2007, 130, 465–478. 10.1085/jgp.200709843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohrasebi A.; Sajadi M. Effect of External Electric Fields on the Potential Energy Profile of K+ions in Selective Filter of the KcsA Potassium Channel. Mol. Simul. 2014, 40, 1067–1073. 10.1080/08927022.2013.840905. [DOI] [Google Scholar]
- Sajadi M.; Lohrasebi A.; Rafii-Tabar H. Modelling the Effect of a GHz Electric Field on the Dynamics of K+ Ions in KcsA Potassium Channel. Mol. Simul. 2014, 40, 399–407. 10.1080/08927022.2013.812789. [DOI] [Google Scholar]
- Li Y.; Chang C.; Zhu Z.; Sun L.; Fan C. Terahertz Wave Enhances Permeability of the Voltage-Gated Calcium Channel. J. Am. Chem. Soc. 2021, 143, 4311–4318. 10.1021/jacs.0c09401. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Wang L.; Li Y.; Zhu Z. Terahertz Waves Enhance the Permeability of Sodium Channels. Symmetry 2023, 15, 427. 10.3390/sym15020427. [DOI] [Google Scholar]
- Liu X.; Qiao Z.; Chai Y.; Zhu Z.; Wu K.; Ji W.; Li D.; Xiao Y.; Mao L.; Chang C.; et al. Nonthermal and Reversible Control of Neuronal Signaling and Behavior by Midinfrared Stimulation. Proc. Natl. Acad. Sci. U. S. A. 2021, 118, e2015685118 10.1073/pnas.2015685118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J.; He Y.; Liang S.; Liao X.; Li T.; Qiao Z.; Chang C.; Jia H.; Chen X. Non-Invasive, Opsin-Free Mid-Infrared Modulation Activates Cortical Neurons and Accelerates Associative Learning. Nat. Commun. 2021, 12, 2730. 10.1038/s41467-021-23025-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan X.; Wu K.; Liu S.; Yuan Y.; Chang C.; Xiong W. Minimal-Invasive Enhancement of Auditory Perception by Terahertz Wave Modulation. Nano Res. 2022, 15, 5235–5244. 10.1007/s12274-022-4127-7. [DOI] [Google Scholar]
- Xiao T.; Wu K.; Wang P.; Ding Y.; Yang X.; Chang C.; Yang Y. Sensory Input-Dependent Gain Modulation of the Optokinetic Nystagmus by Mid-Infrared Stimulation in Pigeons. eLife 2023, 12, e78729 10.7554/eLife.78729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Z. H.; Lv W. P.; Hui D. X.; Wang X. J.; Wang Y. N. Permeability Enhancement of the KcsA Channel under Radiation of a Terahertz Wave. Phys. Rev. E 2022, 105, 024104 10.1103/PhysRevE.105.024104. [DOI] [PubMed] [Google Scholar]
- Zhu Z.; Cheng C.; Chang C.; Ren G.; Zhang J.; Peng Y.; Han J.; Zhao H. Characteristic Fingerprint Spectrum of Neurotransmitter Norepinephrine with Broadband Terahertz Time-Domain Spectroscopy. Analyst 2019, 144, 2504–2510. 10.1039/C8AN02079E. [DOI] [PubMed] [Google Scholar]
- Woods K. N.; Pfeffer J.; Dutta A.; Klein-Seetharaman J. Vibrational Resonance, Allostery, and Activation in Rhodopsin-Like G Protein-Coupled Receptors. Sci. Rep. 2016, 6, 37290. 10.1038/srep37290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang P.; Lou J.; Fang G.; Chang C. Progress on Cutting-Edge Infrared-Terahertz Biophysics. IEEE Trans. Microwave Theory Technol. 2022, 70, 5117–5140. 10.1109/TMTT.2022.3200333. [DOI] [Google Scholar]
- Guozhi L. The Conjectures on Physical Mechanism of Vertebrate Nervous System. Chin. Sci. Bull. 2018, 63, 3864–3865. 10.1360/N972018-01143. [DOI] [Google Scholar]
- Ramundo Orlando A.; Gallerano G. P. Terahertz Radiation Effects and Biological Applications. J. Infrared, Millimeter, Terahertz Waves 2009, 1308–1318. 10.1007/s10762-009-9561-z. [DOI] [Google Scholar]
- Oh S. J.; Kim S. H.; Ji Y. B.; Jeong K.; Park Y.; Yang J.; Park D. W.; Noh S. K.; Kang S. G.; Huh Y. M.; et al. Study of Freshly Excised Brain Tissues Using Terahertz Imaging. Biomed. Opt. Express 2014, 5, 2837–2842. 10.1364/BOE.5.002837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu G.; Chang C.; Qiao Z.; Wu K.; Zhu Z.; Cui G.; Peng W.; Tang Y.; Li J.; Fan C. Myelin Sheath as a Dielectric Waveguide for Signal Propagation in the Mid-Infrared to Terahertz Spectral Range. Adv. Funct. Mater. 2019, 29, 1807862 10.1002/adfm.201807862. [DOI] [Google Scholar]
- Hu E.; Zhang Q.; Shang S.; Jiang Y.; Lu X. Continuous Wave Irradiation at 0.1 Terahertz Facilitates Transmembrane Transport of Small Molecules. iScience 2022, 25, 103966 10.1016/j.isci.2022.103966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshevskaya J. S.; Ratushnyak A. S.; Petrov A. K.; Kozlov A. S.; Zapara T. A.. Effect of Terahertz Electromagnetic Waves on Neurons Systems. In 2008 IEEE Region 8 International Conference on Computational Technologies in Electrical and Electronics Engineering, Novosibirsk, Russia, July 21–25, 2008; pp. 210–211, 10.1109/SIBIRCON.2008.4602607. [DOI] [Google Scholar]
- Ratushnyak A.; Olshevskaya J.; Kozlov A.; Petrov A.; Zapara T. Influence of Terahertz (submillimeter) Laser Radiation on Neurons in Vitro. J. Higher Nerv. Act. 2009, 59, 342–348. [PubMed] [Google Scholar]
- Wu K.; Qi C.; Zhu Z.; Wang C.; Song B.; Chang C. Terahertz Wave Accelerates DNA Unwinding: A Molecular Dynamics Simulation Study. J. Phys. Chem. Lett. 2020, 11, 7002–7008. 10.1021/acs.jpclett.0c01850. [DOI] [PubMed] [Google Scholar]
- Li Y.; Zhu Z.; Sun L.; Xiang Z.; Chang C.; Fan C. Physicochemical Insights on Terahertz Wave Diminished Side Effects of Drugs from Slow Dissociation. ACS Nano 2022, 16, 8419–8426. 10.1021/acsnano.2c02952. [DOI] [PubMed] [Google Scholar]
- Zhang Q.; Yang L.; Wang K.; Guo L.; Ning H.; Wang S.; Gong Y. Terahertz Waves Regulate the Mechanical Unfolding of Tau Pre-mRNA Hairpins. iScience 2023, 26, 107572 10.1016/j.isci.2023.107572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y. K.; Guo L. H.; Wang K. C.; Wang S. M.; Gong Y. B. Molecular Dynamics Simulation of Effect of Terahertz Waves on the Secondary Structure of Potassium Channel Proteins. Acta Phys. Sin. 2021, 70, 248701. 10.7498/aps.70.20211725. [DOI] [Google Scholar]
- Zhao X.; Ding W.; Wang H.; Wang Y.; Liu Y.; Li Y.; Liu C. Permeability Enhancement of Kv1.2 Potassium Channel by a Terahertz Electromagnetic Field. J. Chem. Phys. 2023, 159, 045101 10.1063/5.0143648. [DOI] [PubMed] [Google Scholar]
- Zhu Z.; Chen C.; Chang C.; Song B. Terahertz-Light Induced Structural Transition and Superpermeation of Confined Monolayer Water. ACS Photonics 2021, 8, 781–786. 10.1021/acsphotonics.0c01336. [DOI] [Google Scholar]
- Zhu Z.; Chang C.; Shu Y.; Song B. Transition to a Superpermeation Phase of Confined Water Induced by a Terahertz Electromagnetic Wave. J. Phys. Chem. Lett. 2020, 11, 256–262. 10.1021/acs.jpclett.9b03228. [DOI] [PubMed] [Google Scholar]
- Fowler P. W.; Abad E.; Beckstein O.; Sansom M. S. Energetics of Multi-Ion Conduction Pathways in Potassium Ion Channels. J. Chem. Theory Comput. 2013, 9, 5176–5189. 10.1021/ct4005933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumikama T.; Oiki S. Digitalized K+ Occupancy in the Nanocavity Holds and Releases Queues of K+ in a Channel. J. Am. Chem. Soc. 2016, 138, 10284–10292. 10.1021/jacs.6b05270. [DOI] [PubMed] [Google Scholar]
- Wu Y.; Yan Y.; Yang Y.; Bian S.; Rivetta A.; Allen K.; Sigworth F. J. Cryo-EM Structures of Kv1.2 Potassium Channels Conducting and Non-Conducting. eLife 2023, 12, RP89459 10.7554/elife.89459.1. [DOI] [Google Scholar]
- Jensen M. Ø.; Borhani D. W.; Lindorff-Larsen K.; Maragakis P.; Jogini V.; Eastwood M. P.; Dror R. O.; Shaw D. E. Principles of Conduction and Hydrophobic Gating in K+ Channels. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 5833–5838. 10.1073/pnas.0911691107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mironenko A.; Zachariae U.; de Groot B. L.; Kopec W. The Persistent Question of Potassium Channel Permeation Mechanisms. J. Mol. Biol. 2021, 433, 167002 10.1016/j.jmb.2021.167002. [DOI] [PubMed] [Google Scholar]
- Delemotte L.; Tarek M.; Klein M. L.; Amaral C.; Treptow W. Intermediate States of the Kv1.2 Voltage Sensor from Atomistic Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 6109–6114. 10.1073/pnas.1102724108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H.; Kunkel D.; Schwartzkroin P. A.; Tempel B. Localization of Kv1.1 and Kv1.2, Two K Channel Proteins, to Synaptic Terminals, Somata, and Dendrites in the Mouse Brain. J. Neurosci. 1994, 14, 4588–4599. 10.1523/JNEUROSCI.14-08-04588.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niday Z.; Tzingounis A. Potassium Channel Gain of Function in Epilepsy: An Unresolved Paradox. Neuroscientist 2018, 24, 368–380. 10.1177/1073858418763752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J.; Shen R.; Rohaim A.; Mendoza Uriarte R.; Fajer M.; Perozo E.; Roux B. Computational Study of Non-Conductive Selectivity Filter Conformations and C-type Inactivation in a Voltage-dependent Potassium Channel. J. Gen. Physiol. 2021, 153, e202112875 10.1085/jgp.202112875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostmeyer J.; Chakrapani S.; Pan A.; Perozo E.; Roux B. Recovery from Slow Inactivation in K Channels is Controlled by Water Molecules. Nature 2013, 501, 121–124. 10.1038/nature12395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuello L. G.; Jogini V.; Cortes D. M.; Perozo E. Structural Mechanism of C-Type Inactivation in K+ Channels. Nature 2010, 466, 203–208. 10.1038/nature09153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pless S. A.; Galpin J. D.; Niciforovic A. P.; Kurata H. T.; Ahern C. A. Hydrogen Bonds as Molecular Timers for Slow Inactivation in Voltage-Gated Potassium Channels. eLife 2013, 2, e01289 10.7554/eLife.01289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berneche S.; Roux B. A Gate in the Selectivity Filter of Potassium Channels. Structure 2005, 13, 591–600. 10.1016/j.str.2004.12.019. [DOI] [PubMed] [Google Scholar]
- Boiteux C.; Posson D. J.; Allen T. W.; Nimigean C. M. Selectivity Filter Ion Binding Affinity Determines Inactivation in a Potassium Channel. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 29968–29978. 10.1073/pnas.2009624117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X.; Wang Q.; Ni F.; Ma J. Structure of the Full-Length Shaker Potassium Channel Kv1.2 by Normal-Mode-Based X-Ray Crystallographic Refinement. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 11352–11357. 10.1073/pnas.1000142107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo S.; Kim T.; Iyer V. G.; Im W. CHARMM-GUI: A Web-Based Graphical User Interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- Kopec W.; Köpfer D. A.; Vickery O. N.; Bondarenko A. S.; Jansen T. L. C.; de Groot B. L.; Zachariae U. Direct Knock-On of Desolvated Ions Governs Strict Ion Selectivity in K+ Channels. Nat. Chem. 2018, 10, 813–820. 10.1038/s41557-018-0105-9. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Kutzner C.; Grubmuller H.; de Groot B. L.; Zachariae U. Computational Electrophysiology: The Molecular Dynamics of Ion Channel Permeation and Selectivity in Atomistic Detail. Biophys. J. 2011, 101, 809–817. 10.1016/j.bpj.2011.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutzner C.; Köpfer D. A.; Machtens J.-P.; de Groot B. L.; Song C.; Zachariae U. Insights into the Function of Ion Channels by Computational Electrophysiology Simulations. Biochim. Biophys. Acta, Biomembr. 2016, 1858, 1741–1752. 10.1016/j.bbamem.2016.02.006. [DOI] [PubMed] [Google Scholar]
- English N. J.; Solomentsev G. Y.; O’Brien P. Nonequilibrium Molecular Dynamics Study of Electric and Low-Frequency Microwave Fields on Hen Egg White Lysozyme. J. Chem. Phys. 2009, 131, 035106 10.1063/1.3184794. [DOI] [PubMed] [Google Scholar]
- Astrakas L. G.; Gousias C.; Tzaphlidou M. Structural Destabilization of Chignolin under the Influence of Oscillating Electric Fields. J. Appl. Phys. 2012, 111, 074702 10.1063/1.3699389. [DOI] [Google Scholar]
- Atilhan M.; Aparicio S. Behavior of Deep Eutectic Solvents under External Electric Fields: A Molecular Dynamics Approach. J. Phys. Chem. B 2017, 121, 221–232. 10.1021/acs.jpcb.6b09714. [DOI] [PubMed] [Google Scholar]
- Budi A.; Legge F. S.; Treutlein H.; Yarovsky I. Electric Field Effects on Insulin Chain-B Conformation. J. Phys. Chem. B 2005, 109, 22641–22648. 10.1021/jp052742q. [DOI] [PubMed] [Google Scholar]
- Marracino P.; Havelka D.; Prusa J.; Liberti M.; Tuszynski J.; Ayoub A. T.; Apollonio F.; Cifra M. Tubulin Response to Intense Nanosecond-Scale Electric Field in Molecular Dynamics Simulation. Sci. Rep. 2019, 9, 10477. 10.1038/s41598-019-46636-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- English N. J.; Mooney D. A. Denaturation of Hen Egg White Lysozyme in Electromagnetic Fields: A Molecular Dynamics Study. J. Chem. Phys. 2007, 126, 091105 10.1063/1.2515315. [DOI] [PubMed] [Google Scholar]
- Futera Z.; English N. J. Communication: Influence of External Static and Alternating Electric Fields on Water from Long-Time Non-Equilibrium ab Initio Molecular Dynamics. J. Chem. Phys. 2017, 147, 031102 10.1063/1.4994694. [DOI] [PubMed] [Google Scholar]
- Reale R.; English N. J.; Marracino P.; Liberti M.; Apollonio F. Dipolar Response and Hydrogen-Bond Kinetics in Liquid Water in Square-Wave Time-Varying Electric Fields. Mol. Phys. 2014, 112, 1870–1878. 10.1080/00268976.2013.867081. [DOI] [Google Scholar]
- Reale R.; English N. J.; Marracino P.; Liberti M.; Apollonio F. Translational and Rotational Diffusive Motion in Liquid Water in Square-Wave Time-Varying Electric Fields. Chem. Phys. Lett. 2013, 582, 60–65. 10.1016/j.cplett.2013.07.030. [DOI] [Google Scholar]
- Furutani Y.; Shimizu H.; Asai Y.; Fukuda T.; Oiki S.; Kandori H. ATR-FTIR Spectroscopy Revealing the Different Vibrational Modes of the Selectivity Filter Interacting with K+ and Na+ in the Open and Collapsed Conformations of the KcsA Potassium Channel. J. Phys. Chem. Lett. 2012, 3, 3806–3810. 10.1021/jz301721f. [DOI] [PubMed] [Google Scholar]
- Furutani Y.; Shimizu H.; Asai Y.; Oiki S.; Kandori H. Specific interactions between alkali metal cations and the KcsA channel studied using ATR-FTIR spectroscopy. Biophysics and Physicobiology 2015, 12, 37–45. 10.2142/biophysico.12.0_37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fayer M. D.Ultrafast infrared vibrational spectroscopy; CRC Press, 2013. [Google Scholar]
- Abraham M.; Murtola T.; Schulz R.; Páll S.; Smith J.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Huang J.; Rauscher S.; Nawrocki G.; Ting R.; Feig M.; de Groot B.; Grubmüller H.; MacKerell A. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2016, 14, 71–73. 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A. D. Jr.; Bashford D.; Bellott M.; Dunbrack R. L. Jr.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- Baker C. M. Polarizable Force Fields for Molecular Dynamics Simulations of Biomolecules. WIREs Comput. Mol. Sci. 2015, 5, 241–254. 10.1002/wcms.1215. [DOI] [Google Scholar]
- Jing Z.; Liu C.; Cheng S. Y.; Qi R.; Walker B. D.; Piquemal J. P.; Ren P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394. 10.1146/annurev-biophys-070317-033349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondo H. X.; Yoshida N.; Shirota M.; Kinoshita K. Molecular Mechanism of Depolarization-Dependent Inactivation in W366F Mutant of Kv1.2. J. Phys. Chem. B 2018, 122, 10825–10833. 10.1021/acs.jpcb.8b09446. [DOI] [PubMed] [Google Scholar]
- Cordero-Morales J. F.; Jogini V.; Lewis A.; Vasquez V.; Cortes D. M.; Roux B.; Perozo E. Molecular Driving Forces Determining Potassium Channel Slow Inactivation. Nat. Struct. Mol. Biol. 2007, 14, 1062–1069. 10.1038/nsmb1309. [DOI] [PubMed] [Google Scholar]
- Tan X.-F.; Bae C.; Stix R.; Fernandez-Mariño A.; Huffer K.; Chang T.-H.; Jiang J.; Faraldo-Gómez J.; Swartz K. Structure of the Shaker Kv Channel and Mechanism of Slow C-Type Inactivation. Sci. Adv. 2022, 8, eabm7814 10.1126/sciadv.abm7814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopec W.; Thomson A. S.; de Groot B. L.; Rothberg B. S. Interactions between selectivity filter and pore helix control filter gating in the MthK channel. J. Gen. Physiol. 2023, 155, e202213166 10.1085/jgp.202213166. [DOI] [PMC free article] [PubMed] [Google Scholar]