Understanding the ant’s unique biting system can improve surgical needle holders

Significance

The grasping and holding tools of robotics, microassembly, or endoscopic surgery operate in confined spaces. This limits their maximum size and performance. We studied one of nature’s solutions for this problem: the ant’s mandibles, which combine strong biting performance with elaborate maneuverability of objects. Their mandibles are characterized by gliding joints, tilting axes, and changing power transmission during the opening and closing process. We transferred these three design principles to a commercially available surgical needle holder. That substantially improved the grasping performance of the needle holder.

Abstract

Mechanical grasping and holding devices depend upon a firm and controlled grip. The possibility to improve this gripping performance is severely limited by the need for miniaturization in many applications, such as robotics, microassembly, or surgery. In this paper, we show how this gripping can be improved in one application (the endoscopic needle holder) by understanding and imitating the design principles that evolution has selected to make the mandibles of an ant a powerful natural gripping device. State-of-the-art kinematic, morphological, and engineering approaches show that the ant, in contrast to other insects, has considerable movement within the articulation and the jaw´s rotational axis. We derived three major evolutionary design principles from the ant’s biting apparatus: 1) a mobile joint axis, 2) a tilted orientation of the mandibular axis, and 3) force transmission of the adductor muscle to the tip of the mandible. Application of these three principles to a commercially available endoscopic needle holder resulted in calculated force amplification up to 296% and an experimentally measured one up to 433%. This reduced the amount of translations and rotations of the needle, compared to the needle’s original design, while retaining its size or outer shape. This study serves as just one example showing how bioengineers might find elegant solutions to their design problems by closely observing the natural world.

Grasping and holding are among the most important functions of tools that humans use to manipulate objects (1). In many cases, these tasks must be performed by miniaturized tools in confined spaces. This limits the possibilities of the tool design and leads to a trade-off between tool size and performance (2–5).

This is particularly important in endoscopic surgery, where stitching is performed inside the patient’s body with delicate needle holders (Fig. 1A) (4–6). These needle holders need to enter the body through small ports, thus imposing important limitations on the size of the needle holder (7).

Fig. 1.

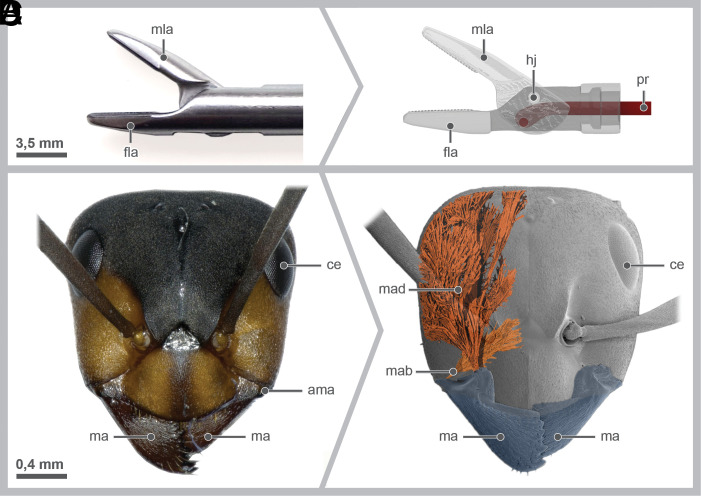
(A) The used commercial needle holder, lateral view; (B) 3D model of the function of the needle holder in the lateral view. Abbreviations: ama: anterior mandibular joint, ce: compound eye, fla: fixed lever arm, hj: hinge joint, ma: mandible, mab: mandibular abductor, mad: mandibular adductor, mla: moveable lever arm, pr: push rod; (C) photograph of the head of the red wood ant Formica rufa in the frontal view; (D) 3D model of the head of F. rufa in the frontal view showing the mandibles and the associated musculature, cuticle rendered transparent.

In most commercial products, the needle is grasped with two jaws that converge into a hinge joint (Fig. 1 A and B). The movable lever arm (mla, Fig. 1 A and B) is controlled by a push rod (pr, Fig. 1B) that delivers force from a handle. Surgeons routinely experience that the needle rotates or tilts in the needle holder, particularly with the so-called “decisive” sutures (8, 9). Consequently, the needle must be regrasped inside the patient’s body, and the stitch must be attempted again, potentially causing reduced accuracy, increased bleeding, and increased surgical time.

To date, PubMed and patent repositories describe over a dozen types of innovative needle holders (e.g., refs. 10 and 11). Yet to our awareness, none of these available needle holders has been modeled after the evolutionary design developed by nature, despite the fact that animals have evolved various specific anatomic solutions for grasping or holding (e.g., refs. 12 and 13).

An elaborate example of such a miniaturized evolutionary grasping device is the biting apparatus of insects (14), the most successful lineage of organisms in terms of species richness on this planet (15). One group of insects that is particularly well adapted to grasping and holding are ants. They use their primary mouthparts, the mandibles (ma, Fig. 1 C and D) to carry food, catch prey, cut leaves, construct nests, or care for their brood (16). These mandibles are moved by two muscles: an adductor (mad, Fig. 1D) and an abductor (mab, Fig. 1D).

In this contribution, we used state-of-the-art 3D approaches from engineering, medicine, and comparative zoology, such as µ-CT, 3D-modeling, and kinematic analyses, to analyze the function, morphology, and kinematics of the primary mouthparts of the red wood ant (F. rufa), in order to digitally reconstruct the potential movements in the ant’s mandible (Fig. 2A). The ant was selected because it is known for carrying material of various shapes, weights, and sizes but also gently handling the offspring. Additionally, it has been reported that ants allow movement within the mandibular articulation (e.g., refs. 17 and 18). We extracted three evolutionary design principles from our data. We then applied these three design principles to a commercially available endoscopic needle holder. Virtual models were created based on each design principle. We evaluated their performance in comparison to a commercially available model (Fig. 1A) with experimental measures (Fig. 3) and theoretical calculations (SI Appendix, Supplementary Material 2). To allow a meaningful comparison of their performance, we held constant the technical parameters, such as surface texture, material pairings, needle position, needle geometry, and the actuator force. Thus, the general performance of the entire device, i.e., the reductions of rotations and translations of the needle hampering accuracy, can be attributed to the optimization of the force transmission. Theoretically, also other parameters such as the shape and surface pattern of the ant mandible, which was addressed by Zhang et al. (19), could improve the needle holder.

Fig. 2.

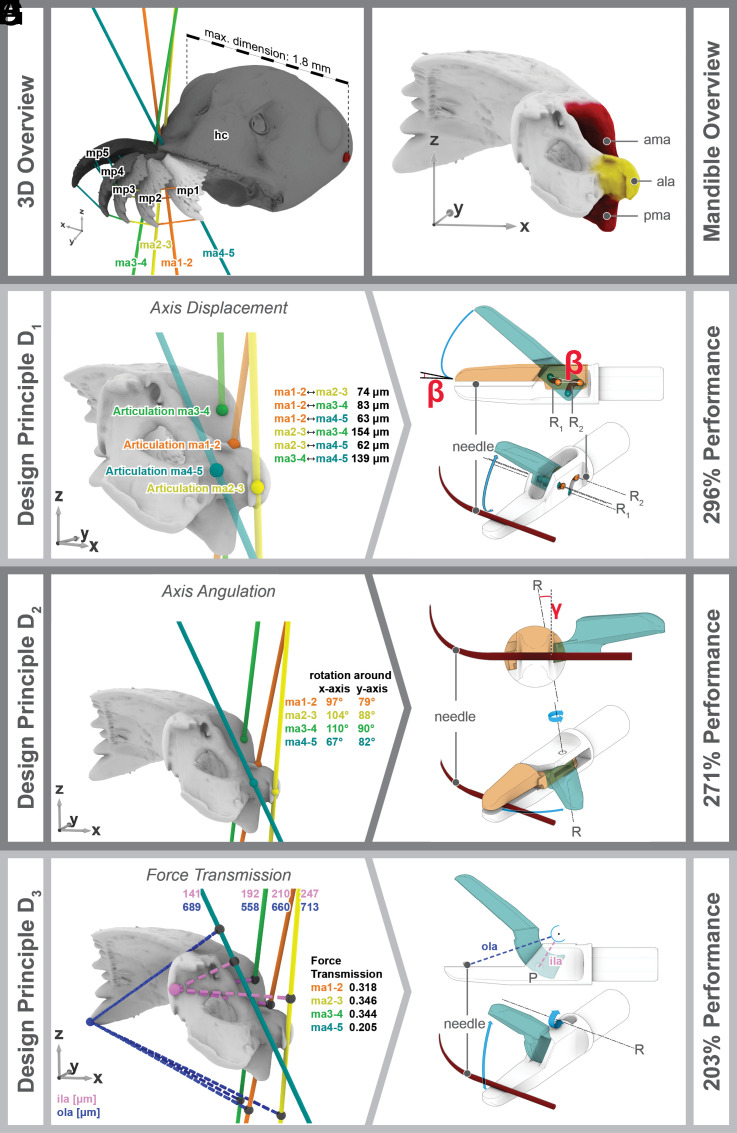
(A) 3D model of the head capsule of F. rufa showing the different studied mandibular positions (mp) and the resulting mandibular axes (ma); (B) articulations of the mandible of F. rufa with the head capsule; (C) 3D model of the mandible of F. rufa in dorsal view showing the points where the mandibular axes meet the surface of the mandibular joint (dots in colors used in A) and the distance between them. (D) Needle holder design D₁ derived from the principle of the moveable joint axis, moveable arm in closed (orange) and fully opened (green) position; (E) mandibular axes and their inclination (in °) toward the X- and Y-axis of the head capsule, colored balls show points of articulations; (F) needle holder design D₂, which is derived from the principle of the tilted axis, shown in frontal view (Top) and dorso-lateral view (Bottom), moveable arm in closed (orange) and fully opened (green) position, angle β is in between the axis of rotation and the plane of the needle; (G) inner (ila) and outer (ola) lever arms of the different mandibular axes (in µm) and the resulting force transmission (= ila/ola); (H) needle holder design D₃ derived from the principle of the force transmission ratio. Abbreviations: ala: alata, ama: anterior mandibular articulation, hc: head capsule, ila: inner lever arm; ma: mandibular axes, ma: mandibular axis, mp: mandibular opening positions, ola: outer lever arm; pma: posterior mandibular articulation, R: rotational axis of the respective needle holder, β: 10° inclination used in D_1, γ: angle between the rotational axis and normal of the gripper surfaces in D₂ (10°)_.

Fig. 3.

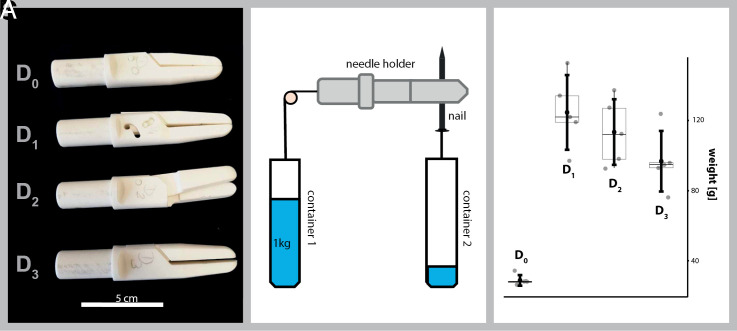
Experimental validation of the needle holders. (A) 3D printed models of the needle holders in scale 10:1. (B) Experimental setup of the experiment. (C) Box plots of the results for the measurements showing the weight of container B in B when in the shown experiment the needle drops out of the needle holder. Gray circles represent individual measurements, thin dark boxes indicate the 25 to 75% quartile with the median as the horizontal line, and thick black lines show the whiskers with the mean as the black dot in the middle. The underlying raw data are provided in SI Appendix, Supplementary Material 3.

Results and Discussion

The mandibular joint of the red wood ant (F. rufa) comprises two articulations with the head capsule: an enlarged anterior one (ama, Figs. 1C and 2B and SI Appendix, Figs. S1 and S2) and a posterior one (pma, Fig. 2B and SI Appendix, Figs. S1 and S2). In the ant studied here, both of them are large flat areas on both the mandible and the head capsule (Fig. 2 A and B and SI Appendix, Supplementary Material 1) that allow a gliding motion in the joint. This agrees with earlier observations of this species (17). Our ultrastructural analyses with scanning electron microscopy show that this area is indeed a completely smooth, patternless surface (SI Appendix, Fig. S1). This construction of ants differs strikingly from all those of other insects with biting mouthparts. In other insects, the mandibles are attached to the head capsule with two fixed ball-and-socket articulations, similar to a door attached to its frame via two hinges (20). Consequently, those insects’ mandibles (like a door) can only swing around a single axis (20).

Evolutionary Design Principle 1: The Mobile Joint Axis.

Ants are the only known group of insects with biting mouthparts with secondarily reduced firm joints (17, 18). This apparently simple reduction from a ball-and-socket articulation to a gliding surface has far-reaching consequences for the function and performance of the ant’s biting. In contrast to the original ball-and-socket joint, the gliding surface of the ant mandible enables movements in different planes instead of movements in a single plane. Based on µ-computer tomographic (µ-CT) scans of various mandibular positions (mp, Fig. 2A), our 3D results show that there is considerable variation in the axes of the different mandibular positions (ma, Fig. 2A, details in SI Appendix, Supplementary Material 1). The actual point of rotation in the joint is the point where the respective mandibular axis intersects with the anterior mandibular articulation (colored points in Fig. 2C). In the red wood ant, this point moves over the entire anterior articulation, including the base of the alata (ala, Fig. 2B). It varies by up to 73 μm in the X-axis, 101 μm in the Y-axis, and 116 μm in the Z-axis (Fig. 2C and SI Appendix, Supplementary Material 1).

Our results support the previously hypothetical assumption that the elongation of the anterior mandibular articulation is associated with the moving axis (21). Zhang et al. (19) hypothesized that this movement within the joint, and the resulting trajectory, provide more possibilities for a gentle grip of the ant’s eggs. Other benefits might be a wider opening of the mandibles or an increased force transmission mediated via the increase of the mechanical advantage.

All traditional surgical needle holders known to us have a fixed joint axis similar to the mandibles of typical winged insects, i.e., the axis of rotation does not change during opening and closing (22). Technical drawings, exploded views, animated videos, and a 3D model of the original needle holder are supplied in SI Appendix, Supplementary Material 2.3, Movie S1/S2, and Dataset S1. By transferring the principle of the moveable joint axis from the ant to the original, commercial needle holder (D₀), we propose design D₁ (Fig. 2D and SI Appendix, Supplementary Material 2.4). This was achieved by creating a second axis of rotation (R₂ in Fig. 2D and SI Appendix, Fig. S10) in the needle holder. When closing the needle holder, the first rotational axis (R₁ in Fig. 2D and SI Appendix, Fig. S10) moves slightly posterior and downward on a trajectory (TR₁ in SI Appendix, Fig. S10) in a 10° inclination (β in Fig. 2D and SI Appendix, Fig. S10), while the second axis (TR₂ in SI Appendix, Fig. S10) makes a posterior and upward movement. Thus, the resulting movement of the mobile arm not only performs the classical closing rotation but also an anterior–posterior translation, which chocks the needle. Drawings, exploded views, animations of the opening process, and a 3D file of this needle holder design are presented in SI Appendix, Supplementary Material 2, Movie S3/S4, and Dataset S2.

Translation and rotation of the needle is the main problem surgeons have during stitching. Therefore, we define the performance of the needle holder as the inverse of the amount of translation and rotation of the needle. As we keep all other technical parameters constant, the reduction of translation and rotation can be attributed to the optimization of the force transmission. SI Appendix, Fig. S8 shows the four degrees of freedom of the needle in the needle holder that are relevant in this context. We measured the force transmission experimentally with 3D printed models of the needle holders (Fig. 3A) and calculated it theoretically (SI Appendix, Supplementary Material 2) in order to compare the performance with regard to the original needle holder D₀. For D₁, the selected inclination of 10° (β in Fig. 2D and SI Appendix, Fig. S10) results in a calculated force transmission of 296% (SI Appendix, Supplementary Material 2.4) and a measured value of 433% (Fig. 3) compared to the original needle holder. The measured value is in D₁ (but also all following designs) higher than the calculated one which might be caused by the experimental setup, the difference in material (plastic in the prints vs. steel in the calculations) or the different values for friction of the steel needle and the plastic needle holder. However, both the calculated and the experimental setup show a significant increase compared to the original design. Theoretically, even higher improvements could be achieved with a smaller value for β (Fig. 2D) but come at the risk of locking the needle holder in the closed position.

Evolutionary Design Principle 2: The Variably Tilted Axes.

The second defining evolutionary characteristic of the ant’s biting apparatus is a variably tilted orientation of the mandibular axis (Fig. 2 A and E). The axes of the two mandibles of the studied ant are not parallel to each other but inclined toward the animal’s yz plane (= midsagittal plane). Furthermore, the amount of tilt is variable; in other words, the axis moves. We found that the axis tilt ranges between 67° to 110° around the x-axis and 79° to 90° around the y-axis (Fig. 2E and SI Appendix, Supplementary Material 1). During the opening process, the axis thereby moves medially and anteriorly. The axis is extremely tilted between the two positions where the mandibles are most opened. This is consistent with earlier observations on trap-jaw ants, where the greatest tilt was observed in extreme angles of the open jaw (23). Inclined axes have been found in many other insects (24), but they do not show the variation we found in the ant as their mandibular axis is fixed.

In the ant, the axis is tilted between 79° and 90° around the y-axis. We transferred this principle to the needle holder by tilting the rotational axis of the needle holder (R in Fig. 2F and SI Appendix, Fig. S11) by 80° counterclockwise around the y-axis. This rotation results in a 10° angle toward the normal of the gripper surfaces (γ in Fig. 2F and SI Appendix, Fig. S11). In order to keep the needle holder simple and manufactural, we did not include an additional rotation around the x-axis (as observed in the ant). As a result of the performed rotation, needle holder design D₂ opens to the side rather than to the top (Fig. 2F and SI Appendix, Fig. S11 and Movies S5–S8). This tilt of the axis of the needle holder locks the needle during the closing process. The device thus acts like a door wedge with the needle being the door leaf and the two arms representing wedges (one between the “door” and the “floor” and one between the door and the “ceiling”). In contrast to the chocking effect of D₁, which is based on an anterior–posterior translation of the upper mobile arm, the effect in D₂ is created by a rotation of the moveable arm. As a result of this modification, the calculated force transmission ratio of the modified design D₂ is 271% (SI Appendix, Supplementary Material 2.5) and the average measured value is 394% (Fig. 3C and SI Appendix, Supplementary Material 3) compared to the original design. Drawings, exploded views, animations of the opening process, and a 3D file of design D₂ are provided in SI Appendix, Supplementary Material 2, Movies S5–S8, and Dataset S3.

Evolutionary Design Principle 3: The Force Transmission.

The third defining feature of the ant’s biting apparatus is the force transmission ratio of the adductor muscle to the tip of the mandible. The force transmission is the ratio between two lines: 1) the inner lever arm of the mandible (ila in Fig. 2G and SI Appendix, Fig. S12; i.e., the line between the point of attachment of the tendon of the adductor muscle and the rotational axis) and 2) the outer lever arm (ola in Fig. 2G, i.e., the shortest (orthogonal) distance between the axis and the tip of the mandible). It is a tradeoff between transmitted force (the higher the value, the greater the transmitted force) and velocity (the smaller the value, the faster the mandibles close). In other insects with a fixed mandibular axis, the force transmission is stable, but in the studied ant, due to the movement in the joint, it ranged between 0.20 and 0.35 (Fig. 2G; discussed as mechanical advantage in detail in ref. 25), implying that 20 to 35% of the muscle force is transmitted to the tip of the mandible. The smallest value for the force transmission in the ant mandible was recorded at the maximum opening, while the largest one was recorded when the mandibles were slightly open. The observation seems plausible as maximum forces would be required when the jaws are almost closed and objects in between them need to be held or crushed with maximum force. The values observed in the ant are in the range of insects that depend on fast mandibular strikes on soft-shelled prey such as predatory aquatic beetles (0.26) or insects that crush hard food such as cockroaches (0.39) and detritivore beetle larvae (0.54) (26, 27).

The observed variability in the force transmission in the ant mandibles may be explained by the fact that they can be considered as multifunctional tools for a variety of tasks: Cutting food and attacking enemies require the whole range of opening angles of the mandibles and strong forces, but handling their own fragile eggs benefits from a well-controlled, gentler grip (16, 19, 23).

The force transmission of the used commercially available needle holder is 0.192 (SI Appendix, Supplementary Material 2.3). That is comparable to the lowest value measured in the ant. An increase of performance could be achieved in two different ways: 1) lengthening the inner lever, i.e., the distance between the axis of rotation and the attachment of the push rod (ila in SI Appendix, Fig. S9), or 2) shortening the outer lever arm, i.e., the distance between the rotational axis and the point where the needle is held (ola in SI Appendix, Fig. S9). However, both approaches have substantial problems in a surgical needle holder. With the first approach, the needle holder itself would increase in diameter, thus requiring a larger port for entry into the body. This would cause a larger surgical wound for the patient (28), which has many associated risks and disadvantages. The second case would shorten the gripping area of the needle holder, thus reducing the surgeon’s control of the needle. This could render certain suturing unsuccessful or even impossible. We addressed these problems in needle holder design D₃ by transforming the hinge joint of the original needle holder into a guiding groove (Fig. 2H and SI Appendix, Fig. S12 and Movie S9/S10). The mobile jaw thus performs a motion following a circular recess on the fixed arm. As a result, the rotational axis projects to a virtual point outside the actual needle holder (R in Fig. 2H and SI Appendix, Fig. S12). This modification achieves the desired effect of increased force transmission without widening the needle holder or shortening the jaws. In contrast to D₀ (and also D₁ and D₂), this design has no single central pin that the mobile arm rotates around. We thus could increase the inner lever from 2.25 mm in the original needle holder (D₀) to 4.67 mm, a raise of 108% (technical drawings, an animation, and a 3D model are found in SI Appendix, Supplementary Material 2.6, Movie S9/S10, and Dataset S4). As a result, the force transmission ratio increased to 0.39 in D₃ (compared to 0.192 in D₀). This is higher than the maximum value we measured in the ant, but it is close to those found in insects that specialize on chewing tough materials, such as the omnivorous cockroach (24). This modification led to a performance that was 2.03 (theoretical calculations; SI Appendix, Supplementary Material 2.6) or 3.36 (experimental measurement, Fig. 3C, and SI Appendix, Supplementary Material 3) times higher than the one of the original needle holder.

Another effect of the proposed modifications in D₃ is the slower closing speed of the needle holder. Due to the increased leverage, our modified needle holder slows down by 51.9 %. This slower but more powerful closing might also give the surgeon more control when grabbing the needle. A similar effect might be found in the ant, which requires slower and more controlled movements to handle its eggs with fully opened mandibles. Increasing the hinge radius while keeping the push rod travel constant results in a smaller maximum jaw opening angle, which does not impede its versatility for suturing. Theoretically, the performance could be increased even higher by incorporating larger force transmission ratios than the one applied. However, this would also increase the radius and thus flatten the guiding groove, which would eventually lead to an unstable construction. Additionally, the closing would be extremely slow which would render suturing tedious.

Conclusions

Theoretically, an even larger force transmission can be obtained through any of the three principles discussed above: 1) by reducing the angle β, 2) by including a particularly strong inclination in D₂, or 3) by further increasing the distance between the rotational axis and the attachment of the push rod (P in Fig. 2H and SI Appendix, Fig. S12) in D₃. However, as mentioned above, any of these extreme measures would have negative consequences that eventually would result in a non-operational needle holder.

We have shown that the derived parameters from the ant’s biting apparatus provide a good compromise between increased force transmission, usability, and control by the surgeon. For future product development, prototypes of these designs should be evaluated in surgical tests. The proposed designs D₁–D₃ are much more complex in manufacturing than the centuries-old original design D₀ with its mobile arm that rotates around a central pin. However, modern manufacturing technologies such as CNC milling and 3D printing now allow their production.

Other parameters than the studied force transmission could be modified in order to reduce the movement of the needle or improve the grip. Potential options include the alteration of the shape or the surface of the needle holder arms (19).

In summary, our results clearly show that the biting apparatus of the ant is a suitable bioinspiration for improving grasping and holding in systems that require high control within a limited space. Theoretically, they could also be transferred to other fields that require a firm and forceful grip under miniaturized conditions, such as robotics, mechatronics, or microassembly (2–4).

Materials and Methods

Ants.

The present study is based on ethanol-fixed workers of F. rufa (Hymenoptera/Formicidae), that were collected in the Paulinenaue Forest, Brandenburg/Germany, in 2014 and 2015 with the permission from Landesamt für Umwelt, Gesundheit, und Verbraucherschutz Potsdam (Permission: LUGV_RW7-4744/46+5#202578/2014). This species was selected as it is known for carrying different shaped, weighted, and sized needles from pine trees and other materials but also gently handling the offspring. A Keyence VHX 2000 was used to photograph the animals or parts of them. For scanning electron microscopy, the specimens were dried with a Balzer CPD 030 critical point dryer and subsequently visualized under a Philips XL30 ESEM.

As we studied a passively induced motion, the described specificity of the mandibular joint might theoretically allow a slightly different motion in the active movement by the ant. We therefore restrained from making any explicit statement about the movement of the mandible.

CT scanning and 3D modeling.

One dried specimen was scanned with an XRadia XCT 200 at the Zoological Institute of the University Greifswald. The resulting data were imported into Amira 5.3 (ThermoFisher) and virtually segmented. The individual structures such as mandibles, muscles, or head capsule were separated using the arithmetic function and exported as tif stacks. Those images were imported into Volume Graphics VGStudio Max 2.2, where volume rendering was performed.

Definition of the coordinate system (SI Appendix, Fig. S4).

For terminology purposes, we define the head of the ant as being orthognathous (the mouthparts facing downward). We define the plane of the occipital ridge in the dorsal inner side of the head capsule of the animal as the yz-plane. The xz-plane is defined as being perpendicular to the yz-plane and going through the two most ventral points of the compound eyes. The xy-plane is perpendicular to the two former ones and runs through the posteriormost points of the compound eyes. The defined axes are illustrated in SI Appendix, Fig. S4.

Determination of the axes.

A freshly killed specimen was fixed in a special sample holder that allows the fixation of the mandible at different angles. Five different mandible positions ranging from complete opening to complete closure were scanned at the Museum Koenig in Bonn with a Bruker Skyscan 1272 CT device (35 kV, 200 µA, 0,4° rotational steps over 360°, 4 µm of spatial resolution). These five scans of mandibles with increasing opening angles were aligned digitally using Rhino3D (Version 6, SR11, Robert McNeel & Associates) and the Grasshopper Plug-in. n = 10 evenly distributed, corresponding points were chosen on the scanned mandibles and the points of each adjacent scan were connected with lines. In the middle of these lines, orthogonal planes were created. The intersections between these 10 planes were calculated, resulting in 45 lines [(n² − n)/2]per pair of adjacent mandible openings. Those 45 lines between two opening stages were averaged to a single line, resulting in four lines in total, each line representing the axis of rotation between the corresponding scans. The detailed procedure is explained in SI Appendix, Supplementary Material 1.3.

Displacement of the axes.

The displacement of the individual axes to each other and thus the movement in the joint was determined by measuring the distance between the upper intersection points of the axes with the mandible. The axis between the two positions with the widest mandibular opening is not intersecting with the mandible. In this case, the point of the minimum distance of this axis to the mandible was chosen as a reference point. A detailed description of this process is provided in SI Appendix, Supplementary Material 1.3.

The force transmission.

The force transmission or mechanical advantage (see ref. 25 for details) is defined as the ratio between two lever arms: 1) the inner lever arm (ila in Fig. 2G, i.e., the distance between the axis of rotation and the attachment of the adductor muscle) and 2) the outer lever arm (ola in Fig. 2G, i.e., the distance between the axis of rotation and the distal tooth of the mandible). The values for the force transmission for each axis ( $\frac{\mathit{ila}}{\mathit{ola}}$ ) are provided in Fig. 2G and SI Appendix, Supplementary Material 1.4.

Needle Holders.

A commercial endoscopic needle holder (5 mm, Richard Wolf, Knittlingen/Germany) was scanned with an XRadia XCT 200 at the Zoological Institute of the University Greifswald. Based on this scan, a virtual model was created using surface rendering in Amira 5.3. SI Appendix, Supplementary Material 2.3 provides models and explosive views of the original needle holder D₀. The Y-axis is defined as following the longitudinal axis of the needle holder while the X-axis is defined as being in the transverse axis of the needle holder (SI Appendix, Fig. S7 provides an image of the defined axes and planes).

We compared the performance of the original needle holder to those of the designs based on the ant´s mandible. To allow a meaningful comparison of their performance, we kept technical parameters such as surface texture, material pairings, geometry, and the actuator force constant. The same applies to the position of the needle, which is in all cases considered as following: 1) perpendicular to the gripper’s longitudinal axis and 2) at 1/3 of the jaw length, measured from the tip of the jaw (SI Appendix, Fig. S8).

We define the performance of the entire device as the reductions of rotations and translations of the needle (SI Appendix, Fig. S8) as this hampers accuracy and provides the major problem during surgery. As we keep all other technical parameters constant, it can thus be attributed to the optimization of the force transmission, which we calculated in detail in SI Appendix. SI Appendix, Supplementary Material 2.3 provides the calculation for the performance of the original needle holder D₀.

We altered this original design (D₀) into three different needle holder prototypes (D₁–D₃) using the 3D CAD software PTC Creo Parametric 3.0. The detailed technical sketches, exploded views, and animated movies of all used designs are provided in SI Appendix of the respective design (SI Appendix, Supplementary Materials 2.4–2.6). To allow comparisons between the modified design and the original needle holder, we defined the following boundary conditions for the improved designs: 1) the length of the fixed arm cannot be altered as it is an important feature for the performance of the surgeon; 2) the outer diameter of the needle holder in the closed position cannot be altered, as the needle holder needs to enter the body through a defined port; and 3) all calculations and experiments deal with a constant force pulling on the push rod. 3D models of all needle holders (D₀–D₃) are provided in (29).

SI Appendix, Supplementary Materials 2.4–2.6 provide the theoretical calculation for the performance of the modified needle holders D₁–D₃.

Validation on Models.

To experimentally validate the results of our calculations, we printed models of all four designs based on the provided models by selective laser sintering on a Formica P 100 (EOS GmbH, 81152 Planegg, Germany) using polyamide PA 12-2200 (EOS). We thereby increased them in size by factor 10 to allow easier handling (Fig. 3A).

The models were firmly fixed in a vise and aligned horizontally with a spirit level. The force of 1 kg of water was attached to the attachment point of the push rod via a string. The needle was replaced by a perfectly straight steel nail that was placed between the arms of the needle holder in an identical position in all designs. It was positioned to be exactly vertically, thus allowing to measure of the displacement in the Y direction. D₂ in particular has a handedness. Thus, the measurements were carried out in both possible orientations. No differences were found. Subsequently, a second container was fixed to the nail with string. This container was slowly filled with water until the nail started to move between the arms of the needle holder. The weight of this container including the nail was measured for five repetitions for each needle holder. The nail was removed between each repetition. Fig. 3B shows the experimental setup.

SI Appendix, Table S1 provides the result of each measurement while Fig. 3C shows them in a box plot diagram (created in R). D₁ could hold an average weight of 433% compared to D₀, D₂ 394% and D₃ 336%. All these values are higher than the theoretically calculated ones (SI Appendix, Supplementary Materials 2.4–2.6). This experimental increase in performance compared to the theoretical calculations might be caused by the experimental setup, the difference in material (plastic in the prints vs. steel in the calculations), or the different friction of the steel needle and the plastic needle holder. However, all measured values are significantly higher than the calculated ones, thus showing even better performance. The measured values also show the same order of performance as the theoretically calculated ones (D₁ > D₂ > D₃).

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Animation of the original needle holder design D₀ during the opening and closing process.

Movie S2.

Animation of the original needle holder design D₀ during the opening and closing process with transparent needle holder. Moveable arm in blue.

Movie S3.

Animation of the modified needle holder design D₁ during the opening and closing process.

Movie S4.

Animation of the modified needle holder design D₁ during the opening and closing process with transparent needle holder. Moveable arm in blue.

Movie S5.

Animation of the modified needle holder design D₂ during the opening and closing process.

Movie S6.

Animation of the modified needle holder design D₂ during the opening and closing process with transparent needle holder. Moveable arm in blue.

Movie S7.

Animation of the modified needle holder design D₂ during the opening and closing process seen in anterior view.

Movie S8.

Animation of the modified needle holder design D₂ during the opening and closing process seen in anterior view with transparent needle holder. Moveable arm in blue.

Movie S9.

Animation of the modified needle holder design D₃ during the opening and closing process.

Movie S10.

Animation of the modified needle holder design D₃ during the opening and closing process with transparent needle holder. Moveable arm in blue.

Data, Materials, and Software Availability

CT scans and 3D model stl. and u3d. files have been deposited in Morphobank (30) and Figshare (29), respectively.