Abstract
Purpose
This study aimed to compare the biomechanical effects of different bone cement distribution methods on osteoporotic vertebral compression fractures (OVCF).
Patients and methods
Raw CT data from a healthy male volunteer was used to create a finite element model of the T12-L2 vertebra using finite element software. A compression fracture was simulated in the L1 vertebra, and two forms of bone cement dispersion (integration group, IG, and separation group, SG) were also simulated. Six types of loading (flexion, extension, left/right bending, and left/right rotation) were applied to the models, and the stress distribution in the vertebra and intervertebral discs was observed. Additionally, the maximum displacement of the L1 vertebra was evaluated.
Results
Bone cement injection significantly reduced stress following L1 vertebral fractures. In the L1 vertebral body, the maximum stress of SG was lower than that of IG during flexion, left/right bending, and left/right rotation. In the T12 vertebral body, compared with IG, the maximum stress of SG decreased during flexion and right rotation. In the L2 vertebral body, the maximum stress of SG was the lowest under all loading conditions. In the T12-L1 intervertebral disc, compared with IG, the maximum stress of SG decreased during flexion, extension, and left/right bending and was basically the same during left/right rotation. However, in the L1-L2 intervertebral discs, the maximum stress of SG increased during left/right rotation compared with that of IG. Furthermore, the maximum displacement of SG was smaller than that of IG in the L1 vertebral bodies under all loading conditions.
Conclusions
SG can reduce the maximum stress in the vertebra and intervertebral discs, offering better biomechanical performance and improved stability than IG.
Keywords: Finite element analysis, Vertebroplasty, Biomechanics, Bone cement distribution, Compression fracture, Osteoporosis
1. Introduction
Osteoporosis is a metabolic skeletal disease that affects the entire body and is characterized by a decline in bone mass and deterioration of bone microstructure [[1], [2], [3]]. This leads to increased bone fragility and a higher risk of fractures. The clinical manifestations primarily include muscle and bone pain, decreased height, spinal deformities, and fractures [4]. Osteoporotic vertebral compression fractures (OVCF), a prevalent type of fracture associated with osteoporosis, are a significant health concern in the elderly population [5,6]. It is estimated that 30%–50% of the population over 50 years of age worldwide are at risk of OVCF, with an average of one case occurring every 3 s [7,8]. This poses a severe threat to the overall health and significantly affects the quality of life of older adults [9,10].
Currently, percutaneous vertebroplasty (PVP) is one of the primary treatment methods for OVCF [11,12]. It involves injecting bone cement into the vertebral body to stabilize the fracture, restore vertebral biomechanical properties, prevent further compression fracture progression, alleviate pain, and enable patients to recover normal functionality within a short period of time [13].
However, with the widespread application of PVP technology, concerns have been raised regarding the increased risk of adjacent vertebral fractures and the potential for reinforced vertebral re-collapse [7,14,15]. Studies have indicated that approximately 20% of patients who undergo vertebral augmentation procedures experience vertebral fractures within one year, with 50%–67% of these fractures occurring in the adjacent vertebra [2,16]. In a retrospective study, Tseng et al. [17] found that 58.8%–63.8% of non-operative vertebral fractures were adjacent to the surgical site, and adjacent vertebral fractures occurred earlier than non-adjacent fractures, significantly affecting long-term effectiveness and patient satisfaction with PVP. Additionally, research has found that the distribution of cement within the vertebra greatly influences surgical outcomes, such as pain relief, adjacent vertebral fractures, and reinforced vertebral re-collapse [18]. Although biomechanical research on adjacent vertebral fractures and reinforced vertebral re-collapse is not comprehensive, it is widely accepted that the distribution of bone cement within the vertebral body is a crucial influencing factor [19,20]. However, relevant biomechanical studies to elucidate the underlying mechanisms are lacking.
Compared with traditional cadaveric specimen studies, the application of finite element analysis (FEA) in spinal biomechanical research is becoming increasingly widespread [[21], [22], [23]]. FEA offers advantages such as low cost, short time requirements, and good repeatability [24,25]. It has become an essential component in studying the biomechanics of the human body and has extensive applications in areas such as the cervical spine, lumbar spine, and joints [[26], [27], [28]]. Meanwhile, previous studies have mostly focused on differences in overall strength, stiffness, and vertebral height recovery with or without bone cement [29]. However, there is currently a lack of biomechanical research specifically addressing connected and unconnected types of bone cement within the vertebral body.
Therefore, this study utilized FEA to compare the biomechanical differences between different distributions of bone cement on the vertebral body and intervertebral discs. This study aimed to provide a theoretical basis for achieving better surgical outcomes and minimizing complications as much as possible.
2. Materials and methods
2.1. Patient data collection and construction of finite element model
The research protocol has been approved by the hospital's ethics committee (NO. [2022]080,701). Additionally, informed consent from the patients has been obtained. A healthy adult male volunteer with no relevant medical history were selected. After signing the informed consent form, the volunteer underwent X-ray, CT, and clinical examinations to exclude any spinal injuries, tumor metastasis, or pathological deformities. A 64-slice spiral CT scanner (GE Company) was used for scanning, covering the range from T11 to L2. The scanning parameters were set as follows:140 kV, 200 mA, slice thickness of 0.625 mm, and no interval [30,31]. The images were saved in the Digital Imaging and Communications in Medicine (DICOM) format and imported into Mimics software (version 21.0, Materialise Company, Leuven, Belgium). Based on the grayscale differences of different tissues, a three-dimensional model of T12 to L2 was constructed using thresholding and the corresponding erasing operations. The model was exported in STL format and imported into the Geomagic Studio 2013 software (Geomagic, USA) for optimization, including smoothing, artifact removal, hole filling, contour editing, surface and lattice construction, and surface fitting. The generated geometric model was saved in STP solid format. Subsequently, the STP 3D model file was imported into the SolidWorks 2018 software (Dassault Systemes Company, USA) to perform feature recognition, surface diagnostics, and surface repair on the geometric model. The articular cartilage, upper and lower endplates, and intervertebral discs were constructed. The intervertebral disc is composed of two main components: the nucleus pulposus and the annulus fibrosus. The nucleus pulposus occupies 43% of the total disc area [32].
2.2. Construction of vertebral fractured model
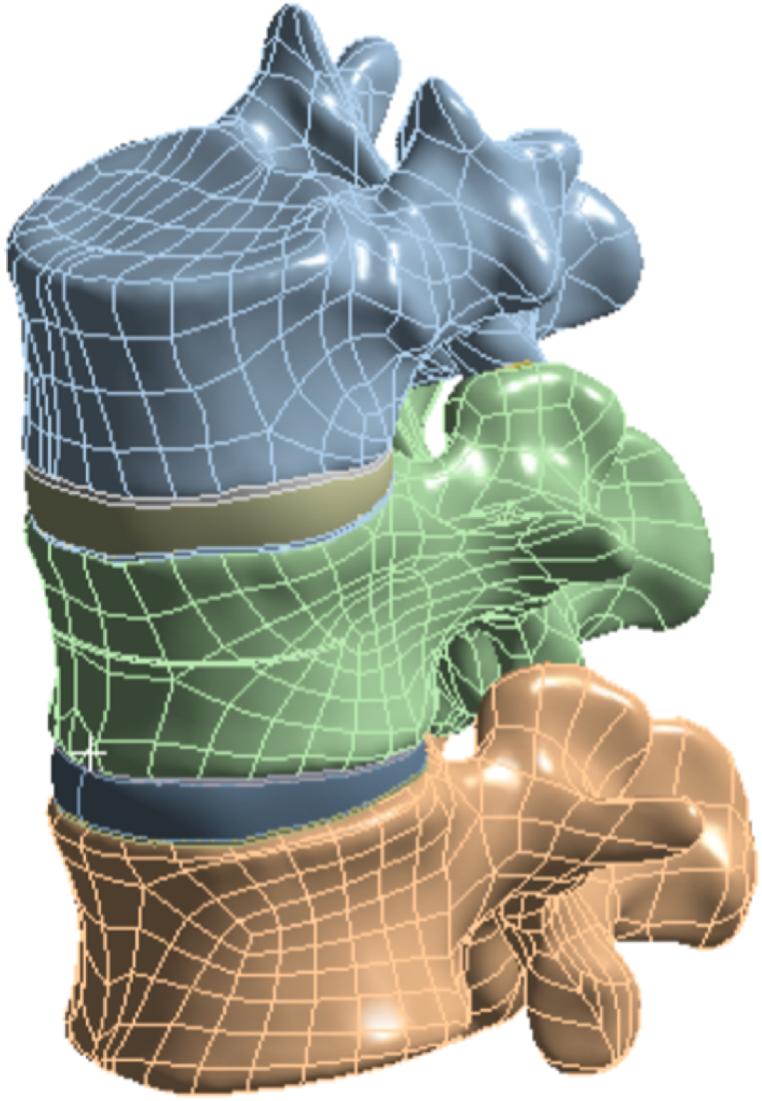
To simulate osteoporosis, the elastic modulus of the vertebral bodies was reduced by specific amounts [[33], [34], [35]]. A previously reported method was utilized to simulate an L1 vertebral fracture, where a fracture line of 0.5 mm was created by cutting the vertebral body [36,37]. The fissure penetrated the vertebral body horizontally through the center of the anterior portion, with 22.5 mm. The depth, width, and height of the fissure were approximately 22.5 mm, 42.5 mm, and 0.5 mm, respectively [10] (Fig. 1).
Fig. 1.
L1 vertebral fracture model.
2.3. Construction of bone cement distribution model
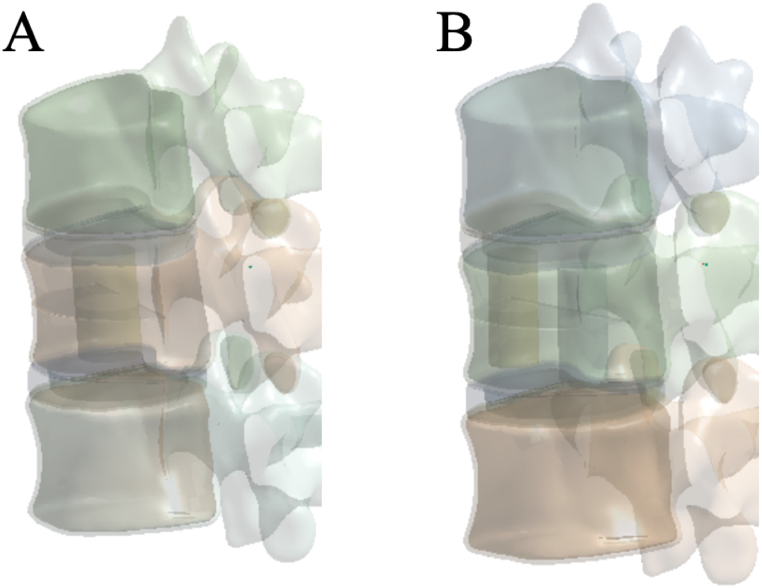
One or two simulated bone cement cylinders were implanted into the fractured vertebral body to simulate the distribution of bone cement within the vertebra [10]. A bone cement cylinder was inserted vertically into the central region of the fractured vertebral body to simulate the block distribution of bone cement (integration group, IG) (Fig. 2A). Additionally, two bone cement cylinders of the same volume were inserted vertically on both sides of the fractured vertebral body to simulate the bilateral distribution of bone cement (separation group, SG) (Fig. 2B). The volume of the bone cement cylinders in both distribution groups was 4 ml.
Fig. 2.
Bone cement distribution model (A: IG; B: SG), IG, integration group; SG, separation group.
2.4. Construction of the complete model
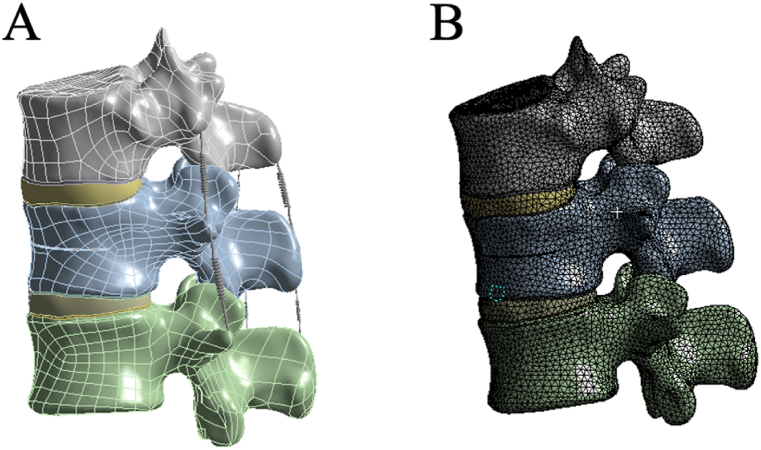
The complete 3D model was imported into ANSYS 19.0 software for FEA. Based on the literature [10,34,38], the material properties were assigned to different components in the analysis material library, including the cortical bone, cancellous bone, post-fracture cortical bone, post-fracture cancellous bone, articular surfaces, nucleus pulposus, annulus fibrosus, and bone cement. The material parameters are listed in Table 1. Additional components included the anterior longitudinal ligament (ALL), posterior longitudinal ligament (PLL), ligamentum flavum (LF), interspinous ligament (ISL), supraspinous ligament (SSL), capsular ligament (CL), and intertransverse ligament (ITL) (Fig. 3A). The contact between the superior and inferior facets was defined as frictional contact, with coefficients of friction of 0.1 [39,40]. All other contacts were defined as bonded. The model was then meshed with control over the type and size of the mesh to ensure that the computational accuracy satisfied the analytical requirements. The mesh size for all the elements was set to 2.0 mm [8,41] (Fig. 3B).
Table 1.
Material parameters of the finite element model.
| Parts | Young modulus/MPa | Poisson's ratio | Sectional area/mm2 | References |
|---|---|---|---|---|
| normal cortical bone | 12,000 | 0.3 | Zhang et al. [42] | |
| osteoporotic cortical bone | 8040 | 0.3 | Liang et al. [37] | |
| normal cancellous bone | 132 | 0.2 | Zhang et al. [42] | |
| osteoporotic cancellous bone | 34 | 0.2 | Zhao et al. [29] | |
| normal endplate | 1000 | 0.4 | Bereczki et al. [34] | |
| osteoporotic endplate | 670 | 0.4 | Salvatore et al. [35] | |
| nucleus pulposus | 1 | 0.499 | Zhang et al. [43] | |
| annulus fibrosus | 4.2 | 0.45 | Zhang et al. [43] | |
| ALL | 20 | 0.3 | 60 | Huang et al. [44] |
| PLL | 20 | 0.3 | 21 | |
| LF | 19.5 | 0.3 | 40 | |
| SSL | 15 | 0.3 | 30 | |
| ISL | 12 | 0.3 | 40 | |
| ITL | 50 | 0.3 | 10 | |
| CL | 7.5 | 0.3 | 67.5 | |
| Bone cement | 3000 | 0.4 | Yang et al. [45] |
ALL, anterior longitudinal ligament; PLL, posterior longitudinal ligament; LF, ligamentum flavum; SSL, supraspinal ligament; ISL, interspinous ligament; ITL, intertransverse ligament; CL, capsular ligament.
Fig. 3.
T12-L2 finite element models (A: Three-dimensional solid Model; B: Mesh division of the finite element model).
2.5. Boundary conditions and load settings
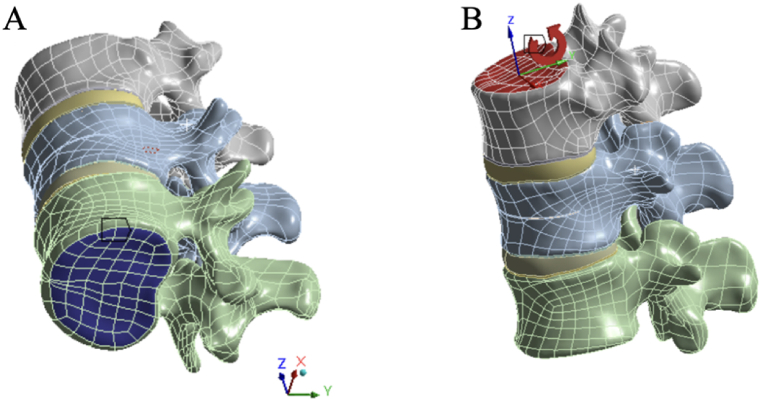
Considering the influence of the paraspinal muscles and intra-abdominal pressure, all the models were fixed at the lower surface of the L2 vertebral body. A vertical load of 400 N was applied to the upper surface of the T12 vertebral body to simulate standing posture [46,47]. Additionally, different directions of moment forces of 10 N m were applied to the upper surface of the T12 vertebral body to simulate six types of motion: flexion, extension, left/right bending, and left/right rotation (Fig. 4 A, B). According to the three-column theory of the spine, 85% of the applied load is distributed on the anterior and middle columns, whereas 15% is distributed on the posterior column [42].
Fig. 4.
A: Applying fixed constraints to the lower surface of L2; B: Applying a vertical load of 400 N and moment forces of 10 N m to the upper surface of T12.
2.6. Observation indicators
The Von Mises stress of the L1 vertebral body, adjacent vertebral bodies, and intervertebral discs, as well as the displacement of the L1 vertebral body, were observed. The von Mises stress has been proposed as a parameter to assess fracture failure [48,49], while the maximum displacement is an indicator of stability [50].
3. Results
3.1. Validation of the model
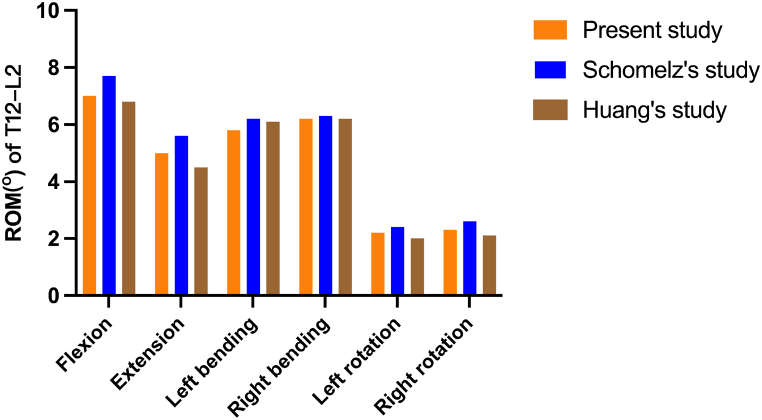
Different loading directions of flexion, extension, left/right bending, and left/right rotation were applied to the vertebral body models to obtain the range of motion data for the T12-L2 segment. The results were compared with biomechanical experimental data from previous literature [44,51] showed good consistency (Fig. 5). This confirms the accuracy and reliability of the model and demonstrates its suitability for subsequent simulation studies.
Fig. 5.
Comparison of the Range of Motion (ROM) of T12-L2 in the model developed in this study with previously reported data.
3.2. Von Mises stress change of the L1 vertebral body
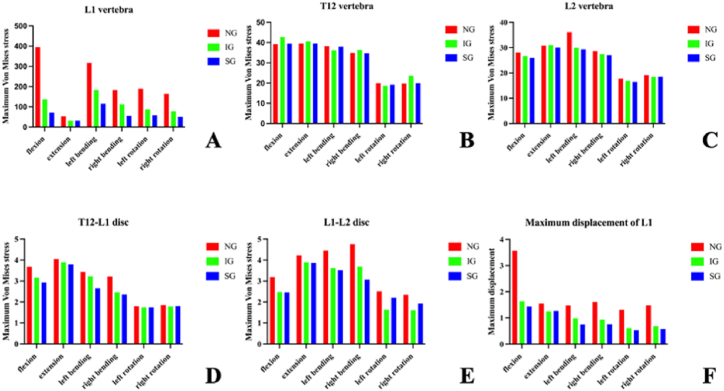
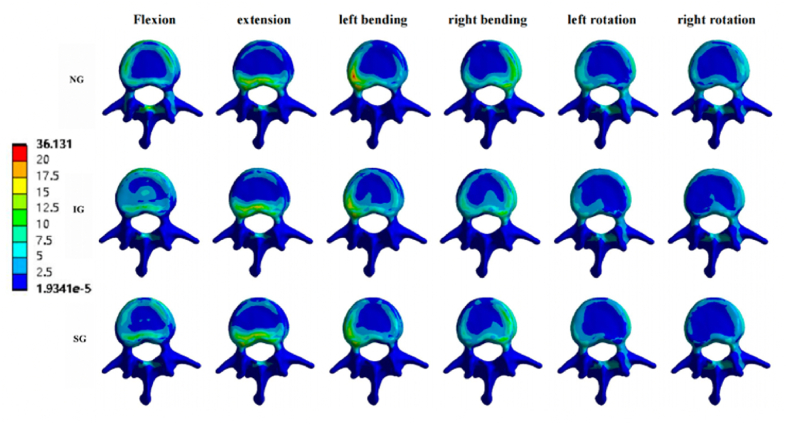
In the L1 vertebral body, compared to the non-injected group (NG), the maximum stresses of IG and SG decreased under the six loading conditions. Compared with IG, the maximum stress of SG decreased during flexion, left/right bending, and left/right rotation, and the maximum stress during extension was basically the same. The maximum IG stresses under the six loading conditions were 136.87, 31.49, 183.71, 112.26, 87.436, and 78.31 MPa, respectively. The maximum stresses of SG under the six loading conditions were 71.257, 31.479, 115.42, 56, 58.073, and 50.402 MPa (Fig. 6, Fig. 7).
Fig. 6.
Maximum Von Mises stress of the vertebra and intervertebral discs, and maximum displacement of L1. NG, non-injected group; IG, integration group; SG, separation group.
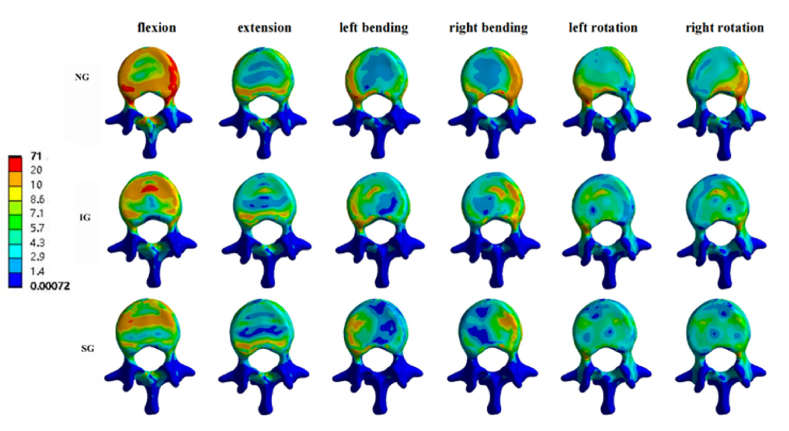
Fig. 7.
Stress cloud pictures of the L1 vertebral body. Stress cloud pictures of the L1 vertebral body in NG, IG, and SG during flexion, extension, left/right bending, and left/right rotation. NG, non-injected group; IG, integration group; SG, separation group.
3.3. Von Mises stress changes of T12 and L2 vertebral body
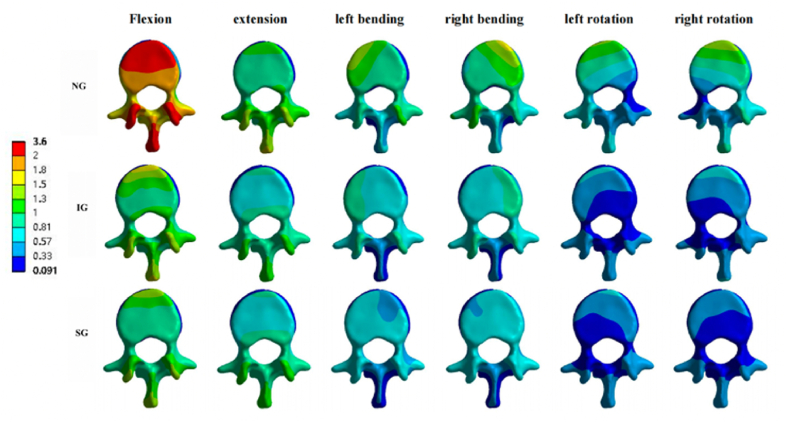
In the T12 vertebral body, compared with NG and SG, the maximum stress of IG increased significantly during flexion and right rotation, and the other loading conditions were basically the same. The maximum IG stresses under the six loading conditions were 43.724, 40.121, 37.990, 35.322, 19.317, and 24.586 MPa, respectively. The maximum stresses of SG under the six loading conditions were 39.474, 39.505, 37.963, 34.705, 19.225, and 19.711 MPa, respectively. (Fig. 6, Fig. 8).
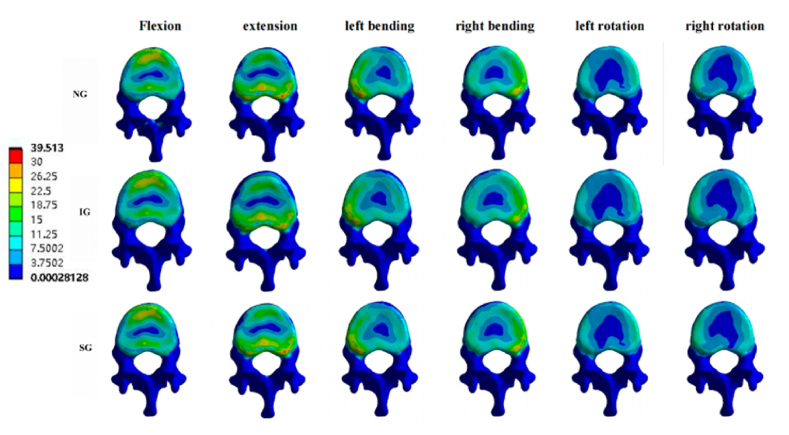
Fig. 8.
Stress cloud pictures of the T12 vertebral body. Stress cloud pictures of the T12 vertebral body in NG, IG, and SG during flexion, extension, left/right bending, and left/right rotation. NG, non-injected group; IG, integration group; SG, separation group.
In the L2 vertebral body, the maximum stress of SG was the smallest under all six loading conditions. (Fig. 6, Fig. 9).
Fig. 9.
Stress cloud pictures of the L2 vertebral body. Stress cloud pictures of the L2 vertebral body in NG, IG, and SG during flexion, extension, left/right bending, and left/right rotation. NG, non-injected group; IG, integration group; SG, separation group.
3.4. Von Mises stress changes of the intervertebral disc
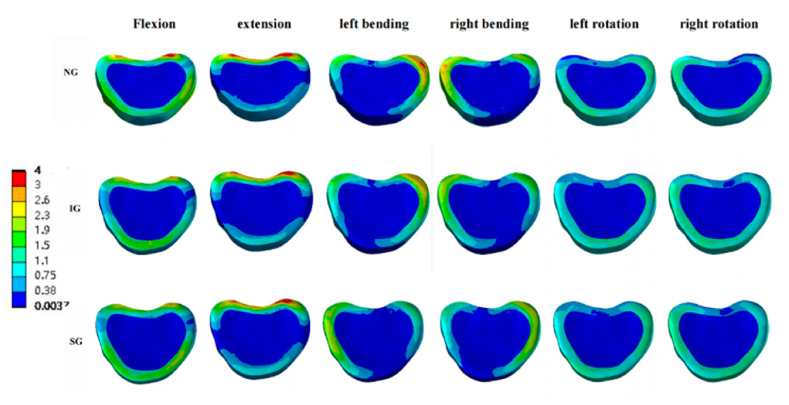
In the T12-L1 intervertebral disc, compared with NG and IG, SG decreased in flexion, extension, and left/right bending, and was basically the same in left/right rotation (Fig. 6, Fig. 10).
Fig. 10.
Von Mises stress cloud pictures of T12-L1 intervertebral disc. Von Mises stress cloud pictures of T12-L1 intervertebral disc in NG, IG, and SG during flexion, extension, left/right bending, and left/right rotation. NG, non-injected group; IG, integration group; SG, separation group.
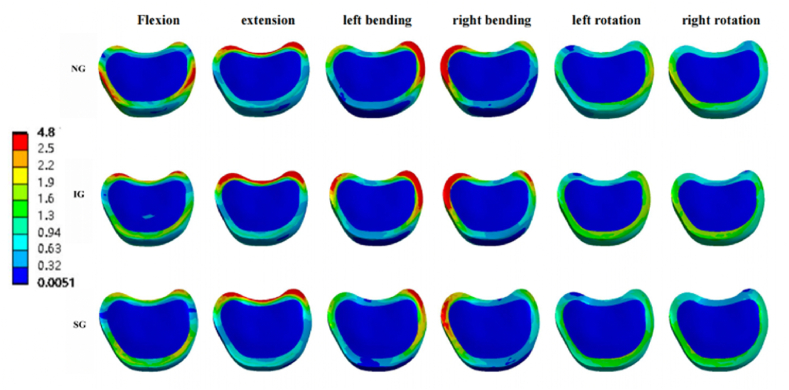
In the L1-L2 intervertebral disc, the maximum stresses of both IG and SG under the six loading conditions decreased compared with NG. However, compared with IG, the maximum stress of SG increased in the left/right rotation. (Fig. 6, Fig. 11).
Fig. 11.
Von Mises stress cloud pictures of L1-L2 intervertebral disc. Von Mises stress cloud pictures of L1-L2 intervertebral disc in NG, IG, and SG during flexion, extension, left/right bending, and left/right rotation. NG, non-injected group; IG, integration group; SG, separation group.
3.5. Maximum displacement of L1
Under the flexion load, the maximum displacements of the L1 vertebral body in NG, IG, and SG were 3.5684, 1.6353, and 1.4316 mm, respectively. Similar trends were observed under the extension, left/right bending, and left/right rotation loads (Fig. 6, Fig. 12). Therefore, compared to NG and IG, the distribution of bone cement in SG reduced the maximum displacement of the L1 vertebral body.
Fig. 12.
Displacement cloud pictures of the L1 vertebral body. Displacement cloud pictures of the L1 vertebral body in NG, IG, and SG during flexion, extension, left/right bending, and left/right rotation. NG, non-injected group; IG, integration group; SG, separation group.
4. Discussion
OVCF commonly occur in the thoracolumbar segment, with the T12 and L1 vertebra particularly susceptible to fractures, which can contribute to the development of kyphotic deformity [52]. Therefore, in this study, we used CT scan data from outpatient volunteers in the thoracolumbar segment to establish a finite element model. Based on previous literature, we modified the material parameters of the skeletal components and assigned different material properties to different regions, allowing us to establish a T12-L2 osteoporotic three-dimensional finite element model. This model effectively simulates fracture models under osteoporotic conditions.
The FEA results showed that the stress of the L1 vertebral body increased significantly after the fracture, whereas it decreased significantly after the injection of bone cement. This indicates that injection of bone cement can significantly reduce stress on the fractured vertebral body. Additionally, in the L1 vertebral body, the maximum Von Mises stress of SG was lower than that of IG under the six loading conditions. This could be attributed to the uniform injection of bone cement on both sides of the vertebral body in a separate distribution, resulting in a more symmetrical stiffness distribution. This symmetry leads to a better balance of stress within the vertebral body, thereby reducing maximum stress levels. Hou et al. [53] discovered that achieving symmetrical distribution of bone cement could effectively decrease the occurrence of recompression in the injured vertebral body. However, owing to the insufficient distribution of cement in the vertebral body, the block shape cannot provide mechanical support for the collapsed vertebral body and the stability of the spine cannot be well restored. Therefore, it is easy to cause a refracture of the operated vertebral body [14,54]. Ha et al. [55] found through FEA that when bone cement is distributed in a block shape, the unfilled part of the bone cement has a stress shielding effect, which can further reduce trabecular bone and accelerate bone loss.
Studies have indicated that load transmission along the longitudinal axis of the spine to the neighboring vertebra is a crucial factor influencing adjacent vertebral fractures [32,36,56]. This study found that in the T12 vertebral body, compared with IG, the maximum stress of SG decreased in flexion and right rotation and was basically the same under other loading conditions. At the same time, in the L2 vertebral body, compared with NG and IG, the maximum stress of SG was the smallest under all six loading conditions. This suggests that separated cement distribution can achieve balanced load transmission, thereby reducing the stress on the adjacent vertebra and minimizing the occurrence of fractures. Liang et al. [37], through FEA, found that when cement is distributed in a concentrated manner without spreading to both sides, it could lead to a significant increase in stress on the adjacent vertebra, thereby increasing the risk of fractures in the adjacent segments. Therefore, in terms of reducing adjacent vertebral fractures, SG has certain biomechanical advantages over IG.
Feng et al. [57] suggested that increased stress during vertebroplasty may affect the nutrient supply to the intervertebral discs, thus influencing disc degeneration. In this study, for T12-L1 intervertebral discs, compared with NG and IG, the maximum stress of SG was lower during flexion, extension, and left/right bending. This suggests that, compared to IG, SG may help reduce stress on the T12-L1 intervertebral disc, thereby decreasing disc degeneration and improving patients' quality of life. Compared with IG, the maximum stress of the L1-L2 intervertebral disc in SG decreased during left/right bending but increased during left/right rotation. This suggests that the separated distribution has a more satisfactory effect on lateral bending. However, it is advisable to avoid rotational movements in the case of separated distribution to prevent an increase in pressure within the intervertebral disc.
According to the three-column theory, spinal instability can increase the risk of spinal recompression [58]. In this study, it was found that SG could decrease the maximum displacement of L1 across various loading conditions, and it was lower than that of IG. This suggests that SG can reduce spinal motion and restore spinal stability more effectively than IG, which was also confirmed by Liebschner M [59]. and Dai [10]. Therefore, SG can also reduce the risk of recompression by improving the stability level.
In vertebroplasty with double-column bone cement, Xu et al. [60] found that when two cement cylinders were implanted into the fractured area of the entire cancellous bone, the cement was distributed within the fracture area and infiltrated the surrounding cancellous bone in an interlocking manner. Liang et al. [37] and Kim et al. [61] also reached the same conclusion using the finite element method, stating that using cylindrical-shaped cement could be a reasonable approach for PVP surgery, as it resembles the cement distribution observed in postoperative imaging and can restore the original height of the fractured vertebra. Our study also found that simulating PVP surgery using a cylindrical cement model may result in different stress and displacement patterns under different loading conditions. However, the overall conclusions were consistent. The primary novelty of this study lies in the simulation of both IG and SG models of bone cement, which is a common occurrence in clinical settings. Subsequently, finite element analysis software was employed to analyze Von Mises stress and displacement in the vertebral body and intervertebral disc.
This study had some limitations. 1. The model used in this study was relatively simplified, assuming homogeneous, isotropic, and linear elastic properties for all tissues, which may have affected the stress and displacement results. 2. The use of cylindrical cement in this study led to conclusions consistent with those of studies that used different cement shapes. This ensures the reproducibility of the research and reduces computational complexity. However, it is important to acknowledge that the cylindrical shape of cement may not fully represent the irregular shapes observed in real clinical scenarios, which could potentially affect the results. 3. Stress on the vertebral body in various motion states in daily life may not be accurately simulated, and force analysis of a specific motion state is only performed under ideal conditions, which has certain limitations.
5. Conclusions
In this study, we used FEA to compare the biomechanical differences between two different distributions of bone cement. The results showed that after L1 vertebral fracture, the stress significantly increased, but the maximum stress reduced after bone cement injection. Furthermore, the separated distribution of bone cement can balance the stress on both sides of the vertebral body, reducing the maximum stress on the vertebral body and intervertebral disc, and thus lowering the incidence of complications.
Ethical Approval
Approved was obtained from the Ethics Committee of the Second Affiliated Hospital of Xuzhou Medical University (NO. [2022]080,701). Informed consent from the participant has been obtained.
Sources of Funding
This study was supported by the Xuzhou Special Fund for Promoting Scientific and Technological Innovation (KC22204).
Data Availability
The data supporting this study's findings are available upon reasonable request from the corresponding author.
CRediT authorship contribution statement
Chengqiang Zhou: Writing – review & editing, Writing – original draft, Software, Data curation, Conceptualization. Xiao Meng: Methodology, Data curation. Shaolong Huang: Formal analysis, Data curation. Han Chen: Investigation. Haibin Zhou: Software. Yifeng Liao: Software, Formal analysis. Zhongjian Tang: Visualization, Validation. Xu Zhang: Visualization, Validation. Hua Li: Validation, Funding acquisition. Wei Sun: Writing – review & editing, Software, Conceptualization. Yunqing Wang: Writing – original draft, Supervision, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We are grateful for the cooperation and support of all orthopedic colleagues at the Affiliated Hospital of Xuzhou Medical University and the Second Affiliated Hospital of Xuzhou Medical University.
Contributor Information
Wei Sun, Email: swyx718323@163.com.
Yunqing Wang, Email: wang.yunqing@163.com.
Abbreviations
- OVCF
osteoporotic vertebral compression fracture
- PVP
percutaneous vertebroplasty
- IG
integration group
- SG
separation group
- NG
non-injected group
- FEA
finite element analysis
- ALL
anterior longitudinal ligament
- PLL
posterior longitudinal ligament
- LF
ligamentum flavum
- SSL
supraspinal ligament
- ISL
interspinous ligament
- ITL
intertransverse ligament
- CL
capsular ligament
References
- 1.Curtis E.M., et al. Recent advances in the pathogenesis and treatment of osteoporosis. Clin. Med. 2015;15(6):s92–s96. doi: 10.7861/clinmedicine.15-6-s92. Suppl 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mao W., et al. Risk factors for secondary fractures to percutaneous vertebroplasty for osteoporotic vertebral compression fractures: a systematic review. J. Orthop. Surg. Res. 2021;16(1):644. doi: 10.1186/s13018-021-02722-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhao G., Liu X., Li F. Balloon kyphoplasty versus percutaneous vertebroplasty for treatment of osteoporotic vertebral compression fractures (OVCFs) Osteoporos. Int. 2016;27(9):2823–2834. doi: 10.1007/s00198-016-3610-y. [DOI] [PubMed] [Google Scholar]
- 4.Gou P., et al. Efficacy of recombinant human parathyroid hormone versus vertebral augmentation procedure on patients with acute osteoporotic vertebral compression fracture. Orthop. Surg. 2022;14(10):2510–2518. doi: 10.1111/os.13470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Alsoof D., et al. Diagnosis and management of vertebral compression fracture. Am. J. Med. 2022;135(7):815–821. doi: 10.1016/j.amjmed.2022.02.035. [DOI] [PubMed] [Google Scholar]
- 6.Park J.S., Park Y.S. Survival analysis and risk factors of new vertebral fracture after vertebroplasty for osteoporotic vertebral compression fracture. Spine J. 2021;21(8):1355–1361. doi: 10.1016/j.spinee.2021.04.022. [DOI] [PubMed] [Google Scholar]
- 7.Yang D., et al. Resources utilisation and economic burden of percutaneous vertebroplasty or percutaneous kyphoplasty for treatment of osteoporotic vertebral compression fractures in China: a retrospective claim database study. BMC Musculoskelet Disord. 2020;21(1):255. doi: 10.1186/s12891-020-03279-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Peng Y., et al. Optimizing bone cement stiffness for vertebroplasty through biomechanical effects analysis based on patient-specific three-dimensional finite element modeling. Med. Biol. Eng. Comput. 2018;56(11):2137–2150. doi: 10.1007/s11517-018-1844-x. [DOI] [PubMed] [Google Scholar]
- 9.Dai C., et al. Risk factors of vertebral re-fracture after PVP or PKP for osteoporotic vertebral compression fractures, especially in Eastern Asia: a systematic review and meta-analysis. J. Orthop. Surg. Res. 2022;17(1):161. doi: 10.1186/s13018-022-03038-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dai H., et al. Biomechanical comparison between unilateral and bilateral percutaneous vertebroplasty for osteoporotic vertebral compression fractures: a finite element analysis. Front. Bioeng. Biotechnol. 2022;10 doi: 10.3389/fbioe.2022.978917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gao W., et al. Establishment and verification of a predictive nomogram for new vertebral compression fracture occurring after bone cement injection in middle-aged and elderly patients with vertebral compression fracture. Orthop. Surg. 2023;15(4):961–972. doi: 10.1111/os.13655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chang X., et al. Vertebroplasty versus kyphoplasty in osteoporotic vertebral compression fracture: a meta-analysis of prospective comparative studies. Int. Orthop. 2015;39(3):491–500. doi: 10.1007/s00264-014-2525-5. [DOI] [PubMed] [Google Scholar]
- 13.Jindal V., Binyala S., Kohli S.S. Balloon kyphoplasty versus percutaneous vertebroplasty for osteoporotic vertebral body compression fractures: clinical and radiological outcomes. Spine J. 2023;23(4):579–584. doi: 10.1016/j.spinee.2022.11.015. [DOI] [PubMed] [Google Scholar]
- 14.Kim Y.Y., Rhyu K.W. Recompression of vertebral body after balloon kyphoplasty for osteoporotic vertebral compression fracture. Eur. Spine J. 2010;19(11):1907–1912. doi: 10.1007/s00586-010-1479-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ko B.S., Cho K.J., Park J.W. Early adjacent vertebral fractures after balloon kyphoplasty for osteoporotic vertebral compression fractures. Asian Spine J. 2019;13(2):210–215. doi: 10.31616/asj.2018.0224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee W.S., et al. Risk factors of developing new symptomatic vertebral compression fractures after percutaneous vertebroplasty in osteoporotic patients. Eur. Spine J. 2006;15(12):1777–1783. doi: 10.1007/s00586-006-0151-7. [DOI] [PubMed] [Google Scholar]
- 17.Tseng Y.Y., et al. Repeated and multiple new vertebral compression fractures after percutaneous transpedicular vertebroplasty. Spine (Phila Pa 1976. 2009;34(18):1917–1922. doi: 10.1097/BRS.0b013e3181ac8f07. [DOI] [PubMed] [Google Scholar]
- 18.Zhou C., et al. Effect of cement distribution type on clinical outcome after percutaneous vertebroplasty for osteoporotic vertebral compression fractures in the aging population. Front Surg. 2022;9 doi: 10.3389/fsurg.2022.975832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Self M., et al. Analysis of injected cement volume and clinical outcomes following kyphoplasty for vertebral compression fractures. Surg. Neurol. Int. 2020;11:56. doi: 10.25259/SNI_22_2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.He D., et al. Cement distribution patterns are associated with recompression in cemented vertebrae after percutaneous vertebroplasty: a retrospective study. World Neurosurg. 2018;120:e1–e7. doi: 10.1016/j.wneu.2018.06.113. [DOI] [PubMed] [Google Scholar]
- 21.Guo W., et al. Effect of ACDF combined with different degrees of partial resection of uncovertebral joints on cervical stability and degeneration: a three-dimensional finite element analysis. J. Orthop. Surg. Res. 2022;17(1):551. doi: 10.1186/s13018-022-03447-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dhar U.K., et al. Factors influencing cage subsidence in anterior cervical corpectomy and discectomy: a systematic review. Eur. Spine J. 2023;32(3):957–968. doi: 10.1007/s00586-023-07530-w. [DOI] [PubMed] [Google Scholar]
- 23.Han Z., et al. Biomechanical studies of different numbers and positions of cage implantation on minimally invasive transforaminal interbody fusion: a finite element analysis. Front Surg. 2022;9 doi: 10.3389/fsurg.2022.1011808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tsuang F.Y., et al. Mechanical performance of porous biomimetic intervertebral body fusion devices: an in vitro biomechanical study. J. Orthop. Surg. Res. 2023;18(1):71. doi: 10.1186/s13018-023-03556-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wu J., et al. Biomechanical evaluation of different sizes of 3D printed cage in lumbar interbody fusion-a finite element analysis. BMC Musculoskelet Disord. 2023;24(1):85. doi: 10.1186/s12891-023-06201-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chethan K.N., et al. Finite element analysis of hip implant with varying in taper neck lengths under static loading conditions. Comput. Methods Progr. Biomed. 2021;208 doi: 10.1016/j.cmpb.2021.106273. [DOI] [PubMed] [Google Scholar]
- 27.Spina N.T., et al. Biomechanical effects of laminectomies in the human lumbar spine: a finite element study. Spine J. 2021;21(1):150–159. doi: 10.1016/j.spinee.2020.07.016. [DOI] [PubMed] [Google Scholar]
- 28.Nandi S., et al. Short single-wedge stems have higher risk of periprosthetic fracture than other cementless stem designs in Dorr type A femurs: a finite element analysis. Hip Int. 2022;32(3):298–303. doi: 10.1177/1120700020949185. [DOI] [PubMed] [Google Scholar]
- 29.Zhao W.T., et al. Biomechanical effects of different vertebral heights after augmentation of osteoporotic vertebral compression fracture: a three-dimensional finite element analysis. J. Orthop. Surg. Res. 2018;13(1):32. doi: 10.1186/s13018-018-0733-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Widmer Soyka R.P., et al. The effectiveness of percutaneous vertebroplasty is determined by the patient-specific bone condition and the treatment strategy. PLoS One. 2016;11(4) doi: 10.1371/journal.pone.0151680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu Y., et al. Biomechanical comparison between metal block and cement-screw techniques for the treatment of tibial bone defects in total knee arthroplasty based on finite element analysis. Comput. Biol. Med. 2020;125 doi: 10.1016/j.compbiomed.2020.104006. [DOI] [PubMed] [Google Scholar]
- 32.Polikeit A., et al. Factors influencing stresses in the lumbar spine after the insertion of intervertebral cages: finite element analysis. Eur. Spine J. 2003;12(4):413–420. doi: 10.1007/s00586-002-0505-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Polikeit A., Nolte L.P., Ferguson S.J. The effect of cement augmentation on the load transfer in an osteoporotic functional spinal unit: finite-element analysis. Spine (Phila Pa 1976. 2003;28(10):991–996. doi: 10.1097/01.BRS.0000061987.71624.17. [DOI] [PubMed] [Google Scholar]
- 34.Bereczki F., et al. Stability evaluation of different oblique lumbar interbody fusion constructs in normal and osteoporotic condition - a finite element based study. Front. Bioeng. Biotechnol. 2021;9 doi: 10.3389/fbioe.2021.749914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Salvatore G., et al. Biomechanical effects of metastasis in the osteoporotic lumbar spine: a Finite Element Analysis. BMC Musculoskelet Disord. 2018;19(1):38. doi: 10.1186/s12891-018-1953-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chiang C.K., et al. Prophylactic vertebroplasty may reduce the risk of adjacent intact vertebra from fatigue injury: an ex vivo biomechanical study. Spine (Phila Pa 1976. 2009;34(4):356–364. doi: 10.1097/BRS.0b013e31819481b1. [DOI] [PubMed] [Google Scholar]
- 37.Liang D., et al. Biomechanical effects of cement distribution in the fractured area on osteoporotic vertebral compression fractures: a three-dimensional finite element analysis. J. Surg. Res. 2015;195(1):246–256. doi: 10.1016/j.jss.2014.12.053. [DOI] [PubMed] [Google Scholar]
- 38.Boger A., et al. Adjacent vertebral failure after vertebroplasty: a biomechanical study of low-modulus PMMA cement. Eur. Spine J. 2007;16(12):2118–2125. doi: 10.1007/s00586-007-0473-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang M., et al. Biomechanics of adjacent segment after three-level lumbar fusion, hybrid single-level semi-rigid fixation with two-level lumbar fusion. Comput. Methods Biomech. Biomed. Eng. 2022;25(4):455–463. doi: 10.1080/10255842.2021.1959557. [DOI] [PubMed] [Google Scholar]
- 40.Zhong Z.C., Chen S.H., Hung C.H. Load- and displacement-controlled finite element analyses on fusion and non-fusion spinal implants. Proc. Inst. Mech. Eng. H. 2009;223(2):143–157. doi: 10.1243/09544119JEIM476. [DOI] [PubMed] [Google Scholar]
- 41.Wang Q.D., Guo L.X. Prediction of complications and fusion outcomes of fused lumbar spine with or without fixation system under whole-body vibration. Med. Biol. Eng. Comput. 2021;59(6):1223–1233. doi: 10.1007/s11517-021-02375-1. [DOI] [PubMed] [Google Scholar]
- 42.Zhang X., et al. A finite element analysis on different bone cement forms and injection volumes injected into lumbar vertebral body in percutaneous kyphoplasty. BMC Musculoskelet Disord. 2022;23(1):621. doi: 10.1186/s12891-022-05522-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhang Q., et al. Finite element analysis of the lumbar spine in adolescent idiopathic scoliosis subjected to different loads. Comput. Biol. Med. 2021;136 doi: 10.1016/j.compbiomed.2021.104745. [DOI] [PubMed] [Google Scholar]
- 44.Huang S., et al. Biomechanical analysis of sandwich vertebrae in osteoporotic patients: finite element analysis. Front. Endocrinol. 2023;14 doi: 10.3389/fendo.2023.1259095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yang P., et al. Pedicle screw fixation with kyphoplasty decreases the fracture risk of the treated and adjacent non-treated vertebral bodies: a finite element analysis. J Huazhong Univ Sci Technolog Med Sci. 2016;36(6):887–894. doi: 10.1007/s11596-016-1680-x. [DOI] [PubMed] [Google Scholar]
- 46.Zhou Q.K., et al. Influence of cement-augmented pedicle screw instrumentation in an osteoporotic lumbosacral spine over the adjacent segments: a 3D finite element study. J. Orthop. Surg. Res. 2020;15(1):132. doi: 10.1186/s13018-020-01650-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Galbusera F., et al. Biomechanics of sacropelvic fixation: a comprehensive finite element comparison of three techniques. Eur. Spine J. 2020;29(2):295–305. doi: 10.1007/s00586-019-06225-5. [DOI] [PubMed] [Google Scholar]
- 48.Fan Z., et al. Biomechanical efficacy of four different dual screws fixations in treatment of talus neck fracture: a three-dimensional finite element analysis. J. Orthop. Surg. Res. 2020;15(1):45. doi: 10.1186/s13018-020-1560-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Li Q.L., et al. Treatment of thoracolumbar fracture with pedicle screws at injury level: a biomechanical study based on three-dimensional finite element analysis. Eur. J. Orthop. Surg. Traumatol. 2013;23(7):775–780. doi: 10.1007/s00590-012-1076-y. [DOI] [PubMed] [Google Scholar]
- 50.Guo L.X., Li W.J. Finite element modeling and static/dynamic validation of thoracolumbar-pelvic segment. Comput. Methods Biomech. Biomed. Eng. 2020;23(2):69–80. doi: 10.1080/10255842.2019.1699543. [DOI] [PubMed] [Google Scholar]
- 51.Schmoelz W., et al. Extent of corpectomy determines primary stability following isolated anterior reconstruction in a thoracolumbar fracture model. Clin. Biomech. 2010;25(1):16–20. doi: 10.1016/j.clinbiomech.2009.09.010. [DOI] [PubMed] [Google Scholar]
- 52.Chen L.H., et al. Repeated percutaneous vertebroplasty for refracture of cemented vertebrae. Arch Orthop Trauma Surg. 2011;131(7):927–933. doi: 10.1007/s00402-010-1236-7. [DOI] [PubMed] [Google Scholar]
- 53.Hou Y., et al. Polymethylmethacrylate distribution is associated with recompression after vertebroplasty or kyphoplasty for osteoporotic vertebral compression fractures: a retrospective study. PLoS One. 2018;13(6) doi: 10.1371/journal.pone.0198407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Yu W., et al. Risk factors for recollapse of the augmented vertebrae after percutaneous vertebroplasty for osteoporotic vertebral fractures with intravertebral vacuum cleft. Medicine (Baltim.) 2017;96(2):e5675. doi: 10.1097/MD.0000000000005675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ha K.Y., et al. Revision surgery after vertebroplasty or kyphoplasty. Clin. Orthop. Surg. 2010;2(4):203–208. doi: 10.4055/cios.2010.2.4.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kim D.J., et al. The proper volume and distribution of cement augmentation on percutaneous vertebroplasty. J Korean Neurosurg Soc. 2010;48(2):125–128. doi: 10.3340/jkns.2010.48.2.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Feng Z., et al. Vertebral augmentation can induce early signs of degeneration in the adjacent intervertebral disc: evidence from a rabbit model. Spine (Phila Pa 1976. 2018;43(20):E1195–E1203. doi: 10.1097/BRS.0000000000002666. [DOI] [PubMed] [Google Scholar]
- 58.Denis F. The three column spine and its significance in the classification of acute thoracolumbar spinal injuries. Spine (Phila Pa 1976. 1983;8(8):817–831. doi: 10.1097/00007632-198311000-00003. [DOI] [PubMed] [Google Scholar]
- 59.Liebschner M.A., Rosenberg W.S., Keaveny T.M. Effects of bone cement volume and distribution on vertebral stiffness after vertebroplasty. Spine (Phila Pa 1976. 2001;26(14):1547–1554. doi: 10.1097/00007632-200107150-00009. [DOI] [PubMed] [Google Scholar]
- 60.Xu K., et al. Influence of the distribution of bone cement along the fracture line on the curative effect of vertebral augmentation. J. Int. Med. Res. 2019;47(9):4505–4513. doi: 10.1177/0300060519864183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kim J.M., et al. Effect of bone cement volume and stiffness on occurrences of adjacent vertebral fractures after vertebroplasty. J Korean Neurosurg Soc. 2012;52(5):435–440. doi: 10.3340/jkns.2012.52.5.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data supporting this study's findings are available upon reasonable request from the corresponding author.