Abstract
Motivation
The selection among substitution models of molecular evolution is fundamental for obtaining accurate phylogenetic inferences. At the protein level, evolutionary analyses are traditionally based on empirical substitution models but these models make unrealistic assumptions and are being surpassed by structurally constrained substitution (SCS) models. The SCS models often consider site-dependent evolution, a process that provides realism but complicates their implementation into likelihood functions that are commonly used for substitution model selection.
Results
We present a method to perform selection among site-dependent SCS models, also among empirical and site-dependent SCS models, based on the approximate Bayesian computation (ABC) approach and its implementation into the computational framework ProteinModelerABC. The framework implements ABC with and without regression adjustments and includes diverse empirical and site-dependent SCS models of protein evolution. Using extensive simulated data, we found that it provides selection among SCS and empirical models with acceptable accuracy. As illustrative examples, we applied the framework to analyze a variety of protein families observing that SCS models fit them better than the corresponding best-fitting empirical substitution models.
Availability and implementation
ProteinModelerABC is freely available from https://github.com/DavidFerreiro/ProteinModelerABC, can run in parallel and includes a graphical user interface. The framework is distributed with detailed documentation and ready-to-use examples.
1 Introduction
Substitution model selection is a traditional step of the phylogenetics pipeline because the applied substitution model can affect the accuracy of phylogenetic tree and ancestral sequence reconstructions, among other evolutionary inferences (Yang et al. 1994, Zhang and Nei 1997, Zhang 1999, Minin et al. 2003, Lemmon and Moriarty 2004, Keane et al. 2006, Ripplinger and Sullivan 2010, Cox and Foster 2013, Arenas and Bastolla 2019, Del Amparo and Arenas 2022, 2023). This need of selection among substitution models is essentially based on the heterogeneous evolutionary processes observed in nature at the molecular level, where genomic regions (Arbiza et al. 2011, Pandey and Braun 2020) and even protein sites (Pupko et al. 2002, Robinson et al. 2003, Echave et al. 2016, Jiménez-Santos et al. 2018, Neverov et al. 2021) often evolve under different selection pressures that better fit with different substitution models. As a consequence, a variety of substitution models of molecular evolution are available and used in the field (see for a review, Arenas 2015a).
At the protein level, two main types of substitution models were developed so far. First, the empirical substitution models, which consist of the relative rates of change among amino acids (exchangeability matrix) and the amino acid frequencies at the equilibrium (Thorne 2000, Yang 2006, Arenas 2015a). These models are traditionally obtained from large empirical datasets of nuclear (Jones et al. 1992, Whelan and Goldman 2001), chloroplast (Adachi et al. 2000), mitochondrial (Yang et al. 1998, Abascal et al. 2007) or virus (Nickle et al. 2007, Dang et al. 2010, Del Amparo and Arenas 2022) proteins, among other biological groups (Thorne 2000, Yang 2006, Arenas 2015a). Empirical substitution models of molecular evolution assume site-independent evolution and also that all the protein sites are modeled with the same exchangeability matrix and amino acid frequencies, which allow them a straightforward implementation into likelihood functions (where the likelihood is site-specific and site-independent) (Yang 2006, Puller et al. 2020) and, in extension, into likelihood-based phylogenetic methods (e.g. Darriba et al. 2011, Kozlov et al. 2019, Tamura et al. 2021). However, those assumptions could also produce proteins with unrealistic amino acid distributions and folding stability (Keane et al. 2006, Bordner and Mittelmann 2014, Arenas et al. 2015b, Arenas and Bastolla 2019). Second, the structurally constrained substitution (SCS) models, which directly consider selection on the protein structure (see for a review Liberles et al. 2012). Some SCS models account for site-dependent evolution and can produce proteins with amino acid distributions and folding stability more realistic than those obtained with empirical substitution models (Arenas et al. 2013). This is hardly surprising because, for example, it is known that residues at the protein core can exhibit substitution patterns different from those located in other regions of the protein (i.e. surface) due to selection on the protein folding stability and activity (Jiménez-Santos et al. 2018, Echave 2019, Perron et al. 2019). Indeed, physicochemical interactions between amino acids located at different protein sites are often observed (Shakhnovich et al. 1996) and can promote coevolution among sites (Starr and Thornton 2016, Neverov et al. 2021, Chaurasia and Dutheil 2022), suggesting that site-dependent substitution models could be preferred to those that ignore coevolution although this should be formally evaluated for every studied data. However, site-dependent models cannot be incorporated into likelihood functions due to the consideration of the site-dependence evolutionary process [notice that current likelihood-based phylogenetic methods calculate site-independent likelihoods (Yang 2006)]. Consequently, these models cannot be compared with other models through the traditional methods for substitution model selection based on likelihoods such as the likelihood ratio test, Akaike Information Criterion and Bayesian Information Criterion, among others (Sullivan and Joyce 2005, Luo et al. 2010, Darriba et al. 2011, 2020). As a consequence, there is a need of likelihood-free methods to perform selection among substitution models of evolution that include substitution models accounting for site-dependent evolution. Importantly, site-dependent SCS models can be used to study protein evolution by likelihood-free methods like those based on computer simulations, including applications for hypothesis testing (Bordner and Mittelmann 2014, Shah et al. 2015, Pascual-García et al. 2019, Del Amparo et al. 2023), validation of analytical frameworks (Arenas et al. 2017, Arenas and Bastolla 2019), and estimation of evolutionary parameters (Bastolla and Arenas 2019, Arenas 2022).
In this regard, as an alternative, the approximate Bayesian computation (ABC) approach is traditionally used to perform model selection in population genetics and ecology without the need of a likelihood function (Beaumont et al. 2002, Beaumont 2010). This approach is based on extensive computer simulations with parameters sampled from prior distributions, summary statistics that extract the information from the query and simulated data and a statistical adjustment (i.e. rejection or multiple linear regression, among others) to obtain the posterior distribution (probability) of the fitting of each evaluated model with the query data (Csilléry et al. 2012). Despite ABC does not require likelihood analyses, it can provide estimates with similar (sometimes higher) accuracy compared to those obtained with some likelihood-based methods (Lopes et al. 2014). Some previous works demonstrated that ABC can be used to study molecular evolution (Wilson et al. 2009, Lopes et al. 2014, Arenas et al. 2015a, Arenas 2015b, Moshe et al. 2022). For example, at the protein level, we previously applied ABC to estimate substitution and recombination rates with acceptable accuracy (Arenas 2022). Key factors for adapting ABC to the evolutionary analysis of protein sequences are the simulation of protein data along evolutionary histories (i.e. phylogenetic trees) under substitution models of evolution and, the design of informative summary statistics to extract evolutionary information from this genetic marker. Concerning the simulation of protein evolution upon evolutionary histories, it was implemented in diverse evolutionary frameworks (see the reviews Arenas 2012, Hoban et al. 2012) although only a few of them include SCS models (Grahnen and Liberles 2012, Arenas et al. 2013). We believe that efforts should still be made in implementing SCS models into computer simulators and, in general, into practical phylogenetic frameworks. Concerning the summary statistics to extract evolutionary information from protein sequences, Arenas (2022) found that several statistics (i.e. mean, standard deviation, skewness and kurtosis) of heterozygosity and pairwise sequence identity are informative for ABC-based analyses of protein evolution under empirical substitution models. However, SCS models produce evolutionary signatures in sequences that could only be detected by evaluating the fitting of the protein sequence with a respective protein structure. Conveniently, there are statistics that could be used for this purpose such as hydrophobicity (Jiménez-Santos et al. 2018), entropy (Goldstein and Pollock 2017), contact interactions (Franzosa and Xia 2009), solvent accessibility (Yeh et al. 2014) and, in general, protein folding stability. We believe that these statistics could allow the application of ABC to study patterns of protein evolution with selection on the protein structure.
Here, we present the application of ABC to perform selection among substitution models of protein evolution that can include site-dependent evolution, thus providing an alternative strategy to evaluate substitution models that, due to their complexity, cannot be implemented into likelihood functions. We implemented the method into a user-friendly computational framework called ProteinModelerABC that showed an acceptable accuracy in distinguishing among these models. As illustrative practical examples, we applied the framework to study the fitting of different site-dependent SCS and empirical models with protein families from diverse organisms of general interest.
2 Materials and methods
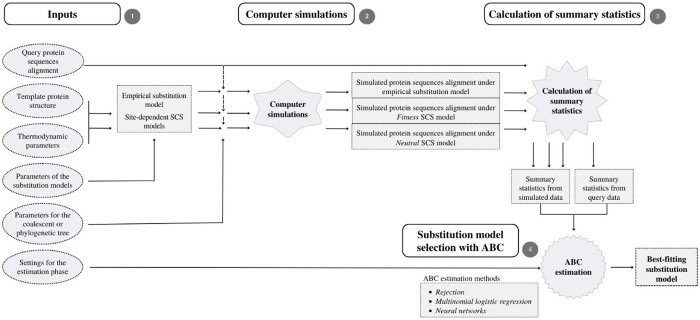
We present an ABC-based method to identify the best-fitting substitution model for a given alignment of protein sequences through a few methodological steps that include the reading of input information, simulation of protein evolution along evolutionary histories under the studied substitution models, calculation of informative summary statistics and, estimation of posterior probabilities for the studied substitution models with common statistical ABC methods (Fig. 1). Details about these steps are presented below.
Figure 1.
Pipeline of substitution model selection with ProteinModelerABC. The framework starts reading the query alignment of protein sequences and diverse user-specified information such as the substitution models to be evaluated and their parameters (Supplementary Table S1), the evolutionary history (simulated with the coalescent or a user-specified phylogenetic tree), the number of simulations and the ABC estimation method, among others. Next, the framework simulates protein evolution under the specified substitution models, obtaining a same number of simulations under each substitution model. In a subsequent step, it calculates the summary statistics for the query and simulated data. Finally, the framework predicts the best-fitting substitution model, among the studied substitution models, according to the posterior probabilities estimated with the ABC method.
Input information. The ABC approach requires making some decisions, such as the number of simulations and the fraction of simulations retained for the estimation (tolerance), that could affect the results. Thus, in addition to the query multiple sequence alignment, the input information includes parameters of the evaluated substitution models of protein evolution, the underlined evolutionary histories and statistical ABC estimation methods (a list of all the parameters implemented in the framework is presented in Supplementary Table S1). A variety of input parameters are optional (including fixed and nuisance parameters, the latter allow user-specified prior distributions) and could provide a more realistic modeling of certain evolutionary processes. For example, the user can optionally specify population genetics parameters to simulate coalescent evolutionary histories (i.e. population size and population growth rate) and the empirical substitution models can include variation of the substitution rate among sites according to a Gamma distribution (Yang et al. 1994) and a proportion of invariable sites (Shoemaker and Fitch 1989). Despite the main aim of ProteinModelerABC is to evaluate the fitting of site-dependent SCS models [note that other well-established methods and frameworks are already available to identify the best-fitting substitution model among a set of empirical substitution models (i.e. Keane et al. 2006, Darriba et al. 2011, Kalyaanamoorthy et al. 2017, Darriba et al. 2020)], it implements a variety of empirical substitution models that allow diverse comparisons between site-dependent SCS and empirical models. In particular, the empirical substitution models implemented in ProteinModelerABC are Blosum62 (Henikoff and Henikoff 1992), CpRev (Adachi et al. 2000), Dayhoff (Dayhoff et al. 1978), DayhoffDCMUT (Kosiol and Goldman 2005), HIVb (Nickle et al. 2007), HIVw (Nickle et al. 2007), JTT (Jones et al. 1992), JonesDCMUT (Kosiol and Goldman, 2005), LG (Le and Gascuel 2008), Mtart (Abascal et al. 2007), Mtmam (Yang et al. 1998), Mtrev24 (Adachi and Hasegawa 1996), RtRev (Dimmic et al. 2002), VT (Müller and Vingron 2000), and WAG (Whelan and Goldman 2001), also any other exchangeability matrix and amino acid frequencies given as input could be evaluated. Concerning site-dependent SCS models, the framework implements two main site-dependent SCS models, hereafter named “Neutral” and “Fitness” (Arenas et al. 2013), that consider the stability of the native state with respect to both unfolding and misfolding states (Minning et al. 2013). The stability includes configurational entropies, hydrophobicity, and site-specific contacts [involving a statistical mechanical treatment of misfolded conformations that is computationally affordable (Bastolla et al. 2005a, 2005b)], among other physicochemical properties (Arenas et al. 2013). Misfolding stability affects the energy of amino acid contacts found in alternative structures (named as negative design to distinguish it from the positive design of protein stability based on native interactions) (Berezovsky et al. 2007, Noivirt-Brik et al. 2009, Minning et al. 2013) and it is important because, if only unfolded states are considered, the modeling of selection tends to artificially increase hydrophobicity (Arenas et al. 2013, Jiménez-Santos et al. 2018). The Neutral model is more general than the Fitness model. The Neutral model considers the fitness as a binary variable where all protein variants with stability above a given threshold (based on a representative protein structure) are considered viable (and equally fit) whereas all protein variants below the threshold are considered lethal and, therefore, discarded (Arenas et al. 2013). Thus, the Neutral model is less sensitive to variations of entropy and thermodynamic temperature (Arenas et al. 2013). Next, the Fitness model additionally considers that the probability of mutations depends on the effective population size, thus showing segregating variation in a population (Arenas et al. 2013). In this case, the fitness is an increasing function of stability and proportional to the fraction of protein variants in the native state (Goldstein 2011, 2013). In addition, the probability of accepting mutation events also considers the effective population size through the Moran’s birth–death process (Ewens 1979, Sella and Hirsh 2005). Thus, the Neutral model includes fewer parameters than the Fitness model and the Fitness model can be reduced to the Neutral model at a low thermodynamic temperature where the fitness tends to be 1 in highly stable proteins and zero in highly unstable proteins (Arenas et al. 2013). In practice, these models can produce different distributions of amino acid frequencies and folding stability of the modeled proteins. The Fitness model produced amino acid distributions more similar to the real observations than those obtained with the Neutral model for some protein families, while the Neutral model was in general more robust than the Fitness model to analyze diverse data (Arenas et al. 2013). For further information about the Neutral and Fitness site-dependent substitution models, we refer the reader to Arenas et al. (2013). As input information, these SCS models require the specification of several thermodynamic parameters and a protein structure (i.e. available from the Protein Data Bank, PDB) representative of the query alignment of protein sequences (Supplementary Table S1). Conveniently, the framework is distributed with a detailed documentation that includes recommendations for the specification of the input parameters.
Computer simulations. The computer simulations of protein data are performed in ProteinModelerABC with a recent version of the simulator ProteinEvolver (Arenas et al. 2013) adapted to ABC (Arenas 2022). Protein evolution is simulated along evolutionary histories that can be previously simulated with the coalescent (Kingman 1982) under diverse population genetics scenarios (Supplementary Table S1) or specified through an input phylogenetic tree. While the latter considers a same phylogenetic tree for all the simulations, the former can include stochasticity to obtain different coalescent evolutionary histories among simulations. The simulation of protein evolution under the studied substitution models is performed forward in time, from the root node to the tip nodes of the evolutionary history. Conveniently, ProteinModelerABC can run the simulations in parallel on a multicore machine to reduce computer time (Supplementary Fig. S1). As expected, a simulation of protein evolution under an empirical substitution model is more rapid (less than a second) than a simulation under a site-dependent SCS model (from seconds to minutes depending on the protein length and sample size) due to the consideration of structural constraints (Supplementary Fig. S2).
Summary statistics. We designed seven summary statistics (SS; details below and in Supplementary Table S2) that showed sufficient evolutionary information to distinguish between the implemented SCS models and between SCS and empirical models (details shown in the following section). In general, these SS comprise the protein folding stability, molecular diversity and physicochemical properties of the amino acids involved in the replacements. Concerning the protein folding stability, we included the mean and standard deviation of the free energy predicted with the framework DeltaGREM (Minning et al. 2013, Arenas et al. 2015b). As a measure of molecular diversity, we considered the number of segregating sites, following previous ABC studies of molecular evolution (Lopes et al. 2014, Arenas et al. 2015a, Arenas 2022). Additionally, we included the site-specific change of physicochemical properties among amino acids by the mean, standard deviation, skewness and kurtosis of the traditional Grantham distances (Grantham 1974).
-
Substitution model selection with ABC. The framework estimates the posterior probability of every studied substitution model with the query protein multiple sequence alignment using statistical methods available from the abc R library (Csilléry et al. 2012). In particular, the framework implements the rejection, multinomial logistic regression, and neural networks methods (Blum and François 2010, Csilléry et al. 2012). In addition to the posterior probabilities, the framework provides the confusion matrix (accuracy of predictions under every studied substitution model) and the goodness of fit of the studied substitution models with the query data. Indeed, the framework supplies distributions of the distance between SS of the retained simulations and SS of the query data for every studied substitution model, which illustrate about the realism of the modeling.
Altogether, ProteinModelerABC provides selection among substitution models of protein evolution including complex models that cannot be implemented in likelihood functions through ABC. The framework is written in Python, C, and R, and can run in parallel on local or cluster computers. Interestingly, the program includes a graphical user interface that can be useful for users that are not familiar with the command line. ProteinModelerABC is freely available from https://github.com/DavidFerreiro/ProteinModelerABC and it is distributed with a detailed documentation and illustrative practical examples.
3 Results
3.1 ProteinModelerABC validation
The use of ABC for selecting among evolutionary scenarios is well-established in population genetics and ecology (e.g. Leuenberger and Wegmann 2010, Sousa et al. 2012, Branco et al. 2022) and we believe that it can provide a proper likelihood-free alternative to evaluate complex substitution models of molecular evolution. Here, we evaluated the accuracy of ProteinModelerABC to perform selection among empirical and SCS models under different scenarios: (i) Number of simulations for training the method (10 000, 50 000, and 100 000), (ii) tolerance (0.005, 0.01, and 0.05), and (iii) ABC estimation method including rejection, multinomial logistic regression, and neural networks. We performed the evaluations using data simulated under the Dayhoff empirical substitution model (which is widely used in the field), the Fitness site-dependent SCS model and the Neutral site-dependent SCS model. The simulations were inspired in the thioredoxin protein family [27 sequences and 316 amino acids (l) with sequence identity of 0.44; Pfam code PF00070] and a representative protein structure (PDB code 1TDE) (Waksman et al. 1994) obtained by homology modeling with SWISS-MODEL (Arnold et al. 2006) from the consensus sequence. Next, we simulated protein sequence alignments upon coalescent evolutionary histories considering a population size (N) of 1000 individuals and a population substitution rate (θ = 4 Nμl, where μ is the substitution rate per site per generation) sampled from a uniform prior distribution between 0 and 500 that include values commonly observed in nature (e.g. Carvajal-Rodriguez, 2006, Lopes et al. 2014, Arenas, 2022). For every scenario (3 substitution models × 3 different numbers of simulations × 3 ABC tolerance levels × 3 ABC estimation methods = 81 scenarios), we evaluated the power of ProteinModelerABC to distinguish between the three substitution models by cross-validation based on 100 permutations (Csilléry et al. 2012). We found that the framework distinguishes between the studied substitution models with acceptable accuracy regardless of the number of simulations used for training the method, the tolerance level and the ABC statistical method used for the estimation (Supplementary Table S3).
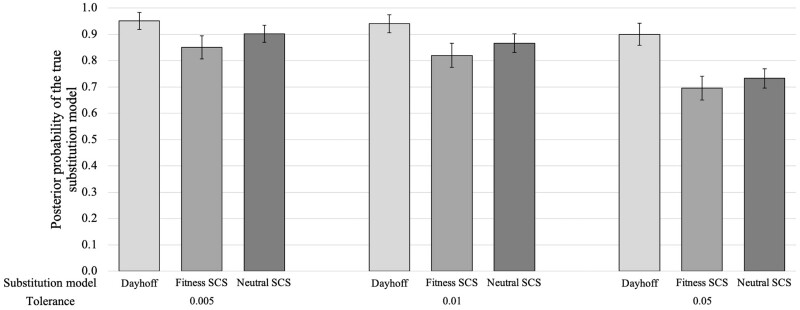
Once we found that the method can distinguish between SCS and empirical models through cross-validation, we evaluated its accuracy in identifying the true substitution model in pseudo-observed (test) data. In particular, we simulated 100 alignments of protein sequences evolved under each studied substitution model (Dayhoff, Fitness SCS and Neutral SCS models) and for each simulated dataset we performed substitution model selection with ProteinModelerABC. These analyses were also performed considering 10 000, 50 000, and 100 000 training simulations, tolerance levels of 0.005, 0.01, and 0.05 and, the three ABC statistical methods. Again, we found that the accuracy of the substitution model selection is not affected by the number of simulations (Supplementary Fig. S3; compare the three plots) and thus 10 000 simulations are sufficient to distinguish between the studied models. Concerning the optimal tolerance, it varied among the studied ABC statistical methods (Supplementary Fig. S3). In particular, the rejection method showed a high robustness in predicting the true substitution model although its accuracy slightly decreased when increasing the tolerance (Fig. 2), a pattern not observed for substitution model selection with the multinomial logistic regression and neural networks methods (Supplementary Fig. S3). However, the latter methods could not converge when the tolerance is small (not enough retained simulations for the estimation) where at least a tolerance of 0.05 was required to obtain accurate estimates (Supplementary Fig. S3). Altogether, the rejection method was less sensitive to the tolerance for substitution model selection and thus we believe that it could be used by default. We did not observe effects of the studied number of simulations used for training the method on the accuracy of the estimates (Supplementary Fig. S3).
Figure 2.
Evaluation of substitution model selection with ProteinModelerABC as a function of the tolerance. Posterior probability of the true substitution model (i.e. Dayhoff, site-dependent Fitness SCS and site-dependent Neutral SCS models) with the ABC rejection method, at different tolerance levels (0.005, 0.01, and 0.05) and using 10 000 training simulations, for 100 pseudo-observed datasets simulated under each substitution model. Error bars indicate 95% confidence intervals from the mean of the posterior probabilities of the true substitution model predicted for the pseudo-observed data. Estimates based on the multinomial logistic regression and neural networks methods are presented in Supplementary Fig. S3
3.2 Illustrative examples of substitution model selection in diverse protein families
We used ProteinModelerABC to identify the best-fitting substitution model, among the best-fitting empirical substitution model previously selected with ProtTest3 (Darriba et al. 2011) and the site-dependent SCS models implemented in ProteinModelerABC, in 10 different protein families (Table 1). These protein families belong to viruses related to human diseases including HIV-1 PR, HIV-1 gag, influenza NS1, SARS-CoV-2 endopeptidase C30 and 2'-O-methyltransferase, Ebola nucleoprotein and, the tumor necrosis factor (TNF) of monkeypox (Mpox) virus. Additionally, we analyzed the highly conserved intracellular signaling Toll-Interleukin protein domain, the squalene epoxidase and the mitochondria membrane translocase, all of them randomly selected but folding in known protein structures. We obtained the protein datasets from the Pfam (Mistry et al. 2021) and PROSITE (Sigrist et al. 2012) databases and they presented diverse sequence length (from 99 to 450 amino acids), sample size (from 8 to 128 sequences) and sequence identity (Table 1). Next, for every dataset, we aligned the sequences with MUSCLE (Edgar 2004) and also we obtained a consensus sequence that we used to identify a representative protein structure by homology modeling with SWISS-MODEL (Table 1). The simulation of protein evolution under site-dependent SCS models and the prediction of protein folding stability (free energy) require homology between the representative protein structure and the sequences of the dataset and thus, sites of the dataset without homology with the protein structure were excluded. Next, we ran ProteinModelerABC with 10 000 simulations under each studied substitution model and under a prior distribution for the substitution rate that produces simulated data with a distribution of sequence identity that includes the sequence identity of the real data (Table 1). Indeed, following results from the previous section, we performed the estimations with the rejection method under a tolerance of 0.005.
Table 1.
Real protein families and their substitution model selection with ProteinModelerABCa.
| Protein family | Sequences database entry | Number of sequences and sequences length | Sequence identity | Prior for the population substitution rate and derived range of sequence identity | Template protein structure | Best-fitting empirical substitution model | Posterior probabilities for substitution model selection | ||
|---|---|---|---|---|---|---|---|---|---|
| Tumor necrosis factor monkeypox | GenBank accession codesb | 10, 160 | 0.95 | Uniform (0–100) | 3on9 | HIVw | Fitness | HIVw | Neutral |
| (1.00–0.65) | 0.22 | 0.01 | 0.77 | ||||||
| HIV protease (PR) | PS50175 | 95, 99 | 0.91 | Uniform (0–150) | 1tcx | HIVb | Fitness | HIVb | Neutral |
| (1.00–0.46) | 0.45 | 0.33 | 0.22 | ||||||
| HIV gag polyprotein | PF00540 | 128, 288 | 0.69 | Uniform (0–500) | 1l6n | RtRev | Fitness | Neutral | RtRev |
| (1.00–0.41) | 0.59 | 0.34 | 0.07 | ||||||
| Influenza NS1 | PF00600 | 25, 202 | 0.83 | Uniform (0–200) | 4oph | JTT | Fitness | JTT | Neutral |
| (1.00–0.54) | 0 | 0.13 | 0.87 | ||||||
| Coronavirus endopeptidase C30 | PF05409 | 30, 299 | 0.53 | Uniform (0–500) | 1lvo | LG | Fitness | LG | Neutral |
| (1.00–0.42) | 0.95 | 0 | 0.05 | ||||||
| Coronavirus 2'-O-methyltransferase | PF06460 | 28, 298 | 0.62 | Uniform (0–500) | 7c2i | LG | Fitness | LG | Neutral |
| (1.00–0.42) | 0.51 | 0.3 | 0.19 | ||||||
| Toll-Interleukin receptor domain | PF01582 | 23, 171 | 0.3 | Uniform (0–700) | 5ku7 | WAG | Fitness | Neutral | WAG |
| (1.00–0.25) | 0.97 | 0.03 | 0 | ||||||
| Mitochondria membrane translocase | PF08038 | 54, 50 | 0.51 | Uniform (0–500) | 6ucv | WAG | Fit ness | Neutral | WAG |
| (1.00–0.14) | 0.36 | 0.44 | 0.2 | ||||||
| Squalene epoxidase | PF08491 | 12, 450 | 0.66 | Uniform (0–500) | 6c6n | WAG | Fitness | Neutral | WAG |
| (1.00–0.50) | 0.97 | 0.03 | 0 | ||||||
| Ebola nucleoprotein | PF05505 | 8, 373 | 0.67 | Uniform (0–500) | 6c54 | LG | Fitness | LG | Neutral |
| (1.00–0.47) | 0 | 0.02 | 0.98 | ||||||
For every studied protein family, the table shows the Pfam or PROSITE accession code (excepting for the first dataset where GenBank accession codes are shown in the table foot), the number of sequences and the sequence length, the sequence identity (average of pairwise sequence identities), the prior for the population substitution rate (including the derived approximate range of average pairwise sequence identity), a representative protein structure (PDB code), the best-fitting empirical substitution model selected with ProtTest3 and the posterior probability of every studied substitution model (empirical, site-dependent Fitness SCS, and site-dependent Neutral SCS models) with ProteinModelerABC (the posterior probability of the selected model is shown in bold).
The goodness of fit analysis showed that, in general, the SS of the real data fall within the SS of the retained simulated data especially for the best-fitting substitution model (illustrative examples are shown in Supplementary Fig. S4). In general, we found that site-dependent SCS models are preferred by most of the summary statistics (in terms of distance to the observed summary statistics) compared to the traditional empirical substitution models (Supplementary Table S4). Indeed, for all the studied real datasets, we found that the site-dependent SCS models fitted better with the real data than the best-fitting empirical substitution model selected with ProtTest3 (Table 1).
4 Discussion
Current methods for substitution model selection are based on the likelihood of fitting the substitution models with the query data. This likelihood is commonly calculated per site, assuming site-independent evolution (Yang 2006, Puller et al. 2020), and none current likelihood function allows the evaluation of substitution models that consider site-dependent evolution. However, these models are increasing in popularity because can produce proteins with more realistic folding stability and distribution of amino acid frequencies than traditional substitution models (i.e. Robinson et al. 2003, Rodrigue et al. 2005, Yu and Thorne 2006, Arenas et al. 2013, Larson et al. 2020) and could be used to analyze protein evolution for diverse applications such as hypothesis testing (Bordner and Mittelmann 2014, Shah et al. 2015, Pascual-García et al. 2019, Del Amparo et al. 2023), validation of analytical frameworks (Arenas et al. 2017, Arenas and Bastolla 2019), and estimation of evolutionary parameters (Bastolla and Arenas 2019, Arenas 2022). Next, the implementation of these substitution models in likelihood-free sampling methodologies such as Monte Carlo and ABC (Beaumont et al. 2002, Rodrigue et al. 2005) becomes relevant for extending their practical applications, including substitution model selection. Here, we present the application of the ABC approach to perform selection among substitution models that can include site-dependent evolution, thus without using likelihood. In particular, we extended our previous ABC studies oriented to estimate parameters of molecular evolution (Arenas et al. 2015a, Arenas 2022), by adapting simulations and summary statistics, to the selection among substitution models of protein evolution that can consider evolutionary constraints from the protein structure. We found that this ABC framework for selection among complex substitution models presents an acceptable accuracy using the implemented set of summary statistics (which was sufficiently informative to distinguish among data simulated under empirical and SCS models, Supplementary Table S4 and Supplementary Fig. S4), and it is especially robust through the implemented ABC rejection method [the implemented logistic and neural networks methods were highly sensible to the tolerance parameter, requiring a high tolerance to ensure accurate model selection as discussed in Beaumont (2010), Fig. 2, and Supplementary Fig. S3]. A low level of tolerance can be convenient to obtain accurate estimates under the rejection method (Sunnåker et al. 2013), as we also found exploring low tolerance levels [i.e. 0.005 and 0.01, the latter was also recommended in previous studies (Csilléry et al. 2012, Nunes and Prangle 2015), Fig. 2]. Regarding the number of simulations, we found that 10 000 simulations can be sufficient to distinguish between the studied substitution models (Supplementary Fig. S3), which is a lower number of simulations than that required to estimate parameters in our previous studies [50 000 simulations in Arenas (2022)] although this is not surprising since parameters estimation usually requires more simulations than model selection.
We implemented the method into a freely available framework named ProteinModelerABC that includes flexibility concerning the underlined evolutionary history (simulated with the coalescent under diverse population genetics processes or specified by the user as a phylogenetic tree, Supplementary Table S1), the modeling of protein evolution (a variety of substitution models are implemented) and the ABC statistical methods to calculate the posterior probability of every studied substitution model with the query data. Next, for subsequent evolutionary analyses, similarly to likelihood-based methods for substitution model selection (Darriba et al. 2011, 2020), we recommend applying the selected best-fitting substitution model, which is the model presenting the highest posterior probability with the study data. The framework can run on the command line of local and cluster computers and includes a graphical user interface (GUI). The required computer time varies depending on the size of the studied data (Supplementary Fig. S2) and, conveniently, the simulations can run in parallel (on both command line and GUI versions) on a multicore machine to reduce the computer time (Supplementary Fig. S1). ProteinModelerABC is distributed with a detailed documentation and several illustrative examples that we recommend exploring.
As illustrative examples of application, we investigated the selection between site-dependent SCS models and the best-fitting empirical substitution model (previously selected with ProtTest3) in diverse protein families of general interest (Table 1). For all the studied real data, we found that site-dependent substitution models explained the real protein evolution better than the best-fitting empirical substitution models. Perhaps the currently available set of empirical substitution models is very limited and more empirical substitution models should be developed to better mimic the evolution of the studied protein families. However, we believe that the main cause of these findings is that site-dependent SCS models are much more specific and realistic than the empirical substitution models because, as indicated in the introduction, the empirical substitution models are usually too generalist, assume a same exchangeability matrix for all the protein sites and ignore coevolution. Note that proteins often present intramolecular interactions that can promote selection toward specific variants through site-dependent evolution (Woo et al. 2014, Rawi et al. 2015, Codoñer et al. 2017, Priya and Shanker 2021, Ferreiro et al. 2022). On the other hand, we find important to mention that the currently implemented site-dependent SCS models assume a representative protein structure for all the sequences of the query data. This could lead to a poor fitting if the query data has sequences poorly represented by the cited protein structure. In this regard, a representative protein structure can be selected from the studied protein sequences by diverse methods (Kuhlman and Bradley 2019) such as the traditional homology modeling [especially when there are protein structures in databases such as PDB likely to resemble the structure of the study sequences (Hameduh et al. 2020)], and the recent deep learning methods implemented in AlphaFold and RoseTTAFold (Baek et al. 2021, Jumper et al. 2021) that are particularly useful when there are not protein structures in databases fitting with the study sequences. Indeed, protein sites present in the study sequences but not in the structure, or disordered, could reduce the fitting of the SCS model with the study sequences due to a lack of structural information in those sites (Kolchanov et al. 1983, Zhang et al. 2011), suggesting a careful modeling and refinement for example also with deep learning methods (Nguyen et al. 2019, Jing and Xu 2021). We believe that the development of more robust SCS models, such as SCS models that consider the evolution and diversity of protein structures, and their implementation into useful frameworks for phylogenetic analyses, are highly demanded in the field to provide more reliable evolutionary estimates. Altogether, we show that ABC can provide a free-likelihood alternative for selecting among complex substitution models of evolution that are often more realistic than the traditional empirical substitution models.
Supplementary Material
Acknowledgements
We thank CESGA (Centro de Supercomputación de Galicia) for the computer resources and for helping with the optimization of the code.
Contributor Information
David Ferreiro, CINBIO, Universidade de Vigo, 36310 Vigo, Spain; Department of Biochemistry, Genetics and Immunology, Universidade de Vigo, 36310 Vigo, Spain.
Catarina Branco, CINBIO, Universidade de Vigo, 36310 Vigo, Spain; Department of Biochemistry, Genetics and Immunology, Universidade de Vigo, 36310 Vigo, Spain.
Miguel Arenas, CINBIO, Universidade de Vigo, 36310 Vigo, Spain; Department of Biochemistry, Genetics and Immunology, Universidade de Vigo, 36310 Vigo, Spain.
Supplementary data
Supplementary data are available at Bioinformatics online.
Conflict of interest
None declared.
Funding
This work was supported by the Spanish Ministry of Science and Innovation [PID2019-107931GA-I00/AEI/10.13039/501100011033]. D.F. was funded by a fellowship from the Xunta de Galicia [ED481A-2020/192]. Funding for open access charge: Universidade de Vigo/CISUG. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Data availability
ProteinModelerABC is freely available from https://github.com/DavidFerreiro/ProteinModelerABC. The simulated and real data used in the study are available from Zenodo at https://doi.org/10.5281/zenodo.10491125.
References
- Abascal F, Posada D, Zardoya R.. MtArt: a new model of amino acid replacement for Arthropoda. Mol Biol Evol 2007;24:1–5. [DOI] [PubMed] [Google Scholar]
- Adachi J, Hasegawa M.. Programs for molecular phylogenetics based on maximum likelihood. Comput Sci Monogr 1996;28:1–150. [Google Scholar]
- Adachi J, Waddell PJ, Martin W. et al. Plastid genome phylogeny and a model of amino acid substitution for proteins encoded by chloroplast DNA. J Mol Evol 2000;50:348–58. [DOI] [PubMed] [Google Scholar]
- Arbiza L, Patricio M, Dopazo H. et al. Genome-wide heterogeneity of nucleotide substitution model fit. Genome Biol Evol 2011;3:896–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M. Simulation of molecular data under diverse evolutionary scenarios. PLoS Comput Biol 2012;8:e1002495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M. Trends in substitution models of molecular evolution. Front Genet 2015a;6:319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M. Advances in computer simulation of genome evolution: toward more realistic evolutionary genomics analysis by approximate Bayesian computation. J Mol Evol 2015b;80:189–92. [DOI] [PubMed] [Google Scholar]
- Arenas M. ProteinEvolverABC: coestimation of recombination and substitution rates in protein sequences by approximate Bayesian computation. Bioinformatics 2022;38:58–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M, Bastolla U.. ProtASR2: ancestral reconstruction of protein sequences accounting for folding stability. Methods Ecol Evol 2019;11:248–57. [Google Scholar]
- Arenas M, Dos Santos HG, Posada D. et al. Protein evolution along phylogenetic histories under structurally constrained substitution models. Bioinformatics 2013;29:3020–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M, Lopes JS, Beaumont MA. et al. CodABC: a computational framework to coestimate recombination, substitution, and molecular adaptation rates by approximate Bayesian computation. Mol Biol Evol 2015a;32:1109–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M, Sánchez-Cobos A, Bastolla U.. Maximum-likelihood phylogenetic inference with selection on protein folding stability. Mol Biol Evol 2015b;32:2195–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M, Weber CC, Liberles DA. et al. ProtASR: an evolutionary framework for ancestral protein reconstruction with selection on folding stability. Syst Biol 2017;66:1054–64. [DOI] [PubMed] [Google Scholar]
- Arnold K, Bordoli L, Kopp J. et al. The SWISS-MODEL workspace: a web-based environment for protein structure homology modelling. Bioinformatics 2006;22:195–201. [DOI] [PubMed] [Google Scholar]
- Baek M, DiMaio F, Anishchenko I. et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021;373:871–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastolla U, Arenas M.. The influence of protein stability on sequence evolution: applications to phylogenetic inference. In: Sikosek T. (ed.) Computational Methods in Protein Evolution. Vol. 1851. Methods in Molecular Biology. New York: Springer, 2019, 215–31. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Porto M, Roman HE. et al. Principal eigenvector of contact matrices and hydrophobicity profiles in proteins. Proteins 2005a;58:22–30. [DOI] [PubMed] [Google Scholar]
- Bastolla U, Porto M, Roman HE. et al. Looking at structure, stability, and evolution of proteins through the principal eigenvector of contact matrices and hydrophobicity profiles. Gene 2005b;347:219–30. [DOI] [PubMed] [Google Scholar]
- Beaumont MA. Approximate Bayesian computation in evolution and ecology. Annu Rev Ecol Evol Syst 2010;41:379–406. [Google Scholar]
- Beaumont MA, Zhang W, Balding DJ.. Approximate Bayesian computation in population genetics. Genetics 2002;162:2025–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berezovsky IN, Zeldovich KB, Shakhnovich EI.. Positive and negative design in stability and thermal adaptation of natural proteins. PLoS Comput Biol 2007;3:e52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blum MGB, François O.. Non-linear regression models for approximate Bayesian computation. Stat Comput 2010;20:63–73. [Google Scholar]
- Bordner AJ, Mittelmann HD.. A new formulation of protein evolutionary models that account for structural constraints. Mol Biol Evol 2014;31:736–49. [DOI] [PubMed] [Google Scholar]
- Branco C, Kanellou M, González-Martín A. et al. Consequences of the last glacial period on the genetic diversity of Southeast Asians. Genes (Basel) 2022;13:384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvajal-Rodriguez A. Recombination estimation under complex evolutionary models with the coalescent composite-likelihood method. Mol. Biol. Evol 2006;23:817–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaurasia S, Dutheil JY.. The structural determinants of intra-protein compensatory substitutions. Mol Biol Evol 2022;39:msac063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Codoñer FM, Peña R, Blanch-Lombarte O. et al. Gag-protease coevolution analyses define novel structural surfaces in the HIV-1 matrix and capsid involved in resistance to protease inhibitors. Sci Rep 2017;7:3717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox CJ, Foster PG.. A 20-state empirical amino-acid substitution model for green plant chloroplasts. Mol Phylogenet Evol 2013;68:218–20. [DOI] [PubMed] [Google Scholar]
- Csilléry K, François O, Blum MGB.. abc: an R package for approximate Bayesian computation (ABC). Methods Ecol Evol 2012;3:475–9. [DOI] [PubMed] [Google Scholar]
- Dang CC, Si Le Q, Gascuel O. et al. FLU, an amino acid substitution model for influenza proteins. BMC Evol Biol 2010;10:99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darriba D, Posada D, Kozlov AM. et al. ModelTest-NG: a new and scalable tool for the selection of DNA and protein evolutionary models. Mol Biol Evol 2020;37:291–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darriba D, Taboada GL, Doallo R. et al. ProtTest 3: fast selection of best-fit models of protein evolution. Bioinformatics 2011;27:1164–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayhoff MO, Schwartz RM, Orcutt BC.. A model of evolutionary change in proteins. In: Dayhoff MO (ed.) Atlas of Protein Sequence and Structure. Vol. 5. Edition, Washington DC: National Biomedical Research Foundation, 1978, 345–52. [Google Scholar]
- Del Amparo R, Arenas M.. Consequences of substitution model selection on protein ancestral sequence reconstruction. Mol Biol Evol 2022;39:msac144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Amparo R, Arenas M.. Influence of substitution model selection on protein phylogenetic tree reconstruction. Gene 2023;865:147336. [DOI] [PubMed] [Google Scholar]
- Del Amparo R, González-Vázquez LD, Rodríguez-Moure L. et al. Consequences of genetic recombination on protein folding stability. J Mol Evol 2023;91:33–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimmic MW, Rest JS, Mindell DP. et al. rtREV: an amino acid substitution matrix for inference of retrovirus and reverse transcriptase phylogeny. J Mol Evol 2002;55:65–73. [DOI] [PubMed] [Google Scholar]
- Echave J. Beyond stability constraints: a biophysical model of enzyme evolution with selection on stability and activity. Mol Biol Evol 2019;36:613–20. [DOI] [PubMed] [Google Scholar]
- Echave J, Spielman SJ, Wilke CO.. Causes of evolutionary rate variation among protein sites. Nat Rev Genet 2016;17:109–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar RC. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res 2004;32:1792–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens WJ. Mathematical population genetics. Berlin, Heidelberg: Springer, 1979. [Google Scholar]
- Ferreiro D, Khalil R, Gallego MJ. et al. The evolution of the HIV-1 protease folding stability. Virus Evol 2022;8:veac115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franzosa EA, Xia Y.. Structural determinants of protein evolution are context-sensitive at the residue level. Mol Biol Evol 2009;26:2387–95. [DOI] [PubMed] [Google Scholar]
- Goldstein RA. The evolution and evolutionary consequences of marginal thermostability in proteins: evolution of protein marginal thermostability. Proteins 2011;79:1396–407. [DOI] [PubMed] [Google Scholar]
- Goldstein RA. Population size dependence of fitness effect distribution and substitution rate probed by biophysical model of protein thermostability. Genome Biol Evol 2013;5:1584–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein RA, Pollock DD.. Sequence entropy of folding and the absolute rate of amino acid substitutions. Nat Ecol Evol 2017;1:1923–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grahnen JA, Liberles DA.. CASS: protein sequence simulation with explicit genotype-phenotype mapping. Trends Evol Biol 2012;4:9. [Google Scholar]
- Grantham R. Amino acid difference formula to help explain protein evolution. Science 1974;185:862–4. [DOI] [PubMed] [Google Scholar]
- Hameduh T, Haddad Y, Adam V. et al. Homology modeling in the time of collective and artificial intelligence. Comput Struct Biotechnol J 2020;18:3494–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff S, Henikoff JG.. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci U S A 1992;89:10915–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoban S, Bertorelle G, Gaggiotti OE.. Computer simulations: tools for population and evolutionary genetics. Nat Rev Genet 2012;13:110–22. [DOI] [PubMed] [Google Scholar]
- Jiménez-Santos MJ, Arenas M, Bastolla U.. Influence of mutation bias and hydrophobicity on the substitution rates and sequence entropies of protein evolution. PeerJ 2018;6:e5549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing X, Xu J.. Fast and effective protein model refinement using deep graph neural networks. Nat Comput Sci 2021;1:462–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Taylor WR, Thornton JM.. The rapid generation of mutation data matrices from protein sequences. Bioinformatics 1992;8:275–82. 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- Jumper J, Evans R, Pritzel A. et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021;596:583–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalyaanamoorthy S, Minh BQ, Wong TKF. et al. ModelFinder: fast model selection for accurate phylogenetic estimates. Nat Methods 2017;14:587–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keane TM, Creevey CJ, Pentony MM. et al. Assessment of methods for amino acid matrix selection and their use on empirical data shows that ad hoc assumptions for choice of matrix are not justified. BMC Evol Biol 2006;6:29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingman JFC. The coalescent. Stoch Process Their Appl 1982;13:235–48. [Google Scholar]
- Kolchanov NA, Soloviov VV, Zharkikh AA.. The effects of mutations, deletions and insertions of single amino acids on the three-dimensional structure of globins. FEBS Lett 1983;161:65–70. [DOI] [PubMed] [Google Scholar]
- Kosiol C, Goldman N.. Different versions of the Dayhoff rate matrix. Mol Biol Evol 2005;22:193–9. [DOI] [PubMed] [Google Scholar]
- Kozlov AM, Darriba D, Flouri T. et al. RAxML-NG: a fast, scalable and user-friendly tool for maximum likelihood phylogenetic inference. Bioinformatics 2019;35:4453–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhlman B, Bradley P.. Advances in protein structure prediction and design. Nat Rev Mol Cell Biol 2019;20:681–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson G, Thorne JL, Schmidler S.. Incorporating nearest-neighbor site dependence into protein evolution models. J Comput Biol 2020;27:361–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le SQ, Gascuel O.. An improved general amino acid replacement matrix. Mol Biol Evol 2008;25:1307–20. [DOI] [PubMed] [Google Scholar]
- Lemmon AR, Moriarty EC.. The importance of proper model assumption in Bayesian phylogenetics. Syst Biol 2004;53:265–77. [DOI] [PubMed] [Google Scholar]
- Leuenberger C, Wegmann D.. Bayesian computation and model selection without likelihoods. Genetics 2010;184:243–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liberles DA, Teichmann SA, Bahar I. et al. The interface of protein structure, protein biophysics, and molecular evolution. Protein Sci 2012;21:769–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes JS, Arenas M, Posada D. et al. Coestimation of recombination, substitution and molecular adaptation rates by approximate Bayesian computation. Heredity (Edinb) 2014;112:255–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo A, Qiao H, Zhang Y. et al. Performance of criteria for selecting evolutionary models in phylogenetics: a comprehensive study based on simulated datasets. BMC Evol Biol 2010;10:242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minin V, Abdo Z, Joyce P. et al. Performance-based selection of likelihood models for phylogeny estimation. Syst Biol 2003;52:674–83. [DOI] [PubMed] [Google Scholar]
- Minning J, Porto M, Bastolla U.. Detecting selection for negative design in proteins through an improved model of the misfolded state: detecting selection for negative design. Proteins 2013;81:1102–12. [DOI] [PubMed] [Google Scholar]
- Mistry J, Chuguransky S, Williams L. et al. Pfam: the protein families database in 2021. Nucleic Acids Res 2021;49:D412–D419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moshe A, Wygoda E, Ecker N. et al. An approximate Bayesian computation approach for modeling genome rearrangements. Mol Biol Evol 2022;39:msac231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller T, Vingron M.. Modeling amino acid replacement. J Comput Biol 2000;7:761–76. [DOI] [PubMed] [Google Scholar]
- Neverov AD, Popova AV, Fedonin GG. et al. Episodic evolution of coadapted sets of amino acid sites in mitochondrial proteins. PLoS Genet 2021;17:e1008711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen SP, Li Z, Xu D. et al. New deep learning methods for protein loop modeling. IEEE/ACM Trans Comput Biol Bioinform 2019;16:596–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickle DC, Heath L, Jensen MA. et al. HIV-specific probabilistic models of protein evolution. PLoS One 2007;2:e503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noivirt-Brik O, Horovitz A, Unger R.. Trade-off between positive and negative design of protein stability: from lattice models to real proteins. PLoS Comput Biol 2009;5:e1000592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunes MA, Prangle D.. abctools: an R package for tuning approximate Bayesian computation analyses. R Journal 2015;7:189–205. [Google Scholar]
- Pandey A, Braun EL.. 2020. Protein evolution is structure dependent and non-homogeneous across the tree of life. In: Proceedings of the 11th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics. Virtual Event USA: ACM. p. 1–11.
- Pascual-García A, Arenas M, Bastolla U.. The molecular clock in the evolution of protein structures. Syst Biol 2019;68:987–1002. [DOI] [PubMed] [Google Scholar]
- Perron U, Kozlov AM, Stamatakis A. et al. Modeling structural constraints on protein evolution via side-chain conformational states. Mol Biol Evol 2019;36:2086–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priya P, Shanker A.. Coevolutionary forces shaping the fitness of SARS-CoV-2 spike glycoprotein against human receptor ACE2. Infect Genet Evol 2021;87:104646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puller V, Sagulenko P, Neher RA.. Efficient inference, potential, and limitations of site-specific substitution models. Virus Evol 2020;6:veaa066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pupko T, Bell RE, Mayrose I. et al. Rate4Site: an algorithmic tool for the identification of functional regions in proteins by surface mapping of evolutionary determinants within their homologues. Bioinformatics 2002;18(Suppl 1):S71–7. [DOI] [PubMed] [Google Scholar]
- Rawi R, Kunji K, Haoudi A. et al. Coevolution analysis of HIV-1 envelope glycoprotein complex. PLoS One 2015;10:e0143245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ripplinger J, Sullivan J.. Assessment of substitution model adequacy using frequentist and bayesian methods. Mol Biol Evol 2010;27:2790–803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson DM, Jones DT, Kishino H. et al. Protein evolution with dependence among codons due to tertiary structure. Mol Biol Evol 2003;20:1692–704. [DOI] [PubMed] [Google Scholar]
- Rodrigue N, Lartillot N, Bryant D. et al. Site interdependence attributed to tertiary structure in amino acid sequence evolution. Gene 2005;347:207–17. [DOI] [PubMed] [Google Scholar]
- Sella G, Hirsh AE.. The application of statistical physics to evolutionary biology. Proc Natl Acad Sci U S A 2005;102:9541–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah P, McCandlish DM, Plotkin JB.. Contingency and entrenchment in protein evolution under purifying selection. Proc Natl Acad Sci U S A 2015;112:E3226–E3235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakhnovich E, Abkevich V, Ptitsyn O.. Conserved residues and the mechanism of protein folding. Nature 1996;379:96–8. [DOI] [PubMed] [Google Scholar]
- Shoemaker JS, Fitch WM.. Evidence from nuclear sequences that invariable sites should be considered when sequence divergence is calculated. Mol Biol Evol 1989;6:270–89. [DOI] [PubMed] [Google Scholar]
- Sigrist CJA, de Castro E, Cerutti L. et al. New and continuing developments at PROSITE. Nucleic Acids Res 2012;41:D344–D347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sousa VC, Beaumont MA, Fernandes P. et al. Population divergence with or without admixture: selecting models using an ABC approach. Heredity (Edinb) 2012;108:521–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starr TN, Thornton JW.. Epistasis in protein evolution. Protein Sci 2016;25:1204–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan J, Joyce P.. Model selection in phylogenetics. Annu Rev Ecol Evol Syst 2005;36:445–66. [Google Scholar]
- Sunnåker M, Busetto AG, Numminen E. et al. Approximate Bayesian computation. PLoS Comput Biol 2013;9:e1002803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura K, Stecher G, Kumar S.. MEGA11: molecular evolutionary genetics analysis version 11. Mol Biol Evol 2021;38:3022–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorne JL. Models of protein sequence evolution and their applications. Curr Opin Genet Dev 2000;10:602–5. [DOI] [PubMed] [Google Scholar]
- Waksman G, Krishna TS, Williams CH. et al. Crystal structure of Escherichia coli thioredoxin reductase refined at 2 A resolution. Implications for a large conformational change during catalysis. J Mol Biol 1994;236:800–16. [PubMed] [Google Scholar]
- Whelan S, Goldman N.. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol Biol Evol 2001;18:691–9. [DOI] [PubMed] [Google Scholar]
- Wilson DJ, Gabriel E, Leatherbarrow AJH. et al. Rapid evolution and the importance of recombination to the gastroenteric pathogen Campylobacter jejuni. Mol Biol Evol 2009;26:385–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo J, Robertson DL, Lovell SC.. Constraints from protein structure and intra-molecular coevolution influence the fitness of HIV-1 recombinants. Virology 2014;454–455:34–9. [DOI] [PubMed] [Google Scholar]
- Yang Z. Computational Molecular Evolution. Oxford: Oxford University Press, 2006. [Google Scholar]
- Yang Z, Goldman N, Friday A.. Comparison of models for nucleotide substitution used in maximum-likelihood phylogenetic estimation. Mol Biol Evol 1994;11:316–24. [DOI] [PubMed] [Google Scholar]
- Yang Z, Nielsen R, Hasegawa M.. Models of amino acid substitution and applications to mitochondrial protein evolution. Mol Biol Evol 1998;15:1600–11. [DOI] [PubMed] [Google Scholar]
- Yeh S-W, Liu J-W, Yu S-H. et al. Site-specific structural constraints on protein sequence evolutionary divergence: local packing density versus solvent exposure. Mol Biol Evol 2014;31:135–9. [DOI] [PubMed] [Google Scholar]
- Yu J, Thorne JL.. Dependence among sites in RNA evolution. Mol Biol Evol 2006;23:1525–37. [DOI] [PubMed] [Google Scholar]
- Zhang J. Performance of likelihood ratio tests of evolutionary hypotheses under inadequate substitution models. Mol Biol Evol 1999;16:868–75. [DOI] [PubMed] [Google Scholar]
- Zhang J, Nei M.. Accuracies of ancestral amino acid sequences inferred by the parsimony, likelihood, and distance methods. J Mol Evol 1997;44(Suppl 1):S139–46. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Huang J, Wang Z. et al. Impact of indels on the flanking regions in structural domains. Mol Biol Evol 2011;28:291–301. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
ProteinModelerABC is freely available from https://github.com/DavidFerreiro/ProteinModelerABC. The simulated and real data used in the study are available from Zenodo at https://doi.org/10.5281/zenodo.10491125.