Abstract
A catalyst possessing a broad substrate scope, in terms of both turnover and enantioselectivity, is sometimes called “general”. Despite their great utility in asymmetric synthesis, truly general catalysts are difficult or expensive to discover via traditional high-throughput screening and are, therefore, rare. Existing computational tools accelerate the evaluation of reaction conditions from a pre-defined set of experiments to identify the most general ones, but cannot generate entirely new catalysts with enhanced substrate breadth. For these reasons, we report an inverse design strategy based on the open-source genetic algorithm NaviCatGA and on the OSCAR database of organocatalysts to simultaneously probe the catalyst and substrate scope and optimize generality as a primary target. We apply this strategy to the Pictet–Spengler condensation, for which we curate a database of 820 reactions, used to train statistical models of selectivity and activity. Starting from OSCAR, we define a combinatorial space of millions of catalyst possibilities, and perform evolutionary experiments on a diverse substrate scope that is representative of the whole chemical space of tetrahydro-β-carboline products. While privileged catalysts emerge, we show how genetic optimization can address the broader question of generality in asymmetric synthesis, extracting structure–performance relationships from the challenging areas of chemical space.
A genetic optimization strategy to discover asymmetric organocatalysts with high activity and enantioselectivity across a broad substrate scope.
Introduction
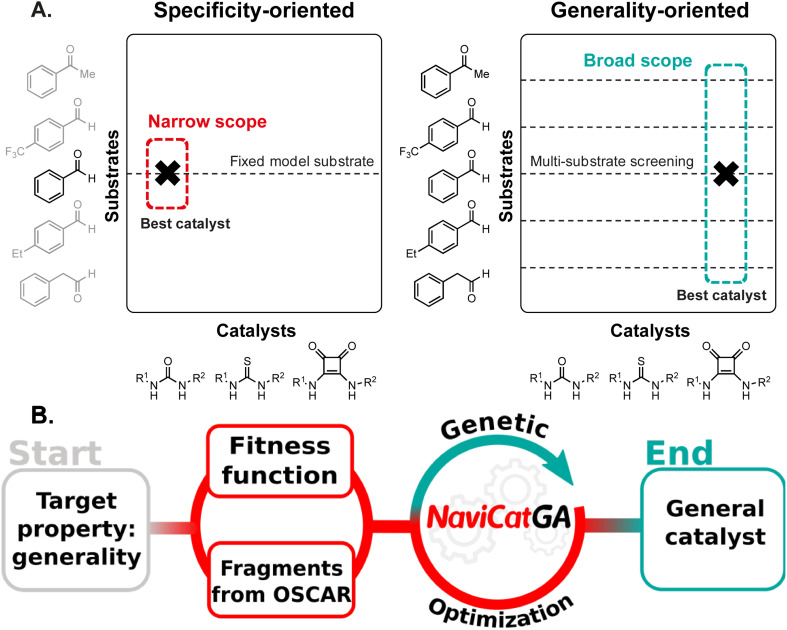
Developing catalytic methods that are tolerant to many functional groups exerting different steric and electronic influences on the reaction center without significant reduction in yield or product selectivity is a long-standing goal of organic chemistry. Despite being a highly desired feature, such “generality” i.e., breadth of substrate scope,1 is rare and only a few transformations become routinely incorporated into the synthetic chemist's toolbox.2,3 This is due to reaction development usually beginning with the examination of a simple, readily available model substrate (Fig. 1A), with subsequent re-optimization on more complex systems guided by empirical trial-and-error.4 Finding species with enhanced substrate breadth requires evaluating wider regions of chemical space derived from a large matrix of diverse catalysts crossed with a panel of substrates that effectively represent the whole target molecule class. Today, “one-pot-multisubstrate” screening5–7 is tractable with high-throughput experimentation techniques,8–12 but has found limited applicability due to issues associated with chemical compatibility and product analysis. The catalyst space investigated remains limited, at best, to tens of candidates and, perhaps worse, the most general ones might be unwittingly excluded from the original screening set, biasing the results.13
Fig. 1. (A) Reaction optimization tactics for the development of catalytic methods: traditional specificity-oriented vs. data-driven multi-substrate screening. (B) Schematic inverse design pipeline powered by NaviCatGA.
In the last decade, data-driven computational methods, in tandem with supervised and unsupervised machine learning algorithms, have been applied to address numerous challenges in organic chemistry,14–17 such as prediction of reaction outcomes,18–20 multistep synthetic planning,21–23 and catalyst discovery.24–28 In particular, Bayesian optimization29,30 has been combined with robotic experimentation to find general conditions for heteroaryl Suzuki–Miyaura coupling.31 Denmark and co-workers have developed a “catalyst selection by committee” to identify general disulfonimides for the atroposelective iodination of a variety of 2-amino-6-arylpyridines,26 and used active learning to provide substrate-adaptive conditions for C–N couplings.32 Recently, Reid et al. have proposed a workflow for assigning and predicting generality through clustering of reaction sets, but manually curated literature databases and a user-defined success value were required.33 Overall, existing data-driven tools are still aimed at accelerating the evaluation of a pre-defined set of catalysts,34 rather than suggesting entirely new species exhibiting high performance across the whole substrate scope.
Generative models35 are an attractive alternative to direct screening by enabling the inverse design of functional molecules and materials.36,37 In this paradigm, the desired functionality (i.e., the target) is first defined, and chemical structures tailored to that property are suggested (Fig. 1B). Although applications of generative models, such as genetic algorithms,38 to homogeneous catalysis are increasingly being reported,39–44 only specificity-oriented catalyst design has been addressed. Optimizing generality as primary target requires adapting existing tools and pipelines to tackle this multi-dimensional problem.
Here, we show how evolutionary experiments performed with the genetic algorithm NaviCatGA,45 leveraging the recently reported OSCAR database of organocatalysts' building blocks,46 are designed to simultaneously probe the catalyst and substrate space and find candidates predicted to exhibit both high turnover and enantioselectivity. We discuss the nature of fitness function used to estimate how close candidate species are to achieving optimal performance, the surrogate models that accelerate fitness evaluation, the database of molecular fragments to generate millions of prospective catalysts on-the-fly, and the strategy followed to choose an unbiased and diverse substrate scope. We select the Pictet–Spengler condensation as a synthetically relevant case study to illustrate how multi-objective genetic optimization across an expansive substrate space affords organocatalysts with good median activity and selectivity, while simultaneously providing information rich data on the areas of chemical space where even the best candidates are underperforming. Analysis of the challenging substrates gives insights into the set of non-covalent interactions that are necessary for generality, and into the structural features of the tetrahydro-β-carboline intermediate that disrupt them. Our pipeline allows us to automatically generate candidates with the broadest scope possible, and also to understand why truly “privileged” organocatalysts across highly diverse substrates are difficult to discover.
Methods: the NaviCatGA pipeline and components
NaviCatGA is a versatile genetic algorithm capable of optimizing homogeneous catalysts by exploiting any suitable fitness function that describes their catalytic performance.45 It manipulates catalyst structures generated on-the-fly from a user-defined library of building blocks (e.g., organocatalysts' scaffolds and substituents from OSCAR46) using any molecular representation, including SMILES strings and XYZ coordinates. By performing an iterative sequence of genetic operations (fitness evaluation, crossover, and mutation), NaviCatGA quickly finds the combination of building blocks that maximizes the fitness function (Fig. 1B).38 The role of the fitness function is evaluating how close a potential catalyst is to achieving optimal performance. In the context of asymmetric catalysis, a good catalyst is both enantioselective (i.e., high enantiomeric excess, often converted to ΔΔG‡, values) and active (i.e., high percentage yield, or turnover frequency, TOF). Measures of selectivity and activity can be obtained either from experiments or computations. Experimental ΔΔG‡ values are notoriously difficult to reproduce accurately with computations,47 while experimental yields, especially in the context of asymmetric organocatalysis, are often not reported (or only high-yielding reactions are reported, see Fig. S1 and S2† for further details).48 During the evolutionary experiment, the structure of new, untested catalyst candidates is generated, and their fitness must be evaluated: this constitutes the bottleneck of genetic optimization.
For these reasons, herein we adopt a hybrid strategy to evaluate catalyst performance: we (1) exploit experimental ΔΔG‡ values curated from the literature to train a statistical model and predict the enantioselectivity of untested catalyst–substrate combinations, and (2) perform DFT computations to construct molecular volcano plots49–51 and estimate a catalyst's TOF via a descriptor variable, training a second surrogate model of activity on the computed volcano plot's descriptor (which, in turn, provides the TOF estimate, vide infra). These surrogate models allow us to bypass otherwise time-consuming experiments or computations and evaluate the fitness of new candidates generated during genetic optimization.
In the following sections, we describe in detail the individual components of the NaviCatGA pipeline (Fig. 1B), highlighting how they are adapted to find organocatalysts with a broad substrate scope. We then discuss the results of the evolutionary experiments, along with the chemical conclusions, in the Results and discussion section.
Target property and reaction database
The target of the inverse design strategy (Fig. 1B) is “generality” i.e., high enantioselectivity and activity across a wide and diverse substrate scope. Inspired by recent work by Jacobsen et al.,10 we investigate the asymmetric Pictet–Spengler reaction53–55 of tryptamine derivatives and carbonyl compounds (Fig. 2A), one of the most important methods for the synthesis of privileged pharmacophores such as tetrahydro-β-carbolines, due to the diversity of catalyst chemotypes capable of inducing high enantioselectivity. Although dozens of systems have been reported,56 employing a variety of organocatalysts such as chiral phosphoric acids (CPAs)57 or single-58 and dual-hydrogen-bond donors (S/DHBD)59 used cooperatively with weak acids or bearing an acidic functional group internally,60 no method has found widespread application, since each study was focused on a limited number of substrates. This reaction constitutes an ideal case study to develop an optimization strategy with generality as primary target.10
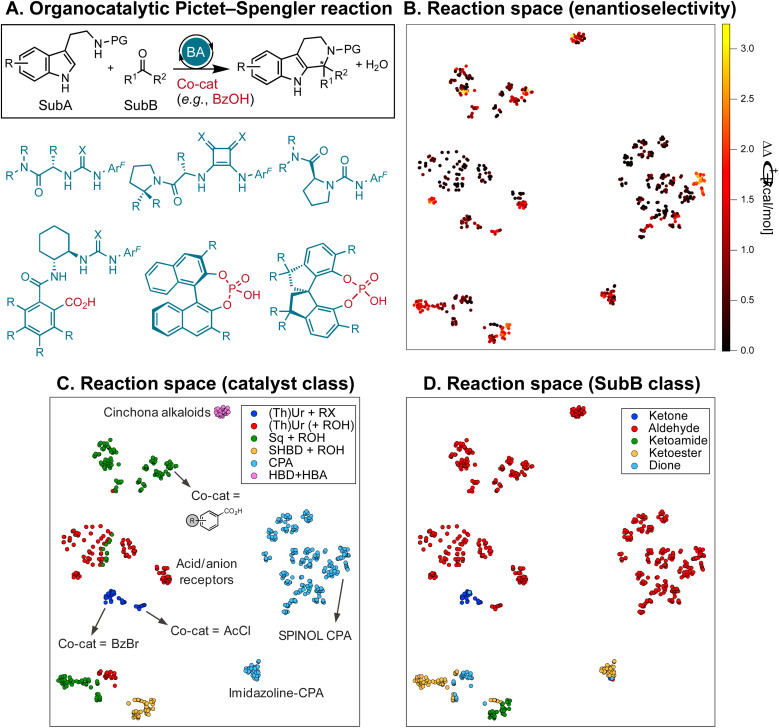
Fig. 2. (A) Pictet–Spengler cyclization of tryptamine derivatives (SubA, PG = protecting group, H, or OH) and carbonyls (SubB) in the presence of chiral organocatalysts and weak acid co-catalysts. Examples of hydrogen-bond donors, acid/anion receptor catalysts, and chiral phosphoric acids are shown. ArF = 3,5-CF3-C6H3, X = O/S. (B)–(D) 2D t-SNE map52 of the reaction space on the basis of the concatenated MFPs of the substrates and catalysts color-coded by the experimental selectivity (ΔΔG‡, B), catalyst class (C), and SubB class (D). (Th)Ur = (thio)ureas, Sq = squaramides, SHBD = single-hydrogen-bond donors, CPA = chiral phosphoric acids, HBA = hydrogen-bond acceptor, RX = benzoyl bromide or acyl chloride (BzBr, AcCl), ROH = carboxylic acid (e.g., BzOH, AcOH).
At the onset of our investigation, we curated a database of 820 Pictet–Spengler condensations from the literature.10,58,61–73 For simplicity, we constrain ourselves to protected or unprotected tryptamines (as shown in Fig. 2A), excluding isotryptamines,74 aryl ethanols,75,76 phenethylamines,77 and other substrates involved in more complex cascade reactions.78–85 The database contains 240 unique transformations (i.e., tetrahydro-β-carboline products) of 33 SubA and 164 SubB (aldehydes, ketones, α-ketoacids/esters/amides, and α-diones), catalyzed by 160 distinct organocatalysts and 30 co-catalysts (carboxylic acids, acyl and benzoyl chlorides and bromides). It is visualized in Fig. 2B with a 2D t-SNE map52 based on the concatenated Morgan FingerPrints86,87 (MFPs) of the catalyst, co-catalyst, and substrates, where each point representing a reaction is colored according to its selectivity (ΔΔG‡ = −RT ln|e.r.|, with e.r. being the experimentally measured enantiomeric ratio). The map is divided into two regions, the right-hand side containing cyclizations catalyzed by CPAs, the left-hand side those with single and dual-HBDs (Fig. 2C); 75% of reactions involve aldehydes as SubB (top and middle parts of the map), while condensations of other carbonyl compounds are located in the lower regions (Fig. 2D).
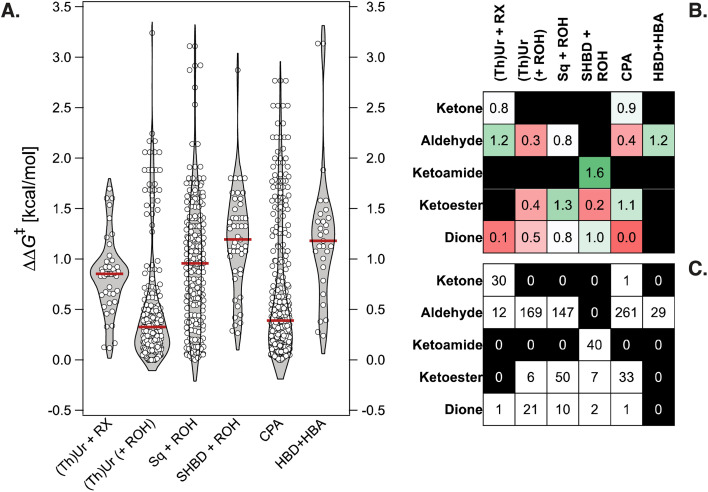
Despite “islands” of high enantioselectivity associated with catalysts being tested on a selected and limited class of carbonyl compounds (e.g., SPINOL CPAs with aldehydes,65 or SHBDs with ketoamides,58cf.Fig. 2B–D), nearly 50% of the transformations display exceedingly low ΔΔG‡ (<0.5 kcal mol−1, and 70% <1 kcal mol−1). The distribution of ΔΔG‡ values for six families of organocatalysts [(thio)ureas with benzoyl bromide or acyl chloride co-catalyst, (thio)ureas, squaramides, or SHBD with carboxylic acid co-catalyst, CPAs, and bifunctional hydrogen-bond donor/acceptor cinchona alkaloids] is shown in Fig. 3A. Although certain chemotypes display high median ΔΔG‡, choosing the catalyst for carrying out an enantioselective Pictet–Spengler reaction on a never-before-tested substrate simply based on literature precedence would lead to biased results, as only few catalyst–substrate combinations have actually been tested. This is emphasized in Fig. 3B and C, which display the median ΔΔG‡ values for different substrate classes, along with the number of reactions reported. Finding general organocatalysts requires evaluating each candidate against a diverse panel of substrates, covering all types of tryptamine derivatives (SubA) and carbonyl compounds (SubB), which quickly becomes too expensive, supporting the need for predictive and generative models.
Fig. 3. (A) Violin plots of experimental ΔΔG‡ values in the literature database of 820 Pictet–Spengler reactions for six different classes of organocatalysts. The median is indicated with horizontal lines. RX = benzoyl bromide or acyl chloride (BzBr, AcCl), ROH = carboxylic acid (e.g., BzOH, AcOH), HBA = hydrogen-bond acceptor. (B) Tabulated median ΔΔG‡ values for different catalyst–substrate combinations from the literature database. (C) Tabulated number of reactions reported for different catalyst–substrate combinations from the literature database.
Fitness function: evaluation of catalyst activity and selectivity
The database of experimental ΔΔG‡ values (and the statistical model trained on it, vide infra) allows us to estimate the enantioselectivity of untested catalyst–substrates combinations. Regarding activity, we evaluate how close a catalyst's turnover is to the maximum achievable one using DFT computations and molecular volcano plots.49–51 Together, these measures of catalytic performance constitute the fitness function of the inverse design pipeline (Fig. 1B).
Molecular volcanos provide a way of connecting a descriptor variable, typically the energy change associated with a step in a catalytic cycle (x-axis), to the overall catalytic performance (y-axis, expressed in terms of energy span or TOF),49,88 while simultaneously giving knowledge of the descriptor value corresponding to the volcano peak or plateau (maximum performance i.e., the target for genetic optimization).45 Volcano plots are built from Linear Free Energy Scaling Relationships (LFESRs, Fig. S3†) that connect the value of the descriptor to the relative energies of the other cycle intermediates and transition states. While extensive details on how these plots are automatically constructed using the toolkit volcanic51 are given in the Computational details and elsewhere,51Fig. 4A shows the mechanism of the Pictet–Spengler reaction,89 whose knowledge is fundamental for building the volcanos. Following condensation of the β-arylethylamine (SubA) with the carbonyl compound (SubB) and formation of iminium ion 1, nucleophilic attack by the aryl group and cyclization can occur either directly at position C2 of the indole viaTS2, or at C3 viaTS1 to form the five-membered aza-spiroindolenine 1B, which undergoes C–C migration to yield 2. Deprotonation of 2 by the conjugate base of the acid co-catalyst, or of the CPA catalyst, is then necessary to form the tetrahydro-β-carboline product.
Fig. 4. (A) General mechanism for the Pictet–Spengler reaction via anion-binding catalysis. (Thio)urea catalysts (X = O/S) with carboxylic acid co-catalysts are shown as an example. (B) The reactions used to construct molecular volcano plots (SRS) are plotted on the t-SNE map from Fig. 2, colored according to the nature of the organocatalyst. (C) Molecular volcano plots based on the C2 and C3 addition mechanism. The shaded areas denote the 95% confidence interval based on the Linear Free Energy Scaling Relationships. Computations were performed at the PCM(toluene)/M06-2X-D3/Def2-TZVP//M06-2X-D3/Def2-SVP level of theory. (D) Distribution of descriptor values and their location on the volcano plot.
Constructing molecular volcanos requires computing the potential energy profiles of a medium-sized pool of sterically and electronically diverse systems.51 44 reactions from the Pictet–Spengler database are selected via farthest point sampling of the 2D t-SNE map. This Scaling Relationships Set (SRS, Fig. 4B) comprises 39 unique transformations (i.e., products) of 11 SubA and 31 SubB, catalyzed by 33 different organocatalysts. Because the mechanism must be the same for all systems investigated, reactions catalyzed by cinchona alkaloid HBD + HBA (corresponding to the pink cluster in the t-SNE map, Fig. 2C) are excluded, as these bifunctional catalysts have been shown to operate via a different mechanism.67 On the other hand, extensive mechanistic studies68,89–93 have demonstrated the viability of the mechanism shown in Fig. 4A for reactions catalyzed by (thio)urea HBDs, acid/anion receptors, and CPAs.
With the SRS, TOF molecular volcanos49 for concerted C2 and stepwise C3 addition are constructed automatically using volcanic51 and the relative energy of intermediate 2 as descriptor (Fig. 4C). Computations are performed at the PCM(toluene)/M06-2X-D3/Def2-TZVP//M06-2X-D3/Def2-SVP level of theory (see the Computational details); although exhaustive conformational sampling of each intermediate 2 is carried out with CREST,94–96 in order to reduce the computational cost only one conformer per stationary point on the Pictet–Spengler potential energy surface (PES) is used to construct the volcanos. The deviations of the points in Fig. 4C (each of which represents a Pictet–Spengler reaction) from the volcano curve may be attributed to differences in conformations between the various catalyst–substrate non-covalently bound complexes, which are characterized by a complex conformational landscape.
Mechanistic aspects of the Pictet–Spengler reaction, including the preferred pathway and the nature of the rate- and enantiodetermining step, have been a topic of intensive research:97 Jacobsen et al. found a strong energetic preference for C2 over C3 addition in reactions catalyzed by chiral thioureas,89 while You and co-workers showed that the spiroindolenine 1B acts as either a productive or non-productive intermediate depending on the shape of the PES.93 Evaluating the mechanism over a broad and diverse catalyst and substrate scope, as afforded by the SRS, reveals that, although the concerted pathways is generally preferred, the difference between the barriers for spiroindolization at C3 and electrophilic aromatic substitution at C2 is on average quite small (the volcanos are close to each other). Additionally, analysis of the LFESRs (Fig. S3†) shows that there is often not one single rate- and enantiodetermining step, as rearomatization via deprotonation (TS3) and C–C bond formation (TS1 or TS2) are almost isoenergetic: indeed, reactions are found for which TS2 and TS3 have similar degree of TOF-control98 (i.e., the reaction rate is limited equally by C–C bond formation and deprotonation, see Fig. S4†). The location of the SRS on the volcano plots indicates that cyclizations of hydroxylamines in the presence of benzoyl bromide co-catalyst (blue points),71 as well as reactions of aldehydes catalyzed by squaramides (green points)70 display the highest TOFs. This observation is in line with the higher reactivity of ketonitrones99 and the stronger H-bonding ability of squaramides, which has been found to correlate with faster turnover.100 Conversely, the performance of CPAs and other DHBDs is strongly dependent on the nature of the substrates, as evinced by the bigger spread of TOF values. Among the poorest performing organocatalysts, sulfinamido urea derivatives101 and carboxylic acids equipped with anion-recognition sites66 are found lower on the volcano.
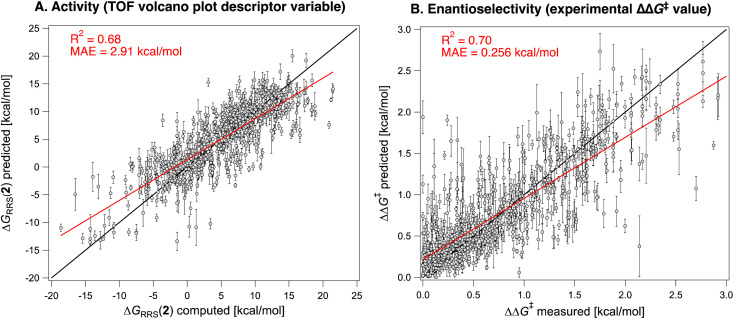
Having constructed the volcano plots and established the identity of the descriptor variable, we compute ΔGRRS(2) for all the reactions in the Pictet–Spengler dataset (703 datapoints i.e., excluding reactions catalyzed by cinchona alkaloids owing to their different mechanism and those where only the carboxylic acid co-catalyst is varied, since HOAc is used throughout, see the Computational details). Structures are generated and optimized according to the pipeline described in the Computational details. Fig. 4D shows the Gaussian-type distribution of ΔGRRS(2) superimposed on the TOF volcano for C2 addition, centered around 7 kcal mol−1. Most Pictet–Spengler reactions are found on the right slopes of the volcano (i.e., weak-binding side), and their turnover is limited by iminium ion formation and deprotonation of the tetrahydro-β-carboline intermediate (or C–C bond formation). Overall, only few condensations have TOF close to the theoretical maximum. We then use this dataset to train a XGBoost machine learning model102 to predict ΔGRRS(2) using the concatenated Morgan FingerPrints of the substrates, catalyst, and co-catalyst (acetic acid, BzBr, or none) as reaction representation (Fig. 5A). A similar model is also trained on the whole Pictet–Spengler database (Fig. 2Bi.e., 820 datapoints, using the real identity of the carboxylic acid co-catalysts rather than acetic acid) to predict the experimental ΔΔG‡ values. Despite the relatively large errors in ΔGRRS(2) predictions (MAE = 2.9 kcal mol−1) and for large ΔΔG‡ values, these models are deemed to be an acceptable compromise between cost and accuracy and are used to accelerate fitness evaluation during genetic optimization (vide infra; see also Fig. S5† and 11 for out-of-sample predictions).38 The choice of the representation and regression method is dictated by the requirement of surrogate models used iteratively in generative molecular design to be fast and affordable. Although linear103 and non-linear104 models using stereoelectronic features105 (see Fig. S7† for multivariate linear regression analysis of the ΔΔG‡ of reactions catalyzed by single- and dual-HBDs) or 3D structures as input106,107 have been extensively developed for reaction outcome prediction,108 they often depend on DFT computations of relatively expensive properties (e.g., vibrational frequencies and intensities, polarizabilities)109 and are not adapted to the purpose of fast (GA) optimization, for which bypassing the DFT bottleneck is key.38 Conversely, 2D descriptors are typically much faster (and less susceptible to bias as they require less user input)110 and have been found to be cost-effective alternatives with good accuracy for experimental targets,110–113 sometimes even rivaling models using DFT features.114 The XGBoost model provides satisfying enantioselectivity predictions (MAE = 0.358 kcal mol−1, MSE = 0.221, Fig. S5†) on 46 out-of-sample reactions115–117 excluded from the original literature database, including condensations involving geminally-disubstituted tryptamines117 that are absent in the training set (Scheme S1†).
Fig. 5. XGBoost models predicting the (A) descriptor variable [ΔGRRS(2)] of the TOF molecular volcano plots, computed at the PCM(toluene)/M06-2X-D3/Def2-TZVP//M06-2X-D3/Def2-SVP level, and (B) the experimentally measured enantioselectivity (expressed as ΔΔG‡) of the Pictet–Spengler reactions from the literature. Predictions are obtained by averaging those from a cross-validation scheme with 100 different random 90/10 train/test splits (633/70 for A, 738/82 for B). The error bars are obtained from the standard deviations from the 100 different train/test splits.
Fig. 11. Energetically lowest-lying TS for the deprotonation/rearomatization step (TS3) of the tetrahydro-β-carboline intermediate of GPS reaction 13 (left) and 47 (right) with the top-performing organocatalyst from generation 32. The distance between the catalyst's amide O and the indole N–H is shown. Computed and predicted enantioselectivity (expressed in terms of ΔΔG‡) and activity [expressed in terms of ΔGRRS(2)] values are reported.
Fragment database: the catalyst and substrate scope
The total combinatorial space explored during the evolutionary experiments is determined by the extent of the library of catalyst components and the scheme chosen to fragment them into building blocks. Here, we leverage the recently reported Organic Structures for CAtalysis Repository (OSCAR),46 which contains 4000 organocatalysts mined from the literature and CSD along with their corresponding molecular fragments. From OSCAR, we select 15 catalyst templates and 402 possible substituents (grouped into 4 categories R1–4 depending on which template they may substitute, see Tables S4 and S5† for a full list). The templates include 10 single- and dual-HBDs [(thio)ureas, (thio)squaramides, and prolyl-(thio)ureas] and 5 CPAs as shown in Fig. 2A (and Fig. S8†), which have been experimentally screened in the asymmetric Pictet–Spengler reaction. They are represented as flexible SMILES strings, written in such a way that different R1–4 can easily be introduced and exchanged, yielding valid SMILES. This results in a total combinatorial space of 2.85 × 108 HBDs and 1428 CPAs. Note that only CPAs with equal substituents at the 6 and 6′ positions of the BINOL/SPINOL scaffold are considered: although this significantly reduces the size of their combinatorial space, it ensures synthetic accessibility, a common problem of generative models.118
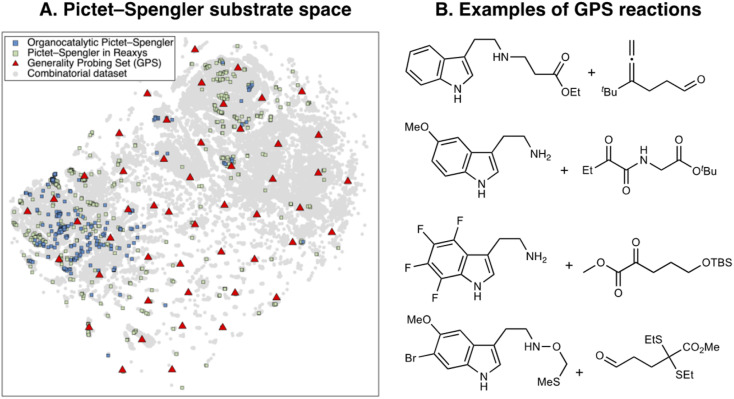
Having established the catalyst scope, we turn our attention to the substrate scope. Since our previous experiments with NaviCatGA were specificity-oriented,45 we implement a different workflow for selecting a representative subset of substrates for generality-driven genetic optimization. Inspired by recent work by Doyle et al.119 and Sigman et al.,120,121 we use the web platform Reaxys® to identify a list of 743 Pictet–Spengler reactions (selective and non-, catalytic and non-) between β-arylethylamines and carbonyl compounds. Additionally, 197 unprotected SubA, filtered according to molecular weight (<300 g mol−1), commercial availability, and functional group compatibility, are included. Combined with the 240 unique organocatalytic reactions from the original Pictet–Spengler database, we obtain 258 distinct tryptamine derivatives (SubA) and 379 carbonyls (SubB). The total combinatorial substrate space, shown in Fig. 6A, encompasses 97 782 possible tetrahydro-β-carboline products (grey circles).
Fig. 6. (A) 2D t-SNE map of the substrate scope on the basis of the concatenated MFPs of SubA and SubB. Blue squares indicate organocatalytic reactions, green squares reactions reported in Reaxys®, red triangles the Generality Probing Set (GPS) from this work. (B) Examples of reactions found in the GPS.
Broadly speaking, examples from the literature (blue and green squares) cover the left half of the chemical space, which corresponds to unsubstituted tryptamines, while the right and bottom areas are sparsely covered. To generate a diverse and unbiased substrate scope for evolutionary experiments, we perform farthest point sampling and select 50 reactions aimed at covering the whole chemical space. Examples of this Generality Probing Set (GPS) are shown in Fig. 6B (the full list is given in Table S6†). Carbonyls (SubB) include predominantly aromatic and aliphatic aldehydes, as reflected by the popularity of these substrates in the Pictet–Spengler reaction (see also Fig. 3C),10 but also less explored α-diones, α-ketoamides, esters, and acids. Substituents on the tryptamine derivative (SubA) are present on all positions of the indole ring through mono-, di-, tri-, and even tetrasubstitution patterns, encompassing both electron-donating (e.g., hydroxyl, methoxy, alkyl) and electron-withdrawing (e.g., nitro, halide, ester) functional groups. This significantly contrasts the previously reported scope (i.e., organocatalytic reactions from the literature or those mined from Reaxys®), dominated by monosubstituted β-arylethylamines. Approximately 60% of SubA in the GPS are unprotected, although a variety of protecting groups (e.g., benzyl, 4-NO2-benzyl, methylthiomethyl ether,122 allyl123) are present.
Results and discussion
Evolutionary experiments
With the different components of the inverse design pipeline at hand (Fig. 1B), we perform evolutionary experiments using the NaviCatGA algorithm.45 Herein, we are trying to optimize multiple properties simultaneously: we are looking for general organocatalysts, meaning that they should exhibit high performance across the whole SubA–SubB substrate scope (represented by the GPS, Fig. 6), and we are looking for candidates with simultaneously high selectivity and activity.
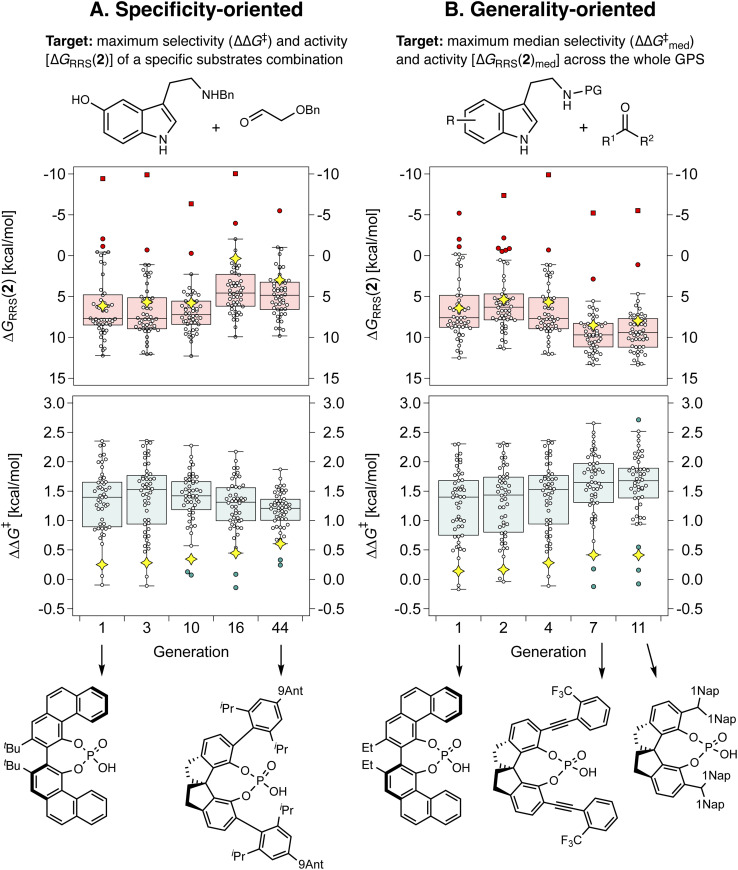
To validate our strategy, we first compare specificity-oriented and generality-oriented optimization on the smaller CPA combinatorial space (i.e., 1428 candidates; a similar experiment on the larger HBD space of 2.85 × 108 possibilities is reported in Fig. S9†): in one case (Fig. 7A) the optimization targets are the selectivity (experimental ΔΔG‡) and activity [ΔGRRS(2), the volcano plot descriptor] for the condensation of Nβ-benzylserotonin and benzyloxyacetaldehyde (reaction 11 in the GPS), predicted with the aforementioned XGBoost models. This particular combination of substrates was found to be associated with poor catalytic performance, and screening of all the 160 organocatalysts in the original literature dataset afforded median ΔΔG‡ and ΔGRRS(2) of only 0.2 and 6.3 kcal mol−1, respectively. Note the volcano peak (maximum activity) corresponds to a ΔGRRS(2) value of −9.0 kcal mol−1. In the other case (Fig. 7B), we optimize the median ΔΔG‡ and ΔGRRS(2) of all 50 reactions in the GPS. Given the multi-objective nature of each experiment (i.e., simultaneous optimization of selectivity and activity), we scalarize124 the two targets seeking a minimum ΔΔG‡ of 2.0 kcal mol−1, trying to reach a ΔGRRS(2) value of −9.0 kcal mol−1, but allowing activity to be marginally degraded if ΔΔG‡ is increased (see the Computational details): this exemplifies a standard situation in which enantioselectivity is to be guaranteed and only subsequently turnover is to be optimized.
Fig. 7. Box-and-whisker charts showing the evolution of ΔΔG‡ and ΔGRRS(2) of the top individual in the CPA population for selected generations (i.e., when the identity of the best-performing catalyst changes). Each datapoint corresponds to a reaction in the GPS, the yellow diamond indicates reaction 11 (shown in the top left). Outliers and far outliers are indicated with filled circles and squares, respectively. In (A), ΔΔG‡ and ΔGRRS(2) of reaction 11 are optimized, whereas in (B) the median ΔΔG‡ and ΔGRRS(2) of all reactions in the GPS are optimized.
Fig. 7 depicts the results of the first set of experiments as box-and-whiskers charts, showing how ΔΔG‡ and ΔGRRS(2) values are distributed across the GPS; only results for the best-performing catalyst in the population and only generations where the identity of the top candidate changes are shown. In the case of specificity-oriented optimization (Fig. 7A), ΔΔG‡ of reaction 11 (yellow diamond) improves from 0.3 to 0.6 kcal mol−1 over the course of 44 generations; ΔGRRS(2) also improves from 6.1 kcal mol−1 to 3.0 kcal mol−1 (i.e., approaching the volcano peak = −9.0 kcal mol−1, cf.Fig. 4C) but higher enantioselectivity comes at the expense of activity (e.g., from generation 16 to 44). Although at the end of the experiment a SPINOL CPA is found with improved (albeit still relatively low) selectivity and good activity, the median ΔΔG‡ decreases during the GA run, meaning that this organocatalyst is less general (conversely, this allows ΔGRRS(2)med to actually improve, once again showing the conflicting nature of the two objectives).
In Fig. 7B,  increases from 1.4 in generation 1 to 1.5 kcal mol−1 in generation 4; activity also improves, with ΔGRRS(2)med going from 7.6 to 6.3 kcal mol−1. To further enhance
increases from 1.4 in generation 1 to 1.5 kcal mol−1 in generation 4; activity also improves, with ΔGRRS(2)med going from 7.6 to 6.3 kcal mol−1. To further enhance  , NaviCatGA is forced to explore solutions in the activity-selectivity Pareto front with higher ΔGRRS(2)med values (generation 7): this iteration corresponds to a change in catalyst scaffold, from VAPOL125 to SPINOL. In agreement with results from Jacobsen et al.,10 the SPINOL scaffold and 1-naphthyl substituents found in generation 11 are associated with good enantioselectivity across the GPS (
, NaviCatGA is forced to explore solutions in the activity-selectivity Pareto front with higher ΔGRRS(2)med values (generation 7): this iteration corresponds to a change in catalyst scaffold, from VAPOL125 to SPINOL. In agreement with results from Jacobsen et al.,10 the SPINOL scaffold and 1-naphthyl substituents found in generation 11 are associated with good enantioselectivity across the GPS ( = 1.7 kcal mol−1), as indicated by the smaller interquartile range (IQR, from 0.9 to 0.5 kcal mol−1). Therefore, even though ΔΔG‡ for reaction 11 is lower than in the specificity-oriented optimization (0.4 kcal mol−1), a more general organocatalyst is discovered. Interestingly, the 2-CF3-phenylalkynyl substituent found in generation 7 was also identified by Denmark and co-workers as important for generality in the atroposelective disulfonimide-catalyzed iodination of 2-amino-6-arylpyridines,26 potentially suggesting that this group is also privileged across mechanistically-distinct reactions.1
= 1.7 kcal mol−1), as indicated by the smaller interquartile range (IQR, from 0.9 to 0.5 kcal mol−1). Therefore, even though ΔΔG‡ for reaction 11 is lower than in the specificity-oriented optimization (0.4 kcal mol−1), a more general organocatalyst is discovered. Interestingly, the 2-CF3-phenylalkynyl substituent found in generation 7 was also identified by Denmark and co-workers as important for generality in the atroposelective disulfonimide-catalyzed iodination of 2-amino-6-arylpyridines,26 potentially suggesting that this group is also privileged across mechanistically-distinct reactions.1
Having validated the inverse design pipeline on the small CPA combinatorial space, we perform a second set of generality-oriented evolutionary experiments on the much larger HBD catalyst scope (2.85 × 108 possible candidates). In the experiment reported in Fig. 8, the targets [ and ΔGRRS(2)med] are scalarized as above, meaning we wish to optimize activity and selectivity simultaneously, but we allow turnover to be degraded in order to achieve higher enantioselectivities. Another GA run where only
and ΔGRRS(2)med] are scalarized as above, meaning we wish to optimize activity and selectivity simultaneously, but we allow turnover to be degraded in order to achieve higher enantioselectivities. Another GA run where only  is optimized (single-objective optimization, SOO) is shown in Fig. S10,† and results are discussed in the following section (the structure of the best-performing catalyst is shown in Fig. 9). Fig. S11† reports a third experiment where only ΔGRRS(2)med is optimized, while in a fourth GA run (Fig. S12†) the two objectives (enantioselectivity and turnover) are scalarized differently i.e., we allow
is optimized (single-objective optimization, SOO) is shown in Fig. S10,† and results are discussed in the following section (the structure of the best-performing catalyst is shown in Fig. 9). Fig. S11† reports a third experiment where only ΔGRRS(2)med is optimized, while in a fourth GA run (Fig. S12†) the two objectives (enantioselectivity and turnover) are scalarized differently i.e., we allow  to be marginally degraded in order to improve ΔGRRS(2)med (see the ESI† for further details).
to be marginally degraded in order to improve ΔGRRS(2)med (see the ESI† for further details).
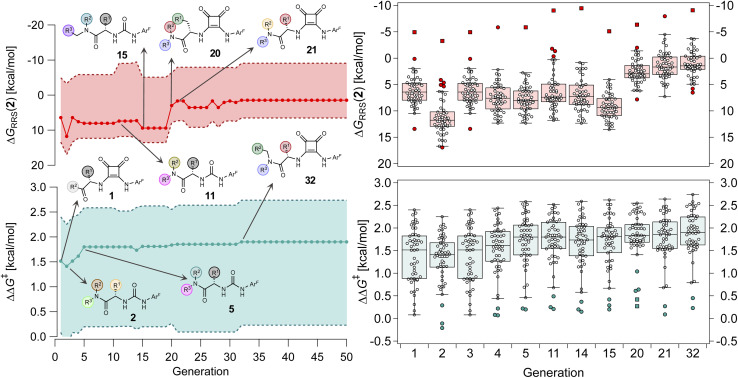
Fig. 8. (Left) Evolution of ΔΔG‡ and ΔGRRS(2) of the top individual in the HBD population over 50 generations. The solid lines indicate the median across the GPS, and the shaded areas represent the upper and lower values. Selected catalysts are shown, with different colored spheres representing different R1–3 substituents. (Right) Box-and-whisker chart of ΔΔG‡ and ΔGRRS(2) for selected generations i.e., only when the structure of the best-performing catalyst changes. Each datapoint corresponds to a reaction in the GPS. Outliers and far outliers are indicated with filled circles and squares, respectively.
Fig. 9. Median selectivity ( ) vs. activity [ΔGRRS(2)med] scatter plot for multi-objective optimization on the HBD scope, color-coded by catalyst generation. The volcano peak (maximum activity) corresponds to ΔGRRS(2) = −9.0 kcal mol−1. The dashed lines show the connections for the set of “noninferior” solutions in the objective space (Pareto optimal solutions). The gray diamond represents the top candidate from the single-objective optimization experiment (SOO, generation 37).
) vs. activity [ΔGRRS(2)med] scatter plot for multi-objective optimization on the HBD scope, color-coded by catalyst generation. The volcano peak (maximum activity) corresponds to ΔGRRS(2) = −9.0 kcal mol−1. The dashed lines show the connections for the set of “noninferior” solutions in the objective space (Pareto optimal solutions). The gray diamond represents the top candidate from the single-objective optimization experiment (SOO, generation 37).
Over the first 5 generations,  increases from 1.5 kcal mol−1 to 1.8 kcal mol−1 while the IQR decreases, indicating that the top candidate is generally more selective across the GPS (Fig. 8). At the onset of the evolutionary experiment, NaviCatGA locates DHBDs with the amide-based template [–C(
O)NR2] as important for selectivity. Indeed, computational studies89 have shown that the amide O engages the substrate through an H-bonding interaction with the indoline N–H. This template126 is preserved throughout the GA run and preferred over catalysts containing the pyrrolidino-moiety:1,127 Jacobsen et al. similarly found that aryl pyrrolidine substituted thioureas had lower generality metric than acyclic amides in the Pictet–Spengler condensation of aldehydes.10 Regarding the identity of the hydrogen-bonding unit, for the first 20 generations ureas are selected over squaramides to increase
increases from 1.5 kcal mol−1 to 1.8 kcal mol−1 while the IQR decreases, indicating that the top candidate is generally more selective across the GPS (Fig. 8). At the onset of the evolutionary experiment, NaviCatGA locates DHBDs with the amide-based template [–C(
O)NR2] as important for selectivity. Indeed, computational studies89 have shown that the amide O engages the substrate through an H-bonding interaction with the indoline N–H. This template126 is preserved throughout the GA run and preferred over catalysts containing the pyrrolidino-moiety:1,127 Jacobsen et al. similarly found that aryl pyrrolidine substituted thioureas had lower generality metric than acyclic amides in the Pictet–Spengler condensation of aldehydes.10 Regarding the identity of the hydrogen-bonding unit, for the first 20 generations ureas are selected over squaramides to increase  but, in accordance with trends extracted from the volcano plots and the lower acidity/H-bonding ability of ureas vs. squaramides,100,128 this results in diminished activity [ΔGRRS(2)med values farther away from the volcano peak of −9.0 kcal mol−1]. This situation exemplifies a typical problem in reaction optimization, where improving one objective is sometimes only possible at the expense of another.129,130 The same amino acid substituent (R1) is also maintained until generation 20, with NaviCatGA favoring the diphenyl group (black spheres in Fig. 8). At this particular iteration of the optimization, the squaramide HBD unit is “rediscovered”, which leads to a noticeable improvement in activity [ΔGRRS(2)med from 9.4 to 3.0 kcal mol−1]. Although this is associated with only marginal increase in
but, in accordance with trends extracted from the volcano plots and the lower acidity/H-bonding ability of ureas vs. squaramides,100,128 this results in diminished activity [ΔGRRS(2)med values farther away from the volcano peak of −9.0 kcal mol−1]. This situation exemplifies a typical problem in reaction optimization, where improving one objective is sometimes only possible at the expense of another.129,130 The same amino acid substituent (R1) is also maintained until generation 20, with NaviCatGA favoring the diphenyl group (black spheres in Fig. 8). At this particular iteration of the optimization, the squaramide HBD unit is “rediscovered”, which leads to a noticeable improvement in activity [ΔGRRS(2)med from 9.4 to 3.0 kcal mol−1]. Although this is associated with only marginal increase in  (1.81 to 1.84 kcal mol−1), the IQR significantly decreases, and most reactions in the GPS have ΔΔG‡ ≥ 1.7 kcal mol−1. Different R1–3 substituents are also selected, and in the remaining generations NaviCatGA explores different substitution patterns to achieve further activity and selectivity enhancements. In particular, ΔGRRS(2)med is decreased to 1.5 kcal mol−1 with small IQR (generation 32), while
(1.81 to 1.84 kcal mol−1), the IQR significantly decreases, and most reactions in the GPS have ΔΔG‡ ≥ 1.7 kcal mol−1. Different R1–3 substituents are also selected, and in the remaining generations NaviCatGA explores different substitution patterns to achieve further activity and selectivity enhancements. In particular, ΔGRRS(2)med is decreased to 1.5 kcal mol−1 with small IQR (generation 32), while  reaches the value of 1.9 kcal mol−1. The most general organocatalyst found at the end of the evolutionary experiment exhibits the 2,4,6-iPr-C6H2 substituent as R1, 3,5-CF3-C6H3 as R2, and the CH(2-tBu-C6H4)2 group in place of R3. Clearly, bulky substituents are privileged in inducing high enantioselectivity and activity across the GPS.
reaches the value of 1.9 kcal mol−1. The most general organocatalyst found at the end of the evolutionary experiment exhibits the 2,4,6-iPr-C6H2 substituent as R1, 3,5-CF3-C6H3 as R2, and the CH(2-tBu-C6H4)2 group in place of R3. Clearly, bulky substituents are privileged in inducing high enantioselectivity and activity across the GPS.
While Fig. 8 focuses on the best catalyst in each generation, Fig. 9 shows how different individuals in a generation occupy the objective space. At each iteration of the NaviCatGA run, a number of solutions to the optimization problem exist, representing tradeoffs between the two objectives. Together, these catalysts constitute a set of nondominated optimal conditions, also known as Pareto front (dashed lines in Fig. 9).129,131 During the evolutionary experiment, the Pareto front moves towards higher  and lower ΔGRRS(2)med values (i.e., closer to the volcano peak, −9.0 kcal mol−1), indicating an overall improvement in generality. The “ideal” organocatalyst i.e., possessing the highest enantioselectivity and turnover possible over the whole substrate scope, would be located in the upper right corner of Fig. 9. The top catalyst from generation 32 constitutes the best compromise between selectivity and activity (
and lower ΔGRRS(2)med values (i.e., closer to the volcano peak, −9.0 kcal mol−1), indicating an overall improvement in generality. The “ideal” organocatalyst i.e., possessing the highest enantioselectivity and turnover possible over the whole substrate scope, would be located in the upper right corner of Fig. 9. The top catalyst from generation 32 constitutes the best compromise between selectivity and activity ( = 1.9, ΔGRRS(2)med = 1.5 kcal mol−1); conversely, nondominated points in the Pareto front of other generations represent candidates with higher activity but lower enantioselectivity (e.g., generation 5,
= 1.9, ΔGRRS(2)med = 1.5 kcal mol−1); conversely, nondominated points in the Pareto front of other generations represent candidates with higher activity but lower enantioselectivity (e.g., generation 5,  = 1.3, ΔGRRS(2)med = −0.5 kcal mol−1). Therefore, the results of an evolutionary experiment may be used to identify catalysts that achieve different activity-selectivity tradeoffs, regardless of how the targets were initially scalarized. Fig. 9 also shows the top candidate from the single-objective optimization experiment (generation 37), which reaches higher
= 1.3, ΔGRRS(2)med = −0.5 kcal mol−1). Therefore, the results of an evolutionary experiment may be used to identify catalysts that achieve different activity-selectivity tradeoffs, regardless of how the targets were initially scalarized. Fig. 9 also shows the top candidate from the single-objective optimization experiment (generation 37), which reaches higher  (2.0 kcal mol−1) at the cost of significantly reduced activity [ΔGRRS(2)med = 7.3 kcal mol−1]. In line with trends extracted from the volcano plot (Fig. 4C), the presence of the thiourea scaffold instead of the squaramide is associated with slower turnover,100 while the 2,4,6-iPr-C6H2 and the CH(2-tBu-C6H4)2 substituents ensure high enantioselectivity.
(2.0 kcal mol−1) at the cost of significantly reduced activity [ΔGRRS(2)med = 7.3 kcal mol−1]. In line with trends extracted from the volcano plot (Fig. 4C), the presence of the thiourea scaffold instead of the squaramide is associated with slower turnover,100 while the 2,4,6-iPr-C6H2 and the CH(2-tBu-C6H4)2 substituents ensure high enantioselectivity.
Chemical insights into generality
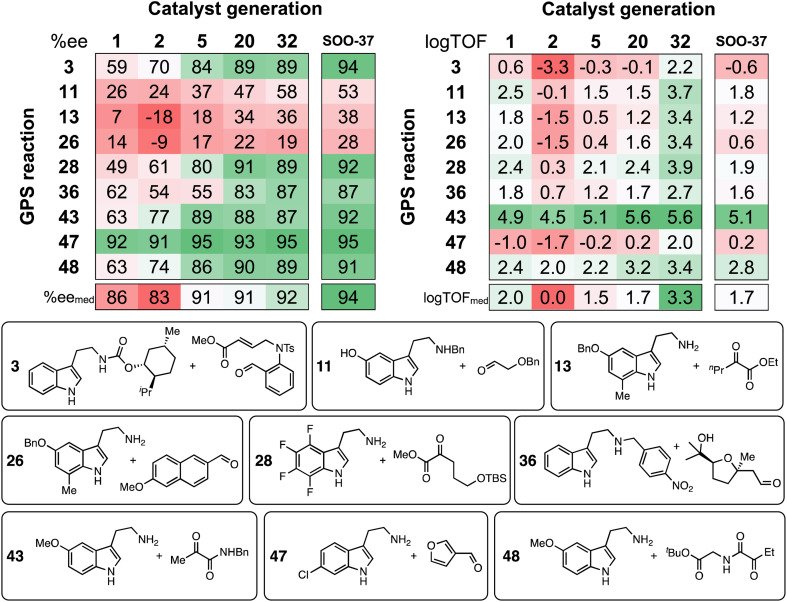
Tabulation of the results of the evolutionary experiments on the HBD space as a heatmap, converted to ee and log TOF values (Fig. 10) shows that, although a catalyst with good median selectivity and activity is found (% eemed = 92, log TOFmed = 3.3), some reactions in the GPS are always associated with poor performance i.e., no matter how the structure of the catalyst evolves during the optimization, certain tetrahydro-β-carboline products may not be obtained in high ee or TOF. This is in contrast to the majority of condensations in the GPS, where selectivity and activity significantly improve as the structure of the organocatalyst is optimized. Reactions 28, 36, and 48 are included in Fig. 10 as examples: these transformations involve a variety of carbonyl compounds (α-ketoester, α-ketoamide, aldehyde) and electron-poor, neutral, and -rich indoles, showing that candidates with good generality across distinct substrate classes are indeed discovered. Note that, due to deviations in the LFESRs associated with the complex conformational space of the catalyst–substrate non-covalently bound complexes (Fig. 4C and S3†), significant differences between predicted and computed TOF values (up to several log units) may be expected.
Fig. 10. Calculated ee and log TOF values from the predicted ΔΔG‡ and ΔGRRS(2), respectively. Results are shown for selected catalyst generations (x-axis) and reactions in the GPS (y-axis), while ee and log TOF median values (bottom) consider all 50 reactions in the GPS. SOO-37 is the top catalyst from the single-objective optimization experiment (structure shown in Fig. 9). Selected SubA and SubB combinations are shown.
Regarding the challenging areas of chemical space, the best-performing HBD organocatalyst from the multi-objective optimization experiment is predicted to achieve ee values of only 36% and 19% in reactions 13 and 26, respectively. Both condensations involve an unprotected β-arylethylamine (SubA) substituted at the 7-position of the indole ring; similarly, Suzuki and co-workers found that 7-methyltryptamine and ethyl 2-oxopentanoate could only be converted in 45% ee.72 These results can be explained in terms of steric effects of the methyl group on the substrate disrupting key non-covalent interactions between the catalyst's amide O and the indole N–H, which are evidently essential for inducing high enantioselectivity.89 The top candidate from the single-objective optimization (SOO-37) affords only marginal improvements for these substrate combinations (38% and 28% ee). Through the specificity-oriented optimization of reaction 13 (Fig. S13†), a urea-based organocatalyst with improved, albeit still low enantioselectivity (53% ee), slow turnover (log TOF = 0.7 s−1) and low generality is discovered, highlighting the limitation of an inverse design strategy based on the combinatorial exploration of known catalyst fragments on pre-described scaffolds.
Considering activity, throughout the NaviCatGA run reactions 3 and 47 are underperforming: according to the volcano plot (Fig. 4C), the formation of the corresponding protonated tetrahydro-β-carboline 2 is energetically unfavorable, in line with the electron-deficient nature of SubA and the electron-withdrawing character of the aldehyde substituent, which hinders the rate-determining deprotonation step. Regardless of the specific substitution patterns the GA may explore during the optimization, finding organocatalysts that non-covalently stabilize such unstable intermediates is clearly a challenge. Reaction 47 also exemplifies a situation where high selectivity and activity are incompatible: while most HBD organocatalysts explored during the evolutionary experiment are predicted to exhibit large ΔΔG‡ values, the TOF always remains far from the theoretical maximum indicated by the volcano. Conversely, reaction 43, which features an electron-rich indole and an α-ketoamide (essentially an activated carbonyl compound),132 has predicted TOF always close to the volcano peak, while selectivity is more challenging to optimize,58 and ee values considerably improve during the GA run (from 63% to 87%).
To verify the accuracy of the ML predictions reported in Fig. 10 and probe the effect of a methyl substituent at the 7-position of the indole ring of SubA, DFT computations are performed on reactions 13 and 47 using the best organocatalyst from generation 32 in the multi-objective optimization (Fig. 11). Full conformational sampling of the two diastereomeric TSs for the rate- and enantiodetermining step (TS3) is carried out with CREST at the GFN2-xTB level, followed by optimization at the PCM(toluene)/M06-2X-D3/Def2-TZVP//M06-2X-D3/Def2-SVP level; enantioselectivity is computed based on the Gibbs free energy difference between the Boltzmann-weighted TSs conformers leading to the (R)- and (S)-tetrahydro-β-carboline products. Good agreement between the computed and predicted ΔΔG‡ values is achieved for both reactions (Fig. 11); as expected from Fig. 5B, the XGBoost model underestimates the larger ΔΔG‡ value of reaction 47, although such comparison must be taken with care since the XGBoost model is trained on experimental ΔΔG‡'s, whereas Fig. 11 reports the results of DFT computations on TS3. Despite such limitation, this approach allows us to directly analyze the structure of the enantiodetermining transition states: as expected, the lowest-lying TS3 for reaction 13 features an elongated indole N–H⋯amide O intermolecular distance (3.85 Å), whereas a stronger hydrogen-bond is present in the catalyst–substrate complex of reaction 47 (1.85 Å). IRC computations133 are then performed to optimize the structure of intermediate 2 for both condensations, leading to relatively good agreement between computed and predicted ΔGRRS(2) values. The higher stability (i.e., faster turnover according to the LFESRs and volcano plot) of the protonated tetrahydro-β-carboline 2 of reaction 13 is consistent with the electron-rich nature of the indole ring and the presence of an activated carbonyl compound such as ethyl 2-oxopentanoate, whereas the formation of 2 for reaction 47 is thermodynamically unfavorable [ΔGRRS(2) = 5.5 kcal mol−1] owing to the electron-poor character of the intermediate, which makes deprotonation slower.
Taken together, the results from the evolutionary experiment suggest that multiple “islands” of high ee or TOF exist in the catalyst–substrate chemical space, and that genetic optimization “expands” them. The discontinuity of the activity/selectivity-response surface is ultimately responsible for limiting generality;134 areas of poor performance are not simply due to structural aspects of the organocatalyst being mismatched to a particular substrates combination,135 but rather to the electronic character of a reaction intermediate inevitably leading to slow turnover or to the disruption of some key non-covalent interactions necessary for stereoinduction.
Conclusions
Given the synthetic utility of catalytic methods that provide high enantioselectivities and activities across a wide assortment of substrates, we have developed an optimization workflow centered on the open-source genetic algorithm NaviCatGA45 and the OSCAR database46 with the aim of demonstrating how generative models35 are an enticing alternative to experimental10 or computational34 high-throughput screening, provided that the various component of the pipeline for de novo catalyst design are adapted to optimize generality as primary target. We have adopted a hybrid approach for scoring candidate organocatalysts that combines a mechanistic-guided strategy (i.e., activity estimations through TOF molecular volcano plots50) with enantioselectivity predictions based on training on experimental data. Catalysts were generated from molecular building blocks extracted from OSCAR.46
We have tested our approach on the asymmetric Pictet–Spengler reaction56 because of the large amount of data available in the literature and the many catalyst chemotypes that have been tested on individual substrate classes, resulting in system-specific islands of high performance.10 We selected a broad and diverse substrate scope guided by mapping the chemical space of commercially and synthetically available tryptamine derivatives and carbonyl compounds tested in the Pictet–Spengler cyclization, and performed evolutionary experiments on this Generality Probing Set (GPS). Through multi-objective optimization, we have explored activity/selectivity trade-offs and located solutions in the Pareto front with good median performance. However, we found that even the top organocatalysts are underperforming in certain areas of substrate space, while other areas are less sensitive to the identity of the HBD/CPA catalyst. Analysis of these outliers provided support to hypotheses on the principle of stereoinduction89 and activity trends extracted from molecular volcanos, demonstrating how genetic optimization also yields mechanistic understanding and reveals structure–property relationships, as long as an unbiased substrate scope is chosen.119
Given these encouraging results, we believe the generality-oriented genetic optimization strategy we have introduced constitutes an efficient, cost-effective tool to probe large catalyst–substrate spaces and identify potential hits with a broad substrate scope, which may then be tested experimentally. The pipeline described herein is generalizable to any asymmetric reaction and can therefore help accelerate the discovery of general chiral catalysts for other transformations of interest.
Computational details
Electronic structure
The structure of both enantiomers of intermediate 2 in the catalytic cycle of the Pictet–Spengler reaction (Fig. 4A, labeled as “Big group pointing Up”, “BU”, or “Big group pointing Down”, “BD”, depending on the relative position of R1 and R2 in 2) were generated by substituting 3D fragments on 20 pre-optimized templates based on work by Jacobsen et al.89 using AaronTools136,137 and optimizing them with the semiempirical GFN2-xTB Hamiltonian138 in the gas phase. In analogy with computational studies by Jacobsen et al.,89 who found no clear trend relating the benzoic acid electronic properties to the reaction rate, the carboxylic acid co-catalyst, which sometimes contains large and bulky groups like triphenylmethyl, 9-anthracentyl, or 1-adamantyl,70 was modelled with acetic acid to simplify the conformational complexity and reduce the computational cost of the system. Conformational sampling of the resulting 703 complexes was carried out using the Conformer-Rotamer Ensemble Sampling Tool94–96 (CREST) at the GFN2-xTB//GFN-FF level of theory,138 constraining positions of the bond-forming atoms. The lowest-energy conformer was selected and optimized at the PCM(toluene)/M06-2X-D3/Def2-TZVP//M06-2X-D3/Def2-SVP level.139–144 The other intermediates and TSs in the SRS were located using scans and IRC computations.133 The PES of only one enantiomeric pathway (corresponding to “BD”-labeled structures) was generated to construct volcano plots (vide infra). Stationary points were characterized on the basis of their vibrational frequencies (minima with zero imaginary frequencies, TSs with one imaginary frequency). Thermal and entropic corrections were calculated using Grimme's quasi-RRHO approximation145 from frequencies computed at 298 K using the GoodVibes program146 with a frequency cut-off value of 100 wavenumbers. All DFT computations were carried out using Gaussian16 (revision C.01).147 The relative Gibbs free energies were automatically post-processed using the toolkit volcanic51 to establish LFESRs, determine the choice of the descriptor variable [the relative energy of intermediate 2, ΔGRRS(2)], and construct TOF–volcano plots. Extensive instructions on how volcano plots are constructed are given elsewhere,51 while the input for volcanic is provided in Table S1.†
Statistical models
MFPs of catalysts, co-catalysts, substrates, and solvents with a fingerprint size of 1024 were generated using RDKit148 from their SMILES strings.149 Chemical space maps were generated using Scikit-learn150 on the basis of the concatenated MFPs with dimensions reduced to 100 using Principal Component Analysis, followed by t-SNE embedding52 with perplexity of 30 to further reduce the featurization to two dimensions for visualization. Random forest models from the XGBoost library were used with default hyperparameters. The input was the concatenated MPFs of Cat, Co-cat, SubA, SubB, and solvent for ΔΔG‡, and of Cat, Co-Cat (i.e., AcOH, BzBr, or none), SubA, and SubB for ΔGRRS(2). A cross-validation scheme was used with 100 different 90/10 training/test splits [738/82 for ΔΔG‡, 633/70 for ΔGRRS(2)]. From the 100 different train/test splits, the target [ΔΔG‡ or ΔGRRS(2)] was predicted approximately 10 times; these test predictions were then averaged to obtain one final prediction. The standard deviation from the test predictions were used to generate the error bars.107
Evolutionary experiments
Genetic optimization was performed with the NaviCatGA algorithm.45 Genes were represented with SMILES strings (see Table S3† for a full list), and the assembler function generated the chromosomes by introducing the SMILES of different R1–4 substituents in a scaffold's SMILES string. The XGBoost models were used for fitness evaluation, with toluene fixed as solvent and benzoic (for ΔΔG‡ evaluation) or acetic acid [for ΔGRRS(2) evaluation] fixed as co-catalyst; no co-catalyst was included in the GA runs on the CPA combinatorial space. Experiments were initiated with 10 randomized individuals per population, a mutation rate of 10%, a selection rate of 25%, and run for 50 generations. Multi-objective optimization was performed by integrating NaviCatGA with the achievement scalarizing function Chimera.124 Four objectives were hierarchically scalarized to obtain the final fitness value for each catalyst candidate i. The first objective was the median selectivity ( ) across the GPS, which was required to be ≥2 kcal mol−1. Secondly, the activity of each candidate i was evaluated as
) across the GPS, which was required to be ≥2 kcal mol−1. Secondly, the activity of each candidate i was evaluated as  , a normalized Gaussian distribution centered on the target x (−9 kcal mol−1, the volcano peak); the median fi value across the GPS was maximized with a 10% degradation threshold. The third and fourth objectives were the standard deviations of
, a normalized Gaussian distribution centered on the target x (−9 kcal mol−1, the volcano peak); the median fi value across the GPS was maximized with a 10% degradation threshold. The third and fourth objectives were the standard deviations of  and median fi in the GPS, which were minimized with a 25% compromise.
and median fi in the GPS, which were minimized with a 25% compromise.
Data availability
Data can be found on the Materials Cloud (https://archive.materialscloud.org/record/2023.175). See the ESI† for further details.
Author contributions
S. G. conceived the project, performed DFT computations, curated the data, and analyzed the results. P. v. G. trained the statistical models. R. L. designed and coded NaviCatGA and implemented it in the evolutionary experiments with help from S. G. L. B. helped curating the database of Pictet–Spengler reactions and generating 3D structures. A. M. ran preliminary computations initiating this work. S. G. wrote the manuscript with help and feedback from all authors. C. C. secured funding and provided supervision throughout.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
S. G. acknowledges the European Research Council (ERC, Grant Agreement No. 817977) within the framework of European Union's H2020 for financial support. The National Centre of Competence in Research (NCCR) “Sustainable chemical process through catalysis (Catalysis)” of the Swiss National Science Foundation (SNSF, grant number 180544) is acknowledged for financial support of P. v. G. and R. L. The authors also acknowledge support from EPFL.
Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc06208b
References
- Strassfeld D. A. Algera R. F. Wickens Z. K. Jacobsen E. N. A Case Study in Catalyst Generality: Simultaneous, Highly-Enantioselective Brønsted- and Lewis-Acid Mechanisms in Hydrogen-Bond-Donor Catalyzed Oxetane Openings. J. Am. Chem. Soc. 2021;143:9585–9594. doi: 10.1021/jacs.1c03992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins K. D. Glorius F. A robustness screen for the rapid assessment of chemical reactions. Nat. Chem. 2013;5:597–601. doi: 10.1038/nchem.1669. [DOI] [PubMed] [Google Scholar]
- Brown D. G. Boström J. Analysis of Past and Present Synthetic Methodologies on Medicinal Chemistry: Where Have All the New Reactions Gone? J. Med. Chem. 2016;59:4443–4458. doi: 10.1021/acs.jmedchem.5b01409. [DOI] [PubMed] [Google Scholar]
- Brethomé A. V. Paton R. S. Fletcher S. P. Retooling Asymmetric Conjugate Additions for Sterically Demanding Substrates with an Iterative Data-Driven Approach. ACS Catal. 2019;9:7179–7187. doi: 10.1021/acscatal.9b01814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao X. Kagan H. B. One-pot multi-substrate screening in asymmetric catalysis. Chirality. 1998;10:120–124. doi: 10.1002/chir.19. [DOI] [Google Scholar]
- Satyanarayana T. Kagan H. B. The Multi-Substrate Screening of Asymmetric Catalysts. Adv. Synth. Catal. 2005;347:737–748. doi: 10.1002/adsc.200505057. [DOI] [Google Scholar]
- Burgess K. Lim H.-J. Porte A. M. Sulikowski G. A. New Catalysts and Conditions for a C-H Insertion Reaction Identified by High Throughput Catalyst Screening. Angew. Chem., Int. Ed. 1996;35:220–222. doi: 10.1002/anie.199602201. [DOI] [Google Scholar]
- Kim H. Gerosa G. Aronow J. Kasaplar P. Ouyang J. Lingnau J. B. Guerry P. Farès C. List B. A multi-substrate screening approach for the identification of a broadly applicable Diels–Alder catalyst. Nat. Commun. 2019;10:770. doi: 10.1038/s41467-019-08374-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prieto Kullmer C. N. Kautzky J. A. Krska S. W. Nowak T. Dreher S. D. MacMillan D. W. C. Accelerating reaction generality and mechanistic insight through additive mapping. Science. 2022;376:532–539. doi: 10.1126/science.abn1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagen C. C. McMinn S. E. Kwan E. E. Jacobsen E. N. Screening for Generality in Asymmetric Catalysis. Nature. 2022;610:680–686. doi: 10.1038/s41586-022-05263-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rein J. Rozema S. D. Langner O. C. Zacate S. B. Hardy M. A. Siu J. C. Mercado B. Q. Sigman M. S. Miller S. J. Lin S. Generality-oriented optimization of enantioselective aminoxyl radical catalysis. Science. 2023;380:706–712. doi: 10.1126/science.adf6177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie W. Wan Q. Sun J. Chen M. Gao M. Chen S. Ultra-high-throughput mapping of the chemical space of asymmetric catalysis enables accelerated reaction discovery. Nat. Commun. 2023;14:6671. doi: 10.1038/s41467-023-42446-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beker W. Roszak R. Wołos A. Angello N. H. Rathore V. Burke M. D. Grzybowski B. A. Machine Learning May Sometimes Simply Capture Literature Popularity Trends: A Case Study of Heterocyclic Suzuki–Miyaura Coupling. J. Am. Chem. Soc. 2022;144:4819–4827. doi: 10.1021/jacs.1c12005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Z. Stuyver T. Coley C. W. Predictive chemistry: machine learning for reaction deployment, reaction development, and reaction discovery. Chem. Sci. 2023;14:226–244. doi: 10.1039/D2SC05089G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strieth-Kalthoff F. Sandfort F. Segler M. H. S. Glorius F. Machine learning the ropes: principles, applications and directions in synthetic chemistry. Chem. Soc. Rev. 2020;49:6154–6168. doi: 10.1039/C9CS00786E. [DOI] [PubMed] [Google Scholar]
- Oliveira J. Frey J. Zhang S. Xu L. Li X. Li S. Hong X. Ackermann L. When machine learning meets molecular synthesis. Trends Chem. 2022;4:863–885. doi: 10.1016/j.trechm.2022.07.005. [DOI] [Google Scholar]
- Schwaller P. Vaucher A. C. Laplaza R. Bunne C. Krause A. Corminboeuf C. Laino T. Machine intelligence for chemical reaction space. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2022;12:e1604. [Google Scholar]
- Schwaller P. Laino T. Gaudin T. Bolgar P. Hunter C. A. Bekas C. Lee A. A. Molecular Transformer: A Model for Uncertainty-Calibrated Chemical Reaction Prediction. ACS Cent. Sci. 2019;5:1572–1583. doi: 10.1021/acscentsci.9b00576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coley C. W. Barzilay R. Jaakkola T. S. Green W. H. Jensen K. F. Prediction of Organic Reaction Outcomes Using Machine Learning. ACS Cent. Sci. 2017;3:434–443. doi: 10.1021/acscentsci.7b00064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei J. N. Duvenaud D. Aspuru-Guzik A. Neural Networks for the Prediction of Organic Chemistry Reactions. ACS Cent. Sci. 2016;2:725–732. doi: 10.1021/acscentsci.6b00219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coley C. W. Green W. H. Jensen K. F. Machine Learning in Computer-Aided Synthesis Planning. Acc. Chem. Res. 2018;51:1281–1289. doi: 10.1021/acs.accounts.8b00087. [DOI] [PubMed] [Google Scholar]
- Szymkuć S. Gajewska E. P. Klucznik T. Molga K. Dittwald P. Startek M. Bajczyk M. Grzybowski B. A. Computer-Assisted Synthetic Planning: The End of the Beginning. Angew. Chem., Int. Ed. 2016;55:5904–5937. doi: 10.1002/anie.201506101. [DOI] [PubMed] [Google Scholar]
- Segler M. H. S. Preuss M. Waller M. P. Planning chemical syntheses with deep neural networks and symbolic AI. Nature. 2018;555:604–610. doi: 10.1038/nature25978. [DOI] [PubMed] [Google Scholar]
- Cordova M. Wodrich M. D. Meyer B. Sawatlon B. Corminboeuf C. Data-Driven Advancement of Homogeneous Nickel Catalyst Activity for Aryl Ether Cleavage. ACS Catal. 2020;10:7021–7031. doi: 10.1021/acscatal.0c00774. [DOI] [Google Scholar]
- Hueffel J. A. Sperger T. Funes-Ardoiz I. Ward J. S. Rissanen K. Schoenebeck F. Accelerated dinuclear palladium catalyst identification through unsupervised machine learning. Science. 2021;374:1134–1140. doi: 10.1126/science.abj0999. [DOI] [PubMed] [Google Scholar]
- Rose B. T. Timmerman J. C. Bawel S. A. Chin S. Zhang H. Denmark S. E. High-Level Data Fusion Enables the Chemoinformatically Guided Discovery of Chiral Disulfonimide Catalysts for Atropselective Iodination of 2-Amino-6-arylpyridines. J. Am. Chem. Soc. 2022;144:22950–22964. doi: 10.1021/jacs.2c08820. [DOI] [PubMed] [Google Scholar]
- Liles J. P. Rouget-Virbel C. Wahlman J. L. H. Rahimoff R. Crawford J. M. Medlin A. O’Connor V. S. Li J. Roytman V. A. Toste F. D. Sigman M. S. Data science enables the development of a new class of chiral phosphoric acid catalysts. Chem. 2023;9:1–20. doi: 10.1016/j.chempr.2023.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karl T. M. Bouayad-Gervais S. Hueffel J. A. Sperger T. Wellig S. Kaldas S. J. Dabranskaya U. Ward J. S. Rissanen K. Tizzard G. J. Schoenebeck F. Machine Learning-Guided Development of Trialkylphosphine Ni(I) Dimers and Applications in Site-Selective Catalysis. J. Am. Chem. Soc. 2023;145:15414–15424. doi: 10.1021/jacs.3c03403. [DOI] [PubMed] [Google Scholar]
- Shields B. J. Stevens J. Li J. Parasram M. Damani F. Alvarado J. I. M. Janey J. M. Adams R. P. Doyle A. G. Bayesian reaction optimization as a tool for chemical synthesis. Nature. 2021;590:89–96. doi: 10.1038/s41586-021-03213-y. [DOI] [PubMed] [Google Scholar]
- Guo J. Ranković B. Schwaller P. Bayesian Optimization for Chemical Reactions. Chimia. 2023;77:31. doi: 10.2533/chimia.2023.31. [DOI] [PubMed] [Google Scholar]
- Angello N. H. Rathore V. Beker W. Wołos A. Jira E. R. Roszak R. Wu T. C. Schroeder C. M. Aspuru-Guzik A. Grzybowski B. A. Burke M. D. Closed-loop optimization of general reaction conditions for heteroaryl Suzuki-Miyaura coupling. Science. 2022;378:399–405. doi: 10.1126/science.adc8743. [DOI] [PubMed] [Google Scholar]
- Rinehart N. I. Saunthwal R. K. Wellauer J. Zahrt A. F. Schlemper L. Shved A. S. Bigler R. Fantasia S. Denmark S. E. A machine-learning tool to predict substrate-adaptive conditions for Pd-catalyzed C–N couplings. Science. 2023;381:965–972. doi: 10.1126/science.adg2114. [DOI] [PubMed] [Google Scholar]
- Betinol I. O. Lai J. Thakur S. Reid J. P. A Data-Driven Workflow for Assigning and Predicting Generality in Asymmetric Catalysis. J. Am. Chem. Soc. 2023;145:12870–12883. doi: 10.1021/jacs.3c03989. [DOI] [PubMed] [Google Scholar]
- Lai J., Li J., Betinol I. O., Kuang Y., Reid J. P., A Statistical Modeling Approach to Catalyst Generality Assessment in Enantioselective Synthesis, ChemRxiv, 2022, preprint, 10.26434/chemrxiv-2022-80fgz [DOI]
- Anstine D. M. Isayev O. Generative Models as an Emerging Paradigm in the Chemical Sciences. J. Am. Chem. Soc. 2023;145:8736–8750. doi: 10.1021/jacs.2c13467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeze J. G. Kelly H. R. Batista V. S. Search for Catalysts by Inverse Design: Artificial Intelligence, Mountain Climbers, and Alchemists. Chem. Rev. 2019;119:6595–6612. doi: 10.1021/acs.chemrev.8b00759. [DOI] [PubMed] [Google Scholar]
- Sanchez-Lengeling B. Aspuru-Guzik A. Inverse molecular design using machine learning: generative models for matter engineering. Science. 2018;361:360–365. doi: 10.1126/science.aat2663. [DOI] [PubMed] [Google Scholar]
- Gallarati S. van Gerwen P. Schoepfer A. A. Laplaza R. Corminboeuf C. Genetic Algorithms for the Discovery of Homogeneous Catalysts. Chimia. 2023;77:39. doi: 10.2533/chimia.2023.39. [DOI] [PubMed] [Google Scholar]
- Vriamont N. Govaerts B. Grenouillet P. de Bellefon C. Riant O. Design of a Genetic Algorithm for the Simulated Evolution of a Library of Asymmetric Transfer Hydrogenation Catalysts. Chem.–Eur. J. 2009;15:6267–6278. doi: 10.1002/chem.200802192. [DOI] [PubMed] [Google Scholar]
- Chu Y. Heyndrickx W. Occhipinti G. Jensen V. R. Alsberg B. K. An Evolutionary Algorithm for de Novo Optimization of Functional Transition Metal Compounds. J. Am. Chem. Soc. 2012;134:8885–8895. doi: 10.1021/ja300865u. [DOI] [PubMed] [Google Scholar]
- Foscato M. Venkatraman V. Jensen V. R. DENOPTIM: Software for Computational de Novo Design of Organic and Inorganic Molecules. J. Chem. Inf. Model. 2019;59:4077–4082. doi: 10.1021/acs.jcim.9b00516. [DOI] [PubMed] [Google Scholar]
- Seumer J. Kirschner Solberg Hansen J. Brøndsted Nielsen M. Jensen J. H. Computational Evolution of New Catalysts for the Morita–Baylis–Hillman Reaction. Angew. Chem., Int. Ed. 2023;62:e202218565. doi: 10.1002/anie.202218565. [DOI] [PubMed] [Google Scholar]
- Strandgaard M., Seumer J., Benediktsson B., Bhowmik A., Vegge T. and Jensen J. H., Genetic algorithm-based re-optimization of the Schrock catalyst for dinitrogen fixation, ChemRxiv, 2023, preprint, 10.26434/chemrxiv-2023-t73mw [DOI]
- Schilter O. Vaucher A. Schwaller P. Laino T. Designing catalysts with deep generative models and computational data. A case study for Suzuki cross coupling reactions. Digital Discovery. 2023;2:728–735. doi: 10.1039/D2DD00125J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laplaza R. Gallarati S. Corminboeuf C. Genetic Optimization of Homogeneous Catalysts. Chem. Methods. 2022:e202100107. doi: 10.1002/cmtd.202100107. [DOI] [Google Scholar]
- Gallarati S. van Gerwen P. Laplaza R. Fabrizio A. Vela S. Corminboeuf C. OSCAR: An Extensive Repository of Chemically and Functionally Diverse Organocatalysts. Chem. Sci. 2022;13:13782–13794. doi: 10.1039/D2SC04251G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laplaza R. Sobez J.-G. Wodrich M. D. Reiher M. Corminboeuf C. The (not so) simple prediction of enantioselectivity – a pipeline for high-fidelity computations. Chem. Sci. 2022;13:6858–6864. doi: 10.1039/D2SC01714H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strieth-Kalthoff F. Sandfort F. Kühnemund M. Schäfer F. R. Kuchen H. Glorius F. Machine Learning for Chemical Reactivity: The Importance of Failed Experiments. Angew. Chem., Int. Ed. 2022;61:e202204647. doi: 10.1002/anie.202204647. [DOI] [PubMed] [Google Scholar]
- Wodrich M. D. Sawatlon B. Solel E. Kozuch S. Corminboeuf C. Activity-Based Screening of Homogeneous Catalysts through the Rapid Assessment of Theoretically Derived Turnover Frequencies. ACS Catal. 2019;9:5716–5725. doi: 10.1021/acscatal.9b00717. [DOI] [Google Scholar]
- Wodrich M. D. Sawatlon B. Busch M. Corminboeuf C. The Genesis of Molecular Volcano Plots. Acc. Chem. Res. 2021;54:1107–1117. doi: 10.1021/acs.accounts.0c00857. [DOI] [PubMed] [Google Scholar]
- Laplaza R. Das S. Wodrich M. D. Corminboeuf C. Constructing and interpreting volcano plots and activity maps to navigate homogeneous catalyst landscapes. Nat. Protoc. 2022;17:2550–2569. doi: 10.1038/s41596-022-00726-2. [DOI] [PubMed] [Google Scholar]
- van der Maaten L. Hinton G. Visualizing Data using t-SNE. Journal of Machine Learning Research. 2008;9:2579–2605. [Google Scholar]
- Pictet A. Spengler T. Über die Bildung von Isochinolin-derivaten durch Einwirkung von Methylal auf Phenyl-äthylamin, Phenyl-alanin und Tyrosin. Ber. Dtsch. Chem. Ges. 1911;44:2030–2036. doi: 10.1002/cber.19110440309. [DOI] [Google Scholar]
- Calcaterra A. Mangiardi L. Delle Monache G. Quaglio D. Balducci S. Berardozzi S. Iazzetti A. Franzini R. Botta B. Ghirga F. The Pictet-Spengler Reaction Updates Its Habits. Molecules. 2020;25:414–495. doi: 10.3390/molecules25020414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stöckigt J. Antonchick A. P. Wu F. Waldmann H. The Pictet–Spengler Reaction in Nature and in Organic Chemistry. Angew. Chem., Int. Ed. 2011;50:8538–8564. doi: 10.1002/anie.201008071. [DOI] [PubMed] [Google Scholar]
- Biswas A. Organocatalyzed Asymmetric Pictet-Spengler Reactions. ChemistrySelect. 2023;8:e202203368. doi: 10.1002/slct.202203368. [DOI] [Google Scholar]
- Maji R. Mallojjala S. C. Wheeler S. E. Chiral phosphoric acid catalysis: from numbers to insights. Chem. Soc. Rev. 2018;47:1142–1158. doi: 10.1039/C6CS00475J. [DOI] [PubMed] [Google Scholar]
- Andres R. Wang Q. Zhu J. Catalytic Enantioselective Pictet–Spengler Reaction of α-Ketoamides Catalyzed by a Single H-Bond Donor Organocatalyst. Angew. Chem., Int. Ed. 2022;61:e202201788. doi: 10.1002/anie.202201788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z. Schreiner P. R. (Thio)urea organocatalysis—what can be learnt from anion recognition? Chem. Soc. Rev. 2009;38:1187–1198. doi: 10.1039/B801793J. [DOI] [PubMed] [Google Scholar]
- Min C. Mittal N. Sun D. X. Seidel D. Conjugate-Base-Stabilized Brønsted Acids as Asymmetric Catalysts: Enantioselective Povarov Reactions with Secondary Aromatic Amines. Angew. Chem., Int. Ed. 2013;52:14084–14088. doi: 10.1002/anie.201308196. [DOI] [PubMed] [Google Scholar]
- Taylor M. S. Jacobsen E. N. Highly Enantioselective Catalytic Acyl-Pictet–Spengler Reactions. J. Am. Chem. Soc. 2004;126:10558–10559. doi: 10.1021/ja046259p. [DOI] [PubMed] [Google Scholar]
- Wanner M. J. van der Haas R. N. S. de Cuba K. R. van Maarseveen J. H. Hiemstra H. Catalytic Asymmetric Pictet–Spengler Reactions via Sulfenyliminium Ions. Angew. Chem., Int. Ed. 2007;46:7485–7487. doi: 10.1002/anie.200701808. [DOI] [PubMed] [Google Scholar]
- Sewgobind N. V. Wanner M. J. Ingemann S. de Gelder R. van Maarseveen J. H. Hiemstra H. Enantioselective BINOL-Phosphoric Acid Catalyzed Pictet–Spengler Reactions of N-Benzyltryptamine. J. Org. Chem. 2008;73:6405–6408. doi: 10.1021/jo8010478. [DOI] [PubMed] [Google Scholar]
- Klausen R. S. Jacobsen E. N. Weak Brønsted Acid–Thiourea Co-catalysis: Enantioselective, Catalytic Protio-Pictet–Spengler Reactions. Org. Lett. 2009;11:887–890. doi: 10.1021/ol802887h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang D. Xu F. Lin X. Wang Y. Highly Enantioselective Pictet–Spengler Reaction Catalyzed by SPINOL-Phosphoric Acids. Chem.–Eur. J. 2012;18:3148–3152. doi: 10.1002/chem.201103207. [DOI] [PubMed] [Google Scholar]
- Mittal N. Sun D. X. Seidel D. Conjugate-Base-Stabilized Brønsted Acids: Catalytic Enantioselective Pictet–Spengler Reactions with Unmodified Tryptamine. Org. Lett. 2014;16:1012–1015. doi: 10.1021/ol403773a. [DOI] [PubMed] [Google Scholar]
- Qi L. Hou H. Ling F. Zhong W. The cinchona alkaloid squaramide catalyzed asymmetric Pictet–Spengler reaction and related theoretical studies. Org. Biomol. Chem. 2018;16:566–574. doi: 10.1039/C7OB02606D. [DOI] [PubMed] [Google Scholar]
- Odagi M. Araki H. Min C. Yamamoto E. Emge T. J. Yamanaka M. Seidel D. Insights into the Structure and Function of a Chiral Conjugate-Base-Stabilized Brønsted Acid Catalyst. Eur. J. Org Chem. 2019;2019:486–492. doi: 10.1002/ejoc.201801024. [DOI] [Google Scholar]
- Andres R. Wang Q. Zhu J. Asymmetric Total Synthesis of (−)-Arborisidine and (−)-19-Epi-Arborisidine Enabled by a Catalytic Enantioselective Pictet–Spengler Reaction. J. Am. Chem. Soc. 2020;142:14276–14285. doi: 10.1021/jacs.0c05804. [DOI] [PubMed] [Google Scholar]
- Chan Y.-C. Sak M. H. Frank S. A. Miller S. J. Tunable and Cooperative Catalysis for Enantioselective Pictet-Spengler Reaction with Varied Nitrogen-Containing Heterocyclic Carboxaldehydes. Angew. Chem., Int. Ed. 2021;60:24573–24581. doi: 10.1002/anie.202109694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch-Colameta T. Greta S. Snyder S. A. Synthesis of aza-quaternary centers via Pictet–Spengler reactions of ketonitrones. Chem. Sci. 2021;12:6181–6187. doi: 10.1039/D1SC00882J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura S. Matsuda Y. Takehara T. Suzuki T. Enantioselective Pictet–Spengler Reaction of Acyclic α-Ketoesters Using Chiral Imidazoline-Phosphoric Acid Catalysts. Org. Lett. 2022;24:1072–1076. doi: 10.1021/acs.orglett.1c04316. [DOI] [PubMed] [Google Scholar]
- Andres R. Sun F. Wang Q. Zhu J. Organocatalytic Enantioselective Pictet–Spengler Reaction of α-Ketoesters: Development and Application to the Total Synthesis of (+)-Alstratine A. Angew. Chem., Int. Ed. 2023;62:e202213831. doi: 10.1002/anie.202213831. [DOI] [PubMed] [Google Scholar]
- Lee Y. Klausen R. S. Jacobsen E. N. Thiourea-Catalyzed Enantioselective Iso-Pictet–Spengler Reactions. Org. Lett. 2011;13:5564–5567. doi: 10.1021/ol202300t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das S. Liu L. Zheng Y. Alachraf M. W. Thiel W. De C. K. List B. Nitrated Confined Imidodiphosphates Enable a Catalytic Asymmetric Oxa-Pictet–Spengler Reaction. J. Am. Chem. Soc. 2016;138:9429–9432. doi: 10.1021/jacs.6b06626. [DOI] [PubMed] [Google Scholar]
- Adili A. Webster J.-P. Zhao C. Mallojjala S. C. Romero-Reyes M. A. Ghiviriga I. Abboud K. A. Vetticatt M. J. Seidel D. Mechanism of a Dually Catalyzed Enantioselective Oxa-Pictet–Spengler Reaction and the Development of a Stereodivergent Variant. ACS Catal. 2023;13:2240–2249. doi: 10.1021/acscatal.2c05484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharf M. J. List B. A Catalytic Asymmetric Pictet–Spengler Platform as a Biomimetic Diversification Strategy toward Naturally Occurring Alkaloids. J. Am. Chem. Soc. 2022;144:15451–15456. doi: 10.1021/jacs.2c06664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raheem I. T. Thiara P. S. Peterson E. A. Jacobsen E. N. Enantioselective Pictet–Spengler-Type Cyclizations of Hydroxylactams: H-Bond Donor Catalysis by Anion Binding. J. Am. Chem. Soc. 2007;129:13404–13405. doi: 10.1021/ja076179w. [DOI] [PubMed] [Google Scholar]
- Muratore M. E. Holloway C. A. Pilling A. W. Storer R. I. Trevitt G. Dixon D. J. Enantioselective Brønsted Acid-Catalyzed N-Acyliminium Cyclization Cascades. J. Am. Chem. Soc. 2009;131:10796–10797. doi: 10.1021/ja9024885. [DOI] [PubMed] [Google Scholar]
- Holloway C. A. Muratore M. E. lan Storer R. Dixon D. J. Direct Enantioselective Brønsted Acid Catalyzed N-Acyliminium Cyclization Cascades of Tryptamines and Ketoacids. Org. Lett. 2010;12:4720–4723. doi: 10.1021/ol101651t. [DOI] [PubMed] [Google Scholar]
- Aillaud I. Barber D. M. Thompson A. L. Dixon D. J. Enantioselective Michael Addition/Iminium Ion Cyclization Cascades of Tryptamine-Derived Ureas. Org. Lett. 2013;15:2946–2949. doi: 10.1021/ol401039h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregory A. W. Jakubec P. Turner P. Dixon D. J. Gold and BINOL-Phosphoric Acid Catalyzed Enantioselective Hydroamination/N-Sulfonyliminium Cyclization Cascade. Org. Lett. 2013;15:4330–4333. doi: 10.1021/ol401784h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai Q. Liang X.-W. Wang S.-G. You S.-L. An olefin isomerization/asymmetric Pictet–Spengler cascade via sequential catalysis of ruthenium alkylidene and chiral phosphoric acid. Org. Biomol. Chem. 2013;11:1602–1605. doi: 10.1039/C3OB00072A. [DOI] [PubMed] [Google Scholar]
- Wang S.-G. Xia Z.-L. Xu R.-Q. Liu X.-J. Zheng C. You S.-L. Construction of Chiral Tetrahydro-β-Carbolines: Asymmetric Pictet–Spengler Reaction of Indolyl Dihydropyridines. Angew. Chem., Int. Ed. 2017;56:7440–7443. doi: 10.1002/anie.201703178. [DOI] [PubMed] [Google Scholar]
- Long D. Zhao G. Liu Z. Chen P. Ma S. Xie X. She X. Enantioselective Pictet–Spengler Condensation to Access the Total Synthesis of (+)-Tabertinggine. Eur. J. Org Chem. 2022;2022:e202200088. doi: 10.1002/ejoc.202200088. [DOI] [Google Scholar]
- Morgan H. L. The Generation of a Unique Machine Description for Chemical Structures-A Technique Developed at Chemical Abstracts Service. J. Chem. Doc. 1965;5:107–113. doi: 10.1021/c160017a018. [DOI] [Google Scholar]
- Rogers D. Hahn M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010;50:742–754. doi: 10.1021/ci100050t. [DOI] [PubMed] [Google Scholar]
- Solel E. Tarannam N. Kozuch S. Catalysis: Energy Is the Measure of All Things. Chem. Commun. 2019;55:5306–5322. doi: 10.1039/C9CC00754G. [DOI] [PubMed] [Google Scholar]
- Klausen R. S. Kennedy C. R. Hyde A. M. Jacobsen E. N. Chiral Thioureas Promote Enantioselective Pictet–Spengler Cyclization by Stabilizing Every Intermediate and Transition State in the Carboxylic Acid-Catalyzed Reaction. J. Am. Chem. Soc. 2017;139:12299–12309. doi: 10.1021/jacs.7b06811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowalski P. Bojarski A. J. Mokrosz J. L. Structure and spectral properties of β-carbolines. 8. Mechanism of the Pictet-Spengler cyclization: an MNDO approach. Tetrahedron. 1995;51:2737–2742. doi: 10.1016/0040-4020(95)00022-Z. [DOI] [Google Scholar]
- Maresh J. J. Giddings L.-A. Friedrich A. Loris E. A. Panjikar S. Trout B. L. Stöckigt J. Peters B. O'Connor S. E. Strictosidine Synthase: Mechanism of a Pictet–Spengler Catalyzing Enzyme. J. Am. Chem. Soc. 2008;130:710–723. doi: 10.1021/ja077190z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overvoorde L. M. Grayson M. N. Luo Y. Goodman J. M. Mechanistic Insights into a BINOL-Derived Phosphoric Acid-Catalyzed Asymmetric Pictet–Spengler Reaction. J. Org. Chem. 2015;80:2634–2640. doi: 10.1021/jo5028134. [DOI] [PubMed] [Google Scholar]
- Zheng C. Xia Z.-L. You S.-L. Unified Mechanistic Understandings of Pictet-Spengler Reactions. Chem. 2018;4:1952–1966. [Google Scholar]
- Grimme S. Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations. J. Chem. Theory Comput. 2019;15:2847–2862. doi: 10.1021/acs.jctc.9b00143. [DOI] [PubMed] [Google Scholar]
- Pracht P. Bohle F. Grimme S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020;22:7169–7192. doi: 10.1039/C9CP06869D. [DOI] [PubMed] [Google Scholar]
- Pracht P. Grimme S. Calculation of absolute molecular entropies and heat capacities made simple. Chem. Sci. 2021;12:6551–6568. doi: 10.1039/D1SC00621E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng C. You S.-L. Exploring the Chemistry of Spiroindolenines by Mechanistically-Driven Reaction Development: Asymmetric Pictet–Spengler-Type Reactions and Beyond. Acc. Chem. Res. 2020;53:974–987. doi: 10.1021/acs.accounts.0c00074. [DOI] [PubMed] [Google Scholar]
- Kozuch S. Shaik S. How to Conceptualize Catalytic Cycles? The Energetic Span Model. Acc. Chem. Res. 2011;44:101–110. doi: 10.1021/ar1000956. [DOI] [PubMed] [Google Scholar]
- Lisnyak V. G. Lynch-Colameta T. Snyder S. A. Mannich-Type Reactions of Cyclic Nitrones: Effective Methods for the Enantioselective Synthesis of Piperidine-Containing Alkaloids. Angew. Chem., Int. Ed. 2018;57:15162–15166. doi: 10.1002/anie.201809799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallarati S. Laplaza R. Corminboeuf C. Harvesting the fragment-based nature of bifunctional organocatalysts to enhance their activity. Org. Chem. Front. 2022;9:4041–4051. doi: 10.1039/D2QO00550F. [DOI] [Google Scholar]
- Xu H. Zuend S. J. Woll M. G. Tao Y. Jacobsen E. N. Asymmetric Cooperative Catalysis of Strong Brønsted Acid–Promoted Reactions Using Chiral Ureas. Science. 2010;327:986–990. doi: 10.1126/science.1182826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Association for Computing Machinery Special Interest Group on Management of Data and ACM Special Interest Group on Knowledge Discovery in Data, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, New York, 2016 [Google Scholar]
- Sigman M. S. Harper K. C. Bess E. N. Milo A. The Development of Multidimensional Analysis Tools for Asymmetric Catalysis and Beyond. Acc. Chem. Res. 2016;49:1292–1301. doi: 10.1021/acs.accounts.6b00194. [DOI] [PubMed] [Google Scholar]
- Ahneman D. T. Estrada J. G. Lin S. Dreher S. D. Doyle A. G. Predicting reaction performance in C–N cross-coupling using machine learning. Science. 2018;360:186. doi: 10.1126/science.aar5169. [DOI] [PubMed] [Google Scholar]
- Gallegos L. C. Luchini G. John P. C. S. Kim S. Paton R. S. Importance of Engineered and Learned Molecular Representations in Predicting Organic Reactivity, Selectivity, and Chemical Properties. Acc. Chem. Res. 2021;54:827–836. doi: 10.1021/acs.accounts.0c00745. [DOI] [PubMed] [Google Scholar]
- Zahrt A. F. Henle J. J. Rose B. T. Wang Y. Darrow W. T. Denmark S. E. Prediction of higher-selectivity catalysts by computer-driven workflow and machine learning. Science. 2019;363:eaau5631. doi: 10.1126/science.aau5631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallarati S. Fabregat R. Laplaza R. Bhattacharjee S. Wodrich M. D. Corminboeuf C. Reaction-based machine learning representations for predicting the enantioselectivity of organocatalysts. Chem. Sci. 2021;12:6879–6889. doi: 10.1039/D1SC00482D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahrt A. F. Athavale S. V. Denmark S. E. Quantitative Structure–Selectivity Relationships in Enantioselective Catalysis: Past, Present, and Future. Chem. Rev. 2020;120:1620–1689. doi: 10.1021/acs.chemrev.9b00425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milo A. Bess E. N. Sigman M. S. Interrogating selectivity in catalysis using molecular vibrations. Nature. 2014;507:210–214. doi: 10.1038/nature13019. [DOI] [PubMed] [Google Scholar]
- Lexa K. W. Belyk K. M. Henle J. Xiang B. Sheridan R. P. Denmark S. E. Ruck R. T. Sherer E. C. Application of Machine Learning and Reaction Optimization for the Iterative Improvement of Enantioselectivity of Cinchona-Derived Phase Transfer Catalysts. Org. Process Res. Dev. 2022;26:670–682. doi: 10.1021/acs.oprd.1c00155. [DOI] [Google Scholar]
- Sandfort F. Strieth-Kalthoff F. Kühnemund M. Beecks C. Glorius F. A Structure-Based Platform for Predicting Chemical Reactivity. Chem. 2020;6:1379–1390. [Google Scholar]
- Tsuji N. Sidorov P. Zhu C. Nagata Y. Gimadiev T. Varnek A. List B. Predicting Highly Enantioselective Catalysts Using Tunable Fragment Descriptors. Angew. Chem., Int. Ed. 2023;62:e202218659. doi: 10.1002/anie.202218659. [DOI] [PubMed] [Google Scholar]
- Metsänen T. T. Lexa K. W. Santiago C. B. Chung C. K. Xu Y. Liu Z. Humphrey G. R. Ruck R. T. Sherer E. C. Sigman M. S. Combining traditional 2D and modern physical organic-derived descriptors to predict enhanced enantioselectivity for the key aza-Michael conjugate addition in the synthesis of Prevymis™ (letermovir) Chem. Sci. 2018;9:6922–6927. doi: 10.1039/C8SC02089B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahrt A. F. Mo Y. Nandiwale K. Y. Shprints R. Heid E. Jensen K. F. Machine-Learning-Guided Discovery of Electrochemical Reactions. J. Am. Chem. Soc. 2022;144:22599–22610. doi: 10.1021/jacs.2c08997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andres R. Wang Q. Zhu J. Divergent Asymmetric Total Synthesis of (−)-Voacafricines A and B. Angew. Chem., Int. Ed. 2023;62:e202301517. doi: 10.1002/anie.202301517. [DOI] [PubMed] [Google Scholar]
- Mauger A. Jarret M. Tap A. Perrin R. Guillot R. Kouklovsky C. Gandon V. Vincent G. Collective Total Synthesis of Mavacuran Alkaloids through Intermolecular 1,4-Addition of an Organolithium Reagent. Angew. Chem., Int. Ed. 2023;62:e202302461. doi: 10.1002/anie.202302461. [DOI] [PubMed] [Google Scholar]
- Seayad J. Seayad A. M. List B. Catalytic Asymmetric Pictet–Spengler Reaction. J. Am. Chem. Soc. 2006;128:1086–1087. doi: 10.1021/ja057444l. [DOI] [PubMed] [Google Scholar]
- Gao W. Coley C. W. The Synthesizability of Molecules Proposed by Generative Models. J. Chem. Inf. Model. 2020;60:5714–5723. doi: 10.1021/acs.jcim.0c00174. [DOI] [PubMed] [Google Scholar]
- Kariofillis S. K. Jiang S. Żurański A. M. Gandhi S. S. Martinez Alvarado J. I. Doyle A. G. Using Data Science to Guide Aryl Bromide Substrate Scope Analysis in a Ni/Photoredox-Catalyzed Cross-Coupling with Acetals as Alcohol-Derived Radical Sources. J. Am. Chem. Soc. 2022;144:1045–1055. doi: 10.1021/jacs.1c12203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas B. C. Goetz A. E. Bahamonde A. McWilliams J. C. Sigman M. S. Predicting relative efficiency of amide bond formation using multivariate linear regression. Proc. Natl. Acad. Sci. U. S. A. 2022;119:e2118451119. doi: 10.1073/pnas.2118451119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang T. Hazra A. Min D. S. Williams W. L. Jones E. Doyle A. G. Sigman M. S. Interrogating the Mechanistic Features of Ni(I)-Mediated Aryl Iodide Oxidative Addition Using Electroanalytical and Statistical Modeling Techniques. J. Am. Chem. Soc. 2023;145:8689–8699. doi: 10.1021/jacs.3c01726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita T. Kawai N. Tokuyama H. Fukuyama T. Stereocontrolled Total Synthesis of (−)-Eudistomin C. J. Am. Chem. Soc. 2005;127:15038–15039. doi: 10.1021/ja055832h. [DOI] [PubMed] [Google Scholar]
- Gobé V. Guinchard X. Stereoselective Synthesis of Chiral Polycyclic Indolic Architectures through Pd0-Catalyzed Tandem Deprotection/Cyclization of Tetrahydro-β-carbolines on Allenes. Chem.–Eur. J. 2015;21:8511–8520. doi: 10.1002/chem.201500273. [DOI] [PubMed] [Google Scholar]
- Häse F. Roch L. M. Aspuru-Guzik A. Chimera: enabling hierarchy based multi-objective optimization for self-driving laboratories. Chem. Sci. 2018;9:7642–7655. doi: 10.1039/C8SC02239A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G. Liang Y. Antilla J. C. A Vaulted Biaryl Phosphoric Acid-Catalyzed Reduction of α-Imino Esters: The Highly Enantioselective Preparation of α-Amino Esters. J. Am. Chem. Soc. 2007;129:5830–5831. doi: 10.1021/ja070519w. [DOI] [PubMed] [Google Scholar]
- Wenzel Mathieu P A. G. L. Jacobsen E. N. Divergent Stereoinduction Mechanisms in Urea-Catalyzed Additions to Imines. Synlett. 2003;2003:1919–1922. [Google Scholar]
- Samha M. H. Wahlman J. L. H. Read J. A. Werth J. Jacobsen E. N. Sigman M. S. Exploring Structure–Function Relationships of Aryl Pyrrolidine-Based Hydrogen-Bond Donors in Asymmetric Catalysis Using Data-Driven Techniques. ACS Catal. 2022;12:14836–14845. doi: 10.1021/acscatal.2c04824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu T. Wheeler S. E. Origin of the Superior Performance of (Thio)Squaramides over (Thio)Ureas in Organocatalysis. Chem.–Eur. J. 2013;19:15141–15147. doi: 10.1002/chem.201302990. [DOI] [PubMed] [Google Scholar]
- Torres J. A. G. Lau S. H. Anchuri P. Stevens J. M. Tabora J. E. Li J. Borovika A. Adams R. P. Doyle A. G. A Multi-Objective Active Learning Platform and Web App for Reaction Optimization. J. Am. Chem. Soc. 2022;144:19999–20007. doi: 10.1021/jacs.2c08592. [DOI] [PubMed] [Google Scholar]
- Dotson J. J. van Dijk L. Timmerman J. C. Grosslight S. Walroth R. C. Gosselin F. Püntener K. Mack K. A. Sigman M. S. Data-Driven Multi-Objective Optimization Tactics for Catalytic Asymmetric Reactions Using Bisphosphine Ligands. J. Am. Chem. Soc. 2023;145:110–121. doi: 10.1021/jacs.2c08513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fromer J. Coley C. Computer-aided multi-objective optimization in small molecule discovery. Patterns. 2023;4:100678–100694. doi: 10.1016/j.patter.2023.100678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthukumar A. Sangeetha S. Sekar G. Recent developments in functionalization of acyclic α-keto amides. Org. Biomol. Chem. 2018;16:7068–7083. doi: 10.1039/C8OB01423J. [DOI] [PubMed] [Google Scholar]
- Fukui K. The path of chemical reactions - the IRC approach. Acc. Chem. Res. 1981;14:363–368. doi: 10.1021/ar00072a001. [DOI] [Google Scholar]
- Olen C. L., Zahrt A. F., Reilly S. W., Schultz D., Emerson K., Candito D., Strotman N. A. and Denmark S. E., Chemoinformatic Catalyst Selection Methods for the Optimization of Copper-Bis(oxazoline) Mediated, Asymmetric, Vinylogous Mukaiyama Aldol Reactions, ChemRxiv, 2023, preprint, 10.26434/chemrxiv-2023-q1g81-v2 [DOI]
- Xu J. Grosslight S. Mack K. A. Nguyen S. C. Clagg K. Lim N.-K. Timmerman J. C. Shen J. White N. A. Sirois L. E. Han C. Zhang H. Sigman M. S. Gosselin F. Atroposelective Negishi Coupling Optimization Guided by Multivariate Linear Regression Analysis: Asymmetric Synthesis of KRAS G12C Covalent Inhibitor GDC-6036. J. Am. Chem. Soc. 2022;144:20955–20963. doi: 10.1021/jacs.2c09917. [DOI] [PubMed] [Google Scholar]
- Guan Y. Ingman V. M. Rooks B. J. Wheeler S. E. AARON: An Automated Reaction Optimizer for New Catalysts. J. Chem. Theory Comput. 2018;14:5249–5261. doi: 10.1021/acs.jctc.8b00578. [DOI] [PubMed] [Google Scholar]
- Ingman V. M. Schaefer A. J. Andreola L. R. Wheeler S. E. QChASM: quantum chemistry automation and structure manipulation. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2021;11:e1510. [Google Scholar]
- Bannwarth C. Ehlert S. Grimme S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019;15:1652–1671. doi: 10.1021/acs.jctc.8b01176. [DOI] [PubMed] [Google Scholar]
- Zhao Y. Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008;120:215–241. [Google Scholar]
- Zhao Y. Truhlar D. G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008;41:157–167. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
- Weigend F. Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/B508541A. [DOI] [PubMed] [Google Scholar]
- Grimme S. Antony J. Ehrlich S. Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Miertuš S. Scrocco E. Tomasi J. Electrostatic interaction of a solute with a continuum. A direct utilization of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981;55:117–129. doi: 10.1016/0301-0104(81)85090-2. [DOI] [Google Scholar]
- Tomasi J. Mennucci B. Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005;105:2999–3094. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- Grimme S. Supramolecular Binding Thermodynamics by Dispersion-Corrected Density Functional Theory. Chem.–Eur. J. 2012;18:9955–9964. doi: 10.1002/chem.201200497. [DOI] [PubMed] [Google Scholar]
- Luchini G. Alegre-Requena J. V. Funes-Ardoiz I. Paton R. S. GoodVibes: Automated Thermochemistry for Heterogeneous Computational Chemistry Data. F1000Research. 2020;9:291–304. [Google Scholar]
- Frisch M., Trucks G., Schlegel H., Scuseria G., Robb M., Cheeseman J., Montgomery J., Vreven T., Kudin K., Burant J., Millam J., Iyengar S., Tomasi J., Barone V., Mennucci B., Cossi M., Scalmani G., Rega N., Petersson G., Nakatsuji H., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Klene M., Li X., Knox J., Hratchian H., Cross J., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R., Yazyev O., Austin A., Cammi R., Pomelli C., Ochterski J., Ayala P., Morokuma K., Voth G., Salvador P., Dannenberg J., Zakrzewski V., Dapprich S., Daniels A., Strain M., Farkas O., Malick D., Rabuck A., Raghavachari K., Foresman J., Ortiz J., Cui Q., Baboul A., Clifford S., Cioslowski J., Stefanov B., Liu G., Liashenko A., Piskorz P., Komaromi I., Martin R., Fox D., Keith T., Laham A., Peng C., Nanayakkara A., Challacombe M., Gill P., Johnson B., Chen W., Wong M., Gonzalez C. and Pople J., Gaussian 16, Revision C.01
- RDKit: Open-Source Chemoinformatics and Machine Learning, https://www.rdkit.org
- Weininger D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988;28:31–36. doi: 10.1021/ci00057a005. [DOI] [Google Scholar]
- Pedregosa F. Varoquaux G. Gramfort A. Michel V. Thirion B. Grisel O. Blondel M. Prettenhofer P. Weiss R. Dubourg V. Vanderplas J. Passos A. Cournapeau D. Brucher M. Perrot M. Duchesnay E. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research. 2011;12:2825–2830. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data can be found on the Materials Cloud (https://archive.materialscloud.org/record/2023.175). See the ESI† for further details.