Investigating the Association Between Dynamic Driving Pressure and Mortality in COVID-19-Related Acute Respiratory Distress Syndrome: A Joint Modeling Approach Using Real-Time Continuously-Monitored Ventilation Data

Abstract

IMPORTANCE AND OBJECTIVES:

COVID-19-related acute respiratory distress syndrome (ARDS) is associated with high mortality and often necessitates invasive mechanical ventilation (IMV). Previous studies on non-COVID-19 ARDS have shown driving pressure to be robustly associated with ICU mortality; however, those studies relied on “static” driving pressure measured periodically and manually. As “continuous” automatically monitored driving pressure is becoming increasingly available and reliable with more advanced mechanical ventilators, we aimed to examine the effect of this “dynamic” driving pressure in COVID-19 ARDS throughout the entire ventilation period.

DESIGN, SETTING, AND PARTICIPANTS:

This retrospective, observational study cohort study evaluates the association between driving pressure and ICU mortality in patients with concurrent COVID-19 and ARDS using multivariate joint modeling. The study cohort (n = 544) included all adult patients (≥ 18 yr) with COVID-19 ARDS between March 1, 2020, and April 30, 2021, on volume-control mode IMV for 12 hours or more in a Mass General Brigham, Boston, MA ICU.

MEASUREMENTS AND MAIN RESULTS:

Of 544 included patients, 171 (31.4%) died in the ICU. Increased dynamic ΔP was associated with increased risk in the hazard of ICU mortality (hazard ratio [HR] 1.035; 95% credible interval, 1.004–1.069) after adjusting for other relevant dynamic respiratory biomarkers. A significant increase in risk in the hazard of death was found for every hour of exposure to high intensities of driving pressure (≥ 15 cm H₂O) (HR 1.002; 95% credible interval 1.001–1.003).

CONCLUSIONS:

Limiting patients’ exposure to high intensities of driving pressure even while under lung-protective ventilation may represent a critical step in improving ICU survival in patients with COVID-19 ARDS. Time-series IMV data could be leveraged to enhance real-time monitoring and decision support to optimize ventilation strategies at the bedside.

KEY POINTS.

Question: How is dynamic, continuously measured driving pressure associated with mortality in patients with concurrent COVID-19 and acute respiratory distress syndrome (ARDS)?

Findings: Our cohort study of 544 patients with concurrent COVID-19 and ARDS from the Mass General Brigham Hospital System finds dynamic driving pressure to be robustly associated with increased mortality risk after adjustment for relevant dynamic respiratory biomarkers and patient characteristics.

Meaning: Continuously and automatically measured driving pressure data may be leveraged to enhance clinical decision support and optimize ventilation strategies in real time.

Over 4.9 million Americans were admitted to hospital due to the novel COVID-19 caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) virus between August 2020 and June 2022 (1). Approximately 33% of hospitalized COVID-19 patients developed acute respiratory distress syndrome (ARDS) (2), which often requires invasive mechanical ventilation (IMV). COVID-19 ARDS is associated with high mortality rates ranging up to 40%, depending upon the wave in the pandemic and other risk factors influencing the baseline hazard of death, including the availability of COVID-19 therapeutics proven to reduce mortality (2, 3). Several studies have reported on their preliminary strategies for the management of individual ventilator parameters for patients with COVID-19 ARDS (2, 4–6). There is substantial heterogeneity in ARDS, and the respiratory system mechanics of patients with ARDS, regardless of COVID-19 status, are broadly similar (7). Several studies have suggested that COVID-19 ARDS presents unique clinical features: more significant hypoxemia, higher lung compliance (5), and longer dependence on IMV (4). Recent literature supports the notion that COVID-19 ARDS requires lung-protective ventilation in a manner similar to non-COVID-19 ARDS (8, 9), including low-tidal volume (V_T) and low-plateau pressure (P_PLAT).

However, mortality in ARDS remains high despite the use of lung-protective ventilation. It has been suggested that driving pressure (ΔP, the ratio of tidal volume to respiratory system compliance), calculated as the P_PLAT minus positive end-expiratory pressures (PEEPs), is strongly associated with survival (10). Using Bayesian joint models (11), Urner et al found each daily increment in driving pressure in non-COVID-19 ARDS to be associated with increased mortality risk (12). A gap in the literature relates to whether the strength of this association between time-varying ΔP and mortality persists in patients with the distinct phenotype of COVID-19 ARDS.

Traditionally, driving pressure is measured via a manual end-inspiratory hold maneuver, typically once or twice a day, and most studies investigating driving pressure consider only the variable measured in this form (10, 12–14). However, recent advances in mechanical ventilation technology have allowed for the automatic calculation of “dynamic” driving pressures measured continuously at the bedside in real-time using estimates of plateau pressure, although research using such data is lacking (15). High-volume and high-velocity ventilation data, along with rich electronic health record (EHR) data, present a unique opportunity to study the association of ventilator parameters with mortality at greater precision. A gap in the literature exists with respect to the time-varying ΔP and mortality relationship where ΔP is used at a more granular level than prior studies (hourly vs. daily measurements of IMV parameters).

In this study, by leveraging high-resolution time-series ventilator data and EHR data, we aimed to contribute to transforming the practice of respiratory medicine to be more dynamic, precise, and personalized. We used multivariate joint modeling of longitudinal and survival data to investigate the association between dynamic driving pressure and ICU mortality in patients with concurrent COVID-19 and ARDS and examine the cumulative effect of driving pressure (11, 16, 17). Compared with more traditional survival analysis methods such as the time-varying Cox model (18), joint modeling has been shown to produce less biased estimates of the associations of time-varying biomarkers and time-to-event outcomes, as well as increased power in estimating treatment effect (19–21). Joint Models account for informative censoring due to death during follow-up. Therefore, the association between a time-varying endogenous covariate and outcome can be measured without selection bias arising from missing values that are related to the outcome (in contrast to time-varying Cox models, which can only deal with exogenous time-varying covariates). We incorporated other relevant time-varying respiratory variables to disentangle the independent effects of each biomarker.

MATERIALS AND METHODS

Study Design and Patient Population

This study was conducted at the Mass General Brigham (MGB), an integrated healthcare delivery network located in Boston, MA. Our study cohort includes all adult ICU patients (≥ 18 yr) with COVID-19 ARDS between March 1, 2020, and April 30, 2021, on volume-control mode IMV for at least 12 hours. COVID-19 diagnosis was based on a positive test result for SARS-CoV-2 by polymerase chain reaction clinical assay. ARDS diagnosis was based on the International Classification of Diseases, 10th Revision Clinical Modification (ICD-10-CM) code J80 (22). We manually validated the ARDS diagnosis for a random subset of 10% (54 patients) of our cohort according to the Berlin Criteria and found the positive predictive value of the ICD-10-CM code to be 96% (23). Patient demographic, clinical, and death data were collected from MGB’s EHR data repository. Data generated from clinical devices (including IMV) at the patient’s bedside were collected at a 1-minute resolution. Ventilation data were collected from Hamilton-G5 and Nihon Kohden 550 mechanical ventilators (24, 25).

This study was performed in compliance with the World Medical Association Declaration of Helsinki on Ethical Principles for Medical Research Involving Human Subjects. The study, entitled “Improving Lung Protective Ventilation (ProLung) using EHR Data” was reviewed by and approved by the MGB institutional review board (IRB) (reference number: 2022P001683) on June 30, 2022. The IRB waived the requirement of consent for this study.

Procedures and Outcomes

Our primary outcome was the hazard of acute decomposition in the ICU during IMV, that is, risk in the hazard of ICU mortality. Patients were followed from the initiation of IMV until death, discharge from the ICU, or liberation from IMV for more than 24 hours, whichever occurred first. These censoring events were treated as multiple competing risks in the joint models.

The independent variables tested as predictors consisted of: 1) time-independent baseline covariates, including gender, race, age, body mass index (BMI), comorbidities, and the Charlson comorbidity index (CCI); and 2) time-dependent (longitudinal) covariates, including driving pressure (cm H₂O), respiratory rate (breaths /min), oxygen saturation (Spo₂) (%), tidal volume per predicted body weight (V_T/PBW) (mL/kg), Po₂ to Fio₂ ratio, Pco₂ (mm Hg), and arterial pH (the measured acid–base balance of the blood). Variables that were recorded multiple times every hour were down-sampled to the hourly mean to optimize the data for computation. We adjusted all analyses for baseline time-independent covariates. We report usage of dexamethasone and remdesivir, which are COVID-19 therapies that have a proven mortality benefit. No usage of baricitinib was found in our cohort.

We calculate dynamic ΔP as the difference between dynamic P_PLAT and measured PEEP. Dynamic P_PLAT is computed every minute by the ventilator via a least squares fit method as outlined by Mojoli et al (15), which is measured at the end of inspiration when flow is at or close to zero and recorded for both mandatory and time-cycled breaths (26). In contrast, static P_PLAT, per standard of care, is manually measured by respiratory therapists about once every 12 hours via an end-inspiratory hold maneuver. Dynamic P_PLAT has been reported to give a good estimation of the actual P_PLAT (15). To verify that dynamic driving pressures reliably approximate static “gold-standard” driving pressures, we conducted a correlation analysis to measure the strength of the linear relationship between dynamic and manually measured static driving pressures.

Statistical Analysis

Patient Characteristics and Longitudinal Variables

Patient characteristics are described as proportions for categorical variables and median (sd) for continuous variables. In the descriptive analyses, p values for each variable were calculated for comparisons between dead and alive patient groups using the Wilcoxon rank-sum and Fisher exact tests, as appropriate.

Baseline Analysis Using Cox Proportional Hazard Models

To examine the basic relationships between baseline ΔP and ICU mortality, we used two types of frequentist baseline measures. One was the mean value of the patient’s dynamic driving pressure on their first day on IMV, and the other was the mean value of first-day manually measured driving pressures, using the 98.9% (538/544) of patients who had both of these measures documented in the EHR. We tested that the assumptions of the Cox proportional hazard model were met (Appendix 1, http://links.lww.com/CCX/B301). Cox proportional hazard models were implemented using restricted cubic splines, to predict the relative hazard of death in ICU with 95% CIs. Additionally, stratified survival curves based on driving pressures at baseline were computed via the Kaplan-Meier estimator. The p values for the comparisons were calculated using a log-rank (Mantel-Cox) test. For these survival curves, we stratified patients using a baseline ΔP cutoff of 15 cm H₂O as this has previously been suggested as an upper safety limit for patients with ARDS (27).

Joint Modeling Analysis

A Bayesian, multivariate joint modeling framework with shared random effects was used to estimate the association of patient-specific longitudinal outcome profiles, that is, dynamic ΔP and other longitudinal variables with ICU mortality. Our joint models use a Cox proportional hazard model for the survival subcomponent and linear-mixed effects models for each of the longitudinal variables (Appendix 1, http://links.lww.com/CCX/B301).

Univariate Joint Modeling Analysis

To assess whether time-varying dynamic ΔP is associated with mortality in patients with concurrent COVID-19 and ARDS, we first constructed a simple, univariate joint model consisting of dynamic ΔP as the sole time-varying variable and baseline patient characteristics: gender, age, race, BMI, CCI, arterial pH, and PF ratio at entry. We used the same modeling approach to quantify the effect of cumulative exposure, that is, by estimating the association between the number of hours with potentially harmful exposure (ΔP ≥ 15 cm H₂O) and ICU mortality.

Multivariate Joint Modeling Analysis

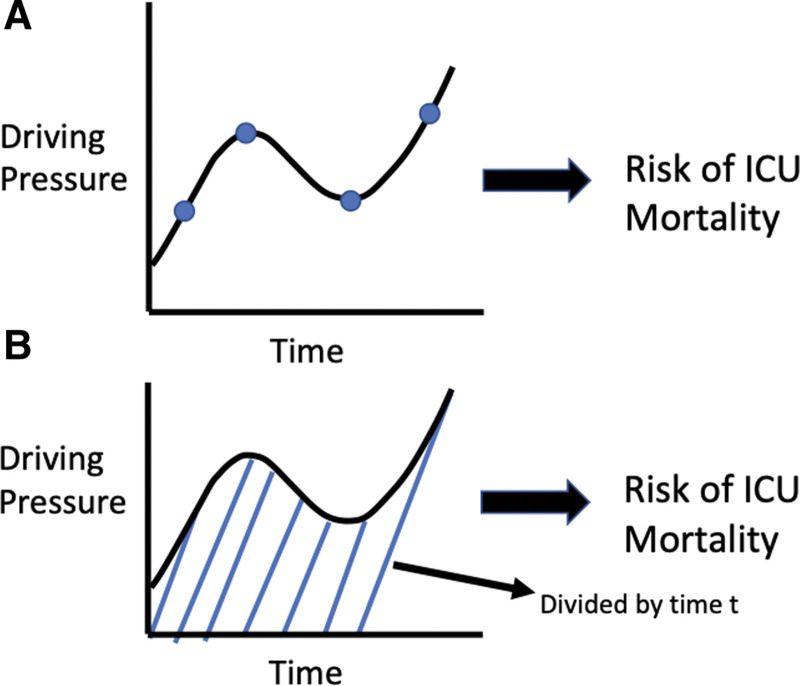
We used multivariate joint modeling to adjust the effect of time-varying ΔP for other time-varying ventilation and gas-exchange variables as described in “Procedures and Outcomes.” Figure 1 visually demonstrates the two distinct functional forms of joint models that we explored in this study.

Figure 1.

Graphical representation of different ways to model the association between dynamic driving pressure and ICU mortality.

Model 1 is a standard, “value-only” joint model. In model 2, we explored the normalized area/cumulative effects functional form, as a recent study suggested that a patient’s history of ΔP levels may be highly relevant to survival (6). We investigated this by incorporating ΔP data from previous time points (i.e., since the start of ventilation). The time-varying normalized cumulative effect of driving pressure is the integral or area under the subject-specific ΔP profile from zero to the current follow-up time t, divided by t. Effectively, this represents the average value of the subject-specific ΔP profile from time 0 to t (Supplementary Equation 3, http://links.lww.com/CCX/B301).

Goodness-of-fit of the multivariate joint models was evaluated using two metrics: the Deviance Information Criterion (DIC) (28), and Widely Applicable Information Criterion (WAIC) (29). Smaller values for DIC and WAIC indicate a better-fitting model. This article is reported according to the Strengthening the Reporting of Observational Studies in Epidemiology guidelines (30).

RESULTS

Demographic Characteristics of the Study Cohort

The final study cohort consisted of 544 patients with concurrent COVID-19 and ARDS with median age of 62 years (interquartile range, IQR, 51–70) and 184 (33.8%) were women. Tables 1 and 2 present descriptive summaries of patient characteristics and time-varying respiratory biomarkers by ICU mortality status. The median number of days in the ICU and on IMV were 16 days (IQR, 10–25) and 15.4 days (IQR, 8.9–24.2), respectively. Overall, 171 (31%) patients died in ICU, with the median age being 67 years (IQR, 57–76 yr) and 50 (29.2%) were women (Table 1). Median ICU and ventilator time were higher in the survival group (17 and 15.8 d, respectively) compared with the deceased group (14 and 13.9 d, respectively) (Table 1). Older age, being of non-Hispanic White descent, a higher CCI, having cardiovascular disease, and having hypertension were all significant risk factors for death.

TABLE 1.

Patient Characteristics by ICU Mortality Status

Variable	All Patients (n = 544)	Alive (n = 373)	Dead (n = 171)	p
Age, yr, mean (IQR)	62 (51–70)	59 (49–68)	67 (57–76)	< 0.0001
Gender, n (%)
Female	184 (33.8)	134 (35.9)	50 (29.2)	0.143
Male	360 (66.2)	239 (64.1)	121 (70.8)	0.143
Race, n (%)
White	233 (42.8)	149 (39.9)	84 (49.1)	0.05
Black	75 (13.8)	51 (13.7)	24 (14.0)	0.894
Asian	33 (6.1)	27 (7.2)	6 (3.5)	0.121
Unknown/other	203 (37.3)	146 (39.1)	57 (33.3)	0.215
Ethnicity, n (%)
Hispanic	156 (28.7)	118 (31.6)	38 (22.2)	0.025
Non-Hispanic	321 (59.0)	211 (56.6)	110 (64.3)	0.092
Unknown	67 (12.3)	44 (11.8)	23 (13.5)	0.577
Body mass index	29.6 (26.1–34.4)	29.3 (26.1–33.5)	30.5 (26–35)	0.265
Comorbidities, n (%)
Chronic liver disease	62 (11.4)	46 (12.3)	16 (9.4)	0.383
Chronic kidney disease	136 (25.0)	91 (24.4)	45 (26.3)	0.67
Diabetes	153 (28.1)	97 (26)	56 (32.7)	0.123
Cardiovascular disease	112 (20.6)	65 (17.4)	47 (27.5)	0.009
Hypertension	232 (42.6)	143 (38.3)	89 (52)	0.003
Charlson Comorbidity Index	0 (0–2)	0 (0–1)	0 (0–3)	0.002
Sequential Organ Failure Assessment	8 (6–11)	8 (6–10)	9 (7–12)	0.003
Medications, n (%)
Remdesivir	110 (20.2)	79 (21.2)	31 (18.1)	0.4904
Dexamethasone	124 (22.8)	96 (25.7)	28 (16.4)	0.016
Time-varying variables
Invasive mechanical ventilation duration	15.4 (8.9–24.2)	15.8 (9.9–25.4)	13.9 (8.6–21.8)	0.072
Driving pressure	13.1 (11.0–16.7)	12.6 (10.5–15.2)	15.0 (11.9–20.0)	< 0.001
Plateau pressure	22.7 (19.0–26.3)	21.9 (17.9–25.8)	24.1 (20.3–28.0)	< 0.001
Positive end-expiratory pressures	10 (6–12)	9 (5–12)	10 (8–12)	< 0.001
Spo2	96.2 (94.4–99.0)	96.4 (94.7–98.1)	95.6 (94.0–97.6)	< 0.001
Respiratory rate	23.0 (18.1–28.0)	22.2 (18.1–27.0)	24.5 (18.4–30.0)	< 0.001
Tidal volume	360.0 (310.0–404.4)	366.5 (318.6–410.0)	340.1 (295.6–396.4)	< 0.001
Tidal volume per predicted body weight	5.9 (5.3–6.3)	5.9 (5.5–6.3)	5.7 (5.0–6.2)	< 0.001
PF ratio	200.0 (156.0–254.3)	215.0 (171.0–268.6)	175.0 (134.9–223.3)	< 0.001
Paco2	45.0 (39.0–51.0)	44.0 (39.0–50.0)	47.0 (41.0–54.0)	< 0.001
Arterial pH	7.39 (7.34–7.44)	7.40 (7.36–7.44)	7.37 (7.31–7.41)	< 0.001
Outcomes, d, mean (IQR)
ICU LOS	16 (10–25)	17 (10–26)	14 (9–22)	0.006
Inpatient LOS	18 (12–27)	19 (12–29)	16 (10–24)	0.003

IQR = interquartile range, LOS = lengths of stay.

TABLE 2.

Results of Multivariate Joint Modelling Analysis

	Δp Value Only		Δp Normalized Area
Variable	HR (95% CI)	p	HR (95% CI)	p
Baseline variables
Male	0.9 (0.516–1.577)	0.71	0.888 (0.527–1.523)	0.651
Age (yr)	1.05 (1.037–1.065)	< 0.001	1.051 (1.035–1.068)	< 0.001
Black (vs. White)	0.381 (0.213–0.636)	0.001	0.407 (0.231–0.695)	< 0.001
Asian (vs. White)	0.749 (0.272–1.765)	0.56	0.713 (0.266–1.574)	0.457
Unknown/other race (vs. White)	1.12 (0.768–1.615)	0.561	1.146 (0.78–1.639)	0.478
Body mass index	1.022 (0.997–1.048)	0.089	1.021 (0.992–1.047)	0.141
Charlson Comorbidity Index	1.024 (0.962–1.088)	0.453	1.032 (0.975–1.092)	0.294
Time-varying variables
Driving pressure (cm H2O)	1.035 (1.004–1.069)	0.021	NA	NA
Normalized area-driving pressure	NA	NA	1.032 (0.986–1.078)	0.177
Spo2 (%)	0.82 (0.798–0.843)	< 0.001	0.812 (0.789–0.839)	< 0.001
Respiratory rate (breaths/min)	1.014 (1.003–1.032)	0.008	1.02 (1.011–1.029)	< 0.001
Tidal volume/predicted body weight (mL/kg)	1.019 (0.933–1.106)	0.627	1.022 (0.957–1.08)	0.497
Pao2/Fio2 ratio (mm Hg)	0.992 (0.989–0.996)	< 0.001	0.992 (0.988–0.995)	< 0.001
Paco2 (mm Hg)	1.021 (1.007–1.039)	0.001	1.027 (1.004–1.045)	0.003
Arterial pHa	0.67 (0.6–0.759)	< 0.001	0.7 (0.605–0.804)	< 0.001

HR = hazard ratio, NA = not applicable.

^aThe HR for arterial pH is the adjusted HR associated with a 1 sd increment in the variable (0.075).

Results of Baseline Analysis

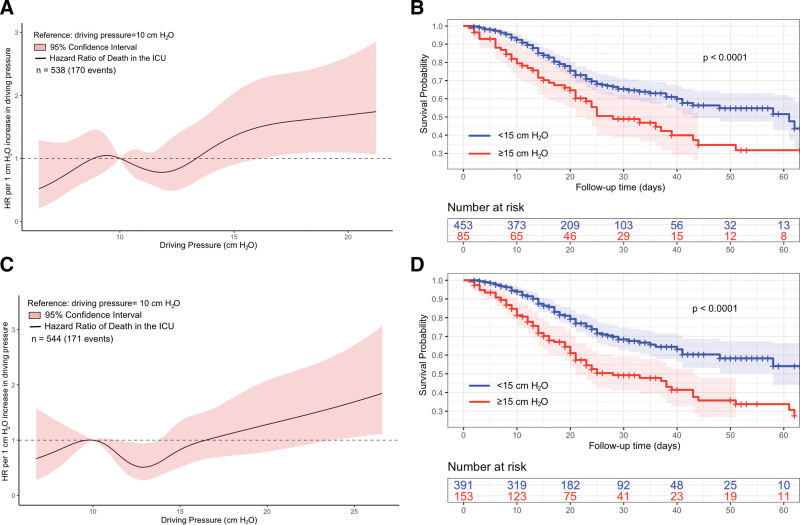
The Cox proportional hazard model assumptions were tested and found to be valid (Appendix 1, http://links.lww.com/CCX/B301). The baseline analysis using Cox proportional hazard models found that baseline static and dynamic ΔP was associated with higher risk in the hazard of ICU mortality (Fig. 2, A and C). Furthermore, patients with static or dynamic ΔP of at least 15 cm H₂O at baseline had significantly poorer survival compared with patients with baseline ΔP less than 15 cm H₂O (Fig. 2, B and D).

Figure 2.

Association of ICU mortality with dynamic and static driving pressures at baseline. A, Unadjusted relationship between baseline static driving pressure (ΔP) and relative hazard of death in the ICU, estimated using a Cox proportional hazards model. B, Differences in ICU survival probability stratified by static ΔP levels greater or less than 15 cm H₂O at baseline. C, Unadjusted relationship between baseline dynamic ΔP and relative hazard of death in the ICU, estimated using a Cox proportional hazards model. D, Differences in ICU survival probability stratified by dynamic ΔP levels greater or less than 15 cm H₂O at baseline. HR = hazard ratio.

Results of the Univariate Joint Modeling Analysis

Our univariate joint modeling analysis found that every 1 cm H₂O increase in ΔP was associated with a 1.079-fold increase in risk in the hazard of ICU mortality during IMV (HR, 1.079 [95% credible interval, 1.056–1.103]; p < 0.001). A 1-hour increase in exposure to ΔP greater than or equal to 15 cm H₂O was found to be associated with a 1.002-fold increase in the risk in the hazard of ICU mortality (HR, 1.002 [95% credible interval, 1.001–1.003]; p < 0.001) (Table 2).

Results of the Multivariate Joint Models

In the first standard (“value-only”) multivariate joint model adjusting for six other time-varying variables, we observed ΔP to be strongly associated with the hazard of ICU mortality (HR, 1.035 [95% credible interval, 1.004–1.069]; p = 0.021) (Table 2). Increased Spo₂ (HR, 0.82 [95% credible interval, 0.798–0.843]; p < 0.001), Pao₂/Fio₂ ratio (HR, 0.992 [95% credible interval, 0.989–0.996]; p < 0.001), and arterial pH (HR, 0.67 [95% credible interval, 0.6–0.759]; p < 0.001) were associated with a lower risk in the hazard of ICU mortality. On the other hand, respiratory rate (HR, 1.009 [95% credible interval, 1.002–1.016]; p = 0.016) and Paco₂ (HR, 1.038 [95% credible interval, 1.011–1.065]; p = 0.008) were independently associated with an increased hazard of ICU mortality. V_T/PBW (HR, 1.019 [95% credible interval, 0.933–1.106]; p = 0.627) was not found to be strongly associated with the hazard of ICU mortality in the multivariate model. In model 2, the normalized area of ΔP (HR, 1.032 [95% credible interval, 0.986–1.078]; p = 0.117) has a small effect (Table 2).

We compared model fit of the joint models based on measures of model fit (WAIC and DIC). Both metrics indicate that model 1 has the best predictive performance (Supplementary Table 2, http://links.lww.com/CCX/B301).

DISCUSSION

Through a multivariate joint modeling framework, we were able to combine survival data with real-time ventilation and gas-exchange information from intubated patients with concurrent COVID-19 and ARDS. Our approach builds on previous studies linking baseline ΔP with the hazard of ICU mortality in patients with non-COVID-19 ARDS by using a more powerful multivariate approach and by incorporating dynamic data at higher resolutions. Similar to previous findings in non-COVID-19 ARDS, our study finds ΔP to be a vital IMV parameter to monitor in patients with concurrent COVID-19 and ARDS which, with modern ventilation technologies can be more conveniently and consistently done in a continuous, automatic monitoring mode rather than as manual, spot static measurements. Use of this dynamic ΔP can allow clinicians to more promptly detect and address the current status of patients’ ΔP levels.

In this study, we observed a cumulative effect over time; every additional hour of exposure to potentially harmful levels of ΔP (≥ 15 cm H₂O) was associated with an increased risk in the hazard of death in the ICU. Our standard, multivariate joint model found a 1 cm H₂O increase in ΔP to be independently associated with a 1.035-fold increase in the hazard of ICU death in patients with concurrent COVID-19 and ARDS after adjustment for other relevant time-varying ventilation and gas-exchange variables. If we normalize this 1.035-fold hazard ratio (HR) from 1 cm H₂O to 7 cm H₂O (i.e., exp [7*log(1.035)] = 1.11), we find that this is similar to the 1.27 relative risk reported by Amato et al (10). This validation increases our confidence that our models correctly estimated the strength of the association.

Tension pneumothorax is a rare, life-threatening ARDS complication resulting in an alveolar rupture potentially due to increased ΔP (31–33). Tension pneumothorax is a critical target for early identification by dynamic clinical decision support (CDS) tools as it is a potential cause of abrupt decompensation if not intervened upon (32, 33). We observed a 104-fold increase in the hazard of ICU death, which makes sense from the literature where we see a 39% mortality rate for patients with ARDS compared with a 91% mortality rate with for patients with tension pneumothorax (2, 32). These patients require immediate intervention. The rarity of the tension pneumothorax event, both in terms of number of patients, but also in terms of how often the signal shows up within individual patients leaves us with a small sample size to work with. Although small sample size is problematic for frequentist statistics, our Bayesian joint models could potentially have smaller credible intervals than what is reported here with the selection of more appropriate priors (34). Computerized CDS interventions or predictive tools aiming to reduce patients’ exposures to high levels of ΔP may be augmented by considering the dynamic ΔP value at the current time point.

Paco₂ and measured respiratory rate were found to be independently associated with increased mortality risk; while an increase in Spo₂, Pao₂/Fio₂, and arterial pH were associated with decreased risk of ICU mortality. After adjusting for ΔP, tidal volume per predicted body weight was not found to be significantly associated with mortality. Given that there was high adherence to lung-protective ventilation (mean V_T/PBW ~5.9) in patients with concurrent COVID-19 and ARDS in this study, this is not unexpected.

Increased adoption of modern ventilators capable of dynamically measuring ΔP presents new opportunities for the development of interventions, strategies, and tools that operate in real time. For instance, the development of a tool that can accurately forecast a patient’s ΔP at future timepoints and make clinical recommendations based on this predicted trajectory may be clinically valuable.

Our study has a few important limitations. Although we manually validated 10% of COVID-19 ARDS cohort as meeting the criteria for ARDS according to the Berlin Criteria (23), the remaining patients were identified with ARDS using ICD-10-CM codes. ICD-10-CM codes may not be completely sensitive and specific, as has been seen with ARDS which is often underdiagnosed for this reason (35). Applying looser criterion dropping the requirement for ICD-10-CM code J80 to be included but necessitating a PF ratio less than 300 mm Hg and a measured PEEP greater than equals to 5 cm H₂O yielded only 27 additional potential patients, of which 6 decompensated in the ICU, to consider for inclusion in the cohort (36). A more sophisticated automated search strategy to identify ARDS patients per the Berlin Criteria could be developed to carry out such a task in a future study. A secondary limitation is that this study was conducted solely on patients within a single-healthcare system (although encompassing different hospitals within this system); differences in clinical protocols and devices with other healthcare systems may limit generalizability of our findings. Replication of our methods using patient cohorts from other hospitals, and with larger sample sizes will be valuable in strengthening the findings of this study. Additionally, the data used in this study are from nearer the start of the pandemic, reflecting the virus’ morphology and characteristics closer to its original state. Further studies need to be conducted to validate the results of this study in emerging COVID-19 variants and potentially in non-COVID-19 ARDS cohorts as well. Future studies may also leverage more sophisticated joint models; for example, a weighted cumulative effects model wherein values of ΔP are weighed differently across different time points, for example, more recent values of ΔP are given differentially greater weighting (37). Or, investigate the potential of these ΔP-based joint models for dynamic, patient-level survival prediction (38).

CONCLUSIONS

ΔP is a critical parameter to monitor in intubated patients with COVID-19 ARDS. Cumulative exposure to higher intensities of ΔP (≥ 15 cm H₂O) is harmful and should be limited if possible. To gain a more comprehensive monitoring of a COVID-19 ARDS patient’s respiratory condition, it would be beneficial to consider the value of dynamic ΔP at a given time point. Strategies or interventions that can harness the power of high-granularity data integration from real-time ventilator physiology data monitoring at the bedside may help limit exposure to high ΔP levels linked to mortality.

ACKNOWLEDGMENTS

We thank members of the Li Zhou’s Research Lab group at Brigham and Women’s Hospital for their contributions to data preparation and continued support throughout this project.

Supplementary Material

cc9-6-e1043-s001.docx ^{(427.7KB, docx)}