Melt electrowriting enabled 3D liquid crystal elastomer structures for cross-scale actuators and temperature field sensors

Abstract

Liquid crystal elastomers (LCEs) have garnered attention for their remarkable reversible strains under various stimuli. Early studies on LCEs mainly focused on basic dimensional changes in macrostructures or quasi–three-dimensional (3D) microstructures. However, fabricating complex 3D microstructures and cross-scale LCE-based structures has remained challenging. In this study, we report a compatible method named melt electrowriting (MEW) to fabricate LCE-based microfiber actuators and various 3D actuators on the micrometer to centimeter scales. By controlling printing parameters, these actuators were fabricated with high resolutions (4.5 to 60 μm), actuation strains (10 to 55%), and a maximum work density of 160 J/kg. In addition, through the integration of a deep learning–based model, we demonstrated the application of LCE materials in temperature field sensing. Large-scale, real-time, LCE grid–based spatial temperature field sensors have been designed, exhibiting a low response time of less than 42 ms and a high precision of 94.79%.

Melt electrowriting creates LCE micrometer- to centimeter-scale 3D actuators and deep learning–based temperature field sensor.

INTRODUCTION

Liquid crystal elastomers (LCEs), composed of cross-linked polymer networks embedded with liquid crystal molecules, have attracted substantial attention in the fields of soft robotics (1), artificial muscles (2), microelectromechanical systems (3), and biomedical applications (4, 5). This can be attributed to their capability to undergo substantial reversible strain (~40%) and programmable shape transformations under various stimuli, including heat (6), light (7–9), electric fields (10), and magnetic fields (11). When cross-linked in a mono-domain, LCEs can reversibly contract in isotropic phases and elongate in nematic phases at transition temperature.

Early studies on the LCE-based actuators primarily focused on basic dimensional changes in macrostructures or quasi–three-dimensional (3D) microstructures (12), such as fiber or film actuators (13–15), pillar arrays (16, 17), and micropatterns (18, 19). In recent years, 3D printing has emerged as a promising technique for fabricating LCE complex geometries of various sizes (20). For instance, the direct ink writing technique deposits millimeter-scale LCE filaments layer by layer to construct centimeter-scale 3D geometries (20–22). In addition, the two-photon polymerization 3D printing technique provides a high resolution of approximately 40 nm, facilitating the fabrication of micrometer-scale intricate objects (23). Furthermore, the digital light processing printing technique enables the fabrication of 3D structures with a hundred-micrometer-level resolution and a macroscopic architecture (24, 25). However, the fabrication of 3D LCE-based cross-scale complex hierarchical structures, spanning from micrometer to centimeter scales, remains exceptionally challenging. Moreover, simultaneous direct orientation and alignment of LCE mesogens in situ, which can significantly improve the feasibility and versatility of LCE-based applications, increase fabrication complexity (26).

To address the aforementioned challenges, this study demonstrated the use of melt electrowriting (MEW) in creating LCE-based microfibers, quasi-3D units, and macroscope 3D structures and demonstrates their capabilities as thermal-responsive cross-scale actuators and spatial temperature field (STF) sensors. MEW is a high-resolution additive manufacturing technique based on the layer-by-layer construction of microfibers that is driven and extruded from a nozzle by applying a high voltage between the nozzle and the substrate (27–30). By controlling printing parameters, including the air pressure, printing speed, temperature, and nozzle size, LCE microfibers with different diameters, ranging from 4.5 to 60 μm, and tailorable properties, including actuation strain of 10 to 55%, actuation stress of 0 to 0.6 MPa, and high work density of 160 J/kg, were printed. These LCE microfiber actuators provided significant mechanical output, lifting and lowering a weight more than 3500 times heavier than themselves under dynamic thermal airflow stimulus at a frequency of 15 Hz. By depositing the LCE microfibers along preprogrammed paths, this study achieved a wide range of 3D actuators spanning from the microscale to the macroscale, including elementary structural units, gradient-responsive LCE wall structures, a 3D spring-shaped actuator, a 1-mm microgripper, and various 3D macrolattice structures. In addition, their deformation responses to the thermal airflow stimulus were demonstrated.

Furthermore, by leveraging the rapid and reversible deformation of the LCE microfiber-based structures when exposed to a dynamically changing thermal airflow, we developed an STF sensor. This sensor, based on a deep learning (DL) model, exhibited a large area (centimeter scale), real-time performance (a 24-Hz sampling frequency), exceptional accuracy (nearly 94.79%), and fine spatial resolution reaching 4 mm. To the best of our knowledge, this is the first application of LCE materials to the field of temperature field sensor. By incorporating the DL techniques, the proposed straightforward but remarkably effective strategy could further advance previously unidentified design, fabrication, and applications of stimulus-responsive smart materials.

RESULTS

MEW-printed LCE microfibers

The MEW technique is a high-resolution 3D printing method based on the layer-by-layer stacking of microfibers, as illustrated in Fig. 1A. The printing LCE ink used in this study was prepared using the Michael addition reaction between liquid crystal mesogens RM257 and chain extender 2,2′-(ethylenedioxy) diethanethiol (EDDET). More information on the ink preparation process can be found in Materials and Methods and fig. S1.

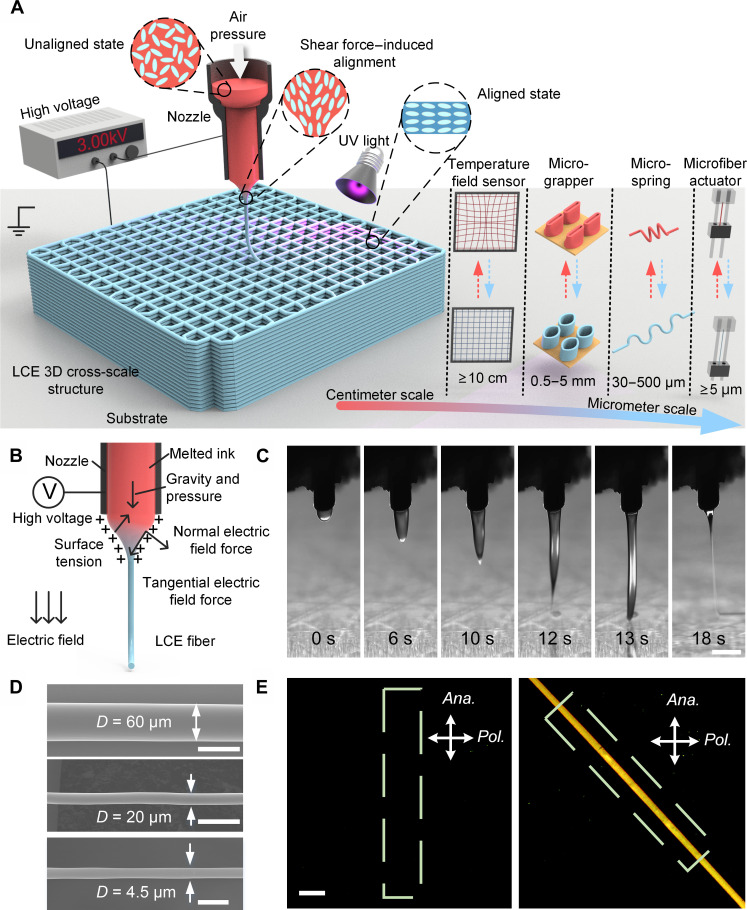
Fig. 1. The 3D MEW-printed LCE microfibers.

(A) Schematic illustration of 3D MEW-printed LCE microfibers and 3D cross-scale structures. A high voltage of 2 to 3 kV was applied between a metal nozzle and the substrate. The melted LCE ink in an unaligned state was driven out of the nozzle to form Taylor cones and fine jets. The powerful shear force inside the Taylor cones gradually aligned and oriented the mesogens of LCE microfibers, which were deposited along preprogrammed paths on the substrate to construct various cross-scale 3D structures. (B) Schematic illustration of the generation of the shear force inside the Taylor cone during the MEW process. (C) Dynamic formation process of Taylor cones and stable LCE microfibers during the MEW process. Scale bar, 500 μm. (D) SEM images of MEW-printed LCE microfibers with different diameters. Scale bars, 50 μm (D = 60 μm and D = 20 μm) and 10 μm (D = 4.5 μm). (E) POM images of the LCE microfibers with aligned mesogens at two different angles relative to the analyzer. Scale bar, 100 μm.

During the printing process, the prepared LCE ink was loaded into a syringe with a metal nozzle with a diameter of 26, 28, or 30 gauge and then placed inside the heating chamber of a self-developed 3D MEW printer (fig. S2). The temperature of the heating chamber varied from 60° to 120°C, with the pressure maintained at 0.2 MPa to extrude the LCE ink through the nozzle. By applying high voltage (2 to 3 kV) to the metal nozzle and grounding the substrate, we created an electric field, which charged the suspended LCE droplets at the nozzle and induced the accumulation of charges on the conical droplet surface. In accordance with the principles of electrohydrodynamic printing (31), the molecules on the surface of the LCE droplets experience electric field forces in both normal and tangential directions, the downward force of gravity, the air pressure exerted by the printer’s air pump, surface tension, and the internal viscosity force within the LCE droplet, as presented in Fig. 1B. With the accumulation of LCE ink at the nozzle, it was attracted to the substrate due to the electric field, thus establishing a Taylor cone, as shown in Fig. 1C. When the electric field force surpassed the surface tension at the tip of the cone, the tapered jet elongated and became thinner and, finally, deposited onto the substrate, and a stable LCE microjet was gradually established, as presented in fig. S3. As shown in the camera view in Fig. 1C and movie S1, the entire process lasted for approximately 20 s. Subsequently, along the designated paths, the resulting microfiber could be used to stack and form 3D structures. By carefully changing the printing conditions, the diameter distribution of the produced MEW LCE microfibers, which ranged from 4.5 to 60 μm, could be precisely controlled (Fig. 1D).

It should be noted that in situ orientation and alignment of the LCE mesogens can also be achieved during the MEW process through the generation of a significant amount of shear force in the Taylor cone. As illustrated in Fig. 1B, the accumulation of charges led to the increase in flow velocity at the surface, which exceeded that of within the jet (32, 33). This facilitated the formation of axial orientation and alignment of the 1D materials, such as nanowires (34), within the jet, resulting in a monodomain state as shown in Fig. 1E. For a monodomain LCE microfiber, when the axial direction of the microfiber is parallel to the polarizer or the analyzer of polarized optical microscopy (POM), the brightness observed was minimum (Fig. 1E, left). In contrast, the brightness increases greatly when the alignment direction is 45° with respect to the polarizer (Fig. 1E, right), indicating good alignment of the LCE mesogens.

Fast-responsive LCE microfiber actuators with tunable actuation performance

We used the MEW to deposit LCE microfibers with different diameters and thermal-induced strains at specified locations, enabling the fabrication and deployment of fiber actuators. Figure 2A shows an LCE microfiber array with a constant diameter of 30 μm, while Fig. 2B displays an LCE microfiber array with varying diameters of 30, 40, and 50 μm. Figure S4 illustrates a single LCE microfiber in a scanning electron microscopy (SEM) image. Precise control of the diameter and thermal-induced strain of the LCE microfibers was achieved by controlling the printing speed, printing temperature, applied voltage, air pressure, and nozzle size, with printing speed and printing temperature being the two most important factors influencing fiber diameter and thermal-induced strain. For a fixed printing nozzle, the printing temperature and air pressure jointly affected the extrusion rate of the LCE ink. Therefore, a constant air pressure of 0.2 MPa was maintained during the printing process. In addition, the printing voltage was in the range of 2 to 3 kV, and a nozzle-to-substrate distance of 2 mm was maintained to ensure a stable high-voltage electric field.

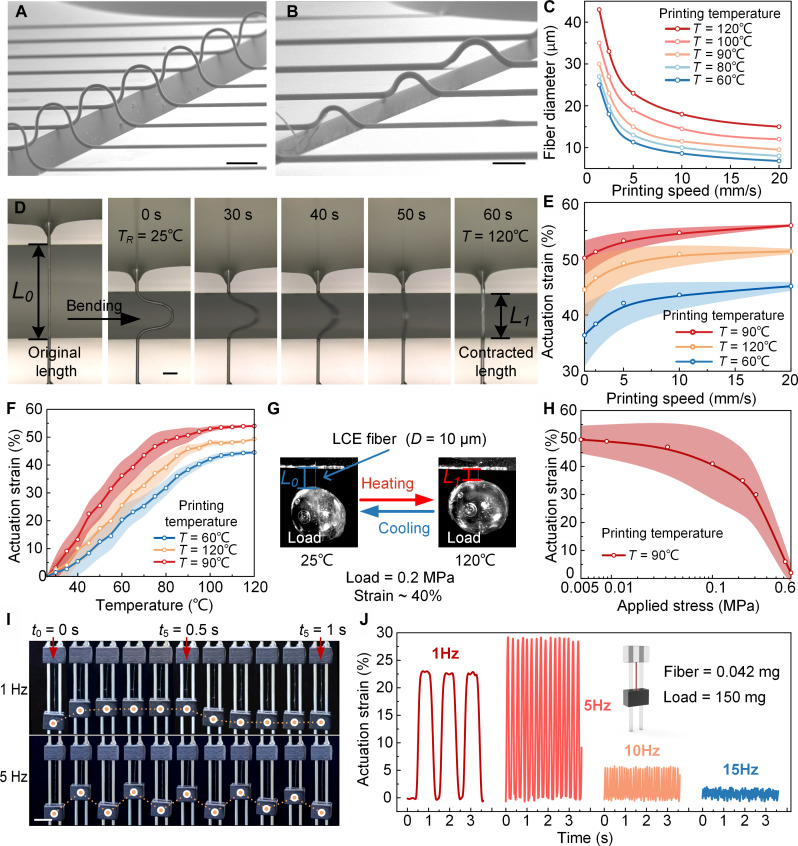
Fig. 2. The MEW-printed LCE microfiber actuators.

(A) The LCE microfiber array with the same diameter of 30 μm was fabricated by MEW. Scale bar, 300 μm. (B) LCE microfiber array with diameters of 30, 40, and 50 μm. Scale bar, 200 μm. (C) LCE microfiber diameter versus printing speed at five printing temperatures. (D) Actuation strain test and the dynamic thermal contraction process of a single LCE microfiber. Scale bar, 50 μm. The LCE microfiber was directly printed onto two adjustable glass slides. The gap distance between the slides was increased until the microfiber was straightened, and then the original length (L₀) of the microfibers was measured. By decreasing the gap distance, the LCE microfiber was bent. Next, the LCE microfiber was heated at a temperature of approximately 120°C, and the gap distance was adjusted until the microfiber was straightened again, and then its contracted length (L₁) was measured. (E) Actuation strain of the LCE microfiber printed at five different printing temperatures versus the printing speed. (F) Actuation strain versus the temperature of single-LCE microfibers printed at different printing temperatures. (G) Actuation stress measurement method of LCE microfibers. The UV-curable adhesive droplet was used as a load. The LCE microfiber with the adhesive droplet was placed inside an oven and heat up to 120°C for actuation stress testing. (H) Actuation strain of the LCE microfibers as a function of the applied actuation stress. (I) Rapid response capability testing of the LCE microfiber actuators at various frequencies. Scale bar, 5 mm. (J) Actuation strain of the LCE microfiber actuator that drives a slider that is 3500 times heavier than it, continuously lifting it up and down under thermal airflow stimuli at frequencies of up to 15 Hz.

The printing temperature was set on the basis of the differential scanning calorimeter (DSC) test results of the LCE ink, as presented in fig. S5. The glass transition temperature (T_g) and the nematic-isotropic phase transition temperature (T_NI) of the LCE ink were −23.37° and 48.37°C, respectively. Therefore, a series of different printing temperatures (i.e., 60°, 80°, 90°, 100°, and 120°C) were used to analyze the variations in microfiber diameter and performance. It should be noted that after the LCE ink was printed and cured by the ultraviolet (UV) light, the T_g and T_NI values increased to −13.11° and 75.22°C, respectively. These temperature changes were used as reference values in the actuation strain tests of the LCE microfiber actuators and 3D cross-scale actuators.

As shown in Fig. 2C, the diameter of the LCE microfiber decreased when the printing speed increased or when the printing temperature decreased. In the experiments, a minimum diameter of 4.5 μm was achieved for the MEW-printed microfiber using a 30-gauge nozzle, with a printing speed of 20 mm/s and a printing temperature of 60°C, as shown in fig. S6. In contrast, the maximum diameter of the fabricated microfiber was 60 μm, which was obtained using a 26-gauge nozzle, with a printing speed of 1 mm/s and a printing temperature of 120°C. It is therefore expected that LCE microfibers of larger diameters can be fabricated using nozzles of larger inner diameters.

The method used to measure the actuation strain of a single LCE microfiber actuator is presented in Fig. 2D. The LCE microfiber was printed directly onto two adjustable glass slides. The gap distance between the slides was increased until the microfiber was straightened, and then, the original length (L₀) of the microfibers was measured. By decreasing the gap distance, the LCE microfiber was bent. Next, the microfiber was heated to approximately 120°C, and the gap distance was adjusted until the microfiber was straightened again, and then, its contracted length (L₁) was measured. Therefore, the actuation strain could be defined and calculated as follows: ε = (L₀ − L₁)/L₀. More details can be found in movie S2. The actuation strain of the fiber actuator gradually increased with the printing speed and finally reached a stable value, as displayed in Fig. 2E. At a printing temperature of 90°C, the actuation strain of the actuator reached its maximum value of approximately 55% when the printing speed was higher than 5 mm/s, as shown in fig. S7 and movie S2.

When the printing temperature was lower than 90°C, increasing the printing temperature could reduce the viscosity of the LCE ink and thus facilitate the alignment of LCE mesogens during MEW. Notably, despite the heating chamber temperature being set at 90°C, the temperatures at the nozzle and the printed LCE microfiber decreased to approximately 40°C (fig. S8), which was below the T_NI. This indicated that the aligned LCE mesogens in the microfiber were securely fixed in their positions and would not revert to an isotropic state. However, when the printing temperature was higher than 90°C, the flowability of LCE ink increased (fig. S9), leading to a reduction in the alignment and consequently a reduction in the strain of the LCE microfiber. The printing temperature was therefore set to 90°C.

To investigate the thermal-induced actuation strain of the LCE microfibers versus ambient temperature, the microfibers were heated in a controlled manner in an oven and the changes in the LCE microfibers’ length were measured, as shown in Fig. 2F. As the oven temperature gradually increased and exceeded 100°C, the actuation strain showed a gradual increase and eventually reached a plateau at 120°C. The MEW-printed LCE microfibers exhibited thermal responsiveness even at low temperatures of 30°C. This could be attributed to the highly efficient thermal convection of microfibers due to the small size of LCE microfiber. Consequently, these findings provide valuable guidelines for the development of temperature field sensors with a wide detection range from 25° to 110°C, as demonstrated in the following context.

Similar to the microfiber actuators, the strain of the LCE fibers was also measured under different loads (stresses), as shown in Fig. 2G. The LCE microfibers were printed on glass slides and cured. A large drop of UV curable adhesive was applied to the LCE fiber as a load, and it was solidified using a UV lamp to firmly attach the adhesive droplet to the LCE fiber. Then, together with the adhesive droplet, the LCE fiber was peeled off and suspended, connecting it to the glass slides. The weight of the adhesive droplet was measured using a precision balance, and the fiber diameter was measured using SEM microscopy. This allowed the stress on the LCE fiber to be calculated. As shown in Fig. 2H, when the applied load was small, the strain of the LCE microfiber actuator remained unaffected. However, at an actuation stress of 0.6 MPa, the microfiber actuator still exhibited a strain of about 3%, which exceeded that of mammalian skeletal muscle of 0.35 MPa (35). Moreover, the actuation stress and strain of the actuators were independent of the microfiber diameter, as presented in movie S3.

Notably, the microfiber actuators demonstrated exceptional actuation durability under external loading, with a rapid temperature sensing capability due to the highly efficient thermal convection and conduction of the LCE fibers (Fig. 2, I and J, and movie S4). A slider was placed between two metal rails, and the LCE microfiber was suspended to lift the slider, allowing it to move rapidly up and down under thermal airflow stimuli. A tensile stress of 0.4 MPa was applied to the microfiber actuator (length: 10 mm, diameter: 22 μm, and weight: 0.042 mg) by a slider load of 150 mg (fig. S10). In previous studies, the external load applied to the LCE actuators in the durability tests typically did not exceed tensile stress of 0.1 MPa (36). As a result, when the LCE microfibers were exposed to a thermal airflow at approximately 120°C with a frequency of 1 Hz, they contracted in 0.2 s, with a 23% reduction in length, while lifting the ultraheavy load that was 3500 times larger than their weight.

When the frequency reached 5 Hz, a resonance phenomenon occurred, causing a significant increase in the strain of the microfiber actuator to approximately 30%. Even at a high frequency of 15 Hz, the microfiber actuator was able to cyclically lift and lower the load with a strain of about 2% in a rapid response time of less than 33 ms. In addition, a long-term durability test conducted at a frequency of 10 Hz revealed that the microfiber could maintain its actuation strain without significant signs of fatigue even after 10,000 cycles, as shown in fig. S11. However, it should be noted that above a thermal airflow frequency of 15 Hz, the dispersion of the thermal airflow required more time, resulting in less noticeable temperature changes in the air. In view of this, tests at higher frequencies were not conducted.

3D high-resolution MEW-printed LCE elementary structural units with graded size and actuation strain

As an additive manufacturing technology, the MEW enables precise deposition of LCE microfibers with different diameters along preprogrammed paths, which facilitates the layer-wise construction of complex 3D objects by computer-aided design. By manipulating various printing parameters, 3D structures were successfully fabricated with predictable and programmable graded sizes and functional changes. The layer-wise printing process of the 3D LCE structures is illustrated in Fig. 3A, where it can be seen that the initial layer of the LCE microfiber was deposited on the substrate, spreading outward and forming a semicircular cross section within the microfiber. Next, the LCE microfibers were continuously deposited and spread out on top of the previous ones, which ensured strong adhesion between adjacent microfibers.

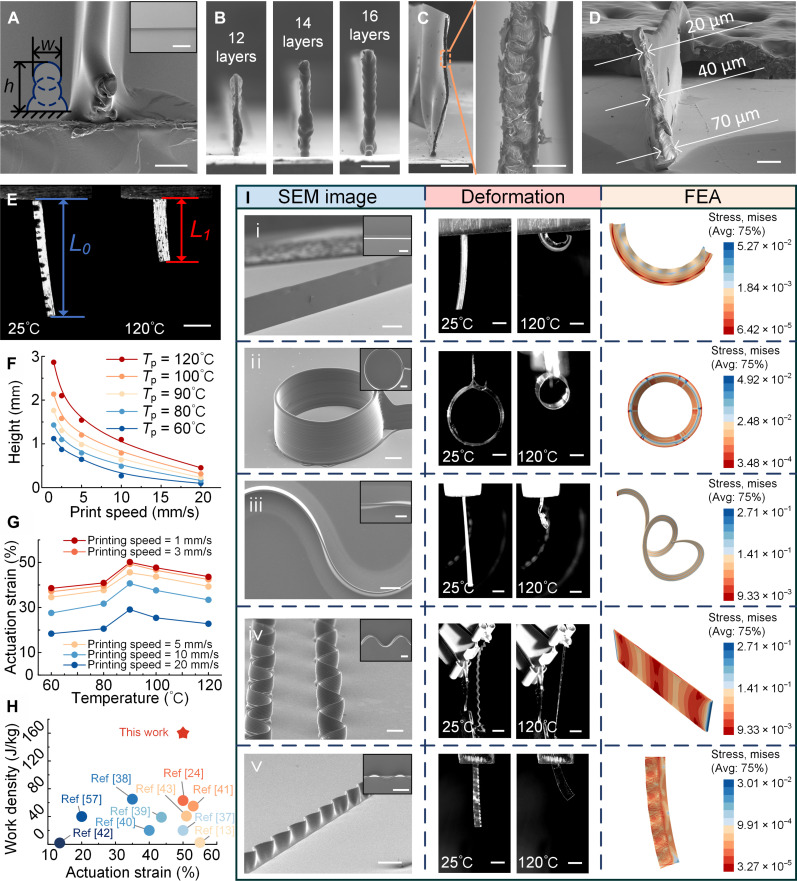
Fig. 3. The 3D MEW-printed LCE elementary structural units with graded size and actuation strain.

(A) SEM image of the cross section of the three-layered LCE wall structure. Scale bar, 50 μm (inset SEM image) and 1 mm. (B) SEM images of three LCE wall structures with different layer numbers (12, 14, and 16 layers). Scale bar, 300 μm. (C) SEM images of the cross section of the 3-mm-high LCE wall structure. Scale bars, 600 μm (left) and 50 μm (right). (D) SEM image of the cross section of the LCE wall structure with varying width (70 to 20 μm). Scale bar, 100 μm. (E) Photograph sequences of the LCE strip unit captured at room temperature and 120°C. Scale bar, 2 mm. (F) Height of printed LCE wall structures as a function of the printing speed and printing temperature. (G) The actuation strain of the LCE wall structures is a function of the printing speed and printing temperature. (H) Ashby plot of work density versus the actuation strain of the MEW-printed LCE actuator, human muscle (57), and other actuators (13, 24, 37–43). (I) Several LCE elementary structural units with graded size and actuation strain, including the LCE strip with varying actuation strain (first row), the LCE cylindrical structure (second row), the LCE spring-shaped structure (third row), the sinusoidal LCE structure (fourth row), and the size-graded sinusoidal LCE curved strip (last row). The leftmost column displays SEM images of structural units, detailing their physical characteristics. The middle column shows photographic sequences of LCE units captured at room temperature and 120°C, demonstrating their thermal response. The rightmost column presents FEA results, predicting the shape-morphing behavior of functionally graded LCE units. Scale bars, 500 μm (SEM images) and 200 μm (photograph sequences).

Precision control over dimensions could be achieved through MEW. As demonstrated in fig. S12, through the repetitive deposition of microfibers in a back-and-forth manner at specific locations, the LCE wall structures with high aspect ratios were fabricated, where the height could be accurately controlled. Three wall structures of 12, 14, and 16 layers were printed using identical printing parameters, as shown in Fig. 3B. The height differences between these structures were consistent, and the wall structures exhibited uniformity and structural integrity over a centimeter scale, as shown in fig. S13. The tallest MEW-printed wall structure here is shown in Fig. 3C with a measured height of approximately 3 mm and a width of 30 μm, resulting in an aspect ratio of 100. This aspect ratio surpassed that achievable with conventional 3D electrohydrodynamic printing methods, which typically yield wall structures with an aspect ratio below 60 (30). In particular, even for tall structures, the adhesion between the internal LCE microfibers remains robust, and no noticeable step-like effects were observed in the cross-sectional view, as demonstrated in Fig. 3C. Furthermore, by adjusting the printing speed during the printing process, wall structures with gradient changes in diameter could be fabricated. As shown in Fig. 3D, the LCE wall structure exhibited a gradual width change, from 70 to 20 μm, with the microfibers firmly adhered to each other without noticeable defects.

All the MEW-printed 3D LCE structures were able to contract under thermal stimuli, as demonstrated in Fig. 3E and movie S5. The LCE wall structures show a maximum strain of up to 50%. The capability of the fabricated LCE structures with both programmable stimuli-responsive properties and designable 3D geometry is shown in Fig. 3 (F and G). The effects of printing temperature and printing speed on the dimensions and actuation performance of the LCE structures were also investigated. To speed up the printing process, a relatively large 26-gauge printing nozzle was used to fabricate all 3D structures. By reducing the printing speed or increasing the printing temperature to reduce ink viscosity, the diameter of deposited fibers could be effectively increased, allowing the rapid fabrication of large-sized 3D structures, as shown in Fig. 3F. Similar to the microfiber actuators, the thermal response of the LCE walls also reduced when the printing temperature exceeded 90°C, as shown in Fig. 3G. However, unlike the microfiber actuators, for the LCE walls, the increase in the printing speed was accompanied by a decrease in the strain. The maximum thermal strain of approximately 50% in the LCE walls was achieved at a printing speed of 1 mm/s and a printing temperature of 90°C. This phenomenon can be attributed to the layer-wise stacking of LCE fibers at higher printing speeds, which impeded sufficient curing time. Consequently, increased rubbing and compression between adjacent LCE microfibers occurred, leading to the disordering of the mesogens at the microfiber edges and a subsequent reduction in the actuation strain of the LCE walls. At the same printing temperature (i.e., 90°C), when the printing speed was increased to 20 mm/s, the resulting LCE wall structures exhibited an actuation strain of approximately 25%. This finding opens up possibilities of constructing 3D LCE structures with graded changes in both sizes and functionality.

The MEW-printed LCE walls exhibited remarkable reversible deformations, making them suitable for use as actuators and artificial muscles. The photographic images of the LCE actuators (0.52 mg) lifting a 2-g load, which exceeded their weight by 3800 times, with a strain of about 24%, and work density reaching its highest value of 160 J kg⁻¹, were displayed in fig. S14. The lifting process is presented in movie S5. Work density represents a key performance metric for actuators and robotic applications. The Ashby plot, which is shown in Fig. 3H, can be used for a comparative analysis of the work density, actuation strain, and corresponding resolution of the human muscles, MEW-printed LCE actuators, and other types of LCE actuators. Currently, some LCE actuators can achieve large reversible deformations of nearly 50% under various stimuli (13, 37, 38), which is similar to the findings of this study. However, the LCE actuator presented in this study exhibited a substantially higher maximum work density of 160 J kg⁻¹ compared to the human muscles and previously reported LCE actuators (24, 38–42), which are all below 70 J kg⁻¹. Regarding the manufacturing process and resolution, most LCE actuators generally have a resolution in the submillimeter range, such as direct writing (39, 43), and only the two-photon direct laser writing (40) can achieve relatively small resolutions (2.9 μm), but its work density is limited to 20 J kg⁻¹. The proposed MEW technology enables the fabrication of complex 3D structures ranging from the micrometer to centimeter scale, with a remarkable resolution of 4.5 μm, superior work density, and actuation strain performance.

Next, several elementary structural units with graded sizes and actuation strains were printed, as shown in Fig. 3I. Their SEM images, photographic sequences at room temperature and 120°C, and finite-element analysis (FEA) results were demonstrated in Fig. 3I. The dynamic contraction processes of the LCE elementary structural units and the comparative FEA images of the structural units’ deformation before and after heating were also reported in movie S6 and fig. S15.

As shown in Fig. 3Ii, when heated up to 120°C, the LCE strips were under imbalanced strain (20% strain on the left and 50% strain on the right), resulting in curling and the formation of an arc-shaped structure. Notably, the excessive strain on the right side led to a wavy-shaped curled appearance in the LCE strip, as demonstrated by both the experimental result and the corresponding FEA analysis in Fig. 3I and fig. S15. Figure 3Iii showcases the thermal actuation of a LCE cylindrical structure. The cylinder with an initial diameter of 4 mm contracted to nearly 2.3 mm in diameter when it was heated to 120°C, which resulted in a 42% reduction in circumference and a 66% decrease in cross-sectional area. Furthermore, several cylindrical structures with different diameters, including a pyramid-shaped cylindrical structure with a gradually decreasing diameter and a gourd-shaped cylindrical structure whose diameter first decreased and then increased, are presented in fig. S16.

Interestingly, when combining the two aforementioned LCE elementary structural units, i.e., the LCE strip with varying strain and the LCE cylindrical structure, the S-shaped structure was created, as shown in Fig. 3Iiii and fig. S17. This S-shaped structure exhibited different strains on its left (30%) and right sides (50%). In the quasi-3D S-shaped cylindrical structure, each arc-shaped unit underwent wave-shaped curling, which resulted in the formation of a spring-like 3D structure. The overall actuation strain reached a remarkable value of 65%.

Images in the fourth row of Fig. 3I show a sinusoidal LCE structure. When the two ends of the LCE curved strip were fixed, the structure contracted into a straight strip upon heating to 120°C. The last row presents a size-graded sinusoidal LCE curved strip, having straight microfibers at the bottom and sinuous microfibers with a gradually increasing curvature toward the top. The photographic sequences and FEA images demonstrated the contraction of the size-graded structure, whose curved segments tended to straighten, which was similar to the behavior shown in the fourth row. However, since the curved microfibers were longer than the straight microfibers, the overall structure bent toward the straight sides. Because of this unique actuation capability, the sinusoidal curved LCE unit was used to create 3D microgrippers, which will be further explained in the following section.

3D MEW-printed flytrap-inspired LCE microgrippers and 3D lattice structures

Venus flytrap has captivated scientists with its remarkable ability to close its two leaves automatically and capture insects within a subsecond upon mechanical stimulation (Fig. 4A) (44). Inspired by the flytrap, this study combined and fabricated two LCE sinusoidal walls, resembling the leaves of the flytrap layer by layer on a substrate. During the MEW printing process, the two sinusoidal walls intersected and adhered to each other at zero-crossing positions, as shown in Fig. 4B and fig. S18. In this way, an array of microgrippers was formed, where each small cavity represented an individual LCE microgripper.

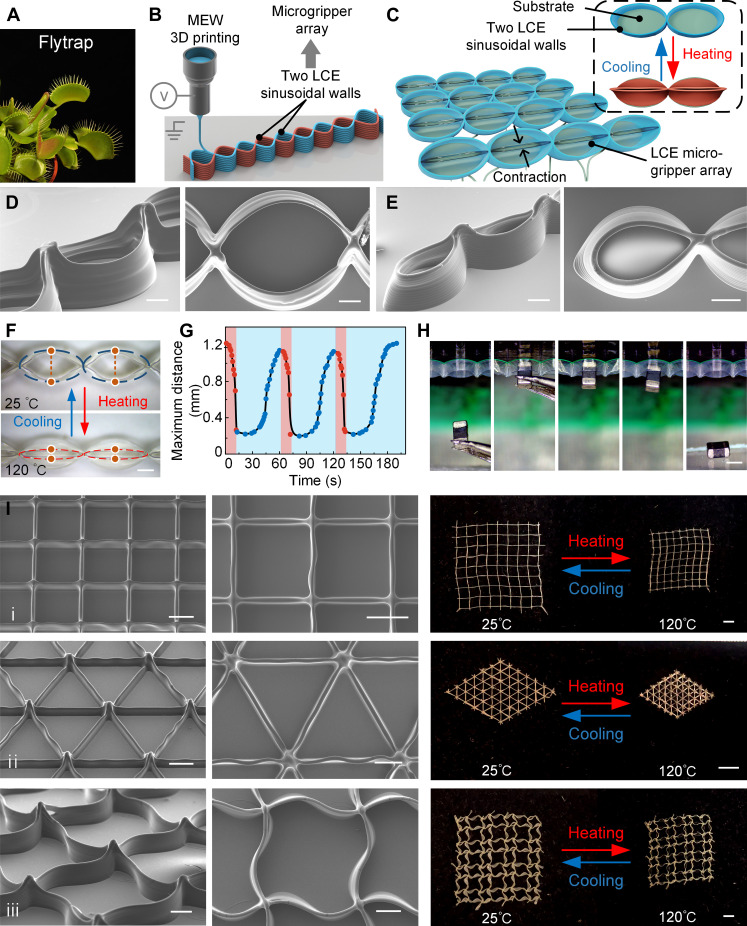
Fig. 4. The 3D MEW-printed flytrap-inspired LCE microgrippers and 3D lattice structures.

(A) Venus flytraps in their closed or open states. (B) Schematic diagram of the LCE microgripper fabrication by MEW. (C) Schematic diagram of the reversible switching process between the open and closed state of the MEW-printed LCE microgripper. (D) SEM images of the LCE microgrippers with a length of 3 mm and a width of 2 mm. Scale bar, 500 μm. (E) SEM images of the LCE microgripper with a length of 1.5 mm and a width of 1 mm. Scale bar, 500 μm. (F) Photographs of the thermal-responsive LCE microgripper in the open and closed states. Scale bar, 500 μm. (G) Cyclic test, where the maximum distance between the two claws of the LCE microgripper changed with time. The maximum distance denoted the distance between the upper and lower points marked on a microgripper in (F). (H) Process of LCE microgripper grasping and subsequently releasing an inductor. The inductor had a length of 2 mm, a width of 1.2 mm, and a height of 0.5 mm. Scale bar, 1 mm. (I) 3D MEW-printed lattice structures. The left two columns display the SEM images of the lattice structures, and the rightmost column shows the photographs of the lattice structures before and after thermal contraction. A square lattice structure, a triangular lattice structure, and a quadrilateral lattice structure composed of sinusoidal curved LCE walls are shown in the first, second, and third rows, respectively. Scale bars, 500 μm (SEM images) and 2 mm (photograph).

The schematic diagram of the reversible switching process between the open and closed states of the MEW-printed LCE microgripper is displayed in Fig. 4C. The substrate of the microgrippers was fixed onto a heat plate, allowing for the adjustment of temperature to the heat of the microgrippers. After heating, the bottom of the LCE microgripper remained firmly adhered to the substrate without contraction. Meanwhile, the top of the microgripper experienced thermal contraction and gradually straightened due to balanced forces at the zero-crossing points of the LCE sinusoidal walls, leading to the closure of the microgrippers’ top, as illustrated in fig. S18. Details of the FEA simulations are presented in fig. S19. By adjusting the printing paths during the MEW process, the LCE microgripper arrays with different sizes could be created, as shown in Fig. 4 (D and E). In this study, small microgrippers, with 1.5 mm length, 1 mm width, and 1 mm height, were successfully fabricated, as shown in Fig. 4E. Additional SEM images of the microgripper arrays are provided in fig. S20.

This study defined the maximum distance as the greatest separation between the upper and lower parts of a microgripper, represented by the distance between two marked points on a single microgripper (Fig. 4F). The maximum distance quantifies the degree of opening or closing of a microgripper before and after heating. To assess cyclic consistency in structural deformations, the variation in the maximum distance over time was examined through cyclic testing, as presented in Fig. 4G and movie S7. The results indicated that the LCE microgrippers exhibited excellent cyclic consistency in structural deformations. The maximum distance decreased from approximately 1.2 to 0.2 mm, which represented a reduction of over 83%, indicating the LCE microgripper’s impressive ability to close and grip objects under thermal stimuli effectively.

Moreover, the gripping and release behavior of the LCE microgripper using a surface mount inductor as the grasping object was illustrated in Fig. 4H and movie S8. This inductor was a rigid rectangular solid with a length of 2 mm, a width of 1.2 mm, and a height of 0.6 mm. A single LCE microgripper weighed 0.3 mg, while the inductor weighted about 10 mg. The results indicated that the lifting ratio, defined as the ratio of the object mass to the gripper mass, exceeded 33. Typically, soft actuators have dimensions greater than 5 mm, and the size of grasped objects is greater than 1 mm (45). Because of the material softness, mechanical compliance, and reduced control complexity of LCE microgrippers fabricated using the MEW technology, it is believed that they could provide a reliable tool for handling solid and complex objects in the submillimeter to millimeter range, such as surface mount device, as mentioned in this study.

Next, the LCE elementary structural units were printed to fabricate 3D lattice structures with a different centimeter scale, as shown in Fig. 4I and movie S9, and their thermal contraction upon heating to 120°C was demonstrated. The first row of Fig. 4I presented a square lattice structure measuring 1.6 cm by 1.6 cm in length and width, where each square unit has a side length of 1 mm. After being placed inside an oven and heated to 120°C, this square lattice structure underwent uniform and proportional contractions. The second row presented a triangular lattice structure measuring 0.6 cm by 0.6 cm in length and width, where each unit has a side length of 1 mm. Last, the last row displayed a quadrilateral lattice structure composed of sinusoidal curved LCE walls measuring 1.6 cm by 1.6 cm in length and width, with each unit having a side length of 2 mm. After heating to 120°C, these two lattice structures also underwent proportional overall contraction. Moreover, as shown in the photographs, the 3D lattice structures showed remarkable structural uniformity over a significant planar area, demonstrating a precise deposition capability of the MEW for LCE microfibers along the predefined paths. The SEM images of the triangular lattice structure were also captured from various view angles (i.e., 45°, 60°, and 90°), as shown in fig. S21. The consistent appearance of lattice units in the vertical direction highlighted the exceptional fabrication ability of the MEW in terms of height direction.

LCE grids: Large-scale, real-time, high-precision STF sensor

In addition to serving as actuators, LCEs combine the birefringence of low molar mass liquid crystals and the mechanical properties of an elastic solid, which allows for their application as optical sensors and photoelastic strain sensors (46, 47). To date, there are no reports on the application of LCEs as sensors that respond to their external stimuli, such as thermal, light, or electromagnetic fields. This limitation arises from the nonlinear and stochastic response exhibited by LCE materials when exposed to external stimuli, as shown in Fig. 2F. Moreover, conventional fabrication methods for LCE structures often provide resolutions in the millimeter range, resulting in slow response and long recovery times that are unsuitable for stimulus source detection.

Inspired by the shape contraction of the 3D lattice structure in Fig. 4I and in response to the increase in spatial temperature inside the oven, this study used the MEW to design a large-scale, real-time, and high-precision STF sensor based on the 3D LCE grids and DL technology, as shown in Fig. 5. Temperature field sensors have been widely used for safety and health monitoring in various environments. For instance, to ensure safe operations in mines, it is crucial to maintain the temperature below 90°C. Moreover, recent advances in automatic fire detection, advanced manufacturing, biomedicine, and oil and gas pipeline monitoring have created an urgent need for temperature field sensors with higher spatial resolution and better real-time response (48, 49). Conventional electrical temperature sensors, such as thermistors and thermocouples, are point sensors and cannot provide temperature field detection, or require a large number of electrical signal input and output channels to form a sensor array. In addition, their physical existence can disrupt the spatial temperature distribution. Currently, distributed temperature sensors are the most mature commercial temperature field sensors, but their spatial resolution is typically above 1 m (48).

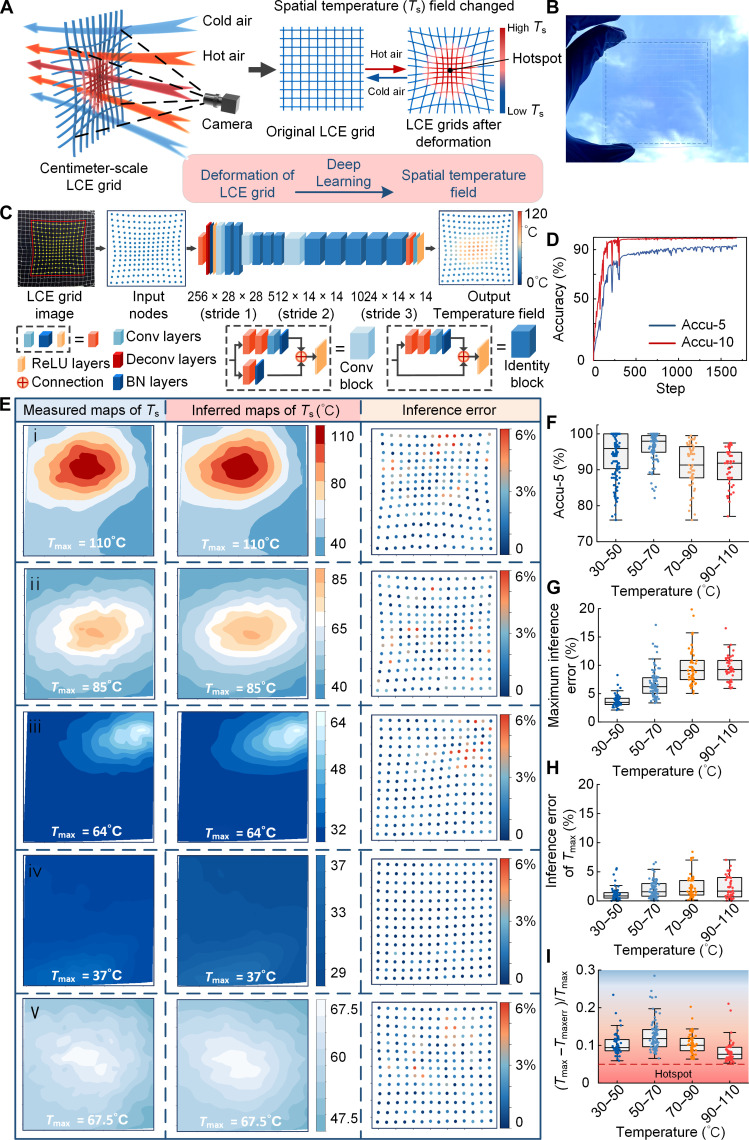
Fig. 5. The LCE grid–based, large-scale, real-time, and high-precision STF sensor.

(A) Schematic diagram of the STF sensor based on LCE grids. (B) Photograph of the LCE grid printed on a glass substrate. (C) The inference process of the temperature field was performed using an integrated DL model. (D) ACCU-5 and ACCU-10 curves in the DL model training process. Accu-5 and Accu-10 are defined as evaluation metrics of inference accuracy. (E) Measured temperature contour maps, inferred temperature contour maps of the STF sensor, and inference error dot plots of the STF sensor. (F to I) STF sensor performance on the test dataset. (F) Boxplot of inference accuracy (Accu-5) of the STF sensor. (G) Boxplot of maximum inference error of the STF sensor. (H) Inference error boxplot of the highest-temperature node. (I) The boxplot illustrates the proximity between the highest-error nodes and the highest-temperature nodes. (T_max − T_maxerr)/T_max is defined as a temperature difference between the highest-temperature node and the highest-error node divided by the highest temperature. The term “hotspot” is defined as a high-temperature zone where the temperature difference does not exceed 5% of the T_max value.

In recent years, DL, derived from research on artificial neural networks, has achieved significant progress in many fields, including computer vision, facial recognition, and image processing (50). Its success originates from its capability to extract higher-level features from raw data and classify information using multiple layers of information modules in a hierarchical structure (51). In this study, thermal contraction of the MEW-printed LCE grid was used to detect the temperature changes of the spatial cold and hot airflow by a camera in real time. By analyzing and inferring the deformation images of the LCE grid using a pretrained ResNet model, which is a type of convolutional neural network model, the distribution of the spatial temperature (T_s) field could be obtained, as illustrated in Fig. 5A.

To create the LCE grid, the MEW-printed perpendicularly intersected three-layered LCE wall structure arrays were used, consisting of LCE microfibers with a diameter of 30 μm. The photographs and SEM images of the LCE grids are presented in Fig. 5B and fig. S22, providing a visualization of the density of the LCE grid. This density refers to the spacing between the LCE wall structures and directly affects the spatial resolution of the LCE grid–based STF sensor. In this study, a minimum grid spacing of 0.4 mm by 0.4 mm was achieved, as shown in fig. S22. In addition, to reduce the computational load of the DL model, a square LCE grid measuring 8 cm by 8 cm with an internal spacing of 4 mm by 4 mm was used to sense the STF. The detailed fabrication process can be found in Materials and Methods and observed in fig. S23.

First, a dataset for the ResNet model training was constructed. It included the grid deformation images and measured STF. The grid deformation images can be easily obtained by a camera, but it is difficult to detect the true air temperature directly by an infrared camera. Therefore, in this study, the temperature of the nodes where the LCE walls intersected in the grid was measured by the infrared camera under the influence of thermal conduction from the surrounding airflow. The measured temperature values of all LCE grid nodes were plotted to create a temperature contour map, which represented the measured STF. This approach was applied because the MEW-printed LCE microfibers could rapidly respond to the thermal airflow stimuli in less than 33 ms, as demonstrated in the previous sections. The dataset construction process can be found in Materials and Methods and observed in figs. S24 and S25 and movie S10. The constructed data included 1355 frames of deformation images and the corresponding 1355 frames of measured temperature field contour maps. Each image frame consisted of a grid with a total of 196 nodes (14 × 14 = 196 nodes). The dataset was divided into training and testing sets by stratified random sampling according to the ratio of 8:2. Last, the deformations and their corresponding thermal responses of more than 260,000 nodes were determined.

Inspired by the ResNet model (52), this study used a two-step integrated model consisting of a feature extractor and an inference module for high-precision inference of the STF, as shown in Fig. 5C. The feature extractor adopted the first three layers of the ResNet50 model but modified the stride of the third layer to one to prevent excessive down-sampling of the feature map. In the temperature inference module, a convolutional neural network with a kernel size of one was used to reduce the channel dimension, enabling temperature inference for the 196 nodes. During the process of DL model inference, the temperature error for each of the 196 nodes in each LCE grid sample was calculated. It should be noted that when the error was below 5%, the inferred temperature was considered accurate. The number of accurately inferred temperature nodes was divided by the total number of nodes to obtain the accuracy for the LCE grid sample. Then, the overall model accuracy was determined as an average accuracy rate across all LCE grids in the training dataset and denoted by Accu-5. The Accu-10 value was obtained following the same approach. After 1679 training iterations, the ResNet model achieved its highest accuracy, with 94.79% for ACCU-5 and 99.67% for ACCU-10, as shown in Fig. 5D. In addition, the loss function quantifies the disparity between the predicted output of a model and the actual target values. A smaller loss value indicates that the model’s predictions are closer to the actual values. The loss curve in this work stabilized around 0.89, signifying the satisfactory convergence performance of the DL model, as demonstrated in fig. S26.

Therefore, the LCE grid–based STF sensors integrated with the DL model could precisely detect the STFs and their testing performance, as shown in Fig. 5E. In the inferred contour maps of the STF sensor test results, the highest temperature of all nodes was denoted by T_max, and the inference error was defined as an absolute difference between the node inference temperature and the measured temperature divided by the measured temperature. The results of the four tests arranged in descending order of temperature are presented in the first to fourth rows in Fig. 5E, respectively. The particular T_max values of the measured maps for the four tests were 37°C, 64°, 85°, and 110°C, and their high-temperature zones were relatively small. Thus, in the temperature range of 30° to 110°C, regardless of the temperature variations, the STF sensor could consistently determine the temperature distribution with high precision. The inferred maps (the middle column of Fig. 5E) generated by the STF sensor closely aligned with the measured maps (the leftmost column of Fig. 5E) captured by the infrared camera, indicating a high consistency in the position and shape of the isothermal contours. This consistency was achieved for a wide temperature range, from the highest temperature of 110°C with a temperature difference exceeding 70°C in the first row of Fig. 5E to the lowest temperature of only 29°C with a temperature difference of merely 8°C in the fourth row. Furthermore, across these four distinct temperature fields, most of the nodes in the inferred maps exhibited inference errors (the rightmost column) within 3%, while all nodes’ inference errors were below 6%.

Then, when the entire STF sensor was exposed to a high-temperature airflow (the fifth row of Fig. 5E), the T_max value was approximately 67.5°C, and the temperature variations were less than 20°C in the 8 cm–by–8 cm area. The results showed a high level of consistency between the inferred maps and measured maps, and the inference error for all nodes remained below 6%. The five inferred temperature maps in Fig. 5E were obtained by the pretrained DL model based on the five LCE grid deformation images presented in fig. S27. In addition, the STF sensor was tested in scenarios where the high-temperature zones were placed at the periphery of the LCE grid, as shown in figs. S28 and S29. It should be noted that this placement did not compromise the sensor’s high-precision detection of varied, complex, large-scale temperature fields, as indicated by the low inference errors.

The test results of the STF sensor on the entire testing dataset consisting of 270 images are presented in Fig. 5 (F to I). For real applications involving temperature fields, such as fires or mining detection, the highest temperature value, T_max, has paramount importance. Therefore, this study used the T_max value to represent the respective temperature field. On the basis of its value, the test dataset was divided into four intervals: 30° to 50°C, 50° to 70°C, 70° to 90°C, and 90° to 110°C. As shown in Fig. 5F, the STF sensor achieved its highest detection accuracy in the temperature range of 50° to 70°C, reaching a median accuracy of 98% and a minimum accuracy of 89%. When the T_max value was between 90° and 110°C, the detection accuracy stabilized at an average value of approximately 92%. Across the entire measurement range, the minimum detection accuracy of the STF sensor exceeded 76%, whereas the maximum detection accuracy reached 100%. The boxplot of the maximum inference error for each of the tested temperature ranges, presented in Fig. 5G, further demonstrated the STF sensor’s high-precision detection capability. Namely, the maximum error increased gradually with the detection temperature, eventually stabilizing with an average value of nearly 9%.

The inference error of the high-temperature nodes was remarkably low, as shown in Fig. 5H. For T_max between 30° and 50°C, the average value was approximately 1%. As temperatures increased, the average T_max error slightly increased, stabilizing at approximately 2% in the temperature range of 90° to 110°C. Across the entire measurement range, the upper limit of T_max inference error remained at only 7%, indicating consistently high precision of the proposed STF sensor in detecting high-temperature regions. A similar conclusion can be drawn from Fig. 5I. In this study, “hotspots” were defined as high-temperature zones where a node’s temperature deviates by less than 5% from T_max. T_maxerr represents the inference temperature of a node with the maximum inference error. As shown in Fig. 5I, nodes with maximum errors typically appeared when the temperature was approximately 10% different from the highest node temperature rather than within the defined hotspot area. This result intuitively demonstrates the precise sensing performance of the MEW-printed STF sensor for high-temperature zones, indicating significant implications for safety and health monitoring.

Rapid response test of 3D MEW-printed STF sensor

In addition to the measurement accuracy, the real-time monitoring performance of overheating or anomalous temperatures is crucial for applications, such as mitigating the risks of fires and equipment damage. Therefore, additional tests were conducted to evaluate the STF sensor’s capacity to detect temperature fields generated by a rapidly moving hot airflow, as shown in Fig. 6.

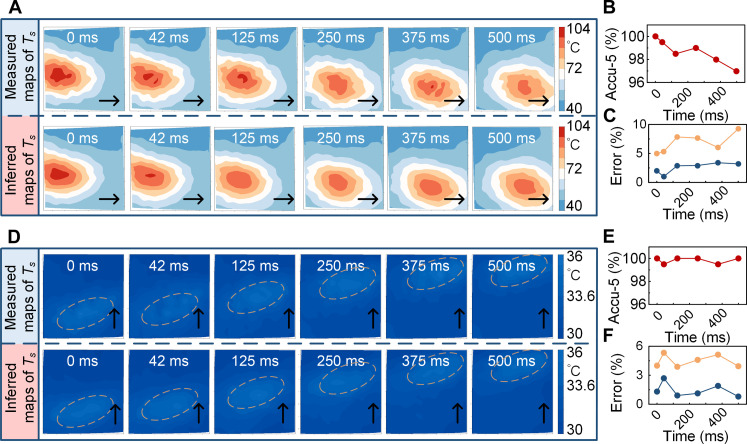
Fig. 6. The rapid response testing of the STF sensor.

(A) Rapid response performance of the STF sensor when the high-temperature airflow swiftly moves from left to right within 500 ms. (B) Real-time accuracy of the STF sensor when the high-temperature airflow moves fast. The measurement accuracy consistently exceeds 96%. (C) Real-time error of the STF sensor when the high-temperature airflow moves fast. The yellow line represents the maximum inference error of the temperature field contour map, and the blue line represents the inference error of the highest-temperature node in the temperature field contour map. (D) Rapid response performance of the STF sensor when the low-temperature airflow swiftly moves from left to right within 500 ms. (E) Real-time accuracy of the STF sensor when the low-temperature airflow moves fast. The measurement accuracy consistently exceeds 99.5%. (F) Real-time error of the STF sensor when the low-temperature airflow moves fast. The yellow line represents the maximum inference error of the temperature field contour map, and the blue line represents the inference error of the highest-temperature node in the temperature field contour map.

In these tests, a heat gun was directed toward the LCE grid, and it oscillated at a velocity of 80 mm/s to simulate the creation of a swiftly moving temperature field. First, a temperature field with a high-temperature zone (T_max of 100°C with a significant temperature difference of 60°C) was simulated, traversing from left to right across the STF sensor, as illustrated in Fig. 6A. Meanwhile, the camera recorded the LCE grid’s deformation at a frequency of 24 Hz, namely, the sampling frequency of the STF sensor was 24 Hz, with a capture interval of 42 ms. These data were fed to the integrated DL model for the temperature field inference. The initial deformation images of the LCE grid captured by the camera are shown in fig. S30. Detailed information on the software and hardware of the STF sensor is provided in Materials and Methods. The entire computational process was completed in 11 ms.

As shown in Fig. 6A, the temperature field contour maps detected by the STF sensor closely resembled those captured by the infrared camera, with nearly overlapping isotherm contours. This result indicates the sensor’s adeptness in responding to rapid movement within a high-temperature zone. In Fig. 6B, the STF sensor maintained consistent detection accuracy exceeding 96% in the rapid detection process. This implied that in each contour map, at least 96% of the nodes exhibited an inferred temperature with a difference of up to 5% from the actual measured temperature. Furthermore, the maximum errors in the sensor’s inferred maps did not exceed 10%, while the inference errors of the highest temperature nodes remained below 4%, as illustrated in Fig. 6C.

The STF sensor’s performance for the temperature field with a low T_max of 36°C is presented in Fig. 6D, where it can be observed that it rapidly traversed from bottom to top across the LCE grid. The simulated temperature distribution featured a compact high-temperature zone, with a temperature difference of only 6°C from a temperature of 30°C. The initial deformation images of the LCE grid captured by the camera are presented in fig. S31. The MEW-printed STF sensor continued to exhibit excellent response speed and measurement accuracy. The detection accuracy consistently exceeded 99.5%, with a maximum error in all resulting inferred maps of up to 6% and an inference error for the highest-temperature nodes of below 3%.

As previously presented, the LCE microfibers responded to thermal airflow stimuli in less than 33 ms, which was shorter than the camera’s interval of 42 ms. In addition, the computation speed of the integrated DL model was less than 11 ms, which was also within the 42-ms interval. These results demonstrate that, even when operating at a high sampling frequency of up to 24 Hz, the proposed MEW-printed STF sensor could maintain exceptionally high large-scale, real-time measurement accuracy.

DISCUSSION

Natural organisms exhibit the ability to autonomously sense and respond to an environment, which has inspired the construction and operation of soft robots and sensors based on stimuli-responsive smart materials, such as LCEs (53–55). While previous studies on LCEs have primarily focused on limited shape changes of macrostructures or quasi-3D microstructures, this study proposes a strategy using the shear forces within Taylor cones during MEW to align the LCE mesogens and fabricate LCE actuators. First, the systematic analysis of printing parameters demonstrated that these microfiber actuators exhibit impressive actuation strain, stress, work density, and response speed when subjected to dynamic thermal airflow stimuli. Meanwhile, the proposed microfiber actuators can be deposited at predefined positions and paths, which is convenient for specific applications. Then, by using a layer-by-layer construction approach for microfibers, this study successfully printed cross-scale LCE actuators, including gradient-responsive structural units, 1-mm microgrippers, and various macro-3D lattice structures. Compared to previous methods, the MEW technique offers a compatible fabrication approach for high-performance 3D actuators spanning micrometer- to centimeter-scale dimensions.

Moreover, leveraging the rapid responsiveness of the MEW-printed LCE microstructures to thermal airflow stimuli, this study applied LCE materials to the field of STF sensing and designed STF sensors with high large-scale, real-time measurement accuracy and spatial resolution. Because of the simplicity but remarkable efficiency of the proposed approach, the authors believe that the application of DL could expand the design and application scope of stimuli-responsive smart materials and enable the detection of various stimuli, such as heat, light, humidity, and solvents.

Last, it is important to note that during MEW, the internal accumulation of charges in fibers can lead to repulsion between adjacent microfibers carrying similar charges. This phenomenon can hinder the successful formation of 3D structures with centimeter-level heights and high fill factors in MEW 3D printing. One potential solution to this issue is the introduction of an electrostatic eliminator during the printing process (56). The electrostatic eliminator ionizes the surrounding air, generating charged electrons that attach to the microfiber surface, thereby achieving in situ charge neutralization of the microfiber charges during MEW and creating more complex high-resolution 3D LCE actuators.

MATERIALS AND METHODS

Materials

Liquid crystal monomers RM257 {1,4-bis-[4-(3-acryloyloxypropyloxy) benzoyloxy]-2-methylbenzene, 98%} used in this study were purchased from Xi’an Caijing Opto-Electrical Science and Technology Co. Ltd. Meanwhile, EDDET, dipropyl amine, butylated hydroxytoluene (BHT), (2-hydroxyethoxy)-2-methylpropiophenone (Irgacure 2959), and methylene chloride (CH₂Cl₂) were purchased from Sigma-Aldrich. All chemicals were used as received without further purification.

LCE ink preparation

The LCE ink was prepared through the Michael addition reaction between the liquid crystal mesogen RM257 and the chain extender EDDET. The chemical structures are shown in fig. S1. In MEW, a minimal amount of LCE ink was used for each printing session. Excess ink, if left in the heating syringe for an extended period, would increase in viscosity. In this study, the liquid crystal monomer RM257 (3.296 g) was dissolved in 20 ml of CH₂Cl₂. Then, the chain extender EDDET (0.875 g) and the catalyst dipropyl amine (0.04 g) were added dropwise. Next, 0.002 g (0.5 wt %) of the radical inhibitor BHT was weighed and added to the mixture. The solution was thoroughly stirred using a magnetic stirrer for 12 hours overnight at room temperature. Afterward, the solution was removed, and 0.08 g of the photoinitiator Irgacure 2959 was weighed and added to the mixture, which was followed by a 20-min stirring for thorough mixing. Last, the mixture was placed in an oven at a temperature of 85°C for 24 hours to allow complete solvent evaporation.

3D MEW-printed LCE microfibers and cross-scale LCE structures

The LCE ink was loaded into a plastic syringe equipped with an industrial metal nozzle, where the nozzle diameter ranged from 26 to 30 gauge. Then, the syringe was inserted into the self-developed 3D MEW printer. During the printing process, an air pump was used to control the flow rate precisely, using a pump pressure of 0.2 MPa. Before printing, the syringe was heated to a predetermined temperature, ranging from 60° to 120°C. To generate the electric field, a positive electrode was connected to the metal nozzle, and a high voltage of 2.0 to 3.0 kV was applied. Once the electric field propelled the LCE ink out of the nozzle, the slide glass substrates were used to collect the resulting LCE microfibers and 3D microstructures. The printing path and speed were governed by the G-code, with speed ranging from 1 to 20 mm/s, to control the diameter and properties of the LCE fibers. The distance between the nozzle and the glass substrate was fixed at 2 mm. During the MEW process, a 365-nm UV lamp was used to treat instantly the LCE fibers and microstructures in situ. The fabrication process is demonstrated in movie S1.

STF sensor fabrication process

The LCE grid was fabricated using the MEW method described above. The grid units had a side length of 4 mm, covering an area of 90 mm by 90 mm. A commercially available UV-curing 3D printer was used to fabricate a 120 mm–by–120 mm framework with a centrally positioned square hole, with a size of 80 mm by 80 mm, as shown in fig. S23. The square framework was inverted and placed onto the printed LCE grid. The UV-curable resin adhesive was applied along the edges of the square hole toward the framework center, ensuring that the framework could adhere to the LCE grid. The adhesive was then treated with UV light for 2 min. After a firm bond was formed, the LCE grid was carefully peeled off from the glass substrate. As a result, the LCE grid within the 80 mm–by–80 mm area at the framework center remained suspended in air, which is suitable for sensing applications.

An iPhone 14 was used as an optical camera to capture the deformation images of the LCE grid. In the DL training process of the STF sensor, calibration of the measured temperature was requested. Here, FLIR X6520sc was used to capture the temperature of the LCE grid when it was exposed to the thermal airflow.

DSC measurement of LCE ink

The DSC measurements were performed using a DSC 1 (Mettler Toledo) in a nitrogen atmosphere. The LCE ink, with a weight of 2 mg, was enclosed in aluminum pans. The heating and cooling scanning rate was set to 5°C/min in the temperature range of −35° to 150°C.

Characterization of LCE microfibers and LCE structures

The diameter of LCE fibers and the three dimensions (i.e., length, width, and height) of LCE structures were measured using different instruments, including an optical microscope (Zeiss), a laser scanning confocal microscope (OLS4000), a field emission scanning electron microscope (SU-8010), and a tungsten filament scanning electron microscope (S-3000 N). The POM images were taken using an OLYMPUS polarized microscope (BX51).

FEA of MEW-printed LCE structure deformations

The 3D model was constructed using the commercial software Solidworks and imported into the commercial software Abaqus for FEA. The LCE was modeled as a linear thermoelastic material with anisotropic thermal expansion coefficients, and a Poisson’s ratio of 0.499 was used. The thermal expansion coefficient α (α ≤ −50%) parallel to the axis of the printed LCE fiber was obtained by measurements, as shown in fig. S15, and the thermal expansion coefficient perpendicular to the axial direction was set to −α/2. The LCE bars in fig. S15 (A, C, and D) exhibited gradient thermal expansion coefficients. In the simulation, the LCE bars fig. S15 (A, C, and D) were fixed at one end. The LCE bar in fig. S15E was fixed at both ends. The LCE tube in fig. S15B was in an independent state. Similar to the experiments, the structure deformation was induced by uniformly increasing the simulation temperature. All stress fields were normalized by Young’s modulus of the material.

DL model dataset construction

The camera of iPhone 14 was used to capture RGB images with a resolution of 2160 × 3840 pixels, and an infrared camera was used to capture infrared temperature images with a resolution of 600 × 500 pixels. Before further analysis, images were preprocessed. First, the four corners of the metal frame were used as registration markers, and perspective transformation was performed to convert the zone of the grid material in the RGB image to a 1000 × 1000–resolution picture. Subsequently, median filtering and contrast enhancement were used to enhance image quality. Furthermore, to reduce computational complexity, this study performed the grayscale gradient detection to detect lines in the images and then merged adjacent lines. Last, the intersection node between the lines and the merged duplicate nodes was obtained, thus completing the automatic extraction of the nodes in the grid material.

To minimize the impact of the nylon frame on the edge grids, this study selected the 14 × 14 = 196 nodes in the framework center as temperature sampling nodes. By using perspective transformation, the grid intersections were transformed from the RGB image coordinate system to the infrared image coordinate system to read the corresponding temperatures. For each image frame, the RGB image coordinates (x and y) and the corresponding temperature (t) of the 196 nodes were obtained to create a dataset, having a total of 1355 image frames. To reduce the uncertainty caused by random sampling, this study performed stratified random sampling and divided the dataset into training and testing datasets according to the ratio of 8:2.

DL model training process and parameter settings

A two-step integrated model, consisting of a feature extractor and a temperature inference module, was used to accomplish the task of temperature inference and enhance accuracy, as shown in Fig. 5C. Inspired by the successful application of the ResNet model, which is a type of residual network, in image recognition tasks, the proposed feature extractor incorporated a convolutional layer followed by a deconvolutional layer. This process adjusted the channel number to 64 and increased the feature map size to 28 × 28. In addition, to improve model stability and convergence speed, both the convolutional and deconvolutional layers were augmented with the batch normalization and ReLU activation functions. Because of the limited size of the constructed dataset, feature extraction was improved by integrating three stages from the ResNet50 model, where the first, second, and third stages included a convolutional block followed by two, three, and five identity blocks, respectively. These stages aided in capturing essential features from the data. In the third stage, the stride was adjusted to one to prevent excessive reduction of the feature map size. Last, in the temperature inference module, a convolutional neural network with a kernel size of one was used to compress the channel number to one, thus enabling temperature inference for the 196 grid nodes.

In this study, the model parameters were set as follows: batch size = 128, learning rate = 0.0001, decay rate of 0.3, with decay applied when the accuracy reaches 0.85. The model was trained for a total of 1683 epochs. The mean squared error (squared L2 norm) loss function was selected to improve the prediction accuracy, particularly in local high-temperature zones.

The experiments were performed on a desktop computer with Windows 10, 32 GB RAM, an AMD Ryzen 9 5900X (12 cores @ 3.70 GHz), and an NVIDIA GeForce GTX 3080. In the experiments, Anaconda Python and the PyTorch DL framework were used. Using this set of hardware and software, an inference time of less than 11 ms was achieved for the STF sensor.

Supplementary Materials

This PDF file includes:

Figs. S1 to S31

Table S1

Legends for movies S1 to S10

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S10