Agent-based methods facilitate integrative science in cancer

Abstract

In this opinion piece we highlight agent-based modeling as a key tool for exploration of cell-cell and cell-environmental interactions that drive cancer progression, therapeutic resistance, and metastasis. These biological phenomena are particularly suited to be captured at the cell-scale resolution only possible within agent-based or individual-based mathematical models. These modeling approaches complement experimental work (in vitro and in vivo systems) through parameterization and data extrapolation, but also feed forward to drive new experiments that test model-generated predictions.

Designing multi-scale mathematical models of cancer

Cancer is an inherently multi-scale disease involving genetics, phenotype selection, ecological interactions, and the break down of tissue-scale homeostatic mechanisms. Due to the complex multiscale interactions at play within tumors, clinical or preclinical data is often collected at each scale: sequencing of genetic information, imaging of tissue-scale tumor density, histology or pathology of environmental or cell biomarkers, and positron emission tomography (PET) scans of the distribution of metastases. A systems approach is key to understanding, predicting, and treating cancer at each scale: intra-cellular, cellular, tissue, and body scale. In this opinion piece, we highlight agent-based modeling as an instrumental tool in the exploration of cell-cell and cell-environmental interactions which drive therapeutic resistance and metastasis. These modeling approaches are often referred to as hybrid modeling frameworks, making use of mathematics to integrate data across multiple temporal and spatial scales [1].

Understanding cancer through a multi-scale, systems perspective

The use of mathematical modeling in cancer treatment has garnered increasing interest in recent years, as both a means of generating or testing hypotheses and as decision-support tools for clinical practice. Though methods in applying mathematics to oncology vary widely (differential equations, stochastic models, partial differential equations, and many more), agent-based mathematical models are particularly suited to capture biological phenomena at the cell-scale resolution. Agent-based approaches, sometimes referred to as individual-based or cell-based, are commonly employed to model stochastic birth-death processes at the resolution of a single cell. The model tracks each individual agent (e.g. a tumor cell or host cell), each of which operates according a prescribed set of rules, which depend on the specific conditions that each cell finds itself in at a given time. Such models are ideal for capturing inherent stochasticity (random variation or noise) involved in cell growth and cell-cell competition. Cell birth and death events are probabilistic and therefore each simulation represents a unique realization of the model. Typically, many stochastic realizations are simulated and averaged, lending agent-based models (see Glossary) the advantage of generating not only the average outcome of a system but also the distribution of possible outcomes. This is ideal for modeling rare events that are difficult to measure or predict, such as accumulation of rare mutations [2], metastatic seeding by circulating tumor cells [3], parasexual recombination [4], and more.

The stochastic nature coupled with cell-scale resolution increases the computational complexity of solving these mathematical constructs. To simplify this process, there exist many software packages to aid the construction of cell-based models of cancer including PhysiCell [5], Hybrid Automata Library [6], and others [1]. Cells can be constrained to regular lattice grid, or in continuous off-lattice space [7]. Although spatial modeling is not necessary for an agent-based model (i.e., cells can compete under a well-mixed assumption where interactions are between all agents at once), modeling the explicit spatial structure of cellular processes often has a significant impact on evolution [8,9]. Furthermore, spatial modeling approaches are necessary for modeling systems where morphogenesis or other biological spatial patterns and structures are of importance [10].

Agent-based methods have been extensively applied to clinical sequencing data by comparing clinical summary statistics of patients to simulated data derived under a variety of assumptions. Branching processes (see Glossary) are simple individual-based models that can be simulated numerically by tracking the number of each cell type over time. These models account for every cell within the tumor, but can simulated in a computationally-tractable manner by storing the total number of each cell type at each timestep in a vector (e.g. x = [x1, x2, x3, …] ). Stochastic branching process approaches can model common patterns of metastasis using subclonal lineage information in primary tumors and metastases. Similar approaches have been used to find that the large majority of driver gene mutations are common to all metastases [11], and to infer that a modest growth rate advantage of new drivers is insufficient to compensate for the time spent waiting for mutations to spontaneously occur [12]. Multi-type branching processes have also been used to study the effect of seeding patterns (single seeding, consecutive seeding, continuous seeding) on the relationship between primary and metastatic heterogeneity [13]. Though mathematical modeling provides perfect information about each simulated cell, error-prone sequencing can be simulated to match the technology-limited depth of sequencing data and providing clinically relevant model-outputs. A key advantage of agent-based methods is their ability to capture stochasticity, particular at the cell-level. Cellular phenomena, such as reproduction and mutation rates, can simulated from probability distributions that lead to stochasticity in the spatial and temporal dimensions.

Agent-based methods facilitate integrative science in cancer

As the title of this manuscript suggests, agent-based approaches are uniquely suited to facilitate integrative science. Integrative science is a term used to define a team-science, as well as a multi-disciplinary, and collaborative style of scientific investigation that brings together mathematicians and biologists [14]. The capacity to collect experimental and clinical cancer data has continuously grown to levels that makes the biology that is inherent within these large datasets very difficult to grasp without mathematical tools. In order to avoid reductionist thinking that is often inevitable when scientific disciplines exist in non-collaborative silos, the skills of data-modelers must be combined with experimental insight.

This integrative science goal is shared by many, yet overcoming the lack of a shared scientific language or lack of shared methods in cross-disciplinary collaboration is difficult. It is our opinion that agent-based approaches provide a unique benefit in facilitating integrative science for several reasons.

First, the design of agent-based models facilitate the development of a shared language. Experimental biologists and clinicians use biological intuition to construct the “rules” of the model (see Box 1: Guide for Beginners) which mathematicians subsequently transcribe into a computational framework. Second, agent-based approaches are complementary to in vivo and in vitro experimental work, facilitating iterative feedback to calibrate parameters and extrapolation of behaviors for experiments not performed. This latter approach drives new experiments that test model-generated predictions [14].

Box 1: Guide for beginners.

There are many software packages with the capability to design and implement agent-based models of cancer. Each software exists on the spectrum from requiring minimal technical knowledge of computer programming (e.g. NetLogo) to intermediate (e.g. Hybrid Automata Library) and advanced flexibility (e.g. PhysiCell). A recommended approach for beginners with the desire to learn programming skills is to start with NetLogo implemented using the “Logo” language and following its design philosophy of low entry threshold without an upper ceiling.

One alternative is to take an integrative science approach: experts in computer programming construct the nuts and bolts of the modeling while experts in cancer biology advise on the construction of rules, expected emergent behavior, and data integration. Importantly, some software (e.g. PhysiCell, Hybrid Automata Library) facilitate iterative collaboration. For example, after the model is constructed it can be exported as a user-friendly graphical-user-interface (PhysiCell uses nanoHUB integration to visualize model output in a web browser), allowing a non-expert to change parameters and visualize the output with a few mouse clicks.

Rule construction:

The first step in designing an agent based model is deciding the “rules” of cell behavior and interaction between cell types and environmental factors. Cellular phenotypes may differ in replicative abilitiy, motility, survival, mutation likelihood, uptake or secretion of diffusible molecules, and more. Two cells in proximity can interact by competing for space upon replication, secreting growth factors. These rules should be implemented with the subject domain knowledge of biologists based on experimental data, biological intuition, or hypothesis generation (see Glossary).

Emergent behavior:

Emergent behaviors are phenomena that are not explicitly programmed into the model a priori. Instead, macroscopic patterns emerge from the complex, non-linear microscopic interactions that are the underlying “rules” of the model.

Data integration:

Integration of data in order to properly parameterize the agent-based model can take one of two forms. First, macroscopic data describing global behavior of the biological system can be fit to the emergent outcome of the model. Second, each underlying “rule” can be parameterized from experimental data in isolation.

Below, we discuss several broad biological processes which have been modeled using agent-based methods to gain insight into cancer progression or treatment: homeostasis, metabolism, tumor-immune ecology, and treatment resistance. Wherever possible, we highlight approaches which utilize integrative science, leveraging the full potential of interdisciplinary collaboration.

Developing a model of homeostasis disruption and melanoma progression through integrative science

Cancer progression must be considered within the context of dynamic feedback between the tumor, its microenvironmental conditions, and interactions with surrounding stromal populations. Normal tissues contain cellular processes, molecular and microenvironmental features which drive tissue function to maintain homeostatic regulation [15]. Viewing cancer as a departure from homeostasis helps consolidate recent findings that driver mutations frequently occur in normal, healthy tissue, albeit with no indications of malignant growth [16]. This provides evidence that driver mutations alone are an insufficient condition for carcinogenesis to occur in individual patients. Constructing a complete view of carcinogenesis, cancer progression, and invasion must account for the coupling of evolutionary processes within the tumor to its dynamic interplay within the patient’s homeostatic ecosystem. While it is arguably difficult to model homeostatic systems experimentally, agent-based models can be constructed from first-principles with the ability to perform otherwise impossible experiments in the early stages of disease progression [17].

An illustrative example of agent-based modeling describing normal homeostatic maintenance of skin and the subsequent disruption as a route for melanoma development [18] is shown in figure 1. In vitro experiments showed that senescent dermal fibroblasts promote the growth of nontumorigenic melanoma cells and promote invasiveness of advanced melanoma cells. Motivated by these experiments, simulations were seeded with a heterogeneous spatial distribution population of senescent fibroblasts. In silico, senescent fibroblasts aid minimally transformed melanocytes with increased proliferation and invasion into the dermis. Fibroblasts produce environmental factors that regulate homeostasis in normal skin tissue. Disruption of fibroblasts during the onset of melanoma will affect skin homeostasis and feedback on initiation and progression.

Figure 1. Multi-scale agent-based model of melanoma:

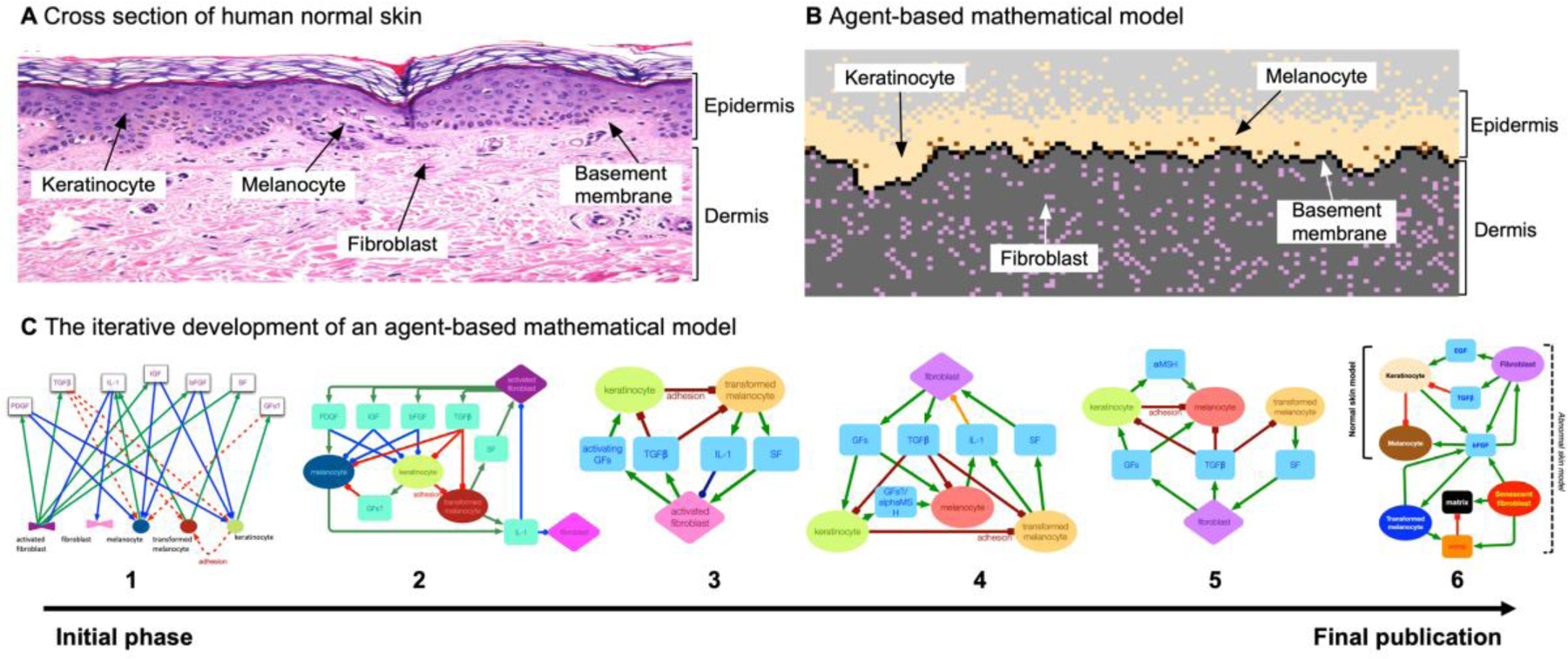
Figure reproduced from ref. 18. (A) Cross section of human normal skin (hematoxylin and eosin stained), where the epidermis contains a basal layer, melanocytes, and keratinocytes, while the dermis contains fibroblasts and extracellular matrix. (B) The computational simulated cross section (bottom) closely mimics the overall qualitative features of normal skin homeostasis. (C) The process to design the multi-scale required iterative discussions within an integrative science team. Experimental biologists in collaboration with mathematicians drew a series of interaction diagrams, culminating in a final model (right) that can recapitulate both normal skin homeostasis and melanoma dynamics.

The iterative process of integrative science is shown in figure 1C. The first step of brainstorming sessions with biologists and mathematical models is very often the construction of interaction diagrams. These diagrams contain the types of “agents” (e.g. fibroblasts, melanocytes, keratinocytes) and their interactions with each other and with diffusible growth factors (e.g. TGFβ, IL-1, etc). The model development was an iterative process through lengthy discussions between mathematicians and biologists of the key factors regulating both normal and transformed skin development and maintenance. Initially, all relevant factors were considered and were subsequently reduced and modified through further discussion and literature search. A key point of this process was to converge on a minimal number of cellular and microenvironmental elements that could both be modeled and quantified experimentally. One problem that arose early was separating factors that modulate normal skin homeostasis versus those that only emerge once cancer initiation has begun. Once we made this separation the final structure of the model emerged.

Only after consideration of homeostatic regulation within the model can accurate predictions be made. The baseline (non-cancerous) model enables us to quantify the contribution of each cell type to the overall aberrant population dynamics. For example, simulations show that systematic up regulation of the senescent fibroblast phenotype was insufficient to drive cancer but sufficient to disrupt the skin architecture, producing mole like structures. Also, in the absence of stromal senescence it was found that tissue homeostasis was able to suppress melanocyte transformation. However, when both melanocyte transformation and stromal senescence are combined then cancer progression rapidly emerged. The model was also used to investigate potential therapeutic opportunities targeting cell-cell or cell-microenvironmental interactions, even if no such therapeutic option currently is available. In silico investigations are useful to identify therapeutic targets, mechanisms of resistance, or critical thresholds in parameter values that drive response or progression. Ideally, mathematical modeling insight feeds an iterative loop to drive more experiments to test the newly generated hypotheses. This paper highlights the ability of agent-based approaches to provide insight into melanoma initiation where it otherwise may be costly or infeasible experimentally. In particular, homeostasis is difficult to model experimentally and in vivo approaches do not offer sufficient temporal detail to tease apart the interactions.

In a similar study for bone metastasis in prostate cancer, agent-based modeling first recapitulated the multicellular process of bone remodeling with mesenchymal stromal cells, osteoblasts, osteoclasts, and precursor cells [19]. The model recapitulates the “vicious cycle” of bone degradation in prostate cancer where cancer cells alter the bone remodeling process through expression of factors like RANKL, inducing bone resorption. Subsequently, growth factors such as TGF𝛽 stimulates the survival and growth of metastatic prostate cancer cells, completing the vicious cycle. The co-opting of the normal homeostatic remodeling process by metastatic tumors yields the vicious cycle of bone degradation and tumor growth. Without careful consideration of homeostatic remodeling, it is difficult to address the treatment considerations of this vicious cycle.

Agent-based modeling is a suitable choice for investigating the role of cell competition and fitness effects in the early stages of malignant transformation. For example, these methods have been applied to show how competition between clones of similar fitness in mormal esophageal epithelium induces mutant cell fate to revert towards homeostasis [20]. Similarly, agent-based methods have shown the role of tissue architecture acting an evolutionary accelerant [21] and overriding cell-specific phenotypes [22]. Agent-based approaches also investigate competition between multiple cell types, including the role of stromal-to-tumor cell density on the efficacy of oncolytic virus treatment [23] or the “engineer versus pioneer” paradigm in degrading extracellular matrix barriers, giving way to cell-intrinsic proliferative phenotypes[24], a paradigm also important in immune escape [25] and cancer metabolism [26].

Iterative modeling elucidates the role of normal homeostasis in clonal expansion

The iterative process of integrative science (i.e. figure 1C) is often hidden to those outside of the original team. Typically, only the final iteration of the mathematical model is published, with previous model versions discarded on the metaphorical trash heap of scientific history. However, the published model in figure 1 underwent further refinement and iteration to address a controversy surrounding neutral evolution and clonal expansion within normal tissues [27]. Substantial accumulation of oncogenic driver mutations can occur in normal, healthy human tissues. These mutations do not appear to substantially disrupt homeostatic normal morphology. It is an open question how a mutant clone is able to expand within normal tissue: primarily the result of arising first and persisting, or the result of arising late, with a selective fitness advantage.

To answer this question, a simplified version of the previously mentioned hybrid cellular automaton model of the human epidermis was implemented (figure 2). In the simulation, the bulk of cellular division occurs within the basal layer with cells pushed upwards with ever-increasing chance of death. This leads to a homeostatic-balanced turnover in the epidermis, such that the overall population size of cells is roughly constant through the simulation. The model then assessed the effect of fitness-enhancing mutations (e.g. NOTCH1 or TP53) on maintaining that homeostatic balance. A cell with NOTCH1 mutations disrupts neutral dynamics through “blocking” neighboring cells from dividing into its local neighborhood and TP53 mutations are not subject to UV damage. Regardless of functional differences, in simulations of homeostatic tissue, non-neutral clones are subject to the same exponential size dependency that neutral clones are. The work suggests that subclone size reflects persistence rather than subclonal selective sweeps. Therefore, NOTCH1 and TP53 mutations must arise early to match observed clonal frequencies.

Figure 2: Multi-scale model of normal human epidermis:

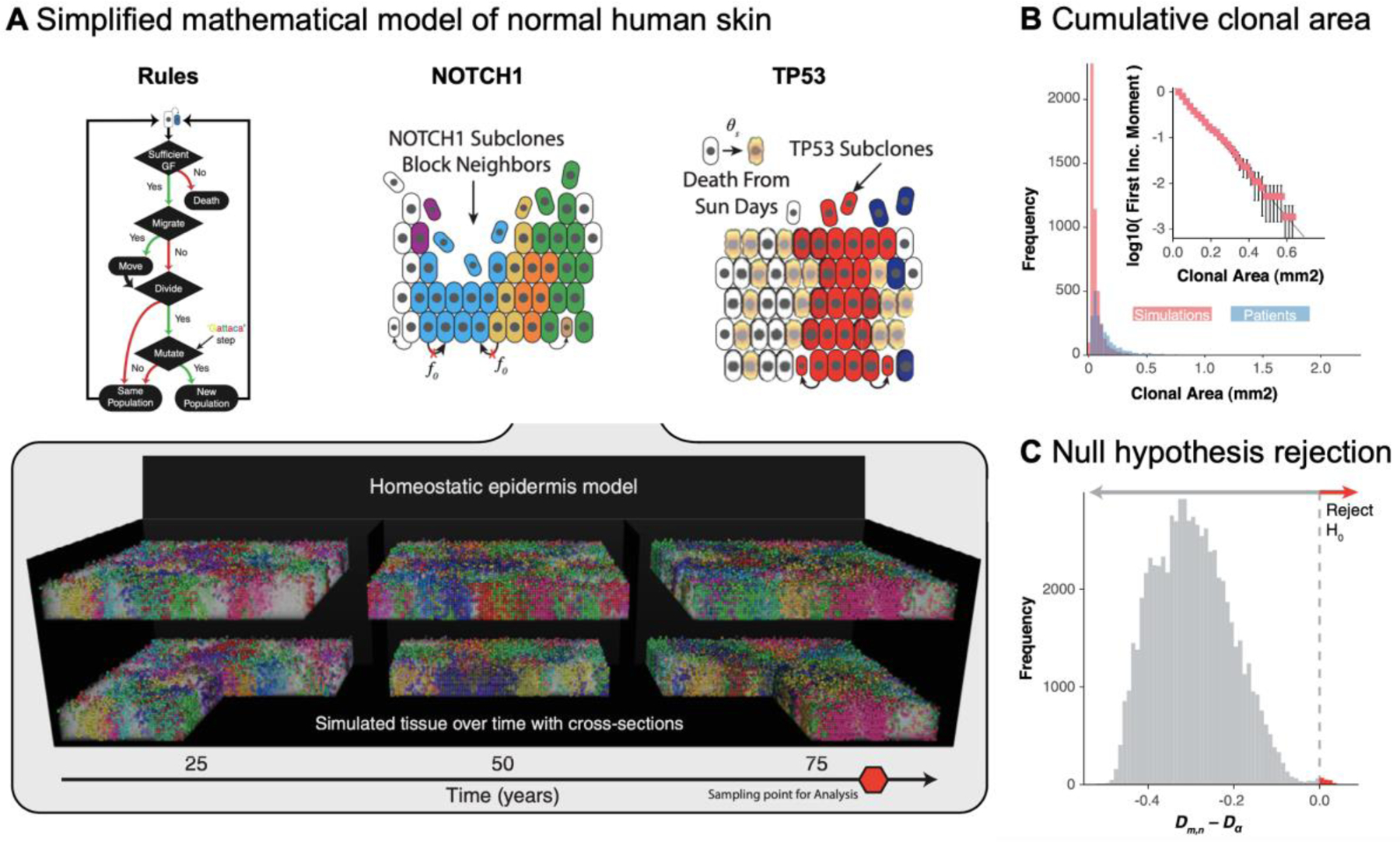
Figure panels are reproduced from ref. 27. A) Homeostatic epidermis model with high-resolution genomes. Rules flowchart shows how loss/replacement in the stem-cell niche at the basal layer are governed by a diffusible gradient of growth factor (GF). The model (bottom) investigates the effect of two fitness-enhancing mutations: NOTCH1 (middle) disrupts neutral dynamics through “blocking” neighboring cells from dividing into its local neighborhood while TP53 (right) are not subject to UV damage. B) Simulated dynamics matches patient biopsy clonal area frequency distributions. The inset shows log-10 transformed first incomplete moment for the same random sampling of patient comparable simulations. C) Difference between Komlogrov–Smirnov test statistic (Dm,n) and critical value (Dα) for all patient biopsies to patient-specific model simulation’s first incomplete moment distributions. Red arrow denotes comparisons where the null hypothesis can be rejected.

The implementation of this model using an agent-based approach is important for several reasons. First, the model enables direct comparison of simulated versus patient genetic data. Each individual simulated cell is embedded with base-pair resolution genes mutating at gene-specific mutation rates [28]. It can model lifelong human skin-cell dynamics that represent tissue architecture within the homeostatic epidermis with realistic mutation accumulation.

Second, the model provides a testbed for simulated experiments. Previous studies modeling clonality within the epidermis ask whether current technology is capable of measuring neutrality in normal tissue [29, 30], whereas this approach develops a testbed model that allows modelers to perform simulated experiments based. These simulated experiments often generate new hypotheses that drive new experiments, as explained in the next section.

Agent-based modeling as a method of generating hypotheses

Complex agent-based modeling is often used when direct measurement of specific parameters for a system is difficult or impossible. While seemingly counter-intuitive, the aim is to focus on specific mechanisms of interest and explore the range of behaviors that such a system generates, across a range of biologically reasonable parameter values. This approach is sometimes referred to as “hypothesis-generating modeling”, or forward modeling [31], where each set of parameter values may represent a different hypothesis. For example, agent-based methods help explain the role of spatial constraints on the “go-or-grow” hypothesis (the idea that cell motility and cell proliferation are dichotomous, antagonistic processes) by modeling competition between proliferative and migratory phenotypes [32]. Agent-based approaches have proved instrumental in determining the limits of currently available sequencing technology to detect the selection advantage of coexisting clones. For example, branching process models have been employed to estimate the selective advantage of driver mutations [2] or the deleterious effect of passenger mutation [33, 34] based on heterogeneity in tumor size and development time. These measurements are not without controversy, because conclusions depend on the choice of model [35], assumptions about spatial interactions [36, 37], turnover rates [21], as well as the number [38] and location [39] of samples taken. An integrative approach where hypothesis testing leads to specific experiments, feeding back to parameterize math models is an ideal workflow [14]. Calibration and parameterization of agent-based models is made challenging by computational complexity (e.g. the time required to perform simulations) and the number of simulations that may be required to mitigate uncertainty arising from intrinsic model stochasticity. This second challenge is addressed in a recent review [40] covering methods for assessing uncertainty and sensitivity of parameters in agent-based models.

Iterative feedback between experimental and mathematical modeling explains the role of cancer metabolism in modulating cancer progression

Figure 3 provides an illustrative example of the power of multi-scale modeling in investigating the interplay between environmental and cellular heterogeneity and immune escape in ductal carcinomas in situ (DCIS). The nature of DCIS as an intrinsically structured disease [41] can be interrogated through the use of agent-based approaches which explicitly account for cell-cell interactions, heterogeneous microenvironments, with dynamic cross talk and feedback [42]. This model of metabolic heterogeneity which consists of a continuous range of glycolytic and acid resistant phenotypes [43] under immune predation [44]. Increased glucose consumption and acid production is a typical result of altered metabolism in cancers. This leads to the acidification of the surrounding microenvironment, ultimately provoking acid-mediated invasion [45]. Heterogeneity in glucose consumption on the cell scale is context-dependent on local variations in nutrients, growth factors, and surrounding cells (normal, stromal, immune), and is in part dependent on local vascularity of the tumor. An example simulation is shown in figure 3, where simulation parameters are tuned to alter vascular context in each quadrant (low/high vascular stability and low/high vascular renewal). Tumor phenotypes evolve through drift: small, random alterations which occur upon cellular division. The figure illustrates the ability of agent-based models to capture spatial and temporal stochasticity and heterogeneity. Variations in microenvironmental conditions of oxygen, pH levels, and glucose concentrations in each quadrant lead to local selection for advantageous phenotypes. Low vascularized regions serve as the breeding ground for aggressive metabolic phenotypes via increased acidity and selection for acid-resistant phenotypes with high rates of glycolysis. In contrast, cells in the well-vascularized regions undergo lower selection pressure, and are less metabolically active. Eventually, the aggressive cells invade from their environment into the better-vascularized regions and accelerate tumor growth significantly.

Figure 3: Mapping immune-escape with multiscale modeling:

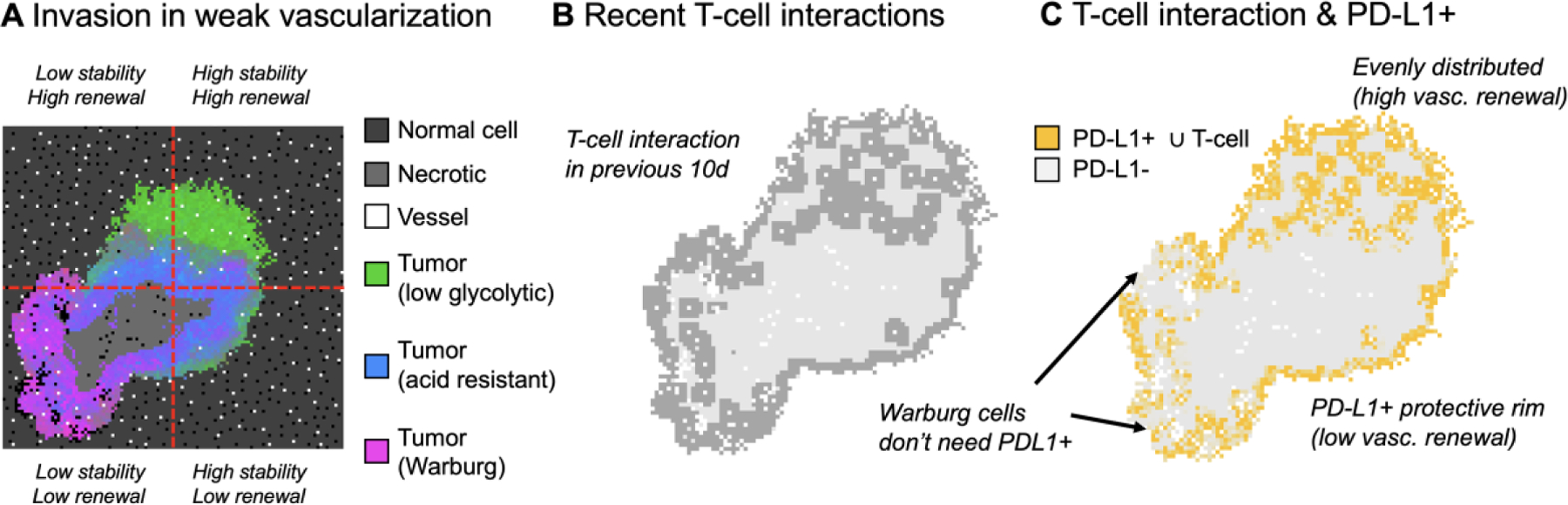
A) Spatial map of the hybrid discrete-continuum mathematical model of cancer metabolism from references 43 and 44. Tumor cells colored by phenotype (normal, acid-resistant, Warburg) interact and compete for resources with normal cells (dark gray). Warburg emerges in areas of weak vascularization (bottom left). B) The tumor in panel A is color-coded to recent immune interactions, which correlates with local vascular density. C) The tumor in panel A color-coded to PD-L1 expression recently employed for immune escape.

This model was developed iteratively through collaboration between mathematical modelers and their experimental colleagues. The initial hypothesis of acid-mediated invasion [46] generated several previous mathematical models that tested various hypotheses about how glycolytic and acid-resistant phenotypes might evolve and/or behave [46–49]. As additional experimental studies of tumor acidosis and its sequelae in cancer development were performed [50–55], the spatiotemporal agent-based model in [43] was developed to further investigate the tumor microenvironment aspects that affected the evolution of these metabolically aggressive phenotypes, and the effect of therapies on this interaction. Initially, the focus of the model was on the tumor intrinsic properties and how they altered the microenvironment in ways that led to invasion. Results from the timing of buffer application in a murine model [53] suggested that there was a threshold effect, wherein early application prevented tumor growth while slightly later application had little effect. This discontinuity led modelers to focus on “critical mass” effects in the model, and the same results were able to be attained in the model regarding buffer timing [43]. This led to hypotheses generated by the model about the success of new metastases based on their phenotype as well as the dose of the buffer, which was subsequently investigated in additional experiments [56]. Interdisciplinary discussions also led to the closer study of the dynamic vasculature, which emerged as a fundamental force shaping evolution in the model. Furthermore, predictions made by the model during its development fueled experimental results [55] that would otherwise have not been expected or tested.

This model has been used to test the accuracy of hypotheses by fitting experimental data using a wide range of assumptions about the rates of phenotypic drift and the cost/benefit ratio of the invasive niche-construction phenotype [42, 56]. This exploration rules out many hypotheses, while keeping others, and also serves to limit the scope of possible mechanisms and their parameterization. Otherwise, precise characterization or measurement of phenotype dynamics within an experimental system may be difficult. In contrast, agent-based approaches provide the modeler with “perfect information” (exact information for each cell), enabling precise tracking of the timing and spatial orientation of tumor-immune interactions (fig. 3B), and the distribution of immune-escape tumor phenotypes like those expressing PD-L1 (fig. 3C).

Integration of experimental data with an extension of this mathematical model was key to investigating the role of acid-responsive macrophages in promoting tumor growth in a follow up study [57]. In silico macrophage behavior was calibrated by fitting a linear model to specific gene expression data collected in different in vitro ecological conditions. This integrative modeling approach was used to explore theoretical treatment targets. For example, when the pH-sensitivity of macrophages was removed from the model, survival rates increased in silico. This finding indicates the promising therapeutic potential of targeting acidic microenvironmental conditions to re-program macrophages to be anti-tumor, increasing patient survival. In contrast, the influence of pH-sensitivity would arguably be technically challenging (if not impossible) to quantify experimentally through direct manipulation of macrophage properties.

Hypotheses of carcinogenesis – and therefore modeling – must account for spatially heterogeneous environmental conditions with variation in cell phenotype response to conditions. Such models are often computationally intensive, requiring scaling simulations down in size or simulating only a two-dimensional slice of tumors. One study used computationally tractable hybrid mesoscale model to develop a new prognostic biomarker (normalized distance from 18F-fluorodeoxyglucose hotspot) by directly comparing model output to PET imaging data at a biologically realistic spatial scale [58]. Another integrative study used agent-based methods to show how gradients of metabolites can alter tumor-associated macrophages differentiation, based on relative distance to vasculature [59].

Tumor ecology: immune and stromal interactions in agent-based modeling

The evolution of tumors is shaped by ecological interactions between tumor cells and the surrounding stroma and microenvironmental factors. Agent-based models often model each immune cell individually, allowing targeting of specific tumor cells and permitting selection for a host of immune-escape mechanisms in localized niches. In the previous example (figure 3), T-cells, recruited from vessels, target tumor cells that then may evolve PD-L1 expression to avoid immune predation. The distribution of PD-L1 roughly matches the distribution of T-cell interactions (figure 3B,C), except where alternative immune-escape mechanisms are available (here, the Warburg phenotypes in lower-left quadrant that acidify the environment, which causes T-cell deactivation). This example shows the complex feedback between tumor phenotype (PD-L1, Warburg), ecology (vasculature and immune recruitment), and invasion into homeostatic tissue. Another study compared simulations to antigen-hot or antigen-cold tumors from TCGA using a stochastic branching process to model negative selection of neoantigens during tumor growth [60]. Negative selection shapes variant allele frequency distributions, providing a signature of immuno-editing that is potentially a biomarker from clinical data [60].

Other models have highlighted the role “immuno-architecture” in predicting the effect of tumor-immune interactions on response to immune checkpoint inhibitors [61, 62] using a three-dimensional multi-scale agent-based modeling approach. Interestingly, although cytotoxic effector T-cells are recruited through spatially heterogeneous vasculature, the model predicted insensitivity to T-cell entry point via vascularization (e.g. core versus rim) on pre-treatment size and PD-L1 expression [61]. Often, immune ecology is studied using hybrid discrete-continuum approaches where microenvironmental factors are modeled using continuous partial-differential equations and immune or tumor cells are modeled as agents. One such study modeled six cell types: normal basal and luminal epithelial cells, tumor epithelium; native stroma (fibroblasts), reactive stroma (cancer-associated fibroblasts), and motile stroma, all interacting with three continuous microenvironmental variables: growth factor, MMP and ECM/basement membrane [63]. Results indicated that stromal ecology correlates with tumor growth, but inversely correlates with tumor phenotypic evolution (the growth factor and MMP production phenotypes).

The spatial location of ecological interactions also has implications for evolutionary dynamics [64]. In one study, clinical sequencing data from clear cell renal cell carcinoma patients indicated the presence of advanced, aggressive subclonal growth in the necrotic, hypoxic tumor center [65]. The tumor core was associated with high somatic copy number alteration (SCNA) burden, with greater propensity to seed metastases. Through clever use of agent-based modeling, authors were able to test the hypothesis that hypoxia-induced necrosis was required to maintain high levels of SCNA burden in the tumor core of the mathematical model.

Agent-based modeling investigates spatial interactions at the cell-scale that modulate treatment resistance

Agent-based approaches have also been used to investigate the effect of cell-cell interactions on treatment resistance. One study investigated the effect of uneven gradients of resource availability within tumor spheroids, noting that fitness differentials can arise from competition for space and oxygen in tumors [50]. The math model allowed only cells with sufficient space and nutrients to proliferate, which creates a decrease in cell fitness going from tumor periphery to core. The authors concluded that lower doses of cyclin-dependent kinase inhibitors control tumor growth and resistance better than high doses, but only when resistance occurs in the tumor core.

Spatial competition with surrounding cells is particularly important to competitive release, which is a resistant population’s release from competition with treatment-sensitive cells after prolonged treatment removes most of the sensitive cells. Adaptive approaches to cancer treatment aim to minimize competitive release and maximize the competitive suppression of resistant cells through well-timed treatment holidays. The key role of spatial competition and heterogeneity in “adaptive therapy” has been investigated using agent-based models [66–68]. In one recent study, cancer cells that evolve along a continuous trade-off between fecundity and resistance (resistant cells proliferate more slowly) [67].

In vivo or clinical data can be used to inform the multiple scales within these agent-based models. For example, an agent-based model of glioblastomas treated with a PDGF-over-expressing retrovirus [69] tracks two cellular phenotypes: proliferative and migratory potential, which are dependent on environmental concentrations of PDGF. Integration of data collected to inform both tissue scale (serial MRI imaging) and cell scale (biopsies) processes were key to optimizing treatment predictions. Employing the same model parameterized by imaging alone led to variability in modeling dynamics with less reliable predictions. It’s important to note that other standard mathematical tools use continuum approaches (e.g. partial differential equations) and cannot account for cell-cell processes on that scale.

Concluding Remarks

As seen in the examples outlined above, agent-based methods facilitate integrative science in cancer research. These methods can integrate a wide variety of data including in vitro or in vivo experiments, sequencing data, and imaging. Given the fundamental unit of most agent-based models is a single cell, it seems obvious that we should try integrate them with newly emerging single-cell technologies to advance our understanding of cancer biology.

Single cell transcriptomics has enabled the quantification of heterogeneous cell populations and the reconstruction of cell fate trajectories through measurement of gene expression in individual cells. Subsequently, RNA velocity methods have estimated the rates of change of expression to predict the future state of individual cells [70, 71]. Even more recently, spatially resolved transcriptomics can quantify cellular heterogeneity while maintaining information of spatial context [72]. However, single cell methods typically do not account for the impact of cell-cell interactions on cell fate or their impact on evolutionary changes in phenotypic abundance over time. The benefit of single cell analysis is a detailed quantification of individual omic and phenotypic properties, but an understanding of competitive or cooperative interactions on the cellular level will be required to quantify the evolutionary dynamics of disease.

Agent-based methods can facilitate this by incorporating single cell data into models that can recapitulate important spatial summary statistics coming from spatial transcriptomics. Agent-based methods were used in a similar fashion to help interpret summary statistics of genetics sequencing data, like the 1/f statistic [21,35–37]. Tools are already in development that integrate single cell sequencing with spatial quantitative systems pharmacology (QSP) modeling [73], providing deep insights for clinical outcome predictions in individual patients. Additionally, tools for base-pair resolution of mutation tracking in agent-based models have become recently available [28].

A major opportunity however, would be to exploit agent based models to integrate detailed single cell phenotyping (of cell relevant states) for a specific tissue with equivalent spatial transcription (of the same tissue) and play them forward in time (and through space) to predict what will happen and what treatment could be leveraged to ch5ange that outcome. The tools and potentially the data are emerging to make such an opportunity a not too distant reality (see Outstanding Questions box).

Outstanding Questions.

1. What spatial and temporal scales are required for agent-based mathematical modeling to recapitulate biological processes: molecular-scale, cell-scale, organism-scale, population-scale?

2. How can integrative science reconcile increasingly complex mathematical models with available biological data?

3. How do we account for agent-based models’ stochasticity when applying it to patient-specific data in a translational setting?

4. Similarly, what are the appropriate clinical summary statistics that are useful to compare mathematical model outputs to clinical data?

5. What are the best practices for integrating data from emerging single-cell technologies into agent-based modeling?

Highlights.

• Agent-based models are well-suited for studying evolutionary and ecological processes in oncology. These models can incorporate many scales of biology, including genetics, molecular dynamics, cellular phenotypes, tissue mechanisms, and systemic properties. In particular, the interactions between these scales and components can be studied in detail.

• Interdisciplinary research in oncology is enhanced by the use of mathematical modeling to integrate knowledge and facilitate communication between fields. This leads to the generation of novel hypotheses that can be extensively explored within a computational model before moving to the wet lab and clinical settings.

Glossary

Agent-based model:

a mathematical model which explicitly tracks individual agents (i.e. cells) and their interactions with each other (either in a spatial or non-spatial setting). Also known as an individual-based model

Hybrid discrete-continuum model:

a mathematical model which combines agent-based models (discrete agents) with continuous partial-differential equation models (continuum). Typically diffusible molecules are modeled on the continuous scale and cells are modeled on the discrete scale

Branching process model:

a simple (and computationally-tractable) individual-based model that tracks the number of each cell type over time. These models are simulated numerically or mean-field approximations of the long-term dynamics and stochastic uncertainty can be used

Hypothesis-generating model:

beginning with a known (or suspected) causality, mathematical models are constructed to express this hypothesis in mathematical terms. The mathematical model is used as motivation for further experiments

Hypothesis-testing model:

beginning with experimental data, mathematical models are constructed to seek potential causalities driving the functional relationships between dependent and independent variables. If the model doesn’t fit the data, the hypothesis is rejected