Unraveling Interface-Driven and Loss Mechanism-Centric Phenomena in 3D/2D Halide Perovskites: Prospects for Optoelectronic Applications

Abstract

In recent years, organic–inorganic metal halide perovskite solar cells (PSCs) have attracted considerable interest due to their remarkable and rapidly advancing efficiencies. Over the past decade, PSC efficiencies have significantly approached those of state-of-the-art silicon-based photovoltaics, making them a promising material. Currently, the scientific community widely recognizes the performance of 3D-PSCs and 2D-PSCs individually. However, when both are combined to form a heterostructure, the lattice and charge dynamics at the interface undergo a multitude of mechanisms that affect their performance. The interface between heterostructures facilitates the degradation of PSCs. The degradation pathways can be attributed to lattice distortions, inhomogeneous energy landscapes, interlayer ion migration, nonradiative recombination, and charge accumulation. This Review is dedicated to examining the phenomena that arise at the interface of 3D/2D halide perovskites and their related photophysical properties and loss mechanism processes. We mainly focus on the impact of lattice mismatch, energy level alignment, anomalous carrier dynamics, and loss mechanisms. We propose a “cause–impact–identify–rectify” approach to gain a comprehensive understanding of the ultrafast processes occurring within the material. Finally, we highlight the importance of advanced spectroscopic and imaging techniques in unraveling these intricate mechanisms. This discussion delves into the future possibilities of fabricating 3D/2D heterostructure-based optoelectronic devices, pushing the boundaries of performance across diverse fields. It envisions the creation of devices with unparalleled capabilities, exceeding the limitations of current technologies.

1. Introduction

The growing gap between the energy supply and demand has widened, driven by global instability. While the goal of bridging this gap seems distant, there is hope as countries increasingly recognize the importance of self-reliance through unconventional energy sources after years of neglecting environmental degradation warnings. Numerous strategic plans for achieving significant reductions in carbon emissions recommend promptly substituting fossil-fuel-based technologies with renewable energy sources and implementing long-duration energy storage systems. Solar photovoltaics show promising and sustainable pathways to withstand the growing trajectory of energy needs. This imperative extends beyond the immediate time frame, as sustained efforts over several decades are required to establish a robust foundation for a sustainable future. As a result, there is a strong argument for increasing the production of silicon solar cells and continuing the pursuit of more cost-effective solar technologies. Organic–inorganic halide perovskites recently emerged as the most promising and cost-effective material for photovoltaic applications, with performance nearly comparable to that of conventional single junction Si-based solar cells. The considerable interest these materials have attracted stems from their notable attributes, including a high absorption coefficient and photoluminescence quantum yield, along with extended charge carrier lifetime and diffusion length. Additionally, their tunable bandgap, lower exciton binding energy (E_b), and defect tolerance further contribute to their appeal among researchers.^1,2 But despite their higher efficiencies, three-dimensional (3D) halide perovskites still face challenges related to stability under external environmental conditions, such as heat, light, and moisture, making them a less practical choice for commercialization.³ Therefore, a relatively new class of materials, i.e., 2D perovskites, has piqued the interest of researchers due to its rich photophysics. Phase pure 2D (n = 1) or quasi-2D (with n > 1 phases present) perovskite structure is formed by slicing the 3D counterpart along the crystallographic facets with bulky organic spacer cations sandwiching inorganic Pb–I sheets, giving rise to the multiple quantum well structure. The reason for the success of these reduced dimensionality perovskites lies in their exceptionally improved stability against moisture.^4,5 But due to the quantum and dielectric confinement,⁶⁻⁸ they exhibit large exciton binding energies and poor conductivity, resulting in poor charge carrier separation and out-of-plane charge transport due to large spacer cations.⁹ Therefore, it is reiterated that what contributes to optoelectronic applications is not a particular advantage but rather a comprehensive performance.

The current narrative confirms that 3D perovskites demonstrate superior efficiency, while 2D perovskites are esteemed for their enhanced stability. However, when considering the practical, real-world application of halide perovskites, it becomes unreasonable to compromise between these pivotal performance parameters. Hence, the concept of 3D–2D (2D-on-3D) bilayer or heterostructures or interspersed type came into being with the significant advantage of stability along with unaffected efficiency.¹⁰ It is proven that the 2D layer over 3D acts as a preserver or passivating layer by reducing the impact of performance-degrading pathways.^11,12 So far, it seems unpretentious that since we had issues with constituent layers alone, their heterostructure is formed to gain a better performance. However, the formation of the heterostructure itself raises complications due to the interface between 2D and 3D layers affecting the photophysical properties of the fabricated devices. The complications at the interface are mainly due to lattice mismatch, energy level misalignment, trap states, interlayer ion migration, and loss mechanisms. Over the past decade, extensive research efforts have focused on gaining a comprehensive understanding of the complex interface.

The focus of recent efforts has been directed toward comprehending the mechanisms underlying photoinduced processes occurring at interfaces, employing a range of spectroscopic and imaging methodologies.^13,14 For instance, the utilization of nondestructive in situ photovoltage spectroscopy was implemented in order to investigate the phenomenon of charge transfer occurring at the nanoscale. The proposed methodology offers a distinctive means of exploring accelerated charge separation at the interface through the utilization of light-varying-frequency-dependent measurements.¹⁵ In addition to bilayer-based characterizations, there has been significant interest in investigating the device characteristics that arise from the incorporation of a 3D/2D heterojunction.^16,17 Although 2D perovskite-based passivating layers have been viewed as a positive addition to the system until now, recent research has presented contrary outcomes. Wang and co-workers demonstrated that phenethylammonium (PEA⁺) and butylammonium (BA⁺), upon reaction with formamidinium ions, deprotonate and form complexes that are detrimental to the device’s thermal photostability. The released ammonia (NH₃) in this process further damages the grain boundaries and interfaces. Therefore, it is suggested to employ cations with a high acid dissociation constant (pK_a) value.¹⁸ Furthermore, it has been observed that the random arrangement of 2D perovskites can lead to adverse consequences in terms of energy transfer and stability, which are closely linked to selection of the spacer cation. The present literature available on these heterojunctions still needs to be developed with clarity on the cause and impact for performance optimization. Investigating charge carrier dynamics across various time scales, from picoseconds to microseconds, using time- and temperature-dependent spectroscopic techniques, along with mathematical models, has profound implications for enhancing device performance.

The advancements from Si solar cells to perovskite-based SC were a breakthrough in the field of photovoltaics. Despite the exponential enhancement in efficiency, exceeding 25%, commercialization of perovskite solar cells, unlike Si, is a limiting factor. The main barrier to large-scale production of perovskite devices is the stability. The long-term stability is assessed with degradation tests. The damp-heat test¹⁹ is one of the standard procedures for verifying the commercialization of perovskite PV modules. For optimal performance resembling a commercial c-Si solar cell (PCE ∼20%), a stabilized PCE must pass a damp-heat test for over 1000 h with <5% relative loss. In this contest, a 2D/3D heterostructure has shown great promise. Azmi et al. constructed a 2D/3D heterostructure PSC with 24.3% PCE in 2022. They met one of the essential industrial stability standards for PV modules by retaining >95% of their initial PCE after >1000 h at damp-heat test conditions.²⁰ This is deemed to be a promising step toward the commercialization of 3D/2D perovskite devices.

This review provides an in-depth analysis of the influences on 3D–2D perovskite interfaces, concentrating on elucidating the intricate photophysics of this interface and examining a multitude of processes from both structural and carrier dynamics perspectives. In this discussion, we aim to offer insights into the significance of 3D−2D perovskites in optoelectronic applications and their broader implications. In light of the increasing shift toward multidimensional materials, the goal of the Review is to provide concise photophysics and accelerate the expedition toward the commercialization of such devices.

2. Formation of 3D–2D Perovskite Interface

As presented in the Introduction, one of the critical aspects of 2D perovskites and, subsequently, 3D–2D heterojunctions is the selection of spacer cations. On the basis of the spacer cation, i.e., monoammonium or diammonium, 2D perovskites can be categorized into three subcategories: Ruddleson Popper (RP), Dion Jacobson (DJ), and Alternating Cation Interlayer (ACI). Depending upon the octahedral offset and tilt associated with each structure, the electronic and structural properties of 2D perovskites vary. In-depth analysis of spacer cations has been reported elsewhere in the literature.^21,22 In order to tackle these challenges mentioned above with 3D perovskites, extensive investigations have been conducted by researchers in the discipline of utilizing diverse 2D spacer cations possessing distinct organic molecules. Most widely known of these are the RP monoammonium cations, which include butylammonium, propylammonium, phenethylammonium, etc. They are found to be efficient in improving the crystallinity and formation of highly oriented thin layers, hence benefiting charge transport and carrier lifetimes.^23,24 On the other hand, DJ perovskites are relatively recent, having diammonium cations including 1,4-butane-diammonium, 3-(aminomethyl)piperidinium, 1,7-heptanediammonium, etc. DJ-perovskites differ from RP in accordance with its stronger interlayer coupling due to shorter interlayer distances.²⁵ Owing to this, a lower confinement effect has been observed in DJ as compared to RP-based perovskites. Another class of 2D layered materials is the alternating cation, having two distinct cations in the interlayer space. Guanidinium cation is the best-known spacer in this category.²⁶ Due to the replacement of a single spacer with two smaller spacers, these spacer cations have piqued the interest of the community. Recently, researchers have employed these in high-efficiency near-infrared PeLEDs due to their better carrier transport and rigid crystal structure owing to H-bonding in GA cations.²⁷ To provide more insights on exciton recombinations and photophysical properties of the lesser explored ACI cations for improved performance for distinct applications, femtosecond-transient absorption (fs-TA) studies were undertaken by Ghosh et al.²⁸ With insights on the role of spacers in 2D perovskites, we will explore the synthesis and mechanisms giving rise to 3D/2D perovskites.

Considering the numerous advantages offered by 3D–2D heterostructures, it is crucial to prioritize the comprehension of the formation process to guarantee the accurate structural stability of the interface. In a typical solution-based process, a 3D perovskite layer is deposited onto the required substrate, followed by annealing for a particular time.

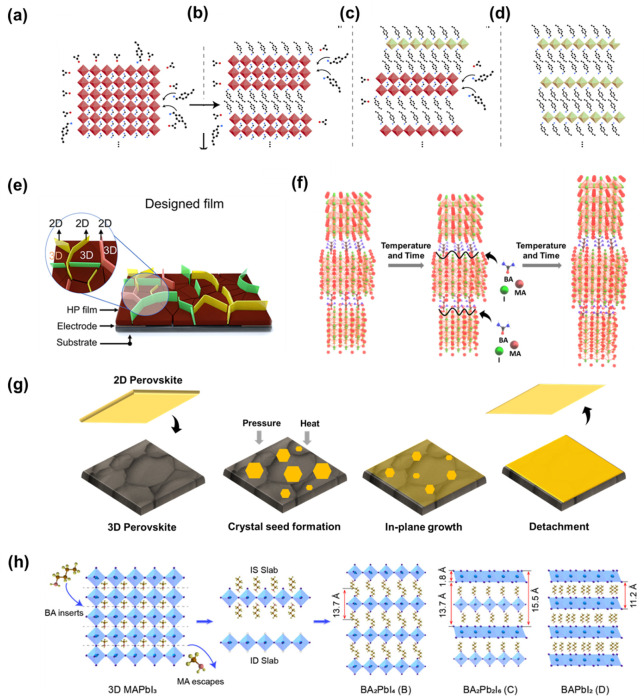
Following this, a solution containing ammonium-based spacer cations (i.e., ligands) mixed in an appropriate solvent forms reduced dimensionality perovskites (RDP) with varying thickness values, i.e., n value. The estimation of the number of octahedra present in inorganic perovskite structures, which are situated between organic spacer cations, is contingent upon the specific value of n. Proppe et al. provided the in situ insights via grazing-incidence wide-angle X-ray scattering (GIWAXS) into intermediate states formed before the formation of final RDPs by bisecting the 3D perovskite.²⁹ In this study, they used MAPbI₃ as a 3D perovskite and added a 4-vinylbenzylammonium bromide spacer cation solution dissolved in IPA for the subsequent formation of a 3D/2D interface. They put forward the mechanism depicted in Figure 1(a,b,c,d), which entails (a) infiltration by spacer cation takes place into a 3D lattice, hence (b) bisecting the 3D perovskite into the lower dimensional structure, and finally (c) bisecting it continuously until (d) reaching n = 1 RDP. The DFT calculations well backed up the mechanism given. The authors discussed the formation of the interface using a particular spacer cation where the infiltration and sequential bisection could be dependent upon its stacking, concentration of ligand solution, or maybe affinity toward the 3D counterpart. Hence, this mechanism may vary accordingly. Similarly, instead of the formation of a layered structure where we may get a gradient distribution of n-valued 2D RPPs, in a more practical situation, we get interspersed 2D domains inside the 3D matrix (see Figure 1(e)).³⁴

Figure 1.

(a–d) Hypothesized transformation of a 3D perovskite surface into RDPs. Reprinted with permission from ref (29). Copyright 2021 Springer Nature. (e) Formation of 2D platelets over a 3D film (red). Reprinted with permission from ref (30) Copyright 2022 Springer Nature. (f) Schematic of proposed intercalation mechanism. Reproduced with permission from ref (31). Copyright 2023 Springer Nature. (g) Top-view and cross-sectional sketches of the manufacturing of a (BA)₂PbI₄ film on a 3D perovskite substrate via the SIG method. Reproduced with permission from ref (32). Copyright 2021 Springer Nature. (h) Schematic illustration of the Pb–I octahedron collapsing and reconstruction model. Reprinted with permission from ref (33). Copyright 2020 American Chemical Society.

One of the critical aspects of the fabrication of the 3D/2D heterojunction has been the purity of the 2D layer. With recent advancements in the synthesis procedures, it is now possible to synthesize phase pure 2D perovskite crystals.³¹ The work discusses how control over temperature and time facilitates crystal growth by employing the kinetically controlled space confinement (KCSC) method. They proposed an intercalation process where the edges of 2D crystals provide a pathway for ions to penetrate the weakly bonded lattice. Figure 1(f) shows the mechanism for the formation of the n = 4 crystal. Initially, three inorganic layers were stacked and separated by BA spacer cations. Eventually, with time, the MA⁺, Pb²⁺, and I^– ions diffused through the edges and attached to the [Pb_nI_3n+1] structure. This solution-processed synthesis necessitates the selection of solvent used to dissolve the 2D and 3D precursors before coating. Sidhik et al. conducted an extensive study of deterministic fabrication of 3D/2D bilayer stacks by evaluating the Gutmann donor number (D_N) and dielectric constant (ε_r).³⁵ They distributed the solvent into three categories: nonpolar, polar protic, and polar aprotic. It was demonstrated that solvents like N-methylpyrrolidone (NMP), dimethylformamide (DMF), and dimethyl sulfoxide (DMSO) dissolve both 3D and 2D, whereas acetonitrile (MeCN), tetramethylsilane (TMS), and propylene carbonate (PC) dissolve 2D but not 3D. These conclusions provide segregation between the different solvents concerning the solubility of 2D and 3D perovskite powders and the subsequent formation of clearly distinct interfaces.

Apart from solution processing, various other 3D/2D processing methods have been proposed. Although solution-processed 3D/2D bilayers are widely used, they still lack adequate thermal stability and the formation of an built-in electric field at the interface. To overcome these issues, Jang et al. fabricated the 3D/2D bilayers using solid-phase in-plane growth (SIG).³² This process incorporates the optimization of pressure and heat for stacking solid 2D layers over a 3D film. Figure 1(g) shows the stepwise preparation with the SIG process. This method, along with control over the thickness of the passivating layer, also showed a superior PCE of 24.35% (certified). Vapor deposition techniques have also been used to avoid the interdiffusion of ions and organic cations at grain boundaries.³⁶ Moreover, it is a green solvent-free and large production method. This technique generally works on the principle of evaporating organoamine in gaseous or liquid form via heating and depositing it on 3D perovskite films. Liu et al. proposed a Pb–I octahedron collapsing and reconstruction model to explain the 3D to 2D transformation.³³Figure 1(h) shows the insertion of BA⁺ ions, which results in the annihilation of the lattice and subsequent replacement of MA⁺. The mechanism further explains the formation of X (halogen) rich (consisting of [PbX₆]^2– octahedra and BA⁺ cations) and X deficient (consisting of halogen vacancies) Pb–X slabs, resulting in multiple products during the in situ GIXRD studies.

The ongoing pursuit of enhancing the efficiency of heterojunctions necessitates the utilization of diverse synthesis techniques. This section discussed a few of these methods, shedding light on their potential contributions. To ensure the formation of the desired bilayer stack with a uniform distribution of ions, it is crucial to conduct a thorough initial characterization. To facilitate this essential step, synchrotron-based GIWAXS has been widely employed to probe the structural characteristics of perovskite thin films.³⁷ Mushtaq et al. used this technique to understand the depth-dependent crystal structure of (PEA)₂Cs₄Pb₅Br₁₆.³⁸ They performed surface- and depth-sensitive measurements to acquire diffraction patterns at 3.7 and 234.9 nm, respectively. They found that there are few PEA layers at the surface, whereas the orientation becomes random inside the bulk. Also, they suggested that the 2D perovskite is preferably oriented parallel to the substrate. Alongside orientation detection, another critical aspect of GIWAXS lies in revealing the byproducts (impurity, unreacted material, etc.) formed, which sometimes cannot be detected by simple XRD characterization.^39,40 With such advancements in in-situ and depth-controlled measurement, these could be highly beneficial to understanding the dynamics and chemical processes occurring at the 3D/2D interfaces.

3. Lattice Mismatch

Box 1.

• The connection between strain and the electronic band structure elucidates the unique photophysical characteristics of perovskite adlayers.

• Exciton dynamics can be modulated via intentional lattice mismatch via variation in the length and bulkiness of the spacer cations.

The term “lattice mismatch” refers to the disparity between the crystal lattice structures of two semiconductor materials that are used in a heterostructure. A crystal lattice is a repeating 3D arrangement of atoms in a solid material. When two semiconductor materials with different lattice structures are used to create a heterostructure, it is possible that their lattice parameters may not perfectly match. The measurement of lattice mismatch is conducted by quantifying the percentage disparity between the lattice constants of the two materials. The degree of misfit (f) due to the lattice mismatch is given by⁴¹eq 1

1

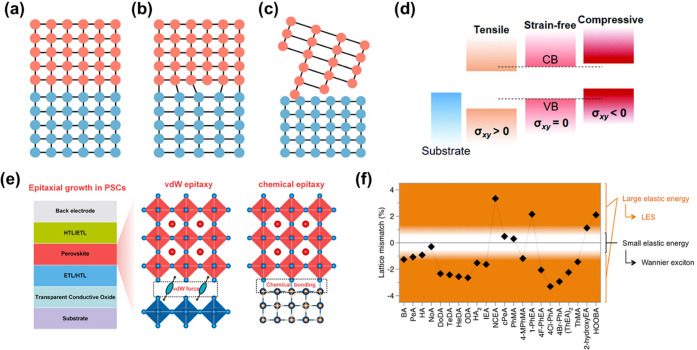
where the a₁ and a₂ are the lattice constants of the corresponding crystal planes of the substrate and epitaxial layer, respectively. Depending on the level of degree of misfit (f), three types of interfaces are commonly formed, i.e., coherent, semicoherent, and incoherent interfaces, which determine the interface properties. A coherent interface occurs when two crystals perfectly align at the interface plane, ensuring a continuous lattice structure across the interface, as illustrated in Figure 2(a). Achieving this perfect alignment requires the interfacial plane to have the same atomic arrangement (including orientation and spacing) in both phases regardless of the chemical composition. The strains associated with a coherent interface result in an increased total energy within the system. When the atomic mismatch between the two crystals is significant, or when the interfacial area is large, it becomes more energetically favorable to replace the coherent interface with a semicoherent interface. In a semicoherent interface, the misfit between the two crystals is accommodated periodically by misfit dislocations, as shown in Figure 2(b). However, when the atomic configuration of the interface plane is vastly different in the two adjoining phases, it is impossible to achieve a good match across the interface. This dissimilarity can result in a notable variance in the atomic arrangement of the two phases or a deviation in interatomic distances exceeding 25%. In either scenario, the interface is categorized as incoherent, as shown in Figure 2(c). Incoherent interfaces result in defects or electronic states at the interface due to the presence of dangling bonds.⁴¹

Figure 2.

Various forms of interfaces: (a) coherent interface, (b) semicoherent interface, and (c) incoherent interface. Reprinted with permission from ref (41). Copyright 2023 American Chemical Society. (d) Band offset of perovskites under in-plane strain. Reprinted with permission from ref (45). Copyright 2021 Royal Society of Chemistry. (e) Nature of interfaces between two materials based on their interaction. Reprinted with permission from ref (41). Copyright 2023 American Chemical Society. (f) Lattice mismatch between various monolayered A₂′PbI₄ perovskites and MAPbI₃. Reprinted with permission from ref (44). Copyright 2018 American Chemical Society.

Strain (ε) is a measure of the localized deformation experienced by a material due to factors like applied stress (σ) and nonuniform temperature gradients. Experimentally determined strains typically manifest as either tensile strain (stretching) or compressive strains (compression). Additionally, there is a noteworthy concept known as “microstrain”, which primarily accounts for the presence of localized regions experiencing both compressive and tensile strain. It arises due to differences in lattice mismatch and coefficient of thermal expansion (CTE) between the substrate and the layer.⁴² These microstrains in the material affect the structure at the interface and, consequently, have different impacts on the efficiency and stability of semiconductor devices. The strain between the two materials can stabilize/destabilize (phase transitions, ion migration, degradation, etc.) the structure depending on the type of strain developed, which may be beneficial/detrimental to improve/worsen the efficiency of the optoelectronic devices. The influence of strain-induced lattice expansion or contraction can significantly impact the strength of chemical bonds within the lattice and subsequently result in modifications to the electronic band structure, as depicted in Figure 2(d). This can lead to a modification in the band alignment of the heterostructures, resulting in either a type-I or type-II configuration, depending on the intended applications.

In semicoherent and incoherent systems, interfacial strain energy will increase proportionally with the lattice mismatch. To mitigate this increase in interfacial energy, misfit dislocations are intentionally created at the interface. These misfit dislocations, also known as threaded dislocations (TD), accommodate the excess strain generated during growth, thereby balancing the system’s energy. In case of significant mismatch, these misfit dislocations may extend into the bulk material. The density of misfit dislocations plays a pivotal role in determining the interface’s quality. Threaded dislocations are one-dimensional defects that form at the interface between two materials and significantly influence the photophysical properties. They act as prominent sites for carrier and light scattering or absorption, ultimately leading to a substantial reduction in the carrier mobility. Additionally, they create nonradiative centers in optoelectronic devices, greatly diminishing photoluminescence (PL) efficiency and device lifetime. Lattice mismatch can also affect the charge carrier dynamics of heterostructures due to changes in the electronic band structure. For example, hole–electron mobilities can be modulated by the nature of the strains present at the interface. Compressive strain initially enhances hole mobility through the reduction in hole effective mass (m_h*) until dislocations create significant issues under excessive strain.⁴³ New surface states can also be introduced due to changes in elastic stored energy created by lattice mismatching. These surface states are often beneficial for the dissociation of excitons.⁴⁴ In heterostructures, the nature of the interface between two materials can also vary based on their interaction. They may form a chemical epitaxy, characterized by a strong chemical bond between the substrate and the epilayer, or van der Waals (vdW) epitaxy, where weak intermolecular forces facilitate the growth of the epilayer film on the substrate (Figure 2(e)). In the context of 3D/2D halide perovskites, the van der Waals interaction is influenced by the tilting of the surface octahedra connected to the organic spacer cation. The unique flexibility of the organic spacer cation allows these materials to accommodate substantial strains, irrespective of the typical constraints related to crystal orientation and lattice constants between nonlayered solid materials.

Conversely, in an investigation conducted by Cahen et al., it was observed that the migration of large cations from 2D halide perovskites to 3D perovskites could occur, as evidenced by high-resolution transmission electron microscopy (HRTEM) analysis.⁴⁶ The deleterious impact of ion migration on the operational efficiency of optoelectronic devices has been well-documented in the literature. Understanding the relaxation of stored elastic energy at the surface of layered halide perovskite (LHP) materials is crucial in practical terms, providing a valuable platform for systematically evaluating and screening LHP compounds with specific functionalities for innovative devices. Building on this, Mohite et al. observed that the internal elastic stored energy in 2D/3D halide heterostructures is intricately linked to the degree of lattice mismatch. By employing a composite model and elastic theory, they revealed that a slight mismatch leads to minimal elastic energy storage. The manipulation of organic cation A exemplifies this significance in RPPs, as depicted in Figure 2f.⁴⁴ For instance, replacing BA with C₉H₁₉NH₃ (n-octyl ammonium) in RPPs significantly reduces elastic energy density,⁴⁷ preventing surface relaxation and preserving bulk Wannier excitons. Conversely, RPPs with (4Cl-C₆H₄NH₃)₂PbI₄ (4Cl-PhA) induce more considerable strain,⁴⁸ promoting significant surface relaxation suitable for electron–hole carrier separation. This comprehensive understanding offers valuable insights for the development of novel materials and devices, underscoring the intricate relationship among elastic energy dynamics, lattice mismatch, and the functionality of 2D/3D halide compounds.

Hence, it is evident that the lattice mismatch, serving as the foundational aspect in these devices, exerts an influence on all of the ensuing characteristics of the heterostructure. In the following section, we will delve into these aspects individually.

4. Energy Level Alignment

In the previous section, we discussed the impact of lattice mismatch, which impacts the 3D–2D interface’s stability and integrity. With a perspective on the structural aspect, we will now move onto the energetic landscape across the interface, i.e., energy alignment, which dictates the carrier dynamics. The energy level bands formed in 3D and 2D perovskite layers depend upon the hybridization of antibonding and bonding states of metal (Pb or Sn) and halogen (I or Br or Cl), hence forming conduction and valence bands. Umebayashi and Akai explored the electronic structure of 3D-MAPbI₃ and 2D-(BA)₂PbI₄ by employing DFT calculations. They showed that due to more structural distortion, the bands are more localized in 2D compared to 3D, resulting from bandwidth narrowing.⁵⁰ The work exemplified the effect of dimensionality on the electronic structure, which further dictates the band alignment at the 3D/2D interface. To design a high-performing optoelectronic device, it is necessary to make a near-perfect interface, allowing easy charge transfer across the layers. This will lead to high charge collection at the contacts, which in turn increases current density (J_SC) and open circuit voltage (V_OC). Nevertheless, charge transfer is not that straightforward in the case of 2D perovskites, and due to high E_b, the charge separation capability is reduced.⁵¹ Therefore, mixed dimensional perovskites with higher n-value 2D perovskites are preferred for better charge separation due to their lower E_b. Also, the built-in electric field formed by the so-called 3D–2D p–n junction plays a significant role in hole extraction and quasi-Fermi level misalignment at the 2D and 3D sides.⁵² Hence, proper band alignment for unhindered charge separation is of utmost importance. The main mechanisms at the 3D–2D heterojunction interfaces are energy cascading between distinct phases and charge separation depending upon the type of band alignment. With the above-made consensus of dimensionality, varying band structures are formed upon considering a perfect case of a layer of 2D and 3D perovskite heterojunctions; the charge and energy transfer may take place via type-I or type-II band alignment. There has been no explicit agreement on the formation of either, but it may vary with the synthesis process,⁵³ organic molecule concentration,⁵⁴ or charge neutrality levels,⁵⁵ etc. Even Zhang et al. proposed that 2D perovskites are prone to energy level misalignments due to strong electron–phonon coupling resulting from thermal fluctuations.⁵⁶ A lot of effort has been put forward to accurately determine the type of band alignment experimentally,^17,57 via mathematical modeling⁵³ and DFT simulations.⁵⁸

Box 2.

• Enhancing band alignment in heterojunctions may boost stability and reduce degradation processes caused by charge buildup at interfaces.^10,49

• The engineering of band alignments at the interface between 3D and 2D materials allows for improved control over carrier energy levels and transport characteristics within the device.

Band alignments in heterojunctions are classified into type I, type II, and type III, namely, straddling, staggered, and broken, respectively. For the sake of this review, type I and II are discussed in detail. Briefly, in the context of type-I band alignment, it is observed that the exciton, i.e., the electron–hole pair bound by Coulombic forces, undergoes a process known as energy funneling. This phenomenon entails the migration of the exciton from a region characterized by a larger bandgap (smaller n) to a region with a smaller bandgap (larger n). As a consequence of this exciton migration, energy is transferred across the heterojunction. In the context of type-II band alignment, it is observed that the transfer of electrons and holes occurs in opposite directions, resulting in the establishment of charge separation across the heterojunction. Specifically, for 2D perovskites, there has still been a debate on accurately predicting the type of band alignment that they show. For instance, in some published literature, butylammonium and phenethylammonium-based 2D perovskites are shown to form type-I alignment,^59,60 whereas contrary results were demonstrated by others.^61,62

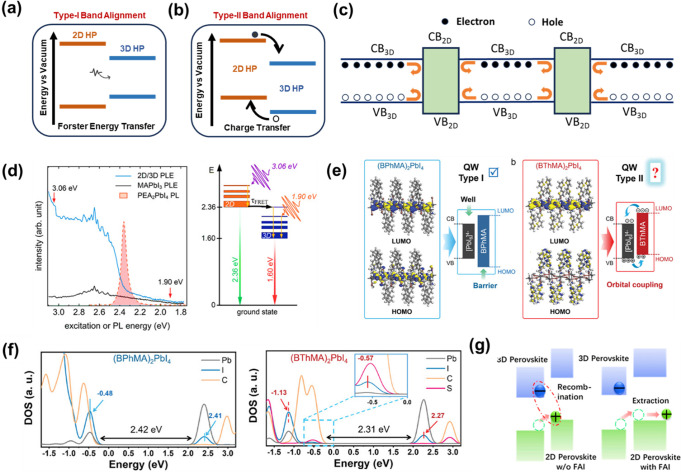
As shown in Figure 3(b), type-II band alignment favors the charge separation at the interface where the CBM and VBM levels of 3D are staggered with respect to 2D band edges. This configuration is efficient for electron (hole) transfer across the interface in p-i-n (n-i-p) structures.^63,64 On the contrary, type-I band (Figure 3(a)) alignment corresponds to the scheme where the CBM and VBM of 3D perovskite lie inside the bandgap of 2D perovskite. This arrangement does not facilitate the charge transfer as both the electrons and holes require some energy to get transferred from one system to another. So, while it may not offer significant advantages for solar cell and photodetector applications, it has been demonstrated to be advantageous in alternative ways: (i) when the heterojunction is formed in a way such that 2D phases are vertically grown at 3D grain boundaries (GBs), carriers are reflected instead of getting trapped at the GBs, as shown in Figure 3(c),⁶⁵ hence reducing recombinations; (ii) the faster energy transfer in quasi-2D perovskites is valuable for efficient light-emitting diodes (LEDs) and laser applications due to energy funneling.⁶⁶

Figure 3.

Energy level representation of (a) type-I and (b) type-II band alignment, and (c) electronic band offsets of the 2D–3D heterojunction indicating carrier blocking at the vertically grown 2D and 3D interface. Reproduced with permission from ref (65) Copyright 2017 Springer Nature. (d) PLE spectra for 2D/3D heterojunction at different excitation intensities and corresponding energy level diagram for energy transfer mechanism. Reprinted with permission from ref (16). Copyright 2023 Wiley-VCH. (e) DFT calculated HOMO, LUMO, and proposed energy levels of organic and (BPhMA)₂PbI₄ (left) and (BThMA)₂PbI₄ (right). Reprinted with permission from ref (58). Copyright 2023 Wiley-VCH. (f) PDOS plots of (BPhMA)₂PbI₄ and (BThMA)₂PbI₄. Reprinted with permission from ref (58). Copyright 2023 Wiley-VCH. (g) Schematic illustration of improved hole extraction after FAI incorporation. Reprinted with permission from ref (77). Copyright 2018 Elsevier.

The above-mentioned energy funneling and charge transfer are extremely fast processes occurring at the femto- to microsecond time scale inside the material. Upon excitation, 2D and 3D perovskites generate free charge carriers or bound excitons at the picosecond (ps) to femtosecond time scale. If the above bandgap excitation takes place, carriers occupy states above the band edge states and are deemed to be hot carriers.⁶⁷ The carrier cools via thermalization, and this takes place at hundreds of picoseconds. The carriers further move toward respective electrodes to get extracted or funnels across bandgaps to recombine radiatively. However, during these processes, they may get captured by defect states and recombine nonradiatively.⁶⁸ To capture and study these phenomena efficiently, ultrafast femtosecond transient absorption (fs-TA) spectroscopy is employed. Many studies employing 3D perovskites detect varying mechanisms such as polaron formation,⁶⁹ carrier cooling,⁷⁰ hot phonon bottleneck,⁷¹ etc. These studies subsequently give in-depth insights into the structural dynamics. With great success in determining complex charge carrier dynamics in 3D and 2D perovskites, fs-TA has been providing crucial information in 3D–2D systems. Fei et al. demonstrated that PAI-doped Cs_0.05FA_0.80MA_0.15Pb(I_0.85Br_0.15)₃ showed reduced recombinations by using TA at the bulk and surface.⁷² In another study, doping 5-ammonium valeric acid iodide (AVAI) cation in α-FAPbI₃ explained the carrier lifetimes by decay rates of ground state bleach and stimulated emissions from TA spectra.⁷³ Energy and charge transfer are detected upon correlating femtosecond-TA spectroscopy with varying carrier injection levels and time-correlated single photon counting (TCSPC) or time-resolved photoluminescence (TRPL).

The synthesis of phase pure 2D perovskites is not easy to accomplish. In the majority of situations, what is synthesized is a quasi-2D perovskite system characterized by mixed values of n. In the work of Yang et al., they prepared a 2D gradient with low n-values at the bottom and high n (3D-like) values at the top using ammonium chloride to segregate the phases. As with the increasing n-value, CBM decreases, whereas VBM remains the same; this built-in band alignment resulted in fluent charge transport.⁷⁴ Along with charge transfer, energy funneling is another prominent effect at the 3D/2D interfaces when type-I band alignment is formed.⁶⁶ This fret energy transfer phenomenon was reinforced at the (PEA)₂PbI₄/MAPbI₃ interface employing photoluminescence (PL) studies. PL excitation (PLE) measurements carried out at different energies shown in Figure 3(d) revealed that both the 3D/2D heterostructure and 3D MAPbI₃ films show an enhancement in PL intensity. An abrupt PL enhancement is observed above 2.36 eV for the 3D/2D perovskite film. Briefly, upon exciting the MAPbI₃ with 1.90 eV, no change in PL intensity was observed as it did not excite (PEA)₂PbI₄, but exciting it at 3.06 eV showed PL enhancement at 2.36 eV, as shown in Figure 3(d), with the addition of the 2D-(PEA)₂PbI₄. This is attributed to type-I band alignment and energy transfer from the low n system to the high n system (MAPbI₃) at the interface.¹⁶ This energy funneling and charge transport from 2D to 3D systems occurs due to lower exciton binding energies associated with high n systems along with the lowering of trap-assisted nonradiative recombinations.^75,76 The next section will dwell upon the concept mentioned above, providing a distinct perspective point that will center around mobility and diffusion.

Until now, organic spacer cations have been thought to affect device performance due to their adverse insulating nature, which, subsequently, hampers carrier transport. More recently, the concept of quantum confinement breaking in 2D perovskites achieved an impressive PCE of 18.05%.⁵⁸ The authors demonstrated the positive effect of orbital coupling between [PbI₆]^4– and organic spacer cations. The bithiophenemethylammonium (BThMA) spacer where coupling was observed, unlike the biphenylmethylammonium (BPhMA) spacer, was used to prove the hypothesis. The formation of a simple but effective arrangement (type II) was due to the narrower bandgap and upshifted highest occupied molecular orbital due to the smaller dihedral angle between aromatic rings in the BThMA spacer as compared to the BPhMA spacer. A larger dihedral angle in BPhMA reduces the conjugation between rings, forming wider bandgaps and turning them into type-I alignment. Hence, orbital hybridization in BThMA organic spacer cations and inorganic [MX₆]^4– gives rise to preferential type-II band alignment (Figure 3(e)). The concept of orbital coupling was strengthened by determining the partial density of states in both systems. As shown in the PDOS plot (Figure 3(f)) for (BPhMA)₂PbI₄, their band structure is formed by I 5p and Pb 6s orbitals, whereas, in (BThMA)₂PbI₄, the new hybridized I 5p state is seen in the PDOS plot, giving evidence for coupling in [PbI₆]^4– and spacers. This molecular optimization had multifold advantages consisting of improved film quality with a better crystal orientation, enhanced dielectric constant, decreased binding energy, and a longer carrier lifetime.

An additional facet of band alignment pertains to the alteration of the conductivity in a 2D layer. The incorporation of conductive channels via p-type doping improved hole extraction. Zhang et al. prepared MAPbI₃/(BA)₂(MA)_n−1Pb_nI_3n+1 to show superior hole extraction properties with and without an organic hole transporting layer, i.e., Spiro-OMeTAD. They successfully showed improved retainment of initial PCE without Spiro-OMeTAD. They further explored the variation in electrical properties of the 2D perovskite layer. They found out that the addition of formamidinium iodide (FAI) in incremental concentrations, i.e., from 5 to 40 mg/mL, increased the Fermi level positions exponentially except for 40 mg/mL, suggesting a change in the electronic properties of the 2D layer via FAI doping. Figure 3(g) shows the energy band structure with and without the addition of FAI. The occurrence was detected by observing a higher photoluminescence (PL) intensity and smaller crystal sizes without FAI. With FAI addition, the crystal size of the 2D layer increased by 2.5 times and much lower PL intensity, pointing toward a lowering in radiative recombinations. Along with the factors mentioned above, they also observed a heterogeneous increase in grain conductivity as confirmed by conductive atomic force microscopy (c-AFM), specifically in regions with high FAI concentration.⁷⁷

The control of phenomena occurring at the interface of nanoscale systems poses considerable challenges owing to the intricate nature of the processes involved. Despite the susceptibility of semiconductor materials to defects that may have negative consequences, energy level alignment of interfaces may offer several benefits if appropriate engineering techniques are applied.

5. Charge Carrier Dynamics at 3D/2D Interface

Box 3.

• The transfer of holes and electrons across the interface is influenced by the carrier mobility in both in-plane and out-of-plane directions.

• Models I and II explain carrier transport with varying band alignments, while Model III evaluates dynamics under illumination.

5.1. Model I: Charge Separation

The elucidation of the structural characteristics and electronic properties of perovskite heterostructures, specifically those composed of 2D and 3D perovskites with a type-II alignment, will be expounded upon by the framework termed Model I (Figure 4(a)). The formation of favorable gradient energy alignment for charge separation is achieved by the gradual phase variation (from low n (2D) to high n (3D)) along the axial direction. The type-II band alignment provides the perfect energy scenario for moving electrons and holes in opposite directions, facilitating effective charge separation at the interface and thus being collected at the respective electrodes. The carrier mobility of 2D perovskites was demonstrated as one of the critical parameters in charge carrier transport.⁷⁸ The carrier mobility for layered organic–inorganic 2D perovskites is highly direction dependent; i.e., the in-plane carrier mobility is several orders of magnitude higher than the out-of-plane carrier transport. The charge carrier transfer in low n Ruddleson Popper (RP) 2D perovskite is restricted to one dimension (1D), consequently altering out-of-plane carrier mobility.⁷⁸ Such a constraint can be overcome by vertically oriented growth of RP 2D perovskite. However, in the case of Dion Jacobson (DJ), 2D perovskite out-of-plane charge transfer is possible with a short-chain spacer cation.⁷⁹ In DJ perovskites, the immobile divalent interlayer spacer cations push the inorganic slabs close to each other. Due to this, the interlayer halide–halide distance is shortened to ∼4.0 Å, which induces a strong coupling between the metal halide octahedra (Figure 4(b)).⁸⁰ Due to strong intralayer coupling and the short interlayer distance between the two inorganic layers, the electron cloud over the metal halide octahedral layers can overlap across the organic spacer cations, thus reducing the quantum confinement that is predominant in RP perovskites. Model I assumes the ideal conditions of PSC fabrication, and thus, there arises a need to explore a more general and practical case further.

Figure 4.

(a) Model I of mixed-dimensional 3D/2D HP films. Schematic diagram of the gradual dimensionality transition along the axial direction, the type-II band alignment of low-n/high-n heterojunctions, and the internal carrier separation along the axial direction. Reproduced with permission from ref (85). Copyright 2023 American Chemical Society. (b) Spinor density for (BA)₂PbI₄ and (MAMP)PbI₄ perovskites illustrating interlayer I–I interactions. Reprinted with permission from ref (80). Copyright 2020 Springer Nature. (c) Model II of mixed-dimensional 3D/2D HP films. Schematic diagram of the interspersing-type phase distribution, the type-I band alignment of low-n/high-n heterojunctions, and the corresponding charge transport. Reproduced with permission from ref (85). Copyright 2023 American Chemical Society. (d) Absorption and PL characteristics of 2D/3D hybrid perovskites with different Cs⁺ doses. Linear absorption (lines) and steady-state PL spectra (areas) (left). Schematic of cascade carrier transfer from small- to large-n phases (right). Reprinted with permission from ref (84). Copyright 2018 Wiley-VCH. (e) Model III of mixed-dimensional 3D/2D HP films. Schematic diagram of the interspersing-type phase distribution, energy band structure of HP junctions, and illustration of the distinct charge transports in darkness and under illumination. White arrows represent charge transport. Reproduced with permission from ref (85). Copyright 2023 American Chemical Society. (f) (i) TA spectra at typical delay times. The PB bands are marked by peak positions (nm). (ii) TA traces of the PB bands (amplitude) as a function of the decay time. Reprinted with permission from ref (83). Copyright 2022 Wiley-VCH.

5.2. Model II: Energy Funneling

The layered axial distribution of varying n-valued 2D perovskite phases upon 3D perovskite is not ideal, as considered in Model I. Instead, it is randomly distributed (or interspersed in 3D domains), making the carrier dynamics complex, as depicted in Model II (Figure 4(c)). One of the ways to understand the charge carrier dynamics is based on the type-I band alignment between 2D and 3D perovskite. The photoexcited charge carriers are believed to be transferred from low n 2D to 3D. If the energy transfers from n = 1 to n = 2 and further on to 3D, it will provide one of the ways to harvest high-energy photons for photovoltaic applications. In the case of LED and LASERs, this type of mechanism is used to produce a narrow distribution of emitted light via an energy cascade, also called energy funneling.⁶⁶ Several research groups have provided evidence showcasing the facilitation of exciton transfer from 2D to 3D through the offset of the CBM and VBM in perovskite heterostructures. In the majority of cases, it has been observed that there is a negligible variation in the VBM, but the CBM undergoes a decrease upon going from low n (2D) to high n (3D) perovskite (see Figure 4(d)).⁷⁵ As a result of this arrangement, the transfer of holes is impeded and the electron exhibits a greater mobility compared to the hole. Hence, exciton dissociation followed by the transfer of electrons leaves excess holes in the valence band, so this hole tries to form an exciton with excess electrons in the conduction band. Further, energy funneling can be understood by Förster resonance energy transfer (FRET) and Dexter-type charge transfer (CT) via carrier diffusion.^79,81,82 The FRET is based on resonant energy transfer from low n 2D to high n via dipole–dipole coupling. However, the CT process occurs due to the charge carrier drift and diffusion induced by the electric field at the heterojunctions of 3D–2D perovskites. Yuan et al. demonstrated that the whole energy funneling followed by the FRET mechanism can be completed after 100 ps.⁷⁵ On the contrary, Gan et al. suggested that the energy funneling that occurred via the CT mechanism takes time longer than 2 ns.⁸³ In his research, the use of TA spectroscopy measurements uncovers that FRET plays a crucial role in ultrafast energy funneling. The TAS spectra for n = 3 quasi-RPP perovskite show the prominent PB at 616 nm. The existence of multiple PB bands indicates that the n = 3 quasi-RPP perovskite contains grains with different n values [Figure 4(f(i))]. As this material has different phases, it is evident that they may form a heterostructure, and depending on the band alignment, there may be energy funneling or charge transfer. To verify this, the authors recorded the excited state population decay profile at various wavelengths corresponding to each PB band. The population decay profile shows that the PB band at 616 nm reaches a maximum within 0.2 ps, whereas other PB bands require a longer time of 1 ps [Figure 4(f(ii))]. It is noted that the difference in time scales was observed due to the ultrafast energy funneling from n = 3 to higher n domains. The coexistence of the charge carrier and energy transfer verified by Wei et al.⁸⁴ reveals that the Coulomb coupling between different perovskite phases enables the ultrafast interfacial charge and energy transfer in 3D–2D perovskites, as demonstrated in Figure 4(d). It can be observed that the PL spectrum is dominated by the 3D perovskite. The PL excitation spectra show peaks corresponding to n = 2, 3, 4 when the PL detection energy is in resonance with 3D perovskite. Similarly, the rise corresponding to n = 2 is found when PL detection energy is in resonance with n = 3. Hence, we can affirm the occurrence of energy transfer from lower n to higher n. The TAS demonstration of ultrafast carrier transfer lends support to the simultaneous presence of both energy funneling and charge transfer.

5.3. Model III: P–N Junction

More recently, Model III explains the charge transfer across the interface by introducing the concept of the PN junction (Figure 4(e)). According to this model, the 3D/2D perovskite heterojunctions are viewed as PN junctions with built-in potential, and they show anomalous behavior upon light irradiation. The model also considers the interspersing phase distribution pattern. Still, it views the 3D/2D interface as the main culprit for diminishing charge transport instead of the 2D layer, as predicted by Models I and II.⁸⁵ This was proven by the fabrication of the ITO/perovskite film/ITO structure, where, under dark conditions, free charge transport between 3D grains and 2D flakes was observed. However, under illumination at low bias, a negative photoconductivity was observed. The model explains that 2D perovskite alone cannot be responsible for hampered charge transport, as none of its drawbacks can potentially reverse the photoconductivity. Therefore, it was concluded that the behavior of the 2D/3D heterojunction in transition from dark to light originates from a built-in potential barrier for charge transport. This was further attributed to the misalignment of the Fermi levels at the 2D and 3D sides.

Hence, Model III suggests that the problem with charge transport and PCE is primarily associated with the 3D/2D interface rather than the individual 2D layer, which is in contrast to Models I and II. The earlier perspectives posited that charge transport issues in 2D perovskite materials could be achieved through enhancements in specific attributes. These attributes encompass the phase orientation, carrier mobility, and phase content. The researchers prioritized the enhancement of the characteristics of the 2D layer rather than directed their attention toward addressing the underlying issue in the 3D/2D interface. Addressing the challenges encountered regarding charge transport at the interface plays a pivotal role in enhancing the overall efficiency and functionality.

6. Loss Mechanisms

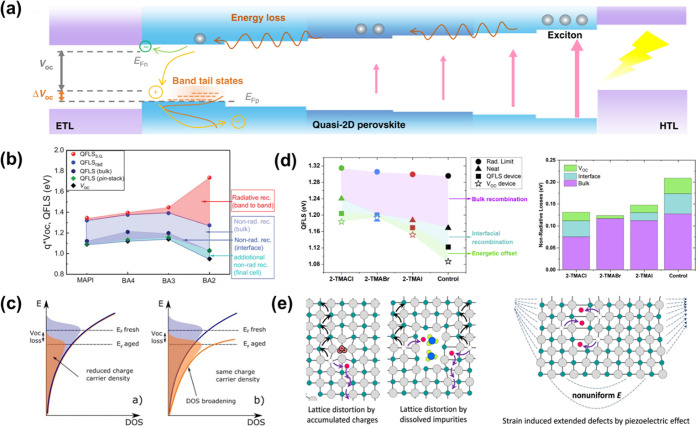
The successful development of an interface between heterostructures necessitates a meticulous approach that takes into consideration the potential loss mechanisms that may arise during the fabrication process or in the operational state. The present section aims to delve into the intricate physics underlying 2D and 3D perovskites, with a particular emphasis on interpreting the mechanisms responsible for the observed drop in performance. The losses can take various forms, such as energy loss, voltage loss, and interfacial recombination losses. Furthermore, the flexible ionic lattice structure in perovskites and, more recently, the dynamic behavior of the spacer cations have further exacerbated the situation. The discussion previously cemented that the dynamics at the interface are dominated by two processes: (i) charge transfer and (ii) energy transfer, and both of these occur at different time scales. The latter, being the faster process, helps the photogenerated carriers to descend to the low bandgap material present in the system, owing to the energy loss (due to hot carrier relaxation).⁸⁶ This energy loss primarily takes place when the inhomogeneous energy distribution exists in the quasi-2D perovskite systems (see Figure 5(a)). Therefore, efforts have moved toward judiciously selecting the spacer cations to maintain flattened energy band structures. These spacer cations have the foremost contribution toward antibonding interactions (due to interlayer electronic coupling⁸⁷), hence shifting VBM up. In contrast, the hybridization of s and p orbitals of halide ions leads to octahedral tilting shifts in both VBM and CBM to produce a nonuniform-energy landscape.⁸⁸ In the context of device fabrication, V_oc and the fill factor (FF) emerge as paramount parameters. Voltage loss in 3D/2D heterojunction-based devices is a significant challenge that arises from the processes previously discussed. The observed phenomena tend to alter the work functions, thereby resulting in a restricted V_oc.⁸⁹ Zhang et al. studied the electro-optical properties of BA₂MA_n–1Pb_nI_3n+1 and MAPbI₃. They identified the impact of recombination currents on quasi-Fermi level splitting (QFLS) losses. There are multiple voltage loss pathways (Figure 5(b)), such as radiative, nonradiative, and interfacial recombination at the perovskite/transport layer. The quantification of nonradiative losses was calculated by measuring the QFLS for the neat perovskite bulk and QFLS at photoluminescence quantum yield (PLQY) = 1, i.e., radiative limit and taking their difference, which was associated with Shockley–Read–Hall recombinations. Using the Shockley–Queisser limit, the maximum QFLS that can be reached theoretically was determined by taking the difference between the red dots and blue dots. Similarly, other losses at the surface and interface can be quantified using comparative analysis of neat and completed devices via the intersection of photoluminescence quantum yield (PLQY), electroluminescence quantum efficiency (EQE_EL), and absorption behavior. Moreover, due to the formation of a disordered structure,⁹⁰ it consequently seeps into the formation of band-tail states. These states extend from the bands into the bandgap of the materials and become recombination centers (see Figure 5(c)). It comes with dual-faceted disadvantages, i.e., (i) increases trap-assisted recombination pathways and (ii) reduces the quasi-Fermi level splitting (which determines the device’s V_oc) by the density of states broadening.⁹¹ Therefore, it is plausible that the occurrence of losses in 3D/2D heterostructures is attributable to disordering phenomenon. This can be attributed to the inherent challenge of effectively controlling the ordered nature at the interface. The Maxwell–Wagner effect model, as described in the literature,⁹² explains the phenomenon of charge accumulation that occurs upon the formation of a heterojunction.⁹⁶ This happens due to the difference in carrier spreading times across the junction. As a result of the accumulation of charges, a potential barrier may form at the interface, leading to a decrease in the open-circuit voltage (V_oc). Eventually, Sutanto et al., upon halide modification in a thiophene-based spacer cation, showed a near perfect interface with zero interfacial losses (see Figure 5(d)). This phenomenon has been attributed to energy level alignment and optimal charge density at the interface, resulting in a decrease in nonradiative recombinations.⁹⁴ As mentioned above, interface rigidity influences the behavior of the components in the lattice or vice versa. However, due to the ionic nature of the perovskite lattice, the ions (Pb²⁺, X^–, MA⁺, FA⁺, or Cs⁺) tend to migrate under heat, electric field, or illumination. As discussed in the third section, lattice mismatch gives rise to local lattice disorder. The pathways depicted in Figure 5(e) illustrate the lattice distortions that give rise to ion migration channels.⁹⁵ Many groups have explored the impact of these channel formation possibilities.⁹⁷⁻¹⁰⁰ It has been proven that this lattice softening is the reason for ion migration inside the perovskite systems, which in turn impacts the photostability, intrasystem phase segregation, increased charge trap states, and hence reduces the V_oc and fill factor of the devices. Considering the significant promise shown by 3D–2D perovskites, it is highly probable that they can serve as replacements in various applications, leading to substantial performance improvements. Nevertheless, as discussed in the earlier review, achieving the desired results depends on the comprehensive examination and subsequent optimization of the heterojunction interface.

Figure 5.

(a) Operation mechanism of quasi-2D perovskite photovoltaics and the correlation between the band structure, energy disorder, and V_oc of the device. Reprinted with permission from ref (80). Copyright 2020 Springer Nature. (b) QFLS is calculated from the PLQY for the neat material and the full device (left), and different types of energy losses are calculated from the left to compare the contribution of the other recombination processes for each system (right). Reprinted with permission from ref (93). Copyright 2019 Wiley VCH. (c) An open-circuit voltage loss can be caused by either increased recombination that lowers the charge carrier density (left) or broadening of the density of states with unchanged charge carrier density (right). Reprinted with permission from ref (89). Copyright 2015 Wiley-VCH. (d) QFLS and V_oc losses are in the bulk and at the interfaces and electrodes. The QFLS obtained in the bulk of the layered perovskites and MAPI (blue hexagons) is impacted by radiative (red shaded area) and nonradiative (light blue shaded area) recombination losses, while the QFLS in the p-i-n stacks (green diamonds) is affected by additional nonradiative interfacial recombination losses (blue shaded area). The presence of the electrodes in the final cell causes additional nonradiative recombination losses concerning the QFLS of the p-i-n stack (turquoise shaded area). Reprinted with permission from ref (94). Copyright 2021 Elsevier. (e) Illustration of the ion migration pathways enabled by lattice distortions due to accumulated charges, dissolved impurities, and nonuniform strain caused by the piezoelectric effect. Reprinted with permission from ref (95). Copyright 2016 American Chemical Society.

Box 4.

• The interface loss mechanism primarily affects the device’s operational efficiency, and it largely depends on the interface recombination process, which includes charge carrier trapping and detrapping.

• The investigation of degradation pathways and underlying mechanisms, including defect formation, ion migration, and phase transitions, holds significant potential for advancing the stability of perovskite devices.

7. Conclusion

The exploration of charge carrier dynamics at the interface in perovskite solar cells has shown significant advancements due to the existence of multiple interfaces within these devices. The adoption of 3D–2D perovskite-based devices has seen a considerable increase. However, several challenges remain during the fabrication process that require a systematic resolution strategy. The fundamental issue of lattice mismatch significantly influences the electronic and structural properties of the interface. Furthermore, the specific type of band alignment formed at the interface is yet to be fully comprehended. Once these issues are successfully optimized, it becomes essential to tackle more complex challenges, particularly the losses that arise during the integration of the absorber layer into the device structure. Hence, we advocate for the use of the “cause-impact-identify-rectify” approach for thorough evaluation. In closing, research on 3D–2D perovskites and their potential applications in high-performance photovoltaics and optoelectronics is still being developed. We posit that a detailed understanding of charge carrier dynamics and loss mechanisms at the perovskite solar cell interface is crucial to overcoming the existing limitations in their performance and functionality.

8. Future Outlook

Among emerging solar technologies, halide perovskite solar cells stand out as one of the most promising options for imminent deployment. They have achieved efficiencies that surpass those of single-junction silicon solar cells. 3D halide perovskites and 2D halide perovskites exhibit strong material compatibility, enabling their integration within a single device by using various design approaches. The incorporation of both 3D and 2D halide perovskites into a single solar cell allows for achieving the stability characteristics of 2D materials without compromising the efficiency associated with 3D materials. Current research lacks the appropriate utilization and development of advanced characterization techniques to study the interface loss mechanism accurately. The challenge that arises in the study of heterostructures is inadequate techniques and limited penetration depth of commonly used incident beams, which hinder the acquisition of information about the interface within the bulk of the material. Therefore, it is essential to employ beamlines that utilize hard X-rays to generate sufficient energy to access the interface. Moreover, recent advancements in science have led to significant progress in the field of attosecond-level spectroscopy as well as high-resolution imaging (∼0.050 nm). These cutting-edge techniques offer a promising avenue for investigating ultrafast processes and exploring the structural intricacies of various interfaces. However, it is essential to note that these spectroscopic techniques (TA spectroscopy, time-resolved photoluminescence, deep-level transient spectroscopy, impedance spectroscopy, etc.) cannot be relied upon solely. Therefore, it is a must to establish a proper correlation between these spectroscopic techniques and imaging techniques (HR-TEM, STM, c-AFM, FE-SEM). A closer inspection of the correlation between these two categories can yield a more precise and complete visual representation of the complex interplay among various mechanisms within the materials under consideration.

The commercialization of 3D–2D-based photovoltaic technology presents several noteworthy issues. To facilitate the charge transport toward their respective electrodes, it becomes necessary to separate the charges effectively. However, the presence of long-chain organic ligands in 2D perovskites has been observed to impede the flow of charges in the thin films. Therefore, additional research efforts are necessary to explore methods to allow charge transfer across organic ligands to inorganic layers or to identify suitable alternatives that can effectively safeguard the integrity of heterostructures while preserving their desirable performance. Furthermore, the integration of 3D–2D heterostructures has emerged as a promising approach in the development of advanced photovoltaic devices, LEDs, and lasers. With the growing emphasis on sustainable energy solutions, 3D–2D perovskite-based devices have become potential candidates for the development of unassisted solar water-splitting systems. The extended durability, stability, and panchromatic absorption properties of the material present potential for harnessing these advantages to convert electrical energy into chemical energy effectively.

Heterojunctions that employ a combination of 2D and 3D materials have recently attracted significant interest in the discipline of light-emitting diodes (LEDs) due to their remarkable photoluminescence quantum yield (PLQY). The advantage is derived from the nanosized perovskite grains as well as the presence of long-chain spacer cations. These factors collectively contribute to the reduction in the exciton diffusion length, resulting in a material that exhibits exceptional efficiency and luminescence properties. The investigation and analysis of 2D perovskites have yielded notable advancements in the efficiency of these devices. This can be attributed to the elevated exciton binding energies inherent in 2D perovskite structures, which consequently facilitate a greater number of radiative recombinations. Moreover, when combined with a 3D counterpart, it not only shows improved luminescent properties but also reduces the trap density, i.e., defect passivation, for better performance. Hence, in the future, exploring the concepts based on energy funneling discussed in this Review could yield ground-breaking LED efficiency. There is a growing demand for medical X-ray imaging to minimize the X-ray dose acquired by the patient down to single-photon sensitivity. Lead halide perovskites make up the most intensely studied class of contender high-Z materials for high-energy photon detection. The X-ray absorption coefficients of halide perovskite are a few-fold higher compared with the most used material, cadmium telluride, for soft X-rays. Moreover, due to their high quantum efficiency, short decay time, and inexpensive cost, halide perovskites could become a top contender for X-ray imaging.

Halide perovskites have garnered significant attention as promising materials for memristors due to their ability to utilize hysteresis, which is based on the motion of defects or ions within the halide perovskite structure. The current state of research regarding the utilization of perovskite materials as memristors is still in its nascent phase. Several obstacles and issues need to be addressed in order to facilitate real-world implementation of halide perovskites in advanced memory devices of the future. Reconfigurable memristors have been successfully developed utilizing halide perovskites, demonstrating the ability to switch between volatile and nonvolatile modes through controllable electrochemical reactions. These reactions involve a combination of both ionic diffusive and drift mechanisms, enabling on-demand switching capabilities. The superior performance in both volatile and nonvolatile modes can be achieved through the careful selection of perovskite nanocrystals and organic capping ligands. At present, conventional computing devices employ silicon- and oxide-based memristors.

More recently, perovskite quantum dots (QDs) have been explored for efficient quantum computing. Researchers exploited rapid photon emission exhibited by perovskites upon laser excitation, and the observed high speed displayed by this phenomenon holds significant implications for quantum computing applications. Additionally, it should be noted that they exhibit minimal engagement with their immediate environment, resulting in enhanced coherence characteristics and heightened stability. The comprehensive understanding of 3D–2D heterostructures presents a pathway for utilization in the field of optoelectronic applications and beyond. Continued research and advancement in this field will open the path for the extensive use of halide perovskite solar cells in the coming years.

Biographies

Balpartap Singh completed his Bachelor of Technology in Textile Engineering from the Indian Institute of Technology Delhi. As a Ph.D. student at the Indian Institute of Science (IISc) under Dr. Rondiya, his focus is on the development of high-efficiency devices by investigating the interfaces of 3D−2D halide perovskites in depth. His goal is to establish fundamental principles to understand loss mechanisms.

Dr. Nilesh G. Saykar received his B.Sc., M.Sc., and M.Phil. degrees from Savitribai Phule Pune University and his Ph.D. degree from the Central University of Punjab, specializing in perovskite solar cells. Currently, he is a Research Associate at the Indian Institute of Science (IISc). Nilesh’s interests include Dion-Jacobson 2D perovskite thin film deposition and charge transfer studies using femtosecond absorption spectroscopy, as well as low-temperature photoluminescence spectroscopy for the fabrication of high-efficiency devices.

Boddeda Sai Kumar completed his B.Tech. in Metallurgical Engineering from Andhra University College of Engineering and his M.Tech. in Materials Science and Metallurgical Engineering at IIT Hyderabad. As a Ph.D. student at the Indian Institute of Science (IISc) Bangalore, under Dr. Rondiya, he focuses on point defects in 2D perovskites. Sai’s interests include uncovering the mechanism behind the order−disorder phase transition of 2D perovskites and understanding the relaxation of octahedral tilting in optoelectronic devices.

Dikshant Afria is a B.S. (Research) student at the Indian Institute of Science (IISc), Bangalore. As a Bachelor’s student at IISc working under the supervision of Dr. Rondiya, his interests include the investigation of the interstitial nature of defects in 2D perovskites and their effects on the recombination process of charge carriers and electronic band structure.

Sangeetha C. K. completed her B.Sc. in Physics from Kannur University and completed her M.Sc. in Physics from Central University of Kerala. As a Ph.D. student at the Indian Institute of Science (IISc) Bangalore, under Dr. Rondiya, her interest lies in defects investigation in chalcogenide materials. She is focusing on understanding the ultrafast electron and hole trapping and relaxation dynamics using various advanced spectroscopic techniques.

Sachin R. Rondiya is an Assistant Professor in the Department of Materials Engineering at the Indian Institute of Science (IISc), Bangalore. Dr. Rondiya leads the “Energy Materials and Devices” group at IISc, specializing in developing novel, sustainable semiconductors and higher-efficiency solar devices. His group focuses on “Point Defects” and “Interface Properties” and with this focused approach, they are striving to improve device performance.

The authors declare no competing financial interest.