Abstract
Non-Newtonian fluid flow is significant in engineering and biomedical applications such as thermal exchangers, electrical cooling mechanisms, nuclear reactor cooling, drug delivery, blood flow analysis, and tissue engineering. The Caputo operator has emerged as a prevalent tool in fractional calculus, garnering widespread recognition. This research aims to introduce a novel derivative by merging the proportional and Caputo operators, resulting in the fractional operator known as the constant proportional Caputo. In order to demonstrate this newly defined operator’s dynamic qualities, it was employed in the analysis of the unsteady Casson flow model. In addition, the current work shows an analytical analysis to determine the Soret effect on the fractionalized MHD Casson fluid over an oscillating vertical plate. Fractional partial differential equations (PDEs) are used to formulate the problem along with IBCs. The introduction of appropriate nondimensional variables converts the PDEs into dimensionless form. The precise solutions to the fractional governing PDEs are then determined by the Laplace transform method. Velocity, concentration, and temperature profiles; the impacts of the Prandtl number; fractional parameter β and γ; and Soret and Schmidt numbers are graphically depicted. The profiles of temperature, concentration, and velocity rise with rising time and fractional parameters. Interestingly, as the Casson flow parameter is higher, fluid velocity decreases closest to the plate but increases away from the plate. Tables showing the findings for the skin-friction coefficient, Sherwood, and Nusselt numbers for a range of flow-controlling parameter values are provided. Furthermore, an investigation is undertaken to compare fractionalized and ordinary velocity fields. The results suggest that the fractional model employing a constant proportional derivative exhibits a quicker decay than the model incorporating conventional Caputo and Caputo-Fabrizio operators.
1. Introduction
Heat and mass transfer processes hold immense significance from an industrial perspective, captivating the attention of numerous researchers and scientists. In the realm of modern technologies and diverse industrial applications, the theory of non-Newtonian fluids exerts a profound influence due to the limitations of Newtonian fluid models in capturing a wide range of flow characteristics. Non-Newtonian fluids exhibit complex relationships involving shear strain rate and stress, transcending the simplistic assumptions of Newtonian fluid models. The theory of non-Newtonian fluids finds significant application in contemporary engineering, namely, within the petroleum sector, where it plays a crucial role in extracting crude oil from various petroleum reservoirs. In contrast to Newtonian fluids, whose properties often prove inadequate, non-Newtonian fluids demand the development of more sophisticated models to accurately represent their intricate behavior. The significance of non-Newtonian fluids has grown exponentially in recent decades, particularly within the research community. These fluids boast a vast array of ever-expanding applications in various industrial sectors, including large-scale heating and cooling systems, plastic extrusion, polymer processing, oil pipeline friction reduction, well drilling, fluid friction minimization, biological materials, flow tracing, plastic foam processing, biomedical flow analysis, food processing industries, lubrication processes, emulsions, chemical processing, slurries, and mud handling.
Numerous scientists have dedicated their efforts to studying non-Newtonian fluids, considering a variety of fluid geometries. For this reason, advancement and improved quality of life are greatly aided by the modeling and simulation of non-Newtonian fluid flow processes. Researchers have investigated a diverse range of non-Newtonian fluid models, each with its own unique computational properties. For instance, while the power-law model effectively captures viscosity characteristics, it fails to account for the effects of elasticity. This motivates researchers and mathematicians to delve deeper into the study of these complex fluids. For theoretical research as well as real-world applications in contemporary engineering, a methodical examination of these fluid flow models is crucial.1−4
There have been several rheological models proposed in order to comprehend the characteristics of flow and heat transmission. Casson flow model5 is one of them. This model does not satisfy Newton’s law of viscosity which was created by Casson (1995). Since Casson fluid’s characteristics relate to the shear stress relation, it is classified as a non-Newtonian fluid. Blood, tomato juices, soup, and juice are a few examples of Casson fluids. Inextricably linked to this model are some freeze flows. Yield stress may be seen in this model. Dash et al.6 investigated how yield pressure affects the motion of a Casson flow in a comparable permeable medium confined in a tube. Fluid with homogeneous and heterogonous reactions is investigated in refs (7–10).
Shashikumar et al.11 was taken into consideration in order to analyze the effects of Casson nanofluids nonlinear flow among plates that are held side by side. Hayat et al.12 studied non-Newtonian Casson flow with magnetohydrodynamics with the impact of Dufour and Soret. This model, along with a variety of flow characteristics and combinations, has been employed by several academics13−15 to achieve a variety of objectives. Fractional models have a few drawbacks since the single Kernel encountered several issues throughout the modeling process. In addition to extending fractional integrals, Caputo and Riemann–Liouville developed the idea of singular Kernel-based fractional derivative operators.
New fractional operators have been introduced in order to address this issue like the fractional derivative of Prabhakar, Caputo–Fabrizio, Atangana–Baleanu, and some others.16,17 Baleanu et al.18 worked with the fractional operator constant proportional Caputo (CPC); the Riemann–Liouville integral and Caputo fractional derivative are combined to produce this. Yavuz et al.19 offered the precise solution and investigation of an operator for a Caputo fractional specified a second grade fractionalized fluid. Caputo and Fabrizio20 discovered novel fractional derivatives enhanced by various scientists to solve practical issues. There are some important references for fractional calculus.21−24
Numerous other scientific disciplines, including mathematics, physics, geophysics, biology, etc., have also adopted the usage of fractional order derivatives. These areas are examined in refs (25–28). Tamoor et al.29 studied the stretching cylinder to look at how the MHD affects the flow of the Casson fluid. Using the stationary motion of a Newtonian flow, Nadeem et al.30 examined the influence of an MHD on a curvilinear surface. A time-dependent micropolar fluid and a curved sheet were used in the investigation. Saleh et al.31 investigated the impact of injection or suction. Today’s food companies criticize the Casson flow model. Casson’s flowing model was used by the cocoa and chocolate manufacturing sectors to show how chocolate behaves rheologically. Additionally, in modern times, the rheological model for human blood is distributed using the Casson model. Casson fluid flows over various geometries in a variety of conditions are mentioned in refs (32–34).
Researchers Damseh et al.35 investigated coupled mass and heat transfer via free convection of a micropolar, viscous, heat-generating or -absorbing fluid flow near a continuously moving vertical porous infinitely long surface in the presence of a first-order chemical reaction. For unsteady coupled mass and heat transfer via mixed convection flow over a vertical cone rotating in an ambient liquid with a time-dependent angular velocity, Chamkha and Rashad36 investigated the Soret and Dufour effects in the presence of a MHD and chemical reaction. Takhar et al.37 discuss the MHD flow across a moving plate in a fluid that rotates with free stream velocity, Hall effects, and a magnetic field.
Chamkha and Khaled38 studied the issue of simultaneous mass and heat transfer by free convection from a semi-infinite inclined plate when an external magnetic field is present and internal heat production or absorption effects are described. The influence of thermophoresis and heat generation or absorption was explored in the Chamkha and Issa39 study of heat and mass transport across a semi-infinite, permeable flat surface in the setting of continuous, two-dimensional, laminar, hydromagnetic flow. Chamkha and Khaled40 showed hydromagnetic coupled mass and heat transfer aided by free convective from a porous surface housed in a fluid-saturated porous medium. Kumar et al.41 explored an electrically conducting, incompressible, and viscous liquid for mixed convective boundary layer flow on a vertical plate amid thermal radiation and an induced magnetic field. In Chamkha,42 coupled heat and mass transport in the presence of electromagnetic radiation and a magnetic field are emphasized together with free convective boundary layer flow across a permeable isothermal truncated cone. Some useful discoveries may be found in refs (43–48).
In the current study, an exact approach is applied to analyze the constant wall concentration and temperature for an unsteady Casson fluid boundary layer flow across a vertically accelerating plate. The set of partial differential equations (PDEs) is analytically solved utilizing the Laplace method. The influence of several dimensionless quantities on concentration, velocity, and heat is thoroughly investigated. Subsequently, Stehfest’s and Tzou’s algorithms are used to invert the transformed results. The solutions obtained for the problem are graphically presented, and the influence of relevant parameters is elucidated using graphs. The influence of the Soret effect is investigated by varying parameters in the governing equations. The concentration, temperature, and velocity profiles obtained using the fractional derivative exhibit a more pronounced decay compared to those obtained with the ordinary derivative. This study is innovative in that it applies the new fractional hybrid operator, the CPC fractional derivative,18 and expands on the work49 for the Casson flow. As far as we are aware, no such conclusion has been achieved for the Casson fluid generated by the Soret effect with CPC fractional derivatives. According to this, the fractional derivative is a more suitable choice for achieving controlled velocity, mass, and heat profiles. The present work holds significant potential for various applications, including the design of geothermal systems, electronic materials, and solar energy systems.
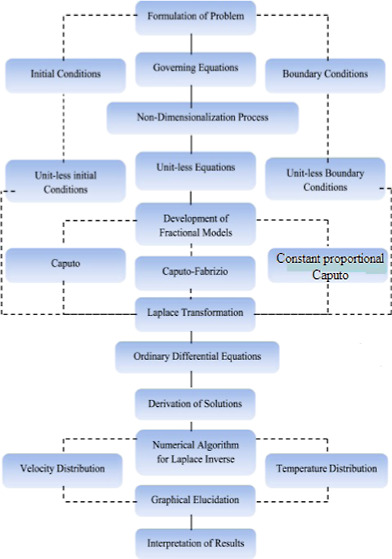
2. Mathematical Formulation
The flow of a Casson flow that is incompressible over an infinitely accelerated vertical plate is examined here. Flow is contained inside the region of y > 0, where y is a perpendicularly measured coordinate to the plate. At initial rest, both the liquid and plate have a constant temperature of T∞ at t = 0. A speed At, where A denotes the oscillation plate, causes the plate to begin accelerating in its plane at time t > 0. The plate’s temperature rises simultaneously to Tw and is then kept constant. Temperature and velocity are dependent on time and space variables y and t, as shown in Figure 1. Following are the forms of the momentum and heat equations when considering unidirectional flow and Boussinesq’s approximation49,50
Figure 1.
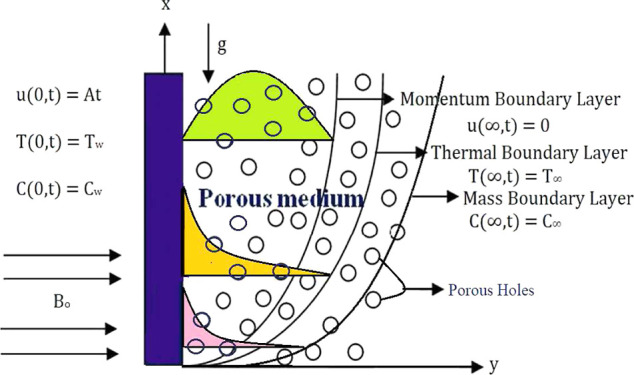
Geometry of flow and coordinate system.
Momentum equation
| 1 |
Energy equation
| 2 |
the generalized Fourier law
| 3 |
Concentration equation with thermo-diffusion
| 4 |
the generalized Fick’s law
| 5 |
with declaration of field variables at the boundary
| 6 |
| 7 |
| 8 |
where the fluid’s velocity is u, fluid temperature is T, C is the fluid concentration, the density of fluid is ρ, the dynamic viscosity is μ, the coefficient of thermal expansion βT, and the mass expansion coefficient βC, electrical conductivity is σ, the constant pressure specific heat at a fixed pressure is Cp, and the identical strength of magnetic field B0, k is the heat conductivity, while chemical molecular diffusivity is D.
The modified typical Ohm’s law for the greater magnitude magnetic field is expressed as follows51−54
| 9 |
Equation 9 is constituent parts are
| 10 |
| 11 |
On solving eqs 10 and 11, we get
| 12 |
| 13 |
the ion slip and Hall effects are neglected in the governing equation because according to our flow supposition, this effect is very minute so it cannot be considered.
By inserting the dimensionless variables given below
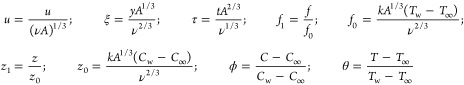 |
14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
where Sr is Soret effect, Gm is mass Grashof number, Gr is Grashof number, Sc is the Schmidt number, M is the magnetic parameter, and Pr is the Prandtl number. The nondimensional IBCs is
| 20 |
| 21 |
| 22 |
3. Fractional Model with CPC Fractional Differential Operator
We will create a fractional modeling of the physical issue in this part. The definition and examples of the novel fractional derivative are found in ref (18)
| 23 |
CPC’s Laplace transform is presented in ref (18)
| 24 |
We obtain the fractional PDEs
| 25 |
| 26 |
| 27 |
| 28 |
Substituting eq 26 in eq 25 and eq 28 in eq 27, we get
| 29 |
| 30 |
The fractional PDEs presented in eqs 29 and 30 are effectively solved using the Laplace technique, a robust technique employed to obtain analytical solutions for initial value problems.
3.1. Solution of Temperature Equation
With the use of the Laplace transform technique, we will solve energy eq 29 with boundary constraints (20)2–(21)2 in this section.
| 31 |
Assuming the following IBCs
| 32 |
Result of eq 31 subject to eq 32, we have
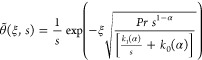 |
33 |
Equation 33 has an exponential expression, and the square root term is complex, hence it is impossible to obtain its direct inverse Laplace transform. To analytically obtain the required result, we thus write it in an alternative form as
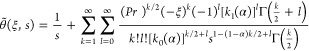 |
34 |
invert Laplace transform to eq 34 gives
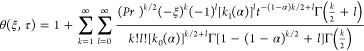 |
35 |
which is the final solution for the temperature field.
3.2. Solution of Concentration Equation
Apply Laplace method on eq 30, we get
| 36 |
Rearrange the above equation
| 37 |
with conditions
| 38 |
The concentration field solution to eq 37 satisfies conditions (38), we have
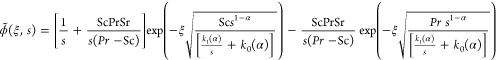 |
39 |
In summation notation, eq 39 is represented as
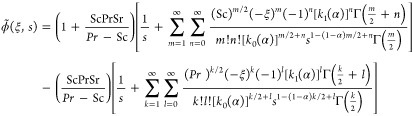 |
40 |
Inverse Laplace transformation of above eq 40 results in
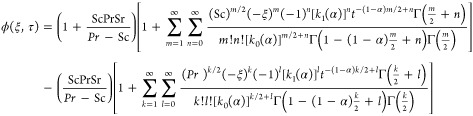 |
41 |
3.3. Solution of Velocity Equation
Using CPC fractional derivative and utilizing the Laplace method to eq 15 with constraints (20)1 and (21)1, we obtain
| 42 |
Putting values of 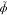 (ξ,s) and θ̃(ξ,s)
in eq 42, we get
(ξ,s) and θ̃(ξ,s)
in eq 42, we get
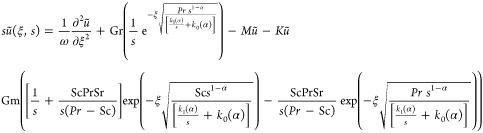 |
43 |
Rearrange the above equation
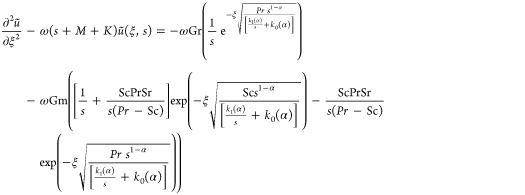 |
44 |
satisfy
| 45 |
We obtain the velocity profile’s using eq 45 in eq 44
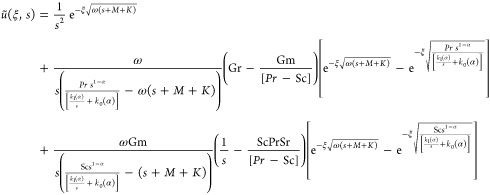 |
46 |
Using Zakian’s procedure
| 47 |
for the inverse Laplace transform form of eq 46. Final calculation for the velocity field is then obtained. Inverse Laplace transform by Zakian’s method is described in refs (55 and 56).
4. Results and Discussion
The Soret effect in the magnetohydrodynamics flow of Casson fractional flow over an accelerated infinite vertical plate in the current study, considering generalized mass and heat transfer through a permeable media. The study presents semianalytical findings for the velocity fields and exact findings for the mass and heat. Additionally, the physical impact of the relevant parameters is illustrated through graphical representations of the heat, mass, and velocity fields.
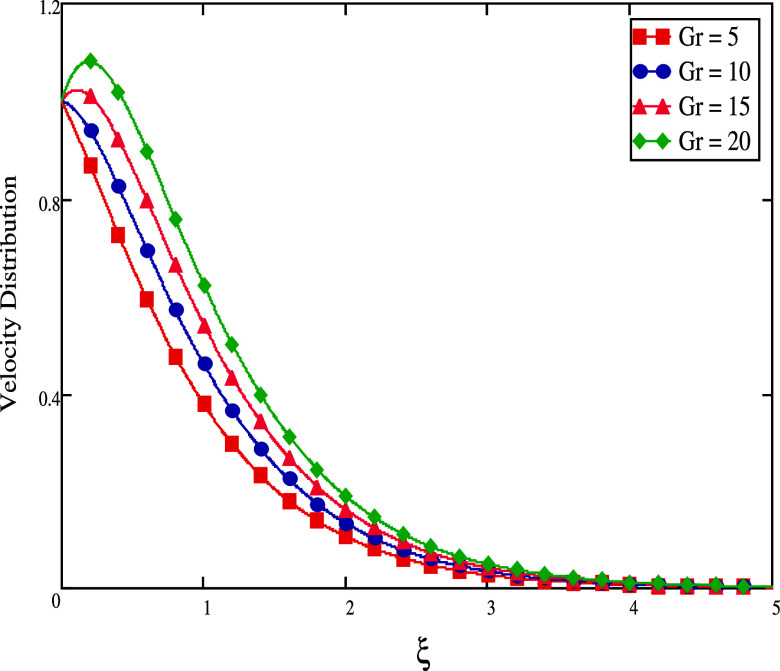
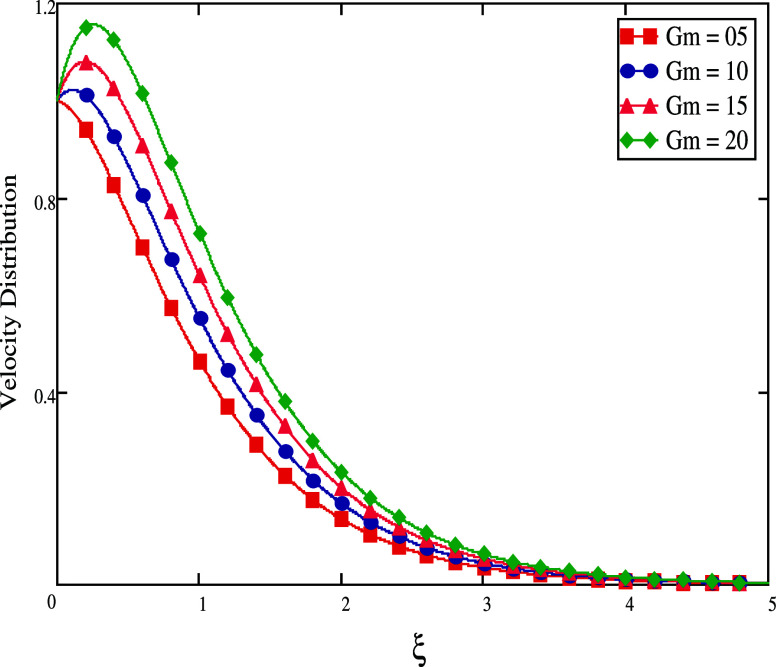
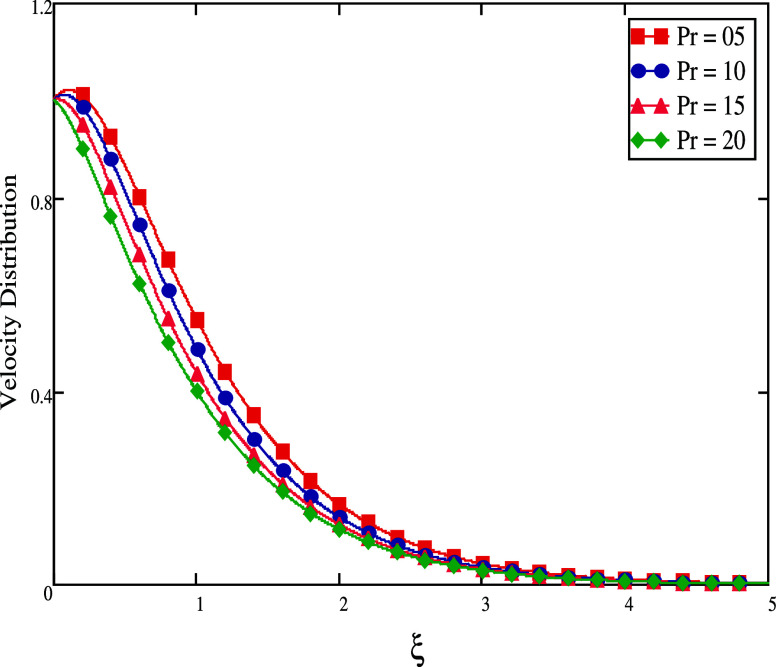
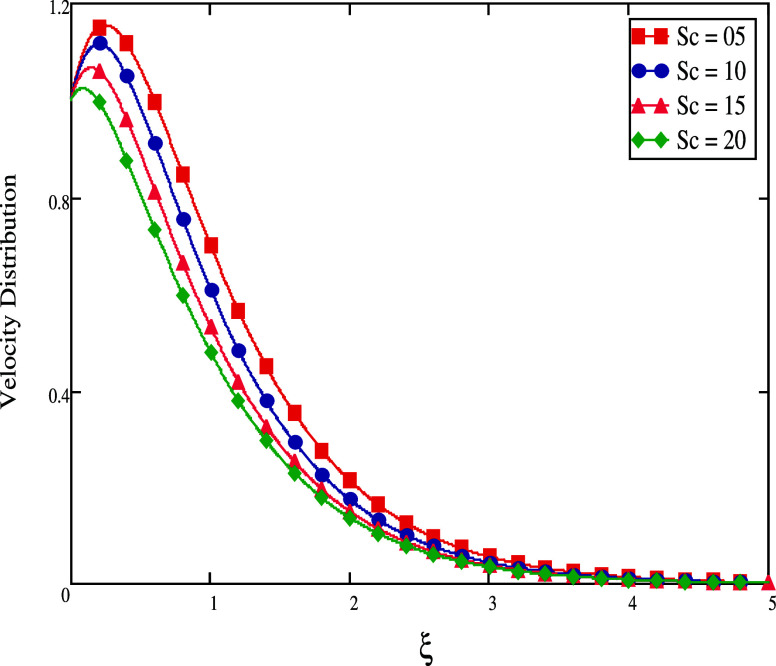
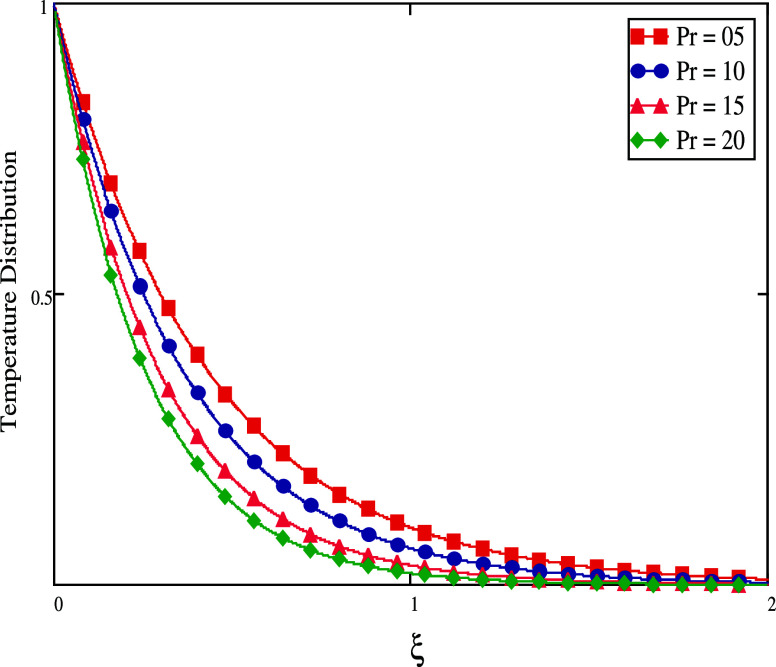
Figure 2 illustrates the impacts of the Grashof number Gr. As we raise the value of Gr, velocity fluid rises. Gr measures the relationship between the heat buoyant force to the viscous force. When Gr = 0, no convection flow exists. If Gr is more than zero, the plate is chilled outside; if Gr is less than zero, the plate is heated externally. Grashof number controls the flow regime in natural convection. Gm effects on the velocity profile is depicted in Figure 3. Velocity is understood to be quicker with higher Gm levels. The speed of the velocity increases because Gm is connected to buoyancy forces, which increase natural convection. In Figure 4, a drop in fluid velocity is evident along with an increase in the Pr (Prandtl number). The temperature gradient would be reduced by increasing the fluid’s heat diffusivity by rising the Pr value. Therefore, the loss of thermal kinetic energy causes a drop in velocity fluid. When the Schmidt number, Sc, varies, Figure 5 depicts the fluid’s behavior. This figure shows that there is a correlation between a rise in the Schmidt number and a fall in fluid velocity. The Schmidt number is the ratio between kinematic viscosity and molecular diffusion. Molecular diffusion tends to decrease as the Schmidt number increases, which slows down fluid movement.
Figure 2.
For different Gr values, velocity profiles.
Figure 3.
For different Gm values, velocity profiles.
Figure 4.
For different Pr values, velocity profiles.
Figure 5.
For different Sc values, velocity profiles.
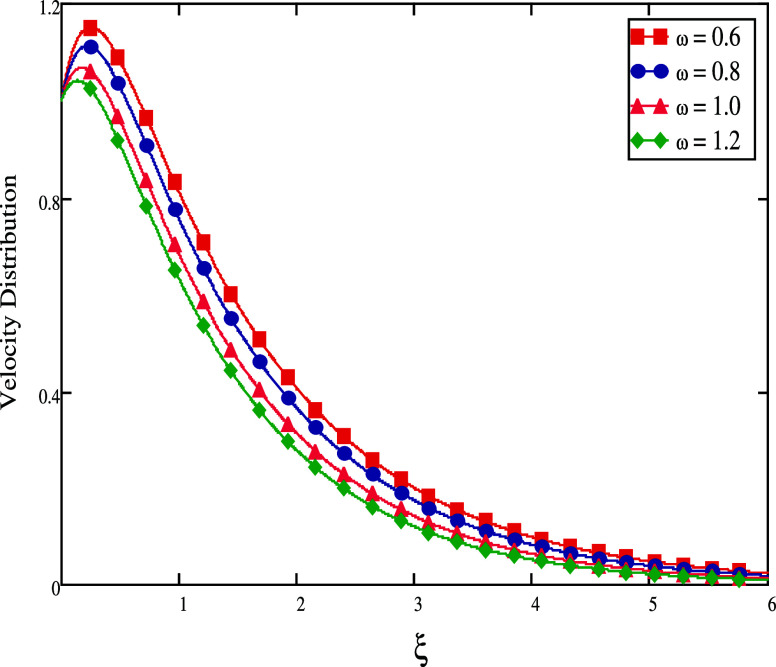
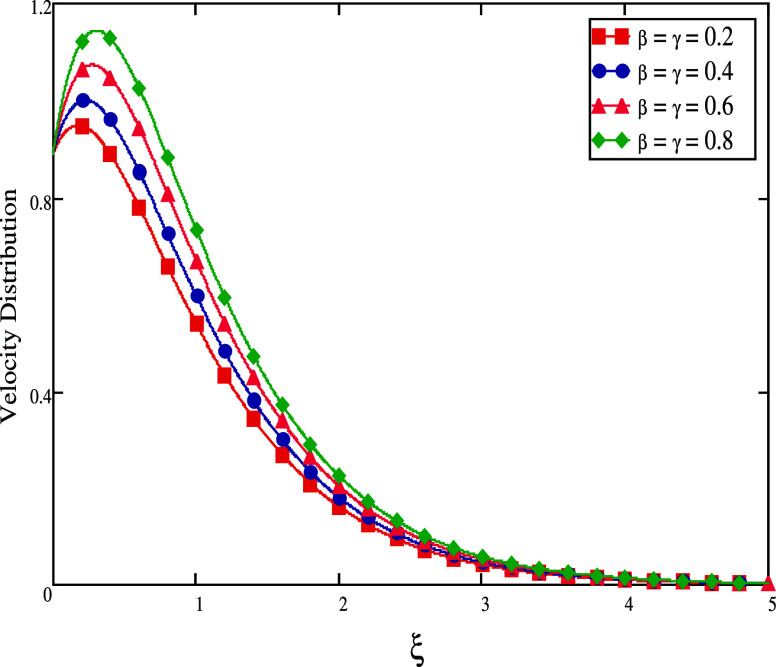
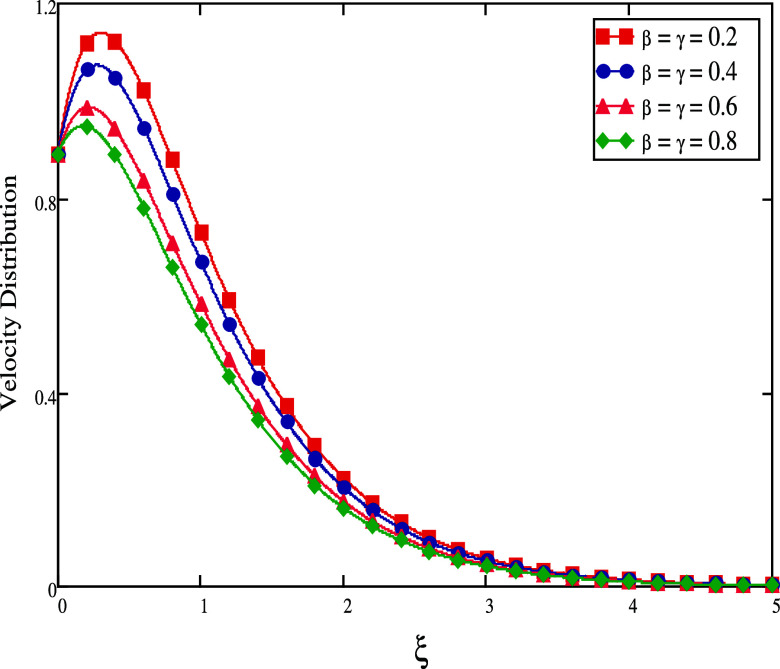
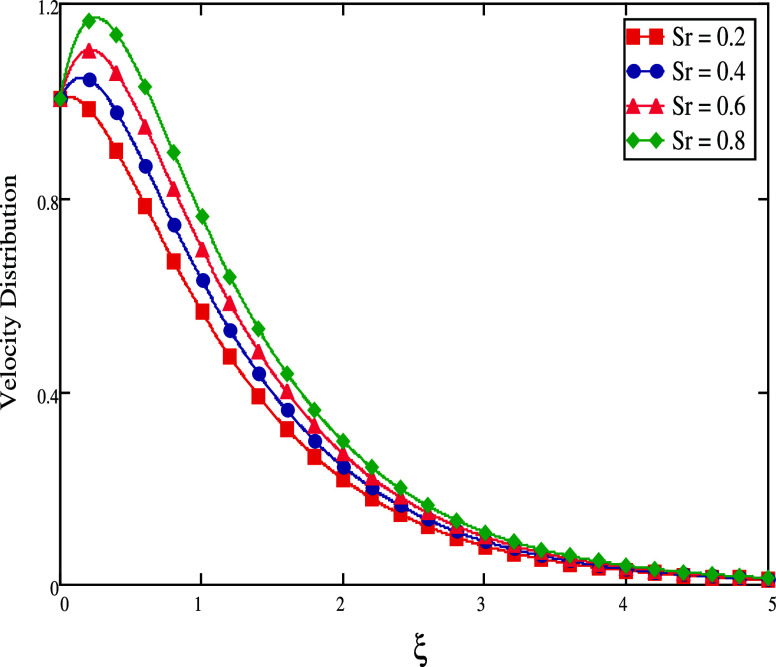
Figure 6 shows how ω affects the velocity field. Increasing ω causes the drag forces to become firmer, which tends to diminish the velocity field, which causes the value of the velocity fluid to decay. Figures 7 and 8 show the influence of velocity fractional parameter profiles for small and large time durations. As we increase the fractional parameter values for a short time period, as shown in Figure 7, the fluid velocity decreases. The velocity rises for large time durations, as seen in Figure 8. This may be explained physically since increasing the β and γ increases the thermal and momentum boundary layers, which in turn rises the velocity distribution for a significant amount of time. The thermo-diffusion or Soret effect (Sr) over the velocity field is discussed in Figure 9. Because of the rising fluctuations in the Sr, an augmenting flow pattern is seen. In the flow domain, the concentration gradient is influenced by the temperature gradient, adding to the mass flux. As a result, when the Sr value increases, there is a corresponding increase in the mass flux, which causes the flow current to rise and the flow speed to increase accordingly.
Figure 6.
For different ω values, velocity profiles.
Figure 7.
Effect of distinct fractional values for large time.
Figure 8.
Effect of distinct fractional values for small time.
Figure 9.
For different Soret values, velocity profiles.
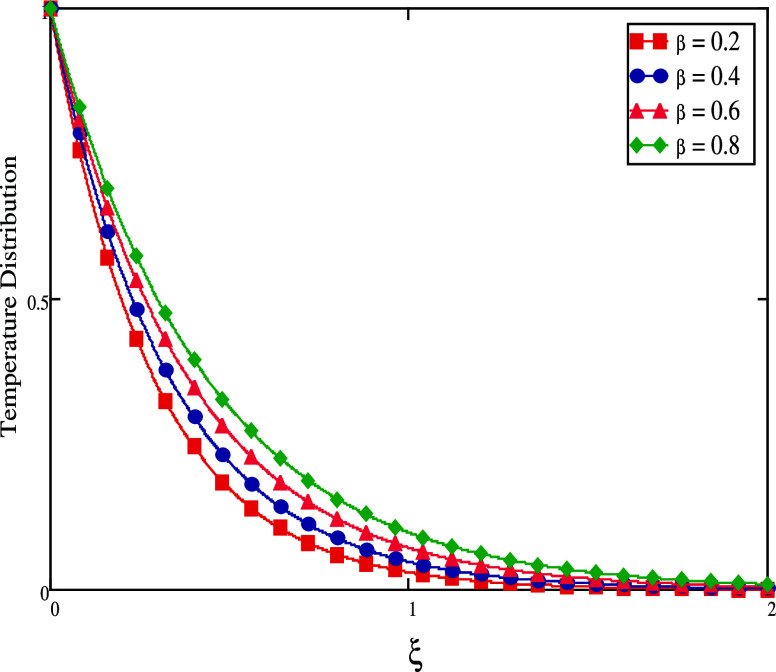
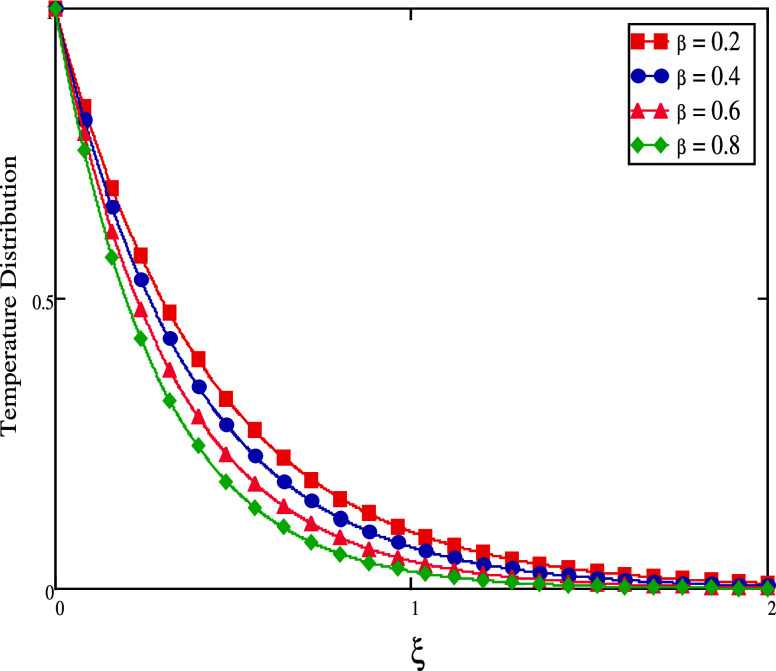
The Pr is used to calculate the thickness of the thermal boundary layer. The drop in heat diffusion rate is brought on by the increase in Pr which dominates momentum diffusivity over fluid movement. As a consequence, Pr increases, thermal boundary layer thickness diminishes, and heat profile becomes lower, as seen in Figure 10. Figures 11 and 12 show, for both short and long times, the impact of β on temperature profiles. When time is short, the fluid temperature drops as the γ values are increased (see Figure 11). The temperature rises as the amount of time increases (see Figure 12).
Figure 10.
Effect of distinct fractional values for small time.
Figure 11.
Temperature profiles for large time.
Figure 12.
Temperature profiles for small time.
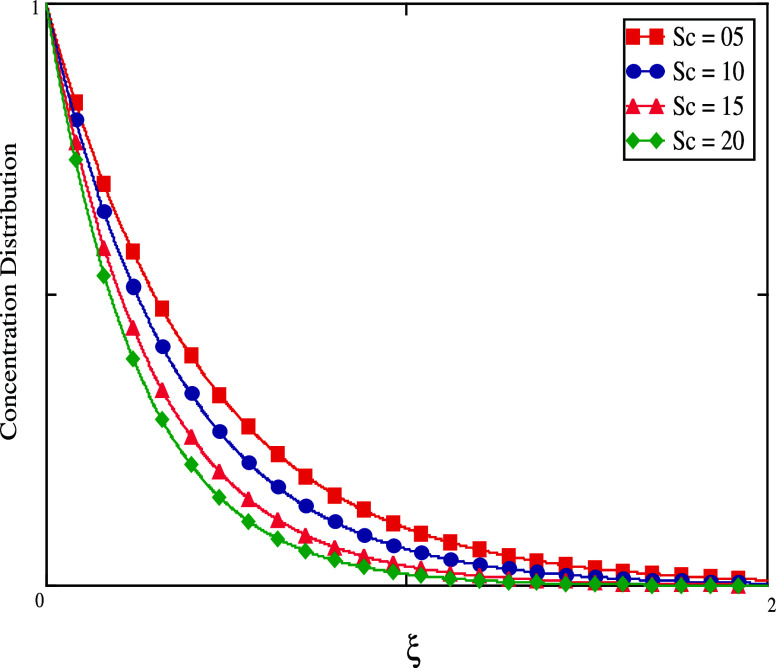
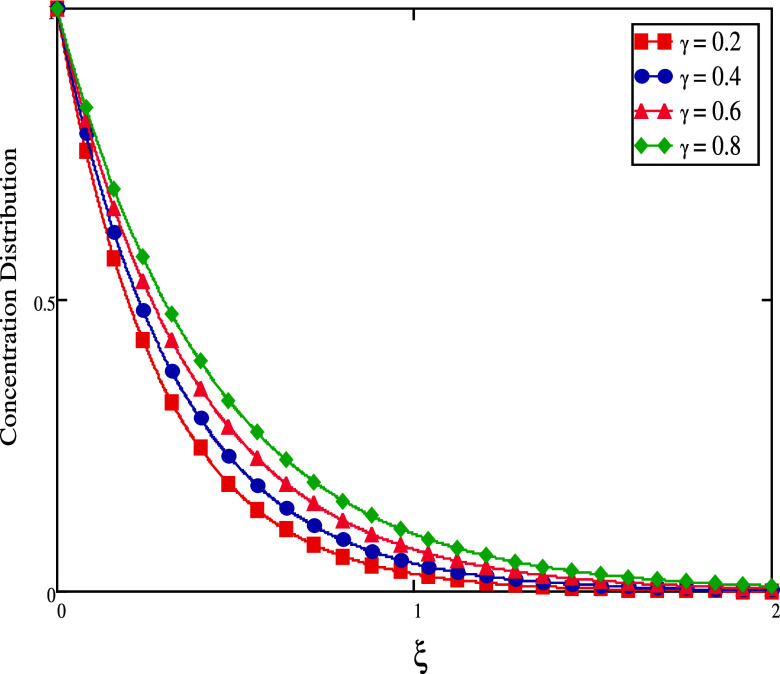
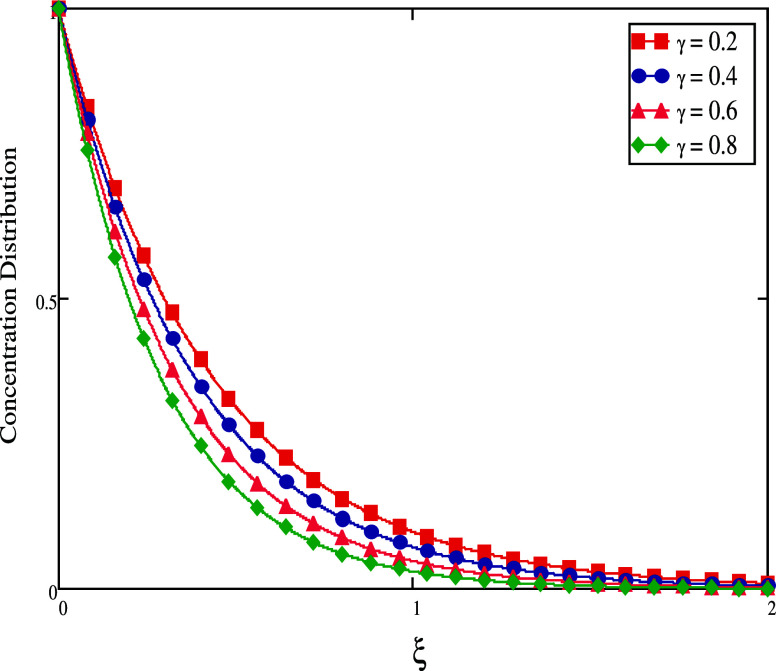
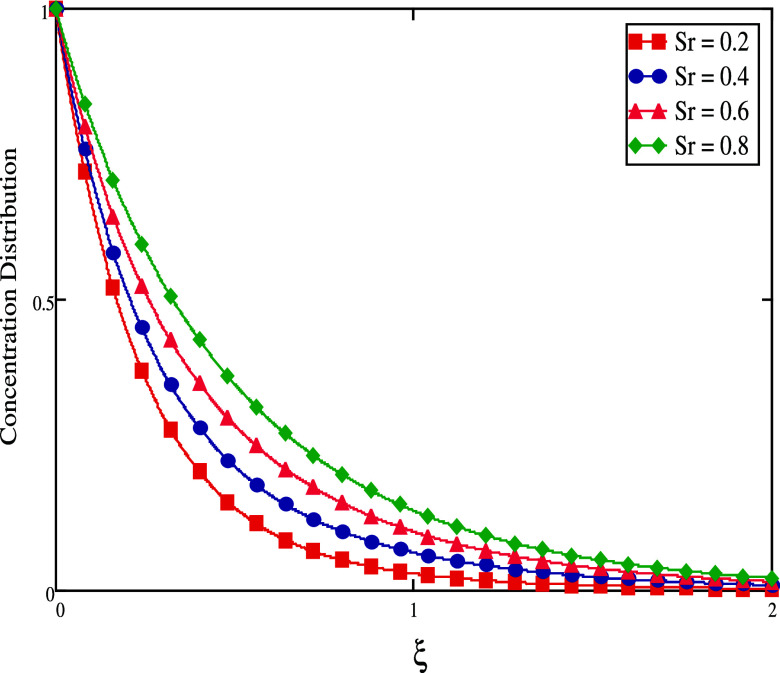
In Figure 13, it is intended to investigate how the Schmidt number has an impact on concentration. By keeping the Schmidt number’s value constant while varying the other factors, it has been discovered that for larger Schmidt number values, accordingly, the field variable concentration cannot be increased. Since this is the situation, increasing the Sc values increases the viscous force that affects fluid flow, hence lowering the concentration flow. Figures 14 and 15 show the impact of γ on mass profiles when time has both small and large values. When time is short, we increase γ values, and the fluid concentration decreases (see Figure 14). When time is big, the concentration rises (see Figure 15). The graphical behavior of Sr on temperature is shown in Figure 16. This figure shows that temperature rises by raising the values of Sr.
Figure 13.
Concentration profiles for distinct Sc values.
Figure 14.
Concentration profiles for large time.
Figure 15.
Concentration profiles for small time.
Figure 16.
Concentration profiles for distinct Sr values.
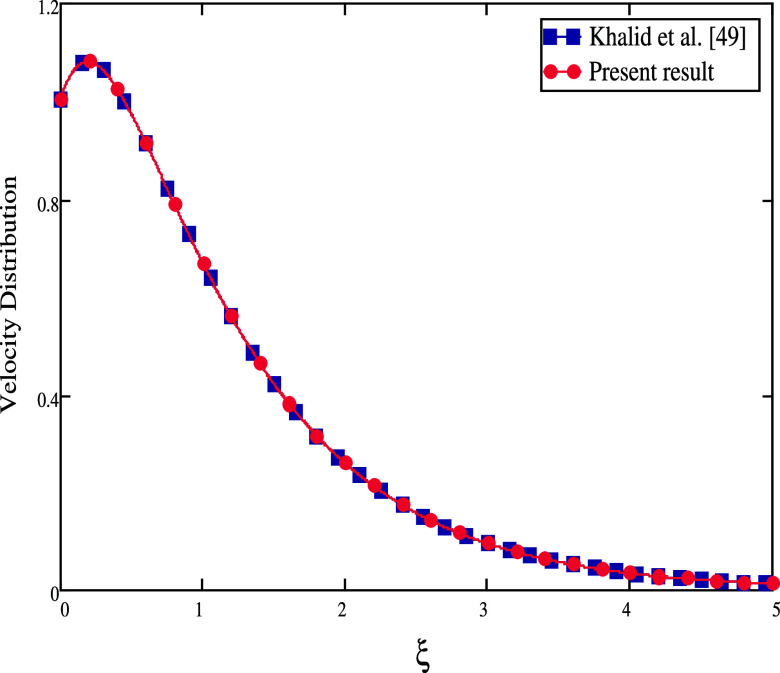
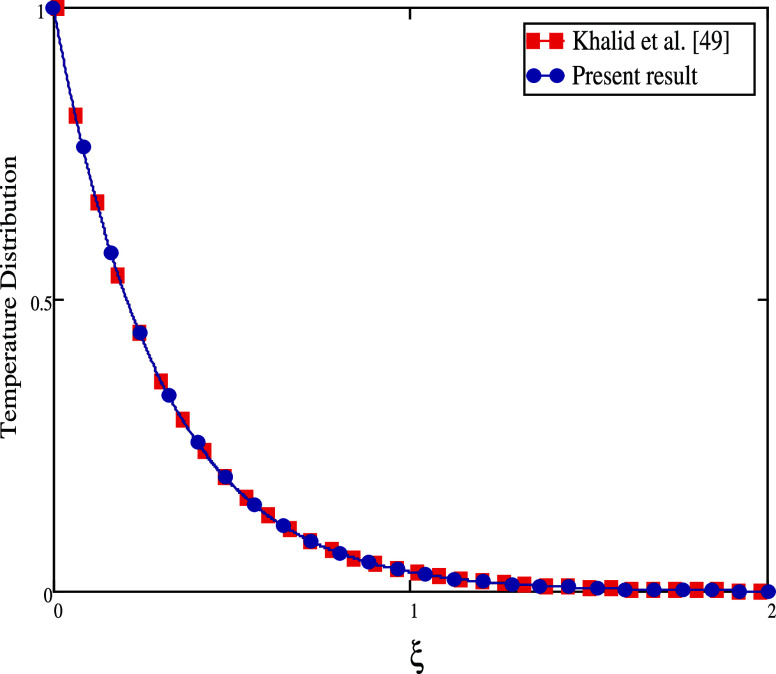
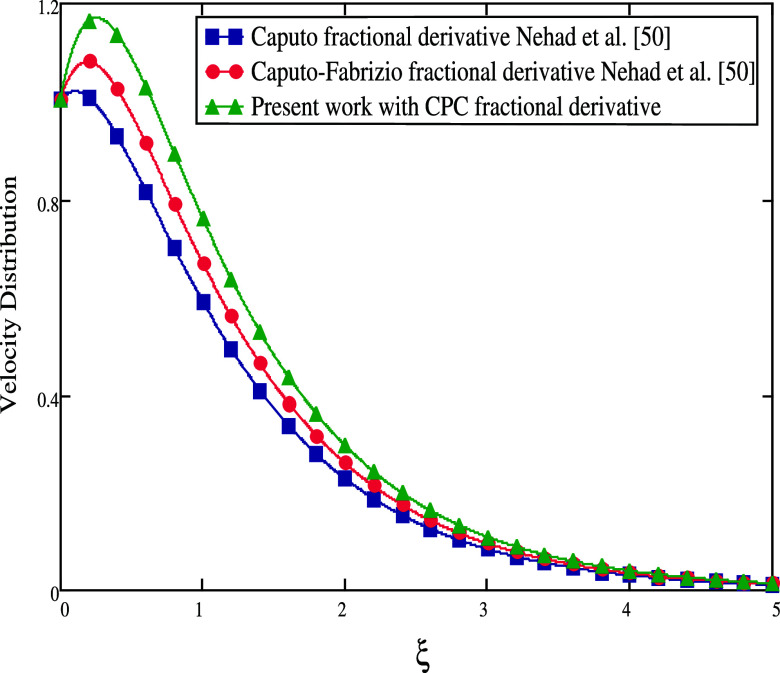
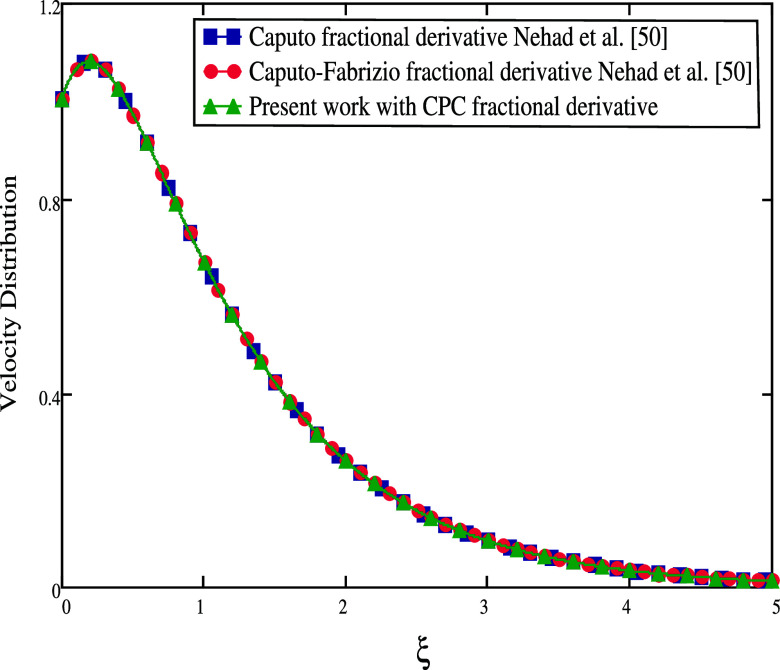
The comparison of the velocity and temperature distribution between the current study and Khalid et al.49 is shown in Figures 17 and 18, respectively. If we take fractional parameters, α = 1, k1 = 0, ko = 1, Gm = 0, K = 0, M = 0, and Sr = 0 in Khalid et al.,33 the fact that the velocity profiles are identical demonstrates the validity of the current work. Additionally, Figure 19 compares the results of the current study with other fractional operators, Caputo and Caputo–Fabrizio, utilized in Nehad et al.50 in the absence of β = ∞, Gm = 0, K = 0, M = 0, and Sr = 0. The fluid profiles are the same as seen in Figure 20 if α is set to 1. A Casson fluid with a CPC fractional derivative is the best option, according to the figures, to improve fluid motion.
Figure 17.
Velocity distribution for comparison of our work with Khalid et al.49 as α = 1, k1 = 0, k0 = 1, Gm = 0, K = 0, M = 0, and Sr = 0.
Figure 18.
Temperature distribution for comparison of our work with Khalid et al.49 as α = 1, k1 = 0, k0 = 1, Gm = 0, and Sr = 0.
Figure 19.
Comparisons between different fractional derivatives α = 0.5.
Figure 20.
Comparisons between different fractional derivatives α → 1.
By raising the fractional parameter values, as shown in Tables 1–3, skin friction, heat, and mass transfer rates can all be improved.
Table 1. Skin Friction.
| β, γ | t = 1 | t = 2 | t = 3 | t = 4 |
|---|---|---|---|---|
| 0.1 | 0.071 | 0.097 | 0.116 | 0.132 |
| 0.2 | 0.076 | 0.103 | 0.124 | 0.141 |
| 0.3 | 0.078 | 0.106 | 0.128 | 0.146 |
| 0.4 | 0.080 | 0.109 | 0.132 | 0.151 |
| 0.5 | 0.083 | 0.113 | 0.136 | 0.166 |
| 0.6 | 0.085 | 0.117 | 0.141 | 0.161 |
| 0.7 | 0.088 | 0.120 | 0.145 | 0.166 |
| 0.8 | 0.091 | 0.124 | 0.150 | 0.172 |
| 0.9 | 0.094 | 0.128 | 0.155 | 0.177 |
| 1.0 | 0.097 | 0.132 | 0.160 | 0.182 |
Table 3. Sherwood Number.
| γ | t = 1 | t = 2 | t = 3 | t = 4 |
|---|---|---|---|---|
| 0.1 | 0.067 | 0.095 | 0.114 | 0.131 |
| 0.2 | 0.073 | 0.102 | 0.123 | 0.142 |
| 0.3 | 0.076 | 0.106 | 0.128 | 0.147 |
| 0.4 | 0.079 | 0.110 | 0.133 | 0.152 |
| 0.5 | 0.082 | 0.115 | 0.138 | 0.158 |
| 0.6 | 0.085 | 0.119 | 0.143 | 0.164 |
| 0.7 | 0.089 | 0.124 | 0.149 | 0.170 |
| 0.8 | 0.092 | 0.128 | 0.154 | 0.177 |
| 0.9 | 0.096 | 0.133 | 0.160 | 0.183 |
| 1.0 | 0.100 | 0.138 | 0.166 | 0.189 |
Table 2. Nusselt Number.
| β | t = 1 | t = 2 | t = 3 | t = 4 |
|---|---|---|---|---|
| 0.1 | 1.151 | 1.177 | 1.196 | 1.212 |
| 0.2 | 1.156 | 1.183 | 1.204 | 1.221 |
| 0.3 | 1.158 | 1.186 | 1.208 | 1.226 |
| 0.4 | 1.160 | 1.189 | 1.212 | 1.231 |
| 0.5 | 1.163 | 1.193 | 1.216 | 1.236 |
| 0.6 | 1.165 | 1.197 | 1.221 | 1.241 |
| 0.7 | 1.168 | 1.200 | 1.225 | 1.246 |
| 0.8 | 1.171 | 1.204 | 1.230 | 1.252 |
| 0.9 | 1.174 | 1.208 | 1.235 | 1.257 |
| 1.0 | 1.177 | 1.212 | 1.240 | 1.262 |
5. Skin Friction
The non-dimensional skin friction is given in eq 48
| 48 |
6. Nusselt Number
According to the Nusselt number, the rate of heat transport is provided by eq 49
| 49 |
7. Sherwood Number
Equation 50 provides the mass transfer rate expressed in terms of the Sherwood number.
| 50 |
Gr, Gm, Pr, Sc, and M are among the variable parameters whose numerical values are used in the study.
The Gr is a nondimensional quantity that is utilized to describe spontaneous or free convection flow. The particular application determines the typical values for Gr. It can vary between 104 and 1012 for flows of vertical plates. It can be anywhere between 108 and 1012 for horizontal plate flows. It may differ considerably more for enclosures and other geometries. The Gm is a nondimensional quantity that describes natural convection induced by buoyancy forces arising from density variations induced by mass gradients. The Gm value range is comparable to that of the Gr for free convection. In typical applications, Gm can span from 10,000 to 1012. A dimensionless quantity known as the Prandtl number (Pr) indicates the ratio of heat diffusivity to the diffusivity of momentum. The Pr typical values vary depending on the fluid under consideration. It is around 0.7 for air, about 7 for water, and anything from 10 to 100 for oils. A dimensionless quantity called the Schmidt number (Sc) is used to quantify how momentum and mass diffusivity interact in a fluid. The fluid under consideration affects the typical values for Sc as well. This equals 600 for water and about 0.7 for air. The magnetic number (M), a dimensionless quantity, is used to describe how a magnetic field affects a fluid’s flow. The magnetic field’s strength and the fluid’s properties determine the typical values for M. It is possible for it to be between 10–6 and 10–3 for light magnetic fields and between 1 and 10 for strong magnetic fields.
Table 4 below lists the ranges of the various parameters that were employed in this investigation.57−59
Table 4. Ranges of the Various Parameters Employed in This Investigation.
| name of parameters | ranges |
|---|---|
| Gm | 3.50–7.20 |
| Gr | 2.50–5.60 |
| M | 1.50–3.50 |
| Pr | 2.20–4.20 |
| Sc | 2.10–4.30 |
8. Conclusions
This work employs precise results for an unsteady Casson fluid boundary layer flows over a vertical plate that is oscillating and has constant wall heat and mass. The Laplace transform is used to solve the nondimensional governing equations. Measured values of temperature, concentration, and velocity are shown graphically. The following parameter includes the Casson parameter, Prandtl number, Grashof number, Schmidt number, Soret number, mass Grashof number, and fractional parameter as well as their impacts on velocity, concentration, and temperature.
The results of this study can be used to design more efficient heat exchangers and chemical reactors.
When Gr, Gm, β, and γ are increased, velocity rises; however, when Pr, Sc, and ω are increased, velocity falls.
Temperature rises when time and fractional parameters are increased but decreases as Pr is raised.
Concentration rises when time and fractional parameters are increased but decreases as Sc is raised.
In biomedical engineering, the Soret effect in Casson fluids can be relevant for drug delivery systems. By exploiting the concentration gradients established by the Soret effect, controlled release of drugs or therapeutic agents can be achieved in targeted regions. The non-Newtonian behavior of the Casson fluid can further influence the flow behavior and enhance the efficiency of drug delivery.
In the oil and gas industry, the Soret effect in Casson fluids can be significant in enhanced oil recovery (EOR) techniques. EOR methods aim to improve the extraction of oil from reservoirs, and the Soret effect in Casson fluids can help enhance the displacement of oil by injecting fluids with specific temperature profiles. This can lead to improved oil recovery rates and increased production efficiency.
The Soret effect in Casson fluids can also impact heat transfer systems. By manipulating the temperature gradient, concentration gradients can be established, which can modify the rate at which heat is transferred through the fluid. This effect can be utilized in applications such as cooling systems, heat exchangers, and thermal management devices to improve thermal transfer efficiency.
In the food sector, the Soret effect in Casson fluids can find uses in processes such as thermal sterilization and pasteurization. By leveraging the concentration gradients established by the Soret effect, heat can be distributed more effectively within the fluid, leading to improved heat treatment processes and preservation of food products.
Acknowledgments
The authors from King Khalid University extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Research Groups Program under Grant No.#RGP.2/427/44.
Data Availability Statement
No data associated in the manuscript.
The authors declare no competing financial interest.
References
- Kahshan M.; Lu D.; Siddiqui A. M. A Jeffrey fluid model for a porous-walled channel: Application to flat plate dialyzer. Sci. Rep. 2019, 9 (1), 15879. 10.1038/s41598-019-52346-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmad M.; Asjad M. I.; Akgül A.; Baleanu D. Analytical solutions for free convection flow of Casson nanofluid over an infinite vertical plate. AIMS Math. 2020, 6 (3), 2344–2358. 10.3934/math.2021142. [DOI] [Google Scholar]
- Abbas S.; Nazar M.; Nisa Z. U.; Amjad M.; Din S. M. E.; Alanzi A. M. Heat and mass transfer analysis of MHD Jeffrey fluid over a vertical plate with CPC fractional derivative. Symmetry 2022, 14 (12), 2491. 10.3390/sym14122491. [DOI] [Google Scholar]
- Khan Z.; Tairan N.; Mashwani W. K.; Rasheed H. U.; Shah H.; Khan W. MHD and slip effect on two-immiscible third grade fluid on thin film flow over a vertical moving belt. Open Phys. 2019, 17 (1), 575–586. 10.1515/phys-2019-0059. [DOI] [Google Scholar]
- Wang Y. Q.; Shafique A.; Nisa Z.; Asjad M.; Nazar M.; Inc M.; Yao S. W. Unsteady flow of Casson nanofluid through generalized Fourier’s and Fick’s law for heat and mass transfer. Therm. Sci. 2022, 26 (Spec. issue 1), 29–38. 10.2298/tsci22s1029w. [DOI] [Google Scholar]
- Dash R. K.; Mehta K. N.; Jayaraman G. Effect of yield stress on the flow of a Casson fluid in a homogeneous porous medium bounded by a circular tube. Appl. Sci. Res. 1996, 57, 133–149. 10.1007/BF02529440. [DOI] [Google Scholar]
- Asjad M. I.; Butt M. H.; Sadiq M. A.; Ikram M. D.; Jarad F. Unsteady Casson fluid flow over a vertical surface with fractional bioconvection. AIMS Math. 2022, 7 (5), 8112–8126. 10.3934/math.2022451. [DOI] [Google Scholar]
- Hayat T.; Khan M. I.; Farooq M.; Yasmeen T.; Alsaedi A. Stagnation point flow with Cattaneo-Christov heat flux and homogeneous-heterogeneous reactions. J. Mol. Liq. 2016, 220, 49–55. 10.1016/j.molliq.2016.04.032. [DOI] [Google Scholar]
- Kameswaran P.; Shaw S.; Sibanda P.; Murthy P. V. S. N. Homogeneous heterogeneous reactions in a nanofluid flow due to a porous stretching sheet. Int. J. Heat Mass Transfer 2013, 57, 465–472. 10.1016/j.ijheatmasstransfer.2012.10.047. [DOI] [Google Scholar]
- Khan W. A.; Alshomrani A. S.; Khan M. Assessment on characteristics of heterogeneous-homogenous processes in three-dimensional flow of Burgers fluid. Results Phys. 2016, 6, 772–779. 10.1016/j.rinp.2016.09.019. [DOI] [Google Scholar]
- Shashikumar N. S.; Archana M.; Prasannakumara B. C.; Gireesha B. J.; Makinde O. D. Effects of nonlinear thermal radiation and second order slip on Casson nanofluid flow between parallel plates. Diffus. Defect Data, Pt. A 2017, 377, 84–94. 10.4028/www.scientific.net/ddf.377.84. [DOI] [Google Scholar]
- Hayat T.; Shehzad S. A.; Alsaedi A. Soret and Dufour effects on magnetohydrodynamic (MHD) flow of Casson fluid. Appl. Math. Mech. 2012, 33, 1301–1312. 10.1007/s10483-012-1623-6. [DOI] [Google Scholar]
- Alotaibi H.; Althubiti S.; Eid M. R.; Mahny K. L. Numerical treatment of MHD flow of Casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Comput. Mater. Continua 2021, 66 (1), 229–245. 10.32604/cmc.2020.012234. [DOI] [Google Scholar]
- Qayyum S.; Khan M. I.; Hayat T.; Alsaedi A. Comparative investigation of five nanoparticles in flow of viscous fluid with Joule heating and slip due to rotating disk. Phys. B Condens. Matter 2018, 534, 173–183. 10.1016/j.physb.2018.01.044. [DOI] [Google Scholar]
- Hayat T.; Ahmad S.; Khan M. I.; Alsaedi A. Simulation of ferromagnetic nanomaterial flow of Maxwell fluid. Results Phys. 2018, 8, 34–40. 10.1016/j.rinp.2017.11.021. [DOI] [Google Scholar]
- Riaz M. B.; Awrejcewicz J.; Rehman A. U.; Abbas M. Special functions-based solutions of unsteady convective flow of a MHD Maxwell fluid for ramped wall temperature and velocity with concentration. Adv. Differ. Equ. 2021, 2021, 500. 10.1186/s13662-021-03657-6. [DOI] [Google Scholar]
- Atangana A.; Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. 10.2298/TSCI160111018A. [DOI] [Google Scholar]
- Baleanu D.; Fernandez A.; Akgül A. On a fractional operator combining proportional and classical differintegrals. Mathematics 2020, 8, 360. 10.3390/math8030360. [DOI] [Google Scholar]
- Yavuz M.; Sene N.; Yıldız M. Analysis of the influences of parameters in the fractional Second grade fluid dynamics. Mathematics 2022, 10 (7), 1125. 10.3390/math10071125. [DOI] [Google Scholar]
- Caputo M.; Fabrizio M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. 2015, 1 (2), 73–85. [Google Scholar]
- Abbas S.; Nazar M.; Gillani S. F. F.; Naveed M.; Ahmad M.; Nisa Z. U. A CPC fractional model of the heat and mass transport mechanism in Carbon nanotubes with slip effects on velocity. Mod. Phys. Lett. B 2023, 2023, 2450100. 10.1142/s0217984924501008. [DOI] [Google Scholar]
- Abbas S.; Ahmad M.; Nazar M.; Amjad M.; Ali H.; Jan A. Z. Heat and mass transfer through a vertical channel for the Brinkman fluid using Prabhakar fractional derivative. Appl. Therm. Eng. 2023, 232, 121065. 10.1016/j.applthermaleng.2023.121065. [DOI] [Google Scholar]
- Abbas S.; Gilani S. F. F.; Nazar M.; Fatima M.; Ahmad M.; Nisa Z. U. Bio-convection flow of fractionalized second grade fluid through a vertical channel with Fourier’s and Fick’s laws. Mod. Phys. Lett. B 2023, 37 (23), 2350069. 10.1142/s0217984923500690. [DOI] [Google Scholar]
- Abbas S.; Nisa Z. U.; Nazar M.; Amjad M.; Ali H.; Jan A. Z. Application of heat and mass transfer to convective flow of Casson fluids in a microchannel with Caputo–Fabrizio derivative approach. Arab. J. Sci. Eng. 2024, 49, 1275–1286. 10.1007/s13369-023-08351-1. [DOI] [Google Scholar]
- Laskin N. Fractional Schrodinger equation. Phys. Rev. 2002, 66 (5), 056108. 10.1103/PhysRevE.66.056108. [DOI] [PubMed] [Google Scholar]
- Naber M. Time fractional Schrodinger equation. J. Math. Phys. 2004, 45 (8), 3339–3352. 10.1063/1.1769611. [DOI] [Google Scholar]
- Asjad M. I.; Karim R.; Hussanan A.; Iqbal A.; Eldin S. M. Applications of fractional partial differential equations for MHD Casson fluid flow with innovative ternary nanoparticles. Processes 2023, 11 (1), 218. 10.3390/pr11010218. [DOI] [Google Scholar]
- Ahmad M.; Asjad M. I.; Nisar K. S.; Khan I. Mechanical and thermal energies transport flow of a second grade fluid with novel fractional derivative. Proc. Inst. Mech. Eng., Part E 2021, 2021, 095440892110535. 10.1177/09544089211053561. [DOI] [Google Scholar]
- Tamoor M.; Waqas M.; Khan M. I.; Alsaedi A.; Hayat T. Magnetohydrodynamic flow of Casson fluid over a stretching cylinder. Results Phys. 2017, 7, 498–502. 10.1016/j.rinp.2017.01.005. [DOI] [Google Scholar]
- Nadeem S.; Khan M. R.; Khan A. U. MHD stagnation point flow of viscous nanofluid over a curved surface. Phys. Scr. 2019, 94, 115207. 10.1088/1402-4896/ab1eb6. [DOI] [Google Scholar]
- Saleh S. H. M.; Arifin N. M.; Nazar R.; Pop I. Unsteady micropolar fluid over a permeable curved stretching shrinking surface. Math. Probl Eng. 2017, 2017, 1–13. 10.1155/2017/3085249. [DOI] [Google Scholar]
- Mythili D.; Sivaraj R. Influence of higher order chemical reaction and non-uniform heat source/sink on casson fluid flow over a vertical cone and flat plate. Mol. Liq. 2016, 216, 466–475. 10.1016/j.molliq.2016.01.072. [DOI] [Google Scholar]
- Pop I.; Sheremet M. Free convection in a square cavity filled with a Casson fluid under the effects of thermal radiation and viscous dissipation. Int. J. Numer. Methods Heat Fluid Flow 2017, 27 (10), 2318–2332. 10.1108/HFF-09-2016-0352. [DOI] [Google Scholar]
- Rao A. S.; Sainath S.; Rajendra P.; Ramu G. Mathematical modelling of hydromagnetic casson non-newtonian nanofluid convection slip flow from an isothermal sphere. Nonlinear Eng. 2019, 8 (1), 645–660. 10.1515/nleng-2018-0016. [DOI] [Google Scholar]
- Damseh R. A.; Al-Odat M. Q.; Chamkha A. J.; Shannak B. A. Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface. Int. J. Therm. Sci. 2009, 48 (8), 1658–1663. 10.1016/j.ijthermalsci.2008.12.018. [DOI] [Google Scholar]
- Chamkha A. J.; Rashad A. M. Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects. Can. J. Chem. Eng. 2014, 92 (4), 758–767. 10.1002/cjce.21894. [DOI] [Google Scholar]
- Takhar H. S.; Chamkha A. J.; Nath G. MHD flow over a moving plate in a rotating fluid with magnetic field, Hall currents and free stream velocity. Int. J. Eng. Sci. 2002, 40 (13), 1511–1527. 10.1016/S0020-7225(02)00016-2. [DOI] [Google Scholar]
- Chamkha A. J.; Khaled A. R. A. Similarity solutions for hydromagnetic simultaneous heat and mass transfer by natural convection from an inclined plate with internal heat generation or absorption. Heat Mass Tran. 2001, 37 (2–3), 117–123. 10.1007/s002310000131. [DOI] [Google Scholar]
- Chamkha A. J.; Issa C. Effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface. Int. J. Numer. Methods Heat Fluid Flow 2000, 10 (4), 432–449. 10.1108/09615530010327404. [DOI] [Google Scholar]
- Chamkha A. J.; Khaled A. R. A. Hydromagnetic combined heat and mass transfer by natural convection from a permeable surface embedded in a fluid-saturated porous medium. Int. J. Numer. Methods Heat Fluid Flow 2000, 10 (5), 455–477. 10.1108/09615530010338097. [DOI] [Google Scholar]
- Kumar B.; Seth G. S.; Nandkeolyar R.; Chamkha A. J. Outlining the impact of induced magnetic field and thermal radiation on magneto-convection flow of dissipative fluid. Int. J. Therm. Sci. 2019, 146, 106101. 10.1016/j.ijthermalsci.2019.106101. [DOI] [Google Scholar]
- Chamkha A. J. Coupled heat and mass transfer by natural convection about a truncated cone in the presence of magnetic field and radiation effects. Numer. Heat Transf.; A: Appl. 2001, 39 (5), 511–530. 10.1080/104077801750111601. [DOI] [Google Scholar]
- Chamkha A. J. Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media. Int. Commun. Heat Mass Tran. 1996, 23 (6), 875–887. 10.1016/0735-1933(96)00070-X. [DOI] [Google Scholar]
- Chamkha A. J. Non-Darcy fully developed mixed convection in a porous medium channel with heat generation/absorption and hydromagnetic effects. Numer. Heat Transf.; A: Appl. 1997, 32 (6), 653–675. 10.1080/10407789708913911. [DOI] [Google Scholar]
- Chamkha A. J.; Issa C.; Khanafer K. Natural convection from an inclined plate embedded in a variable porosity porous medium due to solar radiation. Int. J. Therm. Sci. 2002, 41 (1), 73–81. 10.1016/S1290-0729(01)01305-9. [DOI] [Google Scholar]
- Krishna M. V.; Ahammad N. A.; Chamkha A. J. Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Case Stud. Therm. Eng. 2021, 27, 101229. 10.1016/j.csite.2021.101229. [DOI] [Google Scholar]
- Madhu M.; Kishan N.; Chamkha A. J. Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propuls. Power Res. 2017, 6 (1), 31–40. 10.1016/j.jppr.2017.01.002. [DOI] [Google Scholar]
- Gorla R. S. R.; Chamkha A. Natural convective boundary layer flow over a nonisothermal vertical plate embedded in a porous medium saturated with a nanofluid. Nanoscale Microscale Thermophys. Eng. 2011, 15 (2), 81–94. 10.1080/15567265.2010.549931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalid A.; Khan I.; Shafie S. Exact solutions for unsteady free convection flow of Casson fluid over an oscillating vertical plate with constant wall temperature. Abstr. Appl. Anal. 2015, 2015, 1–8. 10.1155/2015/946350. [DOI] [Google Scholar]
- Shah N. A.; Imran M. A.; Miraj F. Exact solution of time fractional free convectioon flows of viscous fluid over an isothermal vertical plate with Caputo and Caputo-Fabrizio derivatives. J. Prime Res. Math. 2017, 13, 56–74. [Google Scholar]
- Krishna M. V.; Chamkha A. J. Hall and ion slip effects on Unsteady MHD Convective Rotating flow of Nanofluids—Application in Biomedical Engineering. J. Egyptian Math. Soc. 2020, 28 (1), 1. 10.1186/s42787-019-0065-2. [DOI] [Google Scholar]
- Krishna M. V.; Chamkha A. J. Hall effects on MHD squeezing flow of a water-based nanofluid between two parallel disks. J. Porous Media 2019, 22 (2), 209–223. 10.1615/JPorMedia.2018028721. [DOI] [Google Scholar]
- Krishna M. V.; Swarnalathamma B. V.; Chamkha A. J. Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate. J. Ocean Eng. Sci. 2019, 4 (3), 263–275. 10.1016/j.joes.2019.05.002. [DOI] [Google Scholar]
- Chamkha A. J. MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects. Appl. Math. Model. 1997, 21 (10), 603–609. 10.1016/S0307-904X(97)00084-X. [DOI] [Google Scholar]
- Shakeel A.; Ahmad S.; Khan H.; Vieru D. Solutions with Wright functions for time fractional convection flow near a heated vertical plate. Adv. Differ. Equ. 2016, 2016 (1), 51. 10.1186/s13662-016-0775-9. [DOI] [Google Scholar]
- Vieru D.; Fetecau C.; Fetecau C. Time-fractional free convection flow near a vertical plate with Newtonian heating and mass diffusion. Therm. Sci. 2015, 19 (suppl. 1), 85–98. 10.2298/tsci15s1s85v. [DOI] [Google Scholar]
- Asjad M. I.; Ikram M. D.; Sarwar N.; Muhammad T.; Sivasankaran S.; Subaihi S. A. A. Analysis of fractional bioconvection with hybrid nanoparticles in Channel flow. Math. Probl Eng. 2022, 2022, 8600591. 10.1155/2022/8600591. [DOI] [Google Scholar]
- Asjad M. I.; Sarwar N.; Hafeez M. B.; Sumelka W.; Muhammad T. Advancement of non-Newtonian fluid with hybrid nanoparticles in a convective channel and Prabhakar’s fractional derivative-analytical solution. Fractal Fract. 2021, 5 (3), 99. 10.3390/fractalfract5030099. [DOI] [Google Scholar]
- Sheikh N. A.; Ching D. L. C.; Khan I.; Sakidin H. b. Enhancement in heat transfer due to hybrid nanoparticles in MHD flow of Brinkman-type fluids using Caputo fractional derivatives. Sci. Rep. 2022, 12, 14117. 10.1038/s41598-022-18110-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data associated in the manuscript.