Highly Localized Chemical Sampling at Subsecond Temporal Resolution Enabled with a Silicon Nanodialysis Platform at Nanoliter per Minute Flows

Abstract

Microdialysis (MD) is a versatile and powerful technique for chemical profiling of biological tissues and is widely used for quantification of neurotransmitters, neuropeptides, metabolites, biomarkers, and drugs in the central nervous system as well as in dermatology, ophthalmology, and pain research. However, MD performance is severely limited by fundamental tradeoffs between chemical sensitivity, spatial resolution, and temporal response. Here, by using wafer-scale silicon microfabrication, we develop and demonstrate a nanodialysis (ND) sampling probe that enables highly localized chemical sampling with 100 μm spatial resolution and subsecond temporal resolution at high recovery rates. These performance metrics, which are 100–1000× superior to existing MD approaches, are enabled by a 100× reduction of the microfluidic channel cross-section, a corresponding drastic 100× reduction of flow rates to exceedingly slow few nL/min flows, and integration of a nanometer-thin nanoporous membrane with high transport flux into the probe sampling area. Miniaturized ND probes may allow for the minimally invasive and highly localized sampling and chemical profiling in live biological tissues with high spatiotemporal resolution for clinical, biomedical, and pharmaceutical applications.

Microdialysis (MD) enables sampling endogenous and exogenous chemicals from the extracellular space (ECS) in biological tissues.¹ MD is based on the diffusion of chemicals from the ECS over a semipermeable membrane that is continuously flushed with an inlet aqueous flow (perfusate, Figure 1a) to collect analytes in the outlet flow (dialysate, Figure 1a) for subsequent chemical analysis. MD is a widely used method in fundamental and clinical neuroscience and enables quantification of neurotransmitters, neuropeptides, metabolites, biomarkers, and drugs in the central nervous system (CNS).² It is also used widely for monitoring pharmacokinetics and pharmacodynamics in dermatology, ophthalmology, and pain research.³ While versatile, the method has known disadvantages related to fundamental trade-offs between the perfusate flow rate Q, the analyte recovery rate RR, and the probe sampling area S, which result in a competition among the probe’s chemical sensitivity, spatial resolution, and temporal resolution.⁴ While operation at ultraslow-flow (USF) rates of 0.1 μL/min can produce concentration levels of the analyte in the collected sample approaching that in the ECS (recovery rate RR approaching 100%), typical USF perfusion requires long collection times (minutes) to obtain appropriate sample volumes for analyte quantitation. The USF perfusion also significantly decreases the already relatively slow temporal resolution of MD.⁵ In addition, in a typical commercial MD probe with a millimeter long membrane wrapped around a capillary of 200–400 μm in diameter, the resulting active membrane surface area S is of the order of a few mm², which averages out chemical content over large brain volumes. The typically large probe cross-section (0.15–0.5 mm²) also results in inevitable tissue trauma and inflammation during implantation that complicates chemical analysis.

Figure 1.

Design tradeoffs for the deeply scaled ND probe. (a) Schematics of the dialysis process. (b) Recovery rate versus perfusate flow rates for various micro- and nanodialysis probes. The black hatched region corresponds to commercial MD probes. The black dot denotes S = 8 × 10⁷ μm² and R = 3 × 10⁷ s/cm, The blue dot denotes the microfabricated probe of ref (8) with S = 5 × 10⁵ μm² and R = 8 × 10⁶ s/cm. The red denotes the ND probe with S = 1.7 × 10³ μm² and R = 1 × 10⁵ s/cm. (c) Membrane surface area S required to achieve 80% recovery rate versus perfusate flow rate for various membrane resistances. The black hatched region corresponds to commercial MD probes. Blue and red lines are 8 × 10⁶ and 1 × 10⁵ s/cm, respectively. (d) Hydrodynamic resistance for water vs microfluidic channel cross-section for various probes. The right vertical axis is perfusate flow rate per 1 mm of a channel length for a given differential pressure of 100 mbar.

Miniaturization of MD probes using microfabrication technologies⁶⁻¹⁴ has begun to address these issues by decreasing the flow rates to 100 nL/min and below,^8,14 enabling significant reduction of the sampling area down to just a few thousands of μm² that, together with integration with droplet microfluidics,^9−12,14 results in significantly improved temporal resolution down to a few seconds. What are the limits of this miniaturization? Is it possible to design a microfabricated probe that has a sampling area of just 1000 μm², a recovery rate approaching 100%, and the capability to manipulate and deliver sample volumes of just 10 pL to sensitive chemical analysis methods at 1 s temporal resolution, while occupying a cross-section of just 1000 μm² to minimize tissue trauma? While some of these numbers, which correspond to a 100–10000× improvement compared to commercial MD probes, have been demonstrated separately, they have never been realized in a single device due to very restrictive fundamental tradeoffs.

Here we show that by utilizing wafer-scale silicon microfabrication, a nanodialysis (ND) sampling probe with an integrated ultrathin 30 nm nanoporous silicon membrane enables ultralocalized chemical sampling from an area as small as 1700 μm². This superior performance is enabled by the drastic reduction of the microfluidic channel cross-section to 40 μm² and operation at the exceedingly slow flow rates of just a few nL/min. On-chip droplet segmentation of the dialysate flow enables subsecond temporal resolution and on-chip storage of the segmented analytes in a time-preserving sequential droplet train.

Results and Discussion

Design Rules of the Deeply Scaled NanoDialysis (ND) Probe

The governing equation which describes the recovery rate RR of the dialysis probe in the steady-state equilibrium model⁴ is defined as

1

where S is the active area of the membrane, Q is the perfusate flow rate, and R_d, R_m, and R_e are the mass transport resistances for the dialysate, the membrane, and the tissue, respectively. C_out, C_in, and C_ext are the concentrations of analyte in the dialysate, in the perfusate (typically zero), and in the undisturbed tissue, respectively.

To achieve the primary design goal of highly localized chemical sampling, the active probe surface area S has to be minimized while keeping the recovery rate RR considerably large (e.g., >80%). The corresponding product S/Q(R_d + R_m + R_e) in eq 1 should be larger than–ln (1 – 0.8) = 1.6 (Figure 1b). Drastic reduction of this product can be achieved by simply removing the membrane from the design and flushing out the surrounding tissue using balanced push and pull flows^7,9−12,14 (push–pull perfusion, PPP), or just by pulling in the interstitial fluid (ISF) from the ECS with a single open orifice⁹ (ultrafiltration, UF). In all of these implementations, the effective sampling volume is estimated^15,16 to be still of the order of 3 × 10⁶ μm³ (or 3 nL), which is accompanied by a strong depletion of analytes in the tissue surrounding the probe’s flushing site, hence further complicating the analysis.³ Furthermore, while tissue trauma due to exposure to bulk flow into and out of the probe can be minimized at low flow rates,¹⁵ it may be considerable at relatively high μL/min flow rates commonly used in PPP and UF.

An alternative approach to reduce the membrane area by 1000× is to decrease the R_mQ product by a corresponding 1000× (Figure 1C) by decreasing the membrane resistance R_m and the flow rate Q. The pore size, porosity, thickness, and tortuosity of a membrane can be adjusted to decrease R_m. Polymer-based membranes used in commercial MD probes have relatively high R_m of the order of 10⁷ s/cm due to their large thickness (10–40 μm) and tortuosity, which translates into large areas and high flow rates (Figure 1c, black cross-hatched region) to achieve high recovery. A microfabricated MD probe⁸ with an integrated 5 μm thick anodic aluminum oxide (AAO) membrane has been demonstrated, however with just 1% porosity, resulting in a high R on the order of 10⁷ s/cm and S about 10⁵ μm² (Figure 1c, blue). Atomically thin (0.34 nm) graphene-based membranes can provide extremely low resistance,^17,18 which is promising for solvent nanofiltration;¹⁹ however, their defect-induced pore sizes below 1 nm are too small for the commonly targeted molecular weight cutoff (MWCO) of a few kDa. Utilization of molecularly thin (15–50 nm) nanoporous silicon²⁰⁻²² or silicon nitride membranes²³ with low resistances can potentially provide a high RR with active surface areas S down to 1000 μm² (Figure 1c, red). This would require, however, reduction of flow rates Q to the exceedingly slow nL/min range (Figure 1c, red dot) that is at least 100–1000× slower than flow rates used in traditional USF MD⁵ and in microfabricated probes.⁸

Such exceedingly slow flow rates impose numerous challenges in flow control, analyte collection time, sample manipulation, and chemical quantitation. These problems can be mitigated, at least in part, by drastic reduction of the microfluidic channel cross-section from 100000 μm² in traditional MD probes to about 2000 μm² in the microfabricated MD probes^6,8,9,14 and even further to channels as small as 50 μm² using silicon microfabrication.²⁴ Such a dramatic downscaling of channel cross-section results in a corresponding increase of the hydrodynamic resistance (Figure 1D), which is beneficial for maintaining a precise control of nL/min flow rates at reasonable pressures of 100 mbar per 1 mm of the channel length.

Hence, to realize the deeply scaled nanodialysis (ND) probe (Figure 2a) that can be used for highly localized and efficient chemical sampling with minimal tissue damage, the downscaled microfluidic channels enabling exceedingly slow flow rates need to be integrated with an ultrasmall sampling area covered with an ultrathin semipermeable membrane (Figure 2b).

Figure 2.

Schematics of an integrated deeply scaled ND probe. (a) Schematic of an integrated ND probe comprising an ultrathin small area membrane at the tip of a sampling needle, scaled microfluidic channels, a droplet generator, and a delay line for droplet storage. (b) Schematic of the sampling area with open in-plane flow (red arrow) of dialysate and perfusate and an ultrathin membrane to be attached.

Concept and Fabrication of the in-Plane Open-Flow ND Probe

Our ultimate goal is to integrate a nanometer-thin semipermeable membrane with a high density of nanopores into a silicon probe, shown in Figure 2a to achieve a high recovery rate RR with an ultrasmall sampling area S. Besides improving the RR, decrease of the flow rates to nL/min can help to minimize stress on the already fragile membrane that otherwise would result in its rupture that is often observed at high flow rates⁸ even for membranes as thick as 5 μm. To avoid such stress from building up, we adopted an in-plane flow design (Figure 2b), where laminar flows into and out of the sampling area are tightly balanced, hence canceling the out-of-plane bulk flow. This design (Figure 3a) is in striking contrast to the more traditional push–pull sampling approaches, where the microfluidic flows are intentionally redirected from the inside of the probe into the tissue¹² either perpendicular to the in-plane flows inside the probe^7,11,12,14 (Figure 3c) or from the capillary located above the sample orifice^9,10 (Figure 3b). The resulting RR is increasing, however at the expense of bulk flow inside the tissue, which can cause fluid loss/accumulation as well as tissue damage. Instead, the in-plane flow design minimizes stresses toward the external tissue and/or encapsulating membrane. Our design is therefore also conceptually different from the open-flow microperfusion³ and can be called open-flow nanodialysis.

Figure 3.

Concept and fabrication of the open flow ND probe. (a) Schematics of the in-plane open flow nanodialysis. (b) Schematics of the push–pull sampling with adjacent capillary of ref (10). (c) Schematics of the out-of-plane push–pull sampling of ref (12). (d) SEM image of the fabricated ND probe with 3 mm long sampling needle. (e) SEM cross-section of the probe needle showing 2 parallel microfluidic semicircular 5 μm radius channels sealed with a SiNx layer. (f) SEM image of the tip of the completed open flow ND probe with the square sampling area design. (g) SEM image of the tip of the completed open-flow ND probe with the U-shaped sampling area design.

The open-flow ND probe (Figure 3d) is fabricated following a silicon microfabrication process (Figure S1a) that involves 5 layers of aligned photolithography, 2 thin film depositions, and 10 etching steps. The probe sampling needle is designed to be several millimeters long to provide access to deep tissues. Fabrication on silicon-on-insulator (SOI) wafers with a 15 μm device layer enables reduction of the probe needle cross-section to 17 × 70 μm² (1260 μm²), which is the smallest demonstrated thus far (Figure 3e), and is approximately just a few cell bodies across, thus potentially minimizing tissue trauma and inflammation. This cross-section can accommodate up to 3 microfluidic semicircular channels of 5 μm radius etched into the Si device layer and sealed with a 3 μm thick SiNx layer (only 2 channels are used for the design in Figure 3e).

Two separate designs of the probe sampling area at the tip of the needle are explored: a 1540 μm² square design (Figure 3f) and a more complex U-shape design with an area of 1720 μm² (Figure 3 ) with a gradual tapering of the channel width to maintain an in-plane laminar flow (see also Figure S6).

Realization of the in-Plane Pressure-Balanced Open-Flow ND Probe

To characterize the flows and recovery rates of the fabricated ND probe, the probe is released from the processed SOI wafer (Figure S1b,c) and packaged to provide fluidic interfaces with external microfluidic pumps (Figure 4a and Figure S1d). Packaging involves attaching the chip to a 3D-printed holder, insertion of 3 microchannel stubs at the chip edge into glass capillaries, and sealing the junctions with UV-curable resin (Figure S1e–g).

Figure 4.

Realization of the in-plane pressure-balanced open-flow ND probe. (a) Photograph of a packaged ND probe. (b) Equivalent circuit diagram of pull (P1) and push (P2) arms of the microfluidic circuit. (c) Calculated net flow rate as a function of a pressure balance between pull and push channels. (d) Fluorescence microscope image of the packaged probe visualizing the inlet and outlet aqueous flows with dissolved 1 mM fluorescein. (e) Fluorescence microscope image of the sampling tip of the ND probe with the square-shape open sampling area under negative (left, oil suction), nearly zero (middle, balanced), and positive (right, dye overflow) differential pressures ΔP (SI Movie 1).

First, we assess the concept of the in-plane balanced open-flow sampling (Figure 3). The probe in this configuration can be analyzed as an equivalent circuit (Figure 4b) with hydrodynamic resistances R1 and R2, and pressures P1 and P2, corresponding to the pull and push flows, respectively. Since we are aiming to maintain the pressure at the open sampling site to be equal to the atmospheric pressure (or the intracranial pressure for measurements in the brain), we assume both circuit arms are grounded at the sampling site. The interface between the perfusate and the tissue can be elastic; hence, we consider it to be a hydrodynamic capacitor that reflects the volume of the open sampling area changing with differential pressure ΔP = (P1R2 + P2R1)/(R1 + R2) applied to it. Hydrodynamic resistances R1 and R2 were estimated from the cross-section and lengths of the channels and the measured flow velocity for a given pressure (Methods). These hydrodynamic resistances were used to predict the net flow rate at the open-flow sampling site (Figure 4C). Neglecting the capacitance, these flows are perfectly balanced (net flow is zero) when the differential pressure ΔP is zero, corresponding to the blue diagonal in Figure 4c. Along this diagonal, the in-plane flow rate can be tuned continuously from below 5 nL/min in the lower right corner to above 25 nL/min in the upper left corner.

To visualize and measure balanced flows, the packaged ND probe is attached to a glass slide with the sampling needle embedded into a 0.5 mL reservoir (Figure S2) filled with fluorinated oil (FC40, Sigma-Aldrich). Various pressures are applied to the chip’s push and pull channels (Figure 4d). Since the on-chip microfluidic channels are buried under an optically transparent SiNx channel cover, the standard fluorescence microscopy is used to visualize (Figure 4d) aqueous microfluidic flows (fluorescein in DI water) inside the buried channels. Figure 4e shows a series of frames from a movie (SI Movie 1) recorded during a sweep of P2 from 25 to 60 mbar while keeping P1 constant at −100 mbar (vertical cut in Figure 4c). When ΔP at the open-flow area is negative (Figure 4e, left) the oil is suctioned into the outlet channel forming a black elongated droplet, while a positive ΔP results in an overflow of dye solution (Figure 4e, right). A balanced flow is achieved when the push and pull flow rates are nearly equal, resulting in purely in-plane flow (Figure 4e, middle) around the ΔP = 0 predicted from Figure 4c with margins ±30 mbar (SI Movie 1). This margin is consistent with the expected Laplace pressure at the water/oil interface inside the open-flow area, which when overcome, results in suction (negative ΔP) or overflow (positive ΔP).

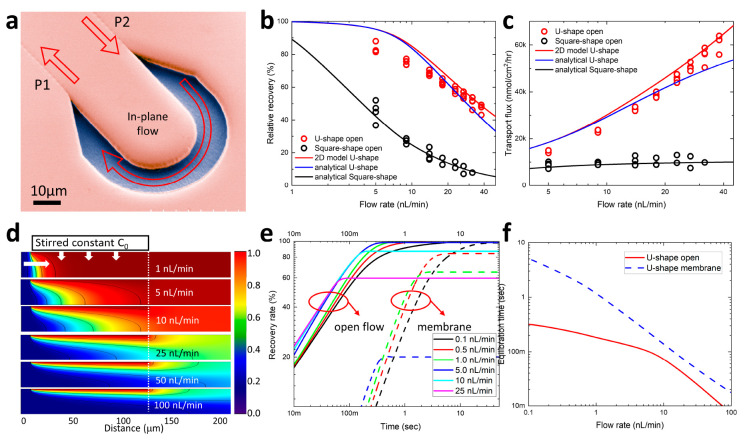
Operation of an Open-Flow ND probe at Balanced Pressure: Ultralocalized Sampling with High Recovery

The established boundaries of the pressure balance correspond to a laminar flow of the perfusate in the open-flow sampling area with minimized out-of-plane bulk flow (Figure 5a). To measure the RR at room temperature (RT) the reservoir is filled with a solution of 1 mM fluorescein in DI water and the dye concentration in the dialysate channel is quantified by measuring the fluorescence intensity with a photomultiplier tube (PMT) attached to a fluorescent microscope (Figure S2). For the square-shaped open-flow area design the RR rapidly increases with a decrease of the flow rate reaching 45.3 ± 6.3% (mean ± standard deviation (SD), n = 4) at 5 nL/min (Figure 5b, black circles). The U-shaped open area design exhibits a much higher RR, reaching 83.3 ± 3.1% (mean ± SD, n = 4) at 5 nL/min. The absolute flux of dye molecules across the open area interface is shown in Figure 5c. For the square-shaped design (Figure 5c, black circles) it remains almost constant at 8819 ± 1243 nmol/(cm² h) (mean ± SD, n = 4) for all flow rates. However, for the U-shaped design (Figure 5c, red circles) the flux exhibits a strong 4× increase from 14204 ± 530 nmol/(cm² h) (mean ± SD, n = 4) at 5 nL/min to 61030 ± 3,525 nmol/(cm² h) (mean ± SD, n = 4) at 38 nL/min.

Figure 5.

Characterization of the open-flow ND probe at balanced pressure. (a) SEM image of the U-shaped open sampling area. (b) Recovery rates of the U-shaped (red circles) and square-shaped (black circles) open-flow ND probes measured at different pressure-balanced perfusate flows at RT. The red curve is the RR calculated by the 2D COMSOL model for 130 μm arc length of the U-shaped design. Blue and black curves correspond to fitting with eq 1. (c) Dye transport flux measured for the U-shaped (red circles) and the square-shaped (black circles) open-flow ND probes measured at different pressure-balanced perfusate flows. The red curve is the RR calculated by the 2D COMSOL model for 130 μm arc length of the U-shaped design. Blue and black curves correspond to fitting with eq 1. (d) Calculated 2D concentration profiles of in-plane dialysate flows. The colors represent the concentration of fluorescein, with blue being 0 mM and red being 1 mM. (e) Calculated transient recovery rates for different flow rates. Solid and dashed lines correspond to the U-shaped design with an open area and an integrated resistive membrane, respectively. (f) Dependence of the equilibration time on flow rates for the U-shaped design with open area (solid red) and integrated resistive membrane (dashed blue).

To get further insight, we performed numerical calculations using a 2D COMSOL model of a steady-state diffusive flux through an open sampling area with the channel depth of 10 μm (Figure S6) for different in-plane laminar flow rates (Figure 5d). Calculated concentration profiles can be understood by comparing the diffusion time τ_D it takes molecules to diffuse vertically to the bottom of the channel, to the residence time τ_R required for molecules to flow along the full length of the open sampling area of 130 μm (Figure S6). Since at low flow rates of a few nL/min, τ_D is shorter than or comparable to τ_R, a nearly constant concentration profile is formed downstream across the whole channel depth (Figure 5d, top) with RR approaching 100% (Figure 5B, red). At high flow rates τ_R is much smaller than τ_D, which leaves the bottom of the channel almost completely depleted of the analytes (Figure 5d, bottom) and therefore significantly diluting the dialysate, with a corresponding strong decrease of the RR (Figure 5b, red). The 2D numerical model produces results consistent with direct fitting using eq 1 (Figure 5b, blue) assuming the transport resistance R_d of 5.4 × 10⁵ s/cm for an open area S of 1760 μm². R_d is the largest at slow flows since the concentration gradient across the interface is the smallest, which results in diminishing flux that is also observed in the results of the U-shaped design in Figure 5c. At higher flow rates the concentration gradient rapidly increases, resulting in smaller R_d and an increase of the flux. For the square design with similar area S of 1540 μm², R_d is 6.5× larger, reaching 3.5 × 10⁶ s/cm (black curve in Figure 5b,c). Correspondingly, the flux is significantly reduced, indicating a much shorter effective sampling length compared to the U-shaped design. Since the RR for the U-shaped design is markedly better than that of the square-shaped design, it is used exclusively for further experiments involving the ND probe with an integrated nanoporous membrane.

Integration of a semipermeable membrane is expected to increase the transport resistance, which can potentially result in an increasingly long time for the concentration to reach the equilibrium steady-state gradients of Figure 5d, thus degrading temporal resolution. The steady-state equilibrium model⁴ of eq 1 does not account for these transients. To evaluate the equilibration time τ_E (time to reach 80% of the equilibrium steady state RR) we used the transient 2D COMSOL model for different transport resistances (Figure 5e, solid lines). For an open area U-shaped design (solid lines in Figure 5e) the calculated τ_E is below 1 s even at a flow rate as low as 0.1 nL/min. The corresponding dependence of τ_E versus flow rate is shown in Figure 5f (red). When the resistance is increased to 10⁷ s/cm, the transient RR exhibits much slower dynamics (Figure 5e, dotted lines) with the calculated τ_E reaching 1 s at 1 nL/min (Figure 5f, blue).

Integration of High Transport Ultrathin Si Nanoporous Membrane

For our ND probe, we adopted a silicon nanoporous membrane²² (SiMPore, NY) (Figure 6A) that has been explored previously for hemodialysis²¹ and showed high permeability²⁵ and molecular selectivity.²⁶ The membrane thickness is just 30 ± 2 nm (mean ± SD, n = 5) with an average pore radius of 23.3 ± 6.6 nm (mean ± SD, n = 208) and a measured porosity of 15.5 ± 6.6% (mean ± SD, n = 10) (Figure S4). The fluorescein transport flux of 2511 ± 502 nmol/(cm² h) (mean ± SD, n = 3) through the Si membrane (Figure S5b) measured at 50 °C using a side-by-side diffusion cell (Figure S3) is 140× higher than that measured for the reference AAO membrane of 18 ± 3 nmol/(cm² h) (mean ± SD, n = 3) with similar pore size and porosity, but with a thickness of 50 μm (InRedox, CO). While for the AAO membrane there is a significant selectivity between anionic fluorescein (332 Da) and methyl orange (327 Da) dyes, and cationic methylene blue (320 Da) dye of similar molecular weights and hydrodynamic diameters (<0.5 nm), the molecular flux through the ultrathin Si nanoporous membrane is independent of the molecule’s charge (Figure 6b and Figure S4) since it is mostly defined by the pore discovery time rather than the transmembrane transport.²⁶

Figure 6.

Characterization and integration of ultrathin Si nanoporous membrane. (a) SEM image of the nanoporous ultrathin silicon membrane. (b) Dye transport fluxes measured with nanoporous Si membrane and with AAO membrane for different dye molecules at 50 °C. (c) Fabrication steps to integrate the ultrathin membrane onto the open sampling area of the ND probe (step 1) using a stamping technique (step 2, see also SI Movie 2), cleaning the wafer (step 3), and releasing the probe from the wafer with front- and back-side etching (step 4). (d) SEM image of the membrane transferred on top of a U-turn sampling area. (e) SEM image of the tip of the completed ND probe with a U-shaped sampling area design. (f) SEM image of the fully processed ND probe with integrated ultrathin Si nanoporous membrane. (g) Relative recovery of a U-shaped ND probe with a Si nanoporous membrane measured at RT. (h) Dye transport flux of a U-shaped ND probe with a Si nanoporous membrane at RT. The dashed horizontal line is the transport flux for a standalone silicon nanoporous membrane at 50 °C.

To integrate the Si nanoporous membrane into the ND probe, we developed a wafer-scale fabrication flow (Figure 6c, Figure S5, and SI Movie 2) adapting a stamping technique²⁷ to detach the membrane from the host substrate using a polydimethylsiloxane (PDMS) substrate, align and attach it to the ND open sampling area (step 2 in Figure 6c), stamp and release the membrane (step 3 in Figure 6c), and clean the residue (Figure 6d). Once the membrane is in place, the wafer undergoes two deep reactive ion etching steps to undercut the sampling needle (step 4 in Figure 6c and Figure 6e). The released ND probe with a Si nanoporous membrane integrated onto the sampling needle with the U-shaped design is shown in Figure 6f.

To measure the recovery rate (Figure 6g) and the dye transport flux (Figure 6h) of the ND probe, the sampling needle is immersed into a reservoir filled with 1 mM fluorescein DI water solution at RT (Figure S2a). While the flow rate dependences (Figure 6g,h) are qualitatively similar to those observed with the open-flow ND probe (Figure 5b,c), the RR at 5 nL/min flow rate is decreased to 15.3 ± 0.3% (mean ± SD, n = 3) due to limited membrane porosity. The transport flux is 2610 ± 44 nmol/(cm² h) (mean ± SD, n = 3) at the slowest flow rate of 5 nL/min that is close to that measured for the standalone membrane (dashed line in Figure 6h) with no flow. The transport flux increases to 4705 ± 550 nmol/(cm² h) (mean ± SD, n = 3) at 38 nL/min, which is among the highest reported for nanoporous membranes.^22,23 Both the 2D numerical COMSOL model (red curves in Figure 6g,h) and analytical eq 1 model (blue curves in Figure 6g,h) provide a good fit to the flow rate dependences in assumption of the total transport resistance R_d + R_m of 9 × 10⁶ s/cm.

On-Chip Droplet Segmentation of Dialysate Flow and Droplet Storage at High Temporal Resolution

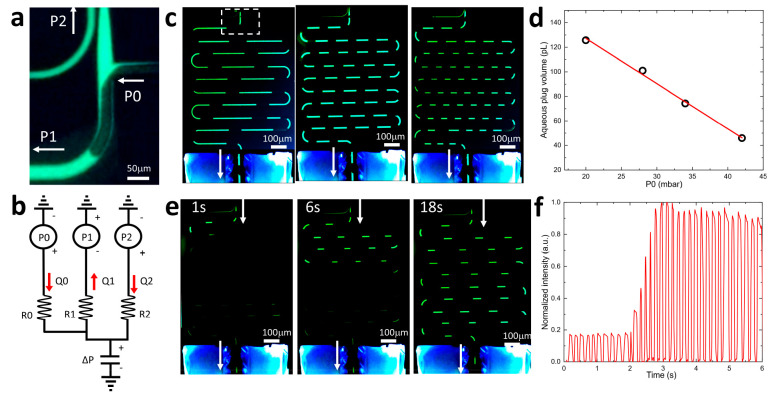
Although the equilibration time for the ND probe with integrated Si membrane at 5 nL/min flow rate is below 1 s (Figure 5f), the overall temporal resolution can be significantly degraded by the lateral Taylor diffusion which occurs in the microfluidic channel that transports the collected dialysate for subsequent chemical analysis. Segmentation of the dialysate flow into a series of oil-isolated nL-volume droplets²⁸ was shown to halt this diffusion and helped to reach temporal resolution in the range of just a few seconds.^8,10−12,14 The drastic reduction of channel cross-section down to 40 μm² enabled by our silicon platform and its operation at exceedingly slow nL/min flow rates allows for stable on-chip generation of droplets with volumes as small as just a few pL.²⁴ We have previously demonstrated an on-chip delivery of such droplets to online mass spectrometry (MS) analysis via an integrated nanoelectrospray ionization (nano-ESI) nozzle²⁹ or printing them one-by-one for matrix-assisted laser desorption ionization (MALDI) MS,³⁰ that yield limits of detection (LOD) at the level of just a few attomoles.³¹ However, it is envisioned that such drastic reduction of flow rates and analyte volumes will impose a specific challenge of interfacing the segmented flows at the ND chip edge. Since the 27 μm diameter of a 10 pL droplet is much smaller than the inner diameter of typical glass capillaries used to connect the chip to the external pumps, to store the droplets,³² and to transport them to chemical analysis, droplets typically tend to intermix or coalesce,¹⁰ thus significantly decreasing temporal resolution.

To address this problem, we designed an on-chip storage delay line (Figure 7) where collected droplets can be kept isolated from each other while preserving their order prior to hyphenation to MS analysis. To decrease the total hydrodynamic resistance R1 of the delay line (Figure 7a) its channel cross-section is increased to 357 μm² by increasing the channel width to 40 μm (Figure S7). Oil flow controlled by the pressure P0 (Figure 7a) is transported through a channel R0 to the T-junction which operates in the squeezing regime (Figure 7b and SI Movie 3) to segment continuous aqueous flow into individual monodisperse (2.5% relative SD) aqueous plugs separated by oil droplets. The volume of the compartments can be continuously tuned (Figure 7c and SI Movie 4) from 40 to 130 pL by adjusting the oil-port pressure P0 and holding P1 constant (Figure 7b). The 26 mm long delay line of Figure 7c can store anywhere from 20 (Figure 7c, left) to 60 (Figure 7c, right) aqueous samples corresponding to up to 1 min of sampling time. The on-chip storage capacity is defined by the sampling frequency, droplet volume, channel length, and hydrodynamic resistances and therefore can be designed beforehand to meet experimental needs.

Figure 7.

On-chip segmentation of dialysate flow and on-chip droplet storage. (a) Fluorescence microscope image of the T-junction area (SI Movie 3). (b) Equivalent circuit diagram with oil port P0 and a T-junction. (c) Segmentation of a dialysate flow into compartments of different volume demonstrating storage capacities of 20, 46, and 66 droplets, left to right, correspondingly. The dashed white rectangle in the left image corresponds to a location of a T-junction in (a). (d) Dependence of the aqueous plug volume on the P0 pressure while P1 is kept constant. (e) Series of still frames from a video (SI Movie 5) taken while the concentration of fluorescein in the reservoir is rapidly changed. (f) Fluorescence intensity measured with a PMT downstream during a rapid change in fluorescein concentration.

The temporal response provided by the flow segmentation is tested in Figure 7e by rapidly changing the fluorescein concentration in the reservoir while monitoring the fluorescence intensity in the downstream channels (Figure 7e and SI Movie 5). Only 4 droplets are required to fully resolve fast changes in the concentration with subsecond temporal resolution (Figure 7f).

Conclusions and Outlook

Our results demonstrate that the designed silicon ND probe with integrated nanoporous membrane can provide high recovery rates, subsecond temporal resolution, and highly localized sampling, simultaneously, within a cross-section that is just a few cell bodies across. These notable performance metrics are a direct result of a 100× downscaling of the microfluidic channel cross-section, a corresponding drastic 100× reduction of flow rates to exceedingly slow few nL/min flows, and an integration of a nanometer-thin nanoporous membrane with high transport flux into the probe sampling area. These engineered improvements were made possible by adopting a wafer-scale silicon microfabrication platform that provides precise control over channel dimensions, a high Young’s modulus to withstand pressure-controlled flows, and optical transparency for flow visualization using standard fluorescence microscopy. Recent development of hyphenation of droplet-segmented analyte flows to sensitive MS methods³³ have shown great promise for chemical quantification of individual droplets with volumes in the low nL down to a few hundreds of pL.⁹⁻¹³ The deeply scaled silicon ND platform demonstrated here enables sampling, on-chip droplet segmentation, and storage of analytes with 10–100× smaller volumes of just a few pL that may impose technical challenges for MS hyphenation. However, previously demonstrated on-chip integration of specially designed nanoelectrospray nozzles using our scaled silicon ND platform^29,30 may enable efficient MS hyphenation of pL-segmented dialysate flows with LOD of just a few attomoles.³¹ The proposed and demonstrated scaling strategy (Figure 1b–d) can potentially be extended even further in miniaturizing the sampling area, while keeping a high recovery rate and temporal resolution. With mature silicon microfabrication technology, it is relatively straightforward to reduce the channel cross-section, and hence control the pressure-driven flow rates below 1 nL/min (Figure 1d). Integration of ultrathin membranes with high transport flux in the ND probe with the in-plane sampling geometry (Figure 5a) can potentially enable reduction of sampling areas down to just 100 μm² (Figure 1c). A corresponding reduction of dialysate volumes to be manipulated and analyzed at a femtoliter range, as well as the required increase of chemical sensitivity to zeptomole levels, are both within reach, especially in view of recent developments in nanofluidics³⁴ and in chemical quantification of single subcellular organelles.³⁵ Equilibration times for a membrane-integrated ND probe will inevitably become slower (Figure 5e), approaching several minutes; however, they can be significantly improved by decreasing the membrane transport resistance (Figure 1c) or by adopting the concept of an open-flow ND (Figure 5a).

Methods

ND Probe Fabrication of Microfluidic Channels

The ND probes are fabricated using a silicon-on-insulator (SOI, UltraSil) wafer with a 425 μm handle thickness, a 1 μm buried oxide (BOX) layer, and a 15 μm device layer. First, 300 nm of SiNx is deposited using plasma-enhanced chemical vapor deposition (PECVD) (PlasmaPro 100, Oxford Instruments) to serve as a hardmask for subsequent etching of the Si device layer (Figure S1a.1). The SiNx hardmask is then patterned with rows of perforations using a direct laser lithography system (MLA 150 Heidelberg) followed by reactive ion etching (RIE) using an inductively coupled plasma (ICP) ICP-RIE etcher (PlasmaPro System100, Oxford Instruments), leaving perforations of 1 μm diameter exposing the Si device layer below (see also Figure S7). Next, the exposed Si is isotropically etched using XeF₂ gas (Xactix, SPTS). During etching the neighboring undercuts from each perforation are merged, forming a continuous microfluidic channel buried underneath the SiNx hardmask (Figure S1a.2). The size of the perforations, the distance between them, and the etching time control the channel cross-section that can be tuned from a semicircular 40 μm² profile with 5 μm radius (single line of perforations, Figure S6e) up to 40 × 10 μm shape with 360 μm² cross-section (4 rows of perforations, Figure S7a). The perforations in the SiNx hardmask layer are then sealed by deposition of 3 μm low stress SiNx via PECVD (Figure S1a.3 and Figure 3e).

ND Probe Open Sampling Area Fabrication

The open sampling sites with square-shaped or U-shaped designs (Figure 3f,g) are defined in the same hardmask layer as the perforations. Therefore, the isotropic Si etching results in a deeper and wider profile than in the buried microfluidic channels (Figure S6) that gradually changes from a 40 μm² (Figure S6e) to 260 μm² (Figure S6d) cross-section, effective slowing down the perfusate flow velocity to achieve higher recovery rates.

ND Probe Perimeter Definition and Release

Lastly, to define the probe perimeter and to release the probe from the wafer, a series of 200 μm wide trenches are patterned on the device side using direct write lithography (Figure S1a.4). The exposed SiNx is etched using ICP-RIE, and the 15 μm thick Si device layer is etched down to the BOX layer using deep reactive ion etching (DRIE) (LpX Pegasus, STS). The BOX layer is etched further down to the handle Si wafer using ICP-RIE. The backside-aligned lithography (EVG620, EVG) is repeated on the handle wafer side followed by a DRIE step to etch all the way through the 425 μm thick handle wafer (Figure S1b). The resulting probe is attached to the wafer via a set of narrow bridges that can be easily broken to release the probe with a sampling needle attached to the probe base (Figure S1c) containing a buried network of microfluidic channels connecting sampling, droplet segmentation, and storage delay line components.

ND Probe Packaging

The fabricated ND chip is released from the wafer and packaged to provide fluidic interfaces (Figure S1e–h). To interface with external microfluidic pumps, the 170 μm wide by 425 μm thick silicon stubs on the chip base (Figure S1e) are shaped to fit into 15 cm long 700 μm ID silica capillaries (TSP700850, Polymicro). The polyimide coating of the glass capillaries is burned out to allow transmission of UV light in subsequent steps. Precise alignment of all 3 capillaries simultaneously is achieved under a microscope with the aid of 3D-printed holders designed for handling the probe and capillaries (Figure S1f) and a pair of x-y-z micromanipulators. The connected stubs are sealed with UV-curable resin (NOA 68T, Norland) to enable continuous operation under high differential pressures (Figure S1g).

Integration of Ultrathin Nanoporous Membrane

Integration of the nanoporous Si membrane into the process flow is introduced after the formation of the microfluidic channels and open sampling sites (Figure 6c) between steps 3 and 4 from Figure S1a using a wafer-scale fabrication flow (Figure 6C, Figure S5, and SI Movie 2). The 30 nm thin silicon nanoporous membrane (US100-P30Q33, SimPore) with 500 × 500 μm² surface area is detached from the Si host substrate using a polydimethylsiloxane (PDMS, Sylgard 184, DOW Chemical) stamp covered with a 2 μm thin poly(methyl methacrylate) (PMMA, MicroChem) layer (Figure S5a and step 1 in SI Movie 2). The wafer is cleaned, treated with oxygen plasma, and preheated above the glass transition temperature of the PMMA to ease the attachment and release of the stamp from the wafer surface (Figure S5b and step 2 in SI Movie 2). The stamp with the attached membrane is aligned to several ND open sampling sites simultaneously (Figure S5b) under a microscope and attached to the wafer (step 2 in SI Movie 2). Then the PDMS stamp is lifted off and the wafer with attached membrane is cooled to room temperature. PMMA residue is removed in acetone for 5 h at 50 °C. Successful attachment and detachment of the PMMA layer can be seen by observing the moving meniscus at the PMMA–substrate interface (red arrows in Figure S5a,b and SI Movie 2). Even though the membrane is just 30 nm thick and is hanging over a large sampling area, it is mechanically robust enough to withstand deposition of thick photoresist layers, double-sided lithography, long DRIE steps, and photoresist stripping and cleaning steps (Figure 6e,f and Figure S6).

Molecular Transport Rate Measurements in Nanoporous Membranes

To characterize the pores of the silicon nanoporous membrane and a reference anodic aluminum oxide (AAO) membrane (AAO-010-020-050, InRedox), SEM images were taken (Hitachi S-4800) at high magnification (Figure S4a) in several areas of the membranes. The raw images were thresholded to isolate pore perimeters from the background, and pore radii, density, and porosity were measured using ImageJ (Figure S4b). Prior to transport measurements, all membranes were exposed to oxygen plasma for 15 min.

To measure the diffusion transport rate, the membranes were placed in the middle of a side-by-side diffusion cell (5G-00-00-15-–05, PermeGear) (Figure S3a) with identical 5 mL feed and permeate volumes to avoid hydrostatic buildup. To measure the transport of molecules with similar weights but different polarities through the membranes, 1 mM solutions of fluorescein (Sigma-Aldrich), methyl orange (ACS reagent, dye content 85%, Sigma-Aldrich), and methylene blue (Sigma-Aldrich) in DI water (18 MΩ, Millipore) were used to fill the feed cell. To ensure uniform concentration distributions in the feed and permeate cells, both cells were continuously stirred using magnetic stir bars. The diffusion cell was held at a constant 50 °C temperature monitored with a thermo-pair. Optical transmission through a receiving permeate cell was analyzed (Figure S3b) using a blue light from a fiber-coupled LED (490 nm, M490F4, Thorlabs) collimated with a pair of high-NA fiber optic collimators (F950FC-A, Thorlabs) and recorded using a fiber-coupled UV–vis spectrometer (Flame Miniature Spectrometer, Ocean Optics). For uniform concentration fields the molar concentration c of the analyte in the permeate cell was calculated from the Beer–Lambert law:

2

where OD is optical density, ε is the molar absorption coefficient, and d is the cell diameter. The transmission through the permeate cell was calibrated by measuring the transmission (Figure S3c), calculating the optical density OD (Figure S3d), and applying a linear fit of OD vs concentration (Figure 4e) for fluorescein (Fluo), methyl orange (MO), and methylene blue (MB) at wavelengths of 498, 503, and 473 nm, respectively. Equation 1 produced a good fit of the Beer–Lambert law for ODs of at least up to 5 with R² > 0.992 and Pearson r_p > 0.995 for all analytes (Figure S3e). Above an OD of 8 the dependence became nonlinear (e.g., Figure S3d) and was not used infitting.

The temporal change of the OD also showed good linearity (R² > 0.995, r_p > 0.998) for all analytes (Figure S4c) for long times, as the experiments lasted as long as several days. Similar dependencies were observed for the AAO membrane (Figure S4d) with high linearity for Fluo (R² = 0.998, r_p = 0.999) and MB (R² = 0.986, r_p = 0.993), and with somewhat lower values for MO (R² = 0.924, r_p = 0.961). The slopes of the linear fits of OD vs time (Figure S4c) were normalized on corresponding calibration curves of OD vs concentration (Figure S3e) to calculate temporal changes in concentration, transport resistances, and transport fluxes reported in Figure 6b.

Visualization and Characterization of Microfluidic Flows with Fluorescence Microscopy

To visualize microfluidic flows, the fully packaged ND probe (Figure 4a) was connected to external pressure-controlled pumps (Flow-EZ Module, LU-FEZ-7000, and LU-FEZ-N800, Fluigent) for push (P2 in Figure 4d) and pull (P1 in Figure 4b,d) aqueous flows, and a push oil flow (P0 in Figure 4d). Since the top SiNx layer of the probe is transparent for visible light, standard fluorescence microscopy was used. Imaging and characterization of flows and droplets were done with an inverted fluorescence microscope (IX73, Olympus) equipped with a photomultiplier tube (PMT 2101, Thorlabs), video cameras (EOS Rebel T7i, Canon, and Hero8, GoPro) and an LED lamp at 400 nm wavelength (pE-300 White, CoolLED) for fluorescence excitation. To visualize the flows (e.g., Figure 4d,e), a fluorescein solution in DI water was used at various concentrations up to 1 mM as specified for each experiment (e.g., Figure 4d).

Calibration and Measurements of Diffusion Fluxes in ND Probes

To visualize the suction or overflow of aqueous flows (Figure 4e), the fully packaged ND probe was attached to a glass slide with its sampling needle embedded into a 0.5 mL reservoir (Figure S2a) filled with fluorinated oil (FC40, Sigma-Aldrich), and various pressures were applied to the chip’s push (P2) and pull (P1) channels (Figure 4e and SI Movie 1).

To measure fluorescein concentration inside the microfluidic channels, the image of a microfluidic channel formed with a 40× objective of the inverted microscope with a field of view (FOV) of 50 μm diameter (inset in Figure S2b) was projected onto a PMT entrance slit, and the voltages were sampled and recorded with a digital multimeter (DMM6500, Keithley). Gain settings for the PMT and power settings for the excitation source were chosen to ensure the highest dynamic range. Example measurements of PMT voltages for 4 consecutive measurements of diffusive transport through an ND probe with an integrated Si nanoporous membrane is shown in Figure S2b. The flow rate was adjusted by changing the P1 and P2 pressures while keeping the pressure at the probe sampling area balanced (Figure 4c).

To convert the recorded PMT voltages (Figure S2b) to concentrations, recovery rates (Figure 6g), and fluxes (Figure 6h), the calibration of PMT voltage was performed (Figure S2c) by flowing solutions of known Fluo concentration at a constant 20 nL/min flow rate resulting with a reasonable linear fit (R² = 0.965, r_p = 0.975). To ensure that the flow rate itself did not affect the calibration, a set of measurements were performed for a constant concentration (1 mM and 10 μM) with flow rate varied (Figure S2d).

Flow Segmentation and Measurements of Hydrodynamic Resistance

To segment aqueous flow into a series of monodisperse plugs, oil flow controlled by the pressure P0 (Figure 7a) is transported through a channel R0 to the T-junction which operates in the squeezing regime (Figure 7b, SI Movie 3). The flow rate ratio between the aqueous and oil flows is controlled by a precise balance of the P0 and P1 pressures (Figure 7d) that defines the volume and frequency of the droplets. As oil droplets are passing through a microscope FOV, the PMT voltage is strongly modulated, enabling detection of the flow velocity. For segmented flows with relatively small oil droplets, the aqueous hydrodynamic resistance can be estimated by linear fitting of the measured flow velocity vs ΔP differential pressure using the known cross-section and length of the microfluidic channel. Normalized hydrodynamic resistances for aqueous (R1 and R2 in Figures 4b and 7b) flows are measured to be 60 and 574 mbar/(pL sec m) for FC40 oil (R0 in Figure 7B). These numbers are in close agreement with predictions using the analytical equation for a rectangular channel cross-section

3

where w and h are the width and height of the channel, L is the channel length, and μ is the dynamic viscosity taken as 8.9 × 10^–4 Pa s for water and 4.1 × 10^–3 Pa s for FC40 at RT.

Measurements of Temporal Response

The temporal response of the ND probe with oil-segmented flow (Figure 7e) was tested by equilibrating the ND probe in a reservoir and then rapidly altering the fluorescein concentration surrounding the probe by using a pipet filled with 1 mM Fluo solution while monitoring fluorescence of aqueous plugs downstream (Figure 7f). Droplet volumes were estimated by measuring droplet lengths and multiplying them by the cross-sectional area of the channel.

Numerical Modeling of Steady-State Diffusion Fluxes for Open Flow ND Probe

Numerical calculations using a 2D model of diffusion flux through an open sampling area for different in-plane laminar flow rates (Figure 5d) were performed using COMSOL Multiphysics 6.1. The microfluidic channel within the sampling area was modeled as a rectangular cross-section with a 11 μm height and 23 μm width to mimic the cross-section observed in experiment (Figure S6). The U-shaped opening was modeled as a straight channel with a length of 130 μm, close to the arc length of the U-shaped opening (Figure S6). Small sections at the inlet and outlet of the sampling area with 10 and 100 μm length, respectively, were added to the model to simulate regions within the push and pull channels, respectively. The fluid flow within the microfluidic channel was modeled with the Navier–Stokes equations by using the “Laminar Flow” module. Convective and diffusive transport of analytes was modeled with the “Transport of Diluted Species” module. The left-side and right-side boundaries were set as an inlet and outlet, respectively, with a fully developed flow at equal constant flow rates (1, 5, 10, 25, 50, and 100 nL/min) and entrance thicknesses equal to the width of the sampling area. The top and bottom boundaries of the microfluidic channel, including the boundary between the sampling area and the external volume, were specified with a no-slip boundary condition that assumes no convection into/out of the sampling area into the outside volume, and that the flow velocity at the boundary is equal to zero. To model the diffusion of analyte into the probe, the top sampling area boundary with the external volume was specified with a constant concentration boundary condition of 1 mM fluorescein, with fluorescein having a diffusion coefficient of 4.9 × 10^–6 cm²/s in water at RT and close to neutral pH. An integrated total flux (mol/s) of the analyte was taken at the outlet boundary and used to calculate recovered concentration. For modeling the steady state equilibrium fluxes (Figure 5b–d), a “Stationary Study” was used.

Numerical Modeling of Steady-State Diffusion Fluxes for ND Probe with Nanoporous Membrane

To model the diffusion flux through an integrated nanoporous membrane (Figure 5c), the top sampling area boundary was replaced with a “Thin Diffusion Barrier” with a no-slip boundary condition. The membrane thickness was set to 30 nm and membrane diffusion coefficient to 2 × 10^–9 cm²/s, a value derived from the experimentally measured transport flux in Figure 6B. Since the constant concentration boundary condition no longer applied to the top sampling area boundary, an additional fluidic cell with a length of 130 μm and height of 1 μm was added above the sampling area to simulate a well-stirred solution at a constant 1 mM concentration of fluorescein at a 100 μL/min flow rate. All other boundaries of this additional cell were set to a constant concentration of 1 mM fluorescein.

Numerical Modeling of Transient Diffusion Fluxes

To model the transient diffusion process (Figure 5e,f) prior to settling into a steady-state equilibrium, a “Time-Dependent Study” was utilized. The initial concentration was set to 0 mM for both the inlet microfluidic channel and within the sampling area. The concentration in the additional fluidic cell above the sampling area was changed stepwise to 1 mM, and the temporal evolution of the concentration profiles was calculated for the following 60 s. To resolve short-term and long-term transients of concentration gradients, gradated time bins were used starting from 0.1 ms for the 0–1 ms interval, 0.5 ms bin for the 1–332 ms interval, and a 50 ms bin for the rest.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.3c09776.

• Fabrication and packaging of ND probe, calibration and measurements of concentration dependence, calibration and measurements of membrane diffusive transport, porosity of Si nanopore membrane and diffusion measurements, integration of ultrathin nanoporous Si membrane onto ND probe, sampling area profile, and library of microfluidic channels, tapers, and T-junctions (PDF)

• Balanced in-plane flow, integration of Si nanoporous membrane, on-chip dialysate segmentation into pL-volume droplets, and temporal response (ZIP)

Author Contributions

^† I.P. , S.K., and C.K.B. contributed equally to this work.

An earlier preprint of this manuscript is available at bioXiv: Highly localized chemical sampling at subsecond temporal resolution enabled with a silicon nanodialysis platform at exceedingly slow flows. Insu Park, Sungho Kim, Christopher Kenji Brenden, Weihua Shi, Hrishikesh Iyer, Rashid Bashir, Yurii Vlasov. bioRxiv 2023.09.08.556607; 10.1101/2023.09.08.556607 (September 12, 2023).

The authors declare no competing financial interest.