Atomically Precise Manufacturing of Silicon Electronics

Abstract

Atomically precise manufacturing (APM) is a key technique that involves the direct control of atoms in order to manufacture products or components of products. It has been developed most successfully using scanning probe methods and has received particular attention for developing atom scale electronics with a focus on silicon-based systems. This review captures the development of silicon atom-based electronics and is divided into several sections that will cover characterization and atom manipulation of silicon surfaces with scanning tunneling microscopy and atomic force microscopy, development of silicon dangling bonds as atomic quantum dots, creation of atom scale devices, and the wiring and packaging of those circuits. The review will also cover the advance of silicon dangling bond logic design and the progress of silicon quantum atomic designer (SiQAD) simulators. Finally, an outlook of APM and silicon atom electronics will be provided.

1. Introduction

CMOS (complementary metal-oxide semiconductor) technology is reaching its ultimate limits for transistor size, and density.¹ Power consumption is also limiting performance improvements, with the ability to dissipate heat efficiently becoming a restrictive factor.^2,3 In order to enable further improvements, innovations in CMOS materials and device structures have been researched and developed.^4,5 This has also created opportunities for alternate modes of logic and memory structures that can focus on high density and performance with minimal size and power consumption. In order to achieve the absolute smallest size and highest density, atoms as the active participants (bits) in the computation process will need to be utilized.

The key advance for the concept of atom scale devices was the invention of the scanning tunneling microscope in 1982 and atomic images a year later.^6,7 This marked the beginning of an era where atoms and atomic structures could be observed and manipulated and it was only a few years later, in 1987, that Becker et al. wrote an atomic bit on Germanium by depositing atoms from the STM tip.⁸ Two years later in 1989, Negative Differential Resistance was measured over atom scale sites on boron exposed silicon.⁹ A year later in 1990, the writing of the letters “IBM” with xenon atoms showed the control of atom manipulation and the power of the STM to perform perfect atom scale lithography.¹⁰ Another year later, the same group demonstrated an atomic switch, when a xenon atom could be controllably located on the tip or sample while detecting the location by changes in the tunnel current.¹¹

The manipulation of xenon atoms was revolutionary in STM and atom devices, but controlled manipulation on semiconductor surfaces, substrates with substantial industrial utility and infrastructure, remained elusive and a key goal. Efforts to control and observe chemical reactions at atomic sites with the STM were initiated in 1988 with the atom resolved chemical reactions of ammonia on silicon (111) 7×7.¹² This lead to other chemical reactions being studied including cycloadditions and many other radical chemical reactions.¹³ In 1991, manipulations of silicon by a scanning tunneling microscope were reported by creating “mounds” and “moats” on Si (111)7×7 as well as controllably ejecting single silicon atoms from the surface.¹⁴ With the manipulation of silicon, the authors speculated that an era of semiconductor microelectronics, called “nanoelectronics” could emerge. However, Si(111) 7×7 had less technological importance than Si(100) surfaces and interfaces. In 1995, a result that set the stage for future developments of atom scale lithography and electronics was published in the journal Science. That work showed that hydrogen could be controllably desorbed from a hydrogen passivated silicon surface with a scanning tunneling microscope tip to create surface silicon dangling bonds (DBs) individually, in groups, or in patterns.¹⁵ Thereafter, hydrogen desorption was studied in detail and technological advances related to atom scale lithography and atom scale electronics proceeded to grow significantly over the years. However, it has taken many years of persistent study and development to at last establish viable capabilities at the atom scale of silicon and semiconductor materials. Today, there are multiple companies (Quantum Silicon Inc.,¹⁶ Zyvex Labs,¹⁷ and Silicon Quantum Computing,¹⁸ as examples) that utilize hydrogen lithography as a primary mode of atom defined or Atomically Precise Manufacturing (APM) to create functional patterns and devices.

The review presented here will focus on details related to APM and Hydrogen Desorption Lithography (HDL) from silicon surfaces with atom defined precision in order to create nano and atom scale devices for nanoelectronics. These atom scale devices are based upon the control and manipulation of surface silicon dangling bonds created through APM and HDL. Background details of the hydrogen terminated silicon surface will also be provided along with imaging and lithographic methods developed to create perfect atom scale patterns and devices. Connection to atom scale devices will also be covered, as will design, simulation and packaging of silicon dangling bond circuits. Finally, an outlook to the future of atom-scale classical and quantum devices based on silicon dangling bonds, will be provided.

2. Silicon Surfaces and Imaging

This section will discuss aspects of silicon surface preparation and imaging. The main focus will be on hydrogen terminated silicon formation (section 2.1) followed by scanning tunneling microscopy and spectroscopy (section 2.2) and atomic force microscopy (section 2.3). Finally, common defects found on the hydrogen terminated surface will be discussed (section 2.4).

2.1. Hydrogen Terminated Silicon

The interaction of hydrogen with semiconductor surfaces, in particular silicon, has been the subject of investigation for some time because of many academic and industrial applications including microelectronics, photovoltaics, and chemical sensor development; some excellent reviews of hydrogen interaction with semiconductor surfaces have been published.¹⁹⁻²² As well, a review from Mayne et al. detailed the scanning probe aspects of adsorption and desorption of hydrogen from surfaces.²³ We will not try to replicate these reviews but will discuss highlights of the surface preparation process and the hydrogen removal process from silicon surfaces as it pertains to atom scale electronic devices.

There are two important silicon surface orientations that can be prepared to have atomically flat and passivated surfaces. Silicon (111) is generally prepared with a wet chemical etching procedure that leaves the surface with a hexagonal surface geometry.²⁴ However, there can be some surface defects from etchant attack at point defects on terraces. As well, the surface, although generally inert to air, can become contaminated with physisorbed material when transferred to an STM that can cause some issues with stable imaging. Ultrahigh vacuum preparation of hydrogen terminated silicon avoids these issues by keeping the environment pristine at all points of the preparation cycle. Unfortunately, UHV prepared hydrogen terminated silicon (111) has surface imperfections that limits the quality of the final surface.²⁵

The hydrogen termination of silicon (100) has been prepared in UHV with very little change to the method since 1976.²⁶ Hydrogen (H₂) is dissociated on a hot filament and then exposed to the clean Si(100)2×1 surface. Depending on the temperature of the silicon surface, monohydride, dihydride or trihydride features are observed and reconstructions of 1×1, 2×1 and 3×1 can be selected.²⁷ The 1×1 and 3×1 reconstructed surfaces are less favored than the 2×1 reconstruction because of the multiple hydride^28,29 species involved and the potential for etching at lower temperatures.¹⁹

An alternative method to prepare Si(100)2×1-H in a Reduced Pressure–Chemical Vapor Deposition (RP-CVD) epitaxy reactor has also been shown.³⁰ In this preparation, a full wafer was processed using wet chemistries, annealing in hydrogen, epitaxial growth of a thin silicon buffer layer by dichlorosilane, followed by a final anneal in hydrogen. STM images showed atomically flat hydrogen terminated silicon.

2.2. STM and STS of Hydrogen Terminated Silicon

While hydrogenation of silicon surfaces toward various ends had been explored since the 1930s,³¹⁻³³ it was examined with STM in 1988 by Wiesendanger et al., who recorded topographic constant-current images of phosphorus-doped hydrogenated amorphous silicon films.³⁴ Subsequently, STM was further applied to hydrogenated Si(111)^35,36 and Si(100) surfaces³⁷⁻³⁹ with most attention given to the hydrogen terminated 2×1 surface.^22,27,40 Unlike the clean surface, in which silicon dimer bistable buckling can occur, the hydrogen terminated surface has a symmetric dimer structure (Figure 1). As well, atom resolving STM can image the hydrogen atoms at either polarity, while the clean H-free surface images the pi and pi* bonds of the silicon dimer.⁴¹ Deuterium terminated surfaces have also been prepared with similar results.^28,29,42,43

Figure 1.

Ball and stick model and STM image of H terminated silicon 100 (2×1). Silicon atoms in yellow and hydrogen atoms in white. Each ball-like structure in the STM image derives from a silicon atom terminated with a hydrogen atom. Dimensions between silicon atoms are shown in the image.

Two modes of STM are common: constant-current and constant-height. In constant-current STM scanning, a fixed bias is applied between probe and sample and a feedback loop controls the tip–sample distance to maintain a current (I) set-point. Features that conduct current easily will appear “higher” (larger tip–sample separation) than features that are less conductive (smaller tip–sample separation).

In constant-height STM mode, a fixed tip–sample distance called z_rel is selected and current is measured as the tip is raster scanned through a surface parallel plane. Constant-height scanning is at times preferable as it can show otherwise masked features as well as reveal the spatial character of gap states. These cannot be imaged in constant current mode because the tip would destructively contact the surface in surrounding regions where the gap states are absent. However, constant height imaging requires a highly stable instrument and is usually only performed when thermal drift and scanner creep can be avoided, usually at cryogenic temperatures.

The preparation of the STM tip is also important in order to produce clean atom resolved images. In order to prepare atomically sharp tips, tips can be sharpened using a field ion microscope prior to imaging in the STM.⁴⁴⁻⁴⁷ This process also creates a nitride coating that helps to stabilize the tip and it has been found that an etched tip with a very slight coating of silicon atoms at the apex, formed by controlled silicon surface contact, is most effective. This was a key advance as stable and reliable imaging on semiconductor surfaces has traditionally been challenging as usual probe preparation methods of indenting into a metal surface were not practical. Figure 2 showcases modern STM imaging of H:Si (100) with constant-current empty and filled state STM images (a,b), respectively, and (c) a constant-height image of the same area.⁴⁸ The constant-height STM image (c) highlights a “cross-shaped” dopant feature^49,50 not visible in the other two panels.

Figure 2.

Different STM imaging modes of the same sample area of H-terminated silicon. (a) STM constant-current empty states image (V = 1.3 V, I = 50 pA). (b) STM constant-current filled states image. (c) STM constant-height image of the same area. (V = 300 mV, z_rel = −300 pm). A pronounced “X” shaped feature due to a near surface dopant becomes clear at these imaging conditions. All images are 25 × 25 nm² in area, and z_rel is a measure of the relative tip–sample height as referenced to a known STM set-point of V = −1.8, I = 50 pA over a hydrogen atom. Reprinted with permission from ref (48). Copyright 2020 Taleana Huff.

STS of a surface site far from defects, adsorbates or dopants is generally quite featureless, only showing the valence and conduction band edges.⁵¹⁻⁵³ The band gap may be measured larger than bulk silicon due to tip induced band bending and because silicon surface states have been replaced by σ – σ* states of the Si–H bonds which are separated by a larger energy gap.⁵⁴ Also, a common observation for UHV thermally prepared Si(100)-H is a shifted Fermi level toward the middle of the gap, especially for n-type samples, not consistent with the known bulk dopant density. Moreover, degenerately doped crystals are often found due to lack an expected dopant state-induced gap current. Dopant current is observed for non-UHV prepared samples.^55,56 These observations were attributed to a driving out of dopants during standard sample annealing at temperatures of 1250 °C.⁵³ When sample heating was restricted to 1050 °C before hydrogen termination, conduction band onset occurred at low voltages, as expected for highly doped material, and the expected dopant induced gap current was also observed. Secondary Ion Mass Spectrometry (SIMS) analysis showed that dopant depletion could occur to depths up to 200 nm with just two fast anneals to 1250 °C. Figure 3 details STS and SIMS data showing the effects of heating and dopant migration.

Figure 3.

(a and b) Scanning tunneling spectra (STS) of hydrogen terminated silicon. The sample was prepared by flash annealing to (a) 1050 °C followed by hydrogen termination. After STS measurement the sample was flash annealed to (b) 1250 °C followed by hydrogen termination. Colors indicate the displaced tip height from the tunneling set point of −2 V, 0.1 nA. Red arrows indicate the location of the valence band onset. It is shifted for the 1250 °C sample. The black arrow indicates the tunneling current resulting from dopant states that are only observed for 1050 °C heated samples. (c–f) SIMS data showing arsenic levels in samples prepared with various annealing methods. Control 1 and 2 experience no high temperature heating. Sample 3 was heated to 1050 °C two times. Sample 4 was heated to 1050 more than 10×. Samples 5 and 6 were heated to 1250 °C two times and greater than ten times, respectively. Dopant levels are depleted significantly for all samples flashed to 1250 °C and for depths over 150 nm. (g) Shows a schematic of the silicon band diagram (not to scale) with varying dopant density according to the SIMS profile, consistent with the observation of a Fermi level within the gap in the near surface region and above the conduction band in the bulk. Reprinted with permission from ref (53). Copyright 2012 American Vacuum Society.

If dopants are not depleted from the surface, they can be easily identified with STM images of the H-terminated surface as dark or bright features depending on the dopant type and the imaging polarity. The clean, H-free surface is effectively pinned, masking the appearance of near surface ionized dopants. The protrusions and depressions seen on the H-terminated surface are a few nanometers in lateral extent and are explained as simple electrostatic charges causing local band bending. For instance, an ionized n-type dopant has a positive charge that pulls bands downward creating depressions in filled state images but protrusions in empty states.⁵⁷⁻⁶⁰ Dopant structures of delta doped phosphorus have also been observed after encapsulation of several layers of deposited silicon using a current imaging tunneling spectroscopy (CITS) method.⁶¹

More recently, dopant location identification has been elucidated using a combination of low temperature STM imaging and calculations.^50,62−64 These observations were initially performed with n-type dopants and exact dopant locations can be identified up to several layers deep in the silicon substrate.

Single dopant atom ionization dynamics have also been observed through the use of all-electronics pump–probe STM spectroscopy with ns time resolution.^65,66 These results showed that ionization and neutralization rates of subsurface dopants could be measured and showed the importance of understanding the charge dynamics of dopants in near surface regions under various STM imaging condition (Figure 4). Dopant ionization of buried dopants have also been investigated by STM for other semiconductor surfaces. For instance, silicon dopant ionization was visualized by STM by the observation of ring structures around dopants. Dopants at various depths could be identified and characterized.⁶⁷

Figure 4.

Illustration of the STM setup used to measure atomically resolved subsurface dopant images. A phosphorus atom is found a few nanometers below the surface of silicon (100) 2×1 and is highlighted in red in (c). Simulated and experimental STM images of the buried dopant are shown. Reprinted by permission from ref (50). Copyright 2016 Springer Nature. www.nature.com/nnano/.

STM study of buried dopants is an important component of silicon-based quantum computation schemes⁶⁸ where the ability to interact with dopant atoms to address coherent electron spin manipulations is highly desired. To this end, recent publications have described measurements on single dopant systems and have shown the ability to control dopant tunnel coupling to a reservoir electrode using subnanometer position control of the STM tip and to control the dopant’s energy level by biasing the gate reservoir.^69,70

Further studies have recently addressed p-type dopants with an aim of electronically addressable spin qubits. Using scanning probe microscopy, Mol et al.⁷¹ explored how dielectric mismatch and quantum confinement affect the ionization energy of single B dopants below the H-terminated Si surface. They directly probed localized single acceptor states using SPM, which revealed a reduction of 5 meV in the ionization energy of the shallow Boron dopant compared to the bulk value and the visualization of a Kramers doublet that could be utilized as a working level for spin qubits.⁷² These studies were extended to pairs of boron dopants where spin–spin interactions were resolved⁷³ and to dopants in high magnetic fields⁷⁴ that led to theoretical proposals for acceptor-based spin–orbit qubits in silicon.^75,76

2.3. AFM Imaging of Hydrogen-Terminated Silicon

Although STM of hydrogen terminated silicon surfaces has been studied for some time, Atomic Force Microscopy (AFM) studies are more recent, especially when imaging atomic structure and sensing charge of atoms. Both AFM and STM involve a sharp scanning probe brought within a fraction of a nanometer of a surface. Both techniques can yield atom-resolved images but the probe-sample interactions employed are not the same, resulting in different and highly complementary information.

AFM is a member of the SPM family and was invented five years after the STM. AFM is routinely used in a wide variety of applications⁷⁷ and was initially developed to address the need for an atom-resolving technique that worked on insulators and at STM-inaccessible energies, such as in bandgaps.⁷⁸ Instead of measuring tip–sample tunneling current, AFM senses the distance dependent force experienced by the probe, manifested by a frequency shift.

Depending on the tip to sample distance, three broad imaging regimes can be experienced; weak attraction, strong attraction, and repulsion. If the oscillation amplitude is sub Angstrom, it is possible to selectively experience and record one particular force regime. Examples of such selective imaging of H:Si(100) are shown in Figure 5. Figure 5(a) shows an empty states STM image of a 3 × 3 nm² area of H:Si(100) 2×1, with (b) the Δf(z) curve taken at the location marked in (a), showing weakly attractive, strongly attractive and repulsive regimes. Figure 5(c–n) display AFM constant-height images of the surface. The images change from poor signal-to-noise to atom-like with the surface hydrogen atoms showing up as spherical white protrusions to features that have bond-like character.

Figure 5.

Constant-height AFM probing of H:Si at different heights with a hydrogen passivated tip. (a) Empty states STM image (V = 1.3 and I = 50 pA) of a 3 × 3 nm² area of H:Si(100) 2×1. (b) Δf(z) spectra taken over top of a hydrogen atom. The spectra location is marked in (a). z_rel = 0 pm is referenced to an STM set-point of I = 50 pA with V = −1.8 V over top of a hydrogen atom. (c–n) Constant-height AFM Δf maps of the same 3 × 3 nm² area taken at different heights. Heights are listed in the lower right corner of every image (V = 0 V and Osc.Amp = 50 pm) and are also marked in (b). Reprinted with permission from ref (48). Copyright 2020 Taleana Huff.

Multiple examples of repulsive images of clean surfaces and of molecules on surfaces have been found to display such bond-like features. In early studies, it was unknown whether bond contrast was dominantly due to having a flexible tip apex and a surface that deformed as the surface was scanned or if so-called Pauli Repulsion was the dominant mechanism⁷⁹⁻⁸³ Labidi et. al’s work⁸⁴ and others^80,85 show that multiple factors are involved; Stick-like image features attributed to bonds among substrate atoms are in some instances accountable as a simple classical convolution effect combined with mechanical flexibility of probe tip apex atoms under strain. In those cases the “bond” appearance has nothing whatsoever to do with bonds between atoms - the effect is reproduced by an entirely classical treatment of repulsive interactions among atom cores, combined with the atom-scale warpage of both the tip and substrate.

An instance of true bond imaging—an innately quantum mechanical effect that classical models cannot capture—has been documented.⁸⁴ The sample under study there was the prime focus of this paper, the H-terminated Si(100) surface. In that work classical convolution bond artifacts and true quantum mechanical bond-derived image features were discerned. Experimental bond-like features could not be reproduced by classical modeling. Only when quantum mechanically accounting for rehybridization of substrate and tip electronic states during the close range imaging process could salient image features be reproduced and accounted for. When a known covalent bond among substrate atoms was artificially eliminated by computational constraints, the bond-like feature disappeared from rigorous quantum mechanically simulated images. Lastly, Labidi⁸⁴ re-emphasized a lesson from early STM literature, that not only “hard-wall” probe-surface interactions can cause tip and substrate distortions during imaging but electronic effects - essentially bonding among tip and substrate - can cause distortions one must be aware of when tip and sample are brought very close. It is therefore not sufficient to model all AFM images with all classical theory, as there are cases where higher-level theory may be required.

This ability to tailor the dominant contributor to image contrast through changing tip–sample distance has application in many experiments, as an AFM user can choose closer imaging for higher resolution^79,86−90 or longer distance imaging to highlight electrostatic contributions.⁹¹⁻⁹⁴

One final AFM spectroscopic tool that must be discussed is Δf(V) measurements. AFM as a technique for detecting single charging events was shown in 1990, where it was used to examine single-charge-carrier recombination events on Si₃N₄ films.⁹⁵ It was taken to spatial resolution limits in 2009, with demonstration of resolving differently charged adatoms by Gross et al.⁹² They showed one-electron charge state changes in gold atoms correspondingly changed the force on the AFM tip by a few pN. Kelvin Probe Force Microscopy (KPFM) was also employed to confirm the charge state changes (Au⁺, Au⁰, and Au^–) by measuring the altered contact potential difference (CPD). Other notable demonstrations include investigation into supramolecular structures and their charge distributions,⁹⁶ contrast formation in Single π-conjugated molecules,⁹⁷ and charge distribution in molecules.⁹⁴ Δf(V) has also been used to examine surfaces⁹⁸⁻¹⁰⁰ and defects.^101−103 A key feature here is that AFM can distinguish between charge states of atoms and structures while achieving atom resolution.

Another consideration for AFM spectroscopy and imaging is apex functionalization, which is an important factor in both Δf(V) and Δf(z) spectroscopy acquisition.¹⁰⁴ The apex atom is known to drastically affect the imaging in AFM.¹⁰⁵ For example, a tungsten tip with apex silicon atoms displays its contrast dominated by the formation of covalent bonds with the surface.^100,106,107 CO functionalized tips^108,109 are said to use Pauli repulsion to give exceptional resolution.⁸⁸ Metal tips are generally nonreactive but can have large induced dipoles due to the Smoluchowski effect,^110,111 where electron redistribution occurs to minimize energy.¹¹² Some tips, like CO, are flexible leading to imaging artifacts.^79,81 Others, like nitrous oxide¹¹³ and copper oxide,⁸⁵ are more rigid due to a higher coordination number. Thus, each functionalization has its own chemical structure, flexibility, and charge distribution,¹⁰⁴ which in turn has consequences for AFM contrast and how perturbative the measurements are. In all cases, the tip/sample contact potential is also an important effect.

2.4. Defects of the H-Si(100)-2×1 Surface

Despite the near perfect surface of the hydrogen terminated silicon 100 surface, there can still be found various defects at the level of a few percent. Most of the 10 or so common defects observed are now understood at the atomic level while a few remain unknown.¹¹⁴ Practically, however, all defects can be experimentally categorized as either charged or neutral species.

Charged defects can be found on the surface, or in the subsurface region in the form of unwanted surface dangling bonds,^22,115−117 as well as buried dopant atoms.^{50,60−63,68,118,119} The often referenced “Type-2” defect has been variously attributed to a negative arsenic dopant,⁶³ a boron dopant,^60,120 and most recently a subsurface Si vacancy,^121−123 as shown in Figure 6.

Figure 6.

Electrostatic shift from charged defects. (a) Δf(V) spectroscopies over a subsurface Arsenic dopant (red, VCPD = −0.53 V), a proposed Si vacancy (blue, VCPD = −0.46 V), and the H-Si surface (green, VCPD = −0.50 V) as shown in the empty states STM image in (b). The image was acquired at V_s = 1.3 V and I_set = 50 pA. Spectra in (a) taken at z_rel = 0 pm. The inset of (b) shows a constant-height image of the arsenic dopant, better highlighting the electronic properties from the bulk (V_s = 0.4 V, Z_rel = −200 pm).

In some situations, surface defects such as dangling bonds can be removed (as described below), however, most subsurface defects are difficult to eliminate and must be identified and avoided during fabrication, particularly if the defect can become charged, thereby modifying the electrostatic environment and causing undesired behaviors of atom-defined devices.

Scanning-probe-based Kelvin probe force microscopy (KPFM)^93,124,125 allowed routine screening for unwanted electrostatic perturbations with nm resolution. By performing a series of Δf(V) spectroscopies across the surface, the local contact potential difference can be identified. Such spectroscopies are shown in Figure 6 (a) above a subsurface arsenic dopant (red), the defect free H-Si surface (green), and a suspected subsurface Si vacancy (blue). Examining the Δf(V) spectroscopy above a defect free area of the surface, a CPD of −0.50 V was obtained, which provides a reference value at this particular tip–sample separation (z_rel = 0 pm), and sample doping concentration. Spectroscopy for the subsurface arsenic dopant shows a CPD of −0.53 V due to the additional electrostatic perturbation of the positively charge Arsenic dopant. The proposed subsurface vacancy defect is seen in a negative charge state resulting in the observed positive shift (V_CPD = −0.46 V). From these results, it was seen that the electrostatic potential can vary on the order of approximately 0.1 V⁴⁹ across areas as small as 10 nm.

Neutral defects, in contrast, create a local strain field that decays rapidly to the point of being unnoticeable within just 1 or 2 nm. These defects can take the form of different hydrogen termination phases,^27,40 added^126−129 or removed^130−132 Si atoms/clusters, as well as chemically different atoms bonded to the surface.^114,133Figure 7 shows several examples of such defects that are commonly found across the surface at a concentration of <1% with normal sample preparation procedures. The imaging of defects on the Si surfaces was originally limited to STM only allowing variations in the electronic properties of these defects to be interpreted. The application of nc-AFM and specifically, a Si functionalized probe^{106,134−136} allowed for the measurement of covalent interactions between the tip and each particular defect type, revealing more detailed atomic idiosyncrasies. Such a difference is highlighted in Figure 6, which features both the empty states STM (V_s = 1.3 V) and Si probe nc-AFM images.

Figure 7.

Common surface defects on the H-Si(100)-2×1 surface. (a) Empty states STM and (b) nc-AFM images of the 3×1 surface reconstruction. (c) Empty states STM and (d) nc-AFM images of the 1×1 surface reconstruction (dihydride pair). (e) Empty states STM and (f) nc-AFM images of a single dihydride defect. (g) Empty states STM and (h) nc-AFM images of a siloxane dimer defect. STM images are acquired at V_s = 1.3 V and I_set = 50 pA. nc-AFM images are acquired at V_s = 0 V and Z_rel = −400 pm ((d) Z_rel = −480 pm). Each image is 2.2 × 2.2 nm². Reproduced from ref (114) (https://doi.org/10.3762/bjnano.11.11. Copyright 2020 Jeremiah Croshaw et al., published by Beilstein-Institut, distributed under the terms of the Creative Commons Attributions 4.0 International License. https://creativecommons.org/licenses/by/4.0).

The 3×1 surface variation^22,137,138 shown in Figure 7(a) and (b) is formed through a combination of 2×1 H-Si dimers and 1×1 H₂-Si dihydrides. Looking at the three H₂-Si dihydrides above and below the row of dimers in (b) (dark features in Figure 7(a)), one can clearly see a split feature that is not evident in (a) and that is identified as two H atoms. Figure 7(c) and (d) show the 1×1 surface phase⁴⁰ commonly referred to as a dihydride pair (or simply dihydride)^27,139−141 when it covers a single dimer site. The absence of any obvious splitting features is due to the steric crowding of the neighboring H₂-Si units. The inner two H atoms experience a greater repulsive interaction resulting in a rotation of each H₂-Si structure. This results in a much weaker measured signal from the outer two H atoms due to their increased distance from the probe apex. It is this steric crowding which prevents the formation of pristine 1×1 surfaces, and has limited DB device fabrication to the much easier prepared 2×1 surface. Figure 7(e) and (f) show another variation of the 1×1 surface phase in which one of the H₂-Si fragments has been ejected from the surface, leaving a single H₂-Si and missing surface atom. Such a defect has only recently been reported¹¹⁴ and awaits further exploration. Lastly, Figure 7(g) and (f) show what is now known as a siloxane dimer after Si-terminated nc-AFM analysis clearly revealed the presence of a third atom inserted into the Si dimer. Originally thought to be a dihydride variation,^142−144 additional studies have correlated its concentration to water contamination leading to the conclusion that the center atom is a bonded oxygen atom.¹³³ A more detailed exploration of commonly seen defects on the H-Si(100)-2×1 surface is presented elsewhere.¹¹⁴ The general point we wish to make is that any atomic silicon circuitry must be aware and accommodating of atomic defects.

3. Dangling Bonds

Dangling bonds are surface silicon atoms that have an unsatisfied valence (silicon atoms with only three bonds to adjacent atoms rather than the usual four). The character of silicon dangling bonds on an otherwise H-terminated silicon surface is what provides the opportunities for silicon atom-defined circuitry—both classical and quantum. Detailed characterizations of DBs are given in Section 3.1. Section 3.2 describes the formation of DBs through controlled lithography and section 3.3 discusses the formation of DB patterns. Section 3.4 reviews charge observations of DBs.

3.1. Dangling Bonds on Hydrogen-Terminated Silicon

During the formation of the hydrogen terminated surface, some surface silicon dangling bonds inevitably remain as a result of incomplete hydrogen termination. The density of the unterminated surface atoms is generally related to the surface temperature during termination and the best surfaces have residual DB densities below 1%.

On an H-Si(100) surface, DB states are not strongly electronically coupled to the conduction or valence band states and their electrons are substantially localized at the host silicon atom. Silicon DBs can have a +1, 0, or −1 charge, depending on the Fermi level and applied fields, among other factors. The neutral and negative states, DB⁰ and DB^–, are occupied orbitals with respectively 1 and 2 electron occupations, while the positive state, DB⁺, with no electron occupation is a virtual orbital.

These orbitals can be calculated by various methods among which density functional theory (DFT) methods are most efficient while providing reasonable accuracy. An example of DFT calculation of the neutral level, DB⁰, is given in Figure 8. Calculations were performed with the AMS-ADF modeling suite^145,146 using a finite-sized H-Si nanocluster comprising 512 Si atoms and 303 H atoms. The cluster comprises 8 Si layers in the z-direction, an H-terminated 2×1 surface reconstruction at the upper layers, and 4×8 surface unit cells in the xy-plane. The whole cluster is capped by H atoms, except at the DB site. The geometry was optimized by spin-polarized DFT using the GGA-PBE functional^147,148 with a DZP basis set fine numerical accuracy.

Figure 8.

Molecular model of an isolated DB in its neutral state. (a) An isosurface (with color phase) of the HOMO, i.e. the neutral DB⁰ orbital, along the [−110] direction. (b) The same DB⁰ isosurface (solid color) seen from the [110] direction compared to the LUMO, i.e. the virtual DB⁰ state depicted as a mesh, which is also found in the bandgap of the bulk silicon. (c) Top view (along the [001] direction) of the same isosurface. Calculations were performed on a H-terminated silicon nanocluster having 8 Si layers in the z-direction and 4×8 surface unit cells in the xy-plane.

The exact energy levels of DBs in the silicon bandgap are somewhat difficult to pinpoint theoretically. The most accurate DFT methods are limited due to the finite size of the nanocluster (nonperiodic systems) or supercell (periodic systems) which can be treated. The choice of exchange-correlation functional can alter results substantially. The accurate band gap of bulk silicon can only be reproduced with computationally expensive functionals. Practically, only up to around a thousand atoms can be effectively treated with DFT methods at the required accuracy. It is generally accepted that the neutral DB state has an occupied spin-polarized state close to the valence band maximum of the bulk Si. For our finite-sized nanocluster mentioned above, we calculated the DB⁰ level to be at 40 meV above the rest of the occupied levels (the highest of which we define as the reference level for a nanocluster, the equivalent of the valence band edge in bulk) and −4.75 eV with respect to the vacuum level, as seen in Figure 9(a). The virtual DB level (of opposite spin) is located 0.8 eV higher than the occupied DB level. These results are similar to other theoretical results in literature^149−151 and consistent with experimental observations.

Figure 9.

DB energy levels in an H:Si nanocluster containing a single DB. (a) A neutral DB has a singly occupied spin-polarized orbital 40 meV above the reference level (red dashed line) of the nanocluster and a virtual orbital higher in energy. (b) A negative DB has a doubly occupied (spin-paired) orbital 610 meV higher than the reference level.

The addition of another electron to the singly occupied DB causes double occupancy of the same orbital, and what is known as on-site Coulomb repulsion or the Hubbard U. Both DB electrons now have the same spatial wave function but paired or opposite spins and have an energy higher than that of DB⁰. This can be seen in Figure 9(b) as the doubly occupied level in the gap 610 meV above the reference level. Notice that the reference levels in (a) and (b) are different because, although the same nanocluster was used to host the DB, the presence of a net −1e charge in case (b) shifts up all the orbitals in the system by about 1 eV as compared to the neutral nanocluster. An additional effect is that the host Si atom of a DB^– is slightly elevated with respect to the other surface Si atoms. This results from the requirement for altered hybridization when fully occupied.

The positive DB⁺ state has a virtual orbital and a downward displacement as compared to the neutral DB state. The type and degree of doping in the silicon crystal as well as the temperature dictates which one of these charge states a DB acquires: if the Fermi level, E_F, is higher than the DB^– orbital level, then the DB will be negative; if E_F is between DB⁰ and DB^– levels, then the DB is neutral. And if E_F is below the DB⁰ level, the DB is positive. All these conditions hold for DBs that do not interact with each other or with external impurities and fields. However, when those interactions are present, the net occupation becomes a matter of local electrostatic potential which, if controllable, can enable manipulation of charge states in DB assemblies. This is turn can constitute the basis for various devices at the atomic scale.

Since the mutually exclusive charge states of a single DB are +, 0, −, each with a different wave function and energy, they all play a role in the way DBs image in STM. During interactions with the rest of the silicon sample and the external factors, such as imaging probes, a single DB can transition between the three charge states. Therefore, in spectroscopic terms, the discrete levels in the bandgap can also be referred to as charge transition levels (CTLs). In Figure 10 we sketch the CTLs in the absence (a) and the presence (b) of an external imaging probe, respectively. In (a), the DB is neutral and the bands are flat. The CTL labeled 0/– coincides with the DB^– electronic level, while +/0 is just the DB⁰ level. In spectroscopy, the CTLs are thresholds for the Fermi level-determined occupation/charging: if E_F is above 0/–, the DB is negative; if below, the DB is neutral. Similarly, the CTL +/0 is a threshold between the neutral and positive DB states.

Figure 10.

Qualitative band diagrams for the DB levels with and without the imaging probe and associated band bending. (a) Unperturbed neutral DB case with no band bending at the surface and the charge transition levels depicted in the band gap. (b) The CTLs in the presence of an external STM imaging probe. E^tip_F and E^Si_F label the tip and sample chemical potentials, respectively, and Γ labels filling and emptying processes. CBM and VBM stand for conduction band minimum and valence band maximum of bulk silicon. Reprinted with permission from ref (117). Copyright 2014 American Physical Society. https://doi.org/10.1103/PhysRevLett.112.256801.

The presence of an external probe (tip) during the STM imaging can significantly alter the energy landscape due to the combination of contact potential and electrostatic field associated with the tip–sample bias. To a good approximation, in most practical cases, the effect can be described by a semiclassical theory commonly known as band bending. In Figure 10(b) we show a typical case of band bending during unoccupied-state STM imaging. Band edges in green correspond to the neutral DB state, while blue curves correspond to the negative DB state. In this altered energy landscape, a single DB receives and transmits tunneling electrons from/to the tip and sample at various rates given mainly by the proximity of other electronic levels. For instance, in (b), the DB is closely coupled to resonant tip levels (situated just across a vacuum gap under 1 nm wide), but because of band bending it is relatively well separated from resonant levels in the sample. A wide tunnel barrier must be crossed (dotted arrows) in order to reach conduction band (CB) or valence band (VB) levels in the bulk. That barrier width is determined by the bulk doping density.

A consequence of this fact is that the outward tunnel rate (discharging from DB into the sample) can be much smaller than the inward rate (charging from the tip). Therefore, the DB can hold a single charge for a relatively long time (on the scale of STM tunnel rates), creating a time-averaged net charged center. This has rather spectacular effects in STM images of DBs.

For room temperature measurements, on highly doped n-type silicon, isolated DBs appear as bright protrusions in filled state images while in empty state images a DB generally shows a complex volcano-like feature, consisting of an outer raised ring, a smaller dark circle and at the center a small maximum. These features are often referred to as “halos”.⁵¹ The relative prominence of these features vary with bias, temperature and local doping density and DBs can appear as bright protrusions in empty state imaging depending on the tunneling conditions^51,152 and Fermi level position (degenerate vs nondegenerate).⁵³ With very sharp tips the nominally circular halo effect is defined by the atomic granularity of the surface, whereas with blunt tips the halo pattern broadens. In the latter case, deviations of tip shape from ideal hemispherical shape are reflected in the shape of the halo.

Silicon samples with low doped n-type or p-type doping typically show dangling bonds as bright protrusions in both biases.^51,153,154 However, silicon preparation parameters (annealing temperature) can have effects on the DB appearance due to nearby subsurface dopants.¹⁵⁵ Charge state differences in dangling bonds have also been sensed by the observation of greatly altered chemical reactions outcomes^155,156 and by the transistor-like gating effects on silicon surface bound molecular assemblies.¹⁵⁷

In Figure 11, we can see typical STM images of a single DB on n-type silicon in both imaging polarities. In the empty-state image (a), the bright central site of the DB is surrounded by dark (“halo” effect), and further bright regions, also captured in the cross section in (c). This is exactly the case matching Figure 10(b): inside this dark halo, the tunnel barrier between the DB and bulk CB is too great to allow electrons held by the DB^– to escape by tunneling into the bulk. There are other channels for discharge,¹⁵⁸ but their characteristic rates are much lower than the rate of tunneling from the tip to the DB (charging). As a consequence, this dark halo is an indication that the DB is “locked” in the negative state in that vicinity. As some of the involved rates are temperature dependent, DB images can also vary with temperature.

Figure 11.

Typical STM images of a single DB in the (a) empty-state imaging, 40 pA, +2 V; and (b) and filled-state imaging, 40 pA, −2 V. (c and d) Cross sections through the indicated dashed lines in each image. Reprinted with permission from ref (158). Copyright 2015 Marco Taucer.

The other charge transfer mechanisms between tip, DB and silicon are outlined in Figure 12. They include the following elastic and inelastic processes:

• 1)Tip–sample tunneling, directly to available CB states
• 2)Inelastic capture of electrons from the tip in the vicinity of the DB, immediately after tunneling
• 3)Direct tip–DB tunneling
• 4)Elastic tunneling from DB to CB
• 5)Thermal excitation from DB to CB (phonon assisted)
• 6)Inelastic recombination of DB electron with a hole in the VB

Figure 12.

(a) Charge transfer mechanisms between the STM tip, DB, and silicon. The DB is marked as purple, Si atoms in green, and H atoms in white. (b,c) Band diagram representations of those mechanisms. (d) Electrostatic potential landscape at the tip-vacuum-silicon interface calculated self-consistently by solving the Poisson–Schrödinger equation in the semiclassical approximation. Reprinted in part with permission from ref (159). Copyright 2011 by the American Physical Society. https://doi.org/10.1103/PhysRevB.84.205416.

Reference (159) by Livadaru et al. describes these in more quantitative detail as a function of tip position and bias (relative to the sample), doping level, temperature, etc. The interplay of all these factors leads to a steady-state, nonequilibrium distribution of the DB charge, one that affects the surface and bulk bands of silicon, thus yielding surprising STM features, not explained otherwise by the conventional theory based on density of states only.

By contrast to the empty-state images, in the filled-state imaging (e.g., Figure 11(b)), the DB appears almost invariably as a simple, relatively small round bright feature. This is due to the fact that the imaging electrons are supplied to the DB from an abundant accumulation layer of electrons created by downward band bending at the silicon surface. Electrons can then readily tunnel fro m the DB to the empty levels of the tip. There is no rate competition as in the empty-filled imaging mode and no nonequilibrium charging and therefore no halo.

3.2. Controlled Lithography

The formation of dangling bonds has been of interest for many years and stimulated desorption of hydrogen from silicon surfaces has been studied by several methods, including electron, photon, and ion stimulated desorption.

Studies of electrons stimulated formation in particular, have generally been divided in three energy ranges; below 10 eV have been used in scanning probe-based work, up to ∼300 eV was examined using electron guns and in the several keV range using SEM type guns and systems.

Electron stimulated desorption using electron guns in the up to ∼300 eV range has been measured by various methods. Madden et al.⁴⁰⁰ determined a desorption threshold voltage of 23 eV for the desorption of hydrogen. In that experiment, the localization of two valence band holes in an Auger final state leads to the breaking of the Si–H surface bond. It was further speculated that a two-hole bond breaking mechanism can also be produced by the Knotek–Feibelman process^160,161 by the Auger decay of a silicon core hole. This was shown to be true by Fuse et al.¹⁶² and Albert and Tolk¹⁶³ and desorption cross section for Si 2s core was determined to be 10^–18/cm² for Si(100)¹⁶² and 10^–19/cm² for Si(111).¹⁶³ Deuterium was also measured to have a 10x smaller cross section than that of H for Si (111). It has also been shown that both H⁺ and H^– species can be detected from desorption, with H^– requiring a more complex process and a significantly reduced yield.¹⁶⁴

Some very low energy desorption directly triggered by a low energy electron collision have shown that threshold energies for hydrogen desorption occurs as low as 6 eV¹⁶⁵ in some studies while others found 12 eV.¹⁶⁶ Desorption probabilities of 2.0 × 10^–6 H per electron were reported.¹⁶⁵

Higher energy electron desorption using electron beams with kV energies have also been studied. Hsu et al. investigated the hydrogen removal from both hydrogen terminated Si(100) 2×1 and 3×1 surfaces.¹⁶⁷ They found desorption cross sections of 4 × 10^–19 to 8 × 10^–18 cm² for the range of 2 keV to 5 keV with decreasing desorption probability with increasing energy. Hallam performed a desorption analysis with a combined STM and SEM system.¹⁶⁸ With a 25 keV beam desorption was evaluated for the formation of various densities of dangling bonds. Single and double dangling bond structures could be resolved and a desorption rate constant of 0.02712 ML/C cm^–2 was determined for the 25 keV beam

Stimulated desorption of hydrogen from dihydride passivated silicon (100) 1×1 has also been observed using ion bombardment. 200 eV Ar⁺ and He⁺ were found to desorb hydrogen with cross sections of 3.4 × 10^–17 cm² and 2.7 × 10^–17cm², respectively.¹⁶⁹ However, removal of hydrogen from the surface was not observed with 1 keV H₂⁺ or 500 eV H⁺ beams that were utilized with Si(111)-H.¹⁷⁰

Desorption of hydrogen from silicon has also been observed with photon irradiation. Pusel et al. compared irradiation desorption between a F₂ laser (7.9 eV) and a XeCl laser (4.0 eV).¹⁷¹ It was found that F₂ laser desorption occurred by direct electronic excitation with a cross section of 1.2 × 10^–20 cm², while the lower energy XeCl laser only caused desorption through a photothermal process of heating the sample and with a lower desorption cross section. High energy photons (1830 eV to 1890 eV) have also been utilized to desorb hydrogen by the excitation of a deep Si 1s level and Auger decay processes.¹⁷² Two distinct yields of H⁺ species (α-H⁺ and β-H⁺) were also observed depending on the photon energy and discriminated by different numbers of localized holes or different ejection angles depending on the silicon hydride species. Laser desorption combined with STM analysis has also been reported and a higher desorption cross section was observed for n-type samples over p-type samples using 157 nm irradiation.¹⁷³ This was explained by laser-induced charging of the surface. STM studies also evaluated the desorption of hydrogen and fast diffusion of dangling bonds under pulsed laser heating studies. Dangling bonds tended to pair on a single dimer after laser heating and hydrogen diffusion rates as high as 10⁸ s^–1 were determined.¹⁷⁴ Hydrogen diffusion was also studied by STM and thermal annealing of samples above 500 K (below 500 K, all DB motion is suppressed). Intra- and interdimer motion was observed and individual silicon dangling bonds were found to diffuse along dimer rows above form clean dimer pairs and reduce the number of individual dangling bonds.^175,176

STM desorption of hydrogen from hydrogen-terminated Si(100)-2×1 surfaces to create dangling bonds has been studied in detail since the demonstration of lithographic capabilities in the early 1990s with an STM tip.^{28,144,177−181} It was determined that there were two different mechanisms available for hydrogen desorption, giving rise to two modes of operation: coarse lithography (with feature sizes larger than 1 nm) and atomically precise lithography. In coarse lithography mode the STM is operating in a field emission regime (bias greater than sample work function), and the Si–H bond can then be broken with direct excitations of electrons from the bonding to the antibonding state when the sample bias exceeds approximately 6 V.^177,182,183 This type of lithography does not have the atomic resolution necessary to precisely remove individual atoms from the surface, but useful for creating larger patterns quickly.^180,184,185

To achieve atomically precise lithography, the STM tip can be used to break single Si–H bonds through multiple vibrational excitations of the Si–H stretch mode with low energy inelastic tunneling electrons (less than 3.5 eV).^180,182,186 The excited lifetime for a Si–H stretch mode is relatively long (approximately 10 ns), requiring four phonons to relax.^182,187 This allows for the possibility of acquiring enough energy from the small fraction of inelastic tunneling electrons available from the large STM tunneling current to break the Si–H bond. The lifetime of the excited stretch mode can change with temperature, altering the efficiency of hydrogen atom extraction (Si–H bond breaking). The highest efficiencies occur at temperatures below 10 K, while at higher temperatures, the competition between excitations and dissipative pathways increases, reducing the likelihood of bond breaking and lowering desorption yields by as much as 300x at room temperature.¹⁸² An isotope effect was also observed, with deuterium desorption efficiency substantially less than that of hydrogen.¹⁸⁸

One class of procedures to remove hydrogen with atomic precision require the active monitoring of STM scan parameters when under feedback control¹⁸⁹ or solely the current channel when feedback control is suspended. With feedback control enabled, the bias and/or current can be ramped to a set condition of desorption parameters until a change in Z position of the STM tip is recorded, signaling a successful event. In contrast, if the scanner is sufficiently stable when the feedback control is suspended, the tip can be held at a fixed height while short (tens of milliseconds) bias pulses are used to induce bond breaking. In these procedures a successful desorption event is detected via a sharp increase in current, signaling a dangling bond has been created as the DB can appear far brighter than the H-terminated surface.

The parameters utilized in either approach vary over a wide range. Tunneling currents of 50 pA to several nanoamps have been reported, along with bias voltages between 1.5 to just over 3 V. Lower voltages and currents have been found to reduce the likelihood of severe tip apex changes, however. All of the parameters would need to be optimized for different temperatures, different doping levels, and different surface passivations.^179,182,190

Hydrogen atom removal has also been achieved via a hole resonance desorption method.¹⁹¹ In this method, desorption was explained by vibrational heating of a H–Si bond by inelastic scattering of tunneling holes with the Si–H 5σ hole resonance. The desorption rate exhibited a power-law dependence on current and a maximum desorption rate at −7 V.

In spite of the atomically precise nature of hydrogen desorption lithography (HDL), some sources of error lead to imperfect lithography. One source of error that arises during fabrication is alignment of the STM tip with the target hydrogen atom. As the tip is moved from site to site, thermal drift and piezo creep can cause uncertainty in its position. Working at cryogenic temperatures can significantly reduce thermal drift and creep while also increasing tip stability. Creep can be further controlled to some extent by allowing sufficient settling time between large tip movements between hydrogen removal sites. Multi-apex tips, which can have more than one roughly equivalent “apex”, can also introduce error during fabrication. Tunneling electrons from these additional apices may induce hydrogen desorption in an undesired location instead of, or in addition to, the intended site. Because of this, it is imperative to work with atomically sharp tips for reliable fabrication.

It is also possible that the hydrogen that is removed during a desorption event can in turn abstract an additional H to create volatile H₂ and another spurious DB in the region.¹⁴⁴ Ballard et al. studied the creation of spurious DBs as a function of both electron dose and pattern size and determined that, for low voltage HDL, the primary source of spurious DBs is not direct electron stimulation but is dependent on the size of the HDL pattern, as seen in Figure 13(a and b). They also determined the lower bound for the observed probability, of creating a spurious DB, to be 10% at room temperature. Hydrogen atoms liberated from the surface could also reattach to DB structures on the surface nearby.

Figure 13.

Reactions of hydrogen atoms after HDL. (a) STM image after HDL with constant dose, variable pattern size. (b) Average number of spurious DBs as a function of pattern size for two separate tips. (c) STM image of a single hydrogen atom (indicated with yellow arrow) physisorbed on the surface after DB formation (1.3 V, 5 nm × 5 nm). (d) Close up of physisorbed H, 1.3 V, 3 nm × 3 nm. However, when the scanning voltage is increased to V = 1.7 V in (e), the hydrogen atom is dragged by the tip and moved close enough to the DB to cap it, as indicated by a change in contrast midway through the image and confirmed by a subsequent STM image of the same area (f). (e) and (f) are larger area 10 × 10 nm images of the area in (c). Reprinted in part with permission from ref (121). Copyright 2018 Springer Nature BV. Reproduced from ref (144) with the permission of AVS: Science & Technology of Materials, Interfaces, and Processing. https://doi.org/10.1116/1.4864302.

Spurious DB formation is generally not observed at low temperature (4 K). At these temperatures, the liberated H atom usually leaves the surface without any further surface reaction. However, in some situations, the desorbed H atom can land on the surface and become physisorbed.¹²¹ The physisorbed H atom can be observed by STM (Figure 13(c and d), and can also be moved by the STM tip and brought back to a DB, where it will react, re-terminating the surface (Figure 13 e and f).

Together, these above factors made it very challenging to fabricate error-free structures using HDL. It was possible to create perfect structures of several DBs in size, but larger structures inevitably contained at least one error. Without a means to correct errors, the creation of the perfect structures required for device applications seemed unlikely.

In order to remove dangling bonds from surfaces, chemical reaction methods were explored in order to cap the DB with a hydrogen atom or with another benign molecule. The molecule TEMPO was initially utilized to form a radical coupling reaction with surface dangling bonds.¹⁹² The TEMPO molecule was shown to readily bond to and thereby annihilate the DB and its distinctive electronic properties. Tempo could also be easily removed by STM imaging at elevated voltages providing a method to protect and deprotect the DB site.¹⁹³ Hydrogen atom donors were also explored where molecules containing weakly bonded hydrogen atoms could cap a dangling bond with a H atom. Two chemicals including diimide and N,N-diethyhydroxylamine were utilized in early studies.^194,195 Diimide, being a very reactive species with the capacity to yield two H atoms, readily donated hydrogen atoms to the surface, but the second available hydrogen atom could abstract other surface hydrogens to form H₂, thereby forming new DBs. DEHA also successfully donate hydrogen atoms to the surface, but in some instances the remaining molecule could react with other surface DBs. Neither of these methods could prepare DB free surfaces.

It was also known that hydrogen atoms could be donated from the STM tip to react with surface silicon. Kuramochi showed that a platinum STM tip could be exposed to hydrogen gas to “load” the tip for imaging for silicon (111) 7×7.¹⁹⁶ The appropriate voltage conditions could then be applied where hydrogen atoms could be field evaporated and transferred from the tip to the surface. In another publication it was shown by Huang that hydrogen atoms could be transferred from the STM tip to single surface DBs on an otherwise hydrogen passivated surface.^197,198 It was later shown that H atoms could be transferred to groups of DBs in order to alter the electronic characteristics of the remaining surface DBs.¹⁵³ These events showed that with better control, improved surfaces could result.

In 2017 these prospects improved dramatically thanks to independent observations by Huff et al.¹⁹⁹ and by Pavlicek²⁰⁰ that provided the framework for the previously absent controlled ability to erase erroneous DBs to create error-free complex DB ensembles. In both reports, an atomic force microscope (AFM) was used to controllably transfer an adsorbed hydrogen atom on the tip apex to a DB on the surface, repassivating it, as shown in Figure 14. In the AFM technique, a small hysteresis in the Δf(z) curve is evident and can be used to confirm the capping of the DB with a hydrogen atom. This work led to the development of a more scalable STM-based hydrogen repassivation (HR) technique by Achal et al.,²⁰¹ which enabled several sequential repassivation events in short succession. This technique, combined with improved lithography techniques, gave rise to the largest perfect structures ever achieved on this medium at that time. Figure 14 and Figure 15 show both the AFM and STM repassivation methods. In the STM methods, hysteresis in the I(z) curves likewise provides an indication of capping success. Statistical data showed that nearly 90% of all events occur before a tip displacement of 550 pm toward the surface.

Figure 14.

Procedure to mechanically induce a hydrogen–silicon covalent bond. (a) Typical filled-state STM image of a silicon dangling bond on the H-Si(100) surface using a single hydrogen atom functionalized tip. The yellow arrow indicates a defect taken as a reference. (b) Δf(z) curve using a H-functionalized tip on a surface hydrogen atom. (c) Ball-and-stick model and (d) Δf(z) curve on a single DB during the mechanically induced Si–H covalent bond capping event. The orange arrow indicates a hysteresis (zoom on inset) characteristic of the change that occurs due to the formation of the Si–H bond. (e) STM image and (f) Δf(z) curve on the Si–H surface subsequent to the mechanically induced reaction in (d). Reprinted with permission from ref (199). Copyright 2017 American Chemical Society.

Figure 15.

Tunneling current signatures of hydrogen repassivation. (a) (V = 0.4 V, T = 4.5 K) The recorded tunneling current as the scanning tunneling microscope (STM) tip (set over a dangling bond (DB) at 1.4 V and 50 pA) is brought toward the surface (blue) and as the STM tip is retracted (red) during hydrogen repassivation (HR). (b) (V = 0.2 V) A second distinct signature (type-II) has also been observed during HR, with a sudden decrease in tunneling current during the approach toward the surface (blue). (c) The tip approach distance where either signature occurred was recorded for 119 unique HR events. Nearly 90% of events occur before 550 pm. The inset depicts the STM tip approaching a DB on the surface. Used with permission of Springer Nature BV from ref (201). Copyright 2018; permission conveyed through Copyright Clearance Center, Inc.

Recently, to improve upon HR further, a faster and simplified procedure for error correction was developed by Achal et al.,²⁰² called molecular hydrogen repassivation (M-HR). With this technique, single molecules of molecular hydrogen (H₂) were now used to erase DB sites (without the use of atoms attached to a scanned probe). Paradoxically, this capability was achieved by precisely adding DBs adjacent to the erroneous DBs, creating an interdimer site, and subsequently capping both of the paired DBs by spontaneous reaction with gaseous H₂.²⁰³ All other DBs are left unaltered. The reaction pathway of hydrogen molecules with these interdimer sites has been well-studied and found to be barrier-free. In order to achieve reliable repassivation speeds, a working background pressure of at least 1 × 10^–9 Torr of hydrogen gas is required in the vicinity of the sample surface. This reaction scheme is shown in Figure 16, where an interdimer site is erased by reaction with H₂. There may arise situations where it is not possible to convert a particular DB site into the appropriate geometry for M-HR. In these situations, the HR technique would then be utilized to erase the DB in question. Together, these two techniques form a complementary and powerful set of tools to enable HDL as a means of creating truly atomic-scale devices.

Figure 16.

Hydrogen molecule reacting with an interdimer site of H-Si(100) at 4 K. (a) Ball and stick diagram. (b) Interdimer site is observed. (c) After exposure to hydrogen gas at 4 K, the interdimer site is capped. Reprinted in part with permission from ref (202). Copyright 2020 American Chemical Society.

3.3. Hydrogen Desorption Patterns on Silicon

With the observation of hydrogen removal from silicon surfaces by STM tips,²⁰⁴ pattern formation was soon undertaken. It was found that desorption of patches of hydrogen could be performed and rows of hydrogen removal could be created with line widths of 1 nm on a 3 nm pitch.¹⁷⁷ These line formations were impressive but still required improvement for their continuity and edge sharpness, as seen in Figure 17(a). Further developments led to cleaner lines, and it was observed that both single DB and paired DBs were formed during some wire formations, Figure 17(b).¹⁵ Patterns beyond lines were also achievable by controlling the movement of the tip in two dimensions; however, patterns still contained positional and removal errors that prevented perfect patterns, Figure 17(c,d).^205,206 Small structures with no error could be achieve at low temperatures where desorption can be more controlled.

Figure 17.

STM images of hydrogen desorption patterns on Si(100)-H. Perfect desorption patterns were not achieved. From ref (15). Copyright 1995. Reprinted in part with permission from AAAS. https://doi.org/10.1126/science.268.5217.1590. Reproduced from ref (177). Copyright 2010, with the permission of AIP Publishing. Reprinted in part with permission from ref (205). Copyright 1998 Springer Nature. Reprinted in part from ref (206). Copyright (2006), with permission from Elsevier.

Creating large patterns of hydrogen desorption can be achieved with sophisticated tip control movements and by varying the conditions of field desorption depending on the accuracy of the pattern required. This has been used very successfully to created delta doped structures and quantum dots by reacting phosphine²⁰⁷ or arsine²⁰⁸ with the exposed silicon. Recently, a two-qubit system was created and measured from a hydrogen lithographed surface pattern (Figure 18(d)).²⁰⁹

Figure 18.

Some mass desorption patterns from dedicated hardware systems with tunneling and field emission desorption and for qubit manufacturing. (a) shows hydrogen desorption in low bias tunneling and high bias field emission regimes. (b and c) show various aligned patterns and patterns created from improved scanner control at different scales. (d) shows the controlled H desorption pattern for quantum dot and electrode formation. Reprinted in part with permission from ref (211). Copyright 2018, with permission from Elsevier. https://doi.org/10.1016/j.mne.2018.11.001. Reprinted in part with permission from ref (209). Copyright 2019 Springer Nature. https://doi.org/10.1038/s41586-019-1381-2.

Complex pattern formation has also gained help from control hardware implementations where complete systems dedicated to reproducing patterns on silicon can be purchased.²¹⁰ These control system can guide the tip through complex motion to reproduce patterns from input structures of bitmaps and CAD drawings using both tunneling desorption and field emission desorption. Example patterns can be seen in Figure 18.²¹¹

The goal of improving lithography accuracy and efficiency gained some insights from Chen et al.²¹² in a study to generate dangling bond lines with atomic precision alignment at room temperature. They demonstrated the reproducible fabrication of sub-1 nm DB lines with near atomic precision and showed that an optimum set of patterning parameter exists. They also studied multiple tips and found that pattern quality is weakly dependent on the STM tip apex quality when the patterning parameters are within the optimum parameter space. Figure 19 shows the formation of a dimer row dangling bond pattern. Three separate tips were tested to compare their desorption characteristics, and the region between the dotted lines represents optimized conditions for low voltage desorption at room temperature.

Figure 19.

Plot of the patterning parameters for single-dimer-row hydrogen desorption. The region between the two dashed lines provides optimal single-dimer-row lithography. Measurements were performed using three different W tips. Patterning parameters used by other groups are shown for comparison (see reference for details within). Inset bottom: a typical single-dimer-row wire patterned with the optimized condition of 3 V, 30 nA, 10 mC cm^–1. Inset top: a typical TEM image of the sharpening tip. Adapted with permission from ref (212). Copyright 2012 IOP Publishing Ltd. https://doi.org/10.1088/0957-4484/23/27/275301.

Hydrogen desorption patterns have also been used for controlled silicon nanostructure growth in 3 dimensions. By removing hydrogen in controlled patterns, the exposed clean silicon can be used for 3D growth. Goh et al.²¹³ utilized alternating disilane adsorption in combination with STM hydrogen desorption cycles to create 3D silicon features. 3D wire structures have also been achieved using a combination of hydrogen desorption lithography followed by overgrowth of epitaxial silicon at low temperatures.²¹⁴ An upper electrode can then be fabricated on the epitaxially overgrown silicon by further removal of hydrogen. ALD of titanium oxide growth from hydrogen controlled lithography patterns has also been shown to create atomically registered nanostructures that may be useful for nanometer metrology of 3D structures.²¹⁵

Although, desorption of hydrogen is now routine, creating perfect patterns, with no positional errors, unintentional desorption and false desorptions, remains challenging. Highly controlled tip motion has been shown to create small perfect patterns of a few atoms for some years now. Taro Hitosugi et al. created single DB lines/wires of various lengths by moving the STM tip along a dimer row while tunneling with conditions to remove the hydrogen²¹⁶ (Figure 20). But the highest accuracy is usually achieved by the controlled desorption of single hydrogen atoms, one silicon position at a time and the best control is also achieved at low temperatures. Using this method has led to the formation and study of various artificial molecules^149,217 (Figure 20). However, these structures are still small enough that, if an error does occur during writing, a new pattern can simply be created at a new location on the surface. For complex patterns that must be written at an absolute position on a surface, close to prefabricated electrodes for example, errors cannot be tolerated and error correction is required. In Figure 20, Achal²⁰¹ et al. show how error correction is utilized in a complex pattern formation to cap an errant DB with a hydrogen atom, thus allowing the pattern to continue in place, without restarting in a new location.

Figure 20.

Perfect patterns form lines/wires in (a) and artificial molecules in (b) and (c). Error correction allows for more complex structures as shown in (d). Reprinted in part with permission from ref (149). Copyright 2013 Springer Nature. https://doi.org/10.1038/ncomms2679. Used with permission of Springer Nature BV from ref (201). Copyright 2018; permission conveyed through Copyright Clearance Center, Inc. Reprinted in part with permission from ref (216). Copyright 2013 American Physical Society. https://doi.org/10.1103/PhysRevLett.82.4034. Reprinted in part with permission from ref (217). Copyright 2018 American Chemical Society.

One critical component for creating atom by atom patterns is the quality of the STM tip. Tips that have been created and conditioned in a field ion microscope, show immediate atom scale resolution with little or no extra conditioning.⁴⁶ This process involves the field assisted chemical etching with nitrogen gas to shape, sharpen and stabilize the apex of the tip down to a single atom, while providing a nitride layer to limit atom diffusion and/or oxidation. It has been found that an etched tip with a very slight coating of silicon atoms, formed by controlled silicon surface contact, is most effective and in cases where tip changes do occur during fabrication of DB structures, some tip reconditioning on the silicon surface is controllably performed. This process has been automated using a machine learning algorithm that can check the state of the tip in order to repair it.²¹⁸ Of the machine learning methods tested, a convolutional neural network (CNN) yielded the greatest accuracy, achieving a positive identification of degraded tips in 97% of the test cases. By using multiple points of comparison and majority voting, the accuracy of the method was improved beyond 99%. Figure 21 shows this process where a “double tip” was detected in the imaging and conditioned using the automated procedure, until a sharp tip was achieved.

Figure 21.

Autonomous tip sharpening used along with atom-scale patterning. (a) An overview (25 × 25 nm²) STM image showing a patterned binary atomic wire, an isolated DB used for tip quality assessment, and a spot (red cross) chosen by the user to perform tip conditioning. (b) Sequence of patterning steps without noticeable tip quality change in between. (c) The tip became double after the creation of the last atom on the right, and the user employed the tip conditioning routine to resharpen it. After three steps of automatic tip conditioning, the tip became sharp and the user carried on the pattering (d). (e) STM images of the isolated DB at the middle left of (a) after each tip conditioning. The CNN used these images to assess the quality of the tip. (f) Output of the CNN for the images in (e). The tunneling conditions were −1.8 V and 50 pA for all images. Reprinted with permission from ref (218). Copyright 2018 American Chemical Society.

CNN can also be used in order to determine the best place to fabricated structures on a surface.²¹⁹ This is important as charged defects require fabrication at distances sufficiently far away to avoid adverse effects. Figure 22 shows an automation method for the identification of defects prior to atomic fabrication via hydrogen lithography using deep learning. A CNN was used to locate and differentiate between surface features on the hydrogen-terminated silicon surface imaged using a scanning tunneling microscope. Once the positions and types of surface features are determined, a predefined atomic pattern can be created in a defect-free area. By training the network to differentiate between common defects the authors were able to avoid charged defects as well as edges of the patterning terraces. Augmentation with previously developed autonomous tip shaping and patterning modules²¹⁸ allowed for atomic scale lithography with minimal user intervention.

Figure 22.

(a) A trace of the defects from the CNN analysis of the scan image shown. The white square shows the area furthest from defects for the corresponding pattern. (b) The resulting surface after patterning the device shown in the inset. Reprinted with permission from ref (219). Copyright 2020 IOP Publishing Ltd. https://doi.org/10.1088/2632-2153/ab6d5e.

3.4. Charge Observations of DBs

Besides the steady state imaging of charged DBs, the dynamic changes of DB charge states can also be observed. The changing charge states of DBs can be observed directly through imaging in the nearby vicinity of DBs on hydrogen terminated silicon.¹¹⁷ This is evident in the top right region of Figure 23(a). At 4.2 K, the region surrounding the DBs while imaging in the empty states can have a high degree of speckle noise at the edge of the feature.

Figure 23.

(a) Topographical STM image of a single DB taken with V = 1.4 V and I = 20 pA. The double-ended arrow shows the range of lateral positions used to acquire the data shown in (a). (b) Histogram of current measurements with the tip at a constant height and a constant voltage of 1.45 V positioned 3.14 nm from the DB. The peak at lowest current corresponds to the negative charge state, while the peaks at intermediate and highest current correspond to the neutral and positive charge states. (c) An example of a current–time trace. The sampling rate is 10 kHz and the entire trace (not shown) is 2 s in length. Reprinted with permission from ref (117). Copyright 2014 American Physical Society. https://doi.org/10.1063/1.111722.

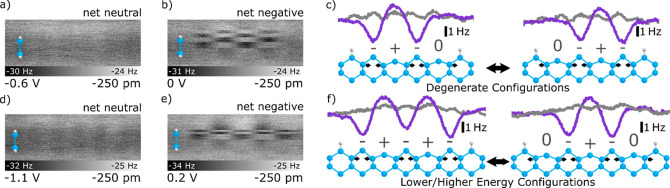
When the tip is positioned in the speckle region, and the tip height is held constant, the measurement of current as a function of time shows unusual jumps among discrete values, as seen in Figure 23. Such current steps are absent when the tip is far (>10 nm) from any DBs. The histogram of current measurements shown in Figure 23(b) demonstrates that there are precisely three dominant current values. These were identified as corresponding to the negative (doubly occupied), neutral (singly occupied), and positive (unoccupied) charge states of the DB. Each charge state of the DB causes a different DB-induced band bending under the tip apex, and thereby creates a different current from tip to sample. One could also extract the relative filling and emptying rates of the dangling bonds. The dynamics extracted from current traces are consistent with a nonequilibrium model¹⁵² in which the DB acts as an atomic quantum dot, tunnel coupled both to the tip and to the bulk Si, and occupation is determined by the competition of filling from the tip and emptying to the bulk.

Scanning tunneling spectroscopy can also display the transitions between charge states. These can be observed as a peak in the dI/dV spectra at low temperature (Figure 24).²²⁰ It was shown that the precise energy of the charge transition varies among different DBs on the same sample and this tuning is related to the proximity of nearby subsurface dopants. Spectroscopic differences for DBs were also observed for samples flashed at different temperatures where dopant migration and concentration could be controlled.

Figure 24.

(a), (b), and (c): 10 × 10 nm² constant-current (30 pA) STM images of a single DB at +1.6 V, −1.8 V, and −1.7 V, respectively. (d) I/V (blue curve) and dI/dV (red curve) spectroscopy of the same DB. (e) dI/dV spectroscopies of a single DB (red curve) and Si:H surface (black curve). (f) Statistics over 69 DBs showing the variation of the charge-state transition peak voltage onset. Reprinted with permission under a Creative Commons CC BY 3.0 License from ref (220). Copyright 2015 IOP Publishing Ltd. https://creativecommons.org/licenses/by/3.0/.

A time-resolved scanning tunneling spectroscopic method can also be used to study the charge dynamic with near single ns time resolution.²²¹ There, the charge transition states of the dangling bond can be observed on a very fast scale (MHz) through an all-electronic pump–probe experiment where the observations were related to charge dynamics of a nearby dopant.

Using this method, interplay of the charge transition levels, denoted (+/0) and (0/−), were observed to create a negative differential resistance when measuring spectroscopy over some dangling bonds.²²² Here the current surprisingly changes from increasing to decreasing as the voltage is increased to more negative values. The initial current onset occurs when the tip Fermi Level aligned with the (0/-) level of the DB. As the tip voltage is increase further, the tip becomes resonant with the (+/0) level, and the current begins to decrease. Since this level is energetically much lower than the (0/−) level, the process is more inelastic (the electron needs to lose kinetic energy through phonon emission before it can be captured by the DB) and hence, occurs at a reduced rate,²²³ resulting in the NDR feature. The NDR persists until the (+/0) level becomes resonant with the bulk valence band due to tip induced band bending (Figure 25). Greater overlap of the DB and the bulk valence band allows for increased current with further increased negative sample voltage.

Figure 25.

(a) Calculated I(V) spectra of a single silicon dangling bond at different tip–sample distances using NEGF (colors are used for clarity). (b)–(e) Energy diagrams of the system of study for all the different energy regimes observed in the I(V) spectra. The Fermi energies of the bulk silicon (E^Si_F) and the tip (E^tip_F) as well as the DB charge transition levels, (+/0) and (0/−), are displayed in the diagram. (b) The tip Fermi level is above both the DB charge transition levels. (c) The tip Fermi level is in resonance with the (0/−) level and above the (+/0) level. (d) The tip Fermi level is in resonance with the (+/0) level. (e) The tip Fermi level is below both charge transition levels, and due to tip induced band bending, the (+/0) level becomes resonant with the bulk valence band edge. Reprinted with permission from ref (222). Copyright 2016 American Physical Society. https://doi.org/10.1103/PhysRevLett.117.276805.

In an extended study of the above NDR, the carrier capture events at single dangling bond states could be tuned by varying the substrate temperature, doping type and doping concentration.⁶⁵ The characteristic NDR feature was observed on both n- and p-type samples and different time constants could be measured depending on the sample annealing parameters. Importantly, the phonon creation rate limited model could account for multiple atom-scale NDR results. Atom specific Kelvin probe force microscopy (KPFM) measurements also confirmed the energetic position of the DB’s charge transition levels, corroborating STS studies. Two features in the KPFM curve are visible (indicated by red arrows) which correspond to the (0/−) charge transition level (approximately −0.20 V) and the (+/0) charge transition level (approximately −1.10 V) shown in Figure 26. Time constants of the electron transition from the (+/0) state to the tip, T_(+/0)t, and from the bulk to the (+/0) state, T_(+/0)b, were measured. For samples heated to 1050 °C, T_(+/0)b, was measured in the 10 ns range, while for 1250 °C heated samples T_(+/0)b was measured in the μs range. T_(+/0)t was determined to be 2.78 ± 0.12 μs on 1250 °C prepared samples.

Figure 26.

(a) KPFM (red) and NDR I(V) (black) curves measured for a DB on a 1250 °C annealed sample. The KPFM curve was measured at z = −330 pm from the reference height of −1.80 V and 50 pA, set over hydrogen. The oscillation amplitude was 100 pm. Two features in the KPFM curve are visible (indicated by red arrows) which correspond to the (0/−) charge transition level (approximately −0.20 V) and the (+/0) charge transition level (approximately −1.10 V). (b) T_(+/0)b time constant of DBs on samples annealed at different temperatures (1250 and 1050 °C) during preparation. (c) T_(+/0)b vs tip height offset measured for a DB on an n-type sample annealed at 1250 °C during preparation. Initial tip height was set at −1.80 V and 50 pA on top of the DB. The time constants are measured at the sample bias of −1.45 V. Reprinted with permission from ref (65). Copyright 2017 American Chemical Society.

Kelvin probe microscopy has also enabled meticulous evaluation of the charge transitions of dangling bonds.⁴⁹ An experimental Δf(V) curve over H:Si(100) is shown in Figure 27(a). The raw data are shown as the black curve, which was then fit with a parabolic function (y = Ax² + Bx + C) shown in blue. The apex of the fit is marked in pink (V_CPD), which is the point where Δf or F_electric has been minimized (the smallest shift off resonance), correlating to a minimization of the CPD. In Figure 27(b), an example of Δf(V) over a single dangling bond is presented. When Δf(V) is taken over entities capable of changing charge state in a discretized way, the switch from one quantized charge state to another presents as a “step” between two parabolas (in the spectra between charge parabolas—or neutral). Some notable literature examples utilizing this include examination of charge transfer between weakly coupled pentacene molecules on insulating NaCl,²²⁴ examination of InAs quantum dots,²²⁵ examination of differently charged gold particles on NaCl,^92,224 scanning quantum dot microscopy,²²⁶ and the use of the charge transition step to make a moveable charge-sensing probe.⁴⁹ In Figure 27(b), a dangling bond which acts as a quantum dot changes from having one extra electron making it negative (blue region), to having no extra electrons and being neutrally charged (red region). The step at V = −0.25 ± 0.01 V signals this charge state change, with the two quantized charge states having their own parabolas and, thus, CPD values associated with those charge states.

Figure 27.

Δf(V) Spectroscopy over Hydrogen and a discrete-charge-state-changing dangling bond. (a) Δf(V) curve (black) taken by an AFM sensor over the center of a surface hydrogen atom on H:Si(100) (z_rel = 0.0 pm, V_range = −0.8 to 0.35 V, and Osc.Amp. = 50 pm). The data has been fitted with a parabolic curve (blue). The maximum of the fit (−0.53 ± 0.02 V) is marked with a pink dot. (b) Δf(V) curve (black) taken by an AFM sensor over the center of a dangling bond on H:Si(100) (z_rel = −300 pm, V_range = −0.8 to 0.35 V, and Osc.Amp. = 50 pm). For voltages in the orange shaded area, the DB is neutral. For voltages in the blue shaded area, the DB gains a single extra electron and is negative. The transition from neutral to negative, or the (0/−) charge transition step, is seen at V = −0.25 ± 0.01 V. Parabolic fits were done for both the neutral (orange) and positive (blue) charge states of the DB. Values of V* could be extracted from the fits for the two charge states, highlighting how even a single electron change can drastically affect the measured CPD offset. Reprinted in part with permission from ref (49). Copyright 2019 American Chemical Society.

The voltage position where the charge transition occurs can be affected by the electrostatics of the sample. Huff et al. measured the change in voltage where the neutral/negative charge transition step occurred for the DB probe at different distances from various charged species, buried dopants, surface defects and other dangling bonds.⁴⁹ In Figure 28(a–i), as the DB is shifted away from the dopant, the charge transition shifts to more positive values, as consistent with a positively charged dopant atom. Other negatively charged defects were also discussed. By fitting each set of shifts as a function of distance with the linearized screened Coulomb energy equation, important material properties such as the Thomas-Fermi screening length, the depth of subsurface charged species, and the dielectric constant of the substrate were found.⁴⁹

Figure 28.

Probing charged species with a movable DB point-probe. (a–g) Constant-height STM images of the DB being moved 0–6 lattice sites away from its initialization point, respectively, from a near-surface arsenic atom (Z_rel = −250 pm and V = 300 mV). (h) Constant-height STM image of the area before addition of a DB, with Δf(V) locations marked (Z_rel = −200 pm and V = 250 mV). (i) Δf(V) spectroscopy taken on top of the DB for each lattice spacing, color coded with the positions in (h), as well as with the frames in (a–g) (Z_rel = −350 pm). Reprinted in part with permission from ref (49). Copyright 2019 American Chemical Society.

The authors also utilized a grid of pointwise 2D KPFM measurements to evaluate the voltage where the contact potential difference between the tip and the surface becomes exactly compensated (V*) for each point in the measurement.⁴⁹ Huff et al. were able to visualize the variations of V* in a 2D map over a 100 nm² area caused by two subsurface species, showing that the background potential was not uniform over this area (Figure 29). Additionally, charges were readily assigned to each species based on the values of V* in their respective vicinities. It was also possible to identify a 64 nm² area with uniform background potential, demonstrating that DBs in this area all exhibited identical charge transition levels as would be expected in such an environment. This kind of mapping and understanding of the local environment will be very important for creating atomic electronic structures with predictable and reproducible properties.

Figure 29.

Varied CPD in small scan areas. (a) Constant-height STM image (V = 300 mV) of a subsurface arsenic dopant (appears as the bright feature in the upper left portion of the image) and an unknown charged species (appears dark in the lower right region), now thought to be a Si Vacancy.¹¹⁴) (b) Constant-current STM image (V = 1.3 V, I = −50 pA) of the same area. (c) KPFM difference map compared to the unperturbed surface (25 × 25 nm² grid, voltage range −1.8 V to −1.0 V. All scale bars are 5 nm. Reprinted in part with permission from ref (49). Copyright 2019 American Chemical Society.

4. Charge Control of DBs

Understanding the charging characteristics of dangling bonds and having the ability to prepare dangling bonds enabled controlled preparation of assemblies of predetermined electron population and position. Section 4.1 describes how the charges in dangling bond assemblies can be observed and controlled. Sections 4.2 and 4.3 focus on spectroscopic and AFM observation and control of charge within DB assemblies.

4.1. Charging in DBs Assemblies

Controlling the charge state of a dangling bond was identified as a key measure to enable important local chemical reactions¹⁵⁵ and to provide control over the current through molecular assemblies.²²⁷ It would also be identified as an important measure to control charge positioning in dangling bond assemblies for information storage and qubit operation and for logic structures.¹²¹ To this extent, there have been various attempts and methods to measure and alter the charge state of dangling bonds.

The simplest measure to vary charge states is through doping control of bulk silicon. Because it is known that p-type and n-type silicon can display positive, neutral and negative DBs through the dopant-associated tuning of the Fermi-level, one could control DB charge by dopant implantation. Nishizawa et al. prepared p–n junctions on Si(111)-H and were able to observe dopants and surface potential distributions.⁵⁹ Although it was not the focus of the paper, one could observe that negative and neutral dangling bonds could be observed in the n-type and p-type regions, showing that controlled implantation could affect the dangling bond charge states. Using another method, Pitters et al. created nanoscale Schottky contacts by creating titanium silicide islands on Si(100)-H 2×1 surfaces.²²⁸ They observed upward band bending around the TiSi islands that created a potential profile in which depleted charges were visible around the islands. Dangling bonds that were observed near the island were imaged as uncharged, consistent with the doping level and upward band bending near the islands, while dangling bonds far from the island were observed as charged,. These two observations showed that potential control could be implemented to control dangling bond charge states, and potentially could be achieved dynamically with supported electrode configurations. This was very recently achieved by Kölker et al.,²²⁹ who used implanted electrodes on a modified STM sample holder to enable application of a gating bias to surface dangling bonds in order to alter their apparent charge state in STM images.

One important observation about the charging state of dangling bonds was that groups of dangling bonds could behave quite differently from isolated ones. For instance, as two isolated dangling bonds are brought closer together, the total charge probability at room temperature changes until an electron is removed from the system due to Coulomb repulsion, and the pair of dangling bonds enter into a tunnel coupled relationship as shown in Figure 30(a).¹⁵⁴

Figure 30.

(Si dimers = blue, H = white, subsurface Si = gray). (a) RT STM image of low doped n-type Si (∼5 × 10¹⁵ cm^–3). 35 × 35 nm², 2 V, 0.1 nA. DBs appear bright. (b) High doped n-type Si (∼5 × 10¹⁸ cm^–3). 35 × 35 nm², 2.2 V, 0.1 nA. DBs appear dark with a central spot. (c) 9 × 9 nm², 2 V, 0.2 nA. Three groups of DBs are prepared. A noncoupled DB pair at 2.32 nm (I). Coupled DB pairs at 1.56 nm (II) and 1.15 nm (III). (d) Calculated one- and two-electron occupation probabilities (black and red curves, respectively) corresponding to the DB pairs in (c). (e,f) Two groups of four spaced at various distances (schematics show the DB positions with respect to the silicon lattice). More closely spaced DBs have a reduced total charge and appear brighter compared to DBs spaced at further distances. (g) Occupation probabilities of a square four-DB structure in the absence of an STM imaging tip as a function of DB–DB separation along the square side. The legend indicates the corresponding symbols for the total number of electrons in the structure, from which the subtraction of 4 yields the number of extra electrons. (h) Group of four DBs spaced greater than 3.5 nm. All four DBs are negatively charged. Reproduced in part from ref (153). Copyright 2011, with the permission of AIP Publishing. Reproduced in part from ref (230). Copyright 2009 American Physical Society. https://doi.org/10.1103/PhysRevLett.102.046805.

Charge sharing within other symmetric clusters (Figure 30(b)) was also evaluated to determine the probable charge states of the clusters.¹⁵³ Charge distribution within cluster composed of different numbers of DBs were also observed to reveal that electron configurations relax to achieve minimum repulsion.^153,154

Importantly the charge distribution within dangling bond assemblies could be controlled electrostatically, providing evidence that bits of information could be encoded as charge position and utilized in a mechanism similar to that in Quantum Cellular Automata (Figure 31).^154,231 This demonstration showed that DB structures could be manipulated and operated upon using external electric fields and was instrumental in guiding future research into the electronics of dangling bond systems.

Figure 31.

A color mapped STM image (6 × 6 nm², 2.5 V, 0.11 nA) of a rectangular 4-DB coupled entity with two additional electrostatically perturbing DBs diagonally placed. The 2 DBs nearest the negative perturbing DBs are relatively high in appearance as a result of unfavored electron occupation at those sites. The average height difference between the violet (higher) and blue colored (lower) DBs is ∼0.4 Å. A grid represents the DB positions on the silicon surface. Reprinted with permission from ref (230). Copyright 2009 American Physical Society. https://doi.org/10.1103/PhysRevLett.102.046805.

4.2. STS and AFM Charge Measurement

Directly measuring the absolute charge in individual dangling bonds is challenging using STM because of the constant passing of current through the structures from the tip to the silicon bulk. However, the effect of charged structures can be measured by performing I(V) spectroscopy on nearby test subjects thereby minimizing direct probe to subject-atom perturbation. This has been performed by measuring the current onset point of a sensor DB in proximity to charged DB structures. The total amount of charge in the DB structure causes an observable shift of the current onset of the I(V) spectrum of the sensor DB; one electron charge and two electron charges shift the current onset by different amounts. Figure 32(202) demonstrates this experiment. In Figure 32(a), the single sensor DB has a current onset at approximately −1 V (blue line). The sharp turn on in current is related to the effect of a nearby subsurface dopant. A second DB (DB2), containing a net charge of one extra electron, is added to the surface 5.4 nm away from DB1, causing the step in the I(V) spectrum of DB1 to shift to the left (Figure 32(f, dark green)). In Figure 32(c), a third DB (DB3) is added near DB2, and no shift in the I(V) spectrum of DB1 is observed (Figure 32(f, light green)). This indicates that only a net charge of 1 extra electron occupies the pair of dangling bonds. DB3 is then removed and added at two new distances (d,e). In both Figure 32(d and e), the spectroscopy is shifted even further. The doubling of the step indicates that the charge in the DB pairs contains a net charge of 2 extra electrons. The number of electrons observed in a group of dangling bonds can be dependent on the doping level and proximity to other charge species and defects. A quick assessment of S/N (signal-to-noise ratio) indicates that such an all-electrical detection approach can obtain fractional charge sensitivity.

Figure 32.

Characterizing charge occupations (V = −1.6 V, I = 50 pA, T = 4.5 K, 6.4 × 6.4 nm²). (a) STM image of a DB on the hydrogen-passivated Si(100)-2×1 surface. The DB (DB1) exhibits a sharp current onset in its I(V) spectrum (blue) due to the ionization of a subsurface arsenic dopant atom caused by the STM tip field. (b) A second DB (DB2), containing a net charge of one electron is added to the surface 5.4 nm away from DB1, causing the step in the I(V) spectrum of DB1 to shift to the left (f, dark green). (c) A third DB (DB3) is added near DB2, and no shift in the I(V) spectrum of DB1 is observed (f, light green). (d, e) The distance between DB2 and DB3 is varied to determine the net charge in the structure for each case. (f) The I(V) spectra taken over DB1, associated with (a–e), showing the sharp onset of current. Reprinted with permission from ref (202). Copyright 2020 American Chemical Society.

Atomic force microscopy can also be used to observe the charged structures of the dangling bond pairs. In the same study,²⁰² AFM images could distinguish between 1 and 2 electron charged structures created respectively by relatively close and longer DB separation separations. Figure 33 shows filled state STM images and AFM images of the same DB structures. In the STM images, the dangling bond pairs appear mostly equivalent with little to discern between close and further separated paired atoms using filled state imaging. However, with the AFM, a charge sensitive measurement collected at 0 V clearly shows a charge difference, where the close pair only has one DB charged, while the further separated pair supports a charge on both dangling bonds.

Figure 33.

STM and AFM images of two DBs with various separations. (a–f) STM images ((a–c, V = 1.3 V, I = 50 pA, T = 4.5 K, 3 × 3 nm²) ((d–f), V = −1.8 V, I = 50 pA, T = 4.5 K, 3 × 3 nm²). (g–i) Constant-height AFM frequency shift images (V = 0 V, Z_rel = −300 pm, T = 4.5 K, 3 × 3 nm²). The dark depressions in AFM represent the location of an electron within each structure. In (g) and (h) there is only a net charge of one additional electron within the structures. In (i) there are two net additional electrons present. STM and AFM. Reprinted in part with permission from ref (202). Copyright 2020 American Chemical Society.

4.3. AFM Charge Control and Monitoring

In addition to local electrostatic effects, the manipulation of electrons within multi-DB structures can also be done using a scanning probe tip. By reducing the separation between the tip and surface DB, an increased attractive force exerted on the DB causes the surface atom to be displaced toward the tip, inducing a rehybridization of that atom, reducing partial sp² character in favor of a greater sp³ character.^116,232,233 This enhanced sp³ character lowers the total free energy of the negatively charged DB state relative to the neutral state leading to the charging of the DB beneath the tip. By controlling the tip height relative to surface DBs, the tip can operate in two distinct regimes, a more benign read regime, where such an interaction does not cause a charge transition, and a write regime, where the interaction with the tip does cause the charge transition.

Figure 34 demonstrates the difference between the two different regimes as measured over a symmetric six-DB structure (shown in Figure 34(e)).²³⁴ As will be shown, this six-DB structure holds 3 negative charges when measured at 0 V. Due to electrostatic effects, the outer two DBs (labeled 1 and 6) host two of these negative charges, while the third switches between the two central DBs (labeled 3 and 4). We can observe this by looking at the structure as a function of time, observing the evolution of charges within the DB structure. Figure 34(f) shows the measurement of the structure in the read regime (Figure 28(a)) where the outer two DBs remain negative and the middle two DBs switch between negative and neutral as the charge switches between these two sites. By reducing the tip sample separation by 50 pm, we enter the write regime (Figure 34(b)). Performing the same measurements, Figure 34(g) shows all DBs within the structure as negative due to the local tip induced charging of the DB under the tip. If instead of measuring in the write regime, we then withdraw the tip to the read regime and measure (Figure 34(c,d)), we can see the evolution of charge within the structure after it has been initialized in the write regime. Figure 34(h) shows the structure scanned in the write regime from left to right. As can be seen, the structure is biased to the right with DB 4 imaged in the negative charge state more often than DB 3. Writing the other direction shows a similar configuration (Figure 34(i)) except now the structure is biased in the reverse direction with DB 3 in the negative charge state more than DB 4. These results demonstrate the ability to position charge within DB structures and observe their evolution with time. Not only double well but also many-well potentials can readily be defined and dynamically tuned to affect occupying electrons.

Figure 34.

Evolution of charge configurations with controlled preparation of a symmetric DB structure. Visualization of scan modes: (a) The tip is scanned from left to right in the read regime only. (b) The tip is scanned from left to right in the write regime only. (c) The tip is first scanned from left to right in the write regime, then scanned in the read regime from right to left. (d) The tip is first scanned from right to left in the write regime, then scanned in the read regime from left to right. (e) Constant-height Δf image of the six-DB structure. (f, g) Line scan maps across the structure in (e) corresponding to scheme (a) shown in (f), (b) shown in (g), (c) shown in (h), and (d) shown in (i). (f), (h), and (i) were measured in the read regime: −270 pm. (g) was measured in the write regime: −320 pm. Scale bar in (e) corresponds to 3 nm. All measurements taken at 0 V. Reprinted in part with permission from ref (234). Copyright 2018 American Physical Society. https://doi.org/10.1103/PhysRevLett.121.166801.

5. Atomic Scale Devices

After the establishment of charge control over DB assemblies, proto-device structures of DBs were created and tested. Section 5.1 describes how one or more pairs of dangling bonds can be utilized to store bits of information and form atomic-scale “binary wires” and logic gates. The above are all devices employing dynamically controlled electrons confined by exactly and reproducibly defined atom structures. As well and more simply, the presence or absence of dangling bonds can be used to encode binary information within an ultradense memory (section 5.2).

Some other molecular and atomic scale systems have also shown some utility in and provided historical motivation for atomic scale electronics (carbon monoxide systems, for example). Some of these systems will be reviewed in section 5.3 while alternative semiconductor systems are discussed in section 5.4. It will emerge that the atom-defined silicon approach as described here has great advantages.

5.1. Bits, Wires, and Gates

As mentioned previously, dangling bonds on the silicon surface behave as quantum dots. While normally an atom in contact with a solid loses its zero-dimensional character as a result of dispersive interactions, Si DBs states exist in the bulk Si bandgap and hereby attain isolation. They can exist in a positive, neutral, or negative charge state in which the unsatisfied orbital hosts 0, 1, or 2 electrons.^{49,121,222,235,236} These charge states are more commonly referenced by their charge transition levels, that is, the energy at which a DB will transition from a positive to neutral charge state (DB(+/0)) or a neutral to negative charge state (DB(0/−)). One of the key features toward the application of these surface DBs is that we can manipulate the energies that these charge transitions occur, enabling us to control the charge state of individual or ensemble DBs. We can manipulate the charge state of these DBs in three ways. (1) By adjusting the Fermi level of the Si crystal, we can tune the charge state of the DB, as shown in Figure 35(a). (2) By placing the DBs next to fixed positive or negative charges (in the form of subsurface dopants, other charged atoms, or with charge or dipole containing molecules, or with other DBs) it lowers or raises the nearby Si energy bands with respect to the crystal Fermi level, as shown with a negative species in Figure 35(b).^49,121,154 (3) By using a scanning probe tip or lithographed solid state gate, we can either empty or fill the DB depending on the alignment of the Si and tip Fermi levels as well as the emptying and filling rates of the DB.^65,222Figure 35(c) shows a tip induced charge transition by emptying an otherwise negatively charged DB faster than it can be filled by the Si bulk. The corresponding DB(+/0) transition can also occur as reported in ref (235).

Figure 35.

Manipulation of the DB charge state. (a) By adjusting the crystal doping level, the alignment of the sample Fermi level (E_F) shifts relative to the DB(0/−) and DB(+/0), putting the DB in a positive (+), neutral (0), or negative (−) charge state (transition positions are illustrative). (b) Patterning a DB next to a fixed negative defect (red) shifts the local bands upward, bringing the DB(0/−) above the E_F and putting the DB in a neutral charge state. (c) By positioning a probe tip near the DB, it enables electrons to tunnel from the DB into the tip. If the emptying rate to the tip is faster than the filling rate from the bulk, then the DB will sit in a neutral charge state.

The energy at which these charge transitions occur are best measured using a nc-AFM.^93,237−241 By performing Δf(V) spectroscopies over the DBs, we can observe a sharp step in Δf as the tip Fermi level passes either the DB(0/−) or DB(+/0) charge transition levels.^49,121,235 This sharp step corresponds to shifts in the DB’s electrostatic and chemical interaction potentials, which are measured as changes in Δf by the probe tip. Figure 36(b) and (d) show the DB(0/−) transition measured over two different DBs as shown in constant-height Δf imaging in Figure 36(a) and (c). Since the DB(0/−) transition occurs at roughly −0.12 V, the DBs imaged at 0 V in (a) and (c) are in the negative charge state. By patterning two DBs with an intervening H-Si atom (0.768 nm), we modify the local electrostatic landscape such that only one of the DBs can be negatively charged. This creates a degenerate system where the extra electron can be located on either the left or right DB in the pair. The degenerate behavior of the DBs is seen in Figure 36(e), where distinct streaks in Δf are seen across the DBs, corresponding to a switching between the (−) and (0) charge state. Based on the Δf(V) in Figure 36, we assume that DBs in the neutral charge state are measured with a less negative Δf than negatively charged DBs. This phenomenon was further explored by Rashidi et al.²³⁴ An additional step is also seen in the Δf(V) spectra in Figure 36(f) at 0.25 V, corresponding to the DB(0/−) transition of the second DB in the pair.

Figure 36.

Binary atomic silicon logic. (a, c, e, g, i) Constant-height Δf images of isolated left (a), isolated right (c), coupled pair (e), biased right (g), and biased left (i) DB assemblies. (b, d, f, h, j) Δf(V) spectra over each of the corresponding DB assemblies. (k) Experimentally measured (red) and TIBB corrected (blue) energy levels of the DB(0/−) transition levels of the DB assemblies. Reprinted in part with permission ref (121). Copyright 2018 Springer Nature BV.

By adding an additional electrostatic perturber, the degeneracy of the DB pair can be broken making it energetically favorable for the additional electron to sit on the DB farthest from the perturber. In this case, an additional negative DB is placed 5 lattice sites away, where tunnel coupling is extremely small compared to that among the paired DBs, but in a position where the electrostatic effect on the pair is substantial. This is shown in Figure 36(g) and (i) with the perturbing DB patterned to the right and left of the DB pair, respectively. Looking at the Δf images, we see that the streakiness in Figure 36(e) is gone and the additional electron sits solely on the left (g) or right (i) side of the pair. The Δf(V) spectra in Figure 36(h) and (j) emphasize the shift in electrostatics with the DB(0/−) transition level of the middle DB (green in (g), blue in (i)) now shifted to roughly 0.32 V. This leads to an energy difference of approximately 0.35 V between the DB(0/−) transition within the DB pair.

As an aside, we note that this and related paramagnetic species enable the movement of a paramagnetic center under simple field control. Moreover, such species exist on a highly n-type doped sample where generally all DBs are negatively charged and not paramagnetic.

A summary of the DB(0/−) transition levels of each DB within these assemblies can be seen in Figure 36(k). It shows both the experimentally measured values as well as the corrected values, which subtract the effect of tip induced band bending as calculated in the SI of ref (121).

By defining a left polarized (Figure 36(g)) DB pair as a binary 0 and a right polarized (Figure 36(i)) DB pair as a binary 1, a fundamental building block to binary atomic silicon logic is established. By extending the shapes of these binary pairs, more complicated logic structures can be created such as binary wires as well as binary OR gates.

The binary wire shown in Figure 37(a) shows a set of 8 binary pairs that have been polarized to the left (binary 0) by the addition of a single perturber at the right end of the wire. In Figure 37(b), the perturbing DB was turned into a binary pair by adding another DB. The binary wire now shows equal polarization to the left and right originating from the midpoint of the wire. By adding a final perturbing DB to the left of the wire, all the binary pairs are polarized to the right (binary 1) demonstrating fully switchable, binary wire functionality. With the addition of positive potentials bipolar actuation for either terminus will become available.

Figure 37.

AFM images of bit propagation in a binary wire. (a) 8 DB pair wire biased by a single negative DB (red dot) on the right. All DB pairs have charge shifted to the left, indicated by the binary number “0” (black dots). (b) The lone negative DB (red) is converted to a pair. The line of 9 DB pairs has a break located near the middle. (c) The 9 DB pair wire is then biased from the left by a single negative DB (red dot). The 9 DB pair wire is converted to all “1”s with the charge to the right side of the DB pair. Reprinted in part with permission from ref (121). Copyright 2018 Springer Nature BV.

Extending these binary pairs into a Y-structure enables two input, one output logic gates such as the OR gate shown in Figure 38. The basic structure is patterned in Figure 38(a), which shows three pairs all polarized away from the middle. By adding a perturbing DB needed to initialize the gate structure (Figure 38(b)), we can define each of the binary pairs to be in the 0 state, as indicated in Figure 38(g). By adding perturbing DBs to the left (Figure 38(c,h)), right (Figure 38(d,i)), or both inputs (Figure 38(e,j)), the corresponding output of the binary pair is shown to match the truth table of an OR gate.

Figure 38.

OR gate constructed from binary pairs. A two input OR gate in (a) the uninitialized state, (b) the initialized state, (c) the “10” input state, (d) the “01” input state, and (e) the “11” input state. (f–j) Corresponding models of the AFM images indicating the presence or absence of any perturbing DB (red) and the charge state of DBs within the pairs (gray, neutral; black, negative). The output bit is marked by the dashed blue line. Reprinted in part with permission from ref (121). Copyright 2018 Springer Nature BV.

Following the success of Binary Atomic Silicon Logic (BASIL), a theoretical modeling tool, SiQAD²⁴² has been developed (section 7), which allows for the simulation of operation of diverse structures and circuits. This study has put forward additional DB designs, which would enable AND, XOR, NAND, and XNOR logic structures as well and will be discuss in section 7.

5.2. Memory

The idea of storing information at the atomic scale is one that is decades old, although it was not until atomically resolved images of individual atoms were obtained using an STM in 1983 that such a feat seemed within reach.⁷ The idea of storing information using single atoms was further solidified by an iconic demonstration in 1990 when Don Eigler et al. at IBM demonstrated the controlled manipulation of xenon atoms at 4 K on the surface of Ni(110) with an STM to fabricate the letters “IBM”.¹⁰ In the years that followed there have been many tour de force demonstrations of the power of atomic-manipulation for data storage.^{201,202,243−248} One of the most substantial modern demonstrations was created by Kalff et al. in 2016 using an STM on the surface of chlorine-passivated Cu(100).²⁴⁷ They were able to manipulate over 8000 surface vacancies to create a kilobyte of rewritable memory, which they used to store an excerpt of Feynman’s motivating lecture, “There plenty of room at the bottom”.

While every demonstration has had a various approaches, material systems, or processes, the majority shared a common unfortunate requirement—extreme cryogenic temperatures (77 K to 4K and below) were needed for the memories to remain stable.^10,246,247 This requirement stemmed from the often-small energy barriers to thermal diffusion of the surface absorbates or vacancies used to represent each bit or piece of information. As a result, slight increases in temperature cause significant reductions in the usable lifetime before the information becomes disordered. Thermal degradation places extreme limitation on the utility of any atom-defined system that is bound together by week van der Waals forces. Moreover, atomic patterns formed on metal substrates will in general have properties of the atomic-assemblies entirely screened electromagnetically, shorted-out electrically and have issues with wire connections. Efforts to circumvent these problems with intervening insulating monolayers unfortunately retain the need for constant cryogenic conditions to retain pattern stability.

One avenue to alleviate cryogenic considerations is to use absorbates or vacancies that are more strongly bonded to the surface. The increased stability, however, comes at the expense of increased difficulty in creating/manipulating each bit/atom. The prime example of this is DB vacancies on the otherwise hydrogen-passivated Si(100)-2×1 surface.^179,182,249 The DBs on the surface experience a minimum diffusion energy barrier of 1.4 eV in every direction,^175,250 rendering them stable against thermal diffusion at room temperature and indeed to 200 °C. For instance, in 2001 Quaade et al. demonstrated a rudimentary 4-bit rewritable DB-based memory using 4 DBs that they created in an array with an STM tip at room temperature (Figure 39).²⁴⁸ They were able to use the STM tip field to induce single DBs in the array to jump between two positions, which were labeled 0 and 1.^248,251 Approaches such as this were limited at the time by the inability to create large error-free DB arrays, and in any case are limited by the absence of practical, non-scanned probe based actuators.

Figure 39.

Four dangling bonds on the same dimer row. The dangling bonds can be switched up or down individually and can thus be represented as binary information. The state of the device can be read by scanning along the dimer row. Setting is accomplished by applying voltage/current pulses on either side of the individual switches. Reprinted with permission from ref (248). Copyright 2001 IOP Publishing Ltd. https://doi.org/10.1088/0957-4484/12/3/311.

As fabrication capabilities matured on the hydrogen-passivated Si(100)-2×1 surface^{15,178,180,201,206,212,252} and the ability to controllably erase individual DBs was developed,^199−201 there was renewed potential in using these thermally robust DBs to store information at the atomic-scale. In 2018 Achal et al. sequentially stored each letter of the alphabet in a rewritable 8-bit DB array by selectively creating and erasing DBs using a low temperature STM. They then went on to create a 192-bit rewritable array to store the beginning 24 notes (simplified and converted into binary) of the Mario theme song (Figure 40).²⁰¹ Enabled by the favorable surface geometry and the ability to precisely address individual lattice sites to add or remove a hydrogen atom, the arrays had a storage density of 1.70 bits/nm², the largest achieved (Figure 41(a)). A total of 64 DBs were required to be fabricated in precise locations in order to store the 24 notes. Thanks to the energetic barriers the DBs experience, it was estimated that the bits in the array would experience an average of one hop in 500 years at room temperature, making it a viable candidate for information archives.²⁰¹ This is now possible thanks to the maturation of fabrication capabilities on the hydrogen-passivated Si(100)-2×1 surface.

Figure 40.

An STM image of a 192-bit DB memory array (V = −1.8 V, I = 50 pA, T = 4.5 K, 21.5 × 10.7 nm²). It stores the beginning 24 notes (simplified and converted into binary) of the Mario theme song. Used with permission of Springer Nature BV from ref (201). Copyright 2018; permission conveyed through Copyright Clearance Center, Inc.

Figure 41.

(a) The geometry of the ultradense memory array, where dangling bonds (DBs) are used to represent one bit of information. It has a maximum bit density of 1.70 bits/nm². The unit memory cell is denoted in red, containing one bit, the sites where hydrogen atoms are removed or replaced to store information are highlighted in green, and the area in gray represents sites used to space each bit from the next. (b) An alternative ultrahigh density storage design, with a maximum storage density of 1.36 bits/nm², which allows for the incorporation of the M-HR technique to rewrite data in a quasi-parallel process. The unit memory cell (red) contains an upper and lower bit (green). Now, to rewrite each bit in the array, the DB/bit is converted into an interdimer site by removing a hydrogen atom (orange/pink), so that an ambient hydrogen molecule can bind to the site to erase it. Reprinted in part with permission from ref (202). Copyright 2020 American Chemical Society.

While possibly attractive for archival applications, the rewriting speeds of these DB arrays needed to be significantly faster to make it more suitable for other storage applications. The main speed-limiting factor was that the STM tip was only capable of erasing a single DB/bit at a time in a serial manner.²⁰¹ In 2020 Achal et al. used the developed M-HR technique to demonstrate the ability to now rewrite DB arrays in a significantly more efficient quasi-parallel manner (Figure 42).²⁰² In order to incorporate the M-HR mechanism as the primary rewriting process, the DB arrays had to be redesigned to ensure each bit in the array could still be individually addressed without altering any neighboring bits (Figure 41(b)). The redesign came at the expense of a slight reduction to 1.36 bits/nm² for maximum storage density.²⁰² Now, however, it was possible to rewrite multiple bits at once (Figure 42(a)), without needing the STM tip present, by first transforming them into highly reactive sites for hydrogen molecules (Figure 42(b,c)). Eventually, as particle beam-based lithographic and holographic readout technologies mature toward atomic-scale precision, it may be possible to use this type of ultrahigh density memory array without any need for an STM. These data storage developments for atomic-scale memories that could bring them into everyday use.

Figure 42.

(a) To store the letter M (01001101) in the array, the bits in line one (11111111) that need to be rewritten are identified. Then, the STM tip removes hydrogen atoms at those sites to convert the already present bits into reactive interdimer sites shown in (b). (b) Ambient hydrogen gas is then able to bind to the reactive sites to erase the bits in parallel without the need for the STM tip. Working at higher hydrogen background pressures speeds up this process. (c) The array has now successfully been rewritten and the letter M is stored on line one (V = −1.65 V, I = 50 pA, T = 4.5 K, 4 × 7.5 nm²). Adapted with permission from ref (202). Copyright 2020 American Chemical Society.

5.3. Other Atom Scale Systems

Atom-scale memory and logic systems have also been described in other material systems. These range from adsorbed gases on metal surfaces, to metal atoms on semiconductors and to molecular systems involving adsorbed C60 molecules. Alternate semiconductor logic systems involving germanium and silicon have also been discussed. We will briefly describe these here.

Since the development of the xenon switch,¹¹ adsorbed gases on metal surfaces have received special attention because of the relative ease in the ability to control the placement of atoms on low temperature surfaces.²⁵³ The xenon experiments showed that atomic switch could be implemented using a STM setup. That research evolved into experiments with carbon monoxide (CO) and led to the developments of CO structures on metal surfaces and the formation of quantum corals.²⁵⁴ Continued experiments with CO lead to the realization that CO could be placed at particular lattice positions to form dimers or a Chevron structure involving 3 CO molecules. Dimers have a bright maximum between the CO molecules while chevron trimers do not. In a very clever experiment,²⁵⁵ a single CO molecule is manipulated so that it interacts with a series of dimers. It initiates the formation of a chevron trimer which then cascades into the series of other dimers to form an extended the chevron system. Using this domino effect and more complicated structures, signals could be transferred between structures and interacting signals could form AND and OR gates to perform logic functions. Crossover and fan-out units were also devised and shown. Figure 43 shows the logical operation of the AND gate. Although, these logic structures were irreversible in function, and only available at low temperatures, they demonstrated that functional atom structures could be created and operated upon.

Figure 43.

Logical AND gate using the CO cascade method. Blue dots indicated CO molecules that hop during device operation, and green dots indicated positions after hopping. (B to D) Sequence of STM images (5.1 nm by 3.4 nm) showing the operation of the AND gate (I = 0.2 nA; V = 10 mV). (B) Initial configuration. (C) Result after input X was triggered manually by moving the top left CO molecule with the STM tip. (D) When input Y was triggered, the cascade propagated all the way to the output. From ref (255). Copyright 2002. Reprinted in part with permission from AAAS.

Similarly, Fölsch et al.¹⁸⁴ used STM to place individual indium atoms on the atomically clean InAs(111) surface. Using this technique, they created various artificial structures and mapped their wave functions. By using the lattice of the surface, the authors were able to control the structures with effectively zero error. Structures including wires and coupled wires were imaged and the DOS map of the confined ground states and excited states of the structures were shown. This system showed that quantum dot architectures could be created which is an important goal of quantum information and fundamental studies of confined electrons. However, despite achieving high reproducibility and precision in placing a single indium atom, they still require low temperatures to avoid atom diffusion.

Memory schemes have also been created from alternate systems. Recently, individual Cl atoms were used to demonstrate rewritable atomic-scale memory of up to 1 kilobyte.²⁴⁷ However, this method also requires cryogenic temperature as the Cl atoms are only stable at low temperatures.

An alternative data storage candidate was proposed to overcome this problem by Nakaya et al.²⁵⁶ They showed rewritable single-molecule data storage at room temperature by manipulating single C₆₀ molecules on three-layer-thick C₆₀ films. By using the STM tip, the authors showed that they could form dimer or trimer C₆₀ structures. These structures appeared as dark spots on an other-wise bright hexagonally structured surface. The modified C60 structures could be observed as a bit of memory and the writing was also shown to be reversible, as seen in Figure 44. Reading and writing was limited to scan probe methods despite the stability of the C₆₀ films at RT.

Figure 44.

C60 memory with writing, erasing and rewriting procedures. Single-molecule-level topochemical data storage using C₆₀ molecules. (a–d) STM images of a three-layer-thick C₆₀ film showing that single-molecule-level writing (a) to (b), erasing (b) to (c), and rewriting (c) to (d) of binary data are possible at RT. A single surface C₆₀ molecule which is used as a bit of data storage represents “1” or “0” of binary data depending on whether the C₆₀ molecule is depressed due to dimerization or trimerization with an underlying C₆₀ molecule or not. Used with permission of John Wiley & Sons – Books, from ref (256). Copyright 2010; permission conveyed through Copyright Clearance Center, Inc.

5.4. Other Semiconductor Atom Systems

To overcome challenges of working on metal surfaces, others have also turned their attention toward semiconductor surfaces. Kolmer et al.²⁵⁷ developed a protocol for fabrication of atomically precise structures on the hydrogen passivated Ge(001)-H surface. The authors prepared clean dimer structures by the removal of hydrogen from a Germanium dimer. They also claimed STM control over the buckling phase of dimer assemblies and stated that the demonstration of the atomic scale construction technology is beneficial for the design of surface logic gates.

The same group also performed experiments on the Si(001)-H surface.²⁵⁸ They reported the design and construction of a prototypical Quantum Hamiltonian Computing (QHC) atom scale Boolean logic gate by scanning tunneling microscopy and atomic manipulation. Dangling bond structures of the QHC NOR/OR logic gates were printed on the silicon surface and STS was performed on different gate structures, showing that spectroscopic signatures varied with the structure input, contributing to the measured truth table showing NOR/OR behavior (Figure 45). A scheme to measure the structure with theoretical gold pads has also been presented.²⁵⁹ and theory descriptions involving molecular latches of acetophenone have been detailed.^260,261 Using the basics of the DB system, along with the molecular latch and theoretical electrical contacts. A complete detailed description of this system has been reviewed and can be found in book format.²⁶²

Figure 45.

(a) Dangling bond NOR/OR logic gates on an Si(001)-(2×1):H surface at 4.5 K. The logical inputs for the different structures of the gate are given on the left side of the STM images (3.5 nm × 3 nm). Gray and red balls depict hydrogenated and bare silicon atoms, respectively. (b) STS dI/dU measurements for different logic gate inputs recorded at 4.5 K over the central part of the gate. Used with permission of Royal Society of Chemistry, from ref (258). Copyright 2015; permission conveyed through Copyright Clearance Center, Inc.

6. Connections to DB Structures

Dangling bond structures will require input and output strategies. Connections could be made with atomic scale wires. Dangling bond wires have been studied through various methods, and sections 6.1 will review STM and AFM measurements. Section 6.2 will cover efforts to measure transport properties of dangling bond wires and other realted structures.

6.1. Dangling Bond Wires

Following the successful development of BASiL components, one of the remaining challenges is to design and fabricate high conductance wiring capable of ex-situ readout and manipulation of such atom scale electronic elements. Significant advancements have been made using encapsulated dopant lines²⁰⁷ which have been coupled to P quantum dots enabling single electron transistor (SET)^217,263,264 and qubit^209,265,266 readout, however, these encapsulated wires have yet to be coupled to surface DBs. Another area actively being explored is the use of 1-D surface DB wires (Figure 46) to couple BASiL components. Initial theoretical and experimental studies revealed strong distinctions in the electronic properties of DB wires based on their patterned surface geometryof Figure 46.

Figure 46.

DB wire types on H-Si(100)-2×1. First and second layer Si atoms shown in blue with H atoms in gray. Wire I (orange) is a continuous DB structure along one side of a dimer row. Wire II (green) shows a DB wire with one H separation between DBs. Wire III (yellow) shows a zig-zag pattern where DBs are positioned on alternating sides of a dimer row. Wire IV (blue) shows a row of bare dimers along a dimer row. Wire V (purple) shows a bare dimer wire, but across neighboring dimer rows. A single DB (black) and a single bare dimer (BD, gray) are also shown. Scale bar is 1 nm.

Taro Hitosugi et al.²¹⁶ showed experimental evidence of strong electron–phonon correlations in DB wires via Jahn–Teller distortions. Variations in the STM images of type I wires were correlated to the calculated atomic geometries which revealed a pairing of second layer Si atoms. These Si atoms which paired up, decreased the back-bond angle of the DB hosting Si atom, raising it from the surface, enhancing its p-like character, and lowering the DB energy level (shown in Figure 47(c,f)). Alternatively, some second layer Si atoms would become spread out, increasing the back-bond angle of the DB hosting Si atom, enhancing its s-like character, and raising the DB energy level. This pairing of second layer Si atoms was later predicted to result in an ionic charge reconfiguration in which raised DBs becoming negative, and lowered DBs becoming positive.^{216,267−269}

Figure 47.

Ionic configuration of net negative DB wires. (a) A 4 DB wire (type I) as imaged by nc-AFM in the net neutral configuration. (b) A net negative 4 DB wire switching between the two degenerate lattice configurations. (c) The two degenerate lattice configurations as imaged in (b) with the Δf line scans in the net negative configuration (purple) and net neutral configuration (gray). Small black arrows indicate the direction of lattice shift of the second layer Si atom with the measured charge state of each DB indicated above. (d) The net neutral configuration of a 5 DB wire. (e) The net negative 5 DB wire switching between the lower and higher energy lattice configurations. (f) Same as (c) except for the 5 DB wire case. (a, b, d, e) 2.5 × 0.9 nm² with the imaged heights and bias indicated below each image. Lattice geometries in (c, f) approximated from Lee.²⁷⁵ Line scans averaged from 50 passes at a relative tip height of −250 pm.

The continued study of such strong correlations within these type I DB wires revealed the possibility of a competing electron–electron correlation in which DB spins would align either ferromagnetically (FM), or antiferromagnetically (antiFM).^{267,268,270−272} The results of several of these studies comparing the ionic lattice distorted and antiFM configurations are shown in Table 1. Notably, all calculations predict an energy lowering effect for both the ionic lattice distorted and antiFM configurations as well the opening of an energy gap. Additionally, any lattice distortion in the antiFM case is absent suggesting these are competing correlations.

Table 1. Comparison of Calculated Height Difference Δd_up-dw (Å) between up and down Atoms in the Distorted DB-Wire, Direct and Indirect Band Gap Energy E_g (eV), and Energy Gain ΔE (meV/DB)^a.

		Δdup-dw(Å)	Edirectg (eV)	Eindirectg (eV)	ΔE (meV/DB)
lattice distorted	(273)	0.16	0.126	0.025	7
	(142)	0.50			47
	(274)	0.67			105
	(269)	0.74	0.68	0.36	43
	(267)	0.78		0.39	49
	(268)VASP	0.78	0.40	0.37	56
	(268)SIESTA	0.81	0.45	0.44	61
antiFM	(267)	0.00		0.63	57
	(268)VASP	0.00	0.55	0.50	41
	(268)SIESTA	0.00	0.63	0.60	56

^aAdapted with permission from ref (268). Copyright 2012 IOP Publishing Ltd.

Experimental insights into the preferred ground state configuration of these type I DB wires were not gained until they were studied within the Si band gap using a nc-AFM.²³⁵ By using a Si functionalized tip, the charge character of the DB wires was more easily observed, revealing unique ionic charge configurations which were correlated to the predicted lattice distortions. It was also found that the formation of these ionic charge configurations was dependent on the net charge of the DB wire. DB wires that were in a net neutral configuration exhibited no ionic redistribution, as shown for DB wires of length 4 and 5 in Figure 47(a) and (d), respectively. Once charged with an extra electron, the DB wires were observed to form an ionic charge distribution (Figure 47(b) and (e)). Looking at Figure 47(b) and (e), the charge state of DBs within the wires can be extracted by comparing the relative Δf of the DBs to H-terminated Si. DBs which show a similar Δf to H-Si are neutral, DBs which measure a less negative Δf are positive, and DBs which measure a more negative Δf are negative. This can more clearly be seen in the extracted line profiles of Δf scans shown in Figure 47(c) and (f). The streakiness across the negatively charged DB wires of Figure 47(b) and (e) is identified as a switching between different ionic and lattice configurations with the same net negative charge. The even length wires exhibit degenerate states where the Si atoms may be in a raised-lowered or lowered-raised configuration. Odd length wires on the other hand, exhibit two energetically different configurations. DB wires in which the outer atoms are raised from the surface are in a lower energy configuration than odd length DB wires with the outer Si atoms lowered toward the surface as predicted by Lee et al.²⁶⁷ Since the net neutral DB wires exhibit no ionic formation, it leaves the possibility of a potential antiFM spin alignment which awaits further studies. Higher order negative charge states were also seen through spectroscopy, indicating DB wires may become charged with more than one extra electron as shown in ref (235).

The identification of such electron–phonon ordering has interesting implications on the conductivity of type 1 DB wires. Theoretical studies have explored such correlations and their effects on the conductivity. When accounting for ionic lattice distortions or antiFM spin alignment, these studies predict significantly reduced conductivity^{267,268,276−280} compared to almost metallic conductivity observed in wires which exclude such potential correlations.^280−283 In response to these results, some groups have explored alternative DB wire designs to the type 1 wires. Kepenekian et al.²⁷⁸ theoretically explored the conductivity of type I, II, III, and IV DB wires. They found that the type I wire showed the greatest correlation effects exhibiting a ground state antiFM spin ordering (which awaits experimental confirmation). The type II configuration showed a similar FM spin ordering which negatively affected the conductivity as well. Experimental explorations of the type II wire by Schofield et. al²³⁶ also revealed varying STM topography images with changing imaging bias suggesting that transitions between ground-state and excited-state orbitals are possible.

The type III and IV DB wires revealed no spin ordering, but the type IV wire demonstrated the commonly seen electron–phonon correlation²⁷² of the unterminated surface^{118,284−289} and single bare dimers^114,290 (BD, Figure 46) leading to dimer buckling which opens a gap in the system due to the formed dimer π bond.^{272,291−293} This new bond has significant overlap with the valence band of the bulk crystal creating a very substantial leakage channel. This leakage channel was observed experimentally by Naydenov and Boland, who showed that type IV wires longer than 4 nm showed no band gap while type I wires remained semiconducting.²⁷⁹ A similar lattice distortion is seen in the type III “zig-zag” DB wire also creating an energy gap in the surface band structure, however, the predicted gap is only ∼0.2 eV compared to the ∼0.9 eV predicted for the antiFM case. These results show promise for some wires for electronic conductivity across the surface.

6.2. Transport Measurements of Nanoscale and DB Wires

Although STM measurements and theoretical calculations of DB wires suggest that good conductivity could be achieved for some wires, there is very little experimental measurements of the transport properties of DB wires on silicon. There have been numerous papers that have evaluated surface conduction on clean silicon surfaces using 4-probe or single probe STM measurements, and these could be used to infer some wire conduction. However, on Si(111)-7×7, reported surface conductivity has spanned several orders of magnitude, depending on the study.^294−302

In order to evaluate the Si(111)-7×7 conduction and create nanowires for measurement, Onoda et al.³⁰³ used a 2-probe STM to create lithographic features and perform transport measurement of the surface states in confined structures. Using a two probe method and ohmic contact to the surface, Onoda measured the surface conductance at low bias voltages, limiting conduction through bulk states, and determined the 2D surface conductivity to be (3.5–4.4) × 10^–6 S/□.

Onoda also used STM lithography to create confined wires of varying aspect ratios and showed that the surface 2D conduction followed the expected conductance for the various shaped features, as shown in Figure 48.

Figure 48.

Conductance measurements of the rectangular Si(111)-(7×7) areas by Ohmic 2P-STM. (a, right) STM image of rectangular areas fabricated by trench lines (V_1P = −2 V and I_t = 1 nA). Probes 1 and 2 were located around the terminals of each wire. (b, left) I–V curves measured by Ohmic 2P-STM on the bare Si surface and different rectangular areas. Inset shows the magnified graph for the case of W = 50 nm with only probe 2 outside of the rectangular areas, indicating the electronic decoupling between the inside and the outside regions. Reprinted with permission from ref (303). Copyright 2021 American Chemical Society.

Onoda went on to measure confined structures of varying lengths and showed that the resistance of wires was related to the length of the wire and that therefore transport is diffusive at RT, as shown in Figure 49. Wires were additionally narrowed at one end causing conduction measurements to depart from metallic and to become asymmetric and nonlinear. These metallic surface wires would be good candidates to connect to surface structures if the Si(111)-7×7 surface became more technologically relevant. However, the measurement methods discussed, could also be implemented on other silicon surfaces.

Figure 49.

Resistance measurements of the open rectangular Si(111)-(7×7) area by Ohmic 1P-STM. (b) Schematic of the resistance measurement with variable L. The tip was moved from the closed terminal to the open one. (c) Equivalent electrical circuit of the experiment in (b). (d) I–V curves measured by Ohmic 1P-STM on the bare Si surface and the open rectangular area with different L. (e) Total resistance measured by Ohmic 1P-STM with different L. Reprinted in part with permission from ref (303). Copyright 2021 American Chemical Society.

Other two probe studies have been performed on Germanium surfaces by Kolmer et al.³⁰⁴ There, a dangling bond wire was created by desorbing hydrogen from the Germanium (100)-2×1 surface (Figure 50). One probe contacted one end of the wire, while the second probe was maintained at the tunneling height above the surface. I–V curves under various distances to the contacted probe were evaluated. At a distance of 48 nm separation, current increased monotonically starting at +0.45 V up to about 1 V. However, for a closer distance of 34.5 nm separation and above +0.4 V, the current is different with the observation of an increase in current and multiple peaks that were attributed to negative differential conductance regions. It was proposed that resonant transport through the surface pi* state was observed but that charge can localize on some parts of the wire to effectively block transport at particular energies.

Figure 50.

(a) STM image of a DB dimer wire on the Ge(0 0 1):H surface at 4.5 K (+1.0 V, 50 pA). The ∼70 nm long wire consists of 156 bare Ge dimers (DB dimers) and has 14 atomic scale defects including 9 single Ge atoms (single DBs) and 5 unknown defects (adsorbates or vacancies). (b) Schematic view of the two-probe experiment geometry. Both STM probes approach the same atomic-scale wire of bare Ge dimers along Ge(0 0 1):H reconstruction rows. (c) SEM image of two tungsten tips approached to the Ge(0 0 1):H surface. (d) STM image of the same DB dimer wire as in (a) (−0.5 V, 50 pA). Insets: two STM images obtained simultaneously by two different tips in the geometry shown in (b) and (c). White arrows point in the slow STM scan direction. Reprinted with permission from ref (304). Copyright 2017 IOP Publishing Ltd. https://doi.org/10.1088/1361-648X/aa8a05.

The authors further published³⁰⁵ two probe STM results on the clean germanium surface where they discussed a method for the determination of the transconductance in a two-probe experimental setup supporting electronic transport through quasi-1D transport channels of the unoccupied surface states on Germanium at 4.5 K. A feature of these surface-propagating electrons was that their coherence is preserved at distances up to 50 nm.

One way to attempt to create metallic like character of DB wires could be to try to metalize the DB structures. This has been achieved by depositing silver on DB wires created on a silicon surface. Silver has been shown to selectively attach to dangling bonds while not reacting with the hydrogen surface itself.³⁰⁶ Silver clusters would also be formed as the deposition of silver was increased. When the DB structures were created as a wire or a cluster of DBs, silver metalized the majority of the wire and cluster structures.

A multiprobe STM measurement was also performed on a silver metalized DB wire (Figure 51).³⁰⁷ the conductance was measured as a function of deposited silver. The authors observed that the conductance shows characteristic features, such as a current flow at the early stage of silver deposition, and a bend in the conductance curve.³⁰⁷ They attributed this shape to possible mechanisms of (1) quantized conduction by ballistic carrier transport, broadened by the influence of temperature or a bulk substrate, or (2) diffusive conduction with intense scattering of carriers at cluster boundaries and surfaces of the nanowire.

Figure 51.

(a) Results of conduction measurements at each amount of deposited silver atoms. The numerical values in the figure indicate the approximate number of silver atoms per dangling bond on the nanowire (nAg) estimated from deposition experiments. The straight lines are the least-squares fits for each data set. The conductance was obtained from these lines of best fit. (b) Conductance of silver nanowire as a function of nAg. Conductance is normalized by units of 2e²/h. Reprinted in part with permission from ref (307). Copyright 2006 IOP Publishing Ltd. https://doi.org/10.1143/JJAP.45.2184.

Lithographed metal (Ti, Pt, and Cr) electrodes have been incorporated with hydrogen terminated silicon surfaces in attempts to connect to DB structures and multiprobe STM measurements have characterized these samples.³⁰⁸Figure 52 shows the SEM image of three probes in close proximity to a Chromium deposited pattern on silicon that had been hydrogen terminated by the wet chemical methods using NH₄F. The STM image shows the metal contacts with atomically flat hydrogen terminated Si(111) between the contacts. The gap between the contacts is approximately 500 nm.

Figure 52.

Cr contacts on Si(111)-H. (a) SEM image of three STM probes approaching the e-beam patterned Si(111)-H surface. 5000× magnification, 4 kV. (b) STM image of atomically flat Si(111)-H between two Cr contacts. 800 nm, 2 V, 300 pA, mixed height and derivative. Reprinted in part with permission from ref (308). Copyright 2009 Janik Zikovsky.

This geometry allowed for various experiments. When the surface was prepared as Si(111) 7×7, a potential could be applied between the two electrodes and the conductance across the contact gap was measured. When dosing molecules, the change in conductance could be measured. Upon exposure to benzene the measured current between the two contacts typically dropped by 85%. Measurements for styrene and 1,2,4-trimethylbenzene showed current drops of 94% and 99.8%.³⁰⁸ The change in conductance during exposure could also be monitored during the dosing of molecules and the sensitivity to doses below 4 × 10^–4 L is achieved which is equivalent to detecting a change in molecular coverages of less than 1/2500th of a monolayer.

Another experiment to characterize the silicon between contacts is Scanning Tunneling Fractional Current Imaging (STFCI), which is a variant of Scanning Tunneling Potentiometry³⁰⁹ (STP). In STFCI, the STM probe is biased and the fractional current to each metal probe is measure and the fractional current to one probe (F_A) can be scaled to be equivalent to the measure potential in a STP experiments.³⁰⁸Figure 53 shows the STFCI image of Si(111) 7×7. The fractional current image shows clearly shows that most of the change in FA occurs at the step edges and shows that a single step is more resistive than the 7×7 terrace.

Figure 53.

STFCI experimental images showing a few steps on Si(111) 7×7. 250 nm, 2 V, 300 pA. (a) Topographies. The yellow numbers indicate the height, in monatomic Si(111) steps, of each terrace. (b) Fractional current image. Adapted with permission from ref (308). Copyright 2009 Janik Zikovsky.

The magnitude of the step resistance can be measured using the multiprobe STM setup in another modified STP setup where height-bias (ZV) spectroscopy is used as a noncontact voltage measurement method.³¹⁰ In this method a potential is applied between two surface contacts and a third probe performs ZV spectroscopy between the contacts. At some point during the tip voltage sweep, the sweeping bias on the tip will match the sample potential, causing the tip to get very close to the surface to compensate for the reduction in current. The ZV spectrum will present a dip corresponding to the surface voltage and because the tip can move around the surface, one can construct a high spatial resolution and nondestructive map of the local potential at the surface.³¹⁰Figure 54 shows this result for four recorded ZV curves at unique surface positions as indicated in the figure inset. Measurement traversing the single step are plotted revealing a step-like jump in the voltage profile correlated with the STM step topography. Dosing of molecules removes this voltage step indicating the loss of surface state conduction. Using this data the surface conductivity was measured at 1.3 ± 0.3 × 10^–6 S/□. Furthermore, they obtained the atomic step conductivity of 2 ± 1 × 10^–8 S/□ and converted the 2D value to a 1D barrier conductivity of 15 ± 7 S/m.

Figure 54.

Potential mapping of Si(111) 7×7. (a) ZV spectra collected at different positions on the diagonal. (b) Potential profile acquired on both clean and dosed (50 L 1,2,4-trimethylbenzene) surfaces. The clean profile displays the fitting function used to calculate the conductivity. The potential difference is 4 V. Inset: STM image showing where the profile was acquired and the monatomic step edge. Some points are identified by colors that match the corresponding potential profile displayed in (a). Reprinted in part with permission from ref (310). Copyright 2014 American Physical Society. https://doi.org/10.1103/PhysRevLett.112.246802.

7. Silicon Quantum Atomic Designer (SiQAD)

Exploration into SiDB logic design and future applications was greatly sped up by the inception of computer-aided design (CAD) tools developed and calibrated specifically for the SiDB platform. SiQAD³¹¹ (Silicon Quantum Atomic Designer) provides a suite of tools to design SiDB layouts and simulate their behavior, as detailed in section 7.1. This has enabled SiDB logic research from the gate level to the application level. In section 7.2, we review logic gates of various topologies that have been designed and validated by SiQAD’s simulations.^311−314 We also review the only existing automated SiDB gate designer,³¹⁵ which leverages reinforcement learning to generate gates conforming to arbitrary truth tables.

Section 7.3 covers research efforts toward higher level SiDB design automation and prospective applications. A design automation framework which is able to place and route SiDB circuits on a hexagonal grid³¹⁶ enables studies at the architecture and application level. Further, it has been integrated into fiction,³¹⁷ a framework for logic synthesis, placement, routing, clocking, and verification of emerging nanotechnologies. Applications in machine learning acceleration³¹⁸ and analog-to-digital conversion³¹⁹ have also been proposed, revealing multiple directions to further develop SiDB logic.

7.1. SiQAD Simulators

SiQAD¹ is the preeminent CAD tool for the design and simulation of SiDB layouts. It provides a graphical user interface to facilitate the placement of SiDBs on the H-Si 2×1 (100) surface and electrodes on metallic structures with arbitrary depth.

It provides physical simulation implementations for ground state charge configuration simulation,^311,318 charge hopping dynamics simulation,¹ and electrostatic landscape solving.^311,319,320

7.1.1. Ground State Simulation

The phenomenon that SiDB layouts tend to relax to the ground state configuration^121,234 is an important feature for SiDB logic design because it has enabled the experimental demonstration of SiDB logic components that encode bit information in the position of charges in SiDB configurations.¹²¹ The ability to accurately simulate the ground state charge configuration of any given SiDB layout allows researchers to rapidly prototype the behavior of SiDB systems and significantly reduce time spent on experimental iterations.

The SiQAD ground state model defines the ground state to be the lowest energy metastable charge configuration(s) for a given SiDB layout. The experimentally fitted energy equation^49,121 of a charge configuration is given by

1

where V^ext_i is the total contribution of external potential sources at the location of the i^th SiDB excepting influences from other SiDBs, n_i is the charge state at each SiDB with possible values 1, 0, and −1 corresponding to the vacant, singly occupied, and doubly occupied states, respectively. V_ij is the screened Coulomb potential given by

2

where r_ij is distance between SiDBs, λ_TF is the Thomas–Fermi screening length, ϵ₀ and ϵ_r are the vacuum and relative permittivities, respectively.

The following metastability constraints are applied in the ground state model:

• configuration stability, where a lower energy configuration does not exist within a single charge hop between any two SiDBs, and

• population stability, where the charge state found for each SiDB is consistent with the energetic position of its charge transition levels relative to the Fermi energy with band bending effects taken into account.

A chemical potential given by μ_– = E_s – E^Si_F is applied to capture the energy difference between the bulk Fermi level, E^Si_F, and the DB(0/−) charge transition level of a single isolated SiDB, E_s. Local band bending effects for individual SiDB sites are modeled as

3

To satisfy the population stability constraint, a SiDB must be negatively charged when V_i + μ_– ≤ 0, positively charged when V_i + μ₊ ≥ 0, and neutral otherwise. It is important to note that this model does not take temperature effects into account, the presence of which may excite the system to take on higher energy charge configurations.

An exact implementation of the ground state model, ExhaustiveGS,³¹⁸ is included with SiQAD. It finds the ground state charge configuration for a given SiDB layout by exhaustively comparing the energy of all available charge combinations that fully satisfy the metastability constraints. However, its application in large scale SiDB layout verification is limited by exponential runtime scaling.

SiQAD also offers a heuristic ground state model implementation, SimAnneal,^311,318 which offers advantageous runtime scaling. It is a simulated annealing algorithm with physically inspired heuristics consisting of two major actions: population control and surface hopping. During the population control phase, charges are allowed to enter or leave SiDBs with probability related to the energetic position of the charge transition levels at that location relative to the Fermi level; as for the surface hopping phase, charges are allowed to hop between SiDBs with hops permitted by an acceptance function inversely proportional to the energy delta that results from the hop. A single-threaded benchmark simulating a layout consisting of 16 SiDBs³¹⁸ revealed an ∼4 orders of magnitude difference in time to solution between SimAnneal and ExhaustiveGS for that problem size with sufficient sampling to achieve 99.7% confidence in the solution.³¹⁸

7.1.2. Charge Hopping Dynamics

HoppingDynamics is a nonequilibrium charge dynamics simulator included in SiQAD.¹ It treats electron transitions via hopping rates, generalized to support multiple hopping models. SiQAD currently offers two such models: Mott Variable Range hopping³²¹ and Marcus hopping.³²² HoppingDynamics only takes neutral and negatively charged SiDBs into account due to their perceived predominant role in SiDB logic design. The inter-SiDB hopping and bulk-SiDB hopping channels are considered. The latter allows charges to be added to and removed from the surface in response to changes in local potentials at the surface. The authors calibrated HoppingDynamics to Rashidi et al.’s experimental AFM line scans over a six SiDB symmetric structure²³⁴ and presented simulated line scan results that resemble experimental AFM line scans.

7.1.3. Electrostatic Landscape Solver

The electrostatic potential landscape at the surface directly influences the operation of SiDB circuits due to the resulting band bending effects.²²⁸ SiQAD includes a finite element method electrostatic solver, PoisSolver,^311,319,320 which allows researchers to characterize the effects of electrodes, surface conduction pads, and dielectric mediums with configurable doping concentration and depletion depth settings.

PoisSolver solves Poisson’s Equation to produce the electrostatic landscape. Multiple definitions of spatial charge density are supported, each with trade-offs between runtime and accuracy. Multiple boundary conditions are also supported. In a comparison between PoisSolver and COMSOL simulation results, PoisSolver’s result was found to be on the same order of magnitude with maximum error below 25%. This allows researchers to rapidly explore electrostatic effects on SiDB systems with a fully integrated tool without additional software licenses.

7.2. SiDB Logic Design

The availability of a calibrated CAD suite for SiDB research has enabled studies of logic implementation from the gate level to the application level. In section 7.2.1, we review efforts in building and verifying SiDB logic components. Simulating these components under different sets of physical parameters reveals limitations to their operational domain, which we review in section 7.2.2. Lastly, we report on efforts toward automated gate design methodologies via reinforcement learning in section 7.2.3.

7.2.1. Logic Platform

The successful experimental demonstration of a sub-30nm² OR gate by Huff et al.¹²¹ introduced an emerging computing platform. Its logic building block encodes bit information in the ground state position of one charge shared by a pair of SiDBs as illustrated in Figure 38. Carefully designed ensembles of these SiDB-pairs can implement logic wires and gates. The use of this basic unit cell is shared by many CAD-driven SiDB logic investigations^{311−314,318,319} and is denoted binary-dot logic (BDL) by some works. An advantage of the SiDB platform is the flexibility to directly implement wide-ranging elementary logic functions in small areal footprints. Ng et al. have proposed multiple elementary 2-input logic gates³¹¹ that take a Y-shaped I/O geometry in the same vein as the OR gate demonstrated by Huff et al.¹²¹ T-shaped 2-input gates were also seen in literature,³¹² presenting an alternative topology that circuit designers may consider. Multiple works have also proposed 3-input BDL gates^311−314 for compact logic implementation. Notably, Vieira et al. proposed a collection of gates that implements all 3-input NPN class representatives.³¹⁴

Simulation-driven research further proposes SiDB circuits that implement more elaborate functions by connecting multiple BDL gates with BDL wires.^{242,312,313,318} An example is provided in Figure 55 where a half adder³¹¹ is implemented using Y-shaped gates with the logic functionality verified in SiQAD. By far, the largest proposed SiDB circuit that can be fully simulated is a full adder³¹² using T- and +-shaped gates. Efforts to design larger and more complex SiDB circuits are possibly limited by simulation runtime constraints³¹⁸ and a lack of well-established design rules. Gates that are designed in isolation often have to undergo modifications when fitted in a circuit due to changes in the electrostatic landscape.³¹¹

Figure 55.

A half adder consisting of an XOR gate, an AND gate, a normal fanout, and a fanout with one inverted output is simulated using SimAnneal. Filled and unfilled circles denote negatively charged and neutral SiDBs, respectively. Reprinted with permission under a Creative Commons CC BY 4.0 license from ref (311). Copyright 2020 IEEE. https://creativecommons.org/licenses/by/4.0/.

An alternative logic unit cell considered in literature³¹¹ resembles quantum-dot cellular automata (QCA) unit cells²³¹ where logic state is represented by pairs of charges in rectangular quantum dot formations taking diagonal positions due to Coulombic repulsion. Elementary gates in QCA implement the Majority-Inverter Graph logic representation structure. A QCA cell made of SiDBs was experimentally demonstrated²³⁰ with the logic state set by two diagonal perturbers. Using SiQAD, Ng et al. proposed a collection of SiDB QCA gates³¹¹ that fully implements elementary QCA functions, for further exploration at the circuit level. It is notable that the flexibility offered by the H-Si(100)-2×1 surface potentially allows it to support multiple sets of QCA cell dimensions and separations. There are opportunities to study the trade-offs between different configurations.

As larger SiDB circuits are considered, there emerges a need for clocking mechanisms to facilitate the flow of signal. It has been shown experimentally that SiDB charge states can be influenced by band bending effects induced by externally applied electrostatic biases.²²⁸ Taking advantage of this phenomenon, a SiDB circuit clocking mechanism that works by modulating the surface electrostatic potential to vary the charge density was demonstrated^311,319,320—regions with fewer charges are considered “off” while regions with sufficient charges for operation are considered “on”. The electric fields are expected to be applied by hanging or buried electrodes.^311,320 Clocked SiDB wires have been demonstrated at a small scale with the use of SiQAD’s PoisSolver and HoppingDynamics simulators.³¹¹ At 1 GHz operation, the power density of hanging clocking networks have been found to be in the order of 10 to 100 μW/cm² depending on the exact clocking electrode layout.³²⁰ However, the exact charge dynamics in SiDB circuits in the presence of an active clocking field and the associated power draw by the population and depopulation of circuit regions remain topics that require further investigation.

7.2.2. Operational Domain

The metastable ground state charge configuration of an SiDB layout (eq 1) is dependent on multiple physical parameters that may vary across different surfaces, such as ϵ_r and λ_TF. μ_– may also vary based on bulk dopant concentration. By sweeping through ϵ_r, λ_TF, and μ_– in ground state simulation for an SiDB layout, one can establish a range of physical parameters within which the expected logically correct ground state can be reached.¹ This is a time-consuming process that has only been applied to select gates in a small number of existing SiDB work.^311,314,318Figure 56 shows the operational domain of Ng et al.’s reproduction of Huff et al.’s OR gate³¹¹ in all input configurations. The intersection of the operational domains across all input combinations reflects the actual operational domain of the gate. Changes in μ_– lead to translations of the operational domain in the ϵ_r direction in log–log scale. A larger operational domain indicates that a gate or circuit is able to reach the intended ground state across a larger range of physical parameters, which is a desirable trait in light of possible lattice and surface imperfections. There exist opportunities to create a figure of merit to evaluate and compare the reliability of SiDB layouts based on their operational domains, which may in turn form the foundation for future circuit design rules.

Figure 56.

Ground state charge population of a slightly modified BDL OR gate³¹¹ for (a) 00, (b) 01/10, and (c) 11 input configurations. The operational domain is colored in dark purple. In (c), an alternative accepted ground state is also included, colored pink. Other colored regions denote the count of negatively charged SiDBs in the ground state configuration at those physical parameters. Uncolored regions represent parameters that yield positive charges in their ground state charge configurations. Reprinted with permission under a Creative Commons CC BY 4.0 License from ref (311). Copyright 2020 IEEE. https://creativecommons.org/licenses/by/4.0/.

7.2.3. Automatic Circuit Design by Reinforcement Learning

The manual design of SiDB layouts is a time-consuming task due to disruptive cascading effects of SiDB placement during the design process. These unintuitive, nonlocal effects obfuscate the realization of general, deterministic strategies for arbitrary SiDB layout design. State-of-the-art layout design is thus prohibitively difficult for nonexperts and is only practiced in tight spheres of academia, hampering the proliferation of SiDB technology. Akin to electronic design automation (EDA) software for semiconductor chip design,³²³ deep reinforcement learning (DRL) has been proposed to realize a scalable and robust solution for the design of general SiDB layouts.³¹⁵

Reinforcement learning (RL), with designs validated by CAD tools, is a uniquely suited optimization method for SiDB layout design. The goal of layout design is to find the configuration of SiDBs in a prescribed design space, given the location of input and output SiDBs, that optimally satisfies a desired logical behavior. The logical behavior is correct if all rows of the logic truth table are satisfied by the layout, and optimality is quantified by the maximal amount of perturbation to the layout’s operating set of physical parameters that does not change the correctness of the logical behavior.³¹¹ It has been demonstrated that simple random sampling design methods, which can be augmented by metaheuristic algorithms, are capable of yielding SiDB layout designs that demonstrate correct logic behavior.³¹⁵ These experiments show that the design landscape is rich with solutions that exhibit correct logic, especially for simpler layouts with two inputs and one output. However, finding the optimal solution for arbitrary logic behavior proves to be challenging due to the characteristics of the DB layout design optimization problem.

First, the design space is extremely large, with the typical 12 × 9 design space of a binary input-unary output circuit posing a 108-dimensional optimization problem, with 3.25 × 10³² possible designs.³¹¹ Although general gradient-based optimization algorithms have been refined by the machine learning community to search much larger domains, these may only be employed on differentiable functions. Furthermore, since no mathematical or physics-based functions have been developed to assist SiDB layout search, there is no underlying function structure that may be exploited during optimization. As a consequence, any global search algorithm applied to SiDB layout design suffers from the no free lunch (NFL) theorem of optimization,³²⁴ meaning that optimizing the global search algorithm for a certain subset of layouts would come at the cost of the performance of an excluded subset of layouts. Second, constructive feedback during the optimization process is sparse. If the SiDB layout design process is framed as an iterative addition of SiDBs until a working layout is reached, like manual design, unconditional logic correctness and optimality feedback is only available at the very end of the design process: either the terminal layout is successful in implementing the desired logical behavior to a certain degree of physical parameter robustness, or it is not. Immediately after a SiDB is placed, there is no optimization function that can be evaluated to determine if the placement helps contribute to finding the optimal design. Furthermore, gaining or losing truth table rows as a consequence of placing an SiDB during the design process is not necessarily indicative of getting closer toward, or straying further away from, a working layout. Indeed, the only way to determine the utility of a chain of SiDB placement decisions is to retroactively evaluate them as a whole after the evaluation of the terminal layout. Lupoiu et al. identified a DRL algorithm that is capable of traversing the automated SiDB layout design optimization space.³¹⁵

In general, RL is a subset of machine learning that trains an agent (the decision-making part of the algorithm) to take the optimal actions in an environment (the system that the agent manipulates) to maximize a cumulative reward (a score that the environment imparts to the agent as a consequence of its actions) over time.³²⁵ The version of RL employed by Lupoiu et al. to automate the design of SiDB layouts is a variant of deep Q-learning (DQL), which is an RL method that trains a neural network to learn the “Quality” function of any arbitrary environment state the agent encounters.³²⁵ For each permitted action in a given state, the Q-function provides the sum of the rewards earned by the agent if it chooses that action and each future action is optimal. General optimization problems thus become trivial: given a perfect Q-function and a rewarding system that is closely aligned with the optimization goal, select the action that maximizes the Q-function at each step until the terminal state is reached. Building a Q-function for problems with tractably sized solution spaces can be done by storing a lookup table in memory containing the Q-values rewarded for taking specific actions at episodic steps. After populating the table with the rewards imparted by the environment for taking specific actions for each time step, the table can then be iteratively referenced to select the actions that result in the maximal future score. Note that this design strategy does not require immediate feedback to select the action that maximizes the sum of all future rewards. For the extremely large SiDB layout design space, using a lookup table to build a Q-function is intractable from both computational and memory perspectives. DQL addresses this by approximating the Q-table with a neural network.³²⁵ DQL is thus a suitable candidate for automated SiDB layout design, given that it supports large optimization spaces through the use of a neural network, delayed action feedback, and does not require training data.

The RL algorithm adapted for automated SiDB layout design by Lupoiu et al.³¹⁵ is illustrated in Figure 57. The automated design tool utilizes double deep Q-learning (DDQL), a variant of DQL.^326−328 Double deep Q-learning utilizes two identical but separate neural networks for action selection and action evaluation (which is used for neural network experience-based training), with learned weights periodically transferred from the latter to the former to help mitigate the neural network overestimation of Q values issue that plagues the vanilla Q-learning algorithm.³²⁷ As input, the tool requires a SiQAD design file with preplaced input and output SiDBs, the specification of the design area that the agent is allowed to manipulate, and the truth table that must be realized.⁵ No restrictions are posed on the number of inputs, outputs, or SiDB placement outside of the design area. The RL algorithm begins with an empty design space at time step 0, and it iteratively adds SiDBs until either a new working layout is discovered or the maximal number of SiDBs for the given area is reached, at which point it restarts. At each time step, there is a chance that the design space is “explored”, by randomly selecting a nonoccupied location in the design space to add a SiDB. Otherwise, the learned design policy is “exploited” by greedily selecting the SiDB location that is predicted by the agent to provide the maximal cumulative sum of future rewards. The future rewards are predicted by a neural network that is trained to predict the maximal cumulative sum of all future rewards using the time step’s design area as input. Unless the new layout is a terminal state, defined as either being an undiscovered working layout or having reached the maximal number of allowable SiDBs in the design space, it is passed as input to the next iteration of the design algorithm. The rewarding strategy provides a small positive reward for gaining a row in the truth table, a small negative reward for losing a row, and a large positive reward for finding a working layout. To push the agent toward the discovery of more robust layouts, the large positive reward is scaled by the operational domain area (as described in section 7.2.2) of the working layout such that those comparable in area–and thus design robustness–to already-discovered layouts are diminished in reward magnitude. State-action-reward experiences are backpropagated through the neural network at set intervals during the layout discovery process to train the network to provide more accurate future reward predictions.

Figure 57.

Overview of the automated SiDB layout-finding reinforcement learning algorithm developed by Lupoiu et al.³¹⁵ Starting from a blank design surface at time step 0, S₀, the reinforcement learning agent iteratively adds SiDB dots in subsequent time steps until either a new working layout is discovered or the maximum number of SiDB dots allowed to be placed in the design area is reached. At each time step, there is a chance that an exploratory, randomly selected action, A^p_t, will be selected according to the random policy. Otherwise, the current time step’s state, S_t, is processed by a neural network to predict the action, A^π_t, that results in the maximum sum of future rewards. The chosen location then gains a DB dot to form the state at the next time step, S_t+1. Reprinted with permission from ref (315). Copyright 2022 Robert Lupoiu.

The automated design tool³¹⁵ demonstrates successful optimization of all binary-input, unary-output layouts and the binary-input, binary output half adder layout manually designed by Ng et al.³¹¹ The tool is demonstrated to converge to learning a set of design rules that maximizes the rewards that the agent receives over design epochs. It is reported that the generated layouts are more spatially compact and take an order of magnitude less time to generate than their hand-designed counterparts. In addition, the automated designer is capable of accounting for physical parameter variations caused by varied dopant concentrations, physical defects, and other external influences, for which manual design rules and procedures do not exist.

The only automated SiDB layout design tool demonstrated thus far stands to be improved by the latest advancements in reinforcement learning and deep learning. For example, the tool suffers from scaling limitations to larger truth tables, with reward convergence taking more epochs and resulting in a lower plateau for the binary input, binary output half adder layout than for the binary input, unary output layouts.³¹⁵ This is because the DDQL algorithm used by the tool requires randomly finding working layouts through exploratory actions in order to learn how to find increasingly more robust layouts,³²⁷ and since the solution space is more sparse for layouts with larger truth tables, convergence takes longer and is more difficult to achieve.³¹⁵ To mitigate scaling issues, a more focused, and thus more efficient, search of the design space may be achieved using Monte Carlo tree search (MCTS) rollouts.^329,330 This exploration method organizes states that it explores as connected nodes in a hierarchical tree structure. The algorithm selects, expands upon, and simulates states that are sorted in the tree using an upper confidence bound formula that takes into account the associated reward value and number of times each node was visited to efficiently explore the domain.³³¹ MCTS rollouts are likely to help mitigate domain complexity scaling issues because this domain exploration algorithm was sufficiently efficient to lead to the demonstration of a Go grandmaster-beating AI algorithm trained with no prior game knowledge—-a game that is notoriously difficult for computer algorithms due to its dauntingly large decision tree.³³⁰ Furthermore, the convolutional neural network (CNN) employed by the design tool processes the SiDB layouts, which are created on the H-Si 2×1 (100) surface, on a regular grid to learn approximations of future values.³¹⁵ The CNN does not make use of important structural information, such as the varying gap lengths between the rows of the surface. Additionally, the input to the CNN must be fixed for any set of learned weights, meaning that training is not directly transferable between structures with different design area sizes—-an issue that is further complicated by the fact that different equally sized areas on the H-Si 2×1 (100) surface are not necessarily congruent. These issues can be resolved by using a graph neural network (GNN) in place of a CNN.³³² The GNN learns relationships for data that is described by passing messages of information between nodes that are connected by edges on arbitrarily structured graphs. The same GNN can also be used to learn data represented on differently structured graphs, allowing for the same network to be transferred to different layouts.

7.3. Design Automation and Future Applications

Looking beyond logic gate design at the physical level, studies have also proposed EDA frameworks for SiDB logic and investigated future applications that SiDBs are well-suited to fulfill. In section 7.3.1, we review a framework that is able to place and route SiDB circuits on a hexagonal grid. In section 7.3.2, two applications are considered: a matrix multiply unit with applications in machine learning proposed by Ng et al.³¹⁸ and an analog-to-digital converter proposed by Chiu et al.³¹⁹

7.3.1. Placement and Routing on Hexagonal Tiles

As a first significant effort toward enabling design automation for SiDB logic, Walter et al. proposed an SiDB logic placement and routing framework³¹⁶ and integrated it into fiction.³¹⁷ Noting that hexagonal tiles are more suitable for the experimentally demonstrated Y-shaped gates¹²¹ than rectangular tiles, they proposed the hexagonal Bestagon gate library to serve as the building blocks for SiDB design automation.³¹⁶ The input and output BDL wires in the tile templates are placed such that outputs of a preceding gate are connected seamlessly to successive ones. The following Bestagon tiles are implemented and verified with SimAnneal: wires (vertical, diagonal, two parallel verticals), wire crossings, fan-out of 2, half adder, and common 2-in-1-out gates including OR, AND, NOR, NAND, XOR, and XNOR. More than half of the Bestagon tiles are designed with the help of Lupoiu et al.’s reinforcement learning agent.^315,333 Examples of select Bestagon tiles are shown in Figure 58. Notably, the agent-designed half adder from the library uses ∼70% fewer SiDBs and smaller area than the Ng et al.’s manually designed counterpart.³¹¹

Figure 58.

Standard component tiles selected from the Bestagon library³¹⁶ depicting a diagonal wire, a straight inverter, a 2-input XOR gate, a half adder, and a wire crossover. Reprinted with permission from ref (316). Copyright 2022 Marcel Walter.

Taking the design of the clocking network into account, the minimum metal pitch is 40 nm at state-of-the-art 7 nm lithography processes.³³⁴ This places a restriction to the minimum addressable size of each SiDB circuit region to be activated by clocking fields. The length of Bestagon tiles are less than 20 nm, which is much smaller than the minimum metal pitch. Walter et al. proposed the idea of super-tiles(316) to circumvent this problem—multiple standard component tiles are grouped into a larger tile to be addressable by clocking electrodes without violating lithography design rules, as illustrated in Figure 59.

Figure 59.

Multiple hexagonal tiles form a super-tile,³¹⁶ with dimensions chosen based on lithographic design rules on clocking electrodes and the clocking floor plan of choice. Reprinted in part with permission from ref (316). Copyright 2022 Marcel Walter.

The physical design flow proposed by Walter et al.³¹⁶ takes a logic level specification (e.g., a gate-level Verilog file) as input. After optimizing the network for number of nodes and depth via cut-based logic rewriting,³³⁵ technology mapping³³⁶ is performed to translate the input network into one that uses available Bestagon gate types. Subsequently, an SMT-based exact placement and routing algorithm³³⁷ is used to generate a gate-level layout. A logic-level equivalence checking step that takes SiDB signal delays into account³³⁸ ensures logical correctness and signal synchronization in the generated gate-level layout. Lastly, the Bestagon library is applied to generate a dot-accurate SiDB layout. As of now, only feed-forward networks are supported. Multiple benchmark suites^339,340 were successfully placed and routed with the application of Bestagon gates, with the largest circuits taking up 32 × 10³ nm² with 651 SiDBs and 30 × 10³ nm² with 1211 SiDBs.

The introduction of design automation tools for SiDBs presents the opportunity to explore SiDB logic at the architectural and application levels at a significantly faster pace than relying on manual designs. Existing design automation tools can be further improved in future work, with some examples including the support of more complex clocking floor plans such as USE(341) at the super-tile level, the improvement of standard component tile libraries to include tiles that have more inputs and outputs, and the capability to route around lattice or other surface defects.

7.3.2. Future Applications

The potential for high frequency³⁴² and low power operation in highly compact component footprint¹²¹ has attracted researchers to study the prospective performance of SiDB logic in sought after applications. The most complete application studies so far are Ng et al.’s matrix multiply unit (MXU),³¹⁸ which has great relevance to machine learning acceleration, and Chiu et al.’s analog-to-digital converter (ADC),³¹⁹ which is in demand in industry and consumer electronics.

Ng et al.’s proposed SiDB MXU focuses purely on applying SiDB logic without taking advantage of other physical or quantum effects. The SiDB MXU takes inspiration from the counterpart in Google’s Tensor Processing Unit version 1 (TPUv1),³⁴³ sharing a systolic array architecture to implement a 8-bit integer matrix multiplier. The MXU takes 8-bit quantized weights and activations as inputs and returns the accumulated products as outputs. Quantization allows smaller hardware footprint and lower power draw at a modest accuracy penalty.^343,344 The systolic array consists of a network of identical processing elements (PEs), each of which acts on the input data and passes the output onto the next PE. Figure 60 illustrates the proposed MXU and an extended component overview in each PE. The PEs contain components laid out in a manner that allows pipeline stages to be fully utilized via input interleaving, which maximizes concurrent operations, improving throughput. Note that although elementary logic components, such as wires, crossovers, and half adders are individually verified in simulation, the MXU design as a whole was not simulated due to computational constraints. Area costs are estimated based on the known sizes of logic building blocks and wires. When pegged to the same clock rate as Google’s TPUv1, Ng et al. estimates that the SiDB MXU offers an improvement of 1 order of magnitude in area efficiency and up to 7 orders of magnitude in power efficiency³¹⁸ using Chiu et al.’s clocking power model.^319,320

Figure 60.

A systolic array MXU. Each PE in the systolic array consists of a control unit, a multiply accumulate (MAC) unit, and a delay line memory. The spatial layout is optimized for pipelined SiDB implementation with the possibility to interleave inputs for concurrent operation. Reprinted in part with permission from ref (318). Copyright 2020 Samuel Ng.

Chiu et al.’s ADC design³¹⁹ takes advantage of the Coulombic behavior of charges in SiDB systems to create compact and sensitive quantum-dot-based voltage comparators in conjunction with SiDB logic, as illustrated in Figure 61. The comparator output is expected to be in thermometer code. A bubble error correction step is present after the comparator stage in case of bit flip errors. Finally, a binary encoding circuit encodes the thermometer code into binary output. Energy per sample estimates are given for 2-, 4-, and 8-bit ADC ranging from 10^–10 to 10^–6 pJ at the low-bound and 10^–5 to 10^–1 pJ at the high-bound. According to these estimates, the SiDB ADC design is highly energy efficient even at the high-bound power estimates compared to existing alternatives.

Figure 61.

A 2-bit SiDB ADC consisting of a comparator array (top), error correction circuit (middle), and binary encoder (bottom). Reprinted with permission from ref (319). Copyright 2020 Hsi Nien Chiu.

8. Protection of Circuits

Dangling bond circuits do have some limitations in that they need to be maintained in a vacuum environment. This is not a problem during the creation of circuits in ultrahigh vacuum where the pressure is in the 10^–11 Torr range and the residual gases (mostly hydrogen) have little reactivity. However, if one wants to remove the circuit from vacuum, some protection must be in place.

One scheme is to develop a wafer capping system where a bonded cap can protect the surface dangling bonds. A step to this has been achieved in systems where the hydrogen terminated surface was created in a clean room reactor. There Si(100)2×1-H was prepared in a Reduced Pressure–Chemical Vapor Deposition (RP-CVD) epitaxy reactor.³⁰ In this preparation, a full wafer was processed using wet chemistries, annealing in hydrogen, epitaxial growth of a thin silicon buffer layer by dichlorosilane, followed by a final anneal in hydrogen. Two wafers where then bonded together and diced into smaller sample pieces. They were then introduced into UHV and separated using a molybdenum blade. STM imaging showed that the hydrogen terminated surface was intact and that DBs could then be prepared. The author’s have also proposed creating hermetically sealed regions where a cap can preserve clean regions of silicon until final processing without direct contact.³⁴⁵

Hydrogen terminated surfaces have also been encapsulated in order to measure 2D electron systems based on hydrogen terminated Si(111) surfaces.^346−348 In these references a series of microfabrication steps prepared a sample and a cap (Figure 62). When bonded together, a void was created where the hydrogen terminated surface could be studied under various conditions.

Figure 62.

Schematic cross section of the Si(111) and SOI substrates before and after bonding. (a) The H-Si(111) substrate has a mesa etched around the edges and n+ contact regions made through P implantation. (b) Within the SOI substrate, the gate and shield layers are created by a double B implantation and are represented by the two p+ doped Si layers. RIE is then used to etch a mesa and a cavity. (c) A H-Si(111) FET, where both substrates [(a) and (b)] are contact bonded in a vacuum. The blue arrows depict the electric field produced by the gate which is terminated at the shield layer except inside the vacuum cavity, where it induces a 2DES on the H-Si(111) surface. Reproduced from ref (346). Copyright 2005, with the permission of AIP Publishing.

Although these packaging approaches are still under development, there is a very large literature base on MEMS packaging with various methods to package air sensitive materials in vacuum environments. Two common bonding methods for MEMS materials either include an intermediate layer to adhere two layers (intermediate layer bonding) or by direct chemical bonding of two interfaces (interfacial bonding).³⁴⁹ Interfacial bonding requires high surface cleanness as well as high surface flatness, and it is usually carried out under high temperature and high pressure conditions that can restrict its application in certain samples. Intermediate layer bonding needs good adhesion materials and can be implemented at relatively low temperature.

These are challenges worth facing as the complexity of DB patterns and circuitry can greatly exceed that of dopant based approaches. The easy addition of quantum properties, including spin functionality make the search for effective encapsulation technology irresistible.

9. Macro Scale Connections

One major issue with utilizing atomic circuits and components described above is the ability to contact to the macroscale world. We have seen that dangling bond wires can interact with dangling bond structures, but those dangling bond wires must connect to metallic macro and micro scale wires, at some point, for the I/O communications to occur.

One method is to use metalized contacts on silicon. This could conceivable done by evaporating metal on clean silicon regions, similar to the silver deposition described earlier.³⁰⁷ But this requires fine control over the surface in order to avoid metal deposition at undesired regions. Metallic silicide wires could also be created,²²⁸ but connections to the DB wires can only occur at interfaces and metal silicide wire integrity at small dimensions can become an issue. Another issue is that of planarity of the silicide wires with the silicon surface, which can be challenging to prepare and difficult to image with scanning probe methods.

One promising plan is to use dopant ion implanted wires in the silicon surface itself.³⁵⁰ This allows for planarity of doped and undoped regions that can be imaged with STM methods. Doping implantation of STM samples has been performed with very nice contrast between p- and n-type regions.^59,351 Dangling bonds within the p- and n-type regions also appear to have different charge states. This observation of varying charge states of dangling bonds has also been observed at metal silicon contact within the depletion region of the contact.²²⁸ Recently, implanted dopant regions have been used to gate the charge state of dangling bonds indicating that active control could be possible.²²⁹ This was shown in STM experiments when Kölker et al. used implanted electrodes on a modified STM sample holder to be able to apply a gating bias to surface dangling bonds. These experiments showed that implanted electrodes can actively control DB structures and could be useful for other structures. Others have used doped regions successfully in other STM experiments. For instance Ng et al.⁷⁰ was able to use an implanted electrode to control the short-range tunnel coupling between a dopant atom and the electrode with a focus characterizing the dopant quantum dot and tuning its energy capacitively with the gate electrode.

One issue with dopants and silicon preparation for STM is that you must avoid high temperatures or risk excess diffusion of the implanted dopants. Ramanayaka et al.¹⁸⁵ used photolithography to define implanted wires for electrical connections. They also connected implanted regions with STM based lithography and phosphine exposure. Critically, they found that the implanted regions could remain isolated (without excessive diffusion) if the thermal treatment of the silicon remained below 1200 °C, which is sufficient for preparing high quality hydrogen terminated Silicon (100) surfaces.

The use of implanted dopant lines to connect dangling bond structures was also described in the thesis by Yong³⁵⁰ and in a patent by Martins,³⁵² where special samples created on Silicon on Insulator (SOI) were created. There, special silicon bridge samples were created so that small regions of suspended silicon could he heated without the requirement to heat the entire sample. This allows any metal contacts to remain at room temperatures, while only doped regions receive the heat treatment. Figure 63 shows this setup where a combination optical and electron beam lithography defines regions for ion implantation and metallic electrical contacts are added after wafer processing but before silicon hydrogen termination. The lithography also included the implantation of deep dopants to provide the electrical charge for the active dangling bond structures. This method allows all of the macro to atom lithography to be performed prior to the atomic circuit fabrication. DB wire fabrication can then connect from the doped wires to the active structures between the contacts.

Figure 63.

The three main components of the macro-to-atom device: (a) I focuses on the nanofabrication of the bulk of the macro-to-atom device, including the ion implanted arsenic (As) conduction lines. (b) II focuses on the electron-beam lithography (EBL) patterned contacts, where narrower electrodes interface with the atomic circuitry patterned in between the gap. (c) III focuses further on the center where atomic-scale lithographic patterning occurs. A heavily doped antimony (Sb) region is embedded under the surface, to provide carriers for the charging of surface dangling bonds (DBs). (d) Side view of (c) heavily doped areas implanted with a Gaussian distribution. The embedded Sb reservoir (green) utilizes a heavier dopant than the As contacts (blue); thus, it has a narrower and sharper dopant profile. Reprinted with permission from ref (350). Copyright 2020 Stephanie Yong.

It may also be possible to add macroscale contacts after circuit encapsulation. This has been achieved for buried phosphorus quantum dot systems.^353,354 In these systems phosphorus dopants and delta doped wires are encapsulated in epitaxially grown silicon (approximately 25 nm thick). Reactive ion etching would then expose regions of the delta doped wires and aluminum metal then deposited to make electrical contact. This system has proven very effective, by creating single atom transistors³⁵⁵ and in characterizing spin qubit systems of quantum dot dopants.^209,265,266 A variation of this process was also adapted by Ramanayaka et al.¹⁸⁵ where implanted wires for electrical connections were utilized along with delta doped regions created by STM lithography.

Others similar contact schemes have been proposed to contact molecular species on hydrogen terminated silicon surfaces.³⁴⁵ Sordes et al. reviewed the use of doped nanovias on SOI samples. The doped nanovias with diameters of 100 nm and 400 nm depth were proposed to connect from the surface of the device layer to the oxide interface of the SOI. At the oxide interface nanovia, metallic interconnects could make the electrical contact to large metallic pads. There are several ways to move forward in macro to atom connections and in encapsulation, all with various technological challenges to overcome in order to create viable dangling bond circuits.

10. Conclusions

In recent years it has become clear that computing performance is plateauing, and it is often said that silicon technology has reached a point of maturity due to fundamental materials limitations. We point out, however, that while CMOS technology is reaching full maturity, there is tremendous growth potential for atom-defined silicon devices that are inherently faster and more energy efficient and allow routine access to the quantum realm.

These atom defined devices can be created using Atomically Precise Manufactuting (APM). APM has been used to describe an array of tools and processes that collectively enable error-free fabrication. To date, multiatom error free designs have only been achieved in few laboratories, but likely the methods will become widespread soon. This ability to make unlimited copies of highly robust, electronically useful, variance-free entities can be expected to have a profound effect on future device design and capabilities.

The APM described in this review covered the technologies related to hydrogen desorption lithography from silicon surfaces. Atom-perfect fabrication has begun to flourish both because of relatively exacting H removal capabilities and because remnant single percent-level placement errors have been eliminated by reliable and programmable editing procedures that erase misplaced DBs by replacing an H atom and then reprinting a DB in the correct position. This has resulted in perfect pattern formation of complex structures. Pattern creation is being enhanced by AI methods that can premap surfaces, identify defects, and write patterns autonomously while correcting any errors or probe problems. With automation becoming ever more established, probe-based manufacture has transitioned from “impractical” to inevitable. In just a few years we will likely see commercial manufacturing of specialized devices. Early devices will be of limited complexity, requiring of order 1000 atoms, but will nevertheless address lucrative niche markets.

In an early proof of concept demonstration, fabrication and actuation of binary wires and logic gates was achieved using APM on hydrogen terminated silicon surfaces. These devices and future circuits have been based upon the silicon dangling bond that has been described as an “atomistic quantum dot” to emphasize its isolated, zero-dimensional character. It also implies that devices previously made of conventional silicon quantum dots, among others, can now be made of identical atoms instead of widely varying dots comprised of many atoms, with attendant advantages. While coupled conventional QDs exhibit symmetric–antisymmetric splitting energies of order 100 μeV, fractional nm spacing among atomistic QDs creates ∼1000× larger interaction energies, of order 100 meV, bringing greater noise immunity. Atomistic QDs also naturally exhibit relatively large Coulomb blockade energies, enabling relaxed cryogenic readout conditions. Unlike dopant spin centers such as substitutional P atoms that display appreciable ionization rates at several tens of Kelvin, thereby limiting spin T1, paramagnetic singly occupied Si dangling bonds sufficiently resist ionization, implying utility even at 300 K.

While proof of concept ultrafast and ultralow power transistor-less classical circuitry is now in-hand, wide deployment in that area is a decade away or more because great circuit complexity is required to be competitive in the classical binary space. The community must incrementally develop ever better tools, including far more rapid nonprobe-based methods for APM before that can happen. It is therefore possible that APM devices will be quantum based. Though customarily thought of as more challenging to make, flawless control over atomic structure renders some aspects of the quantum realm routinely accessible.

It is envisioned that encapsulated, atom-defined chiplet accelerators employing standardized I/O protocols will couple with a CPU, just as a computer graphics chiplet does today. Possible first products would be truly portable with extreme low size, weight, and power and could include a quantum random number generator, simple comparator circuits or a spin-based quantum magnetometer.

The viability of purposefully fabricated paramagnetic silicon dangling bonds as spins in quantum devices is an active research area. Single atom and small ensemble studies of paramagnetic DBs will be analyzed with miniature ESR techniques and with STM- and AFM-based ESR, Rabi and Ramsey measurements. There is no literature characterizing the lifetime and coherence of ideally situated singly occupied dangling bonds such as those described in this review. Only rare measurements of DBs at heterogeneous Si/SiO₂ interfaces are known. While the lifetimes of such nonideal DBs were not compelling, there is reason to believe the prime decohering influences acting there will be absent in better controlled samples. There is disagreement about whether the abrupt symmetry change at a surface can in itself be unfavorable to coherence. We can look forward to these crucial questions soon being resolved.

In any case, whether DBs themselves can be deployed as spins, the APM technology described here greatly enhances the control over traditional spin centers such as B, P, and As. Emerging studies may show the great utility of combining state of the art DB patterning with existing non-ionized dopant and over growth techniques.

This review has been prepared at a time of sharp transition in the APM field: decades of work dedicated to understanding and controlling silicon DBs has progressed to a point where it is expected that the long thought to be impossible task of manufacturing with scanned probes will become a practical reality, and attention can now substantially shift from exploratory research to the deployment of commercially viable atom-defined silicon circuitry.

Glossary

Vocabulary

Scanning Tunneling Microscopy

a mode of atom scale imaging by passing an electric current between a rastered sharp probe and surface atoms

Q-Plus Atomic Force Microscopy

a mode of atom scale imaging by measuring physical forces between a rastered sharp probe, mounted on a vibrating quartz tuning fork, and surface atoms

Dangling Bond

an unsatisfied valence on an atom

Hydrogen Desorption Lithography

breaking of hydrogen atom chemical bonds to surface atoms, leaving a purposeful pattern of dangling bonds

Silicon Quantum Atomic Designer

a computer-aided design tool enabling the rapid design and simulation of computational assemblies of atomic silicon quantum dots

Atomic Scale Devices

functional electronic devices where the main operating components involve atoms

Funding has been supplied by the National Research Council of Canada, Alberta Innovates Technology Futures, Natural Sciences and Engineering Research Council of Canada, and Compute Canada.

The authors declare no competing financial interest.