Abstract
The Easterlin paradox illuminates the counter-intuitive finding that happiness is unlikely to increase with economic growth over time. This study investigates the income–happiness relationship through the concept of β convergence (i.e., the catch-up effect). To this end, we first employed the KPSS panel unit root tests to reveal the time-varying patterns in convergences between the happiness index and real GDP per capita. Then, we conducted analyses of contingency for the linkage between the happiness catch-up and income catch-up effects via estimation using the random coefficient logit model. The data used in this study were obtained from World Database of Happiness and World Development Indicators Database. Our results indicate that both the happiness index and real GDP per capita in selected European countries exhibited signs of catch-up with their benchmark countries over the period of 1975–2020. The average income catch-up effect (generated from group mean of all individual effects) positively impacted the social harmonization of well-being (i.e., the average happiness catch-up effect). Since economic growth is the major force driving the income catch-up effect, the positive linkage between happiness and income catch-up effects provides solid proof of the beneficial effect of economic growth on the social harmonization of well-being.
Keywords: Easterlin paradox, Easterlin illusion, β convergence, Catch-up effect, Stochastic convergence, KPSS panel unit roottest
1. Introduction
1.1. Background
Happiness research has been a compelling area in the field of social science ever since the so-called Easterlin paradox was first proposed [1]. The Easterlin paradox illuminates the counter-intuitive finding that, while happiness is unlikely to increase with economic growth over time, affluent individuals are happier than their counterparts at any given point in time [1]. This paradox was first identified in a US survey [2], and it was later substantiated by large quantities of empirical data collected from developed countries [[3], [4], [5], [6]], developing countries [[6], [7], [8], [9], [10]] and the global economy [11]. In general, the Easterlin paradox is controversial from two perspectives: First, it contradicts the prediction from microeconomic theory that consumers will obtain higher utility levels through increases in consumption due to the growth of income. Second, it directly challenges the essential role of economic growth in fostering a higher standard of living and better quality of life in the process of economic development.
Previous studies seeking to resolve the income–happiness puzzle of the Easterlin paradox were based on three hypotheses: the adaption [12], social comparison [13], and aspiration hypotheses [14]. The adaption hypothesis contends that a rise in income only temporarily raises the level of happiness and that individuals will adapt to their current habituation and eventually return to their original level of happiness. Contrarily, the social comparison and aspiration hypotheses highlight the externality of one's income on others' happiness so that relative income (rather than absolute income) matters in determining individual happiness. The social comparison hypothesis concerns itself with the gap in relative income. Namely, the decline in one's individual happiness will be related to the magnitude of relative deprivation perceived by the individual when comparing their economic circumstances to others. The aspiration hypothesis also refers to the gap in relative income [14]. However, in this case, the perceived gap in relative income informs the individual's expectations for future income growth and, in that way, influences the individual's happiness. The adaption hypothesis has been supported by some studies [[15], [16], [17]], and the results of recent studies investigating the social comparison and aspiration hypotheses are available [[18], [19], [20], [21], [22]].
The adaption, social comparison, and aspiration hypotheses provide theoretical frameworks that can be reconciled with the income-without-happiness phenomenon identified within the Easterlin paradox. Still, the pursuit of economic growth as one of the most important macroeconomic goals is being challenged because the Easterlin paradox is persistently observed in empirical data worldwide [[1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11],23]. In order to validate the importance of economic growth from the economic policy perspective, many studies have switched their focus to the effect of economic growth on happiness inequality. This is because a reduction in happiness inequality equates to an increase in the social harmonization of well-being [24]. If economic growth were found to reduce happiness inequality, then the beneficial effect of economic growth (as a promotor of social harmonization of well-being) would be proved.
The positive association between economic growth and happiness inequality has been addressed in many previous studies. For example, Clark, Flèche, and Senik selected 60 countries with positive economic growth from five waves of the World Value Survey (WVS, 1981–2008) to examine the effect of income growth on happiness inequality. Their findings indicated that economic growth reduced happiness inequality in the context of adequate growth in income inequality [24]. Following this line of research, Ifcher and Zarghhamee utilized the same dataset used in Clark, Flèche, and Senik [24] to investigate the relationship between happiness inequality and economic growth across 97 countries from the period of 1981–2008, and their results also suggested that happiness inequality decreased with an increase in per capita income [25]. Using the same conception of happiness inequality employed by Clark, Flèche, and Senik [24], the negative association between happiness inequality and economic growth was also found in the United Kingdom, West Germany, Australia, and the United States [26], China [27], OECD countries [28], and South Africa [29].
1.2. Income–happiness nexus from theoretical economics
It is important to address that most prior studies on the linkage between happiness inequality and economic (or income) growth (such as the aforementioned studies) utilized standard deviation-type statistics (such as standard deviation, variance, and coefficient variation of the happiness index) to measure happiness inequality. Most of these studies found a downward trend in happiness inequality, suggesting that the dispersion of happiness diminishes over time around the world. In fact, the decrease in happiness variation observed by previous studies over time among different countries is consistent with the so-called σ convergence hypothesis, which asserts that the variation in the target variable within a group of countries will diminish over time [30]. Nevertheless, individual happiness is usually rated by the bounded scale, causing a downward trend in standard deviation of happiness and, in turn, a downward-biased tendency in the dispersion of happiness [24]. Another concept of convergence, the β convergence hypothesis, claims that countries with a lower level of the target variable will catch up with countries with a higher level of the target variable [30]. Therefore, the β convergence hypothesis is also referred as to the catch-up hypothesis in economic growth literature [30]. Consequently, β convergence and the catch-up effect are used interchangeably in this study.
Because only the response of the happiness gap between the target and reference groups to time trend matters in terms of justifying the convergence of the target variables, the concept of β convergence is partially free from the downward-bias problem associated with the diminishing dispersion of happiness over time, as seen when investigating the σ convergence of happiness. Note that both the σ and β convergence hypotheses originated from Solow's growth model [30]. The convergence hypothesis has been investigated in various domains to address social harmonization in the process of economic development, including real GDP per capita [31], healthcare expenditure [32], healthcare financing [33], healthcare utilization [34], welfare states [35], and so forth.
In this study, our objective was to employ the concept of β convergence, originating from economic growth theory, to provide new insights into the income–happiness relationship derived from the Easterlin paradox. The theoretical framework underpinning our research comprises three key components. First, we draw upon the social comparison hypothesis derived from utility theory, suggesting that individual happiness (reflecting individual utility) is contingent on one's own income as well as the income of the reference group. Second, we integrate the catching-up hypothesis of income, represented by β convergence in economic theory, which is commonly observed in the economic development process. Third, the amalgamation of the social comparison hypothesis [13] and the catching-up hypothesis [30] furnishes a sound rationale for applying the concept of β convergence to reevaluating the Easterlin paradox. It follows that the purpose of this research is to examine the effect of the convergence of happiness (measured by the aggregate mean score of self-reported life satisfaction) on the convergence of income (measured by real GDP per capita). To this end, we first applied the newly developed KPSS panel unit root test (KPSS-PUR test, hereafter), which is based on the work of Bahmani-Oskooee, Chang and Wu [36], in order to investigate the β convergence (or catch-up) of income and happiness across eight European countries (namely, Belgium, Denmark, France, Ireland, Italy, Luxembourg, the Netherlands, and the United Kingdom) during the period of 1975–2020, making this the first study of its kind. Secondly, we created binary variables indicating the convergence of income and happiness for each country, and the random coefficient logit model (incorporating unobserved heterogeneities across these countries) was estimated to investigate the association between the income catch-up and happiness catch-up effects over our study period. If the income catch-up effect (β convergence of real GDP per capita) is positively related to the happiness catch-up effect (β convergence of happiness index), then economic growth (a major force triggering the income catch-up effect) across countries over a period of time benefits society by yielding a higher level of happiness (namely, the happiness catch-up effect).
The innovative contribution of this study lies in its capacity to draw attention to the effects of happiness and income catch-up, marking the first endeavor to investigate the intricate connection between these two phenomena. Hence, our study extends beyond exploring the income–happiness relationship discussed previous studies, a metric which traditionally focuses on the mean and variance of happiness in relation to income [[1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29]]. The primary findings of this study are as follows: First, the time-varying convergence patterns of income and happiness were identified, and both happiness index and real GDP per capita in the selected European countries were found to have exhibited signs of catch-up with their benchmark countries during the period of 1975–2020. Second, the average income catch-up effect (generated from the group mean of all individual effects) positively impacted the happiness catch-up effect (referred as to the social harmonization of well-being). Since economic growth is the major force driving the income catch-up effect over time, the positive linkage between the happiness and income catch-up effects is solid proof of the beneficial effect of economic growth on the social harmonization of well-being.
2. Materials and methods
2.1. Materials
The happiness index is obtained using survey questions meant to evaluate one's life satisfaction, such as “On the whole how satisfied are you with the life you lead?”, with ordinal answer choices ranging from one (not at all satisfied) to four (very satisfied). Since this study applied panel data models that required consistent time series data across countries in order to investigate the correlation between income and happiness catch-up effects, we retrieved the longest annual time series data of the happiness index from the World Database of Happiness (https://worlddatabaseofhappiness.eur.nl/) over the period from 1975 to 2020 for eight European countries (i.e., Belgium, Denmark, France, Ireland, Italy, Luxembourg, the Netherlands, and the United Kingdom). It is worth noting that this database is administrated by the Erasmus Happiness Economics Research Organization. There were two values of the happiness index in some countries for given years because multiple surveys of well-being were conducted during certain years. Therefore, imputed the mean values of the happiness index for that year. This imputation procedure is valid only if the happiness index is treated as a cardinal index number. The happiness index (indicating individual utility based on microeconomic theory) should be treated as an ordinal index number. Nevertheless, previous studies confirmed that there is virtually no difference between cardinal and ordinal treatment of the happiness index in terms of the statistical inference of empirical studies [37]. Therefore, most empirical studies have treated the happiness index as a cardinal index number [23,38,39]. In this study, we also treat the happiness index as a cardinal index number in accordance with the conventional treatment of the happiness index used in previous income–happiness relationship studies [23,[37], [38], [39]].
In addition, we used real GDP per capita (constant 2015 US dollar) to measure national income, and the annual data of real GDP per capita were collected from the World Development Indicators Database (https://databank.worldbank.org/source/world-development-indicators) governed by the World Bank. Since the value of the happiness index in Denmark was always higher than that in the rest of our selected countries over our study period, we treated Denmark as a benchmark country for investigating the happiness catch-up effect (or β convergence). In the same way, Luxembourg was selected as a benchmark country for examining the existence of the income catch-up effect (or β convergence) because the real GDP per capita in Luxembourg exceeded that in the rest of our selected countries during our study period.
2.2. The catch-up hypothesis
The empirical procedure used to test the catch-up effect (or β convergence hypothesis) included two steps: First, we applied the KPSS-PUR test, based on the work of Bahmani-Oskooee, Chang and Wu [36], in order to test for stochastic convergence in the happiness index and real GDP per capita across seven European countries during the period of 1975–2020. Second, since stochastic convergence is the only necessary condition, the existence of β convergence was decided by looking at the different signs of the estimated constant term and mean effect of the trend function imposed on the KPSS-PUR test for each country [33]. We verified the presence of β convergence as the sufficient condition using the approach utilized in recent studies to investigate the β convergence hypothesis [31]. Carlino and Mills [40], when introducing the concept of stochastic convergence, implied that the trend stationary process of the log-difference of target variables (such as happiness index and real GDP per capita used in this study) between country i and the benchmark country should be justified. It therefore follows that any unexpected impacts to happiness (real GDP per capita) in country i comparative with that in Denmark (Luxembourg) are temporary. Thus, as suggested by Carlino and Mills [40] and Bernard and Durlauf [41], the unit root test for the trend stationary process of the log-difference of target variables was employed to examine the stochastic convergence of our target variables (namely, happiness index and real GDP per capita). Specifically, stochastic convergence of the happiness index was defined as equation (1) below.
| (1) |
where = ( = ) represents the natural logarithm of happiness index (Hit) in country i (benchmark country-Denmark, ) at time t. The conditional (absolute) convergence for happiness is verified if and only if (). In order to test the absolute convergence of happiness within our selected countries, it is necessary to specify the unit root model specification without constant term and linear trend. This specification is quite restrictive considering the drifts and trends of aggregate time series data that are frequently found in real world data. Thus, employing the concept of conditional convergence is a reasonable choice for analyses of the β convergence hypothesis [40,41]. In this study, we applied the newly developed KPSS-PUR test based on the work of Bahmani-Oskooee, Chang, and Wu [36] to verify the conditional convergence of the happiness index. KPSS-PUR specification is capable of detecting multiple striking breaks, linear trends and smooth transitions in the data generation process (DGP, hereafter) of the happiness index. Specifically, the DGP of the trend stationary series for the happiness index is expressed as follows:
| (2) |
where signifies the log-difference of the happiness index (), and it represents the difference in happiness index (in a natural logarithm scale) between individual country i and Denmark (chosen as the benchmark country) at time t (t = 1,2,3, …,T). The subscript k and denote the kth estimated break point and the optimal number of breaks, respectively. (, if and 0, if other) is the dummy variable used to indicate the upper and lower level of the kth structural break date. TR and (, if and 0, if other) represent the temporal trend and linear trend based on the kth structural break date, respectively. Subscript h indicates the optimal frequency of the non-linear components in the Fourier function (). , , , , , and are unknown parameters for the constant term, TR, , , and , respectively. represents the error term.
It is worth addressing that , , and Fourier function () were used to capture the striking drifts, linear trends, and smooth transitions of the happiness index, respectively. In order to estimate equation (2), we set the initial maximal frequency (h0) as twenty, and the approach introduced by Bai and Perron [42] was utilized to choose the optimal frequency (h). Bai and Perron's approach was also used to choose the optimal number and locations of structural breaks (within the maximal number of breaks set as seven) following the selection of optimal frequency (h*) [42]. To verify whether the Fourier specification is consistent with our happiness time series data, we employed the F test to examine the null hypothesis of the KPSS-PUR model without Fourier function () in equation (2). Nevertheless, Becker, Enders, and Lee proved that the limit distribution of the F statistic derived from the Fourier model specification is a non-standard distribution [43]. Hence, we applied the bootstrap method (replicating samples 10,000 times) to create the finite-sample critical values to examine whether the Fourier specification is appropriate for our panel data.
In addition, we also employed the CD test derived by Pesaran [44] to examine the existence of cross-sectional independence within our selected countries (i.e., H0: non-existence of the cross-sectional dependence versus H1: existence of the cross-sectional dependence). The statistics of the KPSS-PUR test (written as statistic) were computed using the approach introduced by Carrion-i-Silvestre, del Barrio, and López-Bazo [45]. The same condition of a non-standard limit distribution as that seen for the F statistic used to test the nonlinear components in equation (2) applies to the statistic. The statistic would not be expected to follow the standard normal distribution in the case that cross-sectional dependence were found in our panel data. Once the CD test identified the cross-sectional dependence within our selected countries, the bootstrap method (replicating samples 10,000 times) was used to create the finite-sample critical values of the statistic to examine the stochastic convergence of happiness (namely, H0: trend stationarity of the log-difference of the happiness index () for all countries versus H1: unit root of the log-difference of the happiness index () for all countries). The failure to reject the null hypothesis is a sign of the existence of stochastic convergence across our selected countries over the period of 1975–2020. It is also important to mention that the existence of stochastic convergence of the happiness index is an in sufficient but necessary condition to meet the requirement of happiness index β convergence. The sufficient condition of β convergence of the happiness index means that nations with a happiness value below that of Denmark should show positive growth in their values of happiness. In order to gauge whether the levels of happiness in our selected European countries caught up with the level of happiness in Denmark during our study period, we estimated equation (3) below.
| (3) |
where the notations , , , , , , h, and are defined in the same way as they are for equation (2). The kth previous break date for the happiness index of country i is denoted by , with the convention that and . is an indicator ( = 1, if , and 0, if other) for identifying striking breaks, and is a segment variable ( if , and 0, if other) used to model the linear trend. The Fourier function () is specified to capture the smooth transitions of happiness level for each country. Note that the bracketed part of equation (3) () is the trend function in which the slope of the trend function contains time-varying components. In order to evaluate the presence of β convergence, we first derived the slope of the trend function as , and then the mean effect of the trend function for each regime was calculated by averaging the slopes of the trend function. If the sign of the coefficient of the constant term () was different from that of the mean effect of the trend function in some regimes, then the happiness catch-up effect (or β convergence of happiness) for those regimes was determined. Given that the presence of nonlinear components (the rejection of ) in equation (3) was confirmed at the 10%, i.e., a rigorous significance level, the presentation of β convergence (or divergence) suggested by Ref. [33] can be set up as follows:
First, the notation C (D) is utilized to indicate the β convergence (divergence) of happiness in a specific regime if both the coefficients of the constant term () and of the trend () for that regime are statistically significant at the 10% significance level and the sign of the coefficient of the constant term () is opposite (identical) that of the mean effect of the trend function. Second, the notation c (d) is employed to designate the β convergence (divergence) of happiness in the case that either the coefficient of the constant term () or of the trend () for each regime is statistically significant at the 10% significance level and if the coefficient of the constant term () and the mean effect of the trend function show different (identical) signs. The procedures presented for equations (2), (3) can also be used to evaluate the β convergence (divergence) of real GDP per capita, except that must be defined as the log-difference of the real GDP per capita (), representing the difference of real GDP per capita (in a natural logarithm scale) between individual country i and Luxembourg (chosen as the benchmark country) at time t (t = 1,2,3, …,T).
2.3. Linkage of happiness and income convergence
In order to formalize the linkage between happiness and income convergence, we introduce the Cobb-Douglas utility function, indicating the level of happiness, as equation (4) below:
| (4) |
where is the happiness level in country i. () represents real GDP per capita in country i (real GDP per capita in the benchmark country, ) at time t. denotes the unobserved heterogeneity of preference across these countries during our study period. Since a rise in income allows people to meet their need for higher living standards through the purchase of more goods and services, the sign of is positive. Social comparison theory asserts that an income gap between country i and the benchmark country exerts a depressing effect on the happiness level of country i, so the sign of is negative [13]. The presence of the Easterlin paradox is apparent when either + is negative or insignificantly positive. The dynamic catch-up process is given by the log-difference of the happiness index () as follows:
| (5) |
Note that subscript , and , and the KPSS-PUR test is capable of confirming the stochastic convergence (or divergence) of happiness toward Denmark in terms of (or ) across our selected countries over the period of 1975–2020. The stochastic convergence (or divergence) of real GDP per capita toward Luxembourg) can be determined in the same way, that is (or Note that the model specification established for equations (2), (3) can identify multiple structural breaks. This allows us to verify the β convergence (or divergence) of the happiness index and real GDP per capita for each country across various temporal regimes over the period of 1975–2020. Therefore, as expressed in equation (5), the happiness catch-up effect (derived from the left-hand side of equation (5), i.e., ) can be separated into two parts: the first part entails the income catch-up effect (generated from the second bracket of the right-hand side of equation (5), i.e., ), and the second part involves the residual preference catch-up effect (generated from the first bracket of the right-hand side of equation (5), i.e., ).
Three dummy variables can be generated from equation (5) to investigate the relationship between the convergence of the happiness index and the convergence of real GDP per capita. The first dummy variable, HDit, is generated from the β convergence of the happiness index (HDit = 1 for β convergence of the happiness index) and is used to indicate the presence of the happiness catch-up effect in country i at time t. The second dummy variable, YDit, is created from β convergence of real GDP per capita (YDit = 1 for β convergence of real GDP per capita), and is utilized to indicate the presence of the income catch-up effect in country i at time t. The third dummy variable, RDit (determined by HDit and YDit), is used to indicate whether we can identify potential β convergence or divergence of the residual preference. Note that the data for residual preference are not available, meaning β convergence of the residual preference can be determined only if β convergence of the happiness index is present while β convergence of real GDP per capita is absent (namely, HDit = 1 and YDit = 0). This is because convergence of the residual preference must exceed the divergence of real GDP per capita in order to obtain β convergence of the happiness index. The same condition applies when verifying the divergence of the residual preference. The existence of divergence of the residual preference is identified only if divergence of the happiness index is found while β convergence of real GDP per capita is identified (Namely, HDit = 0 and YDit = 1). Thus, it is essential to mention that the other two conditions (which are present when values of HDit and YDit are equal (i.e., HDit = YDit = 0, and HDit = YDit = 1)) involve either β convergence or divergence of the residual preference. In the case of HDit = YDit = 0 (HDit = YDit = 1), β convergence (divergence) of the residual preference is possible as long as the magnitude of the income divergent (catch-up) effect is stronger than that of the residual preference catch-up (divergent) effect, and vice versa. The relationship between happiness and income convergence can be further explored by estimating the random coefficient logit model as follows:
| (6) |
where denotes the probability of the occurrence of the happiness catch-up effect. The definitions of HDit, YDit, and RDit are described in the above paragraph. , , and . (j = 0,1,2) are the means of the distributions of the random parameters (, i = 1,2,3, …,6, owing to the exclusion of the two benchmark countries, i.e., Denmark, and Luxembourg). (j = 0,1,2) are scale parameters for the distributions of the random parameters. (j = 0,1,2) and follows the standard normal and logistic distributions, respectively. Equation (6) was estimated using the maximum simulated likelihood method with 1,000 Halton draws [46]. There are several appealing characteristics of the random coefficient logit model specified by equation (6). First, the conventional random effect logit model is a special case of the random coefficient logit model if we restrict . Second, both the mean effects and the individual effects of the exploratory variables on the dependent variable can be generated from the multiple-level-type model specification imposed on equation (6). If is significantly positive (negative), the average income catch-up effect is positively (negatively) associated with the average happiness catch-up effect (generated by the group mean of all individual effects). The same condition holds for the impact of income catch-up on the happiness catch-up effect for each individual country (i.e., ).
It is essential to state that the data for binary variables used in equation (6) were created using the estimation process of the KPSS-PUR statistics. There are two characteristics of the KPSS-PUR model specification: First, it can accommodate the DGP of the happiness index (and real GDP per capita) with multiple striking breaks and smooth transitions through specifying indicator variables, linear segment, time trend, and Fourier non-linear components in the trend function of happiness. The time-varying (by ways of structural change) specification imposed in the KPSS-PUR test can also locate unknown dates of multiple structural breaks for each of the selected countries. Second, the KPSS-PUR statistics were generated by accommodating the cross-sectional dependence within these selected European countries. These two characteristics assist us in obtaining unbiased statistics for the purposes of testing the catch-up effect (or β convergence) and pinpointing the transition dates in happiness and real GDP per capita for each country. It follows that the binary variables (indicating specific time periods of convergence and divergence of income and happiness across these selected European countries) can be used to estimate the random coefficient logit model. It is also important to point out that the random coefficient logit model not only illustrates the average impact of the income catch-up effect (generated by the group mean of all individual effects) on the happiness catch-up effect, but also demonstrates the linkage of the income catch-up and happiness catch-up effects for each individual country. Given that economic growth is likely to trigger the income catch-up effect, the positive relationship between the income catch-up and happiness catch-up effects may indicate a beneficial effect of economic growth as a contributor to the improvement of happiness levels.
3. Results
3.1. Descriptive statistics
Table 1 presents the summary statistics of happiness index and real GDP per capita across eight European countries (namely, Belgium, Denmark, France, Ireland, Italy, Luxembourg, the Netherlands, and the United Kingdom) during the period of 1975–2020. In order to better demonstrate these data, we drew the time trends of two variables together with two scatter plots used to describe the possible catch-up effects of the happiness index and real GDP per capita in Fig. 1. As illustrated in Fig. 1(a)–(b), we found that the happiness index in Denmark exceeded those in the rest of the seven countries, and that the real GDP per capita in Luxembourg was higher than those in the other seven countries over the period of 1975–2020. In general, we observed upward trends in the happiness index and real GDP per capita in the majority of these eight European countries, but several significant turning points reflected economic recession periods and the process of European integration markets. Fig. 1(c) shows a scatter plot with the mean log-difference of the happiness index (taking Denmark as a benchmark country) on the vertical axis and the mean log of happiness index over the period of 1975–2020 displayed on the horizontal axis. A clearly negative relationship between mean log-difference of the happiness index and mean log of happiness index is revealed and this result suggests that countries with lower levels of happiness index will generate a higher growth rate of happiness relative to Denmark and vice versa. Besides, Fig. 1(d) illustrates the scatter plot with the mean log-difference of real GDP per capita (taking Luxembourg as a benchmark country) against the mean log of real GDP per capita during our study period. This shows the same pattern as seen in Fig. 1(d), with the log of real GDP per capita being obviously negatively associated with the log-difference of real GDP per capita. These findings indicate that countries with a lower level of real GDP per capita will exhibit a higher growth rate of real GDP per capita relative to Luxembourg and vice versa. The evidence obtained from Fig. 1(c)–(d) indicates the possible existence of happiness and income catch-up effects among these selected countries during the period from 1975 to 2020.
Table 1.
Descriptive statistics.
| Variables | Countries | Mean | SD | Min | Median | Max |
|---|---|---|---|---|---|---|
| Happiness Index (measured by life sat-isfaction, and ranged from 1 (not all satisfied) to 4 (very satisfied) |
Belgium (BE) | 3.125 | 0.105 | 2.905 | 3.140 | 3.320 |
| Denmark (DK) | 3.585 | 0.079 | 3.380 | 3.595 | 3.710 | |
| France (FR) | 2.877 | 0.103 | 2.700 | 2.860 | 3.070 | |
| Ireland (IR) | 3.195 | 0.102 | 2.945 | 3.205 | 3.400 | |
| Italy (IT) | 2.744 | 0.118 | 2.510 | 2.743 | 2.955 | |
| Luxembourg (LU) | 3.305 | 0.070 | 3.070 | 3.310 | 3.450 | |
| Netherlands (NL) | 3.392 | 0.069 | 3.240 | 3.396 | 3.520 | |
| United Kingdom (UK) | 3.182 | 0.086 | 3.030 | 3.150 | 3.390 | |
| Real GDP Per capita (constant 2015 US$1,000) |
Belgium (BE) | 32.882 | 6.908 | 20.997 | 33.090 | 43.107 |
| Denmark (DK) | 44.414 | 8.706 | 28.480 | 45.991 | 57.203 | |
| France (FR) | 30.750 | 5.477 | 20.498 | 31.142 | 38.832 | |
| Ireland (IR) | 36.436 | 18.392 | 14.302 | 34.415 | 79.075 | |
| Italy (IT) | 28.191 | 4.659 | 17.847 | 29.804 | 34.081 | |
| Luxembourg (LU) | 78.945 | 26.048 | 38.730 | 80.082 | 112.418 | |
| Netherlands (NL) | 36.263 | 8.144 | 24.010 | 36.756 | 48.444 | |
| United Kingdom (UK) | 35.452 | 8.236 | 21.578 | 36.288 | 47.492 |
Note: Data were covered over the period from 1975 to 2020.
Fig. 1.
Life Satisfaction and real GDP per capita by countries. Note: BE, DK, FR, IR, IT, LU, NL and UK represent Belgium, Denmark, France, Ireland, Italy, Luxembourg, Netherlands, and United Kingdom, respectively.
3.2. The analyses of the stochastic convergence
Table 2 (Panel A) exhibits the number of structural breaks and their corresponding dates for the log-difference of the happiness index () for each country. The KPSS-PUR test identified various numbers of structural breaks for our selected countries, with three breaks for Luxembourg, six breaks for Belgium, and four breaks for the other countries (i.e., France, Ireland, Italy, Netherlands, and the United Kingdom). Structural breaks around the second oil crisis period (1979–1985) were found for all selected countries except for Luxembourg. The KPSS-PUR test showed structural breaks in the late 1980s and early 1990s (1988–1993) for Belgium, France, Luxembourg and Netherlands. Structural breaks were also revealed for all countries except the United Kingdom from the late 1990s to the early 2000s, corresponding to the period during which European market integration occurred. Structural breaks were also found around the subprime loan (2006–2010) and European debt crises (2015–2016) for all selected countries.
Table 2.
Results for the KPSS-PUR Test (Happiness index).
| Panel A: Structural Breaks | ||||||||||
| Countries | # of Brks | Break 1 | Break 2 | Break 3 | Break 4 | Break 5 | Break 6 | Break 7 | ||
| Belgium (BE) | 6 | 1978 | 1986 | 1990 | 1998 | 2011 | 2015 | |||
| Denmark (DK) | Reference Country | |||||||||
| France (FR) | 4 | 1984 | 1993 | 1998 | 2010 | |||||
| Ireland (IR) | 4 | 1987 | 2003 | 2012 | 2016 | |||||
| Italy (IT) | 4 | 1987 | 2000 | 2007 | 2011 | |||||
| Luxembourg (LU) | 3 | 1991 | 2003 | 2015 | ||||||
| Netherlands (NL) | 4 | 1980 | 1984 | 1988 | 2004 | |||||
| United Kingdom(UK) | 4 | 1985 | 1989 | 1999 | 2015 | |||||
| Panel B: Optimal Frequencyrowhead | ||||||||||
| Frequency Selection | Bootstrap critical values | |||||||||
| Countries |
Hypotheses |
Frequency |
F Statistics |
10% |
5% |
1% |
||||
| Belgium (BE) | H0:ρ1 = ρ2 = 0 | 5 | 26.560*** | 2.860 | 3.821 | 5.913 | ||||
|
Denmark (DK) |
Reference Country |
|||||||||
| France (FR) | H0:ρ1 = ρ2 = 0 | 2 | 31.110*** | 2.632 | 3.518 | 5.600 | ||||
| Ireland (IR) | H0:ρ1 = ρ2 = 0 | 13 | 2.861* | 2.446 | 3.209 | 5.204 | ||||
| Italy (IT) | H0:ρ1 = ρ2 = 0 | 18 | 2.929* | 2.461 | 3.336 | 5.517 | ||||
| Luxembourg (LU) | H0:ρ1 = ρ2 = 0 | 12 | 3.982** | 2.442 | 3.291 | 5.134 | ||||
| Netherlands (NL) | H0:ρ1 = ρ2 = 0 | 14 | 4.420** | 2.465 | 3.335 | 5.233 | ||||
| United Kingdom(UK) | H0:ρ1 = ρ2 = 0 | 13 | 6.924*** | 2.441 | 3.234 | 5.269 | ||||
| Panel C: Cross-sectional Dependence Testrowhead | ||||||||||
| Statistic | P value | |||||||||
| CD Test | 4.509*** | <0.01 | ||||||||
| Panel D: KPSS-PUR Test | ||||||||||
| Cross-section independent |
Bootstrap critical values |
|||||||||
| Panel Stationary Test | Statistics | P values | 10% | 5% | 1% | |||||
| Z(λ) Homogeneous | 15.374 | <0.01 | 28.536 | 33.986 | 46.624 | |||||
| Z(λ) Heterogeneous | 36.684 | <0.01 | 63.034 | 72.000 | 93.662 | |||||
Note: “***”, ”**”, and “*” represent 1%, 5%, and 10% significance levels, respectively. The finite sample critical values are computed using the bootstrap method, replicating samples 10,000 times. The maximal number of breaks and frequencies are fixed at 7, and 20, respectively.
Table 2 (Panel B) displays the results for the model specification test determining whether the nonlinear component () specified in the KPSS-PUR test is suitable for our data. The test started with the selection of the optimal frequency (h*) in the nonlinear component () using the approach outlined by Bai and Perron [42]. The KPSS-PUR test selected various optimal frequencies for our selected countries, with two for France, five for Belgium, twelve for Luxembourg, thirteen for Ireland and the United Kingdom, fourteen for the Netherlands, and eighteen for Italy. The F statistics (used for testing the nonlinear model specification of the KPSS-PUR model) rejected the null hypothesis of specification without nonlinear components ( = = 0) for every country at the 10% (or rigorous) level based on finite-sample critical values. In addition, the CD statistic (used to test for the occurrence of the cross-sectional dependence of the log-difference of the happiness index () among the selected countries) is presented in Table 2 (Panel C). The CD statistic generated was 4.509 with a p value smaller than 1%, providing a significant result in favor of the rejection of the null hypothesis of no cross-sectional dependence of the happiness index log-difference () within these selected countries. Finally, the KPSS-PUR test produced both homogeneous and heterogeneous Z(λ) statistics in accordance with assumptions based on homogeneous and heterogeneous long-run variance in error terms, respectively (see Table 2 (Panel D)). It is crucial to note that the p values produced by both the homogeneous and heterogeneous Z(λ) statistics are biased due to the existence of cross-sectional dependence in our panel data [45]. Therefore, we compared both the homogeneous and heterogeneous Z(λ) statistics with their corresponding finite-sample critical values. Both the homogeneous and heterogeneous Z(λ) statistics were smaller than the 10% bootstrap critical values. These results favor the trend of a stationary log-difference of the happiness index () for selected countries during the period of 1975–2020. In turn, we can conclude that there was a stochastic convergence of the happiness index among these countries.
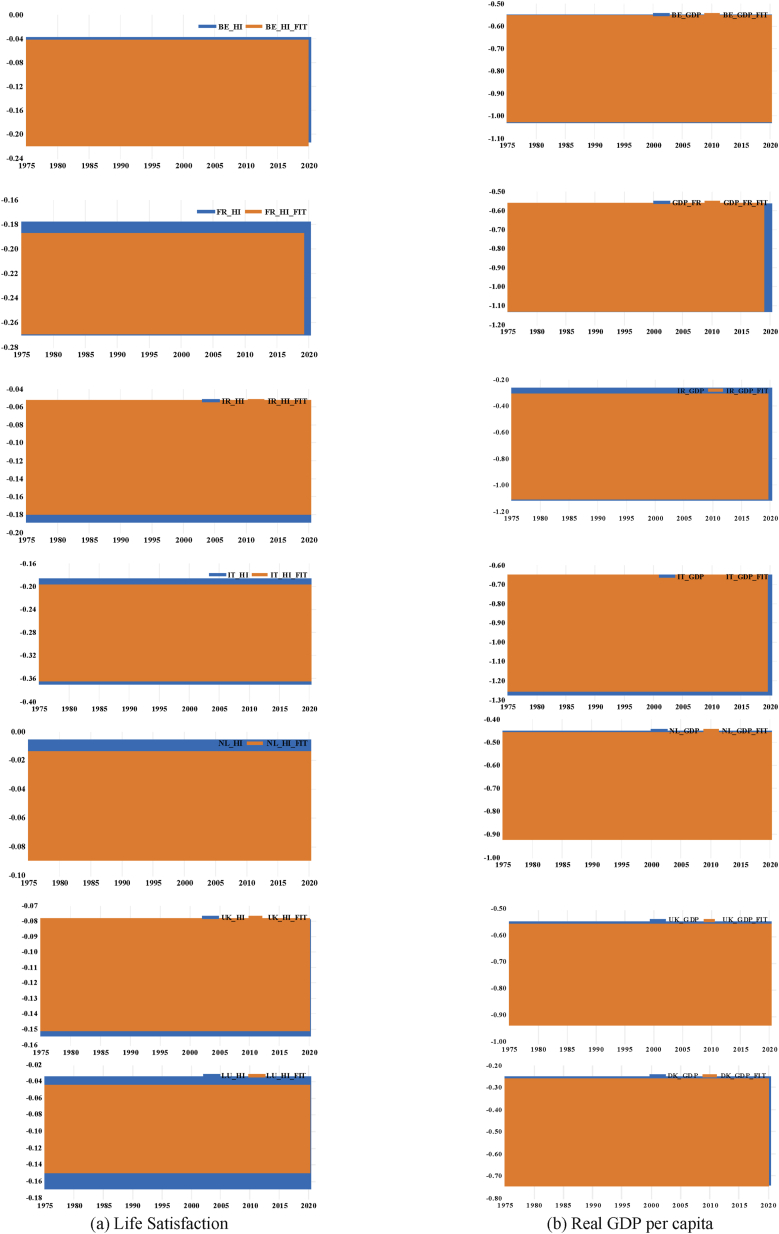
Table 3 exhibits the results for the stochastic convergence of real GDP per capita. All empirical procedures used were consistent with those deployed in the analyses of the stochastic convergence of the happiness index. As indicated in Table 3 (Panel A), the KPSS-PUR test identified six structural breaks for Belgium, Netherlands, Italy, and the United Kingdom, and seven breaks for the other countries (i.e., Denmark, France, and Ireland). Structural breaks during the second oil crisis (1979–1985), the period from the late 1980s to early 1990s (1987–1993), and from the mid-1990s to the early 2000s (1994–2005), as well as during the subprime loan crisis (2006–2010) and European debt crisis (2015–2016) periods were identified for all countries. These structural breaks are consistent with significant economic recessions and the process of European market integration during our study period. As expressed in Table 3 (Panel B), the KPSS-PUR test indicated various optimal frequencies for our selected countries, such as one for Belgium, two for Italy, eight for the United Kingdom, ten for France, Ireland, and Netherlands, and fourteen for Denmark. The F statistics generated from the KPSS-PUR test for all countries were higher than the 10% (or rigorous) finite-sample critical values, and this result indicates that the rejection of the null hypothesis of model specification without the Fourier function is warranted for every country. Additionally, the existence of the cross-sectional dependence of the log-difference of the real GDP per capita () within these selected countries was confirmed because the CD statistic reported in Table 3 (Panel C) produced a p value smaller than 1%, providing evidence in support of the appearance of the cross-sectional dependence of the log-difference of real GDP per capita () among the selected countries. Furthermore, both the homogeneous and the heterogeneous Z(λ) statistics reported in Table 3 (Panel D) were smaller than the 10% bootstrap critical values, and these findings are in support of the trend in stationarity of the log-difference of real GDP per capita () across these selected countries. It follows that the stochastic convergence of real GDP per capita among these selected countries is valid as well. Furthermore, as demonstrated in Fig. 2, the time paths of both the original and fitted series of the log-difference of the happiness index () and real GDP per capita () for each country are quite consistent with many structural changes including striking breaks, linear trends, and smooth transitions over our study period (See Fig. 2(a)–(b) for details). Accordingly, we proved the goodness of fit for the nonlinear specification imposed in the KPSS-PUR test.
Table 3.
Results for the KPSS-PUR Test (Real GDP per capita).
| Panel A: Structural Breaks | ||||||||||
| Countries | # of Brks | Break 1 | Break 2 | Break 3 | Break 4 | Break 5 | Break 6 | Break 7 | ||
| Belgium (BE) | 6 | 1979 | 1985 | 1992 | 1996 | 2006 | 2016 | |||
| Denmark (DK) | 7 | 1984 | 1988 | 1993 | 1997 | 2002 | 2006 | 2016 | ||
| France (FR) | 7 | 1981 | 1985 | 1990 | 1998 | 2006 | 2010 | 2016 | ||
| Ireland (IR) | 7 | 1980 | 1985 | 1993 | 1997 | 2005 | 2009 | 2014 | ||
| Italy (IT) | 6 | 1978 | 1982 | 1987 | 1994 | 1999 | 2010 | |||
| Luxembourg (LU) | Reference Country | |||||||||
| Netherlands (NL) | 6 | 1981 | 1985 | 1990 | 1998 | 2007 | 2016 | |||
| United Kingdom(UK) | 6 | 1982 | 1986 | 1990 | 1998 | 2006 | 2016 | |||
| Panel B: Optimal Frequency | ||||||||||
| Frequency Selection |
Bootstrap critical values |
|||||||||
| Countries |
Hypotheses |
Frequency |
F Statistics |
10% |
5% |
1% |
||||
| Belgium (BE) | H0:ρ1 = ρ2 = 0 | 1 | 20.095*** | 2.768 | 3.739 | 5.947 | ||||
| Denmark (DK) | H0:ρ1 = ρ2 = 0 | 14 | 5.361** | 2.679 | 3.600 | 5.910 | ||||
| France (FR) | H0:ρ1 = ρ2 = 0 | 10 | 13.877*** | 3.131 | 4.205 | 7.154 | ||||
| Ireland (IR) | H0:ρ1 = ρ2 = 0 | 10 | 4.165** | 2.516 | 3.318 | 5.394 | ||||
| Italy (IT) | H0:ρ1 = ρ2 = 0 | 2 | 19.640*** | 2.876 | 3.837 | 6.075 | ||||
| Luxembourg (LU) | Reference Country | |||||||||
| Netherlands (NL) | H0:ρ1 = ρ2 = 0 | 10 | 11.260*** | 2.610 | 3.547 | 5.833 | ||||
| United Kingdom(UK) | H0:ρ1 = ρ2 = 0 | 8 | 3.300* | 2.648 | 3.513 | 5.847 | ||||
| Panel C: Cross-sectional Dependence Test | ||||||||||
| Statistic | P value | |||||||||
| CD Test | 16.565*** | <0.01 | ||||||||
| Panel D: KPSS-PUR Test | ||||||||||
| Cross-section independent |
Bootstrap critical values |
|||||||||
| Panel Stationary Test |
Statistics |
P values |
10% |
5% |
1% |
|||||
| Z(λ) Homogeneous | 6.274 | <0.01 | 7.822 | 8.571 | 9.927 | |||||
| Z(λ) Heterogeneous | 17.425 | <0.01 | 17.945 | 20.704 | 25.962 | |||||
Note: “***”, ”**”, and “*” represent 1%, 5%, and 10% significance levels, respectively. The finite sample critical values are computed using the bootstrap method, replicating samples 10,000 times. The maximal number of breaks and frequencies are fixed at 7, and 20, respectively.
Fig. 2.
The estimated trend function of the KPSS-PUR test for the log-difference of two variables. Note: BE, DK, FR, IR, IT, LU, NL and UK represent Belgium, Denmark, France, Ireland, Italy, Luxembourg, Netherlands, and United Kingdom, respectively. Thick and dot lines represent original series and fitted series of the log-difference of life satisfaction and real GDP per capita.
3.3. The analyses of the β convergence
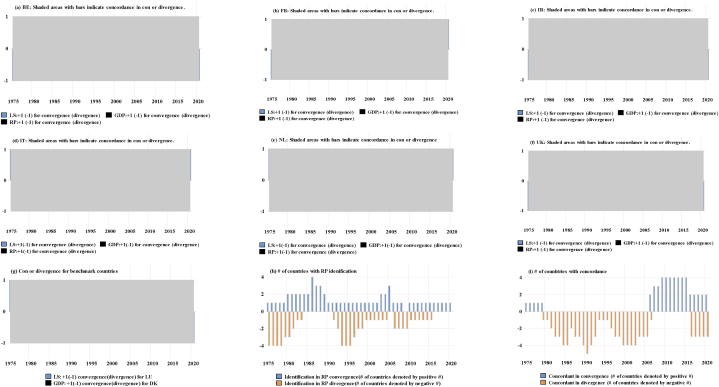
Table 4, Table 5 display the β convergence of the happiness index and real GDP per capita for each country across different regimes under the existence of the stochastic convergence of the happiness index and real GDP per capita among the selected countries, respectively. Since the happiness index in Denmark (serving as the benchmark country for the catch-up effect of happiness) and real GDP per capita in Luxembourg (serving as the benchmark country for the catch-up effect of real GDP per capita) were higher than those in their counterparts over our study period, the signs of the coefficients of the constant term of the trend function (θik) for all countries across different regimes were all negative. It follows that our targeted variables undergo β if the mean effect of the trend function is positive. The notations (referring as to the superscript of the trend function in Table 4, Table 5) were used to indicate β convergence (or divergence), and their definitions were described in Section 2. In order to better interpret results from Table 4, Table 5, the time-varying β convergence (or divergence) of the happiness index and real GDP per capita for selected countries over the period of 1975–2020 were displayed in Fig. 3. In Fig. 3(a)–(g), positive (negative) blue bars and orange-shaded areas represent the periods of β convergence (divergence) of happiness index and real GDP per capita, respectively. In addition, time plots for the β convergence and divergence of the happiness index and real GDP per capita not only assist in defining the dummy variable indicating the exact status (either β convergence or divergence) of residual preference (see green-shaded areas), but they also allow us to determine the periods of concordance of the β convergence and divergence status between the happiness index and real GDP per capita (see orange-shaded areas with bars) and between the happiness index and residual preference (see green-shaded areas with bars). We identified both happiness catch-up towards (away from) Denmark (benchmark country) and income catch-up towards (away from) Luxembourg (benchmark country) in our selected countries across our study period. Fig. 3(h) elucidates the total number of countries for which the precise status of residual preference, namely, either β convergence toward or divergence from Denmark, was determined. Additionally, Fig. 3(i) unveils the concordance in the convergence or divergence status between the happiness index and real GDP per capita for six countries over the period of 1975–2020.
Table 4.
Convergence and divergence classification (Happiness index).
| Belgium (BL) | France (FR) | Ireland (IR) | Italy (IT) | Luxem-bourg (LU) | Netherlands (NL) | United Kingdom (UK) | ||
| Regime 1 | θ1 (t value) | −0.024 (−1.59) | −0.075 (-3.45)*** | −0.047 (-6.63)*** | −0.312 (-44.69)*** | −0.088 (-14.11)*** | −0.070 (-7.31)*** | −0.108 (-25.32)*** |
| γ1 (t value) | −0.016 (-2.79)*** | −0.021 (-6.18)*** | −0.009 (-9.98)*** | 0.005 (5.52)*** | 0.002 (3.81)*** | 0.009 (3.75)*** | −0.001 (−1.54) | |
| Slope (╳10−1) Duration |
−0.021d 1975–1977 |
−0.055D 1975–1983 |
−0.081D 1975–1986 |
0.051C 1975–1986 |
0.027C 1975–1991 |
0.087C 1975–1980 |
−0.012d 1975–1985 |
|
| Regime 2 | θ2 (t value) | −0.042 (-4.14)*** | −0.329 (-15.46)*** | −0.125 (-19.91)*** | −0.202 (-28.94)*** | −0.075 (-9.87)*** | −0.061 (-4.87)*** | −0.138 (-16.91)*** |
| γ2 (t value) | −0.020 (-9.59)*** | 0.006 (2.17)** | 0.001 (1.72)* | −0.004 (-3.98)*** | −0.002 (−1.68) | 0.006 (1.22) | 0.011 (3.59)*** | |
| Slope (╳10−1) Duration |
−0.210D 1978–1985 |
−0.001D 1984–1992 |
−0.003D 1987–2002 |
−0.031D 1987–1999 |
−0.009d 1992–2003 |
0.051c 1981–1984 |
0.080C 1986–1989 |
|
| Regime 3 | θ3 (t value) | −0.174 (-11.49)*** | −0.243 (-16.72)*** | −0.070 (-8.00)*** | −0.197 (-19.63)*** | −0.042 (-5.50)*** | −0.123 (-9.83)*** | −0.136 (-30.33)*** |
| γ3 (t value) | 0.015 (2.74)** | 0.015 (3.79)*** | −0.011 (-6.96)*** | −0.008 (-3.43)*** | −0.006 (-6.19)*** | 0.027 (5.79)*** | −0.001 (−1.29) | |
| Slope (╳10−1) Duration |
0.035C 1986–1989 |
−0.083D 1993–1997 |
0.082C 2003–2011 |
−0.055D 2000–2006 |
−0.057D 2004–2015 |
0.229C 1985–1988 |
0.002c 1990–1999 |
|
| Regime 4 | θ4 (t value) | −0.064 (-6.21)*** | −0.075 (-3.91)*** | −0.206 (-13.77)*** | −0.321 (-22.15)*** | −0.062 (-4.79)*** | −0.045 (-8.43)*** | −0.129 (-37.82)*** |
| γ4 (t value) | −0.021 (-9.93)*** | −0.019 (-6.18)*** | 0.034 (6.18)*** | 0.008 (1.47) | −0.017 (-4.24)*** | −0.002 (-3.65)*** | 0.002 (4.25)*** | |
| Slope (╳10−1) Duration |
−0.140D 1990–1997 |
−0.006D 1998–2009 |
0.2154C 2012–2015 |
0.020c 2007–2010 |
−0.175D 2016–2020 |
−0.006D 1989–2004 |
0.021C 2000–2015 |
|
| Regime 5 | θ5 (t value) | −0.160 (-23.45)*** | −0.342 (-17.69)*** | −0.065 (-4.31)*** | −0.369 (-42.96)*** | −0.056 (-10.40)*** | −0.060 (-8.80)*** | |
| γ5 (t value) | 0.003 (3.14)*** | 0.023 (6.48)*** | −0.017 (-3.06)*** | 0.008 (5.19)*** | 0.0001 (0.24) | −0.015 (-7.10)*** | ||
| Slope (╳10−1) Duration |
−0.023D 1998–2010 |
0.018C 2010–2020 |
−0.074D 2016–2020 |
0.076C 2011–2020 |
0.002c 2005–2020 |
−0.136D 2016–2020 |
||
| Regime 6 | θ6 (t value) | −0.092 (-6.00)*** | ||||||
| γ6 (t value) | −0.030 (-5.30)*** | |||||||
| Slope (╳10−1) Duration |
−0.096D 2011–2014 |
|||||||
| Regime 7 | θ7 (t value) | −0.165 (-12.15)*** | ||||||
| γ7 (t value) | 0.006 (1.45) | |||||||
| Slope (╳10−1) Duration |
−0.068d 2015–2020 |
Note: “***”,”**” and “*” represent 1%, 5% and 10% significance levels, respectively. Bold fonts represent statistical significance at 10% (or rigorous) level. C (D), represents β convergence (divergence) of target variable in the case that both of the coefficients of constant terms () and trends () of each regime are significant and the coefficients of intercepts () and mean effects of the trend function generate different (identical) sign. c (d), represents β convergence (divergence) in the case that either of the coefficients of constant terms () or trends () of each regime is significant and the coefficients of constant terms () and mean effects of the trend function generate different (identical) signs.
Table 5.
Convergence and divergence classification (Real GDP per capita).
| Belgium (BL) | Denmark (DK) | France (FR) | Ireland (IR) | Italy (IT) | Netherlands (NL) | United Kingdom (UK) |
||
| Regime 1 | θ1 (t value) | −0.940 (-16.02)*** | −0.294 (-42.39)*** | −0.634 (-78.19)*** | −1.015 (-67.94)*** | −0.963 (-23.58)*** | −0.459 (-57.94)*** | −0.574 (-49.27)*** |
| γ1 (t value) | 0.018 (2.47)** | 0.003 (2.48)** | 0.008 (4.32)*** | 0.014 (3.63)*** | 0.017 (2.28)** | −0.004 (2.08)** | 0.002 (0.75) | |
| Slope (╳10−1) Duration |
0.037C 1975–1978 |
0.033C 1975–1983 |
0.081C 1975–1980 |
0.130C 1975–1979 |
0.199C 1975–1977 |
−0.042D 1975–1980 |
0.006c 1975–1981 |
|
| Regime 2 | θ2 (t value) | −0.794 (-14.77)*** | −0.217 (-17.46)*** | −0.555 (-44.73)*** | −0.895 (-52.08)*** | −0.891 (-24.45)*** | −0.513 (-42.71)*** | −0.532 (-27.42)*** |
| γ2 (t value) | 0.024 (3.06)*** | −0.046 (-10.06)*** | −0.024 (-5.25)*** | −0.014 (-2.72)** | 0.059 (5.39)*** | −0.012 (-2.64)** | −0.025 (-3.43)*** | |
| Slope (╳10−1) Duration |
−0.138D 1979–1984 |
−0.351D 1984–1987 |
−0.174D 1981–1984 |
−0.090D 1980–1984 |
0.097C 1978–1981 |
−0.105D 1981–1984 |
−0.148D 1982–1985 |
|
| Regime 3 | θ3 (t value) | −0.677 (-13.63)*** | −0.476 (-45.04)*** | −0.704 (-67.95)*** | −1.051 (-83.45)*** | −0.629 (-27.45)*** | −0.610 (-60.61)*** | −0.558 (-28.82)*** |
| γ3 (t value) | 0.009 (1.23) | −0.025 (-7.95)*** | −0.026 (-8.112)*** | −0.005 (-1.95)* | 0.010 (1.35) | −0.029 (-9.58)*** | −0.047 (-6.60)*** | |
| Slope (╳10−1) Duration |
−0.292d 1985–1991 |
−0.262D 1988–1992 |
−0.246D 1985–1989 |
−0.044D 1985–1992 |
−0.214d 1982–1986 |
−0.255D 1985–1990 |
−0.406D 1986–1989 |
|
| Regime 4 | θ4 (t value) | −0.652 (-11.63)*** | −0.574 (-46.14)*** | −0.908 (-119.91)*** | −1.107 (-53.89)*** | −0.546 (-11.82)*** | −0.829 (-112.42)*** | −0.834 (-71.55)*** |
| γ4 (t value) | 0.028 (3.64)*** | 0.012 (2.64)** | −0.004 (-2.71)** | 0.063 (8.27)*** | −0.064 (-8.08)*** | −0.007 (4.642)*** | 0.006 (2.61)** | |
| Slope (╳10−1) Duration |
0.030C 1992–1995 |
0.006C 1993–1996 |
−0.066D 1990–1997 |
0.476C 1993–1996 |
−0.278D 1987–1993 |
0.029C 1991–1998 |
−0.016D 1990–1997 |
|
| Regime 5 | θ5 (t value) | −0.510 (-7.96)*** | −0.558 (-52.79)*** | −0.986 (-130.53)*** | −0.838 (-66.57)*** | −0.952 (-37.70)*** | −0.803 (-116.40)*** | −0.846 (-72.57)*** |
| γ5 (t value) | −0.036 (-5.43)*** | −0.022 (-7.05)*** | −0.012 (-7.96)*** | 0.016 (6.32)*** | −0.053 (-7.94)*** | −0.012 (-9.52)*** | −0.003 (−1.34) | |
| Slope (╳10−1) Duration |
−0.108D 1996–2005 |
−0.152D 1997–2001 |
−0.088D 1998–2005 |
0.211C 1997–2004 |
−0.180D 1994–1998 |
−0.093D 1999–2006 |
−0.024d 1998–2005 |
|
| Regime 6 | θ6 (t value) | −0.921 (-17.57)*** | −0.674 (-54.14)*** | −0.012 (-7.96)*** | −0.669 (-34.00)*** | −1.269 (-39.28)*** | −0.872 (-126.42)*** | −0.948 (-91.48)*** |
| γ6 (t value) | −0.032 (-4.59)*** | −0.001 (−0.20) | −1.114 (-90.01)*** | −0.033 (4.29)*** | 0.024 (3.15)*** | 0.002 (1.48) | 0.009 (5.65)*** | |
| Slope (╳10−1) Duration |
0.074C 2006–2015 |
−0.046d 2002–2005 |
0.003C 2006–2009 |
−0.227D 2005–2008 |
−0.166D 1999–2009 |
0.006c 2007–2015 |
0.079C 2006–2015 |
|
| Regime 7 | θ7 (t value) | −1.218 (-21.33)*** | −0.741 (-106.98)*** | −1.057 (-117.95)*** | −0.860 (-49.90)*** | −0.953 (-20.24)*** | −0.809 (-67.32)*** | −0.786 (-40.51)*** |
| γ7 (t value) | −0.008 (−1.05) | 0.005 (4.70)*** | −0.002 (−0.86) | 0.019 (3.65)** | −0.044 (-5.62)*** | 0.001 (0.14) | −0.023 (-3.28)*** | |
| Slope (╳10−1) Duration |
−0.008d 2016–2020 |
0.046C 2006–2015 |
−0.003d 2010–2015 |
0.100C 2009–2013 |
−0.062D 2010–2020 |
−0.003d 2016–2020 |
−0.156D 2016–2020 |
|
| Regime 8 | θ7 (t value) | −0.655 (-52.64)*** | −0.014 (-82.34)*** | −0.618 (-41.37)*** | ||||
| γ7 (t value) | 0.010 (2.10)** | −0.010 (-2.15)** | 0.055 (14.28)*** | |||||
| Slope (╳10−1) Duration |
0.056C 2016–2020 |
−0.094D 2016–2020 |
0.487C 2014–2020 |
Note: Definitions of all notations used in this Table are the same as those used in Table 4.
Fig. 3.
Contingency Analyses
Note: BE, DK, FR, IR, IT, LU, NL and UK represent Belgium, Denmark, France, Ireland, Italy, Luxembourg, Netherlands, and United Kingdom, respectively.
In order to explore the linkage between the happiness and income catch-up effects, we report the estimated results of the random coefficient logit model in Table 6. We did not apply the conventional fixed and random models for our analyses, because these impose the homogeneous slopes across countries that are inconsistent with the heterogeneous slopes of β convergence analyses derived from the KPSS-PUR test. As indicated in Table 6, the scale parameters corresponding to testing for the validity of the assumptions of the random coefficients of intercept, explanatory variable (YDit, convergence in real GDP per capita), and control variable (RDit, identification of potential β convergence or divergence of the residual preference) were all statistically significant at the 1% level. These model specification tests validate the application of the random coefficient logit model for our analyses. In addition, we found that the income catch-up effect exerted heterogeneous impacts on the happiness catch-up effect among the selected countries. For instants, France and Belgium generated significantly positive and negative effects, respectively, but the rest of countries revealed an insignificant association between the income catch-up and the happiness catch-up effects. Despite the relationship between the convergence of the happiness index and real GDP per capita being ambiguous over our study period, the positive effect dominated the negative effect of income catch-up effect on happiness catch-up. Therefore, the average impact (generated from the group mean of all individual effects) of the income catch-up effect on the average happiness catch-up effect was significantly positive. These results may reconcile the arguments raised by the so-called Easterlin paradox in the literature.
Table 6.
Empirical results for the random coefficient logit model.
| Mean for random parameters | Coefficient | z value |
| Convergence in GDP (Yes = 1) | 0.892 | 3.17*** |
| Heterogeneous slopes for Convergence in GDP | ||
| Belgium (BE) | −5.126 | −6.05*** |
| France (FR) | 6.757 | 6.22*** |
| Ireland (IR) | −0.255 | −0.29 |
| Italy (IT) | 0.269 | 0.62 |
| Netherlands (NL) | −0.579 | −0.96 |
| United Kingdom (UK) |
−0.275 |
−0.37 |
| Mean for random parameters |
Coefficient |
z value |
| Residual Preference (Yes = 1) | −1.989 | −3.90*** |
| Heterogeneous slopes for Residual Preference | ||
| Belgium (BE) | 4.736 | 4.80*** |
| France (FR) | −9.060 | −5.31*** |
| Ireland (IR) | 2.631 | 3.33*** |
| Italy (IT) | −1.062 | −2.18** |
| Netherlands (NL) | 0.962 | 1.69* |
| United Kingdom (UK) |
1.023 |
1.79* |
| Mean for random parameters |
Coefficient |
z value |
| Constant | −1.153 | −4.74*** |
| Heterogeneous Constants | ||
| Belgium (BE) | −3.494 | −5.68*** |
| France (FR) | −3.266 | −4.68*** |
| Ireland (IR) | −2.072 | −3.69*** |
| Italy (IT) | 0.608 | 1.91* |
| Netherlands (NL) | 0.171 | 0.45 |
| United Kingdom (UK) |
0.257 |
0.50 |
| Scale parameters |
Coefficient |
z value |
| σ0 | 1.863 | 6.09*** |
| σ1 | 4.400 | 5.65*** |
| σ2 | 4.575 | 6.32*** |
Note: “***”,”**” and “*” represent 1%, 5% and 10% significance levels, respectively.
4. Discussion
There are two strands of literature focused on the relationship between income and happiness. One strand of happiness literature, termed the Easterlin paradox literature, claims to reveal existence of an insignificant or negative long-run relationship between income and happiness [[1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11],23,38,39]. The other strand of the happiness literature, called the Easterlin illusion literature, has promoted the significantly positive effect of income on happiness [[47], [48], [49]]. The argument arising from these two strands of literature concerns whether income is positively associated with happiness in the long run. It is crucial to point out that an insignificant or negative long-run linkage of income and happiness (as stated in the Easterlin paradox) would not only jeopardize the validity of the idea stemming from microeconomic theory, namely, that there should be a positive income effect on consumer utility, but it also challenges the notion that economic growth can serve as one of the most important macroeconomic goals in the process of economic development. In this study, we applied the concept of β convergence (catch-up effect) established by the economic growth theory [30] in order to reestablish the validity of the positive income effect of happiness underpinned by microeconomic theory and the pursuit of economic growth as an important goal of economic development. Our empirical results yield a number of implications that are deserving of attention and consideration.
4.1. Comparing empirical results with the findings in the existing literature
The existence of the stochastic and β convergence of the happiness index and real GDP per capita, as shown in Table 2, Table 3, Table 4, Table 5, indicates an improvement in happiness status and income level across these countries during our study period because the benchmark countries selected for the analyses exceeded those of the other countries in their value of happiness index and amount of real GDP per capita over our study period. Therefore, countries exhibiting the β convergence of the happiness index and real GDP per capita experienced happiness and income catch-up effects towards their benchmark country during the period of 1975–2020. Our findings, in fact, reconcile the paradox and illusion perspectives of the income–happiness literature through the time-varying patterns of β convergence and the heterogeneous impacts of the income catch-up effect on the happiness catch-up effect [[1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11],23,38,39,[47], [48], [49]]. Evidence from Fig. 3 demonstrates the time-varying patterns of β convergence of the happiness index and real GDP per capita and their convergence (or divergence) over the period of 1975–2020. These time-varying patterns imply the existence of a changing correlation between income and happiness. Additionally, the heterogeneity of the linkage of the income and happiness catch-up effects also exists across our selected countries. It is unsurprising that time-varying and heterogeneous patterns of panel data (such as those revealed in our study) would foster different results and arguments than previous studies in terms of the happiness–income relationship in the field of happiness research [23,38,[48], [49], [50]].
4.2. Practical implication of the empirical results
The results from the CD test, shown in Table 2, Table 3, indicate the presence of cross-sectional dependence of both the happiness index and real GDP per capita within our selected countries. These findings imply that the occurrence of an unanticipated shock (potentially impacting the level of happiness and income) in one country is likely to be conveyed to the other countries due to the Europeanization or globalization process. Evidence for the diffusion of unexpected shocks can be found in the common structural breaks identified among some of the countries in concordance with some specific economic crisis periods (such as the second oil crisis period, 1979–1985, subprime loan crisis period, 2006–2010, and European debt crisis period, 2015–2016), the period during which European market integration proceeded (from the mid-1990s to the early 2000s), and the overlapping periods corresponding to the convergence (or divergence) status of the happiness index and real GDP per capita across the selected countries, as observed in Table 2, Table 3 and Fig. 3. It is crucial to acknowledge that the happiness and income catch-up effects can be regarded as equivalent to the social harmonization process in the long run (due to the usage of data covering a 46-year timespan for our analyses). In contrast to previous studies emphasizing the insignificant correlation between income and happiness in the long run, we argue that the convergence of real GDP per capita serves as an important determinant of the convergence of the happiness index in the long run based on the evidence of the significantly positive linkage between the income catch-up and happiness catch-up effects detected by our analyses of contingency, as seen in Table 6. Given that economic growth is the primary driver behind the catch-up effect of real GDP per capita, our results not only confirm the beneficial effect of economic growth on subject well-being but also validate the essential role of income and economic growth in economic theory.
4.3. Theoretical implications of the research
This research brings to the fore three distinct theoretical implications for the field of happiness studies: First, this study highlights the happiness and income catch-up effects, investigating the relationship between these two effects for the first time. This research goes beyond the analyses of the first moment (average happiness) and second moment (dispersion of happiness) of happiness associated with income. Rather, it concerns the investigation of the beneficial impact of the income catch-up effect on the social harmonization of well-being (i.e., the happiness catch-up effect). Second, we model the time-varying patterns of the β convergence of the happiness index and real GDP per capita and the concordance with their convergence (or divergence) status over the period of 1975–2020. To perform this, we estimate the KPSS-PUR statistics and the random coefficient model. The model specification imposed on the KPSS-PUR test can deal with potential structural changes in the happiness index and real GDP per capita and the cross-sectional dependence among our selected countries during our study period. The random coefficient model allows us to model both mean and individual impacts of the income catch-up effect on the happiness catch-up effect, thus preventing Simpson's Paradox, referring to the fallacy of research that occurs when conclusions drawn from a single homogeneous population, itself comprising heterogeneous populations, contradict those drawn from each heterogeneous population individually [51]. Third, in contrast to previous studies that attempted to resolve the paradox and illusion perspectives of the income–happiness literature through theoretical and empirical analyses of the adaption, social comparison, and aspiration hypotheses, we argue that the empirical results generated when testing for the Easterlin paradox vary during different study periods and across various countries because there is a changing correlation between the income catch-up and happiness catch-up effects over a long period of time and across various countries. The accommodation of structural changes of β convergence and unobserved heterogeneities within our panel data enables us to verify that there is a significant and positive impact of the income catch-up effect on the happiness catch-up effect.
4.4. Limitations and recommendations
Several limitations of this study must be addressed: First, the theoretical concept used to evaluate the level of happiness (or utility) includes income, prices of goods and services, and many other socioeconomic factors (such as demographics, health conditions, and socioeconomic status, etc.). Although factors other than income that influence levels of happiness have been controlled as the residual preference, our analyses are still restricted in the bivariate relationship between income and happiness. Second, the ordinal measure of happiness is recommended by microeconomic theory for the analyses of individual preference. Nevertheless, the unit of analysis employed in this study is the nation, as there is no consistent aggregate time series data available for the ordinal measure of happiness. Consequently, we have to treat the happiness index as the cardinal measure of happiness in concordance with many previous studies [23,37,38]. Third, the happiness index adopted in this study was measured using life satisfaction survey questions, and other standard measures of happiness (or subjective well-being) are not available for us to use to cross-validate our results. Fourth, the data used in the statistical analyses are aggregated data from eight European countries, and this study belongs to a long-run time series analysis describing the trend and convergence of the happiness index and real GDP per capita among our selected countries. Hence, the results generated from this study cannot be used to infer individual behavior in the pursuit of happiness without committing the ecological fallacy of research [52]. Therefore, we recommend that future studies collect individual-level data to delve into the factors influencing individual behavior in the pursuit of happiness or the interactions between income changes and well-being.
5. Conclusions
Many studies have been performed over the preceding decades on the association between income and happiness owing to counter-intuitive findings indicating that happiness is unrelated to economic (or income) growth in the long run [23,37,38]. Following this line of research, the main purpose of this study was to investigate the income–happiness relationship through the concept of β convergence (or catch-up effect), which originated from economic growth theory [30]. To this end, we first employed the sophisticated KPSS-PUR test based on Bahmani-Oskooee, Chang and Wu [36] to reveal the time-varying patterns of convergences of the happiness index and real GDP per capita, and the concordance of convergence (or divergence) between the happiness index and real GDP per capita. Secondly, we estimated the random coefficient logit model to examine the relationship between the happiness catch-up and income catch-up effects.
Our empirical findings indicated that both the happiness index and real GDP per capita in the selected European countries exhibited signs of catching up with their benchmark countries over the period of 1975–2020. Although the relationship between the income and happiness catch-up effects for each individual country was found to be positive (France), negative (Belgium), and insignificant (Ireland, Italy, Netherland, and the United Kingdom), the average income catch-up effect generated from the group mean of all individual effects exerted a significantly positive impact on the average happiness catch-up effect. Since the happiness and income catch-up effects are considered to be equivalent to social harmonization in well-being and income, respectively, the positive association between the happiness catch-up and income effects serves as concrete evidence of the beneficial effect of economic growth on social harmonization of well-being, provided that economic growth is the main force triggering income catch-up.
Funding
This research received no external funding.
Additional information
No additional information is available for this research.
Data availability statement
Data associated with the study are included in this published article.
CRediT authorship contribution statement
Wen-Yi Chen: Writing – review & editing, Writing – original draft, Validation, Methodology, Investigation, Formal analysis, Conceptualization. Lin-Ying Hsu: Writing – original draft, Resources, Project administration, Data curation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors would like to thank the editor of the journal and four anonymous referees for their insightful comments and suggestions that allowed us to improve the quality of this study. A special gratitude goes to Tr. W.W. Liu for her unwavering support throughout the study period. The final proof-reading of the study by Lisa Brutcher (at Washington State University, USA) is deeply acknowledged. All errors are ours. Although this research received no external funding, the Article Processing Charges (APCs) were supported by the Taichung Tzu Chi Hospital, Buddhist Tzu Chi Medical Foundation, Taichung, Taiwan.
Contributor Information
Wen-Yi Chen, Email: chenwen@nutc.edu.tw.
Lin-Ying Hsu, Email: tc1370502@tzuchi.com.tw.
References
- 1.Easterlin R.A. Nations and Households in Economic Growth. Elsevier; 1974. Does economic growth improve the Human Lot? Some empirical evidence; pp. 89–125. [DOI] [Google Scholar]
- 2.Easterlin R.A. Paradox Lost? Review of Behavioral Economics. 2017;4:311–339. doi: 10.1561/105.00000068. [DOI] [Google Scholar]
- 3.Antolini F., Simonetti B. The Easterlin paradox in Italy, or the paradox in measuring? Define happiness before investigating it. Soc Indic Res. 2019;146:263–285. doi: 10.1007/s11205-018-1890-7. [DOI] [Google Scholar]
- 4.Takahashi Y., Fukushima S., Hagiwara R. Determinants of happiness in Japan and The Netherlands: macro and micro analysis and comparison. Asia Pac. Rev. 2018;25:124–150. doi: 10.1080/13439006.2018.1484618. [DOI] [Google Scholar]
- 5.Eren K.A., Aşıcı A.A. The determinants of happiness in Turkey: evidence from city-level data. J. Happiness Stud. 2017;18:647–669. doi: 10.1007/s10902-016-9746-9. [DOI] [Google Scholar]
- 6.Easterlin R.A. Happiness, growth, and public policy. Econ. Inq. 2013;51:1–15. doi: 10.1111/j.1465-7295.2012.00505.x. [DOI] [Google Scholar]
- 7.Lim H.-E., Shaw D., Liao P.-S., Duan H. The effects of income on happiness in east and South Asia: societal values matter? J. Happiness Stud. 2020;21:391–415. doi: 10.1007/s10902-019-00088-9. [DOI] [Google Scholar]
- 8.Li L., Shi L. Economic growth and subjective well-being: analyzing the formative mechanism of Easterlin Paradox. The Journal of Chinese Sociology. 2019;6:1. doi: 10.1186/s40711-018-0090-9. [DOI] [Google Scholar]
- 9.Minkin D., Reyes-García V. Income and wellbeing in a society on the verge to market integration: the case of the Tsimane’ in the Bolivian Amazon. J. Happiness Stud. 2017;18:993–1011. doi: 10.1007/s10902-016-9756-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Easterlin R.A., McVey L.A., Switek M., Sawangfa O., Zweig J.S. The happiness–income paradox revisited. Proc. Natl. Acad. Sci. USA. 2010;107:22463–22468. doi: 10.1073/pnas.1015962107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Opfinger M. The Easterlin paradox worldwide. Appl. Econ. Lett. 2016;23:85–88. doi: 10.1080/13504851.2015.1051650. [DOI] [Google Scholar]
- 12.Brickman P., Campbell D.T. Adaptation Level Theory: A Symposium. Academic Press; 1971. Hedonic relativism and planning the good society; pp. 287–302. [Google Scholar]
- 13.Duesenberry J.S. Harvard University Press; 1949. Income and Saving and the Theory of Consumer Behavior. [Google Scholar]
- 14.Hirschman A.O., Rothschild M. The changing tolerance for income inequality in the course of economic development. Q. J. Econ. 1973;87:544–566. doi: 10.2307/1882024. [DOI] [Google Scholar]
- 15.Wesselbaum D. Happiness over the financial crisis. Oxf. Dev. Stud. 2019;47:113–133. doi: 10.1080/13600818.2018.1524862. [DOI] [Google Scholar]
- 16.Hasan H. Does happiness adapt to increase in income? Evidence from Pakistan socio-economic survey(1988-2001) Pakistan Dev. Rev. 2016;55:113–122. [Google Scholar]
- 17.Latif E. Happiness adaptation to income: evidence from Canada. Econ. Bull. 2015;35:1477–1487. [Google Scholar]
- 18.Davis L. Growth, inequality and tunnel effects: a formal mode. J. Happiness Stud. 2019;20:1103–1119. doi: 10.1007/s10902-018-9991-1. [DOI] [Google Scholar]
- 19.Ifcher J., Zarghamee H., Graham C. Local neighbors as positives, regional neighbors as negatives: competing channels in the relationship between others' income, health, and happiness. J. Health Econ. 2018;57:263–276. doi: 10.1016/j.jhealeco.2017.08.003. [DOI] [PubMed] [Google Scholar]
- 20.Ekici T., Koydemir S. Income expectations and happiness: evidence from British panel data. Applied Research in Quality of Life. 2016;11:539–552. doi: 10.1007/s11482-014-9380-9. [DOI] [Google Scholar]
- 21.Latif E. Happiness and comparison income: evidence from Canada. Soc. Indicat. Res. 2016;128:161–177. doi: 10.1007/s11205-015-1024-4. [DOI] [Google Scholar]
- 22.Schalembier B. The impact of exposure to other countries on life satisfaction: an international application of the relative income hypothesis. Soc. Indicat. Res. 2016;128:221–239. doi: 10.1007/s11205-015-1027-1. [DOI] [Google Scholar]
- 23.Howell R.T., Howell C.J. The relation of economic status to subjective well-being in developing countries: a meta-analysis. Psychol. Bull. 2008;134:536–560. doi: 10.1037/0033-2909.134.4.536. [DOI] [PubMed] [Google Scholar]
- 24.Clark A.E., Flèche S., Senik C. Happiness and Economic Growth. Oxford University Press; 2014. The great happiness moderation; pp. 32–139. [DOI] [Google Scholar]
- 25.Ifcher J., Zarghhamee H. Inequality and Growth: Patterns and Policy. Palgrave Macmillan; 2016. Inequality of happiness: evidence of the compression of the subjective-wellbeing distribution with economic growth; pp. 225–249. [DOI] [Google Scholar]
- 26.Clark A.E., Flèche S., Senik C. Economic growth evens out happiness: evidence from six surveys. Rev. Income Wealth. 2016;62:405–419. doi: 10.1111/roiw.12190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yang J., Liu K., Zhang Y. Happiness inequality in China. J. Happiness Stud. 2019;20:2747–2771. doi: 10.1007/s10902-018-0067-z. [DOI] [Google Scholar]
- 28.Graafland J., Lous B. Income inequality, life satisfaction inequality and trust: a cross country panel analysis. J. Happiness Stud. 2019;20:1717–1737. doi: 10.1007/s10902-018-0021-0. [DOI] [Google Scholar]
- 29.Kollamparambil U. Happiness, happiness inequality and income dynamics in South Africa. J. Happiness Stud. 2020;21:201–222. doi: 10.1007/s10902-019-00075-0. [DOI] [Google Scholar]
- 30.Barro R., Sala-i-Martin X. Massachusetts Institute of Technology Press; 2004. Economic Growth. [Google Scholar]
- 31.Ranjbar O., Chang T., Lee C.-C., Elmi Z.M. Catching-up process in the transition countries. Econ. Change Restruct. 2018;51:249–278. doi: 10.1007/s10644-017-9214-5. [DOI] [Google Scholar]
- 32.Apergis N., Chang T., Christou C., Gupta R. Convergence of health care expenditures across the US states: a reconsideration. Soc Indic Res. 2017;133:303–316. doi: 10.1007/s11205-016-1357-7. [DOI] [Google Scholar]
- 33.Chen W.Y. Does healthcare financing converge? Evidence from eight OECD countries. Int. J. Health Care Finance Econ. 2013;13:279–300. doi: 10.1007/s10754-013-9132-7. [DOI] [PubMed] [Google Scholar]
- 34.Chen W.Y. Do caesarean section rates “catch-up”? Evidence from 14 European countries. Health Care Manag. Sci. 2013;16:328–340. doi: 10.1007/s10729-013-9232-4. [DOI] [PubMed] [Google Scholar]
- 35.Schmitt C., Starke P. Explaining convergence of OECD welfare states: a conditional approach. J. Eur. Soc. Pol. 2011;21:120–135. doi: 10.1177/0958928710395049. [DOI] [Google Scholar]
- 36.Bahmani-Oskooee M., Chang T., Wu T. Revisiting purchasing power parity in African countries: panel stationary test with striking and smooth breaks. Appl. Financ. Econ. 2014;24:1429–1438. doi: 10.1080/09603107.2014.925068. [DOI] [Google Scholar]
- 37.Ferrer‐i‐Carbonell A., Frijters P. How important is methodology for the estimates of the determinants of happiness? Econ. J. 2004;114:641–659. doi: 10.1111/j.1468-0297.2004.00235.x. [DOI] [Google Scholar]
- 38.Ngamaba K.H., Panagioti M., Armitage C.J. Income inequality and subjective well-being: a systematic review and meta-analysis. Qual. Life Res. 2018;27:577–596. doi: 10.1007/s11136-017-1719-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ferrer-i-Carbonell A., Ramos X. Inequality and happiness. J. Econ. Surv. 2014;28:1016–1027. doi: 10.1111/joes.12049. [DOI] [Google Scholar]
- 40.Carlino G.A., Mills L.O. Are U.S. regional incomes converging? A time series analysis. J. Monetary Econ. 1993;32:335–346. doi: 10.1016/0304-3932(93)90009-5. [DOI] [Google Scholar]
- 41.Bernard A.B., Durlauf S.N. Convergence in international output. J. Appl. Econom. 1995;10:97–108. doi: 10.1002/jae.3950100202. [DOI] [Google Scholar]
- 42.Bai J., Perron P. Estimating and testing linear models with multiple structural changes. Econometrica. 1998;66:47–78. doi: 10.2307/2998540. [DOI] [Google Scholar]
- 43.Becker R., Enders W., Lee J. A stationarity test in the presence of an unknown number of smooth breaks. J. Time Anal. 2006;27:381–409. doi: 10.1111/j.1467-9892.2006.00478.x. [DOI] [Google Scholar]
- 44.Pesaran M.H. General diagnostic tests for cross-sectional dependence in panels. Empir. Econ. 2021;60:13–50. doi: 10.1007/s00181-020-01875-7. [DOI] [Google Scholar]
- 45.Lluís Carrion‐i‐Silvestre J., Del Barrio‐Castro T., López‐Bazo E. Breaking the panels: an application to the GDP per capita. Econom. J. 2005;8:159–175. doi: 10.1111/j.1368-423X.2005.00158.x. [DOI] [Google Scholar]
- 46.Greene W.H. Econometric Software, Inc.; 2016. NLOGIT Version 6 Reference Guide. [Google Scholar]
- 47.Muresan G.M., Ciumas C., Achim M.V. Can money buy happiness? evidence for European countries. Applied Research in Quality of Life. 2020;15:953–970. doi: 10.1007/s11482-019-09714-3. [DOI] [Google Scholar]
- 48.Veenhoven R., Vergunst F. The Easterlin illusion: economic growth does go with greater happiness. Int. J. Hydropower Dams. 2014;1:311. doi: 10.1504/IJHD.2014.066115. [DOI] [Google Scholar]
- 49.Hagerty M.R., Veenhoven R. Wealth and happiness revisited-growing national income does go with greater happiness. Soc. Indicat. Res. 2003;64:1–27. doi: 10.1023/A:1024790530822. [DOI] [Google Scholar]
- 50.Easterlin R.A. Feeding the illusion of growth and happiness: a reply to Hagerty and Veenhoven. Soc. Indicat. Res. 2005;74:429–443. doi: 10.1007/s11205-004-6170-z. [DOI] [Google Scholar]
- 51.Simpson E.H. The interpretation of interaction in contingency tables. J. Roy. Stat. Soc. B. 1951;13:238–241. doi: 10.1111/j.2517-6161.1951.tb00088.x. [DOI] [Google Scholar]
- 52.Robinson W.S. Ecological correlations and the behavior of individuals. Am. Socio. Rev. 1950;15:351–357. doi: 10.2307/2087176. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data associated with the study are included in this published article.