Abstract
Molecular qubits offer an attractive basis for quantum information processing, but challenges remain with regard to sustained coherence. Qubits based on clock transitions offer a method to improve the coherence times. We propose a general strategy for identifying molecules with high-frequency clock transitions in systems where a d electron is coupled to a crystal-field singlet state of an f configuration, resulting in an MJ = ±1/2 ground state with strong hyperfine coupling. Using this approach, a 9.834 GHz clock transition was identified in a molecular Pr complex, [K(crypt)][Cp′3PrII], leading to 3-fold enhancements in T2 relative to other transitions in the spectrum. This result indicates the promise of the design principles outlined here for the further development of f-element systems for quantum information applications.
The ability to manipulate coherence in a quantum object enables its use as a quantum bit (“qubit”). This is key to the development of new concepts in quantum information science (QIS), including sensing, communication, and computing.1−9 High-performance systems based on trapped ions10−15 and superconducting qubits16−19 have long coherence times but offer limited scalability and tunability. Recent advances have shown that molecular qubit designs may provide the necessary means for control and functionality, but they are also inherently more coupled to the environment, which tends to diminish performance. Variations of the ligand can provide opportunities to address this shortcoming; however, the principles needed to rationally design new molecular qubits with targeted properties have not been fully developed. Coherence times in molecular qubits can be improved by magnetic dilution20,21 and elimination of atoms with nuclear moments within the molecule.22,23 Limitations to both of these approaches make it desirable to explore alternatives.
Coherence times in electron-spin molecular qubits are improved at avoided energy-level crossings where the dependence of the transition frequency (ν) on the magnetic field (B) vanishes (i.e., dν/dB = 0). As such, the transverse relaxation time (T2) is less sensitive to magnetic noise, engendering resistance to decoherence from nearby magnetic sites24 and other nuclear spins in the molecule.25 Avoided crossings can be generated by nondiagonal perturbations of the spin Hamiltonian such as crystal-field-splitting24 and hyperfine25−27 interactions. For lanthanide systems, hyperfine clock qubits have only been realized with LaII (4f05d1) and LuII (4f145d1)25 centers. These systems have closed f shells, which minimize anisotropy, but this is possible only at the beginning and end of the lanthanide series. There is a significant question of whether coherence enhancements can be realized at hyperfine-derived clock transitions in open-f-shell systems.
Here we provide a framework for identifying clock qubit candidates based on open-shell 4fn5d1 configurations of f elements with even n. Our approach was to identify trivalent 4fn complexes with crystal fields (CFs) that enforce singlet (MJ = 0) ground states (GSs). We hypothesized that reduction to the divalent 4fn5d1 complex would afford an MJ = ±1/2 GS doublet in the MII complex. Open-shell-singlet GSs are well-known in actinide chemistry, with precedent in 5f2, 5f4, and 5f8 systems.28 Equatorial ligand fields provide an additional advantage by promoting occupation of a 5d–6s hybrid orbital,29−38 where d–s hybridization in this singly-occupied molecular orbital increases Fermi contact and induces massive hyperfine couplings,39 bringing clock transitions to higher frequency. Both of these criteria were met by Cp′3PrIII (1) (Cp′ = trimethylsilylcyclopentadienyl), which has a singlet GS, as evidenced in published magnetometry data29 by the limiting value near 0 for χT at low temperatures. These data also indicate a 4f25d1 configuration for divalent [K(crypt)][Cp′3PrII] (2) (crypt = [2.2.2]cryptand). Combined with the large hyperfine coupling40,41 and 100% natural abundance of 141Pr, the Cp′3Pr system is ideal for testing the hypothesis described above.
 |
1 |
While the published magnetometry data for 1 were consistent with a singlet GS, in the C3h pseudosymmetry of the molecule there are in fact three possible singlet states with MJ = 0 and (|+3⟩ ± |−3⟩)/√2, where the latter pair is generated by the B66 component of the CF. Fortuitously, CF modeling of optical data has been reported for 1,42 indicating that the ground state is MJ = 0. We have further confirmed this by fitting43 the reported magnetometry data to the model Hamiltonian in eq 2:
| 2 |
with Zeeman, spin–orbit, and CF terms (see section S2.1 in the Supporting Information for a full discussion). The slight differences in CF parameters relative to those previously reported (Table 1) are most likely due to the more simplistic model used for the present treatment. These parameters afforded the state diagram shown in Figure 1, indicating that the GS of this molecule is |J, MJ⟩ = |4, 0⟩, which is separated from |4, ±1⟩ by 190 cm–1.
Table 1. CF Parameters for 1 and 2 Determined by Fitting Magnetometry Data Reported in Reference (29); The Optical CF Parameters in the First Column Are Taken from Reference (42)a.
| 1 (opt.) | 1 (mag.) | 2b | |
|---|---|---|---|
| B02 | –2485 | –3129(19) | –810(60) |
| B04 | 1323 | 1980(20) | 1230(40) |
| B06 | 555 | 484(11) | 484c |
| B66 | –1956 | –1760(60) | –1760c |
| k | – | 0.98c | 0.98c |
All CF values are in units of cm–1. λ was fixed at 380 cm–1, which is 90% of the optimized free ion value.43
Fit includes an empirical TIP component of 7.4 × 10–4 emu mol–1. The exchange coupling, j, was set to 10,000 cm–1.
Fixed during the fit.
Figure 1.
(top) Best fits of eqs 2 and 3 to the published magnetometry data29 for 1 and 2, respectively. (bottom) Empirical state-energy diagrams for the ground multiplets of 1 (3H4, left) and 2 (4H7/2, right).
We next set out to model the magnetometry for 2 to assess the effect of the d electron on the state ordering. The reduced high-temperature magnetic moment of 2 relative to 1 is consistent with an LS coupling scheme,29,44 and eq 2 may be used to model the magnetometry data for 2 with S = 3/2 and L = 5, affording an MJ = ±1/2 GS of 4H7/2 parentage (see section S2.2 for fit details). However, the CF treatment in this model is unrealistic, as V̂CF operates on all three electrons.
Instead, we elected to model the data by coupling the 4f angular momentum to a second S = 1/2 spin system representing the 5d–6s hybrid electron. This Hamiltonian is shown in eq 3:
| 3 |
where V̂4f indicates the CF term acting only on the 4f electrons and j is a large, positive, isotropic exchange coupling describing the interaction between the 4f and 5d electron spins. This model has the advantage of allowing a direct comparison of 4f CF parameters between 1 and 2. We assumed that the 4f CF was only perturbed by the additional 5dz2 electron, which should impact only the B02 and B04 parameters of the 4f CF Hamiltonian (section S2.3). These parameters and a residual temperature-independent paramagnetism (TIP) were the only parameters allowed to vary from those of 1 (section S2.2). The results of this fit to the magnetometry data for 2 are shown in Figure 1, and the best-fit parameters are shown in Table 1. Crucially, the GS from both models can be assigned as |7/2, ±1/2⟩, consistent with a conserved 4f state ordering relative to 1. The reduction of the B02 and B04 CF parameters and smaller separation between the ground and first excited state (120 cm–1 vs 190 cm–1) indicate that the CF potential felt by the 4f electron is weakened upon addition of the 5d electron. This result is predictable, as the 5d electron itself responds to the ligand field and thus occupies orbitals that generate an antipodal potential with respect to that of the ligands.
Following confirmation of the MJ = ±1/2 GS in 2, we set out to characterize its hyperfine and relaxation behavior using X-band EPR spectroscopy on a magnetically dilute powder of ca. 1% 2 in [K(crypt)][Cp′3YbII] (2Yb), which is diamagnetic due to a 4f14 configuration.30,31 While no spectral features attributable to 2 were observed using continuous-wave (cw) detection, it was possible to collect an echo-detected field-swept (EDFS) spectrum of 2 (Figure 2a). The spectrum was integrated across a range of delay times to suppress distortion due to electron spin echo envelope modulation (ESEEM) from 1H hyperfine coupling.45 This X-band spectrum is highly complex and cannot be immediately attributed to a spin system with pseudoaxial symmetry and hyperfine coupling to a 141Pr nucleus. However, this spectrum could be consistent with 2 in the weak-field limit,39 a possibility that we probed using higher-frequency EPR spectroscopy.
Figure 2.

X-band EPR spectroscopy of 1% 2 in 2Yb at 5 K. (a) EDFS X-band EPR spectrum of 2 (integrated over ca. 1 μs delay times) together with a simulated spectrum based on the parameters in Table 2. (b) Variable-delay EDFS spectra of 2 showing the more rapid decay of spectral components above about 100 mT. (c) Variable-frequency EDFS spectra integrated over 8 μs delays showing a sharp transition at zero field and 9.834 GHz; spectra were mirrored around zero field for clarity. (d) Empirical state energy diagram for the ⊥ orientation of 2 showing allowed transitions at 9.834 GHz in blue. The clock transition is highlighted in red. (e) Primary echo decay curves at various frequencies and fields from 0 to 100 mT together with results of fitting exponential decays to determine T2. A decay at 378 mT is shown for comparison.
The 70 GHz spectrum of an undiluted powder of 2 is shown in Figure 3 together with a simulated spectrum. In contrast to the X-band results, this spectrum is pseudoaxial with a clear hyperfine coupling, enabling the modeling of the g⃡ and A⃡ tensors. Analysis of both X-band and the high-frequency EPR spectra of 2 is based on the effective spin Hamiltonian (SH)46 in eq 4 using a pseudospin (S = 1/2) system coupled to an I = 5/2 nuclear spin:
| 4 |
with electron and nuclear Zeeman contributions and hyperfine terms (see section S5.1).
Figure 3.

Simulation (red) and experimental 70 GHz cw EPR spectrum (blue) of an undiluted powder of 2 at 5 K. The small sharp peak at ca. 2.5 T is a minor g = 2 impurity.
The SH parameters from the 70 GHz spectrum (Table 2) enabled modeling of the X-band spectrum using eq 4. In this case, the spectrum could be modeled using an axial SH, with the g⊥ and A⊥ values near the average of gx,y and Ax,y extracted from the 70 GHz data. The higher apparent symmetry at X-band may be due to the presence of near-neighbor magnetic sites in the concentrated sample, which may be sufficient to desymmetrize the SH. These g values are somewhat different from those predicted for a 4H7/2MJ = ±1/2 GS (g⊥ = 2.67, g∥ = 0.67) but are in good agreement with those predicted by PHI43 using the model based on eq 3 (g⊥ = 2.43, g∥ = 0.81), supporting our assignment of the GS.
Table 2. Parameters from Simulating Multifrequency EPR to a Rhombic (70 GHz) or Axial (9.834 GHz) Pseudospin Hamiltonian and g Values Predicted by the Two Spin Hamiltonians for an MJ = ±1/2 Doublet.
ν or 
|
⊥ | ∥ | ||
|---|---|---|---|---|
| 70a | g | 2.60 | 2.21 | 0.94 |
| A | 4.70a | 3.70a | 0.87a | |
| 9.834a | g | 2.43 | 0.94 | |
| A | 4.33a | 0.87a | ||
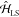 (4H7/2) (4H7/2) |
g | 2.67 | 0.67 | |
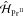 |
g | 2.42 | 0.81 | |
In GHz.
The state energy versus magnetic field diagram from this model (Figure 2d) has an avoided energy level crossing generated by a nondiagonal term in the hyperfine coupling with a transition frequency of 9.834 GHz in the perpendicular orientation at low magnetic fields. Variable-frequency EPR spectroscopy shows a dramatic enhancement in signal intensity at 0 mT and 9.834 GHz (Figure 2c), and the primary echo decay shows no evidence of ESEEM. Both of these observations are consistent with a clock transition,47 although the vanishing 1H Larmor frequency at zero field may also contribute to the lack of ESEEM. Intriguingly, all of the features in the range of 0–100 mT have decay constants in the range of 2–3 μs, while the higher-field transitions, which arise from Zeeman splitting, have T2 times closer to 1 μs (Figure 2b,e). The longest relaxation times do not occur precisely at the zero-field clock transition but rather were observed slightly away at 9.850 GHz and 36 mT (T2 = 2.94 μs).
The origin of the T2 enhancement over this wide field range can be explained by the nearly field-independent nature of the state energy of the two |F, MF⟩ states involved in the relevant transitions (F = J + I is the combined electronic and nuclear angular momentum). In this range, a number of the parent |MJ, MI⟩ states sequentially approach one another in energy, and mixing between them to form the final |F, MF⟩ states at low field leads to the extended weak dependence of the state energy on the field. These transitions invariably relax slower than those at higher fields (by a factor of 2–3), consistent with a clocklike enhancement of the relaxation due to the weak dependence of the frequency on the field. We additionally note that the T1 (longitudinal) relaxation times determined for 2 were also ca. 3 μs at 5 K (Figure S4), which may limit the degree to which T2 can be enhanced at the clock transition.
The combined magnetometry and EPR results presented above support the fundamental hypothesis that coupling of an open-shell-singlet 4f configuration to an electron in an s–d hybrid orbital results in an MJ = ±1/2 doublet, with large hyperfine couplings that give rise to high-frequency clock transitions with longer T2 relaxations. This was accomplished by enforcing a low-anisotropy 4f configuration, enabling performance that is normally possible only with the closed-4f-shell configurations at either end of the lanthanide series. Future work will focus on using these design principles to target new molecular hyperfine qubits based on lanthanide and actinide centers with both f and d electrons.
Acknowledgments
This work was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Chemical Sciences, Biosciences, and Geosciences Division at Lawrence Berkeley National Laboratory under Contract DE-AC02-05CH11231. Work performed at the National High Magnetic Field Laboratory was supported by the U.S. National Science Foundation (DMR-2128556) and the State of Florida. W.J.E. thanks the U.S. National Science Foundation under CHE-2154255 and the Eddleman Quantum Institute for support.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c12725.
The authors declare no competing financial interest.
Supplementary Material
References
- Chuang I. L.; Yamamoto Y. Simple quantum computer. Phys. Rev. A 1995, 52, 3489. 10.1103/PhysRevA.52.3489. [DOI] [PubMed] [Google Scholar]
- Schliemann J.; Khaetskii A. V.; Loss D. Spin decay and quantum parallelism. Phys. Rev. B 2002, 66, 245303. 10.1103/PhysRevB.66.245303. [DOI] [Google Scholar]
- Arute F.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. 10.1038/s41586-019-1666-5. [DOI] [PubMed] [Google Scholar]
- Huang H. Y.; Broughton M.; Cotler J.; Chen S.; Li J.; Mohseni M.; Neven H.; Babbush R.; Kueng R.; Preskill J.; McClean J. R. Quantum advantage in learning from experiments. Science 2022, 376, 1182–1186. 10.1126/science.abn7293. [DOI] [PubMed] [Google Scholar]
- Bennett C. H.; Brassard G.; Ekert A. K. Quantum cryptography. Sci. Am. 1992, 267, 50–57. 10.1038/scientificamerican1092-50. [DOI] [Google Scholar]
- Gisin N.; Ribordy G.; Tittel W.; Zbinden H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. 10.1103/RevModPhys.74.145. [DOI] [Google Scholar]
- Perdomo-Ortiz A.; Dickson N.; Drew-Brook M.; Rose G.; Aspuru-Guzik A. Finding low-energy conformations of lattice protein models by quantum annealing. Sci. Rep. 2012, 2, 571. 10.1038/srep00571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershenfeld N.; Chuang I. L. Quantum Computing with Molecules. Sci. Am. 1998, 278, 66–71. 10.1038/scientificamerican0698-66.9418300 [DOI] [Google Scholar]
- Grover L. K.A fast quantum mechanical algorithm for database search. In Proceedings of the 28th Annual ACM Symposium on Theory of Computing, Philadelphia, PA, May 22–24, 1996; ACM, 1996; pp 212–219.
- Cirac J. I.; Zoller P. Quantum Computations with Cold Trapped Ions. Phys. Rev. Lett. 1995, 74, 4091–4094. 10.1103/PhysRevLett.74.4091. [DOI] [PubMed] [Google Scholar]
- Monroe C.; Kim J. Scaling the ion trap quantum processor. Science 2013, 339, 1164–1169. 10.1126/science.1231298. [DOI] [PubMed] [Google Scholar]
- Wang P.; Luan C. Y.; Qiao M.; Um M.; Zhang J.; Wang Y.; Yuan X.; Gu M.; Zhang J.; Kim K. Single ion qubit with estimated coherence time exceeding one hour. Nat. Commun. 2021, 12, 233. 10.1038/s41467-020-20330-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivas R.; Löschnauer C. M.; Malinowski M.; Hughes A. C.; Nourshargh R.; Negnevitsky V.; Allcock D. T. C.; King S. A.; Matthiesen C.; Harty T. P.; Ballance C. J. Coherent Control of Trapped Ion Qubits with Localized Electric Fields. Phys. Rev. Lett. 2023, 131, 020601. 10.1103/PhysRevLett.131.020601. [DOI] [PubMed] [Google Scholar]
- Maksymov A.; Nguyen J.; Chaplin V.; Nam Y.; Markov I. L.. Detecting Qubit-Coupling Faults in Ion-Trap Quantum Computers. In 2022 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Korea, April 2–6, 2022; IEEE, 2022; pp 387–399.
- Akhtar M.; Bonus F.; Lebrun-Gallagher F. R.; Johnson N. I.; Siegele-Brown M.; Hong S.; Hile S. J.; Kulmiya S. A.; Weidt S.; Hensinger W. K. A high-fidelity quantum matter-link between ion-trap microchip modules. Nat. Commun. 2023, 14, 531. 10.1038/s41467-022-35285-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed M. D.; DiCarlo L.; Nigg S. E.; Sun L.; Frunzio L.; Girvin S. M.; Schoelkopf R. J. Realization of three-qubit quantum error correction with superconducting circuits. Nature 2012, 482, 382–385. 10.1038/nature10786. [DOI] [PubMed] [Google Scholar]
- Devoret M. H.; Schoelkopf R. J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. 10.1126/science.1231930. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Pagano G.; Hess P. W.; Kyprianidis A.; Becker P.; Kaplan H.; Gorshkov A. V.; Gong Z.-X.; Monroe C. Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 2017, 551, 601–604. 10.1038/nature24654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.; Eddins A.; Anand S.; Wei K. X.; van den Berg E.; Rosenblatt S.; Nayfeh H.; Wu Y.; Zaletel M.; Temme K.; Kandala A. Evidence for the utility of quantum computing before fault tolerance. Nature 2023, 618, 500–505. 10.1038/s41586-023-06096-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu C.-J.; von Kugelgen S.; Krzyaniak M. D.; Ji W.; Dichtel W. R.; Wasielewski M. R.; Freedman D. E. Spin and Phonon Design in Modular Arrays of Molecular Qubits. Chem. Mater. 2020, 32, 10200–10206. 10.1021/acs.chemmater.0c03718. [DOI] [Google Scholar]
- Bader K.; Dengler D.; Lenz S.; Endeward B.; Jiang S.-D.; Neugebauer P.; van Slageren J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. 10.1038/ncomms6304. [DOI] [PubMed] [Google Scholar]
- Graham M. J.; Yu C.-J.; Krzyaniak M. D.; Wasielewski M. R.; Freedman D. E. Synthetic Approach To Determine the Effect of Nuclear Spin Distance on Electronic Spin Decoherence. J. Am. Chem. Soc. 2017, 139, 3196–3201. 10.1021/jacs.6b13030. [DOI] [PubMed] [Google Scholar]; PMID: 28145700.
- Zadrozny J. M.; Niklas J.; Poluektov O. G.; Freedman D. E. Millisecond coherence time in a tunable molecular electronic spin qubit. ACS Cent. Sci. 2015, 1, 488–492. 10.1021/acscentsci.5b00338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiddiq M.; Komijani D.; Duan Y.; Gaita-Ariño A.; Coronado E.; Hill S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. 10.1038/nature16984. [DOI] [PubMed] [Google Scholar]
- Kundu K.; White J. R.; Moehring S. A.; Yu J. M.; Ziller J. W.; Furche F.; Evans W. J.; Hill S. A 9.2-GHz clock transition in a Lu(II) molecular spin qubit arising from a 3,467-MHz hyperfine interaction. Nat. Chem. 2022, 14, 392–397. 10.1038/s41557-022-00894-4. [DOI] [PubMed] [Google Scholar]
- Wolfowicz G.; Tyryshkin A. M.; George R. E.; Riemann H.; Abrosimov N. V.; Becker P.; Pohl H.-J.; Thewalt M. L. W.; Lyon S. A.; Morton J. J. L. Atomic clock transitions in silicon-based spin qubits. Nat. Nanotechnol. 2013, 8, 561–564. 10.1038/nnano.2013.117. [DOI] [PubMed] [Google Scholar]
- Zadrozny J. M.; Gallagher A. T.; Harris T. D.; Freedman D. E. A Porous Array of Clock Qubits. J. Am. Chem. Soc. 2017, 139, 7089–7094. 10.1021/jacs.7b03123. [DOI] [PubMed] [Google Scholar]
- Edelstein N. M.; Lander G. H. In The Chemistry of the Actinide and Transactinide Elements; Morss L. R., Edelstein N. M., Fuger J., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp 2225–2306. [Google Scholar]
- Meihaus K. R.; Fieser M. E.; Corbey J. F.; Evans W. J.; Long J. R. Record High Single-Ion Magnetic Moments Through 4fn5d1 Electron Configurations in the Divalent Lanthanide Complexes [(C5H4SiMe3)3Ln]−. J. Am. Chem. Soc. 2015, 137, 9855–9860. 10.1021/jacs.5b03710. [DOI] [PubMed] [Google Scholar]
- MacDonald M. R.; Bates J. E.; Ziller J. W.; Furche F.; Evans W. J. Completing the Series of + 2 Ions for the Lanthanide Elements: Synthesis of Molecular Complexes of Pr2+, Gd2+, Tb2+, and Lu2+. J. Am. Chem. Soc. 2013, 135, 9857–9868. 10.1021/ja403753j. [DOI] [PubMed] [Google Scholar]
- Fieser M. E.; MacDonald M. R.; Krull B. T.; Bates J. E.; Ziller J. W.; Furche F.; Evans W. J. Structural, spectroscopic, and theoretical comparison of traditional vs recently discovered Ln2+ ions in the [K(2.2.2-cryptand)][(C5H4SiMe3)3Ln] complexes: The variable nature of Dy2+ and Nd2+. J. Am. Chem. Soc. 2015, 137, 369–382. 10.1021/ja510831n. [DOI] [PubMed] [Google Scholar]
- Windorff C. J.; MacDonald M. R.; Meihaus K. R.; Ziller J. W.; Long J. R.; Evans W. J. Expanding the Chemistry of Molecular U2+ Complexes: Synthesis, Characterization, and Reactivity of the {[C5H3(SiMe3)2]3U}− Anion. Chem. - Eur. J. 2016, 22, 772–782. 10.1002/chem.201503583. [DOI] [PubMed] [Google Scholar]
- Fieser M. E.; et al. Evaluating the electronic structure of formal LnII ions in LnII(C5H4SiMe3)31– using XANES spectroscopy and DFT calculations. Chem. Sci. 2017, 8, 6076–6091. 10.1039/C7SC00825B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fieser M. E.; Palumbo C. T.; La Pierre H. S.; Halter D. P.; Voora V. K.; Ziller J. W.; Furche F.; Meyer K.; Evans W. J. Comparisons of lanthanide/actinide +2 ions in a tris(aryloxide)arene coordination environment. Chem. Sci. 2017, 8, 7424–7433. 10.1039/C7SC02337E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su J.; Windorff C. J.; Batista E. R.; Evans W. J.; Gaunt A. J.; Janicke M. T.; Kozimor S. A.; Scott B. L.; Woen D. H.; Yang P. Identification of the Formal +2 Oxidation State of Neptunium: Synthesis and Structural Characterization of {NpII[C5H3(SiMe3)2]3}1–. J. Am. Chem. Soc. 2018, 140, 7425–7428. 10.1021/jacs.8b03907. [DOI] [PubMed] [Google Scholar]
- Ryan A. J.; Darago L. E.; Balasubramani S. G.; Chen G. P.; Ziller J. W.; Furche F.; Long J. R.; Evans W. J. Synthesis, Structure, and Magnetism of Tris(amide) [Ln{N(SiMe3)2}3]1– Complexes of the Non-traditional + 2 Lanthanide Ions. Chem. - Eur. J. 2018, 24, 7702–7709. 10.1002/chem.201800610. [DOI] [PubMed] [Google Scholar]
- Fang M.; Lee D. S.; Ziller J. W.; Doedens R. J.; Bates J. E.; Furche F.; Evans W. J. Synthesis of the (N2)3– Radical from Y2+ and Its Protonolysis Reactivity To Form (N2H2)2– via the Y[N(SiMe3)2]3/KC8 Reduction System. J. Am. Chem. Soc. 2011, 133, 3784–3787. 10.1021/ja1116827. [DOI] [PubMed] [Google Scholar]
- Woen D. H.; Chen G. P.; Ziller J. W.; Boyle T. J.; Furche F.; Evans W. J. Solution Synthesis, Structure, and CO2 Reduction Reactivity of a Scandium(II) Complex, {Sc[N(SiMe3)2]3}−. Angew. Chem. 2017, 129, 2082–2085. 10.1002/ange.201611758. [DOI] [PubMed] [Google Scholar]
- Abragam A.; Bleaney B.. Electron Paramagnetic Resonance of Transition Ions; Clarendon Press: Oxford, U.K., 1970. [Google Scholar]
- Bleaney B. Hyperfine Interactions in Rare-Earth Metals. J. Appl. Phys. 1963, 34, 1024–1031. 10.1063/1.1729355. [DOI] [Google Scholar]
- Morton J.; Preston K. Atomic parameters for paramagnetic resonance data. J. Magn. Reson. (1969) 1978, 30, 577–582. 10.1016/0022-2364(78)90284-6. [DOI] [Google Scholar]
- Jank S; Reddmann H; Amberger H.-D. The electronic structure of organometallic complexes of the f elements: XL. Crystal field strength of η5-cyclopentadienyl ligand estimated on the basis of the crystal field parameters of (Me3SiC5H4)3PrIII. J. Alloys Compd. 1997, 250, 387–390. 10.1016/S0925-8388(96)02554-6. [DOI] [Google Scholar]
- Chilton N. F.; Anderson R. P.; Turner L. D.; Soncini A.; Murray K. S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. 10.1002/jcc.23234. [DOI] [PubMed] [Google Scholar]
- Anderson D. M.; Cloke F. G. N.; Cox P. A.; Edelstein N.; Green J. C.; Pang T.; Sameh A. A.; Shalimoff G. On the stability and bonding in bis(η-arene)ianthanide complexes. J. Chem. Soc., Chem. Commun. 1989, 53–55. 10.1039/C39890000053. [DOI] [Google Scholar]
- Rowan L. G.; Hahn E. L.; Mims W. B. Electron-Spin-Echo Envelope Modulation. Phys. Rev. 1965, 137, A61. 10.1103/PhysRev.137.A61. [DOI] [Google Scholar]
- Stoll S.; Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- Kundu K.; Chen J.; Hoffman S.; Marbey J.; Komijani D.; Duan Y.; Gaita-Ariño A.; Stanton J.; Zhang X.; Cheng H.-P.; Hill S. Electron-nuclear decoupling at a spin clock transition. Commun. Phys. 2023, 6, 38. 10.1038/s42005-023-01152-w. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




