Systematic evaluation of MRI-based characterization of tumor-associated vascular morphology and hemodynamics via a dynamic digital phantom

Abstract.

Purpose

Validation of quantitative imaging biomarkers is a challenging task, due to the difficulty in measuring the ground truth of the target biological process. A digital phantom-based framework is established to systematically validate the quantitative characterization of tumor-associated vascular morphology and hemodynamics based on dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI).

Approach

A digital phantom is employed to provide a ground-truth vascular system within which 45 synthetic tumors are simulated. Morphological analysis is performed on high-spatial resolution DCE-MRI data (spatial/temporal resolution = 30 to $300\mu \mathrm{m}/60\mathrm{s}$) to determine the accuracy of locating the arterial inputs of tumor-associated vessels (TAVs). Hemodynamic analysis is then performed on the combination of high-spatial resolution and high-temporal resolution (spatial/temporal resolution = 60 to $300\mu \mathrm{m}/1$ to 10 s) DCE-MRI data, determining the accuracy of estimating tumor-associated blood pressure, vascular extraction rate, interstitial pressure, and interstitial flow velocity.

Results

The observed effects of acquisition settings demonstrate that, when optimizing the DCE-MRI protocol for the morphological analysis, increasing the spatial resolution is helpful but not necessary, as the location and arterial input of TAVs can be recovered with high accuracy even with the lowest investigated spatial resolution. When optimizing the DCE-MRI protocol for hemodynamic analysis, increasing the spatial resolution of the images used for vessel segmentation is essential, and the spatial and temporal resolutions of the images used for the kinetic parameter fitting require simultaneous optimization.

Conclusion

An in silico validation framework was generated to systematically quantify the effects of image acquisition settings on the ability to accurately estimate tumor-associated characteristics.

1. Introduction

Tumor-induced vascularization is one of the fundamental hallmarks of cancer.¹ It is central to tumor expansion as it provides direct access to nutrients and oxygen, as well as tumor control as it provides delivery of systemically administered therapies.² Blood vessels associated with tumors differ from normal vessels in both their structural and functional properties; in particular, tumor-related vasculature is typically irregular, dilated, tortuous, and leaky, which leads to irregular blood flow patterns and abnormal interstitial environments.^1,3,4 Thus, given their central roles in tumor development and response to therapy, both the morphology and function of tumor associated vessels (TAVs) are natural sources of biomarkers for cancer diagnosis and prognosis, as well as targets for cancer treatment.^5–7

Imaging biomarkers quantitatively reporting on vascular characteristics have long been studied with the goal of improving both diagnostic and prognostic capabilities.^2,8–13 For example, maximum intensity projections of dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) data have revealed increased vascularity in breast tumors compared to the contralateral healthy breast,^14–18 as well as a strong association between the presence of vessels adjacent to a malignant tumor.^19–21 A recent study identified TAVs in 3D from DCE-MRI and further supported its use for improving the diagnostic specificity of breast cancer.²² Beyond morphology, many imaging efforts have been devoted to characterizing the hemodynamics associated with blood flow through tumor vasculature. Quantitative and semi-quantitative analyses of DCE-MRI can return estimates of the plasma volume fraction, extracellular extravascular volume fraction, vessel permeability, and perfusion.^2,9 Furthermore, we have recently developed a technique that enables the extraction of both morphological and hemodynamic features of tumor-associated vasculature, potentially increasing the diagnostic accuracy of suspicious tumors.²³

Validation of imaging-based characterization of tumor-associated vascular properties is a challenging task (as it is for many imaging biomarkers). Unlike the biomarkers derived from tissue samples, measurements from non-invasive, clinical imaging techniques provide only indirect characterization of the target biological process. Thus, conventional methods of validating biomarkers may not be appropriate for imaging measures. Comparing in vivo and ex vivo images is extremely challenging because of deformation that can happen during the tissue fixation process, let alone the fact that many in vivo dynamic quantities are hard to measure with ex vivo experiments.^24,25 Radioactive microspheres,²⁶ Doppler flowmetry,²⁷ or implanted probes^28,29 have been used to measure dynamic vascular features (e.g., pressure and flow) in vivo, but their utility is limited by their invasive character. Recent efforts also developed multi-contrast optical imaging systems to quantitatively characterize hemodynamics in microvasculature.³⁰ However, these optical imaging techniques are limited by the complexity of assembling such systems, as well as their limited depth of tissue penetration.

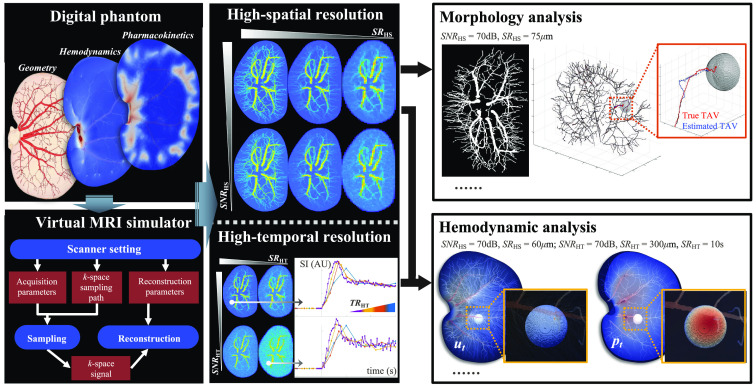
An alternative strategy for validating imaging biomarkers is to use physical or digital phantoms, which can provide tunable ground-truth values of properties or processes of interest.³¹ For example, we have recently developed an in silico validation framework to virtually generate DCE-MRI data.³² This framework consists of (1) a digital phantom that provides detailed, realistic vascular structure, tissue properties, perfusion, and time-resolved contrast agent delivery of a murine kidney, and (2) a virtual MR scanner³³ to produce realistic DCE-MRI data based on the digital phantom under various (user-defined) acquisition settings including spatial resolution, temporal resolution, and signal-to-noise ratio (SNR). This digital-phantom-based validation framework provides a unique opportunity to validate methods employing DCE-MRI data to characterize both tumor-associated vascular morphology and hemodynamics. In this contribution, we employ the digital phantom to generate ground-truth (virtual) DCE-MRI data for systematically evaluating the accuracy of our tumor-associated vascular morphology and hemodynamics analysis^22,23 over a range of image acquisition settings (Fig. 1). This allows for rigorously determining realistic acquisition settings, which balance the demands of the analyses with what is experimentally feasible, thereby enabling the image processing techniques to be widely available for applications in oncology.

Fig. 1.

Overview of the virtual validation framework. The “digital phantom” and “virtual MRI simulator” were used to generate virtual DCE-MRI data with two protocols: “high-spatial resolution” and “high-temporal resolution” imaging. The high-spatial resolution imaging sets were generated with a range of two acquisition parameters: spatial resolution ($S{R}_{\mathrm{HS}}$) and SNR ($SN{R}_{\mathrm{HS}}$). The high-temporal resolution imaging sets were generated with a range of three parameters: spatial resolution ($S{R}_{\mathrm{HT}}$), temporal resolution ($T{R}_{\mathrm{HT}}$), and SNR ($SN{R}_{\mathrm{HT}}$). “Morphological analysis” was performed on the high-spatial resolution imaging sets to determine the accuracy of locating the arterial inputs of TAV. “Hemodynamic analysis” was then performed on the combination of high-spatial and high-temporal resolution imaging sets to determine the accuracy of estimating tumor-associated hemodynamic characteristics [interstitial pressure ($p_t$), interstitial flow velocity (${\mathbf{u}}_t$), etc.]. The goal of this framework is to systematically quantify the effects of image acquisition parameters on the ability to accurately estimate tumor-associated characteristics.

2. Methods

2.1. Digital Vascular Phantom

A digital phantom developed in our previous study³² was used to realize a ground-truth vascular system. Briefly, the generation of the geometric model is based on the MR histology data of excised rat kidneys published by Xie et al.³⁴ The kidney volume is segmented by applying a $k$-means clustering algorithm on the $T_1$-weighted images. The vasculature is extracted by applying a semi-automatic algorithm on the $T_2^{*}$-weighted images. In particular, the algorithm is initialized with a manually identified starting point within the renal artery, from which vessel centerlines are automatically tracked to determine the local vascular radius and orientation along the main trunk. Manually selected branching points are identified along the main trunk, and the algorithm is repeated along these branches to identify subsequent generations of vascular branches. The final result is the hierarchical, tree-like structure of vasculature.

Note that while the phantom is based on the anatomy of a rat kidney, it was designed to serve as a general vascular phantom. This geometry was chosen because it provides a clear, representative, and realistic visualization of a hierarchical vascular network (i.e., from input arteries to small arterioles). Such a geometry is essential for achieving detailed simulations of blood flow and interstitial transportation. To the best of our knowledge there is no three-dimensional characterization of a vascular tree that depicts the branching patterns throughout space in such detail as this ex vivo MRI³⁴ data set.

2.2. Virtual DCE-MRI Generation

Using the in silico validation framework,³² virtual DCE-MRI data were generated with two protocols to mimic two separate clinical acquisition scenarios: a conventional acquisition, which seeks to achieve high-spatial resolution (and only modest temporal resolution), and an ultra-fast acquisition, which seeks to achieve high-temporal resolution (and only modest spatial resolution). High-spatial resolution images can reveal detailed anatomy of enhanced tissues; conversely, high-temporal resolution images can reveal detailed kinetics of the wash-in and wash-out of contrast agents.

We perform morphological analysis on high-spatial resolution images²² and perform hemodynamic analysis on the combination of high-spatial resolution images and high-temporal resolution images.²³ In particular, high-spatial resolution DCE-MRI data sets are generated with a range of spatial resolution ($S{R}_{\mathrm{HS}}$) and SNR ($SN{R}_{\mathrm{HS}}$); see Table 1 for all combinations. (We note that the range of candidate spatial resolutions is chosen to match the size of investigated vessels in the digital phantom derived from a rat kidney.³¹ If used for validating and optimizing parameters for human imaging, the digital phantom needs to be modified and the range of candidate spatial resolutions can be changed correspondingly; see Sec. 4 for more exposition on this important point). Each high-spatial resolution scan consists of one pre- and one post-contrast image, each acquired with a temporal resolution of 1 min. The high-temporal resolution DCE-MRI data sets are generated with a range of spatial resolution (${SR}_{\mathrm{HT}}$), temporal resolution ($T{R}_{\mathrm{HT}}$), and SNR ($SN{R}_{\mathrm{HT}}$); see Table 1 for all combinations. Each high-temporal resolution scan consists of five pre- and multiple post-contrast images acquired for 1 min, with various temporal resolutions from 1 to 10 s. These data are used to evaluate the tumor-associated hemodynamic analysis based on our imaging-based computational fluid dynamics model.²³

Table 1.

Control of acquisition parameters.

Entity			Symbol	Measure
Acquisition parameters	High spatial resolution	Spatial resolution	$S{R}_{\mathrm{HS}}$	30, 45, 60, 75, 90, 120, 150, 180, 210, 240, 270, $300\mu \mathrm{m}$
		Signal-to-noise ratio	$SN{R}_{\mathrm{HS}}$	5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70 dB
	High temporal resolution	Spatial resolution	${SR}_{\mathrm{HT}}$	when $S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$	60, 150, $300\mu \mathrm{m}$
				when $S{R}_{\mathrm{HS}}=150\mu \mathrm{m}$	150, $300\mu \mathrm{m}$
				when $S{R}_{\mathrm{HS}}=300\mu \mathrm{m}$	$300\mu \mathrm{m}$
		Temporal resolution	$T{R}_{\mathrm{HT}}$	1, 4, 7, 10 s
		Signal-to-noise ratio	$SN{R}_{\mathrm{HT}}$	5, 15, 70 dB

For evaluation of the morphological analysis, 168 combinations of $S{R}_{\mathrm{HS}}$ (12 values) and $SN{R}_{\mathrm{HS}}$ (14 values) are used. For evaluation of the hemodynamic analysis, 72 combinations of $S{R}_{\mathrm{HS}}$, $S{R}_{\mathrm{HT}}$, $T{R}_{\mathrm{HT}}$, and $SN{R}_{\mathrm{HT}}$ are used ($SN{R}_{\mathrm{HS}}$ is not included due to its minimal effect on segmentation, see Sec. 3.1 for more details). In particular, we enforced that the spatial resolution of the high-temporal resolution images to be modest comparing to that of the high-spatial resolution images (i.e., $S{R}_{\mathrm{HT}}\ge S{R}_{\mathrm{HS}}$), with $S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$ (three values of $S{R}_{\mathrm{HT}}$), $150\mu \mathrm{m}$ (two values of $S{R}_{\mathrm{HT}}$), or $300\mu \mathrm{m}$ (one value of $S{R}_{\mathrm{HT}}$) at four different $T{R}_{\mathrm{HT}}$ and three different $SN{R}_{\mathrm{HT}}$. This decision is based on the consideration that in practical situations, the high-temporal resolution images are usually acquired with a lower spatial resolution than that of high-spatial resolution images. For clarity, each combination of acquisition settings is assigned an ID (see Fig. S1 in the Supplemental Material).

2.3. Evaluation of the Accuracy of Morphological Analysis

2.3.1. Synthetic tumor cohort

We focused on quantitatively determining the ability of our image analysis algorithm to accurately identify the tumor-associated vasculature. As no tumor existed within the original digital phantom,³² 45 spherical volumes are simulated within the tissue at arbitrary locations and with a fixed radius of 1 mm. Each volume represents a unique tumor “case,” thereby yielding the “tumor cohort” ($n=45$).

2.3.2. Identification of tumor-associated vessels

The morphological analysis of TAVs²² was applied on the high-spatial resolution DCE-MRI data. Briefly, a Hessian-based filter is applied to the difference between the post- and pre-contrast frames (i.e., the “subtraction” image) to segment the whole vasculature within the image volume. A gap filling process is then applied to refine the connectivity of the segmented vasculature. Then, regarding one synthetic tumor (see previous section), we investigate each vessel having a termination close to the tumor, and a tracking algorithm previously developed²² is used to compute the lowest-cost path (i.e., the tracking path) from the termination of this vessel to other vessels and the edge of tumor. If the lowest-cost path leads to the tumor, the investigated vessel is identified as a TAV. Two metrics (Table 2) are defined to quantitatively evaluate the accuracy of the estimated TAVs: (1) spatial distance bias (SDB) and (2) source detection accuracy (SDA). The equations for SDB and SDA are in the next section.

Table 2.

Metrics for evaluating the accuracy of image analysis.

Entity			Symbol	Measure
Metrics measuring the accuracy of image analyses	Morphological analysis	Spatial distance bias	SDB	Difference between estimated and true location of TAV for each tumor
		Source detection accuracy	SDA	Agreement between estimated and true arterial input of TAV for each tumor
	Hemodynamic analysis	Kolmogorov–Smirnov distance	KS	Difference between estimated and true distributions of the hemodynamic characteristics $(p_t,{\mathbf{u}}_t,q_v,q_e)$ for each tumor
		Percentage error	PE	Difference between estimated and true median of the hemodynamic characteristics $(p_t,{\mathbf{u}}_t,q_v,q_e)$ for each tumor

2.3.3. Accuracy of estimated tumor-associated vessels

For each synthetic tumor, the true TAVs are identified by determining the overlap between the true vasculature and the tumor volume and labeled as the set, $\mathbf{V}=\{V_i{\}}_{i=1,\dots ,N_t}$, where $N_t$ is the number of true TAVs for the $t$’th tumor, and $i$ is the index of each true TAV for this tumor [Fig 2(a)]. Similarly, the estimated TAVs are obtained from each high-spatial resolution dataset as described in Sec. 2.3.2 and labeled as the set, $\hat{\mathbf{V}}=\{\widehat{V_i}{\}}_{i=1,\dots ,N_t}$ [Fig 2(b)]. Thus, the SDB is defined to measure the physical distance between the estimated TAVs and the corresponding true TAVs for each tumor. Specifically, a spatial distance (SD) from each $V_i$ to its closest estimated TAV, $\widehat{V_i}$, and tracking path, $\widehat{P_i}$, is defined as

$${\mathrm{SD}}_i=\mathrm{SD}(V_i,\{\widehat{V_i},\widehat{P_i}\}),$$ (1)

where SD is defined as the averaged Euclidean distance from each point along $V_i$ to the set $\{\widehat{V_i},\widehat{P_i}\}$ [Fig 2(c)]. Note that $\widehat{P_i}$ is empty if no tracking path is found. Then, ${\{{SD}_i\}}_{i=1,\dots ,N_t}$ are averaged to produce the SDB:

$$\mathrm{SDB}=\frac{{\sum }_{i=1}^{N_t}{SD}_i}{N_t}.$$ (2)

Fig. 2.

Illustrations showing how the accuracy of the estimated TAVs is evaluated. (a) The true vasculature (dark red lines) and an example tumor (orange region), where vessel $l_7$ is connected to the tumor and is defined as a true TAV (i.e., $V_1=l_7$). The entire arterial input is the set ${\mathbf{S}}_1=\{l_7,l_5,l_1\}$. (b) An example of the estimated TAV. In particular, $\widehat{l_5}$ is a vessel with its termination point close to the tumor. The tracking algorithm is applied to verify it is a TAV with the tracking path $\widehat{P_1}=\widehat{p_1}$ (blue dots), yielding the arterial input set $\widehat{{\mathbf{S}}_1}=\{\widehat{l_5},\widehat{l_3},\widehat{l_1}\}$ (blue lines). To quantify the accuracy of the estimated TAV, the Euclidean distance is calculated from each point along the true TAV, $V_1$, to the estimated TAV and associated tracking path, $\{\widehat{V_1},\widehat{P_1}\}$ [see, e.g., point $x$ in (c)]. The set of distances for all points along $V_1$ are averaged to represent the SD between true and estimated TAVs, yielding a value of SDB. To assess the accuracy of the arterial input, the true TAV arterial input [bright red vessels in (a)] is projected onto the segmented vasculature to yield the set ${\widehat{{\mathbf{S}}_1}}^0=\{\widehat{l_5},\widehat{l_3},\widehat{l_1}\}$ [red lines in (d)], which is then compared to the estimated arterial input, $\widehat{{\mathbf{S}}_1}$, yielding a value of SDA. Specifically, the example in (b) has $\mathrm{SDB}=SD(l_7,\{\widehat{l_5},\widehat{p_1}\})$ and SDA = #$(\{\widehat{l_5},\widehat{l_3},\widehat{l_1}\}\bigcap \{\widehat{l_5},\widehat{l_3},\widehat{l_1}\})$/#$(\{\widehat{l_5},\widehat{l_3},\widehat{l_1}\})=1$, where # denotes the cardinality of a set. This is a successful estimation of a TAV.

Given the branching pattern of the true vasculature, the entire arterial input of a true TAV ($V_i$) can be identified as the group of vessels connecting $V_i$ to the arterial input of the breast vasculature; we term this entire path ${\mathbf{S}}_i$ [Fig 2(a)]. For each true TAV ($V_i$), $\widehat{V_i}$ provides the closest estimation of $V_i$ and the arterial input of $\widehat{V_i}$ is defined as $\widehat{{\mathbf{S}}_i}$ [Fig 2(b)]. Note that ${\mathbf{S}}_i$ consists of the vessels comprising the true vasculature, and ($\widehat{{\mathbf{S}}_i}$) consists of vessels estimated from the segmentation process. To quantify the differences between ${\mathbf{S}}_i$ and ($\widehat{{\mathbf{S}}_i}$), we project the true arterial input onto the segmented vasculature. In particular, for each true vessel in ${\mathbf{S}}_i$ [for example, $l_1$ in Fig 2(a)], we investigate all vessels in the segmented vascular and calculate the SD between the true vessel and each investigated segmented vessel. If an investigated segmented vessel has an average distance to the true vessel that is smaller than the diameter of the true vessel, this segmented vessel will be considered a “projection of the true vessel” in the segmented vasculature [for example, $\widehat{l_1}$ in Fig 2(d)]. This projection results in a representation of the true arterial input (${\mathbf{S}}_i$) in the segmented vasculature, defined as ${\widehat{{\mathbf{S}}_i}}^0$, where ${\widehat{{\mathbf{S}}_i}}^0$ is the best estimate of ${\mathbf{S}}_i$ that can be achieved from $\widehat{V_i}$ [Fig 2(d)]. We then define the $i$’th “source accuracy” ($S{A}_i$) as the agreement between the estimated and true arterial inputs of each $V_i$ as

$${SA}_i=\#(\widehat{{\mathbf{S}}_i}\cap {\widehat{{\mathbf{S}}_i}}^0)/\#({\widehat{{\mathbf{S}}_i}}^0),$$ (3)

where $\#(·)$ is the cardinality of ${\widehat{{\mathbf{S}}_i}}^0$. $\{{SA}_i{\}}_{i=1,\dots ,N_t}$ is averaged to produce the SDA via,

$$\mathrm{SDA}=\frac{{\sum }_{i=1}^{N_t}{SA}_i}{N_t}.$$ (4)

Thus, the SDA quantifies the average agreement between the estimated arterial input and the projection of the true arterial input.

The metrics SDB and SDA are calculated with respect to each tumor and each high-spatial resolution dataset. The Wilcoxon test is then applied to compare each metric (within the tumor cohort) across different datasets to quantify the effect of the image acquisition settings on the estimation of TAVs, with $P<0.05$ indicating statistical significance.

2.4. Evaluation of the Accuracy of Hemodynamic Analysis

2.4.1. Summary of hemodynamic analysis

The hemodynamic analysis estimates tumor-related blood and interstitial flow²³ and requires both high-spatial resolution images and high-temporal resolution images. Briefly, a computational fluid dynamic model was established based on Poiseuille’s law for flow in the vascular network, Starling’s law for the interaction between the blood plasma and interstitial fluid, and Darcy’s law for interstitial flow.²³ The high-spatial resolution images are segmented to provide the vascular and tissue masks, which are then meshed to provide the modeling domains. The high-temporal resolution DCE-MRI data are fit to a simplified Kety–Tofts model³⁵ to estimate the bolus arrival time (BAT), volume transfer coefficient ($K^{\mathrm{trans}}$), and plasma volume fraction ($v_p$). The BAT is used to determine blood flow directions and inlet pressure in the vascular network, $v_p$, is used to estimate the radius of the segmented vasculature within each voxel, and $K^{\mathrm{trans}}$ is used to calibrate spatially resolved maps of vascular hydraulic conductivity and permeability via a linear scaling as outline in Ref. 23. Given each combination of the high-spatial and high-temporal resolution datasets (Fig. S1 in the Supplemental Material), the image-guided computational fluid dynamics model estimates four hemodynamic characteristics: the blood pressure field ($p_v$) and interstitial pressure field ($p_t$) throughout the tissue, thereby enabling calculation of the vascular fluid extraction rate ($q_e$) and interstitial flow velocity (${\mathbf{u}}_t$).

2.4.2. Accuracy of estimated hemodynamic characteristics

Recall that the digital phantom provides detailed, spatially resolved maps of whole-tissue hemodynamics (including $p_t$, ${\mathbf{u}}_t$, $p_v$, and $q_e$), which will serve as the ground truth³² for the subsequent studies. Thus, for each tumor, the hemodynamics can be identified over both the true tumor mask and the TAVs. To compare the true and estimated hemodynamics, we compute the Kolmogorov–Smirnov distance (KS)³⁶ and the percentage error (PE) between the two as defined in Table 2. The KS quantifies the difference between the true and estimated hemodynamics for a tumor via

$$K{S}_h=\max |F(h)-F(\widehat{h})|,$$ (5)

where $h$ refers to one of the hemodynamic characteristics (i.e., $h=p_t$, ${\mathbf{u}}_t$, $p_v$, or $q_e$), $F(h)$ and $F(\hat{h})$ represent the empirical distribution functions for the true and estimated hemodynamic characteristic, respectively. The PE is defined as the percent difference between the true and estimated hemodynamics via

$${\mathit{PE}}_h=\frac{|M(h)-M(\hat{h})|}{|M(h)|}\times 100\%,$$ (6)

where $M(h)$ and $M(\hat{h})$ represent the median of the true and estimated hemodynamic characteristic, respectively.

$K{S}_h$ and $P{E}_h$ are calculated with respect to each tumor, and each combination of high-spatial and high-temporal resolution datasets. The same synthetic tumor cohort described in Sec. 2.3.1 is also used in this analysis. The Wilcoxon test is used to compare each metric across the different generated datasets to evaluate the effect of the imaging acquisition settings on the estimation of the tumor-associated hemodynamic characteristics. The significance threshold is set as 0.05.

3. Results

3.1. Evaluation of Morphological Analysis

Figure 3 visualizes the estimated TAVs for one example tumor whose images were simulated at different spatial resolutions. Comparing Figs. 3(a)–3(c) to Fig. 3(d), the locations of the estimated TAVs are (qualitatively) less accurate as the spatial resolution decreases. However, when the spatial resolution is too low (e.g., $S{R}_{\mathrm{HS}}\ge 150\mu \mathrm{m}$) for the true TAVs to be identified during segmentation, the tracking paths still provide an acceptable estimation of the true TAVs location. For example, in Figs. 3(c) and 3(d), when $S{R}_{\mathrm{HS}}=150$ and $300\mu \mathrm{m}$, the distance between estimated and true TAVs (i.e., SDB) are 1.32 and 1.66 mm, respectively. In contrast, the arterial inputs of the TAVs are still successfully detected as the spatial resolution decreases. Even when the spatial resolution is too low (e.g., $S{R}_{\mathrm{HS}}\ge 150\mu \mathrm{m}$), the tracking is still very likely to estimate the correct arterial inputs of tumors. For example, in Figs. 3(c) and 3(d), when $S{R}_{\mathrm{HS}}=150$ and $300\mu \mathrm{m}$, the tumor arterial inputs are both estimated with 100% accuracy ($\mathrm{SDA}=100\%$).

Fig. 3.

3D visualization of estimated TAVs. The $x$-, $y$-, and $z$-axes represent the coronal, axial, and sagittal views, respectively. (a)–(d) TAVs for one example tumor detected from images with $SN{R}_{\mathrm{HS}}$ of 70 dB and $S{R}_{\mathrm{HS}}$ of 30, 75, 150, and $300\mu \mathrm{m}$, respectively. The segmented vasculature (thin black lines), estimated TAVs (bold red lines), and tracking paths (bold blue lines) leading from the vasculature to the tumor (green volume) are presented in each panel, along with their arterial inputs (bold black lines). Estimating the TAVs with $S{R}_{\mathrm{HS}}=30\mu \mathrm{m}$ yields 100% accuracy. As the spatial resolution decreases from 30 to $300\mu \mathrm{m}$, the accuracy of the arterial input of the estimated TAVs is preserved, but the accuracy of the location of the estimated TAVs is reduced.

3.1.1. Quantify accuracy of estimated TAV location

The effect of spatial resolution on the SDB was compared across different values of $S{R}_{\mathrm{HS}}$ with an ${SNR}_{\mathrm{HS}}$ fixed at a value ranging from 5 and 70 dB in increments of 5 dB. As presented in Figs. 4(a) and 4(b), when $S{R}_{\mathrm{HS}}\le 60\mu \mathrm{m}$ the spatial error of the estimated TAVs is very small with a median $\mathrm{SDB}\le 0.32\mathrm{mm}$. When $60\mu \mathrm{m}<S{R}_{\mathrm{HS}}\le 90\mu \mathrm{m}$, the spatial error of the estimated TAVs increases from a median SDB of 0.32 to 0.86 mm. When $S{R}_{\mathrm{HS}}>90\mu \mathrm{m}$, the spatial error of the estimated TAVs plateaus to median SDB of $\sim 1\mathrm{mm}$. Moreover, the SDB is significantly different when $S{R}_{\mathrm{HS}}\le 60\mu \mathrm{m}$ and $S{R}_{\mathrm{HS}}>90\mu \mathrm{m}$, and no significant difference is observed when $S{R}_{\mathrm{HS}}\le 60\mu \mathrm{m}$ or when $S{R}_{\mathrm{HS}}>90\mu \mathrm{m}$. Overall, the ability to detect the location of the TAVs is preserved with a high accuracy over the investigated range of $S{R}_{\mathrm{HS}}=[\mathrm{30,300}]\mu \mathrm{m}$. Furthermore, as shown in Figs. 4(c) and 4(d), the effect of ${\mathit{SNR}}_{\mathrm{HS}}$ on SDB is small provided $5\mathrm{dB}\le {\mathit{SNR}}_{\mathrm{HS}}\le 70\mathrm{dB}$; in particular, no significant difference in SDB was observed between any ${\mathit{SNR}}_{\mathrm{HS}}$ values. Thus, within the investigated range of ${\mathit{SNR}}_{\mathrm{HS}}$ from 5 to 70 dB, the ability to accurately estimate the location of the TAVs is not significantly affected by the SNR.

Fig. 4.

Accuracy of the location of estimated TAVs. (a) and (b) plot the SDB of estimated TAVs for the tumor cohort ($n=45$; see Sec. 2.3.1) over all tested $S{R}_{\mathrm{HS}}$, with $SN{R}_{\mathrm{HS}}$ fixed at 5 and 70 dB, respectively. One gray cross at each $S{R}_{\mathrm{HS}}$ indicates an SDB value obtained from the corresponding dataset for each tumor; thus, there are 45 points at each value of $S{R}_{\mathrm{HS}}$. The red dots and blue bars represent the median and interquartile range across the whole tumor cohort, respectively. Similarly, (c) and (d) plot the SDB of the estimated TAVs for the whole tumor cohort over all tested $SN{R}_{\mathrm{HS}}$, with $S{R}_{\mathrm{HS}}$ fixed at 300 and $60\mu \mathrm{m}$, respectively. Overall, the accuracy of estimating the location of TAVs decreases as the spatial resolution decreases, but it is preserved with a high value over the investigated range of $S{R}_{\mathrm{HS}}$. Importantly, the accuracy of estimating the location of TAVs is not sensitive to the SNR within the investigated range of $SN{R}_{\mathrm{HS}}$.

3.1.2. Quantify accuracy of estimated TAV arterial input

The effect of spatial resolution on the SDA was compared across different values of $S{R}_{\mathrm{HS}}$ with an ${\mathit{SNR}}_{\mathrm{HS}}$ fixed at each candidate value between 5 and 70 dB. As shown in Figs. 5(a) and 5(b), when $S{R}_{\mathrm{HS}}\le 120\mu \mathrm{m}$, the arterial input of the TAVs is estimated with a median $\mathrm{SDA}>90\%$. When the $S{R}_{\mathrm{HS}}$ is between 120 and $300\mu \mathrm{m}$, the accuracy of estimating the arterial input of the TAVs falls to a median $\mathrm{SDA}>60\%$. Interestingly, an increase in the SDA is observed when the spatial resolution falls from 210 to $300\mu \mathrm{m}$. A possible reason for this observation is that when the spatial resolution is too low, the method cannot identify small vasculature branches. Thus, only the major arterial branches are preserved in the segmentation and there will be fewer options to “guess” the arterial input of TAVs, thereby simplifying the estimation of the arterial inputs. The patterns just described are identified as trends by the Wilcoxon tests, but no significant differences are found between different $S{R}_{\mathrm{HS}}$. Overall, the ability to detect the arterial inputs of the TAVs is preserved with high accuracy over the investigated range of $S{R}_{\mathrm{HS}}$ from 30 to $300\mu \mathrm{m}$. Furthermore, as shown in Figs. 5(c) and 5(d), the effect of ${\mathit{SNR}}_{\mathrm{HS}}$ on SDA is small provided $5\mathrm{dB}\le {\mathit{SNR}}_{\mathrm{HS}}\le 70\mathrm{dB}$; no significant difference in SDB is observed between any ${\mathit{SNR}}_{\mathrm{HS}}$ values. Thus, within the investigated range of ${\mathit{SNR}}_{\mathrm{HS}}=[\mathrm{5,70}]\mathrm{dB}$, the accuracy of the estimation of the arterial inputs of TAVs is not significantly affected by the SNR. In addition, even though the accuracy of estimating locations and arterial inputs of TAVs is demonstrated to be quite high, we acknowledge that a few outlier cases exist, which failed the identification of their TAVs. A further investigation on the source of these outlier cases can be found in Sec. 2 in the Supplemental Material.

Fig. 5.

Accuracy of the arterial inputs of estimated TAVs. (a) and (b) Plot the SDA of the estimated TAVs for the tumor cohort ($n=45$; see Sec. 2.3.1) over all tested $S{R}_{\mathrm{HS}}$, with $SN{R}_{\mathrm{HS}}$ fixed at 5 and 70 dB, respectively. One gray cross at each $S{R}_{\mathrm{HS}}$ indicates an SDA value obtained from corresponding dataset for each tumor; thus, there are 45 points at each value of $S{R}_{\mathrm{HS}}$. (Note that the visualization may give the impression of many outliers because the outliers spread out in the figures while the regular data points are mostly overlapping with each other.) The red dots and blue bars represent the median and interquartile range across the whole tumor cohort, respectively. Similarly, (c) and (d) plot the SDA of the estimated TAVs for the whole tumor cohort over all tested $SN{R}_{\mathrm{HS}}$, with the $S{R}_{\mathrm{HS}}$ fixed at 300 and $60\mu \mathrm{m}$, respectively. Overall, the accuracy of estimating the arterial inputs of TAVs decreases as the spatial resolution decreases, but it is preserved with a high value within the investigated range of $S{R}_{\mathrm{HS}}$. Importantly, the accuracy of estimating the arterial inputs of TAVs is not significantly affected by the SNR within the investigated range of $SN{R}_{\mathrm{HS}}$.

3.2. Evaluation of the Hemodynamic Analysis

Figure 6 presents hemodynamic characteristics estimated from three different image acquisition settings. Figures 6(a)–6(c) show the interstitial pressure fields ($p_t$) calculated for the whole tissue with vasculature segmented from images with $S{R}_{\mathrm{HS}}=60$, 150, and $300\mu \mathrm{m}$, respectively. Correspondingly, Figs. 6(d)–6(f) visualize the streamlines of interstitial flow fields (${\mathbf{u}}_t$) calculated for the whole kidney with the vasculature segmented from images with $S{R}_{\mathrm{HS}}=60$, 150, and $300\mu \mathrm{m}$, respectively. Qualitatively, the $S{R}_{\mathrm{HS}}$ has a clear effect on the magnitude and distribution of the computed hemodynamic characteristics in the whole tissue.

Fig. 6.

Estimated hemodynamic characteristics from example datasets. (a)–(c) The interstitial pressure ($p_t$) fields estimated for the cases of $S{R}_{\mathrm{HS}}=60$, 150, and $300\mu \mathrm{m}$, respectively, with $SN{R}_{\mathrm{HT}}=70\mathrm{dB}$, $S{R}_{\mathrm{HT}}=300\mu \mathrm{m}$, and $T{R}_{\mathrm{HT}}=1\mathrm{s}$. The colormap represents the magnitude of $p_t$. Similarly, (d)–(f) show the streamlines of interstitial flow (${\mathbf{u}}_t$) fields solved for the cases of $S{R}_{\mathrm{HS}}=60$, 150, and $300\mu \mathrm{m}$, respectively, with $SN{R}_{\mathrm{HT}}=70\mathrm{dB}$, $S{R}_{\mathrm{HT}}=300\mu \mathrm{m}$, and $T{R}_{\mathrm{HT}}=1\mathrm{s}$. The colormap represents the magnitude of ${\mathbf{u}}_t$. The magnitudes estimated for both $p_t$ and ${\mathbf{u}}_t$ within the whole organ decrease as the spatial resolution of the images used for vasculature segmentation decreases.

3.2.1. Effects of acquisition parameter on estimated hemodynamic characteristics

We individually evaluate the effects of four image acquisition parameters ($S{R}_{\mathrm{HS}}$, $SN{R}_{\mathrm{HT}}$, $T{R}_{\mathrm{HT}}$, and $S{R}_{\mathrm{HT}}$) on the accuracy of the estimated hemodynamic characteristics (i.e., $p_t$, ${\mathbf{u}}_t$, $p_v$, and $q_e$). The effect of ${\mathit{SNR}}_{\mathrm{HS}}$ is not specifically evaluated because the results in Sec. 3.1 indicate that ${\mathit{SNR}}_{\mathrm{HS}}$ has very little effect on the segmentation of vasculature provided $5\mathrm{dB}\le {\mathit{SNR}}_{\mathrm{HS}}\le 70\mathrm{dB}$.

First, the higher the spatial resolution of the images used for segmenting the vasculature, the better the estimation of both interstitial (i.e., $p_t$ and ${\mathbf{u}}_t$) and vascular characteristics (i.e., $p_v$ and $q_e$). For example, increasing $S{R}_{\mathrm{HS}}$ from 300 to 150 to $60\mu \mathrm{m}$ results in a median (interquartile range) of $K{S}_{pt}=0.91$ (0.55 to 1.00), 0.38 (0.21 to 0.54), and 0.13 (0.08 to 0.20), respectively. The same trends are also observed for $K{S}_{ut}$, $K{S}_{pv}$, and $K{S}_{qe}$ when increasing $S{R}_{\mathrm{HS}}$. This effect is consistent across most settings of $SN{R}_{\mathrm{HT}}$, $T{R}_{\mathrm{HT}}$, and $S{R}_{\mathrm{HT}}$ [(a)–(c) of Figs. S2–S5 in the Supplemental Material]. Thus, no matter what acquisition settings are used for the high-temporal kinetic images, the spatial resolution of images used for segmentation always dominates the final estimation of the hemodynamic parameters; that is, an accurate segmentation of the vasculature is essential for accurate hemodynamic analysis.

Second, the effects of $SN{R}_{\mathrm{HT}}$ do not significantly change the KS values in most situations [(d)–(f) of Figs. S2–S5 in the Supplemental Material]. This observation is consistent across most settings of $SN{R}_{\mathrm{HT}}$, $T{R}_{\mathrm{HT}}$, and $S{R}_{\mathrm{HS}}$. Thus, the accuracy of the estimated hemodynamic characteristics is not significantly affected by the SNR of the DCE-MRI data used for computing the pharmacokinetic parameters (i.e., $K^{\mathrm{trans}}$ and $v_p$) within the investigated range ($5\mathrm{dB}\le SN{R}_{\mathrm{HT}}\le 70\mathrm{dB}$).

Third, the effects of $T{R}_{\mathrm{HT}}$ and $S{R}_{\mathrm{HT}}$ are highly correlated, and the trends are not consistent across different combinations of $T{R}_{\mathrm{HT}}$, $S{R}_{\mathrm{HT}}$, and $S{R}_{\mathrm{HS}}$; thus, the optimization of the high-temporal resolution acquisition requires simultaneous tuning of $T{R}_{\mathrm{HT}}$ and $S{R}_{\mathrm{HT}}$. For the interstitial characteristics, increasing temporal resolution tends to improve the estimation accuracy of interstitial characteristics in most cases [(g)–(i) in Figs. S2 and S3 in the Supplemental Material]. However, the significance of the trends depends on the combinations of $S{R}_{\mathrm{HT}}$ and $S{R}_{\mathrm{HS}}$. Furthermore, decreasing the spatial resolution of high-temporal resolution images tends to improve the accuracy of the estimation for the interstitial characteristics in most cases [(j)–(l) in Figs. S2 and S3 in the Supplemental Material], and this effect is significant for most cases provided $T{R}_{\mathrm{HT}}\ge 4\mathrm{s}$. Conversely, for the vascular characteristics, no clear trend is consistently observed when changing each acquisition parameter [(g)–(l) in Figs. S4 and S5 in the Supplemental Material]. For example, when $S{R}_{\mathrm{HT}}=300\mu \mathrm{m}$ and $S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, increasing the temporal resolution significantly improves the accuracy of estimating $p_v$ (Fig. S4g in the Supplemental Material). However, when $S{R}_{\mathrm{HT}}=S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, increasing the temporal resolution is ineffective or, even, harmful to the estimating $p_v$ (Fig. S4h in the Supplemental Material).

3.2.2. Optimization of acquisition settings for the hemodynamic analysis

Based on the evaluation of each hemodynamic characteristic, the optimal acquisition settings can be identified by finding the datasets, which achieve the lowest medians of KS and PE in the tumor cohort (Figs. 7 and 8). Specifically,

Fig. 7.

Systematic evaluation of the effects of image acquisition settings on the estimate of the interstitial characteristics $p_t$ and ${\mathbf{u}}_t$. In all four panels, the columns (1 to 72) refer to the combinations of acquisition parameters that were investigated (corresponding to case ID in Fig. S1 in the Supplemental Material), the rows (1 to 45) refer to each tumor, and row “M” presents the median across the tumor cohort. (a) and (b) The heat maps for $K{S}_{pt}$ and $P{E}_{pt}$, respectively, (c) and (d) the heat maps for $K{S}_{ut}$ and $P{E}_{ut}$, respectively. Identifying the minimal value in “M” yields the best acquisition setting for estimating $p_t$ is {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=150\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=4\mathrm{s}$, $SN{R}_{\mathrm{HT}}=15\mathrm{dB}$} (red arrow), which minimizes $K{S}_{pt}=0.06$ and $P{E}_{pt}=3.31\%$; the best acquisition setting for estimating ${\mathbf{u}}_t$ is {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=150\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=1\mathrm{s}$, $SN{R}_{\mathrm{HT}}=5\mathrm{dB}$}, which minimizes $K{S}_{ut}=0.16$ and $P{E}_{ut}=6.66\%$. In addition to these optimal acquisition settings, a larger range of acquisition settings still yields acceptable errors (pink bars).

Fig. 8.

Systematic evaluation of the effects of image acquisition settings on the estimate of the vascular characteristics $p_v$ and $q_e$. In all four panels, the columns (1 to 72) refer to the combinations of acquisition parameters that were investigated (corresponding to case ID in Fig. S1 in the Supplemental Material), the rows (1 to 45) refer to each tumor, and row “M” refers to the median across the tumor cohort. (a) and (b) The heat maps for $K{S}_{pv}$ and $P{E}_{pv}$, respectively, (c) and (d) the heat maps for $K{S}_{qe}$ and $P{E}_{qe}$, respectively. Identifying the minimal value in “M” yields, the best acquisition setting for estimating $p_v$ is {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=150\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=7\mathrm{s}$, $SN{R}_{\mathrm{HT}}=5\mathrm{dB}$} (red arrow), which minimizes $K{S}_{pv}=0.27$ and $P{E}_{pv}=18.17\%$; the best acquisition setting for estimating $q_e$ is {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=60\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=4\mathrm{s}$, $SN{R}_{\mathrm{HT}}=15\mathrm{dB}$}, which minimizes $K{S}_{qe}=0.31$ and $P{E}_{qe}=27.58\%$. In addition to these optimal acquisition settings, a larger range of acquisition settings still yields acceptable errors (pink bars).

• (a)The optimal settings for estimating $p_t$ are {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=150\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=4\mathrm{s}$, $SN{R}_{\mathrm{HT}}=15\mathrm{dB}$}; these choices yield a minimum of $K{S}_{pt}=0.06$ and $P{E}_{pt}=3.31\%$.
• (b)The optimal settings for estimating ${\mathbf{u}}_t$ are {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=150\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=1\mathrm{s}$, $SN{R}_{\mathrm{HT}}=5\mathrm{dB}$}; these choices yield a minimum of $K{S}_{ut}=0.16$ and $P{E}_{ut}=6.66\%$.
• (c)The optimal settings for estimating $p_v$ are {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=150\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=7\mathrm{s}$, $SN{R}_{\mathrm{HT}}=5\mathrm{dB}$}; these choices yield a minimum of $K{S}_{pv}=0.27$ and $P{E}_{pv}=18.17\%$.
• (d)The optimal settings to estimate $q_e$ are {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}=60\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}=4\mathrm{s}$, $SN{R}_{\mathrm{HT}}=15\mathrm{dB}$}; these choices yield a minimum of $K{S}_{qe}=0.31$ and $P{E}_{qe}=27.58\%$.

It should be noted that other combinations of parameter settings will still yield acceptable results. For example, for $p_t$, choosing {$S{R}_{\mathrm{HS}}=60\mu \mathrm{m}$, $S{R}_{\mathrm{HT}}\ge 150\mu \mathrm{m}$, $T{R}_{\mathrm{HT}}\le 4\mathrm{s}$, $SN{R}_{\mathrm{HT}}\ge 5\mathrm{dB}$} yields $K{S}_{pt}<0.10$ and $P{E}_{pt}<4.76\%$ [Figs. 7(a) and 7(b)]. More details on acceptable ranges of alternative acquisition settings are presented in Table 3.

Table 3.

Optimization of acquisition settings for each hemodynamic characteristic.

	$S{R}_{\mathrm{HS}},S{R}_{\mathrm{HT}},T{R}_{\mathrm{HT}},SN{R}_{\mathrm{HT}}$	KS	PE (%)
$p_t$	$60\mu \mathrm{m}$, $300\mu \mathrm{m}$, $\le 7\mathrm{s}$, $\ge 5\mathrm{dB}$	<0.10	<4.76
	$60\mu \mathrm{m}$, $150\mu \mathrm{m}$, $\le 4\mathrm{s}$, $\ge 5\mathrm{dB}$
	$60\mu \mathrm{m}$, $150\mu \mathrm{m}$, 10 s, $\ge 5\mathrm{dB}$
	$60\mu \mathrm{m}$, $60\mu \mathrm{m}$, $\le 4\mathrm{s}$, $\ge 5\mathrm{dB}$
${\mathbf{u}}_t$	$60\mu \mathrm{m}$, $300\mu \mathrm{m}$, $\le 7\mathrm{s}$, $\ge 5\mathrm{dB}$	<0.20	<8.50
	$60\mu \mathrm{m}$, $150\mu \mathrm{m}$, $\le 4\mathrm{s}$, $\ge 5\mathrm{dB}$
	$60\mu \mathrm{m}$, $60\mu \mathrm{m}$, $\le 4\mathrm{s}$, $\ge 5\mathrm{dB}$
$p_v$	$60\mu \mathrm{m}$, $300\mu \mathrm{m}$, $\le 7\mathrm{s}$, $\ge 5\mathrm{dB}$	<0.38	<31.48
	$60\mu \mathrm{m}$, $150\mu \mathrm{m}$, 7 s, $\ge 5\mathrm{dB}$
	$60\mu \mathrm{m}$, $60\mu \mathrm{m}$, 10 s, $\ge 5\mathrm{dB}$
$q_e$	$60\mu \mathrm{m}$, $150\mu \mathrm{m}$, $\le 4\mathrm{s}$, $\ge 5\mathrm{dB}$	<0.40	<38.61
	$60\mu \mathrm{m}$, $60\mu \mathrm{m}$, $\le 4\mathrm{s}$, $\ge 5\mathrm{dB}$

4. Discussion

The pathway to validation of a particular imaging measurement requires a long period of effort and debate resulting in a consensus document.^37–42 In the last decade, investigators have made concerted efforts to accelerate this process. For example, since 2008 the National Cancer Institute has sponsored the Quantitative Imaging Network^43–45 to promote development, validation, and optimization of quantitative imaging tools and methods for improving diagnosis and monitoring response to therapies. In parallel, the Radiological Society of North America organized the Quantitative Imaging Biomarker Alliance^46,47 in 2007 to unite researchers, healthcare professionals, and industry to improve the value and practicality of quantitative imaging biomarkers. However, as the central mission of these collaborations is to improve standardization, they are frequently focused on techniques that are already widely utilized. These entities may not be appropriate for newly emerging techniques. In such cases, digital phantoms provide more feasible opportunities⁴⁸ to efficiently validate new imaging approaches. Although further experimental studies are still necessary before the techniques can be reliably used in the clinical setting, the results obtained from in silico validation can provide a rigorous guide for experiment design and substantially reduce the overall time and cost of validation.

We have established an in silico validation framework based on a dynamic digital phantom and virtual MRI simulation to systematically evaluate and optimize a DCE-MRI-based characterization of tumor-associated vascular morphology and hemodynamics. Specifically, the evaluation of morphological analyses demonstrates that the TAVs can be identified accurately ($\mathrm{SDA}>60\%$ and $\mathrm{SDB}<1.27\mathrm{mm}$) with all investigated imaging spatial resolution and SNR (i.e., spatial resolution better than $300\mu \mathrm{m}$ and SNR higher than 5 dB). Even when the imaging spatial resolution is too low (i.e., $<120\mu \mathrm{m}$) to directly visualize small vessels feeding a tumor, the vessel tracking can successfully find the most plausible path of vessels extending from major vascular trunks to the tumor. These results indicate that the TAVs can be identified from DCE-MRI with high accuracy, which is essential for exploring its further applications in cancer diagnosis, prognosis, and the development of vascular-related interventions. In particular, this analysis could be used to assess the delivery of chemotherapies and radiolabeled molecules to tumors through the feeding vascular network, as well as changes in delivery as vessels and cancers change during therapy.⁴⁹ In addition, our current morphological analysis used a Hessian-based algorithm for segmentation of the vasculature in 3D. It is possible that a machine learning-based segmentation could improve the accuracy of the segmentation.⁵⁰

The evaluation of the hemodynamic analyses demonstrates that its accuracy relies on the imaging quality of both the high-spatial resolution images (used for segmenting and identifying the vasculature) and the high-temporal resolution images (used for estimating tissue properties). With optimized acquisition settings, the estimation of interstitial characteristics (i.e., $p_t$ and ${\mathbf{u}}_t$) can be very accurate ($P{E}_{pt}<4.76\%$ and $P{E}_{ut}<8.50\%$). These results indicate that our analysis can identify interstitial features from DCE-MRI with high accuracy. Importantly, previous studies demonstrated that high interstitial pressure can result in an accumulation of systemic therapies near the surface of blood vessels surface, limiting penetration into the tumor, and therefore cause treatment failure.⁵¹ Thus, our hemodynamic analysis could prove useful for quantifying the interstitial characteristics of tumors, including vascular normalization and reducing interstitial pressure via anti-angiogenesis therapies,^52,53 and increasing intra-tumoral interstitial flow via heat or ultrasound stimulation.⁵⁴ An imaging-based technique that can reliably characterize interstitial characteristics could monitor the outcome of these approaches longitudinally to guide subsequent interventions on a patient-specific basis.

In contrast to the interstitial parameters, our evaluation indicates greater error when estimating vascular characteristics (i.e., $p_v$ and $q_e$), only achieving accuracies of $P{E}_{pv}<31.48\%$ and $P{E}_{qe}<38.61\%$ for the best acquisition situations. This is probably because the estimation of vascular characteristics depends on the accuracy of both the hemodynamic computation as well as detection of TAVs, which makes the task more challenging. For example, as shown in Fig 2(c), when the end of the true $\mathrm{TAV}(V_1)$ is too small to identify via segmentation, the estimated TAV only corresponds to part of the true TAV—even when the tracking path successfully identified the location of estimated TAV ($\widehat{V_1}$). Thus, the computed vascular characteristics along the estimated TAV are biased when compared to the values along the true TAV. This bias could manifest itself as error within the hemodynamic computation and increase the uncertainty in estimating tumor-associated vascular characteristics.

Together with previous reports,^22,23 this study demonstrates the DCE-MRI-derived vascular morphology and hemodynamics can potentially be accurate biomarkers for tumor characterization. Future experimental validation is still desired to support the accuracy of these techniques. For example, pre-clinical studies could be conducted to obtain highly resolved whole vasculature via vascular casting and micro (x-ray) computed tomography,^55,56 which would provide the ground-truth for the DCE-based morphology analysis. Invasive methods such as implanted probes^28,29 can be used to directly measure the blood and interstitial flows in xenograft models and provide the ground truth for the DCE-based hemodynamic analysis.

The optimization of imaging settings will also benefit from more preclinical or clinical evidence, with results from the present in silico study serving as guidance. Importantly, two core findings of this study should be considered when designing the DCE-MRI acquisition protocol:

• •If the acquired data are to be used for morphological analysis, especially identification of TAVs, increasing imaging spatial resolution is helpful but not necessary, because the location and arterial input of TAVs can be recovered quite well even if the imaging resolution is $300\mu \mathrm{m}$. Imaging noise has little effect, provided the SNR is above 5 dB.
• •If the acquired data are to be used for hemodynamic analysis, especially estimation of tumor-associated blood flow and interstitial transport, increasing the spatial resolution of the images used for vessel segmentation is essential; in fact, increasing the spatial resolution almost linearly improves the estimation accuracy. The spatial and temporal resolutions of the images used for the kinetic parameter fitting require simultaneous optimization as their effects on estimation are highly correlated. Again, the imaging noise of either high-spatial or high-temporal resolution images has little effect, provided the SNR is above 5 dB.

A few key points should be considered when applying the results of the in silico study to actual imaging experiments. First, in this study, we evaluated the effects of spatial resolution, temporal resolution, and SNR separately. In real imaging experiments, these three parameters are intimately connected with each other and depend on a complex set of factors related to scanner hardware (e.g., field strength, gradient strength, shimming). Second, the dynamic digital phantom used for this study is based on the anatomy and physiology of a rat kidney,³² while we have designed it to be a general vascular phantom. Thus, this phantom may not accurately recapitulate the kidney-specific filtration processes, and the vascular size and perfusion in this digital phantom are different from that in human kidney or in other organs/tissues. The specific numerical values regarding the imaging acquisition parameters resulted from this study may not be directly applicable to that of the clinical setting. Moreover, this study only used one kidney to generate the phantom. Generating more phantoms from different datasets to evaluate the effect of different vascular structures may prove beneficial. Third, we synthetized spherical volumes with a fixed size to represent tumors in this study, but tumors can (of course) have arbitrary shapes and sizes. We did, though, perform a sensitivity analysis on the effect of tumor shape and size on the identification of TAVs (see Sec. S1 in the Supplemental Material). The results indicate that the change in the tumor size and shape—especially size—has effects on the evaluation of MRI-based TAV characterization, but they do not change the conclusion presented in the main text.

In spite of the limitation listed in the previous paragraph, the digital phantom and the associated methodology presented in this study can be made to readily represent human organs. For example, appropriate scaling is all that is required to convert the vascular geometry of the digital phantom to match the size of corresponding human vessels, and the ground-truth hemodynamics of the digital phantom could be recalculated by the adjusted vessel size and heart rate. With the digital phantom adjusted according to the specific clinical or preclinical application, the validation methodology presented in this study could be employed to provide specific guidance on image acquisition parameters. Moreover, this study also represents a practical example of employing digital phantoms to validate the accuracy and to optimize the performance of novel imaging acquisition, reconstruction, and processing methods.

5. Conclusion

We have established a novel in silico validation framework to systematically evaluate quantitative DCE-MRI analyses for characterizing tumor-associated vasculature and several of its hemodynamic properties. The TAV identification and hemodynamic analyses—especially the estimation of interstitial characteristics—were found to be reliable. This study also indicates that the in silico validation framework can rigorously optimize acquisition settings, thereby providing a robust system for systematically testing imaging methods for vascular characterization.

Biography

Biographies of the authors are not available.

Disclosures

Authors have no relevant financial interests in the manuscript and no other potential conflicts of interest to disclose.

Code and Data Availability

All data in support of the findings of this paper are available within the article or as Supplemental Material. The digital phantom used in this study is publicly available in an open toolkit, R2D2, at https://github.com/ChengyueWu/R2D2_toolkit. The virtual MRI simulator used in this study is publicly available in GitHub at: https://github.com/tyo8/ECA_Demo.