The effect of frequency (64 – 498 MHz) on specific absorption rate adjacent to metallic orthopedic screws in MRI: a numerical simulation study

Abstract

Background:

The imaging of patients with implanted electrically-conductive devices via magnetic resonance imaging at ultra-high fields is hampered by uncertainties relating to the potential for inducing tissue heating adjacent to the implant due to coupling of energy from the incident electromagnetic field into the implant. Existing data in the peer-reviewed literature of comparisons across field strengths of tissue heating and its surrogate, the specific absorption rate (SAR), is scarce and contradictory, leading to further doubts pertaining to the safety of imaging patients with such devices.

Purpose:

The radiofrequency-induced SAR adjacent to orthopedic screws of varying length and at frequencies of 64 to 498 MHz was investigated via full-wave electromagnetic simulations, to provide an accurate comparison of SAR across MRI field strengths.

Methods:

Dipole antennas were used for RF transmission to achieve a uniform electric field tangential to the screws located 120 mm above the antenna midpoints, embedded in a bone-mimicking material. The input power to the antennas was constrained to achieve the following targets without the screw present: (i) E = 100 V/m, (ii) B₁⁺ = 2 μT, and (iii) global-average-SAR = 3.2 W/kg. Simulations were performed with a spatial resolution of 0.2 mm in the volume surrounding the screws, resulting in 76–137 MCells, noting the maximum 1g-averaged SAR value in each case. Simulations were repeated at 128 MHz and 297 MHz for screws embedded in muscle tissue.

Results:

The peak SAR, occurring at the resonant screw length, substantially increased as the frequency decreased when the input power to the dipole antenna was constrained to achieve constant electric field in background tissue at the screws’ locations. A similar pattern was observed when constraining input power to achieve constant B₁⁺ and global-average-SAR. The dielectric properties of the tissue in which the screws were embedded dominated the SAR comparisons between 297 and 128 MHz.

Conclusions:

The study design allowed for a direct comparison to be performed of SAR across frequencies and implant lengths without the confounding effect of variable incident electric field. Lower frequencies produced substantially larger SAR values for implants approaching the resonant length for the worst-case uniform incident electric field along the screws’ length. The data may inform risk-benefit assessments for imaging patients with orthopedic implants at the new clinical field strength of 7 Tesla.

Introduction

Patients with implanted electrically-conductive devices such as orthopedic screws, rods and pins are routinely imaged with MRI at field strengths of 1.5 T and 3 T. However, uncertainty remains regarding the safety of imaging such devices at the new clinical field strength of 7 T. Only a handful of devices have been certified by manufacturers as MR Conditional at 7 T^1,2, and there is a common belief that radiofrequency-induced tissue heating adjacent to such devices is always worse as the magnetic field strength (and hence Larmor frequency) increases. As a result, many patients and research subjects are denied a 7 T MRI examination.

The heating of tissue adjacent to conducting implants results from the interaction of the incident electromagnetic field transmitted by the radiofrequency (RF) coil with the implant. For long, thin implants such as orthopedic screws, the incident electric field drives conduction currents along its length, with the largest effect occurring when the incident electric field is parallel to the implant. An impedance mismatch exists at the interface between the implant and tissue, due to their vastly different dielectric properties, and hence significant electrical charge build-up occurs particularly at the ends. This charge build-up creates a secondary ‘scattered’ electric field in the adjacent tissue, which drives eddy currents in the lossy tissue environment, thereby resulting in ohmic heating. The transfer function, first introduced by Park et al. in 2007³, describes how the scattered field can be calculated from knowledge of the incident electric field along an implant’s length.

The conduction current created in the implant by the incident electric field exhibits a resonant behavior due to the ‘antenna effect’, where the implant is considered to behave like an antenna and hence can preferentially support standing wave current patterns when the implant length equals a ‘resonant’ length, typically at a certain fraction (or multiples thereof) of the RF wavelength^4–7. This resonant length ranges from 0.3λ to 0.5λ, depending on the dielectric properties of the surrounding tissue^8–10. The magnitude of the conduction currents depends on the magnitude of the incident electric field, reaching a maximum when the electric field is parallel to and uniform along the length of the implant.

Many prior peer-reviewed studies^3,8–13 have investigated RF-induced tissue specific absorption rate (SAR) adjacent to conducting implants in a variety of both physical and simulation environments, with only a handful reporting SAR at several frequencies / magnetic field strengths, mainly 1.5T/3T^3,14–20. A limitation of these studies was a lack of knowledge of or control over the incident electric field along the full length of the implant. The highly heterogeneous spatial distribution of the electric fields produced by the birdcage-type RF coils²¹ used in those studies inevitably resulted in a high (and unknown) degree of variability of the resulting SAR, invalidating a direct comparison of SAR across field strengths. A further limitation of these studies was the limited range of implant lengths investigated, which may or may not have been close to a resonant length at the specific conditions investigated.

The aim of this simulation study was to investigate the effects of frequency from 64 to 498 MHz (corresponding to magnetic field strength 1.5 – 11.7 Tesla for ¹H) on the RF-induced SAR adjacent to orthopedic screws of varying lengths (18 – 183 mm) embedded in a tissue-mimicking dielectric environment. This experimental design ensured that the worst-case SAR could be compared across field strengths and implant lengths, without confounding effects such as variable incident electric fields and a limited range of implant lengths. The hypothesis was that comparative data on the worst-case SAR will inform risk-benefit analyses for 7 T examinations of patients with passive elongated implant devices such as orthopedic screws.

Materials and Methods:

Full wave electromagnetic simulations were performed using a finite-difference time-domain (FDTD) solver package (version 6.2, Sim4Life, ZMT, Switzerland). An open-source orthopedic cortical bone screw model (grabcad.com/library/4-5mm-cortex-screw-1) (Figure 1) was embedded in a medium with dielectric properties mimicking cancellous bone tissue at each frequency covering the resonant frequency for ¹H from 1.5 to 11.7 Tesla. Because the aim was to compare RF-induced SAR as a function of frequency, the choice of bone, while relevant for orthopedic devices, was not particularly important so long as consistency across frequencies was maintained. The screw model was varied in 24 discrete lengths from 18 – 183 mm, with a constant screw diameter of 4 mm in each case, and assigned the dielectric properties of titanium. The screws were placed 120 mm from the center of a dipole antenna, with their long axis parallel to the dipole. This ensured the screws were located in a region of uniform background electric field oriented parallel to the screws’ long axis, where ‘background’ here refers to the electric field produced by the dipole in the absence of the screw. Dipole antennas were used to generate the electromagnetic fields in this study due to their recognized beneficial properties for imaging at ultra-high fields (i.e. ≥ 7 Tesla; improved B₁⁺ efficiency at greater depths and more uniform transmit-receive profiles compared to stripline or loop designs) together with their ability to generate an optimally uniform electric field parallel to their long axis^22–25.

Figure 1:

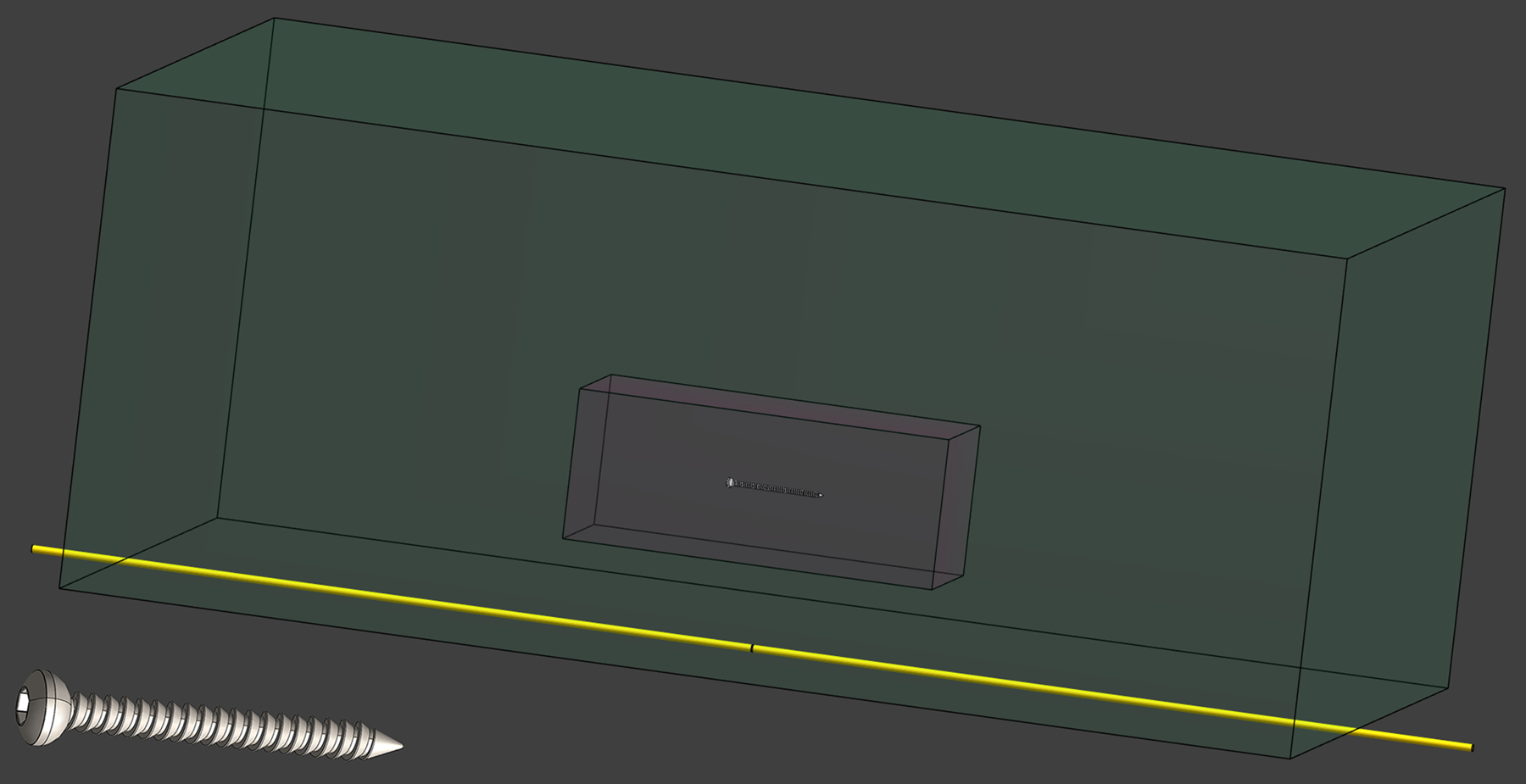
Schematic from the simulation environment showing the location of the 78 mm screw within the tissue-mimicking volume (green) above the dipole antenna (yellow). The white dashed box centered on the screw is the 5 kg tissue volume over which the 3.2 W/kg global-average SAR was measured. A magnified view of one screw is shown in the lower left corner.

On going from 64 to 498 MHz, λ/2 dipole lengths were used to achieve the respective resonant frequencies. An alternative approach would be to keep the dipole length constant by introducing appropriate inductive elements into the dipole at each frequency to achieve resonance, as typically employed in fractionated dipole antennas²²; however, this approach was not employed due to potential confounds to the uniformity of the background electric field arising from such variable inductances in the dipole design. The dipoles were modeled as perfect electric conductors. The tissue-mimicking volume was simulated at a geometric resolution of 0.1 mm and maximum step size of 0.2 mm in a subgrid volume of 3 × 3 × 22.5 cm³ surrounding the screws, increasing to a geometric resolution of 0.2 mm and maximum step size of 8 mm in the surrounding volume of 40 × 60 × 100 cm³. Figure 1 shows the screw location within the tissue volume relative to the dipole antenna location (78 mm screw, 128 MHz dipole). The dipoles were simulated with a geometric resolution of 0.5 mm and maximum step size of 0.9 mm, and were placed in air 6 mm below the larger tissue-mimicking volume. The rest of the simulation volume, including an additional 25 cm buffer in each direction, was simulated at a geometric resolution of 1 mm and maximum step size of 8 mm, with perfectly absorbing radiation boundaries at the periphery to avoid boundary effects. Simulations thus averaged 76 – 137 MCells and took on average approximately 0.5 – 3 hours to reach convergence at a level of −50 dB, using a dedicated GPU (RTX A6000, NVIDIA, USA). Details of the simulation and dipole parameters are presented in Table 1. Background simulations were also executed in the absence of screws at each field strength. The coupling of the screws to the dipole antenna were determined by noting the S₁₁ values (using a linear scaling) from each simulation and compared to the values obtained without the screws in situ.

Table 1:

Details of the excitation frequencies, corresponding magnetic fields for ¹H, wavelength, dipole lengths and frequency-dependent dielectric properties of bone tissue used in the simulations.

Frequency [MHz]	64	128	213	297	400	498
Magnetic Field [T]	1.5	3	5	7	9	11.7
Wavelength [m]	4.68	2.34	1.40	1.00	0.748	0.602
Dipole Length [m]	2.34	1.17	0.70	0.50	0.374	0.301
Conductivity [S/m]	0.1608	0.1799	0.1986	0.2152	0.2346	0.2535
Relative Permittivity (${\epsilon }_r$)	30.869	26.284	24.199	23.181	22.442	21.958

The specific absorption rate, averaged over a volume of 1 g, was used as a surrogate of tissue heating. The maximum 1g-average SAR value (hereafter referred to as ‘SAR_max’) within the tissue-mimicking volume, always located near the tip of the screws, was recorded for each screw length and magnetic field strength. An additional set of simulations were performed to investigate the effects of the dielectric properties of different tissue types (specifically: bone and muscle) on the SAR_max values at 297 MHz (7 T). This was accomplished by performing simulations with the dielectric properties and density of either muscle (σ = 0.77 S/m, ε_r = 58.23, ρ = 1090.4 kg/m³) or bone (σ = 0.215 S/m, ε_r = 23.18, ρ = 1178.3 kg/m³) assigned to the uniform tissue-mimicking volumes in which the screws were implanted.

Three normalization methods were implemented for the radiofrequency power at the dipole antenna excitation port:

1. E field normalization: to achieve a total E field magnitude of 100 V/m at the center of the screw location, in the absence of the screw;

2. B₁⁺ normalization: to achieve a B₁⁺ magnitude of 2 μT at the center of the screw location, in the absence of the screw;

3. Global-average SAR normalization: to achieve an equivalent 3.2 W/kg global-average SAR within a centrally located 5 kg tissue block in the absence of the screw.

The 5 kg tissue block over which the 3.2 W/kg global-average SAR was measured is indicated by the red inner box in Figure 1.

The uniformity of the E_x field (i.e. the E-field component parallel to the screws’ long axis) produced by dipole antennas increases with frequency. To correct for underestimations in SAR_max deriving from this slight nonuniformity of the E_x-field magnitude and therefore allow for an accurate comparison across frequencies the SAR data was multiplied by a scaling factor for each screw length and each frequency, determined from:

$$\mathit{\text{Scaling}}\mathit{\text{factor}}={\left(\frac{E_{\mathit{\text{center}}}.l}{\int E_{\mathit{\text{profile}}}dl}\right)}^2$$ (1)

where E_center is the background E_x-field value measured at the location corresponding to the center of each screw (simulated without the screw present), l is the screw length, E_profile is the background E_x-field profile measured along the location of the screws’ axis (again, simulated without the screw present), and the integral is performed along the screw length in each case. The quadratic term was used considering SAR ∝ E².

To demonstrate the increase in SAR due to the presence of the screw, the normalized SAR elevation was calculated as²⁶:

$$\mathit{\text{Normalized}}\mathit{\text{SAR}}El\mathit{\text{evation}}=\frac{{\mathit{\text{SAR}}}_{\mathit{\text{screw}}}–{\mathit{\text{SAR}}}_{\mathit{\text{background}}}}{{\mathit{\text{SAR}}}_{\mathit{\text{background}}}}$$ (2)

where SAR_screw and SAR_background are the SAR_max values with the screw present and absent, respectively.

Results:

Table 2 shows the input power values to the dipole antennae that were used to achieve the target E field (100 V/m), B₁⁺ (2 μT) and global-average SAR (3.2 W/kg) at the location of the screw, in the absence of the screw. The increased input power required at lower fields to achieve the target values was due to the longer antennae at lower fields which transmit electromagnetic fields over a larger tissue volume, resulting in lower electromagnetic field energy density per unit input power (note: for birdcage-type RF coils, the opposite trend of decreased power at lower frequencies typically occurs). Also shown in Table 2 are the relative differences in S₁₁ values with the longest screw (183 mm) present versus no screw present at each frequency, demonstrating the minimal coupling between the dipole antennas and screws in all experimental situations.

Table 2:

Input power to the dipole antennae drive ports that were used to achieve the target E field (100 V/m), B₁⁺ (2 μT) and global-average SAR (3.2 W/kg) at the location of the screw, in the absence of the screw. The change in S₁₁ values with the longest screw present compared to no screw present is also shown.

Frequency [MHz]	64	128	213	297	400	498
100 V/m E Field [W]	203.6	171.9	130.2	101.9	83.8	77.2
2 μT B1+ [W]	347.9	291.2	299.8	249.7	220.9	209.3
3.2 W/kg global-average SAR [W]	519.2	329.4	222.8	171.6	152.7	152.3
Change in S11 (screw / no screw) [%]	1.5	− 0.5	0.6	−0.1	−0.5	1.2

Representative plots of the background E_x and B₁⁺ fields are shown in Figure 2 for the case of 297 MHz, demonstrating their uniformity at the screw location. Variations of up to 31% were found in the background E_x-field magnitude along the largest screw length at 498 MHz, decreasing to 2.5% at 64 MHz; the corresponding scaling factors for these longest screws were 1.228 and 1.017, respectively. Figure 3 shows the scaling factor as a function of frequency and screw length. Scaling factors greater than 1.05 were only observed for screw lengths well above the resonant lengths; at the resonant lengths for all field strengths, the scaling factors were all less than 1.015.

Figure 2:

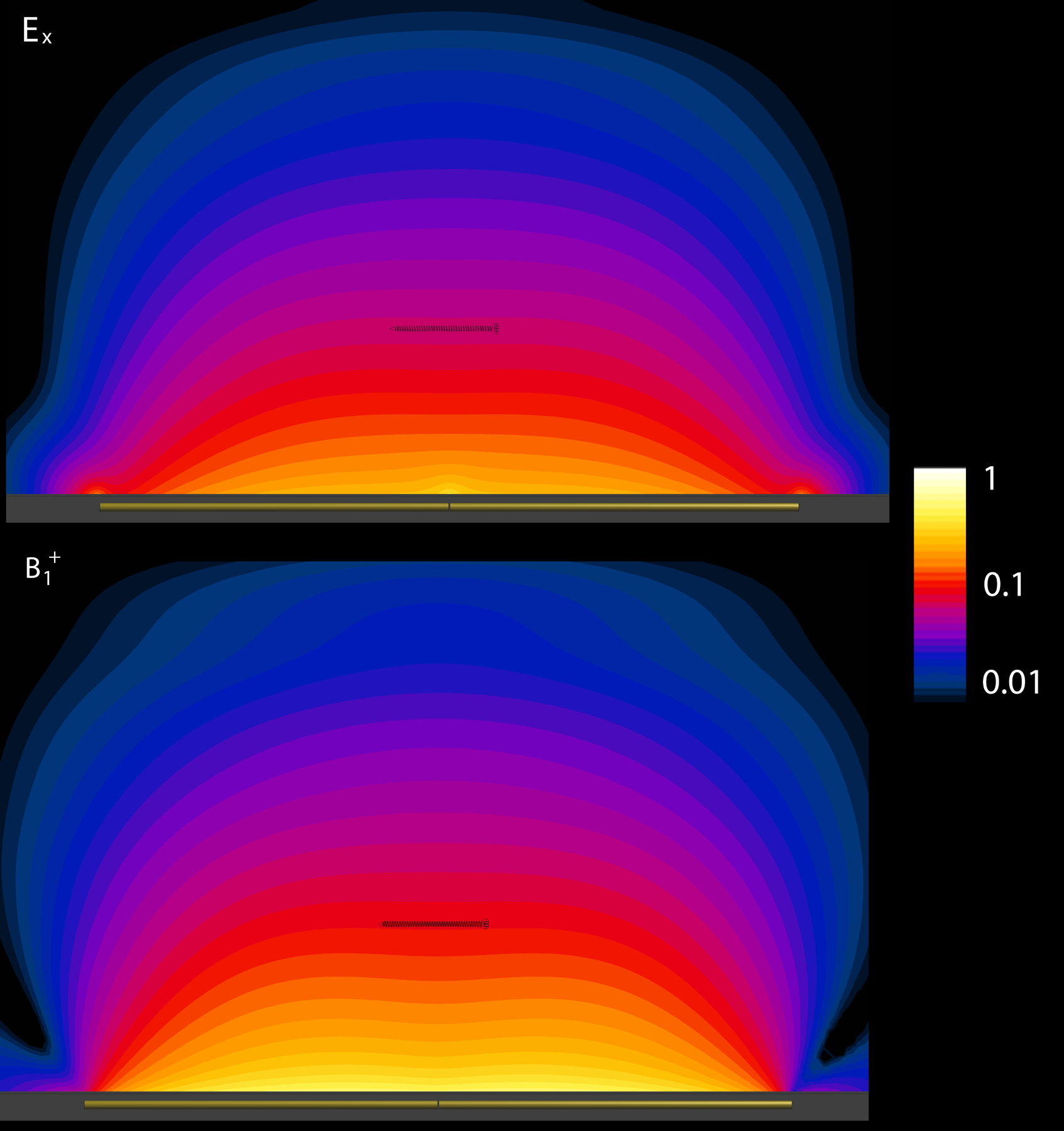
Representative plots of the relative background E_x (top) and B₁⁺ (bottom) field profiles in the tissue-mimicking region in the plane parallel to the dipole antenna axis at 297 MHz (7 T), demonstrating their uniformity at the screw location. The 78 mm screw, shown here for illustrative purposes only, was not included in the simulations.

Figure 3:

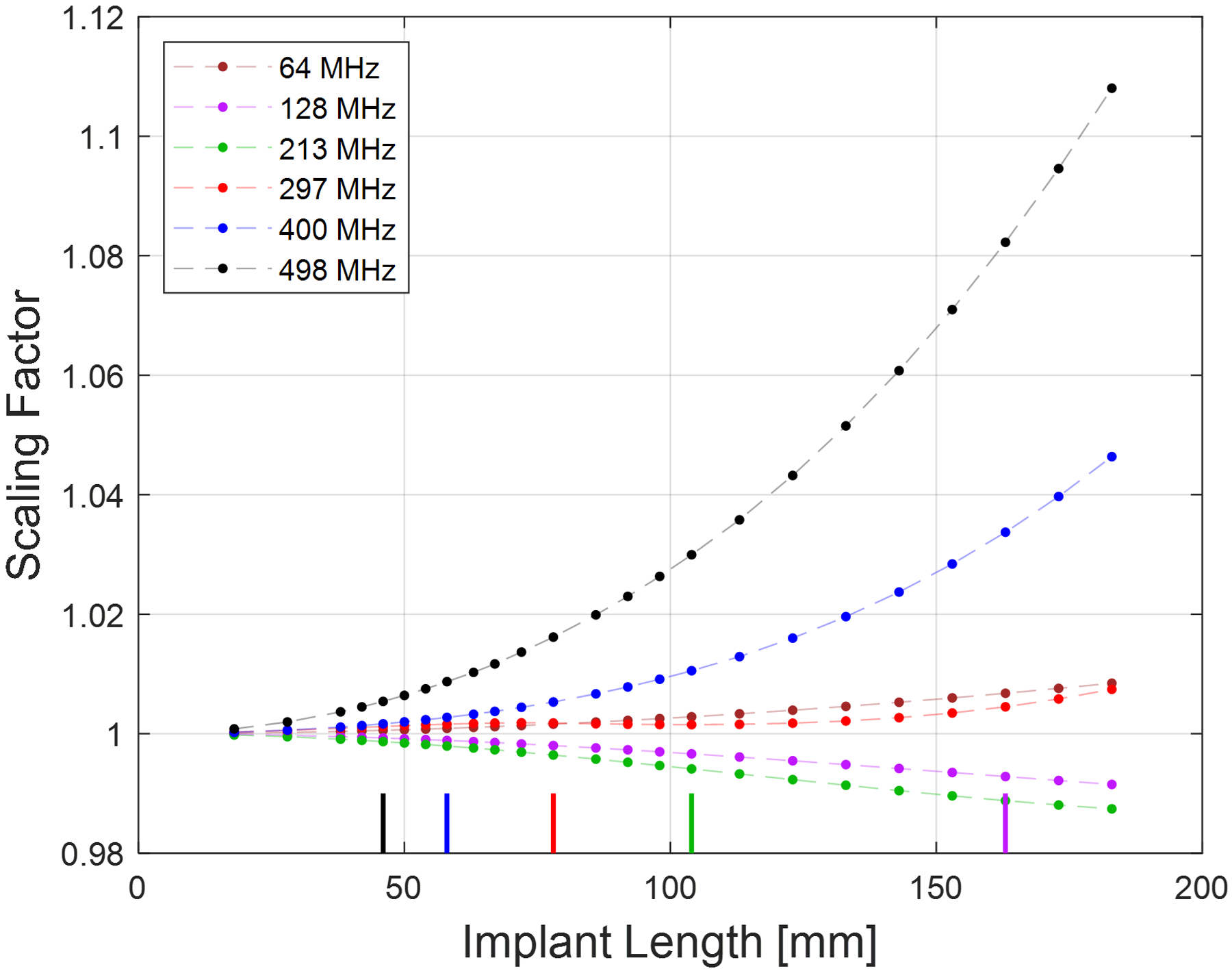
Plot showing the scaling factor (per Equation 1) at each field strength as a function of screw length. The color-coded bars along the x-axis indicate the approximate resonant length at each frequency (except 64 MHz, where the resonant length exceeded 200 mm).

A representative image showing the spatial distribution of the 1g-averaged SAR near one of the orthopedic screws (78 mm, simulated at 297 MHz) is shown in Figure 4, demonstrating the SAR_max value close to the tip of the screw.

Figure 4:

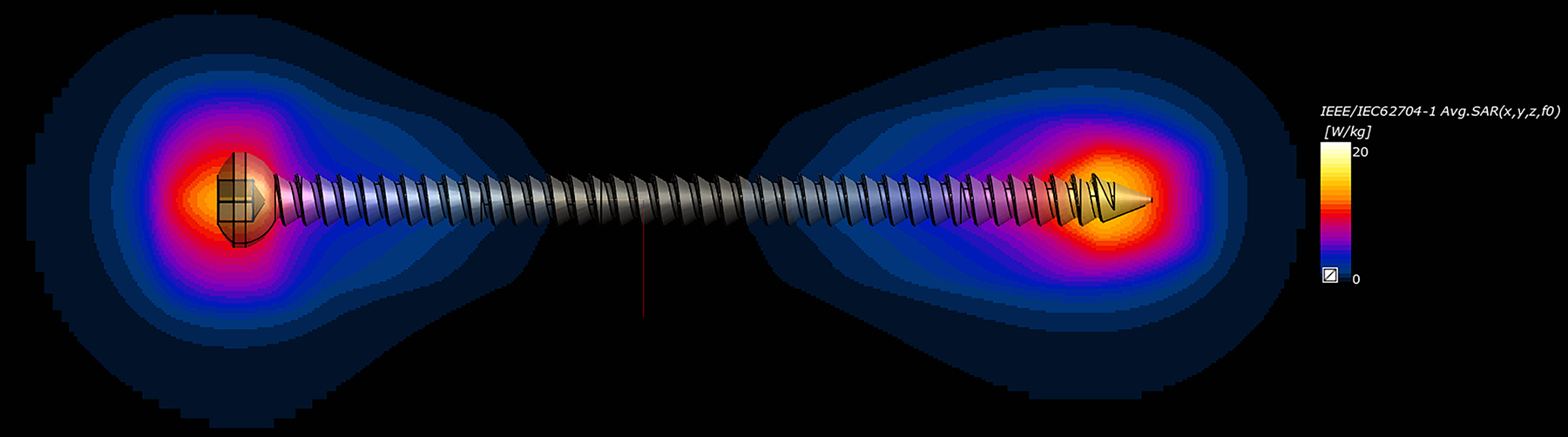
Representative spatial distribution of the 1g-averaged SAR near one of the orthopedic screws (78 mm, simulated at 297 MHz), demonstrating the SAR_max value close to the tip, as expected. The SAR elevation adjacent to the screw head is less than that at the tip due to the more rounded shape of the head, which creates a less intense scattered electric field at that location.

The scaling factor-corrected SAR_max values across all screw lengths and frequencies are presented in Figure 5, for the three computed RF power normalizations. As expected, all data exhibit the resonant length effect whereby the SAR_max values reach a peak for screw lengths equal to the resonant lengths at each frequency, and decrease thereafter. Several features are worth noting:

• for screw lengths up to the resonant lengths, the SAR_max was higher at higher frequencies

• the peak SAR_max, occurring at the resonant screw lengths, were consistently lower at higher frequencies

• for screw lengths above the resonant lengths, the SAR_max was lower at higher frequencies.

Figure 5:

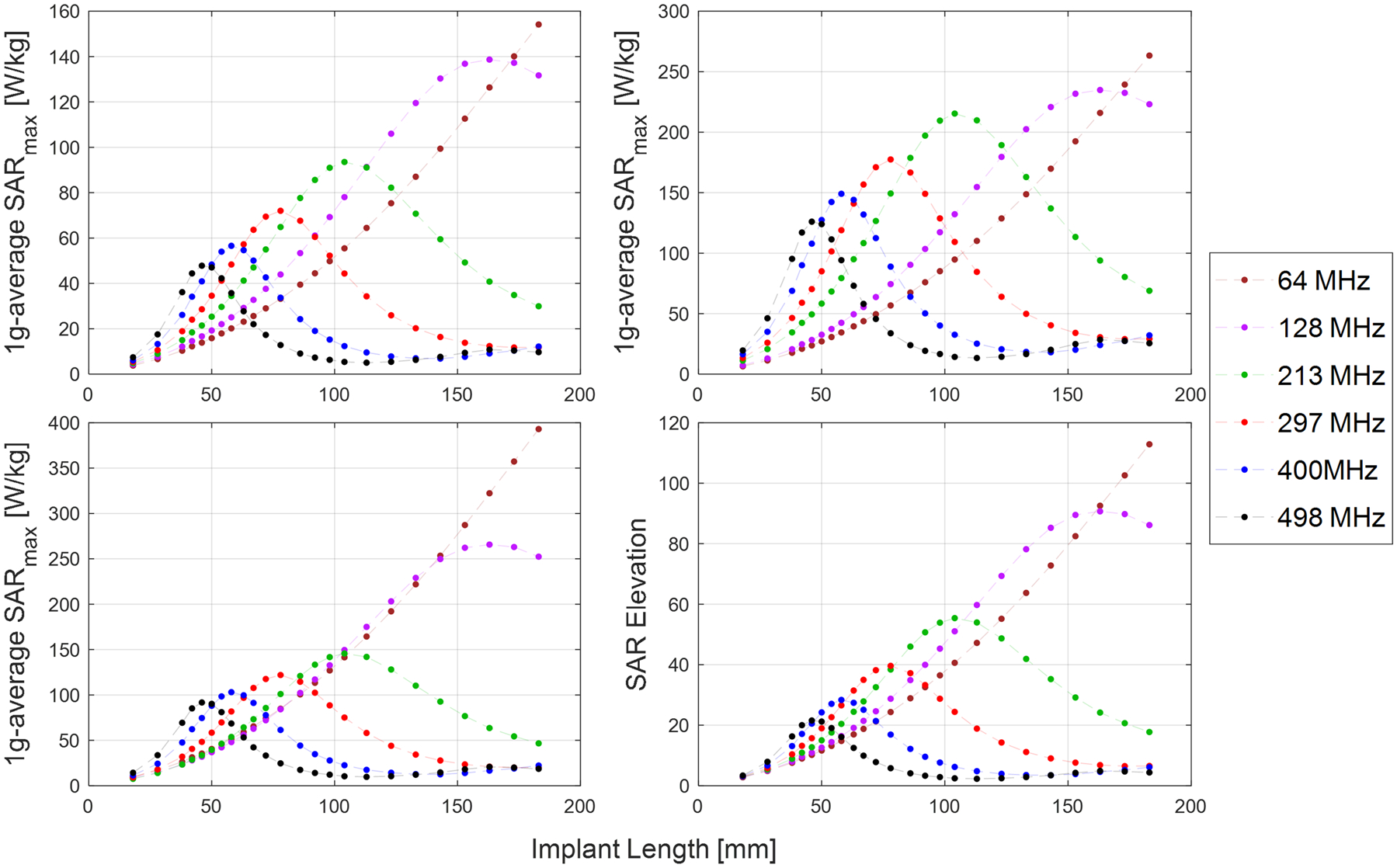
Plots of the SAR_max as a function of screw length and frequency, when normalized for constant E-field (top row, left), B₁⁺ (top row, right), and global-average SAR (bottom row, left). The plot of SAR elevation is also shown (bottom row, right)

The SAR Elevation as a function of field strength is also presented in Figure 5. Due to the inherent normalization to the input power used to calculate this parameter, the SAR Elevation was the same for each of the three computed RF power normalizations. A similar pattern of lower SAR Elevation at higher frequencies was evident.

Data from the simulations performed at 128 MHz and 297 MHz comparing the muscle- and bone-mimicking tissues are presented in Figure 6. A similar resonant-length effect was observed here, wherein the peak SAR_max value was measured in screw lengths of approximately one-third of the wavelength in all simulated tissue types. The peak SAR_max value decreased in magnitude and occurred at shorter screw lengths as the tissue conductivity and permittivity increased. This data illustrates the strong dependance of the SAR values on the dielectric properties of the tissue in which the screw is implanted. An interesting comparison can be made for specific screw lengths, for example the 78 mm screw indicated by the vertical red line in Figure 6. The SAR for this specific screw length is higher at 297 MHz compared to 128 MHz when it is embedded in bone, because this particular screw length is close to the resonant length at 297 MHz but far from the resonant length at 128 MHz. However, when embedded in muscle, the opposite trend emerges because this screw length is now closest to the resonant length at 128 MHz, resulting in higher SAR at that frequency. This illustrates how the implant length relative to the resonant length for each frequency and tissue type dominates the resultant induced SAR, and how SAR comparisons which only consider one or a small range of implant lengths could lead to erroneous conclusions regarding the frequency which gives rise to the highest induced SAR values.

Figure 6:

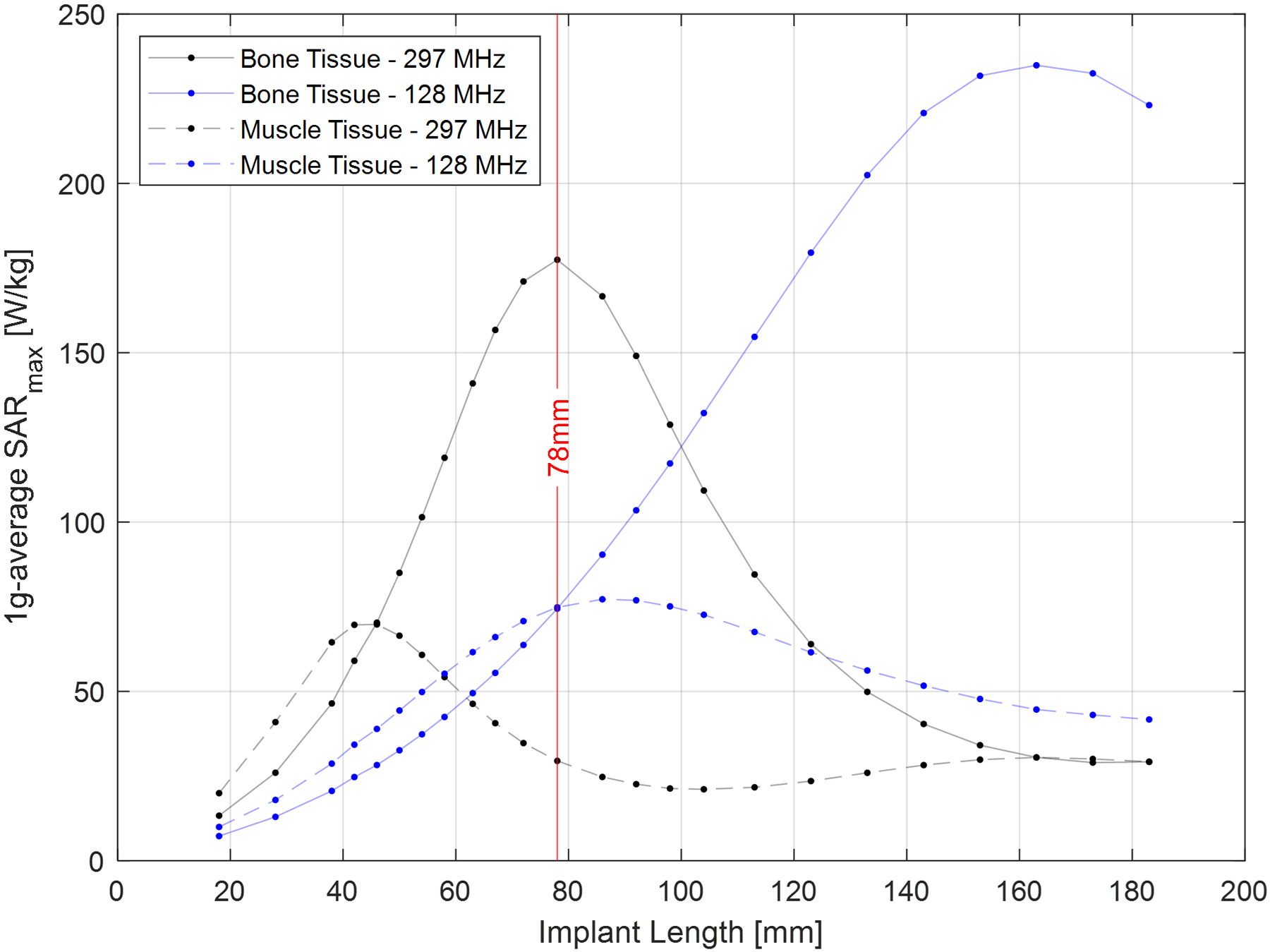
Plot of the SAR_max values at 297 MHz as a function of screw length for the screw embedded in uniform tissue regions mimicking the dielectric properties and densities of bone and muscle (input power was normalized to produce B₁⁺_rms = 2 μT at the screw location). Muscle tissue has higher conductivity and permittivity values, and hence the peak SAR_max value for muscle was lower and occurred at shorter screw lengths. The vertical red line highlights the data for the 78 mm screw, to illustrate how the implant length relative to the resonant length for each frequency and tissue type dominates the resultant induced SAR.

Discussion

The main finding of this study was the dominant effect that the implant length relative to the resonant length at each frequency has on the RF-induced SAR in tissue adjacent to the orthopedic screws, with higher peak SAR values (occurring at the resonant length) found at lower frequencies. The same pattern was found when the input power to the dipole antennae were controlled to achieve constant values for the electric field, B₁⁺ field and global-average SAR at the location of the implants for all field strengths.

A motivating factor for this study was the scarce and contradictory data in the published literature describing the effect of increasing frequency on the RF-induced SAR in tissue close to electrically conductive implants. For example, in comparisons between 64 and 128 MHz, some studies reported higher SAR levels at higher frequencies while others reported the opposite^3,14–18. Similarly, in a recent study investigating SAR for various DBS lead trajectories across field strengths (1.5 T to 10.5 T), higher SAR was reported at higher fields when the input power to the RF transmitters was adjusted to produce a B₁⁺ field of 2 μT, while lower SAR was reported up to 7 T, increasing at 10.5 T, when the input power was adjusted to produce a global average SAR of 3 W/kg²⁰. A contributing factor to the different apparent trends in the reported SAR versus frequency in these prior studies was the variability of the incident electric field impinging on the implanted devices which, while not typically considered for imaging, is crucial when comparing SAR as a function of frequency. As a result, it is difficult to draw conclusions from the data on the effect of increasing frequency on SAR, due to the many additional variables which invariably contributed to the reported SAR values. For example, a higher SAR in one scenario might merely be due to a higher incident electric field integrated along the implant (dependent on many experimental factors), and hence not necessarily due to a change in frequency. An assessment of the effect of increasing frequency on SAR must remove any variability of the incident electric field along the length of the implant. Indeed, the ASTM measurement standard for assessing RF-induced heating near passive implants states that the incident electric fields should be “sufficiently homogenous (i.e. ± 1 dB variability) in magnitude and phase”²⁷, which are unlikely to be realized in most testing scenarios, particularly those using birdcage-type RF coils²¹, leading to the current uncertainties in the literature. The current study specifically aimed to control the incident electric field along the length of the implant, to allow for an accurate comparison of SAR across all field strengths / frequencies investigated.

In the current study, control over the incident electric field was ensured by using dipole antennae for RF transmission: dipole antennae produce a uniform electric field parallel to the antennae axis^1,28,29. The implants were positioned at a location within the tissue-mimicking volume where the electric fields were as uniform as possible considering the boundary conditions (attenuation and reflection of the RF waves), and far enough away from the antennae to minimize any coupling between the antennae and implants at all frequencies / field strengths investigated. The use of a scaling factor to account for the residual small nonuniformity of the incident electric field only effected a minor change in the SAR values across frequencies and did not alter the relative pattern of lower peak SAR values at higher frequencies. This allowed for a comparison of the SAR due to a worst-case uniform incident electric field, where the only variables were the frequency and implant length.

The pattern of decreased peak SAR values at the resonant lengths at higher frequencies may be due to an interplay between the shorter resonant lengths and increased attenuation of the RF current. The shorter resonant lengths result in less charge build-up at the implant ends due to the smaller spatial extent over which incident electric field can resonantly act to create a standing wave current pattern along the implant. For longer implants that can support higher harmonics of the standing wave patterns, the increased impedance of the implant (specifically, the inductive reactance component, which increased linearly with frequency) may serve to attenuate the RF current that is induced along the implant, thereby further reducing the SAR, compared to that occurring at lower frequencies³⁰.

The strong dependance of the SAR on the dielectric properties of the tissue in which an implant is embedded is illustrated by the data in Figure 6, which illustrates the approximately three times greater SAR_max found when the screw was implanted in tissue mimicking the properties of bone compared to muscle at 7 T. The high conductivity of muscle tissue compared to bone results in increased loading of the screw when embedded in muscle, increasing the impedance of the screw with the consequent impact on SAR. Considering that tissue dielectric properties vary with frequency, this data illustrates the importance of using the correct tissue dielectric properties when comparing SAR across frequencies. Figure 6 also illustrates how any SAR comparison as a function of frequency must consider the length of the implant under investigation relative to the resonant lengths encountered in the experimental set-up. For example, a 78 mm screw alternatively produces either a higher or lower SAR at 297 MHz compared to 128 MHz depending on the material in which it is embedded. Previous studies only investigated one or a small range of implant lengths^{14–20,31,32}, which could lead one to erroneously conclude that one frequency or the other produced the worst SAR.

The trend reported here of lower peak SAR at higher frequencies was found when the input power to the dipole antennas was normalized to achieve identical values of B₁⁺, electric field and global average SAR at the screw. However, it is important to note that lower RF powers are typically required when imaging at lower frequencies to achieve a given B₁⁺ value, which would tend to lower the concomitant electric fields and hence lower SAR compared to ultra-high fields where the far-field regime dominates due to the shorter wavelengths. Furthermore, the spatial distribution of the SAR in realistic in vivo situations will depend critically on many local factors which affect the magnitude and polarization of the local electric field at the implant location (the RF transmitter, the implant, the anatomy), and the pattern reported here of higher SAR at lower frequencies will not be realized in all scenarios. For example, in the study by Guerin et al, simulations performed in a range of realistic deep brain stimulation electrode lead configurations revealed some scenarios exhibiting higher SAR at 1.5 T compared to 3 T, while others revealed the opposite¹⁶. Similar work by Golestanirad et al^31,32 reported variable results for 1.5 T – 3 T comparisons. The inherent complexity of such clinically-relevant scenarios, with the associated large variability in the incident electric field impinging on the implant along its tortuous path in the body, give rise to the observed broad distribution of SAR outcomes. The aim of the current study was not to investigate realistic in vivo scenarios, but rather to perform a SAR comparison where the only variable was frequency and with the worst-case of an incident electric field parallel to and uniform along the length of the implant. The finding that the worst-case SAR is not necessarily higher as we move to higher field strength systems may inform assessments of safety for implants such as orthopedic screws and pins which are imaged routinely at 1.5 T and 3 T in First Level RF mode, yet remain the subject of some trepidation at 7 T and above.

Regarding study limitations, the data presented in this study show the effect of magnetic field strength / frequency on the SAR in a rather simple model system comprising a uniform tissue volume surrounding the implant, with a dipole antenna used for RF transmission. As such, care is needed in extrapolating results to other experimental set-ups. While the use of a more realistic in vivo scenario involving heterogeneous electric field distributions (arising from, say, other RF transmitter designs and/or anthropomorphic body models) may provide a better estimate of SAR for those specific scenarios investigated, this approach would introduce many additional uncontrolled variables and consequently would invalidate the comparison of SAR across frequencies. The use of screws up to 183 mm exceeds the typical lengths that are used clinically, however the results of this study can be generalized to any implant length, such as orthopedic rods or pins which routinely reach such lengths. A further limitation of the current study was that no correction was performed to account for the phase variation of the incident electric field along the screw lengths. However, the use of the dipole antenna ensured that the phase variations were small in all situations investigated, and hence not likely to alter the findings. Finally, although coupling between the antennae and screws was extremely low for all screw lengths and frequencies investigated, nevertheless the effect of any residual (albeit small) coupling on the induced current in the screws was not investigated.

Conclusions

The model simulation set-up used in this study allowed for a direct comparison of the RF-induced SAR across frequencies and screw lengths. For a constant incident electric field, substantially higher peak SAR values were produced adjacent to orthopedic screws at lower magnetic fields compared to higher magnetic fields, driven predominately by resonant length effects. These results are independent of the specific device used to transmit the RF energy, as it considers the worst-case of a uniform incident electric field along the length of the implant as a function of increasing frequency, evaluated for identical values of the B₁⁺ field, electric field and global-averaged SAR at the screw location. The finding that the worst-case SAR is not necessarily higher as we move to higher field strength systems may inform assessments of safety for implants such as orthopedic screws and pins located within the RF transmit field, particularly at the new clinical field strength of 7 Tesla.

Data Availability Statement

The CAD model used in this study is available at this link: URL