Abstract
Delays in meeting math requirements can impede the progress among community college students who aspire to earn a baccalaureate degree. To investigate this issue, we used state administrative data from Texas to examine the prevalence and predictors of math course repetition and how math course repetition predicts transfer students’ outcomes. More than a third of community college transfer students take additional introductory mathematics coursework despite having fulfilled the requirement—a phenomenon we referred to as “horizontal repetition”—and one sixth of community college students take redundant coursework within a given mathematics course sequence, referred to as “vertical repetition.” Using regression models controlling for student backgrounds, academic experiences, and institutional fixed effects, we found that horizontal repetition was linked to lower GPA and, among degree recipients, increased time to degree and excess credits. Vertical repetition was negatively associated with GPA and degree completion and positively linked to increased time to degree and excess credits. Location of course repetition shaped student outcomes, where math course repetitions occurring at the university appear to drive many of the negative associations between both horizontal and vertical repetition and student outcomes. As community colleges and universities across the country consider the efficacy of course sequences and transfer pathways, our research offers insights into patterns and implications of course repetition in core math courses.
Keywords: Coursetaking, Mathematics, Course repetition, Degree attainment, Excess credits, Community college
Community colleges provide open access to higher education for about a third of college students in the United States, providing a space for students to develop the knowledge and skills necessary for social and economic mobility (Schudde & Goldrick-Rab, 2015; U.S. Department of Education, 2019). The vast majority of students enter community colleges with the intention of earning a baccalaureate degree or higher. However, among community college transfer students, only 14% earn a baccalaureate degree within six years (Shapiro et al., 2017). Math coursework is an important predictor of degree attainment (Calcagno et al., 2007; Wang et al., 2017; Zhang, 2019), yet inefficient course-taking patterns—especially in introductory coursework like entry-level math—can lead to delays in degree attainment and excess credits among community college transfer students (Fink et al., 2018; Schudde et al., 2021).
To ensure that their math coursework applies towards their intended baccalaureate degrees, transfer-intending community college students must familiarize themselves with course requirements of their intended program of study at both their community college and their desired transfer destinations (Calcagno et al., 2007; Jenkins & Bailey, 2017; Schudde, Bradley, et al., 2020). Despite increased attention to the role math coursework plays in community college students’ persistence and degree attainment (e.g., Bahr, 2008; Ngo, 2020; Park et al., 2020), however, little information is available about students’ math course–taking patterns within and across institutions of higher education (IHEs) and the role redundant math coursework plays in community college transfer student outcomes. Because transfer students must navigate the course requirements of multiple IHEs in order to achieve their degree attainment goals, we focused our inquiry on students who initially enrolled in public two-year colleges and transferred to four-year IHEs, anticipating math course repetitions across institutional sectors due to different requirements.
In this study, we used student-level state administrative data from Texas to examine how redundancy (hereafter repetition) in math coursetaking predicts transfer student outcomes, including grade point average (GPA), baccalaureate (BA) degree attainment, time to degree, and excess credits. Leveraging detailed transcript data, we examined two types of math course repetition among two different populations of Texas community college transfer students: horizontal repetition and vertical repetition. Horizontal repetition occurs when students enroll in and earn credit for more than one different entry-level mathematics course (e.g., college algebra and quantitative reasoning). Vertical repetition occurs when students take redundant coursework within a given mathematics course sequence (e.g., repeat the same math course after earning credit or enroll in a lower-level course, like college algebra, after earning credit in a higher-level math course, like trigonometry). Our delineation between the two types of course repetition was driven by evolving research on the consequences of math pathways, a reform model that allows major-specific introductory math courses—rather than only college algebra—to fulfill college-level math requirements. Schudde and Keisler (2019) argued that increased flexibility in introductory math requirements may eventually lead some students to take more than one introductory math course, particularly if they switch majors. We anticipated that students’ motivation for repeating across introductory math courses (e.g., major switching or major exploration) likely differs from their motivation for repeating within the same vertical sequence.
Our results suggest that there are different predictors of math course repetition depending on whether repeating occurs within (vertical) or across (horizontal) a given sequence, and that the two patterns of math course repetition appear to have distinct implications for success. Horizontal repetition is more prevalent for courses taken at the community college, whereas vertical repetition is more prevalent for courses taken at the university. Both horizontal repetition and vertical repetition are negatively linked to cumulative GPA and, among baccalaureate recipients, positively correlated with time to degree and excess credits, but vertical repetition is also negatively associated with baccalaureate degree attainment. We found variation in the relationship across the location of repetition with no repeaters. Math course repetitions at the university were linked to longer time to degree, whereas repetitions at the community college were not. Also, while horizontal repetition at the community college was positively associated with an increase baccalaureate degree attainment, there was no relationship between horizontal repetition at the university. Students who repeated the same or a lower-level course (vertical repetition) at the university were less likely to earn a bachelor’s degree than those who did not, but there was no relationship between vertical repetition at the community college and bachelor’s degree attainment. These findings suggest that differentiating between types of math course repetition and examining repetition by location are necessary to fully understand the magnitude of repetition across institution types and the association between math course repetition and student outcomes.
Coursetaking and Community College Student Outcomes
Community college students must progress through required coursework to earn credentials, whereupon even coursework accrued early in the college career has important implications for subsequent outcomes. In a study examining the link between course-taking patterns and transfer, Hagedorn et al. (2010) found that starting in college-level math or taking a higher level of English at college entrance was associated with persistence through transfer for students from all racial/ethnic backgrounds. The timing of course completion also predicts student outcomes. Completing developmental education (dev-ed) math and English courses and subsequent required math and science coursework in the first three years of college positively predicts transfer and graduation (Cohen & Kelly, 2019).
Math coursetaking in particular appears consequential for student persistence and degree attainment (Adelman, 2005; Bahr et al., 2017; Calcagno et al., 2007; Cohen & Kelly, 2019). Completing college-level math in the first year of community college is associated with associate degree attainment and successful transfer (Adelman, 2005; Calcagno et al., 2007; Wang et al., 2017). Interestingly, Wang et al. (2017) found that students who meet their math requirements in the first term and those who complete the math requirements in the fourth or fifth terms have higher odds of completing a degree than their peers who complete in the interim. Perhaps early math requirement completion spurs momentum toward degree requirements (Calcagno et al., 2007), whereas later completion occurs among persisting students who are then more likely to take the appropriate math course for their program of study. Still, 29% of community college students who took at least one mid-level or advanced math course did not earn a credential or transfer to a four-year IHE (Bahr et al., 2017). Taking more math courses is associated with transfer student outcomes; among transfer students, those who earn additional college-level math credits are more likely to earn a baccalaureate degree than students who do not (Adelman, 2005; Zhang, 2019).
Mathematics literacy—including adequate mastery of quantitative reasoning, statistics, and/or algebra—allows students to engage with program content and prepare for post-collegiate life; structurally, completing math coursework is necessary to meet degree requirements (Hagedorn et al., 2006; NASEM, 2016; Packard et al., 2012). Early completion of college-level math is especially important in fields that require math as a foundation for subsequent coursework (Calcagno et al., 2007; Schulmerich & Hurley, 2015; Wang et al., 2017; Zhang, 2019). In a study of community college students intending to work in science, technology, engineering, and mathematics (STEM) careers, Hagedorn and DuBray (2010) described the “mathematics developmental climb,” in which students must move through a series of dev-ed courses before they can enroll in required college-level courses (p. 38). In a study of nursing students, taking at least one dev-ed math course was associated with course repetition in biological sciences and nursing courses (Schulmerich & Hurley, 2015). Early progress through math requirements may shape students’ trajectories, including major selection. Community college transfer students who took at least one college-level mathematics course in their first term at a four-year IHE were more likely to earn a STEM baccalaureate degree than a non-STEM baccalaureate degree (Zhang, 2019).
Math Sequences and Course Repetition
Redundant math coursework—whether repeating high school math or math coursework at the college level—seems especially prevalent at community colleges, where many students are placed in a lower level of math than their high school course-taking experience would suggest is necessary (Bailey et al., 2010; Chen, 2016; Melguizo & Ngo, 2020; Ngo, 2020; Ngo & Velasquez, 2020). As a result, many community college students—even those with demonstrated readiness—cannot escape “math traps” that place them in courses with repetitive material (Ngo, 2020; Ngo & Velasquez, 2020, p. 9).
The magnitude of course repetition—overall or in math more specifically—among college students in the United States is unclear. The literature on repeating courses is much more robust in K–12 education, where grade retention (i.e., having to repeat an entire year of courses) is more common (e.g., Alexander et al., 1994; Fong et al., 2014; Hill, 2014). The few extant studies of postsecondary course repetition were performed in contexts outside of the United States, where grade retention and course repetition among college students is more systematic and often attributable to poor performance (e.g., Tafreschi & Theimann, 2016; Nasser & Nauffal, 2012)—which is different from the phenomenon we explore here, where students who pass math courses ultimately repeat in some way.
Although research that explicitly explores course repetition is slim, much of the literature highlighting inefficiencies in community college pathways acknowledges course repetition as a contributor. Bahr et al.’s (2017) study of math pathways illustrated that introductory math coursework may include substantial course repetition. A large proportion of students who passed college algebra or general education math ultimately exited the sequence to move into other pathways. The authors explained that 20% of students who passed algebra moved on to another sequence, where the “most common other destination was statistics” (p. 442). That is, instead of passing algebra and taking trigonometry (the next course in the sequence), a substantial proportion of students who passed college algebra instead took a different math course at the same introductory level—a phenomenon we refer to as horizontal course repetition. Horizontal course repetition may occur when students decide to switch majors and/or realize that the completed course does not align with requirements in their program of study.
Another course repetition scenario occurs among students who are committed to staying in the same sequence—students retake the same course (or an earlier course in the sequence) even if they have already passed it—what we refer to as vertical repetition. At some institutions, students may be encouraged or required to repeat a course if they earned a C, which counts as passing but may not be adequate for subsequent coursework in some majors (Kovacs, 2016). Research suggests that students who have taken a course online are more likely to engage in vertical course repetition—where they repeat the same course they already passed—than their peers who took the course face-to-face (Hart et al., 2018). Thus, some vertical course repetition decisions are likely strategic; repetition allows students a second chance at learning material or improving their grades (Fong et al., 2014; Hom, 2007).
Although research has not yet explored the implications of horizontal or vertical course repetition, research suggests that course redundancy makes students’ educational trajectories less efficient. Research on course-taking patterns among nursing students illustrates the negative correlation between repeating courses and graduating on time (Schulmerich & Hurley, 2015). Course repetition may also lead to the accrual of excess credits—credits earned beyond those required for a given credential. When students complete more than one introductory math course, they likely end up with excess elective credits, as programs of study typically specify one introductory math requirement (Schudde et al., 2021). Many community college transfer students who earn bachelor’s degrees accumulate excess credits (Fink et al., 2018; Zeidenberg, 2015). Fink et al. (2018) illustrated that community college transfer students who took more introductory courses at the 100 and 200 levels at the community college were at greater risk of accruing excess credits. Course-taking decisions at the community college have long-term consequences for transfer students as well, as the number of credits earned at the community college before transfer is positively associated with credit loss upon transfer (Giani, 2019). Thus, unnecessary course repetitions may lead to additional costs for students—due both to the added costs of completing a given course and to the opportunity costs of delaying graduation and entering the labor market (Romano et al., 2011; Schulmerich & Hurley, 2015; Zeidenberg, 2015).
There is a growing sense among community college stakeholders that the way students consume math in college does not align with students’ academic or career goals (Bryk & Treisman, 2010; President’s Council of Advisors on Science & Technology, 2012). Many reformers emphasize that completing college algebra is a barrier for many students and that other types of mathematical reasoning, including statistical reasoning or basic quantitative reasoning, may be more relevant to students seeking careers in non-STEM fields (Bryk & Treisman, 2010). Math pathways reforms—a math corollary to the Guided Pathways movement—offer alternatives to college algebra, including quantitative reasoning or statistics, to increase completion of introductory math courses and, ultimately, allow students to attain their desired degree (Carnegie Math Pathways, 2020; Dana Center, 2020; Roksa et al., 2009). As more institutions work to offer alternatives to the “algebra-for-all” model, further challenges for students, including course redundancy, may arise as colleges work to revise math course recommendations (Schudde & Keisler, 2019). Transfer students may be particularly susceptible to taking more than one introductory math course as they navigate different math course requirements across degree plans in different programs (Schudde et al., 2021).
Our study is a quantitative effort to understand course repetition in math among students who began at community colleges and transferred to a four-year IHE. The literature includes broad studies of math course–taking patterns and their link to student outcomes, but no research, to our knowledge, has explored course repetition, including the differentiation between horizontal repetition among various introductory courses and vertical repetition within a given math sequence. Given the widespread reform efforts underway at community colleges and their potential to provide viable pathways to bachelor’s degree attainment, there is a pressing need to understand both the prevalence of math course repetition within and across IHEs and the association between different types of repetition and student outcomes. To address this need, we examine math course repetition among transfer students who initially entered higher education through Texas community colleges and the relationship between math course repetition and those students’ subsequent GPA, baccalaureate attainment, time to degree, and excess credit outcomes.
Research Questions
To understand the prevalence of math course repetition and how repetition predicts student outcomes among community college transfer students, we address the following research questions using statewide administrative data from Texas:
What proportion of community college transfer students experience vertical and horizontal math course repetition? Which students are most likely to experience math course repetition and at which institutional level?
What are the predictors of vertical and horizontal math course repetition?
- What is the relationship between each type of math course repetition and college outcomes, including cumulative GPA, bachelor’s degree attainment, time to bachelor’s degree, and excess credits?
- How does the location of repetition—at the community college or university—predict college outcomes?
Conceptual Framework
Our analytic models predict course repetition (RQ2) and longer-term achievement and attainment measures (RQ3). Research on community college student outcomes, including those of transfer students, primarily focuses on persistence and completion (Braxton et al., 2014; Roksa, 2006; Schudde, 2019). We have drawn on that extant literature to support our decisions to include additional variables for inclusion in our statistical models (other than capturing horizontal and vertical repetition, described above). Based on our review of prior literature, we identified three main constructs that have been linked to community college student success: student background, academic experiences, and achievement.
Student Background
Individual demographic characteristics—such as race and ethnicity, gender, age, socioeconomic status and other financial indicators—are associated with persistence, transfer, and baccalaureate degree attainment among community college students (Bailey et al., 2005; Schudde, 2019). Survey research also suggests variation in student behavior during college across demographic groups, such as race and gender, including how frequently students engage with advisors and faculty, who may play a role in students’ course-taking decisions (CCSSE, ). Financial aid receipt may predict community college entrants’ course-taking patterns, including decisions to drop and retake courses in order to meet eligibility standards for need-based aid, as well as their long-term outcomes, including bachelor’s degree attainment and time to degree (Scott-Clayton & Schudde, 2020).
Academic Experiences
Students’ academic experiences—such as enrollment behavior, initial course taking patterns, and major decisions—shape their subsequent course-taking decisions and long-term outcomes. Research links enrollment patterns, such as attending part time or stopping out (taking a break from college followed by re-enrollment), to persistence and degree attainment (Bailey et al., 2015; Fike & Fike, 2008; Park, 2012). Although researchers have not examined the relationship between enrollment patterns and course repetition, community-college reformers emphasize the importance of consistent fulltime enrollment for remaining connected to support staff at the college and making timely progress toward a degree (Bailey et al., 2015).
Participation in dual credit—college-level credits taken during high school—can improve student momentum toward a degree, whereas participation in dev-ed coursework—preparatory courses that do not count toward a college credential—may hinder student progress and delay time to degree (Bahr, 2008; Wang et al., 2015, 2017). The slow pace of dev-ed sequences, particularly in math, may function as a detour in students’ journey toward a degree (Bryk & Treisman, 2010). Furthermore, students placed in dev-ed courses are not always aware that those courses do not count toward a degree, creating frustration with unanticipated prolonged time to degree attainment.
Student major may predict both math course repetitions and subsequent degree outcomes. Colleges across the country, including those in our Texas sample, now guide students into math pathways specific to their desired major, where they may take quantitative reasoning (QR), statistics, or algebra as appropriate (Bryk & Treisman, 2010). Yet a large proportion of community college students—up to 40 percent—switch majors, which has been linked to a lower probability of baccalaureate degree attainment (Liu et al., 2021; Schudde, Ryu, et al., 2020). Students who switch majors may be more likely to experience math course repetition because the new major might have different requirements to earn a baccalaureate degree (Bailey et al., 2016).
Academic Achievement
Students’ prior achievement and attainment—such as course grades, cumulative GPA across all college credits, and associate degree attainment—are likely to predict subsequent baccalaureate degree attainment and time to degree (Belfield, 2013; Wang et al., 2015, 2017). Research suggests that student grades predict subsequent degree attainment and time to degree (Clovis & Chang, 2021; Yue & Fu, 2017). We also expect that students’ grades in their first college-level mathematics courses may predict course repetition. Astorne-Figari and Speer (2019) found that earning lower grades within a given major field increased the probability that students switch to majors that are very different from the ones they leave. Although they focused on bachelor’s degree recipients, we anticipate that this process may similarly hold among community college transfer students, whose lower grades in initial math courses may predict switching to a different math pathway (horizontal repetition). Belfield (2013) illustrated the benefits to completing an associate degree prior to transfer for long-term outcomes, though it is unclear whether completing an associate degree prior to transfer may contribute to redundancy in coursework.
Overall, we anticipate that a host of demographic characteristics, academic experiences, and achievement measures will predict student course repetition and subsequent degree outcomes. Additionally, research illustrates that variation in institutional practices for transfer may shape variation in transfer-out rates at community colleges and baccalaureate attainment rates among transfer students at destination four-year IHEs (Jenkins & Fink, 2016). Articulation agreements also vary across institutional partners, especially in state contexts that favor bilateral transfer agreements, such as Texas, which may result in varying levels of overlap in math requirements depending on the feeding community college and the destination university. For this reason, it is important to control for variation across institutions students attended (we elaborate on this point in the methods section).
State Context
The Texas public higher education system comprises 80 two-year institutions, which include technical and community colleges, and 39 four-year institutions (Texas Higher Education Coordinating Board [THECB], 2017). These entities together form the public higher education pipeline for students who start at a two-year school and aim to earn a baccalaureate degree. Like many states, Texas lacks incentives for two-year and four-year institutions to work together to implement existing transfer policies and build clearer transfer pathways (Bailey et al., 2016). The state primarily relies on bilateral transfer agreements made between individual institutions rather than on a statewide agreement, which leaves students and advisors to navigate specific agreements between colleges and programs in efforts to understand which course sequences will lead to their desired degree (Root, 2013; Schudde, Bradley, et al., 2020). Transfer-intending community college students must “curate” and “synthesize” information from a variety of resources to understand which courses to take to increase the likelihood that they will achieve their educational goals (Schudde, Bradley, et al., 2020, p. 11).
In Texas, four entry-level math courses are offered to satisfy general education math requirements: college algebra, quantitative reasoning, statistics, and math for business. Recent reform efforts, like the Texas Pathways strategy and math pathways reforms, seek to ensure that required math courses align with a student’s field of study (Carnegie Math Pathways, 2020; Dana Center, 2020; Flores & Fabianke, 2019). Math coursework is frequently cited as a challenge for credit transfer (Bailey et al., 2016; Schudde et al., 2021); yet there is little evidence about what math course-taking patterns look like at Texas IHEs. Illumination of common issues with math course repetition could inform ongoing reforms.
Methods
To address our research questions, we used longitudinal statewide administrative data from the Texas Educational Research Center (ERC), a repository for data capturing the entire population of K–12 and college students in the state. We relied on descriptive statistics to capture the prevalence of different types of math course repetition and discern whether the repetition primarily occurs at community colleges or at destination universities (since our sample is comprised of transfer students). We ran regression analyses to examine the relationships between course repetitions (both vertical and horizontal repetition in a separate analysis) and student background and academic characteristics. We also used regression to study the relationship between location of math course repetition and student outcomes.
Data
The Texas ERC data includes student-level data for the entire population of secondary and postsecondary students in Texas. We primarily relied on data collected by THECB, including college student enrollment records; student schedule data (course numbers, credits, grades); and degree outcomes, along with financial aid information. Given our interest in course repetition among community college transfer students, we focused our analytic sample on first-time community college entrants in Fall 2011 and Fall 2012 who transferred to a public university within three years of college entrance (N = 19,667). We tracked students over seven years. In line with prior research, we restricted the sample to students who had taken more than 10 credits at community colleges (N = 19,511), which allows us to focus on non- “incidental” students with at least one semester of full-time equivalent coursework (Adelman, 1999, p. 40; 2005). Finally, we further restricted the analytic sample to include only students who had earned credit in at least one college-level math course by completing it with a passing grade (D or better) (N = 13,908). Because this study did not include students who did not previously pass a college-level math course (which also eliminates students who only took a dev-ed math), it is not representative of the full population of community college students. These restrictions were necessary to examine our research questions.
To examine college-level math course repetition among community college transfer students, we first had to identify and match math courses across community colleges and public universities in Texas. We used the Texas Common Course Numbering System (TCCNS) and the Texas Transfer Inventory Guide (TTIG) to create a list of math course prefixes and numbers for all public institutions. The TCCNS includes standard course prefixes and numbers for lower-division courses in the state (e.g., MATH 1314 for college algebra), a step that is mandated for community colleges and optional for public universities. Although TCCNS includes college-level math courses for most public institutions, it does not include math courses for all public universities. For that reason, we also used the TTIG—a list, collected by the Charles A. Dana Center, that captures transferrable math courses across all public postsecondary institutions, including universities that do not use TCCNS course prefixes and numbers (Dana Center, 2020). We identified college-level math courses using naming conventions (e.g., course numbers that begin with zero are developmental courses, whereas those that start with one or above are college level) and confirmed our identifications using the state’s Academic Course Guide Manual, a list of available courses that includes recommended course numbers. Using course prefixes and numbers, we identified 12 types of college-level math courses available at both public community colleges and universities. Figure 1 illustrates how those 12 math courses fall into sequences through which horizontal or vertical course repetition may occur. There are four introductory college-level math courses (top row), two of which—quantitative reasoning and elementary statistics—do not have subsequent courses in the sequence. The longest math course sequence is the college algebra sequence (which leads to Calculus I through III) (Fig. 1).
Fig. 1.
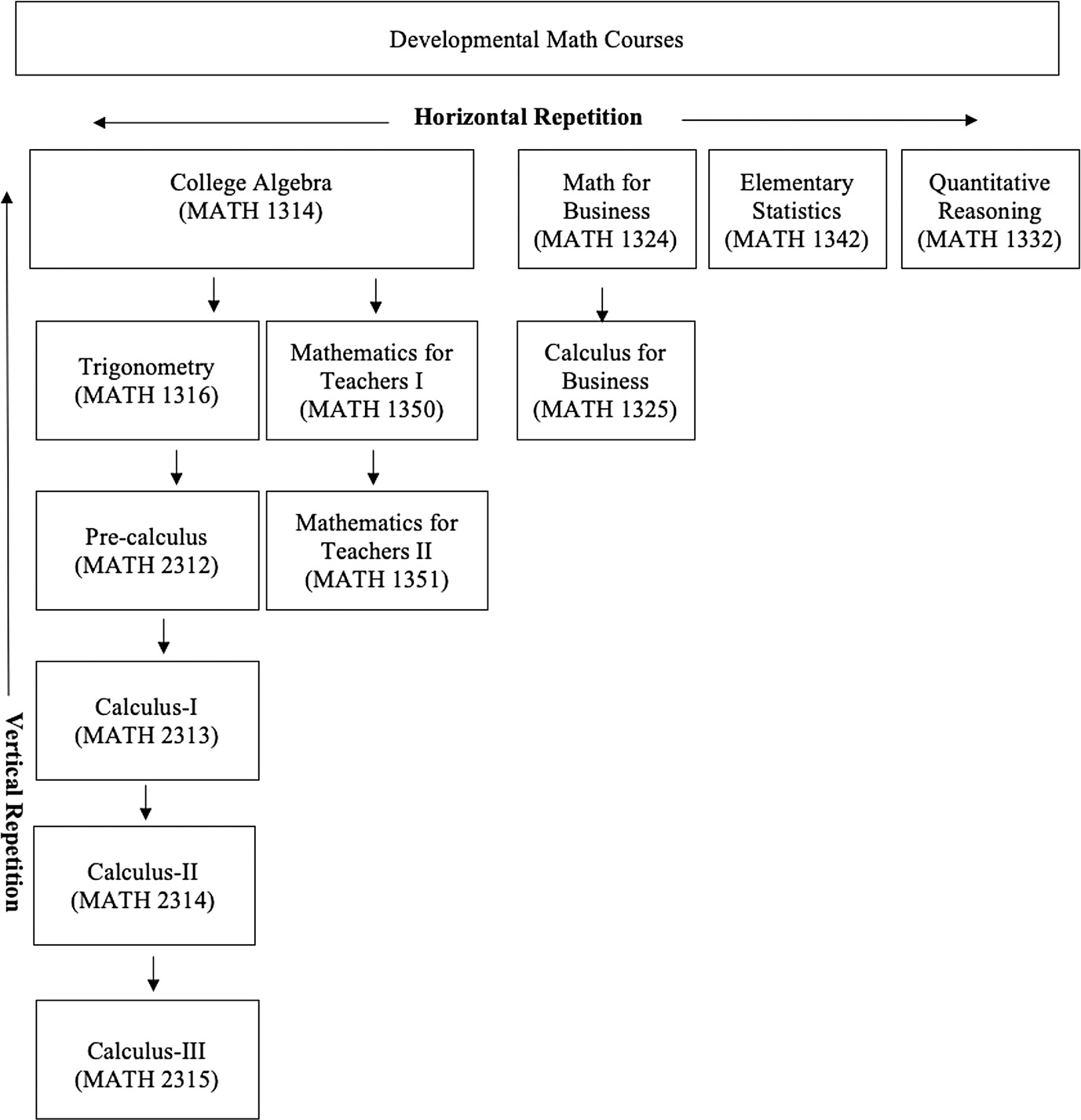
Horizontal and Vertical Course Repetitions in Mathematics. Figure shows names and course numbers for 12 types of college-level math offered at public institutions of higher education in Texas. Horizontal repetition occurs when students complete an introductory math course and then enroll in a different introductory math course (i.e., it only occurs among introductory coursework). Vertical repetition occurs when students repeat a math course in the same sequence (repeating the same specific course or one earlier in the same sequence).
We merged our resulting list of college-level math courses with the ERC’s student-level transcript data (referred to as THECB “schedule” data). For semesters enrolled, we identified each student’s math courses—creating indicators of college-level math courses that they had passed with a D or above—across both community colleges and universities. We created a flag for the first instance when they took and passed a college-level math course. We captured it as their first college-level math course completed.
The math course identifiers allowed us to determine which students repeated math courses and helped us narrow our analytic samples to examine the two types of math course repetition. We created two distinct (though overlapping) analytic samples: 1) introductory college-level math completers, which includes community transfer students who completed at least one of the four introductory college-level math courses (college algebra, elementary statistics, quantitative reasoning, and business for math) with a passing grade at a community college (N = 12,254); 2) any college-level math completers, which includes community college transfer students who completed any of 12 college-level mathematics courses with a passing grade at a community college (N = 13,908).
Analytic Strategy
We used descriptive statistics to examine each type of math course repetition, where it occurs (at the community college level versus at the university level), and the characteristics of students who experienced it (RQ1). We then used ordinary least squares (OLS) regression to examine which student background characteristics and academic experiences predict each type of math course repetition, holding other measures constant (RQ2). To address the final research question (RQ3), we fitted OLS regression models to examine the relationship between each type of math course repetition (with separate regressions for horizontal and vertical repetition indicators) and each college outcome. Then to examine how the presence and location of repetition predicts outcomes, we ran OLS models that included a categorical measure of repetition and location (replacing the dichotomous measure of course repetition) capturing four conditions: never repeated, repeated course at a community college, repeated at a university, and repeated at both community college and university. For our dichotomous outcome, baccalaureate attainment, we also ran logistic regressions, as is sometimes preferred for binary outcomes. We found similar results using OLS (an approach referred to as a linear probability model). We present results from the linear probability model because it improves interpretability of the results; it allows readers to interpret a given coefficient as the change in the predicted probability of the outcome per additional unit in the independent variable.
We ran separate regression models for each math repetition type to estimate the relationship between each type of math course repetition and our four outcomes: cumulative GPA, bachelor’s degree attainment, time to a bachelor’s degree, and excess credits. The models included our variable of interest (dichotomous indicator of either horizontal or vertical course repetition); demographic background variables; academic experiences (student enrollment patterns, associate degree status, major); and achievement indicators (earned dev-ed math credits, earned dual enrollment credits, and GPA), described in the sections below. Because transfer rates and transfer students’ baccalaureate degree attainment vary across institutions, we included fixed effects for feeder (pre-transfer) community college and destination university in all regression models to help address this endogeneity (Cameron & Miller, 2015).1 We performed regressions predicting cumulative GPA and baccalaureate degree attainment on the full analytic samples. For the regression analyses run on time to bachelor’s degree and on excess credits, we restricted the analytic samples to only students who had earned a bachelor’s degree because we could assess those outcomes only for baccalaureate recipients. In the analyses predicting time to degree and excess credits, following the example of Fink et al. (2018), we excluded students with fewer than 80 cumulative credits, because those students had likely earned credits that were not captured in state administrative data—this often occurs when students earn some credits from out of state or from private institutions.
Independent Variables of Interest: Horizontal and Vertical Math Course Repetition
Horizontal repetition occurs among students who previously completed introductory collegelevel math (e.g., college algebra, math for business, quantitative reasoning, or elementary statistics) with a passing grade when they subsequently take a different introductory collegelevel math course. As shown in Fig. 1, horizontal repetition occurs among students who take more than one introductory math course at the same level. For instance, horizontal repetition occurs when a community college student takes college algebra in the first semester and then takes quantitative reasoning in the second semester even though they have already satisfied the introductory college-level math requirement. Vertical repetition could occur among students who completed any college-level math course, if they retake the same course or take a lower college-level math course within a prescribed sequence—duplicating a step within the same math sequence. For example, vertical repetition occurs when a student takes college algebra or trigonometry after having completed trigonometry with a passing grade.
We created a horizontal repetition indicator to capture whether students took multiple first-time college-level math courses (college algebra, math for business, elementary statistics, and quantitative reasoning) and a vertical repetition indicator to capture whether students took redundant courses in a specific sequence (e.g., repeating same course or lower in the college algebra or business math sequence). Because of our interest in community college transfer students and the potential for course redundancy when moving between institutions, we also captured where course redundancy occurred (at the community college or university) among those who had experienced either type of math course repetition. We used the measures capturing location of course repetition in descriptive and inferential analyses.
Additional Variables
Table 1 describes our variables, including our independent variables of interest; additional predictors associated with student outcomes (e.g., demographic characteristics, enrollment patterns, and achievement measures); and outcomes measures. We captured various demographic measures—such as race and ethnicity, gender, age, and financial aid receipt—associated with community college persistence and transfer (Bailey et al., 2005; Schudde, 2019). Because family income is available only for students who filed for financial aid, we could not include the measure in our models; doing so would have drastically reduced the final analytic sample. Instead, we included indicators for whether students had applied for financial aid and whether they had ever received the Pell Grant.2
Table 1.
Description of Variables
| Variable name | Description | Introductory Math Completersa | All Math Completersb |
|---|---|---|---|
| Mean | Mean | ||
|
| |||
| Independent Variables | |||
| Independent Variable of Interest | |||
| Horizontal Repetition | Dichotomous measure indicating student repeated entry college-level math course | 0.372 | |
| Vertical Repetition | Dichotomous measure indicating student repeated same or previous course in college-level math sequence | 0.166 | |
| Additional Repetition Descriptors c | |||
| Occurred at University | Flag capturing whether repetition occurred at a four-year institution | 0.183 | 0.094 |
| Occurred at Comm. College | Flag capturing whether repetition occurred at a community college | 0.213 | 0.082 |
| Within the college | Among those who experienced math course repetition at a community college, flag for whether those course repetitions occurred within the same community college | 0.912 | 0.910 |
| Demographics | |||
| Race | Reported race/ethnicity of the student, obtained from THECB enrollment data | ||
| White (reference) | Identified as non-Hispanic White | 0.436 | 0.442 |
| Black | Identified as non-Hispanic Black | 0.067 | 0.063 |
| Asian | Identified as Asian | 0.045 | 0.053 |
| Hispanic | Identified as Hispanic | 0.403 | 0.392 |
| Other Race | Identified as another race, including Native Hawaiian or Other Pacific Islander, Native American and unknown | 0.003 | 0.002 |
| Two or More Races | Identified as two or more races | 0.046 | 0.047 |
| Female | Dichotomous indicator of identifying as female (vs. male) in THECB enrollment data | 0.582 | 0.555 |
| Age | Age of the student at initial enrollment; obtained from THECB enrollment data | 18.664 | 18.638 |
| Financial Aid Applicant | Dichotomous measure of whether student had a FADS file in the financial aid data in the first year, which indicates whether the student ever filed for federal or state financial aid; obtained from THECB Financial Aid Data System (FADS) data | 0.790 | 0.789 |
| Pell Grant Recipient | Indicator of whether student ever received Pell Grant in the first year; obtained from THECB Financial Aid Data System (FADS) data | 0.418 | 0.408 |
| Enrollment Intensity | Categorical measure of whether student enrolled part time, full time, or a mix of part and full time in the first year enrolled, derived from schedule data; full time = enrolled in at least 12 credits per term in year 1, part time = enrolled in less than 12 credits per term, mixed intensity = mix of full and part time across terms | ||
| Full Time (reference) | 0.639 | 0.645 | |
| Part Time | 0.091 | 0.087 | |
| Mixed Intensity | 0.270 | 0.268 | |
| Other Academic Measures | |||
| Stop-Out Count | The number of periods of nonenrollment followed by enrollment (i.e., count of terms in which a student enrolled during a Fall/Spring term after nonenrollment in the prior term, excluding summer); derived from THECB enrollment data | 0.204 | 0.199 |
| Earned Associate Degree | Dichotomous measure of whether the student earned an associate degree; obtained from THECB graduation data | 0.385 | 0.376 |
| Switched Major | Indicates whether student switched their major after transferring to a four-year institution. Measure derived from program codes in enrollment data; students who switched broad Classification of Instructional Programs (CIP) codes (first two digits) between the time of transfer and their last enrolled term at university coded as switching majors | 0.409 | 0.404 |
| Initial Major | Categorical measure of students’ first major at community college, obtained from enrollment data and constructed using first two digits of CIP code | ||
| Humanities and Liberal Arts (reference) | Includes: Liberal Arts, Interdisciplinary Studies, Philosophy, Theology, History | 0.430 | 0.430 |
| Industrial, Manufacturing, and Construction | Agriculture, Construction, Mechanic, Precision, Transportation | 0.023 | 0.021 |
| Natural Sciences | Natural Sciences, Biology, Physics, Science Technologies | 0.052 | 0.056 |
| Business | Architecture, Business | 0.114 | 0.109 |
| Social and Behavioral Sciences | Cultural Studies, Family Studies, Legal Studies, Psychology, Social Sciences | 0.042 | 0.038 |
| Communication Sciences | Communication, Communication Technologies, Library Science | 0.014 | 0.013 |
| Literature, Linguistics, and Fine Arts | Linguistics, English, Visual and Performing Arts | 0.039 | 0.037 |
| Math and Computer Sciences | Computer Science, Mathematics | 0.028 | 0.042 |
| Education, Social Services, and Policy | Education, Security, Public Administration | 0.090 | 0.084 |
| Engineering and Related Fields | Engineering, Engineering Technologies | 0.026 | 0.037 |
| Service Oriented | Personal and Culinary Services, Military Studies, Parks and Recreation, Leisure | 0.024 | 0.022 |
| Health | Health-Related Programs and Residency Programs | 0.078 | 0.073 |
| Other | Other Majors | 0.039 | 0.039 |
| Earned Dual Credit | Categorical measure of whether the student earned a dual credit; derived from THECB schedule data | 0.248 | 0.222 |
| Earned Dev-Ed Math Credit | Categorical measure of whether the student earned any dev-ed math credit; obtained from THECB schedule data | 0.287 | 0.301 |
| First Math Course Graded | First passing grade student earned in a college-level math course | ||
| B or better | 0.679 | 0.684 | |
| C | 0.248 | 0.246 | |
| D (reference) | 0.073 | 0.070 | |
| Outcomes: | |||
| Cumulative college-level GPA | Cumulative grade point average from college-level courses (excludes remedial coursework grades); derived from THECB schedule data | 3.358 | 3.374 |
| Bachelor’s Degree | Dichotomous measure of whether student earned a bachelor’s degree within 7 years of initial enrollment; obtained from THECB graduation data | 0.721 | 0.730 |
| Time to a Bachelor’s Degree | Number of semesters student takes to complete a bachelor’s degree within 7 years (analytic samples restricted to degree-earners; N = 7,132 for introductory math completers and N = 8,078 for any math completers); derived from THECB graduation data and enrollment data | 14.980 | 14.959 |
| Excess Credits | College course credits that students earned more than 120 credits; derived from THECB graduation and schedule data | 13.900 | 13.882 |
| N | 12,254 | 13,908 | |
Introductory college-level math completers comprise the population of students eligible for horizontal course repetition (may repeat entry-level math course)
All college-level math course completers comprise the population of students eligible for vertical repetition (may repeat the same or lower math course within a sequence)
The indicators of whether the repetition occurred at a university or community college were used them to explore descriptive patterns for our first research question. We included a categorical measure capturing presence and location of repetition—never repeated, repeated at community college, repeated at university, repeated at both—in additional regression models (see Tables 5 and 7)
First math course grade was included only in the regression models predicting course repetition and cumulative GPA (models for other student outcomes controlled for cumulative GPA, which includes math grades)
Enrollment patterns, such as attending part time or stopping out (taking a break from college followed by re-enrollment), have been linked to persistence and degree attainment (Bailey et al., 2015; Fike & Fike, 2008; Park, 2012). To capture student enrollment patterns, we created measures of first-year enrollment intensity—captured as part-time, full-time, or mixed enrollment—and total number of stop-outs. We also included other academic measures likely to predict bachelor’s degree attainment, such as cumulative GPA across all college credits, associate degree attainment, and participation in dual credit or dev-ed coursework (Bahr, 2008; Belfield, 2013; Wang et al., 2015, 2017). In the regression models predicting math course repetition, we also included a measure of students’ grade in their first college-level math course.
We created indicators for students’ initial majors, using the first two digits of their Classification of Instructional Programs (CIP) code from their community college. To capture whether students switched majors after transferring, we also created a dichotomous measure capturing whether students had a different broad major field in the semester directly before transfer and in their final semester at the university.3 We anticipated that students who switched majors after transfer might require additional credits to earn a baccalaureate degree, as different majors sometimes require different math coursework (Bailey et al., 2016).
Descriptive Statistics
Table 1 also presents variable means for both analytic samples: introductory math completers, the subpopulation of transfer students in which we examine horizontal repetition, and all math completers, the subpopulation of transfer students in which we examine vertical repetition. In both analytic samples of community college transfer students, approximately 44% of the students identified at White, 40% as Hispanic, 7% as Black, between 4 and 5% as Asian, and the remainder as another race or more than one race. About four-fifths of the students filed for financial aid in the first year, and two-fifths of students received a Pell Grant in the first year. A majority of students—63%—enrolled full time in college during their first year, with the bulk of remaining students attending as a mix of part and full time across terms. Twenty-nine percent of students in the introductory math completers subpopulation had previously completed dev-ed math, whereas 30% of all college-level math completers had. The most common initial college major was humanities and liberal arts, which includes general studies, and almost 40% of students switched majors after transfer (where their first term post-transfer had a different two-digit CIP code than their last term at the community college).
Limitations
Because we relied on regression, the results we present do not represent causal relationships but rather correlations. However, given our interest in understanding the prevalence of math course repetition and predictors of repetition, using descriptive statistics and regressions with covariates is an appropriate strategy for addressing our research questions. To minimize bias in the regression for both RQ2 and RQ3, we included controls for demographic background, academic background and experiences, major choice, and community college and university fixed-effects; but it is feasible that omitted variables may explain at least some of the observed patterns. Despite these potential limitations, the dearth of literature on course repetition and its relationship with college outcomes means that our analysis stands to make a strong contribution to higher education research and can serve as a base for future research in this area.
Results
In the following sections, we present the descriptive and inferential findings from our analyses. First, we describe the prevalence of horizontal and vertical math course repetition among community college transfer students and illustrate which students are most likely to experience math course repetition (and at which institutional level). We show the characteristics of students who experience horizontal and vertical math course repetition compared with those of their peers who do not experience repetition. Next, we examine predictors of each type of math course repetition, exploring whether observed descriptive patterns hold when statistical controls are included. Finally, we present estimates of the association between each type of math course repetition and college outcomes and estimates capturing the association between the location of course repetition and student outcomes.
Math Course Repetition: Exploring Descriptive Patterns
Descriptive statistics from Table 1 illustrate a high prevalence of horizontal repetition among our sample of introductory college-level math completers. Two-fifths of introductory math completers (37.2%) took at least one extra introductory college-level math course.4 Vertical repetition was less common, but still substantial: 16.6% of students who had previously completed a college-level math course retook the same course or a lower course in the same math sequence.5 We also explored whether the course repetition occurred prior to transfer, at the community college, or post-transfer, at the university. Transfer students who experienced horizontal repetition primarily experienced that repetition at a community college (21.3% of all introductory math completers) rather than at university (18.3% of introductory math completers). Note that some students—about 2.4% of introductory math completers—experienced horizontal repetition at both the university and the community college. For introductory math course completers who experienced horizontal repetition at the community college, 91% of pre-transfer horizontal course repetition occurred at the same community college (i.e., repetition was not attributed to the student’s repeating the introductory math course at a different community college). College-level math course completers who experienced vertical repetition were slightly more likely to experience it at the university level (9.4% of all math completers) than at the community college (8.2%) (and about 1% of students experienced vertical repetition within both sectors). Among students who experienced vertical repetition at the community college, 91% repeated that coursework within a single community college rather than across multiple community colleges.
Table 2 shows student background characteristics, college experiences, and student outcomes across course repetition status for both analytic samples, with percentages displayed for dichotomous measures and means for continuous measures. We distinguish between horizontal repeaters (or nonrepeaters) in the analytic sample of introductory math completers and vertical repeaters (or nonrepeaters) in the analytic sample of any college math course completers. Horizontal repetition was particularly common among Asian students—nearly half (48%) of students who identified as Asian took more than one different introductory math course. The average for White, Black, and Hispanic students varied (37%, 45% and 34%, respectively). Among introductory math course completers, women were more likely to experience horizontal math course repetition than men. Among all collegelevel math course completers, men were more likely to experience vertical math course repetition than women. In both analytic subsamples, students who applied for financial aid appeared less likely to experience either horizontal and vertical repetition than their peers who did not file a FAFSA. We also observe variation in horizontal repetition across enrollment intensity among introductory math completers, where students who enrolled part time during their first year of college appeared less likely to repeat math courses horizontally than their full-time or mixed-intensity peers. The descriptive results provide support for our decision to include demographic and academic measures in the regression models.
Table 2.
Description of vertical and horizontal repeaters compared with nonrepeaters
| Introductory Math Completers | Any Math Completers | |||||
|---|---|---|---|---|---|---|
|
|
|
|||||
| Horizontal Repetition | Vertical Repetition | |||||
|
|
|
|||||
| Yes | No | N | Yes | No | N | |
| % or Mean | % or Mean | % or Mean | % or Mean | |||
|
| ||||||
| Race | ||||||
| White | 36.6% | 63.4% | 5337 | 16.7% | 83.3% | 6150 |
| Black | 45.2% | 54.8% | 821 | 17.6% | 82.4% | 875 |
| Asian | 47.9% | 52.1% | 557 | 16.8% | 83.2% | 731 |
| Hispanic | 34.1% | 65.9% | 4942 | 16.5% | 83.5% | 5458 |
| Other | 43.8% | 56.3% | 32 | 20.6% | 79.4% | 34 |
| Two or More | 46.2% | 53.8% | 565 | 15.3% | 84.7% | 660 |
| Gender | ||||||
| Female | 39.4% | 60.6% | 7133 | 14.9% | 85.1% | 7713 |
| Male | 34.0% | 66.0% | 5121 | 18.9% | 81.1% | 6195 |
| Age | 18.525 | 18.746 | 12,254 | 18.327 | 18.7 | 13,908 |
| Financial Aid Applicant | ||||||
| Yes | 36.6% | 63.4% | 9684 | 16.1% | 83.9% | 10,972 |
| No | 39.1% | 60.9% | 2570 | 18.5% | 81.5% | 2936 |
| Pell-Grant Recipient | ||||||
| Yes | 35.5% | 64.5% | 5120 | 14.8% | 85.2% | 5679 |
| No | 38.4% | 61.6% | 7134 | 17.9% | 82.1% | 8229 |
| Enrollment Intensity | ||||||
| Full time | 37.5% | 62.5% | 7835 | 16.1% | 83.9% | 8967 |
| Part time | 32.9% | 67.1% | 1111 | 16.1% | 83.9% | 1213 |
| Mixed enrollment | 37.8% | 62.2% | 3308 | 18.1% | 81.9% | 3728 |
| Stop-Out Count | .208 | .201 | 12,254 | .203 | .198 | 13,908 |
| Earned Associate Degree | ||||||
| Yes | 38.1% | 61.9% | 4715 | 13.8% | 86.2% | 5225 |
| No | 36.6% | 63.4% | 7539 | 18.3% | 81.7% | 8683 |
| Switched Major | ||||||
| Major switcher | 41.3% | 58.7% | 5012 | 18.3% | 81.7% | 5622 |
| Non-major switcher | 34.3% | 65.7% | 7242 | 15.5% | 84.5% | 8286 |
| Initial Major | ||||||
| Humanities and Liberal Arts | 39.4% | 60.6% | 5274 | 15.3% | 84.7% | 5975 |
| Industrial, Manufacturing, and Construction | 37.0% | 63.0% | 281 | 15.4% | 84.6% | 292 |
| Natural Sciences | 40.9% | 59.1% | 641 | 18.4% | 81.6% | 782 |
| Business | 37.4% | 62.6% | 1394 | 18.3% | 81.7% | 1519 |
| Social and Behavioral Sciences | 32.7% | 67.3% | 511 | 13.4% | 86.6% | 530 |
| Communication Sciences | 33.3% | 66.7% | 171 | 9.2% | 90.8% | 174 |
| Literature, Linguistics, and Fine Arts | 30.9% | 69.1% | 482 | 12.2% | 87.8% | 508 |
| Math and Computer Sciences | 26.4% | 73.6% | 348 | 31.3% | 68.7% | 584 |
| Education, Social Services, and Policy | 24.7% | 75.3% | 1104 | 13.5% | 86.5% | 1162 |
| Engineering | 24.0% | 76.0% | 317 | 24.6% | 75.4% | 517 |
| Service Oriented | 43.3% | 56.7% | 300 | 21.5% | 78.5% | 311 |
| Health | 47.8% | 52.2% | 959 | 14.6% | 85.4% | 1,010 |
| Other | 39.8% | 60.2% | 472 | 19.3% | 80.7% | 544 |
| Earned Dual Credit | ||||||
| Yes | 34.1% | 65.9% | 3516 | 16.5% | 83.5% | 4193 |
| No | 38.4% | 61.6% | 8738 | 16.7% | 83.3% | 9715 |
| Earned Dev-Ed Credit | ||||||
| Yes | 37.2% | 62.8% | 3039 | 14.4% | 85.6% | 3092 |
| No | 37.1% | 62.9% | 9215 | 17.3% | 82.7% | 10,816 |
| First Math Course Grade | ||||||
| B or better | 38.3% | 61.7% | 8324 | 12.9% | 87.1% | 9513 |
| C | 34.4% | 65.6% | 3040 | 15.4% | 84.6% | 3418 |
| D | 36.2% | 63.8% | 890 | 57.1% | 42.9% | 977 |
| Outcomes | ||||||
| Cumulative GPA | 3.359 | 3.358 | 12,254 | 3.241 | 3.400 | 13,908 |
| Bachelor’s Degree | .722 | .720 | 12,254 | .669 | .742 | 13,908 |
| Time to Bachelor’s Degree | 15.16 | 14.873 | 8798 | 15.393 | 14.88 | 10,105 |
| Excess Credits | 16.999 | 12.053 | 8798 | 20.004 | 12.774 | 10,105 |
| Total (N) | 4554 | 7700 | 2314 | 11,594 | ||
N (introductory math completers) = 12,254. N (all math course completers) = 13,908. The table shows the characteristics of students who experienced (vs. never experienced) horizontal and vertical math course repetition. It presents the number of community college transfer students (N) within different repetition types and the corresponding percentage (%) of students (for categorical measures) or means (for continuous measures, including three of the outcomes: cumulative GPA, time to degree, and excess credits). Within each analytic sample (introductory math vs. all math course completers), the percentages add up to 100% across the row
Table 2 also shows college student outcomes of transfer students in the two subpopulations by their horizontal and vertical repetition status. Among introductory math completers, the average cumulative GPA is quite similar across horizontal repetition status (3.36 for both repeaters and nonrepeaters). Bachelor’s degree attainment appears similar among horizontal repeaters and nonrepeaters. Among baccalaureate recipients, students who experienced horizontal repetition accumulated about five additional credits on average and took 0.3 semester longer to complete a baccalaureate degree. The patterns by vertical repetition status look slightly different. Among all math course completers, students who experienced vertical repetition had slightly lower GPAs than those who did not experience vertical math course repetition. Vertical repeaters appeared less likely to earn a bachelor’s degree within seven years: 74% of vertical nonrepeaters earned a degree compared with 67% of vertical repeaters. Among baccalaureate recipients, vertical repeaters took slightly longer to finish and accumulated more excess credits than nonvertical repeaters.
Predictors of Horizontal and Vertical Math Course Repetition
Table 3 presents regression results from our models that estimate predictors of each type of math course repetition, allowing us to consider how the patterns we observed in Table 2 hold after covariate adjustment. As in our descriptive patterns above, there appears to be a correlation between race/ethnicity and horizontal repetition. Among introductory college-level math completers, students who identify as Hispanic, Black, and more than one race have a higher probability of horizontal repetition than White students. Despite the descriptive finding of a higher prevalence of horizontal repetition among Asian students compared with White students, the Asian coefficient was not significant once we controlled for other covariates in a regression model (i.e., the inclusion of covariates explained away observed variation in horizontal repetition across Asian and White students). Women appear more likely to experience horizontal repetition and less likely to experience vertical repetition than men, even after controlling for other demographic and academic characteristics. Age appears to negatively predict both forms of math course repetition. Among introductory math completers, each additional year of age is associated with a 0.4-percentage-point decrease in the probability of experiencing horizontal repetition (β = − 0.004, SE = 0.001, p < 0.001); among any college-level math completers, each additional year is associated with a 0.2-percentage-point decrease in the probability of vertical repetition (β = − 0.002, SE = 0.001, p < 0.05).
Table 3.
Predictors of horizontal and vertical math course repetition: regression results
| Variables | Course Repetition Outcome | |
|---|---|---|
|
|
||
| Horizontal | Vertical | |
|
| ||
| Race (Reference = White) | ||
| Asian | 0.018 | 0.005 |
| (0.022) | (0.015) | |
| Black | 0.059** | 0.006 |
| (0.019) | (0.014) | |
| Hispanic | 0.023* | 0.013 |
| (0.011) | (0.008) | |
| Two or More | 0.058** | −0.022 |
| (0.021) | (0.014) | |
| Other | 0.076 | 0.033 |
| (0.083) | (0.060) | |
| Female | 0.041*** | −0.017** |
| (0.009) | (0.006) | |
| Age | −0.004** | −0.002* |
| (0.001) | (0.001) | |
| Pell Grant Recipient | −0.007 | −0.004 |
| (0.010) | (0.007) | |
| Financial Aid Applicant | −0.011 | −0.015 |
| (0.012) | (0.008) | |
| Initial Major (Reference = Humanities and Liberal Arts) | ||
| Industrial, Manufacturing, and Construction | 0.041 | −0.031 |
| (0.030) | (0.022) | |
| Natural Sciences | 0.051* | 0.004 |
| (0.020) | (0.014) | |
| Business | −0.005 | 0.005 |
| (0.015) | (0.011) | |
| Social and Behavioral Sciences | −0.027 | −0.025 |
| (0.022) | (0.016) | |
| Communication Sciences | −0.027 | −0.029 |
| (0.037) | (0.027) | |
| Literature, Linguistics, and Fine Arts | −0.058* | −0.046** |
| (0.023) | (0.017) | |
| Math and Computer Sciences | −0.082** | 0.090*** |
| (0.026) | (0.016) | |
| Education, Social Services, and Policy | −0.100*** | −0.013 |
| (0.016) | (0.012) | |
| Engineering and Related Fields | −0.117*** | 0.112*** |
| (0.028) | (0.017) | |
| Service Oriented | 0.066* | 0.013 |
| (0.029) | (0.021) | |
| Health | 0.073*** | 0.026* |
| (0.017) | (0.013) | |
| Other | −0.026 | −0.005 |
| (0.025) | (0.017) | |
| Enrollment Intensity (Reference = Full time) | ||
| Part time | −0.041** | −0.008 |
| (0.015) | (0.011) | |
| Mixed Enrollment | 0.010 | −0.001 |
| (0.010) | (0.007) | |
| Earned a Dev-Ed Math Credit | −0.003 | −0.013 |
| (0.011) | (0.008) | |
| Earned Dual Credit | −0.026** | −0.006 |
| (0.010) | (0.007) | |
| First Math Course Grade (Reference = D) | ||
| B or Higher | 0.013 | −0.455*** |
| (0.017) | (0.012) | |
| C | −0.019 | −0.426*** |
| (0.018) | (0.013) | |
| Cohort (Reference = Fall 2012) | −0.027** | 0.001 |
| (0.008) | (0.006) | |
| Constant | 0.191 | 0.582*** |
| (0.158) | (0.101) | |
| Observations | 12,254 | 13,908 |
| R-squared | 0.112 | 0.151 |
The table presents coefficients with standard errors in parentheses from ordinary least squares regression models performed on a pooled sample of community college students who entered college in Fall 2011 or Fall 2012, where each column represents a separate regression. Both models include students who transferred to a four-year institution within first 3 years of initial enrollment and capture course repetition over 7 years; the analysis in column 1 includes introductory math completers as the analytic sample, and the analysis in column 2 includes students who previously completed any college-level math course. All models include community college and university fixed effects
p < 0.001
p < 0.01
p < 0.05
It seems that major does play some role in math course repetition. Among introductory college-level math completers, students in humanities and liberal arts (the most common broad major, which includes general studies students) appear more likely to experience horizontal repetition than students with most other broad majors. However, among students who completed any college-level math course, students in STEM-related majors are more likely than those in humanities and liberal arts to experience vertical repetition. For example, students studying math and computer sciences are nine percentage points more likely to repeat vertically than the reference group (β = 0.090, SE = 0.016, p < 0.001). Among all college-level math completers, students who passed their first college-level math course with B or better or C are significantly less likely to experience vertical repetition than are students with a D.
The Relationship Between Math Course Repetition and Student Outcomes
To understand whether the relationship between each type of course repetition and college outcomes holds after controlling for student background and college experiences, we ran a series of regressions. Table 4 presents results from regressions run on the analytic sample of introductory math course completers estimating the relationship between horizontal math course repetition—a dichotomous indicator—and four student outcomes: cumulative GPA, baccalaureate attainment, time to degree, and excess credits. Results reveal a positive relationship between horizontal repetition status and time to a baccalaureate degree and excess credits, where horizontal repetition is associated with an increase of 0.24 semester (β = 0.242, SE = 0.058, p < 0.001) and an increase of 3.6 excess credits (β = 3.570, SE = 0.382, p < 0.001). Also, there is a small negative6 correlation between horizontal repetition status and cumulative GPA (β = − 0.018, SE = 0.008, p < 0.05).
Table 4.
Relationship Between Horizontal Math Course Repetition and Student Outcomes
| Variables | Outcomes | |||
|---|---|---|---|---|
|
|
||||
| Cumulative GPA | Bachelor’s Degree Attainment | Time to Degree | Excess Credits | |
|
| ||||
| Horizontal Repetition | −0.018* | 0.008 | 0.242*** | 3.570*** |
| (0.008) | (0.008) | (0.058) | (0.382) | |
| Race (Reference = White) | ||||
| Asian | −0.003 | −0.004 | 0.147 | 4.642*** |
| (0.019) | (0.019) | (0.144) | (0.944) | |
| Black | −0.128*** | 0.002 | 0.120 | 2.846*** |
| (0.016) | (0.016) | (0.126) | (0.824) | |
| Hispanic | −0.051*** | 0.015 | 0.145* | 0.721 |
| (0.009) | (0.009) | (0.070) | (0.457) | |
| Two or More Races | −0.059*** | −0.027 | 0.083 | 1.318 |
| (0.018) | (0.018) | (0.136) | (0.892) | |
| Other | −0.036 | 0.049 | −0.150 | −2.949 |
| (0.070) | (0.071) | (0.523) | (3.429) | |
| Female | 0.085*** | 0.037*** | −0.427*** | −2.418*** |
| (0.008) | (0.008) | (0.058) | (0.380) | |
| Age | 0.019*** | 0.000 | −0.061*** | −0.491*** |
| (0.001) | (0.001) | (0.009) | (0.059) | |
| Pell Grant Recipient | −0.021* | −0.039*** | 0.097 | 0.713 |
| (0.009) | (0.009) | (0.067) | (0.442) | |
| Financial Aid Applicant | 0.003 | 0.002 | −0.024 | −0.137 |
| (0.010) | (0.010) | (0.074) | (0.488) | |
| Enrollment Intensity (Reference = Full time) | ||||
| Part time | −0.088*** | −0.103*** | 0.864*** | −2.668*** |
| (0.013) | (0.013) | (0.104) | (0.685) | |
| Mixed Enrollment | −0.077*** | −0.064*** | 0.519*** | −1.871*** |
| (0.008) | (0.009) | (0.065) | (0.428) | |
| Stop-Out Count | −0.049*** | −0.126*** | 0.454*** | −1.807*** |
| (0.008) | (0.008) | (0.073) | (0.476) | |
| Earned Associate Degree | 0.091*** | 0.046*** | 0.072 | 2.936*** |
| (0.008) | (0.008) | (0.059) | (0.389) | |
| Switched Major | −0.035*** | −0.009 | 0.309*** | 5.021*** |
| (0.008) | (0.008) | (0.059) | (0.385) | |
| Initial Major (Reference = Humanities and Liberal Arts) | ||||
| Industrial, Manufacturing, and Construc | 0.029 | −0.017 | −0.640*** | 0.370 |
| (0.025) | (0.026) | (0.184) | (1.209) | |
| Natural Sciences | 0.023 | −0.016 | 0.106 | 5.156*** |
| (0.017) | (0.017) | (0.132) | (0.868) | |
| Business | −0.005 | 0.039** | −0.526*** | −2.705*** |
| (0.012) | (0.013) | (0.092) | (0.600) | |
| Social and Behavioral Sciences | 0.021 | 0.037 | −0.380** | −2.536** |
| (0.019) | (0.019) | (0.140) | (0.920) | |
| Communication Sciences | 0.028 | 0.025 | −0.435 | −2.324 |
| (0.031) | (0.031) | (0.232) | (1.521) | |
| Literature, Linguistics, and Fine Arts | 0.050** | −0.025 | 0.205 | 2.856** |
| (0.019) | (0.020) | (0.148) | (0.970) | |
| Math and Computer Sciences | 0.039 | −0.063** | 0.242 | 5.612*** |
| (0.022) | (0.023) | (0.178) | (1.167) | |
| Education, Social Services, and Policy | −0.011 | 0.041** | −0.240* | −1.025 |
| (0.014) | (0.014) | (0.101) | (0.663) | |
| Engineering and Related Fields | 0.010 | −0.053* | 0.868*** | 10.501*** |
| (0.023) | (0.024) | (0.193) | (1.264) | |
| Service Oriented | −0.022 | −0.008 | 0.091 | 3.512** |
| (0.024) | (0.025) | (0.179) | (1.177) | |
| Health | −0.026 | −0.012 | 0.216 | 3.841*** |
| (0.015) | (0.015) | (0.117) | (0.766) | |
| Other | 0.017 | −0.030 | −0.111 | 0.777 |
| (0.021) | (0.021) | (0.153) | (1.006) | |
| Earned a Dev-Ed Math Credit | −0.033*** | −0.007 | 0.394*** | 5.375*** |
| (0.010) | (0.010) | (0.074) | (0.488) | |
| Earned Dual Credit | 0.033*** | 0.047*** | −0.614*** | −7.662*** |
| (0.008) | (0.009) | (0.063) | (0.410) | |
| Cumulative GPA | 0.192*** | −1.129*** | −7.065*** | |
| (0.008) | (0.069) | (0.452) | ||
| First Math Course Grade (Reference = D) | ||||
| B or Higher | 0.539*** | |||
| (0.014) | ||||
| C | 0.169*** | |||
| (0.015) | ||||
| Cohort (Reference = Fall 2012) | 0.010 | 0.001 | −0.074 | −0.403 |
| (0.007) | (0.007) | (0.054) | (0.357) | |
| Constant | 2.285*** | 0.286* | 19.346*** | 36.527*** |
| (0.134) | (0.137) | (1.041) | (6.826) | |
| Observations | 12,254 | 12,254 | 8,798 | 8,798 |
| R-squared | 0.346 | 0.241 | 0.179 | 0.254 |
The table presents coefficients with standard errors in parentheses from ordinary least squares regression models performed on a pooled sample of community college students who entered college in Fall 2011 or Fall 2012, where each column represents a separate regression for each outcome. Regressions for GPA and bachelor’s degree attainment include full analytic sample. Regressions for time to degree (captured in semesters) and excess credits include only baccalaureate recipients with more than 80 college-level semester credits. All models include community college and university fixed effects
p < 0.001
p < 0.01
p < 0.05
Table 5 conducts a similar analysis to Table 4, but replaces the independent variable of interest to examine the relationship between a 4-category measure of horizontal repetition–capturing both presence and location of horizontal repetition—and student outcomes. Where results from Table 4—which used a dichotomous measure capturing whether students ever experienced horizontal repetition—illustrate a negative relationship between horizontal repetition and GPA, results from Table 5 suggest that horizontal repetition experienced at the university drives that relationship. Repeating an introductory course at the university is associated with a 0.05-unit decrease in cumulative GPA (or 0.1-unit decrease, for those experiencing horizontal repetition at both institution types) compared with never repeating introductory math (β = − 0.045, SE = 0.010, p < 0.001; β = − 0.103, SE = 0.023, p < 0.001). We observe a similar relationship between location of horizontal repetition and time to degree: introductory math course repetition at the university, as shown in Table 5, appears to drive the observed positive relationship between the dichotomous indicator of horizontal repetition and time to degree we presented in Table 4. The null overall relationship between horizontal math repetition and bachelor’s degree attainment appears to be driven by the conflicting roles played by repeating introductory math coursework at the community college and the university—horizontal repetition at the community college, compared with no repetition, positively and significantly predicts degree attainment; repetition at the university (or at both community college and university) does not appear to predict degree attainment (the coefficients are negative and nonsignificant).
Table 5.
Relationship between horizontal math course location and student outcomes
| Cumulative GPA | Bachelor’s Degree Attainment | Time to Degree | Excess Credits | |
|---|---|---|---|---|
|
| ||||
| Location of Horizontal Repetition (Reference = No Repetition) | ||||
| Horizontal Repetition at community college | 0.015 | 0.030** | 0.053 | 2.221*** |
| (0.010 | (0.010) | (0.070) | (0.459) | |
| Horizontal Repetition at university | −0.045*** | −0.013 | 0.489*** | 5.051*** |
| (0.010) | (0.011) | (0.083) | (0.542) | |
| Horizontal Repetition at both | −0.103*** | −0.034 | 0.541** | 7.695*** |
| (0.023) | (0.024) | (0.185) | (1.216) | |
| Student Backgrounds | YES | YES | YES | YES |
| College Experiences | YES | YES | YES | YES |
| Academic Experiences | YES | YES | YES | YES |
| Institutional Fixed Effects | YES | YES | YES | YES |
| Observations | 12,254 | 12,254 | 8,798 | 8,798 |
| R-squared | 0.348 | 0.242 | 0.181 | 0.257 |
The table presents coefficients with standard errors in parentheses from ordinary least squares regression models performed on a pooled sample of community college students who entered college in Fall 2011 or Fall 2012, where each column represents a separate regression for each outcome. Regressions for GPA and bachelor’s degree attainment include full analytic sample. Regressions for time to degree (captured in semesters) and excess credits include only baccalaureate recipients with more than 80 college-level semester credits. All models include community college and university fixed effects. See full table with all regression coefficients in appendix Table A9
p < 0.001
p < 0.01
p < 0.05
Table 6 presents results from regressions estimating the relationship between vertical math course repetition—a dichotomous indicator—and student outcomes among all college-level math course completers. After the full set of statistical controls were included, the results suggest that experiencing vertical course repetition—compared with never experiencing vertical course repetition—generally predicts poorer performance on all student outcomes we captured. Vertical math course repetition is associated with a 0.04-unit decrease in students’ cumulative GPA and a 5.1-percentage-point decrease in the probability of earning a baccalaureate degree (β = − 0.037, SE = 0.010, p < 0.001; β = − 0.051, SE = 0.009, p < 0.001). Among students who earned a bachelor’s degree, vertical course repetition is correlated with a 0.6-semester increase in time to degree and a 7.4-credit increase in excess credits (β = 0.537, SE = 0.072, p < 0.001; β = 7.421, SE = 0.475, p < 0.001).
Table 6.
Relationship Between Vertical Math Course Repetition and Student Outcomes
| Variables | Outcomes | |||
|---|---|---|---|---|
|
|
||||
| Cumulative GPA | Bachelor’s Degree Attainment | Time to Degree | Excess Credits | |
|
| ||||
| Vertical Repetition | −0.037*** | −0.051*** | 0.537*** | 7.421*** |
| (0.010) | (0.009) | (0.072) | (0.475) | |
| Race (Reference = White) | ||||
| Asian | −0.001 | −0.001 | 0.183 | 3.930*** |
| (0.017) | (0.017) | (0.126) | (0.830) | |
| Black | −0.125*** | 0.002 | 0.106 | 2.859*** |
| (0.015) | (0.015) | (0.120) | (0.795) | |
| Hispanic | −0.051*** | 0.014 | 0.155* | 0.572 |
| (0.009) | (0.009) | (0.065) | (0.429) | |
| Two or More | −0.060*** | −0.021 | 0.135 | 1.711* |
| (0.016) | (0.016) | (0.125) | (0.822) | |
| Other | −0.007 | 0.022 | −0.064 | −2.013 |
| (0.067) | (0.068) | (0.510) | (3.366) | |
| Female | 0.075*** | 0.038*** | −0.446*** | −2.552*** |
| (0.007) | (0.007) | (0.054) | (0.356) | |
| Age | 0.019*** | −0.001 | −0.070*** | −0.539*** |
| (0.001) | (0.001) | (0.009) | (0.057) | |
| Pell Grant Recipient | −0.021** | −0.033*** | 0.100 | 0.844* |
| (0.008) | (0.008) | (0.063) | (0.416) | |
| Financial Aid Applicant | 0.000 | −0.005 | −0.054 | 0.000 |
| (0.009) | (0.009) | (0.069) | (0.456) | |
| Enrollment Intensity (Reference = Full time) | ||||
| Part time | −0.093*** | −0.103*** | 0.840*** | −2.945*** |
| (0.012) | (0.012) | (0.099) | (0.653) | |
| Mixed Enrollment | −0.077*** | −0.067*** | 0.524*** | −2.037*** |
| (0.008) | (0.008) | (0.061) | (0.401) | |
| Stop-Out Count | −0.042*** | −0.127*** | 0.406*** | −2.305*** |
| (0.008) | (0.008) | (0.069) | (0.454) | |
| Earned Associate Degree | 0.087*** | 0.043*** | 0.087 | 2.738*** |
| (0.007) | (0.007) | (0.056) | (0.368) | |
| Switched Major | −0.034*** | −0.008 | 0.310*** | 4.866*** |
| (0.007) | (0.007) | (0.055) | (0.363) | |
| Initial Major (Reference = Humanities and Liberal Arts) | ||||
| Industrial, Manufacturing, and Constr | 0.013 | −0.022 | −0.668*** | −0.270 |
| (0.024) | (0.025) | (0.180) | (1.188) | |
| Natural Sciences | 0.027 | −0.013 | 0.043 | 5.111*** |
| (0.016) | (0.016) | (0.119) | (0.785) | |
| Business | −0.012 | 0.044*** | −0.585*** | −3.645*** |
| (0.012) | (0.012) | (0.087) | (0.572) | |
| Social and Behavioral Sciences | 0.010 | 0.030 | −0.404** | −2.701** |
| (0.018) | (0.019) | (0.137) | (0.905) | |
| Communication Sciences | 0.017 | 0.023 | −0.434 | −2.511 |
| (0.030) | (0.031) | (0.229) | (1.513) | |
| Literature, Linguistics, and Fine Arts | 0.044* | −0.034 | 0.189 | 2.580** |
| (0.019) | (0.019) | (0.143) | (0.943) | |
| Math and Computer Sciences | 0.060*** | −0.033 | 0.308* | 4.666*** |
| (0.018) | (0.018) | (0.136) | (0.897) | |
| Education, Social Services, and Policy | −0.010 | 0.036** | −0.301** | −1.977** |
| (0.013) | (0.013) | (0.098) | (0.645) | |
| Engineering and Related Fields | 0.000 | −0.035 | 0.744*** | 7.398*** |
| (0.019) | (0.019) | (0.148) | (0.975) | |
| Service Oriented | −0.034 | −0.007 | 0.044 | 3.079** |
| (0.023) | (0.024) | (0.175) | (1.155) | |
| Health | −0.028 | −0.012 | 0.148 | 3.639*** |
| (0.014) | (0.014) | (0.113) | (0.746) | |
| Other | 0.018 | −0.035 | −0.078 | −0.002 |
| (0.019) | (0.020) | (0.143) | (0.946) | |
| Earned a Dev-Ed Math Credit | −0.041*** | −0.006 | 0.419*** | 5.432*** |
| (0.009) | (0.009) | (0.072) | (0.475) | |
| Earned Dual Credit | 0.028*** | 0.042*** | −0.640*** | −7.562*** |
| (0.008) | (0.008) | (0.058) | (0.382) | |
| Cumulative GPA | 0.185*** | −1.061*** | −6.111*** | |
| (0.008) | (0.065) | (0.428) | ||
| First Math Course Grade (Ref. = D) | ||||
| B or Higher | 0.528*** | |||
| (0.014) | ||||
| C | 0.158*** | |||
| (0.015) | ||||
| Cohort (Reference = Fall 2012) | 0.014* | −0.000 | −0.073 | −0.773* |
| (0.007) | (0.007) | (0.051) | (0.336) | |
| Constant | 2.491*** | 0.183 | 19.894*** | 41.145*** |
| (0.113) | (0.115) | (0.917) | (6.052) | |
| Observations | 13,908 | 13,908 | 10,105 | 10,105 |
| R-squared | 0.347 | 0.238 | 0.176 | 0.251 |
The table presents coefficients with standard errors in parentheses from ordinary least squares regression models performed on a pooled sample of community college students who entered college in Fall 2011 or Fall 2012, where each column represents a separate regression for each outcome. Regressions for GPA and bachelor’s degree attainment include full analytic sample. Regressions for time to degree (captured in semesters) and excess credits include only baccalaureate recipients with more than 80 college-level semester credits. All models include community college and university fixed effects
p < 0.001
p < 0.01
p < 0.05
We further examine the relationship between vertical repetition—taking into account location of the course repetition—in Table 7, which illustrates estimated relationships between the 4-category measure of vertical repetition and student outcomes among all college-level math completers. The role that vertical repetition plays in predicting student outcomes is more consistent across repetition location than what we observed for horizontal repetition, though results suggest that vertical repetition at the university does appear to drive the negative relationship between vertical repetition and bachelor’s degree attainment and positive association between vertical repetition and time to degree. The coefficients for vertical repetition at the university and at both institution types are significantly different than the reference category of no repetition, whereas vertical repetition at the community college is not significantly different than the reference for both outcomes). Vertical repetition at all locations is positively correlated with additional excess credits (and negatively related to GPA), though magnitudes of excess credit accumulation are larger when students repeat the same or a lower-level math course at the university (11.9 additional excess credits compared with never repeating) or at both institution types (16.8 additional excess credits compared with never repeating) (β = 11.900, SE = 0.658, p < 0.001; β = 16.893, SE = 2.068, p < 0.001).
Table 7.
Relationship between vertical math course repetition location and student outcomes
| Cumulative GPA | Bachelor’s Degree Attainment | Time to Degree | Excess Credits | |
|---|---|---|---|---|
|
| ||||
| Location of Vertical Repetition (Reference = No Repetition) | ||||
| Vertical Repetition at community college | −0.030* | −0.014 | −0.049 | 2.433*** |
| (0.014) | (0.013) | (0.097) | (0.640) | |
| Vertical Repetition at University | −0.039** | −0.073*** | 1.062*** | 11.900*** |
| (0.012) | (0.012) | (0.100) | (0.658) | |
| Vertical Repetition at both | −0.079* | −0.136*** | 1.668*** | 16.893*** |
| (0.035) | (0.035) | (0.314) | (2.068) | |
| Student Backgrounds | YES | YES | YES | YES |
| College Experiences | YES | YES | YES | YES |
| Academic Experiences | YES | YES | YES | YES |
| Institutional Fixed Effects | YES | YES | YES | YES |
| Observations | 13,908 | 13,908 | 10,105 | 10,105 |
| R-squared | 0.347 | 0.239 | 0.183 | 0.261 |
The table presents coefficients with standard errors in parentheses from ordinary least squares regression models performed on a pooled sample of community college students who entered college in Fall 2011 or Fall 2012, where each column represents a separate regression for each outcome. Regressions for GPA and bachelor’s degree attainment include full analytic sample. Regressions for time to degree (captured in semesters) and excess credits include only baccalaureate recipients with more than 80 college-level semester credits. All models include community college and university fixed effects. See full table with all regression coefficients in Appendix Table A10
p < 0.001
p < 0.01
p < 0.05
Discussion and Implications
Math course requirements can serve as a bottleneck for college students (Riegle-Crumb & Grodsky, 2010), yet little is known about how math course repetition predicts student outcomes. In this study, we investigated the prevalence of math course repetition among community college transfer students in Texas and explored the relationship between redundant math coursework and student outcomes. Although repeating a math course may be necessary after an unsuccessful course outcome, such as a failing grade or a withdrawal, the repercussions of math course repetition after receiving a passing grade are unclear. We examined math course repetition among two populations of Texas community college transfer students: those who passed a math course and either took an additional course at the same level (horizontal repetition) and those who previously completed any collegelevel math course and repeated a course in the same sequence (vertical repetition). Our study offers insights into the prevalence and location of community college transfer students’ horizontal and vertical repetition and the association between each type of course repetition and student outcomes.
We found that horizontal and vertical repetition was fairly common among community college transfer students; 38% of students who completed an introductory college-level math course experienced horizontal repetition, and 17% of students who completed any college-level math course experienced vertical repetition. Horizontal repetition appeared to be driven primarily by redundant coursework at the community college level as almost two-thirds of horizontal math course repetition occurred at community colleges (where it was not due to students’ enrolling at more than one community college but predominantly occurred within the same institution). This finding supports previous work that identified inefficiencies in community college pathways to desired goals (e.g., Bailey et al., 2015; Fink et al, 2018). The remaining horizontal course repetition occurred at universities, where students repeated entry-level math coursework previously completed at community colleges. This inter-sector misalignment seems analogous to the math misalignment and redundancy observed at the secondary-to-postsecondary transition (Melguizo & Ngo, 2020; Ngo, 2020). Our findings support the push to improve support for students in their course selections and to ensure they are taking the appropriate coursework early in their college careers to meet their major and career aspirations. It is also feasible to assume that some of the observed redundancy in coursetaking at community colleges is a result of poor messaging about which classes transfer-intending students should take if they hope to earn a baccalaureate; thus, a system-level approach to reforms, in which both community colleges and universities offer clear transfer pathways and major requirements, may be key to reducing horizontal course repetition (Schudde et al., 2021).
We found that among all math completers, vertical repetition was equally likely to occur at community colleges and at universities. Thus, vertical repetition in math sequences is a phenomenon that cannot be attributed to one specific sector. This suggests that transfer students would benefit from investigations by both sectors into mechanisms that cause vertical repetition and structural changes that reduce unnecessary vertical repetition.
We posited that vertical repetition may be driven by students’ choices of major and their intent to strengthen their preparation for higher-level math. Indeed, we did find that major choice was associated with vertical repetition, as STEM student, particularly engineering and math/computer science majors, were more likely to experience vertical repetition than those in liberal arts. Because STEM majors, especially in math/computer science or engineering, require a strong math foundation for success, it is plausible that vertical repetition occurred because earning a specific grade in a math course or mastering certain skills is particularly consequential for aspirants in these fields. Among all college-level math course completers, students who earned a lower grade in their first college-level math course appear more likely to vertically repeat. While a grade of D is considered passing, many students, particularly those receiving federal financial aid, may repeat a course to improve their GPAs as many community colleges allow for course replacement in internal GPA calculations (Scott-Clayton & Schudde, 2020). Additionally, many community colleges and universities require a grade of C to meet prerequisite math course requirements, and certain competitive programs in both sectors have formal and informal grade requirements for admission. It may be the case that students with low grades leverage vertical repetition to improve their academic standing so they can maintain funding, progress in a math sequence, or be more competitive for admission to certain programs.
On the other hand, there was no difference in the frequency of horizontal repetition among introductory math completers with different passing grades, suggesting that students’ grades are likely not the reason they may take an additional introductory math course. Initial major choice, however, was associated with horizontal repetition. That is, students who initially chose majors in humanities and liberal arts, including general studies, were generally more likely to experience horizontal repetition than students in other majors. One reason might be that later major switching or specialization in general studies resulted in different math requirements. Additional research is necessary to further study the link between major selection and horizontal repetition.
Our descriptive and regression findings suggest that horizontal repetition—repeating introductory math courses—makes pathways to a degree less efficient. On average, students who experienced horizontal repetition accrued more than three excess credits and increased their time to degree attainment by 0.24 semesters; they also achieved slightly lower GPAs than non-horizontal-repeaters. In our regression analyses on the subsample of introductory math course completers, we found that accounting for the location of horizontal repetition dramatically sharpened our understanding of the link between horizontal repetition and student outcomes. For example, compared with not repeating an introductory math course, horizontal repetition at the community college was associated with a slight increase in the likelihood of earning a baccalaureate degree while horizontal repetition at the university was not. Repeating introductory courses at the university, compared with nonrepetition, was negatively associated with cumulative GPA and positively associated with time to degree, whereas repetition at the community college did not appear significantly different than nonrepetition. These findings suggest different consequences for horizontal repetition across locations. Experiencing more than one introductory math course at the community college, perhaps in the process of major exploration, generates excess credits, but it does not appear detrimental to degree attainment. In fact, it may improve degree attainment, perhaps because completing a math course specific to the student’s final major provides a better foundation for their post-transfer academic trajectory. On the other hand, post-transfer horizontal course repetition—taking additional introductory courses at the university—is associated with reduced achievement (GPA) and increased time to degree.
The different findings for the location of horizontal repetition suggest that students may benefit from policies and practices that reduce the need for post-transfer horizontal repetition, such as improved alignment of math requirements across sectors and inter-sector collaboration on transfer advising to help students anticipate math course needs for their desired degree program. To better understand the mechanisms associated with horizontal repetition, researchers might further examine course-taking behaviors, mining program maps for their math course requirements to distinguish between students enrolled in multiple math courses to meet specific requirements and those who may be shopping for a final major.
When we examined vertical repetition among all college-level math completers, we found that vertical repetition negatively predicts student outcomes, perhaps to a greater extent than horizontal repetition. The most striking finding from our regression analysis is that, after controlling for other factors, vertical repeaters accrue, on average, 7.4 more excess credits than nonrepeaters, which, coupled with an average half-semester lengthening of time to degree, highlights the cost of vertical repetition to students. Moreover, our regression results show that while vertical repetition at any location positively predicted excess credits, the estimates were substantially larger among students who experienced repetition at the university level. Further, vertical repetition at the university appeared to drive the negative association between vertical repetition and baccalaureate degree attainment as the relationship between vertical repetition at the community college and degree attainment was not statistically different than nonrepetition. While repeating a math course within the same sequence is inherently costly at any location, repeating at the community college may serve to motivate students seeking to transfer while repeating post-transfer may discourage students.
Overall, the greater negative consequences of vertical course repetition at the university than at the community college suggest that improvements in advising with regard to math sequences at the university might reduce unnecessary course repetitions and improve student outcomes. However, we acknowledge that the link between vertical repetition and student outcomes may be partially due to omitted variable bias. For example, students who are inclined toward vertical repetition may also be less likely to get good grades or earn a degree. However, given that we captured initial course grade as a predictor of cumulative GPA and cumulative GPA as a predictor of all degree outcomes, we assume that our model least partially captures the role of prior performance.
Overall, our findings support the need for two constructs in the study of math course repetition, given the different origins of repetition for students retaking entry-level math courses (horizontal repetition) and students repeating within a sequence of math courses (vertical repetition). Horizontal repetition occurs more frequently at the community college level, while vertical repetition occurs somewhat more frequently at the university. The location of course repetition matters: both horizontal and vertical repetition at the university had larger negative consequences for student outcomes than repetition at the community college.
Our findings suggest that there may be different mechanisms undergirding horizontal and vertical math course repetition patterns, which is worthy of additional study. Given the limitations of our data set, we cannot rule out that math course repetition is associated with other factors that impact student performance, either at the entry level or along a math pathway. For this reason, we emphasize the need to interpret our findings with caution and hope our study will spur additional research with data that can capture additional statistical controls, including more detailed measures of student experiences (e.g., student engagement), that we could not capture in administrative data. Moreover, future research could replicate this study to explore vertical and horizontal repetition among community college and university entrants in other contexts and timeframes, especially as more IHEs work to align course sequences using guided pathways. We also see the need, given the prevalence of horizontal repetition within the community college, for research that focuses on full cohorts of community college entrants.
Implications for Practice
Since vertical and horizontal repetition among transfer students occurred at both community colleges and universities, reducing unnecessary repetition will require structural changes and intersector collaboration by multiple stakeholders. Our findings suggest that both community colleges and universities should develop specific strategies for reducing math course repetition, first focusing on internal deterrence, and then working with partner institutions to devise further measures to avert both pre- and post-transfer repetition. In particular, our findings suggest a greater need to prevent math course repetition at the university level. Although horizontal repetition at the community college was linked to excess credits, which is not ideal, it otherwise positively predicted bachelor’s degree attainment, whereas both types of course repetition at the university level were unequivocally negative for student outcomes.
The guided pathways framework for whole-college design has the potential to reduce unnecessary math course repetition within and across institutions, but only if universities actively participate in reforms (Bailey et al., 2015; Flores & Fabianke, 2019; Jenkins et al., 2017, 2018; Schudde et al., 2021). All IHEs interested in addressing course redundancy may benefit from these comprehensive reform efforts, which include structural changes like developing intersector meta-majors, clusters of programs that lead to similar career goals and require the same courses early in college and share the same entry-level math course. IHEs should also streamline transfer agreements between two- and four-year partners by crafting articulation agreements and transfer guides for that specify from the outset which courses are required and how those courses will transfer and apply toward a degree (Ganga & Mazzariello, 2018). If community colleges and universities are to address transfer issues fully, they will need to understand the relationship between math course repetition and its location— both among introductory courses (horizontal) or within sequences (vertical)—and student outcomes.
Implementing math pathways in which the content of entry-level math aligns with students’ broad major (i.e., meta-major) and career goals should theoretically reduce horizontal course repetition, if these pathways are implemented alongside robust career exploration and program advising that enables students to quickly decide upon and enter a defined meta-major at the start of college, and if meta-major requirements are fully accepted at the university. Early work on math pathways interventions for dev-ed math students shows promising improvements in short-term student outcomes, such as math course persistence and completion (Ganga & Mazzariello, 2018; Rutschow et al., 2017; Schudde & Keisler, 2019; Schudde & Meiselman, 2019). The Texas Success Center (2019)—an organization that facilitates the guided pathways initiative in the state—emphasizes that creating math pathways aligned with meta-majors could decrease unnecessary horizontal repetition for community college entrants who start college with at least a broad idea of their area of interest and should be advised to take courses that fulfill the requirements for a broad set of related majors. During the initial transition to meta-majors and math pathways, horizontal repetition may increase as students face shifting program requirements and must compare requirements across degree plans. Indeed, recent evidence from Florida suggests that offering math pathways for college-level courses improved the rate of passing introductory math but also created conditions conducive to horizontal math course repetition (Mokher & Hu, 2022). To reduce repetition during the early phases of adopting math pathways, community colleges and universities may consider accepting older program plans or offering noncredit or short-term bridge courses to provide necessary math skills to students who have existing entry-level math credits.
Within any IHE, the purposeful use of internal data analytics could decrease course repetition and reduce excess credits. Institutional research (IR) offices at community colleges and universities could use an approach similar to the one used in this study, identifying different types of course repetition to examine patterns at their college. In a case study of one community college, Jenkins and Pellegrino (2019) demonstrated how the IR office used student transcript data to identify challenging courses, highlighting the importance of using data to understand impediments to students’ progress. We similarly recommend that IR offices use data to identify courses with high rates of repetition, which could help them target courses and sequences in which students need additional support to reduce credit redundancy. IR offices at receiving universities should focus on course repetition patterns at feeding community colleges and work with those exhibiting higher repetition rates to reduce this rate, perhaps, for example, by improving transfer agreements and pre-transfer advising.
Advisors can use information gleaned from IR studies to enhance their advising practices. Advisors and math department faculty can work together to identify repetition patterns and examine the reasons for horizontal and/or vertical repetition, such as inadequate information about programs and/or transfer requirements or difficult course sequences or combinations. Together, faculty and student support staff could develop and provide necessary program information, as well as in-semester support services, to help students meet their academic goals before, during, and after transfer. Additionally, IR offices, math departments, and advisors could work together to create an early flagging system in which a warning would come up in their case management systems when students attempted to register for courses that were redundant with requirements they had already fulfilled, allowing advisors to target those students for additional guidance.
Conclusion
In this study, we differentiated between two different types of math course repetition among community college transfer students—horizontal and vertical repetition. Among community college transfer students who earn excess credits toward a baccalaureate, accruing too many introductory courses can contribute to credit inefficiencies in a community college pathway to a baccalaureate degree (Fink et al., 2018). Our strategy of differentiating between horizontal and vertical course repetition helped us further understand how course redundancy patterns predict student outcomes. We found that vertical repetition was slightly more likely to occur at the university level than at the community college level (though the rates were approximately equal), whereas horizontal repetitions occurred primarily at community colleges. Not only did we find differences in the relationships between course repetition types and student outcomes, but we also found that the link between course repetition and outcomes was shaped by where the repetitions occurred. Overall, vertical repetition (repeating within the same sequence) was associated with more negative student outcomes than horizontal repetition. The associations between both types of repetition and student outcomes were more likely to be negative when they occurred at the university. These patterns may prove useful as community colleges and universities collaborate to implement reforms to support more efficient and effective course-taking for students. By examining measures of horizontal and vertical repetition by location, IHEs can identify areas for further improvement and determine how reforms can help students achieve more efficient course-taking patterns.
Supplementary Material
Footnotes
In Appendix Tables A1 and A2, we report horizontal and vertical repetition rates by the most common feeding community colleges, the most common destination universities and the most common transfer pathways from community colleges to universities. There is substantial variation among even the top 10 most common institutions. These descriptive data support our decision to use institutional fxed efects. For example, among top 10 feeding community colleges, horizontal rates vary from 54% in Houston Community College to 19% in South Texas College. Blinn College to Texas A&M University is one of the most common transfer pathways. While the horizontal rate for students who transferred from Blinn College to Texas A&M University is slightly below the average (34%), the vertical repetition rate is well above the average (32%).
We included both fnancial aid applicant and Pell recipient indicators since they capture two diferent populations. While about 79% of frst-year students applied for fnancial aid, only 41–42% of those students receive a Pell grant. Among fnancial aid flers, half of those students received a Pell grant (51.8% for any math completers and 52.9% for introductory math completers). To determine if our results were sensitive to the inclusion of both measures, we ran all the models in Table 4 and Table 6 without using the fnancial aid applicant indicator. The patterns of results did not change. The additional results are available upon request.
We presented horizontal repetition rates by the most common major-switching patterns from community college to university in Table A3 in the appendix. Among the most common major-switching categories (from undecided major at community college to business at university), the highest horizontal repetition rate is 66%. We did not include major-switching in the main models in Table 3 because some students experienced repetitions before major switching. Given the causal order issue, we preferred not to include major switching in our main model specifcation, but reported supplemental models predicting repetitions with major-switching as a covariate in Table A4 in the appendix.
We report horizonal repetition patterns by students’ frst introductory college-level mathematics courses in the appendix (see Table A5 in Appendix). For example, after students frst completed college algebra, 41% of those students took another introductory college-level mathematics course. Of the repeaters, 18% took math for business, 3% took quantitative reasoning and 24% took elementary statistics.
We report more detailed vertical repetition patterns in the college algebra-calculus sequence in the Appendix (see Table A6). For example, among students who completed and earned credit for pre-calculus, 7% repeated the same or a lower-level course in the college algebra-calculus sequence, where 5% repeated the same pre-calculus course and the remainder retook a lower-level course (trigonometry or college algebra).
We present stepwise regression models for each outcome in the appendix, where Table A7 and Table A8, respectively, illustrate the change in the horizontal and vertical repetition indicator as additional blocks of variables are incorporated into the model. The coefcient of horizontal repetition indicator became negative in the fnal step—when institutional fxed efects were added to the model—in predicting cumulative GPA (see Table A7).
Supplementary Information The online version contains supplementary material available at at https://doi.org/10.1007/s11162-022-09706-7.
References
- Adelman C (1999). Answers in the tool box: Academic intensity, attendance patterns, and bachelor’s degree attainment. U.S. Department of Education. https://files.eric.ed.gov/fulltext/ED431363.pdf [Google Scholar]
- Adelman C (2005). Moving into town—and moving on: The community college in the lives of traditional-age students. U.S. Department of Education. http://www2.ed.gov/rschstat/research/pubs/comcollege/movingintotown.pdf
- Alexander K, Entwistle D, & Dawber SL (1994). On the success of failure: A reassessment of the effects of retention in the primary grades. Cambridge University Press. [Google Scholar]
- Astorne-Figari C, & Speer JD (2019). Are changes of major changes? The roles of grades, gender, and preferences in college major switching. Economics of Education Review, 70, 75–93. 10.1016/j.econedurev.2019.03.005 [DOI] [Google Scholar]
- Bahr PR (2008). Does mathematics remediation work? A comparative analysis of academic attainment among community college students. Research in Higher Education, 49(5), 420–450. 10.1007/s11162-008-9089-4 [DOI] [Google Scholar]
- Bahr PR, Jackson G, McNaughtan J, Oster M, & Gross J (2017). Unrealized potential: Community college pathways to STEM baccalaureate degrees. Journal of Higher Education, 88(3), 430–478. 10.1080/00221546.2016.1257313 [DOI] [Google Scholar]
- Bailey TR, Jenkins PD, & Leinbach DT (2005). Community college low-income and minority student completion study: Descriptive statistics from the 1992 high school cohort. Community College Research Center, Columbia University. 10.7916/D8FF3QF6 [DOI] [Google Scholar]
- Bailey T, Jeong DW, & Cho SW (2010). Referral, enrollment, and completion in developmental education sequences in community colleges. Economics of Education Review, 29(2), 255–270. 10.1016/j.econedurev.2009.09.002 [DOI] [Google Scholar]
- Bailey TR, Jaggars SS, & Jenkins D (2015). Redesigning America’s community colleges: A clearer path to student success. Harvard University Press. [Google Scholar]
- Bailey TR, Jenkins D, Fink J, Cullinane J, & Schudde L (2016). Policy levers to strengthen community college transfer student success in Texas: Report to the Greater Texas Foundation. Community College Research Center, Columbia University. 10.7916/d8js9w20 [DOI] [Google Scholar]
- Belfield C (2013). The economic benefits of attaining an associate degree before transfer: Evidence from North Carolina. (CCRC Working Paper No. 62). 10.7916/D8GB2229 [DOI]
- Braxton JM, Doyle WR, Hartley HV, Hirschy AS, Jones WA, & McLendon MK (2014). Rethinking college student retention. Jossey-Bass. [Google Scholar]
- Bryk A, & Treisman U (2010). Make math a gateway, not a gatekeeper. Chronicle of Higher Education, 56(32), B19–B20. [Google Scholar]
- Calcagno JC, Crosta P, Bailey T, & Jenkins D (2007). Stepping stones to a degree: The impact of enrollment pathways and milestones on community college student outcomes. Research in Higher Education, 48(7), 775–801. 10.1007/s11162-007-9053-8 [DOI] [Google Scholar]
- Cameron AC, & Miller DL (2015). A practitioner’s guide to cluster-robust inference. Journal of Human Resources, 50(2), 317–372. 10.3368/jhr.50.2.317 [DOI] [Google Scholar]
- Carnegie Math Pathways. (2020). https://carnegiemathpathways.org/
- Community College Survey of Student Engagement [CCSSE]. (2021a). 2021 Means report by race/ethnicity. https://www.ccsse.org/survey/reports/2021/standard_reports/ccsse_2021_coh_means_byRace.pdf
- Community College Survey of Student Engagement [CCSSE]. (2021b). 2021 Means report by gender. https://www.ccsse.org/survey/reports/2021/standard_reports/ccsse_2021_coh_means_byGender.pdf
- Chen X (2016). Remedial coursetaking at US public 2-and 4-year institutions: Scope, experiences, and outcomes. Statistical analysis report. (NCES 2016–405). National Center for Education Statistics. https://files.eric.ed.gov/fulltext/ED568682.pdf [Google Scholar]
- Clovis MA, & Chang M (2021). Effects of academic momentum on degree attainment for students beginning college at 2-Year institutions. Journal of College Student Retention: Research, Theory & Practice, 23(2), 322–336. 10.1177/1521025119826245 [DOI] [Google Scholar]
- Cohen R, & Kelly AM (2019). The impact of community college science and mathematics coursetaking on graduation, transfer, and non-completion. Review of Higher Education, 42(2), 595–617. 10.1353/rhe.2019.0008 [DOI] [Google Scholar]
- Center Dana. (2020). Texas transfer inventory guide. https://dcmathpathways.org/resources/texas-transfer-inventory-guide-2018-19-exce
- Deil-Amen R, & Rosenbaum JE (2002). The unintended consequences of stigma-free remediation. Sociology of Education, 75(3), 249–268. 10.2307/3090268 [DOI] [Google Scholar]
- Fike DS, & Fike R (2008). Predictors of first-year student retention in the community college. Community College Review, 36(2), 68–88. 10.1177/0091552108320222 [DOI] [Google Scholar]
- Fink J, Jenkins PD, Kopko EM, & Ran X (2018). Using data mining to explore why community college transfer students earn bachelor’s degrees with excess credits (CCRC Working Paper No.100). Columbia University, Community College Research Center. 10.7916/D8NC7CNF [DOI] [Google Scholar]
- Flores KP, & Fabianke J (2019). Progress implementing guided pathways in Texas community colleges. Texas Success Center, Texas Association of Community Colleges. https://tacc.org/sites/default/files/2020-01/SOAA%20Report%202019_0.pdf [Google Scholar]
- Fong AB, Jaquet K, & Finkelstein N (2014). Who repeats Algebra-I, and how does initial performance relate to improvement when the course is repeated? (REL 2015–059). Regional Educational Laboratory West. https://eric.ed.gov/?id=ED548534 [Google Scholar]
- Ganga E, & Mazzariello A (2018). Math pathways: Expanding options for success in college math. Education Commission of the States. https://eric.ed.gov/?id=ED590584 [Google Scholar]
- Giani MS (2019). The correlates of credit loss: How demographics, pre-transfer academics, and institutions relate to the loss of credits for vertical transfer students. Research in Higher Education, 60(8), 1113–1141. 10.1007/s11162-019-09548-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagedorn LS, Moon HS, Cypers S, Maxwell WE, & Lester J (2006). Transfer between community colleges and 4-year colleges: The all-American game. Community College Journal of Research and Practice, 30(3), 223–242. 10.1080/10668920500322384 [DOI] [Google Scholar]
- Hagedorn LS, Cabrera A, & Prather G (2010). The community college transfer calculator: Identifying the course-taking patterns that predict transfer. Journal of College Student Retention: Research, Theory & Practice, 12(1), 105–130. 10.2190/CS.12.1.g [DOI] [Google Scholar]
- Hagedorn LS, & DuBray D (2010). Math and science success and nonsuccess: Journeys within the community college. Journal of Women and Minorities in Science and Engineering, 16(1), 31–50. 10.1615/JWomenMinorScienEng.v16.i1.30 [DOI] [Google Scholar]
- Hart CMD, Friedmann E, & Hill M (2018). Online coursetaking and student outcomes in California community colleges. Education Finance and Policy, 13(1), 42–71. 10.1162/edfp_a_00218 [DOI] [Google Scholar]
- Hill AJ (2014). The costs of failure: Negative externalities in high school course repetition. Economics of Education Review, 43, 91–105. 10.1016/j.econedurev.2014.10.002 [DOI] [Google Scholar]
- Hom EKI (2007). The academic goals, course repetition, and completion ratios of Asian and Latin American international students in urban community colleges [Doctoral dissertation, The University of Southern California]. Proquest Dissertations and Theses Global. https://search.proquest.com/docview/304806896?pq-origsite=gscholar&fromopenview=true [Google Scholar]
- Jenkins PD, & Fink J (2016). Tracking transfer: New measures of institutional and state effectiveness in helping community college students attain bachelor’s degrees. Columbia University, Community College Research Center. 10.7916/D8C24W80 [DOI] [Google Scholar]
- Jenkins D, & Bailey T (2017). Early momentum metrics: Why they matter for college improvement (CCRC Working Paper No.65). Columbia University, Community College Research Center. https://ccrc.tc.columbia.edu/publications/early-momentum-metrics-college-improvement.html
- Jenkins D, Lahr HE, & Fink J (2017). Implementing guided pathways: Early insights from the AACC Pathways colleges. Community College Research Center, Teachers College, Columbia University. 10.7916/D86D608W [DOI] [Google Scholar]
- Jenkins D, Lahr HE, Fink J, & Ganga EC (2018). What we are learning about guided pathways. Community College Research Center, Teachers College, Columbia University. 10.7916/D8KW6Z78 [DOI] [Google Scholar]
- Jenkins D, & Pellegrino L (2019). Collaborating to break down barriers to student success: Guided pathways reforms at San Jacinto College. (Series on Change Management at AACC Pathways Colleges: Case Study 3 of 5). Community College Research Center, Teachers College, Columbia University. https://files.eric.ed.gov/fulltext/ED598447.pdf [Google Scholar]
- Kovacs K (2016, September 23). When a C isn’t good enough. Inside Higher Ed. https://www.insidehighered.com/news/2016/09/23/students-who-earn-cs-gateway-courses-are-less-likely-graduate-new-data-show#.YGNTphtatH8.link
- Liu V, Mishra S, & Kopko EM (2021). Major decision: The impact of major switching on academic outcomes in community colleges. Research in Higher Education, 62(4), 498–527. 10.1007/s11162-020-09608-6 [DOI] [Google Scholar]
- Melguizo T, & Ngo FJ (2020). Mis/Alignment between high school and community college standards. Educational Researcher, 49(2), 130–133. 10.3102/0013189X19898697 [DOI] [Google Scholar]
- Mokher C, & Hu S (2022). Diverging paths: Exploring the association between initial math pathways and college students’ subsequent math performance. Journal of Postsecondary Student Success, 1(3), 50–74. [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine [NASEM]. (2016). Barriers and opportunities for 2-year and 4-year STEM degrees: Systemic change to support diverse student pathways. New York: National Academies Press. [PubMed] [Google Scholar]
- Nasser R, & Nauffal D (2012). Frequency of repeated courses its relation to persistence and performance in Lebanon’s higher education. Higher Education Studies, 2(1), 20–26. 10.5539/hes.v2n1p20 [DOI] [Google Scholar]
- Ngo FJ (2020). High school all over again: The problem of redundant college mathematics. Journal of Higher Education, 91(2), 222–248. 10.1080/00221546.2019.1611326 [DOI] [Google Scholar]
- Ngo FJ, & Velasquez D (2020). Inside the math trap: Chronic math tracking from high school to community college. Urban Education. 10.1177/0042085920908912 [DOI] [Google Scholar]
- Packard BW, Gagnon JL, & Senas AJ (2012). Navigating community college transfer in science, technical, engineering, and mathematics fields. Community College Journal of Research and Practice, 36(9), 670–683. 10.1080/10668926.2010.495570 [DOI] [Google Scholar]
- Park T (2012). The role of the community college in Texas: The impact of academic intensity, transfer, and working on student success [Doctoral dissertation, Vanderbilt University]. https://etd.library.vanderbilt.edu/available/etd-03242012-094629/unrestricted/Park_Dissertation_Final_Version.pdf
- Park ES, Ngo F, & Melguizo T (2020). The role of math misalignment in the community college STEM pathway. Research in Higher Education. 10.1007/s11162-020-09602-y [DOI] [Google Scholar]
- President’s Council of Advisors on Science and Technology. (2012, February). Engage to excel: Producing one million additional college graduates with degrees in science, technology, engineering, and mathematics. https://obamawhitehouse.archives.gov/sites/default/files/microsites/ostp/pcast-engage-to-excel-final_2-25-12.pdf
- Riegle-Crumb C, & Grodsky E (2010). Racial-ethnic differences at the intersection of math coursetaking and achievement. Sociology of Education, 83(3), 248–270. 10.1177/0038040710375689 [DOI] [Google Scholar]
- Roksa J, Jenkins D, Jaggars SS, Zeidenberg M, Cho SW (2009). Strategies for promoting gatekeeper course success among students needing remediation: Research report for the Virginia Community College System (CCRC Working Paper). Columbia University, Community College Research Center. https://files.eric.ed.gov/fulltext/ED507392.pdf
- Roksa J (2006). Does the vocational focus of community colleges hinder students’ educational attainment? Review of Higher Education, 29(4), 499–526. 10.1353/rhe.2006.0038 [DOI] [Google Scholar]
- Romano RM, Losinger R, & Millard T (2011). Measuring the cost of a college degree: A case study of a SUNY community college. Community College Review, 39(3), 211–234. 10.1177/0091552111416226 [DOI] [Google Scholar]
- Root M (2013). Essential elements of state policy for college completion. Southern Regional Education Board. https://vtechworks.lib.vt.edu/bitstream/handle/10919/98994/StateTransfer.pdf?sequence=1&isAllowed=y [Google Scholar]
- Rutschow EZ, Diamond J, & Serna-Wallender E (2017). Math in the real world: Early findings from a study of the Dana Center Mathematics Pathways. (Research Brief). Center for the Analysis of Postsecondary Readiness. https://files.eric.ed.gov/fulltext/ED583571.pdf [Google Scholar]
- Schudde L, & Goldrick-Rab S (2015). On second chances and stratification: How sociologists think about community colleges. Community College Review, 43(1), 27–45. 10.1177/0091552114553296 [DOI] [Google Scholar]
- Schudde L (2019). Short- and long-term impacts of engagement experiences with faculty and peers at community colleges. Review of Higher Education, 42(2), 385–426. 10.1353/rhe.2019.0001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schudde L, & Keisler K (2019). The relationship between accelerated dev-ed coursework and early college milestones: Examining college momentum in a reformed mathematics pathway. AERA Open, 5, 1. 10.1177/2332858419829435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schudde L, & Meiselman AY (2019). Early outcomes of Texas community college students enrolled in Dana Center Mathematics Pathways prerequisite developmental courses. (Research Brief). Center for the Analysis of Postsecondary Readiness. https://files.eric.ed.gov/fulltext/ED597974.pdf [Google Scholar]
- Schudde L, Bradley D, & Absher C (2020). Navigating vertical transfer online: Access to and usefulness of transfer information on community college websites. Community College Review, 48(1), 3–30. 10.1177/0091552119874500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schudde LT, Ryu W, & Brown RS (2020). Major movement: Examining meta-major switching at community colleges. The Review of Higher Education, 44(2), 189–235. 10.1353/rhe.2020.0044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schudde L, Jabbar H, & Hartman C (2021). How political and ecological contexts shape community college transfer. Sociology of Education, 94(1), 65–83. 10.1177/0038040720954817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulmerich SC, & Hurley TV (2015). Remediation and course repetition: The domino effect on academics and economics. Contemporary Nurse, 51(2–3), 232–244. 10.1080/10376178.2015.1124725 [DOI] [PubMed] [Google Scholar]
- Scott-Clayton J, & Schudde L (2020). The consequences of performance standards in need-based aid evidence from community colleges. Journal of Human Resources, 55(4), 1105–1136. 10.3368/jhr.55.4.0717-8961R2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro D, Dundar A, Huie F, Wakhungu PK, Yuan X, Nathan A, & Hwang Y (2017). Tracking transfer: Measures of effectiveness in helping community college students to complete bachelor’s degrees. (Signature Report No. 13). National Student Clearinghouse. https://files.eric.ed.gov/fulltext/ED580214.pdf [Google Scholar]
- Tafreschi D, & Thiemann P (2016). Doing it twice, getting it right? The effects of grade retention and course repetition in higher education. Economics of Education Review, 55, 198–219. 10.1016/j.econedurev.2016.10.003 [DOI] [Google Scholar]
- Texas Success Center. (2019). Texas pathways coaching manual. https://tacc.org/sites/default/files/flipbooks/2019-01/texas_pathways_coaching_manual_010419_0.pdf
- Texas Higher Education Coordinating Board [THECB]. (2017). Texas public higher education almanac: A profile of state and institutional performance and characteristics. Author. [Google Scholar]
- U.S. Department of Education. (2019). Number of students enrolled in postsecondary institutions annually, by sector of institution: 2018–2019. https://nces.ed.gov/ipeds/TrendGenerator/app/build-table/2/2?rid=1
- Wang X, Chan H-Y, Phelps LA, & Washbon JI (2015). Fuel for success: Academic momentum as a mediator between dual enrollment and educational outcomes of two-year technical college students. Community College Review, 43(2), 165–190. 10.1177/0091552115569846 [DOI] [Google Scholar]
- Wang X, Wang Y, Wickersham K, Sun N, & Chan H-Y (2017). Math requirement fulfillment and educational success of community college students. Community College Review, 45(2), 99–118. 10.1177/0091552116682829 [DOI] [Google Scholar]
- Yue H, & Fu X (2017). Rethinking graduation and time to degree: A fresh perspective. Research in Higher Education, 58(2), 184–213. 10.1007/s11162-016-9420-4 [DOI] [Google Scholar]
- Zeidenberg M (2015). Valuable learning or “spinning their wheels”? Understanding excess credits earned by community college associate degree completers. Community College Review, 43(2), 123–141. 10.1177/0091552115571595 [DOI] [Google Scholar]
- Zhang YL (2019). Early academic momentum: Factors contributing to community college transfer students’ STEM degree attainment. Journal of College Student Retention: Research, Theory & Practice. 10.1177/1521025119881130 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


