The Consequences of Performance Standards in Need-Based Aid

Abstract

Even need-based financial aid programs typically require recipients to meet Satisfactory Academic Progress (SAP) requirements. Using regression discontinuity and difference-in-difference designs, we examine the consequences of failing SAP for community college entrants in one state. We find heterogeneous academic effects in the short term, but, after six years, negative effects on academic and labor market outcomes dominate. Declines in credits attempted are two to three times as large as declines in credits earned, suggesting that SAP may increase aid efficiency. But students themselves are worse off, and the policy exacerbates inequality by pushing out low-income students faster than their higher-income peers.

I. Introduction

College is a high-return investment on average, even for academically marginal students (Ost, Pan, and Webber 2018; Zimmerman 2014) and even at the subbaccalaureate level (Jepsen, Troske, and Coomes 2014; Belfield and Bailey 2011). Out of concerns that too few qualified students take advantage of this high-return investment—whether due to information constraints or financial constraints—the federal government invests more than $120 billion annually to encourage college enrollment and completion (Scott-Clayton 2017).

But college is also a risky investment, particularly at the community college level, where only about one-third of first-time students complete any degree within six years (Baum, Little, and Payea 2011). Of course, some dropout is to be expected even in a well-functioning postsecondary system, as students learn more about their preferences and abilities, and a system with zero dropout would likely signify too few students taking the risk (Fischer 1987; Manski 1988, 1989; Manski and Wise 1983; Altonji 1993). Furthermore, it has long been recognized that financial aid could increase dropout rates by inducing some students with lower-than-average graduation propensities to enroll (Manski 1988, 1989). Still, the financial and behavioral factors that lead students to underenroll in college in the first place may also lead students to drop out too soon, and this has led to substantial research and policy efforts aimed at understanding and improving completion rates (Deming and Dynarski 2010).

The prevalence of academic performance standards—which kick students off aid, and/or out of school, before they want to leave—thus represents an interesting theoretical and policy puzzle that has received far less attention. Whether a student receives aid or not, academic performance standards, which typically require students to maintain a minimum grade point average (GPA) or risk being placed on probation and eventually dismissed, can send important signals about institutional expectations for success and provide incentives for increased effort while enrolled—incentives to which students appear to respond (Lindo, Sanders, and Oreopoulos 2010; Casey, Cline, Ost, and Qureshi 2018). But, at least in the four-year context, it appears that the students pushed out of college as a result experience substantial labor market losses compared with similar students who just barely passed the minimum requirement and were allowed to continue (Ost, Pan, and Webber 2018).

While this is clearly bad for the affected students, students are not the only stake-holders involved, and the benefits they receive from continued enrollment may or may not outweigh the costs of continuing to subsidize their study. The question of whether some low-performing students might persist in the “college experiment” longer than they should has particular importance for financial aid policy, as aid by design attracts a higher-risk population. Students themselves face much more immediate financial consequences. Finally, the policymakers who administer financial aid policy have a direct interest in understanding whether performance criteria enhance or undermine the cost-effectiveness of their investments. The trade-off may be particularly important at community colleges, given their high rates of noncompletion. If students with a high risk of noncompletion experience additional difficulty as a result of academic performance standards, the policy could, at least partially, undermine the government’s investment.

In this study, we examine the consequences of federal Satisfactory Academic Progress (SAP) requirements, which students receiving Pell Grants, student loans, and other need-based federal aid must meet to maintain eligibility for aid, for community college entrants in one state. To assess the effects of this policy, we use regression discontinuity and difference-in-difference designs, informed by theory, to examine the consequences of SAP failure on academic and labor market outcomes up to six years after entry.

Institutions have flexibility regarding how they define and enforce SAP, but they commonly require students to maintain a cumulative GPA of 2.0 or higher and to complete at least two-thirds of the course credits that they attempt. Meeting SAP is a nontrivial hurdle for many students: in earlier work, we find that 25–40 percent of first-year Pell recipients at public institutions have performance low enough to place them at risk of losing financial aid, representing hundreds of thousands to more than a million college entrants each year (Schudde and Scott-Clayton 2016).

Though minimum performance standards have existed in the need-based federal student aid programs for nearly 40 years, we have little direct evidence regarding how students respond to them. Studies of performance-based scholarships generally find that students are responsive to performance incentives, though such scholarships typically focus on GPA thresholds well above 2.0 (Carruthers and Özek 2016; Cornwell, Lee, and Mustard 2005; Cornwell, Mustard, and Sridhar 2006; Dynarski 2008; Scott-Clayton 2011) and examine the marginal effect of receiving extra aid rather than the effect of losing foundational need-based assistance (Angrist, Lang, and Oreopoulos 2009; Patel and Valenzuela 2013; Barrow, Richburg-Hayes, Rouse, and Brock 2014; Barrow and Rouse 2018; Richburg-Hayes et al. 2009). A series of experiments with supplementary performance-based scholarships (provided in addition to Pell Grants) conducted by MDRC are particularly relevant given their low-income target population and 2.0 GPA threshold, which corresponds to the SAP threshold. In these studies, students assigned to the treatment group increased the time they spent on academic activities, earned more credits, and were more likely to persist (Patel and Valenzuela 2013; Barrow, Richburg-Hayes, Rouse, and Brock 2014; Barrow and Rouse 2018).

Another strand of literature examines how students react to performance standards in general but does not consider implications for financial aid policy. The most closely related empirical work is the Lindo, Sanders, and Oreopoulos (2010) study of the causal effects of academic probation for students regardless of financial aid status at one large baccalaureate institution in Canada. Using regression discontinuity, the authors compare persistence, grades, and graduation rates for students just above and below the first-year GPA threshold for placement onto academic probation. The authors find that being placed on probation induces some students to drop out but increases GPA for those that return, with a net negative impact on graduation for students near the cutoff. A recent paper by Casey, Cline, Ost, and Qureshi (2018) replicates these findings using data from a U.S. public four-year institution but finds that some of the increase in GPA is due to strategic course selection. Ost, Pan, and Webber (2018) find that students who leave college due to just barely failing a performance standard experience lower earnings years later than those who just barely met the standard. Finally, our own prior work documenting the prevalence of SAP failure (Schudde and Scott-Clayton 2016) includes an analysis of the academic effects of standards for Pell recipients in a different state than examined here, with our preferred strategy suggesting that falling just below standard may lead to bigger effects on dropout for Pell recipients than nonrecipients.

This study builds on the prior work in three ways. First, rather than focusing exclusively on students’ behavioral responses, we outline a simple model to highlight the trade-offs faced by a social planner weighing whether to set performance standards in the context of financial aid. Second, our preferred difference-in-difference (DID) design allows us to look at impacts of SAP for students further below the performance threshold. This is important because evaluating the policy depends upon estimating average rather than local effects, which theory predicts will differ in this case. Finally, we examine a broader range of outcomes, including earnings and estimated aid eligibility, and track students for longer (six years) than prior research on the policy.

Using administrative records on aid recipients at more than 20 community colleges in one state, we first apply a regression discontinuity (RD) design similar to that used in prior work, as well as an RD-DID approach that compares discontinuities at the threshold for aided versus unaided students. However, our preferred estimates use a DID, where unaided students serve as a control group. This technique allows us to net out any effects of academic probation in general and to estimate effects for students further away from the performance threshold, and it also provides greater statistical power. While the DID estimates are of greater policy relevance in terms of determining whether SAP requirements are effective overall, the RD and RD-DID results replicate prior work and help provide support for our causal interpretation.

In line with theoretical predictions and consistent with prior work, we find evidence of heterogeneous effects of SAP failure during the period after students have been warned they are at risk of losing aid (but before they have faced actual consequences). Also consistent with our model, we find that discouragement (dropout) effects are larger for students further below the threshold, while encouragement (improved GPA) effects appear larger for those nearest the threshold. But once consequences begin to be enforced in Year 3, negative effects start to dominate. All of our specifications indicate significant reductions in enrollment and credits attempted by the end of Year 3, with no improvement in cumulative GPA, except perhaps for those nearest the cutoff.

By the end of Year 6, negative effects persist or increase, while any positive effects have washed out. There are indications of negative effects on certificate and associate degree completion, though magnitude and significance vary across specification. Our preferred DID specification also finds statistically significant reductions in earnings for those who fail SAP, consistent both with a reallocation of effort towards schooling in early years and small decline in certificate completion that may reduce earnings in later years.

Evaluating SAP policy as a whole requires weighing the value of human capital foregone against the cost of continuing to subsidize enrollment. By the end of Year 6, students who failed SAP in their first year attempted 3.4 fewer credits (a 10 percent decline) but completed only 1.4 fewer credits (a 6–7 percent decline), suggesting that the marginal credit no longer attempted had a low probability of being completed. While a complete assessment of net benefits is beyond the scope of this paper, this suggests that SAP appears to improve the efficiency of aid dollars. But students themselves are no better off, and policymakers may be concerned about the equity implications, as our results clearly indicate that aid recipients with low GPAs leave college more quickly than academically similar but financially unassisted peers. Further, our results suggest that Pell Grant recipients—students from low-income households—are somewhat more sensitive to the negative effects of SAP failure than other aid recipients, which may mean SAP pushes out students who are already at higher risk of noncompletion and would benefit the most from college.

The remainder of the paper proceeds as follows: Section II provides additional background on SAP policy. Section III introduces the theoretical framework and key predictions. Section IV describes our data, Section V describes our empirical strategy, and Section VI presents our main results. Section VII concludes with a discussion of policy implications and unanswered questions.

II. Policy Background

SAP regulations have been a part of need-based federal student aid since 1976 when an amendment to the Higher Education Act of 1965 stipulated that students must demonstrate “satisfactory progress” toward a degree in order to continue receiving aid (Bennet and Grothe 1982). The regulations give institutions flexibility regarding how they define SAP, though in practice it is typical for institutions to require a cumulative GPA of 2.0 or higher and completion of at least two-thirds of the course credits that students attempt (Schudde and Scott-Clayton 2016).¹

SAP policy applies to federal Pell Grant recipients, student loan borrowers, and work-study participants, and state and institutional need-based aid programs often piggy-back their minimum performance rules on the federal standards.² While our empirical analysis will group students receiving any type of aid, the federal Pell Grant is the single largest source of need-based financial aid in the country and the main form of aid received at most community colleges (Baum and Payea 2013).³ For example, among the aid recipients in our community college sample, 70 percent received Pell, compared to 44 percent receiving state grants and 20 percent receiving loans.⁴ Average awards among all aid recipients were $2,385 in Pell, compared to just $407 in state grants and $729 in federal student loans.

SAP standards layer on top of “academic good standing” policies that apply to all students regardless of aid status. In the state community college system (SCCS) that we examine, a 2.0 cumulative GPA, or a C average, is required to earn a credential. This is a fairly typical graduation standard at public institutions nationally. Many students in our sample are potentially affected by this criterion; the average first-year GPA is only 2.32 on a four-point scale, and approximately one-third of full-time students fall below the 2.0 threshold at the end of their first year.

Students who fall below a 2.0 in any semester are placed on academic warning status, and a notification will appear on their transcript.⁵ However, besides warning students that they are not on track to graduate, academic warning in this system has little durable consequence except for those students receiving financial aid, who can lose aid after two years if they do not sufficiently improve. Still, the system’s guidelines emphasize that even if an academic warning does not itself lead to dismissal, students will not be able to earn a degree with a GPA of less than 2.0.⁶ The 2.0 GPA threshold does not appear to be systematically linked to other outcomes, such as the ability to transfer to a four-year institution.⁷ More immediate consequences are reserved for students who fall below a 1.5 GPA; these students may be immediately placed on probation and required to file an appeal in order to continue enrolling or receiving aid. It’s also important to note that students with GPAs just above the 2.0 threshold are not necessarily “safe” from future consequences and thus may also feel pressure to improve. However, these students will not receive any formal academic warning, nor will they need to improve their performance in subsequent semesters (since SAP is based on cumulative GPA, those who fall below need to dig out of a hole, while those who are above may even be able to afford reduced performance in a subsequent term).

Our review of college catalogs describing SAP and academic good standing policies suggests performance standards may be less than perfectly transparent to students—indeed, we found them challenging to decipher ourselves. In the years pertaining to our sample, policies appear to vary somewhat across colleges, and the thresholds and timelines for SAP evaluation do not always seem to correspond to the thresholds and timelines for broader institutional academic standards. We will return to this complexity in our discussion section. Nonetheless, for the period and sample under consideration, all students with a GPA below 2.0 received at least some notification that they were at academic risk by the end of their first year, but students were unlikely to face binding consequences (such as financial aid loss or dismissal) before the end of their second year unless they fell below a 1.5 GPA.

III. Theoretical Framework

Our theoretical framework is based on Bénabou and Tirole (2000), who present a simple principal–agent model in which agents choose between shirking, a low-effort/low-benefit task, and a high-effort/high-benefit task. Lindo, Sanders, and Oreopoulos (2010) use an even simpler version of this model in their analysis of academic probation, focusing on the agent’s decision while accounting for heterogeneity in their ability (conceptualized as a probability of success at either the low-effort/ low-benefit task or the high-effort/high-benefit task). The key insight emphasized by Lindo, Sanders, and Oreopoulos (2010) is the heterogeneity of behavioral impactswhen performance standards are applied: higher ability individuals are motivated to work harder, while lower ability individuals are discouraged and drop out. (See Online Appendix A for a more detailed theoretical discussion and graphical illustrations.)

For our analysis, we are also interested in the principal’s (policymaker’s) perspective. Imposing a standard is only worthwhile if the increase in value coming from those induced to work harder exceeds the loss of value attributable to those induced to dropout. We are also interested specifically in the role of financial aid in this context. The Pell Grant and other scholarship programs provide another means by which policymakers can encourage greater investment in education. But if the planner provides an upfront scholarship based on enrollment alone, this induces more individuals into the low-effort/low-benefit option, but no more into the high-effort/high-benefit option.⁸ Thus, relative to providing a given scholarship without any performance standard, tying aid to performance is unambiguously worthwhile if the total benefit of the low-effort option is lower than the value of the scholarship.⁹ Assuming that there is some minimal level of effort that generates benefits less than the cost of the scholarship, then performance standards are always desirable. The question is where to set the minimal standard and how to implement them to maximize the desired behavioral effects.

Though our model highlights some factors that can influence the optimal threshold, our empirical analysis here only evaluates the apparent costs and benefits of the current threshold. We see the key insights of this model as threefold. First, even before turning to the data, the model reveals that some minimal performance standard is desirable, so if current policy is ineffective, this suggests considering implementation issues and/or alternative thresholds rather than eliminating standards completely. Second, the implication of heterogeneous effects by ability suggests the importance of examining impacts beyond those near the given threshold. Third, the model highlights the importance of considering a range of outcomes beyond academic impacts: if performance standards reduce aid expenditures without harming (or potentially even increasing) earnings, they may be socially desirable even if they reduce academic attainment for some students.

This theoretical framework helps guide our empirical contribution. First, our DID identification strategy will net out the effects of academic probation policies that apply to all students and provide a broader view of the hypothesized heterogeneous effects among affected students, compared with an RD that considers only aided students near the cutoff. Second, our inclusion of labor market earnings outcomes (at least in the medium term) provides a broader view of the policy’s effects than an analysis of academic outcomes alone. For example, it is possible to imagine scenarios under which students themselves benefit from leaving school earlier: they may reallocate their time from unproductive studies to more productive work in the labor market.¹⁰ Third, our analysis over a longer time frame (six years) than prior research allows us to provide a more comprehensive summary of human capital outcomes. Finally, recognizing that policymakers’ and students’ interests may diverge, we will roughly weigh the value of any impacts on human capital attained against the impacts on estimated scholarship outlays.

While the theoretical model focuses on agents’ actions in a single period under performances incentives, in our empirical context we consider three distinct periods: the first is an evaluation period in which students learn about their ability, the second period is a warning period in which individuals know where their performance falls relative to the standard but are not yet subject to loss of aid, and the third period is an enforcement period in which aid recipients who do not improve to meet the standard lose their aid.¹¹ These periods are reasonably well-defined for aid recipients in our sample as the first, second, and third year (and beyond) relative to entry.¹² The second period is when we are most likely to observe heterogeneous behavioral responses by ability. In the third period, when consequences are enforced, we may see less heterogeneity if even students who fall closer to the performance threshold are unable to improve enough to avoid losing aid.

IV. Data

We use de-identified state administrative data on first-time students who entered one of more than 20 community colleges in a single eastern state between 2004 and 2010. Only fall entrants are included in the data. We focus on students who enrolled full-time in their first semester to ensure enough courses are attempted to compute a reliable first-year GPA (an additional justification is that performance standards may not be assessed until students have attempted at least 12 credits). We follow all students’ outcomes for six years after initial entry.

The data include demographic information, transcripts, placement test scores, financial aid received in the first year, and credentials earned. All measures of enrollment, GPA, credits attempted and completed, and certificates and associate degrees completed are derived from the community college transcripts and are aggregated across colleges for those who enrolled in more than one community college during the followup period. The data are linked to two additional databases: the National Student Clearinghouse (NSC), which we use to capture transfer to four-year (public or private not-for-profit) and/or for-profit institutions and individual quarterly employment and earnings data from state Unemployment Insurance (UI) records. We use the UI data to construct measures of student labor supply during the second through sixth years post-entry, as well as to create controls for first-year employment status and earnings.

The data do not include any explicit measure of academic warning. We infer who is under a warning status based upon students’ cumulative grade point averages (GPAs). Because SAP policy in this system also requires students to complete two-thirds of the credits they attempt, we know that some students above the threshold will also be warned they are failing SAP.¹³ This waters down the magnitude of our estimated effects. We are not able to explicitly identify students who lost Pell eligibility as a result of SAP failure. However, this is not necessary for our analysis, which focuses on the initial threat of losing Pell (based on first-year GPA) as a key dimension of treatment rather than considering only students who experience the actual loss of aid.

Table 1 describes our full sample and provides mean outcome levels for all full-time entrants to this state system as well as for our analytic samples, which limit the sample by GPA (and for the RD, by aid status). Average first-year GPA is 2.4 overall, but closer to 2 for our analytic samples. About two-thirds of entrants are pursuing liberal arts degrees, which may indicate an intent to transfer, and about one-quarter to one-third transfer within six years. More than 60 percent re-enrolled in fall of the second year, but fewer than 10 percent remained enrolled by the end of the six-year followup period.

Table 1.

Descriptive Statistics, State Community College Sample (2004–2010 First-Time, Full-Time Fall Entrants)

Variable	Full Sample	RD Sample	RD-DID Sample	DID Sample
Background variables
Age (years)	20.0	19.6	19.1	19.2
Female (percent)	53	57	50	49
White (percent)	66	58	65	64
Black (percent)	21	31	22	23
Hispanic (percent)	6	6	7	7
Total aid, Y1 ($)	2,171	4,132	2,178	2,157
Pell recipient (percent), Y1	38	71	37	38
Pell amount (percent), Y1	1,277	2,502	1,318	1,324
Federal loan recipient (percent), Y1	11	21	11	11
Federal loan amount ($), Y1	390	776	409	410
Cumulative GPA <2.0, Y1	30	41	42	48
Comp. <67% credits, Y1	37	43	40	52
Credits attempted, Y1	27.2	28.4	27.9	27.0
Credits earned, Y1	20.2	20.0	19.8	17.7
Took placement test (percent)	79	83	81	82
Needs remediation (percent, predicted)	73	80	75	76
Ever dual-enrolled (percent)	18	24	21	19
Intent: Occ. associate’s (percent)	23	23	22	22
Intent: Occ. cert. (percent)	13	14	12	12
Intent: Liberal arts AA/AS (percent)	64	63	66	66
First-year GPA	2.37	2.06	2.06	1.87
Outcome variables
Fall Year 2
Enrolled (percent), fall Y2	62	62	66	61
Term GPA, fall Y2	2.24	1.97	1.98	1.85
Credits attempted, fall Y2	7.52	7.35	7.86	7.10
Credits earned, fall Y2	5.66	4.78	5.19	4.47
Quarterly earnings ($), Y2	1,872	1,987	1,925	1,937
Year 3
Still enrolled (percent), end of Y3	32	34	37	34
Cumulative GPA, end of Y3	2.32	2.04	2.06	1.91
Credits attempted, Y2–Y3	24.36	23.89	25.64	23.04
Credits earned, Y2–Y3	18.76	16.35	17.74	15.40
Quarterly earnings ($), Y2–Y3	2,112	2,235	2,172	2,186
Year 6
Still enrolled (percent), end of Y6	8	8	9	9
Cumulative GPA, end of Y6	2.35	2.08	2.10	1.96
Total credits attempted, Y2–Y6	31.1	32.2	34.6	31.8
Total credits earned, Y2–Y6	23.8	22.6	24.3	21.9
Earned certificate (percent), by Y6	13	11	11	9
Earned AA/AS (percent), by Y6	26	17	19	16
Transferred: Pub/NFP 4-yr (percent), by Y6	35	26	30	26
Transferred: For-profit (percent), by Y6	7	9	7	8
Quarterly earnings ($), Y2–Y6	2,639	2,684	2,656	2,637
Sample size	115,205	13,453	25,525	34,752

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time. Y1 = Year 1, Y2 = Year 2, Y3 = Year 3, Y6 = Year 6.

V. Empirical Strategy

Because all students in our sample face performance standards by the end of their first year, and about 54 percent of our sample receives financial aid in their first year, we can compare the effects of introducing performance standards for aided and unaided students. The data suggest two possible approaches: regression discontinuity (RD) analysis for aid recipients just above and below the GPA threshold to remain in good standing and/or a difference-in-difference (DID) analysis comparing students above and below this threshold for aid recipients versus nonrecipients. An RD-DID, though underpowered, helps provide a linkage between the two methods.

A. Regression Discontinuity

The only assumption required is that the underlying relationship between first-year GPA and the outcome of interest (in the absence of the performance standard) is continuous through the threshold. Following Imbens and Lemieux (2008), we use a local linear specification with the bandwidth restricted to a narrow range around the 2.0 threshold. We focus on a bandwidth of 0.5 GPA units, guided by graphical plots, an optimal bandwidth analysis, and by the concern that other school policies might come into play below 1.5 or above 2.5.¹⁴ Still, we test for sensitivity to bandwidth selection by reestimating results using half this bandwidth (0.25), twice this bandwidth (1.0), or allowing the bandwidth to vary for each outcome according to an optimal-bandwidth calculator.¹⁵

The basic model, which we run on the sample restricted to aid recipients within the given bandwidth, takes the form:

$$\begin{gathered} Y_i=B_0+{\text{β}}_1\left(Belo{w}_i\right)+{\text{β}}_2\left(GPADistanc{e}_i\ast Belo{w}_i\right) \\ \hspace{1em}\hspace{1em}+{\text{β}}_3\left(GPADistanc{e}_i\ast Abov{e}_i\right)+CollegeFE+CohortFE+{\text{β}}_n{X}_i+{\text{ε}}_i \end{gathered}$$ (1)

where $Y_i$ represents the outcome for student $i$, and ${\text{β}}_1$ is the estimate of the effect of falling below the SAP cutoff on the outcome. CollegeFE is a vector of institutional fixed effects (entered as a set of dummy variables indicating the institution initially attended, with one institution excluded); this is important because the financial aid officers responsible for enforcing performance standards are nested within institutions. CohortFE is a vector of cohort fixed effects, a necessary inclusion because of potential changes in the student population over time. $X_i$represents a vector of individual-level covariates, including race, gender, age at initial enrollment, whether students were exempt from placement testing in reading and math (indicators of prior achievement), placement test scores for those who were not exempt, whether the student was predicted to be assigned to remedial coursework, whether the student had previously enrolled in college as a high school student, and dummies for the student’s degree intent at entry (occupational associate degree, occupational certificate, or academic associate degree), and major at entry.¹⁶ We also include additional controls to capture elements of the student’s first-year experience, including total credits attempted in the first year, whether the student worked for pay, and how much the student earned during the school year.¹⁷ We cluster standard errors by institution–cohort.¹⁸ We test the sensitivity of our results to models with and without covariates.

B. Grade Heaping

Using GPAs as the running variable in an RD introduces an additional challenge. Given the nature of the state’s grading system—in which only whole letter grades are awarded—we find “heaping” in whole-number GPAs across the distribution, including at our cutoff value of 2.0. Moreover, the fewer credits a student has attempted, all else equal, the more likely they are to have a whole-number GPA. This problem, however, is surmountable.¹⁹ Excluding students with precisely a 2.0, a McCrary (2008) test indicates the distribution of cumulative GPAs is continuous around the threshold. This suggests that the observed heaping is due to grading policy and not to students precisely manipulating whether they fall above or below the threshold. Thus, following the recommendations of Barreca, Lindo, and Waddell (2011) (see also Barreca, Guldi, Lindo, and Waddell 2011), we rely on “donut-RD” estimates, dropping observations with precisely a 2.0 GPA. Figure 1 shows the distribution of first-year GPAs for aid recipients and nonrecipients before removing whole-number GPAs.

Figure 1.

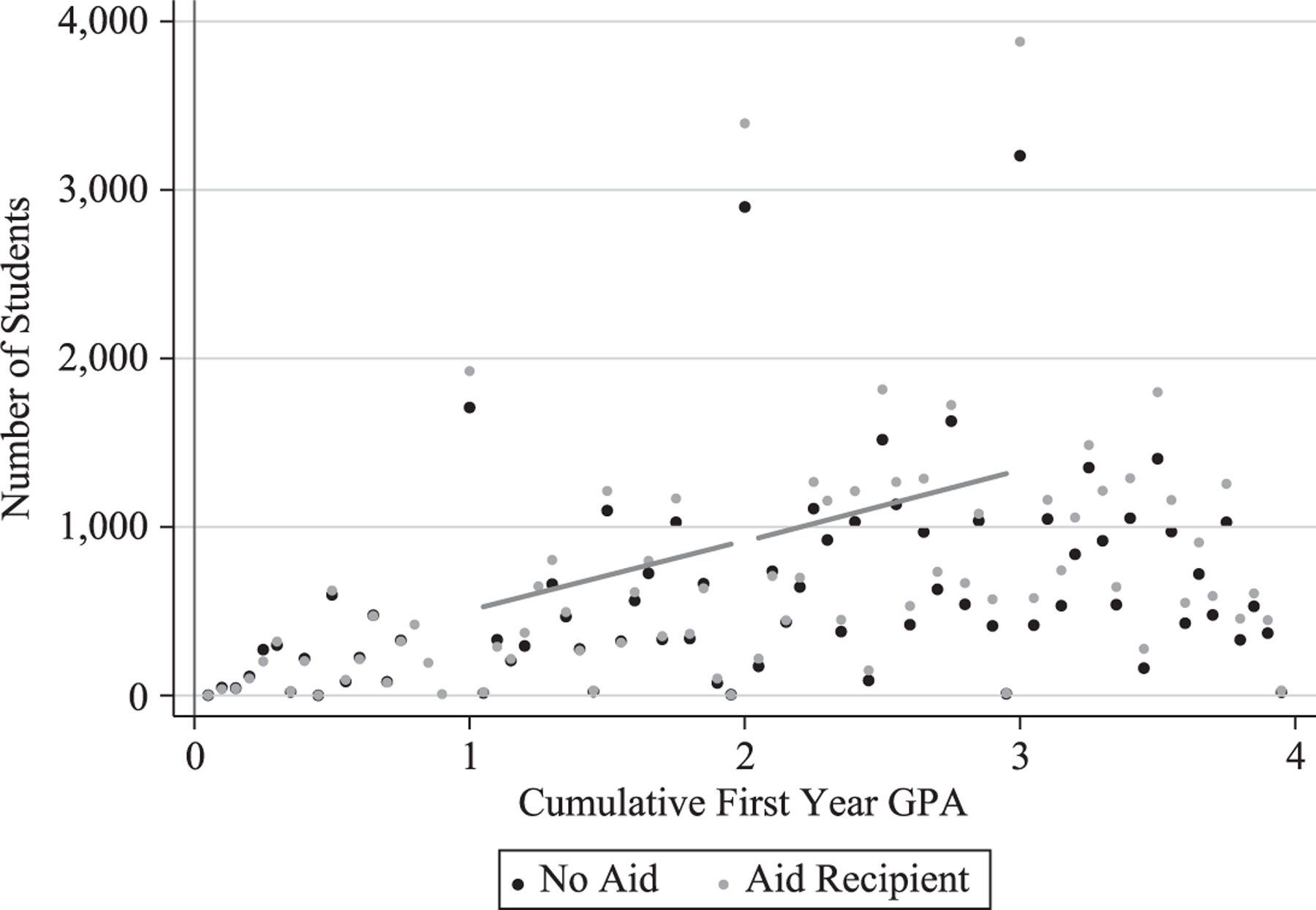
Distribution of GPA before Eliminating Heaping at GPA = 2.0

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Note: Fitted lines are shown for aid recipients above and below the cutoff after disregarding GPA = 2.0.

The RD estimates capture the total effect of performance standards for aid recipients, including general standards at the institution as well as the effects of SAP policy specifically. To net out the effects of general academic standards and isolate the effects of SAP, we also run the following RD-DID regression:

$$\begin{array}{l}{Y}_i+{\text{γ}}_0+{\text{γ}}_1\left(Belo{w}_i\ast Ai{d}_i\right)+{\text{γ}}_2\left(Belo{w}_i\right)+{\text{γ}}_3\left(Ai{d}_i\right)\\ \hspace{1em}\hspace{1em}+{\text{γ}}_4\left(GPADistanc{e}_i\ast Belo{w}_i\ast Ai{d}_i\right)+{\text{γ}}_5\left(GPADistanc{e}_i\ast Abov{e}_i\ast Ai{d}_i\right)\\ \hspace{1em}\hspace{1em}+{\text{γ}}_6\left(GPADistanc{e}_i\ast Belo{w}_i\ast NoAi{d}_i\right)+{\text{γ}}_7\left(GPADistanc{e}_i\ast Abov{e}_i\ast NoAi{d}_i\right)\\ \hspace{1em}\hspace{1em}+CollegeFE+CohortFE+{\text{γ}}_n{X}_i+{\text{ε}}_i\end{array}$$ (2)

The ${\text{γ}}_i$ in this regression provides an estimate of the difference in the two RD estimates. While these estimates have the advantage of isolating the effects of SAP relative to other policies at the 2.0 threshold, like the RD it remains limited only to students near the cutoff, and both approaches are relatively weakly powered.

C. Difference-in-Difference

Compared to the RD or RD-DID, a DID approach has several advantages: it isolates the effects of SAP separate from other policies at the 2.0 cutoff, examines a wider range of students affected by the policy, and provides greater statistical power than either the RD or the RD-DID. The main drawback is that the DID requires stronger assumptions about the relationship between first-year GPA and subsequent outcomes, namely by assuming that whatever differences in potential outcomes exist between aided and unaided students, these differences are fixed as we move across the range of first-year GPAs (after controlling for any differences in observable characteristics).²⁰ This assumption could be violated if, for example, unaided students have unobserved advantages that are larger for those with particularly poor first-year performance. Before presenting our results, we will examine the plausibility of the DID assumption by visually inspecting outcome patterns for aided and unaided students by GPA, by examining the same patterns earlier in college before SAP warnings are given and by testing whether the DID indicates significant “impacts” on background characteristics (a type of covariate balance check).

Our specification allows for a very flexible relationship between GPA and potential outcomes by replacing the Below and GPADistance interactions from Equation 1 with a set of fixed effects for GPA bins (with width of 0.05):

$$\begin{gathered} Y_i={\text{α}}_0+{\text{α}}_1\left(Belo{w}_i\ast Ai{d}_i\right)+{\text{α}}_2\left(GPABin{05}_i\right)+{\text{α}}_3\left(Ai{d}_i\right) \\ \hspace{1em}\hspace{1em}+CollegeFE+CohortFE+{\text{α}}_n{X}_i+{\text{ε}}_i \end{gathered}$$ (3)

We continue to limit the bandwidth above the cutoff to those below a 2.5 GPA; however, we extend the bandwidth below the cutoff to those above 1.0 GPA in order to capture more of the population affected by SAP failure. In a separate specification, we directly test for heterogeneity in the DID model by adding additional interactions for those further below the cutoff (from 1.5 to 1.85 GPA) and furthest below the cutoff (from 1.0 to 1.5 GPA). This allows us to test our hypothesis that discouragement effects will be bigger in the DID as we include students further below the threshold, while encouragement effects may be smaller.

VI. Main Results

A. Graphical Analysis and Covariate Balance Checks

Figures 2–5 show average outcomes by first-year GPA in bins of 0.05 and with the size of the circles reflecting numbers of observations. Discontinuities in the outcomes of aid recipients below versus above the cutoff are visible in some but not most of the graphs (see Figure 3, for example, which shows enrollment and credits attempted by the end of Year 3). Even in graphs where there is no clear discontinuity for the aided group, it appears that the difference between aided and unaided students widens noticeably below the cutoff. Above the cutoff outcomes for aided students generally appear much more similar to those of unaided students. For example, reenrollment rates and credits attempted in Year 2 (Figure 2), end of Year 3 (Figure 3), and after six years (Figures 4–5) appear much lower for aided students below the cutoff than for unaided students, while the two groups appear much more similar above the cutoff. The earnings graphs follow a somewhat different pattern, with aided and unaided students appearing more similar below the cutoff, and some indication that gaps may widen the further we look above the cutoff.

Figure 2.

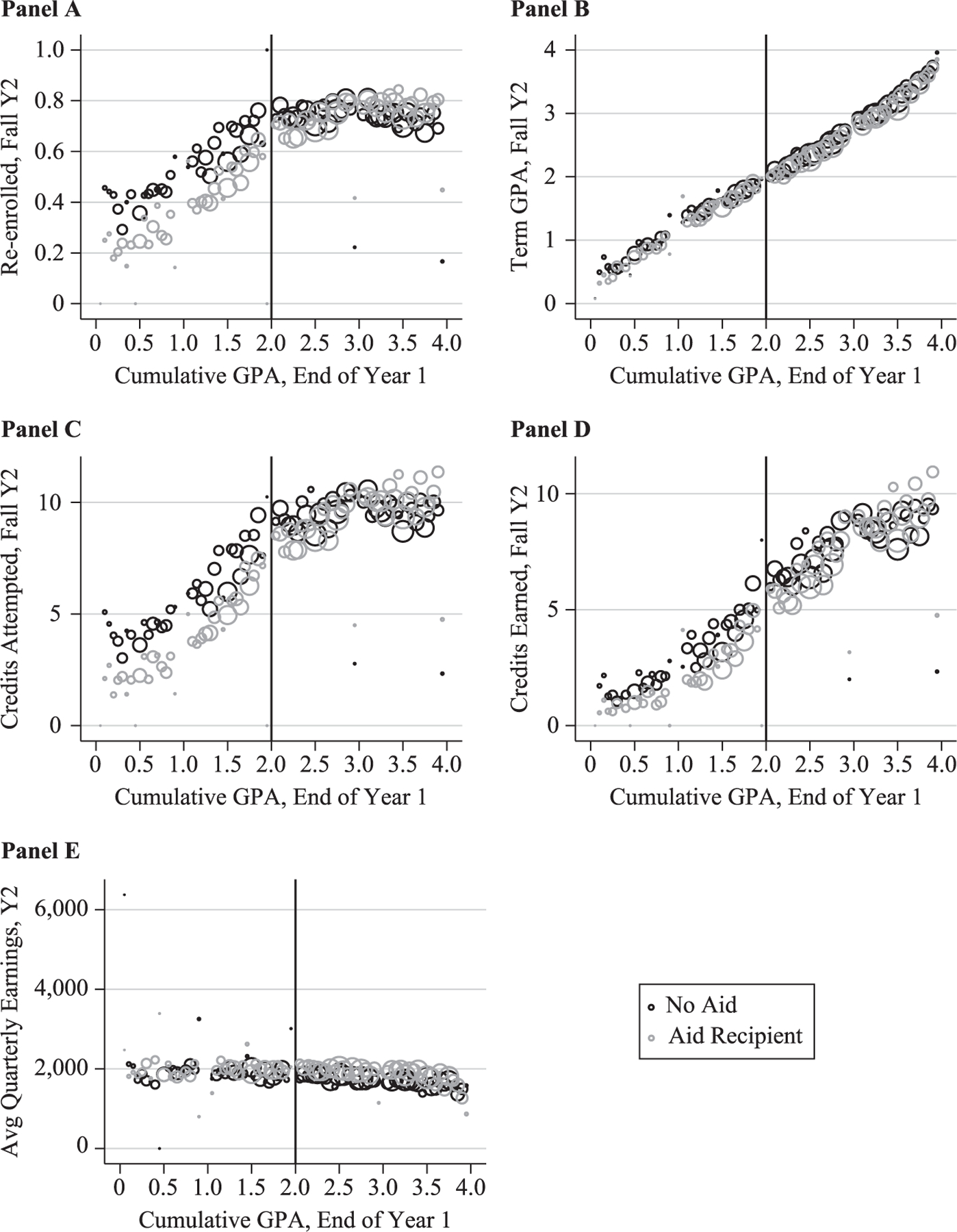
Fall Year 2 Outcomes

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Figure 5.

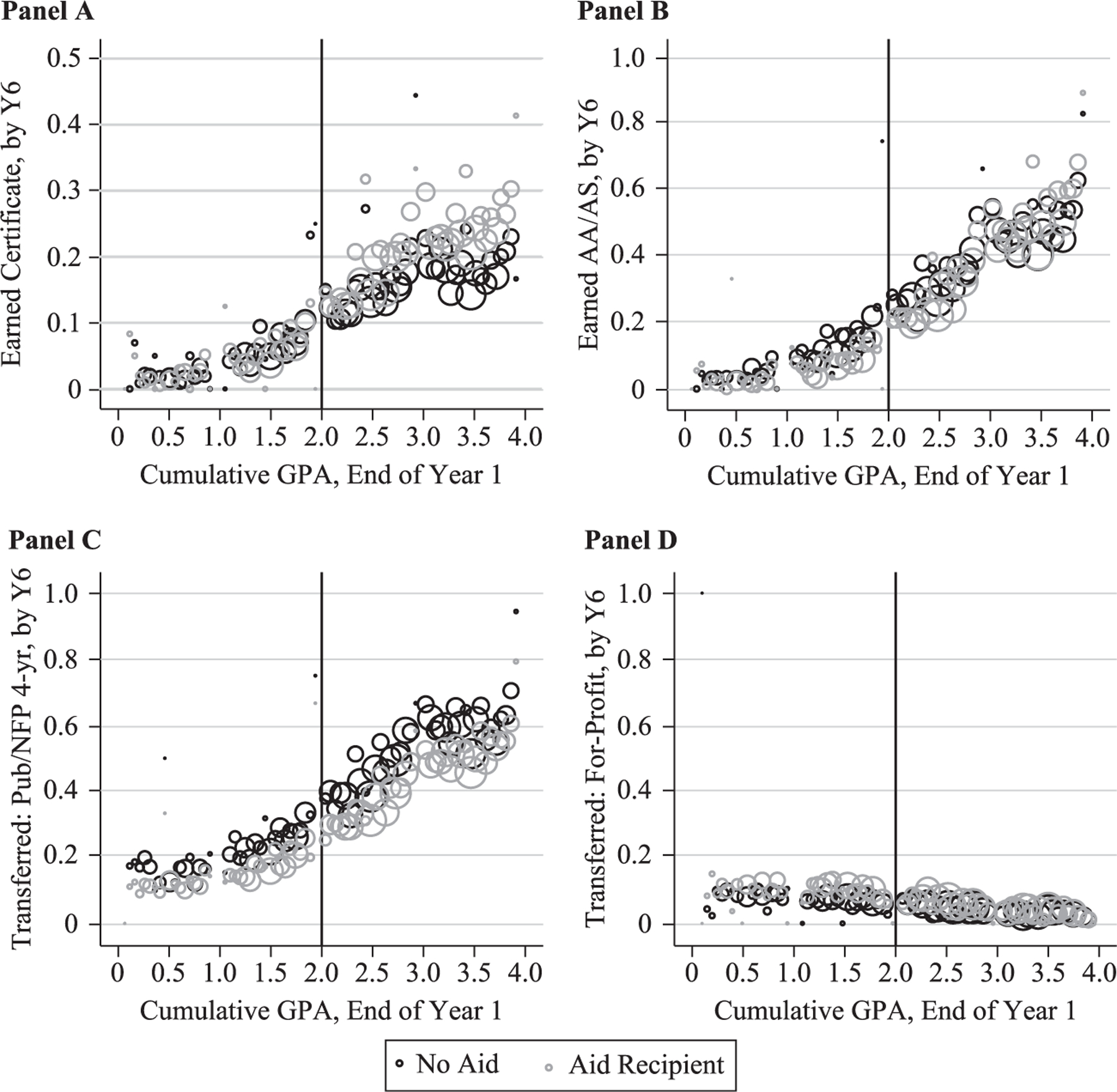
Degree Attainment and Transfer Outcomes, End of Year 6

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Figure 3.

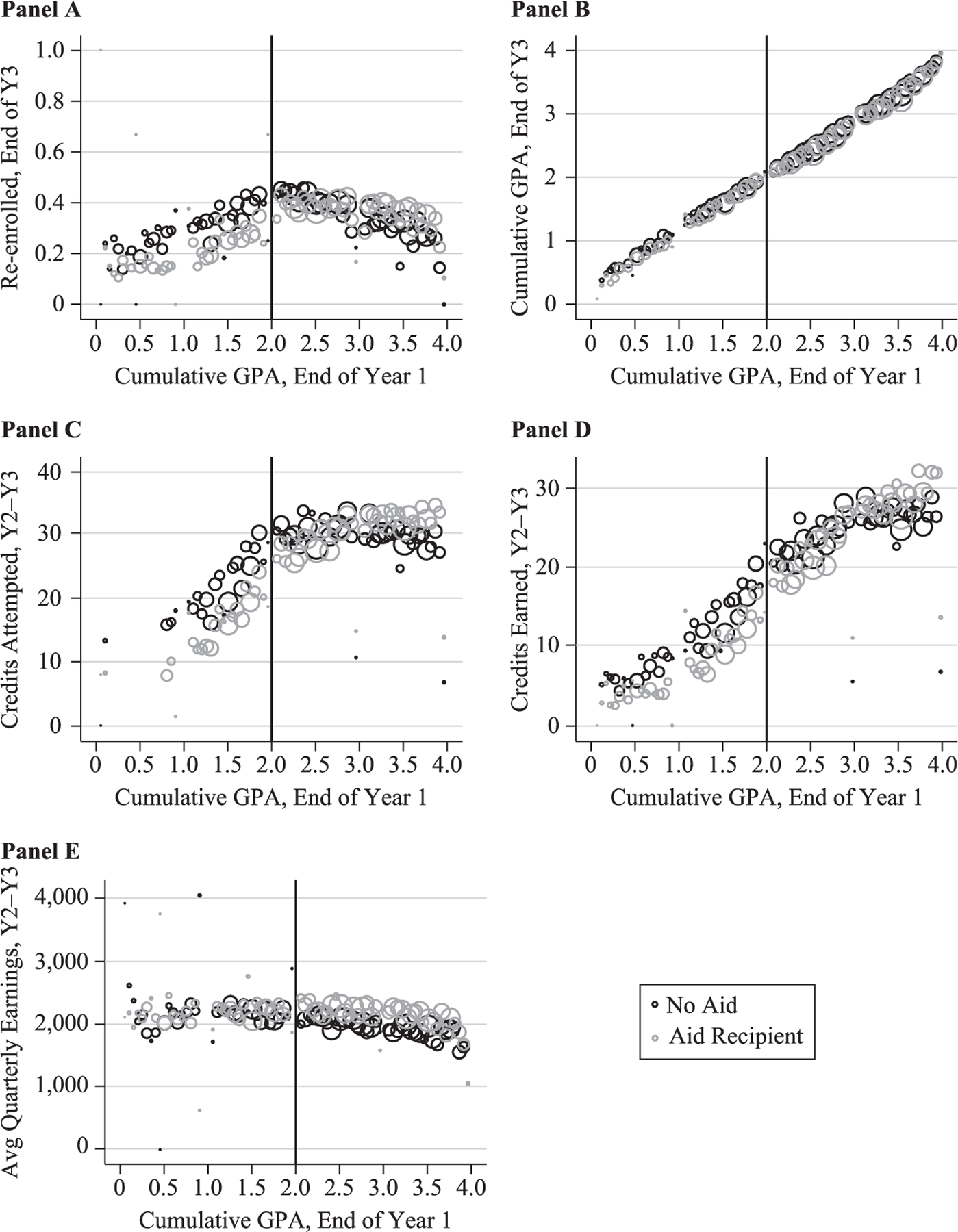
Cumulative Outcomes after 3 Years

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Figure 4.

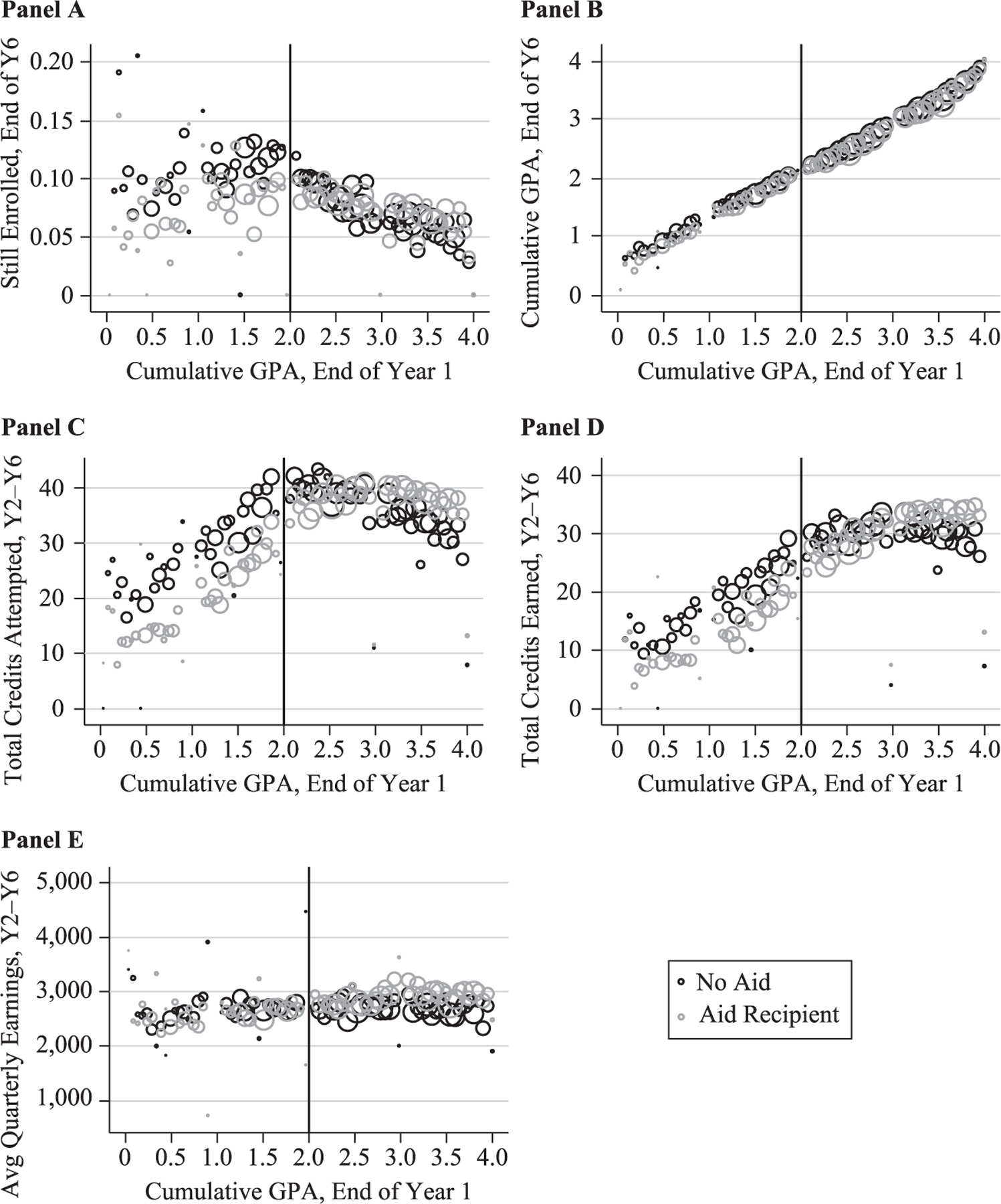
Cumulative Outcomes, End of Year 6

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Notes: Aid recipients are in gray; nonrecipients are in black.

The patterns in these graphs provide some reassurance about the stronger identification assumptions required for the DID, namely, that any differences between aided and unaided students should be fixed across the range of GPAs, except due to the effects of the difference in exposure to SAP policy. Above and below the cutoff, the lines for aided and unaided students look reasonably parallel, particularly for the range of data we focus on for the regressions, between 1.0 and 2.5. Above 2.5 or 3.0, outcomes for aided students actually begin to exceed those of unaided students—this could result if unaided students at high GPAs are more likely to transfer—but we do not include students this far from the threshold in our main specifications.

As a further check, in Figure 6 we also look at similar graphs of the spring Year 1 enrollment, credits, and GPAs (before students generally receive SAP warnings) based on the fall of Year 1 GPA. If the relationship between initial college GPA and subsequent outcomes is simply different for aided and unaided students, it should show up in these first-year graphs as well, yet in these graphs it appears the two lines are largely over-lapping across almost the whole range of GPA.

Figure 6.

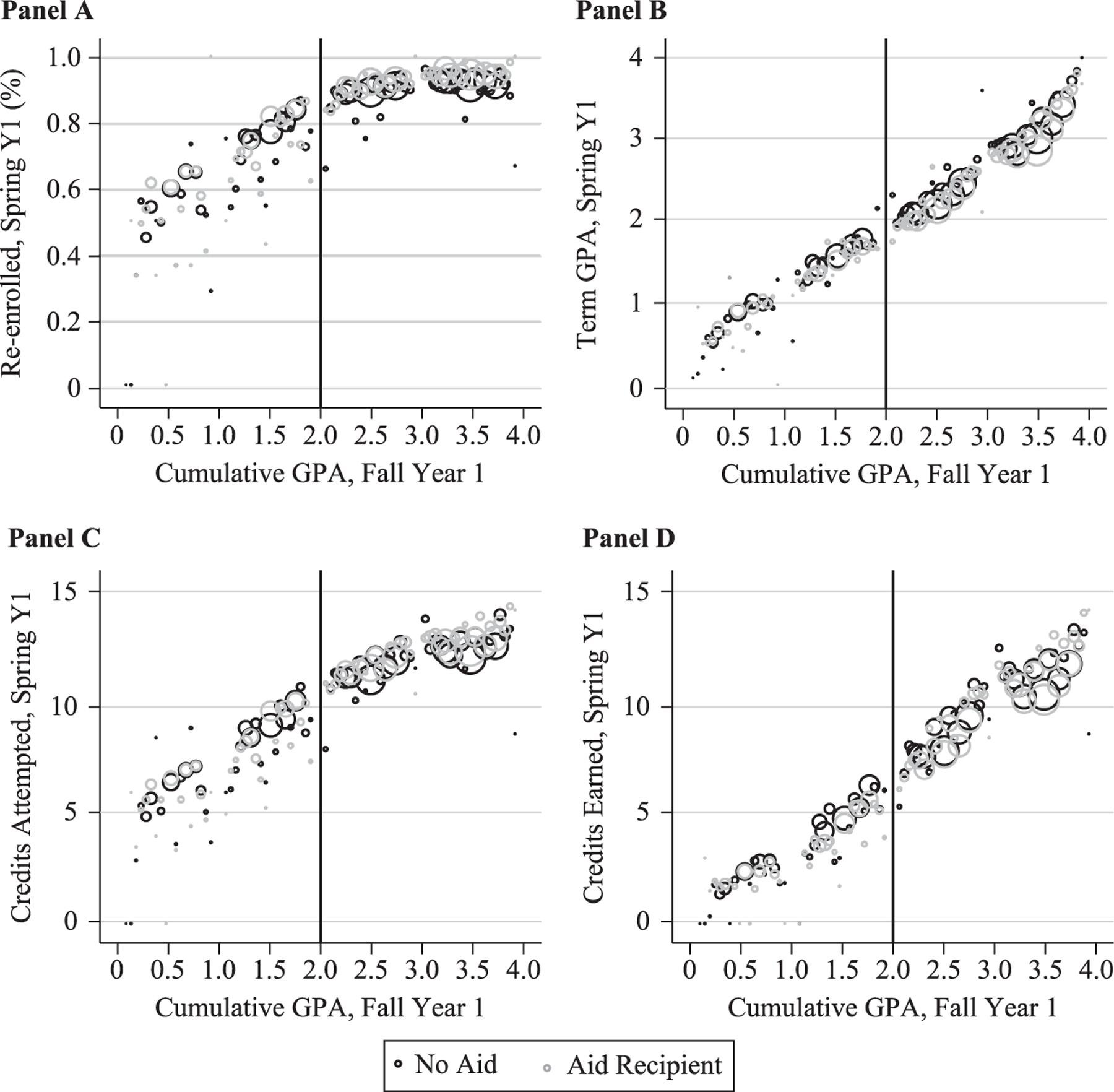
Spring Year 1 Outcomes as Function of Fall Year 1 GPA.

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

In Table 2, we formally evaluate whether any of our identification strategies may be biased by selection on observables. Rather than testing for a lack of balance on each pre-treatment characteristic individually, we instead follow a method employed by Carrell, Hoekstra, and Kuka (2018) that takes account not only of the magnitude of any differences in covariates, but also how much these differences in aggregate relate to the outcomes under study. To do this, we first run a set of regressions in which we predict each outcome using the full set of covariates listed in Online Appendix Table B1.²¹ Then, we run each of our main estimating equations (excluding covariates) with the predicted outcome variable on the left-hand side. We hope to see that the effects on predicted outcomes are insignificant and close to zero in magnitude.

Table 2.

Placebo Impacts on Predicted Outcomes Based on Observable Covariates

	RD (±0.5)		RD-DID (±0.5)		DID (+0.5/–1.0)
Predicted Outcome	Coef.	(SE)	Coef.	(SE)	Coef.	(SE)
Year 2
Enrolled, fall Y2	0.00	(0.006)	0.01	(0.007)	0.00	(0.003)
Term GPA, fall Y2	0.02	(0.006)***	0.02	(0.008)**	0.00	(0.003)
Credits attempted, fall Y2	0.08	(0.085)	0.17	(0.108)	0.02	(0.038)
Credits earned, fall Y2	0.09	(0.067)	0.17	(0.082)**	0.01	(0.031)
Quarterly earnings ($), Y2	14	(54)	77	(70)	18	(27)
Year 3
Still enrolled, end of Y3	0.00	(0.004)	0.00	(0.005)	0.00	(0.002)
Cumulative GPA, end of Y3	0.02	(0.006)***	0.02	(0.008)***	0.00	(0.003)
Credits attempted, Y2–Y3	0.26	(0.280)	0.57	(0.355)	0.04	(0.135)
Credits earned, Y2–Y3	0.27	(0.219)	0.53	(0.274)*	0.02	(0.109)
Quarterly earnings ($), Y2–Y3	11	(48)	71	(65)	13	(25)
Year 6
Still enrolled, end of Y6	0.00	(0.001)	0.00	(0.001)	0.00	(0.000)
Cumulative GPA, end of Y6	0.02	(0.006)***	0.02	(0.008)***	0.00	(0.003)
Total credits attempted, Y2–Y6	0.27	(0.336)	0.53	(0.423)	0.03	(0.165)
Total credits earned, Y2–Y6	0.28	(0.262)	0.51	(0.327)	0.01	(0.133)
Earned certificate, by Y6	0.00	(0.003)	0.01	(0.004)*	−0.003	(0.001)**
Earned AA/AS, by Y6	0.01	(0.005)*	0.01	(0.006)*	0.00	(0.002)
Transferred: Pub/NFP 4-yr, by Y6	0.01	(0.006)	0.01	(0.008)	0.00	(0.003)
Transferred: For-profit, by Y6	0.00	(0.002)	0.00	(0.003)	0.00	(0.001)
Quarterly earnings ($), Y2–Y6	1	(45)	70	(64)	3	(24)
Sample size		13,453		25,525		34,752

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Notes: Pseudo-impacts on predicted outcomes are taken from separate regressions following our main RD, RD-DID, and DID specifications (with no other covariates included) with the predicted outcome as the dependent variable. Predicted outcomes are obtained by first running regressions to predict each outcome using all available covariates (for a full list of covariates included, see Online Appendix Table B1).

The first take-away from this analysis is that, perhaps surprisingly, the DID appears most robust to selection concerns, with only one statistically significant pseudo-impact out of 19 predicted outcomes tested: a −0.003 reduction in certificate completion.²² For the RD and RD-DID, this method reveals statistically significant, but very small, positive impacts on GPA (0.02 grade points) and associate degree completion (one percentage point), with some additional small positive effects on predicted credits and certificate completion in the RD-DID. Of course, we can control for these small differences in observed covariates when we run our actual impact regressions, and, ultimately, we will show a highly consistent pattern of findings with or without these controls included. Still, to the extent these small observable differences might indicate other, unobservable differences, if anything this would suggest a slight positive bias in the RD and RD-DID, with those just below the cutoff having slightly higher ability/motivation.

B. RD and RD-DID Results

Table 3 provides the results from the RD and RD-DID specifications for several aspects of student behavior that our model suggests should be affected, measured separately during the fall of Year 2 (the first warning period), through the end of Year 3 (including the enforcement period when individuals could be actually prohibited from reenrolling or receiving aid), and cumulatively through Year 6. The first column of the table shows our preferred RD specification, while the subsequent column shows an alternative specification with no covariates. The final column shows the RD-DID results. Results for alternative bandwidths are presented in Online Appendix Table B2 and are consistent in overall patterns and magnitudes, though the widest bandwidth generates more statistically significant results.

Table 3.

RD-Estimated Effects of Failing GPA Performance Standard at End of Year 1, Aid Recipients Only

	RD (±0.5 GPA Points)				RD-DID
	With Covariates		No Covariates		With Covariates
Outcome	Coef.	(SE)	Coef.	(SE)	Coef.	(SE)
Year 2
Enrolled, fall Y2	−0.01	(0.02)	−0.01	(0.02)	−0.03	(0.03)
Term GPA, fall Y2	0.06	(0.04)	0.07	(0.04)*	0.05	(0.05)
Credits attempted, fall Y2	−0.26	(0.26)	−0.23	(0.26)	−0.64	(0.40)
Credits earned, fall Y2	−0.04	(0.24)	0.00	(0.25)	−0.15	(0.36)
Quarterly earnings ($), Y2	28	(83)	29	(96)	−27	(118)
Year 3
Still enrolled, end of Y3	−0.07	(0.02)***	−0.07	(0.02)***	−0.07	(0.03)**
Cumulative GPA, end of Y3	0.01	(0.02)	0.01	(0.02)	−0.01	(0.03)
Credits attempted, Y2–Y3	−1.86	(0.93)**	−1.72	(0.97)*	−2.84	(1.42)**
Credits earned, Y2–Y3	−1.00	(0.82)	−0.86	(0.85)	−1.23	(1.21)
Quarterly earnings ($), Y2–Y3	32	(88)	27	(95)	−31	(118)
Year 6
Still enrolled, end of Y6	0.01	(0.01)	0.01	(0.01)	0.00	(0.02)
Cumulative GPA, end of Y6	0.00	(0.02)	0.01	(0.02)	−0.03	(0.03)
Total credits attempted, Y2–Y6	−1.55	(1.30)	−1.35	(1.37)	−3.39	(2.16)
Total credits earned, Y2–Y6	−0.96	(1.09)	−0.75	(1.15)	−2.12	(1.75)
Earned certificate, by Y6	−0.01	(0.02)	−0.01	(0.02)	−0.03	(0.02)
Earned AA/AS, by Y6	−0.05	(0.02)***	−0.05	(0.02)***	−0.03	(0.03)
Transferred: Pub/NFP 4-yr, by Y6	−0.02	(0.02)	−0.01	(0.02)	0.02	(0.03)
Transferred: For-profit, by Y6	0.00	(0.01)	0.00	(0.01)	0.02	(0.02)
Quarterly earnings ($), Y2–Y6	68	(99)	53	(103)	−59	(150)
Sample size	13,453		13,453		25,525

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Notes: Robust standard errors clustered by institution–year in parentheses. All specifications use local linear regression with observations at precisely 2.0 GPA dropped. Control variables include all covariates listed in Table 2: age, gender, race dummies, placement test scores if available, placement test flags, flag for predicted remedial need, flag for ever dual enrolled, degree intent at entry, major at entry, first-year credits attempted, first-year employment status, and first-year earnings. For term-GPA estimates, term GPA is imputed to the last known cumulative GPA (this ensures that any impacts on this measure come only from students who reenroll without introducing attrition bias; see Online Appendix Table B3 for alternative approaches to computing the fall of Year 2 term-GPA impact). Fall Year 2 credits attempted/ completed are zero if the student is not enrolled. See Online Appendix Table B2 for results from alternative bandwidths.

We first examine reenrollment rates, term GPAs, and credits in the fall of Year 2. Note that for dropouts, term GPAs are imputed to the last known cumulative GPA to ensure that impacts only come from those who reenroll, without introducing attrition bias.²³ Credits attempted/completed are zero for those who are not enrolled. For aid recipients near the cutoff, failing SAP appears to have little effect on initial reenrollment decisions or on measures of credits attempted and completed, though coefficients are consistently negative but generally very small in magnitude. We find a marginally insignificant increase of 0.06 GPA points (p = 0.14) in term GPA in the fall of the second year, and no evidence of effects on earnings.²⁴

By the end of Year 3, during which students may have experienced the loss of aid, more clearly negative effects begin to appear. Most notably, by the end of Year 3, aid recipients who just barely failed the GPA standard were seven percentage points (p < 0.01) less likely to still be enrolled, consistent across both the RD and RD-DID. We find a significant reduction of about 1.9 credits attempted (about a 19 percent reduction), with a smaller, but statistically nonsignificant reduction of one credit completed (a 14 percent reduction), with slightly larger magnitudes in the RD-DID.

By the end of the six-year followup period, no significant effects remain on the likelihood of still being enrolled or on cumulative GPAs (as shown in Table 1, very few students remain enrolled after six years, regardless). The reductions in credits attempted and completed largely persist (and in the RD-DID, increase in magnitude), but increases in standard errors render these effects no longer statistically significant. We find a significant five-percentage-point reduction in associate degree completion, though we interpret this result cautiously as it is sensitive to bandwidth selection (see Online Appendix Table B2) and smaller in the RD-DID. Coefficients on certificate completion and transfer to a four-year institution are also negative, but small and not statistically significant. Finally, we find no effects on quarterly earnings averaged across Years 2–6.

Overall the clearest result from the RD and RD-DID is that failing SAP leads students to drop out sooner than they would otherwise and possibly to earn fewer degrees, with very limited evidence of any positive effects beyond the marginally insignificant 0.06 GPA effect in the fall of Year 2.

C. Difference-in-Difference Results

As discussed in Section III, a major drawback of both the RD and the RD-DID is that effects are estimated only for students near the 2.0 threshold. Yet our model clearly predicts heterogeneous effects by ability. We expect encouragement effects to be strongest for students just below the threshold, while we expect discouragement effects to grow as we move further down the GPA distribution. Our DID specification enables us to capture the effects of SAP policy for a wider range of students affected, while also increasing statistical power.

Our results are shown in Table 4. The main results in the first column show the average effects of falling below the GPA standard for students with as low as a 1.0 GPA (the comparison group includes students with GPAs up to 2.5).²⁵ Results for specifications with no covariates are shown in Online Appendix Table B4 and are virtually identical. The subsequent columns show results from a single regression in which we allow for heterogeneity in treatment effects depending on how far below the threshold the student falls. Column 2 shows the main effect of falling below the 2.0 cutoff, while Columns 3 and 4 test whether there is any significant differential effect for those further below the cutoff (1.5–1.85 GPA) and furthest below the cutoff (1.0–1.5 GPA), respectively. To obtain the total effects for those further/furthest from the cutoff, the main effect in Column 2 and additional effect in Column 3 or 4, respectively, should be added together. For those between 1.85 and 1.99 GPA, the main effect in this model is equivalent to the total effect.

Table 4.

DID Estimated Effects of Failing GPA Performance Standard at End of Year 1

	Baseline DID				DID Allowing for Heterogeneity by GPA
	1.0 < GPA< 2.5		Main Effect of Aided*Below2.0		Additional Effect for those Further Below (1.5–1.85 GPA)		Additional Effect for those Furthest Below (1.0–1.5 GPA)
Outcome	Coef.	(SE)	Coef.	(SE)	Coef.	(SE)	Coef.	(SE)
Year 2
Enrolled, fall Y2	−0.06	(0.01)***	−0.04	(0.02)	−0.01	(0.02)	−0.04	(0.02)*
Term GPA, fall Y2	0.03	(0.02)	0.11	(0.05)**	−0.07	(0.05)	−0.09	(0.05)*
Credits attempted, fall Y2	−0.66	(0.13)***	−0.79	(0.32)**	0.21	(0.34)	0.08	(0.33)
Credits earned, fall Y2	−0.06	(0.11)	−0.18	(0.29)	0.20	(0.28)	0.08	(0.30)
Quarterly earnings ($), Y2	−33	(41)	−203	(92)**	250	(91)***	132	(92)
Year 3
Still enrolled, end of Y3	−0.04	(0.01)***	−0.04	(0.03)	−0.01	(0.03)	0.01	(0.03)
Cumulative GPA, end of Y3	0.00	(0.01)	0.04	(0.02)**	−0.04	(0.02)*	−0.05	(0.02)***
Credits attempted, Y2–Y3	−2.27	(0.41)***	−2.65	(1.04)**	0.16	(1.12)	0.63	(1.11)
Credits earned, Y2–Y3	−0.58	(0.35)*	−0.69	(0.96)	−0.02	(0.99)	0.25	(1.00)
Quarterly earnings ($), Y2–Y3	−91	(41)**	−241	(90)***	266	(92)***	80	(95)
Year 6
Still enrolled, end of Y6	−0.01	(0.01)**	−0.01	(0.02)	−0.01	(0.02)	0.00	(0.02)
Cumulative GPA, end of Y6	−0.01	(0.01)	0.03	(0.02)	−0.03	(0.02)	−0.05	(0.02)**
Total credits attempted, Y2–Y6	−3.36	(0.59)***	−3.40	(1.40)**	−0.04	(1.47)	0.12	(1.42)
Total credits earned, Y2–Y6	−1.40	(0.46)***	−1.35	(1.17)	−0.07	(1.19)	−0.06	(1.17)
Earned certificate, by Y6	−0.02	(0.01)***	−0.03	(0.02)	0.01	(0.02)	0.01	(0.02)
Earned AA/AS, by Y6	0.00	(0.01)	−0.03	(0.02)	0.03	(0.02)	0.05	(0.02)**
Transferred: Pub/NFP 4-yr, by Y6	0.01	(0.01)	−0.01	(0.02)	0.02	(0.02)	0.02	(0.02)
Transferred: For-profit, by Y6	0.00	(0.00)	−0.01	(0.01)	0.01	(0.01)	0.01	(0.01)
Quarterly earnings ($), Y2–Y6	−111	(49)**	−203	(125)	$58	(125)	53	(127)
Sample size	34,752				34,752

Source: Authors’ calculations using restricted SCCS administrative data, 2004–2010 first-time fall entrants who initially enrolled full-time.

Notes: Robust standard errors clustered by institution–year in parentheses. All specifications limited to those with first-year GPA between 1.0 and 2.5. In addition to the main treatment interaction (Aided*Below), all specifications include fixed effects for first-year GPA bin in increments of 0.05, an indicator for aid recipients, and all covariates listed in Table 2: age, gender, race dummies, placement test scores if available, placement test flags, flag for predicted remedial need, flag for ever dual enrolled, degree intent at entry, major at entry, first-year credits attempted, first-year employment status, and first-year earnings. For term-GPA estimates, term GPA is imputed to the last known cumulative GPA (this ensures that any impacts on this measure come only from students who reenroll without introducing attrition bias; see Online Appendix Table B3 for alternative approaches to computing the fall of Year 2 term-GPA impact). Fall Year 2 credits attempted/completed are zero if the student is not enrolled. The coefficients in the Columns 2–4 columns are from a separate specification that separates the treatment effect into a main effect of Aided*Below2.0, with additional interactions for those further below [Aided*Below*(1.5 – 1.85 GPA)] and furthest below [Aided*Below*(1.0 – 1.5 GPA)] the cutoff. See text for details.

The baseline DID results in the first column generally follow the patterns seen in the RD and RD-DID, but are more accentuated with many more significant effects, including a six-percentage-point reduction in enrollment in the fall of Year 2.²⁶ Columns 2–4 highlight a clear pattern of heterogeneity: encouragement effects appear strongest, and discouragement effects appear weakest, for those just below the cutoff (Column 2). For example, the estimated four-percentage-point decline in Year 2 reenrollment for those just below the cutoff is not statistically significant but is significantly more negative for those furthest below the cutoff (for whom enrollment declines by a total of eight percentage points).²⁷ Conversely, compared with the 0.11 GPA point improvement in Year 2 for those nearest the cutoff, the effect is significantly smaller for those furthest below (for a total improvement of just 0.02 GPA points). On the other hand, credits attempted and completed do not appear to vary much by distance from the threshold, either in the short or longer term. This may be because students near the margin may reduce their course load in an effort to improve their GPAs, while those further away reduce course load out of discouragement. Overall, the DID suggests a decrease of 3.4 credits attempted and 1.4 credits completed after six years, roughly similar to the RD-DID.

The DID suggests a modest but statistically significant two-percentage-point decline in certificate completion. The RD and RD-DID had also suggested declines of one to three percentage points (though these were not statistically significant). But one outcome on which the RD and DID results diverge is on associate degree completion: the RD suggested a significant negative effect, while the DID finds no effect overall, with effects less negative or even positive for those furthest below the cutoff. It is surprising that any degree completion impacts would become less negative when including students further below the threshold. This could simply be attributable to floor effects in the outcome; perhaps only those close to the threshold are even on the margin of completing a degree.

We also see markedly more negative estimates on average quarterly earnings in the DID as compared with the RD (though estimates were also negative in the RD-DID, they were smaller and not significant), with affected students estimated to earn $111 less per quarter on average (roughly a 5 percent decline over Years 2–6) than those unaffected by the policy. These negative effects are concentrated among those closest to the cutoff (see Column 2) and become less negative for those further away, though this heterogeneity is not always statistically significant. The negative earnings effects show up in Year 2 while the majority of the sample is still enrolled, suggesting some students may be reallocating time from work to school in order to improve their GPAs. On the other hand, the fact that the effects persist and may even grow over time suggests another possible channel for earnings effects besides the school–work time allocation trade-off: it may be connected to the declines in credits completed (or the decline in certificate completion).²⁸

Overall, the pattern of results in the DID—with negative effects on credits, larger effects on credits attempted versus completed, negative effects on certificate completion, and no persistent positive effects on GPA—is quite similar to the patterns observed in the RD-DID, except that the smaller standard errors in the DID lead to many more statistically significant findings. The main differences are that the DID suggests more negative effects on earnings but a less negative effect on associate degree completion.

D. Additional Robustness Checks

As noted earlier, there are two main components of SAP failure, only one of which is the GPA criterion. The other criterion is that students must complete two-thirds (67 percent) of the credits that they attempt. Because the two criteria are highly correlated, with GPA being the more determinative (and more continuously distributed than the credit-completion percentage, especially after just one year of enrollment), we focus on the GPA criterion for our analysis. But, in Online Appendix Table B5, we replicate our main specifications using the credit-completion percentage as the running variable. The RD results are more sensitive, but the RD-DID and DID results using this alternative approach are both highly consistent with the patterns discussed above.

Finally, we also examine whether results varied across subgroups, focusing on our preferred DID specification (these results are available in Online Appendix Tables C1–C3). We find very similar patterns for both men and women, with the exception of term GPA in the fall of Year 2, where men showed a significant increase of 0.07 GPA points compared with null effects on term GPA for women. We see little indication that pre-recession and post-recession entry cohorts (entering before versus after 2008) responded differently to SAP policies, with one exception—the post-recession group experienced larger negative impacts on average quarterly earnings, particularly cumulatively over Years 2–6.

We do find evidence that effects differ across different types of aid recipients (see Online Appendix Table C3). When we split aided students into those receiving any Pell Grant, those receiving other grants but not Pell (primarily state aid), and those receiving loans only, we find that our results appear driven by those receiving some type of grant assistance (Pell or other grants). In the short term (fall of Year 2), Pell recipients appear more sensitive to SAP failure than recipients of other grant aid, but the pattern of results is not very different over the longer term.

VII. Discussion

In this paper, we provide a conceptual framework for thinking about the role and consequences of imposing performance standards in the context of financial aid. The framework suggests that some minimum standard is desirable. Determining whether a standard is effective in a given context requires weighing the value of encouragement effects for those who are motivated to work harder against the discouragement effects for those who are induced to dropout.

Consistent with the model and with prior research by Lindo, Sanders, and Oreopoulos (2010), we find behavioral effects in the expected directions. We also find discouragement effects appear larger, and encouragement effects smaller, for students further below the GPA threshold. In our preferred DID specification, failing the SAP grade standard decreases enrollment in fall of the second year by six percentage points overall, but increases GPAs by 0.11 grade points for those nearest the threshold. These results are also consistent with Schudde and Scott-Clayton (2016), who applied a DID specification to examine SAP policy in a different state and found significant negative effects on reenrollment and positive (but small and insignificant) effects on GPAs in the second year.

Evaluating the policy overall requires examining impacts over the longer term. Our DID results suggest reductions of 3.4 credits attempted and 1.4 credits earned after six years. Considering the average credits attempted in Year 1 (shown in Table 1), the decrease in attempted credits represents over a 10 percent decline. It’s also likely that not every student receives the average effect; a 10 percent decline could also be generated if one-fourth of treated students dropped out one full-time semester (12 credits) earlier than they would have otherwise, or if half the students dropped to nine credits instead of 12 credits per term for an entire year.

The 1.4-credit (6–7 percent) decline in credits completed is obviously much smaller than the effects on credits attempted. This difference in magnitudes is a key finding, suggesting that students were discouraged from attempting some credits they were unlikely to complete, and thus SAP policy may improve the efficiency of aid distributed. If we multiply the decline in credits attempted by an estimate of students’ per credit aid eligibility, the decline corresponds to a $524 decline in estimated aid disbursed per student in the second through sixth years.²⁹ Moreover, this could underestimate of the cost savings since tuition itself is subsidized and because even some of the students in our sample who reenroll after failing SAP may have done so without aid.

Clearly, however, treated students themselves do not appear to receive much benefit from SAP policy.³⁰ The short-term improvements in GPA are not sustained over the long term, and in addition to the small but persistent decline in credits completed, our preferred DID specification suggests a two-percentage-point decline in certificate completion. While, in theory, students with a low likelihood of completing the courses they attempt might benefit from leaving school sooner rather than later in order to devote more time to gaining experience in the labor market, our preferred DID specification indicates a significant $111 decline in quarterly earnings. The cumulative earnings decline—$2,220 over the five followup years—more than outweighs the estimated government savings in financial aid.³¹ Unfortunately, we do not have data on cumulative debt loads over the followup period to know whether students may be leaving school with less debt.

The reduction in quarterly earnings appears about twice as large as what we would expect from the declines in credits or certificates completed, suggesting some of the decline may be due to students reducing labor supply in an effort to improve their academic standing.³² If even small negative earnings effects persist over the lifetime from the decline in credits and certificates, the costs of the policy could outweigh the benefits in terms of financial aid savings by a substantial amount.³³

Taken broadly, the pattern of effects here suggests that SAP policy is only partly doing its job. It does appear to reduce some unproductive reenrollments while providing some encouragement for students to perform better. But, for many students, by the time they receive their first warning it may too late for them to improve their GPAs sufficiently to maintain their aid eligibility. Our review of college catalogs, as well as anecdotal reports from college staff, suggest that many students may not learn about SAP until they lose aid. Staff reported that the timing of notification is not aligned with an early warning system or with student enrollment periods. If students are not informed until after the warning period, this is a missed opportunity: if students are poorly informed, it will mute the incentive effects of standards, and the longer it takes for students to realize they are failing, the harder it will be for them to get back above the GPA threshold.

From an equity stance, the implications of SAP policy are complex. Poor academic performance is widespread across student demographics. SAP policy targets undergraduates from America’s most disadvantaged families: median family income among aid recipients in our sample is about $28,000. Students who are reliant on federal financial aid face the consequences of academic standards more quickly than students who can afford to pay for college out of pocket. A student with unlimited funds can, theoretically, continue to enroll in community college for as many iterations as necessary to attain the 2.0 cumulative GPA required for graduation. A student who relies on federal funding to cover tuition expenses ultimately receives fewer chances to “get it right.” The consequences may reverberate for years; RD evidence from Ost, Pan, and Webber (2016) indicates that four-year college students who just barely miss minimum academic performance cutoffs earn significantly less later in life than those who just barely meet such standards. Heterogeneous effects within the economically disadvantaged group may further exacerbate inequality. Though we cannot examine it here, prior work by Barrow and Rouse (2018) suggests that students with children are less able than those without children to shift their time allocation towards academics in order to meet performance incentives.

Finally, an open question is how the effects of SAP may be different following a significant tightening of the standards in 2011, too late for us to examine in our sample. The new regulations mean that students who fail SAP cannot receive aid for more than one subsequent term without filing an appeal. Even if the appeal is successful, students can only receive aid for one additional term unless they improve sufficiently to pass the SAP standard (Satisfactory Academic Progress, 34 C.F.R. § 668.34 2012; U.S. Department of Education, Federal Student Aid 2014). As a result, SAP policy is likely to affect more students more quickly than it has in the past—the stakes are high to understand its impacts for both students and public coffers.