Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Feb 24;128(9):1715–1724. doi: 10.1021/acs.jpca.3c08158

W4Λ: Leveraging Λ Coupled-Cluster for Accurate Computational Thermochemistry Approaches

Emmanouil Semidalas †, Amir Karton ‡, Jan M L Martin †,*
PMCID: PMC10926103  PMID: 38400740

Abstract

graphic file with name jp3c08158_0006.jpg

High-accuracy composite wave function methods like Weizmann-4 (W4) theory, high-accuracy extrapolated ab initio thermochemistry (HEAT), and the Feller–Peterson–Dixon (FPD) approach enable sub-kJ/mol accuracy in gas-phase thermochemical properties. Their biggest computational bottleneck is the evaluation of the valence post-CCSD(T) correction term. We demonstrate here, for the W4-17 thermochemistry benchmark and subsets thereof, that the Λ coupled-cluster expansion converges more rapidly and smoothly than the regular coupled-cluster series. By means of CCSDT(Q)Λ and CCSDTQ(5)Λ, we can considerably (up to an order of magnitude) accelerate W4- and W4.3-type calculations without loss in accuracy, leading to the W4Λ and W4.3Λ computational thermochemistry protocols.

1. Introduction

Chemical thermodynamics and thermochemical kinetics are not just cornerstones of chemistry but arguably its very foundations. As the evaluation of absolute energies of molecules is a Sisyphian task (see Section 5 of ref (1) for a detailed discussion), the most fundamental thermochemical property of a molecule is generally taken to be the heat of formation. While this cannot be directly evaluated computationally, through the heats of formation of the gas-phase atoms, it can be related to the molecular total atomization energy (TAE)—the energy required to break up a molecule into its separate ground-state atoms. This latter quantity—a “cognate” of the heat of formation, if the reader permits a linguistic metaphor—is amenable to computation.

Experimental and theoretical thermochemical techniques have been recently reviewed by Ruscic and Bross.2 Nowadays, by far the most reliable source of experimental (or hybrid) reference data are the Active Thermochemical Tables (ATcT) database,3 in which a thermochemical network of reaction energies is jointly (rather than sequentially) solved4,5 for the unknown heats of formation viz. TAEs and their respective uncertainties.

For small molecules, TAEs can now be evaluated by composite wave function [ab initio] theory (cWFT) approaches to a kJ/mol accuracy or better. Such approaches include Weizmann-4 (W4)6,7 and variants (such as W4-F12,8,9 W3X-L,10 and Wn-P3411), the high-accuracy extrapolated ab initio thermochemistry (HEAT) by an international consortium centered on Stanton,12−15 the Feller–Peterson–Dixon (FPD) approach,16,17 which is less a specific cWFT than a general strategy, and the like. These approaches have been extensively validated against ATcT and other information: see, e.g., Karton18 for a recent review.

The “Gold Standard of Quantum Chemistry” (T. H. Dunning, Jr.), CCSD(T) (coupled-cluster with all single and double substitutions with a quasiperturbative correction for triple substitutions),19,20 performs much better than it has any right to, owing to a felicitous error compensation amply documented in refs (6, 7, and 12–15) (see Stanton21 for a different perspective why this occurs). Post-CCSD(T) valence correlation corrections are the essential component that sets apart W4, HEAT, and the like from lower-accuracy approaches such as the correlation consistent composite approach (ccCA) by the Wilson group,22 Gaussian-4 (G4) theory,23,24 our own minimally empirical variants of these,25,26 or indeed Weizmann-1 (W1) and W2 theory27 and their explicitly correlated versions.28 In all but the smallest cases, its evaluation is the single greatest “bottleneck” in W4 and HEAT calculations, owing to the extremely steep CPU time scaling of higher-order coupled-cluster approaches. [For fully iterative coupled-cluster up to m-fold connected excitations, the CPU time asymptotically scales as nmNm+2virt × Niter, where Niter is the number of iterations, n is the number of electrons correlated, and Nvirt is the number of virtual (unoccupied) orbitals. For quasiperturbative approximations, the corresponding scaling is nm–1Nm+1virtNiter for the underlying CC(m – 1) iterations and nmNm+1virt for the final step].

Hence, any way to significantly reduce their computational cost or make their scaling less steep would extend the applicability of W4- and HEAT-type approaches.

As quasiperturbative triples, (T), proved so successful in ground-state coupled-cluster theory, attempts were then made to add them to excited-state equation-of-motion coupled-cluster theory with all singles and doubles (EOM-CCSD). This led also for the ground state to the so-called Λ coupled-cluster methods,29−32 which recently seemed to show promise for computational thermochemistry as well.33,34 Moreover, a recent study35 on spectroscopic properties of small molecules likewise appeared to show that the Λ quasiperturbative series—CCSD(T)Λ, CCSDT(Q)Λ, CCSDTQ(5)Λ, ...—converges more rapidly than the ordinary quasiperturbative expansion CCSD(T), CCSDT(Q), CCSDTQ(5), ... There was even a tantalizing hint in ref (35) that e.g., CCSDT(Q)Λ might be superior to CCSDTQ owing to a similar error compensation as one sees in CCSD(T) vs CCSDT.

This of course calls for a broader thermochemical exploration: we offer one in the present paper, focusing on the W4-17 benchmark36 of 200 first- and second-row molecules, its W4-11 subset37 published 6 years earlier, and the latter’s W4-08 subset.38 We shall show not only that Λ coupled-cluster indeed accelerates convergence but also that it can be exploited, with no loss in accuracy, for faster and less resource-intensive variants of W4 and W4.3 theory.

2. Computational Methods

All calculations were carried out on the Faculty of Chemistry’s HPC facility ChemFarm at the Weizmann Institute of Science.

Geometries of the W4-17 set of molecules, originally optimized at the CCSD(T)/cc-pV(Q+d)Z level with only valence correlation included, were taken from the electronic supporting information (ESI) of the W4-17 paper36 and used as-is, without further optimization.

Most of the post-CCSD(T) electronic structure calculations, and all of the post-CCSDTQ calculations, were carried out using the arbitrary-order coupled-cluster code39−42 in the MRCC program system of Kállay and co-workers.43 The specific levels of theory considered include CCSDT,44 CCSDT[Q],45 CCSDT(Q),39 CCSDT(Q)A,41 CCSDT(Q)B,41 CCSDTQ,46 CCSDTQ(5),41 and CCSDTQ5.47

Coupled-cluster jobs were run in a “sequential restart” fashion where, e.g., CCSDT takes initial T1 and T2 amplitudes from the converged CCSD calculation, CCSDTQ in turn uses the converged CCSDT amplitudes as initial guesses for the T1, T2, and T3 amplitudes, and so forth. For the open-shell species, unrestricted Hartree–Fock references were used throughout, except that higher-order triple excitation contributions, T3 – (T), were also evaluated restricted open-shell in semicanonical orbitals as per the original W4 protocol.

The most demanding CCSDT, CCSDT(Q), CCSDT(Q)Λ, and CCSDTQ calculations were carried out using a prerelease version of the NCC program developed by Matthews and co-workers as part of CFOUR.48

Basis sets considered are the cc-pVnZ basis sets of Dunning and co-workers49,50 or truncations thereof. The abbreviated notation we use for truncated basis sets is probably best illustrated by example: VDZ(p,s) refers to cc-pVDZ truncated at p functions for nonhydrogen and at s functions for hydrogen, VDZ(d,s) refers to the untruncated cc-pVDZ basis set on nonhydrogen atoms, and the p polarization functions on hydrogen are removed.

It is well-known (e.g., refs (51 and 52)) that for second-row atoms in high oxidation states, tight (i.e., high-exponent) d functions are energetically highly important at the CCSD(T), or even the Hartree–Fock (!), level. (This was ultimately rationalized53 chemically as back-donation from chalcogen and halogen lone pairs into the vacant 3d orbital, which drops closer to the valence orbitals in energy as the oxidation state increases. A similar phenomenon involving tight f functions and vacant 4f and 5f orbitals exists in heavy p-block compounds.54) However, do tight d functions significantly affect post-CCSD(T) contributions? One of us55 considered this question and found the total contribution to be quite modest and to largely cancel between higher-order triples and connected quadruples.

3. Results and Discussion

3.1. Higher-Order Connected Sextuples

Table 1 summarizes our results using coupled-cluster methods for the molecular sets considered in this study.

Table 1. Overview of Post-CCSD(T) Methods and Basis Sets Used for Molecules in the W4-17 Database.

method basis set #species data seta
CCSDT VDZ(p,s) through    
  VQZ(f,d) 200 W4-17
  VQZ(g,d) 199 W4-17 except n-pentane
  V5Z(h,f) 65 “W4.3” subset
CCSDT(Q) VDZ(p,s) 200 W4-17
  VDZ(d,s) 200 W4-17
  VTZ(d,p) 199 W4-17 except C2Cl6
  VTZ(f,p) 198 W4-17 except C2X6 (X = F, Cl)
  VTZ(f,d) 197 W4-17 except n-pentane, C2X6 (X = F, Cl)
  VQZ(d,p) 137 W4-11
  VQZ(f,d) 132 W4-11: excluding 5 speciesb
  VQZ(g,d) 122 W4-11: excluding 12 species, W4-08: without 3c
  V5Z(h,f) 59 “W4.3” subset excluding 6 speciesd
CCSDT(Q)Λ VDZ(p,s) 200 W4-17
  VDZ(d,s) 200 W4-17
  VTZ(d,p) 188 W4-17: excluding 12 speciese
  VTZ(f,p) 157 W4-11 plus 20 species from W4-17
  VQZ(g,d) 122 W4-11: excluding 12 species, W4-08: without 3f
CCSDTQ VDZ(p,s) 200 W4-17
  VDZ(d,s) 184 W4-17: excluding 16 species
  VTZ(d,p) 134 W4-08 except AlF3, AlCl3, BF3, O2F2, S4, SO3 plus 25 species from W4-11 and 19 from W4-17
  VTZ(f,p) 65 “W4.3” subset
  VQZ(g,d) 50 “W4.3” subset except 15 speciesg
CCSDTQ(5) VDZ(p,s) 193 W4-17 except 7 speciesh
  VDZ(d,s) 165 W4-17 except 32 species; W4-11 except CH3COOH, CF4, and SiF4
  VTZ(f,p) 53 “W4.3” subset except 12 species
CCSDTQ(5)Λ VDZ(p,s) 193 W4-17 except 7 speciesh
  VDZ(d,s) 163 W4-17 except 34 species; W4-11 except CH3COOH, CF4, and SiF4
  VTZ(f,p) 53 “W4.3” subset except 12 species
CCSDTQ5 VDZ(p,s) 96 W4-08
  VDZ(d,s) 65 “W4.3” subset
CCSDTQ5(6) VDZ(p,s) 95 W4-08 except O2F2
CCSDTQ5(6)Λ VDZ(p,s) 95 W4-08 except O2F2
CCSDTQ56 VDZ(p,s) 88 W4-08 except BF3, C2N2, O2F2, AlF3, P4, SO3, S4, AlCl3
core–valence post-CCSD(T) correlation contributions
CCSDT – CCSD(T) CVTZ(f,p) 136 W4-11except cis-HOOO
CCSDT(Q) – CCSDT CVTZ(f,p) 118 W4-08: excluding 8 species; W4-11: except 11 speciesi
Open in a new tab
a

W4-17, W4-11, and W4-08 data sets include 200, 137, and 96 species, respectively; the “W4.3” subset for which W4.3 results were obtained in earlier work contains 65 species.

b

Without acetic acid, ethanol, CF4, C2H5F, and propane.

c

Excluding from W4-08: FO2, O2F2, and ClOO; excluding from W4-11: acetaldehyde, formic and acetic acids, ethanol, glyoxal, cis-HOOO, CF4, SiF4, C2H5F, propane, propene, and propyne.

d

Without CH2CH, CH2NH, NO2, N2O, H2O2, and F2O.

e

Without n-pentane, benzene, C2X6 (X = F, Cl), PF5, SF6, cis-C2F2Cl2, cyclopentadiene, beta-lactim, ClF5, n-butane, and allyl.

f

Excluding from W4-11: acetaldehyde, formic and acetic acids, ethanol, glyoxal, cis-HOOO, CF4, SiF4, C2H5F, propane, propene, and propyne; excluding from W4-08: FO2, O2F2, and ClOO.

g

Without CH2C, CH2CH, C2H4, CH2NH, HCO, H2CO, CO2, NO2, N2O, O3, HOO, H2O2, F2O, SSH, and HOF.

h

Without n-pentane, C2X6 (X = F, Cl), cyclopentadiene, silole, beta-lactim, and ClF5.

i

Excluding from W4-08: AlCl3, AlF3, BF3, S4, S3, CS2, SO3, and P4; excluding from W4-11: allene, propyne, propane, F2CO, C2F2, C2H5F, SiF4, CF4, cis-HOOO, glyoxal, and acetic acid.

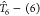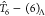The smallest contribution we will consider here are the higher-order connected sextuple excitations, CCSDTQ56 – CCSDTQ5(6) or Inline graphic for short, and CCSDTQ56 – CCSDTQ5(6)Λ or Inline graphic for short. A box-and-whiskers plot of these contributions is given in Figure 1. It can be seen there that Inline graphic has an extremely narrow spread, and that the largest outlier by far is C2 at just 0.015 kcal/mol. We can hence consider CCSDTQ5(6)Λ to be essentially equivalent to CCSDTQ56 in quality.

Figure 1.

Figure 1

Open in a new tab

Box-and-whiskers plots of Inline graphic (on the left) and Inline graphic (on the right) using the VDZ(p,s) basis set for the W4-08 data set (excluding BF3, C2N2, O2F2, AlF3, P4, SO3, S4, and AlCl3). In this and subsequent box plots, the box boundaries represent the 25th and 75th percentile of the data, and the whiskers extend to the last point within 1.5 times the interquartile range (IQR) from the box, following the standard Tukey definition. Outliers are shown as filled circles if located more than 1.5 IQR from the box edge, while extreme outliers are represented by open circles when positioned more than 3 IQR from the box edge.

For CCSDTQ56 – CCSDTQ5(6), the spread is still very narrow, but now we have some small positive and negative outliers, BN −0.026, N2O +0.015, SiO +0.009, P2 +0.006 kcal/mol.

Since these tiny contributions are much smaller than the basis set incompleteness error in the larger components (see below), we feel justified in neglecting higher-order connected sextuples altogether.

3.2. CCSDTQ5(6)Λ – CCSDTQ(5)Λ

The quasiperturbative sextuple contributions were evaluated only for the VDZ(p,s) basis set. A box plot can be seen in Figure 2. Whiskers are at +0.02 and −0.01 kcal/mol, around a median of basically 0.00 kcal/mol. The largest positive and negative outliers are +0.04 and −0.03 kcal/mol, respectively. In almost all situations, this contribution can be safely neglected.

Figure 2.

Figure 2

Open in a new tab

Box-and-whiskers plots of (6)Λ – (5)Λ (on the left) and (6)Λ – T5 (on the right) using the VDZ(p,s) basis set for the W4-08 data set.

If we used full iterative CCSDTQ56 – CCSDTQ5 instead (at massively greater computational expense), we would get binding contributions throughout (small as they might be), topping out at 0.069 kcal/mol for C2.

We argue that this contribution can be omitted in all but the most accurate work.

This is not the case for CCSDTQ5(6) – CCSDTQ(5), given the well-known deficiencies of CCSDTQ(5).7,40

3.3. CCSDTQ(5)Λ – CCSDT(Q)Λ

We now move on to the Λ connected quintuples contribution, CCSDTQ(5)Λ – CCSDT(Q)Λ. The largest basis set for which we were able to evaluate even a subset (53 species) was VTZ(f,p).

As can be seen in Figure 3, the box is centered near 0.0 while the whiskers are ±0.04 kcal/mol in the largest basis set, VTZ(f,p). For the “W4.3” subset of 65 species, the root-mean square deviation (rmsd) between VDZ(p,s) and VTZ(f,p) is 0.06 kcal/mol, while that between VDZ(d,s) and VTZ(f,p) shrinks to just 0.02 kcal/mol.

Figure 3.

Figure 3

Open in a new tab

Box-and-whiskers plots of contributions to TAEs of (5)Λ – (Q)Λ terms for (a) “W4.3” subset, (b) W4-08, and (c) W4-11 data sets.

For the smallest basis set, VDZ(p,s), there are sizable outliers, at −0.63 kcal/mol (for C2) and +0.43 kcal/mol (for B2). These shrink to −0.24 and +0.34 kcal/mol, respectively, for VDZ(d,s), i.e., upon expanding the nonhydrogen basis sets from double-ζ to polarized double-ζ.

Obviously, for small “troublemakers” like C2, BN, and B2, switching to a basis set larger than VDZ(p,s) is not an issue at all.

In contrast, for CCSDTQ5 versus CCSDTQ, most contributions are positive. VDZ(p,s) has a box at about 0.08 kcal/mol with whiskers spanning 0.2 kcal/mol (outliers at 0.4 kcal/mol) while VDZ(d,s) has a smaller box (0.06 kcal/mol), and its whiskers span 0.14 kcal/mol (outliers up to 0.42 kcal/mol) (see Figure S1 in Supporting Information).

Therefore, aside from the much lower cost of CCSDTQ(5)Λ compared to CCSDTQ5, the CCSDTQ(5)Λ – CCSDT(Q)Λ contribution is close enough to zero that “in a pinch” it can be omitted altogether.

Nevertheless, let us also consider the quintuples contributions relative to CCSDTQ. For the 53 VTZ(f,p) species, the rms CCSDTQ(5)Λ – CCSDTQ is just 0.08 kcal/mol with the VTZ(f,p) basis set. For the same contribution, the rmsd between VDZ(p,s) and VTZ(f,p) basis sets is just 0.02 kcal/mol, while that between VDZ(d,s) and VTZ(f,p) shrinks to just 0.01 kcal/mol. (Box plots of CCSDTQ(5)Λ – CCSDTQ contributions to TAEs are shown in Figure S2 of Supporting Information).

What about (5) vs (5)Λ contributions compared to full iterative CCSDTQ5 – CCSDTQ? We have [CCSDTQ5 – CCSDTQ]/VDZ(d,s), or if you like, Inline graphic/VDZ(d,s) available for the “W4.3” subset of molecules, with which the rmsd of (5) is 0.05 kcal/mol, compared to just 0.01 kcal/mol for (5)Λ. 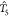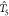For the small VDZ(p,s) basis set, the rmsd between (5) and Inline graphic is 0.04 kcal/mol, compared to 0.01 kcal/mol between (5)Λ and Inline graphic. We believe that this adequately shows the superiority of (5)Λ.

3.4. Higher-Order Quadruples

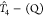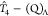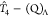The relevant statistics for the higher-order quadruples, Inline graphic and Inline graphic, are given in Table 2, complemented by two box plots as shown in Figures S3 and S4 while the outliers are listed in Table S1 in Supporting Information. It can be seen in Table 2 that complete neglect beyond CCSDT(Q) would cause an error of 0.255 kcal/mol, but only 0.111 kcal/mol beyond CCSDT(Q)Λ. Introducing a low-cost CCSDTQ/VDZ(p,s) calculation would reduce rmsd to 0.094 kcal/mol for Inline graphic but 0.062 kcal/mol for Inline graphic—the latter is small enough that one is tempted to substitute a single CCSDTQ(5)Λ/cc-pVDZ(p,s) calculation for the W4 theory combination of CCSDTQ/cc-pVDZ and CCSDTQ5/cc-pVDZ(p,s).

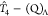Table 2. rmsd and Mean Signed Deviations (MSDs) in kcal/mol of Inline graphic and Inline graphic Terms for the “W4.3” Subset.

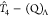basis set Inline graphica
 Inline graphicb
  rmsd MSD rmsd MSD
neglecting 0.255 0.109 0.111 0.044
VDZ(p,s) 0.094 0.039 0.062 0.007
VDZ(d,s) 0.030 0.011 0.014 0.001
VTZ(d,p) 0.015 0.003 0.010 0.001
VTZ(f,p) 0.012 0.006 0.007 0.005
VQZ(g,d) REF REF REF REF
Open in a new tab
a

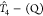Inline graphic/VQZ(g,d) is used as reference.

b

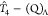Inline graphic/VQZ(g,d) is used as reference. A total of 50 data points are used in all comparisons.

Similarly, with the cc-pVDZ(d,s) basis set, we have rmsd = 0.030 kcal/mol for 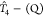Inline graphic , but just 0.014 kcal/mol for 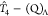Inline graphic. With 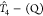Inline graphic, one needs to escalate to VTZ(f,p) (like in W4.3 theory) to achieve a comparable rmsd = 0.012 kcal/mol.

3.5. (Q)Λ – (Q)

The difference between ordinary parenthetical quadruples and their Λ counterpart approaches zero for systems dominated by dynamical correlation but becomes quite significant when there is strong static correlation. [In ref (6), we defined the %TAE[(T)] diagnostic, the percentage of the CCSD(T) TAE that is due to connected triples, as a “pragmatic” diagnostic for static correlation (see also refs (56 and 57) for other diagnostics)]. Between %TAE[(T)] and %TAE[(Q)Λ – (Q)], and upon eliminating the irksome BN diatomic, the coefficient of determination R2 for 160 closed-shell species is 0.7164 with the cc-pVDZ(d,s) basis set, which increases to 0.7407 upon additionally eliminating ClF5. While this is not something one would want to substitute for an actual evaluation, it does indicate a relationship between the two quantities.

Compared to the largest basis set for which we have sufficient data points available, namely, VQZ(g,d), the rmsd is 0.066 kcal/mol for VDZ(p,s) but drops to 0.027 kcal/mol for VDZ(d,s) and to 0.01 kcal/mol or less for a VTZ basis set.

In W4 theory, we combined6 CCSDT(Q)/VTZ(f,d) with [CCSDTQ – CCSDT(Q)]/VDZ(d,p). If, for the sake of argument, we split up the latter term into [CCSDT(Q)Λ – CCSDT(Q)]/VDZ(d,p) plus [CCSDTQ – CCSDT(Q)Λ]/VDZ(d,p), then based on the previous section, we could prune the basis set for the second step to VDZ(p,s) and greatly reduce computational expense.

Continuing this line of argument, in the W4.3 and W4.4 theories, CCSDT(Q)/V{T,Q}Z extrapolation is combined with [CCSDTQ-CCSDT(Q)]/VTZ(f,d). If we again partition the latter term into a relatively cheap [CCSDT(Q)Λ – CCSDT(Q)]/VTZ(f,p) and a very expensive [CCSDTQ – CCSDT(Q)Λ]/VTZ(f,p) step, we could again take down the basis set for the latter to VDZ(d,s).

Why not do the largest basis set (Q)Λ to begin with? The extra computational expense of evaluating the “left eigenvector” is of course one factor but not the main one: in practice, we find the additional memory requirements to be a greater impediment for large molecules and basis sets.

3.6. Parenthetical Connected Quadruples (Q)

In W4lite and W4 theory, the (Q) contribution is included via scaling, as it was shown6 that extrapolation of (Q) from too small basis sets yields erratic results for highly polar molecules like H2O and HF.

For calibration, we used V{Q,5}Z extrapolation for 58 species (“W4.3” subset minus CH2CH, CH2NH, NO2, N2O, H2O2, and F2O). Minimizing rmsd against that (see Table 3), we find the cheapest option that still has a tolerably small rmsd to be VDZ(d,s) scaled by 1.227, close enough to the 5:4 used in the past for 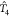Inline graphic in W3 theory.58 The error drops to 0.082 kcal/mol with 1.17 × VTZ(d,p) and to 0.038 kcal/mol with 1.099 × VTZ(f,p), only semantically different from 1.1 × VTZ used in W4 theory. This is roughly half the rmsd of V{D,T}Z extrapolation, at rmsd = 0.074 kcal/mol (Figure S5).

Table 3. rms (kcal/mol) of CCSDT(Q)-CCSDT Errors for TAEs in the “W4.3” Subset.

basis set rmsd
VDZ(p,s) 0.413
VDZ(d,s) 0.249
VTZ(d,p) 0.183
VTZ(f,p) 0.109
VTZ(f,d) 0.108
VQZ(f,d) 0.058
VQZ(d,p) 0.149
VQZ(g,d) 0.044
V5Z(h,f) 0.021
1.227 × VDZ(d,s)a 0.139
1.170 × VTZ(d,p)a 0.082
1.099 × VTZ(f,p)a 0.038
V{D(d,s),T(f,p)}Zb 0.074
V{T(d,p),Q(f,d)}Za 0.010
V{T(f,p),Q(g,d)}Zb 0.006
(Q)/V{Q(g,d),5(h,f)}Z REF
Open in a new tab
a

Scaling factor obtained from rmsd minimization.

b

Extrapolation exponent a = 2.85 for V{D,T}Z and a = 3.25 for V{T,Q}Z; no change occurs with Karton’s extrapolation exponents (a = 2.9968 and a = 3.3831) from Table 5 in ref (59). A total of 58 species are included in all comparisons.

V{T,Q}Z as used for W4.3 theory in ref (6), at rmsd = 0.006 kcal/mol is essentially as accurate as the reference. Importantly, however, deleting the highest angular momentum in both basis sets is found to cause only negligible further loss of accuracy, to rmsd = 0.01 kcal/mol. This offers an attractive way to reduce the cost of W4.3 calculations (see below).

3.7. Higher-Order Connected Triples, CCSDT – CCSD(T)

For a subset of 65 molecules within W4-08—the so-called “W4.3” subset for which we were able to perform W4.3 calculations in refs (36 and 37)—we managed to carry out CCSDT/cc-pV5Z calculations, and hence, we used CCSD(T)/V{Q,5}Z extrapolation as the reference value. These limits are apparently not very sensitive to the extrapolation exponent, as there is just 0.007 kcal/mol rms difference between values obtained using a fixed 3.0 and Karton’s optimized value59 of 2.7342. That means that the reference we are using is pretty insensitive to details of the extrapolation procedure; hence it makes sense to calibrate the 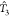Inline graphic – (T) higher-order connected triples contribution to TAE by comparison with [CCSDT – CCSD(T)]/V{Q,5}Z extrapolations.

The rms Inline graphic – (T) contribution is 0.684 kcal/mol. It is obvious from Figure 4 and Table 4 that untruncated and truncated cc-pVDZ basis sets are barely better than doing nothing, with rms errors over 0.5 kcal/mol. A cc-pVTZ basis set recovers a more respectable chunk, but still leaves 0.18 kcal/mol rmsd, which increases to 0.25 kcal/mol if the f functions are omitted. In order to get below 0.1 kcal/mol without extrapolation, at least a cc-pVQZ basis set is required, although the g function can apparently be safely omitted. V5Z reaches 0.05 kcal/mol.

Figure 4.

Figure 4

Open in a new tab

Errors for 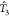Inline graphic – (T) terms vs 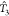Inline graphic – (T)/V{Q(g,d),5(h,f)}Z for the “W4.3” subset with 65 molecules.

Table 4. rmsd 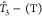Inline graphic against 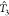Inline graphic – (T)/V{Q,5}Z (kcal/mol) for the “W4.3” Subset.

basis set rmsda
neglecting 0.684
VDZ(p,s) 0.554
VDZ(d,s) 0.545
VTZ(d,p) 0.248
VTZ(f,d) 0.179
VTZ(f,p) 0.181
VQZ(f,d) 0.094
VQZ(g,d) 0.090
VQZ(d,p) 0.194
V5Z(h,f) 0.049
Schwenke coefficient ALb rmsda
V{D,T}Z 0.503 0.041
V{D,T}Z 0.498c 0.041
V{D,T}Z 0.570 0.052
V{T,Q}Z 0.950 0.012
V{T(d,p),Q(f,d)}Z 0.528d 0.042
V{Q,5}Z-v2 1.049 0.007
V{Q,5}Z 1.210 REF
Open in a new tab
a

All 65 molecules of the “W4.3” subset are considered for all comparisons.

b

The energy is extrapolated with the Schwenke60 two-point formula E∞ = E + AL(E(L) – E(L – 1)).

c

Exponent taken from Karton.59

d

Obtained from rmsd minimization.

Extrapolation from cc-pV{D,T}Z, as practiced in W4 theory,6 brings down rmsd to just 0.041 kcal/mol with the exponent 2.7174 optimized by Karton:59 if one substitutes the 2.5 recommended in refs (6 and 7), rmsd slightly increases to 0.052 kcal/mol. For cc-pV{T,Q}Z, Karton’s exponent is functionally equivalent to 2.5, and we obtain rmsd = 0.012 kcal/mol—that level as used in W4.36 and W4.47 can credibly be used as a reference. Alas, unlike for (Q), removal of the top angular momenta of both basis sets increases the error to the same as cc-pV{D,T}Z, presumably primarily because of the impact on cc-pVTZ.

3.8. Post-CCSD(T) Core–Valence Contributions

Core–valence 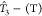Inline graphic is required for W4.2 and W4.3 theory6 while core–valence (Q) corrections enter in W4.4 theory.7 In the original papers,6,7 we employed the cc-pCVTZ basis set;61 in the present work, we employed the combination of cc-pCVTZ on nonhydrogen atoms and cc-pVTZ(no d) on hydrogen—abbreviated, CVTZ(f,p). Full CCSDT proved feasible for all of W4-11 (except for cis-HOOO, owing to an SCF convergence issue) while (Q) was feasible for W4-08 minus eight species (seven of which contain multiple second-row atoms with their [Ne] cores) and for the additional W4-11 species minus 10 larger first-row species and SiF4.

The rms core–valence Inline graphic contribution was 0.046 kcal/mol and the rmsd core–valence (Q) term was 0.037 kcal/mol—larger than the remaining errors in the valence post-CCSD(T) part of W4.3 theory and hence not negligible.

W4.2 theory is identical to W4 theory except for the core–valence 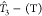Inline graphic term. As discussed in ref (6), it removes the dependence on the specific definition of frozen-core CCSD(T) for restricted open-shell references (semicanonicalization before transform as in Gaussian,62 MRCC, and CFOUR versus transform before semicanonicalization as in MOLPRO63).

3.9. Composite Approaches

First, let us concentrate on W4 itself. In composite A, we retain the Inline graphic component from original W4, except that we remove the top angular momentum from hydrogen: CCSDT/{VDZ(d,s),VTZ(f,p)}. Next, we add (Q)/VTZ(f,p) and scale the contribution by 1.11. Then, we add [(Q)Λ – (Q)]/VDZ(d,s) and CCSDTQ(5)Λ/VDZ(p,s) – CCSDT(Q)Λ/VDZ(p,s). In effect, we replace the CCSDTQ/VDZ(d,s) and CCSDTQ5/VDZ(p,s) steps with a single CCSDTQ(5)Λ/VDZ(p,s) step.

Composite A is feasible for the entire W4-17 data set except for seven species where the quintuples present an obstacle. As they are expected to be of minor importance in these species, one can substitute CCSDTQ/VDZ(p,s) as a fallback option, leaving us with a complete W4-17 set. By way of illustration, for NCCN (dicyanogen) on 16 cores of an Intel Ice Lake server at 2.20 GHz with 768 GB RAM and local SSD, the CCSDT(Q), CCSDTQ, and CCSDTQ5 steps of standard W4 theory take 16.2 h wall time, compared to 5.4 h for the corresponding steps in Composite A, making it 3 times faster. We thus renamed composite A to W4Λ. The rmsd between this W4Λ and standard W4 is 0.066 kcal/mol for the post-CCSD(T) contributions to TAEs of the W4-08 data set.

Now, let us consider W4.3. In composite B, we retain the Inline graphic component from original W4, except that we remove the top angular momentum from hydrogen: CCSDT/{VTZ(f,p),VQZ(g,d)}. The (Q) we extrapolate from (Q)/{VTZ(d,p),VQZ(f,d)}. Then, we add [(Q)Λ – (Q)]/VTZ(f,p) and CCSDTQ(5)Λ/VDZ(d,s) – CCSDT(Q)Λ/VDZ(d,s).

This composite B is feasible for nearly all of the W4-11 set; in conjunction with the CCSDT/CVTZ(f,p) core–valence contribution, we dub it here W4.3Λ. The rmsd between W4.3Λ and standard W4.3 is only 0.019 kcal/mol for the TAEs of 65 species in the “W4.3” data set.

In composite C, we add a CCSDTQ5(6)Λ/VDZ(p,s) – CCSDTQ(5)Λ/VDZ(p,s) component to composite B. Together with the CCSDT(Q)/CVTZ(f,p) core–valence contribution, we propose this as W4.4Λ.

What about lower-cost options? A form of W4lite,Λ can be created by scaling (Q)Λ/VDZ(d,s) by an empirical scale factor obtained by minimizing the rmsd from W4.3Λ: we thus find a scale factor of 1.249 (in practice, 5:4) and rmsd = 0.149 kcal/mol.

At a reviewer’s request, the final leaf of the ESI workbook compares the original W4-17 atomization energies at W4 and W4.n levels with their Λ counterparts. As the differences between them are essentially confined to the post-CCSDT terms (leaving aside the small differences in T3 – (T) owing to the present omission of the highest angular momentum in the hydrogen basis set), differences between the two are very small as expected, with an IQR = 0.04 kcal/mol. The one glaring exception is FOOF, where the discrepancy reached nearly 1 kcal/mol. Upon close scrutiny, we were able to identify an error in the published W4-11 and W4-17 values for that molecule and to trace those to a CCSDT(Q)/cc-pVTZ calculation where a malfunctioning restart from saved amplitudes (back in 2007) yielded an erroneous total energy of −349.4117061 Eh rather than the correct value of −349.4131206 Eh. As a result, the published36 TAEe value of 151.00 kcal/mol should read 151.89 kcal/mol, and its TAE0 counterpart of 146.00 should read 146.89 kcal/mol instead. In addition, in Table S2 of the article mentioned above, the T4 contribution for FOOF should read 3.18 rather than 2.29 kcal/mol.

3.10. Timing Comparison of Composite Approaches

The total electronic energy of a W4-type composite approach is the sum of CCSD(T) energy near the basis set limit and various post-CCSD(T) terms, detailed in previous sections. As for all but the smallest molecules, the cost of the post-CCSD(T) contributions dwarfs that of the CCSD(T)/CBS step, our timing comparison can focus exclusively on the former. For example, three separate single-point energy calculations are needed for W4: (a) CCSDTQ5/VDZ(p,s); (b) CCSDTQ/VDZ(d,s); and (c) CCSDT(Q)/VTZ(f,p). The 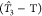Inline graphic/V{D,T}Z term is a byproduct of parts (b) and (c). Note that CCSDT(Q), CCSDTQ5, and CCSDTQ56 scale with system size as N9, N12, and N14, respectively.18

Figure 5 shows total wall clock times (note the logarithmic y axis) for calculating the post-CCSD(T) terms of several composite approaches across five species in the W4-08 data set. Calculations were performed on 16 cores and in 340 GB of RAM on otherwise empty nodes with dual 26-core Intel Ice Lake CPUs at 2.2 GHz, 7.0 TB of local solid state disk, and 768 GB of RAM. Wall clock times and percentages of time elapsed per step are provided in Tables S2 and S4 of Supporting Information.

Figure 5.

Figure 5

Open in a new tab

Wall clock time for calculating the post-CCSD(T) terms of various composite schemes for five molecules in the W4-11 data set. The y axis is in the logarithmic scale.

Λ-based composites, especially for larger molecules, exhibit significant speedups over non-Λ counterparts. For cyanogen, standard W4 takes 16.3 h, while W4Λ only requires one-third as much (5.4 h); W4.3 requires 522.3 h, but W4.3Λ only one-eighth thereof (65.6 h). Both W4lite and W4lite,Λ are almost of equivalent cost for the molecules considered. As can be seen from Table S4, for W4 the highest-order coupled-cluster step, CCSDTQ56/VDZ(p,s), will dominate the CPU time as the molecules grow larger; in contrast, for W4Λ, the CCSDT(Q)/VTZ step remains the dominant one. If the calculation is carried out wholly using MRCC, then the (Q) step benefits from almost perfect parallelism, which offers a further way to speed up the W4Λ calculation if enough cores are available. If, on the other hand, the CCSDT(Q) step is carried out using the very fast NCC module in CFOUR, then this will further favor W4Λ over W4 as the dominant iterative quintuples step in the latter is not amenable to NCC at present. For much larger systems, the total cost of canonical calculations would of course become intractable, but their CPU time scaling can be nearly linearized by substituting localized natural orbital coupled-cluster, LNO-CCSDT(Q),64−66 for conventional CCSDT(Q). The performance of the latter is presently being investigated in our laboratory.

4. Conclusions

Using the W4-17 data set (and the W4-11 and W4-08 subsets thereof) as our “proving ground”, we have reconsidered post-CCSD(T) corrections in computational thermochemistry in light of Λ coupled-cluster methods. It is apparent that the Λ approach converges more rapidly and smoothly with the substitution levels. Our findings corroborate our earlier conjecture35 that the coupled-cluster series has two more “sweet spots” (performance-price optima) beyond CCSD(T), namely, CCSDT(Q)Λ and CCSDTQ(5)Λ. These findings are then exploited to drastically reduce the computational requirements of the W4 and W4.3 computational thermochemistry protocols; we denote the modified versions W4Λ and W4.3Λ, respectively.

Acknowledgments

Research at Weizmann was supported by the Israel Science Foundation (grant 1969/20), by the Minerva Foundation (grant 2020/05), and by a research grant from the Artificial Intelligence for Smart Materials Research Fund, in memory of Dr. Uriel Arnon. E.S. thanks the Feinberg Graduate School (Weizmann Institute of Science) for a doctoral fellowship and the Onassis Foundation (Scholarship ID: FZP 052-2/2021-2022). J.M.L.M. is the incumbent of the Baroness Thatcher [of Kesteven] Professorial Chair in Chemistry. The authors would like to thank Drs. John F. Stanton, Devin A. Matthews, and Branko Ruscic for helpful discussion and Dr. Margarita Shepelenko for proofing the draft manuscript. J.M.L.M. would like to dedicate this paper to the memory of his untimely deceased colleague and friend, Prof. Abraham Minsky (1952–2024), Renaissance man and physical organic chemist turned structural biologist extraordinaire. May his memory be blessed.

Data Availability Statement

This material is also freely available from the Figshare repository at http://doi.org/10.6084/m9.figshare.24806913. Additional data can be obtained from the authors upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.3c08158.

  • Total energies, TAE contributions, and statistics (ZIP)

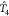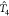  • Box plots of CCSDTQ5 – CCSDTQ contributions to TAEs, CCSDTQ(5)Λ – CCSDTQ contributions, CCSDTQ – CCSDT(Q) and CCSDTQ – CCSDT(Q)Λ basis set convergence, CCSDT(Q) – CCSDT differences; relative errors of Inline graphic – (Q) and Inline graphic – (Q)Λ compared to [Inline graphic – (Q)]/VQZ(g,d) and [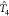Inline graphic – (Q)Λ]/VQZ(g,d); wall clock times of composite approaches for selected species; wall clock times per post-CCSD(T) step of each composite approach; refs (43, 62, 63) with full author lists (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp3c08158_si_001.zip (2.5MB, zip)
jp3c08158_si_002.pdf (330.5KB, pdf)

References

  1. Martin J. M. L. Electron Correlation: Nature’s Weird and Wonderful Chemical Glue. Isr. J. Chem. 2022, 62, e202100111 10.1002/ijch.202100111. [DOI] [Google Scholar]
  2. Ruscic B.; Bross D. H.. Chapter 1-Thermochemistry. Computer Aided Chemical Engineering; Elsevier, 2019; Vol. 45, pp 3–114. 10.1016/B978-0-444-64087-1.00001-2. [DOI] [Google Scholar]
  3. Ruscic B.; Bross D. H.. Active Thermochemical Tables (ATcT) Values Based on ver. 1.130 of the Thermochemical Network; Argonne National Laboratory: Lemont, IL, 2022. http://atct.anl.gov (accessed Dec 14, 2023).
  4. Ruscic B.; Pinzon R. E.; Morton M. L.; von Laszewski G.; Bittner S. J.; Nijsure S. G.; Amin K. A.; Minkoff M.; Wagner A. F. Introduction to Active Thermochemical Tables: Several “Key” Enthalpies of Formation Revisited. J. Phys. Chem. A 2004, 108, 9979–9997. 10.1021/jp047912y. [DOI] [Google Scholar]
  5. Ruscic B.; Pinzon R. E.; von Laszewski G.; Kodeboyina D.; Burcat A.; Leahy D.; Montoy D.; Wagner A. F. Active Thermochemical Tables: thermochemistry for the 21st century. J. Phys.: Conf. Ser. 2005, 16, 561–570. 10.1088/1742-6596/16/1/078. [DOI] [Google Scholar]
  6. Karton A.; Rabinovich E.; Martin J. M. L.; Ruscic B. W4 theory for computational thermochemistry: In pursuit of confident sub-kJ/mol predictions. J. Chem. Phys. 2006, 125, 144108. 10.1063/1.2348881. [DOI] [PubMed] [Google Scholar]
  7. Karton A.; Taylor P. R.; Martin J. M. L. Basis set convergence of post-CCSD contributions to molecular atomization energies. J. Chem. Phys. 2007, 127, 064104. 10.1063/1.2755751. [DOI] [PubMed] [Google Scholar]
  8. Sylvetsky N.; Peterson K. A.; Karton A.; Martin J. M. L. Toward a W4-F12 approach: Can explicitly correlated and orbital-based ab initio CCSD(T) limits be reconciled?. J. Chem. Phys. 2016, 144, 214101. 10.1063/1.4952410. [DOI] [PubMed] [Google Scholar]
  9. Kesharwani M. K.; Sylvetsky N.; Köhn A.; Tew D. P.; Martin J. M. L. Do CCSD and approximate CCSD-F12 variants converge to the same basis set limits? The case of atomization energies. J. Chem. Phys. 2018, 149, 154109. 10.1063/1.5048665. [DOI] [PubMed] [Google Scholar]
  10. Chan B.; Radom L. W2X and W3X-L: Cost-Effective Approximations to W2 and W4 with kJ mol–1 Accuracy. J. Chem. Theory Comput. 2015, 11, 2109–2119. 10.1021/acs.jctc.5b00135. [DOI] [PubMed] [Google Scholar]
  11. Chan B. Accurate Thermochemistry for Main-Group Elements up to Xenon with the Wn-P34 Series of Composite Methods. J. Chem. Theory Comput. 2021, 17, 5704–5714. 10.1021/acs.jctc.1c00598. [DOI] [PubMed] [Google Scholar]
  12. Tajti A.; Szalay P. G.; Császár A. G.; Kállay M.; Gauss J.; Valeev E. F.; Flowers B. A.; Vázquez J.; Stanton J. F. HEAT: High accuracy extrapolated ab initio thermochemistry. J. Chem. Phys. 2004, 121, 11599–11613. 10.1063/1.1811608. [DOI] [PubMed] [Google Scholar]
  13. Bomble Y. J.; Vázquez J.; Kállay M.; Michauk C.; Szalay P. G.; Császár A. G.; Gauss J.; Stanton J. F. High-accuracy extrapolated ab initio thermochemistry. II. Minor improvements to the protocol and a vital simplification. J. Chem. Phys. 2006, 125, 064108. 10.1063/1.2206789. [DOI] [PubMed] [Google Scholar]
  14. Harding M. E.; Vázquez J.; Ruscic B.; Wilson A. K.; Gauss J.; Stanton J. F. High-accuracy extrapolated ab initio thermochemistry. III. Additional improvements and overview. J. Chem. Phys. 2008, 128, 114111. 10.1063/1.2835612. [DOI] [PubMed] [Google Scholar]
  15. Thorpe J. H.; Lopez C. A.; Nguyen T. L.; Baraban J. H.; Bross D. H.; Ruscic B.; Stanton J. F. High-accuracy extrapolated ab initio thermochemistry. IV. A modified recipe for computational efficiency. J. Chem. Phys. 2019, 150, 224102. 10.1063/1.5095937. [DOI] [PubMed] [Google Scholar]
  16. Dixon D. A.; Feller D.; Peterson K. A. A Practical Guide to Reliable First Principles Computational Thermochemistry Predictions Across the Periodic Table. Annu. Rep. Comput. Chem. 2012, 8, 1–28. 10.1016/B978-0-444-59440-2.00001-6. [DOI] [Google Scholar]
  17. Feller D.; Peterson K. A.; Dixon D. A. The Impact of Larger Basis Sets and Explicitly Correlated Coupled Cluster Theory on the Feller–Peterson–Dixon Composite Method. Annu. Rep. Comput. Chem. 2016, 12, 47–78. 10.1016/bs.arcc.2016.02.001. [DOI] [Google Scholar]
  18. Karton A. Quantum mechanical thermochemical predictions 100 years after the Schrödinger equation. Annu. Rep. Comput. Chem. 2022, 18, 123–166. 10.1016/bs.arcc.2022.09.003. [DOI] [Google Scholar]
  19. Raghavachari K.; Trucks G. W.; Pople J. A.; Head-Gordon M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. 10.1016/S0009-2614(89)87395-6. [DOI] [Google Scholar]
  20. Watts J. D.; Gauss J.; Bartlett R. J. Coupled-cluster methods with noniterative triple excitations for restricted open-shell Hartree–Fock and other general single determinant reference functions. Energies and analytical gradients. J. Chem. Phys. 1993, 98, 8718–8733. 10.1063/1.464480. [DOI] [Google Scholar]
  21. Stanton J. F. Why CCSD(T) works: a different perspective. Chem. Phys. Lett. 1997, 281, 130–134. 10.1016/S0009-2614(97)01144-5. [DOI] [Google Scholar]
  22. Peterson C.; Penchoff D. A.; Wilson A. K. Chapter One - Prediction of Thermochemical Properties Across the Periodic Table: A Review of the correlation consistent Composite Approach (ccCA) Strategies and Applications. Annu. Rep. Comput. Chem. 2016, 12, 3–45. 10.1016/bs.arcc.2016.04.001. [DOI] [Google Scholar]
  23. Curtiss L. A.; Redfern P. C.; Raghavachari K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. 10.1063/1.2436888. [DOI] [PubMed] [Google Scholar]
  24. Curtiss L. A.; Redfern P. C.; Raghavachari K. Gn theory. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2011, 1, 810–825. 10.1002/wcms.59. [DOI] [Google Scholar]
  25. Semidalas E.; Martin J. M. L. Canonical and DLPNO-Based G4(MP2)XK-Inspired Composite Wave Function Methods Parametrized against Large and Chemically Diverse Training Sets: Are They More Accurate and/or Robust than Double-Hybrid DFT?. J. Chem. Theory Comput. 2020, 16, 4238–4255. 10.1021/acs.jctc.0c00189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Semidalas E.; Martin J. M. L. Canonical and DLPNO-Based Composite Wavefunction Methods Parametrized against Large and Chemically Diverse Training Sets. 2: Correlation-Consistent Basis Sets, Core–Valence Correlation, and F12 Alternatives. J. Chem. Theory Comput. 2020, 16, 7507–7524. 10.1021/acs.jctc.0c01106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Martin J. M. L.; Parthiban S.. W1 and W2 Theories, and Their Variants: Thermochemistry in the kJ/mol Accuracy Range. In Quantum-Mechanical Prediction of Thermochemical Data; Cioslowski J., Ed.; Understanding Chemical Reactivity; Kluwer Academic Publishers: Dordrecht, 2002; Vol. 22, pp 31–65. 10.1007/0-306-47632-0_2. [DOI] [Google Scholar]
  28. Karton A.; Martin J. M. L. Explicitly correlated Wn theory: W1-F12 and W2-F12. J. Chem. Phys. 2012, 136, 124114. 10.1063/1.3697678. [DOI] [PubMed] [Google Scholar]
  29. Stanton J. F.; Gauss J. A simple correction to final state energies of doublet radicals described by equation-of-motion coupled cluster theory in the singles and doubles approximation. Theor. Chim. Acta 1996, 93, 303–313. 10.1007/BF01127508. [DOI] [Google Scholar]
  30. Crawford T. D.; Stanton J. F. Investigation of an asymmetric triple-excitation correction for coupled-cluster energies. Int. J. Quantum Chem. 1998, 70, 601–611. . [DOI] [Google Scholar]
  31. Kucharski S. A.; Bartlett R. J. Noniterative energy corrections through fifth-order to the coupled cluster singles and doubles method. J. Chem. Phys. 1998, 108, 5243–5254. 10.1063/1.475961. [DOI] [Google Scholar]
  32. Kucharski S. A.; Bartlett R. J. Sixth-order energy corrections with converged coupled cluster singles and doubles amplitudes. J. Chem. Phys. 1998, 108, 5255–5264. 10.1063/1.475962. [DOI] [Google Scholar]
  33. Thorpe J. H.; Feller D.; Bross D. H.; Ruscic B.; Stanton J. F. Sub 20 cm–1 computational prediction of the CH bond energy — a case of systematic error in computational thermochemistry. Phys. Chem. Chem. Phys. 2023, 25, 21162–21172. 10.1039/D2CP03964H. [DOI] [PubMed] [Google Scholar]
  34. Franke P. R.; Stanton J. F. Rotamers of Methanediol: Composite Ab Initio Predictions of Structures, Frequencies, and Rovibrational Constants. J. Phys. Chem. A 2023, 127, 924–937. 10.1021/acs.jpca.2c06686. [DOI] [PubMed] [Google Scholar]
  35. Spiegel M.; Semidalas E.; Martin J. M. L.; Bentley M. R.; Stanton J. F. Post-CCSD(T) corrections to bond distances and vibrational frequencies: the power of Λ. Mol. Phys. 2024, 122, e2252114 10.1080/00268976.2023.2252114. [DOI] [Google Scholar]
  36. Karton A.; Sylvetsky N.; Martin J. M. L. W4–17: A diverse and high-confidence dataset of atomization energies for benchmarking high-level electronic structure methods. J. Comput. Chem. 2017, 38, 2063–2075. 10.1002/jcc.24854. [DOI] [PubMed] [Google Scholar]
  37. Karton A.; Daon S.; Martin J. M. L. W4–11: a high-confidence benchmark dataset for computational thermochemistry derived from first-principles W4 data. Chem. Phys. Lett. 2011, 510, 165–178. 10.1016/j.cplett.2011.05.007. [DOI] [Google Scholar]
  38. Karton A.; Tarnopolsky A.; Lamère J. F.; Schatz G. C.; Martin J. M. L. Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A 2008, 112, 12868–12886. 10.1021/jp801805p. [DOI] [PubMed] [Google Scholar]
  39. Bomble Y. J.; Stanton J. F.; Kállay M.; Gauss J. Coupled-cluster methods including noniterative corrections for quadruple excitations. J. Chem. Phys. 2005, 123, 054101. 10.1063/1.1950567. [DOI] [PubMed] [Google Scholar]
  40. Kállay M.; Gauss J. Approximate treatment of higher excitations in coupled-cluster theory. J. Chem. Phys. 2005, 123, 214105. 10.1063/1.2121589. [DOI] [PubMed] [Google Scholar]
  41. Kállay M.; Gauss J. Approximate treatment of higher excitations in coupled-cluster theory. II. Extension to general single-determinant reference functions and improved approaches for the canonical Hartree-Fock case. J. Chem. Phys. 2008, 129, 144101. 10.1063/1.2988052. [DOI] [PubMed] [Google Scholar]
  42. Kállay M.; Surján P. R. Higher excitations in coupled-cluster theory. J. Chem. Phys. 2001, 115, 2945–2954. 10.1063/1.1383290. [DOI] [PubMed] [Google Scholar]
  43. Kállay M.; Nagy P. R.; Mester D.; Rolik Z.; Samu G.; Csontos J.; Csóka J.; Szabó P. B.; Gyevi-Nagy L.; Hégely B.; et al. The MRCC program system: Accurate quantum chemistry from water to proteins. J. Chem. Phys. 2020, 152, 074107. 10.1063/1.5142048. [DOI] [PubMed] [Google Scholar]
  44. Noga J.; Bartlett R. J. The full CCSDT model for molecular electronic structure. J. Chem. Phys. 1987, 86, 7041–7050. 10.1063/1.452353. [DOI] [Google Scholar]
  45. Kucharski S. A.; Bartlett R. J. An efficient way to include connected quadruple contributions into the coupled cluster method. J. Chem. Phys. 1998, 108, 9221–9226. 10.1063/1.476376. [DOI] [Google Scholar]
  46. Kucharski S. A.; Bartlett R. J. The coupled-cluster single, double, triple, and quadruple excitation method. J. Chem. Phys. 1992, 97, 4282–4288. 10.1063/1.463930. [DOI] [Google Scholar]
  47. Musiał M.; Kucharski S. A.; Bartlett R. J. Formulation and implementation of the full coupled-cluster method through pentuple excitations. J. Chem. Phys. 2002, 116, 4382–4388. 10.1063/1.1445744. [DOI] [Google Scholar]
  48. Matthews D. A.; Cheng L.; Harding M. E.; Lipparini F.; Stopkowicz S.; Jagau T. C.; Szalay P. G.; Gauss J.; Stanton J. F. Coupled-cluster techniques for computational chemistry: The CFOUR program package. J. Chem. Phys. 2020, 152, 214108. 10.1063/5.0004837. [DOI] [PubMed] [Google Scholar]
  49. Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  50. Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. 10.1063/1.464303. [DOI] [Google Scholar]
  51. Martin J. M. L. Basis set convergence study of the atomization energy, geometry, and anharmonic force field of SO2: The importance of inner polarization functions. J. Chem. Phys. 1998, 108, 2791–2800. 10.1063/1.475670. [DOI] [Google Scholar]
  52. Dunning T. H.; Peterson K. A.; Wilson A. K. Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited. J. Chem. Phys. 2001, 114, 9244–9253. 10.1063/1.1367373. [DOI] [Google Scholar]
  53. Martin J. M. L. Heats of formation of perchloric acid, HClO4, and perchloric anhydride, Cl2O7. Probing the limits of W1 and W2 theory. J. Mol. Struct.: THEOCHEM 2006, 771, 19–26. 10.1016/j.theochem.2006.03.035. [DOI] [Google Scholar]
  54. Mehta N.; Martin J. M. L. The Importance of Tight f Basis Functions for Heavy p-Block Oxides and Halides: A Parallel With Tight d functions in the Second Row. J. Phys. Chem. A 2023, 127, 2104–2112. 10.1021/acs.jpca.3c00544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Karton A. Tightening the Screws: The Importance of Tight d Functions in Coupled-Cluster Calculations up to the CCSDT(Q) Level. J. Phys. Chem. A 2022, 126, 8544–8555. 10.1021/acs.jpca.2c06522. [DOI] [PubMed] [Google Scholar]
  56. Fogueri U. R.; Kozuch S.; Karton A.; Martin J. M. L. A simple DFT-based diagnostic for nondynamical correlation. Theor. Chem. Acc. 2013, 132, 1291. 10.1007/s00214-012-1291-y. [DOI] [Google Scholar]
  57. Martin J. M. L.; Santra G.; Semidalas E.. An Exchange-Based Diagnostic for Static Correlation. AIP Conference Proceedings, 2022; Vol. 2611, p 020014. 10.1063/5.0119280. [DOI]
  58. Boese A. D.; Oren M.; Atasoylu O.; Martin J. M. L.; Kállay M.; Gauss J. W3 theory: Robust computational thermochemistry in the kJ/mol accuracy range. J. Chem. Phys. 2004, 120, 4129–4141. 10.1063/1.1638736. [DOI] [PubMed] [Google Scholar]
  59. Karton A. Effective basis set extrapolations for CCSDT, CCSDT(Q), and CCSDTQ correlation energies. J. Chem. Phys. 2020, 153, 024102. 10.1063/5.0011674. [DOI] [PubMed] [Google Scholar]
  60. Schwenke D. W. The extrapolation of one-electron basis sets in electronic structure calculations: How it should work and how it can be made to work. J. Chem. Phys. 2005, 122, 014107. 10.1063/1.1824880. [DOI] [PubMed] [Google Scholar]
  61. Peterson K. A.; Dunning T. H. Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited. J. Chem. Phys. 2002, 117, 10548–10560. 10.1063/1.1520138. [DOI] [Google Scholar]
  62. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, 2016. http://www.gaussian.com.
  63. Werner H.-J.; Knowles P. J.; Manby F. R.; Black J. A.; Doll K.; Heßelmann A.; Kats D.; Köhn A.; Korona T.; Kreplin D. A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. 10.1063/5.0005081. [DOI] [PubMed] [Google Scholar]
  64. Nagy P. R.; Kállay M. Optimization of the linear-scaling local natural orbital CCSD(T) method: Redundancy-free triples correction using Laplace transform. J. Chem. Phys. 2017, 146, 214106. 10.1063/1.4984322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Nagy P. R.; Kállay M. Approaching the Basis Set Limit of CCSD(T) Energies for Large Molecules with Local Natural Orbital Coupled-Cluster Methods. J. Chem. Theory Comput. 2019, 15, 5275–5298. 10.1021/acs.jctc.9b00511. [DOI] [PubMed] [Google Scholar]
  66. Szabó P. B.; Csóka J.; Kállay M.; Nagy P. R. Linear-Scaling Local Natural Orbital CCSD(T) Approach for Open-Shell Systems: Algorithms, Benchmarks, and Large-Scale Applications. J. Chem. Theory Comput. 2023, 19, 8166–8188. 10.1021/acs.jctc.3c00881. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp3c08158_si_001.zip (2.5MB, zip)
jp3c08158_si_002.pdf (330.5KB, pdf)

Data Availability Statement

This material is also freely available from the Figshare repository at http://doi.org/10.6084/m9.figshare.24806913. Additional data can be obtained from the authors upon reasonable request.

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES