Abstract
Purpose:
Inverse finite element analysis (iFEA) of the atrioventricular heart valves (AHVs) can provide insights into the in vivo valvular function, such as in vivo tissue strains; however, there are several limitations in the current state-of-the-art that iFEA has not been widely employed to predict the in vivo, patient-specific AHV leaflet mechanical responses. In this exploratory study, we propose the use of Bayesian optimization (BO) to study the AHV functional behaviors in vivo.
Methods:
We analyzed the efficacy of Bayesian optimization to estimate isotropic Lee-Sacks material coefficients in three benchmark problems: an inflation test, a simplified leaflet contact model, and an idealized AHV model. Then, we applied the developed BO-iFEA framework to predict the leaflet properties for a patient-specific tricuspid valve under a congenital heart defect condition.
Results:
We found that the BO could accurately construct the objective function surface compared to the one from a grid search analysis. Additionally, in all cases the proposed BO-iFEA framework yielded material parameter predictions with average element errors less than (normalized by the simulation-specific characteristic length). Nonetheless, the solutions were not unique due to the presence of a long-valley minima region in the objective function surfaces. Parameter sets along this valley can yield functionally equivalent outcomes (i.e., closing behavior) and are typically observed in the inverse analysis or parameter estimation for the nonlinear mechanical responses of the AHV.
Conclusion:
In this study, our key contributions include: (i) a first-of-its-kind demonstration of the BO method used for the AHV iFEA; and (ii) the evaluation of a candidate AHV in silico modeling approach wherein the chordae could be substituted with equivalent displacement boundary conditions, rendering the better iFEA convergence and a smoother objective surface.
Keywords: in-silico modeling, constitutive model parameters, statistics-based modeling, heart valve biomechanics
1. Introduction
Inverse finite element analysis (iFEA) can serve as a non-invasive method for understanding the biomechanical properties of soft tissues in vivo and facilitating digital realization of organ-level function; however, this is a computationally expensive problem with many hurdles to be addressed before it can be used effectively under clinical settings.
In the literature of heart valve biomechanics, iFEA has been used to predict the tissue properties within an ex vivo beating heart apparatus [1, 3], via in vivo animal models [24, 33, 25, 20, 21], or from human in vivo medical imaging data [42, 28, 38, 7, 29]. A distinct advantage of ex vivo studies is the ability to systematically validate the iFEA framework with high-fidelity benchtop experimental measurements. For example, Abassi. et al. (2016) performed iFEA for a bioprosthetic semi-lunar valve using a camera-equipped ex vivo pulse duplicator system and validated the tissue material responses predicted from an anisotropic Fung-type constitutive model against the mechanical data from biaxial testing [1]. Aggarwal et al. (2016) used iFEA in conjunction with a structural constitutive model to assess the accuracy, sensitivity, and feasibility of the iFEA framework for the semi-lunar valves [3]. From their work, they found that using multiple imaging time points in the residual calculations and a more pronounced heterogeneity in the leaflet strains improved the objective function surface (e.g., convexity and smoothness – the features that can help the iFEA performance).
On the other hand, in vivo animal models have also been used to perform iFEA of the cardiac valves. This category of studies is advantaged by the use of surgically implanted sonocrystals that provides a superior temporal resolution for capturing the rapid motion of the valve during cardiac cycles. In these studies, the dynamic motion of individual leaflets (rather than the full valve apparatus) are analyzed, with a finite element mesh being constructed for the area delimited by the sonocrystal markers and the marker displacements applied as boundary conditions to the edges of the 3D leaflet geometry [24, 33, 25]. Using this technique, Lee et al. (2014, 2017) analyzed a central region of the sonocrystal-tracked ovine mitral valve anterior leaflet and noted that a fiber-based structural model yielded the most accurate reconstruction of the in vivo tissue displacements [24, 25], similar to what was later found in the aforementioned semi-lunar valve study [3]. Alternatively, iFEA using animal models can be performed by digitally reconstructing the full valve leaflets with the corresponding chordae attachments and prescribed displacement/pressure boundary conditions [20, 21]. Interestingly, Krishnamurthy et al. (2008, 2010) used this technique to analyze the ovine mitral valve anterior leaflet and identified a few other challenges associated with iFEA: (i) they suggested that the leaflet strains in vivo may not initiate the high-stiffness tissue behaviors; however, this may be due to the use of an orthotropic linear elastic model [20]; and (ii) they found that the leaflets are active structures (e.g., interstitial cells) with dynamic stiffening behaviors [21]. An additional challenge for iFEA was identified by Rausch et al. (2013), where they observed that the inclusion of leaflet tissue pre-strains to an in-silico mitral valve model can yield substantial differences for the predicted tissues stiffness (i.e., up to four orders of magnitude) [33].
The last category of studies includes the use of iFEA for human in vivo heart valves. To date, a material parameter-predicting iFEA framework for the atrioventricular heart valves (AHVs) has not been achieved. The existent “inverse” analyses for in vivo human data are formulated with constitutive model parameters fit to benchtop (or ex vivo) biaxial testing data of valve leaflets from other species or cadavers [42,28]. Currently, patient-specific computational models for the mitral/tricuspid valves are instead based on forward simulations using presumed material parameters and chordae topologies, and the majority of these studies do not assess the model accuracy by comparisons between the simulation-predicted and in vivo leaflet surfaces [38, 7]. To circumvent the challenges in material parameter identification in the AHVs, Pham et al. (2017) proposed an interesting alternative approach where the chordae tendineae topology and pre-tensions are optimized to achieve a good agreement with the in vivo mitral valve geometry [29].
In short, the in vivo properties of the AHV leaflets have not been holistically determined using non-invasive computational modeling. The translation of iFEA for use with medical imaging data of the AHVs faces many hurdles, including high computational costs associated with simulating complex leaflet contact and tissue nonlinearity, difficulties in reconstructing the valve geometry due to limitations in imaging resolution (e.g., chordae are typically too thin to be seen in echocardiograms), and the existence of non-unique solutions limiting the potential use of iFEA-derived material parameters for subsequent simulations of virtual surgical treatments of the valves.
One attractive method to address these challenges for iFEA of the AHVs is Bayesian optimization (BO). In this approach, the optimization search space is fit with a surrogate model that is iteratively updated following a defined search criterion and Bayes’ rule. When used appropriately, the BO method provides distinct advantages over traditional derivative-based optimization methods or global optimization techniques, especially within the context of iFEA, including: (i) fewer evaluations (i.e., saving computational costs), (ii) a trained surrogate model (which can be used for other analyses and applications), and (iii) a deterministic optimization for certain criterion and parameters. More specific details can be found in Section 2.1 as well as the recent review of BO within the context of experimental design [13]. Specific to modeling of biological systems, BO has been leveraged to infer in vivo constitutive model parameters for the left ventricle of the heart [6], determine the properties of atherosclerotic coronary arteries from in vivo data [40], and assess the in vivo myocardial growth during exercise [10]. However, the application of Bayesian optimization to the AHVs remains an area to be explored/investigated.
Thus, the objective of this work is to apply BO, a derivative-free optimization method, to iFEA of the AHVs. We begin with a series of synthetic test cases to establish our framework and verify the applicability of BO to this class of biological structures. Then, we perform a first-of-its-kind application of the BO-IFEA framework to patient-specific echocardiogram data from a newborn with hypoplastic left heart syndrome (HLHS) – one of the most common single-ventricle congenital heart defects [35].
2. Materials and Methods
2.1. Inverse Finite Element Analysis
2.1.1. The Objective Function
Commonly, the goal in medical imaging-based iFEA is to match the shape of the studied organ between the simulation and the ground truth surface (e.g., obtained from image segmentation point cloud data). To this end, we defined the objective function as the bidirectional local distance between the element centroids and the image-derived 3D point cloud data (see also Figure 2 of Kim et al. (2012) [19]). The metric was chosen owing to the improved reliability in point projection to complex contours and providing a more accurate comparison in surfaces with significant curvature, as opposed to other alternative measures such as the normal distance or minimum distance. Then, the objective function value was computed by
| (1) |
where is the number of the finite elements, is the 3D valve leaflet surface constructed by the imaging-derived 3D point cloud, is the corresponding finite element surface to be determined from the iFEA framework, and is the bi-directional local distance (B-LD) associated with the centroid of the element, that is calculated as the larger value between the forward minimum Euclidean distance and the backward maximum distance :
| (2) |
| (3) |
Fig. 2.

(a) Schematic of the simplified model for two leaflets in contact. (b) Elementwise bidirectional local distance (B-LD) errors for the optimal BO solution normalized by the characteristic length (4.03 mm). (c) Mean Gaussian process surface from the BO procedure.
Herein, denotes the backward minimum (Euclidean) distance from the set of imaging-derived 3D point cloud to the element centroid .
2.1.2. Mathematical Preliminaries for Bayesian Optimization
In the BO method, the calculation of the objective function value is treated as a “black box” and fitted with a surrogate function that is generally a Gaussian process (GP) [12]. First, a prior distribution is formulated in a generic form for the points of the estimated model parameters y:
| (4) |
where is the normal (Gaussian) distribution with the mean function (usually a constant) and the covariance function (e.g., the Gaussian kernel). Then, with progressive iterations of the BO solver, the data points sampled from the Gaussian process in conjunction with the corresponding function values are used to determine the posterior probability distribution for a prospective set of model coefficients using Bayes’ rule:
| (5) |
Herein, the posterior covariance is the updated form of the prior variance function after considering the objective function evaluations at the sampled points , i.e., , and is the BO iteration counter.
At each iteration of the BO procedure, the point to be evaluated is determined using an acquisition function that is informed by the GP. In this study, we used the Expected Improvement (EI) acquisition function, where the value of the prospective points are determined based on the potential improvement of . The expected improvement is mathematically written as:
| (6) |
where is the current optimal observed point, is a tunable hyperparameter to balance the exploitation (first term) and the exploration (second term), and are the probability density function and cumulative density function of the GP, respectively, and the normalized coefficient is defined as:
| (7) |
The unique advantage of BO is that while may be expensive to evaluate, the approximation is computationally very efficient. Thus, can be maximized through with a good computational efficiency to provide the model parameter estimate at the next iteration, i.e., . Furthermore, is deterministic for a given value of leading to reproducible approximations. In this work, we used BO to predict the set of constitutive model parameters (y) that minimize the objective function value in Eq. (1).
2.1.3. Implementation of Bayesian Optimization
The BO algorithm was implemented using the bayesopt function in MATLAB (MathWorks, MA, USA), equipped with the acquisition function expected–improvement. In the function, the amount of exploration versus exploitation of the solution search space can be tuned using the exploration ratio hyper-parameter, , where represents equal weighting between the search preferences. For our investigations, we used based on our findings from an intermediate study and verification of the BO routine, while ensuring a balance between the exploration and exploitation of the anticipated complexity of the objective surfaces (see Supplemental Information 1). The Bayesian optimization for all test cases was performed with 9 parallel workers (Intel Xeon Gold 6136 CPU at 3.00GHz) with the terminating condition of 100 maximum iterations or . This maximum number of iterations was chosen to keep the computations day (a more desirable feature for eventual clinical usage).
2.1.4. Analysis of Optimization Results
Biomechanics-focused iFEA was performed to determine an optimal set of constitutive model parameters that best describe the mechanical behaviors of the soft tissues. In the case of analyzing the heart valve leaflets, it is likely that without additional information, such as patient-specific leaflet microstructure, the solution may be non-unique [3, 24]. To examine if has multiple minima or a “flat” global minima, we proposed to report the mean and standard error of the mean (SEM) of the optimized parameters corresponding to the top 5% percent of all the evaluated . If the SEM is found to be relatively large, it may represent a non-unique solution, the presence of multiple minima, or a poorly posed optimization problem (e.g., insufficient iterations to explore the search space). In addition, we also chose to plot the mean of the trained Gaussian process, when possible, which can provide additional information about the optimization search space (e.g., as shown in Section 3.1).
2.1.5. Constitutive Modeling of the AHV Leaflets and Chordae
Isotropic Lee-Sacks Model for Valve Leaflets
To model the mechanical behaviors of the AHV leaflets, we used the Lee-Sacks model [24]. This exponential-type model was selected due to its widespread use, with the added advantage that we can render a twoparameter problem that can be easily visualized using contour or 3D surfaces [44, 16, 2, 18, 45]. Specifically, we adopted the following strain energy function (SEF) form:
| (8) |
where , and are the material parameters, is the first invariant of the right Cauchy-Green tensor , is the deformation gradient, is the upper bound of used to stabilize the material model at non-physiologic stresses , and is a penalty parameter to enforce tissue incompressiblity (i.e., ). Using the incompressibility condition and assuming zero transmural stress, can be analytically determined as:
| (9) |
where denotes the derivative of the SEF with respect to . For material model parameter estimation, was set as , whereas and were to be estimated from the BO procedure.
Chordae Tendineae Model
In the simulation cases involving chordae tendineae of the AHV, we used a tension-only hyperelastic form [24]:
| (10) |
where , , is the Green-Lagrange strain of the chordae, and is the Macaulay bracket to prevent compressive chordae behaviors.
2.2. Inverse Finite Element Analysis Test Cases
For the analysis of the residual search space and verification of our implementation of BO, we used three test cases: (i) an inflation test with a hyperelastic thin membrane; (ii) a pressure-induced contact between the central regions of two valve leaflets; and (iii) a valvular closing behavior with an idealized valve geometry. In these test cases, the synthetic 3D point cloud was generated using the element centroid locations from a forward simulation with target material parameters. These three test cases allow us to make one-to-one comparison between the synthetic solution (i.e., ground truth) and the BO-obtained solution on the same finite element mesh. Following the three test cases, we then used the knowledge generated to perform BO-iFEA of a real, patient-specific tricuspid valve geometry based on a point cloud obtained from echocardiographic images.
The purposes of each test case as well as the illustrative examples in Supplemental Information 1 and Supplemental Information 2 are summarized as follows:
Test Case 1: To examine the ability of the BO method to reconstruct the objective function surface (compared to the one from the grid search) and to evaluate both the accuracy in reproducing the target model parameters and the sensitivity (e.g., effects of noise and spatially varied thicknesses and model parameters – see Supplemental Information 3).
Test Case 2: To analyze the objective function surface in the simulation that involves contact and to assess BO performance in a more complex problem.
Test Case 3: To present and evaluate a new method of prescribing boundary conditions on the TV leaflets that can facilitate a smoother objective surface for improved BO performance.
Test Case 4: To test the BO performance on heart valve closing behavior with an idealized TV geometry, that involves more complex leaflet self-contact, buckling behaviors and increased computational cost.
Supplemental Information 1: To study the appropriate choice of the hyperparameter in the adopted BO algorithm and to examine the reproducibilty in capturing all the three global minima with the analytical Branin function.
Supplemental Information 2: To further examine the BO performance considering the analytical 2D Ackley function with one global minimum.
All simulations were performed using Abaqus Explicit dynamics (Abaqus Simulia, Dassault Systèmes, France) with a total simulation time of , adaptive time-stepping with a maximum time step of , as well as a general contact model with a contact stiffness of 0.5 in conjunction with a damping pressure of in the cases involving leaflet contact or valve closing [24, 25, 20, 33]. All valve leaflet geometries were constructed as 4-node shell (S4) elements. In the cases involving chordae tendineae, we used the 2-node truss (T3D2) elements with a tension-only mechanical response.
2.2.1. Test Case 1: An Inflation Test with a Hyperelastic Thin Membrane
In the first numerical test case, we considered a square thin membrane with a curvature of that was discretized into 625 equally sized four-node shell elements (Fig. 1a). The nodes on the outside edges of the geometry were pinned while a pressure equivalent to 120 mmHg (i.e., ) was applied to the top surface over of simulation time to capture the large displacement of the material (maximum displacement of ). A synthetic solution was obtained from a forward FE simulation with arbitrarily selected (target) model parameters and .
Fig. 1.

(a) Geometry of the inflation test (Test Case 1). (b) Element-by-element bidirectional local distance (B-LD) errors depicted for the optimal solution. (c) Surface of the mean Gaussian process (GP) from Bayesian optimization. (d) Contour plot of the mean Gaussian process and the mean and standard error of the mean (SEM) of the top 5% of the BO-evaluated solutions (numbers in blue indicate the value of normalized by the characteristic length (2 mm) for each contour level, in mm/mm). (e) Optimization history showcasing the value of normalized by the characteristic length (2 mm).
To demonstrate the ability of BO to reconstruct the objective function surface, we first adopted the conventional sweeping method over parameter space and with a uniformly spaced grid. The objective function values were then used to generate a contour plot for visualization of the parameter search space. In addition, BO was performed within the same parameter domain using the simulation settings described in Section 2.1.3, and the mean GP surface and contour plot were produced and reported for comparison with the grid search-generated contour surface.
We used Test Case 1 for additional sub-studies that are described in the Supplemental Information 3. These sub-studies were performed to analyze the effects of (i) the addition of artificial noise in the solution (to replicate the situation of imprecise medical image segmentation) [43], and (ii) spatially heterogeneous vs. homogeneous leaflet thicknesses and leaflet material properties [26,39,23] on the BO performance and the associated objective function surface.
2.2.2. Test Case 2: Two Leaflets in Contact
For the next test scenario, we generated a simplified model of the valve leaflet contact that only considers the central regions of two separated leaflets [31]. By removing the commissure regions from the simulation, we reduced the computational cost of each simulation as no buckling or self-contact was involved.
The geometry was constructed as two curved, rectangular geometries, each consisting of 576 four-node shell elements (Fig.2a). To emulate the in vivo-equivalent measurements of the tricuspid valve, the leaflet height and width were , and , respectively, with a leaflet separation distance of [9]. Also, six free-edge chordae tendineae were equally spaced around each of the leaflet perimeters stemming from the model origin. The boundary conditions included pinning the top edge of each leaflet and applying a pressure of to the ventricular (i.e., outer) surface. The Bayesian optimization was performed within the parameter space: and , considering the target model parameters as and .
2.2.3. Test Case 3: An Enhanced Approach for iFEA of Valve Leaflet Contact
In an effort to improve the performance of the optimization process, we performed a modification to the iFEA approach for the AHV leaflets that does not consider the chordae attachments. Instead, a displacement boundary condition was prescribed to the leaflet free edges to guide the movement of the valve closing. This approach has a clinically relevant benefit–the chordae tendineae cannot typically be segmented in lower-resolution imaging methodologies, such as echocardiography, and the assumptions regarding chordae topologies or material properties can be avoided.
To test this new approach, we performed a three-step procedure: (i) a forward simulation for the leaflet contact model of known properties in Section 2.2.2; (ii) extraction of the time-varying displacements of the leaflet free edge nodes from the synthetic solution; and (iii) generation of a new leaflet contact model with no chordae attachments but with the time-varying displacement boundary condition applied to the leaflet nodes at the free edge for use with the BO-iFEA (Fig. 3a). Here, Bayesian optimization was performed within the search space and . Similarly, we considered and as the target material parameters.
Fig. 3.

(a) Illustration of the process for developing the leaflet contact optimization Test Case 3 with prescribed leaflet free edge displacements (Test Case 2). (b) Contour surface of the objective function when using free-edge leaflet displacements and the mean and standard error of the mean (SEM) of the top 5% of the BO-evaluated solutions. Note the contour surface is generated from the mean Gaussian process model and the numbers in blue indicate the value of for each contour level normalized by the characteristic length (4.03 mm). (c) Element-by-element bidirectional local distance (B-LD) measures for the optimal solution.
2.2.4. Test Case 4: Idealized Tricuspid Valve Closing
Next, an idealized AHV simulation was performed using a cylinder-shaped geometry with an elliptical annulus (major diameter, 15 mm; minor diameter, 10 mm), and leaflet and commissure heights of 20 mm and 13 mm, respectively [16, 22]. Briefly, the leaflet free edge contour was generated using a smoothing cubic spline fitted to points generated below the annulus curve at the desired leaflet-to-free edge distances. Then, the annulus and leaflet contours were subdivided circumferentially into 55 evenly spaced points, and the mesh was constructed, composed of 770 four-node shell elements with thickness values of . The boundary conditions for the model were as follows: (i) a smoothstepped transvalvular pressure gradient of 25 mmHg was applied to the ventricular surface of the leaflets over of simulation time (total simulation duration of as observed in the patient’s echocardiogram); and (ii) the self-contact of the leaflets was facilitated using the general algorithm in Abaqus, with a contact penalty stiffness of 0.5.
For the target (synthetic) solution, we followed the same procedure as in Section 2.2.3, where the forward simulation had a simplified chordae geometry with papillary muscle tips located below each commissure, and two, single-strand free edge chordae per group. The leaflet free edge displacements were similarly retrieved from the target solution, i.e., material parameters of and (Fig. 4a,b). Then, a valve model without chordae and using the leaflet free edge displacement condition was used for the Bayesian optimization in a search space and .
Fig. 4.
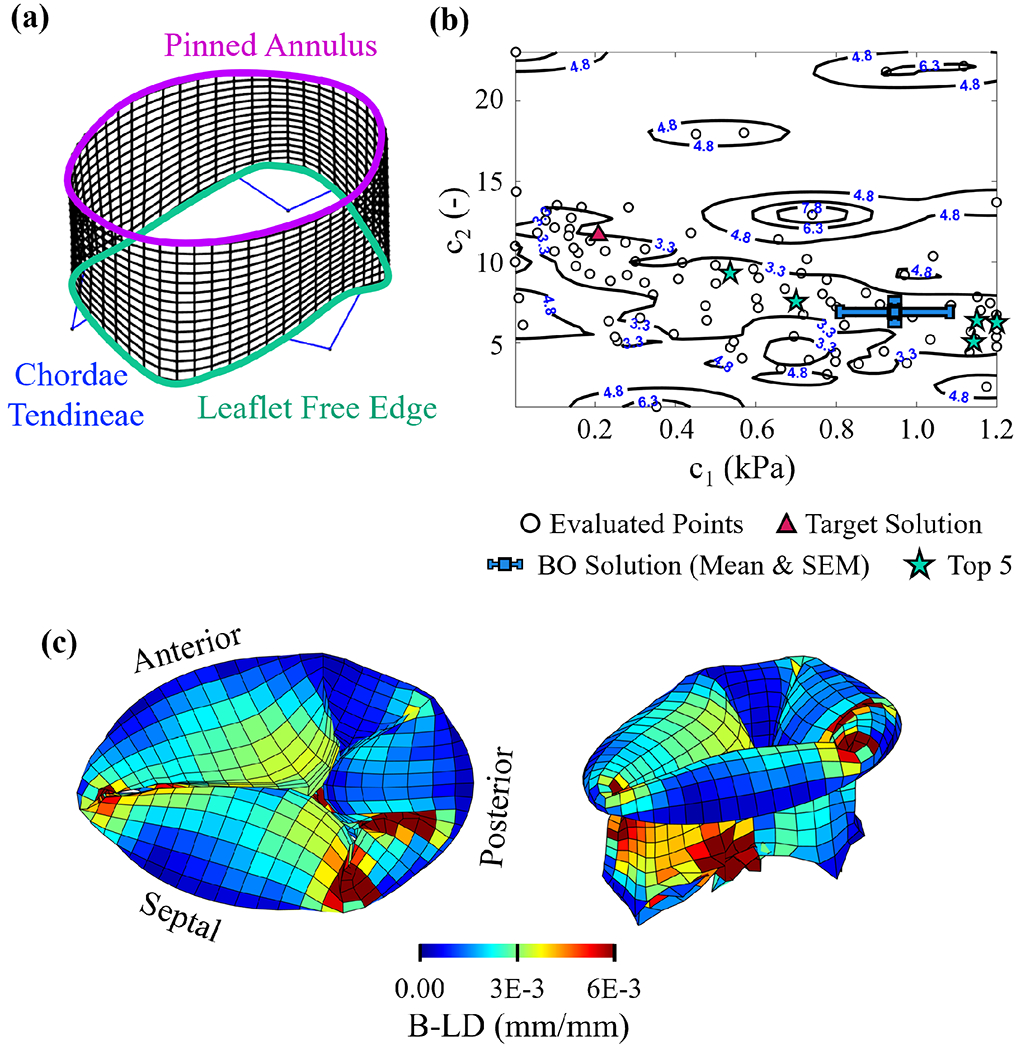
(a) Tricuspid valve model used in the forward simulation of the target (synthetic) solution (Test Case 3). (b) Contour surface of the objective function and the mean and standard error of the mean (SEM) of the top 5% of the BO-evaluated solutions (numbers in blue indicate the value of for each contour level normalized by the characteristic length (79.28 mm)). (c) Element-by-element bidirectional local distance (B-LD) measures for the optimal solution (left: superior view; right: isometric view).
2.2.5. Applicational Problem: Analysis with a Representative Patient Imaging Data
Finally, we analyzed a patient-specific tricuspid valve (TV) geometry from a newborn with hypoplastic left heart syndrome [36]. In this section, we perform two sub-studies using the patient-specific valve geometry: (i) optimization of a 6-parameter problem with a target (synthetic) solution; and (ii) optimization of a 6-parameter problem using the real echocardiogram-derived leaflet point cloud segmentation to recreate the realistic in vivo deformed tricuspid valve surface (true solution). In the 6-dimensional (6D) problem, each leaflet has a unique set of and , resulting in six model parameters to be estimated.
For the valve geometry, we used transthoracic 4-dimensional echocardiographic (4D TEE) imaging data from a representative patient, as collected using a Philips EPIQ ultrasound machine (Philips, NV) equipped with 5- and 7-MHz matrix-array transducers [36]. Then, the 4DTEE imaging data was imported to a segmentation software (3D Slicer) [11] for retrieval of the TV annulus and the free edge at all available imaging time points between the open and closed valve configurations, i.e., between the right ventricular minimum volume and the end diastole, respectively (Fig. 5a). Moreover, the three TV leaflets were individually identified based on the commissure locations obtained from the echocardiographic images. Next, the annulus and leaflet free edge point clouds were fit with a smoothing spline, and the mesh was constructed by linear interpolation between the two contours at the open valve state, resulting in 980 shell elements (Fig. 5b). The annulus and leaflet point clouds at each segmented time instance were used to inform the displacement boundary conditions for the nodes on the TV annulus and papillary muscle tips (Fig. 5c). Transvalvular pressure of 25 mmHg was applied as the pressure loading condition to the valve leaflet surface that mimics the typical physiological condition observed for patients with hypoplastic left heart syndrome. A simulation duration of was chosen to emulate the time frame of tricuspid valve closure as observed in the patient’s echocardiogram.
Fig. 5.

(a) Illustration of image segmentation of the patient-speciifc echocardiogram to retrieve the TV annulus, free edge, and leaflet point clouds. (b) Generated finite element mesh for the three TV leaflets. (c) Dynamic displacement conditions prescribed for the TV annulus and leaflet free edge (t1 = right ventricle minimum volume and t4 = end diastole).
For the BO process, we used a larger search domain because we did not know the true material parameters for the in vivo tissues of this congenital patient. In the first sub-study, the 6D synthetic solution was constructed by randomly sampling values within the search domain of and . For the three leaflets, the target parameters were: TVSL, and ; TVAL, and ; and TVPL, and . The maximum number of BO iterations for this application was set to be 200.
Ethical Approval Declarations
The study protocol for using the patient echocardiograms was reviewed and approved by the institutional review board (IRB) at the University of Oklahoma Health Sciences Center (OUHSC IRB#14112). This is a retrospective enrollment of patients diagnosed with HLHS from July 2019 to present. Due to the retrospective nature of the study, patient consent has been deemed not required by the OUHSC IRB.
3. Results
3.1. Results of Test Case 1: Inflation Testing
The error surface for the optimum BO solution is shown in Fig. 1b, the mean GP surface from the BO is shown in Fig. 1c, and the contour surface with the mean and SEM of the top 5% of evaluated BO solutions is shown in Fig. 1d. From the results of this test case, We found a valley-shaped surface in the objective function approximated by the Gaussian process model, which was in agreement with the contour surface generated from the grid search (Fig. 6). This valley-shaped function caused a large spread of parameter values for the top 5% of BO-evaluated points , but relatively small fluctuation in the objective function values with the minimum objective function value observed at iteration 42.
Fig. 6.

Comparison of the Gaussian process model approximation of the objective function surface (shaded contour map) against the contour map generated from a uniform grid search (white solid lines) normalized by the characteristic length (2 mm).
3.2. Results of Test Case 2: Two Leaflets in Contact
In the 2nd test case, we found that the GP-approximated objective function surface was generally non-smooth (variations of ) for the leaflet contact scenario (Fig. 2b). Despite the non-smooth objective function, the Bayesian optimization obtained a solution with a relatively small error of (i.e., average error per element of ). However, the optimized parameter values were found as and , and the BO was not able to reconstruct the desired synthetic solution (i.e., the ground truth constitutive parameters: and . The misprediction may be explained by the large variations in element centroid locations with small perturbations in the prescribed model parameters, which inspired our enhanced leaflet contact modeling approach (Fig. 2c).
3.3. Test Case 3: Revised Leaflet Contact
Using the “guided free-edge” approach, we found a well-defined, wide-valley-shaped contour surface (Fig. 3b), and the minimal errors in the finite element surface (exempting buckling variations at the free edge, Fig. 3c). We also found a smaller residual value for the optimized Bayesian solution compared to the in vivo-emulating model: (i.e., average error per element of ); ; . Furthermore, the optimal solution was obtained at iteration 24/100 in the revised leaflet contact approach, as opposed to iteration 90/100 in the in vivo-emulating approach (Test Case 2). While the optimized parameter ranges in our enhanced approach do not exactly cover the synthetic solution, the 61.9% decrease in the objective function value and the faster solution convergence demonstrated the advantage of the revised simulation approach.
3.4. Results of Test Case 4: Idealized Valve Closing
From the analysis of an idealized TV, we found the presence of a wide and less smooth, valley of nearly equivalent solutions in the GP-approximated objective function contour surface (Fig. 4b), and the largest element-wise errors in the commissural regions (Fig. 4c). From BO, we found a large range of parameters in the top 5% of evaluated solutions, with a small range of residual values: (i.e., average error per element of ). The wide SEM for the parameters is likely caused by the wider shape of the valley, and the variations in tissue folding behaviors in the commissure regions.
3.5. Real Application: BO-iFEA for Patient-Specific TV
3.5.1. Synthetic Solution
For the 6D synthetic solution using the TV geometry derived from patient imaging data, the optimized parameters were found at iteration 138 (out of the maximum 200 iterations specified in the BO algorithm) as: (i) TVSL, and ; (ii) TVAL, and ; and (iii) TVPL, and ; (i.e., average error per element of ) (Fig. 7a–b). We found that the optimized solution is within the vicinity of the target parameters, with the relatively smaller errors likely being attributed to the existence of a region of near-equivalent solutions in the hyperspace.
Fig. 7.

(a) Top-down and isometric views of the element-wise bidirectional local distance (B-LD) errors normalized by the characteristic length (56.46 mm) and (b) qualitative comparisons with the leaflet point cloud for the optimized TV surface with the 6D synthetic and (c, d) true solutions. Note that for improved visualization a denser finite element mesh was generated than what was used in the real optimization.
3.5.2. True Solution from Medical Imaging Data
In the patient-specific optimization using the real locations of the leaflet point cloud segmented from patient imaging data, the BO-determined parameters were found at iteration 171 out of the maximum number of 200 iterations as (i) TVSL, and ; (ii) TVAL, and ; and (iii) TVPL, and . The corresponding objective function values were found to be (i.e., average error per element of ) (Fig. 7c–d). The larger objective function value was likely caused by noise in the point cloud stemming from the low-resolution imaging modality. This phenomenon also explains the wider IQR for the optimized parameters, but a more narrow IQR for the objective function as compared to the synthetic 6D problem.
4. Discussion
In this work, we have built upon existing applications of BO to biological systems by evaluating and applying BO for inverse finite element analysis of the atrioventricular heart valves. Specifically, we used a series of carefully designed test cases to understand the search space for nonlinear, hyperelastic materials (such as the AHV leaflets) and verify the use of BO for this class of tissues. Then, we provided a first-of-its-kind application of BO to in vivo imaging data for a TV geometry with HLHS. In tandem, we evaluated a new method for removing the chordae tendineae from consideration in iFEA of the AHVs and found that our new “guided free-edge” approach improved convergence and reduced variation the residual search space. In summary, this work provides a new BO framework for iFEA of the AHVs, which represents substantial progress towards determining the in vivo properties of the AHV tissues.
4.1. Bayesian Optimization
From our test cases, we found that Bayesian optimization is capable of reconstructing the objective function surface and locating the region of the global optima within a reasonable number of iterations in cases with both smooth and non-smooth residual search spaces (all simulations performed in day in our laboratory). In the inflation testing case (i.e., Test Case 1), the synthetic solution was effectively captured within 42 iterations. Meanwhile, in the leaflet contact and the tricuspid valve simulation (Test Cases 2-4), the exact solution was not reconstructed; however, the objective function values were reasonable and the obtained solutions were in the vicinity of the user-prescribed parameter values. We were also able to predict patient-specific valve behavior using constitutive model parameters found using BO, albeit the BO solution appeared to converge to a region of equivalent solutions in the hyperspace. Overall, we found these results to be satisfactory for the present study and a strong demonstration of the potential of BO as a tool for inverse in silico modeling.
4.1.1. Improvements to BO
In our work, we used a relatively simple implementation of the BO algorithm for our demonstration of the technique. Moving forward, it may prove beneficial to implement modifications of BO that have been proposed by other researchers. For example, the BO routine can be parallelized using Thompson sampling as an acquisition function, providing an efficient random sampling method for each of the parallelized processes [8]. More complicated parallelization scheme relies on modifying the acquisition functions for batch processing, such as with local penalization or Monte-Carlo methods [4]. In future works, it would be valuable to compare the efficiency and accuracy of the different parallel processing schemes for biomechanics-iFEA problems. Another modification to improve BO is using a “dynamic search domain” for solving problems where the ideal search domain is unknown [37]. This method is specifically interesting for the biomechanics-focused iFEA studies, because, while in vitro testing of soft tissues may provide an estimate for the ideal search space, phenomena such as pre-strains could change the predicted material parameters by four orders of magnitude [33, 32]. Other possible directions for improving BO could be related to the definition of the GP, such as using a composite GP [4], or a least squares-inspired approach [41].
4.2. Ongoing Challenges in Inverse Analysis for the Atrioventricular Heart Valves
iFEA for the atrioventricular heart valves depends on accurate, high-fidelity image data to target during the optimization process. Unfortunately, 4D echocardiography (the common modality for the cardiac valves) can suffer from substantial noise, image dropout, low frame rates, and the inability to accurately estimate tissue thicknesses [14]. Furthermore, user segmentation of the heart valve to acquire the requisite point cloud data for iFEA can introduce user-specific bias into the target geometry. Each of these will likely influence the target surface for iFEA, potentially leading to imprecise constitutive model parameters or in vivo predictions. Future studies could overcome these challenges by using emerging deep learning methods for valve segmentation [14]. Otherwise, researchers must carefully design ex vivo or in silico experiments to characterize how noise or uncertainty influence iFEA results. Our preliminary assessment of the noise-related effects for Test Case 1 (Pressure Inflation) are provided in the Supplemental Information 3; however, more detailed analyses related to heart valve function are warranted but outside of the scope of the present investigation.
The conventional method of simulating the mitral or tricuspid valve closing from medical image data involves generating a chordae structure that may or may not emulate the true in vivo condition. For example, Khaligi et al. [17] developed a “functionally equivalent” chordae topology model; however, the implementation may have some shortfalls for in vivo data analysis due to inaccuracies in measuring the chordae thicknesses or when simulating the diseased valves. Additionally, determining the material properties of the chordae further complicates the optimization routines, especially when considering the three mechanically distinct types of chordae (i.e., basal, marginal, strut) [30]. While BO could theoretically be used to optimize the chordae and leaflet properties at the same time (BO can solve up to 20-dimensional problems), the convergence of the solution may be infeasible or extremely expensive. With these limitations, our question was: Can we simulate the AHV function without the chordae tendineae to improve BO IFEA? This philosophy has been shared in other investigations focused on determining in vivo valve mechanics [34, 27]; however, in our experience, the use of a chordae-emulating force can over-estimate leaflet coaptation and lead to further challenges in an iFEA framework that does not benefit from penalty-based shape enforcement. Thus, we proposed our novel “guided free-edge” approach, which we found to provide faster solution convergence. We also noted a substantial reduction in variation of the residual when using the guided freeedge approach, which suggests that this approach can help reduce erroneous predictions stemming from challenges with the chordae.
The logical next step for our framework using this new approach is verification using an ex vivo heart simulator in conjunction with an excised human, animal, or synthetic AHV. In this scenario, the tissues could be characterized experimentally and compared with the iFEA-predicted material properties, and the images obtained from ultrasound probes could be compared with higher resolution imaging methods to verify the accuracy of the optimization and imaging methods, respectively. This integrated experimentalcomputational approach could also facilitate investigations into the effects of imaging noise, prescribed free edge motions, considering more sophisticated material models (e.g., full structural models), and relating tissue mechanics to cellular biosynthetic processes if used within a bioreactor environment.
4.3. Limitations
This study is not without limitations. First, the material parameters that were obtained for the patient-specific geometry may not be truly representative of the tissue material behaviors due to our “guided free-edge” approach; the chordae material properties may be embedded in the predicted leaflet properties. Future works using an ex vivo heart simulator (see also Section 4.2) would allow careful investigation of this effect and provide validation of our model beyond the synthetic cases used herein. Consequently, the future patient conditions or therapy outcomes can not be predicted using our framework. Second, the exponential constitutive model causes a valley of nearly equivalent solutions (i.e., non-unique solutions). Despite this, a high-resolution iFEA-retrieved digital reconstruction of the valve surface provides rich detail about the geometry and mechanics of the valve, which may be useful in predicting adverse tissue remodeling caused by excessive strains [15], or for surgical planning using these high-fidelity visualizations. However, it should be noted that medical imaging has intrinsic noise that may influence the point cloud definition and the accuracy of subsequent BO analyses. Preliminary analyses exploring a similar effect to that of medical imaging noise for Test Case 1 (Inflation Testing) can be found in Supplemental Information 3. Third, we considered a relatively simple constitutive model to ensure reasonable computing times. Future investigations may consider more sophisticated constitutive models (e.g., the full structural model); however, these may suffer from the curse of dimensionality, which would increase computation time and reduce solution accuracy [5]. Finally, in our simulations of the real patient TV, we observed non-physiologic behaviors at the leaflet free edge due to minor errors in the image segmentation and contour smoothing process affecting the prescribed displacements. Some of this may be attributed to the coarse mesh density used to provide manageable computation times, and future works will more carefully explore how mesh density and point cloud density influence the results. This issue could likely be remedied by a semiautomated or automated image segmentation routine that more accurately maintains the leaflet lengths throughout the segmentation process (e.g., contour propagation).
4.4. Conclusion
Overall, this exploratory study of the iFEA problem for the AHVs represented two primary contributions to the field of AHV biomechanical modeling: (i) a demonstration of Bayesian optimization, with recommendations on standardized reporting of results (i.e., mean and SEM of the top 5% of the BO-evaluated solutions); and (ii) an enhanced method for iFEA of the atrioventricular heart valve function using “guided free-edge displacement”, rather than an assumed chordae topology. We have found that BO has advantages over derivative-free or derivative-based solvers, including faster computational times, and the ability to cheaply reconstruct the objective function surface. While there are still remaining challenges for performing inverse analysis of the heart valve structures, BO could be used to obtain information about the leaflet strains and coaptation in a relatively short time frame (each inverse analysis problem was performed within one day in our laboratory). With continued efforts in this field, a long-term vision can be realized of a patient-specific framework for the prediction of surgical outcomes and disease progression in newborns with congenital heart defects such as hypoplastic leaf heart syndrome.
Supplementary Material
Acknowledgment
We gratefully acknowledge the supports from the Presbyterian Health Foundation, American Heart Association (AHA) Scientist Development Grant Award (16SDG27760143), Oklahoma Center for the Advancement of Science and Technology (OCAST, HR23-003), and grant R01 HL159475 from the National Institutes of Health. CJR was supported by the National Science Foundation Graduate Research Fellowship (GRF 2020307284). CHL was in part supported by the IBEST-OUHSC Funding for Interdisciplinary Research, and the research funding from OU’s Research Council.
Appendix A: Comparison of Bayesian Optimization (BO) with the Conventional Grid Search Method
Similar to the results presented in Section 3.1 (Fig. 6), a grid search was performed to render contour surfaces for comparison with the BO-estimated objective surface in the newly proposed leaflet simulation method (Section 2.2.3) and the idealized valve analysis (Section 2.2.4). Comparing these surfaces (Fig. 8), we found a reasonable agreement between the grid- and BO-based objective surfaces. The discrepancies between the BO surface and the grid-based surface may be attributed to the BO terminating condition of 100 iterations. Nevertheless, the BO approach captures general features of the contour, such as the valley shape in Fig. 8a and the local region of large residuals in Fig. 8b, in 25% of the computation time of the grid-based search. This distinct advantage of the BO approach for these complex simulations will help translate iFEA to clinical applications where patient-specific material properties may improve clinical outcomes.
Fig. 8.

Comparison of the Gaussian process model approximation of the objective function (shaded contour map) with the contour map generated from a uniform grid search (solid lines) for (a) the proposed leaflet simulation method (Section 2.2.3) normalized by the characteristic length (4.03 mm) and (b) the full valve analysis test case (Section 2.2.4) normalized by the characteristic length (79.28 mm).
Footnotes
Conflict of Interest
The authors of this paper have no financial or personal relationships with other people or organizations that could inappropriately influence (bias) our work.
References
- 1.Abbasi M, Barakat MS, Vahidkhah K, and Azadani AN Characterization of three-dimensional anisotropic heart valve tissue mechanical properties using inverse finite element analysis. J Mech Behav Biomed Mater 62:33–44, 2016. [DOI] [PubMed] [Google Scholar]
- 2.Aggarwal A, Hudson LT, Laurence DW, Lee C-H, and Pant S A bayesian constitutive model selection framework for biaxial mechanical testing of planar soft tissues: Application to porcine aortic valves. J Mech Behav Biomed Mater 138:105657, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aggarwal A and Sacks MS An inverse modeling approach for semilunar heart valve leaflet mechanics: exploitation of tissue structure. Biomech Model Mechanobiol 15:909–932, 2016. [DOI] [PubMed] [Google Scholar]
- 4.Balandat M, Karrer B, Jiang D, Daulton S, Letham B, Wilson AG, and Bakshy E BoTorch: A framework for efficient Monte-Carlo Bayesian optimization. In: Advances in Neural Information Processing Systems 33 (NeurIPS 2020). 2020. [Google Scholar]
- 5.Bessa MA, Bostanabad R, Liu Z, Hu A, Apley DW, Brinson C, Chen W, and Liu WK A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Computer Methods in Applied Mechanics and Engineering 320:633–667, 2017. [Google Scholar]
- 6.Borowska A, Gao H, Lazarus A, and Husmeier D Bayesian optimisation for efficient parameter inference in a cardiac mechanics model of the left ventricle. International Journal for Numerical Methods in Biomedical Engineering 38:e3593, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Conti CA, Della Corte A, Votta E, Del Viscovo L, Bancone C, De Santo LS, and Redaelli A Biomechanical implications of the congenital bicuspid aortic valve: a finite element study of aortic root function from in vivo data. J Thorac Cardiovasc Surg 140:890–896, 2010. [DOI] [PubMed] [Google Scholar]
- 8.Dai Z, Low BKH, and Jaillet P Federated Bayesian optimization via Thompson sampling. In: Advances in Neural Information Processing Systems 33 (NeurIPS 2020). 2020. [Google Scholar]
- 9.David TE, David CM, and Manlhiot C Tricuspid annulus diameter does not predict the development of tricuspid regurgitation after mitral valve repair for mitral regurgitation due to degenerative diseases. J Thorac Cardiovasc Surg 155:2429–2436, 2018. [DOI] [PubMed] [Google Scholar]
- 10.Fan Y, Coll-Font J, Van den Boomen M, Kim JH, Chen S, Eder RA, Roche ET, and Nguyen CT Characterization of exercise-induced myocardium growth using finite element modeling and bayesian optimization. Frontiers in Physiology p. 1264, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin J-C, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M et al. 3d slicer as an image computing platform for the quantitative imaging network. Magn Reson Imaging 30:1323–1341, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Frazier PI A tutorial on bayesian optimization. arXiv preprint arXiv:1807.02811, 2018. [Google Scholar]
- 13.Greenhill S, Rana S, Gupta S, Vellanki P, and Venkatesh S Bayesian optimization for adaptive experimental design: A review. IEEE access 8:13937–13948, 2020. [Google Scholar]
- 14.Herz C, Pace DF, Nam HH, Lasso A, Dinh P, Flynn M, Cianciulli A, Golland P, and Jolley MA Segmentation of tricuspid valve leaflets from transthoracic 3d echocardiograms of children with hypoplastic left heart syndrome using deep learning. Frontiers in Cardiovascular Medicine 8:735587, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Howsmon DP, Rego BV, Castillero E, Ayoub S, Khalighi AH, Gorman RC, Gorman JH III, Ferrari G, and Sacks MS Mitral valve leaflet response to ischaemic mitral regurgitation: from gene expression to tissue remodelling. J R Soc Interface 17, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Johnson EL, Laurence DW, Xu F, Crisp CE, Mir A, Burkhart HM, Lee C-H, and Hsu M-C Parameterization, geometric modeling, and isogeometric analysis of tricuspid valves. Comput Methods Appl Mech Eng 384:113960, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Khalighi AH, Rego BV, Drach A, Gorman RC, Gorman JH, and Sacks MS Development of a functionally equivalent model of the mitral valve chordae tendineae through topology optimization. Ann Biomed Eng 47:60–74, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kiendl J, Hsu M-C, Wu MC, and Reali A Isogeometric kirchhoff–love shell formulations for general hyperelastic materials. Comput Methods Appl Mech Eng 291:280–303, 2015. [Google Scholar]
- 19.Kim HS, Park SB, Lo SS, Monroe JI, and Sohn JW Bidirectional local distance measure for comparing segmentations. Med Phys 39:6779–6790, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Krishnamurthy G, Ennis DB, Itoh A, Bothe W, Swanson JC, Karlsson M, Kuhl E, Miller DC, and Ingels NB Jr. Material properties of the ovine mitral valve anterior leaflet in vivo from inverse finite element analysis. Am J Physiol Heart Circ Physiol 295:H1141–H1149, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Krishnamurthy G, Itoh A, Swanson JC, Miller DC, and Ingels NB Jr. Transient stiffening of mitral valve leaflets in the beating heart. Am J Physiol Heart Circ Physiol 298:H2221–H2225, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Laurence DW, Lee C-H, Johnson EL, and Hsu M-C An in-silico benchmark for the tricuspid heart valve-geometry, finite element mesh, abaqus simulation, and result data set. Data Br 39:107664, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Laurence DW, Ross CJ, Jett SV, Johns CH, Echols AL, Baumwart R, Towner RA, Liao J, Bajona P, Wu Y, and Lee C-H An investigation of regional variations in the biaxial mechanical properties and stress relaxation behaviors of porcine atrioventricular heart valve leaflets. J Biomech 83:16–27, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee C-H, Amini R, Gorman RC, Gorman JH III, and Sacks MS An inverse modeling approach for stress estimation in mitral valve anterior leaflet valvuloplasty for in-vivo valvular biomaterial assessment. J Biomech 47:2055–2063, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lee C-H, Zhang W, Feaver K, Gorman RC, Gorman JH, and Sacks MS On the in vivo function of the mitral heart valve leaflet: insights into tissue-interstitial cell biomechanical coupling. Biomech Model Mechanobiol 16:1613–1632, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mansi T, Voigt I, Georgescu B, Zheng X, Mengue EA, Hackl M, Ionasec RI, Noack T, Seeburger J, and Comaniciu D An integrated framework for finite-element modeling of mitral valve biomechanics from medical images: Application to MitralClip intervention planning. Med Image Anal 16:1330–1346, 2012. [DOI] [PubMed] [Google Scholar]
- 27.Narang H, Rego BV, Khalighi AH, Aly A, Pouch AM, Gorman RC, Gorman JH III, and Sacks MS Pre-surgical prediction of ischemic mitral regurgitation recurrence using in vivo mitral valve leaflet strains. Annals of biomedical engineering pp. 1–13, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Oomen P, Loerakker S, van Geemen D, Neggers J, Goumans M-J, van den Bogaerdt AJ, Bogers AJ, Bouten CV, and Baaijens FP Age-dependent changes of stress and strain in the human heart valve and their relation with collagen remodeling. Acta Biomater 29:161–169, 2016. [DOI] [PubMed] [Google Scholar]
- 29.Pham T, Kong F, Martin C, Wang Q, Primiano C, McKay R, Elefteriades J, and Sun W Finite element analysis of patient-specific mitral valve with mitral regurgitation. Cardiovasc Eng Technol 8:3–16, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pokutta-Paskaleva A, Sulejmani F, DelRocini M, and Sun W Comparative mechanical, morphological, and microstructural characterization of porcine mitral and tricuspid leaflets and chordae tendineae. Acta Biomater 85:241–252, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Prot V, Skallerud B, and Holzapfel G Transversely isotropic membrane shells with application to mitral valve mechanics. constitutive modelling and finite element implementation. Int J Numer Methods Eng 71:987–1008, 2007. [Google Scholar]
- 32.Rausch MK and Kuhl E On the effect of prestrain and residual stress in thin biological membranes. J Mech Phys Solids 61:1955–1969, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rausch MK, Tibayan FA, Ingels NB, Miller DC, and Kuhl E Mechanics of the mitral annulus in chronic ischemic cardiomyopathy. Ann Biomed Eng 41:2171–2180, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rego BV, Khalighi AH, Drach A, Lai EK, Pouch AM, Gorman RC, Gorman JH III, and Sacks MS A noninvasive method for the determination of in vivo mitral valve leaflet strains. International journal for numerical methods in biomedical engineering 34:e3142, 2018. [DOI] [PubMed] [Google Scholar]
- 35.Reyes A 2nd, Bove EL, Mosca RS, Kulik TJ, and Ludomirsky A Tricuspid valve repair in children with hypoplastic left heart syndrome during staged surgical reconstruction. Circulation 96:II–341, 1997. [PubMed] [Google Scholar]
- 36.Ross CJ, Trimble EJ, Johnson EL, Baumwart R, Jolley MA, Mir A, Burkhart HM, and Lee C-H A pilot investigation of the tricuspid valve annulus in newborns with hypoplastic left heart syndrome. JTCVS Open 10:324–339, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Stander N and Craig K On the robustness of a simple domain reduction scheme for simulation-based optimization. Eng Comput 19:431–450, 2002. [Google Scholar]
- 38.Stevanella M, Maffessanti F, Conti CA, Votta E, Arnoldi A, Lombardi M, Parodi O, Caiani EG, and Redaelli A Mitral valve patient-specific finite element modeling from cardiac mri: application to an annuloplasty procedure. Cardiovasc Eng Technol 2:66–76, 2011. [Google Scholar]
- 39.Sun W, Martin C, and Pham T Computational modeling of cardiac valve function and intervention. Annu Rev Biomed Eng 16:53–76, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Torun SG, Torun HM, Hansen HH, de Korte CL, van der Steen AF, Gijsen FJ, and Akyildiz AC Multicomponent material property characterization of atherosclerotic human carotid arteries through a bayesian optimization based inverse finite element approach. journal of the mechanical behavior of biomedical materials 126:104996, 2022. [DOI] [PubMed] [Google Scholar]
- 41.Uhrenholt AK and Jensen BS Efficient bayesian optimization for target vector estimation. In: Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, volume 89 of Proceedings of Machine Learning Research, pp. 2661–2670. 2019. [Google Scholar]
- 42.Wang Q and Sun W Finite element modeling of mitral valve dynamic deformation using patient-specific multi-slices computed tomography scans. Ann Biomed Eng 41:142–153, 2013. [DOI] [PubMed] [Google Scholar]
- 43.Weis JA, Miga MI, Granero-Moltó F, and Spagnoli A A finite element inverse analysis to assess functional improvement during the fracture healing process. J Biomech 43:557–562, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wu MC, Zakerzadeh R, Kamensky D, Kiendl J, Sacks MS, and Hsu M-C An anisotropic constitutive model for immersogeometric fluid–structure interaction analysis of bioprosthetic heart valves. J Biomech 74:23–31, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wu W, Ching S, Maas SA, Lasso A, Sabin P, Weiss JA, and Jolley MA A computational framework for atrioventricular valve modeling using open-source software. J Biomech Eng 144:101012, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


