Confusion cannot explain cooperative behavior in public goods games

Significance

A common assumption in behavioral economics experiments is that motivations can be inferred from individuals’ choices. This assumption is challenged by previous research showing that cooperation in a public goods game is primarily due to participants’ confusion. We show that if participants are well instructed, confusion is reduced and it can be shown that social preferences matter. Our results support the assumption in behavioral economics that choices reveal motivations.

Abstract

Some scholars find that behavioral variation in the public goods game is explained by variations in participants’ understanding of how to maximize payoff and that confusion leads to cooperation. Their findings lead them to question the common assumption in behavioral economics experiments that choices reflect motivations. We conduct two experiments, in which we minimize confusion by providing participants with increased training. We also introduce a question that specifically assesses participants’ understanding of payoff maximization choices. Our experimental results show that the distribution of behavior types is significantly different when participants play with computers versus humans. A significant increase in contributions is also observed when participants play with humans compared to when they play with computers. Moreover, social norms may be the main motive for contributions when playing with computers. Our findings suggest that social preferences, rather than confusion, play a crucial role in determining contributions in public goods games when playing with humans. We therefore argue that the assumption in behavioral economics experiments that choices reveal motivations is indeed valid.

Public goods games are frequently employed to investigate how people value the welfare of others in collective action dilemmas. Canonical findings from public goods game experiments show that average contributions are between 40 and 60% of endowments in one-shot games or in the first period of repeated games and usually decrease over time to about 10% despite non-cooperation being a profit-maximizing strategy (1–17). Most of the existing explanations of this empirical regularity rely on social preferences (2, 7–9, 13, 17), whereas some scholars explain it by confusion, suggesting that people cooperate because they misunderstand the game (18–24).

Scholars have attempted to distinguish between cooperation motivated by social preferences and cooperation motivated by confusion. However, there is no consensus as to which explanation is most valid. It seems widely accepted that the observed contributions are most likely driven by some combination of confusion and social preferences (18, 19, 25, 26, SI Appendix, Discussion). In contrast, Burton-Chellew, El Mouden, and West (21, hereinafter “BEW”) argued that social preferences do not explain human cooperation, whereas confusion does.

The experiment of BEW adopted the paradigm developed by Houser and Kurzban (19), characterized by the introduction of nonhuman, computer players programmed to execute pre-determined contribution sequences. Since participants are aware that their contribution decisions have no effect on the behavior of the computer players and that only the real person (i.e., themselves) will receive money, it is assumed that contributions when playing with computer players are due to confusion, and the difference in contributions between playing with computer players and playing with human players could be attributed to social preferences.

Unlike previous studies that used direct response methods and between-subjects designs to compare participants’ contribution behavior in the computer and human treatments (e.g., ref. 19), BEW used within-subjects designs (i.e., computer and human conditions) and applied the strategy method in the computer condition to elicit participants’ behavior types and then examined their unconditional contributions when playing with computers and humans. BEW also introduced a test question to examine whether participants understood how to maximize payoff in the game. They believed that their test question could distinguish between confused and informed subjects. According to their results, only 22% of the participants correctly answered the 10 standard control questions developed by Fischbacher and Gächter (9); only 29% of the participants correctly answered their test question. In other words, about 70 to 80% of the participants were confused. Moreover, their results showed, first, that the distribution of behavior types in their computer condition was similar to that in the human treatment of previous studies (9, 10). Second, participants made similar unconditional contributions regardless of whether their groupmates were humans or computers. Third, the level of cooperation was similar between the informed and confused participants. BEW concluded that cooperative behavior in the public goods game is better explained by variation in understanding of how to maximize payoff, and that confusion (i.e., misunderstanding the game) leads to cooperation. They further concluded that “the previous division of humans into altruistic cooperators and selfish free riders was misleading” and that “other existing paradigms from the fields of behavioral economics might be built on incorrect conclusions from experimental studies” (21, p. 1295).

It is worth noting, however, that there are two key points in the experiment of BEW. These points may in fact have exaggerated the role of confusion. The first is that BEW required the participants to complete 10 standard control questions without telling them the correct answer. These 10 standard control questions have been widely used in previous studies to help participants understand the game (9, 10), and it is common practice to ensure that participants answer them all correctly before the experiment begins.

Second, BEW tested whether the participants understood the public goods games by asking each player at the end of the experiment, “In the game, if a player wants to maximize his or her earnings in any one particular round, does the amount they should contribute depend on what the other people in their group contribute?” (21, p. 1294). Based on their assumption, answering “no” implies that the participants understood the game correctly; otherwise, it implies that they misunderstood it. However, answering “yes” to their question does not necessarily imply a misunderstanding of the game. In fact, BEW’s test question about the payoff-maximizing strategy is much more relevant to participants’ actual decision-making than to their understanding of the game. The actual decision may involve normative considerations, beliefs about others’ actions, and some other behavioral motives (8, 27). That is, their question does not distinguish between confused participants who are unaware of the opportunity to free-ride on others’ contributions and informed participants who consciously choose to forgo this opportunity due to other concerns. Some of their confused players may in fact be the informed. Therefore, their test question to examine participants’ understanding of the game is potentially flawed.

In light of the aforementioned points, BEW’s conclusions can be questioned. Given the importance of public goods games in analyzing social dilemmas and developing policy-relevant designs for problems outside the laboratory, the present research attempts to reevaluate their views.

To this end, we conducted two experiments. Experiment 1 conducted a classic linear public goods game using a between-subjects design. After ensuring that all participants had correctly answered all 10 standard control questions, we used our test question to examine whether participants understood the nature of the public goods game. Participants were asked how much they should contribute to the group project in a one-shot game, given the contributions of other group members, if they wanted to maximize their own earnings. Since the payoff-maximizing strategy is to contribute zero, if a participant correctly understands the essential nature of the game, they will contribute zero (of course, their actual contribution may not be zero); otherwise, they will make a non-zero contribution. We also explored behavioral motives in the game using post-experimental questionnaires and two additional experiments.

To increase the robustness of the results of experiment 1 and to facilitate a direct comparison with BEW’s study, we conducted experiment 2, which replicated BEW’s experiment (21). The only modification is that we told participants the correct answers to the 10 control questions. This modification is designed to examine whether BEW’s results can be replicated when participants understand the instructions. Moreover, after completing all replicated stages of BEW’s experiment, we also assessed participants’ understanding of the game with our test questions.

Results of Experiment 1

Understanding the Game.

In this experiment, all participants were randomly assigned to groups of four players (computers or humans), with each player assigned 20 monetary units (MU). All contributions to the group project were multiplied by two and then shared equally among four group members. That is, the private marginal return to the contributor is 0.5. Consequently, the strategy that maximizes payoff is to contribute zero.

We first tested whether participants understood the experiment using the 10 control questions (9). After participants correctly answered the 10 standard control questions, we asked an additional question: “In a one-shot game, given that the amount contributed to the project by the other group members of your group is 30 MU, if you want to maximize your own benefit, how much should you contribute to the project (of course, your actual contribution may be different)?” Different from BEW’s test question, our question asks participants to make a supposed contribution if they only consider their own interests in a more explicit contribution scenario. If a participant answers “zero,” it means they understand the game, otherwise it means they misunderstand it.

In the human treatment, only 2.5% (3 of 120) of participants answered “non-zero,” and in the computer treatment, only 2.5% (3 of 120) did. This implies that approximately 98% of the participants understood the game correctly, which almost eliminated the effect of confusion. This also suggests that correctly answering these 10 standard control questions effectively ensures that players understand the public goods games.

Distribution of Behavior Types.

We classified our participants into four behavior types: free riders, conditional cooperators, humped/triangle cooperators, and others. Free riders were those who followed the payoff-maximizing strategy, i.e., they contributed 0 MU regardless of how much their groupmates contributed. By contrast, conditional cooperators contributed more when their groupmates contributed more. Humped cooperators were defined as those who “increased their contributions with the contributions of others up to a point” and then “decreased their own contributions as others contribute more.” Anyone who did not fit into one of these categories was referred to as other.

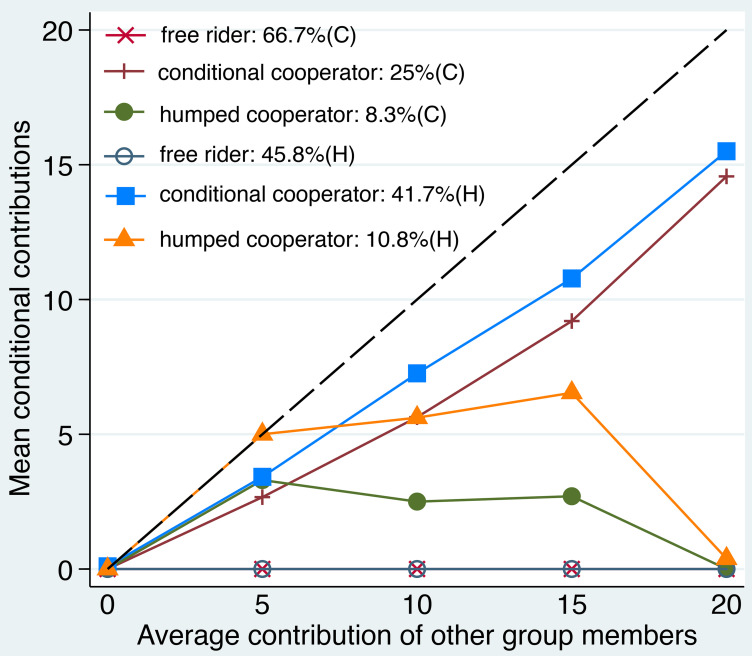
In the computer treatment, 66.7% (80 of 120) of participants were free riders, and 25% (30 of 120) were conditional cooperators. The remaining 8.3% (10 of 120) exhibited a pattern of humped cooperators. In the human treatment, 45.8% (55 of 120) of participants were free riders, and 41.7% (50 of 120) were conditional cooperators. The remaining 12.5% (15 of 120) of the human players exhibited other patterns, of which 10.8% (13 of 120) were humped cooperators and 1.7% (2 of 120) were others (Fig. 1 and SI Appendix, Fig. S3 and Results).

Fig. 1.

Average of one’s own contribution for the average contribution of other group members in experiment 1. H denotes human treatment, C denotes computer treatment, and N = 120 for each treatment.

The distribution of behavior types in game with computer players significantly differed from that in game with human players [Fisher’s exact test (FET): P < 0.01]. This is also not consistent with BEW’s results (21; FET for human treatment: P < 0.01; FET for computer treatment: P < 0.01). According to previous studies (10, 26, 28–30), the difference between the two treatments is used to estimate cooperation driven by the social preferences. Therefore, our results suggest that a substantial proportion of the participants exhibited social preferences.

Conditional Cooperation Level.

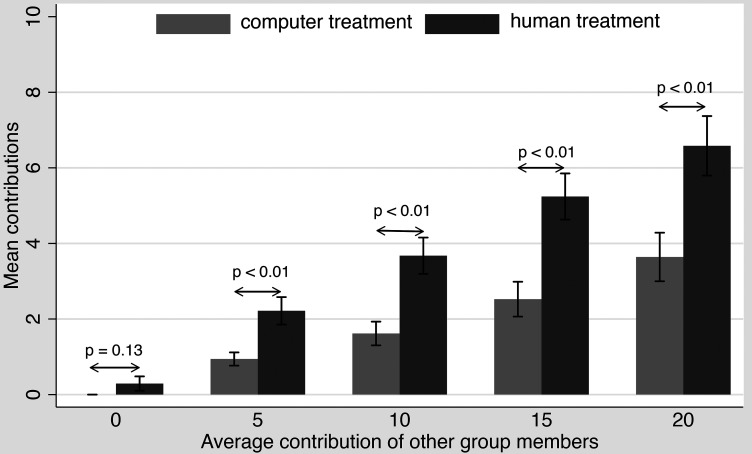
When comparing the conditional contribution level in the computer and human treatments, it is found that the mean contributions in the human treatment were significantly greater (t test: all ps < 0.01 for an average of 5, 10, 15, and 20 MU contribution by others; P = 0.13 for an average of 0 MU contribution by others; Fig. 2 and SI Appendix, Table S1 and Results). In general, although the participants in both treatments showed a tendency to cooperate, their slopes were significantly different (slope = 0.18 and 0.31 for the computer and human treatments, respectively, P < 0.01).

Fig. 2.

Average conditional contribution levels in computer (light gray) and human treatments (dark gray) of experiment 1. Error bars indicate ±1 SE. SE denotes the SEM.

Underlying Motives for Conditional Cooperation.

As we controlled for the effect of confusion on cooperation, the difference in cooperation between computer and human treatments showed that social preferences do affect the level of cooperation. Besides, after controlling for the effect of confusion on cooperation, the level of contribution remained significantly greater than zero when participants played with computer players. Hence, we explore the underlying motives for such contributions. The six confused participants were not included in the analysis of motives.

Participants first answered the question, “Did your decision depend on the contributions of other members of your group?” The results showed that 56% and 43% of the participants in the human and computer treatments, respectively, answered “yes” (Table 1).

Table 1.

Distribution of answers on whether participants’ decisions depended on others’ contribution

	Treatment
	Human		Computer
Type	Yes*	No	Yes	No
Free rider	5	48	13	67
Conditional cooperator	47	2	27	0
Humped cooperator	12	1	10	0
Other	2	0	0	0

^*Response to the question of whether participants’ contributions depended on others’ contributions. Question asked: “In the decision you just made, did your contribution depend on the contributions of other members of your group?” The six confused participants were not included in the analysis of motives. N = 117 for each treatment.

Various types of motives influence cooperation (5–10, 31–38). Throughout the course of our experiment, the participants were not allowed to communicate with each other, and we did not provide any feedback about payoffs or group members’ behavior. Although these designs prevent signaling, reciprocity, and learning (39–41), several motives can influence cooperative behavior. First, altruistic preference is an important motive (6, 40, 42). Second, people cooperate because they believe that most people do the same; that is, because they adhere to social norms (8, 43–46). Third, when individuals contribute inadequately to their group project, they may feel that they are sacrificing the interests of others, which may further generate feelings of guilt or shame. That is, individuals may experience threats to their self-image (47–49). Fourth, although all decisions and payments were made anonymously, some participants may have thought that the experimenters could observe their behavior. And they were concerned about their social image (49–52), which led them to avoid being too selfish. Therefore, in the human treatment, altruism, social norms, self-image concerns, and social image concerns were included to test participants’ underlying motives. In the computer treatment, altruism was excluded and social norms, self-image concerns, and social image concerns were considered as possible motives (SI Appendix, Methods).

In the human treatment, 91% (48 of 53) of free riders answered that the contributions of other group members did not influence their contributions. Their motives were mainly self-interest and social norms, accounting for 50% and 42%, respectively. Only 9% (5 of 53) of free riders answered “yes,” and their motive was social norms. Ninety-six percent (47 of 49) of conditional cooperators reported that other members’ contributions influenced their decisions. Their most common motive was social norms (47%), followed by altruism and self-image concerns (19% and 21%, respectively). Only 4% (2 of 49) of conditional cooperators answered “no,” but they were motivated by social norms rather than self-interest. Almost all humped cooperators indicated that their decisions were affected by others’ contributions and that the main motive was social norms (75%, Table 2 and SI Appendix, Tables S2 and S3 and Results). In general, differences in altruism, self-image concerns, and self-interest are significant when comparing free riders and cooperators (FET: altruism: P < 0.01; social norms: P = 0.58; self-image: P < 0.01; social image: P = 1.000; self-interest: P < 0.01).

Table 2.

Distribution of motives in the human and computer treatments

		Treatment
		Human					Computer
Type		Free rider (N = 53)	Conditional cooperator (N = 49)	Humped cooperator (N = 13)	Other (N = 2)	Free rider (N = 80)	Conditional cooperator (N = 27)	Humped cooperator (N = 10)	Other (N = 0)
* Motives for answering “yes”	Altruism	0	9	2	1	–	–	–	–
	Social norm	5	22	9	1	10	18	6	–
	Self-image	0	10	0	0	0	6	1	–
	Social image	0	1	0	0	0	1	1	–
	Other	0	5	1	0	3	2	2	–
Motives for answering “no”	Self-interest	24	0	1	0	47	0	0	–
	Social norm	20	2	0	0	17	0	0	–
	Other	4	0	0	0	3	0	0	–

^*Response to question whether participants’ contributions depended on others’ contributions. Question asked: “In the decision you just made, did your contribution depend on the contributions of other members of your group?”

In the computer treatment, 84% (67 of 80) of free riders reported that their decisions were not influenced by others’ contributions, and that self-interest and social norms were their most important motives, accounting for about 70% and 25%, respectively. Sixteen percent (13 of 80) of free riders answered “yes,” with social norms being the main motive, accounting for 77%. All conditional and humped cooperators answered “yes,” and the social norms motive accounted for about 67% and 60%, respectively (Table 2 and SI Appendix, Tables S4 and S5 and Results). Differences in social norms, self-image concerns, social image concerns, and self-interest are significant when comparing free riders and cooperators (FET: social norms: P < 0.01; self-image: P < 0.01; social image: P = 0.10; self-interest: P < 0.01).

The above results suggest that social norms are the main motivation for individuals to contribute when playing with computers. To further clarify the social norms of free riders and cooperators when they play games with computers, we conducted two additional experiments (each with 72 participants) in which participants were incentivized to reveal their perceptions of social norms (SI Appendix, Methods). Additional experiment 1 used Krupka and Weber’s (53) method, in which participants were asked for their incentivized beliefs about what is commonly regarded as appropriate or inappropriate behavior (54, 55). Additional experiment 2 used the method of Bicchieri and Xiao (56), which follows the work of Bicchieri (57). Using a two-step procedure, this method first elicits non-incentivized reports of participants’ personal normative beliefs about what one ought to do in a given situation. Then participants are incentivized to indicate their empirical and normative expectations. Empirical expectations capture what the individual believes to constitute common behavior in the situation (i.e., what most other people do). Normative expectations are second-order beliefs that describe an individual’s beliefs about what others believe they ought to do.

The results of additional experiment 1 showed that free riders rated contributing 0 as the most socially appropriate, regardless of the amount contributed by the three computers, whereas cooperators correspondingly rated 0, 5, 10, 15, and 20 as most socially appropriate when the computer players’ contributions were 0, 5, 10, 15, and 20, respectively (SI Appendix, Figs. S4 and S5 and Results). The results of additional experiment 2 showed that the three beliefs, i.e., personal normative belief, empirical expectation, and normative expectation, exhibited significant differences between free-riders and cooperators when the computer players made non-zero contributions (SI Appendix, Table S6 and Results). These results confirm that while both free riders and cooperators adhered to social norms, their behavior differed because their perceived social norms were distinct. The social norms adhered to by free riders involve making contributions close to zero, whereas the social norms among cooperators involve increasing cooperation as groupmates’ contributions increase.

Unconditional Cooperation.

We compared how well the strategy method described the above predicted behavior in unconditional games in which participants simultaneously and privately contributed money to a group project (9, 21, 58). After completing the conditional contributions, participants were asked to make a one-shot unconditional contribution decision. The order of decisions in our experiment was not counterbalanced because we wanted to first classify the participants based on their behavior in the conditional decisions and then examine whether the behavior in the conditional game predicted their behavior in the unconditional game (21, 59, 60).

Overall, the behavioral types from the conditional decisions can predict the level of cooperation in the subsequent unconditional contribution (9, 21, 60–62), both in the computer treatment [generalized linear model (GLM), F = 23.36, P < 0.01, $R_{\mathit{adj}}^2$ from a linear model = 0.28] and in the human treatment (GLM, F = 19.70, P < 0.01, $R_{\mathit{adj}}^2$ from a linear model = 0.33).

Results of Experiment 2

In experiment 2, which replicated the BEW’s experiment, all participants answered the 10 standard control questions correctly through training, whereas in BEW’s experiment, only 22% of the participants answered the standard questions correctly.

Question About the Payoff-Maximizing Strategy.

As in the experiment of BEW, we asked participants to answer BEW’s test question at the end of experiment 2, “In the game, if a player wants to maximize his or her earnings in any one particular round, does the amount they should contribute depend on what the other people in their group contribute?” (21, p. 1294). According to BEW, answering “no” meant that the participants understood the experiment correctly; otherwise, it meant that they misunderstood the game.

The results of experiment 2 showed that 19 (26%) of our participants answered that the payoff-maximizing strategy does not depend on what others contribute in a one-shot game; 40 (56%), 12 (17%), and 1 (1%) answered “yes,” “sometimes,” and “unsure,” respectively. Recall that in experiment 2, participants’ confusion was minimized with increased training; however, the distribution of responses to this question remained similar to that found by BEW (FET: P = 0.15). The result from the logistic GLM on the probability of answering this question as a function of the behavior type also showed that the behavioral scheme cannot significantly predict BEW’s standard of understanding the game (GLM: F = 1.36, P = 0.26). These results imply that BEW’s test question is in fact not directly relevant to the misunderstanding of the game.

We also assessed participants’ understanding of the game with our test questions: “In a one-shot game, given that the amount contributed to the project by the other group members of your group is 30/10/60 MU, if you want to maximize your own benefit, how much should you contribute to the project (of course, your actual contribution may be different)?” Participants answered these questions after all replicated stages of BEW’s experiment. We found that only 4% (3 of 72) of participants answered non-zero, that is, approximately 96% of the participants understood the game. This is similar to the result of experiment 1. This further suggests that correctly answering the 10 standard control questions can effectively ensure that participants understand the public goods games.

Distribution of Behavior Types.

In experiment 2, 11 of 72 participants (15%) were conditional cooperators. Ten participants (14%) were humped cooperators. The remaining 51 participants (71%) were free riders (SI Appendix, Fig. S6, Table S7, and Results). The distribution of behavior types in experiment 2 was significantly different from the result of BEW (FET: P < 0.01). Moreover, the distribution of behavior types in experiment 2 was similar to that of the computer treatment in experiment 1 (FET: P = 0.181), and significantly different from that of the human treatment in experiment 1 (FET: P < 0.001). This also provides evidence that a great number of participants were driven by social preferences.

Play with Computers versus Humans.

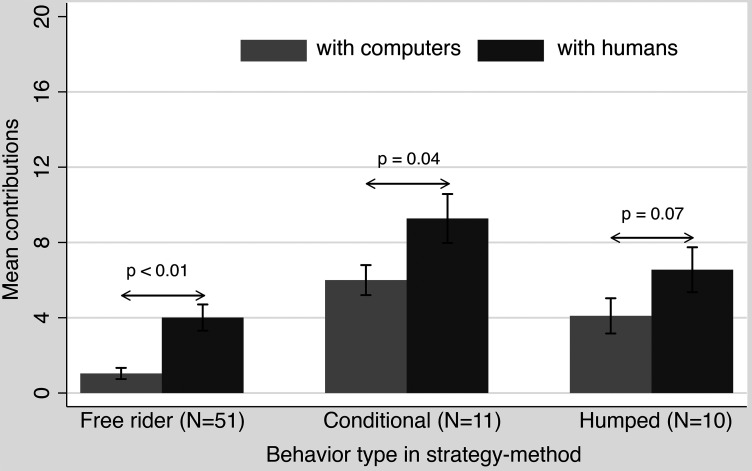
In experiment 2, the behavior types from the strategy method significantly predicted the level of cooperation in the subsequent unconditional games, both with computers (GLM, contribution ~ type: F = 24.27, P < 0.01, R²_adj = 0.4) and with humans (GLM, mean-contribution over six rounds ~ type: F = 6.08, P < 0.01, R²_adj = 0.14) (Fig. 3 and SI Appendix, Results). It is worth noting that although our results also showed that the behavior types predicted the level of cooperation in the subsequent unconditional games, the predictive power in the computer condition was much greater than in the human condition, whereas BEW reported that the predictive power was similar between the two conditions. Furthermore, there was a significant difference in the mean unconditional contributions between games with computers or humans (paired t test: t = 5.07, P < 0.01, SI Appendix, Table S8 and Results).

Fig. 3.

Average unconditional contribution levels grouped by behavior type in experiment 2. Error bars indicate ±1 SE. SE denotes the SEM. For all types, the mean levels of cooperation were significantly different when playing with computers (light gray) vs. when playing with humans (dark gray).

Results Comparison of Experiments 1 and 2 and BEW’s Experiment.

To sum up, our experiment 2 does not reproduce BEW’s results (SI Appendix, Table S11 and Results). The only difference between BEW’s experiment and our experiment 2 is the manipulation of understanding the game. Previous studies have suggested that participants may become informed as the experiment progressed (18, 19). In BEW’s experiment, most players did not understand the game at the beginning; some confused players might become informed over the course of the experiment, but their test question failed to measure how many confused players became informed. Their results seem to be a mixed artifact, reflecting the behavior of both confused and informed players. In our experiment 2, more than 95% of players understood the game, and informed players were responsible for the observed contribution pattern. Therefore, our replicated experiment further suggests that BEW’s conclusion is questionable.

Moreover, the results of experiment 1 also provide supporting evidence that cooperative behavior in the public goods games cannot be attributed to confusion. On the one hand, participants’ understanding of the nature of the game was tested immediately after they correctly answered the 10 standard control questions in experiment 1. This partially rules out the possibility that participants became informed as the experiment progressed. On the other hand, instruction for the computer treatment in experiment 1 was explicitly explained with a computer framing, while that of experiment 2 was explained with a human framing at first. In this way, confusion due to the framing of the instruction can be controlled. Both experiments 1 and 2 show that people exhibit social preferences toward human players.

General Discussion

BEW investigated the role of confusion in explaining cooperative behavior in the public goods game. They first proposed a direct measurement method to test whether players understood the nature of the game and concluded that contributions in public goods games were mainly due to confusion. The present research conducted two experiments, in which participants’ confusion was minimized through increased training. We also proposed an applicable test question about the payoff-maximizing action, which is much more relevant to understanding of the game. Based on the results that the distribution of behavior types is significantly different when participants play with computers versus humans and that participants would contribute more when playing with humans than with computers, we suggest that cooperative behavior in public goods games is not a pure artifact of confusion. We argue that the assumption in behavioral economics experiments that choices reveal motivations is substantiated.

First, our study contributes to the messy topic of whether contribution in public goods games can be attributed to confusion. Burton-Chellew et al. serve as a prominent voice advocating for the dominated role of confused participants in shaping the contribution pattern observed in the game (20–24). Upon thorough examination of BEW’s experimental approaches, we argue that their conclusions mainly stem from an uncontrolled experimental implementation and thus deliberately exaggerate the role of confusion.

In the BEW’s experiment, participants were asked to answer the 10 standard control questions but were never given the correct answer. This practice will introduce a significant degree of variability. Such variability can arise from many sources, including individual differences in interpretation of the task and understanding of the rules and dynamics of the game. It is reasonable to infer that the decision noise caused by this variability may obscure the effect of social preferences. Experiment 2, which replicated BEW’s experiment, introduced a simple modification: telling participants the correct answer to the control questions. We then found a significant difference in cooperative behavior when participants interacted with computers versus humans, both in the strategy method and in direct responses. Therefore, mitigating decision noise through measures like clear instructions and control questions seems necessary for researchers.

Previous research has assumed that answering the standard control questions can ensure that participants understand the game (6, 9, 10). The control questions used in these studies are not exactly the same. For example, refs. 9 and 10 used 10 standard control questions, whereas ref. 6 used eight standard control questions. Although researchers often reported that they ensured that participants answered these questions correctly, whether these questions are sufficient to enable participants to understand the experiment remains an open question, as the existing studies have not provided further verification.

BEW explored this question by directly measuring whether participants understood the game. However, their payoff-maximizing test question may lead to an overestimation of the proportion of participants deemed confused. In fact, their test question measures whether a player’s “what he/she actually did” depends on what others do, rather than the “what he/she should have done” in their perceptions. Understanding the game and identifying the optimal strategy (i.e., what someone should do) in a given situation is relatively simple, while actual decision-making may involve normative considerations, image concerns, beliefs about others’ actions, and some other behavioral motives (8, 27, 63–65). There is also evidence that selective engagement in prosocial behavior across different contexts is not an error or a violation of rationality, but rather a natural consequence of people caring about norms, reputation, and some unobserved factors (e.g., refs. 63–65). In other words, there may be a subtle gap between the understanding of payoff-maximizing strategy and the practice of payoff-maximizing strategy in the context of public goods games.

From this perspective, our test question provides a direct and reliable measure of whether participants are confused about the experiment, as it is more relevant to understanding than to actual action. Participants were asked to report a supposed contribution if they only considered their own interests. This supposed contribution allows for a difference from the actual contribution, depending on the type of participant. It shows that the vast majority of participants in experiments 1 and 2 chose to contribute 0 in the “supposed” way we asked, while only 26% of participants in experiment 2 answered the test question of BEW correctly. Based on our standard for understanding the game, we show that correctly answering 10 standard control questions, widely used in previous studies (9, 10), can ensure that over 95% of participants understand the nature of the game. We also believe that it is necessary to introduce test question in the economic experiments in order to verify participants’ understanding of the game.

Second, we provide insights into the motives for contributions when playing with computers beyond confusion. Previous studies have typically tracked computer treatment in public goods game experiments, where players are grouped with “virtual players” (19, 26, 27). It is assumed that contributions in the computer condition are due to confusion. Participants in our experiments 1 and 2 all answered the standard control questions correctly and more than 96% understood the nature of the game, but still a significant proportion of participants made non-zero contributions in the computer condition. Therefore, we conducted a preliminary investigation of this phenomenon by post-questionnaires and two additional experiments.

Results showed that concerns about social norms, social image, self-image, and self-interest differed significantly between free riders and cooperators. Some scholars might argue that these factors are broad experimenter demand effects, specifically social norms and image concerns, as participants do not want to behave as if they are greedy in the presence of the experimenter. Following this standard, it can be said that even if participants understand the game, they may still contribute in the computer condition to please the experimenter. More importantly, we provide additional evidence that participants tend to behave in accordance with their own perceived social norms. Not only the heterogeneity in the normative rules that govern behavior in a certain context, but also heterogeneity in one’s sensitivity to following social norms can alter the nature and extent of social behavior (63). In brief, our research shows that there are many factors that influence contributions in computer condition beyond misunderstanding the game. Although these factors may be viewed as broad experimenter demand effects, our investigation provides insight into the motives behind the contributions that do not fit the rational assumptions.

Third, the present research adds solid evidence that social preferences, but not confusion, are the main reason of human cooperation. Revisiting the two competing explanations that aim to elucidate the cooperation in the public goods games, Houser and Kurzban suggest that the observed contributions are most likely due to a combination of confusion and social preferences (19), while BEW reject this explanation outright. Our experiments 1 and 2 indicated that the contribution levels were significantly higher when playing with humans than that when playing with computers. Even under the strictest assumption that cooperation in the computer condition is entirely due to confusion, and that the difference between the two treatments provides an estimate of the contribution driven by social preferences in the human treatment (19), our results suggest that social preferences account for about half of the contributions when playing with humans. Thus, we refute the argument of BEW and support the widely accepted view that social preferences, rather than confusion, are the main reason for human cooperation.

In summary, by providing increased training to the participants, the effect of confusion about the game can be controlled to an acceptable level in the laboratory experiment. Given that it is a standard practice in experimental economics to train participants to understand the game, BEW’s arguments of “the previous division of humans into altruistic cooperators and selfish free riders was misleading” and “other existing paradigms from the fields of behavioral economics might be built on incorrect conclusions from experimental studies” (21, p. 1295) appear to be arbitrary. Research or governmental policy based on the behavior in the public goods games continues to yield significant insights and understanding.

Methods

There were 240 participants (117 males and 123 females, mean age = 21.19 y, SD = 2.08) in experiment 1 and 72 participants (38 females and 34 males, mean age = 21.10 y, SD = 1.79) in experiment 2, respectively. The experiments were programmed and conducted using z-Tree (66) at the Institute for Study of Brain-like Economics, Shandong University, China. All participants signed informed consent prior to experiments, which were performed in accordance with the Declaration of Helsinki and approved by the Ethics Committee of College of Economics, Shandong University (SI Appendix, Methods).

Experiment 1: Experiment 1 applied a between-subject design, and the marginal per capita return in the public good game is 0.5. Participants were asked to make two sets of decisions, i.e., a “conditional contribution” schedule and an “unconditional” decision. Specifically, the contribution schedule of the five possible average contributions of the other three group members (0, 5, 10, 15, and 20) was shown, and participants had to make their corresponding contributions for each of the five values. For unconditional contributions, participants simultaneously and privately contributed money to a group project. Experiment 1 was one-shot, and the participants were aware of this.

Experiment 2: The procedures of experiment 2 were rigorously aligned with those of BEW. The only difference was that participants were given information about the correct answer and how the correct answer was calculated for each of the 10 standard control questions. After participants completed the entire experimental procedure of BEW, participants answered the following question: “In a one-shot game, given that the amount contributed to the project by the other three group members in your group is 30 (10, 60) MU, if you want to maximize your own benefit, how much should you contribute to the project (of course, your actual contribution may be different)?” This ensures that the participants’ previous decisions were not affected.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Anonymized xls data have been deposited in Open Science Framework (10.17605/OSF.IO/V7Y8B) (67). All other data are included in the manuscript and/or SI Appendix.