Resolution Limit in Infrared Chemical Imaging

Abstract

Chemical imaging combines the spatial specificity of optical microscopy with the spectral selectivity of vibrational spectroscopy. Mid-infrared (IR) absorption imaging instruments are now able to capture high-quality spectra with microscopic spatial detail, but the limits of their ability to resolve spatial and spectral objects remain less understood. In particular, the sensitivity of measurements to chemical and spatial changes and rules for optical design have been presented, but the influence of spectral information on spatial sensitivity is as yet relatively unexplored. We report an information theory-based approach to quantify the spatial localization capability of spectral data in chemical imaging. We explicitly consider the joint effects of the signal-to-noise ratio and spectral separation that have significance in experimental settings to derive resolution limits in IR spectroscopic imaging.

Graphical Abstract

INTRODUCTION

Spatial resolution in optical microscopy is fundamentally limited by diffraction, with a spatial cutoff frequency quantifying the resolution limit. Today, many techniques have circumvented this classical limit to recognize objects at much smaller scales.^1,2 One set of approaches rely on attenuating fluorescence emission to narrow the point-spread function in methods such as stimulated emission depletion microscopy. Another set of modalities such as photoactivated localization and stochastic optical reconstruction microscopies rely on spatial sparsity and temporally separated emissions to enhance spatial resolution. In these approaches, the underlying problem of extracting information can be formulated as a spatial-temporal mapping problem to recognize point objects. Hyperspectral imaging systems can invoke a different form of information encoding, namely a spectral—spatial mapping.

Chemical imaging is a class of label-free hyperspectral imaging techniques that derive contrast from molecular composition. Molecular vibrational frequencies are coincident with optical frequencies in mid-infrared (IR), for instance, resulting in light being quantitatively absorbed proportional to the concentration of the molecular species present. This molecular record provides the ability to recognize objects via analyses of spectral variations within acquired images.³ Spectral analyses⁴ in a variety of applications have been conducted with the simplest and most prevalent configuration of an IR source and detector, a common motif in spectral recording.⁵ Much recent effort has been focused on adding greater molecular information^6–13 and speed,^14,15 while the image quality is commonly accepted to be optimized by following optical design rules from theoretical models. The emergence of quantum cascade lasers (QCL) is also challenging the conventional performance of IR imaging by offering possibilities for recording and analyses to optimize instrument capability that go beyond Fourier transform IR imaging systems.^16,17 The speed and signal-to-noise ratio (SNR) tradeoffs in emerging systems are enabling us to ask more fundamental questions on how data quality, optical configuration, and spectral processing may act in concert to maximize information from chemical imaging.

Modeling the optical resolution limit to account for SNR¹⁹ provides a start to understand the limits of IR imaging. The framework cannot be directly applied to IR imaging, however, as spectra offer both further possibilities and complications. Spectral variation has been used to propose computational methods that realize subdiffraction localization^20–27 as well as provide a cohesive theoretical framework^28–33 to understand image formation in the mid-IR region. However, the acquisition of high SNR, high optical fidelity data to realize these ideas has remained challenging. Taking advantage of QCLs, novel techniques such as balanced detection are now enabling high-sensitivity measurements that are pushing the detection limits^17,18 for IR spectroscopy. Custom-designed optical configurations are similarly providing high spatial fidelity with greatly reduced speckle effects from laser coherence.^14,15 To systematically take advantage of these developments for object recognition by molecular means, a clear definition for achievable resolution is necessary.

THEORY

We report a decision-theoretic-based approach that formulates the two-point resolution limit in terms of the chemical imaging system’s ability to distinguish two spectrally different samples at a specific SNR. We seek to provide an analytical relation that explicitly captures the impact of spectral dependence on the spatial sensitivity to infer a resolution limit. One advantage of this treatment is that the idea of resolution can be generalized beyond the model of separating two-point sources by invoking the information capacity of the optical system.²⁰ Finally, we seek to provide an analysis of current performance limits and propose new benchmarks for future developments that are experimentally relevant. We do note that there are configurations using optical and physical detection mechanisms in which the IR wavelength is not the primary determinant of image quality; we do not discuss those systems and point the reader to theoretical analysis on performance of such systems.^34,35 However, the overall concept of understanding resolution limits in terms of the IR wavelength and SNR targeted here will also help understand performance of these other configurations.

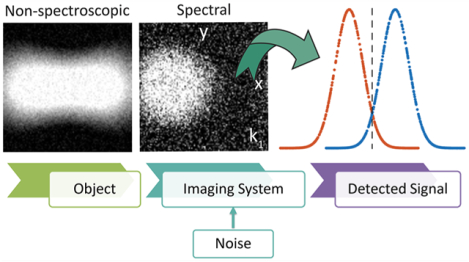
Inspired by the classical resolution limit and decisiontheoretic analysis for nonspectral optical imaging systems,³⁶ we consider two deterministic objects to be imaged by a spectral imaging system. Given two-point objects with absorption spectra ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ that are separated by spatial distance $d$, we establish this problem in terms of total information content that can be precisely retrieved by the detector (Figure 1). The imaging data are assumed to be sampled on a $m\times m\times n$ grid at coordinates ${\mathbf{r}}_i=\left(x_i,y_i\right),i\in \left[1,m^2\right]$ at the detector plane with a magnification of unity and at spectral bands $k_j,j\in [1,n]$.

Figure 1.

Schematic of a chemical imaging system. Two spectrally distinct samples, $S_1$ and $S_2$, that are separated by distance $d$ are imaged. The signal D detected by the detector is mapped on a $m\times m\times n$ grid.

Absorption by point scatterers is manifest in the point spread function (PSF) of the optical system convolved with the incident illumination intensity, scaled by the spectral response. In the paraxial limit for a circular aperture and in the absence of noise, the recorded data are $\mathbf{D}\left({\mathbf{r}}_i,k_j\right)=\mathbf{A}\left({\mathbf{r}}_i,k_j\right)+ϵ$, where $ϵ=𝒩\left(0,{\sigma }^2{\mathbf{I}}_{m\times m\times n}\right)$ is approximated by Gaussian-distributed random variable with standard deviation $\sigma$. The mathematical model is considerably simplified by assuming that each element of $ϵ,{ϵ}_{ij}$, is statistically independent and identically distributed. Physically, the recorded data, D, would have nonlinear contributions from multiple scattering effects and interactions arising from the incident and scattered fields. However, these effects can be neglected as a first approximation for the low-contrast point emitters in consideration^30–32 and for signals dominated by absorption. The problem of reproducing the original object from a noisy image can be modeled by using a decision-theoretic approach^{19,20,24–27} wherein the task can be formulated as deciding between two mutually exclusive and exhaustive hypotheses, ${\mathscr{H}}_1$ and ${\mathscr{H}}_2$, that relate to the presence of two different objects. Here, we formulate the problem comprising of two samples, $S_1$ and $S_2$. The null hypothesis, ${\mathscr{H}}_1$, is that $S_1$ is present, and the alternative hypothesis, ${\mathscr{H}}_2$, is that $S_2$ is present.

The conditional probability distribution functions for the recorded data, $\mathbf{D}$, can be analytically described in terms of the likelihood of these hypotheses as

$$ℒ\left({\mathscr{H}}_1\right)=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{n/2}}\prod _{j=1}^n \text{exp}\left\{-\frac{{∥D\left({\mathbf{\text{r}}}_i,k_j\right)-A_1\left({\mathbf{\text{r}}}_i,k_j\right)∥}^2}{2{\sigma }^2}\right\}$$ (1)

where $ℒ\left({\mathscr{H}}_1\right)$ is the likelihood that the set of readings $\mathbf{D}$ is due to the presence of $S_1$. Alternatively, the likelihood that the set of images is due to $S_2$ is

$$ℒ\left({\mathscr{H}}_2\right)=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{n/2}}\prod _{j=1}^n \text{exp}\left\{-\frac{{∥D\left({\mathbf{\text{r}}}_i,k_j\right)-A_2\left({\mathbf{\text{r}}}_i,k_j\right)∥}^2}{2{\sigma }^2}\right\}$$ (2)

In the spatial domain, Harris³⁶ showed that the Bayes decision favoring either of the two hypotheses can be described by a decision function under these conditions. In the spectral domain, without regard to the specific structure of the data or any prior knowledge, we can sum over the entire spectral range to obtain the decision function. In terms of a log likelihood ratio $\left(\psi \right)$, the decision function is described by

$$\psi =\frac{2{\sigma }^2}{1}\text{log}\left(\frac{ℒ\left({\mathscr{H}}_1\right)}{ℒ\left({\mathscr{H}}_2\right)}\right)=\sum _{j=1}^n{\left(D\left({\mathbf{\text{r}}}_i,k_j\right)-A_2\left({\mathbf{\text{r}}}_i,k_j\right)\right)}^2-{\left(D\left({\mathbf{\text{r}}}_i,k_j\right)-A_1\left({\mathbf{\text{r}}}_i,k_j\right)\right)}^2$$ (3)

Note that taking a logarithm or applying any other monotonically increasing function does not change the statistical formulation of the decision. Thus, if $\psi >0$, then the first hypothesis ${\mathscr{H}}_1$ is more likely, and if $\psi <0$, then the alternate hypothesis ${\mathscr{H}}_2$ is more likely. Stating this problem as a binary hypothesis test allows us to formulate the object recognition at each pixel, ${\mathbf{r}}_i$ as

$$\begin{gathered} {\mathscr{H}}_1:\mathbf{\text{D}}={\mathbf{\text{A}}}_1+ϵ:\psi >0 \\ {\mathscr{H}}_2:\mathbf{\text{D}}={\mathbf{\text{A}}}_2+ϵ:\psi <0 \end{gathered}$$ (4)

Now, the next step is to calculate the probability that the application of the decision function, $\psi$, described above will result in an incorrect or a correct decision. Note that due to noise, the decision function, $\psi$, is randomly distributed with mean $\mu ={{∥{\mathbf{A}}_2-{\mathbf{A}}_1∥}_2}^2$ and variance ${{\sigma }_0}^2=4{\sigma }^2{{∥{\mathbf{A}}_2-{\mathbf{A}}_1∥}_2}^2$. A major consequence of this formulation is the elegant result that $\psi ~𝒩\left(\mu ,{\sigma }^2\right)$, and this distribution is the only information required to make the optimal decision. For a special case of nonimaging spectrometer, let $\Delta$ denote the normalized quadratic spectral distance³⁶ given by $\Delta ={∥{\mathbf{A}}_2-{\mathbf{A}}_1∥}_2^2$.

Figure 2 (A) shows ${\text{S}}_1$ and ${\text{S}}_2$ and their Euclidean distance for each combination of object pair and measurement system. The columns correspond to point sources with spectrally distinct sources. Inset rows in the object’s column show $x-y$ projections and $y-k$ slices of $S_1$ and $S_2$ for each type of sample. The quadratic spectral distance calculated at 1730 cm⁻¹ by using a representative hyperspectral imaging case is shown. The corresponding spectral band is marked on the $y-k$ projection.

Figure 2.

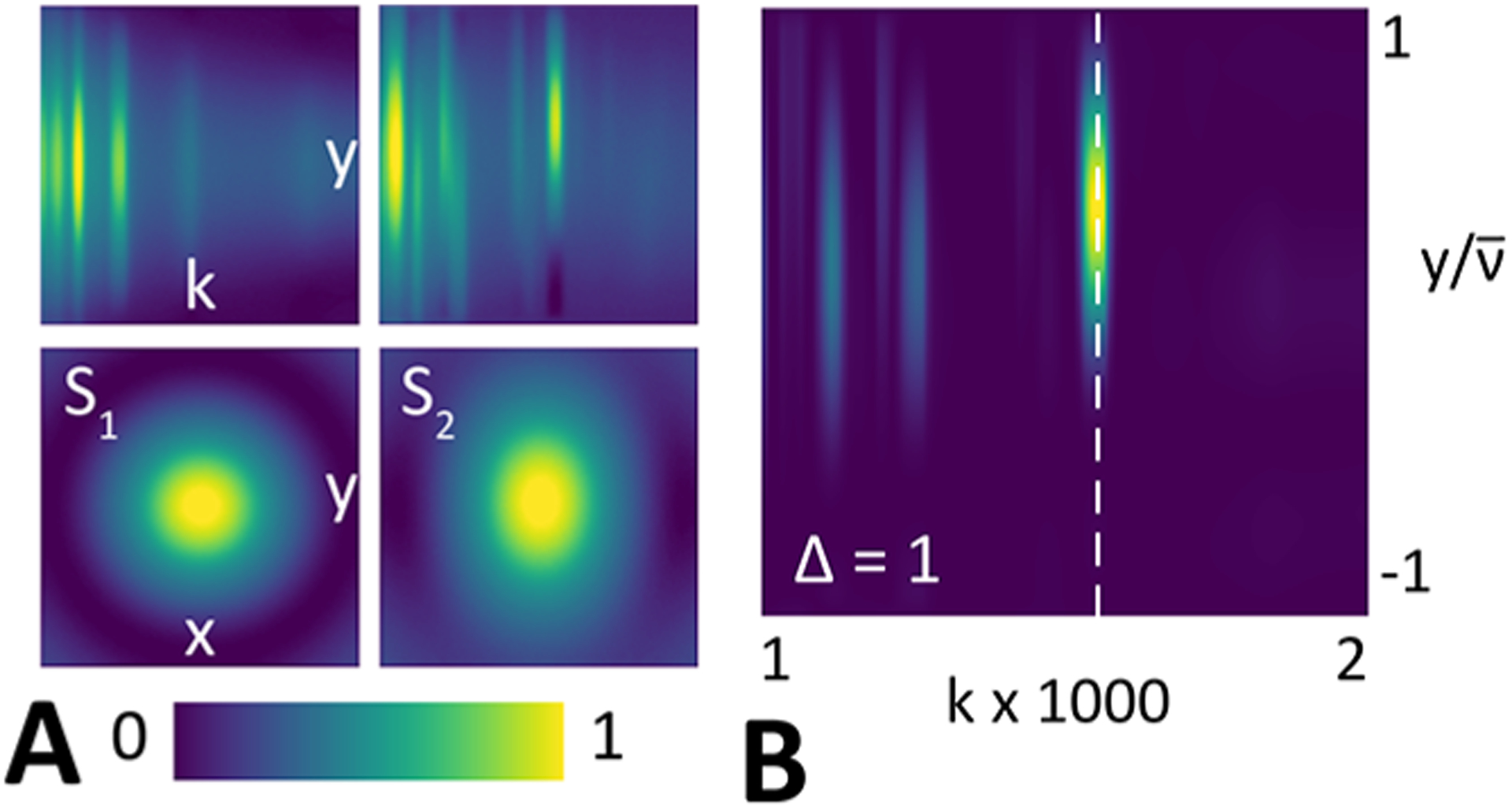
(A) Images show the signals produced by the objects, $S_1$ and $S_2$, and their corresponding $x-y$ projections. (B) Spectral distance at high-contrast spectral band, 1730 cm ⁻¹, for hyperspectral imaging for PEG and PMMA with standard coherent illumination.

The spectral difference, as quantified by the Euclidean distance between $S_1$ and $S_2$, is mathematically indistinguishable from a spatial separation. This property is the key difference between resolution considerations in chemical imaging and optical microscopy and motivates the approach here as computational spectral distinction is the very basis (contrast) in IR image formation. Assuming equal priors, the chance of making an incorrect decision if ${\mathscr{H}}_1$ is true $(\psi <0)$ gives the probability of error as

$$P_{\text{err}}=Q\left(\frac{\mu }{2{\sigma }_0}\right)=\frac{1}{2}\text{erfc}\left(\frac{\Delta }{4\sigma }\right)$$ (5)

where erfc is the complementary error function. It depends on the native properties of the materials (Euclidean spectral distance), spatial distance, and the characteristic of the measurement (noise). As the emitters become spectrally distinct, the quadratic spectral distance, $\Delta$, between $S_1$ and ${\text{S}}_2$ increases, and the probability of error reduces. Likewise, the probability of error increases as the variance in measurement (noise) increases. The relationship also implies that collocated scatterers with identical spectra cannot be distinguished, i.e., $P_{\text{err}}\to 0.5$.

RESULTS AND DISCUSSION

Now, we cast the problem in the decision-theoretic domain such that for chemical imaging a minimum separation distance can then be interpreted as the resolution limit $(\hat{d}/\lambda )$. We use the quadratic spectral separation, $\Delta$, between $S_1$ and $S_2$ in the formulation of spatial resolution. The object information contained in the acquired far-field intensity image at the detector is encompassed by the PSF and can be expressed in terms of the Fisher information, $ℐ\left(\hat{d}\right)$, where $\hat{d}$ is the estimate of $d$. Because image acquisition is typically a Gaussian-noise dominated process, the Fisher matrix^37,38 can be formulated as follows:

$$ℐ\left(\widehat{d}\right)=\beta {\left(k_j\text{NA}\right)}^{2}f\left(d\right)$$ (6)

where $\beta$ is the normalization constant, NA is the numerical aperture of the imaging objective lens, $J_{\alpha }$ is the Bessel function of order $\alpha$, and $f\left(d\right)=\int \frac{1}{{\sigma }^2}\left(\frac{J_1{J}_2}{{r_1}^3}{\text{e}}^{-{\mathbf{A}}_1}+\frac{J_1{J}_2}{{r_2}^3}{\text{e}}^{-{\mathbf{A}}_2}\right)\text{d}{x}_i\text{d}{y}_i$, with $r_{1/2}^2={\left(x_i\pm \frac{d}{2}\right)}^2+y_i^2$. The problem of minimizing the distinguishable distance, i.e., spatial resolution limit for the imaging system, is equivalent to maximizing the Fisher information, which is an analytical formulation of the sensitivity in PSF to the spatial separation. The measurement D is constrained by the maximum signal power and the uncertainty in the Euclidean distance, $\mathbb{E}\left[{\mathbf{D}}^2\right]\le I_0\left(1+4{\Delta }^2\right)+{\sigma }^2$

$$ℐ\left(\widehat{d}\right)\ge {\text{log}}_2\left(\frac{I_0+{\sigma }^2+4{\Delta }^2{I}_0}{{\sigma }^2}\right)$$ (7)

Using a decision-theoretic approach, we can formulate the variance in the estimate of the variable $d$ in terms of spectral distance, $\Delta$, as

$$\mathbb{E}\left[(d-\hat{d}{)}^2\right]\ge \frac{1}{{\text{log}}_2\sqrt{1+\text{SNR}\left(1+4{\Delta }^2\right)}}$$ (8)

Combining (6) and (8) and using the Cramer-Rao inequality, the minimum spatial separation is then bounded by the inverse of the Fisher information. Parametrically, the lower bound is achieved for the unbiased estimator of $d$ given by $\hat{d}$

$$\widehat{d}=\frac{\lambda }{\text{NA}}\frac{1}{{\text{log}}_2\sqrt{1+\text{SNR}\left(1+4{\Delta }^2\right)}}$$ (9)

where $\lambda$ is the wavelength, the signal-to-noise ratio ${\left(\text{SNR}\right)=I}_0/{\sigma }^2$, and NA is the numerical aperture of the system.

Notably, the form of this equation is similar to common expressions of spatial resolution limits in optical microscopy. The practical significance of eq 9 can be seen in comparing simulations of hyperspectral and spectrally insensitive imaging. Figure 3A shows the predicted minimum resolvable distance, $\hat{d}/\lambda$, as a function of SNR for two different configurations, and for a NA of 0.4 and 0.9 for each of the two cases. We note a reduction in $\hat{d}/\lambda$ by including spectral contrast. Here, we use $\Delta =1$ and a SNR of 1–10⁴ as typical values that represent the absorbance range and ratios of absorbance to baseline noise, respectively.³ As expected, we observe an improvement in achievable resolution using a higher NA lens and the addition of spectral contrast providing information that increases the ability to distinguish between objects. Notably, spectral data can provide advantages in maximizing resolution, especially at low SNR. Next, we examine the joint dependence of $\hat{d}/\lambda$ on $\Delta$ and SNR in Figure 3B. For our specific case of imaging spectrally distinct point scatterers, the formalism predicts diffraction-limited performance $(\hat{d}/\lambda =0.61)$ for SNR values as low as 10. Our approach specifically deals with chemical imaging systems with no specialized illumination or postprocessing, where spatial localization is improved by using spectral content. Our predictions broadly support previous experimental and theoretical derivations of optimal pixel size and indicate a likely limit of $\hat{d}/\lambda ~0.10$ for most practical SNR values. Finally, we provide a direct analytical formulation that relates the resolution and the SNR required to achieve the enhanced image.

Figure 3.

(A) Minimum resolvable distance, $\widehat{d}$$/\lambda$, is compared for a hyperspectral and a nonspectroscopic optical imaging system as a function of SNR and NA. The classical diffraction-limited resolution is shown as a dashed line. (B) Contour plot showing the variation of the minimum resolvable distance, $\hat{d}/\lambda$, as a function of $\Delta$ and SNR, with the isoline indicating the Rayleigh limit for optical microscopy (red).

The resolution limit formulation in (9) also provides a convenient means to visualize the trade-off between spatial and spectral content as well as the influence of noise, as shown in Figure 4 by signal distributions in wavelength normalized space for imaging systems with an illustrative NA of 0.4. Figure 4A shows the limiting case that corresponds to spectrally insensitive imaging (i.e., the common optical microscopy case, where $\Delta =0$). Along each column, we show representative simulations for increasing variance (namely, ${\sigma }^2=0.001-10)$ that correspond to a SNR of 1000 to 0.1. The predicted limits of spatial separation $\hat{d}/\lambda$ increases as a function of higher noise (lower SNR), as expected. For each noise magnitude, the corresponding signals for spectrally distinct points are shown across the row. Comparing the effects of spectral content shows that a spectroscopic imaging system $(\Delta \ne 0)$ can achieve the same spatial resolution limits at much higher noise levels than a spectrally insensitive imaging system $(\Delta =0)$. Specifically, for $\Delta =0.5,{\sigma }^2$ can be up to 2 times higher or for $\Delta =1,{\sigma }^2$ can be up to 5 times higher to achieve the same performance. Thus, spectral separation not only enables a higher perceived system resolution limit but also emphasizes the critical role played by the noise levels. It must be noted that the higher SNR in spectral systems usually requires a much greater cost (larger time for acquisition, more complicated hardware, and needs for handling data), emphasizing that achieving spectral enhancement of limits is not without effort. Finally, with a higher NA, a better resolution limit is expected for each case that scales linearly with 1/NA. The approach uses the Cramer—Rao lower bound, which is a weak lower bound, and alternative approaches can establish a tighter bound. Alternately, improved estimates of images may be obtained by using sparse image retrieval and restoration algorithms such as ref 39 or deep learning methods.⁴⁰ These approaches can indeed provide images with sharper detail, but we emphasize that such reconstructions are still limited in their uncertainty by the SNR of the recorded data. The goal of this report is not to discuss the impacts of these computational super-resolution techniques but to provide a rigorous analytical formulation for the resolution limit in chemical imaging, on which further computational enhancements can be made and one that serves as a baseline performance to evaluate such efforts.

Figure 4.

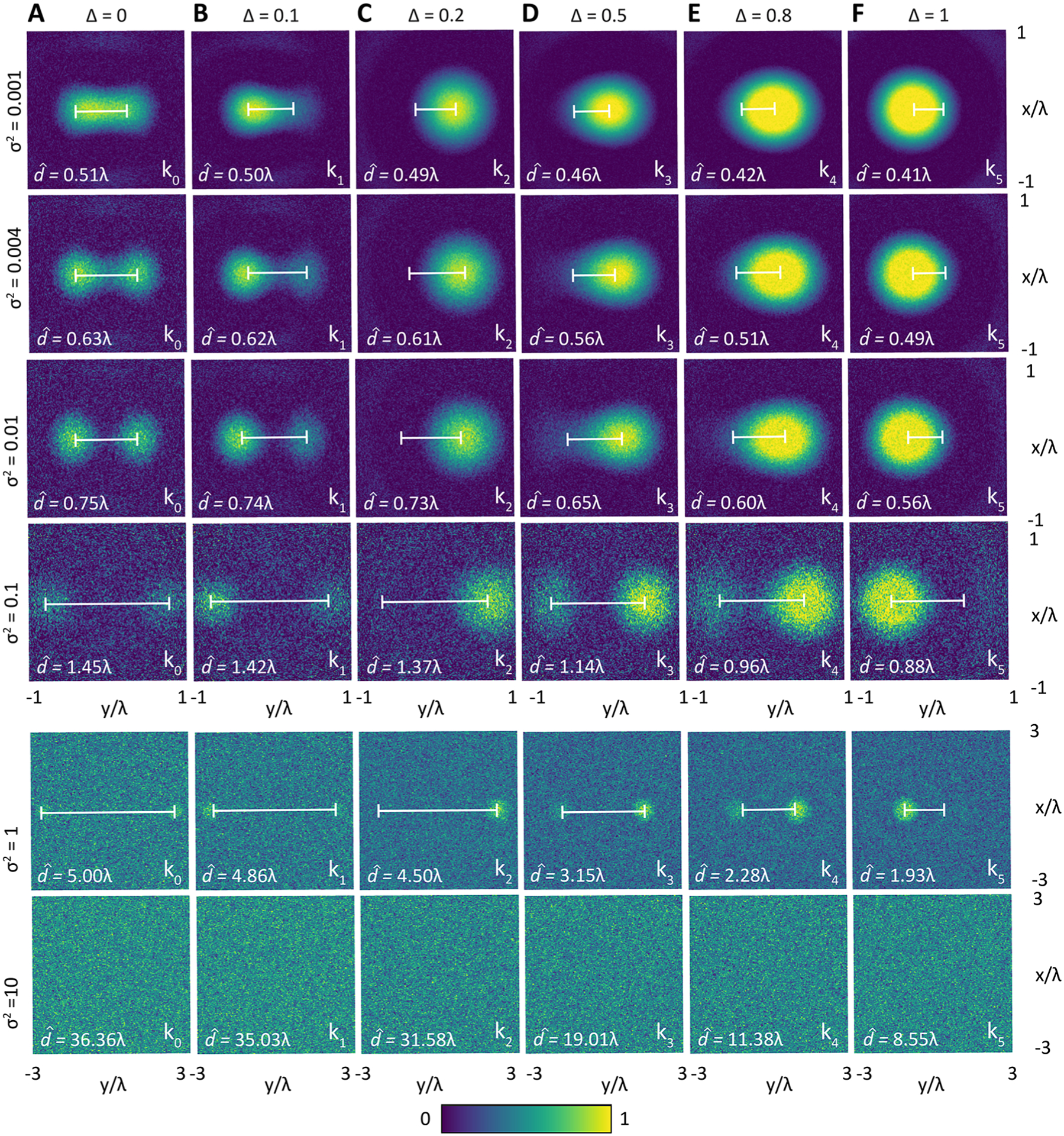
Simulation of the spatial $(x-y)$ signal distributions produced by the objects, $S_1$ and $S_2$, for different spectral separations: (A) $\Delta =0$ corresponding to optical imaging and (B–F) corresponding to spectral imaging cases. The spectral bands are respectively 1450, 1440, 1010, 1110, 1020, and 1730 cm⁻¹. The noise is simulated for levels indicated to the left of each row.

This study generalizes ideas from optics to chemical imaging microscopes and can be extended to other emerging techniques as well as modalities with different mechanisms of chemical contrast. One exciting new area is the combination of infrared and optical frequencies to record data by using the photothermal effect,^41–49 for example. The probing wavelength in these cases is much shorter (typically, visible), which facilitates submicrometer optical resolution but does not yet provide the SNR of all-IR laser scanning microscopy.¹⁵ Thus, the optical configuration and measurement quality both become important to understand limits of performance. Although we focus on use of a single IR wavelength for imaging throughout the optical train for simplicity, the formalism developed here can also be modified to suit these emerging modalities. The analytical framework can also be extended to other techniques, including second-order nonlinear spectroscopies such as sum frequency generation (SFG)^50–53 or second-harmonic generation (SHG) microscopy,^54,55 with an additional constraint on signal localization arising from the signal origin being from the interfaces.⁵⁶

For SNR values that have recently become practical, a hyperspectral configuration is shown to have improved resolving power compared to a nonspectroscopic design. Thus, having a good estimate of the system transfer function, and a sufficient SNR, it is possible to resolve the objects beyond the classical nonspectral resolution limit. This finding should spur further investigations into methods to practically realize these advantages of IR imaging. Similar to other superresolution modalities and attempts to increase the resolution by means of apodization or by inverse filtering and extrapolation, we emphasize that spectroscopic microscopy does not surpass the diffraction limit. It enables users to identify essential information about the probed sample by acquiring spectral data that yields more information than microscopic or spectroscopic measurements alone. Combined with prior information, the spectral dimension can thus be considered to encode information about the spatial dimensions. The provided analysis should allow an understanding of this linkage and spur further investigations into the capabilities of chemical imaging systems.

CONCLUSIONS

Chemical imaging measurements enable both a molecular and an optical probing the sample, thus yielding more information than optical microscopic or spectroscopic measurements alone. Combined with prior sample information, the relationship between the spectral and spatial dimensions can be formulated as a unified set of information that jointly determines the limits of performance. Here, we have formulated the joint influence to test the evidence for one of the two hypotheses that rigorously evaluates spatial separation between two-point emitters. We provide a quantitative measure of the likelihood of accurately identifying two objects in chemical imaging that depends on the Euclidean spectral—spatial distance in the sample as well as the noise in the imaging system. This results in a standard decision-theoretic treatment of resolution that is influenced explicitly by both optical and spectroscopic quality. The work should enable a better understanding of the spatial resolution of molecular composition using concepts that are traditionally applied to optical microscopy, especially as we formulate the expression for chemical imaging in the same form as the more commonly understood spatial resolution limits for morphological optical imaging.