基于影像组学的logistic回归模型预测胶质瘤分级

Abstract

目的

胶质瘤是最常见的颅内原发中枢神经系统肿瘤，胶质瘤的分级对临床治疗及随访方案的选择、预后的评估有重要指导意义。本研究目的在于探讨基于影像组学的logistic回归模型预测胶质瘤病理分级的可行性。

方法

回顾性收集2012年1月至2018年12月经手术病理切片证实为胶质瘤的146例患者。手动分割患者增强T₁加权成像(contrast-enhanced T₁-weighted imaging，T₁WI+C)图像中的胶质瘤区域，形成3D感兴趣区(region of interest，ROI)；提取41个影像特征；采用最小绝对收缩和选择运算(least absolute shrinkage and selection operator，LASSO)二元logistic回归法筛选与胶质瘤病理分级最相关的特征并计算影像组学得分(radiomics score，Rad-score)；采用单因素logistic回归建模方法建立预测模型；用受试者操作特征(receiver operating characteristic，ROC)曲线评估模型的区分能力，评估指标为曲线下面积(area under the curve，AUC)。利用Hosmer-Lemeshow检验衡量模型预测的准确性。

结果

筛选出5个与胶质瘤病理分级最相关的特征，用这5个特征构建的预测胶质瘤病理分级的logistic回归模型的ROC曲线AUC为0.919，具有很好的区分能力，其校准曲线经Hosmer-Lemeshow检验，与理想曲线的差异无统计学意义(P=0.808)，预测准确性高。

结论

基于影像组学的logistic回归模型可以有效地对胶质瘤病理分级进行预测，有望成为术前预测胶质瘤分级的辅助方法。

胶质瘤是最常见的颅内原发中枢神经系统肿瘤，发病率(4.67~5.73)/100 000^[1]。根据2016版WHO中枢神经系统肿瘤分类^[2]，胶质瘤包括星形细胞瘤、少突胶质细胞瘤、室管膜瘤、混合性神经元-神经胶质肿瘤及其他来源胶质瘤。根据病理组织学，胶质瘤分为I~IV级，其中I~II级为低级别，III~IV级为高级别，胶质瘤的分级对临床治疗及随访方案的选择、患者的预后有重要指导意义^[2-4]。目前胶质瘤的分级主要还是依靠活检或手术后的病理诊断，病理诊断虽是分级的金标准，但有创、耗时长等缺点限制了其应用。在常规影像学图像中有很多潜在的信息无法被人眼发现，导致其在胶质瘤精准分级方面的应用仍面临巨大挑战。随着人工智能及精准医疗的飞速发展，影像组学已成为临床研究的热点。影像组学通过挖掘数据提取疾病影像数据中所包含的定量特征，进而找出疾病的影像标志物或预测疾病分类、分级，具有无创、经济、高效和可重复的优点，有助于临床决策。基于此，近年来研究者们利用影像组学数据对胶质瘤进行分级取得了较好的效果，但使用何种影像序列及何种模型效果最好尚有待探索^[5-11]。本研究采用手动方式分割患者增强T₁加权成像(contrast-enhanced T₁-weighted imaging，T₁WI+C)图像中的胶质瘤区域，并进一步提取影像特征，通过筛选特征并构建logistic回归模型在术前对高、低级别胶质瘤进行分级，以期满足临床上胶质瘤的术前精准预测及个性化治疗的需求。

1. 对象与方法

1.1. 对象

回顾性收集中南大学湘雅医院2012年1月至2018年12月经手术病理证实的胶质瘤患者。纳入标准：1)术前在同一台机器采集MRI数据；2)扫描MRI前未接受穿刺、放射治疗和化学治疗；3)术后病理学诊断具有精确分级。排除标准：1)MRI数据伪影大；2)合并其他严重的神经系统疾病。

1.2. MRI扫描方法

采用GE Signa HDx 3.0T磁共振成像仪及8通道头部相控阵线圈采集患者的颅脑MRI平扫+增强数据，并在线圈的内部填充适量的MRI兼容的泡沫以固定被试头部，减少扫描过程中的头动伪影。1)轴位T₂加权成像(T₂-weighted imaging，T₂WI)序列参数：重复时间(time of repetition，TR)=4 480 ms，回波时间(time of echo，TE)=120 ms，层厚=5 mm，层间距=1.5 mm，层数=20，视野(field of view，FOV)=240 mm×240 mm，矩阵=320×288。2)轴位T₂液体衰减反转恢复成像(T₂-fluid attenuated inversion recovery，T₂FLAIR)序列参数：TR=8 500 ms，TE=168 ms，矩阵=320×256，层厚、层间距、层数及FOV与T₂WI一致。3)轴位T₁加权成像(T₁-weighted imaging，T₁WI)序列参数：TR=2 000 ms，TE=24 ms，矩阵=320×224，FOV、层厚、层间距、层数与T₂WI一致。4)轴位增强T₁加权成像(contrast enhancement T₁-weighted imaging，T₁WI+C)序列参数：TR=1 725 ms，TE= 24 ms，矩阵=320×256，层厚、层间距、层数及FOV与T₂WI一致。

1.3. 图像分析

1.3.1. 图像和病灶感兴趣区的获取

图像来自中南大学湘雅医院放射科影像归档和通信系统(picture archiving and communication systems，PACS)。基于MATLAB的图形用户界面(graphic user interface，GUI)获取病灶感兴趣区(region of interest，ROI)。首先由2名具有3年以上工作经验的影像医师独立手动分割每例患者T₁WI+C图像中的胶质瘤区域，形成3D ROI图像；然后交由1位高级职称影像医师进行审核，当审核者认为ROI绘制错误或者差异过大时，则返回上一步骤进行修改；最终使用的ROI为2名医师各自勾画ROI的重叠区域。胶质瘤区域的分割标准基于轴位T₁WI+C图像中的肿瘤实性区域，包括肿瘤异质性导致的无强化区，排除内部明显的坏死、囊变区域。对于部分无对比增强或强化不明显的低级别胶质瘤，肿瘤分割需要同时参考轴位T₂WI及T₂FLAIR序列。

1.3.2. 影像特征的提取

根据既往研究^[10]提取41个影像特征。1)3个全局特征：峰度、偏度、方差。2)7个灰度共生矩阵(gray-level co-occurrence matrix，GLCM)特征：对比度、相关性、能量、熵、均数和、同质性、方差。3)13个灰度游程矩阵(gray-level run-length matrix，GLRLM)特征：长程强调度、短程强调度、游程非一致性、游程方差、游程百分比、灰度非一致性、灰度方差、高灰度游程强调度、低灰度游程强调度、长程低灰度强调度、短程低灰度强调度、长程高灰度强调度、短程高灰度强调度。4)13个灰度区域大小矩阵(gray-level size zone matrix，GLSZM)特征：高灰度区域强调度、低灰度区域强调度、区域百分比、区域大小非一致性、区域方差、灰度非一致性、灰度方差、大区域高灰度强调度、小区域高灰度强调度、大区域低灰度强调度、小区域低灰度强调度、大区域强调度、小区域强调度。5)5个邻域灰度差矩阵(neighborhood gray-tone difference matrix，NGTDM)特征：繁度、糙度、复杂度、对比度、劲度。与既往研究^[10]不同的是，这41个影像特征均基于3D图像进行计算。本研究建立logistic回归模型的最终目的是预测胶质瘤样本的病理分级，而单一的样本数据无法进行类似群体数据的归一化处理，故在本研究中，影像特征均使用其原始值，不进行归一化处理。

1.3.3. 影像特征的筛选

上述41个影像特征对于胶质瘤的病理分级并非都有用，其中包含一些冗余的特征，而选取特征过多会增加过拟合的风险，因此降低影像特征的维度以选择与肿瘤级别高度相关的指标是非常必要的^[12]。本研究采用最小绝对收缩和选择运算(least absolute shrinkage and selection operator，LASSO)二元logistic回归法筛选变量，该方法通过在回归方程中引入1个惩罚系数λ，对冗余变量进行“惩罚”，即将其系数逐步压缩至0，可以有效地筛选出与结局最相关的变量，降低自变量维度，从而避免过拟合的风险^[13]。

1.4. 模型的建立

采用单因素logistic回归建模方法建立预测模型。首先，将筛选得到的影像特征的权重加和，得到总体的影像组学得分(radiomics score，Rad-score)；然后，用Rad-score与胶质瘤的病理分级进行单因素logistic回归分析，得到拟合后的logistic回归方程，建立模型。该模型计算出样本为高级别胶质瘤的概率，并根据约登指数最大原则划定预测概率阈值，大于阈值的为高级别胶质瘤，小于阈值的为低级别胶质瘤^[14]。

1.5. 统计学处理

采用MATLAB中的统计工具包进行统计学分析。分别使用两样本t检验、卡方检验分析高级别胶质瘤组与低级别胶质瘤组年龄、性别构成差异是否有统计学意义。采用组间相关系数(inter-class correlation coefficient，ICC)评估2名医师独立获取的肿瘤ROI影像特征的一致性，ICC>0.75被认为一致性良好^[15]。用受试者操作特征(receiver operating characteristic，ROC)曲线评估模型的区分能力，评估指标为曲线下面积(area under the curve，AUC)。利用Hosmer-Lemeshow检验来判断校准曲线与理想曲线是否存在差异，继而衡量模型预测的准确性^[16-17]。P<0.05为差异有统计学意义。

2. 结 果

2.1. 一般资料

共纳入胶质瘤患者146例，其中高级别胶质瘤患者(高级别组)70例，低级别胶质瘤患者(低级别组)76例。高级别组与低级别组在年龄、性别构成上的差异无统计学意义(均P>0.05，表1)。

表1.

低级别胶质瘤与高级别胶质瘤患者的基本情况比较

Table1 Comparison of basic conditions between high-grade glioma and low-grade glioma

组别	n	男/女	年龄/岁
总体	146	59/87	19.7~73.3(47.6±11.9)
高级别组	70	29/41	20.5~70.2(50.3±12.7)
低级别组	76	30/46	19.7~73.3(44.2±11.3)

2.2. 一致性检验结果

2名影像医师提取的ROI影像特征ICC为0.893~0.967，提示2名医师提取ROI具有较高的组间一致性。

2.3. 特征筛选结果

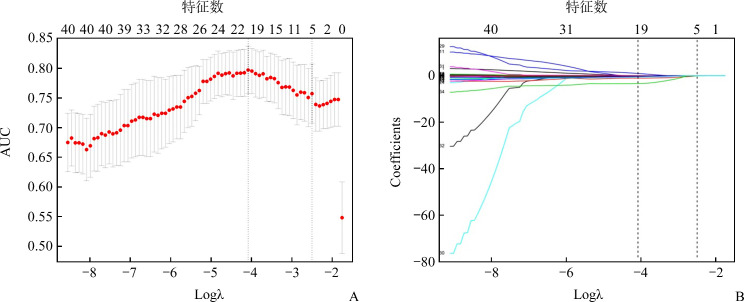
在图1A中，横坐标表示惩罚系数λ的对数(logλ)，纵坐标表示模型的AUC，曲线上方的数字表示模型中剩余的特征数量，可见随着惩罚系数λ逐渐变大，特征数量逐步减少。左侧虚线表示AUC最大时对应的λ值和筛选到的特征数量，右侧虚线表示在最大AUC的基础上增加1倍标准误时模型中剩余特征的数量进一步减少。选用1倍标准误时对应的参数可以在简化模型的同时保证一定的准确率，提高模型的效能^[16]。

图1.

LASSO回归变量筛选图

Figure 1 Feature selection using LASSO

A: Variation of AUC. The horizontal axis shows logλ and the vertical axis shows the AUC. The numbers above the curve represent the number of feature of nonzero coefficient. The left dotted line represents the feature number corresponding to the maximum AUC, while the right dotted line represents that corresponding to 1 standard error of AUC. B: The shrinkage plot of coefficients. The horizontal axis shows logλ and the vertical axis shows coefficient. The numbers above the curve represent the number of features with nonzero coefficient.

在图1B中，横坐标表示惩罚系数λ的对数(logλ)，纵坐标表示模型中特征的系数，曲线上方的数字表示模型中系数不为0的特征的数量。随着λ逐渐变大，越来越多的特征系数被压缩为0，在1倍标准误时(右侧虚线处)只剩余5个非0特征。因此，通过LASSO二元logistic回归法共筛选得到5个最相关的影像特征(表2)。最终Rad-score的计算便是将这5个影像特征的值与其系数(权重)的乘积相加。

表2.

LASSO二元logistic回归法筛选得到的影像特征

Table 2 Radiomics features selected by LASSO binary logistic regression

类别	中文名称	英文名称	英文缩写	系数
灰度共生矩阵	均数和	sum average	SA	0.048
	方差	variance		0.009
灰度游程矩阵	灰度非一致性	gray-level non-uniformity	GLN	-0.015
灰度区域大小矩阵	区域大小非一致性	zone-size non-uniformity	ZSN	-0.092
邻域灰度差矩阵	对比度	contrast		0.116

2.4. Logistic回归模型

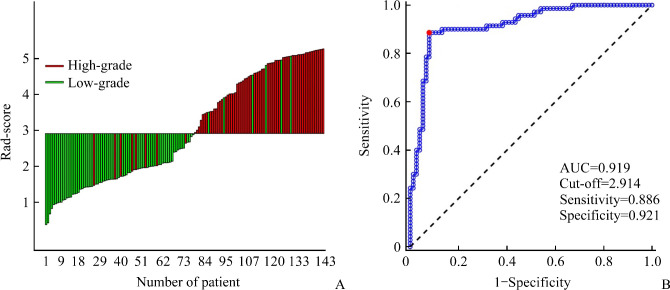
146例胶质瘤患者的Rad-score瀑布图见图2A：红色为高级别胶质瘤，绿色为低级别胶质瘤，每根柱子所对应高度的纵坐标值即为相应患者的Rad-score。根据ROC曲线(图2B)，算得截断值为2.914，AUC值为0.919，敏感度为0.886，特异度为0.921。用Rad-score进行单因素logistic回归建模，以胶质瘤级别为结局变量(高级别为1，低级别为0)，算得Rad-score回归系数为1.584(P<0.0001)，表明Rad-score与胶质瘤级别显著相关。其最终的logistic回归方程为：

图2.

Rad-score瀑布图及ROC曲线

Figure 2 Waterfall plot and ROC curve

A: Waterfall plot of Rad-score. The vertical axis shows the value of Rad-score; red bars represent patients with actual high-grade glioma; green bars represent patients with actual low-grade glioma; the transverse line represents the cut-off point in ROC curve. Bars under the transverse line represent the predicted patients with low-grade glioma, bars above the transverse line represent the predicted patients with high-grade glioma. B: ROC curve of Rad-score. The red point represents the sensitivity and specificity at the cut-off point.

$$P=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{4.780}-\mathrm{1.584}\times \mathrm{R}\mathrm{a}\mathrm{d}-\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e})}$$

其中P表示样本为高级别胶质瘤的概率。

2.5. 模型校准度评估

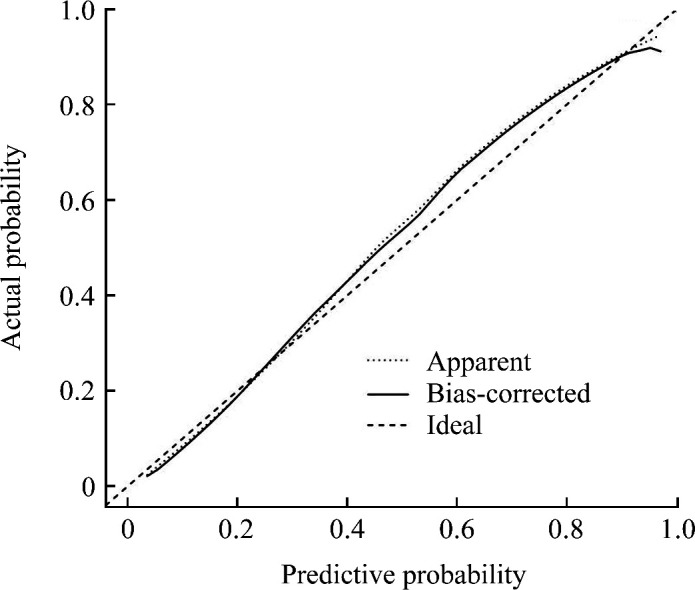
通过建立的模型可计算得到各样本为高级别胶质瘤的概率(预测概率)。为比较预测概率与实际概率是否相符，进一步行预测模型的校准曲线分析^[18]。图3显示该模型的校准曲线，虚线所示的校准线与理想模型的对角线稍有偏差，但接近吻合，Hosmer-Lemeshow检验结果显示差异无统计学意义(P=0.808)。

图3.

预测模型的校准曲线

Figure 3 Calibration curve for the predictive model

The P value of Hosmer-Lemeshow test for calibration is 0.808, showing no significant difference. This result indicates good agreement between the predictive probability and the actual probability.

3. 讨 论

目前，影像组学已成为影像学领域的研究热点之一。相比于医学影像的传统视觉阅片方式，影像组学可通过机器学习的方法深入挖掘医学影像的生物学本质，提取影像图像潜在的定量特征。影像组学是在大数据背景下医学影像、计算机、人工智能等多学科交叉的产物，可为精准医疗、个体化诊疗的实施提供支持。近年来，已尝试将影像组学应用于肿瘤分级、鉴别诊断、预后、疗效检测甚至分子水平诊断^{[9, 19-21]}。本研究采用基于影像组学的logistic回归模型作为分类器，可以有效地对胶质瘤病理分级进行预测，并发掘出基于5个影像组学指标的Rad-score。Rad-score可作为影像学上的标志物，基于影像组学的logistic回归模型预测胶质瘤分级有望成为术前预测胶质瘤分级的辅助方法。

本研究通过Rad-score建立logisitic回归模型并将其应用于胶质瘤分级的预测，结果表明该模型可以准确地对胶质瘤的高、低级别进行二分类判别。关于影像组学研究采用哪些序列图像建模更有效，目前尚未达成一致意见。Tian等^[5]采集153例胶质瘤患者(低级别胶质瘤42例，高级别胶质瘤111例)的术前多模态MRI(包括T₁WI、T₂WI、T₁WI+C、多b值弥散加权成像、三维动脉自旋标记灌注加权像)进行影像组学分析，预测胶质瘤病理分级，结果表明：单序列中T₁WI+C序列纹理特征效能最高，全部模态组合的预测效能高于单序列，结构模态组合(T₁WI、T₂WI、T₁WI+C)、扩散模态(多b值弥散加权成像)的预测效能均高于灌注模态(三位动脉自旋标记灌注加权像)，但是该研究存在样本量不均衡的局限性。邓慧媛等^[8]利用logistic多因素回归分析发现：从弥散加权成像(diffusion-weighted imaging，DWI)序列提取的特征Percentile-75对高、低级别胶质瘤的诊断效能最高(AUC=0.7930)，而该研究在T₂WI序列及T₁WI+C序列中未筛选出与肿瘤分级相关的特征。本研究采用T₁WI+C序列中影像组学信息，通过LASSO二元logistic回归法筛选与胶质瘤病理分级最相关的特征，对高、低级别胶质瘤进行预测，取得较满意的效果(AUC=0.919)，说明常规MRI图像中也包含有意义的影像组学特征。

ROI分割包括手动分割、半自动分割、自动化分割3种方式。尽管有研究^[22]提出用软件自动分割ROI的算法可减轻人力负担及避免主观因素的影响；但是在病理状态下，胶质瘤的影像学表现差异较大，由高水平的影像医师进行手动分割仍是目前研究的主流^[5]。本研究采用2名影像医师各自独立勾画病灶的ROI，再由另一名高年资上级医师审核，这种肿瘤ROI分割方法耗时相对较长，但是结果更准确，也更便于理解。

与既往研究仅关注一个或一类纹理特征分析不同，本研究基于胶质瘤患者术前T₁WI+C影像图像，通过手工分割病灶，提取146例患者的41个影像特征，通过LASSO二元logistic回归法筛选特征，旨在构建更简洁且更具诊断价值的综合影像特征。LASSO二元logistic回归法是目前在数据挖掘与建模分析中应用较广的一种变量降维方法^[23-24]。本研究采用LASSO二元logistic回归法筛选出5个特征，这5个特征与我们之前研究^[10]中人工神经网络的最终输入特征一致。在之前的人工神经网络研究中，我们用两样本t检验筛选出7个特征，将这7个特征逐一加入模型，发现仅使用前5个特征便能使模型的准确率达到平台水平。显然本研究用LASSO回归筛选变量效率更高，且能计算出每个变量的系数(即相对权重)，从而进一步构建出一个综合的Rad-score，定量计算样本为高级别胶质瘤的概率。

本研究采用ROC曲线的AUC及校准曲线的P值共同评估模型对高、低级别胶质瘤的分类效能。AUC越接近1，表明分类效能越好^[25-26] 。本研究构建的模型区分高、低级别胶质瘤的AUC为0.919，表明模型对高、低级别胶质瘤具有很好的区分能力；且校准曲线与理想曲线吻合度较好，偏差很小(P=0.808)，说明模型预测的概率与实际情况十分接近。

虽然本研究构建模型的预测效能稍低于人工神经网络模型(AUC=0.9486)^[10]，但是本研究的模型具有以下优势：1)模型基于肿瘤的3D ROI数据更能反映肿瘤的异质性。针对本研究中的数据，3D方式建模的logistic回归模型的AUC明显高于3D方式建模(之前的研究^[10]为2D方式建模)的神经网络模型(0.919 vs 0.6873，P<0.001)。2)Logistic回归模型可以精确地量化预测概率，且结果显示预测概率与实际概率一致性高，这使得logistic回归模型的临床可解释性更强，这一点是神经网络模型无法做到的。3)对于一个模型的评价，光有区分度是不够的，还需要考察其准确度(也就是校准度)。Logistic回归模型很容易做到这一点，但是神经网络模型的结果并非概率值，也无法进行校准曲线分析。因此，我们认为logistic回归模型优于人工神经网络模型。

本研究的局限性在于：1)样本量相对不足，因此无法将病例再分为训练集和验证集来进行外部验证。根据目前较为公认的样本量估计方法^[27]，二分类结局中数量较少组的样本量至少应为进入模型中变量数的10倍，达到15倍以上较为适宜。尽管最终我们的建模变量仅为1个合成后的变量(Rad-score)，但我们在LASSO二分类逻辑回归中筛选到5个变量，因此样本数至少应为100例以上，达到150例可认为LASSO回归结果相对稳定。因此我们现阶段的样本量刚好仅适用于建模，而无法再分出验证集。2)仅依靠影像组学指标建模，未将临床资料纳入建模分析。我们将会深化目前的工作，在后续研究中进一步完善上述不足。

基金资助

国家自然科学基金(81701847)；湖南省自然科学基金(2017JJ3497，2017JJ2387)。

This work was supported by the National Natural Science Foundation (81701847) and the Natural Science Foundation of Hunan Province (2017JJ3497, 2017JJ2387), China.

利益冲突声明

作者声称无任何利益冲突。

原文网址

http://xbyxb.csu.edu.cn/xbwk/fileup/PDF/202104385.pdf