Assessing the impact of areal unit selection and the modifiable areal unit problem on associative statistics between cases of tick-borne disease and entomological indices

Abstract

The modifiable areal unit problem (MAUP) is a cause of statistical and visual bias when aggregating data according to spatial units, particularly when spatial units may be changed arbitrarily. The MAUP is a concern in vector-borne disease research when entomological metrics gathered from point-level sampling data are related to epidemiological data aggregated to administrative units like counties or ZIP Codes. Here, we assess the statistical impact of the MAUP when calculating correlations between randomly aggregated cases of anaplasmosis in New York State during 2017 and a geostatistical layer of an entomological risk index for Anaplasma phagocytophilum in blacklegged ticks (Ixodes scapularis Say, Acari: Ixodidae) collected during the fall of 2017. Correlations were also calculated using various administrative boundaries for comparison. We also demonstrate the impact of the MAUP on data visualization using choropleth maps and offer pycnophylactic interpolation as an alternative. Polygon simulations indicate that increasing the number of polygons decreases correlation coefficients and their variability. Correlation coefficients calculated using ZIP Code tabulation area and Census tract polygons were beyond 4 standard deviations from the mean of the simulated correlation coefficients. These results indicate that using smaller polygons may not best incorporate the geographical context of the tick-borne disease system, despite the tendency of researchers to strive for more granular spatial data and associations.

Introduction

The modifiable areal unit problem (MAUP) is a source of bias that arises when data are aggregated into areal units, whereby changing the boundaries of the areal unit may produce different results in analysis or visualization (Buzzelli 2020). First named in 1979, the MAUP is considered a special case of the ecological fallacy; a problem in statistical inference where relationships estimated from group-level data differ from relationships estimated from individual-level data (Robinson 1950, Openshaw and Taylor 1979, Openshaw 1984, Kousser 2001). The first papers to explore the ecological fallacy give examples that can also be categorized as examples of the MAUP (Gehlke and Biehl 1934, Robinson 1950). Specifically, these papers highlight how correlation coefficients vary when different areal Census units are used for aggregation, however, the potential for bias from the MAUP is not limited to the analysis of Census data. The field of geography and its subdisciplines are generally concerned with the MAUP, including spatial epidemiology (Nakaya 2000, Swift et al. 2014), human geography (Sémécurbe et al. 2016, Nielsen and Hennerdal 2017), physical geography (Dark and Bram 2007), and ecology (Moat et al. 2018, Ju et al. 2021).

The study of tick-borne diseases (TBDs) often falls under the scope of spatial epidemiology, ecology, and/or geography, and may be sensitive to bias from the MAUP (Kitron 1998, Jackson et al. 2006, Eisen et al. 2010, Wilson 2010). Both TBD cases and vector-related data are routinely aggregated to administrative areal units for convenience (Jackson et al. 2006) either for visualization, analysis, or both. Common areal units used for aggregation in the published literature include ZIP Codes/ZIP Code Tabulation Areas (ZCTAs) (Eisen et al. 2006, O’Connor et al. 2021, Russell et al. 2021), towns (Diuk-Wasser et al. 2014, Walter et al. 2016, Fernández-Ruiz et al. 2023), counties (Eisen and Eisen 2008, Porter et al. 2019, Tran et al. 2020, 2021), and states (Rosenberg et al. 2018). Aggregating point-level TBD case data to areal units can be a useful public health tool to display and communicate risk for TBD infection. However, it should not discourage individual protective measures for TBD prevention based on the boundaries in a choropleth map, as the boundaries may not accurately reflect risk of TBD infection. Similarly, the risk of acquiring a TBD may be estimated by calculating ecological metrics that incorporate pathogen prevalence and density of a tick population, often referred to as entomological risk index (ERI) (Mather et al. 1996). Other studies may assess entomological risk by examining either pathogen prevalence or tick density (Eisen et al. 2006, Khatchikian et al. 2012, Tran et al. 2020, 2021). Like case counts and aggregations, ERI, and other metrics can also be used for visualization and analysis, again introducing bias from the MAUP (Eisen et al. 2006, Russell et al. 2021, Prusinski et al. 2023). When ecological metrics are compared to observed cases of a TBD at matching areal units or nearby locations, bias from the MAUP extends to the results of the observed relationship between the 2 variables.

The impact of the MAUP on bivariate (Openshaw and Taylor 1979) and multivariate statistics (Fotheringham and Wong 1991, Amrhein 1995) is generally understood, yet, analysis of the impact of the MAUP in geographic sub-fields remains important. Studies in the published literature examining the impact of the MAUP on health data are plentiful (Nakaya 2000, Cockings and Martin 2005, Schuurman et al. 2007, Swift et al. 2008, Parenteau and Sawada 2011, Burden and Steel 2016, Roquette et al. 2018, Lee et al. 2020), however, few TBD studies directly mention bias from the MAUP as a concern (Jackson et al. 2006, Tran and Waller 2015). The TBD risk system presents a unique case where the MAUP should be taken into consideration, as risk for acquiring a TBD exists at the intersection of the spatiality of human behaviors and host–tick ecology. The blacklegged tick (Ixodes scapularis Say, Acari: Ixodidae) is the tick vector responsible for the spread of multiple pathogens in New York State (NYS) within the United States (Prusinski et al. 2014, Tokarz et al. 2017, Wroblewski et al. 2017, Yuan et al. 2020, Keesing et al. 2021), and its spatial distribution is partially owed to the movement of vertebrate hosts, including white-tailed deer (Odocoileus virginianus Zimmerman, Artiodactyla: Cervidae) (Watts et al. 2018). The movement potential of vertebrate hosts is often described by forest patch metrics including connectivity, patch area, and wildlife–urban interface that may be used to assess the risk of acquiring a TBD (Brownstein, Skelly, et al. 2005, McClure and Diuk-Wasser 2018, VanAcker et al. 2019, Diuk-Wasser et al. 2021). Meanwhile, the process of human–tick interaction additionally incorporates human behavioral traits which may be related to geographic location. Examples of spatially varying human behavioral traits include concern about contracting Lyme disease (Kim et al. 2020), understanding proper methods to prevent Lyme disease infection (Gould et al. 2008), and clinical provider knowledge (Hill and Holmes 2015).

Geographers tend to agree that the MAUP is not “fixable” but can be coped with (Buzzelli 2020). One such method to cope with the MAUP is to select areal units that best represent the natural system the investigator wishes to assess (Jackson et al. 2006), though the intersection of ecology and human behavior makes properly selecting areal units difficult. Many studies will incorporate spatial features relevant to tick ecology (Brownstein, Skelly, et al. 2005, McClure and Diuk-Wasser 2018, VanAcker et al. 2019, Diuk-Wasser et al. 2021), yet, this method does not necessarily represent the process by which humans interact with infected I. scapularis (McClure and Diuk-Wasser 2018). It follows that the selection of areal units for aggregation should incorporate both systems related to TBD risk: the dynamics of the spatial distribution of ticks, associated pathogens, and human behaviors related to risk of acquiring TBDs, however, areal units that properly incorporate both sets of processes may not exist. To our knowledge, Jackson et al. (2006) is the only study to purposefully assess how selecting areal units that best match the TBD system can impact statistical output. Jackson et al. (2006) examined the impact of different selected spatial units on the explanatory power of a multivariate model relating the incidence of Lyme disease to land-cover metrics including percent forest and herbaceous cover, and an edge metric quantifying forest and herbaceous adjacency. Polygons were aggregated as either 10-km² grid cells, 36-km² grid cells, or were delineated according to major roadways as an attempt to better approach the natural process of vertebrate host movement related to forest patch connectivity. Their results indicated that different polygon aggregation schemes exhibited similar rate ratios for all independent variables in their multivariate model. However, their results indicated that using major roads as polygon delineations increased the explanatory power of their models, potentially pointing to the importance of selecting polygons that best approximate the natural system in question.

The analysis conducted by Jackson et al. (2006) provided evidence that the MAUP is a concern when analyzing TBD data but did not directly examine the MAUP from the broader geographic contexts of place and scale. Place can be defined as a meaningful segment of geographical space, and can apply to both social spaces and physical landscapes (Cresswell 2008). The place may also be described under the context of “sense of place,” where individuals are aware of the significant impact places have on them (Tuan 1990). In this way, the place becomes an important consideration when selecting areal units, as administrative units (ZIP Codes/ZCTAs, towns, counties, and states) may or may not reflect a sense of place specific to knowledge, attitudes, or behaviors surrounding TBDs or the landscapes relevant to tick ecology. Similarly, the spatial scale should receive special consideration when selecting areal units, as different units reflect different processes in TBD and tick ecology systems. For example, peridomestic exposure to ticks primarily occurs at local scales, while the impact of climate and climate change operates at large geographic scales (Diuk-Wasser et al. 2021).

Place and scale can be reasonably approximated by 2 biases arising from the MAUP termed “the scale effect” and “the zone effect.” These effects may result in changes to statistical output as the size or shape of polygons are changed, respectively (Buzzelli 2020). These biases have been analyzed since the conceptualization of the MAUP (Openshaw and Taylor 1979). Openshaw and Taylor (1979) first addressed these unique biases by repeatedly simulating sets of polygons of varying sizes and testing the correlation between 2 variables under these aggregations. Here, we employ a similar technique by assessing the impact of the scale and zone effects of the MAUP on correlation statistics for anaplasmosis, a TBD locally endemic and considered reportable under public health law in NYS (O’Connor et al. 2021, Russell et al. 2021). Anaplasmosis is caused by the bacterium Anaplasma phagocytophilum (Rickettsiales: Anaplasmataceae) (Bakken et al. 1994), particularly the Ap-ha genotype (Massung et al. 2002, 2005), and is transmitted to humans via the bite of an infected I. scapularis tick (Chen et al. 1994). We also demonstrate the impact the MAUP has on visualizing anaplasmosis risk using previously reported, and publicly available case data aggregated to county polygons (New York State Department of Health 2017). Specifically, we demonstrate the shortcomings of choropleth maps and instead offer the alternative of using a pycnophylactic interpolation (Tobler 1979). To our knowledge, our study is the first to consider the MAUP’s impact of visualizing risk and directly assess the impact of the scale and zoning on correlation statistics between cases of a TBD and entomological risk measures derived from field-collected tick specimens.

Methods

Anaplasmosis Case Criteria and Geocoding

Anaplasmosis is a reportable disease under the New York State Sanitary Code (10NYCRR 2.10, 2.14). Cases of anaplasmosis occurring in 2017 were gathered from the New York State Department of Health Communicable Disease Electronic Surveillance System (CDESS). Cases were selected for inclusion if they were considered “confirmed” or “probable” by the Council of State and Territorial Epidemiologists (2008) case definition (Council of State and Territorial Epidemiologists 2008). The use of confirmed and probable case definitions for anaplasmosis case selection criteria has been described previously (O’Connor et al. 2021). Variables assessed from anaplasmosis case records were limited to the address and geographic coordinates of residence. In the event that a case record was missing geographic coordinates for residence, address information was geocoded in ArcMap v. 10.8 (ESRI 2019) using the pre-installed military grid reference system lookup table. Cases of anaplasmosis within the 5 boroughs of New York City were excluded from the analysis.

Tick Sampling and Pathogen Testing

Host-seeking ticks were sampled during October and November of 2017 via standardized flagging surveys conducted on publicly accessible forested lands as described previously (Prusinski et al. 2014). Briefly, sampling sites were selected according to the presence of habitat suitable for adult and nymphal I. scapularis, particularly sites with northern hardwood trees, leaf-litter, and low-lying vegetation. All sampling sites were located on publicly owned land. The GPS coordinates of each collection site location were recorded at the initial site visit. Field-collected ticks were immediately placed in 99.5% ethanol and stored on cold packs in an insulated cooler until returned to the laboratory. Specimens were stored at 4°C until sorted by developmental stage on a chill table (Model 1431, BioQuip, Gardena, CA). Ticks were then identified under a dissecting microscope (Model SMZ1000, Nikon, Tokyo, Japan) to species using a dichotomous key (Keirans and Clifford 1978, Keirans et al. 1996), and I. scapularis were placed into 1.5 ml Eppendorf tubes containing 99.5% ethanol and stored at −20°C until nucleic acid extraction.

A maximum of 50 individual adult I. scapularis per collection site underwent automated total genomic DNA extraction via Qiagen QIAcube HT using the QIAamp 96 kit (Qiagen USA, Germantown, MD) according to manufacturer protocols. Extracted DNA was then tested for the presence of (target gene) A. phagocytophilum (msp2), Babesia microti (Piroplasmida: Babesiidae) (18s rDNA), B. burgdorferi (16S rDNA), and B. miyamotoi (Spirochaetales: Spirochaetaceae) (16S rDNA) using a quadplex real-time PCR assay as previously described (Piedmonte et al. 2018). All samples testing positive for A. phagocytophilum by quadplex PCR were further tested using a custom Taqman^® SNP genotyping PCR assay to differentiate between the Ap-ha and Ap-V1 variants of A. phagocytophilum as originally described by Krakowetz et al. (2014), and with modifications described previously (Prusinski et al. 2023).

Entomological Risk Index Calculation and Geostatistical Modeling

We estimated the risk of exposure to Ap-ha A. phagocytophilum by calculating an entomologic risk index (ERI) for each site sampled (Mather et al. 1996, Prusinski et al. 2023), as the product of tick density (number of adult I. scapularis collected per m²) and the proportion of I. scapularis testing positive for Ap-ha A. phagocytophilum. If a sampling site was visited multiple times during the autumn of 2017, the corresponding ERI values were averaged. All calculations were performed with R v 4.1.0.

An ordinary kriging geostatistical model was built to interpolate site-level ERI values to achieve a continuous surface of ERI across NYS for use in statistical analysis. The ordinary kriging interpolation method is used to make general ERI predictions without incorporating other predictive variables (Matheron 1971, Cressie 1986). Variogram models were built with the “automap” package in R (Hiemstra et al. 2009). Ordinary kriging interpolations were then performed with the “gstat” package in R (Pebesma 2004).

Cartography, Data Visualization, and Map Comparisons

We compared the differences in visual representation of anaplasmosis incidence between choropleth maps and smoothed pycnophylactic interpolation. Pycnophylactic interpolation generates a continuous surface from attributes aggregated to polygons for the purpose of smoothing abrupt changes in attribute value at polygon boundaries (Tobler 1979). Pycnophylactic interpolation was performed using the “predicts” package in R (Hijmans 2023) and anaplasmosis incidence was gathered from publicly available data (New York State Department of Health 2017). All maps and charts shown were created with the “tmap” and “ggplot2” R packages, respectively (Wickham 2016, Tennekes 2018).

Polygon Simulation

Voronoi polygons were randomly simulated for reaggregation using 2 procedures. The first procedure randomly generated uniformly distributed spatial points using the “sp” package in R (Pebesma and Bivand 2005, Bivand et al. 2013). These sample points were then fed into the “voronoi” function in the “dismo” package in R to generate the Voronoi tessellations (Hijmans et al. 2021). The second procedure used a population-weighted sampling scheme to generate spatial points. The formula for population-weighted sampling is shown in Equation 1.

$${\displaystyle \begin{array}{l}{\displaystyle P(x)=\frac{p_i}{{\displaystyle \sum _{i=1}^n}{p}_i}}\end{array}}$$ (1)

where p_i is the population within 30-arc-second grid cell i and P(x) is the probability of placing a spatial point grid cell i. Grid cells were selected without replacement. Probabilities for weighted sampling were calculated from the Gridded Population of the World, Version 4 (GPWv4): Population Count, Revision 11 dataset at 30-arc-second resolution (Center For International Earth Science Information Network-CIESIN-Columbia University 2018). Sample points generated with this procedure were then used to generate Voronoi tessellations under the same process as the randomly selected sample points. Polygons generated from this scheme will henceforth be referred to as “population-weighted” polygons. Each procedure of generating Voronoi polygons was repeated from 30 to 3,000 polygons, 10 times each, creating polygons with similar average sizes to commonly used administrative units. Administrative units included: NYS counties, congressional districts, upper and lower state legislative districts, county subdivisions, ZCTAs, and NYS Department of Environmental Conservation wildlife management areas (WMAs). In all, 29,710 sets of polygons were generated for the random sampling and population-weighted sampling procedures, for a total of 59,420 sets of polygons.

After each set of Voronoi polygons was created, the total number of reported anaplasmosis cases within the generated polygons was calculated with the “sf” package in R (Pebesma 2018). Population-at-risk within each generated Voronoi polygon was calculated by extracting the GPWv4 dataset within each polygon using the “exactextractr” package in R (Baston 2022). The “exactextractr” package functions by summing the raster value within each cell that falls within the overlaid polygons. This method corrects for polygon edges that intersect raster cells by totaling only the portion of the cell within the polygon. The total number of reported anaplasmosis cases within each polygon was then divided by the resulting population-at-risk to generate anaplasmosis incidence per 100,000 individuals. In addition, the predicted values of Ap-ha ERI from ordinary kriging were averaged across the Voronoi polygons with each new simulated set.

Statistical Analysis

Spearman’s ρ correlation between anaplasmosis incidence and ordinary kriged Ap-ha ERI was assessed for each set of polygons for a total of 59,420 correlation coefficients. Correlation coefficients were compared to those generated from commonly used administrative units. P-values generated from Spearman’s ρ were adjusted via the Bonferroni–Holm adjustment due to concerns of multiple testing (Holm 1979).

Linear models were used to assess the impact of the scale effect by comparing the relationship between the number of polygons used for aggregation and to resulting correlation coefficients. The zone effect was assessed by calculating the variance of ρ values within the same number of simulated polygons. Linear models were used to compare the resulting variance to the number of polygons simulated to determine if the zone effect varies across polygon scales.

Results

Anaplasmosis Cases

A total of 1,112 confirmed and probable cases of anaplasmosis were gathered from CDESS. Of the 1,112 cases, 1,072 (96.40%) contained coordinate information and 39 (3.51%) were successfully geocoded to coordinates. One case (0.09%) did not contain coordinate information or address information for geocoding and was excluded from further analysis. A map containing the point-locations of anaplasmosis cases randomly jittered ± 0.05°C latitude and longitude is shown in Fig. 1. A previous analysis of these data aggregated to ZCTAs indicated these data are spatially autocorrelated (Russell et al. 2021). Figure 2 provides examples of the MAUP on choropleth maps of anaplasmosis incidence. A choropleth map of anaplasmosis incidence aggregated to NYS counties is shown alongside a pycnophylactic interpolation (Fig. 3).

Fig. 1.

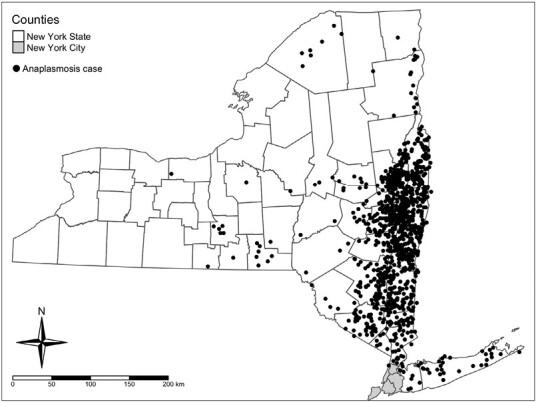
Cases of anaplasmosis in New York State (2017), jittered ± 0.05°C latitude and longitude.

Fig. 2.

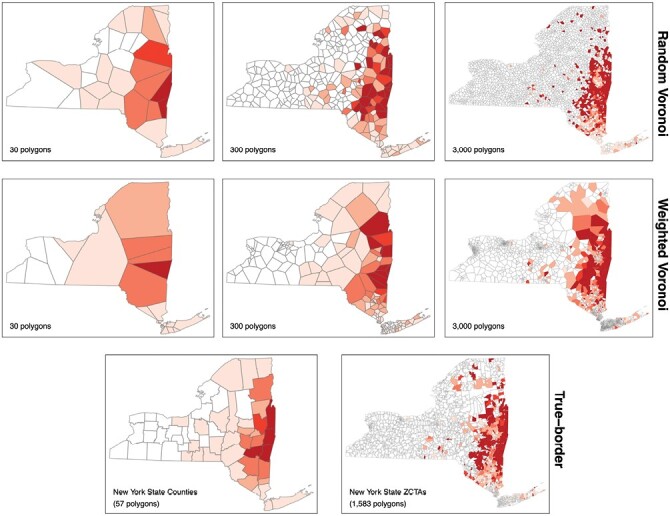
Choropleth maps of anaplasmosis incidence using different polygons for aggregation.

Fig. 3.

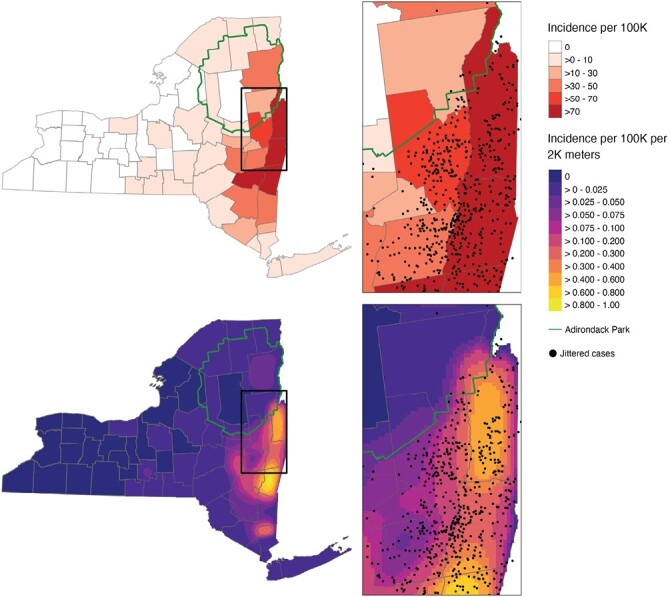
A choropleth map of anaplasmosis incidence aggregated to NYS county level (top). A pycnophylactic interpolation of anaplasmosis incidence aggregated to NYS county level (bottom). Jittered anaplasmosis cases are overlaid to demonstrate risk distribution. The border of the Adirondack Park is overlaid to demonstrate a boundary that better represents risk.

Tick Sampling, Pathogen Testing and Geostatistical Modeling

The results of host-seeking adult I. scapularis sampling and PCR testing are shown in Table 1. Entomological risk index of Ap-ha aggregated to site-level is shown in Fig. 4. Moran’s I (I = 0.2207, P < 0.0001) and variogram modeling indicated that site-level ERI was spatially autocorrelated (Supplementary Figs. S1 and S2). Ordinary kriging predictions of Ap-ha ERI obtained from variogram models are shown in Fig. 5.

Table 1.

Adult Ixodes scapularis sampling and Anaplasma phagocytophilum genotyping results in New York State (2017)

		n	%
Site visits		220	-
Specimens collected		9,822	–
Specimens tested		4,246	43.23%
	(+) A. phagocytophilum	305	7.18%
Specimens genotyped
	(+) Ap-ha	227	74.43%

Fig. 4.

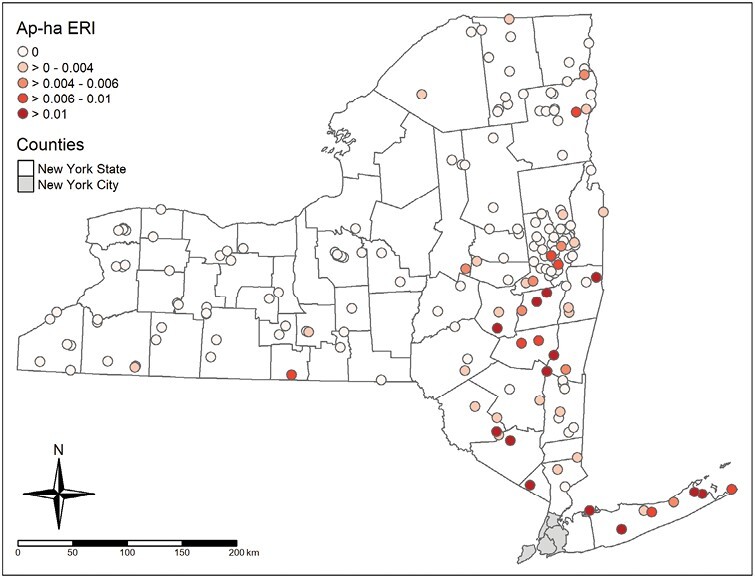
Ap-ha entomological risk index aggregated to sampling sites.

Fig. 5.

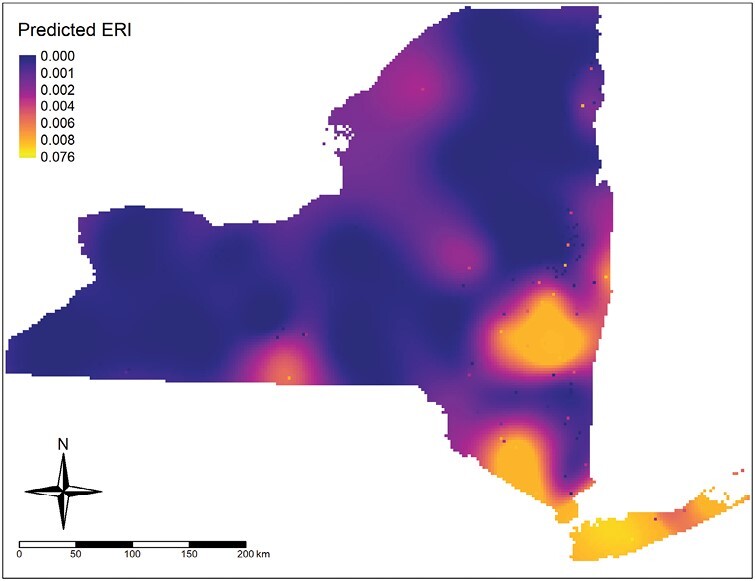
Ap-ha entomological risk index values generated using ordinary kriging interpolation.

Polygon Simulation and Statistical Analysis

Anaplasmosis incidence and ordinary kriged Ap-ha ERI were successfully reaggregated to 59,420 unique sets of randomly generated Voronoi polygons. Anaplasmosis incidence and ordinary kriged Ap-ha ERI were statistically significantly correlated in 29,694 (99.95%) sets of randomly generated polygons and 6,414 (21.59%) sets of polygons generated using the population-weighted sampling method. Correlation coefficients obtained using ordinary kriged Ap-ha ERI ranged from 0.204 to 0.780 using randomly generated polygons and from −0.180 to 0.614 for polygons generated using population-weighted sampling. Correlation coefficients calculated from simulated polygon aggregations and true polygon border aggregations are shown in Fig. 6.

Fig. 6.

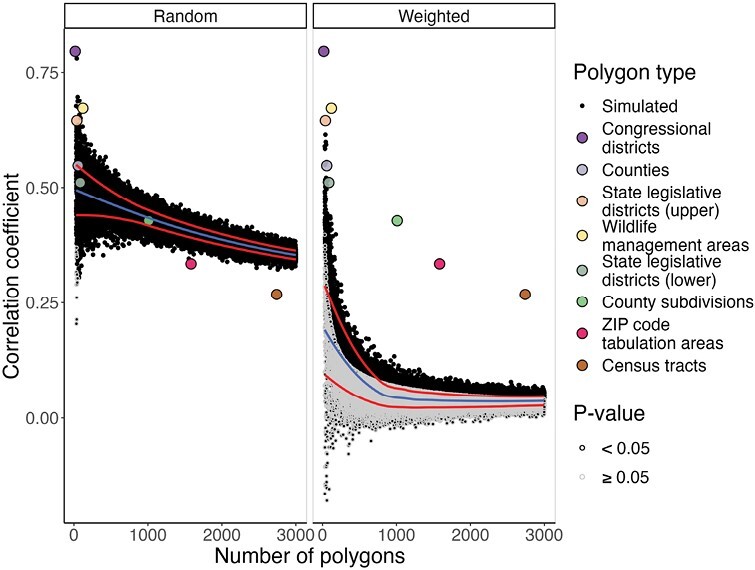
Spearman’s ρ correlation coefficients between kriged Ap-ha entomological risk index and anaplasmosis incidence using random and population-weighted sampling schemes. Administrative border polygons are included for reference and are listed by increasing number of polygons in the legend. The center/blue line is a locally estimated scatterplot smoothing (LOESS) line of the correlation coefficients, and red lines above and below are LOESS lines one standard deviation above and below the mean correlation coefficient for each number of simulated polygons (30–3,000).

Linear regression models built using randomly generated polygons indicate a negative relationship between the number of polygons used for aggregation and the resulting correlation coefficient (β = −4.754 × 10⁻⁵, P < 0.0001). Linear models built using polygons generated using the population-weighted sampling scheme also indicated a negative relationship between the number of polygons used and correlation coefficients (β = −3.076 × 10⁻⁵, P < .0001). Results of the regression models used to estimate the impact of the scale effect are shown in Table 2.

Table 2.

Regression models assessing the impact of the number of polygons simulated on the correlation coefficient

Polygon generation		β a	P
Random
	Intercept	0.48540	<0.0001
	Number of polygons	−0.00475	<0.0001
Population-weighted
	Intercept	0.10200	<0.0001
	Number of polygons	−0.00308	<0.0001

^aNumber of polygons divided by 100 to increase interpretability. A change in 100 polygons used for aggregation changes the correlation coefficient according to the beta values shown.

Linear regression models assessing the relationship between the variance of correlation coefficients and the number of polygons generated from random sampling indicated a negative slope (β  = −5.902 × 10⁻⁷, P < 0.0001). The relationship between the variance of correlation coefficients and the number of polygons generated from population-weighted sampling was also negative (β  = −1.710 × 10⁻⁶, P < 0.0001). Results of the regression models used to estimate the impact of the zone effect are shown in Table 3.

Table 3.

Regression models assessing the impact of the number of polygons simulated on the variance of the correlation coefficient

Polygon generation		β a	P
Random
	Intercept	0.00138	<0.0001
	Number of polygons	−0.00006	<0.0001
Population-weighted
	Intercept	0.00373	<0.0001
	Number of polygons	−0.00017	<0.0001

^aNumber of polygons divided by 100 to increase interpretability. A change in 100 polygons used for aggregation changes the correlation coefficient according to the beta values shown.

Discussion

Our study is the first to use repeated polygon simulation to assess the impact of the MAUP on visualizing TBD risk and associative statistics between cases of TBD and entomological risk indices. Our results demonstrate that special attention should be given to the selection of areal units as they pertain to spatial scale and/or epidemiological and ecological phenomenon. This result is demonstrated visually in Fig. 2, as the scale used by choropleth risk maps can misrepresent the locally specific risk of acquiring a TBD. Specifically, Fig. 2 shows that using the same underlying data for creating a choropleth map can arbitrarily change the areas deemed as “risky.” Additionally, choropleth risk maps using large administrative units can fail to approximate the underlying system causing changes in risk. Figure 3 demonstrates a reduction in the frequency of anaplasmosis cases demarcated at the boundary of the Adirondack Park. The Adirondack Park is a nearly 1 million hectare land area with elevations ranging from 30 to 1,600 m containing mixed deciduous–coniferous forest (Glennon and Porter 2005). ERI has generally been low from targeted drag and flag surveys within the Adirondack Park, categorizing this area as low risk for acquiring a TBD (Khatchikian et al. 2012). The difference in ecology in the Adirondack Park and its historically low ERI should necessitate incorporating this boundary for risk visualization. However, the use of county-level data aggregation prevails out of simplicity. Figure 3 brings forth the use of pycnophylactic interpolation as a feasible alternative to address this issue. Despite only having access to county-level data, the pycnophylactic interpolation depicted in Fig. 3 demonstrates that the smoothing can potentially account for changes brought on by features other than the administrative polygons used in a choropleth map. The pycnophylactic interpolation results in a gradual decrease in TBD risk from outside the Adirondack Park to within the park, whereas the county-level choropleth map indicates an instantaneous demarcation of risk only at county boundaries.

Apart from visualizing risk, much of TBD research aims to assess the associations between TBD incidence and entomological risk factors over varying spatial scales (Diuk-Wasser et al. 2021), where results are often attributed to different etiological pathways or phenomenon across these scales. As described by Diuk-Wasser et al. (2021), such pathways include: B. burgdorferi genetics, interaction with the wildlife–urban interface, peridomestic exposure, and travel-related exposure. However, it is important to note that changes in point estimates from statistical tests will inherently vary when switching between scales, regardless of the change in disease etiology or ecological process. The phenomenon of changing statistical point estimates due to the scale and zone effects of the MAUP illuminate the potential for improper TBD risk assessments and etiologies over varying spatial scales.

The use of polygon simulation to assess the MAUP’s impact on statistical metrics is not novel and the distribution of correlation coefficients using the randomly generated polygons corroborates previous research (Openshaw and Taylor 1979). Particularly, correlation coefficients and their variance are higher when fewer random polygons are used, demonstrating the impact of the scale effect (Fig. 6). This result was originally described by Clark and Avery (1976), and can be further understood when examining the variance of the kriged Ap-ha ERI and the logged variance of anaplasmosis cases, population at risk, and incidence per 100,000 (Fig. 7). Among the polygons generated by random sampling, the variance of kriged Ap-ha ERI exhibits minimal change as the number of polygons change, while the logged variance of incidence per 100,000 decreases with the number of polygons. The reduction in variance when using fewer polygons is caused by a smoothing effect, and results in increasing correlation coefficients (Clark and Avery 1976, Fotheringham and Wong 1991). Openshaw and Taylor (1979) found the same effect when aggregations using more polygons had lower correlation coefficients. Similarly, Fotheringham and Wong (1991) noted that regression slope parameters decreased with increasing aggregation under multivariate regression.

Fig. 7.

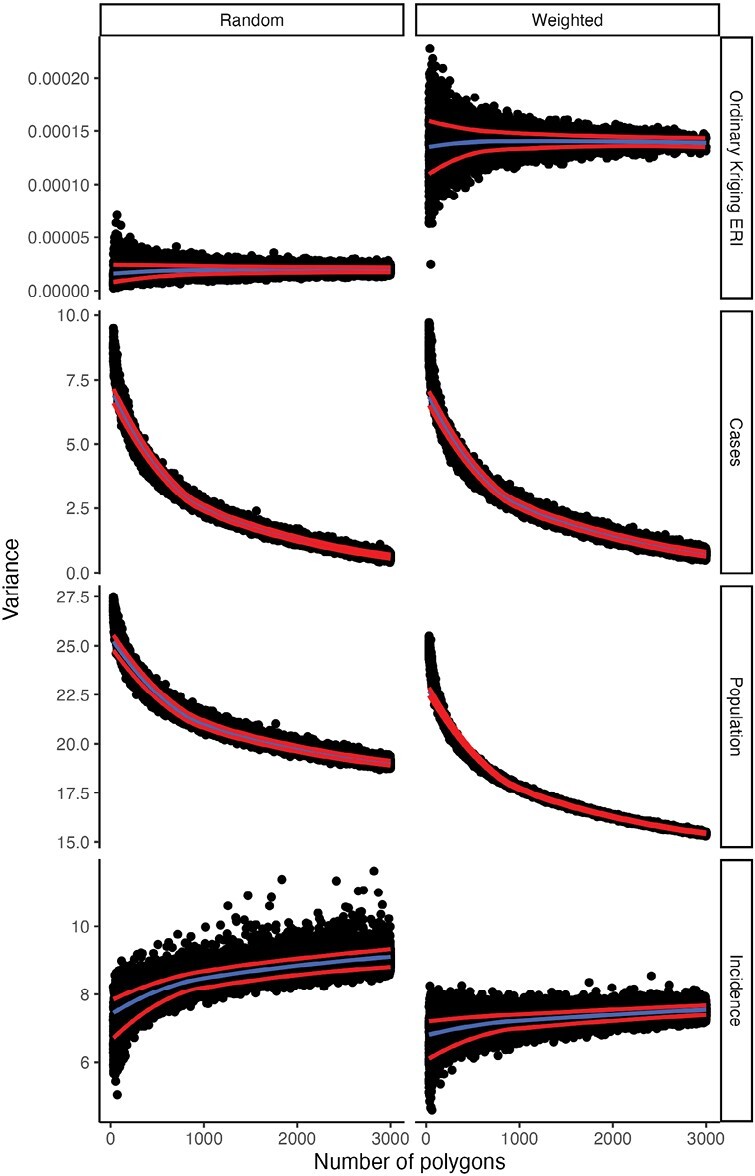
Between-polygon variances of variables reaggregated to simulated polygons. Variance of cases, population at risk, and incidence are depicted on the log scale. The center/blue line indicates a LOESS line of the variances. Red lines above and below indicate a LOESS line one standard deviation above and below the mean of the simulated variance for each number of simulated polygons (30–3,000).

Correlation coefficients calculated from population-weighted polygons indicate a decreased likelihood of statistically significant correlation relative to the randomly generated polygons. The relative difference in correlation coefficients between the random and population-weighted polygons can be attributed to the variance and covariance of incidence and kriged ERI between the different schemes. Specifically, the variance of anaplasmosis incidence is lower in population-weighted polygons than in randomly generated polygons, while the variance of kriged ERI is higher in population-weighted polygons than in randomly generated polygons. The reduced variance of incidence can be attributed to the population of polygons generated using the population-weighting scheme. As more polygons are generated in areas with higher population densities, the distribution of polygon populations becomes homogenous. Furthermore, increasing the number of polygons in major metropolitan areas where there are few or zero cases of anaplasmosis in NYS may also decrease the variance of case counts, but our results do not demonstrate this (Fig. 7). Meanwhile, variances of kriged ERI using population-weighted polygons are much higher than those from randomly generated polygons. This result is likely due to increasing the number of polygons (i.e., pseudoreplication) in high-density areas with both high and low values for ERI (Figs. 2 and 5). Kriged ERI values were generated using ordinary kriging at the scale of NYS, resulting in smoothed predicted ERI values that fail to incorporate ecotones. As a result, a higher number of polygons are created in the highly dense, southeastern part of NYS. These polygons are then improperly assigned high ERI values. At the same time, a higher number of polygons are created in other highly dense urban areas in the central and western parts of NYS, which have low ERI values. Overall, an increase in the variance of kriged ERI and a decrease in anaplasmosis incidence in the population-weighted polygons results in a reduction of covariance between these variables, ultimately reducing the correlation coefficients (Fig. 6).

The distribution of correlation coefficients in our study agrees with previous research, particularly because the nature of the data used in this study is not unique. Global and local spatially autocorrelated count data are a common occurrence in many disciplines, as are spatially continuous risk measures. The informative nature of our findings lies in how correlation coefficients generated from simulated polygons relate to those calculated from polygons commonly used by public health agencies and academic researchers. When examining TBD case data, agencies and researchers may select spatial units based on case data availability. Two commonly chosen areal units are counties and ZIP Code/ZCTAs. The correlation coefficients generated from county polygons appear to be within one standard deviation from the mean correlation coefficients using simulated polygons (Fig. 6). Meanwhile, the correlation coefficients generated from ZCTAs are greater than 4 standard deviations from the mean correlation coefficients using simulated polygons. The differences in correlation coefficients between the simulated polygons and true border polygons demonstrate the statistical impact of the MAUP’s scale and zone effects and provide evidence for the importance of considering spatial scale and place as they relate to the phenomenon being examined.

When the spatial scale of an analysis in a TBD study decreases, the phenomenon being considered should also change. For example, studies occurring over large geographic areas often examine climate change or theoretical species distributions of tick vectors (Brownstein et al. 2003, Brownstein, Holford, et al. 2005, Jung Kjær et al. 2019). Meanwhile, studies at the smallest scales investigate more individual-specific phenomena, for example, peridomestic exposure (Moon et al. 2019, Keesing et al. 2022). It follows that as the scale decreases, place as a consideration for TBD risk may also decrease, as individuals may consider their individual risk situation as unique and not associated with a space beyond their home. This situation is analogous to the ecological fallacy, where individuals may feel that risk levels specific to a group do not apply to them. Furthermore, it is likely that as polygons become smaller, their boundaries must become more accurate to capture both the place and the system under investigation. For example, ZCTAs are used by the United States Census Bureau and are representations of ZIP Codes, which were created to incorporate logistics for mail delivery (Grubesic and Matisziw 2006). Although delineations based on mailing logistics will incorporate place in some respects, ZIP Codes and ZCTAs differ from other Census Bureau delineations in that they were not designed with place in mind. Failing to incorporate place introduces challenges in epidemiological data analysis, as these ZIP codes and ZCTAs may not represent meaningful space related to disease risk (Grubesic and Matisziw 2006). However, our results also demonstrate that Census tracts may similarly fail to capture place for TBD risk. Furthermore, larger polygons (counties, congressional districts, state legislative districts, and WMAs) generally have higher correlation coefficients than smaller polygons (county subdivisions, ZCTAs, and Census tracts). Part of the decrease in correlation coefficients is expected due to the known impacts of the scale effect on the MAUP, however, it can be noted that correlation coefficients decrease faster using non-simulated polygons than they do with the randomly generated simulated polygons. As all simulated polygons have zero representation of place, it follows that the impact of place could cause a sharper decrease in correlation coefficients.

The zone effect is another MAUP bias that pertains to statistical output and the concept of place. Here, we measured the impact of the zone effect statistical output as we changed the borders of polygons while keeping their average size the same. Figure 6 demonstrates that the zone effect results in a higher variation in correlation coefficients among simulated polygons at higher levels of aggregation. The zone effect can be assessed under the context of place by comparing the placeless, simulated polygons to irregularly shaped polygons used by political entities (Figs. 2 and 6), though this relationship is difficult to disentangle from the impact of the scale effect. Figure 6 indicates that correlation coefficients from ZCTAs and Census tracts are more than 4 standard deviations below the mean of simulated correlation coefficients, while larger polygons are above the mean.

Given that small administrative units may be poor measures of place for TBDs, it should be considered why these areal units are used by TBD researchers. One possible explanation is the quest for “more accurate” spatial analysis. Tobler’s first law of geography states: “everything is related to everything else, but near things are more related than distant things” (Tobler 1970). Following this heuristic under the context of TBD epidemiology, i.e., where exposure to an infected tick is required to contract a TBD, researchers may be confronted with the notion of using the smallest feasible areal unit for analysis. As previously mentioned, this procedure may sacrifice the operationalization of place in favor of pinpointing the closest environment surrounding a case of a TBD. Importantly, this procedure may prevent polygons from capturing travel-related risk that larger polygons may otherwise capture, i.e., as areal units decrease, risky areas like public parks will be treated as separate from cases linked to home addresses. In addition, arbitrarily decreasing the scale of areal units can be classified as pseudoreplication, as increasing the number of units artificially creates new observations for use in statistical testing, increases the variance of observations, and creates small, spatially autocorrelated units.

Our study is not without limitations, primarily attributable to data quality and availability. The geographic location of anaplasmosis cases is linked to home address, thus, the position where a case acquired A. phagocytophilum is unknown. This presents a potential for bias where individuals living in population-dense areas may have traveled to rural areas and acquired A. phagocytophilum, despite their geographic location being linked to their home address. Such a situation would improperly display geographic risk and alter the results of statistical testing. Additionally, our study only assessed one TBD over a single year. Ideally, the impact of the MAUP can be assessed specifically for unique TBDs, as ecologies may differ between diseases. Further, cases of anaplasmosis in NYS are clustered (Fig. 1, Supplementary Fig. 2; Russell et al. 2021), increasing the impact of spatial autocorrelation on MAUP bias. Meanwhile, cases of Lyme disease in NYS are endemic statewide, and a study using Lyme disease case data may be informative (New York State Department of Health 2017). Despite these limitations, our results emphasize findings specific to cartographic visualization of TBD risk and analyses using associative statistics. In the context of data visualization, when using large areal units in choropleth maps, we recommend that a pycnophylactic interpolation may better display the spatially-continuous nature of TBD risk, and may even indirectly incorporate part of the TBD system not included in the areal unit selection. For statistical analysis, we recommend that TBD researchers and public health agencies should be cautious and aim to properly incorporate place when selecting areal units. Though ZCTAs provide an obvious example of areal units that fail to incorporate place for TBDs, determining which units emphasize place is less obvious and often context-dependent. Considering the potential for pseudoreplication, we also emphasize that researchers should first consider using larger areal units in spatial research before selecting polygons of decreasing size. Though many larger areal units will not best approximate individual risk in the TBD system, they should be preferred to smaller areal units as they may better incorporate regional-specific place and TBD risk. These results also demonstrate that TBD research operating across scales should be mindful of the impact of change scale and reaggregation which may unintentionally alter statistical estimates. The careful selection of analysis units should reduce bias from the MAUP and will allow researchers and officials to better disseminate information about risks and associations within TBD ecology and epidemiology.

Funding

This work was supported by the NYSDOH, the National Institutes of Health (grants AI097137 and AI142572) and the Centers for Disease Control and Prevention (award U01CK000509) and the CDC Emerging Infections Program TickNET (Cooperative Agreement NU50CK000486). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health, the Centers for Disease Control and Prevention or the Department of Health and Human Services.

Author contributions

Collin O'Connor (Conceptualization [lead], Formal analysis [lead], Investigation [lead], Methodology [lead], Software [lead], Visualization [lead], Writing—original draft [lead], Writing—review & editing [equal]), Melissa Prusinski (Data curation [lead], Funding acquisition [equal], Project administration [lead], Resources [equal], Supervision [equal], Writing—review & editing [equal]), Jared Aldstadt (Conceptualization [supporting], Resources [equal], Supervision [equal], Writing—review & editing [equal]), Richard Falco (Investigation [supporting], Writing—review & editing [supporting]), JoAnne Oliver (Investigation [supporting], Writing—review & editing [supporting]), Jamie Haight (Investigation [supporting], Writing—review & editing [supporting]), Keith Tober (Investigation [supporting], Writing—review & editing [supporting]), Lee Ann Sporn (Investigation [supporting], Writing—review & editing [supporting]), Jennifer White (Investigation [supporting], Project administration [supporting], Writing—review & editing [supporting]), Dustin Brisson (Investigation [supporting], Project administration [equal], Resources [equal], Writing—review & editing [supporting]), and P. Backenson (Investigation [supporting], Project administration [equal], Resources [equal], Writing—review & editing [supporting])

Data availability

Code used to conduct data gathering, cleaning, and analysis are available at https://github.com/coconn41/TBD_MAUP. Code can be used to recreate the analysis using modified publicly available data. Original data are available upon request.