Application of an advanced maximum likelihood estimation restoration method for enhanced-resolution and contrast in second-harmonic generation microscopy

Summary

Second-harmonic generation (SHG) microscopy has gained popularity because of its ability to perform submicron, label-free imaging of noncentrosymmetric biological structures, such as fibrillar collagen in the extracellular matrix environment of various organs with high contrast and specificity. Because SHG is a two-photon coherent scattering process, it is difficult to define a point spread function (PSF) for this modality. Hence, compared to incoherent two-photon processes like two-photon fluorescence, it is challenging to apply the various PSF-engineering methods to improve the spatial resolution to be close to the diffraction limit. Using a synthetic PSF and application of an advanced maximum likelihood estimation (AdvMLE) deconvolution algorithm, we demonstrate restoration of the spatial resolution in SHG images to that closer to the theoretical diffraction limit. The AdvMLE algorithm adaptively and iteratively develops a PSF for the supplied image and succeeds in improving the signal to noise ratio (SNR) for images where the SHG signals are derived from various sources such as collagen in tendon and myosin in heart sarcomere. Approximately 3.5 times improvement in SNR is observed for tissue images at depths of up to ~480 nm, which helps in revealing the underlying helical structures in collagen fibres with an ~26% improvement in the amplitude contrast in a fibre pitch. Our approach could be adapted to noisy and low resolution modalities such as micro-nano CT and MRI, impacting precision of diagnosis and treatment of human diseases.

Introduction

In recent years, second-harmonic generation (SHG) microscopy has increased in popularity due to its ability to provide submicron, optically sectioned, label-free images of noncentrosymmetric biological structures, such as fibrillar collagen and myosin, with high contrast and specificity. Although the SHG process was first demonstrated in 1961 (Franken et al., 1961), a year after the invention of the laser, the use of SHG for biological imaging did not come about until ~30 years ago in 1986 when it was first used to study collagen fibre orientation in rat tail tendons (Freund & Deutsch, 1986). Since that time there has been a growing understanding in biology that the extracellular matrix (ECM) environment is at least as important to biological function as the cells they bind together. Hence, noninvasive imaging of the three-dimensional (3D) collagen network, which comprises a significant portion of the ECM, could help elucidate the underlying mechanisms behind various connective tissue diseases and problems relevant to mechanobiology. As a result, SHG microscopy has been applied to problems of importance to human health, such as quantifying the 3D collagen organisational structure in the cervical microenvironment (Lau et al., 2013), mapping the changes in stromal collagen fibres in breast biopsies as a function of pathologic condition (Ambekar et al., 2012b) and quantifying tendon structural integrity under tendinopathy in chicken (Sivaguru et al., 2010) and in horses (Sivaguru et al., 2014a).

Similar to two-photon fluorescence (TPF), SHG microscopy exploits a two-photon effect to achieve 3D optical sectioning (Denk et al., 1990; Sivaguru et al., 2012). However, unlike TPF microscopy, SHG does not involve energy transitions between real electronic states, and as a result, there is no molecular absorption—only scattering takes place. This particular characteristic is advantageous in mitigating light-induced photo-damage. Moreover, fluorescent techniques are amenable to both optical and position-localisation based resolution-enhancement microscopy techniques (Hell et al., 2015), but adapting such methods to SHG microscopy has proved challenging. In addition, due to the coherent nature of the SHG process, there are difficulties in obtaining a point spread function (PSF), which is often used to determine the imaging properties, for example, spatial resolution, of the optical system (microscope). In particular, SHG is phase preserving with respect to the input optical pump beam, thereby imposing directionality to the generated second-harmonic signal. This is in contrast to the incoherent nature of fluorescence, which results in an isotropic radiation pattern. Thus, a subwavelength fluorescent bead is often used to experimentally obtain a microscope’s PSF, whereas for the SHG case the radiation pattern is polarisation sensitive and would be donut shaped (Saleh et al., 1991; Pawley, 1995; Terakawa & Nedyalkov, 2016). In line with this observation, there have thus far only been a few attempts to improve the SHG image resolution, for example, utilising subtractive imaging methods (Tian et al., 2015; Korobchevskaya et al., 2016) to observe a modest increase in contrast and resolution. Furthermore, in general, determination of the PSF requires tracing the propagation of the complex amplitude of the PSF generated at the sample plane through a scattering medium (Pawley, 1995). However, for SHG microscopy, this procedure is complicated by the fact that the complex amplitude of the SHG signal depends on the square of the complex amplitude of the excitation light. Thus, this nonlinear effect cannot be described by the conventional 3D PSF used for incoherent processes (Tang et al., 2004). In addition, these challenges present basic limitations for applying digital restoration methods such as linear deconvolution for a nonlinear modality. It is true that the ‘SHG-modality’, that is, SHG signal generation process is nonlinear. However, our working hypothesis is that despite the SHG signal inherently nonlinear at the point of generation (objective-sample-excitation light interface), the generated photons are still affected by the collection optics (PSF) as the signal registered in a photomultiplier tube in a linear manner, as in any other linear optical modality. Deconvolution is a common technique from signal and image processing that has found applications in many areas of engineering and science because of its utility in separating a desired signal from all unwanted contributions from the experimental system. In the context of image processing of acquired microscopy images, deconvolution has been used extensively in both widefield and confocal microscopy (Goldraij et al., 2006; Sivaguru et al., 2012) to remove image blur due particularly to out-of-focus light in 3D datasets (Pawley, 1995; Sivaguru et al., 2012). Generally, it is the high-spatial frequency components associated with the fine details in an image that are severely attenuated by the blurring action of out-of-focus light. Deconvolution is an approach to amplify these high-spatial frequencies on the condition that the noise contribution in the system such as photon and electronic shot noise is sufficiently small relative to the amplitude of the high-spatial frequency components. Therefore, for an accurately measured 3D PSF, an optical system can be sufficiently well characterised so that the deleterious effects of out-of-focus light and photon shot (Poisson) noise can be deterministically mitigated. In this paper, we employ an advanced maximum likelihood estimation method (AdvMLE) based on the Richardson-Lucy (RL) algorithm (Biggs, 2010a, b), which relies on iterative statistical method and the optical parameters to estimate the system PSF. Beginning with an initial guess PSF, we use the AdvMLE algorithm to develop a synthetic PSF to improve the resolution of SHG images. To the best of our knowledge this is the first implementation of the RL based deconvolution algorithm to improve SHG image resolution. The algorithm is applied to SHG images of gold nanoparticles, chicken tendon and mouse heart sarcomere.

Material and methods

Ethics statement

All animal protocols were approved by the Institutional Animal Care and Use Committee at Loyola University Chicago (LU#205109) and were performed in accordance with the guidelines listed in the Guide for the Use and Care of Laboratory Animals published by the National Institutes of Health.

Chicken tendon and mouse heart sample preparation.

Wild type mouse hearts in the FVB/N (WT) background were euthanised in a carbon dioxide (CO₂) chamber by slow flow of CO₂ (10–30% of chamber volume per min) as described previously (Lynch et al., 2015; Sivaguru et al., 2015). This treatment was continued for 15–30 min after breathing stops. The mouse hearts were dissected from anesthetised mice, the blood was drained and, the tissue was fixed in 10% formalin. The hearts were bisected longitudinally and dehydrated through graded ethanol series and embedded in paraffin wax. Five-micrometre thick step-serial sections were made and stained with haematoxylin and eosin (H&E). These sections were imaged using the SHG microscope setup configured for forward-signal collection, as described in subsequent sections.

Chicken tendon samples were procured from a local grocery store (chicken drumsticks). A surgical blade was used to cut open a 1 cm vertical slit/window in intact tendon in order to expose the major superficial tendon. The entire leg of the chicken was placed in a petri dish containing phosphate buffered saline pH 7.4 (Fig. S1). Tendons from the same batch of chicken legs were also dissected out (1 cm in length) and processed for cryostat sectioning as described previously (Sivaguru et al., 2010; Sivaguru et al., 2014a).

In the next step, the tendons were fixed in Notox (Scientific Device Laboratory, Des Plaines, IL, USA) for 1 h, followed by washing three times with PBS (phosphate buffered saline), incubated with PBS/10% sucrose for 2 h, PBS/20% sucrose for 2h and then PBS/30% sucrose overnight. They were then embedded in cryostat mould using 50% OCT (Optimum Cutting Temperature) plus 50% PBS containing 30% sucrose. For cryostat sectioning, the samples were brought to −20°C from −80°C from storage temperature and cut to 20-μm thick sections optimal for SHG microscopy as described previously (Sivaguru et al., 2010; Sivaguru et al., 2014a) using a cryostat (Leica CM 3050S). The sections were thawed, secured between two cover glasses (#1.5) with a PBS buffer mounting medium and imaged immediately.

Preparation of gold nanoparticles.

Monodispersed gold nanoparticles suspended in water (100-nm diameter in size) were purchased from TedPella Inc. (Redding, CA, USA). The surface of the particles had trace amounts of citrate to stabilise the particle in the solution. The size of the particles was characterised and verified by the supplier with transmission electron microscopy (TEM). The initial number of particles in the solution was 5.6 × 10⁹ particles mL⁻¹, which was diluted with distilled water to prepare a 1:1000 dilute aqueous solution. The solution was allowed to dry on a high performance #1.5 cover glass from Carl Zeiss (0.170 ± 0.005 mm, Cat # 474030-9010-000, Carl Zeiss, Jena, Germany) in a fume hood at room temperature.

Optical setup of second-harmonic imaging microscopy.

A schematic of the experimental optical setup can be found elsewhere (Sivaguru et al., 2010; Sivaguru et al., 2014a). The LSM 710 system is equipped with a tunable Ti:Sapphire laser source that produces 70-fs duration pulses at a repetition rate of 80 MHz. We used the 780-nm excitation wavelength and a quarter-wave plate to generate circularly polarised light (the fundamental laser is plane polarised) to gather isotropic SHG signals from collagen fibres at all orientations in a single image (Sivaguru et al., 2010; Sivaguru et al., 2014a). The laser light is reflected by a 760 nm dichroic (short-pass) beam splitter and focused onto the sample using a Zeiss 40×X C Apochromat 1.2 numerical aperture (NA) water-immersion objective. The incident power at the sample plane is ~10 mW. The emitted backward SHG signal is collected by the same objective, whereas the forward signal is collected by a condenser objective (0.55 NA) using a transmitted photomultiplier tube. Both transmitted and reflected SHG signals were integrated by a set of X and Y galvanometric mirrors at a pixel dwell time of ~1.58 μs and four-line averaging to minimise noise. Two filters are positioned in each image acquisition (forward and backward); one IR blocking filter (Semrock FF01-680/SP-25) is used to block the laser pump wavelengths, and the other band pass filter is used to collect the SHG signal at 390 nm (Semrock FF01-390/18-25). Photomultiplier tubes (Hamamatsu R6357 multialkali) record the forward and backward SHG images.

LSM inverter scope.

The LSM Tech inverter (Inverter Scope Model-300, LSM Tech Inc., Etters, PA, USA) is used to convert the inverted microscope in to an upright microscope (Fig. S1). Here, a long-working distance 40× water dipping objective with a Teflon tip (Zeiss 40× LD Achroplan, 1.0 NA) is used without any cover glass. In this case, the images are collected only in the backward SHG modality (reflected light). Using the Z-axis motor of the microscope, the objective is used to collect a series of optical sections in the Z-axis direction up to 400-μm deep from the surface of the tissue without any physical sectioning.

Image acquisition, restoration procedures and analysis.

The images were acquired with either 512 × 512 or 1024 × 1024 pixel dimensions and saved in LSM format. The voxel dimensions (XYZ) in microns used for all images are given as follows: 0.19 × 0.19 × 0.4 for chicken tendon images, 0.10 × 0.10 × 0.30 for heart sarcomere images, 0.41 × 0.41 × 0.60 for intact tendon images and 0.08 × 0.08 × 0.10 for gold nanoparticles. The master gain and laser powers were optimised for the images. In most cases, multiple 2D images were taken through the Z axis for 3D reconstruction of the entire sample or to assess depth penetration. Images from all planes were used in applying two different restoration algorithms. The images were presented mostly in the median plane out of the multiple 3D stacks.

Deconvolution algorithm

Description of AdvMLE deconvolution process.

Deconvolution is a mathematical technique for correcting the out-of-focus blur that occurs when light passes through an optical system. The PSF describes how each point of light from the specimen is observed by the camera or detector, and in a system where the PSF is spatially invariant, the image formation can be modelled mathematically as a convolution. The microscopic image $\left(g\right)$ is a result of a convolution $(\otimes )$ between the ground truth $\left(f\right)$ and the PSF $\left(h\right)$, plus a noise component $\left(n\right)$ that is Poisson distributed from photon counting statistics. The expression that describes this is given by Lucy (1974) and Richardson (1972)

$$g=f\otimes h+n,$$ (1)

where each variable is a 3D volume of intensity values. The process of estimating the true data $\left(f\right)$ from the observation $\left(g\right)$ is termed deconvolution. There are many approaches to achieving deconvolution and may be single step filtering (linear) or iterative in nature (nonlinear) (Pawley, 1995). One of the most popular approaches is the Richardson-Lucy (RL) iterative algorithm (Richardson, 1972; Lucy, 1974), which is based on maximum likelihood estimation (MLE) with a log-likelihood measure assuming Poisson distributed noise. The simplified log-likelihood $\left(logL\right)$ can be written as (Biggs, 2010a)

$$\log (L)=\sum g·\log \left(r_k\right)-r_k,$$ (2)

where $r_k={\widehat{f}}_k\otimes h$ is the reblurred estimate calculated by convolving the $k$th estimate of the true image $\left(f\right)$ with the known PSF $\left(h\right)$. The basic RL iteration for restoring the image is (Biggs, 2010a)

$${\widehat{f}}_{k+1}={\widehat{f}}_k\cdot \left(h\star \frac{g}{r_k}\right),$$ (3)

where ★ is the correlation operator and · is element-wise multiplication. As negative signals are not observed by detectors, each iteration is guaranteed to preserve nonnegativity of the image and the PSF. In addition the likelihood measure is also increased, which is maximised when $r_k=g$. Additionally, the RL iterations are known to converge slowly, so there are a variety of methods for both reducing the noise amplification and increasing the speed of convergence (Richardson, 1972; Lucy, 1974).

A further extension of the standard deconvolution method is that of blind deconvolution where the PSF can be estimated along with the image as stated above. Using the RL approach, this can be simply achieved by switching the image and PSF variables such that (Biggs, 2010a)

$${\widehat{h}}_{k+1}=\frac{1}{\sum {\widehat{f}}_k}{\widehat{h}}_k\cdot \left({\widehat{f}}_k\star \frac{g}{r_k}\right).$$ (4)

Application of AdvMLE to SHG images.

The algorithm discussed in the previous subsection is applied to SHG images. As mentioned earlier, in the specific case of SHG, the coherent scattering nature of the process makes it challenging to obtain a PSF. However, as a two-photon process, the illumination PSF $\left(h_{il}(x,y,z)\right)$ dictates the resolution (Diaspro, 2001). This PSF is proportional to the square of the one-photon illumination PSF ${\left(h_{il}(x,y,z)\right)}^2$ and depends on the excitation wavelength, numerical aperture of the objective lens and refractive index of the lens immersion medium.

The logical flow of the application is presented in a flow chart in Figure 1. In this implementation, the supplied raw image is blurred with the initial theoretical guess PSF, which is developed based on the parameters mentioned in the previous paragraph. Subsequently, the image and PSF are updated alternatively; the PSF is kept fixed while the image estimate is updated, and the image is kept fixed while the PSF estimate is updated if there are visible reconstruction artifacts. For both the updated image and PSF, a reblurred image is formed by convolving the current image and PSF estimates together, which is then compared with the raw image. If the modified image and PSF estimates are correct then the reblurred image will match the raw image within the predefined noise limits. This procedure is based on the Richardson-Lucy algorithm (Richardson, 1972; Lucy, 1974) for restoration in the presence of Poisson distributed photon noise, which allows the PSF to adapt to the actual blur function present in the data when the initial theoretical PSF does not exactly match. This adaptive nature of the algorithm, solves the issue of not having a PSF for a scattering modality such as SHG imaging. The user is provided with a choice of applying only MLE deconvolution (choice ‘NO’) or perform the additional convergence acceleration provided by the AdvMLE algorithm (choice ‘YES’). This allows us to compare the quality and convergence rate of the two processes. The algorithm can restore a 3D image in no more than 20 iterations without excessive noise amplification. Note that, before the algorithm is applied, the edge artefacts in the image are minimised by padding the image and blending the edges in all three directions. The intensity values for the added border pixels are calculated by linear interpolation between the intensity values of the opposing edge pixels.

Fig. 1.

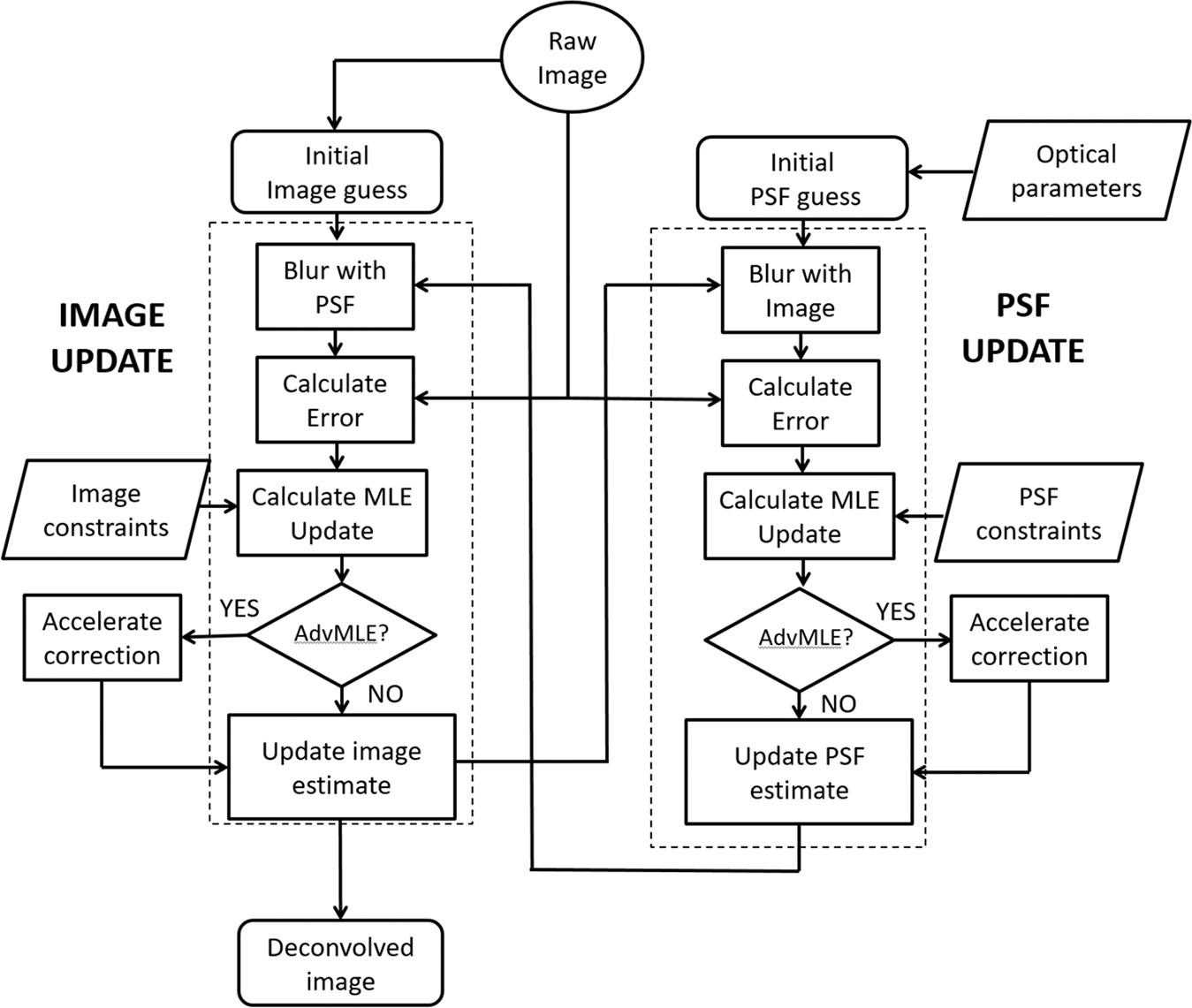
Flow sequence and operation logic of the MLE and AdvMLE algorithm as applied to SHG images. The PSF update and image update processes are highlighted with dotted boxes. See text for details.

The AdvMLE deconvolved data from tendon and heart sarcomere SHG images were obtained in either XY projection (combining all planes in a z-stack) or single median plane (centre focal plane of the Z stack). Most images were made in single channel in 8-bit black and white (256 shades of grey) or pseudo-coloured to green for back-scattered SHG (BSHG) and red for forward-scattered SHG (FSHG) in merged images. Both raw and deconvolved image intensities were adjusted to display the minimum and maximum intensity of pixels available in the image for optimal representation of the full dynamic range. The RGB pseudo coloured images were converted to 8 bit in the program ImageJ (NIH open source software), calibrated to appropriate the voxel dimension as in the raw data, and the fast Fourier transform (FFT) was performed to identify the extent of frequencies recovered after deconvolution. For all the FFT images, a predefined uniform threshold was used for optimum performance and appropriate comparison, before and after AdvMLE deconvolution. The bandwidth gain images were obtained by subtracting the raw-FFT images from the AdvMLE-FFT images using inbuilt image math function of ImageJ. FFT frequency traces were made on the images using the same program along the maximum frequency distribution through the centre (frame to frame) of the FFT image (see Fig. S2) and spatial frequency per unit micron was calculated (see Data S1 for source data and calculation methods). The same ImageJ program was used to draw a dotted line at multiple representative locations of the images and the position information was saved in the ROI (region of interest) manager of the ImageJ. Using the ROI manager, the data were compared from exactly the same location from the images before and after deconvolution. The line graphs were made using Origin 8.6 (Origin Lab Corporation, Northampton, MA, USA).

Results

AdvMLE deconvolution takes ~30 s for a standard 512 × 512 pixel 3D image having around ~30 optical sections. First we test the efficacy of our AdvMLE algorithm for 3D SHG images by using 100-nm spherical, Au nanoparticle as our initial test sample. A single Au nanoparticle on glass yields an appreciably strong SHG signal. The results are discussed in detail in the Supplementary Information and depicted in Figure S3. Both lateral and axial plane images demonstrate appreciable increase in higher spatial frequencies after AdvMLE processing. To identify improvements in spatial resolution, we calculated the full width at half maximum (FWHM) from line intensity profiles across raw and AdvMLE-processed gold nanoparticle images, which showed us an improvement of ~29% and 31% for lateral and axial images, respectively.

Our algorithm is next applied to SHG images of chicken tendon and the results are shown in Figure 2. Figures 2(A) and (B) show FSHG images of tendon collagen fibres XY (median plane) and XZ planes for the raw and AdvMLE-processed images. Similarly, the corresponding BSHG images are shown in Figures 2(C) and (D). In both cases, individual collagen fibres are more clearly distinguished in the AdvMLE-processed images, providing a better resolution and contrast. In addition, AdvMLE processing removes signal contribution from out-of-plane fibres, which appear as a blurred structure in the raw image (red arrow in Fig. 2A). Plots of the line intensity profiles for select positions (dotted lines in Figs. 2A, C) for the FSHG and BSHG images are obtained for raw and AdvMLE-processed images and shown in Figures 2(E) and (F), respectively. We observe sharp, distinct peaks (better SNR) for the processed images with larger intensities than the raw image, thereby reiterating the observation of the enhanced resolution and contrast for the processed images. The FSHG line intensity profile shows several regions of zero intensity (flat horizontal line) whereas the corresponding profile for BSHG image does not. This observation can be explained by the fact that the BSHG signal contains significant noise contribution (Houle et al., 2015). When AdvMLE is applied to a BSHG image, this noise is reduced enhancing the signal from the fibres. For FSHG, the signal has a relatively lower noise contribution. Hence, only the background noise is reduced through AdvMLE leading to regions with zero intensity (flat line). Figures 2(G) and (H) plot the average peak intensity for raw and AdvMLE images. Here, we observe that the AdvMLE-processed images show significantly larger average peak intensities for both BSHG and FSHG images (ranging from ~1.8- to 3.5-fold) in comparison to the raw unprocessed images. Finally, in Figures 2(I) and (J), we see that the AdvMLE-processed images have an average FWHM that is ~ 20% smaller compared to the unprocessed images.

Fig. 2.

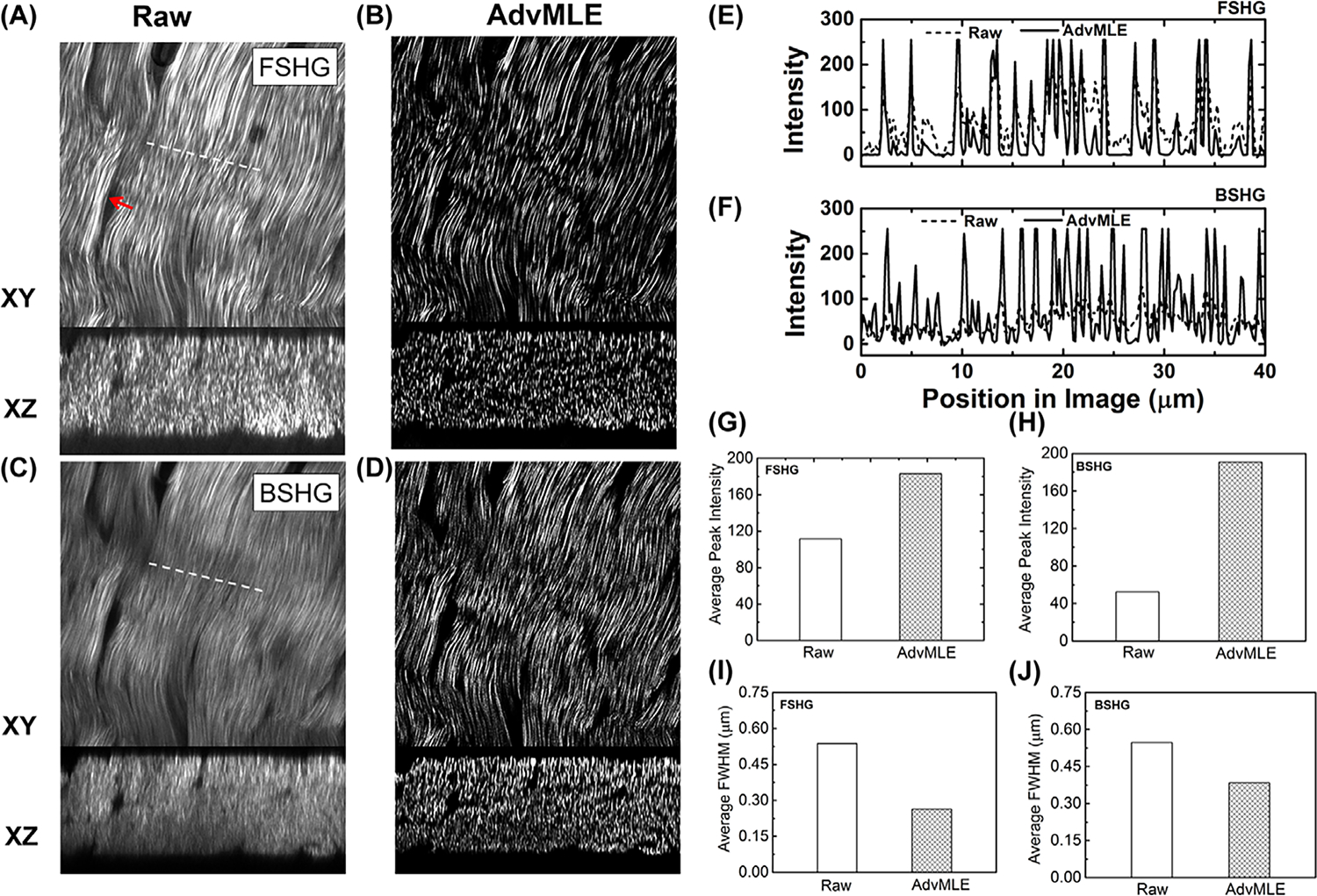
AdvMLE enhances resolution in forward and backward SHG images of chicken tendon. (A), (B) FSHG and (C), (D) BSHG images of chicken tendon for (A), (C) raw and (B), (D) AdvMLE-processed images are compared. Red arrow in (A) indicates AdvMLE processing removes signal contribution from out-of-plane fibres, which appear as a blurred structure in the raw image. The images shown are from individual optical sections in the median plane of a Z stack. Line intensity profiles along the white dashed lines shown in (A), (C) are given for the raw and AdvMLE-processed FSHG (E) and BSHG (F) images. Similar dashed lines were placed on the AdvMLE images (B), (D) in identical locations to the raw images. The average peak intensity and average peak FWHM are provided between raw and AdvMLE-processed images for FSHG (G), (I) and BSHG (H), (J). The length of lines in images (A), (C) represents 40 μm and is used as the scale bar.

Figure 3 shows magnified raw (see also Video S1) and AdvMLE (see also Video S2) processed images of collagen fibres in the chicken tendon, revealing the helical arrangement of the collagen fibre structure. To the best of our knowledge, this is the first demonstration of the collagen fibre helical organisation using SHG imaging. In Figure 3(B), the helical pattern is visible with increased clarity compared to the raw image after AdvMLE processing (see Fig. S4 for full field-of-view). In addition, tracing a line intensity profile along a representative fibre from the images (Fig. 3B), we observe that the amplitude contrast in the fibre pitch is improved by ~26% after AdvMLE processing.

Fig. 3.

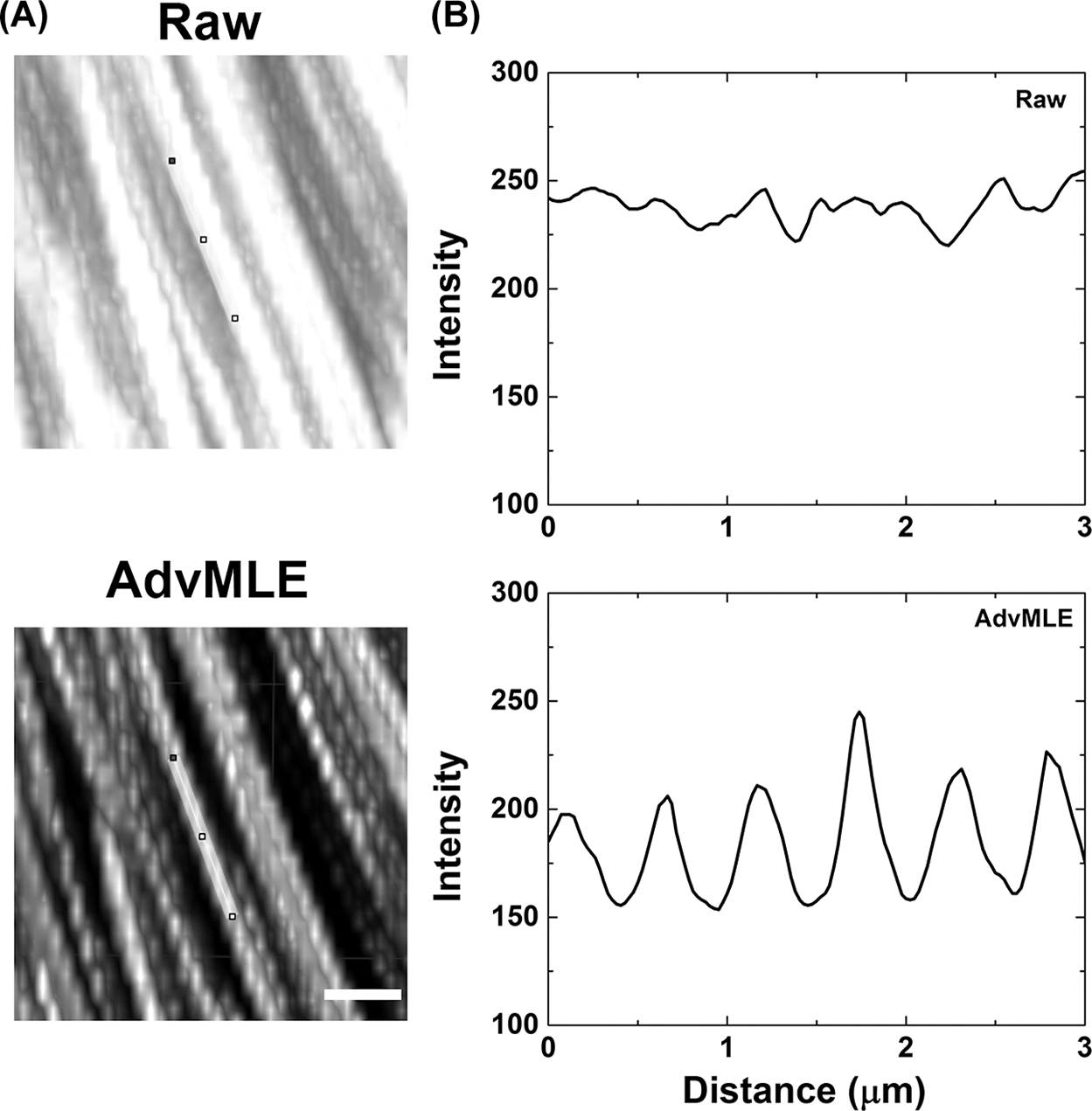
AdvMLE-processed images showing enhanced structural information. Helical structure of collagen fibrils (chicken tendon) showed in FSHG images in raw (a, top row) and after AdvMLE processing (a, bottom row). At a representative location on each image of (A), a 3-μm long intensity profile was drawn in (B), showing the pitch of the helical pattern traced along a single fibre (line traced on images). Scale bar corresponds to 2 μm.

Figure 4 shows application of the AdvMLE algorithm to FSHG images of mouse heart sarcomere. Observations similar to those discussed in Figure 3 for the tendon images are made. In comparison to the raw SHG images (Fig. 5A and Video S3), deconvolution using AdvMLE (Fig. 4B and Video S4) permits better resolved images of heart sarcomeres. The line intensity profiles along the dashed lines 1, 2 and 3 indicated in Figure 4(A) are compared in Figure 4(C) for raw and AdvMLE-processed images. It is clear that the AdvMLE-processed images are again sharper with high SNR and have more distinct features than raw unprocessed images. As expected, the AdvMLE-processed images also show a higher average peak intensity along lines 1, 2 and 3 in comparison to the raw unprocessed images (Fig. 5D), which is consistent with the expected higher SNR. The corresponding average FWHM for the AdvMLE-processed myosin fibres are around ~ 54% narrower along the same selected line 2 in the raw image (Fig. 4E).

Fig. 4.

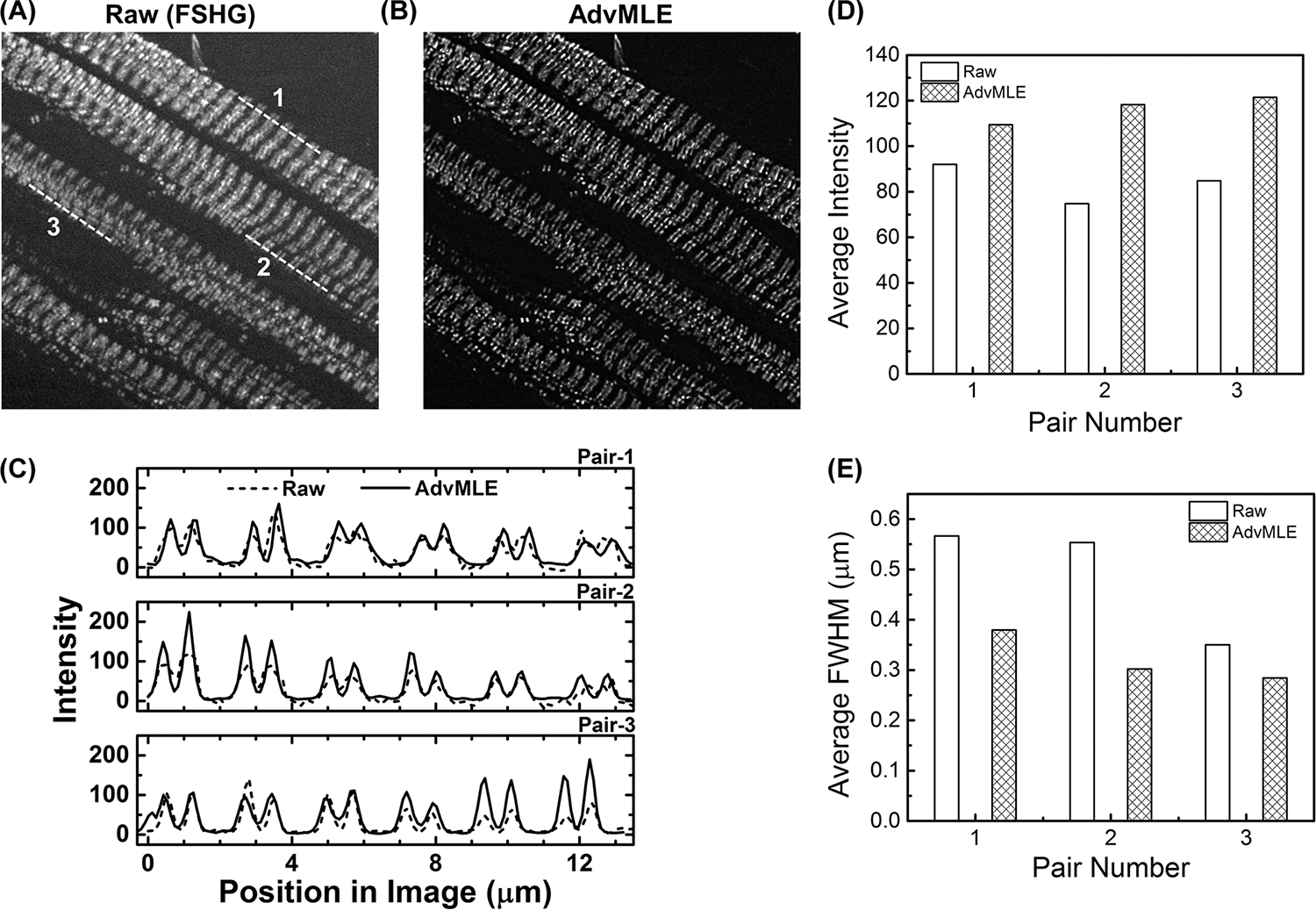
AdvMLE enhances resolution in forward SHG images of mouse heart sarcomere. Parts (A) and (B) show raw and AdvMLE-processed FSH Gimages of normal adult mouse heart (FvB/N strain) sarcomere, respectively. Average peak intensity (C) along lines 1, 2 and 3 shown in the FSHG image for raw (A) and corresponding locations in AdvMLE-processed images (B). The average peak intensity and average peak FWHM are provided in (D) and (E) for each pair of lines in raw and AdvMLE-processed images. The length of the lines in image (A) represents 13 μm and is used as a scale bar.

Fig. 5.

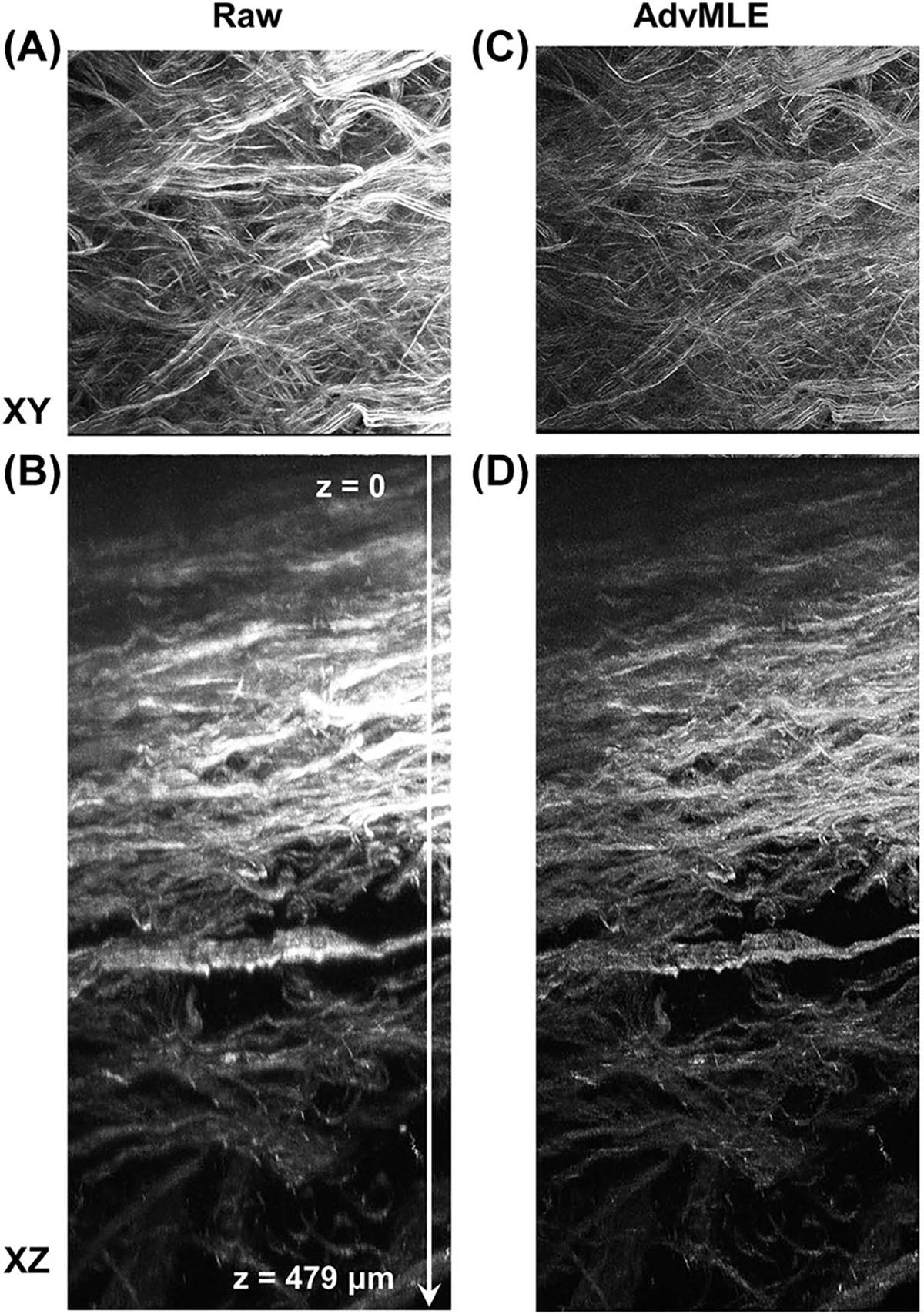
AdvMLE enhances resolution in backward deep tissue SHG images of intact chicken tendons. Raw and AdvMLE-processed SHG images of intact chicken tendon are obtained, and the (A), (C) XY and (B), (D) XZ planes are shown. The images are maximum intensity projection of all optical slices through a depth of around 479 μm (surface to the deepest plane signal, top to bottom indicated by an arrow in B, which is also used as a scale bar).

In comparison to the linear microscopy techniques, a major advantage of SHG microscopy is the increased depth penetration in tissues. In this study, we use an Inverter Scope (Fig. S1) and a specialised long-working distance objective to image intact tendon in the BSHG mode as opposed to conventional imaging using sectioned tissue in a microtome, as sectioning could lead to artefacts. The results are shown in Figure 5 for both XY and XZ plane raw (Video S5) and AdvMLE-processed images (Video S6). It is clear from the XZ-plane images that a maximum penetration depth of 479 μm is achievable in intact chicken tendon in the backward direction. Moreover, we again observe that the fibres are more clearly distinguished after the AdvMLE processing compared to raw data, even at several hundred μm deep from the surface in the intact tissue.

To determine how, why and where the improvement in spatial resolution is gained using the AdvMLE algorithm, we evaluate the optical transfer function (OTF) by taking the Fourier transform of the chicken tendon and normal adult mouse heart as shown in Figure 6. In all cases, we see that AdvMLE-processed images result in a much larger extent of the OTF, a direct result of an increased spatial-frequency bandwidth. By taking the difference between the AdvMLE-processed images and the raw SHG images, we obtain the difference in Figures 6 (C), (G) and (K), which represents the increase in spatial-frequency bandwidth. It is interesting to note that the BSHG tendon image starts off with much lower spatial-frequency bandwidth, compared to FSHG (Figs. 6A, E) but both ends with much increased bandwidth after the AdvMLE processing (Figs. 6B, F). However, the retrieved frequencies are still lower in BSHG compared to FSHG. This is a likely result of the fact that the BSHG signal undergoes increased scattering from the tissue, and thus reduces the maximum attainable spatial resolution compared to coherent, high SNR FSHG. Figures 6(D), (H) and (L) allow us to quantitatively plot the improvement in the OTF for the raw and AdvMLE-processed FSHG and BSHG images of the tendon and mouse heart along the longest axis of frequencies (Fig. S2). As expected, the AdvMLE-processed images show the highest retrieval of intensities for the highest spatial frequencies ~2.5 cycles μm⁻¹, corresponding to a transverse spatial resolution of ~400 nm, close to the theoretical diffraction limit. A summary of AdvMLE improvements across SHG sources is presented in Table 1.

Fig. 6.

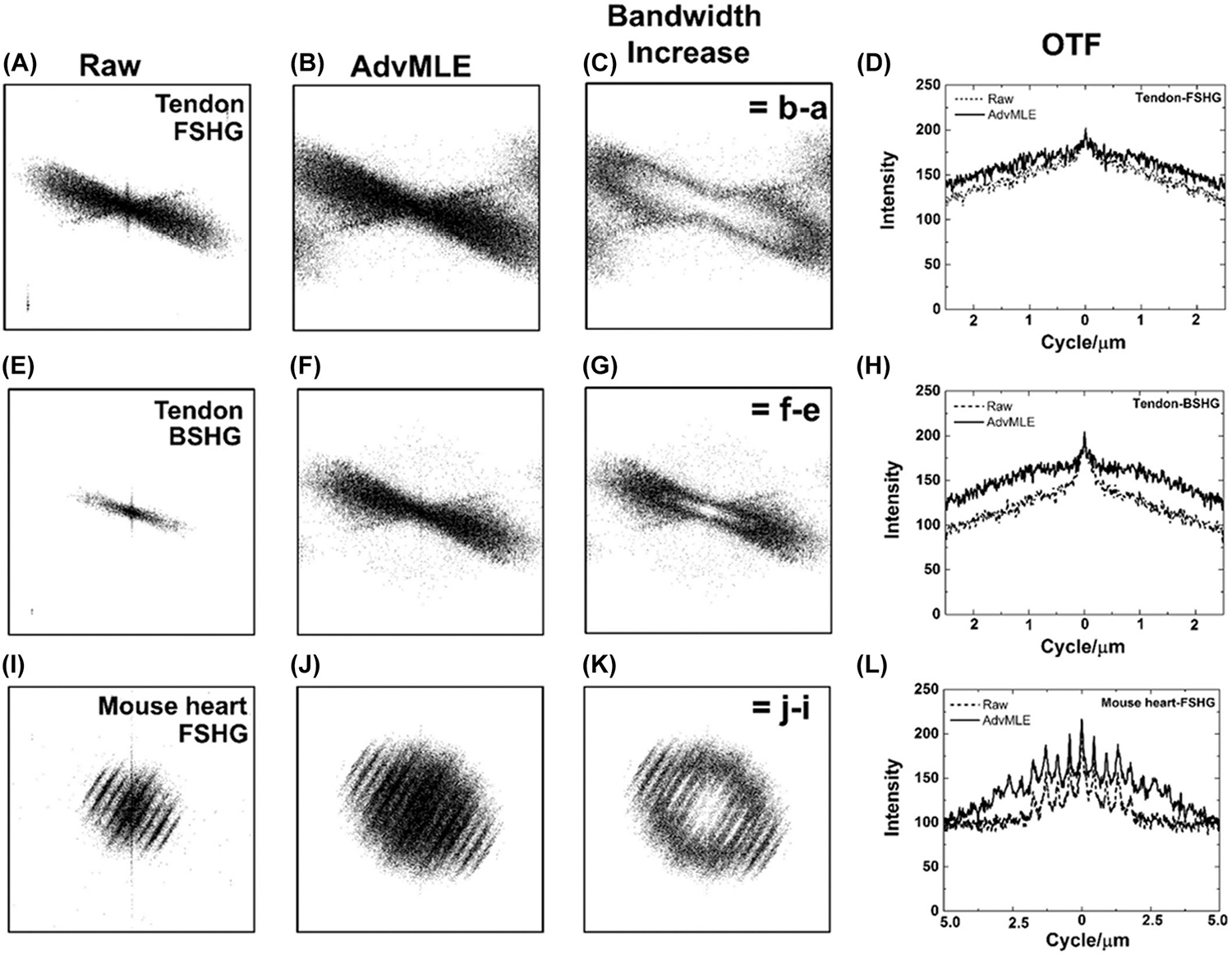
Impact of AdvMLE processing on spatial-frequency bandwidth and optical transfer function. The FFT of images in Figures 2 and 4 and their optical transfer function (OTF) showing the spatial-frequency bandwidth for (A)–(D) FSHG and (E)–(H) BSHG images chicken tendon, and (I)–(L) FSHG images of mouse heart sarcomere. The bandwidth increase for (C), (G), (K) AdvMLE-processed images is obtained by subtracting the corresponding raw from the processed images in the frequency spectrum. A line intensity profile drawn across the maximum width of the frequency distribution (see Fig S2) calibrated to indicate the OTF metric showing location (cycles μm⁻¹) of the frequency improvement for images (C), (G) and (K). The frame (left, right and top and bottom) of each image (A)–(C), (E)–(G) and (I)–(K) represents 0.39 μm cycle⁻¹, the centre wavelength of the collected SHG signal of the two-photon excitation wavelength 780 nm.

Table 1.

Summary of results showing AdvMLE performance over SHG images of various structures. The values in the parenthesis indicate percent improvement.

Parameter/tested samples	Peak intensity		modality	Resolution (FWHM) (μm)
	Raw	AdvMLE		Raw	AdvMLE
Gold nanoparticles (BSHG)	Not applicable			2.58 (XZ)	1.79 (31%)
				0.97 (XY)	0.69 (29%)
Collagen (FSHG)	111	182 (63%)a		0.53	0.26 (51%)a
Collagen (BSHG)	52	190 (265%)a		0.54	0.37 (31%)a
Heart sarcomere (FSHG)	84	116 (39 ± 19)b		0.49	0.30(31 ± 13)b

^aThe values are mean average peak intensity across multiple fibres.

^bThe values are mean average peak intensity across multiple fibres at three different locations ± SD.

Discussion

Owing to the fact that SHG is a second-order nonlinear optical scattering process, it may perhaps be surprising that AdvMLE deconvolution algorithm works so well on the acquired SHG images. However, it is useful to realise that the nonlinearity in SHG microscopy is essentially in the frequency conversion from pump photons to frequency-doubled signal photons. Once the SHG signal is generated, the problem can be reasonably approximated as wave propagation in a linear medium with modest noise contribution, similar to that of any linear microscopy technique, assuming that the medium has minimal scattering. However, in the coherent nature of the second-harmonic generation process means that the second-harmonic signal generated from the point particle is not isotropically emitted. This prevents a direct application of linear systems theory because, in general, PSFs are for incoherent processes. Hence, the developed AdvMLE algorithm makes an initial guess based on the SHG imaging optical parameters and then creates a PSF adaptively using the provided SHG image data set (see Fig. 1). It is for this reason that the developed deconvolution algorithm worked well in this study and could be adapted to other coherent, nonlinear optical imaging techniques such as coherent anti-Stokes Raman scattering microscopy, third-harmonic generation imaging and stimulated Raman scattering microscopy.

An important pointto note is that a multiple scattering medium would hamper the application of deconvolution because strong scattering introduces nonlinearity. This would be true for any optical imaging modality. However, the tissues studied in this work do not have sufficient scattering to prevent the application of the AdvMLE deconvolution algorithm. Interestingly, as noted earlier, we do see some effects of scattering when we compare the spatial-frequency bandwidth of BSHG tendon images to that of the FSHG images. Owing to the fact that the resolution enhancement is limited by the SNR of the data, the application of the deconvolution algorithm to FSHG images is more effective than to BSHG images as the latter has lower SNR and reduced multiple scattering compared to the former. This is implied by the OTF plots we have obtained from these modalities. The higher amplitude of the OTFs in AdvMLE-processed BSHG images compared to raw BSHG images emphasises the fact that better noise removal is observed for BSHG images compared to FSHG images.

One of the immediate benefits of the algorithm used in this work to SHG microscopy is in their potential to improve the accuracy in quantitative SHG imaging calculations. For example, Fourier transform second-harmonic generation (FT-SHG) imaging has been used extensively to quantify the collagen fibre spatial organization in tissues such as bone (Ambekar et al., 2012a), horse tendon (Sivaguru et al., 2010; Sivaguru et al., 2014a), chicken tendon (Sivaguru et al., 2014b) and cervical microenvironment (Lau et al., 2013). In these cases, FT-SHG is used to estimate the spread in relative collagen fibre orientation, which is subsequently used as a metric for biological assessment. The deconvolution algorithms we have presented in this work could be used to better resolve the imaged collagen fibres in studies such as these. As a result, quantitation of their relative orientation, in both 2D and 3D, would become more accurate. The improved accuracy will also help in quantitative SHG imaging based on the use of the forward to backward SHG signal ratio (Williams et al., 2005; Sivaguru et al., 2010). Visualisation of the helical pattern of the collagen after application of our algorithm could potentially lead to identification of changes in this pattern due to tendon diseases or rupture due to sports injury (Sivaguru et al., 2010; Sivaguru et al., 2014a,b).

Conclusion

In this paper, we have demonstrated resolution enhancement in SHG images using an AdvMLE deconvolution algorithm. Beginning with a synthetic guess PSF our deconvolution algorithm develops a PSF for the supplied SHG image and improves the spatial resolution and SNR for SHG images of collagen in tendon and myosin in heart sarcomere. The algorithm further enhances the SNR in SHG images by ~3.5 times, thereby revealing underlying helical structures of collagen fibres in SHG images with an ~26% increase in amplitude contrast in the fibre pitch. It is available as a part of image analysis deconvolution package with the Olympus CellSens program.

Several changes can be proposed to improve the results presented in this paper. The observed SNR can be further enhanced by introducing coherent detection techniques, such as the use of heterodyning, which could offer yet at least another order of magnitude enhancement (Tsuji et al., 1997). Furthermore, because of the efficient reassignment of out-of-focus photons that deconvolution provides, the overall method could be combined with holographic SHG microscopy (Smith et al., 2013), where this latter modality would benefit from removal of artefacts for improved localisation of objects in a volume (Latychevskaia et al., 2010). This approach could also be extended in similar approaches already made to contrast enhancement in medical imaging techniques used for disease diagnostics and treatments such as micro-nano computer tomography (Benzarti & Amiri, 2013), X-ray (Jiang & Wang, 2003) and magnetic resonance imaging (Usha & Perumal, 2016), to narrow down the tumour area or swelling in biological tissues there by targeting the treatment to a much narrower focal volume (such as in radiation therapy), thereby reducing the amount of normal tissue damage and complications.