Summary:
We consider methods for causal inference in randomized trials nested within cohorts of trial-eligible individuals, including those who are not randomized. We show how baseline covariate data from the entire cohort, and treatment and outcome data only from randomized individuals, can be used to identify potential (counterfactual) outcome means and average treatment effects in the target population of all eligible individuals. We review identifiability conditions, propose estimators, and assess the estimators’ finite-sample performance in simulation studies. As an illustration, we apply the estimators in a trial nested within a cohort of trial-eligible individuals to compare coronary artery bypass grafting surgery plus medical therapy versus medical therapy alone for chronic coronary artery disease.
Keywords: causal inference, clinical trials, double robustness, generalizability, observational studies, transportability
1. Introduction
When effect modifiers influence who participates in randomized trials, causal inferences from randomized individuals need to be generalized (extended) to the population of all trial-eligible individuals (Rothwell, 2005). The need to extend trial findings arises naturally when trials are nested in cohort studies that collect baseline covariate data from all eligible individuals, including those who are not randomized. In this setting, treatment and follow-up data from non-randomized individuals might be unavailable or unreliable. For example, investigators might wish to use treatment and outcome information only from randomized individuals to avoid confounding of the treatment effect among non-randomized individuals (Torgerson and Sibbald, 1998; Silverman and Altman, 1996).
In this paper, we build on the emerging literature on “generalizing” and “transporting” inferences from randomized trials to a target population (Cole and Stuart, 2010; Tipton, 2012; O’Muircheartaigh and Hedges, 2014; Hartman et al., 2013; Rudolph and van der Laan, 2017; Zhang et al., 2016) to show how data from randomized trials nested within cohorts of eligible individuals can be used to generalize inferences from randomized individuals to the target population of all trial-eligible individuals. We review identifiability conditions and propose estimators for the potential (counterfactual) outcome means and average treatment effects in the target population. We assess the finite-sample performance of different estimators in simulation studies. Lastly, we illustrate the application of the estimators in the Coronary Artery Surgery Study (CASS), a randomized trial nested within a cohort of trial-eligible individuals to compare coronary artery bypass grafting surgery plus medical therapy versus medical therapy alone for chronic coronary artery disease.
2. Targets of inference
Consider a trial nested in a cohort of trial-eligible individuals and let be the set of treatments evaluated in the randomized trial. For each treatment , we use the random variable to denote the potential (counterfactual) outcome under intervention to receive treatment (Splawa-Neyman, 1990; Rubin, 1974; Robins and Greenland, 2000). We only consider a finite number of distinct treatments (e.g., comparisons of treatment vs. control, or comparisons between two or more active treatments).
Baseline covariate information is collected from all cohort members, but treatment and outcome information is only collected (or only deemed reliable) from randomized individuals. We model the data as independent and identically distributed realizations of the random tuple , , where is the number of randomized individuals, is the number of non-randomized individuals, and is the total number of trial-eligible individuals; is the indicator for being randomized ( for randomized individuals; for non-randomized trial-eligible individuals); is a vector of baseline covariates; is the (randomized) treatment assignment indicator; and is the observed outcome. An example data structure for binary treatment , along with the potential outcomes, is depicted in Table 1 (throughout, we use uppercase letters to denote random variables and lowercase letters to denote realizations). For simplicity, we assume that full adherence to assigned treatment, absence of measurement error, and no dropout in the trial. Though the methods we propose can be extended to address these issues, we do not pursue these extensions here to simplify exposition and maintain focus on selective trial participation. Extensions of our results will be considered in future work.
Table 1:
The left-hand-side of the table depicts the data structure, including baseline covariates , the trial participation indicator ( for the randomized indviduals and for the non-randomized individuals), the binary treatment (), and the observed outcome (). The right hand side of the table depicts the potential outcomes and under treatment and , respectively. The consistency assumption allows us to equate some of these potential outcomes with the observed outcomes, depending on trial participation and treatment assignment. Dashes denote missing values in the observed data.
| Individual | ||||||
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | ||||
| 2 | 1 | 1 | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 1 | 1 | |||||
| 1 | 0 | |||||
| 1 | 0 | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 1 | 0 | |||||
| 0 | – | – | ||||
| 0 | – | – | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 0 | – | – |
We are interested in using the data to draw causal inferences about all trial-eligible individuals. Key targets of inference are the potential outcome means , for each , and the average treatment effects , for any pair of treatments , . In general, ; in our setup, differences arise when effects are heterogeneous over baseline covariates that are not equidistributed among randomized and non-randomized individuals (Dahabreh et al., 2016).
3. Identifiability conditions for potential outcome means
The following conditions are sufficient to identify the potential outcome means for : (I) Consistency of potential outcomes: for individuals who receive treatment , the observed outcome equals the potential outcome under treatment , that is, if , then , for every . (II) Mean exchangeability in the trial: for every . (III) Positivity of treatment assignment probability in the trial: for every and every such that . (IV) Mean generalizability (i.e., mean exchangeability over ): for every . The mean generalizability condition is implied by, but does not imply, the often invoked (and stronger) condition of generalizability in distribution, . (V) Positivity of trial participation: for every such that .
Conditions I through III are expected to hold for well-defined interventions compared in randomized trials (Hernán and Robins, 2018). Of note, implicit in our notation is an assumption that the invitation to participate in the trial and trial participation itself do not affect the outcome except through treatment assignment – this assumption is often plausible in pragmatic randomized trials (Ford and Norrie, 2016). Conditions IV and V are needed to extend inferences about the potential outcome means (or the average treatment effect) from randomized individuals to the target population of all trial-eligible individuals.
As is common in the causal inference literature, we use the term “exchangeability” to mean that two or more groups are expected to have the same outcome functionals had they received the same treatment (Greenland and Robins, 1986). This notion differs from other uses of the term in statistics. Furthermore, in this section, we used the term “consistency” for the condition linking potential (counterfactual) and observed outcomes; later, we will use the same term to refer to the property of an estimator that converges to its estimand; the intended meaning should be clear from context.
4. Identification
Under the identifiability conditions listed in the previous section, the conditional potential outcome mean in the target population of all trial eligible individuals for each treatment can be identified,
It follows that we can identify the potential outcome means,
where the subscript denotes expectation with respect to the target population distribution of . Using this result, we can identify average treatment effects by differencing,
Furthermore, we can identify any other measure of effect defined in terms of the potential outcome means (Hernán, 2004); for example, for binary , we can identify the causal risk ratio comparing treatments and in the target population,
In the Appendix, we show that identification of average treatment effects is possible under weaker identifiability conditions, which do not, however, suffice to identify the potential outcome means. Because these potential outcome means are of inherent scientific and policy interest in most applications, in the remainder of the paper we focus on estimating them.
5. Estimation
We now discuss estimators of the functional . Specifically, we consider (1) outcome model-based estimators that rely on modeling the expectation of the outcome; (2) inverse probability (IP) weighting estimators that rely on modeling the probability of participation in the trial; and (3) augmented IP weighting estimators that rely on modeling both the expectation of the outcome and the probability of participation in the trial. Hereafter, “convergence” and the symbol “” denote convergence in probability; estimators that converge to their corresponding estimands are termed “consistent” (see the Web Appendix for additional information).
5.1. Outcome model-based estimator
The outcome model-based estimator is obtained by fitting a conditional outcome mean model among trial participants and marginilizing over the empirical covariate distribution of all trial-eligible individuals (Robins, 1986),
| (1) |
where is an estimator of for . Typically, we posit a parametric outcome model with finite-dimensional parameter for each treatment , and estimate the model parameters by standard methods. In applications, we recommend fitting separate outcome models among the treated and untreated randomized individuals to better capture effect modification over baseline covariates. When the outcome models are correctly specified, and for each .
5.2. IP weighting estimators
An alternative approach for generalizing inferences from randomized individuals to the target population relies on estimating the probability of trial participation followed by IP weighting, an approach related to the analysis of sampling surveys (Horvitz and Thompson, 1952) and to IP weighting methods for confounding control in observational studies (Robins, 1999). Specifically, we can use the IP weighting estimator
| (2) |
where is an estimator for and is an estimator for for . When trials are nested within cohorts of eligible individuals, we do not know the probability of trial participation, but we can estimate it, typically using a parametric model . The probability of treatment in the trial is under the control of the investigators and does not need to be estimated. Nevertheless, estimating the probability of treatment among randomized individuals, say using a parametric model , can improve efficiency in finite samples. Heuristically, modeling the probability of treatment is beneficial because it addresses random imbalances in baseline covariates among randomized individuals, provided that we properly account for the estimation of (Hahn, 1998; Lunceford and Davidian, 2004, Williamson et al., 2014). When the model for the probability of participation is correctly specified, and given that the model for the probability of treatment among randomized individuals is always correctly specified, and for every .
The estimator in (2) is unbounded, in the sense that it can produce point estimates that fall outside the support of , particularly in the presence of extreme weights (Robins et al., 2007). Using the identity
| (3) |
which holds when positivity conditions III and V hold, we can construct a bounded IP weighting estimator by normalizing the weights to sum to 1 (Hájek, 1971),
| (4) |
Even when not intending to use IP weighting estimators, analysts should inspect the distribution of the estimated probabilities of trial participation to examine overlap between randomized and non-randomized individuals. Furthermore, analysts should examine whether the sample analog of (3) is approximately satisfied, that is,
5.3. Augmented IP weighting estimators
We can combine modeling the probability of trial participation with modeling the expectation of the outcome among randomized individuals to obtain more efficient (augmented) IP weighting estimators (Robins et al., 1994; Bang and Robins, 2005). Augmented IP weighting estimators are also doubly robust in the sense that they are consistent and asymptotically normal when either the model for the probability of participation or the model for the expectation of the outcome is correctly specified. Because background knowledge is often inadequate to correctly specify the outcome model, the improved efficiency of augmented IP weighting estimators is often the primary motivation for using them (Tan, 2007), provided the model for the probability of trial participation can be (approximately) correctly specified.
The theory of augmented IP weighting estimation is extensive and multiple estimators, with different behavior in finite samples, are doubly robust (Robins et al., 1994, 2007). Here, we examine three estimators that are easy to implement in standard statistical packages.
We begin by considering the augmented IP weighting estimator
| (5) |
with , , and as defined above.
We can normalize the weights, as we did for the IP weighting estimators, to obtain
| (6) |
Alternatively, we can obtain a bounded regression-based augmented IP weighting estimator by fitting an IP weighted parametric multi-variable regression model for the outcome among randomized individuals and then standardizing the predictions over the empirical covariate distribution of all trial-eligible individuals,
| (7) |
where is the vector of estimated parameters from the IP weighted outcome regression. This estimator is doubly robust when the outcome is modeled with a linear exponential family quasi-likelihood (Gourieroux et al., 1984) and the canonical link function (Robins et al., 2007; Wooldridge, 2007).
In the Web Appendix we show that the estimator in (5) is the one-step in-sample estimator suggested by the influence function for and argue that it is locally efficient (Robins et al., 1994; Robins and Rotnitzky, 1995). The estimators in (6) and (7) are asymptotically equivalent to the estimator in (5). In finite samples, augmented IP weighting estimators will tend to produce more precise results than non-augmented IP weighting estimators, sometimes strikingly so. When using any augmented IP weighting estimator, as for the outcome model-based estimator in (1), we recommend fitting separate outcome models in each treatment group in the randomized trial.
6. Simulation studies
We conducted simulation studies to compare the finite-sample performance of different estimators, for binary and continuous outcomes. Details about the simulation study methods and code to replicate the analyses are provided in the Web Appendix; the simulation results are summarized in Appendix Tables A.2 through A.19. In brief, our numerical studies confirmed that, when all models were correctly specified, all estimators were approximately unbiased even with small numbers of randomized individuals and small total cohort sample sizes (when one model was incorrectly specified, the augmented IP weighting estimators were also approximately unbiased; results not shown). The outcome-model based estimator had the lowest variance, followed closely by the two doubly robust estimators; IP weighting estimators had substantially larger variance than all other estimators, especially when using non-normalized weights.
7. The Coronary Artery Surgery Study (CASS)
7.1. CASS design and data
CASS was a comprehensive cohort study that compared coronary artery bypass grafting surgery plus medical therapy (henceforth, “surgery”) versus medical therapy alone for individuals with chronic coronary artery disease; details about the design of CASS are available elsewhere (William et al., 1983; Investigators, 1984). In brief, individuals undergoing angiography in 11 participating institutions were screened for eligibility and the 2099 trial-eligible individuals who met the study criteria were either randomized to surgery or medical therapy (780 individuals), or included in an observational study (1319 individuals). We excluded 6 individuals for consistency with prior CASS analyses and in accordance with CASS data release notes; in total we used data from 2093 individuals (778 randomized; 1315 non-randomized). Baseline covariates were collected from randomized and non-randomized individuals in an identical manner. No randomized individuals were lost to follow-up in the first 10 years of the study; we did not use information on adherence among randomized individuals, in effect assuming that the non-adherence would be similar among all eligible individuals, so that intention-to-treat effects are transportable.
7.2. Statistical analysis
Estimands.
We estimated the 10-year mortality risk under surgery and medical therapy, and the risk difference and risk ratio comparing the treatments for the target population of all trial-eligible individuals.
Model specification.
We fit logistic regression models for the probability of participation in the trial, the probability of treatment among randomized individuals, and the probability of the outcome (in each treatment arm) with the following covariates: age, severity of angina, history of previous myocardial infarction, percent obstruction of the proximal left anterior descending artery, left ventricular wall motion score, number of diseased vessels, and ejection fraction. We chose these variables based on a previous analysis of the same data (Olschewski et al., 1992) and did not perform any model selection.
Missing baseline covariate data.
Of the 2093 trial-eligible individuals, 1686 had complete data on all baseline covariates (731 randomized, 368 in the surgery group and 363 in the medical therapy group; 955 non-randomized). For simplicity, in the main text we only report analyses restricted to individuals with complete data. To examine whether missing data influenced our results, we repeated our analyses using (1) multiple imputation with different models for the missing data conditional on the observed data (multivariate normal multiple imputation and multiple imputation with chained equations) (Little and Rubin, 2014) and (2) IP of missingness weighting for non-monotone missing data (Sun and Tchetgen Tchetgen, 2018).
Inference.
For all analyses, we used bootstrap resampling (with 10,000 samples) to obtain normal distribution-based 95% confidence intervals (results using percentile intervals were very similar and are not shown).
7.3. Results
Baseline characteristics, overlap, and balance.
Web Appendix Table A.20 summarizes baseline covariate information for randomized and non-randomized individuals. The left panel of Figure 1 presents kernel densities of the estimated probabilities of trial participation for randomized and non-randomized individuals; there was good overlap and the smallest estimated probability for trial participation for randomized individuals was approximately 0.273. The right panel of Figure 1 presents the kernel density of the estimated weights among randomized individuals, obtained as the inverse of the estimated probability of trial participation times the inverse of the estimated probability of receiving the treatment actually received among randomized individuals. The sample average of the estimated weights was approximately 1.001, both in the surgery and medical therapy groups; the largest estimated weight was less than 10. Taken together, these results suggest that the observed covariate distributions of randomized and non-randomized individuals had sufficient overlap for attempting to extend inferences from the trial to the target population of all eligible individuals. Baseline covariates in randomized and non-randomized individuals were balanced after IP weighting (Web Appendix Table A.21).
Figure 1:
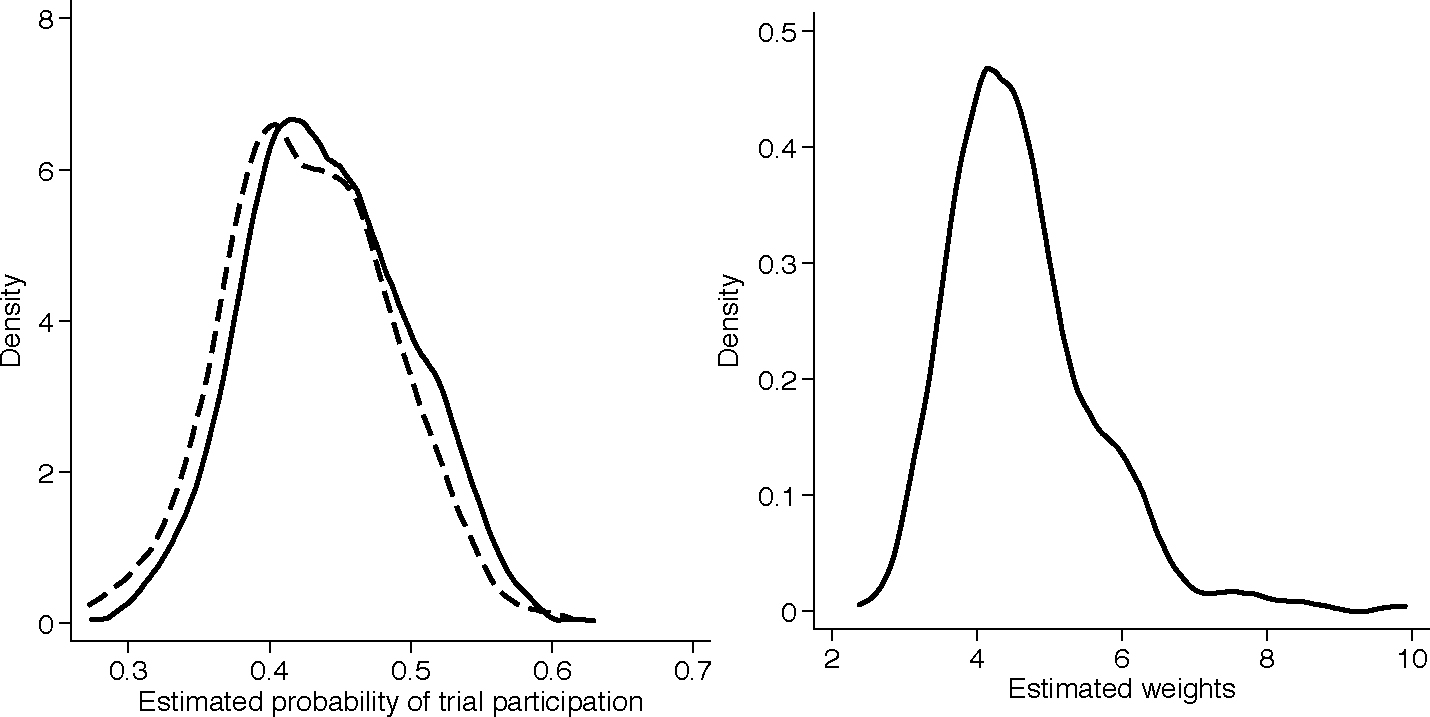
Kernel densities of the estimated probabilities of trial participation (left panel) for randomized (solid line) and non-randomized (dashed line) individuals and estimated weights (right panel) for randomized individuals.
Treatment-specific risks and treatment effects.
Estimates of the 10-year mortality risk and treatment effects at 10 years are shown in Table 2. All generalizability methods produced similar results: the mortality risk in the target population was about 18% for surgery and 20% for medical therapy, corresponding to a risk difference of about 2% and a risk ratio of about 0.9, in favor of surgery. Because different methods rely on different parametric models, agreement across their point estimates suggests that inference is not driven by model specification. The similar confidence interval widths produced by different generalizability estimators reflect the binary nature of the outcome as well as the absence of strong selection on measured baseline covariates in this particular application. The mortality risk among randomized individuals was about 17.3% for surgery and 20.9% for medical therapy, corresponding to a risk difference of about 3.5% in favor of surgery. The closeness of estimates from the randomized trial and our generalizability analyses probably reflects the absence of strong selection on measured baseline covariates in this application.
Table 2:
Estimated 10-year mortality risk (%) for surgery and medical therapy, and risk difference and risk ratio comparing the treatments among randomized individuals and all trial-eligible individuals in the Coronary Artery Surgery Study. For each point estimate we provide bootstrap confidence intervals from 10,000 re-samplings. Surgery = coronary artery bypass grafting surgery plus medical therapy; CI = confidence interval; Medical = medical therapy; RD = risk difference; RR = risk ratio; Trial-only = unadjusted analysis using only observations from randomized individuals; OM = outcome model-based standardization; IPW1 = inverse probability weighting; IPW2 = inverse probability weighting with normalized weights; AIPW1 = augmented inverse probability weighting; AIPW2 = augmented inverse probability weighting with normalized weights; AIPW3 = inverse probability weighted regression; (eq.) gives the equation number for each estimator.
| Target population | Estimator (eq.) | Surgery (%) | 95% CI | Medical (%) | 95% CI | RD (%) | 95% CI | RR | 95% CIS |
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| Randomized individuals | Trial-only | 17.4 | (13.5, 21.3 ) | 20.1 | (15.9, 24.3 ) | −2.7 | (−8.5, 3.0) | 0.86 | (0.59, 1.14) |
|
| |||||||||
| All trial-eligible individuals | OM (1) | 18.5 | (14.3, 22.6) | 20.0 | (15.9, 24.0) | −1.5 | (−7.2, 4.2) | 0.93 | (0.64, 1.21) |
| IPW1 (2) | 18.0 | (13.9, 22.1) | 19.9 | (15.9, 24.0) | −2.0 | (−7.7, 3.8) | 0.90 | (0.62, 1.18) | |
| IPW2 (4) | 18.0 | (13.9, 22.0) | 19.9 | (15.9, 24.0) | −2.0 | (−7.7, 3.8) | 0.90 | (0.62, 1.18) | |
| AIPW1 (5) | 18.3 | (14.2, 22.4) | 20.0 | (15.9, 24.0) | −1.6 | (−7.3, 4.1) | 0.92 | (0.64, 1.20) | |
| AIPW2 (6) | 18.3 | (14.2, 22.4) | 20.0 | (15.9, 24.0) | −1.6 | (−7.3, 4.1) | 0.92 | (0.64, 1.20) | |
| AIPW3 (7) | 18.3 | (14.2, 22.4) | 19.9 | (15.9, 23.9) | −1.6 | (−7.2, 4.1) | 0.92 | (0.64, 1.20) | |
Using treatment and outcome data on non-randomized individuals to evaluate the generalizability analyses.
In CASS, data on treatment and outcome were collected among non-randomized individuals, even though such data are not necessary for identification under the conditions in Section 3. To evaluate whether outcome models built among randomized individuals were reasonable, we compared the empirical mortality risk among non-randomized individuals who received treatment against the average outcome predictions for the same group of individuals, using models estimated among randomized individuals. The similarity of the empirical risk in non-randomized individuals to the average of the predictions provides some reassurance that the models were not grossly inappropriate for generalizing trial results: for surgery, the empirical risk was 18.6% and the average of the predictions was 19.8%; for medical therapy, the empirical risk was 19.1% and the average of the predictions was 18.9%.
The comparison in the preceding paragraph is only indirectly relevant to the goal of generalizing inferences to the target population of all trial-eligible individuals; after all, the comparison is conditional on treatment received among non-randomized individuals. Another way to evaluate the generalizability analyses, is to compare them against an observational analysis that uses all the data (regardless of ). The validity of such observational analysis requires exchangeability of treatment groups, , and positivity, , for , but does not require identifiability conditions IV or V (which are necessary to endow the generalizability estimators with a causal interpretation). Using an IP weighting regression estimator for confounding control in the entire CASS dataset (Robins et al., 2007), the potential outcome mean estimates were 17.9% and 19.6% for surgery and medical therapy, respectively; these estimates are similar to those from the generalizability analyses. Because the observational and generalizability analyses rely on different identifiability conditions, agreement between them provides some mutual support (but does not establish the validity of either).
Comparison of methods for handling missing data.
Web Appendix A.22 presents descriptive statistics for missing covariate data; the missing data pattern for baseline covariates was non-monotone. The point estimates from analyses using multiple imputation or IP weighting for missing baseline covariates were nearly identical to those of the complete case analyses and only slightly more precise (Web Appendix Tables A.23 through A.25).
8. Discussion
We examined methods for extending inferences from randomized individuals to the target population of trial-eligible individuals, using trials nested within cohorts for outcomes observed at a single time-point post-randomization. Our work adds to the literature on “generalizability” and “transportability” (Cole and Stuart, 2010; O’Muircheartaigh and Hedges, 2014; Tipton, 2012; Hartman et al., 2013; Zhang et al., 2016; Rudolph and van der Laan, 2017), and connects with the literature on selection bias (Keiding and Louis, 2016; Infante-Rivard and Cusson, 2018).
The methods we propose rest on two identifiability conditions beyond those supported by randomization: mean generalizability from randomized to non-randomized individuals and positivity of trial participation. Directed acyclic graphs can facilitate reasoning about the mean generalizability condition (Pearl, 2015; Pearl and Bareinboim, 2014). Arguably, the identifiability conditions are most plausible in studies explicitly designed to collect information on all trial-eligible individuals, including those who are not randomized. Our methods are therefore appropriate for “comprehensive cohort studies” (Olschewski et al., 1985, 1992; Schmoor et al., 1996), randomized preference designs (Torgerson and Sibbald, 1998; Lambert and Wood, 2000), and pragmatic trials embedded within healthcare systems (Fiore and Lavori, 2016; Choudhry, 2017). Though our approach is useful for extending inferences from randomized individuals to trial-eligible individuals in these designs, it does not address individuals who are candidates for treatment but do not meet the trial eligibility criteria.
Our approach uses treatment and outcome data only from randomized individuals, to avoid confounding of the treatment effect among non-randomized individuals and eliminate the need to follow them up. Nevertheless, if treatment and outcome data from non-randomized individuals are available, analysts can use them to assess model specification, as we did in the CASS reanalysis. When such data are available and substantive knowledge suggests that the observed covariates suffice to adjust for confounding among non-randomized individuals, it may be useful to compare the results of generalizability methods against the results of observational analyses of the entire cohort. These analyses target the same causal quantities but rest on different identifiability conditions: generalizability analyses require mean generalizability from randomized to non-randomized individuals whereas observational analyses require mean exchangeability of treated and untreated individuals. As in our CASS reanalysis, similarity of results from analyses that rest on different identifiability conditions provides mutual support for their validity (but does not definitively establish it).
Methods for generalizing inferences from randomized individuals to all trial-eligible individuals exploit models for the expectation of the outcome in the trial or the probability of trial participation. Investigators typically rely on parametric working models and model misspecification can lead to inconsistency, even if mean generalizability holds. Approximately correct specification of the model for the probability of participation may be more feasible, because inverstigators can use surveys or qualitative studies to investigate what drives eligible individuals to participate in a randomized trial (Ross et al., 1999). The findings from these investigations can be used to specify models for trial participation and obtain consistent IP weighting estimators.
Augmented IP weighting estimators are consistent when either working model is correctly specified, providing two opportunities for valid inference. Misspecification of just one of the models can adversely affect how these estimators perform. And misspecification of both models, in some cases (Waernbaum and Pazzagli, 2017), can make augmented IP weighting estimators perform worse than the (misspecified) outcome model-based estimator (Kang and Schafer, 2007). Serious bias can also occur when IP weights are highly variable, though this problem is to some extent mitigated with bounded estimators (Robins et al., 2007). Even when the outcome model is misspecified, augmented IP weighting estimators may still be preferred for their typically increased efficiency compared to non-augmented IP weighting estimators; their performance may be further improved with approaches that explicitly attempt to minimize variance (Cao et al., 2009; Rotnitzky et al., 2012) or reduce bias (Vermeulen and Vansteelandt, 2015) under model misspecification.
Supplementary Material
Acknowledgments
This work was supported by Patient-Centered Outcomes Research Institute (PCORI) awards ME-1306–03758 and ME-1502–27794 and National Institutes of Health (NIH) grant R37 AI102634. Statements in this paper do not necessarily represent the views of the PCORI, its Board of Governors, the Methodology Committee, or the NIH. The data analyses in our paper used CASS research materials obtained from the NHLBI Biologic Specimen and Data Repository Information Coordinating Center. This paper does not necessarily reflect the opinions or views of the CASS or the NHLBI. The authors thank Christopher H. Schmid and Bora Youn (both at Brown University) for helpful discussions.
Footnotes
9. Supplementary Materials
Web Appendices, Tables, and Figures referenced in Sections 5 through 7, including example R code implementing the methods, are available with this paper at the Biometrics website on Wiley Online Library.
References
- Bang H and Robins JM (2005). Doubly robust estimation in missing data and causal inference models. Biometrics 61, 962–973. [DOI] [PubMed] [Google Scholar]
- Cao W, Tsiatis AA, and Davidian M (2009). Improving efficiency and robustness of the doubly robust estimator for a population mean with incomplete data. Biometrika 96, 723–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choudhry NK (2017). Randomized, controlled trials in health insurance systems. New England Journal of Medicine 377, 957–964. [DOI] [PubMed] [Google Scholar]
- Cole SR and Stuart EA (2010). Generalizing evidence from randomized clinical trials to target populations: the ACTG 320 trial. American Journal of Epidemiology 172, 107–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahabreh IJ, Hayward R, and Kent DM (2016). Using group data to treat individuals: understanding heterogeneous treatment effects in the age of precision medicine and patient-centred evidence. International Journal of Epidemiology 45, 2184–2193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiore LD and Lavori PW (2016). Integrating randomized comparative effectiveness research with patient care. New England Journal of Medicine 374, 2152–2158. [DOI] [PubMed] [Google Scholar]
- Ford I and Norrie J (2016). Pragmatic trials. New England Journal of Medicine 375, 454–463. [DOI] [PubMed] [Google Scholar]
- Gourieroux C, Monfort A, and Trognon A (1984). Pseudo maximum likelihood methods: Theory. Econometrica: Journal of the Econometric Society pages 681–700. [Google Scholar]
- Greenland S and Robins JM (1986). Identifiability, exchangeability, and epidemiological confounding. International Journal of Epidemiology 15, 413–419. [DOI] [PubMed] [Google Scholar]
- Hahn J (1998). On the role of the propensity score in efficient semiparametric estimation of average treatment effects. Econometrica 66, 315–331. [Google Scholar]
- Hájek J (1971). Comment on “An essay on the logical foundations of survey sampling by D. Basu”. In Godambe VP and Sprott DA, editors, Foundations of Statistical Inference. [Google Scholar]
- Hartman E, Grieve R, Ramsahai R, and Sekhon JS (2013). From SATE to PATT: combining experimental with observational studies to estimate population treatment effects. Journal of the Royal Statistical Society Series A (Statistics in Society) 10, 1111. [Google Scholar]
- Hernán MA (2004). A definition of causal effect for epidemiological research. Journal of Epidemiology and Community Health 58, 265–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán MA and Robins JM (2018). Causal inference (forthcoming). Chapman & Hall/CRC, Boca Raton, FL. [Google Scholar]
- Horvitz DG and Thompson DJ (1952). A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association 47, 663–685. [Google Scholar]
- Infante-Rivard C and Cusson A (2018). Reflection on modern methods: selection bias?a review of recent developments. International Journal of Epidemiology. [DOI] [PubMed] [Google Scholar]
- Investigators CP (1984). Coronary artery surgery study (CASS): a randomized trial of coronary artery bypass surgery: comparability of entry characteristics and survival in randomized patients and nonrandomized patients meeting randomization criteria. Journal of the American College of Cardiology 3, 114–128. [PubMed] [Google Scholar]
- Kang JD and Schafer JL (2007). Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science pages 523–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keiding N and Louis TA (2016). Perils and potentials of self-selected entry to epidemiological studies and surveys. Journal of the Royal Statistical Society. Series A (Statistics in Society) 179, 319–376. [Google Scholar]
- Lambert MF and Wood J (2000). Incorporating patient preferences into randomized trials. Journal of clinical epidemiology 53, 163–166. [DOI] [PubMed] [Google Scholar]
- Little RJ and Rubin DB (2014). Statistical analysis with missing data, volume 333. John Wiley & Sons. [Google Scholar]
- Lunceford JK and Davidian M (2004). Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Statistics in Medicine 23, 2937–2960. [DOI] [PubMed] [Google Scholar]
- Olschewski M, Scheurlen H, et al. (1985). Comprehensive cohort study: an alternative to randomized consent design in a breast preservation trial. Methods Archive 24, 131–134. [PubMed] [Google Scholar]
- Olschewski M, Schumacher M, and Davis KB (1992). Analysis of randomized and nonrandomized patients in clinical trials using the comprehensive cohort follow-up study design. Controlled Clinical Trials 13, 226–239. [DOI] [PubMed] [Google Scholar]
- O’Muircheartaigh C and Hedges LV (2014). Generalizing from unrepresentative experiments: a stratified propensity score approach. Journal of the Royal Statistical Society. Series C (Applied Statistics) 63, 195–210. [Google Scholar]
- Pearl J (2015). Generalizing experimental findings. Journal of Causal Inference 3, 259–266. [Google Scholar]
- Pearl J and Bareinboim E (2014). External validity: from do-calculus to transportability across populations. Statistical Science 29, 579–595. [Google Scholar]
- Robins JM (1986). A new approach to causal inference in mortality studies with a sustained exposure period – application to control of the healthy worker survivor effect. Mathematical Modelling 7, 1393–1512. [Google Scholar]
- Robins JM (1999). Association, causation, and marginal structural models. Synthese 121, 151–179. [Google Scholar]
- Robins JM and Greenland S (2000). Causal inference without counterfactuals: comment. Journal of the American Statistical Association 95, 431–435. [Google Scholar]
- Robins JM and Rotnitzky A (1995). Semiparametric efficiency in multivariate regression models with missing data. Journal of the American Statistical Association 90, 122–129. [Google Scholar]
- Robins JM, Rotnitzky A, and Zhao LP (1994). Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association 89, 846–866. [Google Scholar]
- Robins JM, Sued M, Lei-Gomez Q, and Rotnitzky A (2007). Comment: Performance of double-robust estimators when “inverse probability” weights are highly variable. Statistical Science 22, 544–559. [Google Scholar]
- Ross S, Grant A, Counsell C, Gillespie W, Russell I, and Prescott R (1999). Barriers to participation in randomised controlled trials: a systematic review. Journal of Clinical Epidemiology 52, 1143–1156. [DOI] [PubMed] [Google Scholar]
- Rothwell PM (2005). External validity of randomised controlled trials: “to whom do the results of this trial apply?”. The Lancet 365, 82–93. [DOI] [PubMed] [Google Scholar]
- Rotnitzky A, Lei Q, Sued M, and Robins JM (2012). Improved double-robust estimation in missing data and causal inference models. Biometrika 99, 439–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology 66, 688. [Google Scholar]
- Rudolph KE and van der Laan MJ (2017). Robust estimation of encouragement design intervention effects transported across sites. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 79, 1509–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmoor C, Olschewski M, and Schumacher M (1996). Randomized and non-randomized patients in clinical trials: experiences with comprehensive cohort studies. Statistics in Medicine 15, 263–271. [DOI] [PubMed] [Google Scholar]
- Silverman WA and Altman DG (1996). Patients’ preferences and randomised trials. The Lancet 347, 171–174. [DOI] [PubMed] [Google Scholar]
- Splawa-Neyman J (1990). On the application of probability theory to agricultural experiments. essay on principles. section 9. [Translated from Splawa-Neyman, J (1923) in Roczniki Nauk Rolniczych Tom X, 1–51]. Statistical Science 5, 465–472. [Google Scholar]
- Sun B and Tchetgen Tchetgen EJ (2018). On inverse probability weighting for non-monotone missing at random data. Journal of the American Statistical Association 113, 369–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan Z (2007). Comment: Understanding OR, PS and DR. Statistical Science 22, 560–568. [Google Scholar]
- Tipton E (2012). Improving generalizations from experiments using propensity score subclassification assumptions, properties, and contexts. Journal of Educational and Behavioral Statistics 38, 239–266. [Google Scholar]
- Torgerson DJ and Sibbald B (1998). Understanding controlled trials. what is a patient preference trial? BMJ: British Medical Journal 316, 360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vermeulen K and Vansteelandt S (2015). Bias-reduced doubly robust estimation. Journal of the American Statistical Association 110, 1024–1036. [Google Scholar]
- Waernbaum I and Pazzagli L (2017). Model misspecification and bias for inverse probability weighting and doubly robust estimators. arXiv preprint arXiv:1711.09388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- William J, Russell R, Nicholas T, et al. (1983). Coronary artery surgery study (CASS): a randomized trial of coronary artery bypass surgery. Circulation 68, 939–950. [DOI] [PubMed] [Google Scholar]
- Williamson EJ, Forbes A, and White IR (2014). Variance reduction in randomised trials by inverse probability weighting using the propensity score. Statistics in medicine 33, 721–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wooldridge JM (2007). Inverse probability weighted estimation for general missing data problems. Journal of Econometrics 141, 1281–1301. [Google Scholar]
- Zhang Z, Nie L, Soon G, and Hu Z (2016). New methods for treatment effect calibration, with applications to non-inferiority trials. Biometrics 72, 20–29. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


