Measurements of Nonlinear Polarization Dynamics in the Tens of Gigahertz

Abstract

Frequency-dependent linear-permittivity measurements are commonplace in the literature, providing key insights into the structure of dielectric materials. These measurements describe a material’s dynamic response to a small applied electric field. However, nonlinear dielectric materials are widely used for their responses to large applied fields, including switching in ferroelectric materials, and field tuning of the permittivity in paraelectric materials. These behaviors are described by nonlinear permittivity. Nonlinear-permittivity measurements are fraught with technical challenges because of the complex electrical coupling between a sample and its environment. Here, we describe a technique for measuring the complex nonlinear permittivity that circumvents many of the difficulties associated with other approaches. We validate this technique by measuring the nonlinear permittivity of a tunable ${\mathrm{B}\mathrm{a}}_{0.5}{\mathrm{S}\mathrm{r}}_{0.5}{\mathrm{T}\mathrm{i}\mathrm{O}}_3$ thin film up to 40 GHz and comparing our results with a phenomenological model. These measurements provide insight into the dynamics of nonlinear dielectric materials down to picosecond timescales.

I. OVERVIEW

Ferroelectric and related materials have many applications that rely on a nonlinear relationship between the electric field and the polarization [1]. For example, the switching of the built-in polarization leads to both non-volatile memory and alternative transistor designs that utilize switching dynamics to increase power efficiency [2–8]. In microwave electronics, tunability of the permittivity with applied electric field enables components such as filters and phase shifters to be reconfigured by applying a dc voltage [9–12]. These switching and tuning processes can have complex time dependence that is difficult to measure at microwave frequencies.

In nonlinear dielectric materials, mesoscale structure, including domain walls and polar nanoregions (PNRs), [13–20] strongly influences the dynamics of nonlinear dielectric materials under an applied electric field. For example, PNRs in ${\mathrm{B}\mathrm{a}}_x{\mathrm{S}\mathrm{r}}_{1-x}{\mathrm{T}\mathrm{i}\mathrm{O}}_3$ thin films affect microwave-frequency dielectric loss and dispersion. Several reports also attribute the broad temperature dependence of the ferroelectric-paraelectric phase transition to PNRs [17–19,19,21–26]. While a great deal of previous research focused on understanding the effects of nanostructure on dielectric properties, in recent years researchers are making rapid progress in designing specific nanostructures in dielectrics to induce specific properties. Examples include low-loss tunable Ruddlesden-Popper (RP) superlattices [27], superlattices with polar vortices [28,29], and nanoparticles with vortex domains [30,31]. In all of these cases, theoretical tools (mesoscale theory and density-functional theory) could predict the static dielectric properties [27–30], but the dynamic properties remain more difficult to describe. Notably, even though reducing dielectric loss is a main motivation for the development of RP dielectrics, the current physical picture of loss mechanisms in those materials is qualitative, rather than predictive [20, 27]. In this case, the experimental characterization is limited to linear permittivity and static tuning. The addition of nonlinear-permittivity measurements would provide additional information that could aid in the development and validation of dynamic models.

Figure 1 schematically shows two approaches to nonlinear measurements. At low frequencies, the interpretation of time-domain measurements is straightforward [Fig. 1(a)]. One applies a steplike voltage pulse to a capacitor, and measures the current that flows as the capacitor charges [32–35]. The current is proportional to the time-derivative of the polarization. At short timescales (10 s of ps), this approach becomes more difficult because it becomes increasingly hard to account for all of the sources of signal distortion in the experiment [34,35]. Time-domain calibrations are possible in principle, but require specialized instrumentation and would add a great deal of complexity to a measurement system [36]. We are unaware of any attempts to use time-domain calibrations in this context. Instead, Refs. [34,35] relied on a circuit model that described the coupling between pulse width, the linear capacitor charging time, and the switching dynamics of the material they measured. As a consequence, the physical interpretation of their measurements depended on their model.

FIG. 1.

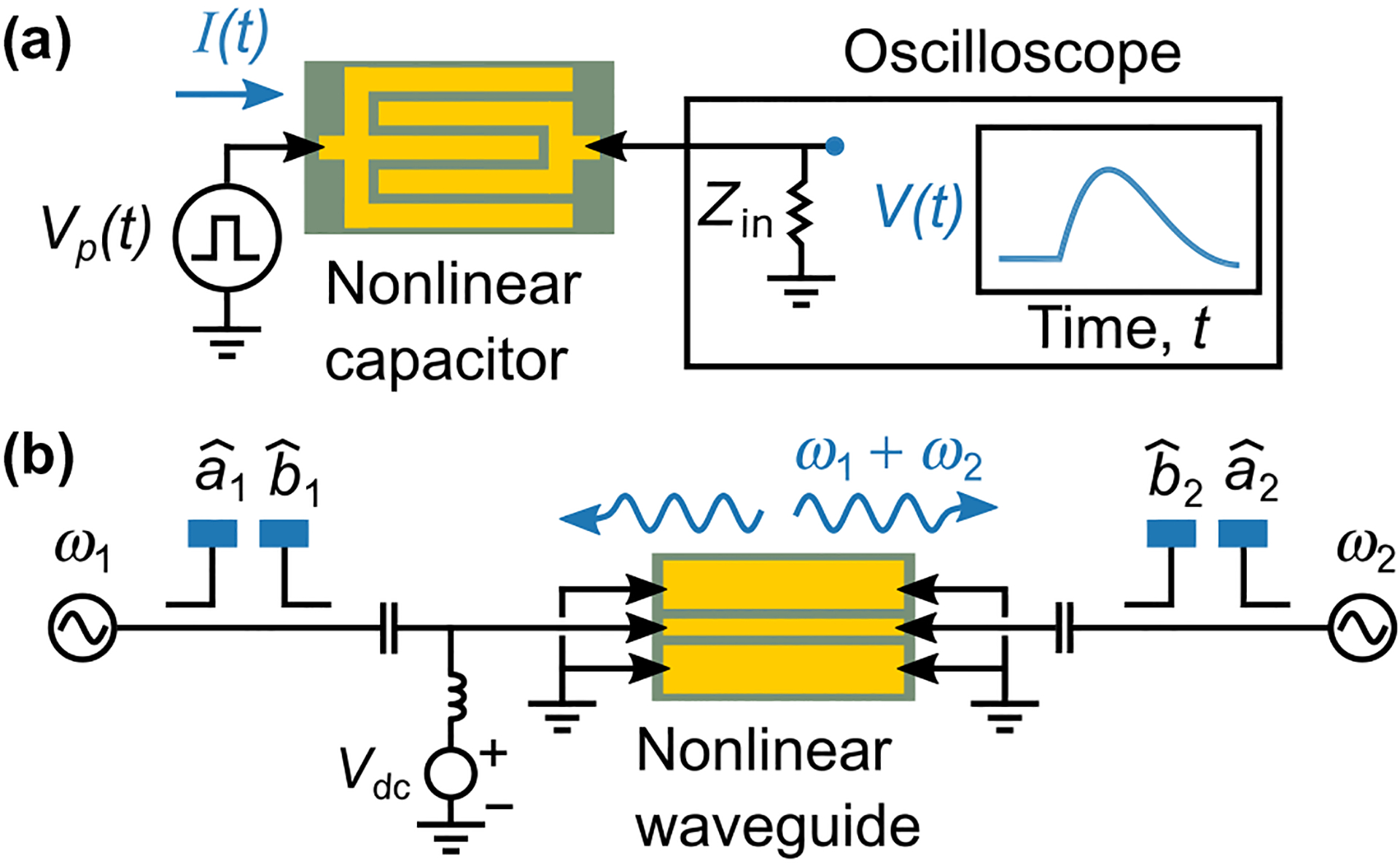
Schematic picture of nonlinear measurements of thin films. (a) In time-domain measurements, tuning dynamics are characterized by applying a voltage pulse $V_p\left(t\right)$ to a capacitor and measuring the current $I\left(t\right)=V\left(t\right)/Z_{\text{in}}$ that flows as the capacitor charges. This current is related to the change of the polarization with respect to time. (b) We characterize tuning dynamics by exciting a waveguide patterned on a nonlinear material with two microwave frequencies ${\omega }_1$ and ${\omega }_2$, and measuring the waves generated by nonlinear mixing. The complex amplitudes $\hat{a}$ and $\hat{b}$ correspond to the forward (towards the sample) and backward (from the sample) traveling waves, respectively. This method can be extended to much higher frequencies than time-domain measurements.

In principle, frequency-domain measurements [Fig. 1(b)] can circumvent these obstacles because one can correct for signal distortion (Sec. III A). Frequency-domain measurements quantify dynamics in terms of harmonics and frequency mixing products generated by nonlinear processes within a material. Most frequency-mixing measurements use either low-frequency ($<1\mathrm{G}\mathrm{H}\mathrm{z}$) [25,26,37], or optical [1,21,38] techniques. These frequency ranges allow for useful approximations that simplify nonlinear-permittivity measurements. At low frequencies, one can use lumped-element circuit analysis; while at optical frequencies one can use the slowly varying envelope approximation. In the microwave regime, lumped-element models are increasingly difficult to apply at high frequencies. Larger test devices can show distributed effects. These effects can be mitigated by using smaller devices, but then the calibration is more sensitive to the difficult-to-model electromagnetic fields near the probes. At the same time, the slowly varying amplitude approximation is not viable due to sample size and dielectric loss.

Another challenge of microwave-frequency measurements is that the phase of the mixing products relative to the incident signals, which carries vital information about the dynamics, is difficult to determine. While the relative phase of two microwave signals at the same frequency can be measured by mixing the two signals, cross-frequency phase relationships are much harder to establish. These phase relationships are important because they are necessary to describe the shape of a time-domain waveform influenced by nonlinear processes. For example, the phase of the mixing products distinguishes between nonlinear gain and loss, and between increases and decreases in phase velocity.

Here, we describe a frequency-domain technique that resolves the frequency-dependent complex nonlinear permittivity. Specifically, we use a large-signal network analyzer (LSNA) to demonstrate nonlinear-permittivity measurements from 0 to 40 GHz with cross-frequency phase resolution and absolute power calibration. In our experiments, we fabricate waveguides on a nonlinear ${\mathrm{B}\mathrm{a}}_{0.5}{\mathrm{S}\mathrm{r}}_{0.5}{\mathrm{T}\mathrm{i}\mathrm{O}}_3$ (BST) thin film, and measure the waves generated by nonlinear mixing within the waveguide. The key contributions are cross-phase calibration, power calibration, and our ability to interpret our results as fundamental materials properties rather than as ad hoc circuit parameterizations [39–41].

This paper is organized as follows. Section II describes how to relate nonlinear permittivity to experimentally accessible currents and voltages. Section III describes how we perform calibrated nonlinear microwave measurements of lithographically fabricated waveguide structures, and how these measurements can determine linear and nonlinear permittivity. Section IV then describes how we expect the measurements to look on the basis of phenomenological theory, and finally in Sec. V, we compare the results of a preliminary set of measurements to these theoretical expectations.

II. NONLINEAR CIRCUIT THEORY

Figure 2 illustrates how the nonlinear behavior of a dielectric leads to small-signal frequency mixing and harmonic generation. The model we use here is given explicitly in Sec. IV [42], but in this section we focus on its qualitative behavior. To reflect the basic features of our experimental data (Sec. V), we chose a model that does not show any hysteresis but is nonlinear in the sense that the permittivity changes in response to a large applied electric field. Equivalently, this changing permittivity can also be expressed as a nonlinear relationship between D and E [Fig. 2(a)]. When a field is applied, the material takes some time to relax to a new configuration. The relaxation dynamics lead to a difference between the response to a time-varying field [the cyan line in Fig. 2(a)] and the response to a dc field (the black line). While the model does not include hysteresis, the time lag between the response of the material and the applied field leads to loops in the $D-E$ plot.

FIG. 2.

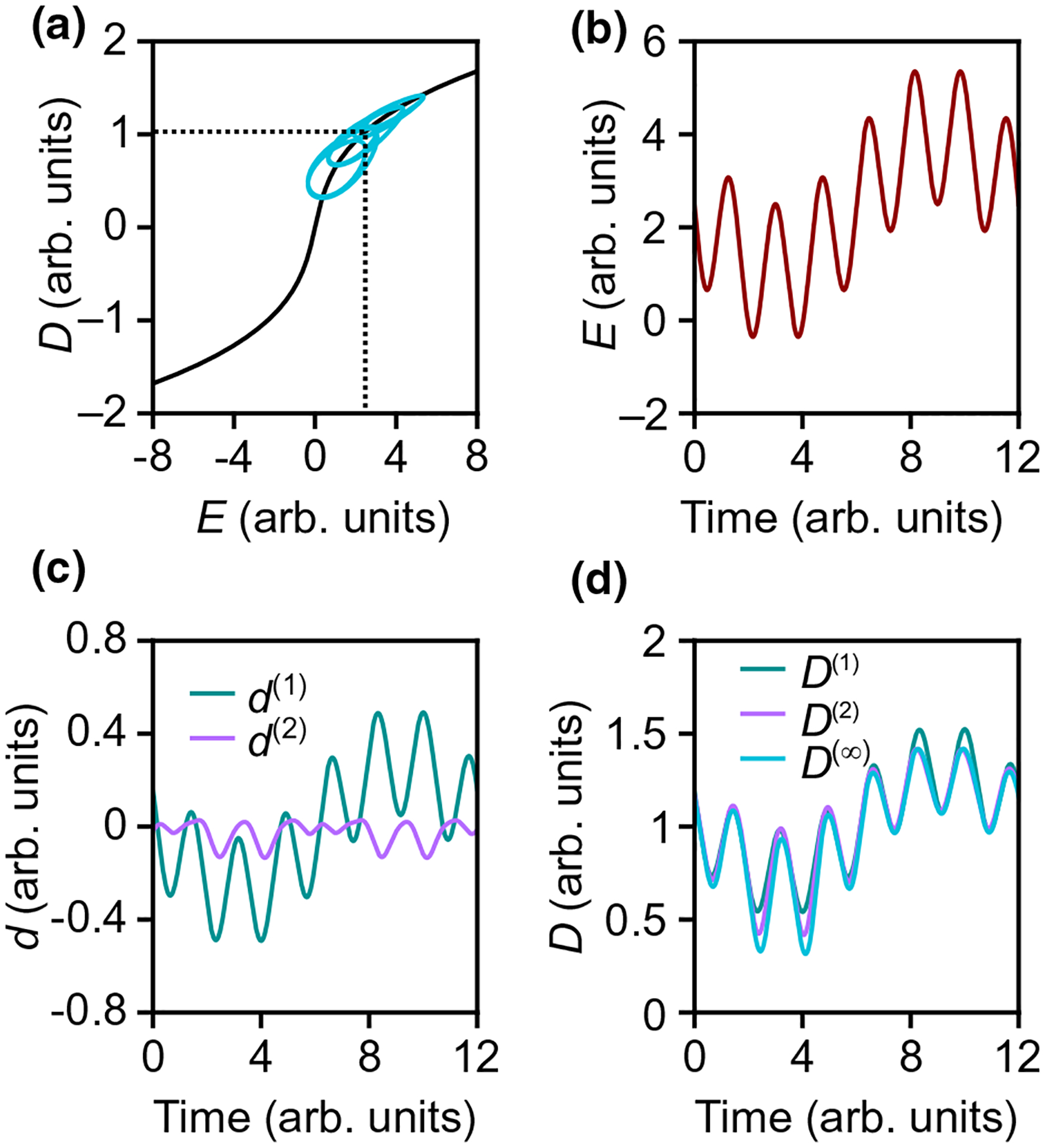
Illustration of the Volterra representation of dynamics. (a) Time-varying nonlinear relationship between the displacement field $D\left(t\right)$ and the electric field $E\left(t\right)$ superimposed with the dc $D-E$ curve. (b) Two-tone input signal $E\left(t\right)$. (c) First-order $\left[d^{\left(1\right)}\left(t\right)\right.$, teal line] and second-order $\left[d^{\left(2\right)}\left(t\right)\right.$, magenta line] contributions to the output signal. (d) Comparison of the first-order approximation $D^{\left(1\right)}\left(t\right)$ (teal line), second-order approximation $D^{\left(2\right)}\left(t\right)$ (purple line), and a solution obtained by direct numerical solution of the equation of motion $D^{\left(\infty \right)}\left(t\right)$ (cyan line).

In our experiment, we characterize the dynamic nonlinear behavior using small sinusoidal electric fields. For reference, the amplitude of the sinusoidal signals is below $0.003\mathrm{V}\mu {\mathrm{m}}^{-1}$ root-mean-square, while the field necessary to change the permittivity by about 33% is $8\mathrm{V}\mu {\mathrm{m}}^{-1}$. At lower frequencies it is possible to reconstruct a full $D\left(E\right)$ curve by applying a large, time-varying electric field and measuring harmonics of the input signal [43]. However, at microwave frequencies, small signals are convenient for several reasons. First, dielectric loss increases with frequency, and a microwave-frequency signal large enough to significantly change the dielectric properties of a sample will also change the sample through heating. Another difficulty is that the nonlinear behavior in the measurement equipment can obscure the nonlinear response of the sample. While the nonlinearity of the measurement equipment can be mitigated, this is typically only possible in a narrow frequency range [44,45]. At the power levels we employ, we only detect the leading-order nonlinear response, the second-order mixing products. We measure these mixing products in the presence of a large applied dc field, because without this field, the second-order mixing products we seek to measure are suppressed by symmetry.

In Fig. 2, we show a simulation analogous to our experiment: a superposition of a dc field and two sinusoidal signals at different frequencies ${\omega }_1$ and ${\omega }_2$ [Fig. 2(b)] is applied to the material. Conceptually, one sinusoidal signal alters the permittivity of the material, and the second signal probes this change in permittivity. The response of the material includes a linear response, $d^{\left(1\right)}$, which consists of the Fourier components with frequencies ${\omega }_1$ and ${\omega }_2$, as well as a second-order nonlinear response $d^{\left(2\right)}$ with Fourier components ${\omega }_1+{\omega }_2,\left|{\omega }_1-{\omega }_2\right|,2{\omega }_1,2{\omega }_2$, and dc. In Fig. 2(c), we plot $d^{\left(1\right)}$ and $d^{\left(2\right)}$. Figure 2(d) compares three models of the response of the material: a linear approximation $D^{\left(1\right)}=D_{\mathrm{d}\mathrm{c}}+d^{\left(1\right)}$, the second-order nonlinear approximation $D^{\left(2\right)}=D_{\mathrm{d}\mathrm{c}}+d^{\left(1\right)}+d^{\left(2\right)}$, and a solution obtained by Euler integration $D^{\left(\infty \right)}$. We see that the amplitude of the higher-frequency oscillations in $D^{\left(\infty \right)}$ is larger when $E\left(t\right)$ is smaller. This asymmetry arises because the permittivity of the material is higher with a smaller applied field. The second-order correction, $d^{\left(2\right)}$, restores this asymmetry (tuning) that the linear approximation fails to capture. Note that the relative phase of the linear response $d^{\left(1\right)}$ and the nonlinear response $d^{\left(2\right)}$ determines whether the nonlinearity enhances the amplitude of $D\left(t\right)$ or diminishes it.

Formally, we model the behavior of a material by a Volterra-series expansion, which expresses a nonlinear process by a power-series expansion of the response of a system in powers of the stimulus [46]. The $n$th term in the expansion, ${\mathbf{d}}^{\left(n\right)}\left(t\right)$, is proportional to the $n$th power of $\mathbf{e}\left(t\right)$. The relationship between these variables can be expressed in either the frequency domain or the time domain. The terms in the frequency-domain Volterra series can be written

$${\hat{d}}_k^{\left(1\right)}\left(\omega \right)={\epsilon }_0{\hat{\epsilon }}_{jk}^{\left(1\right)}\left(\omega \right){\hat{e}}_j\left(\omega \right),$$ (1)

$${\hat{d}}_l^{\left(2\right)}\left(\omega \right)={\epsilon }_0\int d{\omega }_1\int d{\omega }_2\delta \left(\omega -{\omega }_1-{\omega }_2\right)\times {\hat{\epsilon }}_{jkl}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right){\hat{e}}_j\left({\omega }_1\right){\hat{e}}_k\left({\omega }_2\right),$$ (2)

$${\widehat{d}}_{k_{n+1}}^{\left(n\right)}\left(\omega \right)={\epsilon }_0\int d\underset{\_}{\omega }\delta \left(\omega -\Sigma \underset{\_}{\omega }\right){\widehat{\epsilon }}_{k_1,\dots ,k_{n+1}}^{\left(n\right)}\left(\underset{\_}{\omega }\right)\prod _{j=1}^n{\widehat{e}}_{k_j}\left({\omega }_j\right),$$ (3)

where $\delta$ is the Dirac delta function, and ${\widehat{\epsilon }}^{\left(n\right)}\left(\underset{\_}{\omega }\right)$ is the $n$th-order permittivity. In this formulation, the nonlinear permittivity tensors depend on dc bias field, and in the case of hysteretic materials, also depend on the past history of the applied bias field. Equation (3) states that when the material is stimulated by $n$ sinusoidal signals whose frequencies sum to $\omega$, the amplitude of the mixing product ${\widehat{d}}^{\left(n\right)}\left(\omega \right)$ is proportional to the $n$th-order permittivity ${\widehat{\epsilon }}^{\left(n\right)}\left(\underset{\_}{\omega }\right)$. To express the model more compactly, we define $\underset{\_}{\omega }=\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)$ and $\Sigma \underset{\_}{\omega }={\omega }_1+{\omega }_2+\cdots +{\omega }_n$.

Using a Volterra-series approach, we develop an equivalent circuit theory to describe how a nonlinear dielectric perturbs a waveguide mode. We follow the logic of Ref. [47], which derives the well-known telegraphers equations from Maxwell’s equations in a single-mode waveguide. Reference [47] defines a voltage $\hat{V}$ and a current $\hat{I}$ that are proportional to the transverse electric field ${\stackrel{\mathbf{ˆ}}{\mathbf{e}}}_{\mathbf{T}}$ and the transverse magnetic field ${\stackrel{\mathbf{ˆ}}{\mathbf{h}}}_{\mathbf{T}}$, respectively:

$${\hat{\mathbf{h}}}_{\mathbf{T}}=\frac{\hat{I}\left(z\right)}{I_0}\hat{\mathcal{H}}(x,y),$$ (4)

$${\hat{\mathbf{e}}}_{\mathbf{T}}=\frac{\hat{V}\left(z\right)}{V_0}\hat{\mathcal{E}}(x,y).$$ (5)

Here, $\stackrel{\mathcal{ˆ}}{\mathcal{H}}$ and $\stackrel{\mathcal{ˆ}}{\mathcal{E}}$ are normalized transverse fields that do not depend on z. According to Ref. [47], there is not a universally accepted way to determine the normalization constants $I_0$ and $V_0$. However, they are partially determined by a power-based normalization convention: in the situation where there is a wave propagating in one direction, the power traveling down the waveguide is given by $V{I}^{*}$.

We make an additional simplifying assumption, which is that our waveguide supports a transverse electric-magnetic (TEM) mode whose electric and magnetic fields are in the plane perpendicular to the propagation direction. This approximation is good so long as the gap width $W$ is much less than the wavelength of the guided mode [48]. To model the nonlinear material properties, we include the first two terms in the Volterra-series expansion of $\stackrel{\mathbf{ˆ}}{\mathbf{d}}$, and assume the materials involved have a linear magnetic response. From energy-based arguments, in direct analogy with Ref. [47], we obtain a generalized form of the telegrapher’s equations:

$$\frac{d}{dz}\hat{V}(\omega ,z)=-\hat{Z}\left(\omega \right)\hat{I}(\omega ,z),$$ (6)

$$\frac{d}{dz}\hat{I}(\omega ,z)=-{\hat{Y}}^{\left(1\right)}\left(\omega \right)\hat{V}(\omega ,z)-\hat{N}(\omega ,z),$$ (7)

$$\widehat{N}\left(\omega ,z\right)=\int d\underset{\_}{\omega }\delta \left(\omega -\Sigma \underset{\_}{\omega }\right){\widehat{Y}}^{\left(2\right)}\left(\underset{\_}{\omega }\right)\prod _{j=1}^2\widehat{V}\left({\omega }_j,z\right).$$ (8)

These equations are parameterized by a distributed admittance ${\hat{Y}}^{\left(1\right)}\left(\omega \right)$, nonlinear admittance ${\hat{Y}}^{\left(2\right)}\left(\underset{\_}{\omega }\right)$, and impedance $\hat{Z}\left(\omega \right)$. These coefficients are given by expressions involving surface integrals over the $x-y$ plane:

$$\hat{Z}\left(\omega \right)=\frac{i\omega }{{\left|I_0\right|}^2}\int dS\left[{\hat{\mu }}_{jk}\left(\omega \right){\hat{\mathscr{H}}}_j^{*}\left(\omega \right){\hat{\mathscr{H}}}_k\left(\omega \right)\right],$$ (9)

$${\hat{Y}}^{\left(1\right)}\left(\omega \right)=\frac{i\omega }{{\left|V_0\right|}^2}\int dS\left[{\widehat{ℰ}}_{jk}^{\left(1\right)}\left(\omega \right){\widehat{ℰ}}_j^{*}\left(\omega \right){\widehat{ℰ}}_k\left(\omega \right)\right],$$ (10)

$${\hat{Y}}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)=\frac{i\left({\omega }_1+{\omega }_2\right)}{{\left|V_0\right|}^2{V}_0}\int dS\times \left[{\hat{\epsilon }}_{jkl}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right){\widehat{ℰ}}_j^{*}\left({\omega }_1+{\omega }_2\right){\widehat{ℰ}}_k\left({\omega }_1\right){\widehat{ℰ}}_l\left({\omega }_2\right)\right].$$ (11)

Equations (9) and (10) agree with the expressions given in Ref. [47] in the special case that there are no electric or magnetic fields in the propagation direction. Reference [47] did not consider the case of nonlinear materials and did not offer any expression for ${\hat{Y}}^{\left(2\right)}$. Similar expressions to Eq. (11) can be derived for nonlinear magnetic materials, or materials with a higher-order dielectric nonlinearity.

A. Solution of the nonlinear telegrapher’s equations

To a good approximation, we can solve Eqs. (6)–(8) perturbatively, treating ${\hat{Y}}^{\left(2\right)}$ as a small parameter [49]. In our experiment, the microwave-frequency electric fields in the waveguide are much smaller than the electric field required to change the permittivity of the nonlinear dielectric film by a substantial amount. We assume a solution of the form $\hat{V}\left(\omega ,z\right)={\hat{V}}^{\left(1\right)}\left(\omega ,z\right)+{\hat{V}}^{\left(2\right)}\left(\omega ,z\right),\hat{I}\left(\omega ,z\right)={\hat{I}}^{\left(1\right)}(\omega ,z)+{\hat{I}}^{\left(2\right)}(\omega ,z)$, where ${\hat{I}}^{\left(1\right)}\gg {\hat{I}}^{\left(2\right)}$ and ${\hat{V}}^{\left(1\right)}\gg {\hat{V}}^{\left(2\right)}$. The first-order voltage and current, ${\hat{V}}^{\left(1\right)}$ and ${\hat{I}}^{\left(1\right)}$, represent the externally-applied signals, while the second-order voltage and current ${\hat{V}}^{\left(2\right)}$ and ${\hat{I}}^{\left(2\right)}$ represent the waves generated by nonlinear mixing in the dielectric material. To lowest order, we set ${\hat{Y}}^{\left(2\right)}=0$, and Eqs. (6)–(8) reduce to the well-known telegrapher’s equations. These equations admit traveling wave solutions:

$${\hat{V}}^{\left(1\right)}\left(z\right)=V^{+}{e}^{-\gamma z}+V^{-}{e}^{\gamma z},$$ (12)

$${\hat{I}}^{\left(1\right)}\left(z\right)=\frac{V^{+}}{Z_0}{e}^{-\gamma z}-\frac{V^{-}}{Z_0}{e}^{\gamma z}.$$ (13)

Here, $\gamma =\sqrt{\hat{Z}{\hat{Y}}^{\left(1\right)}}$ is the propagation constant and $Z_0=\sqrt{\hat{Z}/{\hat{Y}}^{\left(1\right)}}$ is the characteristic impedance. The unknown coefficients $V^{+}$ and $V^{-}$ are determined by boundary conditions. Once these coefficients are determined, we approximate the nonlinear term in Eq. (8) by

$$\widehat{N}\left(\omega \right)\approx \int d\underset{\_}{\omega }\delta \left(\omega -\Sigma \underset{\_}{\omega }\right){\widehat{Y}}^{\left(2\right)}\left(\underset{\_}{\omega }\right)\prod _{j=1}^2{\widehat{V}}^{\left(1\right)}\left({\omega }_j\right).$$ (14)

With this approximation, Eqs. (6)–(8) can be solved by a Green’s function approach. To construct a solution, we seek functions $G_V$ and $G_I$ that satisfy the following differential equations:

$$\frac{d{G}_V\left(z,z^{\prime }\right)}{dz}=-\hat{Z}\left(\omega \right)G_I\left(z,z^{\prime }\right),$$ (15)

$$\frac{d{G}_I\left(z,z^{\prime }\right)}{dz}=-{\hat{Y}}^{\left(1\right)}\left(\omega \right)G_V\left(z,z^{\prime }\right)+\delta \left(z-z^{\prime }\right)$$ (16)

Here, $\delta \left(z-z^{\prime }\right)$ is the Dirac $\delta$ function and models a pointlike current source at position $z^{\prime }$. Once $G_I\left(z,z^{\prime }\right)$ and $G_V\left(z,z^{\prime }\right)$ have been computed, the voltage and current may be determined by integrating the contributions of waves generated by the nonlinear current source $\hat{N}\left(\omega ,z^{\prime }\right)$ at each position along the transmission line (with length $l$).

$${\hat{V}}^{\left(2\right)}(\omega ,z)=-{\int }_0^{l}d{z}^{\prime }{G}_V\left(z,z^{\prime }\right)\hat{N}\left(\omega ,z^{\prime }\right),$$ (17)

$${\hat{I}}^{\left(2\right)}\left(\omega ,z\right)=-{\int }_0^{l}d{z}^{\prime }{G}_I\left(z,z^{\prime }\right)\hat{N}\left(\omega ,z^{\prime }\right).$$ (18)

B. Boundary conditions

We use boundary conditions based on the experimentally accessible quantities $\hat{a}$ and $\hat{b}$ to solve for both the first-order solution, $V^{\left(1\right)}$ and $I^{\left(1\right)}$, and for the form of the Green’s function. The wave parameters $\hat{a}$ and $\hat{b}$ are defined with respect to an arbitrary, real, reference impedance $Z_{\text{ref}}$ in terms of the current $\hat{I}$ and voltage $\hat{V}$ [47].

$${\hat{a}}_n\equiv \frac{\hat{V}+Z_{\mathrm{r}\mathrm{e}\mathrm{f}}\hat{I}}{2},$$ (19)

$${\hat{b}}_n\equiv \frac{\hat{V}-Z_{\mathrm{r}\mathrm{e}\mathrm{f}}\hat{I}}{2}.$$ (20)

The subscript $n$ refer to ports 1 and 2, which we define to be the left and right edges of the waveguide. Note that the current is defined as flowing away from the port, so for ${\hat{a}}_2$ and ${\hat{b}}_2,\hat{I}$ has the opposite sign as in Eqs. (13). The LSNA calibration that we describe in Sec. III allows us to measure the $\hat{a}$ and $\hat{b}$ waves at the edge of our waveguides. In our analysis, we solve for the coefficients $V^{+}$ and $V^{-}$ assuming that the $\hat{a}$ wave at each end of the waveguide is given by its measured value.

We employ slightly different boundary conditions for the Green’s function than the first-order solution. Green’s functions have homogeneous boundary conditions [50], and so we set the $\hat{a}$ wave to 0, rather than its measured value. In principle, we should also account for an inhomogeneous (proportional to $\hat{a}$) contribution to the $\hat{b}$ waves at the frequencies of the mixing products. In our case, we find that the $\hat{a}$ waves at these frequencies are negligible. We expect the $\hat{a}$ waves to be small because the LSNA is not sourcing any power at the frequencies of the mixing products, and we did not employ any highly reflective components in our setup. We found that including measured $\hat{a}$ waves in our analysis seemed to add noise to our results, because in our experiment these waves are near the limit of detection.

If the left side of a waveguide is connected to a probe, we can assume as a boundary condition that $\hat{a}$ wave at $z=0$ has the value ${\hat{a}}_1$. We arrive at the following relationship:

$$\hat{V}\left(0\right)+Z_{\mathrm{r}\mathrm{e}\mathrm{f}}\hat{I}\left(0\right)=2{\hat{a}}_1.$$ (21)

Meanwhile, if the right side of a waveguide is connected to a probe, we can assume as a boundary condition that $\hat{a}$ wave at $z=l$ has the value ${\hat{a}}_2$.

$$\hat{V}\left(l\right)-Z_{\text{ref }}\hat{I}\left(l\right)=2{\hat{a}}_2.$$ (22)

In our measurements, we employ both two-port transmission lines, and one-port terminated transmission lines. One end of the terminated waveguide is connected to the probe, and the other is terminated by an open cirucit with a small capacitance compared to the rest of the transmission line. In terms of the impedance associated with this termination, ${\hat{Z}}_l$, the boundary condition on the right end of the terminated waveguide is

$$\hat{V}\left(l\right)={\hat{Z}}_l\hat{I}\left(l\right).$$ (23)

The equations given in Sec. IIA, with the boundary conditions in this section, allowed us to extract the nonlinear admittance from the measured wave parameters. In Sec. III, we discuss how to calibrate our measurements so that these boundary conditions can be applied.

III. EXPERIMENTAL APPROACH

A. Nonlinear calibration

To interpret LSNA measurements of our on-wafer waveguides, we need to characterize the relationship between ${\hat{a}}_n^r$ and ${\hat{b}}_n^r$, the raw signals measured by the receivers of an LSNA, and ${\hat{a}}_n$ and ${\hat{b}}_n$, the forward and backward waves at the edges of an on-wafer device. This relationship (calibration) accounts for signal distortion by all of the circuitry between the receivers of the LSNA and the sample, including the internal circuitry of the LSNA, the coaxial cables connecting the test ports of the LSNA to the probes, the bias tees and the wafer probes. We use a linear model to account for this distortion.

Figure 3 schematically shows the error model that we employ. We define three reference planes: the raw measurements, a coaxial reference plane at the connector to the wafer probes, and an on-wafer reference plane. As we discuss, this two-tiered structure is necessary for phase and amplitude calibrations. The $2\times 2$ complex-valued matrices $X_1,Y_1,X_2$, and $Y_2$ are in $T$-parameter form, and describe how the $\hat{a}$ and $\hat{b}$ waves change between reference planes.

FIG. 3.

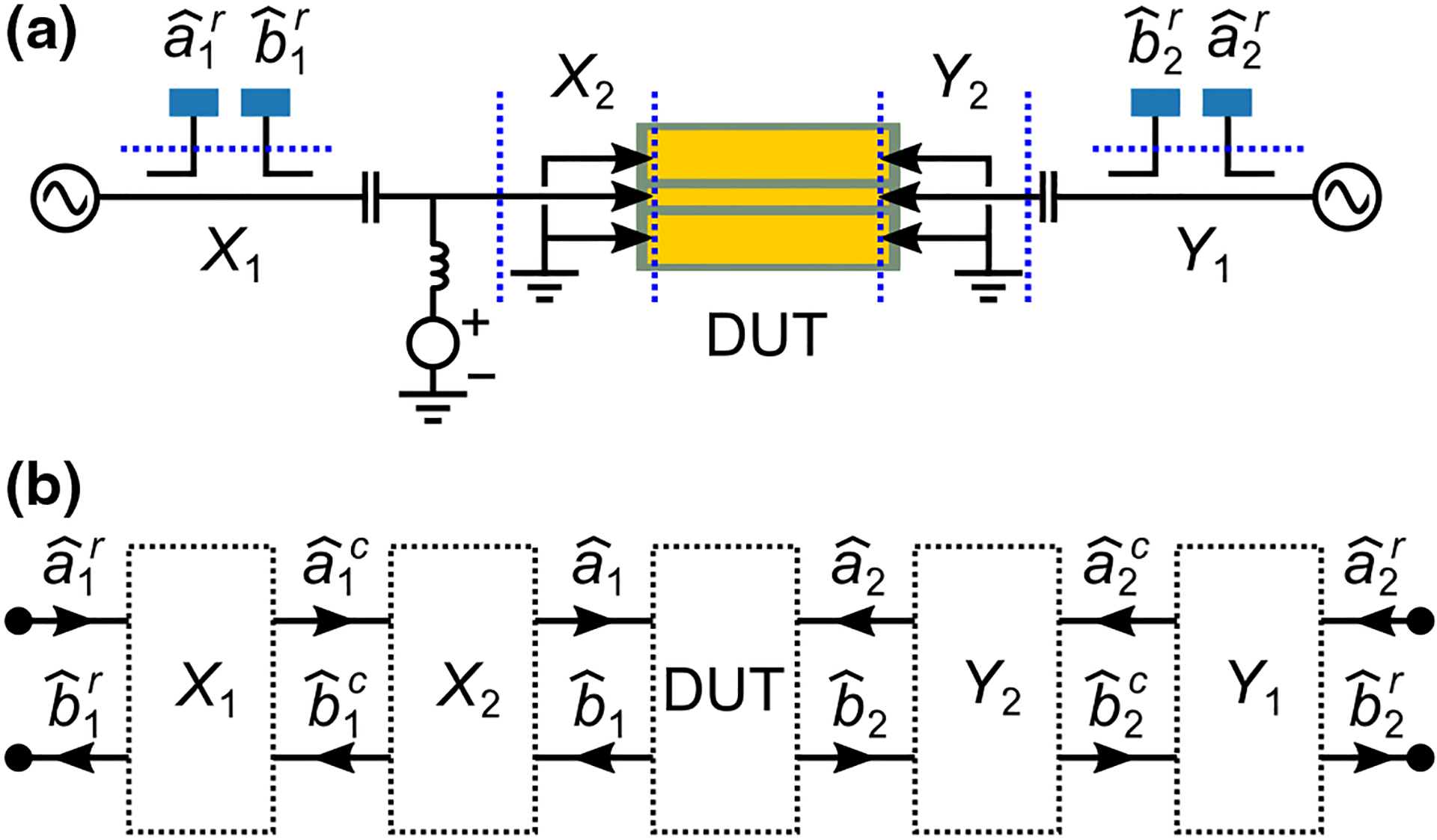
Error model. (a) Physical location of the reference planes. The raw wave parameters, ${\hat{a}}_n^r$ and ${\hat{b}}_n^r$, are measured by the detectors of the LSNA. The wave parameters at the coaxial plane, ${\hat{a}}_n^c$ and ${\hat{b}}_n^c$ are measured at the ends of the coaxial connectors that attach to the wafer probes. The wave parameters of the device under test (DUT), ${\hat{a}}_n$ and ${\hat{b}}_n$, are measured at the wafer probe tips. (b) Schematic representation of the error model relating the wave parameters at the different reference planes. The error model has 16 parameters defined independently at each frequency point: $X_1,Y_1,X_2$ and $Y_2$, are all $2\times 2$ complex-valued matrices.

The LSNA calibration is a generalization of a traditional linear network analyzer calibration that also allows for phase and power calibrations. We model the relationship between the measured $T$ parameters of a linear device $\left(M\right)$ and their true values $\left(T\right)$ by $M=XTY$. In our two-tiered calibration model, $X=X_1{X}_2$ and $Y=Y_2{Y}_1$. By measuring a set of linear passive devices with known $T$ parameters, we determine seven of the eight complex numbers in $X$ and $Y$ [51]. The remaining ambiguity is a feature of any linear error model determined solely from measurements of passive devices [52]. One way to resolve this ambiguity is to assume that either $X$ or $Y$ represents a reciprocal network [51]. However, the first-tier error parameters $X_1$ and $Y_1$ include the LSNA, and the signals measured by its receivers are subject to an unknown, and potentially nonreciprocal, scaling in magnitude and frequency. To determine the phase and amplitude of the $\hat{a}$ and $\hat{b}$ waves, one must measure these quantities directly at some reference plane [52].

We determine the phase and amplitude by measuring these quantities at the coaxial reference plane immediately before the wafer probes. This reference plane is necessary because we lack on-wafer phase and power standards. Apart from an overall phase and amplitude, we use a short-open-load-thru (SOLT) calibration to determine the parameters in $X_1$ and $Y_1$ up to 40 GHz [53]. To establish the cross-frequency phase, we use a comb generator that produces periodic pulses in the time domain. The comb generator has a repetition rate of 10 MHz, and its Fourier spectrum consists of evenly spaced harmonics from 10 MHz up to 40 GHz. We attach a comb generator to port 3 of the LSNA for the duration of the experiment to serve as a phase reference. Thus, the phase of any signal at ports 1 or 2 could be determined by comparing to the phase of the reference at port 3, as long as all of the frequencies involved are multiples of 10 MHz. We also need to account for the fixed phase relationship between the phase reference and the signals measured at ports 1 and 2, and this relationship is determined by measuring a second comb generator attached to coaxial port 1. To calibrate the power of the $\hat{a}$ and $\hat{b}$ waves, we measure the power sourced by the LSNA at port 1 at the coaxial reference plane.

B. On-wafer calibration

In order to interpret our mixing products in physical terms, we need to understand the relationship between the measured $\hat{a}$ and $\hat{b}$ waves, and the guided modes of on-wafer waveguides. This involves measuring waveguides with well-understood properties, and constructing an error model from these measurements. Our on-wafer calibration standards are shorts, loads, and transmission lines, allowing for a multiline thru-reflect-line (MTRL) calibration [51]. The on-wafer calibration standards had an identical cross-sectional geometry to the test devices on the BST chip, but are patterned directly on a substrate with negligible dielectric dispersion at microwave frequencies $\left[\mathrm{t}\mathrm{a}\mathrm{n}\right(\delta )<0.005]$. The calibration substrate also has a similar relative permittivity $\left({\epsilon }^{\left(1\right)\prime }\approx 24\right)$ to the substrate that the BST film was deposited on $\left({\epsilon }^{\left(1\right)\prime }\approx 22\right)$. We do not need any phase or power calibration to construct our secondtier error parameters, $X_2$ and $Y_2$. These matrices represent wave propagation through the wafer probes, which are made of reciprocal materials. This reciprocity removes any ambiguity in $X_2$ and $Y_2$.

Transmission lines make good calibration standards because their scattering parameters can be derived from fundamental electromagnetic theory. If one chooses $Z_{\mathrm{r}\mathrm{e}\mathrm{f}}=Z_0$, then the $T$-parameter model of a transmission line is described by one unknown parameter, $\gamma$. Let $M_1$ and $M_2$ be $T$-parameter measurements of two transmission lines with lengths $l_1$ and $l_2=l_1+\Delta l$. Reference [51] showed that the eigenvalues of matrix $M_1\left(M_2^{-1}\right)$ are $\mathrm{e}\mathrm{x}\mathrm{p}(\pm \gamma \Delta l)$. This relationship means that, without any calibration, we can determine the propagation constant $\gamma$ from measurements of two transmission lines with different lengths. By measuring a reflect standard and set of transmission lines, we can determine the error matrices $X$ and $Y$ [51,54].

In practice, it is more convenient to set the reference impedance $Z_{\text{ref}}$ to $50\Omega$ than $Z_0$. The coaxial cables and probes leading up to the sample are designed to have a characteristic impedance near $50\Omega$, and hence it is a natural choice for many measurements. To set the reference impedance, we make use of the fact that $Z_0=\gamma /\hat{Y}$. Our calibration transmission lines are fabricated on a substrate with little to no dielectric dispersion. In this case, we make the approximation ${\hat{Y}}_1=i\omega C_0$, where $C_0$ is a frequency independent capacitance per unit length. This model of the admittance is justified by Eq. (10) under the assumption that the mode is TEM, and therefore the electric field is frequency-independent. To estimate the capacitance per unit length $C_0$, we use the method described in Ref. [55]. We then modify the error matrices $X$ and $Y$ to set the reference impedance to $50\Omega$ [56]. By insisting that the capacitance is frequency independent, we implicitly determine the constant $V_0$ in Eq. (10). The power normalization condition determines the product $I_0^{*}{V}_0$, so the waveguide current and voltage are unambiguously defined in terms of the guided mode electric and magnetic fields by the MTRL calibration.

In principle, there is some error in the calibration because the transmission lines on the BST test chip has a higher capacitance per unit length than the calibration standards by a factor of about 3/2 [56]. The systematic error introduced by this discrepancy should not influence our linear-permittivity estimates because our estimator of $\gamma$ is based on the eigenvalues of measurements of pairs of transmission lines, and is therefore independent of the calibration [51]. To assess the magnitude of this uncertainty in our nonlinear measurements, we modeled the effect of a small parasitic capacitance to our analysis. As expected, this added error did not change our linear-permittivity estimates. Our nonlinear-permittivity estimates changed by less than the error bars. So, we conclude that the difference in distributed capacitance between our test structures and our calibration standards does not significantly degrade the quality of our data. We caution that for thicker films, or films with higher permittivity, some modifications to this calibration approach may be necessary to account for this effect.

C. Measurement configurations

Figure 4 shows two experiment configurations we use to measure 2nd order nonlinear mixing products. We use these two configurations because in our nonlinear measurements we encounter a trade-off between dynamic range and bandwidth. The dominant source of error in our nonlinear measurements is the nonlinearity of the sources and receivers in the LSNA, which generated their own mixing products at exactly the frequencies of interest. Consequently, in our frequency-swept nonlinear measurements [Fig. (4a)], we have about 10 dB of dynamic range even though the nonlinear signals from our sample are about 40 dB above the noise floor. In our voltage-swept nonlinear measurements [Fig. (4b)], we improve the dynamic range by fixing the source frequencies, using one-port devices, and employing filters to suppress spurious signals from the LSNA.

FIG. 4.

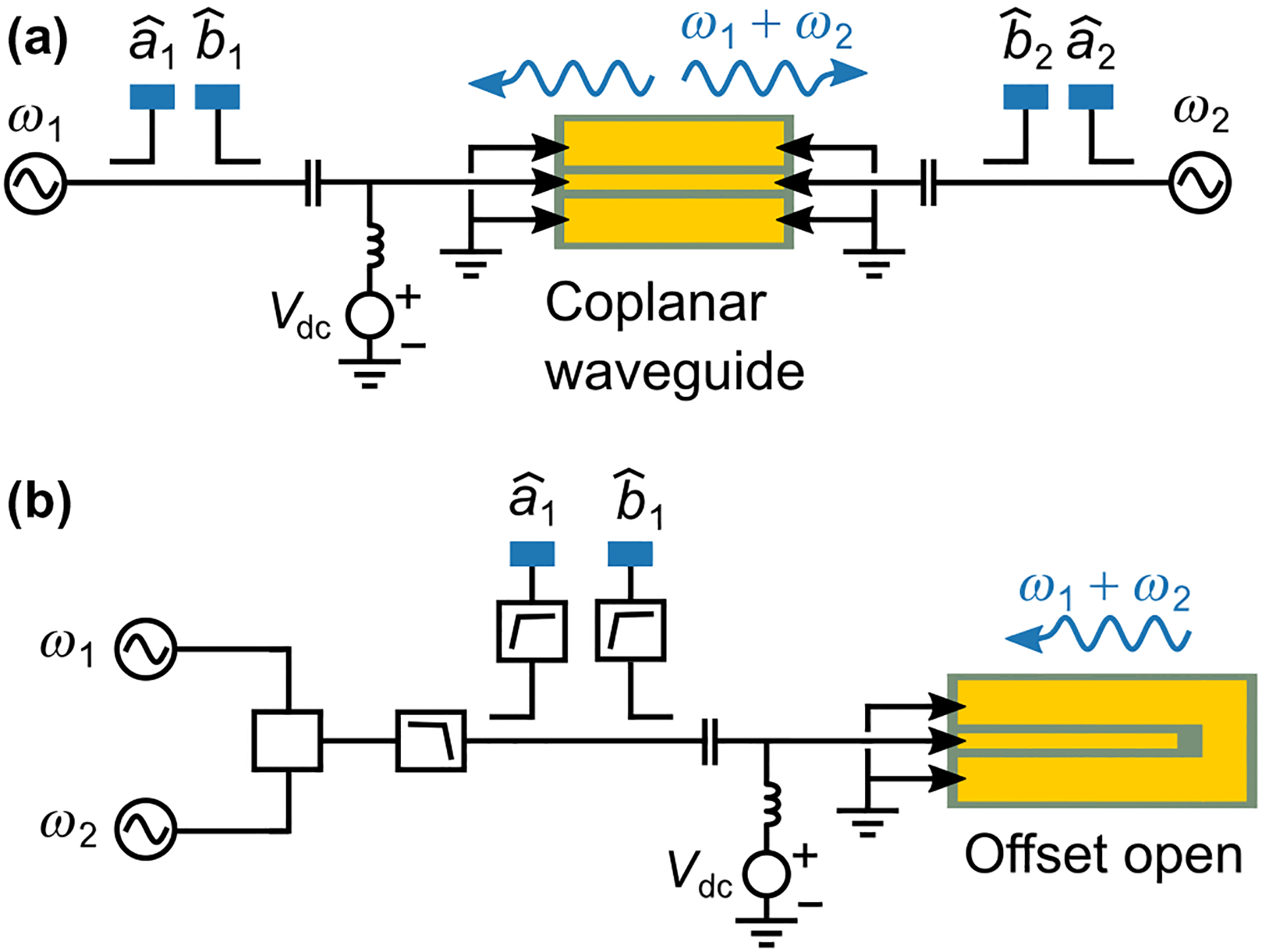
Measurement configurations. (a) For broadband measurements, we use coplanar waveguides, and excite the waveguide from both edges. (b) For narrow-band measurements, we use a one-port configuration, with waveguides terminated by a gap to ground. This allows us to use filters to minimize spurious signals generated within the LSNA.

In the one-port measurements of the terminated transmission lines, we use a low-pass filter to remove signal content at $2{\omega }_1,2{\omega }_2$, and ${\omega }_1+{\omega }_2$ generated by the sources. Likewise, high-pass filters placed in front of the receivers attenuated the signals at ${\omega }_1$ and ${\omega }_2$ and prevented mixing in the receivers. With these filters, the dynamic range increased to about 30 dB for the frequencies under test in a narrow band around 7.8 GHz.

D. Sample preparation

To facilitate our measurements, we fabricate coplanar-waveguide transmission-line structures and coplanar waveguide offset open structures on the film (Fig. 5). We prepare our sample through standard deposition and lithography techniques. The BST film is grown to a thickness of 200 nm by pulsed laser deposition on the (001) surface of a ${\left({\mathrm{L}\mathrm{a}\mathrm{A}\mathrm{l}\mathrm{O}}_3\right)}_{0.3}{\left({\mathrm{S}\mathrm{r}\mathrm{T}\mathrm{a}\mathrm{A}\mathrm{l}\mathrm{O}}_6\right)}_{0.7}$ (LSAT) substrate heated to 760 °C. The KrF ablation laser produced an incident laser fluence of $0.4\mathrm{J}/{\mathrm{c}\mathrm{m}}^2$ at a repetition rate of 5 Hz. The film growth occurred under a background oxygen pressure $\left(P_{{\mathrm{O}}_2}\right)$ of 40 Pa (30 mTorr). We pattern the test structures on the BST film by photolithography, followed by electron-beam deposition of a 500-nm-thick gold layer with a 10-nm-thick titanium adhesion layer. We fabricated the calibration standards on the (001) surface of a ${\mathrm{L}\mathrm{a}\mathrm{A}\mathrm{l}\mathrm{O}}_3$ (LAO) substrate by the same process.

FIG. 5.

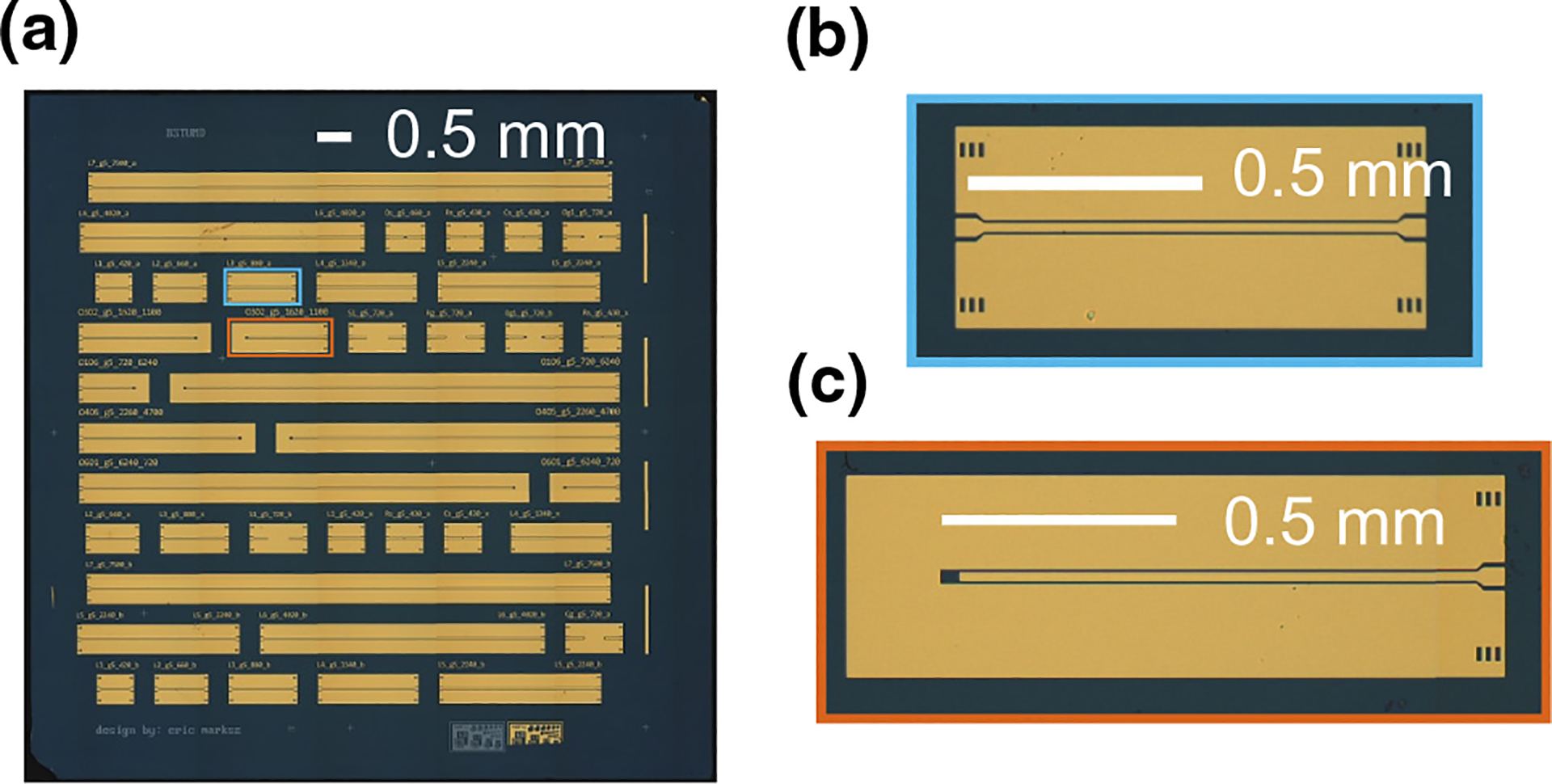
Our BST sample. (a) Photograph of the BST chip with the waveguide structures fabricated on it. Because the chip is larger than the microscope’s field of view, this photograph is stitched together from many smaller images. (b) Example of a two-port device, a coplanar-waveguide (CPW) transmission line with a length of 0.880 mm. (c) Example of a one-port device, a coplanar waveguide offset open with a length of 1.100 mm.

Photographs of the BST chip are shown in Fig. 5. The test devices on the BST thin film consisted of a collection of CPW structures and offset open structures of varying lengths: $l=\{0.420,0.660,0.880,1.340,2.240,4.020$, and $7.500\}\mathrm{m}\mathrm{m}$ for the CPWs, and $l=\{0.720,1.100,1.620,2.260,4.700,$ and $6.240\}\mathrm{m}\mathrm{m}$for the offset opens. The CPWs had $20\mu \mathrm{m}$ wide center conductors, $200\mu \mathrm{m}$ wide ground planes, and a $5\mu \mathrm{m}$ gaps between the center conductor and the ground planes. The offset open structures have the same cross-sectional geometry as the CPWs, but are terminated at one end with a $40\mu \mathrm{m}$ gap to the ground plane.

E. Analysis overview

After performing the two-tiered calibration described in Sec. III, we perform both a linear and nonlinear characterization of our BST film to determine the permittivities ${\hat{\epsilon }}^{\left(1\right)}$ and ${\hat{\epsilon }}^{\left(2\right)}$ from the measured wave parameters. We treat these permittivities as complex frequency-dependent scalars because we do not have enough information to independently determine all of the tensor elements. Because of the linear relationships between the admittances ${\hat{Y}}^{\left(1\right)}$ and ${\hat{Y}}^{\left(2\right)}$ and the permittivities ${\hat{\epsilon }}^{\left(1\right)}$ and ${\hat{\epsilon }}^{\left(2\right)}$, our strategy is to determine ${\hat{Y}}^{\left(1\right)}$ and ${\hat{Y}}^{\left(2\right)}$ from measurements, and then use simulations to relate these quantities to ${\hat{\epsilon }}^{\left(1\right)}$ and ${\hat{\epsilon }}^{\left(2\right)}$.

The first step is a linear characterization to determine the circuit parameters ${\hat{Y}}^{\left(1\right)}$ and $\hat{Z}$ as a function of dc bias voltage and frequency. To do this, we measure a collection of transmission lines fabricated on the materials we wish to characterize, and make use of the fact that, if $M_1$ and $M_2$ are $T$-matrix measurements of two transmission lines whose lengths differ by $\Delta l$, the eigenvalues of $M_1\left(M_2^{-1}\right)$ are $\mathrm{e}\mathrm{x}\mathrm{p}(\pm \gamma \Delta l)$ (Sec. III B). On our BST thin-film sample, we fabricate seven CPWs, leading to 21 different measurements (six independent measurements) of the quantity $\gamma \Delta l$, and use linear regression against $\Delta l$ to estimate $\gamma$. The linear admittance ${\hat{Y}}^{\left(1\right)}$, is related to the propagation constant by $\gamma =\sqrt{\hat{Z}{\hat{Y}}^{\left(1\right)}}$. Under the assumption of single-mode TEM propagation, $\hat{Z}$ depends only on the CPW geometry and metal conductivity [47, 57]. We estimate the value of $\hat{Z}$ with the model described in Ref. [57]. From the theoretical $\hat{Z}$ and measured $\gamma$, we can compute ${\hat{Y}}_1$. We use these linear circuit parameters in the nonlinear analysis.

Figure 6 illustrates our process for estimating ${\hat{Y}}^{\left(2\right)}$ from mixing product measurements. To measure the mixing products, we apply microwave power from both ends of the CPW as shown in Fig. 1(b). The incident power from port 2 is about −4 dBm, and the incident power from port 1 varied with frequency between −10 and −23 dBm. According to Eqs. (6)–(8), a waveguide excited by signals at ${\omega }_1$ and ${\omega }_2$ generates voltage and current waves at ${\omega }_1+{\omega }_2$. The key insight from Sec. II that enables our nonlinear analysis is that the amplitudes of these mixing products are directly proportional to ${\hat{Y}}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)$. In other words, the complex amplitude of the measured mixing products, $\hat{b}\left({\omega }_1+{\omega }_2\right)$, is given by

$$\hat{b}\left({\omega }_1+{\omega }_2\right)={\hat{b}}_{\text{model }}\left({\omega }_1+{\omega }_2\right){\hat{Y}}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)$$ (24)

where ${\hat{b}}_{\text{model}}\left(\omega \right)$ is the hypothetical strength of the mixing products under the condition that ${\hat{Y}}^{\left(2\right)}=1$. To estimate ${\hat{Y}}_2\left(\underset{\_}{\omega }\right)$, we measure the mixing product ${\hat{b}}_2\left(\omega \right)$ at ${\omega }_1+{\omega }_2$ for our seven transmission lines, and use linear regression against ${\hat{b}}_{\text{model}}\left({\omega }_1+{\omega }_2\right)$ to determine ${\hat{Y}}_2\left(\underset{\_}{\omega }\right)$. We also measure ${\hat{Y}}_2$ at the other second-order mixing frequencies: $\left|{\omega }_1-{\omega }_2\right|,2{\omega }_1$, and $2{\omega }_2$, but we focus on ${\omega }_1+{\omega }_2$ for brevity.

FIG. 6.

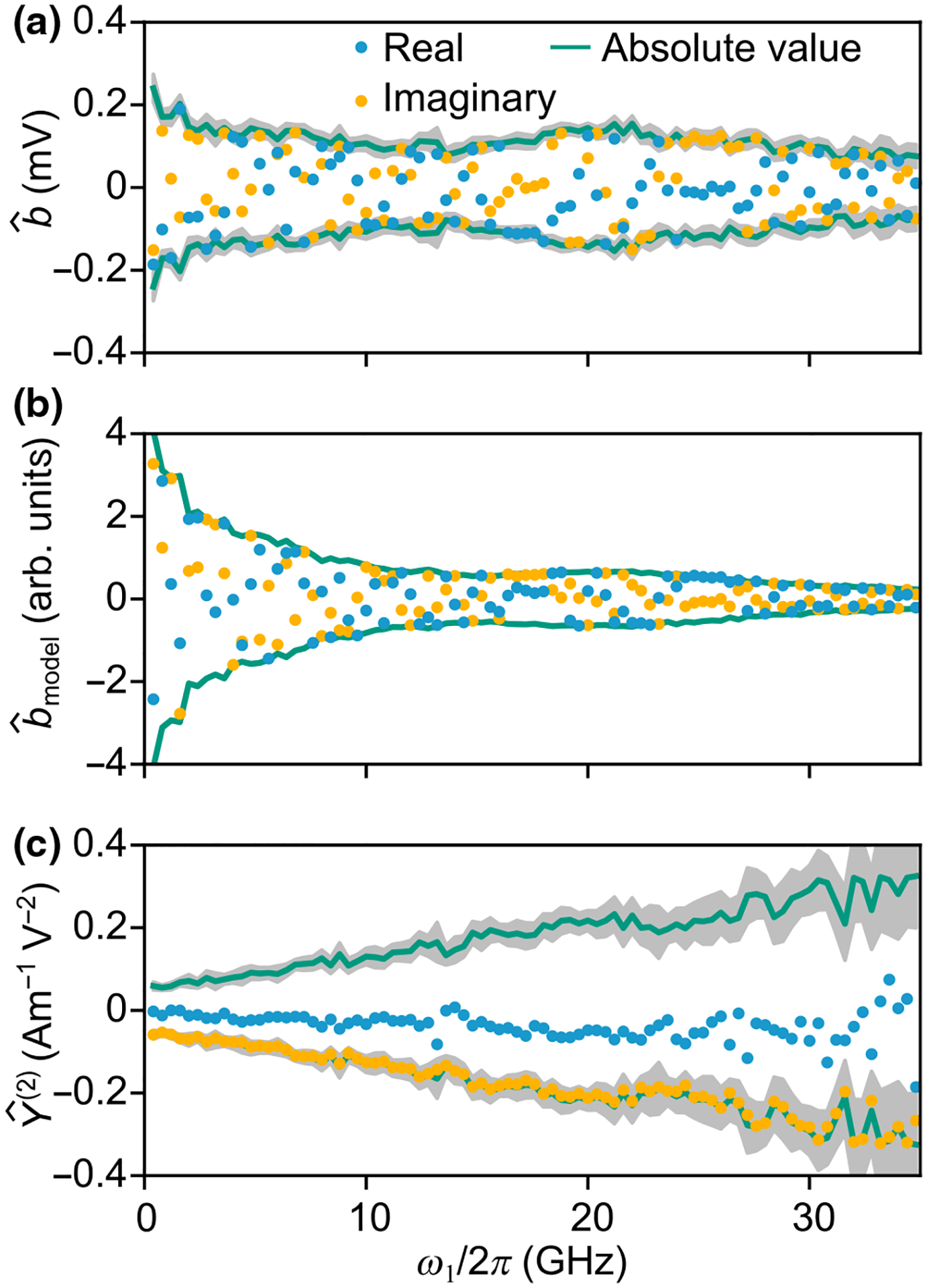
Example of the nonlinear admittance estimation from measurements. (a) Measured mixing product, $\hat{b}\left({\omega }_1+{\omega }_2\right)$ of a CPW of length $1.340\mathrm{m}\mathrm{m}.{\omega }_2=2\pi \times 5\mathrm{G}\mathrm{H}\mathrm{z}$. (b) ${\hat{b}}_{\text{model}}\left({\omega }_1+\left.{\omega }_2\right)\right.$, the hypothetical value of the mixing product under the condition ${\hat{Y}}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)=1$. The estimated uncertainty in (b) from uncertainty in ${\hat{Y}}^{\left(1\right)}$ is smaller than the width of the line. (c) ${\hat{Y}}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)$ estimated by ${\hat{Y}}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)=\hat{b}\left({\omega }_1+\left.{\omega }_2\right)/{\hat{b}}_{\text{model}}\left({\omega }_1+{\omega }_2\right)\right.$. Error bars in (a) and (c) represent a 95% confidence interval estimated from the distribution of ${\hat{Y}}^{\left(2\right)}$ estimates from CPWs of different lengths. We omit error bars on individual data points for visual clarity.

The quantity ${\hat{b}}_{\text{model}}$ is fully determined by the linear characterization. The first step to calculating ${\hat{b}}_{\text{model}}$ is to reconstruct the spatial variation of the incident voltage waves from the measured values ${\hat{a}}_1\left({\omega }_1\right),{\hat{a}}_2\left({\omega }_1\right),{\hat{a}}_1\left({\omega }_2\right)$, and ${\hat{a}}_2\left({\omega }_2\right)$. Using the boundary conditions from Sec. II B, we can determine the traveling wave amplitudes $V^{+}$ and $V^{-}$. From those amplitudes, and Eq. (12), we can estimate the spatial shape of the nonlinear current source density $\hat{N}\left(z\right)$ through Eq. (8). At this point, we solve for ${\hat{b}}_{\text{model}}$ using a Green’s function approach. The Green’s function is given in Sec. IIA, and the unknown coefficients in the Green’s function are determined from Eqs. (15) to (16) with the boundary conditions from Sec. II B. With the Green’s function known, and the nonlinear current density $\hat{N}\left(z\right)$ known, the currents and voltages at the frequencies of the mixing products are determined through Eqs. (17) and (18). These currents and voltages in turn can be used to determine ${\hat{b}}_{\text{model}}$.

The last step in our analysis is to relate the admittances ${\hat{Y}}^{\left(1\right)}$ and ${\hat{Y}}^{\left(2\right)}$ to the permittivities ${\hat{\epsilon }}^{\left(1\right)}$ and ${\hat{\epsilon }}^{\left(2\right)}$. To simplify this relationship, we note that the electric field of a TEM mode is frequency independent. Therefore, the relationship between the admittances ${\hat{Y}}^{\left(1\right)}$ and ${\hat{Y}}^{\left(2\right)}$ and the permittivities ${\hat{\epsilon }}^{\left(1\right)}$ and ${\hat{\epsilon }}^{\left(2\right)}$ is also frequency independent. In our geometry, the linear admittance and the permittivity are approximately related by ${\hat{Y}}^{\left(1\right)}\left(\omega \right)/i\omega =c_0+c_1{\hat{\epsilon }}^{\left(1\right)}\left(\omega \right)$ [47,58,59]. The constants $c_0$ and $c_1$ can be computed through quasistatic finite-element methods. The nonlinear admittance ${\hat{Y}}^{\left(2\right)}\left(\underset{\_}{\omega }\right)$ is linearly related to the strength of the dielectric nonlinearity, ${\hat{\epsilon }}^{\left(2\right)}\left(\underset{\_}{\omega }\right)$. To relate the nonlinear permittivity ${\hat{\epsilon }}^{\left(2\right)}$ to the admittance, ${\hat{Y}}^{\left(2\right)}$, we assume that the electric field in our waveguide (both microwave and dc) is given by the voltage between the center conductor and ground plane, divided by the gap width, $W$. This approximation leads to the relation ${\hat{Y}}^{\left(2\right)}=i\omega \left(c_1/W\right){\hat{\epsilon }}^{\left(2\right)}$. From the agreement between our data and model (Fig. 8), we estimate that the error introduced by this approximation is about 20% in the worst-case scenario (strong dc bias).

FIG. 8.

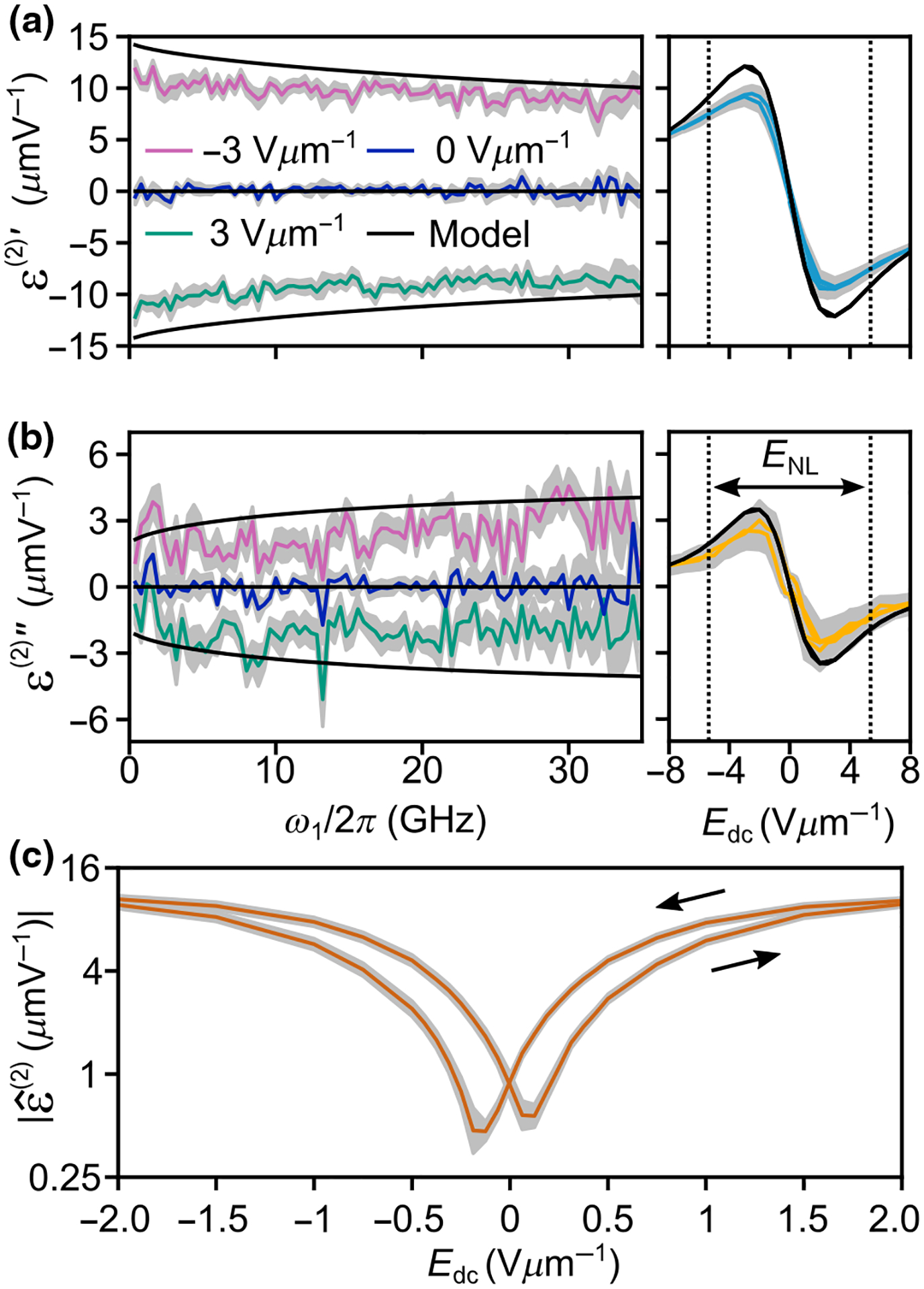
Second-order nonlinear permittivity, ${\hat{\epsilon }}^{\left(2\right)}={\epsilon }^{\left(2\right)\prime }-i{\epsilon }^{\left(2\right)\prime \prime }$, inferred from the ${\omega }_1+{\omega }_2$ mixing product. In the frequency-dependent measurements, we vary the angular frequency of one of the stimulus signals, ${\omega }_1$, while the other stimulus frequency, ${\omega }_2$, is held constant at $2\pi \times 5\mathrm{G}\mathrm{H}\mathrm{z}$. In our bias-swept measurements we set ${\omega }_1=2\pi \times 7.84\mathrm{G}\mathrm{H}\mathrm{z}$ and ${\omega }_2=2\pi \times 7.76\mathrm{G}\mathrm{H}\mathrm{z}$. To facilitate comparison to Fig. 7, we indicate an interval of width $E_{\mathrm{N}\mathrm{L}}$ centered around the $E_{\mathrm{d}\mathrm{c}}=0\mathrm{V}\mu {\text{m}}^{-1}$. The error bars (gray) are the 95% confidence interval from the standard error of the mean. (a) Real part, ${\epsilon }^{\left(2\right)\prime }$. (b) Imaginary part, ${\epsilon }^{\left(2\right)\prime \prime }$. (c) Absolute value of ${\hat{\epsilon }}^{\left(2\right)}$ near $0\mathrm{V}\mu {\mathrm{m}}^{-1}$.

IV. THERMODYNAMIC MODEL

We compare our results to a physical model that predicts the nonlinear response of our BST thin film. To be comparable with our experiment, the model needs to describe the time dependence of the polarization, describe the change of the polarization in response to a large applied field, and be amenable to a small-signal Volterra-series expansion. Mesoscale models meet these requirements, but require detailed knowledge of the nanostructure of the material. The small-signal requirement rules out models like the Ishibashi-Orihara model, which assume the amplitude of the time-varying field is large enough to completely pole the material [60,61]. Many models, like the spherical-random-bond-random-field model, are not suitable because they do not describe the time dependence of the material [62].

In BST thin films, the relaxation dynamics of PNRs lead to permittivity that varies over a broad range of frequencies, often modeled by a distribution of relaxation times [17–20]. To our knowledge, there is no universally accepted first-principles method to predict the distribution of relaxation times for a given material. Even a conceptual picture of PNR dynamics remains a subject of current research [13,14].

Given the complexity of a first-principles model, we take a phenomenological approach to interpreting our measurements. We chose a model that uses a heuristic interpretation of PNR dynamics and the Landau-Ginzburg-Devonshire (LGD) free energy. This model, introduced in Ref. [37], incorporates the salient features of our data: tuning of the permittivity with an applied electric field and a distribution of relaxation times. It was used to describe the temperature dependence and frequency dependence of the third harmonic up to 100 kHz in $\mathrm{P}\mathrm{b}\left({\mathrm{M}\mathrm{g}}_{1/3}{\mathrm{N}\mathrm{b}}_{2/3}\right){\mathrm{O}}_3$. We expect this model to also apply to BST in the tens of GHz because BST has qualitatively similar tuning behavior and dispersion.

The model describes the tuning processes in terms of the LGD free energy. In its simplest form, the LGD free energy $U$ can be expressed in terms of the polarization $P$ and the phenomenological parameters $\alpha$ and $\beta$ as $U=(1/2)\alpha P^2+(1/4)\beta P^4$. The one-dimensional model is justified because in our CPW structures, the electric fields are mostly in plane. The distribution of relaxation times is modeled by a function $f\left(t\right)$. The time evolution of the polarization is described by

$$P\left(t\right)={\epsilon }_0\Delta \epsilon \int d{t}^{\prime }f\left(t-t^{\prime }\right)\left[E\left(t^{\prime }\right)-\beta P^3\left(t^{\prime }\right)\right],$$ (25)

where $\Delta \epsilon ={\left({\epsilon }_0\alpha \right)}^{-1}$. Essentially, Eq. (25) models the polarization of a macroscopic region as a sum many coupled relaxation processes within identical anharmonic free-energy wells.

To model the nonlinear permittivity of our sample, we develop a perturbative expansion of Eq. (25) in powers of the electric field. We begin by writing the electric field as $E\left(t\right)=E_{\mathrm{d}\mathrm{c}}+e\left(t\right)$ and the polarization as $P\left(t\right)=P_{\mathrm{d}\mathrm{c}}+p^{\left(1\right)}\left(t\right)+p^{\left(2\right)}\left(t\right)+p^{\left(3\right)}\left(t\right)+\cdots$. We then substitute these series expansions into Eq. (25), and iteratively solve for $p^{\left(n\right)}$ in terms of $p^{\left(1\right)},\dots ,p^{(n-1)}$. Setting $e\left(t\right)=0$ and $p\left(t\right)=0$, Eq. (25) admits a closed-form solution for $P_{\mathrm{d}\mathrm{c}}$ if $\beta >0:P_{\mathrm{d}\mathrm{c}}={\epsilon }_0\Delta \epsilon E_{\mathrm{N}\mathrm{L}}T\left(E_{\mathrm{d}\mathrm{c}}/E_{\mathrm{N}\mathrm{L}}\right)$, with $T\left(x\right)=\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}\left[(1/3){\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}}^{-1}\left(3x\right)\right]$[63,64]. We introduce the parameter $E_{\mathrm{N}\mathrm{L}}={\left(4{\alpha }^3/3\beta \right)}^{1/2}$ with units of electric field to describe the strength of the nonlinearity. The function $T\left(x\right)$ has a sigmoidal shape, with a slope of unity for small arguments. With the dc polarization determined, calculating the Fourier transform of Eq. (25) yields

$${\hat{\epsilon }}^{\left(1\right)}\left(\omega \right)={\epsilon }_{\infty }+\Delta \epsilon {\hat{f}}_E\left(\omega \right),$$ (26)

$${\hat{\epsilon }}^{\left(2\right)}\left(\underset{\_}{\omega }\right)=\frac{-4P_{\mathrm{d}\mathrm{c}}}{{\epsilon }_0{\left(E_{\mathrm{N}\mathrm{L}}\right)}^2}{\hat{f}}_E\left(\Sigma \underset{\_}{\omega }\right){\hat{f}}_E\left({\omega }_1\right){\hat{f}}_E\left({\omega }_2\right).$$ (27)

For convenience, we define the function ${\hat{f}}_E\left(\omega \right)=\hat{f}\left(\omega \right)/\left[1+4T^2\left(E_{\mathrm{d}\mathrm{c}}/E_{\mathrm{N}\mathrm{L}}\right)\hat{f}\left(\omega \right)\right]$, where $\hat{f}\left(\omega \right)$ is the Fourier transform of $f\left(t\right)$ in Eq. (25). We also add an additional parameter ${\epsilon }_{\infty }$, which describes the high-frequency limit of the permittivity [17,18]. Qualitatively, both the real and imaginary parts of ${\hat{\epsilon }}_1\left(\omega \right)$ peak at $E_{\mathrm{d}\mathrm{c}}=0{\mathrm{V}\mathrm{m}}^{-1}$. The parameter $E_{\mathrm{N}\mathrm{L}}$ can be interpreted as a characteristic dc field strength necessary to cause appreciable tuning (about 64% at dc). On the other hand, ${\hat{\epsilon }}_2\left(\omega \right)$ vanishes at $E_{\mathrm{d}\mathrm{c}}=0{\mathrm{V}\mathrm{m}}^{-1}$, and is antisymmetric about $0{\mathrm{V}\mathrm{m}}^{-1}$. Note that the second-order permittivity is inversely related to $E_{\mathrm{N}\mathrm{L}}$, so this parameter quantifies both the width of the tuning curve and the strength of the second-order nonlinearity.

V. RESULTS AND DISCUSSION

As we expect from the model, the real and imaginary parts of the frequency-dependent permittivity tuned with the application of an electric field (Fig. 7). As we show in Fig. 1, we apply the bias voltage between the center conductor and the ground planes. This resulted in a mostly in-plane dc and microwave electric field, which are superimposed onto one another. To check if the BST sample had hysteresis, we sweep the electric field in a cycle $0\mathrm{V}\mu {\mathrm{m}}^{-1}\to 8\mathrm{V}\mu {\mathrm{m}}^{-1}\to -8\mathrm{V}\mu {\mathrm{m}}^{-1}\to 8\mathrm{V}\mu {\mathrm{m}}^{-1}\to 0\mathrm{V}\mu {\mathrm{m}}^{-1}$. No hysteresis larger than the measurement uncertainties is present. Both the real and imaginary parts of the permittivity have a peak near $0\mathrm{V}\mu {\mathrm{m}}^{-1}$, and decrease as the magnitude of the bias field increases.

FIG. 7.

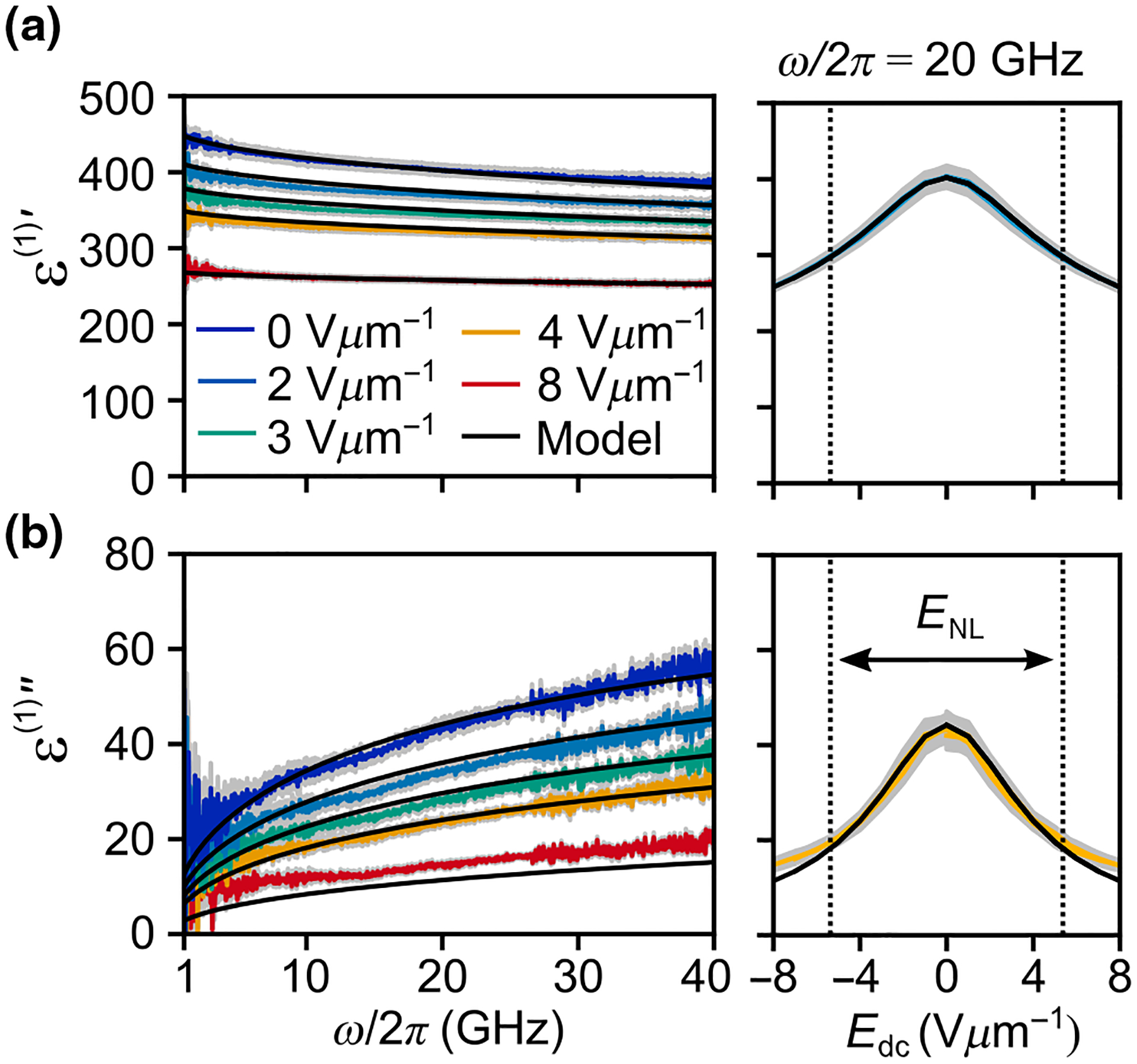
Linear permittivity, ${\hat{\epsilon }}^{\left(1\right)}={\epsilon }^{\left(1\right)\prime }-i{\epsilon }^{\left(1\right)\prime \prime }$ as a function of frequency, and as a function of bias electric field at 20 GHz. An interval of width $E_{\mathrm{N}\mathrm{L}}$ centered around $E_{\mathrm{d}\mathrm{c}}=0{\mathrm{V}\mathrm{m}}^{-1}$ is indicated. The error bars (gray) are the 95% confidence interval from the standard error of the mean. (a) Real part, ${\epsilon }^{\left(1\right)\prime }$. (b) Imaginary part, ${\epsilon }^{\left(1\right)\prime \prime }$.

Equation (26) captures the basic features of the electric field and frequency dependence of the data. We assume that $\hat{f}\left(\omega \right)$ is given by the Cole-Cole function $\hat{f}\left(\omega \right)={\left[1+{\left(i\omega {\tau }_0\right)}^a\right]}^{-1}$ [19]. The parameter ${\tau }_0$ is a phenomenological characteristic timescale. The parameter $a$ describes the shape of the distribution of relaxation times, with the value $a=1$ corresponding to the Debye model (one relaxation time), and smaller values describing wider distributions. This parameter also describes the limiting behavior of the dielectric loss at low frequencies ${\epsilon }^{\left(1\right)\prime \prime }\propto {\omega }^a$. The model illustrates the close link between the dielectric loss and the tuning. The parameters ${\tau }_0=0.49\mathrm{p}\mathrm{s},a=0.50,E_{\mathrm{N}\mathrm{L}}=10.7{\mathrm{V}}_{\mu }{\mathrm{m}}^{-1},{\epsilon }_{\infty }=106$, and $\Delta \epsilon =354$ are estimated by a least-squares fit. Equation (25) states that the polarization relaxes to the lowest free energy by a superposition of coupled gradient descent processes. The free-energy gradient is steeper at large dc fields, so the relaxation is faster. This field-dependent relaxation speed manifests as a field-dependent loss tangent, and the imaginary part of the permittivity tunes more strongly (66% at $8{\mathrm{V}\mu m}^{-1}$) compared with the tuning of the real part (33% at $8\mathrm{V}\mu {\mathrm{m}}^{-1}$).

As in the linear case, the model predicts the salient features of the dependence of ${\hat{\epsilon }}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)$ on bias field and frequency (Fig. 8). Note that the black line in Fig. 8 is a prediction, rather than a fit. The parameters in Eq. (27) are determined from the linear-permittivity data in Fig. 7. The model predicts the relaxationlike trend of ${\hat{\epsilon }}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)$ with frequency, but somewhat overestimates the value of ${\hat{\epsilon }}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)$. More notably, even though we see no hysteresis in the linear data, we see some hysteresis in the field dependence of ${\hat{\epsilon }}^{\left(2\right)}$. Figure 8(c) shows that the absolute value of ${\hat{\epsilon }}^{\left(2\right)}$ takes differing values on increasing and decreasing voltage sweeps, and that this difference is larger than the measurement uncertainties [65].

Extending this model to include spatial variation in the polarization could improve the accuracy of the model and provide physical insight. The electric field varies over the scale of the CPW gaps, causing different regions of the film to experience different dc bias. This large-scale inhomogeneity may impact the voltage dependence of the linear and nonlinear admittance. The polarization also varies on the scale of nanometers to hundreds of nanometers due to grain boundaries and PNRs. We speculate that interactions among PNRs might lead to different nonlinear coupling [other forms of the $P^3$ term in Eq. (25)]. While we conclude that Eq. (25) predicts most of the features of our data, we cannot exclude other models of nonlinear coupling. The samples that we characterize have relatively low dielectric loss, leading to a fairly flat frequency dependence for ${\hat{\epsilon }}^{\left(2\right)}\left({\omega }_1,{\omega }_2\right)$. In the future, we hope to evaluate more lossy samples and extend our measurements to higher frequencies. In this report, our main finding is that the measurement technique allows for broadband, calibrated, and model-independent measurements of material nonlinearity.

VI. CONCLUSIONS

In conclusion, we demonstrate the ability to measure nonlinear permittivity up to 40 GHz and develop a thermodynamic model informed by the data. We expect this technique to apply to a broad range of materials because the measurements and analysis used to produce Figs. 7 and 8 made no physical assumptions about the sample. These nonlinear-permittivity measurements provide a measurable quantity, independent of linear permittivity, that can be used to probe the complex dynamics of ferroelectric and related materials. The dynamics of these materials arise due to an interaction of many mechanisms including electrostatic energy, gradient energy, strain, and flexoelectricity. Nonlinear-permittivity measurements are a way to test models that include these different physical mechanisms. There are endless possibilities for manipulating the coupling between these effects to control domain structures and dielectric properties. For these materials to be used in high-speed electronics applications, it is necessary to understand their linear and nonlinear dynamics under an applied field.

The experimental data presented here is available online [66].