When Data Are Lacking: Physics-Based Inverse Design of Biopolymers Interacting with Complex, Fluid Phases

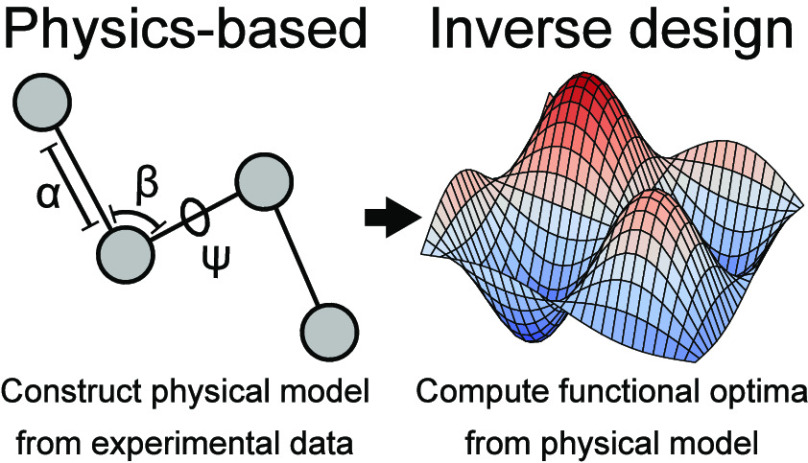
Abstract

Biomolecular research traditionally revolves around comprehending the mechanisms through which peptides or proteins facilitate specific functions, often driven by their relevance to clinical ailments. This conventional approach assumes that unraveling mechanisms is a prerequisite for wielding control over functionality, which stands as the ultimate research goal. However, an alternative perspective emerges from physics-based inverse design, shifting the focus from mechanisms to the direct acquisition of functional control strategies. By embracing this methodology, we can uncover solutions that might not have direct parallels in natural systems, yet yield crucial insights into the isolated molecular elements dictating functionality. This provides a distinctive comprehension of the underlying mechanisms.In this context, we elucidate how physics-based inverse design, facilitated by evolutionary algorithms and coarse-grained molecular simulations, charts a promising course for innovating the reverse engineering of biopolymers interacting with intricate fluid phases such as lipid membranes and liquid protein phases. We introduce evolutionary molecular dynamics (Evo-MD) simulations, an approach that merges evolutionary algorithms with the Martini coarse-grained force field. This method directs the evolutionary process from random amino acid sequences toward peptides interacting with complex fluid phases such as biological lipid membranes, offering significant promises in the development of peptide-based sensors and drugs. This approach can be tailored to recognize or selectively target specific attributes such as membrane curvature, lipid composition, membrane phase (e.g., lipid rafts), and protein fluid phases. Although the resulting optimal solutions may not perfectly align with biological norms, physics-based inverse design excels at isolating relevant physicochemical principles and thermodynamic driving forces governing optimal biopolymer interaction within complex fluidic environments. In addition, we expound upon how physics-based evolution using the Evo-MD approach can be harnessed to extract the evolutionary optimization fingerprints of protein–lipid interactions from native proteins. Finally, we outline how such an approach is uniquely able to generate strategic training data for predictive neural network models that cover the whole relevant physicochemical domain. Exploring challenges, we address key considerations such as choosing a fitting fitness function to delineate the desired functionality. Additionally, we scrutinize assumptions tied to system setup, the targeted protein structure, and limitations posed by the utilized (coarse-grained) force fields and explore potential strategies for guiding evolution with limited experimental data. This discourse encapsulates the potential and remaining obstacles of physics-based inverse design, paving the way for an exciting frontier in biomolecular research.

Introduction

The development of novel chemical targets, such as in material design or drug candidates, has historically been based on a process of lead optimization, where initial (natural) molecules are selected and put through an iterative process of adaptation and testing to selectively improve key properties.¹ While this strategy produces more optimized solutions, only a minuscule fraction of the imaginable combinations is considered.

To alleviate this, research increasingly focuses on the exploration of this so-called chemical space.^2,3 Here, the main challenge—and interest, as evidenced by the number of citations—arises from the astronomical size of chemical space, estimated at around 10⁶³ unique combinations for small molecules alone.⁴ To this end, large chemical libraries of compounds and molecular fragments have been constructed, which see application in virtual screening and de novo design.^3,5 As part of the initial stage in the development process, these in silico strategies can increase the efficiency of the research through early identification of viable candidates.² However, due to the involved dimensions, the limitations of standard design approaches quickly become apparent.

Inverse Design

Inverse design—where the process begins with the desired functionality, instead of the molecular structure—is particularly suited to such research due to its ability to efficiently handle many-dimensional problems.¹ Involved methods seek to create order from the massive chemical space through computation of the functional space, relating chemical structure(s) to a measure of the corresponding desired functionality (fitness). While computation of the entire functional space is infeasible, intelligent methods act by sampling positions in the functional space and—depending on subsequently computed local gradients—are capable of efficiently exploring this space to discover positions with better functionality.¹ A variety of methods can be applied in this regard, with the choice of method depending on factors such as the continuity of the functional space and the availability of (computational) resources. Several examples of inverse design and search space exploration strategies have been highlighted in Figure 1A–F.

Figure 1.

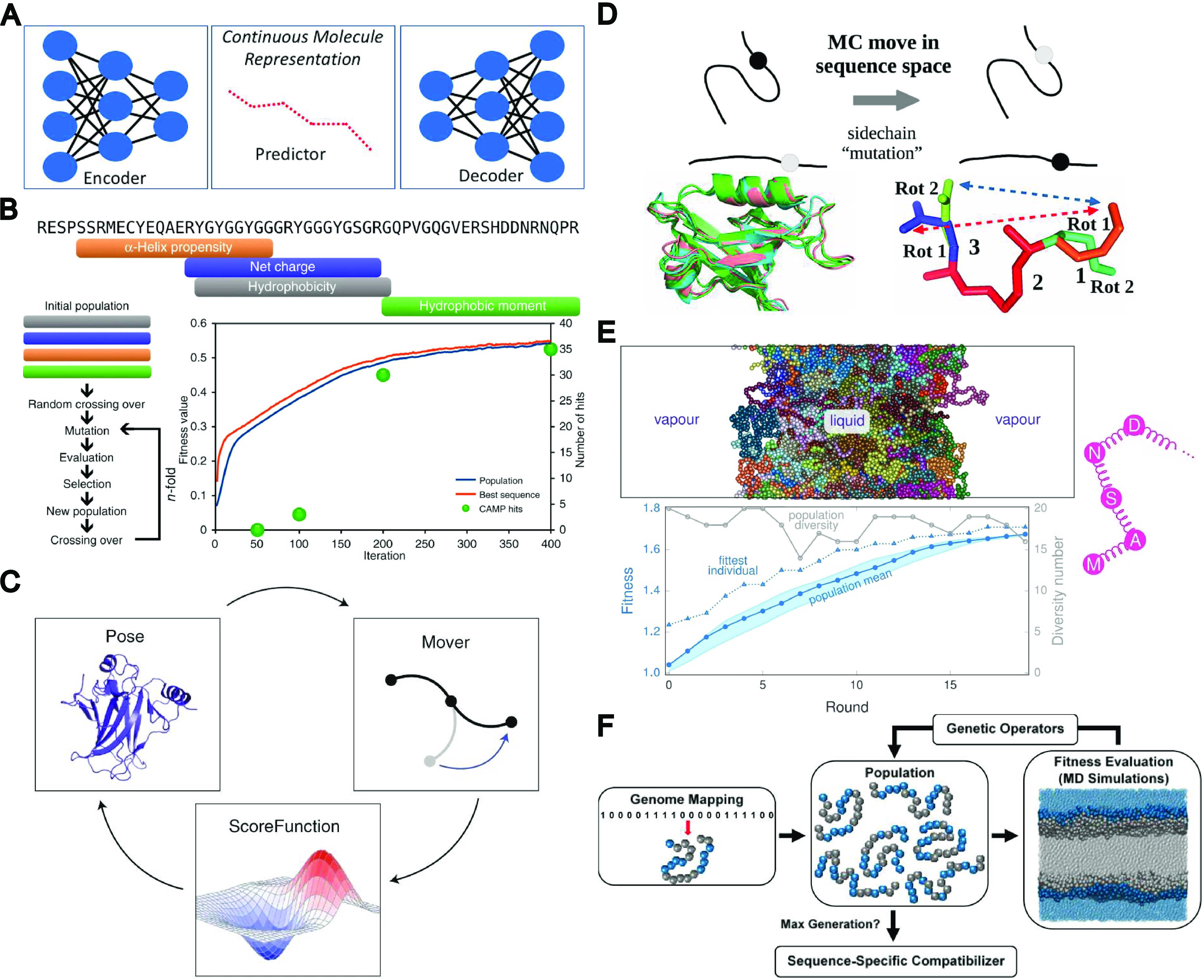
Collection of various inverse design and chemical space exploration approaches. (A) Generative model, encoding molecules of interest into a continuous latent space which can be explored to identify new molecules with similar properties. Reprinted with permission from ref (5). Copyright 2018 American Chemical Society. This is a commonly applied strategy in virtual screening. (B) Sequence-based genetic algorithm seeded with fragments that maximize specific physicochemical properties. Fitness values are directly calculated from sequence. Adapted from re (6). Copyright 2018 The Authors under a Creative Commons CC BY license, published by Springer Nature. (C) Simplified overview of the Rosetta protocol. Biomolecule configurations are iteratively modified and evaluated according to a prespecified scoring function of various energetic functions. Adapted with permission from ref (7). Copyright 2020 Nature Springer America, Inc. (D) Physics-based redesign of proteins using Monte Carlo and Boltzmann sampling. Adapted with permission from ref (8). Copyright 2020 American Chemical Society. (E) Combining genetic algorithms with amino-acid-scale coarse-grained MD simulations for local optimization of existing liquid–liquid phase separating proteins. Reprinted with permission from ref (9). Copyright 2021 The Authors under Creative Commons Attribution International license, published by PLOS. (F) Combining genetic algorithms with MD simulations using a binary coarse-grained copolymer model for de novo optimization of copolymer compatibilizers. Reprinted with permission from ref (10). Copyright 2017 American Chemical Society.

Learning from Evolution

Evolutionary strategies, such as the genetic algorithm (GA), function through an iterative process inspired by Darwinian evolution.¹¹ In optimization problems, candidate solutions are encoded as sequences of bits or characters, where each position in the sequence represents a specific property that is free to be adapted by the optimization algorithm. These sequences can be evaluated according to a specified fitness function, which assigns fitness values to the sequences based on how well they perform in the given problem.

The GA proceeds by generating a population of candidate sequences, either based on some existing (natural) solution which is to be optimized or generated randomly to better explore the overall functional space. All sequences in this population are then evaluated according to the fitness function and ranked based on the resulting fitness values. The best performers are selected from the population, and parts of their sequences are combined with each other to generate a new population. Random mutations are introduced in the new sequences to maintain diversity within the population. This process of evaluation, selection, and recombination repeats until a desired target is achieved.¹¹

The underlying assumption behind this approach is that the functional properties of a solution are inherently encoded within its sequence, and through recombination of high-performing sequences more high-performing sequences are produced. Random crossover and mutation of these sequences allows for sporadic increases in functionality, leading to a steady increase in the fitness of a population over time until it converges to some optimal solution.¹¹

Notably, such evolutionary operations are fairly trivial within the chemical space of biopolymers, since they topologically consist of linear chains of repeating autonomous units and therefore the chemical design rules are well-defined. A straightforward example of this concept in practice can be seen in peptide optimization problems, where the solutions (peptides) are simply encoded as sequences of amino acids, which are then evaluated using a fitness function that considers one or several amino acid-dependent factors, such as hydrophobicity or helix-forming propensities.⁶ In the case of small organic molecules, however, encoding into chemical space is far from trivial due to the inherently nonlinear and three-dimensional nature of the structures, typically involving conversions into continuous and high-dimensional descriptor spaces.^1,12

Solutions obtained through natural evolution are optimized with respect to a complex environment—taking into account factors like cell toxicity, competition between molecules, variations within the environment, energetic cost, and so on, to ensure that the overall fitness of an organism is not negatively affected. As many of such factors are in conflict with each other (e.g., toxicity putting limitations on the possible chemistry and concentrations of molecules), it is conceivable that more optimal “solutions” exist when we consider only specific functionalities of interest. Part of the strength of inverse design strategies lies with the transparency of the fitness function, as it allows us to precisely define those factors we are interested in, and leave out those which we are not. This selectivity allows us to move beyond what is seen in natural evolution. Although not directly applicable in natural systems, solutions found in this manner allow for the identification of the isolated molecular features that dictate functionality and therefore provide unique insight in the underlying mechanisms. The resulting knowledge can potentially assist in the development of new drug targets.

Physics-Based Inverse Design

Physics-based inverse design operates on the principle that the physical driving forces governing functionality are encoded within independently parametrized energy functions, such as molecular force fields. By employing inverse design approaches, functional molecular structures can be identified from these energy functions. In such approaches, the chemical space is sampled directly through thermodynamic ensemble averaging of observables, either through Hamiltonian dynamics in molecular dynamics (MD) simulations or through explicit calculation of Boltzmann factors subject to detailed balance in Monte Carlo (MC) simulations.

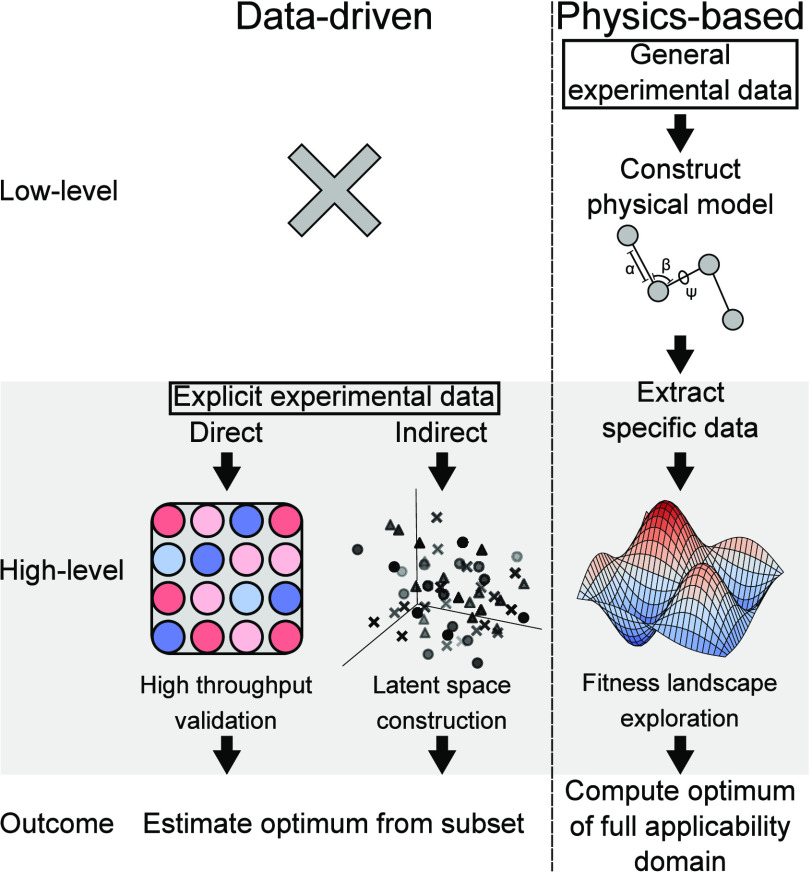
Data-driven inverse design approaches, on the other hand, often rely on constructing a latent space, a high-dimensional vector space comprising physicochemical and structural descriptors of biomolecules.¹ These approaches, such as quantitative structure–activity relationship (QSAR) models, aim to establish a quantitative relationship between the descriptor vector and the corresponding functionality. Inverse design in these approaches involves the identification of optima in the latent space and subsequent translation into corresponding chemical structures.¹² Data for constructing latent spaces can come from experiments or computational high-throughput methods such as molecular simulations or molecular docking. This distinction is visualized in Figure 2.

Figure 2.

Comparing “data-driven” to “physics-based” methods. To clarify the distinction, we look to the relation between experimental data and the desired outcome. In data-driven methods, the experimental data are of the same class as the result (high-level)—i.e., to optimize protein–ligand binding, one needs protein–ligand binding experimental data. In contrast, physics-based methods utilize general, indirect experimental data (low-level) to construct physical models, from which data specific to the desired optimization (high-level) can be extracted using inverse design techniques.

Physics-based design offers a distinct advantage over data-scientific approaches by eliminating the need for the construction of a latent space, addressing the three primary drawbacks associated with data-driven methods: First, the requirement for large experimental data on functionality can be challenging to fulfill or access. Second, the construction of a latent space relies on a priori known descriptors, which may omit significant determinants and lead to suboptimal predictions. In contrast, physics-based design approaches can enhance optimization efficiency by reducing the dimensionality of the physical molecular space through techniques like coarse-graining. Third, a latent space may restrict the applicability domain of sequence generation, resulting in generated molecules resembling the training data. Physics-based inverse design approaches overcome this limitation by exploring the entire available amino acid sequence space, enabling the identification of global optima in lipid–protein interactions even within a vast sequence space (e.g., 20²⁴ sequences).

Physics-Based Design of Proteins

One prominent example of physics-based design in biopolymer or protein design is Rosetta.⁷ Rosetta operates on the principle that native protein structures represent free energy minima, aiming to determine the sequence corresponding to the minimal free energy state. The approach combines knowledge-based potentials derived from the PDB database with physical energy terms like van der Waals and electrostatic interactions. Rosetta is widely used in protein design to obtain desired folding patterns, binding pockets, and more (see Leman et al.⁷ for a comprehensive review). However, existing protein design methods, including Rosetta, are primarily focused on single molecular structures in simplified solvent environments. Consequently, their energy functions, often relying on knowledge-based potentials, may fail to accurately capture scenarios where energy minimization is influenced by complex, fluidic, and responsive environments such as biological lipid membranes and protein liquid phases.

Proteins Interacting with Complex Fluid Phases

The main focus of this perspective lies on conducting physics-based design of biopolymers, optimized for interaction with fluid phases. We posit that in such scenarios the fold of a biopolymer is often not the determining factor for functionality. This notion is supported by the discovery of highly functional disordered proteins and protein regions in recent decades.^13,14 Furthermore, the fold can often be assumed or predetermined. For instance, the design of α-helical peptides that sense lipid packing defects typically yields sequences with a high propensity for α-helical structure, as functionality is primarily driven by intermolecular interactions at the membrane interface.¹⁵ This optimization process tends to “bake-in” the imposed structure. Consequently, the energy function should focus on accurately and efficiently describing interactions with the environment, favoring physical molecular force fields over knowledge-based potentials. Coarse-grained force fields are particularly advantageous due to the computational costs associated with inverse design using molecular dynamics simulations in conjunction with evolutionary algorithms.

Moreover, in structure-focused protein design, even minor alterations can have a significant impact within the tightly sculpted angstrom-resolution world of protein cavities.^16,17 This leads to a search space which is highly localized around unique solution sequences, aligning with the key–lock hypothesis for molecular recognition. In contrast, interactions with fluid phases involve weak, transient, and dynamic interactions with individual constituents of the fluid phase such as, for example, a lipid membrane^15,18,19 or a protein liquid condensate.^9,20−25 These interactions feature search spaces characterized by smoothness and a high degree of degeneracy in relevant physicochemical properties. In other words, due to the smoothness of the search space, the optimum is represented by a potentially large set of equally valid and degenerate solutions, rather than a single “holy grail” sequence that outperforms all others. We argue that these aspects often facilitate convergence to a global rather than a local optimum, even in search spaces containing 20²⁰ or more sequences.

In the following sections, we will present various examples of biopolymer design for interaction with complex fluid phases, introduce our recently developed evolutionary molecular dynamics approach, and discuss the potential, challenges, culprits, and shortcomings of current physics-based design methods.

Recent Applications of (Physics-Based) Inverse Design

Inverse design strategies involved in the design of biopolymers commonly focus on the optimization of existing (natural) sequences,⁸ effectively constraining the potential exploration of the search space to regions of known functionality. Reduction of the search space in this manner decreases the computational requirements, which can instead be directed toward a more thorough analysis (considering large population sizes and many iterations) for inverse design methods with relatively simple fitness functions. Sequence-based fitness functions as applied by Porto et al. are a prime example of cost-effective evaluations of peptide features, scoring candidate sequences as a function of amino acid hydrophobicity and helicity scales.⁶ Alternatively, fewer evaluations (i.e., small population sizes and few iterations) can be performed using more complex and resource-intensive fitness functions capable of exploring the dynamic features of candidate biopolymer sequences as applied in physics-based inverse design. An example of this is seen in the work of Lichtinger et al., where MD simulations are integrated into a genetic algorithm with the aim of identifying stabilizing and disruptive features of liquid–liquid phase separation in intrinsically disordered proteins.⁹

While this approach has proven effective, there are several drawbacks. Initializing the optimization using known sequences has the potential for getting trapped in local optima as large regions of the search space remain unexplored. Initialization of the population with random sequences instead provides a relatively uniform distribution over the search space while eliminating a potential source of input bias, potentially identifying new solutions as previously unknown regions of the search space are explored.²⁶ Most importantly, starting from independent random populations allows for discrimination between local optima and a potential global optimum, thereby providing unique information on the main physicochemical determinants that underpin solution space.

The main challenges of physics-based inverse design strategies involve the heavy computational and time requirements that arise from the integration of (resource-heavy) physics-based techniques into metaheuristic inverse design strategies. While conventional fitness functions used in, for example, genetic algorithms can typically be evaluated in the order of (milli)seconds to minutes,¹¹ physics-based techniques such as molecular simulations require essential computation of ensemble averages which lies magnitudes of order above that, ranging from hours to days for most coarse-grained systems, to potentially weeks or months for larger atomistic or quantum simulations. The product of physics-based evaluations and inverse design strategies, where tens of thousands of evaluations must be performed to produce reliable results, leads to slow methods which are heavily reliant on computational resources to perform a complete optimization.

To ensure the viability of physics-based inverse design strategies, particularly in the absence of prior knowledge during initialization, a balance should be struck between the thoroughness of the inverse design process (e.g., population size and number of iterations) and the depth and accuracy of the fitness function (e.g., resolution and simulation time). Recent literature support the feasibility of such approaches, through the use of smart strategies and manageable search spaces. The field of polymer science in particular sees benefit from such approaches.^27,28 For example, Meenakshisundaram et al. have applied the combination of genetic algorithms with coarse-grained MD simulations to identify synthetic copolymer compatibilizers, capable of stabilizing polymer–polymer interfaces.¹⁰ Due to the computationally intensive nature of the MD simulations, time spent on simulations should be kept to a minimum.

An alternative strategy entails the use of surrogate models—in particular artificial neural network models trained by performing extensive molecular simulations of targets—in place of actual physics-based simulations. Surrogate models are capable of predicting simulation results at orders of magnitude faster than what would be achievable by directly performing the simulation,^29,30 providing an attractive alternative to direct simulations in the inverse design process. While such models bear similarities to data-driven strategies,¹ training of surrogate models relies on molecular simulations and can therefore be considered as part of a physics-based strategy. However, reliance on extrapolation, particularly the case for machine learning-based models, may limit optimization when exploring untrained regions of the search space.^10,29 Hybrid strategies that integrate surrogate models into the optimization workflow, combined with systematic retraining of the model during optimization, could provide the best of both worlds.^23,31

In our recent works, we have demonstrated applications of physics-based inverse design strategies in the de novo design of functional membrane peptides, relying solely on direct molecular simulation. The main challenge in protein design lies with the immense search spaces that are available to explore, with 20²⁴ possible combinations existing for a 24 amino acid long peptide when considering 20 natural amino acids. While problems of this magnitude might seem computationally intractable, identification of the optimal transmembrane cholesterol attractor¹⁸ and optimal membrane curvature sensor¹⁵ peptides support the viability of the strategy for in silico identification of candidate peptides, hinting to the potential of physics-based inverse design strategies in various fields.

Synthetic Polymers

Although not strictly biopolymers, the research on synthetic polymers also highly benefits from physics-based inverse design strategies, as recently reviewed by Patra.²⁷ While many similarities exist between the fields, the main difficulties that set biopolymers apart involve the larger chemical spaces often considered as well as the interactions and functionalities that are considered for optimization. Biopolymers such as polynucleotides and polypeptides contain many more elements per position than what is generally considered for polymer optimization, producing significantly larger search spaces. Optimizing interactions for biopolymers primarily involves their intricate, heterogeneous environments, such as lipid membranes, where they are localized or influenced. In contrast, polymer optimization typically focuses on the bulk properties of the materials. Nonetheless, valuable lessons can be learned that apply to either field. In particular perspectives on multiobjective optimization and the integration of automated experimental characterization could also be of relevance to the design of biopolymers.²⁷

Evolutionary Molecular Dynamics: Principle of EVO-MD

We introduce EVO-MD as an example implementation of the physics-based inverse design concept, which we have applied in the development of membrane-interacting peptides.^15,18,32EVO-MD integrates molecular simulations based on building-block coarse-grained force fields, such as the Martini model, into a custom genetic algorithm wrapper program, allowing for the automated setup, production, and subsequent analysis of MD simulations based on candidate sequences selected by the genetic algorithm. The concept of EVO-MD is inspired by the work on virtual creatures performed by Karl Sims in the 1990s.^33,34 Virtual creatures, as simulated by Karl Sims, involve the evolution of virtual block creatures in a simulated dynamic environment. These creatures are created within a computer and undergo a process of variation and selection to improve their ability to perform specific tasks, such as swimming or walking, or even competition for food (see Figure 3). The goal is to create creatures with successful behaviors through the evolution of their virtual genes. At its heart, EVO-MD uses the idea of virtual creatures to guide the evolution of biomolecules within a molecular dynamics environment. It harnesses the laws of physics and thermodynamic forces to shape biomolecules starting from completely random sequences.

Figure 3.

Virtual creatures in action. The snapshots (from left to right) illustrate a scenario where the evolution of virtual creatures is being driven by food competition (green colored block). Adapted with permission from ref (34). Copyright 1994 MIT.

The heavy computational and time requirements associated with physics-based inverse design, particularly when considering both large search spaces (e.g., exceeding 20²⁴ combinations) and random initialization, are mitigated using strategies that maximize information extraction from the available simulation data. The largest gain in efficiency follows from the use of relatively short coarse-grained MD simulations for the fitness evaluations. While the simulations are not yet converged within these time frames and the measured observable(s) are therefore far from accurate, genetic algorithms do not require the absolute value of an observable. All that is required for evolution to proceed is an estimation of the relative ranking of the solutions within a population as this is the sole criterion on which the selection is based. As long as a “better” solution relatively outperforms most other solutions, evolution proceeds in the proper direction. However, the closer we approach the (global) optimum in evolution, the smaller the spread in fitness within the population pool and thus the more relevant robust sampling becomes.

Undersampling of simulation observables does pose a problem for the selection step, as outliers—being excessively overestimated observables with respect to their actual value due to undersampling—would almost fully constitute a selection pool after evaluation. We devised several approaches to combat this: (i) We assume that the outliers are due to undersampling and that the distributions of the mean values are (mostly) sequence independent. From this follows that outliers of better solutions (i.e., with high “true” values for their observable(s)) are more likely to exceed the outliers of worse results, and therefore allows us save time in our simulations by intentionally undersampling (within reason). (ii) We optimize the time that we allocate for sampling through the use of simulation replicas. This can provide a more efficient and accurate estimation of the observable(s) compared to a single, longer simulation—in particular when the largest relaxation time in the system of interest is in the order of the time scale of the simulation.^35,36 (iii) We eliminate outliers by verifying the best results of each iteration and maintaining high-performing solutions between iterations. The usage of elitism—where the best performing solutions in a population are directly copied over to the new population—leads to solutions occurring which have already been evaluated. To verify the best performers, the corresponding observable(s) are again estimated using independent simulations. The new value is then computed from the weighted average of previous estimations and the new simulation result. This process effectively adds additional replicas into a solution’s evaluation, increasing accuracy and thereby removing outliers from the selection pool. Sequences that maintain their high-performing status are retained through a second elitism procedure, to ensure that high-performing solutions are not lost.

Applications

Optimizing Transmembrane Peptides for Cholesterol Attraction

Development of EVO-MD was centered around the optimization of transmembrane proteins for protein–cholesterol interaction. In an attempt to identify potential linear cholesterol-recognition motifs using evolutionary strategies, we discovered a thermodynamically driven effect of attraction, based on hydrophobic mismatching between peptide and membrane and the membrane-snorkeling ability of cholesterol molecules¹⁸ (see Figure 4).

Figure 4.

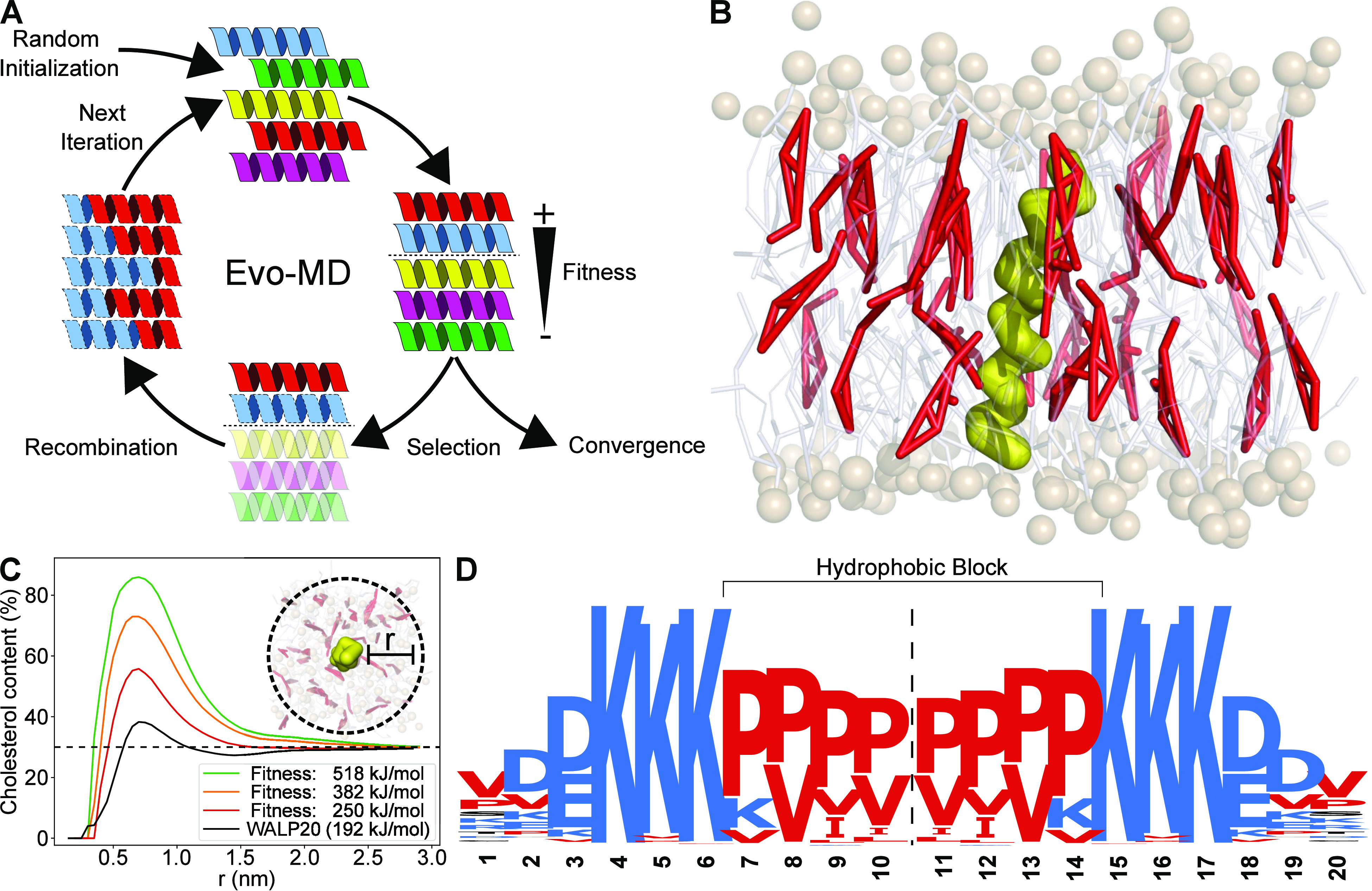
Inverse design of the optimal transmembrane cholesterol-attracting peptide sequence using Evo-MD. Reprinted with permission from ref (18). Copyright 2021 The Authors, preprinted by Cold Spring Harbor Laboratory. (A) Graphical overview of the Evo-MD approach. (B) Side view of an example simulation system used for fitness evaluation. The candidate peptide (yellow) is transversely positioned in a POPC (white/brown) and cholesterol (red) bilayer membrane. Fitness is computed from the time-averaged interaction energy between peptide and all cholesterol molecules. (C) Plot of cholesterol enrichment in a shell surrounding the peptide. As Evo-MD produces higher fitness sequences, we see an increase in the accumulation of cholesterol around these peptides. (D) Sequence logo visualizing the characteristics of the optimal transmembrane cholesterol attractor, revealing highly conserved lysine patches located deep within the membrane, and a short block consisting of small hydrophobic amino acids.

The project yielded two valuable lessons for advancing the realm of physics-based biopolymer design. First, we demonstrated that it is in fact feasible to perform directed evolution starting from completely random sequences, using a fitness function that is evaluated through coarse-grained molecular dynamics simulations. Considering the many limitations brought about by this approach—constraining the method to relatively small population sizes, low numbers of iterations, and significant undersampling—we show that it is indeed possible to converge toward the global optimum, as is evident by reproducing the same solution despite starting from different random sequences and sequence population sizes. Interestingly, this suggests that the solution space of protein–lipid interactions—in our example cholesterol attraction—comprises a function with a well-defined single maximum/optimum. As a result, the fitness of the optimization converges rapidly toward the global optimum.

Second, the usage of evolutionary strategies allows for a more thorough exploration of the search space, where the search itself is less dependent on researcher’s bias. This bias, however, is effectively transferred to other aspects of the approach such as in the definition of the fitness function. An example of this can be seen in the definition of cholesterol recognition. Are we interested in a sequence that attracts and therefore clusters as much cholesterol around it as possible (aspecific binding) or instead a sequence that allows for the strongest binding to a single specific cholesterol molecule, preventing dissociation afterward (specific binding). A fitness function which simply maximizes interaction energy between protein and lipid, which we applied in our cholesterol recognition project,¹⁸ would result in the former example, while a fitness function optimizing the latter case might instead require an alternative measurement/definition for binding, possibly considering the duration at which a specific cholesterol molecule stays bound to the protein. Such distinctions are easy to overlook, yet evolutionary algorithms are extremely sensitive to them. Precisely because of this sensitivity, important insights can be gained into what it is that natural evolution truly optimizes for.

Curvature Sensing Peptides

We also applied EVO-MD to the inverse design of surface peptides that sense hydrophobic defects in the lipid packing that arise when membranes are strongly curved.^15,32 In line with elastic theory,³⁷ we found that the optimal physics-based curvature sensor is extremely hydrophobic and bulky (rich in phenylalanine and tryptophan residues), allowing for deep insertion into the outer membrane leaflet and maximization of asymmetric leaflet tension. Obtaining these fundamental insights through a data-driven approach, devoid of reliance on physics-based principles, is a nontrivial task. The answers lie beyond the practical domain of native water-soluble peptide sequences. Herein lies the strength of physics-based inverse design, which empowers true physical optimization, unconstrained by biological limitations or researcher biases. However, this emphasis on physical optimization does not preclude the exploration of practical applications. On the contrary, in addition to the valuable contributions physical optimization offers for fundamental understanding, one can incorporate pragmatic “posthoc” adjustments based on the theoretical optimum.

For instance, it is possible to restrict the optimization within a “biologically feasible” search space, aligning with criteria imposed by biology such as solubility, membrane-binding selectivity, and fine-tuned protein–protein interactions. Starting from the theoretical optimum, one can argue that this approach expands the exploration of a much broader search space, especially when employing the data to train a neural network model for fitness prediction, as is utilized in surrogate models.³⁰ This model can then be utilized to further optimize the solution while subjecting it to additional pragmatic constraints. The result may unveil additional feasible solutions that might otherwise remain undiscovered when exclusively working within the confines of biologically viable configurations.

With the large body of MD data we acquired during the Evo-MD optimization of these curvature sensors, we trained a convolutional neural network (CNN) that can predict sensing free energy of a peptide from its primary amino acid sequence alone.¹⁵ On average, the (root mean squared) error of these predictions was in the same range as the typical sampling error from MD simulations. Interestingly, we found that the CNN-predicted free energies better describe qualitative experimental trends (derived from literature) than the MD trajectories they were trained on. We suggest that this is due to a smoothing effect in both chemical space (the CNN is trained on data for >100000 unique sequences) and in the MD sampling itself, which, overall, leads to more robust predictions.

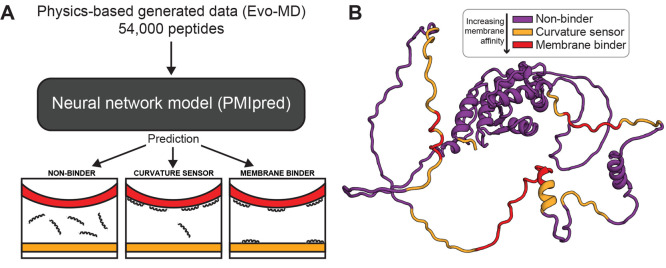
The observed accuracy of neural networks trained by Evo-MD data has motivated us to launch the protein–membrane interaction prediction (PMIpred) server (https://pmipred.fkt.physik.tu-dortmund.de/),¹⁹ which utilizes a transformer model trained by physics-based generation (EVO-MD) of over 54000 curvature-sensing peptide sequences to predict the membrane-interaction behavior of peptide sequences (Figure 5A). Moreover, PMIpred enables users to (i) scan protein structures (PDB files) for the presence of membrane-binding domains, (ii) quantify curvature sensing, (iii) discriminate between membrane binding and curvature sensing (see Figure 5B for an example), and (iv) quantify the contribution of each individual amino acid to membrane binding, thereby easing the design of point deleterious mutations. Using training data generated by evolutionary optimization has the important advantage that it encompasses the full thermodynamic range of possibilities over a vast search space (20²⁴ sequences in this particular case), whereas a data set of natural peptides (if available in the first place) would be strongly constrained to a certain biologically feasible regime that only comprises peptides with highly similar physicochemical characteristics. Therefore, we argue that such a training set can substantially improve both the applicability domain as well as the accuracy of neural network models, despite many of the generated sequences not necessarily being biologically relevant. This principle is equivalent to fitting an unknown function to data points that are well-spaced over the whole range of the applicability domain versus data points that are only clustered within a narrow window. Particularly, precise knowledge of the maxima (and minima) of a function—which a physics-based optimization is able to resolve—will benefit the quality of a fit or model, also within the biologically relevant domain of the search space.

Figure 5.

Overview of PMIpred: on-the-fly prediction of peptide–membrane interaction using physics-based inverse design. Adapted with permission from ref (19). Copyright 2023 The Authors, preprinted by Cold Spring Harbor Laboratory. (A) Data produced using physics-based inverse design approaches such as Evo-MD can be used to train deep learning models, allowing for quick but accurate evaluation of entire proteins while avoiding the overhead of MD simulations. PMIpred incorporates a transformer model trained on Evo-MD generated data for optimizing curvature sensing, allowing for the classification of peptides and regions of proteins as either nonbinding, curvature sensing, or membrane binding. (B) Example output of PMIpred showing the protein structure of ArfGAP1. Regions of interest are labeled according to the model, indicating regions likely to exhibit curvature sensing, membrane binding, or nonbinding behavior.

Considerations

Hyperparameter Optimization

Results obtained from our work with EVO-MD substantiate the viability of physics-based inverse design as a tool for efficient in silico exploration of extensive search spaces. However, the demanding nature of the method makes it rather difficult to perform performance optimizations with regard to the inverse design segment of the approach, as this would require performing multiple runs of the algorithm to evaluate the effect of various hyperparameters on convergence efficiency and search space exploration. It is therefore likely that there exists significant room for improvement regarding the optimization of algorithm parameters. This becomes apparent when we compare to more common use cases for such methods. For example, general genetic algorithm applications often make use of individual evaluations that are on a much shorter time span ((milli)seconds to minutes), rather than the hours seen in molecular simulations.¹¹ In such cases, it is relatively easy to perform large scale hyperparameter and performance tests to find algorithm parameters that optimize the search for efficient convergence and a reduced chance of getting stuck in suboptimal solutions of the search space (local optima).

Surrogate models, as applied in similar strategies,^27,29,31 could provide an alternative scheme for more efficient debugging and parameter testing within a physics-based inverse design context. This would involve (1) running a short preliminary optimization using physics-based models with default parameters, (2) training a surrogate model (e.g., neural network) on the gathered data, (3) replacing the physics-based fitness function (hours) with the surrogate model (seconds), and (4) performing the parameter testing with the highly efficient surrogate-based genetic algorithm. The resulting parameters can then be applied to the original physics-based genetic algorithm.

Secondary Structure Prediction

The gain in efficiency achieved through the use of the Martini coarse-grained force fields is vital to the feasibility of the approach. However, a major trade-off with respect to protein simulations is the models failure to represent changes in secondary structure during simulations. Secondary structure must therefore be defined prior to the simulation and is fixed using specific parameters for the affected beads.³⁸ This is not necessarily a limiting factor in the physics-based inverse design of sequences interacting with fluidic systems, where optimizing the interactions with the environment dominates protein functionality.^20,21 The forcing of a specific structure, while the sequence might not adhere to this structure in reality, in fact avoids a potential source of bias. While the quality of secondary structure prediction tools has seen significant advances through implementation of machine learning techniques, prediction remains limited to 84% accuracy.³⁹ Viable solutions might therefore be excluded from the search space. In addition, although sequence-based exclusion of nonhelical solutions might guarantee structurally valid peptides, it essentially restricts regions of the search space and thereby limits exploration during the inverse design process. Structurally invalid solutions might still exhibit favorable aspects, and could therefore serve as a stepping stone toward higher fitness solutions. Finally, such solutions still yield unique insight into the physicochemical driving forces underpinning functionality, and obtained optima could alternatively serve as templates for synthetic peptide mimics. Once optimization has been performed, more realistic sequences can be produced based on the optimized results.

An example of this procedure can be seen with the optimization of the transmembrane cholesterol attractor peptide.¹⁸ Due to the (thermo)dynamic nature of this problem, most solutions do not impose hard requirements on the specific type and position of specific amino acids. Instead, analysis of the produced solutions leads to the identification of groups of amino acids that produce similar effects. Based on this analysis, we can then select amino acids suiting a specific structure constraint based on the user’s need. For the transmembrane cholesterol attractor, we sought to produce an α-helical peptide and therefore enforced this structure in the simulations. This allowed the search to produce solutions that would not conform to the desired secondary structure in laboratory experiments. However, after analysis of the produced sequences, alternative amino acids could be selected that both complied with the given structure yet still produced the desired functionality.

Finally, advances in the field of (secondary) structure prediction have led to tools such as AlphaFold⁴⁰ and Porter5,⁴¹ which do not require specific experimental data and can be integrated as part of the sequence generation step should a (semi)accurate structure representation be desired for individual sequences. Such preliminary exclusion of structurally invalid solutions reduces the search space and therefore allows for a faster convergence of the inverse design process, although it may converge toward local optima.

Outlook

In Silico Optimization in Dynamic Environments

We have thus far only scratched the surface of the potential utility of physics-based evolutionary optimization within the field of molecular sciences. We in particular envision physics-based inverse design to open new and unique avenues in the (inter)facial recognition of biological lipid membranes, e.g., the inverse design of peptide drugs and peptide-based drug vehicles capable of selectively targeting the fluid membranes of viruses, microbes, and cancer cells; since their membrane leaflets are characterized by pronounced differences in curvature⁴² and/or lipid composition.⁴³ Here, structure-based molecular design approaches are rendered ineffective beyond the level of targeting individual lipid species due the diffusive and fluid nature of lipid membranes.

Mystery of Lipid Rafts

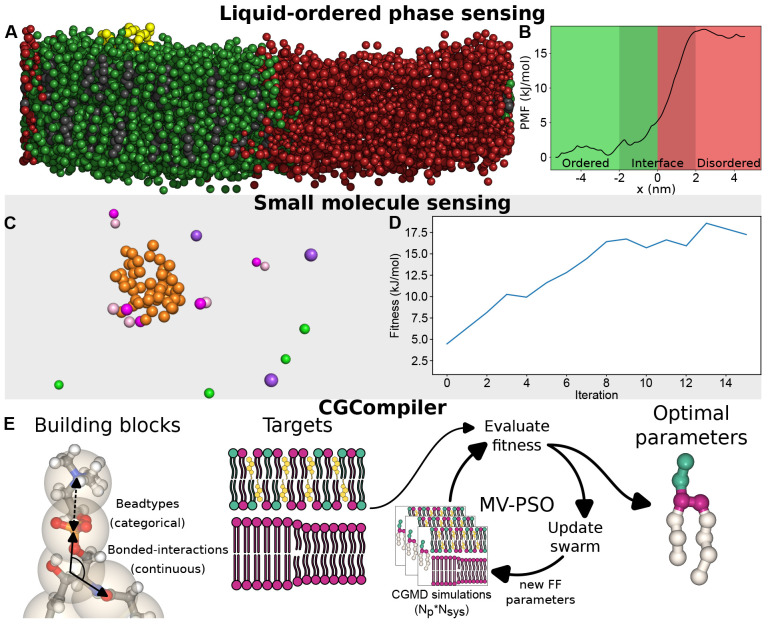
A closely related design challenge emerges within research domains investigating the interactions between proteins and lipid rafts. Lipid rafts are organized but transient regions of the cellular membrane where the formation is primarily driven by lipid–lipid interactions, in particular saturated lipids, glycosphingolipids, and cholesterol.⁴⁵ Lipid rafts are expected to be in the liquid-ordered phase. While such domains have been extensively studied in model membranes,⁴⁵ the highly dynamic nature of these domains complicates in vivo detection and therefore investigation.⁴⁵ An important question is whether motifs might exist in native proteins capable of sensing and potentially inducing such phase compositions in lipid membranes, as is hinted at by the discovery of several features for transmembrane protein–raft association.⁴⁶ In this context, leveraging physics-based inverse design emerges as a pivotal tool, providing a framework for the direct optimization of protein-raft interactions, specifically focusing on the affinity of proteins for liquid ordered phases over liquid disordered phases (see Figure 6A,B). Subsequently, a follow-up analysis to determine raft affinity in native protein sequences could be streamlined by employing a neural network trained in a manner similar to PMIpred.¹⁹ However, the main challenge will be in translating the affinity derived from simplified in silico models of lipid rafts to the complex and dynamic lipid rafts in vivo.

Figure 6.

A peek into the (potential) near-future of physics-based inverse design. All illustrated quantitative data are symbolic and only serve as an impression of the aimed result. Discovering lipid raft sensing motifs using Evo-MD. (A) Suggested coarse-grained system for the optimization of a membrane binding peptide (yellow), showing preference for liquid-ordered (Lo) regions (green) over liquid-disordered (Ld) regions (red). Cholesterol is labeled in black. (B): The potential of the mean force plot of a Lo-phase binding peptide would show a pronounced preference for the bulk Lo phase over either Ld phase or the interface. Evolution of a short disordered glutamate-sensing motif. (C) Visualization of an unstructured peptide sequence responsive to the presence of glutamate molecules (magenta), chloride ions (green), and sodium ions (purple). (D) Impression of the evolution of fitness (for example, measurement of peptide–glutamate enthalpic interactions) over the course of GA iterations. CGCompiler: automated coarse-grained molecule parametrization. (E) Both categorical (bead type) and continuous (bond/angle/dihedral) properties of molecules are able to be tuned simultaneously using mixed-variable particle swarm optimization. Simulation results are optimized with respect to target data obtained from atomistic simulations and/or experiments. Adapted with permission from ref (44). Copyright 2023 American Chemical Society.

Molecular Recognition in Structureless Proteins

Beyond the field of lipid membranes, physics-based inverse design methods also have an interesting potential for the field of intrinsically ordered proteins (IDPs).⁴⁷ The discovery of IDPs has profoundly transformed our understanding of protein structure and function. Nevertheless, our comprehension of how unstructured biomolecules can effectively recognize and bind to specific small molecules remains limited. Physics-based design could provide insight by engineering short disordered peptide sequences, where the conformational ensemble, such as radius of gyration, is responsive to the presence of small molecules in the solution (see Figure 6C,D). This approach could not only address essential questions regarding potential, alternative mechanisms of molecular recognition in IDPs, but also explore the boundaries of their molecular sensitivity. The primary challenge remains with the fact that coarse-grained models like the Martini model maintain predefined secondary structure, limiting the potential for transient secondary and even tertiary structures to occur. Nonetheless, it would be worthwhile to investigate the limits of molecular recognition within entirely unstructured configurations.

Allocation of Computational Power

The heavy reliance of physics-based inverse design on computing power demands a careful allocation of resources. A large gain in performance is obtained from restricting the often astronomical search space, for example through consideration of binary genes in copolymer optimization (producing search spaces of 2^N), or through mirroring of transmembrane peptide sequences (reducing the 20^N search space to 10^N). Other strategies include the intentional undersampling of simulations to allow the algorithm to complete within a reasonable time frame, and the choice for small population pools and a minimal number of iterations to limit the total number of fitness evaluations that must be performed.

As the availability and affordability of computational power continues to advance, the opportunity arises to enhance parts of the approach. Although we could improve simulation accuracy to reduce the occurrence of outliers, or increase fitness evaluations (larger population pool, more iterations) to increase the chance of convergence to optimal solutions, we are currently able to manage considerable search space exploration despite these limiting factors. A compelling allocation could involve employing more sophisticated fitness evaluations. Examples of this include the use of higher resolution simulations (e.g., all atom, or united atom force fields; for example as applied by Zhou et al.⁴⁸) to better capture nuances of the design space. The application of larger simulation systems containing more complex environmental factors, think of more realistic membrane models containing membrane proteins that might affect processes of interest, might allow for better transferability between in-silico results and in vivo verification. Finally, expanding the chemical space through more elaborate encodings, for example longer peptides/proteins or a broader pool of available elements (e.g., non-natural amino acids), may allow for the discovery of previously inaccessible solutions.

Multiobjective Optimization

Multiobjective optimization enables the concurrent evaluation of multiple properties of interest during the inverse design process, of particular relevance in the design of biopolymers due to their intricate interactions with the environment. While naive implementations are straightforward to implement with little decrease in efficiency, for example penalties to the fitness score of a supposed surface-bound peptide based on its actual positioning during the simulation, they may inadvertently constrain search space exploration by limiting diversity.

“True” implementations of multiobjective optimization, for example the NSGA algorithms,^49,50 avoid this issue by computing the Pareto front, a collection of solutions that represent optimal compromises between the various optimization targets supplied to the algorithm. The main limitation remains with the substantial computational demands of physics-based inverse design, as these algorithms typically necessitate additional fitness evaluations. Nevertheless, the trade-off may be justifiable depending on the problem’s complexity.

Moving beyond (Bio)polymers

Furthermore, while this perspective mainly focuses on the optimization of biopolymers, the approach is not limited to genetic material alone. When considering evolutionary algorithms for inverse design, the common origin between such algorithms and the (genetic) biopolymers is a straightforward relation to draw, and it is easy to miss the wide spectrum of problems that could be tackled by the approach. Indeed, all that is required for a problem to be considered for evolutionary optimization is an encoding of the problem suited to the selected inverse design method. For example, one might consider a similar approach as used for peptides but instead applied to small molecule design, encoding moieties as building blocks into a chromosome representation¹—although this would require the introduction of search constraints since the dimension of the small molecule universe becomes otherwise intractable. Furthermore, optimization targets outside the single-molecule scope can be envisioned as well, such as encoding variable system properties (e.g., temperature, pressure, and system size), system composition (e.g., type and number of molecules present, initial position), and combinations thereof.

Continuous Optimization Problems

While genetic algorithms are particularly suited for discrete optimization problems, semicontinuous encodings can be envisioned for real-value optimization. However, inherently continuous strategies like particle swarm optimization (PSO)—also falling under the category of population-based heuristic approaches—show a higher computational efficiency for such problems.⁵¹ The general idea behind PSO algorithms is that each candidate solution (particle) is represented by a position and a velocity in parameter space, and particles are updated by utilizing information from earlier good solutions of the swarm (the collection of particles).^52,53 Thus, candidate solutions are efficiently guided toward good solutions. Similar to genetic algorithms, PSO algoritms can be combined with MD-based fitness functions in an EVO-MD scheme to allow for physics-based optimization within continuous search spaces.

Automating Force-Field Parametrization

The computational efficiency and accuracy of available coarse-grained molecular force fields has been pivotal for the here-discussed physics-based design of biopolymers. Developing accurate parametrizations of these models remains a challenging task due to the complexity and interdependence of the involved interaction parameters. Seemingly paradoxical, force field development is in itself a physics-based inverse design problem, as the tuning of interaction parameters essentially boils down to a complex optimization problem where its performance is evaluated using physics-based force fields. Evaluation of sets of parameters using corresponding simulations and subsequent comparison to expected values (obtained from experimental or ab initio methods) could serve as a fitness function for inverse design strategies, particularly when targeting macroscopic properties.⁵⁴ Such implementations have been demonstrated in various works. For example, Messerly et al. describe an algorithm for the optimization of nonbonded interaction parametrization for reproduction of vapor–liquid equilibria properties, using surrogate models which rely on molecular configurations obtained from simulation.²⁹ Other examples include the optimization of existing coarse-grained force-field parameters for the modeling of intrinsically disordered protein properties, relevant to their role in liquid–liquid phase separation.^24,25,55

While such models show promise when applied within their respective domains, extension toward the broader chemical domain (e.g., including new molecules or targeting different properties) requires reparametrization of the force-field parameters. Building-block-type force fields such as the Martini force field provide a solution by parametrizing thermodynamical properties of groups of atoms, from which complete molecules can be constructed. However, this remains a complex task due to the complexity of the possible interactions.⁴⁴ The most recent version of the Martini force field, Martini 3, rebalances the density of interactions by introducing an even larger number of possible interaction types, often rendering the parametrization of molecules a nontrivial problem to common users.⁵⁶ Automation of the coarse-grained parametrization of molecules could provide a solution, especially in the construction of large databases of molecules. Importantly, parametrization of bonded and nonbonded parameters should ideally be performed simultaneously since bonded and nonbonded interactions are not independent—instead, they are directly influencing each other via the density of interactions.^56,57 The primary hurdle lies with the nonbonded parameters of building-block force fields, such as the Martini force field, which are constructed of discrete and predefined fixed variables. In contrast, the bonded parameters involve continuous variables. This gives rise to a parametrization challenge that entails managing a mixed variable problem. To this aim, we have pioneered the use of mixed-variable particle swarm optimization in the automated parametrization of molecules within the Martini 3 coarse-grained force field by matching both structural (e.g., RDFs) and thermodynamical data (e.g., phase-transition temperatures).⁴⁴ An important advantage of this “CGCompiler approach” is that both bonded and nonbonded interactions are simultaneously optimized while conserving the search efficiency of vector guided particle swarm methods over heuristic search methods (see Figure 6E).

Integration of Direct Experimental Feedback

Finally, while in silico optimization has undeniably emerged as a valuable tool for designing chemical structures across diverse domains, including drug and material design,^1,58 it is imperative to recognize its inherent limitations in completely replacing experimental characterization. In silico models, by their nature, tend to oversimplify the intricate complexities of biological systems. Consequently, there is a growing need for a more seamless integration of experimental feedback into the process of inverse design.

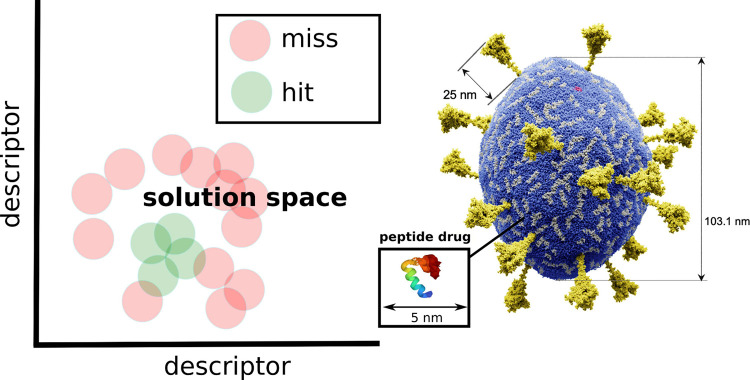
One potential approach toward achieving this integration involves harnessing empirical data to influence the generation of the genetic pool within physics-based inverse design, facilitated by genetic algorithms. Such an integration strategy is poised to steer the search toward solutions that are inherently more contextually relevant. One such idea involves mapping the “misses” and “hits” obtained from experimental assays into a continuous high-dimensional descriptor space, which comprises descriptor vectors, such as the descriptors being developed for antimicrobial peptides.⁵⁹ This map acts as an evolutionary constraint on the generation of the sequence pool within physics-based inverse design driven by genetic algorithms. New peptides generated within this protocol that are too closely related to past “misses” within the descriptor space are omitted from entering the sequence pool (see Figure 7), a concept akin to support vector machines (SVMs).

Figure 7.

Integration of experimental feedback within physics-based peptide design. (A) Using a descriptor space to integrate experimental feedback on desired activity into biasing the physics-based evolution of peptides. The red dots indicate forbidden regions in solution space that are not being revisited in the course of peptide evolution enforcing the sampling of new regions. (B) Impression of a designed antiviral peptide targeting the SARS-CoV-2 viruses. Experimental feedback on “hits” and “misses” is envisioned to, for example, gradually improve the physics-based design of antiviral peptides. Adapted with permission from ref (60). Copyright 2023 Elsevier Ltd.

The overarching objective is 2-fold: first, to reduce the dimensionality of the descriptor space through principal component analysis (PCA), and second, to continually refine the constraints on the descriptor space during the course of experimental validation. This iterative process aims to seek improved exclusion and inclusion criteria that optimally guide the retrospective prediction of collected experimental data.

The implementation of experimental feedback holds the potential not only to enhance future design but also to uncover shared physicochemical characteristics among “hits” or “misses”, which may further aid in identifying potential mechanisms of action. The primary challenge in implementing this integrated approach lies in the demand for sophisticated high-throughput experimental techniques tailored to the specific problems studied, as well as imposing efficient constraints in a high-dimensional descriptor space where points are predominantly located on a hypersurface. Nevertheless, as our knowledge and experience in this field continue to evolve, we anticipate that this integration will increasingly define the future of research and design across various domains.

Conclusion

We have outlined how physics-based inverse design can open a promising new avenue for the inverse design of biopolymers interacting with complex, fluid phases. Physics-based inverse design could introduce a quantum leap in the development of biomolecular sensors and peptide drugs that either recognize or selectively target membrane curvature, membrane lipid composition, or membrane phase (e.g., lipid rafts), and even protein condensates. Furthermore, even when the generated optimal solutions are not of direct biological relevance, physics-based inverse design uniquely enables pin-pointing of relevant physicochemical principles and thermodynamic driving forces on how biopolymers optimally interact with complex fluidic environments. In addition, physics-based evolution can be exploited to isolate the fingerprints of evolutionary optimization within native proteins, such as in the optimization of protein–cholesterol interactions within transmembrane domains.

Sequences generated in the course of the evolution span the entire physicochemical applicability domain of the targeted functionality. Therefore, generation of such training data in conjunction with neural network models additionally paves the road for novel (quantitative) prediction tools in the public domain, as shown with the PMIpred server¹⁵ for sequence-based prediction of membrane binding free energies. It is straightforward to extend this concept to other applications, for example in the scoring of the ability of peptide sequences to recognize/attract cholesterol or on their affinity for liquid ordered phases (lipid rafts).¹⁸

A main challenge of physics-based inverse design is the appropriate choice of the fitness function that specifies a desired functionality, as well as the underlying assumptions in the used system setup, adopted/targeted protein structure, and (coarse-grained) force field.

Finally, as physics-based methods effectively extract implicit information from the underlying force field, integration of improved (coarse-grained) force fields—for example, the recent Martini 3^56,61 and the Spica force-field^62,63—in conjunction with the integration of groundbreaking protein structure prediction methodology—for example, the Alphafold 2 project⁶⁴—could further facilitate these applications.

The authors declare no competing financial interest.