Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Feb 14;20(5):2202–2208. doi: 10.1021/acs.jctc.3c01230

Low-Scaling GW Algorithm Applied to Twisted Transition-Metal Dichalcogenide Heterobilayers

Maximilian Graml †,‡, Klaus Zollner †, Daniel Hernangómez-Pérez , Paulo E Faria Junior †, Jan Wilhelm †,‡,*
PMCID: PMC10938508  PMID: 38353944

Abstract

graphic file with name ct3c01230_0005.jpg

The GW method is widely used for calculating the electronic band structure of materials. The high computational cost of GW algorithms prohibits their application to many systems of interest. We present a periodic, low-scaling, and highly efficient GW algorithm that benefits from the locality of the Gaussian basis and the polarizability. The algorithm enables G0W0 calculations on a MoSe2/WS2 bilayer with 984 atoms per unit cell, in 42 h using 1536 cores. This is 4 orders of magnitude faster than a plane-wave G0W0 algorithm, allowing for unprecedented computational studies of electronic excitations at the nanoscale.

1. Introduction

Electronic excitations in matter play a pivotal role in various physical phenomena, including light absorption and transport. The characteristics of these excitations are strongly influenced by the host material. Excitons, which are bound electron–hole pairs, exhibit a remarkable and unusually strong electron–hole binding in low-dimensional semiconductors that have emerged in the past decade.1 When stacking two atomically thin semiconductors on top of each other, the atomic alignment between the layers can exhibit periodic variations, leading to a new type of in-plane superlattice known as the moiré superlattice. Excitons in moiré structures have gained enormous attention recently2−12 thanks to their highly unusual exciton properties which include spatial confinement due to the moiré potential,2 interlayer,5,6 and intralayer charge transfer.9 Furthermore, electronic properties of moiré lattices can be tuned by the band alignment and the twist angle between the layers such that moiré structures hold great promise as an exciting platform for probing electronic and photonic quantum phenomena over the next decade.12

Gaining insight into excitons in moiré structures can be achieved through a combination of experiments, theoretical models, and computations. As an example, low-angle MoSe2/WS2 moiré structures have shown an interesting interplay of intra- and interlayer exciton hybridization because of the nearly degenerate conduction bands of the MoSe2 and WS2 layers. The conduction band offset and the wave function hybridization between layers, however, are still under debate.3,7,13−15 Detailed knowledge about the electronic band structure of the MoSe2/WS2 moiré bilayer and the implications for exciton formation and binding is thus crucial to resolving this controversy.

In this work, we focus on the GW method from many-body perturbation theory,16−18 which is an approximation for the electronic self-energy that allows for computing the electronic band structure of a given material. Importantly, GW accounts for the nonlocal, frequency-dependent screening of the interaction between electrons, which is crucial in moiré bilayers. The GW band structure is then the basis for the description of excitons via the Bethe–Salpeter equation.17,19 Currently available plane-wave-based GW algorithms are, however, incapable of treating low-angle moiré cells that contain thousands of atoms,20 despite their computational scalability to the largest supercomputers.21−25 Stochastic GW methods26 may enable large-scale GW calculations; however, it remains uncertain as to whether applying periodic boundary conditions27 within the framework of stochastic GW can be achieved seamlessly.28 To compute the GW band structure in large moiré cells, the pristine unit-cell matrix projection (PUMP) has been suggested.9,20 PUMP is based on expanding the moiré cell wave functions in terms of the pristine unit-cell wave functions. By construction, PUMP cannot capture the nanometer-scale atomic reconstruction of moiré structures which can dramatically influence their electronic band structure.4

The GW space–time method29 offers a promising route toward large-scale GW calculations. This is because the computational scaling is reduced from O(N4atN2k) for standard GW algorithms to O(N3atNk) in the GW space–time method, where Nat is the number of atoms in the unit cell and Nk is the number of k points used to discretize the Brillouin zone. To achieve the scaling reduction, it is required to use a spatially local basis instead of plane waves. The local basis can be chosen as a real-space grid where studies of unit cells of up to 100 atoms have been reported.29,30 Another choice of the spatially local basis is an atomic-orbital-like basis.31 This choice is highly efficient in the GW space–time method, enabling GW calculations on molecules with more than 1000 atoms.32−36

Periodic boundary conditions in the GW space–time method with atomic-orbital-like basis functions have not yet been reported. The main inhibiting factor has been the inclusion of k-dependent Coulomb interactions which represent a major challenge regarding computational efficiency and numerical precision.37−39 In this work, we overcome this challenge by employing real space representations of the polarizability, the screened Coulomb interaction, and the self-energy. The real-space representation allows us to use the minimum image convention (MIC)40,41 (i.e., each atomic orbital in the simulation interacts only with the closest image of another atomic orbital). We benchmark the algorithm on G0W0 band gaps of monolayer MoS2, MoSe2, WS2, and WSe2, finding an average deviation of only 0.06 eV from reference calculations.42,43 We also apply the GW algorithm to a MoSe2/WS2 bilayer with an unprecedented cell size of 984 atoms which has an order of magnitude more atoms than previous state-of-the-art large-scale GW calculations.25

2. Algorithm

The GW algorithm presented in this work starts from a density functional theory (DFT) calculation,

2. 1

where εnk represents the eigenvalues of the Kohn–Sham Hamiltonian ĥKS(k). Bloch orbitals ψnk are expanded in Gaussians,44

2. 2

where the molecular orbital coefficients Cμn(k) are optimized in DFT and ϕRμ(r) are Gaussian-type basis functions being centered on an atom in cell R.

Following the GW space–time method,29 we compute the Green’s function in imaginary time at the Γ point,32

2. 3

The irreducible polarizability χPQ(iτ) at k = 0 in the Gaussian auxiliary basis {φRP(r)} follows,35

2. 4

using three-center matrix elements

2. 5

of the truncated Coulomb operator

2. 6

with cutoff radius rc. The tensor (μν|P) can be understood as originating from the resolution of the identity with the truncated Coulomb metric (RI-tCm),35,45,46 where rc is typically chosen to be 3 Å.35,46,47 The locality of Vrc(r, r′) ensures that the tensor (μν|P) is sparsely occupied, making the GW algorithm computationally efficient. RI-tCm ensures that the resolution of the identity quickly converges with the size of the auxiliary basis {φRP(r)}.35,45,46 We use Tikhonov regularization48 for the RI expansion to prevent linear dependencies of fit coefficients, as we discuss in detail in the Supporting Information.

The polarizability χPQ(k, iτ) is needed on a dense k-point mesh because it is later multiplied with the bare Coulomb interaction V(k) that diverges at the Γ point and thus requires a fine k-point sampling. The atom-centered basis allows us to decompose the Γ-point result (eq 4), χPQ(k = 0, iτ), using

2. 7

where χRPQ is the real-space representation of the irreducible polarizability and φRP denotes an auxiliary Gaussian orbital which is localized in cell R. For nonmetallic systems, the polarizability χ(r, r′, iτ) is space-local (i.e., χ(r, r′, iτ) exponentially decays with increasing |r – r′|).49,50 The matrix element χRPQ thus vanishes in the case of a large distance between the center of φ0P and the center of φRQ. We employ MIC (i.e., we assume that χRPQ(iτ) in eq 7 is nonzero only if the atomic center of φ0P and the atomic center of φRQ are closest together among all cells R). In this way, we extract χRPQ(iτ) from eq 7,

2. 8

which is exact in the limit of a large, nonmetallic unit cell. Using eq 8, we obtain the polarizability at any k point at negligible computational cost,

2. 9

We transform the irreducible polarizability to an imaginary frequency,29,30,51

2. 10

We have observed that χPQ(k, iω) computed from eq 10 features spurious negative eigenvalues with small absolute values. The reason is that eq 9 together with eq 8 is exact only in the limit of large unit cells. We remove negative eigenvalues from χPQ(k, iω), which requires costly diagonalization for every k point and every frequency point ω. Once having a positive definite matrix χPQ(k, iω), we compute the dielectric function

2. 11

where Id is the identity matrix and the truncated Coulomb matrix M(k) appears due to the RI-tCm,

2. 12

We regularize M–1(k) to prevent linear dependencies in the RI expansion; see details in the Supporting Information.

V(k) in eq 11 denotes the Coulomb matrix38,52

2. 13

The sum over R reaches over the entire crystal. Following the elaborate discussion in the Appendix of ref (52), we evaluate the lattice sum (eq 13) on a finite set of cells {R}. The subset fulfills ∑{R}e–ik·R = 0 for all k in our k-point mesh to ensure absolute convergence of the lattice sum (eq 13) for 2D periodic systems.52 Typically, we employ a few thousand neighbor cells to evaluate the lattice sum (eq 13) which is computationally affordable thanks to analytical Coulomb integrals.53

We decompose the screened Coulomb interaction W = V + (ϵ–1 – 1)V into the bare Coulomb interaction V and the correction (ϵ–1 – 1)V due to screening. The bare interaction leads to the exchange self-energy Σx, and it is well known54,55 that truncating the bare interaction in Γ-only Hartree–Fock calculations leads to fast convergence in the supercell size. We therefore use the truncated Coulomb operator VrHFc from eq 6 for the bare interaction,

2. 14

For the cutoff radius rHFc in eq 14, we set half the minimum of inner box wall distances in periodic directions, which is the common choice in periodic Hartree–Fock calculations.55

We transform W to real space,

2. 15

where ΩBZ is the Brillouin zone (BZ) volume. Special care is required for the BZ integral as WPQ(k, iω) diverges at the Γ point with 1/k for two-dimensional materials if φP and φQ are s-type basis functions.37,38,56 We evaluate WPQ(k, iω) using a 4 × 4 Monkhorst–Pack k-point mesh57 {kj}Nkj=1, Nk = 8,58 and a 6 × 6 Monkhorst–Pack k-point mesh {qj}Nqj=1, Nq = 18. We extrapolate the BZ integration (eq 15) with the inverse square root of the number of k points.38,59 In practice, we extrapolate with respect to k points by discretizing eq 15 to

2. 16

where k-point extrapolation is absorbed in integration weights

2. 17

Following the GW space–time method,29,30 we compute the self-energy Σ(r, r′, iτ) = iG(r, r′, iτ) W(r, r′, iτ).29 Σ(r, r′, iτ) is space-local as G(r, r′,iτ) is space-local,49 and only elements of W(r, r′, iτ) with small |r – r′| contribute to Σ. We thus continue with the minimum image of eq 15

2. 18

where the cell vector

2. 19

gives the smallest distance between the atomic centers RP of φ0P and the atomic center RQ + R of φRQ. We include the Γ-point RI metric matrix M from eq 12,

2. 20

which leads to the self-energy at the Γ point,

2. 21

k points in Σ follow from MIC at negligible computational cost (cf. eqs 8 and 9),

2. 22

We transform the self-energy to real energy18,29,30,32,35 and to the Bloch basis to compute quasiparticle energies εG0W0nk,

2. 23

where vxcnk is the diagonal of the exchange-correlation matrix.

3. Numerical Precision

The numerical trick in the presented GW algorithm is the MIC used in eqs 8, 18, and 22. MIC is exact in the limit of a large unit cell. We determine the critical cell size for the validity of MIC by computing the G0W0 band gap of monolayers MoS2, MoSe2, WS2, and WSe2, presented in Figure 1. For the four materials, the band gap changes on average by only 11 meV between the 10 × 10 supercell (300 atoms in the unit cell) and the 14 × 14 supercell (588 atoms in the unit cell). We conclude that the GW algorithm from this work can be used to study unit cells that are as large as a 10 × 10 supercell or larger. In the Supporting Information, we show additional convergence tests on the basis set size, the number of time and frequency points, the k-point mesh size, the filter threshold for sparse operations, and the vertical box height.

Figure 1.

Figure 1

Open in a new tab

G0W0 band gap of monolayer WS2, MoS2, WSe2, and MoSe2 calculated from eq 23 as a function of the supercell size (TZVP-MOLOPT basis set,60 without spin–orbit coupling (SOC)).

We compare the G0W0 band gap of monolayers MoS2, MoSe2, WS2, and WSe2 to the G0W0 band gap computed from three different plane-wave codes;39,42,43 see Table 1. We find that our G0W0 band gaps deviate on average by only 0.06 eV to the band gaps from plane-wave-based codes. This small discrepancy might be due to the use of different pseudopotentials and the difficulty in reaching the complete basis set limit.

Table 1. G0W0@PBE Band Gap (in eV, without SOC) of Monolayers MoS2, MoSe2, WS2, and WSe2 Computed from Equation 23 (TZV2P-MOLOPT Basis,60 10 × 10 Supercell, Detailed Convergence Test in the SI) and Computed from Plane-Wave Codes39,42,43a.

Software package MoS2 MoSe2 WS2 WSe2
This work (CP2K61) 2.47 2.07 2.81 2.37
GPAW42 2.53 2.12 2.75 2.30
BerkeleyGW39 2.45 2.09 2.61 2.34
VASP43 2.50 2.06 2.70 2.34
Open in a new tab
a

Details of BerkeleyGW calculations are given in the SI. We have removed SOC from the GPAW band gaps.42.

4. Computational Effort

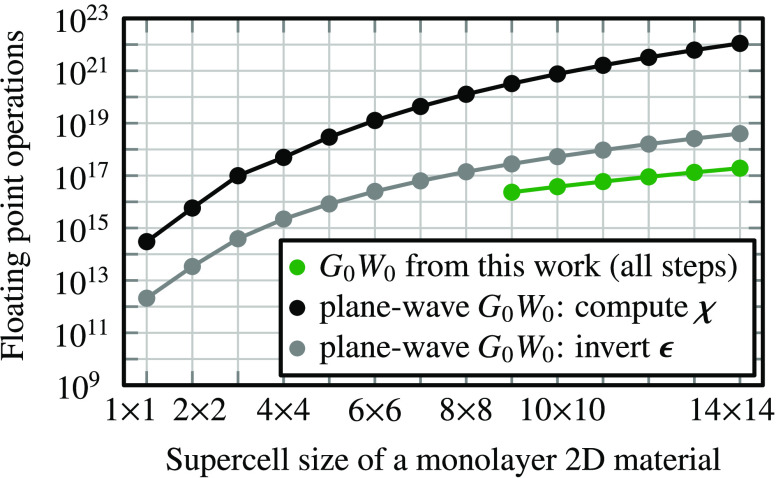
The presented G0W0 algorithm has a significantly reduced computational cost compared to plane-wave-based G0W0 algorithms. We show the number of floating point operations to compute the irreducible polarizability χ in a plane-wave G0W0 algorithm in Figure 2 in black. As a comparison, we show the execution of our low-scaling G0W0 algorithm via green traces. Our G0W0 algorithm requires 40,000 times fewer floating point operations for a 14 × 14 supercell as computing χ in plane waves for a 14 × 14 supercell. One might reduce the computational cost for computing χ in plane waves by a stochastic evaluation of the unoccupied band summation.23 For such an algorithm, the inversion of the dielectric matrix ϵ remains a computationally costly step. As we show in Figure 2, inverting ϵ in a plane-wave basis requires an order of magnitude more floating point operations compared to executing our whole G0W0 algorithm.

Figure 2.

Figure 2

Open in a new tab

Number of floating point operations (real double precision) needed for executing G0W0 algorithms. Green: low-scaling G0W0 algorithm from this work using a TZVP-MOLOPT basis set.60 Black: computing the irreducible polarizability χ in a plane-wave basis. Gray: inverting the dielectric matrix ϵ in a plane-wave basis. Underlying computational parameters are typical for monolayers MoS2, MoSe2, WS2, and WSe2; see the detailed raw data and discussion available in the SI.

Further advantages compared to plane-wave-based algorithms include the cheap diagonalization of the Kohn–Sham matrix to obtain Bloch states thanks to the compact Gaussian basis. Also, nonperiodic directions are easily dealt with in our GW algorithm by restricting the sum over cells R to periodic directions. It is not necessary to truncate the Coulomb operator in nonperiodic directions as in plane-wave algorithms.39,62 Moreover, the self-energy (eq 22) is available in the full Gaussian basis set, which allows us to compute the G0W0 correction for all Bloch states at negligible computational cost.

We measured the computation time of the algorithm, shown in Figure 3. The computation time is moderate; as an example, a G0W0 calculation on the 10 × 10 MoSe2 supercell (300 atoms) takes only 7 h on 576 cores. Assuming ideal scalability starting from the 9 × 9 cell, we estimate that a G0W0 calculation on 4500 atoms is in reach.63 Scalability improvements are the subject of ongoing work to achieve this system size in practice.

Figure 3.

Figure 3

Open in a new tab

Execution time of a G0W0 calculation for MoSe2 9 × 9–14 × 14 supercells (TZVP-MOLOPT basis set) on Supermuc-NG (Intel Skylake Xeon Platinum 8174). Magenta points show the computational cost to diagonalize the polarizability χ(k), which allows us to remove all spurious negative eigenvalues of χ(k) to ensure numerical stability. Dashed lines show a fit of αNβat to the execution time, where α and β are fit parameters. Raw data are available in the SI.

5. Application: 2D Heterobilayer

We now focus on an application of the G0W0 algorithm to transition-metal dichalcogenide heterobilayers which recently gained increased attention due to twist-angle-dependent moiré potentials and interlayer excitons.3,4,7−9,12−15 Recent large-scale plane-wave-based GW calculations on twisted heterostructures were limited to 75 atoms in the unit cell.25 This GW computation25 has been described to be highly cumbersome, and it was achieved only by using an advanced accelerated large-scale version of the BerkeleyGW code which scales to entire leadership high-performance computers with more than half a million cores.22,23 Small unit cells with 75 atoms allow for only the study of heterobilayers with selected, large twist angles and absent atomic reconstruction.

In order to illustrate the large-scale capabilities of our G0W0 algorithm beyond monolayers, we focus on prototypical MoSe2/WS2 twisted heterostructures. On one hand, the different lattice parameters of MoSe2 and WS2 give rise to a considerably large moiré periodicity at zero twist angle (∼8 nm), thus requiring a large number of atoms in the structure. On the other hand, low-angle MoSe2/WS2 has shown an interesting interplay of intra- and interlayer exciton hybridization because of the nearly degenerate conduction bands. This feature, however, is still under debate in the literature.3,7,13−15 The underlying electronic structure is thus crucial to resolve this controversy and is exactly the kind of problem that requires large-scale GW calculations. Here we considered MoSe2/WS2 moiré superstructures with twist angles of between 9.3 and 26.6° (Figure 4) that have corresponding unit cells of up to 984 atoms. We emphasize that in all cases the strain of the individual monolayers is <0.01% compared to the experimentally determined lattice constants,64,65 which is important because the band gap is very sensitive to strain.66,67 The G0W0 band gap of the MoSe2/WS2 bilayer depends on the twist angle changing from 1.86 eV (9.3°) to 1.92 eV (26.8°), in line with experimental observations of the exciton emission energy.13 Our GW calculation on the 984-atom heterostructure takes 42 h on only 1536 cores, which is a factor of 30,000 faster than with a plane-wave algorithm; see the estimate in the SI. Such large-scale GW calculations are an ideal starting point for further analysis of the electronic structure of these materials. For example, with our GW algorithm, the calculation of deep moiré potentials4 is within reach because of atomic reconstruction and height variations. Both crucially influence the interlayer screening that is captured by the GW method. On top of a GW calculation, the Bethe-Salpeter equation17,19 will enable the study of excitons in large-scale moiré structures. Our computationally efficient scheme also holds great promise for nanoscale excited-state dynamics in low-dimensional materials with Green’s function methods.

Figure 4.

Figure 4

Open in a new tab

Band gap of a MoSe2/WS2 heterostructure as a function of the twist angle. Inset: The unit cell (black rhomboid) for a 19.4° twist angle contains 984 atoms.

6. Conclusions

We have presented a low-scaling GW algorithm with periodic boundary conditions employing localized basis functions and the minimum image convention. The GW algorithm is numerically precise and requires up to 5 orders of magnitude fewer floating point operations compared to plane-wave codes. We carried out a G0W0 calculation on a MoSe2/WS2 heterostructure with 984 atoms in the unit cell which is an order of magnitude more than the state of the art.25 Our GW algorithm will enable routine applications of GW and its time-dependent variants to low-dimensional, nanostructured materials that were previously computationally highly challenging.

Acknowledgments

We thank Mauro Del Ben, Maria Camarasa-Gomez, Ferdinand Evers, Dorothea Golze, Jürg Hutter, Ole Schütt, and Shridhar Shanbhag for helpful discussions. K.Z. and P.E.F.J. acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), SFB 1277 (project no. 314695032, projects B07 and B11), SPP 2244 (project no. 443416183), and the European Union Horizon 2020 Research and Innovation Program under contract number 881603 (Graphene Flagship). D.H.-P. acknowledges support from a Minerva Foundation Grant (7135421), an ERC Starting Grant (101041159), and the DFG through SFB 1277 (no. 314695032, project B10). J.W. acknowledges funding by the DFG via the Emmy Noether Programme (project no. 503985532). The Gauss Centre for Supercomputing is acknowledged for providing computational resources on SuperMUC-NG at the Leibniz Supercomputing Centre under the project ID pn72pa. The Quantum Espresso and BerkeleyGW computations were carried out at the Max Planck Computing and Data Facility Cluster.

Data Availability Statement

The low-scaling GW algorithm is implemented in the open-source CP2K package,61 which is freely available from GitHub.68 Inputs and outputs of the calculations are also available on GitHub.69

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c01230.

  • Further computational parameters underlying our calculations (Sec. S1); regularized resolution of the identity used in the GW algorithm (Sec. S2); numerical convergence of our benchmark monolayer band gaps (Sec. S3, S4); resolution of the identity with the truncated Coulomb metric in Sec. S5; periodic, low-scaling GW algorithm from the manuscript to a GW algorithm with standard scaling (Sec. S6); the number of required floating point operations in our low-scaling Gaussian algorithm, a standard-scaling Gaussian algorithm and in planewave algorithms (Sec. S7 – S11); timings of our algorithm (Sec. S12); comparison of the supercell convergence of our algorithm to the supercell convergence of stochastic GW (Sec. S13) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ct3c01230_si_001.pdf (177.4KB, pdf)

References

  1. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
  2. Seyler K. L.; Rivera P.; Yu H.; Wilson N. P.; Ray E. L.; Mandrus D. G.; Yan J.; Yao W.; Xu X. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 2019, 567, 66–70. 10.1038/s41586-019-0957-1. [DOI] [PubMed] [Google Scholar]
  3. Zhang L.; Zhang Z.; Wu F.; Wang D.; Gogna R.; Hou S.; Watanabe K.; Taniguchi T.; Kulkarni K.; Kuo T.; Forrest S. R.; Deng H. Twist-angle dependence of moiré excitons in WS2/MoSe2 heterobilayers. Nat. Commun. 2020, 11, 5888. 10.1038/s41467-020-19466-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Shabani S.; Halbertal D.; Wu W.; Chen M.; Liu S.; Hone J.; Yao W.; Basov D. N.; Zhu X.; Pasupathy A. N. Deep moiré potentials in twisted transition metal dichalcogenide bilayers. Nat. Phys. 2021, 17, 720–725. 10.1038/s41567-021-01174-7. [DOI] [Google Scholar]
  5. Karni O.; et al. Structure of the moiré exciton captured by imaging its electron and hole. Nature 2022, 603, 247–252. 10.1038/s41586-021-04360-y. [DOI] [PubMed] [Google Scholar]
  6. Schmitt D.; et al. Formation of moiré interlayer excitons in space and time. Nature 2022, 608, 499–503. 10.1038/s41586-022-04977-7. [DOI] [PubMed] [Google Scholar]
  7. Gobato Y. G.; de Brito C. S.; Chaves A.; Prosnikov M. A.; Woźniak T.; Guo S.; Barcelos I. D.; Milošević M. V.; Withers F.; Christianen P. C. M. Distinctive g-Factor of Moiré-Confined Excitons in van der Waals Heterostructures. Nano Lett. 2022, 22, 8641–8646. 10.1021/acs.nanolett.2c03008. [DOI] [PubMed] [Google Scholar]
  8. Barré E.; Karni O.; Liu E.; O’Beirne A. L.; Chen X.; Ribeiro H. B.; Yu L.; Kim B.; Watanabe K.; Taniguchi T.; Barmak K.; Lui C. H.; Refaely-Abramson S.; da Jornada F. H.; Heinz T. F. Optical absorption of interlayer excitons in transition-metal dichalcogenide heterostructures. Science 2022, 376, 406–410. 10.1126/science.abm8511. [DOI] [PubMed] [Google Scholar]
  9. Naik M. H.; et al. Intralayer charge-transfer moiré excitons in van der Waals superlattices. Nature 2022, 609, 52–57. 10.1038/s41586-022-04991-9. [DOI] [PubMed] [Google Scholar]
  10. Rivera P.; Yu H.; Seyler K. L.; Wilson N. P.; Yao W.; Xu X. Interlayer valley excitons in heterobilayers of transition metal dichalcogenides. Nat. Nanotechnol. 2018, 13, 1004–1015. 10.1038/s41565-018-0193-0. [DOI] [PubMed] [Google Scholar]
  11. Jin C.; Ma E. Y.; Karni O.; Regan E. C.; Wang F.; Heinz T. F. Ultrafast dynamics in van der Waals heterostructures. Nat. Nanotechnol. 2018, 13, 994–1003. 10.1038/s41565-018-0298-5. [DOI] [PubMed] [Google Scholar]
  12. Huang D.; Choi J.; Shih C.-K.; Li X. Excitons in semiconductor moiré superlattices. Nat. Nanotechnol. 2022, 17, 227–238. 10.1038/s41565-021-01068-y. [DOI] [PubMed] [Google Scholar]
  13. Alexeev E. M.; et al. Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 2019, 567, 81–86. 10.1038/s41586-019-0986-9. [DOI] [PubMed] [Google Scholar]
  14. Tang Y.; Gu J.; Liu S.; Watanabe K.; Taniguchi T.; Hone J.; Mak K. F.; Shan J. Tuning layer-hybridized moiré excitons by the quantum-confined Stark effect. Nat. Nanotechnol. 2021, 16, 52–57. 10.1038/s41565-020-00783-2. [DOI] [PubMed] [Google Scholar]
  15. Ma X.; Fu S.; Ding J.; Liu M.; Bian A.; Hong F.; Sun J.; Zhang X.; Yu X.; He D. Robust Interlayer Exciton in WS2/MoSe2 van der Waals Heterostructure under High Pressure. Nano Lett. 2021, 21, 8035–8042. 10.1021/acs.nanolett.1c02281. [DOI] [PubMed] [Google Scholar]
  16. Hedin L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. 10.1103/PhysRev.139.A796. [DOI] [Google Scholar]
  17. Onida G.; Reining L.; Rubio A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. 10.1103/RevModPhys.74.601. [DOI] [Google Scholar]
  18. Golze D.; Dvorak M.; Rinke P. The GW Compendium: A Practical Guide to Theoretical Photoemission Spectroscopy. Front. Chem. 2019, 7, 377. 10.3389/fchem.2019.00377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Blase X.; Duchemin I.; Jacquemin D.; Loos P.-F. The Bethe–Salpeter Equation Formalism: From Physics to Chemistry. J. Phys. Chem. Lett. 2020, 11, 7371–7382. 10.1021/acs.jpclett.0c01875. [DOI] [PubMed] [Google Scholar]
  20. Li H.; Xiang Z.; Naik M. H.; Kim W.; Li Z.; Sailus R.; Banerjee R.; Taniguchi T.; Watanabe K.; Tongay S.; Zettl A.; da Jornada F. H.; Louie S. G.; Crommie M. F.; Wang F.. Imaging Moiré Excited States with Photocurrent Tunneling Microscopy. arXiv 2306.00859, 2023. [DOI] [PubMed]
  21. Sangalli D.; et al. Many-body perturbation theory calculations using the yambo code. J. Phys.: Condens. Matter 2019, 31, 325902 10.1088/1361-648X/ab15d0. [DOI] [PubMed] [Google Scholar]
  22. Del Ben M.; da Jornada F. H.; Canning A.; Wichmann N.; Raman K.; Sasanka R.; Yang C.; Louie S. G.; Deslippe J. Large-scale GW calculations on pre-exascale HPC systems. Comput. Phys. Commun. 2019, 235, 187–195. 10.1016/j.cpc.2018.09.003. [DOI] [Google Scholar]
  23. Del Ben M.; Yang C.; Li Z.; Jornada F. H. d.; Louie S. G.; Deslippe J. Accelerating Large-Scale Excited-State GW Calculations on Leadership HPC Systems. SC20: International Conference for High Performance Computing, Networking, Storage and Analysis 2020, 1–11. 10.1109/SC41405.2020.00008. [DOI] [Google Scholar]
  24. Yu V. W.-Z.; Govoni M. GPU Acceleration of Large-Scale Full-Frequency GW Calculations. J. Chem. Theory Comput. 2022, 18, 4690–4707. 10.1021/acs.jctc.2c00241. [DOI] [PubMed] [Google Scholar]
  25. Kundu S.; Amit T.; Krishnamurthy H. R.; Jain M.; Refaely-Abramson S. Exciton fine structure in twisted transition metal dichalcogenide heterostructures. Npj Comput. Mater. 2023, 9, 186. 10.1038/s41524-023-01145-x. [DOI] [Google Scholar]
  26. Neuhauser D.; Gao Y.; Arntsen C.; Karshenas C.; Rabani E.; Baer R. Breaking the Theoretical Scaling Limit for Predicting Quasiparticle Energies: The Stochastic GW Approach. Phys. Rev. Lett. 2014, 113, 076402 10.1103/PhysRevLett.113.076402. [DOI] [PubMed] [Google Scholar]
  27. Brooks J.; Weng G.; Taylor S.; Vlček V. Stochastic many-body perturbation theory for Moiré states in twisted bilayer phosphorene. J. Phys.: Condens. Matter 2020, 32, 234001 10.1088/1361-648X/ab6d8c. [DOI] [PubMed] [Google Scholar]
  28. We discuss challenges in stochastic GW calculations on two-dimensional materials in detail in the Supporting Information.
  29. Rojas H. N.; Godby R. W.; Needs R. J. Space-Time Method for Ab Initio Calculations of Self-Energies and Dielectric Response Functions of Solids. Phys. Rev. Lett. 1995, 74, 1827–1830. 10.1103/PhysRevLett.74.1827. [DOI] [PubMed] [Google Scholar]
  30. Liu P.; Kaltak M.; Klimeš J.; Kresse G. Cubic scaling GW: Towards fast quasiparticle calculations. Phys. Rev. B 2016, 94, 165109 10.1103/PhysRevB.94.165109. [DOI] [Google Scholar]
  31. Rohlfing M.; Krüger P.; Pollmann J. Efficient scheme for GW quasiparticle band-structure calculations with applications to bulk Si and to the Si(001)-(2 × 1) surface. Phys. Rev. B 1995, 52, 1905–1917. 10.1103/PhysRevB.52.1905. [DOI] [PubMed] [Google Scholar]
  32. Wilhelm J.; Golze D.; Talirz L.; Hutter J.; Pignedoli C. A. Toward GW Calculations on Thousands of Atoms. J. Phys. Chem. Lett. 2018, 9, 306–312. 10.1021/acs.jpclett.7b02740. [DOI] [PubMed] [Google Scholar]
  33. Förster A.; Visscher L. Low-Order Scaling G0W0 by Pair Atomic Density Fitting. J. Chem. Theory Comput. 2020, 16, 7381–7399. 10.1021/acs.jctc.0c00693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Duchemin I.; Blase X. Cubic-Scaling All-Electron GW Calculations with a Separable Density-Fitting Space–Time Approach. J. Chem. Theory Comput. 2021, 17, 2383–2393. 10.1021/acs.jctc.1c00101. [DOI] [PubMed] [Google Scholar]
  35. Wilhelm J.; Seewald P.; Golze D. Low-Scaling GW with Benchmark Accuracy and Application to Phosphorene Nanosheets. J. Chem. Theory Comput. 2021, 17, 1662–1677. 10.1021/acs.jctc.0c01282. [DOI] [PubMed] [Google Scholar]
  36. Förster A.; Visscher L. Quasiparticle Self-Consistent GW-Bethe–Salpeter Equation Calculations for Large Chromophoric Systems. J. Chem. Theory Comput. 2022, 18, 6779–6793. 10.1021/acs.jctc.2c00531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ren X.; Merz F.; Jiang H.; Yao Y.; Rampp M.; Lederer H.; Blum V.; Scheffler M. All-electron periodic G0W0 implementation with numerical atomic orbital basis functions: Algorithm and benchmarks. Phys. Rev. Materials 2021, 5, 013807 10.1103/PhysRevMaterials.5.013807. [DOI] [Google Scholar]
  38. Zhu T.; Chan G. K.-L. All-Electron Gaussian-Based G0W0 for Valence and Core Excitation Energies of Periodic Systems. J. Chem. Theory Comput. 2021, 17, 727–741. 10.1021/acs.jctc.0c00704. [DOI] [PubMed] [Google Scholar]
  39. Qiu D. Y.; da Jornada F. H.; Louie S. G. Screening and many-body effects in two-dimensional crystals: Monolayer MoS2. Phys. Rev. B 2016, 93, 235435 10.1103/PhysRevB.93.235435. [DOI] [Google Scholar]
  40. Paier J.; Diaconu C. V.; Scuseria G. E.; Guidon M.; VandeVondele J.; Hutter J. Accurate Hartree-Fock energy of extended systems using large Gaussian basis sets. Phys. Rev. B 2009, 80, 174114. 10.1103/PhysRevB.80.174114. [DOI] [Google Scholar]
  41. Irmler A.; Burow A. M.; Pauly F. Robust Periodic Fock Exchange with Atom-Centered Gaussian Basis Sets. J. Chem. Theory Comput. 2018, 14, 4567–4580. 10.1021/acs.jctc.8b00122. [DOI] [PubMed] [Google Scholar]
  42. Gjerding M. N.; et al. Recent progress of the Computational 2D Materials Database (C2DB). 2D Mater. 2021, 8, 044002 10.1088/2053-1583/ac1059. [DOI] [Google Scholar]
  43. Camarasa-Gómez M.; Ramasubramaniam A.; Neaton J. B.; Kronik L. Transferable screened range-separated hybrid functionals for electronic and optical properties of van der Waals materials. Phys. Rev. Mater. 2023, 7, 104001 10.1103/PhysRevMaterials.7.104001. [DOI] [Google Scholar]
  44. Blum V.; Gehrke R.; Hanke F.; Havu P.; Havu V.; Ren X.; Reuter K.; Scheffler M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. 10.1016/j.cpc.2009.06.022. [DOI] [Google Scholar]
  45. Jung Y.; Sodt A.; Gill P. M. W.; Head-Gordon M. Auxiliary basis expansions for large-scale electronic structure calculations. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6692–6697. 10.1073/pnas.0408475102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Luenser A.; Schurkus H. F.; Ochsenfeld C. Vanishing-Overhead Linear-Scaling Random Phase Approximation by Cholesky Decomposition and an Attenuated Coulomb-Metric. J. Chem. Theory Comput. 2017, 13, 1647–1655. 10.1021/acs.jctc.6b01235. [DOI] [PubMed] [Google Scholar]
  47. We discuss the choice rc = 3 Å in the Supporting Information.
  48. Goncharsky A.; Stepanov V.; Tikhonov A.; Yagola A.. Numerical Methods for the Solution of Ill-Posed Problems; Kluwer Academic Publishers: Dordrecht, 1995. [Google Scholar]
  49. Kohn W. Density Functional and Density Matrix Method Scaling Linearly with the Number of Atoms. Phys. Rev. Lett. 1996, 76, 3168–3171. 10.1103/PhysRevLett.76.3168. [DOI] [PubMed] [Google Scholar]
  50. Martin R. M.; Reining L.; Ceperley D. M.. Interacting Electrons; Cambridge University Press, 2016. [Google Scholar]
  51. Azizi M.; Wilhelm J.; Golze D.; Giantomassi M.; Panadés-Barrueta R. L.; Delesma F. A.; Buccheri A.; Gulans A.; Rinke P.; Draxl C.; Gonze X. J. Open Source Softw. 2023, 8, 5570. 10.21105/joss.05570. [DOI] [Google Scholar]
  52. Grundei M. M. J.; Burow A. M. Random Phase Approximation for Periodic Systems Employing Direct Coulomb Lattice Summation. J. Chem. Theory Comput. 2017, 13, 1159–1175. 10.1021/acs.jctc.6b01146. [DOI] [PubMed] [Google Scholar]
  53. Golze D.; Benedikter N.; Iannuzzi M.; Wilhelm J.; Hutter J. Fast evaluation of solid harmonic Gaussian integrals for local resolution-of-the-identity methods and range-separated hybrid functionals. J. Chem. Phys. 2017, 146, 034105. 10.1063/1.4973510. [DOI] [PubMed] [Google Scholar]
  54. Spencer J.; Alavi A. Efficient calculation of the exact exchange energy in periodic systems using a truncated Coulomb potential. Phys. Rev. B 2008, 77, 193110. 10.1103/PhysRevB.77.193110. [DOI] [Google Scholar]
  55. Guidon M.; Hutter J.; VandeVondele J. Robust Periodic Hartree-Fock Exchange for Large-Scale Simulations Using Gaussian Basis Sets. J. Chem. Theory Comput. 2009, 5, 3010–3021. 10.1021/ct900494g. [DOI] [PubMed] [Google Scholar]
  56. Wilhelm J.; Hutter J. Periodic GW calculations in the Gaussian and plane-waves scheme. Phys. Rev. B 2017, 95, 235123. 10.1103/PhysRevB.95.235123. [DOI] [Google Scholar]
  57. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  58. We employ the k symmetry k ↔ −k.
  59. Laughon K.; Yu J. M.; Zhu T. Periodic Coupled-Cluster Green’s Function for Photoemission Spectra of Realistic Solids. J. Phys. Chem. Lett. 2022, 13, 9122–9128. 10.1021/acs.jpclett.2c02534. [DOI] [PubMed] [Google Scholar]
  60. VandeVondele J.; Hutter J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. 10.1063/1.2770708. [DOI] [PubMed] [Google Scholar]
  61. Kühne T. D.; et al. CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. 10.1063/5.0007045. [DOI] [PubMed] [Google Scholar]
  62. Hüser F.; Olsen T.; Thygesen K. S. Quasiparticle GW calculations for solids, molecules, and two-dimensional materials. Phys. Rev. B 2013, 87, 235132. 10.1103/PhysRevB.87.235132. [DOI] [Google Scholar]
  63. The computation time is T = (Nat/243)21870 core hours + (Nat/243)3443 core hours, where we took the execution time of quadratic and cubic steps as shown in Figure 3. The maximum job size on Supermuc-NG is 150 000 cores for 24 h, making 3.6 Mio. core hours, allowing for a G0W0 calculation on 4500 atoms.
  64. Schutte W. J.; De Boer J. L.; Jellinek F. Crystal structures of tungsten disulfide and diselenide. J. Solid State Chem. 1987, 70, 207–209. 10.1016/0022-4596(87)90057-0. [DOI] [Google Scholar]
  65. James P. B.; Lavik M. T. The crystal structure of MoSe2. Acta Crystallogr. 1963, 16, 1183–1183. 10.1107/S0365110X6300311X. [DOI] [Google Scholar]
  66. Zollner K.; Junior P. E. F.; Fabian J. Strain-tunable orbital, spin-orbit, and optical properties of monolayer transition-metal dichalcogenides. Phys. Rev. B 2019, 100, 195126. 10.1103/PhysRevB.100.195126. [DOI] [Google Scholar]
  67. Chaves A.; et al. Bandgap engineering of two-dimensional semiconductor materials. npj 2D Mater. Appl. 2020, 4, 29. 10.1038/s41699-020-00162-4. [DOI] [Google Scholar]
  68. https://github.com/cp2k/cp2k, accessed December 20, 2023.
  69. https://github.com/JWilhelm/Inputs_outputs_low_scaling_GW_TMDC, accessed December 20, 2023.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct3c01230_si_001.pdf (177.4KB, pdf)

Data Availability Statement

The low-scaling GW algorithm is implemented in the open-source CP2K package,61 which is freely available from GitHub.68 Inputs and outputs of the calculations are also available on GitHub.69

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES