Room Temperature Skyrmions in Strain-Engineered FeGe thin films

Abstract

Skyrmions hold great promise for low-energy consumption and stable high density information storage, and stabilization of the skyrmion lattice (SkX) phase at or above room temperature is greatly desired for practical use. The topological Hall effect can be used to identify candidate systems above room temperature, a challenging regime for direct observation by Lorentz electron microscopy. Atomically ordered FeGe thin films are grown epitaxially on Ge(111) substrates with ~ 4 % tensile strain. Magnetic characterization reveals enhancement of Curie temperature to 350 K due to strain, well above the bulk value of 278 K. Strong topological Hall effect was observed between 10 K and 330 K, with a significant increase in magnitude observed at 330 K. The increase in magnitude occurs just below the Curie temperature, a similar relative temperature position as the onset of Skx phase in bulk FeGe. The results suggest that strained FeGe films may host a SkX phase above room temperature when significant tensile strain is applied.

Magnetic skyrmions are topologically protected magnetic spin configurations that can have size of ~5 nm or less [1] and yet can be manipulated using ultra-low current densities on the order of ~10⁶ A/m², much less than that required for driving ferromagnetic domain walls [2–6]. These properties have attracted significant interest for spintronic applications as they could provide high information density at low power in a non-volatile package. However, widespread use of skyrmion technology requires new technological approaches [7] and new materials with sufficient Curie temperature to enable the skyrmions at or just above room temperature. Skyrmions exist in either bulk chiral magnets lacking inversion symmetry or at the interface of magnetic multilayer stacks lacking mirror inversion symmetry [8–12]. Due to inversion symmetry breaking, the neighboring spins evolve at a finite angle with respect to each other to form the non-collinear spin textures [3, 13–16] as a result of competition between the spin-orbit coupling induced Dzyaloshinskii-Moriya (DM) interaction and symmetric Heisenberg exchange interaction.

Skyrmion crystal lattice (SkX) phases have been observed directly by a variety of techniques: in B20 FeGe [2] and MnSi [17] using Lorentz transmission electron microscopy (LTEM), FeCoSi [18] and Co₈Zn₈Mn₄ [19] using small-angle neutron scattering (SANS), and in Fe/Ir multilayer stacks using spin-resolved scanning tunneling microscopy (STM) [9]. The potential for skyrmionic behavior can also be detected by topological Hall effect (THE) measurements [20, 21] and ac magnetic susceptibility measurements [22]. Recently, antiskyrmions-analogous to skyrmions, but with opposite topological charge - have been demonstrated by LTEM in Heusler compounds with $D_{2d}$ symmetry well above room temperatures [23]. Although topological Hall effect (THE) measurements are not conclusive, they have the advantage of being widespread, and unlike the previous techniques can be readily performed at room temperature without modification or concerns of thermal signal broadening.

A major obstacle to integrating skyrmions into spintronic devices is their instability in the absence of a magnetic field, since topological protection does not guarantee skyrmion stability against thermal agitation. In thin films with thickness less than or comparable to that of the helical wavelength, the helical ground state is suppressed, favoring skyrmion formation over a wide range of temperatures [2]. Magnetic multilayer stacks are fertile playgrounds to generate skyrmions, as they have high operating temperature [12, 24, 25], but the required current density to drive skyrmions in magnetic multilayer stacks (~10¹¹ A/m² [24]) is much higher than in B20 compounds (~10⁶ A/m² [4, 6]). In addition, magnetic multilayer stacks have a longer helical wavelength resulting in lower skyrmion density in the SkX phase [3, 26].

Studies have shown that the ordering temperature, ${\text{T}}_c$, can be tuned in B20 magnets via substrate-induced strain [27, 28]. FeGe is an obvious candidate as it has the highest known ${\text{T}}_c\sim 278\text{K}$ [2–4] within this class. In this letter, we report epitaxial growth of FeGe thin films on Ge(111) substrates, demonstrate strain induced ${\text{T}}_c$ enhancement, and topological Hall resistivity (THE) above transition temperature comparable to those seen previously in SkX phases [20, 27], suggesting potential SkX formation above room temperature.

Epitaxial FeGe films of thickness 18 nm, 72 nm, and 102 nm were grown on Ge(111) substrates in an Ar atmosphere by sputter beam epitaxy, utilizing shuttered and beam-shaped off-axis direct-current (DC) magnetron co-sputtering of elemental Fe and Ge targets [29–31]. Films were grown with base pressure 6.7 × 10⁻⁷ Pa (5 × 10⁻⁹ Torr), growth pressure 0.7 Pa (5 mTorr), and substrate temperature 300 °C. An Al capping layer (~ 2.7 nm) was deposited at 100 °C in order to prevent intermixing with the FeGe layer.

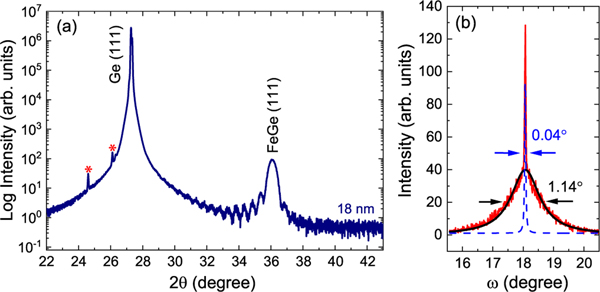
Energy dispersive x-ray (EDX) spectroscopy and Rutherford back-scattering (RBS) determined the stoichiometry of both films in this study to be 51 % ± 3 % Fe and 49 % ± 3 % Ge. Crystal structure, epitaxial quality, and film thickness were measured with x-ray diffraction (XRD) and x-ray reflectivity (XRR). Fig. 1(a) shows the out of plane x-ray diffraction for 18 nm thick FeGe films (see Supplemental Material [32] for detailed XRD results of all three films). Pronounced Laue oscillations in the XRD patterns indicate a smooth film-substrate interface. The out of plane <111> d-spacing is 2.487(2) Å, 7.9 % smaller than the bulk 2.701 Å and indicative of a high tensile epitaxial strain [33–35]. Off-axis measurements show axial distortion of the (100) peak, suggesting rhombohedral distortion due to epitaxial strain [36]. Measurements taken in the $(4\overline{1}0)$ and [201] directions suggest a rhombohedral angle $\alpha ={94.0}^{\circ }$ and an in-plane lattice constant of 4.87(4) Å, matching the Ge substrate lattice constant of 5.658 Å with 30° in-plane rotation (4.899 Å). Although the error in estimating an in-plane lattice constant with rhombohedral distortion and mosaic twinning (see below) is significant, the above values are not found to change appreciably in the 72 nm film and so we can safely assume our film maintains the 4.1 % tensile epitaxial strain indicated by the lattice mismatch.

FIG. 1.

$2\theta -\omega$ XRD scan of 18 nm thick FeGe film epitaxially grown on Ge(111). Asterisks (*) indicate substrate peaks (b) Rocking curve scan of FeGe(111) peak showing a FWHM = 0.040°(7) with a broad background with a FWHM = 1.14° indicative of the mosaicity spread in crystal structure caused by lattice mismatch.

The rocking curve scan of the FeGe(111) peak is shown in Fig. 1(b). A full width at half maximum (FWHM) of 0.06° is measured, with a sharp peak (fit as blue dashed line, FWHM 0.04°) overlaid with a broader mosaic spread peak (black solid line) likely from in-plane (black solid line) likely from in-plane twinned regions in the film. This mosaic feature implies that the FeGe (111) planes are distorted within a small angular range from the substrate (111) plane to compensate for lattice mismatch while maintaining epitaxy.

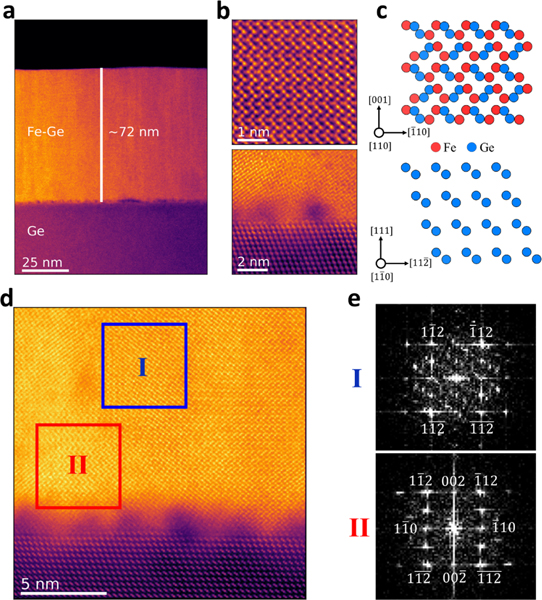
The 72 nm FeGe film was imaged by aberration-corrected scanning transmission electron microscopy (STEM) (see Supplementary Material [32] for details). The atomic resolution high-angle annular dark-field imaging (HAADF) image in Fig. 2(b) (top) shows the formation of the B20 phase, with its corresponding atomic model [37] and crystallographic orientation in Fig. 2(c) (top). Fig. 2(b) (bottom) shows the Ge(111) substrate and the Ge-FeGe interface, with the corresponding crystal and orientation of Ge(111) substrate shown in Fig. 2(c) (bottom).

FIG. 2.

(a) HAADF image showing Ge substrate and FeGe film. (b) Atomic resolution HAADF images showing the B20 phase (top) and Ge-FeGe interface (bottom). (c) Atomic model of B20-phase (top) and Ge with crystal orientation consistent with their respective HAADF images in (b). (d) Regions I (blue) and II (red) highlight two regions with different orientations of FeGe film. (e) Fast Fourier transform (FFT) patterns of the regions I (top) and II (bottom).

We observe a ~ 1 nm thick interfacial layer between the Ge substrate and the FeGe films, as shown in Fig. 2(b) (bottom), possibly due to imperfect epitaxy or defects left on the substrate surface during pre-growth oxide removal by HCl etch. The film also shows small regions of non-uniform crystal orientation (B20) within the film: Fig. 2(d) shows a wide field-of-view HAADF image with two regions highlighted as I (blue) and II (red). The respective fast Fourier transform (FFT) patterns of regions I and II are shown in Fig. 2(e), which suggests different crystal orientation for these two regions. The presence of small twinned volumes is corroborated semiquantatively by 60° offset twinning peaks in XRD Phi ($\varphi$) scan (see FIG. S3, Supplemental Material [32]) where the intensity of twinned volumes is ~1 % of that of the primary orientation peak intensities. The different crystal orientation observed in TEM corroborates the twinning observed in XRD and explains the mosaicity spread observed in rocking curve measurements.

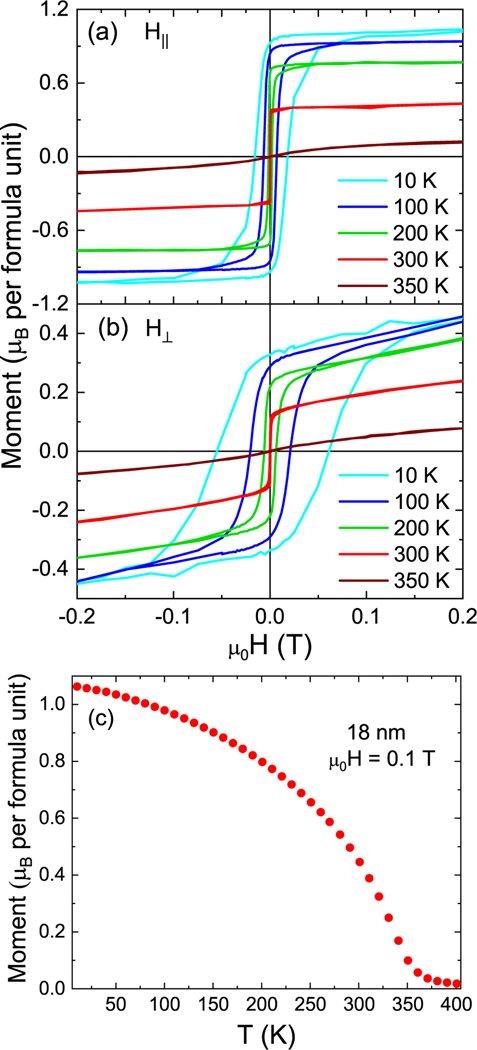
Magnetic properties were measured using a superconducting quantum interference device (SQUID) magnetometer. Magnetic hysteresis measured in the in-plane and out-of-plane geometry at 10 K to 350 K are shown in Figs. 3(a) and (b) respectively. We obtained a saturation magnetization ${\text{M}}_s=1.15\pm 0.06{\mu }_B$ per formula unit (f.u). at 10 K for the 18 nm thick film. Fig. 3(c) shows an M as a function of T curve for the same film at an applied field of 0.1 T. The transition temperature is found to be 350 K using the Arrott plot technique [38], showing a strong Curie temperature enhancement compared to the bulk value of 278 K [2–4]. While the magnetic spins in bulk FeGe arrange themselves in a conical fashion along the body diagonal [111] crystallographic direction, strain along the body diagonal [111] decreases the distance between the nearest Fe planes, thereby increasing the strength of exchange interaction and favoring strong polarization of magnetic moments. Thus, more thermal energy is required to disrupt the magnetic moments and Curie temperature is enhanced.

FIG. 3.

SQUID data: Magnetic hysteresis loop at different temperatures for the 18 nm thick FeGe film for both (a) in-plane (field parallel to film plane) and (b) out-of-plane (field perpendicular to film plane) configuration. (c) The temperature dependence of magnetization for the 18 nm thick FeGe film.

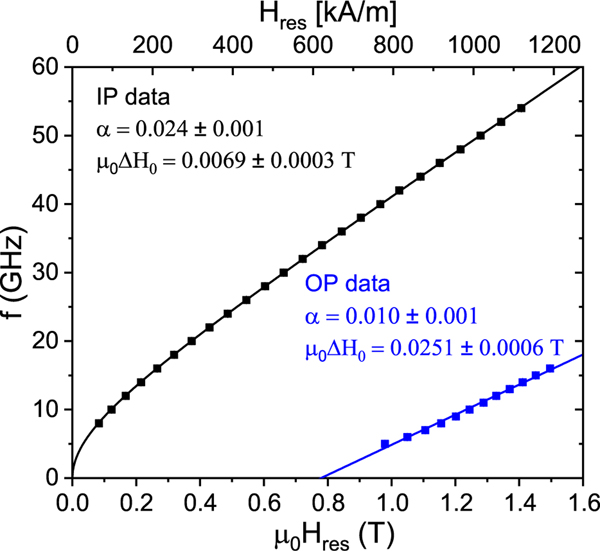
Broadband ferromagnetic resonance (FMR) spectroscopy was used to probe the magnetic dynamic properties of strained FeGe films at room temperature. The raw FMR signal was fitted using a Lorentzian line-shape [39] in order to extract the resonance field $H_{res}$ and peak to peak linewidth, $\text{Δ}{H}_{pp}$. The out of plane $H_{res}$ data were fitted using the Kittel formula to determine the gyromagnetic ratio ${\gamma }^{\prime }$ and effective magnetization $M_{eff}$ at RT which were found to be 21.97 ± 0.51 GHz/T and 620 ± 9 kA/m respectively. The observed value for ${\gamma }^{\prime }$ is lower than for typical ferromagnetic materials (${\gamma }^{\prime }=\frac{g{\mu }_B}{h}=28\text{GHz}/\text{T}$ for $\text{g}\simeq 2$), this may be attributed to the fact that the sample is not fully saturated even for the largest field in FMR experiment (1.6 T). FMR measurement in the unsaturated regime can underestimate the value for ${\gamma }^{\prime }$ while at the same time overestimating the effective magnetization [40] for the out of plane configuration. If the samples are not fully saturated, then one may assume, to the first approximation, that effective magnetization has a linear response to the applied field, which would validate the observed lower value of ${\gamma }^{\prime }$ for the out-of-plane configuration. Fig. 4 also shows a nonlinear frequency dependence on $H_{res}$ for the out-of-plane configuration at fields smaller than 1.2 T. This may be due to the non-collinear spin texture in FeGe film [28].

FIG. 4.

Kittel plot (frequency as a function of $H_{res}$) at room temperature for 18 nm thick FeGe film for both in-plane (IP) and out-of-plane (OP) configuration.

The effective Gilbert damping parameter, ${\alpha }_{eff}$, is determined by fitting the measured linewidths, $\text{Δ}{H}_{pp}$, as a linear function of the microwave frequency [41–43],

$$\text{Δ}H(f)=\text{Δ}{H}_o+\frac{2}{\sqrt{3}}\frac{{\alpha }_{eff}}{{\gamma }^{\prime }}f,$$ (1)

assuming there is no field dragging of magnetization, where $f$ is the microwave frequency. The extrinsic linewidth for the out of plane configuration was determined to be 0.0251 ± 0.0006 T, less than that observed by Turgut et al. [44]. Similarly, the effective damping parameter, ${\alpha }_{eff}$, was found to be 0.01 ± 0.001, which is significantly smaller than ${\alpha }_{eff}=0.28\pm 0.02$; reported by Beg et al. [45] and smaller than ${\alpha }_{eff}=0.038\pm 0.005$ at T = 258 K; observed by Turgut et al. [44] for FeGe film grown on Si(111) substrates.

Topological Hall resistivity data at a series of temperatures (10 K to 330 K) for a field range spanning from negative to positive are shown in Fig. 5. A standard Hall bar structure was patterned from 18 nm thick FeGe film for electrical Hall measurements. Both the longitudinal (${\rho }_{xx}$) and transverse Hall (${\rho }_{xy}$) resistivity measurements were taken using a probe station at 10 K, 100 K, 290 K, 300 K, and 330 K. An electron traversing through the skyrmionic texture follows the local magnetization profile and is deflected by Lorentz force due to an emergent magnetic field, thus giving rise to the topological Hall effect [3, 27, 46–51], a signature of skyrmionic phase [46]. The total Hall effect can be expressed as

$${\rho }_{xy}=R_{OH}{H}_{\perp }+R_{AH}{M}_{\perp }+{\rho }_{TH},$$ (2)

where $H_{\perp }$ is the applied magnetic field, $M_{\perp }$ is the out-of-plane magnetization, $R_{OH}$ and $R_{AH}$ are the ordinary and anomalous Hall coefficients, and ${\rho }_{TH}$ is the topological Hall resistivity. The ordinary Hall effect scales with $H$, whereas the anomalous Hall effect scales with the magnetization of the sample. Two types of scattering contribute to the anomalous Hall effect; scattering independent mechanism ($\alpha {\rho }_{xx}^2$), and skew-scattering ($\beta {\rho }_{xx}$) mechanism caused by impurities and phonons [50]. It can be expressed as

$$R_{AH}=\alpha {\rho }_{xx}^2+\beta {\rho }_{xx},$$ (3)

where ${\rho }_{xx}$ is the longitudinal resistivity. The magnetoresistance, defined as $\text{Δ}{\rho }_{xx}/{\rho }_{xx}=\left[{\rho }_{xx}(H)-{\rho }_{xx}(0)\right]/{\rho }_{xx}(0)$, across all temperatures was found to be less than 0.02 % suggesting ${\text{R}}_{AH}$ to be constant with applied magnetic field. The intrinsic contribution to the anomalous Hall effect depends on the details of the band structure and is largely scattering independent. The total anomalous Hall effect can be approximated to be dominated by scattering independent mechanism and the contribution from the skew scattering mechanism can be ignored [52] as previously shown for FeGe thin films [20, 53, 54]. At fields greater than saturation field, FeGe films are in a field polarized state, meaning ${\rho }_{TH}=0$. The total Hall resistivity can then be plotted as a function of magnetization, $R_{OH}H$ can be quantified - from the intercept, and ${\mu }_0{R}_{AH}M$ - from the slope [53]. The topological Hall resistivity (${\rho }_{TH}$) is then obtained by subtracting ordinary and anomalous Hall resistivities from the total Hall resistivity.

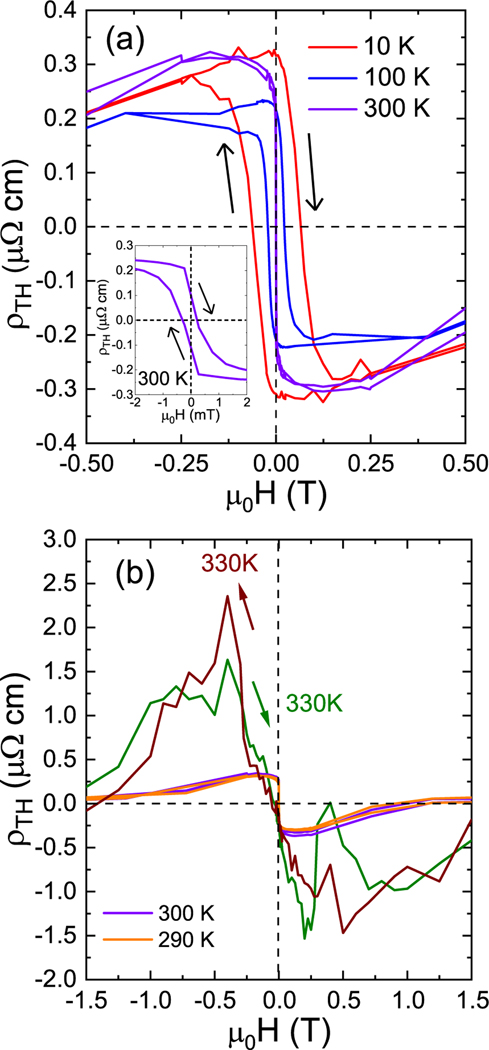
FIG. 5.

The topological Hall resistivity (${\rho }_{TH}$) hysteresis loops for the 18 nm thick FeGe film at (a) 10 K, 100 K, and 300 K (b) 290 K, 300 K, and 330 K. A clear THE resistivity hysteresis loop at (a) 10 K, 100 K, and 300 K (inset) is the indicative of a non-collinear phase.

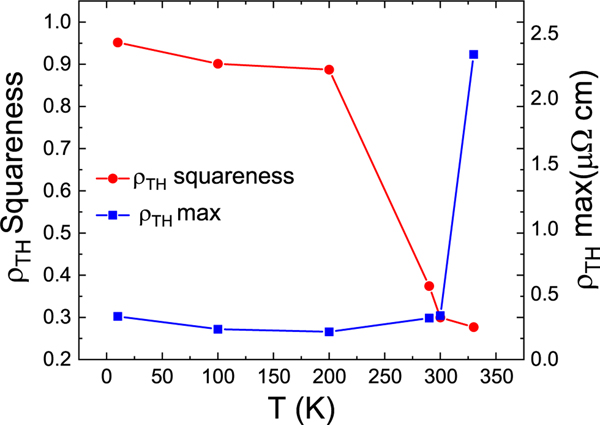
As shown in Fig. 5, the 18 nm film exhibits clear topological Hall resistivity hysteresis loops with strong non-zero ${\rho }_{TH}$ values at zero fields up to 300 K, demonstrating a non-collinear phase up to RT. A significant topological Hall effect $\left({\rho }_{TH}=326\text{nΩ}\text{cm}\right)$ is observed at 10 K which gradually decreases up to 290 K and then sharply increases $\left({\rho }_{TH}=2.34\mu \text{Ω}\text{cm}\right)$ at 330 K. This temperature, relative to ${\text{T}}_c$, is consistent with the temperature range expected for skyrmion lattice formation in bulk FeGe and B20 magnets in general [6, 20]. This observed ${\rho }_{TH}$ value at 330 K is significantly larger than in metallic multilayers [25] and in unstrained FeGe thin films [20]. Significant directional dependence for the maximum ${\rho }_{TH}$ is observed at 330 K at ± 0.4 T when the field is scanned from positive (negative) to negative (positive). It should be noted that competing magnetic phases (e.g. helical and conical) can persist at the low-temperature regime. These phases can potentially contribute to the topological Hall resistivity and cannot be excluded completely. As shown in Fig. 6, the maximum value of ${\rho }_{TH}$ remains relatively constant close to RT and then suddenly spikes above RT, whereas the squareness $\left({\rho }_{TH}(H=0)/{\rho }_{TH}(max)\right)$ of ${\rho }_{TH}$ plummets above 200 K, suggesting a possible metastable SkX phase.

FIG. 6.

The squareness of the topological Hall resistivity (${\rho }_{TH}$) for corresponding maximum value of (${\rho }_{TH}$) for 18 nm FeGe film between 10 K and 330 K.

The topological Hall effect is frequently attributed as a signature of the magnetic spin texture and the observed Hall anomaly close to ${\text{T}}_c$ reminiscent of the skyrmion lattice phase. However, it is worth recalling that other mechanisms have been either theorized or observed to contribute to the total Hall effect in chiral magnets with perpendicular magnetic anisotropy, e.g. thermal fluctuations of topological excitations [55, 56]. However, the magnitude of observed THE in our film is much larger and so can probably be ruled out as this thermal effect. The increased noise level at 330 K at lower fields departing from the field polarized state can be attributed to low current needed to measure Hall data on a film on narrow-bandgap Ge substrate at elevated temperature without exceeding 2 % leakage current during the measurement. Attempts to perform LTEM at elevated temperature have been unsuccessful as data acquisition is greatly affected above room temperature. Small angle neutron scattering is proposed to resolve this issue and corroborate skyrmion formation in strained FeGe thin films.

In conclusion, we have grown phase-pure epitaxial FeGe films on Ge(111) substrate with coherent ~4 % tensile strain, and demonstrate strain induced ${\text{T}}_c$ enhancement well above room temperature while preserving B20 crystal structure, albeit with slight structural distortions. A small value for the effective Gilbert damping parameter is measured compared to previous reports, critical for potential application in spintronics. Additionally, significant ${\rho }_{TH}$ at zero field is observed in a wide temperature window from 10 K to 330 K and a strong ${\rho }_{TH}=2.34\mu \text{Ω}\text{cm}$ at 330 K close to observed ${\text{T}}_c$ with distinct TH peaks at ± 0.4 T. These features can be attributed to the emergent magnetic field caused by the non-collinear spin arrangement and suggest potential skyrmion formation above room temperature.