Abstract
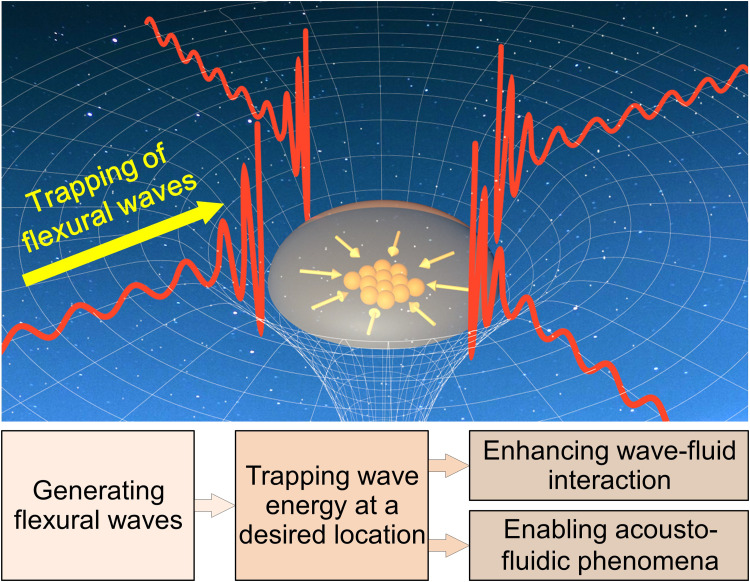
Acoustic black holes offer superior capabilities for slowing down and trapping acoustic waves for various applications such as metastructures, energy harvesting, and vibration and noise control. However, no studies have considered the linear and nonlinear effects of acoustic black holes on micro/nanoparticles in fluids. This study presents acoustofluidic black holes (AFBHs) that leverage controlled interactions between AFBH-trapped acoustic wave energy and particles in droplets to enable versatile particle manipulation functionalities, such as translation, concentration, and patterning of particles. We investigated the AFBH-enabled wave energy trapping and wavelength shrinking effects, as well as the trapped wave energy–induced acoustic radiation forces on particles and acoustic streaming in droplets. This study not only fills the gap between the emerging fields of acoustofluidics and acoustic black holes but also leads to a class of AFBH-based in-droplet particle manipulation toolsets with great potential for many applications, such as biosensing, point-of-care testing, and drug screening.
Acoustofluidic black holes enable the trapping of acoustic waves for in-fluid particle manipulation.
INTRODUCTION
The past several decades have witnessed a tremendous advancement in precision manipulation techniques that exploit optics (1, 2), magnetics (3, 4), electrical fields (5, 6), atomic force microscopy (7, 8), and acoustofluidics (9–14) for assorted applications in biology, chemistry, medicine, and micro/nanosystems (15–18). Among them, acoustofluidics-based precision manipulation techniques have garnered considerable interest (16, 19–24) because of their versatility, simplicity, low power requirement, and contactless nature (10, 11, 25, 26).
Acoustofluidic techniques typically use surface acoustic waves (27–33) or bulk acoustic waves (34–39) to apply acoustic radiation forces and acoustic streaming–induced drag forces on micro/nanoparticles and further control their motions and positions. To achieve better manipulation performance and enable more functionalities, the latest breakthroughs in the field of acoustic physics are gradually introduced to the development of acoustofluidic techniques, such as recent advances in tunable acoustic vortices for in vivo manipulation of kidney stones (40), phononic crystals for channel-less translation of cells (41, 42), and acoustic holography for printing tissues with complex and high-resolution patterns (43, 44). However, no studies have introduced recent innovations in acoustic black holes to the field of acoustofluidics.
A black hole is a region of spacetime where gravity is so strong that nothing can escape from it (45). In the field of acoustics, an acoustic black hole is a region that can trap wideband incoming acoustic waves (46). Acoustic black holes have been attracting increasing attention in the communities of acoustics and structural dynamics, owing to their outstanding capabilities of trapping wideband waves (46–48). The acoustic black holes for trapping flexural waves with bending wave motions in plate-like structures typically have properly tailored material thickness profiles at user-specified positions (46, 49). From the edge to the center of an acoustic black hole, the substrate’s thickness gradually decreases, leading to tailored wave characteristics, such as gradient wave speeds and impedances. Therefore, when flexural waves encounter acoustic black holes, they can be slowed down and trapped (46, 47, 50) and their intensities can be locally enhanced (50, 51). Because of these features, acoustic black holes have successfully been implemented for many applications such as elastic metastructures, energy harvesting, vibration mitigation, and noise control. However, to the best of our knowledge, no studies have been conducted to investigate the linear and nonlinear effects of acoustic black holes on micro/nanoparticles dispersed in fluids. The knowledge of these effects could be crucial for developing next-generation acoustofluidic devices for assorted biological, medical, and chemical applications.
This study presents acoustofluidic black holes (AFBHs) that leverage controlled interactions between trapped acoustic energy in AFBHs and particles in droplets to achieve versatile in-droplet particle manipulation functionalities (such as translation, concentration, and redistribution of particles in droplets) in a customizable, high-throughput, low-power, and easy-to-use manner. In particular, by trapping wideband flexural waves in plate-like substrates, AFBHs can increase local wave intensities at targeted locations and further enhance dynamic wave-fluid and wave-particle interactions to enable strong acoustofluidic effects, such as applying acoustic radiation forces on in-droplet particles and inducing acoustic streaming in droplets to apply drag forces on in-droplet particles. Our study shows that these forces induced by trapped wave energy in AFBHs can efficiently manipulate and enrich in-droplet particles, even using a low-power wave source. Moreover, by controlling in-AFBH mode shapes, AFBHs can reshape internal acoustic pressure fields, change pressure antinode numbers, and change acoustic streaming fields for robustly controlling particle distributions in droplets. Furthermore, a large number of AFBHs can be arranged in a customized array for trapping acoustic energy in multiple sites to manipulate (e.g., enrich or redistribute) particles in a large array of droplets in a parallel and high-throughput manner.
To investigate and leverage the AFBH-enabled features, we developed three types of AFBH-based acoustofluidic devices: an AFBH-based elliptical substrate device, an AFBH-based dual transducer device, and an AFBH array–based device. Through finite element simulations and experiments, we successfully demonstrated multiple particle manipulation functionalities enabled by these AFBH-based acoustofluidic devices, including controlled enrichment of in-droplet particles, quantitative characterization of in-droplet particle concentrations, enhancement of fluorescence signal intensities, control of in-droplet particle distributions, and parallel manipulation of particles in an array of droplets. We expect that this study could spur the development of AFBH-based lab-on-a-chip platforms for biomedical and chemical research.
RESULTS
Principle and design of AFBH-based acoustofluidic devices
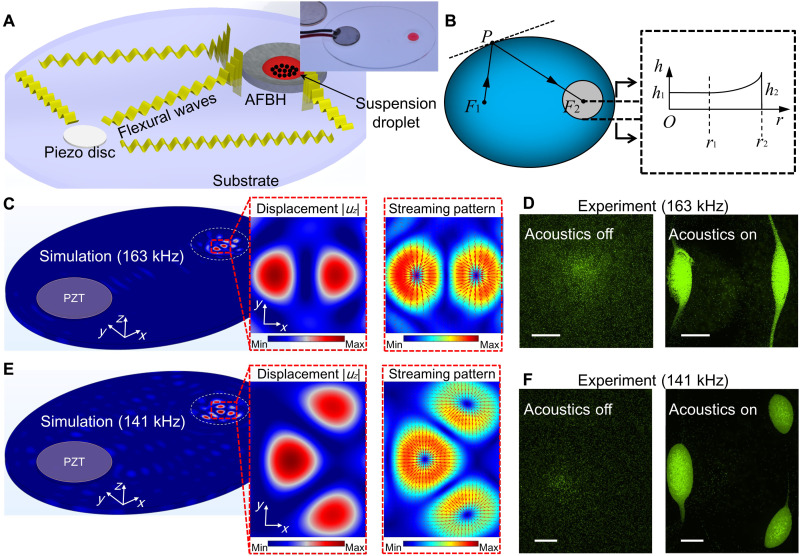
As illustrated in Fig. 1, when an AFBH is created in a specific region of a plate-like structure, incoming structural-borne flexural waves from all directions can be trapped by the AFBH. With this feature, wave energy can be efficiently delivered into a particle-laden droplet placed in the AFBH for markedly enhancing linear and nonlinear wave-fluid and wave-particle interactions. These interactions further lead to a series of acoustofluidic phenomena, such as acoustic radiation forces on particles, acoustic streaming, enrichment of particles, and reshaping of particle distributions within the droplet. Figure 2 (A and B) shows three-dimensional (3D) and 2D schematics of a representative AFBH-based acoustofluidic device, i.e., an AFBH-based elliptical substrate device. In this device, a circular piezoelectric transducer is bonded to the left focal point F1 of an elliptical polymethyl methacrylate (PMMA) substrate to generate flexural waves in the substrate. When these flexural waves encounter an arbitrary point P on the elliptical substrate’s free boundary, they are reflected and redirected to the other focal point F2 of the elliptical substrate because the angle between the boundary’s normal direction and F1P naturally equals the angle between the boundary’s normal direction and F2P. Because of this wave redirection effect, flexural waves reflected by the elliptical boundary can be focused, leading to marked enhancement of the local wave intensity around the focal point F2.
Fig. 1. Schematic for illustrating the principle of an AFBH.
Fig. 2. Numerical and experimental results for manipulating in-droplet particles using an AFBH-based elliptical substrate device.
(A and B) 3D and 2D schematics for illustrating the mechanism of an AFBH-based elliptical substrate device. (A) Inset: A photo of a fabricated device with a piezoelectric transducer [disc-like lead-zirconate-titanate (PZT)] bonded at the left focal point of an elliptical PMMA substrate. (C) Left: A simulated flexural wave field (out-of-plane displacement amplitude |uz|) in the solid domain at an excitation frequency of 163 kHz. Right: The corresponding acoustic streaming field with drag forces illustrated by red arrows. (D) Distributions of 10-μm fluorescent polystyrene particles in an AFBH before applying acoustic waves and after 3 min of acoustic waves. Scale bars, 500 μm. For this experiment, the excitation voltage, frequency, droplet volume, and initial particle concentration are 10 Vpp, 163 kHz, 20 μl, and 8.25 × 105 ml−1, respectively. (E) A simulated flexural wave field and an acoustic streaming field at an excitation frequency of 141 kHz. (F) Distributions of 10-μm fluorescent polystyrene particles in an AFBH before applying acoustic waves and after 3 min of acoustic waves. Scale bars, 500 μm. For this experiment, the excitation voltage, frequency, droplet volume, and initial particle concentration are 10 Vpp, 141 kHz, 20 μl, and 8.25 × 105 ml−1, respectively.
In addition to redirecting and focusing flexural waves enabled by the elliptical substrate boundary, an AFBH with its center at the focal point F2 is adopted to further trap the focused flexural waves. As shown in a cross-sectional view (Fig. 2B), the AFBH has a well-like geometry with the remaining substrate thickness h(r) following a relation as
| (1) |
where r is the distance to the focal point F2. As described in this equation, the AFBH has a flat bottom to the distance r1 and a power-law profile from the distance r1 to r2. Because of this power-law profile (46), the AFBH can trap omnidirectional incoming flexural waves and further enhance in-AFBH wave intensities. Therefore, by leveraging both an elliptical substrate to redirect and focus flexural waves at the focal point F2 and an AFBH at F2 to further trap the focused waves, the local wave intensities in the AFBH will be much higher than those in the substrate’s rest area. Moreover, when a particle-laden droplet is dispensed in the AFBH, the trapped flexural waves will be strong enough to induce acoustic streaming and apply drag forces on particles in the droplet, as well as apply acoustic radiation forces on those particles. These forces will be able to move particles and rearrange their distributions.
To investigate the wave intensity enhancement effect of our AFBH-based elliptical substrate device in Fig. 2A, we analyzed the flexural wave fields in the solid domain and the acoustofluidic effects in the fluid domain through finite element simulations. The detailed parameters for our simulations are provided in tables S1 and S2. Figure 2C (left) shows a simulated flexural wave field (i.e., the out-of-plane displacement amplitude |uz|) at a frequency of 163 kHz. It can be seen that there are two adjacent wave antinodes near the AFBH’s center, and the maximum displacement amplitude in the AFBH is much larger than that in the rest area. We also simulated the flexural wave field in an elliptical substrate without an AFBH at the same frequency of 163 kHz. The result (fig. S1A) shows that the displacement amplitude |uz| near the focal point F2 is larger than that in the rest area of the elliptical substrate, proving the wave focusing effect enabled by the elliptical substrate configuration. Moreover, by comparing the simulation results of cases with (Fig. 2C, left) and without (fig. S1A) an AFBH, it can be found that the maximum wave displacement amplitude in the AFBH is about 2.75 times that in an elliptical substrate without an AFBH. This means that an AFBH can further enhance the local wave intensity by trapping the flexural waves that are initially focused by the elliptical substrate boundary.
To further investigate the in-droplet particle manipulation enabled by trapped flexural waves in the AFBH, we simulated the acoustic pressure field, the acoustic radiation force field (for 10-μm polystyrene particles), and the acoustic streaming field in a particle suspension droplet in the AFBH. To perform acoustofluidic simulations, the out-of-plane displacements of simulated flexural waves are coupled to the bottom of the droplet. The simulated 3D acoustic pressure field in the droplet and its 2D distribution at the droplet’s bottom are shown in fig. S2A. It can be seen that there are two adjacent acoustic pressure antinodes near the center. Typically, one would expect acoustic radiation forces to move particles to acoustic pressure nodes rather than antinodes, which is normally observed in traditional surface and bulk acoustic wave–based acoustofluidic devices (9–11). However, according to our simulation results for acoustic radiation forces (fig. S3A) and acoustic streaming–induced drag forces (Fig. 2C), particles should be moved to the acoustic pressure antinodes rather than nodes. This is because our AFBH device leverages flexural waves, which typically lead to in-plane acoustic radiation and acoustic streaming–induced drag forces that point to antinodes (39, 52, 53).
To validate our simulation results, we conducted particle manipulation experiments using a fabricated AFBH-based elliptical substrate device (Fig. 2A, top right). The acquired fluorescence microscopy images (Fig. 2D, left and right) show the distributions of 10-μm fluorescent polystyrene particles in the AFBH before applying acoustic waves and after 3 min of acoustic waves. For this experiment, the excitation voltage, frequency, droplet volume, and particle concentration used were 10 peak-to-peak voltage (Vpp), 163 kHz, 20 μl, and 8.25 × 105 ml−1, respectively. A recorded video of the particle manipulation process can be seen in movie S1. As shown in this experimental result, after applying acoustic waves, 10-μm polystyrene particles gradually aggregate near the two antinodes. This experimental observation (Fig. 2D) agrees well with our numerical prediction (Fig. 2C). In addition, we carried out comparison experiments using the same wave generation conditions while dispensing droplets at locations outside the AFBH. The comparison shows that few particles can be moved, indicating that flexural waves without the AFBH-based intensity enhancement cannot effectively manipulate in-droplet particles.
Controlling in-droplet particle patterns via different in-AFBH mode shapes
By generating different in-AFBH mode shapes, an AFBH can reshape acoustic pressure fields and acoustic streaming fields to further control particle patterns in droplets. To investigate this capability, we simulated the flexural wave field in the solid domain (Fig. 2E, left), the acoustic pressure field in the fluid domain (fig. S2B), the acoustic radiation force field in the fluid domain (fig. S3B), and the acoustic streaming field in the fluid domain (Fig. 2E, right) at multiple excitation frequencies. The results at 141 kHz reveal the wave focusing effect enabled by the elliptical boundary (fig. S1B), as well as the wave trapping effect enabled by the AFBH (Fig. 2E, left). By comparing the maximum wave displacement amplitudes in Fig. 2E and fig. S1B, it can be found that the maximum wave displacement amplitude in the elliptical substrate with an AFBH is nearly 11.43 times that in the elliptical substrate without an AFBH. These simulation results indicate that our device can greatly enhance the local wave intensities by leveraging both the elliptical boundary–enabled wave focusing effect and the AFBH-enabled wave trapping effect. Moreover, by comparing the simulation results at 163 kHz (Fig. 2C) and 141 kHz (Fig. 2E), it can be found that different wave frequencies can lead to different in-AFBH mode shapes with different numbers of antinodes. Therefore, by tuning the wave frequency and changing the in-AFBH mode shape, our device should be able to change the acoustic forces applied on particles in a droplet and further rearrange the distributions of particles.
To validate the simulation results, we performed experiments using our AFBH-based elliptical substrate device (Fig. 2A) at a frequency of 141 kHz. The rest of the experimental parameters were the same as those used for the experiments at 163 kHz. Our acquired microscopy images (Fig. 2F) show the distributions of 10-μm fluorescent polystyrene particles in a droplet before applying acoustic waves and after 3 min of acoustic waves. The particle manipulation process can be seen in movie S2. This experimental result shows that in-droplet particles can be gradually moved to and enriched at the three antinodes, and the constructed particle pattern at 141 kHz is different from that at 163 kHz. These results prove that an AFBH holds the capability of controlling in-droplet particle distributions by changing in-AFBH mode shapes.
Single-site enrichment of particles
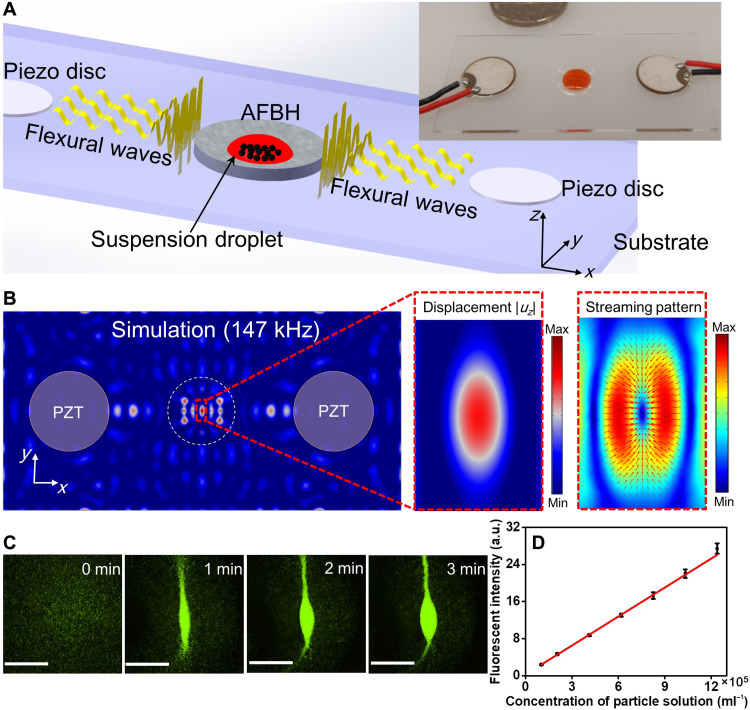
We created an AFBH-based dual transducer device for enabling controlled enrichment of particles at a targeted location. As shown in Fig. 3A (a schematic and a photo), two piezoelectric transducers are bonded on a rectangular PMMA substrate to generate standing flexural waves. An AFBH is located between the two piezoelectric transducers for trapping the generated standing flexural waves and enhancing local wave intensities. For the dual transducer configuration, by changing the AFBH’s inner radius r1, it becomes possible to control the numbers of nodes and antinodes generated in the AFBH. Moreover, the distance between the adjacent wave nodes can be reduced by an AFBH, as shown in fig. S4. This is because the AFBH’s bottom with a thinner wall thickness theoretically supports flexural waves with a larger wave number and a smaller wave speed compared with the region outside the AFBH (46, 49). Furthermore, the AFBH-based dual transducer device can shift the flexural wave node and antinode positions by tuning the phase difference between the two excitation sources, as shown in our simulation results (fig. S4).
Fig. 3. Numerical and experimental results for enriching particles using an AFBH-based dual transducer device.
(A) Left: A schematic for illustrating the mechanism of an AFBH-based dual transducer device. Right: A photo of a fabricated device with a pair of piezoelectric transducers for generating flexural waves. (B) Left: A simulated flexural wave field (out-of-plane displacement amplitude |uz|) in the substrate at a frequency of 147 kHz showing that an antinode can be generated at the AFBH center. Right: The corresponding acoustic streaming field in the fluid domain showing that streaming-induced drag forces (red arrows) converge at the antinode. (C) Time-lapse microscopy images showing that 10-μm fluorescent polystyrene particles can be gradually enriched at the antinode in the AFBH. Scale bars, 1 mm. For this experiment, the excitation voltage, frequency, droplet volume, and initial particle concentration are 10 Vpp, 147 kHz, 20 μl, and 8.25 × 105 ml−1, respectively. (D) Quantitatively characterized mean fluorescence intensities for droplets with different initial particle concentrations. For all the test groups, the excitation voltage, frequency, droplet volume, and duration of acoustic waves are kept as 10 Vpp, 147 kHz, 20 μl, and 3 min, respectively. a.u., arbitrary units.
When a particle suspension droplet is dispensed in an AFBH with a small radius r1 of 3 mm, which only supports one flexural wave antinode at the AFBH’s center, this antinode will be able to enrich in-droplet particles at a single site. To understand this mechanism, finite element simulations were performed at an excitation frequency of 147 kHz. We simulated the flexural wave field in the solid domain (Fig. 3B, left), the acoustic radiation force field in the fluid domain (fig. S5), and the acoustic streaming field in the fluid domain (Fig. 3B, right). Our simulation results show that a wave antinode can be generated at the AFBH’s center. Moreover, both simulated in-plane acoustic radiation forces and acoustic streaming–induced drag forces converge at this antinode. Driven by these forces, in-droplet particles should be gradually moved to the AFBH’s center and enriched. To validate this numerical prediction, experiments were performed using a fabricated device (Fig. 3A, right). The excitation voltage, frequency, droplet volume, and particle concentration used were 10 Vpp, 147 kHz, 20 μl, and 8.25 × 105 ml−1, respectively. The acquired time-lapse images (Fig. 3C) show that 10-μm fluorescent polystyrene particles in a droplet can be gradually moved to the antinode and enriched to form a cluster (see movie S3 for the enrichment process). To better understand the mechanism behind the particle enrichment, we provided side-by-side simulation and experimental results in fig. S6. The simulation results show that the in-plane vectors of acoustic streaming point to the antinode. Our experimental result shows that particles are enriched at the acoustic antinode. Moreover, the shape of the particle cluster formed by enrichment is analogous to the shape of the region with weak acoustic streaming (i.e., the blue region of the simulated acoustic streaming pattern). Our observation agrees with the findings presented in other acoustofluidic studies using low-frequency flexural waves for particle manipulation (39, 52, 53).
Because the enrichment of fluorescent particles can gradually increase the fluorescence intensity, our AFBH-based device could potentially be used for quantitative fluorescence-based biosensing assays (20, 21, 54, 55). As a proof of concept, we performed a series of particle enrichment experiments using droplets with different initial particle concentrations and monitored the mean fluorescence intensity of the aggregated particle cluster for each case. As indicated by our quantitative characterization results in Fig. 3D, the mean fluorescence intensity linearly increases with the increase in initial in-droplet particle concentration. This result indicates that our AFBH-based device holds great potential as a robust tool for assisting fluorescent signal amplification, quantitative biochemical sensing, and point-of-care testing applications.
Manipulating particles in a droplet array via an array of AFBHs
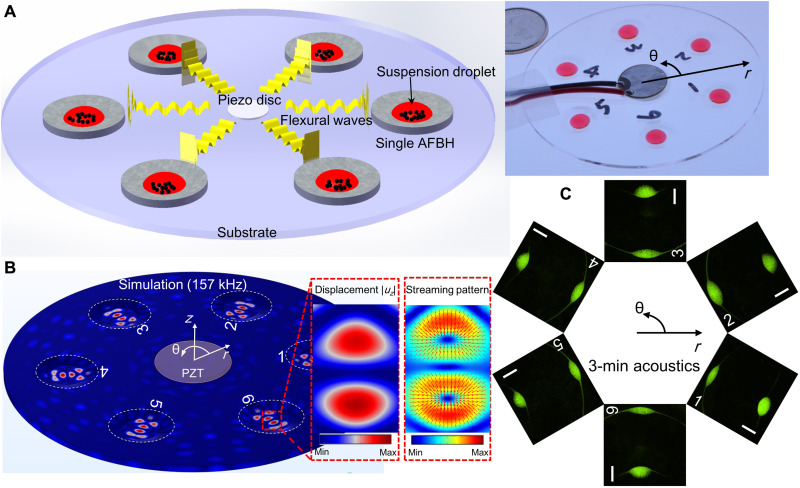
By leveraging a circular AFBH array and a radially flexural resonance mode of a circular substrate, we established an AFBH platform for simultaneously manipulating (e.g., redistributing and enriching) particles in multiple droplets placed in an array of AFBHs. As shown in Fig. 4A (a schematic and a photo), six AFBHs with the same design are distributed on a circular PMMA substrate with a rotationally symmetric configuration. A circular piezoelectric transducer is bonded at the center of the circular substrate to generate omnidirectional flexural waves, which can be trapped and locally enhanced by the six AFBHs. With this feature, our platform can manipulate (e.g., redistribute and enrich) particles in six droplets placed in the six AFBHs simultaneously.
Fig. 4. Numerical and experimental results for manipulating particles in a droplet array using an AFBH array.
(A) Left: A schematic for illustrating the mechanism of an AFBH array–based device. Right: A photo of a fabricated AFBH array–based device with a bonded circular piezoelectric transducer for generating omnidirectional flexural waves. (B) Left: A simulated flexural wave field (out-of-plane displacement amplitude |uz|) in a circular PMMA substrate at a frequency of 157 kHz. It can be seen that the mode shapes in all the AFBHs are nearly the same, and there are two antinodes at in each AFBH. Right: The corresponding acoustic streaming field in the fluid domain showing that streaming-induced drag forces (red arrows) converge at the two antinodes. (C) Acquired fluorescence microscopy images showing that 8-μm fluorescent polystyrene particles can be redistributed to form two particle clusters in each AFBH. Scale bars, 500 μm. The particle distributions in six AFBHs are nearly the same, indicating that the six AFBHs have similar particle manipulation performance. For this experiment, the excitation voltage, frequency, droplet volume, initial particle concentration, and duration of acoustic waves are 10 Vpp, 157 kHz, 20 μl, 7.38 × 105 ml−1, and 3 min, respectively.
To investigate the mechanism of our AFBH array, we simulated the flexural wave field in the solid domain (Fig. 4B, left), the acoustic radiation force field in the fluid domain (fig. S7), and the acoustic streaming field in the fluid domain (Fig. 4B, right). Among them, the simulated wave displacement amplitude field (Fig. 4B, left) at 157 kHz shows that the flexural waves can be trapped in the individual AFBHs with high intensities. In the fluid domain, both the acoustic radiation force (fig. S7) and the acoustic streaming (Fig. 4B, right) converge to the wave antinodes. These simulation results indicate that in-droplet particles in each AFBH can be manipulated by flexural waves with enhanced intensities. Moreover, the particle manipulation phenomena should be similar in all the AFBHs because the mode shapes in these AFBHs are nearly the same (Fig. 4B, left).
To validate our numerical prediction, we performed experiments using a fabricated device with an array of six AFBHs (Fig. 4A, right) to manipulate an array of particle suspension droplets dispensed in the AFBH array. The excitation voltage, frequency, droplet volume, particle concentration, and duration of acoustic waves used were 10 Vpp, 157 kHz, 20 μl, 7.38 × 105 ml−1, and 3 min, respectively. The acquired fluorescence microscopy images for the individual droplets are given in Fig. 4C. These images show that the particles can be successfully manipulated and redistributed to form two particle clusters at the two antinodes in each AFBH. Moreover, the shapes of particle clusters in all the AFBHs are nearly the same, proving that the individual AFBHs have similar wave trapping effects and particle manipulation performance. Although this experimental study is for the in-AFBH mode shape with two antinodes, other in-AFBH mode shapes (e.g., a mode shape with three antinodes in Fig. 2E and a mode shape with one antinode in Fig. 3B) could also be generated to achieve different in-droplet particle distributions by carefully optimizing the parameters of the AFBH array–based device (such as wave frequency, dimension and material of substrate, and AFBH’s center location). In addition to the demonstrated case with six AFBHs, our platform can be extended to configurations with more AFBHs. For example, when a circular array of 18 AFBHs is constructed, our simulation result (fig. S8) shows that all the AFBHs can successfully trap flexural waves with enhanced intensities and support similar in-AFBH mode shapes. We expect this capability to benefit many potential applications, such as parallel fabrication of cell spheroids by concentrating cells in multiple droplets, as well as parallel enrichment of particles with fluorescent biomarkers in multiple droplets for fluorescence signal enhancement.
DISCUSSION
In this study, we introduced, investigated, and demonstrated AFBHs, which leverage controlled linear and nonlinear interactions between trapped acoustic energy in AFBHs and particle suspension droplets to enable versatile particle and fluid manipulation functionalities, such as translation, concentration, and redistribution of particles, as well as the generation of fluidic streaming. Through finite element simulations and acoustofluidic experiments, the mechanisms of AFBHs were investigated. Our study shows that AFBHs can increase local wave intensities by trapping wideband flexural waves and, therefore, notably enhance wave-fluid and wave-particle interactions to enable strong acoustofluidic effects, such as applying acoustic radiation forces on in-droplet particles and generating acoustic streaming to apply drag forces on in-droplet particles. Our experiments show that these forces can effectively manipulate and enrich in-droplet particles, thanks to the wave trapping and intensity enhancement caused by AFBHs. Second, by controlling their internal flexural mode shapes, AFBHs can reshape internal acoustic energy distributions, change acoustic radiation and streaming-induced forces applied on in-droplet particles and, therefore, change in-droplet particle distributions. Third, our study shows that multiple AFBHs can be arranged in a customized array to simultaneously trap acoustic energy in AFBHs at multiple locations and, therefore, manipulate particles in a large array of droplets in a parallel and high-throughput manner. In addition to focusing and trapping flexural waves, the AFBH has the potential to locally shrink the wavelength. As shown in our simulation results (fig. S4), the wavelength in the AFBH with a reduced thickness is much smaller than that in the region outside the AFBH. This is because the flexural mode’s wavelength decreases with the decrease in material thickness. In the future, we will further experimentally investigate the wavelength shrinking effect enabled by an AFBH and leverage this mechanism for finer particle manipulation. We also plan to perform studies on increasing the frequency of acoustofluidic experiments and scaling down the AFBH-based devices using high-resolution 3D printing techniques such as digital light processing–based stereolithography and Nanoscribe two-photon lithography.
The AFBHs presented in this study not only fill the gap between the fields of acoustofluidics and acoustic black holes but also lead to novel AFBH-based acoustofluidic devices, including an AFBH-based elliptical substrate device, an AFBH-based dual transducer device, and an AFBH array–based device. By leveraging the trapped flexural waves in AFBHs and the enhanced wave-particle and wave-fluid interactions, our devices successfully achieved different particle manipulation functionalities, including in-droplet particle concentration, control of particle distributions, and simultaneous manipulation of particles in an array of droplets. Compared with other types of acoustofluidic devices, such as devices based on surface acoustic waves and bulk acoustic waves, the AFBH-based devices offer multiple appealing features. The AFBH-based device can easily manipulate particles in multiple droplets in a parallel manner with only one acoustic source. In addition, the AFBH-based device has a simple and easy-to-fabricate design (i.e., a piezoelectric transducer bonded on a plate with tailored holes), and the AFBH-based particle manipulation mechanisms can easily be integrated with different plate-like substrates for developing portable point-of-care devices. With these advantages, we believe that AFBHs hold great potential for developing versatile tools for a wide range of applications such as particle enrichment, fluorescence signal amplification, cell patterning, quantitative biochemical sensing, parallel particle manipulation, point-of-care testing, and high-throughput construction of cell spheroids.
MATERIALS AND METHODS
Numerical simulations
The commercial finite element software COMSOL Multiphysics 5.6 (Burlington, MA, USA) was adopted for numerical simulations. The flexural wave fields in solid domains were computed using the coupled Piezoelectricity-Solid module. The acoustic pressure fields in fluid domains were computed using the Pressure Acoustics module. The acoustic radiation force fields (i.e., vector fields) were derived through the postprocessing of the simulated in-fluid acoustic fields based on the Gor’kov radiation force equation (39). With the simulated in-fluid acoustic fields, the in-fluid acoustic streaming fields were computed on the basis of the Reynolds stress method (52) using the Laminar Flow module. More details of our numerical models and the related equations for acoustic radiation force and acoustic streaming can be found in section S1.
Device fabrication and characterization
Our devices are composed of substrates with AFBHs and circular piezoelectric transducers. In this study, PMMA is selected for device fabrication because PMMA plates are transparent and it is easy to fabricate AFBHs on PMMA plates. The PMMA plates were fabricated by a computer numerical control machining (HK GS Rapid Co. Limited, China) to form PMMA substrates with AFBHs. The profiles of AFBHs were designed on the basis of the relation in Eq. 1. To characterize the manufactured AFBH, we took an image of the thickness profile of a PMMA substrate with an AFBH (see fig. S9). The comparison between the measured thickness profile and the designed profile shows that the material thickness errors in the AFBH region are less than 70 μm. To improve the fabrication accuracy, the feasibility of using microfabrication and high-resolution 3D printing techniques for manufacturing AFBHs will be investigated in the future. For generating flexural waves in PMMA substrates, circular piezoelectric transducers (SMD12T06R412WL, Steiner & Martins Inc., USA) were bonded on PMMA substrates at optimized locations using an epoxy kit (Permatex, USA). For device characterization, a vector network analyzer (E5063A, Keysight) was used to acquire reflection coefficient S11 curves (fig. S10) for a free piezoelectric transducer and a piezoelectric transducer bonded on an elliptical PMMA substrate.
Particle sample preparation
For our experimental studies, both 8- and 10-μm fluorescent polystyrene beads (Phosphorex Inc., USA) were chosen because their material properties are similar to those of cells. These particles were diluted and mixed in deionized water and then ultrasonically dispersed for 1 min for preparing particle suspensions.
Experimental setup
Our experiments were conducted on the stage of an inverted microscope (Nikon TE2000U, Japan). The excitation signals for piezoelectric transducers were generated by a function generator (SDG1050, Siglent, Germany). Images and videos were taken using Nikon imaging software (NIS-Elements Advanced Research, Nikon, Japan) through a charge-coupled device digital camera (CoolSNAP HQ2, Photometrics, Tucson, AZ, USA). The fluorescence intensities in acquired images were postanalyzed using the ImageJ (National Institutes of Health, USA) software.
Acknowledgments
Funding: We acknowledge support from the National Natural Science Foundation of China (11974183), Zhejiang Provincial Natural Science Foundation of China under Grant No. LR22C200006, the National Science Foundation (CMMI-2104526), and the start-up fund from Duke University. P.L. and K.Y. acknowledge support from the China Scholarship Council (CSC).
Author contributions: P.L. conceived the idea. P.L., K.Y., H.H., J.C., and Q.M. contributed to the experimental design and scientific presentation. P.L., Z.T., and K.Y. performed all the experiments and data analysis. P.L. and Z.T. performed all the numerical simulations. P.L. fabricated the devices. All the authors wrote the paper. Z.T., X.X., J.H., and T.J.H. provided overall guidance and contributed to the experimental design and scientific presentation.
Competing interests: T.J.H. has cofounded a start-up company, Ascent Bio-Nano Technologies Inc., to commercialize technologies involving acoustofluidics and acoustic tweezers. The authors declare that they have no other competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Section S1
Figs. S1 to S10
Tables S1 and S2
References
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S3
REFERENCES AND NOTES
- 1.Lin L. H., Hill E. H., Peng X. L., Zheng Y. B., Optothermal manipulations of colloidal particles and living cells. Acc. Chem. Res. 51, 1465–1474 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lin L., Wang M. S., Peng X. L., Lissek E. N., Mao Z. M., Scarabelli L., Adkins E., Coskun S., Unalan H. E., Korgel B. A., Liz-Marzan L. M., Florin E. L., Zheng Y. B., Opto-thermoelectric nanotweezers. Nat. Photonics 12, 195–201 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hejazian M., Nguyen N. T., Magnetofluidic concentration and separation of non-magnetic particles using two magnet arrays. Biomicrofluidics 10, 044103 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Feng H. F., Xu X., Hao W. C., Du Y., Tian D. L., Jiang L., Magnetic field actuated manipulation and transfer of oil droplets on a stable underwater superoleophobic surface. Phys. Chem. Chem. Phys. 18, 16202–16207 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Zheng T. Y., Zhang Z. Z., Zhu R., Flexible trapping and manipulation of single cells on a chip by modulating phases and amplitudes of electrical signals applied onto microelectrodes. Anal. Chem. 91, 4479–4487 (2019). [DOI] [PubMed] [Google Scholar]
- 6.Park S., Zhang Y., Wang T. H., Yang S., Continuous dielectrophoretic bacterial separation and concentration from physiological media of high conductivity. Lab Chip 11, 2893–2900 (2011). [DOI] [PubMed] [Google Scholar]
- 7.Moreno-Moreno M., Ares P., Moreno C., Zamora F., Gomez-Navarro C., Gomez-Herrero J., AFM manipulation of gold nanowires to build electrical circuits. Nano Lett. 19, 5459–5468 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Liu H. Z., Wu S., Zhang J. M., Bai H. T., Jin F., Pang H., Hu X. D., Strategies for the AFM-based manipulation of silver nanowires on a flat surface. Nanotechnology 28, 365301 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Connacher W., Zhang N. Q., Huang A., Mei J. Y., Zhang S., Gopesh T., Friend J., Micro/nano acoustofluidics: Materials, phenomena, design, devices, and applications. Lab Chip 18, 1952–1996 (2018). [DOI] [PubMed] [Google Scholar]
- 10.Friend J., Yeo L. Y., Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 83, 647–704 (2011). [Google Scholar]
- 11.Ozcelik A., Rufo J., Guo F., Gu Y. Y., Li P., Lata J., Huang T. J., Acoustic tweezers for the life sciences. Nat. Methods 15, 1021–1028 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Melde K., Mark A. G., Qiu T., Fischer P., Holograms for acoustics. Nature 537, 518–522 (2016). [DOI] [PubMed] [Google Scholar]
- 13.Baudoin M., Gerbedoen J. C., Riaud A., Matar O. B., Smagin N., Thomas J. L., Folding a focalized acoustical vortex on a flat holographic transducer: Miniaturized selective acoustical tweezers. Sci. Adv. 5, eaav1967 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pereno V., Aron M., Vince O., Mannaris C., Seth A., de Saint Victor M., Lajoinie G., Versluis M., Coussios C., Carugo D., Stride E., Layered acoustofluidic resonators for the simultaneous optical and acoustic characterisation of cavitation dynamics, microstreaming, and biological effects. Biomicrofluidics 12, 034109 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yeo L. Y., Chang H. C., Chan P. P. Y., Friend J. R., Microfluidic devices for bioapplications. Small 7, 12–48 (2011). [DOI] [PubMed] [Google Scholar]
- 16.Li P., Huang T. J., Applications of acoustofluidics in bioanalytical chemistry. Anal. Chem. 91, 757–767 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Moroni L., Burdick J. A., Highley C., Lee S. J., Morimoto Y., Takeuchi S., Yoo J. J., Biofabrication strategies for 3D in vitro models and regenerative medicine. Nat. Rev. Mater. 3, 21–37 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Su B., Wu Y. C., Jiang L., The art of aligning one-dimensional (1D) nanostructures. Chem. Soc. Rev. 41, 7832–7856 (2012). [DOI] [PubMed] [Google Scholar]
- 19.He Z. Y., Ranganathan N., Li P., Evaluating nanomedicine with microfluidics. Nanotechnology 29, 492001 (2018). [DOI] [PubMed] [Google Scholar]
- 20.Zhang L. Y., Tian Z. H., Bachman H., Zhang P. R., Huang T. J., A cell-phone-based acoustofluidic platform for quantitative point-of-care testing. ACS Nano 14, 3159–3169 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hao N. J., Pei Z. C., Liu P. Z., Bachman H., Naquin T. D., Zhang P. R., Zhang J. X., Shen L., Yang S. J., Yang K. C., Zhao S. G., Huang T. J., Acoustofluidics-assisted fluorescence-SERS bimodal biosensors. Small 16, 2005179 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sazan H., Piperno S., Layani M., Magdassi S., Shpaisman H., Directed assembly of nanoparticles into continuous microstructures by standing surface acoustic waves. J. Colloid Interface Sci. 536, 701–709 (2019). [DOI] [PubMed] [Google Scholar]
- 23.Nichols M. K., Kumar R. K., Bassindale P. G., Tian L. F., Barnes A. C., Drinkwater B. W., Patil A. J., Mann S., Fabrication of micropatterned dipeptide hydrogels by acoustic trapping of stimulus-responsive coacervate droplets. Small 14, 1800739 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Zhang P. R., Bachman H., Ozcelik A., Huang T. J., Acoustic microfluidics. Annu. Rev. Anal. Chem. 13, 17–43 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ding X. Y., Li P., Lin S. C. S., Stratton Z. S., Nama N., Guo F., Slotcavage D., Mao X. L., Shi J. J., Costanzo F., Huang T. J., Surface acoustic wave microfluidics. Lab Chip 13, 3626–3649 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xie Y. L., Bachman H., Huang T. J., Acoustofluidic methods in cell analysis. TrAC Trends Anal. Chem. 117, 280–290 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bussiere V., Vigne A., Link A., McGrath J., Srivastav A., Baret J. C., Franke T., High-throughput triggered merging of surfactant-stabilized droplet pairs using traveling surface acoustic waves. Anal. Chem. 91, 13978–13985 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Reboud J., Auchinvole C., Syme C. D., Wilson R., Cooper J. M., Acoustically controlled enhancement of molecular sensing to assess oxidative stress in cells. Chem. Commun. 49, 2918–2920 (2013). [DOI] [PubMed] [Google Scholar]
- 29.Collins D. J., Morahan B., Garcia-Bustos J., Doerig C., Plebanski M., Neild A., Two-dimensional single-cell patterning with one cell per well driven by surface acoustic waves. Nat. Commun. 6, 8686 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Destgeer G., Cho H., Ha B. H., Jung J. H., Park J., Sung H. J., Acoustofluidic particle manipulation inside a sessile droplet: Four distinct regimes of particle concentration. Lab Chip 16, 660–667 (2016). [DOI] [PubMed] [Google Scholar]
- 31.Collins D. J., Ma Z. C., Han J., Ai Y., Continuous micro-vortex-based nanoparticle manipulation via focused surface acoustic waves. Lab Chip 17, 91–103 (2017). [DOI] [PubMed] [Google Scholar]
- 32.Gu Y. Y., Chen C. Y., Mao Z. M., Bachman H., Becker R., Rufo J., Wang Z. Y., Zhang P. R., Mai J., Yang S. J., Zhang J. X., Zhao S. G., Ouyang Y. S., Wong D. T. W., Sadovsky Y., Huang T. J., Acoustofluidic centrifuge for nanoparticle enrichment and separation. Sci. Adv. 7, eabc0467 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tian Z. H., Yang S. J., Huang P. H., Wang Z. Y., Zhang P. R., Gu Y. Y., Bachman H., Chen C. Y., Wu M. X., Xie Y. B., Huang T. J., Wave number-spiral acoustic tweezers for dynamic and reconfigurable manipulation of particles and cells. Sci. Adv. 5, eaau6062 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Carugo D., Octon T., Messaoudi W., Fisher A. L., Carboni M., Harris N. R., Hill M., Glynne-Jones P., A thin-reflector microfluidic resonator for continuous-flow concentration of microorganisms: A new approach to water quality analysis using acoustofluidics. Lab Chip 14, 3830–3842 (2014). [DOI] [PubMed] [Google Scholar]
- 35.Ku A., Lim H. C., Evander M., Lilja H., Laurell T., Scheding S., Ceder Y., Acoustic enrichment of extracellular vesicles from biological fluids. Anal. Chem. 90, 8011–8019 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Christakou A. E., Ohlin M., Onfelt B., Wiklund M., Ultrasonic three-dimensional on-chip cell culture for dynamic studies of tumor immune surveillance by natural killer cells. Lab Chip 15, 3222–3231 (2015). [DOI] [PubMed] [Google Scholar]
- 37.Augustsson P., Karlsen J. T., Su H. W., Bruus H., Voldman J., Iso-acoustic focusing of cells for size-insensitive acousto-mechanical phenotyping. Nat. Commun. 7, 11556 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Drinkwater B. W., Dynamic-field devices for the ultrasonic manipulation of microparticles. Lab Chip 16, 2360–2375 (2016). [DOI] [PubMed] [Google Scholar]
- 39.J. Hu, Ultrasonic Micro/Nano Manipulations: Principles and Examples (World Scientific, 2014). [Google Scholar]
- 40.Maxwell A. D., Bailey M., Cunitz B. W., Terzi M., Nikolaeva A., Tsysar S., Sapozhnikov O. A., Vortex beams and radiation torque for kidney stone management. J. Acoust. Soc. Am. 139, 2040–2040 (2016). [Google Scholar]
- 41.Reboud J., Bourquin Y., Wilson R., Pall G. S., Jiwaji M., Pitt A. R., Graham A., Waters A. P., Cooper J. M., Shaping acoustic fields as a toolset for microfluidic manipulations in diagnostic technologies. Proc. Natl. Acad. Sci. U.S.A. 109, 15162–15167 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wilson R., Reboud J., Bourquin Y., Neale S. L., Zhang Y., Cooper J. M., Phononic crystal structures for acoustically driven microfluidic manipulations. Lab Chip 11, 323–328 (2011). [DOI] [PubMed] [Google Scholar]
- 43.Gu Y. Y., Chen C. Y., Rufo J., Shen C., Wang Z. Y., Huang P. H., Fu H., Zhang P. R., Cummer S. A., Tian Z. H., Huang T. J., Acoustofluidic holography for micro- to nanoscale particle manipulation. ACS Nano 14, 14635–14645 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ma Z. C., Holle A. W., Melde K., Qiu T., Poeppel K., Kadiri V. M., Fischer P., Acoustic holographic cell patterning in a biocompatible hydrogel. Adv. Mater. 32, 1904181 (2020). [DOI] [PubMed] [Google Scholar]
- 45.R. M. Wald, General Relativity (University of Chicago Press, 1984). [Google Scholar]
- 46.Pelat A., Gautier F., Conlon S. C., Semperlotti F., The acoustic black hole: A review of theory and applications. J. Sound Vib. 476, 115316 (2020). [Google Scholar]
- 47.Krylov V. V., Acoustic black holes: Recent developments in the theory and applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61, 1296–1306 (2014). [DOI] [PubMed] [Google Scholar]
- 48.Drinkwater B. W., An acoustic black hole. Nat. Phys. 16, 1010–1011 (2020). [Google Scholar]
- 49.V. Giurgiutiu, Structural Health Monitoring with Piezoelectric Wafer Active Sensors (Elsevier Inc., Academic Press, ed. 2, 2014). [Google Scholar]
- 50.Krylov V. V., Tilman F. J. B. S., Acoustic ‘black holes’ for flexural waves as effective vibration dampers. J. Sound Vib. 274, 605–619 (2004). [Google Scholar]
- 51.Zhao L. X., Conlon S. C., Semperlotti F., An experimental study of vibration based energy harvesting in dynamically tailored structures with embedded acoustic black holes. Smart Mater. Struct. 24, 065039 (2015). [Google Scholar]
- 52.Lei J. J., Formation of inverse Chladni patterns in liquids at microscale: Roles of acoustic radiation and streaming-induced drag forces. Microfluid. Nanofluid. 21, 50 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Vuillermet G., Gires P. Y., Casset F., Poulain C., Chladni patterns in a liquid at microscale. Phys. Rev. Lett. 116, 184501 (2016). [DOI] [PubMed] [Google Scholar]
- 54.Liu P. Z., Tian Z. H., Hao N. J., Bachman H., Zhang P. R., Hu J. H., Huang T. J., Acoustofluidic multi-well plates for enrichment of micro/nano particles and cells. Lab Chip 20, 3399–3409 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mao Z. M., Li P., Wu M. X., Bachman H., Mesyngier N., Guo X. S., Liu S., Costanzo F., Huang T. J., Enriching nanoparticles via acoustofluidics. ACS Nano 11, 603–612 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.A. F. Bower, Applied Mechanics of Solids (CRC Press, 2009). [Google Scholar]
- 57.D. T. Blackstock, Fundamentals of Physical Acoustics (Wiley-Interscience, 2000). [Google Scholar]
- 58.L. E. Kinsler, A. R. Frey, A. B. Coppens, J. V. Sanders, Fundamentals of Acoustics (Wiley, ed. 4, 1999). [Google Scholar]
- 59.Tang Q., Hu J. H., Analyses of acoustic streaming field in the probe-liquid-substrate system for nanotrapping. Microfluid. Nanofluid. 19, 1395–1408 (2015). [Google Scholar]
- 60.Gor’kov L. P., On the forces acting on a small particle in an acoustical field in an ideal fluid. Soviet Phys. Dokl. 6, 773–775 (1962). [Google Scholar]
- 61.Nyborg W. L., Acoustic streaming due to attenuated plane waves. J. Acoust. Soc. Am. 25, 68–75 (1953). [Google Scholar]
- 62.Lighthill J., Acoustic streaming. J. Sound Vib. 61, 391–418 (1978). [Google Scholar]
- 63.Liu P. Z., Tang Q., Su S. F., Hu J. H., Principle analysis for the micromanipulation probe-type ultrasonic nanomotor. Sens. Actuators A 318, 112524 (2021). [Google Scholar]
- 64.Tang Q., Liu P. Z., Hu J. H., Analyses of acoustofluidic field in ultrasonic needle-liquid-substrate system for micro−/nanoscale material concentration. Microfluid. Nanofluid. 22, 46 (2018). [Google Scholar]
- 65.Zhu P. F., Hu J. H., Modeling and analysis of the droplet-ultrasonic stage system for nano concentration. Sens. Actuators A 225, 111–118 (2015). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Section S1
Figs. S1 to S10
Tables S1 and S2
References
Movies S1 to S3