Deeply integrating latent consistent representations in high-noise multi-omics data for cancer subtyping

Abstract

Cancer is a complex and high-mortality disease regulated by multiple factors. Accurate cancer subtyping is crucial for formulating personalized treatment plans and improving patient survival rates. The underlying mechanisms that drive cancer progression can be comprehensively understood by analyzing multi-omics data. However, the high noise levels in omics data often pose challenges in capturing consistent representations and adequately integrating their information. This paper proposed a novel variational autoencoder-based deep learning model, named Deeply Integrating Latent Consistent Representations (DILCR). Firstly, multiple independent variational autoencoders and contrastive loss functions were designed to separate noise from omics data and capture latent consistent representations. Subsequently, an Attention Deep Integration Network was proposed to integrate consistent representations across different omics levels effectively. Additionally, we introduced the Improved Deep Embedded Clustering algorithm to make integrated variable clustering friendly. The effectiveness of DILCR was evaluated using 10 typical cancer datasets from The Cancer Genome Atlas and compared with 14 state-of-the-art integration methods. The results demonstrated that DILCR effectively captures the consistent representations in omics data and outperforms other integration methods in cancer subtyping. In the Kidney Renal Clear Cell Carcinoma case study, cancer subtypes were identified by DILCR with significant biological significance and interpretability.

INTRODUCTION

Cancer is a complex and diverse disease regulated by multiple factors at the cellular level in the human body. The same type of cancer often exhibits multiple cancer subtypes, each carrying distinct biological significance. Accurate cancer subtyping can help clinicians to assess the condition of cancer patients and to formulate personalized treatment plans to improve the life quality of patients [1]. Early cancer subtyping traditionally relied on assessing tumor morphological features such as morphology, size and location to determine the extent of tumor progression and prognosis [2]. With the advancement of biotechnology, cancer subtyping that utilizes specific omics data (e.g. gene expression) has achieved promising results [3–5]. Nevertheless, existing studies have shown that only using single-omics data can neither fully describe the information of cancer subtypes nor effectively capture the subtleties of cancer [6–8]. Comprehensive analysis multi-omics data can effectively reveal distinct effects at the cellular level, such as those manifested at the genomic and epigenomic levels [9]. It is now relatively easy to obtain comprehensive and accurate omics information for various types of cancer with the evolution of high-throughput technology. The Cancer Genome Atlas (TCGA) utilized high-throughput technology to collect genomic data and clinical information from many cancer patients. TCGA provides cancer researchers with omics and clinical survival data for 33 different human cancers, including Breast Invasive Carcinoma (BRCA), Colon Adenocarcinoma (COAD), Glioblastoma Multiforme (GBM), etc. Each cancer dataset includes heterogeneous omics data from the same patient, such as messenger RNA (mRNA) expression, DNA methylation and micro RNA (miRNA) expression. TCGA has made the utilization of multi-omics data for cancer subtyping possible.

Although comprehensively analyzing multi-omics data can provide information at different omics levels, effectively integrating the consistent information from different omics data remains challenging [10]. Based on the stage of integration, existing methods can be classified into three categories: early integration methods, late integration methods and intermediate integration methods [9]. Early integration methods construct a matrix by directly connecting expression data between different omics and dividing cancer subtypes through single-omics clustering methods such as K-means. However, inappropriate standardization can lead to weight imbalance between various omics data, and direct connection may increase dimensionality. In order to address these issues, iCluster [11], iClusterBayes [12] and LRAcluster [13] project the connected data to a lower dimension through probabilistic modeling to achieve joint dimensionality reduction. Meanwhile, MCCA [14] and MultiNMF [15] achieve the purpose of dimensionality reduction through canonical correlation analysis and joint matrix decomposition, pushing the clustering solution of each view to a common consensus. Late integration methods cluster the single-omics data separately and then integrate the clustering results of each omics. This approach allows each omics to select the most suitable clustering algorithm based on the characteristics of its own data. For instance, PINSPlus [16] clusters each omics data using a perturbation clustering method and constructs a connectivity matrix to make the clustering results robust.

Currently, most multi-omics cancer subtyping methods belong to intermediate integration methods, which aim to integrate multi-omics information by capturing the consistency and complementarity information between different omics. The intermediate integration methods can be further divided into kernel learning, subspace learning and machine learning methods. The kernel learning method maps samples to a high-dimensional space using a kernel function (e.g. Gaussian kernel) to extract nonlinear features and cluster them (e.g. rMKL-PP [17], hMKL [18]). Part of the method uses the kernel function to construct a patient similarity network to operate on the similarity relationship between observation pairs in a high-dimensional space [19, 20]. Among them, SNF [21] builds multiple similarity networks by calculating the sample similarity in different omics data and then integrates them through message passing. The subspace learning method assumes that the data samples are distributed in the union of multiple low-dimensional subspaces and achieves cancer subtyping through subspace segmentation (e.g. NEMO [22], Subtype-WESLR [23]).

Chaudhary et al. [24] were the first to use a deep autoencoder [25] model to predict the survival of patients with hepatocellular carcinoma. Autoencoder and variational autoencoder (VAE) [26] reconstruction-based methods only use the input data as supervision to compress the input data into one that can retain the most original data information. The low-dimensional representation meets the requirements for data dimension when multi-omics integration is performed. Numerous machine learning methods have also been applied to cancer subtyping. MAUI [27] uses an autoencoder to measure the similarity between colorectal cancer (CRC) and disease models such as cancer cell lines. Subtype-GAN [28] is based on multiple-input multiple-output neural networks, using consensus clustering and Gaussian mixture models to identify molecular subtypes of tumor samples. DCAP [29] notices the noise problem in omics data and proposes using denoise in the encoder to learn patient-pair feature representations. DLSF [30] proposes to integrate the multi-omics data by learning consistent manifolds in the latent sample space for disease subtypes identification. DSIR [31] simultaneously captures the global structures in sparse subspace and local structures in manifold subspace from multi-omics data and constructs a consensus similarity matrix by utilizing deep neural networks. MRGCN [32] simultaneously encodes and reconstructs multiple omics expression and similarity relationships into a shared latent embedding space.

Despite existing methods attaining encouraging results, several unresolved problems persist. Firstly, while the addition of regularization terms or the adoption of feature selection methods can mitigate some of the noise, they can potentially inadvertently disregard important patient information. Secondly, the straightforward concatenation of low-dimensional omics features assigns the same weight to each omics, but this fails to reflect the actual scenario accurately. Finally, reconstruction-based methods typically prioritize reconstruction at the expense of clustering performance. Based on the above problems, we proposed Deeply Integrating Latent Consistent Representations (DILCR). It aims to alleviate the integration problem of high-noise multi-omics data by capturing the latent consistent representations and adequately integrating their respective information. To obtain better consistent representations, we assumed that each dataset consists of two irrelevant variables: noise variable and consistency variable. The consistency variable encompasses low-frequency information associated with clustering, whereas the noise variable encompasses much high-frequency information unrelated to clustering. Therefore, we used VAE to split noise and consistency variables from the latent omics space and augment this ability using contrastive learning. And we proposed Attention Deep Integration Network (ADINet) to deeply integrate the latent consistency variable of each omics and use integrated variable for the next cancer subtyping. We make integrated variable clustering friendly by self-supervised clustering optimization. By comparing 14 methods, the experimental results indicate that DILCR performs better than most methods, and the identified cancer subtypes by it have higher confidence and more significant biological significance.

METHODS

Method overview

DILCR is a VAE-based deep learning model designed to effectively alleviate the integration problem of high-noise levels multi-omics data. As shown in Figure 1, the model comprised three main modules: Separating Noise and Consistency Variables, ADINet and Self-supervised Clustering Optimization.

Figure 1.

Overview of the DILCR model. (A) Separating Noise and Consistency Variables by reconstructing the expression matrix of each omics and combining it with the contrastive learning, inputting the information from each omics expression matrix and obtaining consistency variable and noise variable during the intermediate process. (B) Attention Deep Integration Network. It outputs integrated variable by deeply integrating the latent consistency variable between each omics. (C) Self-supervised Clustering Optimization. It minimizes the soft assignment and target distribution loss to make the learned integrated variable more suitable for cancer subtyping, and get the final cancer subtyping of the -th patient by . Note: The part inside the dotted line box indicates that all omics have the same structure (not shared), where takes the value .

In the separating noise and consistency variables module, we utilized independent VAE structure and contrastive loss function to effectively separate noise and consistency variables in omics data. Moreover, we used ADINet to deeply integrate the consistency variable between each omics and used the integrated variable for cancer subtyping. In self-supervised clustering optimization module, we introduced the Improved Deep Embedded Clustering (IDEC) algorithm [33] to fine-tune the integrated variable, making them more suitable for cancer subtyping. In the following sections, we describe the implementation details of DILCR.

Separating noise and consistency variables

For omics expression data , where the -th omics expression data . Each column represents different gene expression values for each patient, and each row represents the expression value of the same gene in different samples. A sample in the -th omics data is denoted as . To capture better consistent representations, we postulated that each omics comprised consistency variable associated with clustering and irrelevant noise variables, i.e.

(1)

where is the proportion of in , and are the consistency variable and noise variable for any sample in the -th omics data, respectively.

That is, for the consistency variable and noise variable, we first obtained a low-dimensional feature with mixed clustering information and noise through the independent encoder . Subsequently, the low-dimensional feature was divided into two distinct components: the consistency variable layer and the noise layer to separate the two variables. The process of learning the latent consistency variable can be expressed as follows:

(2)

where is a mapping function and takes as a parameter, is the consistency variable layer parameter of -th omics, and are the independent encoder and encoder parameter of -th omics, respectively. The process of learning the noise variable can be expressed as follows:

(3)

where and are the parameters of learning and , respectively. Add in order to make the sampling step differentiable and suitable for backpropagation.

Contrastive loss function

To obtain better consistency variable for subsequent tasks, we proposed a novel contrastive loss function to enhance the quality of consistency variable. The objective of contrastive learning is to minimize the distance between positive sample pairs while maximizing the distance between negative sample pairs in a given space [34], i.e.

(4)

where is the distance function, , are positive counterparts and negative counterparts of sample , respectively.

In this paper, our goal was to make the consistency variable between each omics as similar as possible and to ensure it remained far away from cluster-irrelevant information in space. To achieve this, we defined consistency variable from different omics in the same sample as positive samples for each other. In other words, for the -th omics, the positive sample of the -th sample was defined as . On the other hand, we defined the noise variable of all samples as negative samples for each sample. Specifically, for the -th omics, the negative sample of the -th sample was defined as . Our final proposed contrastive learning loss function was defined as follows:

(5)

where

(6)

(7)

where is the unsampled noise variable, is a temperature hyperparameter, which controls the model’s discrimination against negative samples, and are the positive sample score and negative sample score, respectively. And is cosine similarity function, is exponential function.

Attention deep integration network

Because the quality of the integrated variable directly impacts the final performance of the model, it is crucial to integrate these variables efficiently after obtaining the consistency variable for each omics. However, existing methods often achieve integration by simply concatenating them, which gives equal weight to different omics. To obtain omics-cross information, we proposed using a typical TransformerEncoder [35] to deeply integrate consistency variables in each omics and assign adaptive weights to different omics. Its ADINet process could be expressed as follows:

(8)

(9)

(10)

where is the connected variable, is the integrated variable, a is an arbitrary vector input to the function, and are learnable parameters. And is vector connection, is vector length.

When reconstructing raw expression data, we used the integrated variable to reconstruct omics-common information in all omics data and the noise variable to reconstruct omics-specific information in the -th omics data. The reconstructed raw data could be expressed as follows:

(11)

where is reconstructed data of -th omics data, and and are the independent decoder and decoder parameter of -th omics, respectively.

Self-supervised clustering optimization

After obtaining the integrated variable, to address the issue that the learned low-dimensional space features based on reconstruction models may not be suitable for cancer subtyping, we introduced the IDEC algorithm for fine-tuning the integrated variable used for cancer subtyping. Self-supervised clustering optimization is achieved by minimizing the following loss:

(12)

where is Kullback–Leibler (KL) divergence that measures the distance between two distributions, is the number of clusters, is the similarity measure between the -th sample integrated variable and the cluster center , using the -distribution as the kernel:

(13)

where the target distribution in Eq.(12) is generated by :

(14)

As shown in Eq.(14), the quality of the target distribution depends on the soft distribution . Therefore, the target distribution should not be updated at each iteration but only when the soft assignment has an excellent representation to avoid instability. In practice, we update target distribution using all embedded points every iterations. The -th sample label assignment obtained when updating the target distribution was given by the following equation:

(15)

We also followed the original paper and stopped training if the percentage change in label assignment for the target distribution was less than a threshold for two consecutive updates.

Variational lower bound

The objective of variational inference was to maximize the log-likelihood function of multi-omics real data [36]. Here, we introduced the noise variable and the integrated variable . Using Jensen’s inequality, the log-likelihood function of our model is formulated as follows:

(16)

where is the true distribution of -th omics data, which consists of two independent continuous variable and ; let denote all views’ data, i.e. , is the Evidence Lower Bound (ELBO) of the -th omics. In variational inference, maximizing the likelihood is equal to maximizing the ELBO. Given that and were two independent variables, then , so the Eq.(16) could be written as follows:

(17)

where are the posterior distribution of and , respectively. The derivation process of Eq.(16) to Eq.(17) can be seen in Supplementary Eq.(1). Specifically, separating noise and consistency variables module is achieved by minimizing the following loss:

(18)

where is the reconstruction loss implemented by Mean Squared Error, is KL divergence terms in Eq.(17).

Overall loss function

Because random initialization of cluster centers could lead to poor performance of IDEC, we needed to first iteratively optimize the clustering variable using the model to obtain a better representation, rather than a random and poor representation. The loss in our network was as follows:

(19)

where , , and are all adjustable hyperparameters to balance the impact of each loss.

RESULT

TCGA dataset and data processing

To validate the effectiveness of DILCR, we selected 10 typical cancer datasets for subsequent analysis, including Acute Myeloid Leukemia (AML), BRCA, COAD, GBM, Kidney Renal Clear Cell Carcinoma (KIRC), Liver Hepatocellular Carcinoma (LIHC), Lung Squamous Cell Carcinoma (LUSC), Ovarian Serous Cystadenocarcinoma (OV), Sarcoma (SARC) and Skin Cutaneous Melanoma (SKCM). Each cancer dataset included mRNA expression data, DNA methylation data, miRNA expression data and clinical information for each patient. The multi-omics data and patient clinical information were obtained from this reference [9].

When preprocessing data, to prevent the model from underfitting by a lack of sample data, we retained as many samples as possible during data processing instead of deleting too many samples. Specifically, we processed each cancer dataset as follows:

• Firstly, we removed patient data for duplicates in the survival data.

• Secondly, we removed omics data for patient data without survival data.

• Finally, we used the mean value to fill in the missing data for each omics data according to the number of remaining samples in the survival data.

The number of missing omics data for the retained samples, based on survival data, is presented in Supplementary Table S1. Furthermore, a comprehensive description of each cancer dataset is provided in Table 1.

Table 1.

The details of the TCGA dataset used in this paper. They are, respectively, described as the feature dimension of mRNA expression, DNA Methylation, miRNA expression and the number of patients in each dataset

Dataset	mRNA expression	DNA methylation	miRNA expression	Sample number
AML	20531	5000	705	187
BRCA	20531	5000	1046	1227
COAD	20531	5000	705	444
GBM	12042	5000	534	571
KIRC	20531	5000	1046	536
LIHC	20531	5000	1046	373
LUSC	20531	5000	1046	587
OV	20531	5000	705	598
SARC	20531	5000	1046	265
SKCM	20531	5000	1046	467

Comparison of DILCR with the state-of-the-art methods on 10 cancer datasets

Comparison methods. We selected 14 state-of-the-art integration methods comparing with DILCR to demonstrate the effectiveness. These include the early integration method LRAcluster [13], the late integration method PINSPlus [16] and 12 intermediate integration methods. The intermediate integration methods include six traditional methods and six latest deep learning integration methods: SNF [21], rMKL-LPP [17], MCCA [14], MultiNMF [15], iClusterBayes [12], NEMO [22], DCAP [29], DLSF [30], DSIR [31], MRGCN [32], MOCSS [37] and DMCL [38]. Among them, DCAP, DLSF, MOCSS and DMCL are deep learning integration methods designed to solve the noise in heterogeneous omics data.

Parameter settings. To address the limited amount of cancer patient data and the high-dimensional features, we designed a shallow model for easy training in the separating noise and consistency variables module. The encoder of DILCR used a three-layer multi-layer perceptron structure, where the input layer had the same dimension as the features from different omics. The other two hidden layer dimensions are set to 1024 and 512 to handle the dimension differences of different omics features. We then separated the noise and consistency variables from the feature representation and set their dimensions to 128. Finally, the dimensions of , and are set to 10, 10 and 20, respectively. Moving on to the ADINet module, we used a layer of 1024-dimensional TransFormerEncoder and directly utilized the dimension after the consistency variable connected of all omics, i.e. 384-dimensional, for the final dimension used for cancer subtyping. In the self-supervised clustering optimization module, IDEC algorithm updated the target distribution iteration interval as 50, and the training stopped when the threshold reached 1e-6. Regarding the hyperparameters which need manual setup during training, we set the balance coefficients of , , and to 0.9, 0.3, 0.1 and 10, respectively. Additionally, for the number of subtypes in each cancer, we referred to the settings in previous articles [9, 20, 23, 30], and we selected three clustering numbers of 3, 4 and 5. The number of cancer subtypes was determined by the P-value of survival analysis. Results for several other classes are provided in the Supplementary Table S2. The final number of subtypes for each cancer dataset is shown in parentheses in Table 2.

Table 2.

The results of DILCR were compared with 14 state of the art integration methods on 10 cancer datasets. In each cell , is the number of enriched clinical parameters, is the P-value of survival analysis and is the number of clusters. The bold values are significant results (P-value < 0.05). Means is the average value of the algorithm. Sig is the number of datasets with significant results and enriched clinical parameters

Methods	AML	BRCA	COAD	GBM	KIRC	LIHC	LUSC	OV	SARC	SKCM	Means	Sig
LRAcluster	1/0.3(4)	1/0.7(5)	0/0.7(5)	1/2.9(4)	2/2.0(9)	2/2.4(12)	1/1.3(5)	1/0.8(4)	2/2.5(13)	1/6.2(4)	1.2/2.0	9/6
PINSPlus	1/0.5(4)	1/0.9(2)	1/0.5(2)	1/0.2(2)	1/1.2(2)	1/0.9(9)	0/0.1(2)	1/0.1(4)	2/1.0(3)	1/5.8(3)	1.0/1.1	9/1
SNF	1/2.7(5)	1/0.4(4)	1/0.1(2)	1/3.8(3)	2/6.0(3)	1/0.2(2)	0/0.1(3)	1/0.6(3)	2/2.1(3)	1/2.0(2)	1.1/1.8	9/5
rMKL-LPP	1/2.4(6)	5/0.6(7)	0/0.5(6)	2/3.0(6)	1/1.1(11)	3/1.0(6)	0/0.3(6)	1/0.1(6)	2/2.5(6)	1/2.6(7)	1.6/1.4	8/4
MCCA	1/1.5(2)	1/1.6(5)	1/0.1(2)	2/1.7(4)	2/5.5(2)	1/0.3(5)	0/0.5(5)	1/0.4(5)	2/1.9(5)	1/6.4(5)	1.2/2.0	8/6
MultiNMF	0/1.3(2)	0/1.3(2)	0/0.3(2)	1/2.1(3)	1/1.9(2)	3/2.9(3)	1/0.3(2)	0/0.3(2)	2/1.1(2)	2/4.5(2)	1.0/1.6	7/6
iClusterBayes	1/1.5(2)	0/1.3(3)	0/0.2(2)	1/3.1(2)	4/7.3(2)	2/2.2(3)	0/1.5(2)	2/0.9(2)	2/0.9(2)	2/3.7(2)	1.4/2.2	7/6
DCAP	1/1.6(5)	1/3.1(5)	0/0.2(2)	2/4.5(5)	1/0.2(2)	2/1.4(5)	0/1.8(3)	1/0.6(2)	2/3.8(4)	1/8.7(4)	1.1/2.6	9/7
DLSF	1/2.5(5)	2/1.9(3)	1/0.1(4)	2/4.5(5)	3/2.8(4)	3/3.3(3)	1/0.1(3)	1/0.03(4)	2/2.4(10)	3/3.9(5)	1.9/2.2	10/7
NEMO	1/3.2(5)	1/0.3(4)	1/0.1(4)	1/4.6(10)	2/3.9(3)	2/2.7(5)	0/0.3(3)	1/0.4(3)	2/1.9(3)	1/3.2(10)	1.2/2.1	9/6
DSIR	1/2.7(7)	3/6.8(12)	1/1.1(5)	2/3.0(9)	4/1.4(4)	2/2.0(10)	2/1.8(3)	1/1.0(3)	2/2.6(3)	3/3.7(8)	2.1/2.6	10/8
MRGCN	1/3.0(10)	4/6.7(4)	1/0.6(7)	2/3.8(8)	4/2.4(9)	2/1.7(10)	1/1.5(13)	1/0.8(5)	2/3.3(8)	3/4.5(5)	2.1/2.8	10/8
MOCSS	1/5.9(4)	1/7.0(5)	2/0.8(5)	2/3.5(5)	2/3.6(4)	1/3.6(5)	0/0.6(5)	1/1.1(5)	1/4.4(5)	1/4.2(5)	1.2/3.5	9/7
DMCL	1/2.7(2)	1/2.9(5)	2/0.5(2)	1/5.7(2)	2/3.4(6)	1/3.0(2)	0/0.9(3)	1/1.1(4)	1/4.5(4)	1/2.4(2)	1.1/2.7	9/7
DILCR	1/6.1(3)	4/8.8(5)	3/1.0(4)	2/8.3(3)	5/7.9(4)	3/4.3(5)	0/2.9(3)	1/2.4(3)	1/6.1(5)	2/9.4(5)	2.2/5.8	9/9

Evaluation method. We used two evaluation methods to assess the performance of DILCR. Firstly, we used the log-rank test to calculate the P-value of survival analysis, comparing whether significant differences exist between the cancer subtypes identified by DILCR. Secondly, we aimed to test for the enrichment of clinical labels in the clusters. We chose six clinical labels for which we tested enrichment: age at initial diagnosis, gender and four discrete clinical-pathological parameters: measuring the progression of the tumor (pathologic T), cancer in lymph nodes (pathologic N), metastases (pathologic M) and total progression (pathologic stage). In the clinical label enrichment analysis, we used the Chi-Square test for discrete clinical parameters, and for numeric parameters, we used the Kruskal–Wallis test. Additionally, not every cancer dataset could obtain these six clinical parameters, and the specific clinical parameter information used in each dataset is described in the Supplementary Table S3.

DILCR performance on 10 cancer datasets. As shown in Table 2, we display DILCR with 14 other comparison methods in terms of P-value of survival analysis, the number of enriched clinical parameters and the number of clusters used in 10 cancer datasets. Our proposed method has higher P-value of survival analysis than the other 14 methods in nine datasets, indicating that the cancer subtypes identified by DILCR have more significant differences. Although the DILCR has a lower P-value than the DSIR on COAD dataset, it has a higher number of enriched clinical parameters than other methods. As shown in Figure 2, the results reveal that DILCR outperforms all other methods in the number of significant results datasets, and it is the number of enriched clinical parameters which is only less than one compared with the best method. Specifically, the clinical parameters enriched by different methods are shown in Supplementary Table S4. In Figure 3, we also plotted the Kaplan–Meier survival curves of DILCR on 10 cancer datasets to illustrate that DILCR could well distinguish the survival of different subtypes of patients. The results show that the survival curves of the cancer subtypes identified by DILCR on the 10 datasets can be well separated.

Figure 2.

The number of datasets with significant results and enriched clinical parameters of different algorithms on 10 cancer datasets. The red is our method DILCR.

Figure 3.

Kaplan-Meier survival curves were plotted to analyze the cancer subtypes identified by DILCR on ten cancer datasets. The dashed line represents the median survival line, and different colored curves represent different cancer subtypes. The extent of separation between the curves indicates the degree of significance in survival differences among patients with various subtypes, with greater separation showing more pronounced differences in survival outcomes.

Effectiveness and robustness evaluation of DILCR on synthetic datasets

We referred to the method of Shi et al. [39] to generate simulated multi-omics data and compared the performance of DILCR with other methods on simulated data. We generated mRNA, DNA methylation and miRNA expression data for 400 patients with real clusters. Specifically, the mRNA, DNA methylation and miRNA expression data were separately produced from real genomic profiles GSE10645 [40], GSE51557 [41] and GSE73002 [42]. Since all methods can perform better under good generation conditions, we use some parameters different from Shi et al. settings when generating simulated data. When generating data with clustering characteristics, , generates simulated data under bad conditions. Finally, in the simulated data, the real clusters are 1–100, 100–200, 200–300 and 300–400.

We generated simulated data for three different noise scenarios to evaluate the effectiveness and robustness of DILCR. We added 0%, 20% and 30% extra noise to the original simulated data to simulate low-noise, medium-noise and high-noise conditions, respectively. We conducted 50 random experiments under different noise conditions and compared three traditional methods (SNF, NEMO, MCCA) with four deep learning methods designed for handling noise in heterogeneous omics data (DCAP, DLSF, MOCSS, DMCL). We used Normalized Mutual Information (NMI) [43], Adjusted Rand Index (ARI) [44] and the score [45] as evaluation metrics. NMI and ARI have value ranges of [0, 1] and [−1, 1], respectively, to assess the similarity between the clustering results and the real clusters. A higher value indicates closer clustering results to the real clusters. The score considers precision and recall, with a value range of [0, 1]. As shown in Figure 4, DILCR can obtain better results than other comparison methods in simulated data under different noise intensities, and the smaller box also shows that DILCR has better robustness. In addition, in terms of robustness and effectiveness, deep learning methods perform better than traditional methods.

Figure 4.

Comparison of NMI, ARI and between DILCR and seven comparison methods on (A) low-noise, (B) medium-noise (C) and high-noise simulated data, respectively.

Validation of subtypes identified by DILCR

We compared the cancer subtypes identified by DILCR on the BRCA dataset with the molecular characteristics of BRCA and the molecular typing of PAM50 RNAseq of BRCA [46], and the results are shown in Supplementary Figure S1 and Supplementary Table S5. Furthermore, when considering the expression of estrogen receptor (ER), human epidermal growth factor receptor 2 (HER2), and progesterone receptor (PR), different cancer subtypes exhibit distinct characteristics. Patients with the Basal-like subtype exhibit negative expressions of ER, HER2 and PR. Patients with the HER2-enriched subtype display positive HER2 expression but negative ER and PR expression, while Luminal-A and Luminal-B subtypes are positive for ER and PR, but they are negative for HER2. As shown in Figure S1 and Table S5, Subtype-0 and Subtype-2 identified by DILCR on the BRCA dataset can clearly match Basal-like and Luminal-A, respectively. Additionally, Subtype-1 contains five different real subtypes, which may be heterogeneous. On the other hand, Subtype-3 and Subtype-4 are a mix of Luminal-A and Luminal-B. We believe that clustering some Luminal-A and Luminal-B samples into the same subtype is due to the high similarity in certain sample features across both subtypes.

Case study of identified subtypes on KIRC

As shown in Table 2, DILCR demonstrates good performance (P-value = 7.9, number of enriched clinical parameters = 5) on the KIRC dataset. Moreover, as shown in Figure 3, the Kaplan–Meier survival curves of different subtypes are clearly separated, indicating the ability of DILCR to distinguish the survival outcomes of patients with different subtypes.

To further elucidate the biological significance of DILCR, we analyzed the four cancer subtypes identified by DILCR on the KIRC dataset. We first screened the differentially expressed genes (DEGs) between the subtypes using a t-test, followed by GO/KEGG enrichment analysis to reveal the molecular pathways and biological functions involved in all DEGs. Finally, we analyzed the survival risk of patients with different gene expression levels in the pathways affected by single genes.

Firstly, we used t-test (P-adjust 0.05, FoldChange = 1) to screen for genes that show significant differentially expressed in mRNA between different cancer subtypes. As shown in the heatmap in Figure 5, we observe that the DEGs exhibit inter-group differences in mRNA expression between different cancer subtypes, further demonstrating the good interpretability and biological significance of the cancer subtypes identified by DILCR. In addition, among the DEGs we identified, EGFR, ESRRG, ALDOB, BIRC5 and other genes are consistent with some previous studies [47–49].

Figure 5.

Heatmaps of significantly differentially expressed mRNA among identified subtypes by DILCR on KIRC. The rows and columns represent DEGs and patients, respectively. (A) subtype 0 and subtype 1; (B) subtype 0 and subtype 2; (C) subtype 0 and subtype 3; (D) subtype 1 and subtype 2; (E) subtype 1 and subtype 3; (F) subtype 2 and subtype 3.

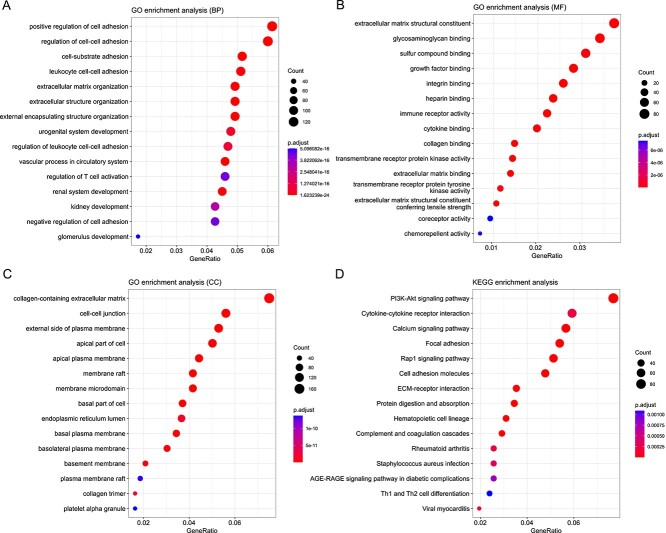
To reveal the molecular pathways and biological functions involved in these genes and better understand their biological significance, we used the HiPlot online tool (https://hiplot.com.cn/) to perform GO/KEGG enrichment analysis on the DEGs we identified. The top 15 pathways with the highest enrichment count from the enrichment results were displayed using a bubble plot, as shown in Figure 6. The most highly enriched GO pathways (BP, MF, CC) were positive regulation of cell adhesion, channel activity and collagen-containing extracellular matrix, respectively. The most enriched KEGG pathway was the PI3K-Akt signaling pathway. These enriched pathways are consistent with some previous studies [23, 48].

Figure 6.

The top 15 enriched pathways on the GO (BP, MF, CC)/KEGG signal pathway. The X-axis represents the gene proportion, that is, the proportion of differentially expressed proteins annotated by this pathway in species, and the Y-axis represents the name of the pathway. In the bubble chart, the size and color of the bubbles represent the number of enriched genes and the P-value level, respectively.

To understand the biological roles and potential functions of the whole differentially expressed mRNA, we selected the path with the largest GeneRatio from the above four pathways, and chose one gene from each to analyze its impact on survival prognosis (including NPNT, TMEM150C, FREM2, PIK3R3). We divided the patients into high-expression and low-expression groups based on the mean expression value of the gene and examined whether patients with different expression levels had significant differences in survival. As shown in the Figure 7, patients with different expression groups affected by a single gene displayed significant differences in survival, and the overlap between the confidence intervals of the survival curves between groups was very small, indicating that our results have strong credibility. Specifically, NPNT, FREM2 and PIK3R3 are associated with patient survival prognosis in existing studies [50–52], and can also be identified as molecular complex detection components in protein interaction networks (Supplementary Figure S2). Although there are few studies related to TMEM150C, in the survival analysis of TMEM50C gene, the Kaplan–Meier curve showed complete separation, and the survival rate of patients in the high expression group was significantly higher than that of patients in the low expression group. This suggests that the cancer subtypes we identified provide important guidance for future cancer diagnosis, treatment and discovery of relevant important genes. Additionally, we screened DEGs on the remaining nine cancer datasets according to consistent criteria and performed GO/KEGG pathway enrichment analysis on them. The most enriched pathways on GO/KEGG for other dataset are detailed in Supplementary Table S6.

Figure 7.

Survival prognostic analysis was influenced by NPNT, TMEM150C, FREM2 and PIK3R3 genes on the KIRC dataset. The red curve is the high expression group of the gene, and the blue curve is the low expression group of the gene. The dashed line is the median survival probability line. The red and blue blocks represent confidence intervals.

Evaluation DILCR performance on BRCA

We compared the three methods of K-means (baseline method), DILCR and DILCR-DI (without adding contrastive loss function) on BRCA with noise. The purpose was to illustrate that our model can handle real high-noise omics data and to prove that the contrastive learning method can effectively enhance the model’s ability to deal with noise. We introduced 10 different intensities of random noise ranging from 5% to 50% and added them to the original omics data. Subsequently, we observed the extent to which the performance of the three methods attenuated after the addition of noise. The data used by K-means was obtained by combining the expression data of each omics of BRCA in the patient dimension. To assess the clustering performance of the different methods, we employed the molecular typing of PAM50 RNAseq of BRCA [46] as the ground truth clustering of BRCA. This subtype categorizes BRCA into five subtypes: Luminal-A, Luminal-B, HER2-enriched, Basal-like and Normal-like, which are widely acknowledged in clinical practice. As shown in the Figure 8, the NMI of DILCR does not decrease significantly as the noise intensity increases and always maintains a high level. The ARI and of DILCR are significantly better than that of DILCR-DI. In a high-noise environment, the performance of DILCR-DI dropped significantly, while the performance of DILCR did not drop significantly. This shows that the contrastive loss function can effectively enhance the model’s learning ability on high-noise data. Furthermore, to demonstrate the ability of DILCR to handle missing omics data, we compared the omics data by randomly removing some expression values and using mean imputation. As shown in Supplementary Figure S3, we found that DILCR can adapt to highly missing omics data.

Figure 8.

Clustering performance of K-means, DILCR-DI and DILCR on BRCA dataset with varying degrees of additional noise. The X-axis represents the intensity of noise, and the Y-axis represents clustering performance.

Ablation study on BRCA

We evaluated the effects of adding and combining different modules on the DILCR method without any modules. We formed seven other methods. Some details of each method are briefly described below:

• DILCR-NA: No modules are added. The contrastive loss coefficient is set to 0, and the consistency variable of each omics was clustered using K-means after direct concatenation without passing through the ADINet module. The IDEC algorithm is also not used at the end.

• DILCR-C, DILCR-I, DILCR-D: Contrastive loss function, IDEC algorithm and ADINet module are added, respectively, to the DILCR-NA method.

• DILCR-CI, DILCR-DC, DILCR-DI: Different combinations of the contrastive loss function and IDEC algorithm, ADINet module and contrastive loss function and ADINet module and IDEC algorithm are added, respectively, to the DILCR-NA method.

• DILCR: The three modules are added to the DILCR-NA method.

The results shown in Figure 9 demonstrate that the performance of DILCR consistently increases with the addition of different modules, compared with the baseline method (K-means). Notably, adding the ADINet module significantly improves the model’s performance. This finding suggests that the proposed module effectively integrates the consistent information in the omics data, providing a strong feature representation for predicting cancer subtypes. Finally, the method that added all three modules outperforms the other methods that lack some modules.

Figure 9.

Comparison of clustering performance of seven different combination methods with K-means and DILCR. K-means is used as the baseline method, and the highest bar is the DILCR performance. The X-axis represents different clustering indicators, and the Y-axis represents the values of various methods corresponding to these indicators.

DISCUSSION AND CONCLUSION

Accurate cancer subtyping aids clinicians in personalizing cancer treatment, thereby reducing patient toxicity and treatment costs. However, integrating multi-omics data faces challenges due to the high noise levels of omics data. In this paper, we proposed a deep integrating multi-omics model called DILCR, which alleviated the noise problem associated with integrating multi-omics data. The experimental results demonstrated that DILCR effectively captured better consistent representations by separating the noise and consistency variables, and it can adapt to a real high-noise environment.

To evaluate the performance of DILCR, we compared 14 methods on 10 cancer datasets from TCGA. DILCR achieved better cancer subtyping results. We obtained significant P-value of survival analysis and enriched clinical parameters on nine datasets. Specifically, DILCR achieved 7.9 P-value of survival analysis and enriched five clinical parameters on the KIRC dataset, indicating that the cancer subtypes identified by DILCR demonstrate well-interpretable biological significance. The Kaplan–Meier curve on KIRC showed a clear separation between the curves of the identified cancer subtypes, indicating noticeable survival differences. Furthermore, the KIRC cancer dataset analysis revealed DEGs and enrichment pathways aligned with previous studies, demonstrating a reasonable correlation at the molecular level. DILCR also outperformed other comparative methods on most cancer datasets, and we attributed this improvement to the essential role played that we proposed attention deep integration module. The attention mechanism adaptively captured the different effects of different omics on cancer subtypes.

Despite DILCR demonstrating better results on the majority of TCGA datasets, it is evident that there remains room for further improvement. In data preprocessing, we attempted to preserve the utmost omics data, but the mean-filling method yielded unsatisfactory results when confronted with many missing values, such as the COAD dataset. Furthermore, we tried seven different preprocessing methods in Supplementary Table S7 to explore the effects of various preprocessing and filling methods on the performance of DILCR. The results showed that filling-based preprocessing methods outperformed deletion-based preprocessing methods, and better filling methods can also improve the performance of the DILCR. In future studies, exploring better filling methods or mining the underlying topology between patients enhances the model’s effectiveness. Additionally, despite the successful identification of cancer subtypes based solely on omics expression data, including patient clinical information through the utilization of multimodal technology in future research endeavors can enhance the model’s performance further.

Key Points

• DILCR captured better consistent representations by separating two irrelevant variables: noise variable and consistency variable.

• We proposed an ADINet to integrate consistency variables in each omics.

• The IDEC algorithm was introduced to optimize the integrated variable, making it cluster-friendly.

• Compared with other existing methods, DILCR identified more significant biological significance cancer subtypes and effectively adapted to high-noise multi-omics data.

Yueyi Cai is currently working toward an M.S. degree in computer system architecture at the School of Information Science and Engineering at Yunnan University, Yunnan, China. He received a B.S. degree in computer science and technology from Leshan Normal University, Sichuan, China, in 2022. His interests include bioinformatics and artificial intelligence.

Shunfang Wang is currently a professor of School of Information Science and Engineering, Yunnan University, China. She received her Ph.D. degree in probability theory and mathematical statistics from Yunnan University in 2005. She was a Visiting Scholar with Texas A&M University in USA in 2010. She has published over 100 scientific papers as the first author or corresponding author in internationally renowned journals and conferences such as Bioinformatics, IEEE/ACM TCBB, Computers in Biology and Medicine, BMC Genomics, BMC Bioinformatics, Biomedical Signal Processing and Control, and BIBM, etc. She has been supervising Ph.D. students since 2016. Her research interests include bioinformatics, machine learning, medical image analysis and computational statistics.

FUNDING

This work is supported by the National Natural Science Foundation of China (62062067), and Yunnan University Graduate Research Innovation Project (KC-23233880).

DATA AVAILABILITY STATEMENTS

All data are from publicly available datasets. The complete code for DlLCR can be accessed at https://github.com/ykxhs/DILCR.