Abstract
B cell epitope prediction methods are separated into linear sequence-based predictors and conformational epitope predictions that typically use the measured or predicted protein structure. Most linear predictions rely on the translation of the sequence to biologically based representations and the applications of machine learning on these representations. We here present CALIBER ‘Conformational And LInear B cell Epitopes pRediction’, and show that a bidirectional long short-term memory with random projection produces a more accurate prediction (test set AUC=0.789) than all current linear methods. The same predictor when combined with an Evolutionary Scale Modeling-2 projection also improves on the state of the art in conformational epitopes (AUC = 0.776). The inclusion of the graph of the 3D distances between residues did not increase the prediction accuracy. However, the long-range sequence information was essential for high accuracy. While the same model structure was applicable for linear and conformational epitopes, separate training was required for each. Combining the two slightly increased the linear accuracy (AUC 0.775 versus 0.768) and reduced the conformational accuracy (AUC = 0.769).
Keywords: epitope prediction, machine learning, BiLSTM, embedding, protein structure
INTRODUCTION
B cells are produced in the bone marrow and are characterized by the presence of a unique receptor on their surface denoted as the B cell receptor (BCR) [1]. When a B cell encounters an antigen, the BCR binds to the antigen, via interactions between the BCR binding site and a specific region of the antigen called an epitope and triggers a series of events that lead to the production of a clone of B cells producing antibodies specific to that antigen [2]. B cells also play a role in the development of immunological memory, which allows the immune system to respond rapidly to future encounters with the same antigen [3].
The epitopes bound by BCRs are typically on the surface of antigens [4]. In protein-based antigens, B-cell epitopes can be linear or conformational. Linear epitopes are a continuous sequence of amino acid (AA) residues, while conformational epitopes consist of the spatially continuous ones, which may be sequence-wise discontinuous AA [5].
The identification of B-cell epitopes is crucial for peptide-based vaccines [6], diagnostic tools [7, 8] and the selection of high-affinity antibodies for immuno-therapy and immuno-diagnostics [9]. Experimental epitope-identification methods examine large arrays of potential epitope candidates and are expensive and time-consuming [10].
To overcome these limitations, a large number of tools were developed to predict B-cell epitopes. Those tools can be classified into two approaches: full peptide prediction and single AA prediction. In the single AA prediction approach (e.g. BepiPred-3.0 [11] and DiscoTope2 [12]), one studies a protein or chain and predicts for each AA whether it is part of an epitope or not. Full peptide prediction approaches (e.g. epitope1D [13], DeepLBCEPred [14], LBCEPred [15], NetBCE [16]) receive a candidate peptide within a protein and predict whether it is an epitope or not. Full peptide prediction methods are limited to linear epitopes. Moreover, they cannot be used to screen all candidate peptides. Single AA-based methods are usually trained on conformational (nonlinear) epitopes, although they can be applied also to linear epitopes, where each residue in the epitope is considered by itself. Besides the general epitope prediction algorithms above, models were developed to predict epitopes for a specific antibody [2, 17–20]. The advantage of such models is that they use the antibody information and their prediction may be more accurate. Their limitation is that they cannot be used for general screening of candidate epitopes for any antibody in a protein, as required for example, when looking for positions in viral proteins that can be targeted [21].
However, current prediction algorithms suffer from some limitations. When screening for epitopes in a protein, one may look for either linear or conformational epitopes. All current approaches treat the predictions of such epitopes as distinct tasks. Moreover, full-epitope prediction algorithms require an estimate of the epitope length, which is often not available. Finally, for conformational epitope, most algorithms require either predicted or observed 3D structure that is often not available.
We here propose to bridge the gap between linear and nonlinear epitopes and improve prediction accuracy. We present CALIBER a bidirectional long short-term memory (BiLSTM) [22] model that assign each residue the probability that it is part of an epitope.We denote this algorithm CALIBER (Conformational And LInear B cell Epitopes pRediction). We show that this model can be applied to linear and conformational-epitopes, and suggests an extended framework for detecting linear or conformational epitopes. We show that this model significantly improves on the current state-of-the-art (SOTA) of linear-epitope predictions, and is as good or better than the SOTA in conformational epitopes. CALIBER is available as a server at https://caliber.math.biu.ac.il or a stand-alone Python code at https://github.com/louzounlab/epitope_b_cells_predictor.
We compare the predictions of CALIBER with existing models. There are many epitope-prediction tools [11–16, 23–29], and others. We describe here the main SOTA methods. BepiPred-2.0 [23] is a sequence-based B-cell epitope prediction. It predicts for each antigen residue (except for the first and last four residues in antigen) the probability of being a part of an epitope. Each residue is encoded using biochemical features of all the residues in a nine-residue sliding window centered on the residue itself. Then, a Random Forest algorithm was trained on these structural features.
BepiPred-3.0 [11] improves on BepiPred-2.0 using representations from the protein language model Evolutionary Scale Modeling (ESM)-2 [30]. Instead of the structural information, they represent the residues by embedding extracted from the ESM-2 model of each residue in a window of size 9. Each window is an input for Feed Forward Neural Network. DiscoTope-2 [12] combines a statistical difference in AA composition between epitope and non-epitope residues and a definition of the spatial neighborhood for integrating log-odds ratios in residue proximity. GraphBepi [24] is a graph-based model. GraphBepi first generates the sequence representations and protein structures from antigen sequences by a pre-trained language model and AlphaFold2 [31], respectively. This information is the input of an edge-enhanced deep graph neural network [32] and of a BiLSTM neural networks [33] in parallel. Those are combined to predict B cell epitopes using a multilayer perceptron (MLP). EpiDope [25] is a linear epitope single residue predictor. It is based on deep neural networks to detect epitopes in proteins based on their primary AA sequence.
While existing models consecutively improved the prediction accuracy, the accuracy is still not high enough for the clinical estimate of epitopes, and more advanced models are required. Moreover, almost all linear epitope models predict whether a full peptide is an epitope rather than providing a score for each residue in the peptide to allow an estimate of how precise is the prediction per residue. We here propose such a model.
MATERIALS AND METHODS
Datasets
Linear epitopes
The dataset used to train and evaluate the models was taken from the Immune Epitope Database (IEDB) [34], following the linear test set used in BepiPred-2.0. The peptides were divided into positive and negative. Negative peptides or peptides that were confirmed as positive only in one experiment were dropped. B cell epitopes tend to be 5 to 25 AAs [35], therefore longer or shorter epitopes were also dropped. Then every peptide was matched with its original protein sequence. We used only the proteins that contained a positive peptide. Protein sequences with non-standard AA symbols were discarded from the dataset. The final dataset contained 11 725 proteins, where 10% of the proteins were used as an external test set (Table 1).
Table 1.
Pro. Len.—Average and standard deviation of the protein length in the training and test sets of each dataset. Epitope Len.—Number of epitope residues in each protein. Fraction—Fraction of residues in the protein that are in epitopes. Num. of Pro.—number of proteins. Residue epitope—the number of all residues that are in epitopes. Residue non-epitope—the number of residues that are not in epitopes
| Pro. len | Epitope len | Fraction | Num of Pro. | Residue epitope | Residue non-epitope | ||
|---|---|---|---|---|---|---|---|
| Linear | Train |
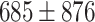
|
|
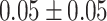
|
10 552 | 147 646 | 7078 382 |
| Linear | Test |
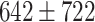
|
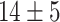
|
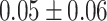
|
1173 | 16 414 | 737 189 |
| Conformational | Train |
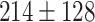
|
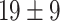
|
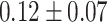
|
1320 | 24 958 | 256 971 |
| Conformational | Test |
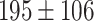
|
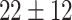
|
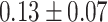
|
146 | 3204 | 25 222 |
Conformational epitopes
We used the antigen training dataset from BepiPred-3.0. The dataset was obtained from the Protein Data Bank (PDB). We included only structures that contain at least one complete antibody, and at least one non-antibody (antigen) protein chain, with a resolution lower than 3Å and R-factor (a metric that gauges how well the proposed crystallographic model aligns with the actual experimental X-ray diffraction data) lower than 0.3, the resolution and R-factor values were chosen according to BepiPred-3.0 [11] dataset preparation. This resulted in 582 antigen-antibody structures. We kept only the antigen chains that had at least one epitope residue and a sequence length of 39 or more. We obtained a total of 1466 antigens. Ten percent of the data set is used as an external test set. Proteins that appear in the training set were not included in the test set.
Protein features
Each protein residue was represented by different embeddings. We tested Kidera [36] factors, biochemical properties or the ESM-2 embedding for the linear epitopes, and ESM-2 or ESM-IF1 (inverse folding) embeddings for the conformational epitopes. Kidera factors are a set of 10 physico-chemical properties used to describe the As [36]. An additional vector of eight properties was calculated for each residue on a sequence of nine (the residue itself, and four before and after), or less if the size of the residue from the start/end of the sequence is less than 4 AA: the molecular mass of the sequence [37], average of KD score on sequence [38], fraction of helix [39], aromaticity [40], instability index [41], isoelectric point [42], the molar extinction coefficient assuming cysteines (reduced) and cysteines residues (Cys-Cys-bond) [43]. Those eight properties were Z-scored.
ESM-2 encoding [30] was calculated by the pre-trained ESM-2 transformer which returns for an entire antigen sequence a 1280 dimensions encoding for each AA in the protein. ESM-IF1 [44] is based on the protein structure; hence a PDB file is required as input. The encoding is a vector in size 512 for each AA.
Relative Surface Accessibility (RSA) was also calculated using NetSurfP-3.0 [45], as an additional feature for the ESM embedding, and for the biochemical features.
Model architecture
The output of all models was the input of an MLP with one hidden layer which returns a single value per residue, and then a sigmoid 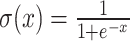 function is applied to the output to get a probability value. The difference between the models is in the initial layers.
function is applied to the output to get a probability value. The difference between the models is in the initial layers.
BiLSTM
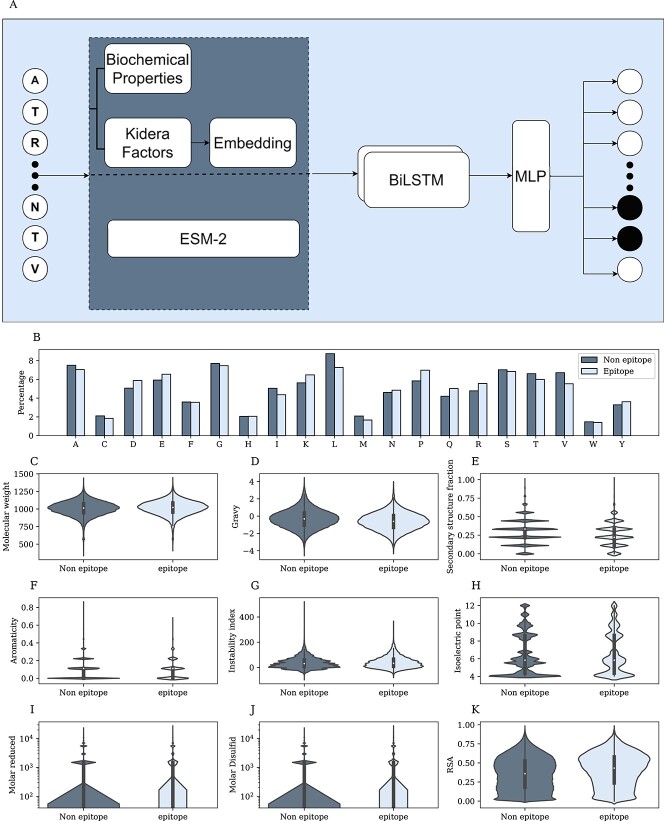
The first step was performed on four kinds of initialization: (1) random embedding, (2) the Kidera Factors vector that was used to initialize the embedding layer, (3) the Kidera Factors with biochemical features; the Kidera Factors vector was used to initialize the embedding layer, and the embedding output concatenated to the biochemical features vector. For each of these methods, the embedding layer was learned in each epoch. (4) ESM-2 pretrained embedding. In the next step, one of the initialization methods of the entire protein was the input of a BiLSTM. The BiLSTM network outputs a vector for every residue of the protein. The output is a concatenation of the two LSTM directions, hence the output is fed into an MLP with one layer to combine the results (Figure 1A). This model requires only the protein sequence and does not consider the structure.
Figure 1.
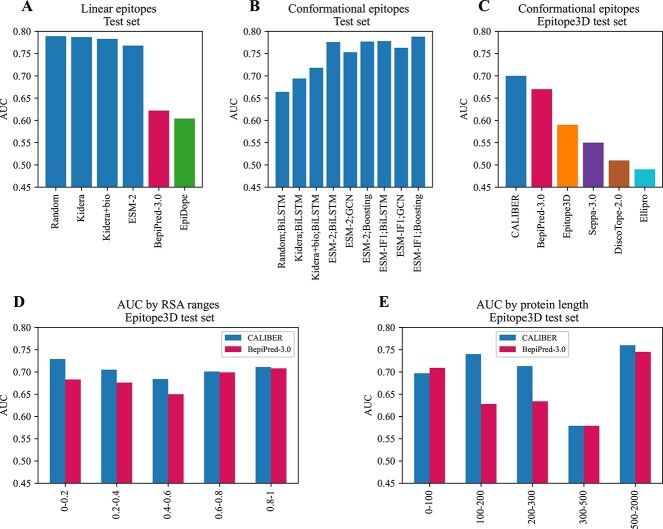
Linear epitopes. A) Model architecture. First, choose an encoding for each residue—ESM-2, Kidera factors. Then embed the vector and concatenate it to the biochemical properties of the residue. The combined sequence is the input of a BiLSTM, and the output is the input of an MLP. B) Percentage of each AAa from the protein sequences that are epitopes(light color) and non-epitope (dark color). C-J) Distribution of epitope and non-epitope for different properties, where each residue was represented by the average feature of the ninemer around it. I-J) Y-axis in log scale. K) RSA distribution of epitope and non-epitope residues.
Graph convolutional networks
Each protein was represented as a graph, where each node is a residue. The node features were ESM-2 or ESM-IF1 pre-trained embedding concatenated or not to the RSA (Figure 2A). An edge exists between two residues if the distance (calculated from the PDB) of them is less or equal to 5 (this value was chosen through a grid search); the edges were unweighted.
Figure 2.
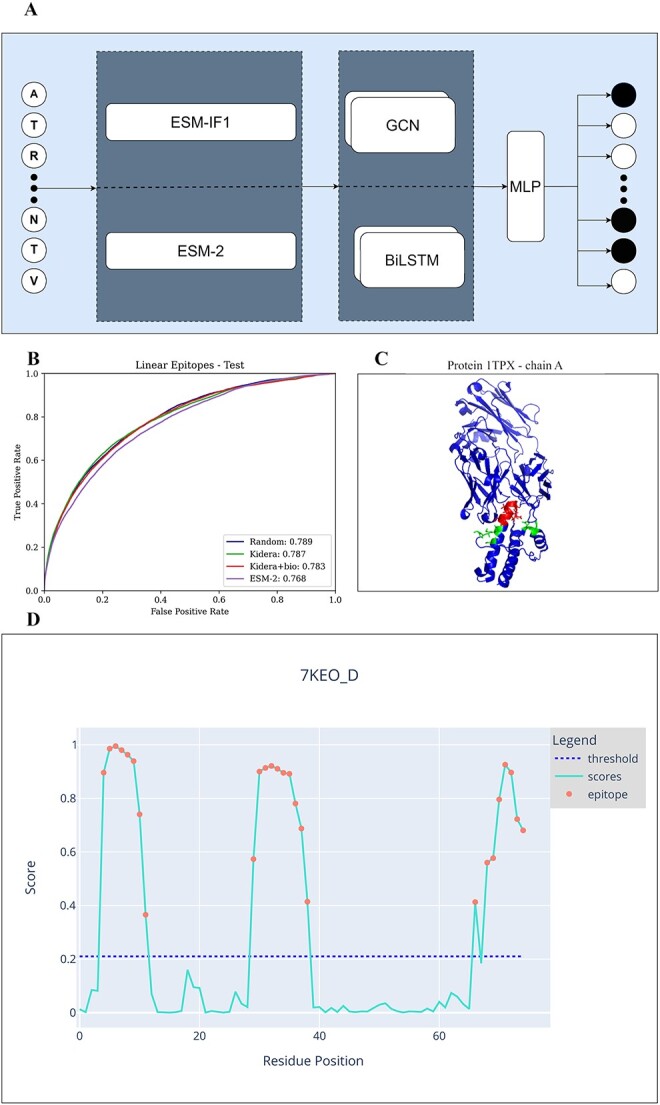
A) Model architecture. First, choose an encoding - ESM-2 or ESM-IF1. Then, the whole sequence is the input of either a BiLSTM or GCN. Finally, the output of these models is the input of an MLP.B) Chain A of the protein 1TPX. Residues that are part of a linear epitope are colored red, residues that are part of a Conformational epitope are colored green, and those that are not a part of an epitope are colored blue. C) ROC curve of linear epitopes on the test sets of all 4 methods. D) An example of the graphical diagram that the CALIBER website produces for each protein in the input. The x-axis represents the residue position, and the y-axis the CALIBER scores. The dashed line represents the threshold. Each residue with a score over the threshold is colored in red. The threshold can be set on the website.
The distance was computed using the observed PDB files. We calculated the distances between every two atoms that appear in the structure. The distance between each pair of AA was determined to be the minimal distance between the atoms of each AA.
The protein graph was the input of a graph convolutional network (GCN) model with two layers. The activation function was a Rectified Linear Unit [46], and a dropout between each layer was performed. This model requires the protein structure, regardless of the chosen embedding, since the graph is based on the distances.
Hyper-parameters tuning
A Binary Cross-Entropy loss was used. The optimizer was Adam. An early stopping mechanism was set to stop the training process after 10 consecutive epochs of decreasing validation Area under the ROC Curve (AUC). All the model hyperparameters were optimized using a grid search using an internal validation AUC as a score. The following ranges were used: learning rate in the range of 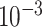 to
to 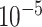 , encoding dimension for the random embedding in the range of 10 to 100, L2-regularization in the range of 0 to 0.1, drop-out rate in the range of 0 to 0.3, LSTM hidden size in the range of 10 to 100, LSTM number of layers in the range of 1 to 4, 1–7 GCN layers, 10–30 neurons per GCN hidden layer, the distance between two residues to determine edges in the range of 3–10 Å. The hyper-parameters were selected to maximize the AUC in the internal validation set. The hyper-parameters for the linear epitopes models and the joint training of both linear and Conformational epitopes were - learning rate = 0.001, dropout rate = 0.25, LSTM hidden size = 100, LSTM number of layers = 2, L2 regularization =
, encoding dimension for the random embedding in the range of 10 to 100, L2-regularization in the range of 0 to 0.1, drop-out rate in the range of 0 to 0.3, LSTM hidden size in the range of 10 to 100, LSTM number of layers in the range of 1 to 4, 1–7 GCN layers, 10–30 neurons per GCN hidden layer, the distance between two residues to determine edges in the range of 3–10 Å. The hyper-parameters were selected to maximize the AUC in the internal validation set. The hyper-parameters for the linear epitopes models and the joint training of both linear and Conformational epitopes were - learning rate = 0.001, dropout rate = 0.25, LSTM hidden size = 100, LSTM number of layers = 2, L2 regularization = 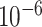 , encoding dimension = 10. The hyper-parameters for the Conformational epitopes models - learning rate =0.0001, dropout rate = 0.2, LSTM hidden size = 10, LSTM number of layers = 2, L2 regularization =
, encoding dimension = 10. The hyper-parameters for the Conformational epitopes models - learning rate =0.0001, dropout rate = 0.2, LSTM hidden size = 10, LSTM number of layers = 2, L2 regularization = 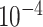 , GCN layers = 16, distance = 5.
, GCN layers = 16, distance = 5.
Performance evaluation
Each residue received a score whether it is an epitope. The entire protein/chain was used in the training and the evaluation, except when we used ESM-2, the model returns the embedding up to 1023 first residues, therefore for longer proteins, we used only the first 1023 residues. The model was first evaluated by the AUC over a 5-fold cross-validation, to find the optimal hyper-parameters. Then it was evaluated on an external test set. For each model, we report the following outcomes:
AUC—the area under the curve of the recall/sensitivity (TP/(TP+FN)) versus the false positive rate or specificity (FP/(FP+TN)).
Area under the precision-recall curve (PR-AUC)—the AUC of the positive predictive value (PPV)/precision (TP/(TP+FP)) versus the recall/sensitivity (TP/(TP+FN)).
Balanced accuracy (BAC)—The average of recall/sensitivity and specificity
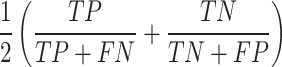 |
Matthews correlation coefficient (MCC) -
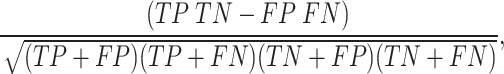 |
where TP=True Positive, TN=True Negative, FP=False Positive, and FN=False Negative.
Statistical tests
To examine whether the difference between the results of the different algorithms is statistically significant, we performed a one-sample t-test, since we examined the performances on a single test set. We used the standard error of the validation set, calculated over the cross-validation. A total of 25 validations for the boosting model (five for BiLSTM, five for GCN and all their combinations for the boosting).
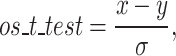 |
(1) |
where for each measure tested, 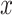 is the CALIBER performance score on the test set,
is the CALIBER performance score on the test set, 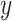 is the performance score of the other tested algorithms and
is the performance score of the other tested algorithms and 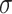 is the standard error of the validation set by CALIBER.
is the standard error of the validation set by CALIBER.
RESULTS
Epitopes in proteins can be linear or conformational. Typically conformational epitopes are computed using an available structure [12, 47, 48]. However, often such a structure is unavailable. We first tested for linear epitopes whether it is better to use an embedding based on biological insight or a purely data-oriented approach. Epitopes are presented on the surface of the protein. As such, one could expect multiple biochemical properties to differ significantly between residues in epitopes and not within epitopes. We checked whether specific AA properties are associated with linear epitopes. We then trained different models, with either AA biochemical properties, random embedding or properties of the entire protein, and tested what model produces the most accurate prediction of linear epitopes on a test set.
Linear epitopes properties
We compared the biochemical properties of AAs within and outside epitopes in 11 725 proteins from the IEDB [34] (see methods). Each AA was represented by the average feature of the ninemer around it. For each residue we measured its RSA and a 9 AA window moving average of the following features: the molecular mass, the KD score, the fraction of helices residues, aromaticity, instability index, iso-electric point, the molar extinction coefficient assuming cysteine (reduced) and cysteine residues (Cys-Cys-bond) (see Methods). All distributions are not sampled from a normal distribution (Shapiro–Wilk test 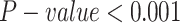 ) We compared the distributions and performed a Mann–Whitney U-test of the distributions of each of these properties for ninemers where the central residue was within or outside epitopes. Significant differences were obtained for the molecular mass of the sequence, the average KD score, the fraction of helices, the instability index, the isoelectric point and RSA. However, the differences in the distributions (Figure 1 B–K) were very limited, and not enough to separate the two groups (epitopes and non-epitopes). Indeed, the AUC of the classification of residues into inside and outside of epitopes, based on each property by itself, are all around 0.5 (Table 2).
) We compared the distributions and performed a Mann–Whitney U-test of the distributions of each of these properties for ninemers where the central residue was within or outside epitopes. Significant differences were obtained for the molecular mass of the sequence, the average KD score, the fraction of helices, the instability index, the isoelectric point and RSA. However, the differences in the distributions (Figure 1 B–K) were very limited, and not enough to separate the two groups (epitopes and non-epitopes). Indeed, the AUC of the classification of residues into inside and outside of epitopes, based on each property by itself, are all around 0.5 (Table 2).
Table 2.
AUC for epitope residues using each feature by itself in Linear epitope.
| Feature | AUC |
|---|---|
| Molecular weight | 0.526 |
| Gravy | 0.419 |
| secondary structure fraction | 0.446 |
| Aromaticity | 0.5 |
| Instability index | 0.524 |
| Isoelectric point | 0.507 |
| Molar reduced | 0.5 |
| Molar disulfide | 0.5 |
| RSA | 0.57 |
Linear-epitopes models
Given the low accuracy of predictors based on single features, we tested more complex classifiers. Linear epitope prediction can be treated as a text classification problem. To test the accuracy of such models, We trained BiLSTM models with the embedding of each AA as an input with different encodings: 1) a randomly initialized embedding layer further trained by the model, 2) an embedding layer initialized with the Kidera factor further trained by the model, 3) an embedding layer initialized with the Kidera factor further trained by the model concatenated to biochemical features (fraction of helix, aromaticity, instability index, isoelectric point, the molar extinction coefficient assuming cysteines (reduced) and cystines residues (Cys-Cys-bond)), and the RSA of the AAs. The prediction was for each AA whether it is part of an epitope. 4) pre-trained ESM-2 embedding. The BiLSTM output was fed into an MLP with 2 layers.
We trained each model over a 5-fold cross-validation. When the input of the model was random AA embedding, Kidera or Kidera with biochemical properties, the average AUC was 0.8 on the validation dataset. For the ESM-2 embedding the average AUC on the validation dataset was 0.77 (Supp. Mat. Table S1). When the input is the ESM-2, the validation set is not equal to the AA embedding input, since ESM-2 embedding is limited to the 1,023 first residue and so on the output. We checked the AUC of the AA embedding up to the first 1,023 residues of the proteins, the validation average AUC is 0.76. This is a similar validation AUC as the AA embedding. However, it is much more computationally expensive. The runtime of the random AA embedding is 0.08 sec versus 14.34 sec for ESM-2 on average on 50 proteins from the test (Table 3) on a single GPU, and it can be applied to all protein lengths.
Table 3.
CALIBER (above line) and other models (below lines) Linear epitope prediction performance on the external test set. CALIBER is applied with different embedding methods: AA random embedding, ESM-2, Kidera embedding, Kidera embedding + biochemical properties, to other algorithms: BepiPred-3.0 and EpiDope. The run times of CALIBER in seconds per protein (averaged over 50 proteins from the test.
| AUC | BAC | MCC | PR-AUC | Time | |
|---|---|---|---|---|---|
| Random | 0.789 | 0.71 | 0.13 | 0.12 | 0.08 |
| Random up to 1023 | 0.764 | 0.69 | 0.14 | 0.13 | - |
| Kidera | 0.787 | 0.71 | 0.13 | 0.12 | 0.08 |
| Kidera+bio | 0.783 | 0.71 | 0.13 | 0.12 | 0.15 |
| ESM-2 | 0.768 | 0.7 | 0.14 | 0.13 | 14.34 |
| BepiPred-3.0 | 0.622 | 0.59 | 0.06 | 0.04 | - |
| EpiDope | 0.604 | 0.58 | 0.05 | 0.03 | - |
The MCC and PR-AUC validation are equal for all methods. The BAC of the random initial embedding is the highest and is 0.73 (Supp. Mat. Table S1). Since epitope prediction can be used for large-scale screening, one may require much shorter times. As such, given that both models have similar performances, we prefer the model with the shorter run time.
To ensure the results of CALIBER are not the effect of parameter hyper-tuning, we performed an additional test on samples that the model was not exposed to during training or parameter tuning. The model-based on random embedding, Kidera embedding and Kidera embedding with biochemical properties inputs yielded a higher AUC,0.789, 0.787, and 0.783, respectively versus ESM-2 AUC of 0.768 (Figures 2C, 3A), while ESM-2 yielded a higher PR-AUC of 0.13 versus 0.12. (Table 3) We compared our method with Bepipred-3.0 and EpiDope on the external test set. DiscoTope-2 required the protein structure, therefore it was not included in this comparison. The accuracy of CALIBER is higher than BepiPred-3.0 and EpiDope by all measures (Table 3, Figure 3A).
Figure 3.
AUC of the test dataset. The blue bars are the results of CALIBER. A) Linear epitopes test set AUC of CALIBER and of BepiPred-3.0 and EpiDope by the different initialization methods. B) Conformational epitopes test set AUC of CALIBER by the different initialization methods and the different models (in the label name, separated by ’;’). C) Conformational epitopes test set AUC of CALIBER (ESM-IF1;Boosting) versus other models on the Epitope3D dataset. D) Performance comparison of CALIBER and BepiPred-3.0 on the blind test set Epitope3D, on different ranges of RSA. E) Performance comparison of CALIBER and BepiPred-3.0 on the blind test set Epitope3D, on different ranges of chain length.
Conformational epitopes
Conformational epitopes are typically discontinuous (See Figure 2B for example). Most prediction algorithms use the structure for the prediction of AA belonging to such epitopes [12, 47, 48]. However, given the accuracy of the linear models above, we tested the trained linear model with the four initialization methods: random embedding, Kidera factors, Kidera factors concatenated to biochemical features, and ESM-2 on the conformational epitopes test set; The AUC values were 0.62,0.62,0.54 and 0.56, respectively. Thus, the sequence-based models above do not apply to conformational epitopes.
To test whether the source of the difference is the model or the data, we trained the same models with the conformational epitopes training set and evaluated the AUC on the test set; the AUC were 0.66, 0.69,0.72, and 0.78, respectively (Table 4, and the validation results in Supp. Mat. Table S2). Thus, at least for the ESM-2-based model, the required model architecture is similar for linear and conformational epitopes. However, the models should be trained independently.
Table 4.
CALIBER Conformational epitope prediction performance of BiLSTM, GCN, and boosting models on the Test dataset. Comparing the different embedding methods: Random initialization. Kidera, Kidera + biochemicals, ESM-2 and ESM-IF1.
| Embedding | Model | AUC | BAC | MCC | PR-AUC |
|---|---|---|---|---|---|
| Random | BiLSTM | 0.664 | 0.62 | 0.16 | 0.18 |
| Kidera | BiLSTM | 0.694 | 0.64 | 0.18 | 0.21 |
| Kidera+bio | BiLSTM | 0.718 | 0.66 | 0.21 | 0.25 |
| ESM-2 | BiLSTM | 0.776 | 0.7 | 0.27 | 0.35 |
| ESM-2 | GCN | 0.753 | 0.69 | 0.25 | 0.32 |
| ESM-2 | Boosting | 0.777 | 0.68 | 0.23 | 0.37 |
| ESM-IF1 | BiLSTM | 0.778 | 0.7 | 0.28 | 0.34 |
| ESM-IF1 | GCN | 0.763 | 0.68 | 0.24 | 0.33 |
| ESM-IF1 | Boosting | 0.788 | 0.69 | 0.24 | 0.38 |
We further tested, whether including the physical distance between the residues would improve the precision. We thus tested a GCN, or the combination of a GCN with the model above, as well as boosting both models (See methods). We trained and optimized the models again over a 5-fold cross-validation. When the structure is given, one can also produce an ESM-IF1 embedding. The models were trained with either ESM-2 or ESM-IF1 initial embedding. We further trained all models either with (Supp. Mat. Table S3) or without RSA (Table 4, Figure 3B, Supp. Mat. Table S2). The performances were similar, so we used the model without the RSA input. To summarize, as was the case in the linear models, explicitly adding information on the protein structure to the language models had a limited contribution to the accuracy.
Given the high accuracy of the ESM-2 model on both types of epitopes, we tested whether a single model could be produced for both types of epitopes, training the BiLSTM model with ESM-2 as an input on the linear and conformational epitopes simultaneously. The resulting AUC for the linear test was 0.775 and AUC for the conformational 0.769 (Table 5, 3B). This is slightly lower than each model by itself. However, this is the first combined model that gives better than SOTA results for both types of epitopes.
Table 5.
CALIBER Performance of the BiLSTM model initialized with ESM-2 trained on both datasets of Linear and Conformational epitopes, on the Test datasets.
| Dataset | AUC | BAC | MCC | PR-AUC |
|---|---|---|---|---|
| Linear | 0.775 | 0.7 | 0.14 | 0.13 |
| Conformational | 0.769 | 0.62 | 0.17 | 0.34 |
Conformational epitope predictions comparison
We compared our model with existing conformational epitope prediction methods, using an additional external test set including 45 proteins provided in Epitope3D [48].
To ensure consistency with existing methods, the test measures were calculated only on surface residues with an RSA above 15%, as evaluated in Epitope3D publication (Table 6, Figure 3C). We performed a one-sample t-test between CALIBER results and all other models for all measures. The results are significantly different with 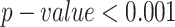 . The AUC values were extracted from the Bepipred-3.0 publication, and BAC and MCC were extracted from the Epitope3D publication, except for the Bepipred-3.0 which was computed directly using Bepipred-3.0. We did not compare with GarphBepi, since neither the code nor the website produced results. CALIBER and BepiPred-3.0 which both used protein language models outperformed the other models, while CALIBER used all protein/chain sequences for prediction and BepiPred-3.0 only used local information suggests again that information beyond the embedding and the language model has minimal contribution to the accuracy. We further tested the AUC of CALIBER and BepiPred-3.0 for different ranges of RSA, we included all residues with RSA in the range from all proteins in the test set. CALIBER has a higher AUC for all RSA ranges (Figure 3D, Supp. Mat. Table S5). In addition, We tested the AUC of CALIBER and BepiPred-3.0 for different ranges of chain length, we included all residues of chines in the length range from all proteins in the test set. For proteins up to a length of 100, BepiPred-3.0 slightly outperformed CALIBER (AUC of 0.709 versus 0.697), for proteins in the 300–500 range, the AUC is equal for both methods and is lowest for all length ranges (AUC of 0.579). For the other length range groups, CALIBER outperformed BepiPred-3.0 (Figure 3E, Supp. Mat. Table S6).
. The AUC values were extracted from the Bepipred-3.0 publication, and BAC and MCC were extracted from the Epitope3D publication, except for the Bepipred-3.0 which was computed directly using Bepipred-3.0. We did not compare with GarphBepi, since neither the code nor the website produced results. CALIBER and BepiPred-3.0 which both used protein language models outperformed the other models, while CALIBER used all protein/chain sequences for prediction and BepiPred-3.0 only used local information suggests again that information beyond the embedding and the language model has minimal contribution to the accuracy. We further tested the AUC of CALIBER and BepiPred-3.0 for different ranges of RSA, we included all residues with RSA in the range from all proteins in the test set. CALIBER has a higher AUC for all RSA ranges (Figure 3D, Supp. Mat. Table S5). In addition, We tested the AUC of CALIBER and BepiPred-3.0 for different ranges of chain length, we included all residues of chines in the length range from all proteins in the test set. For proteins up to a length of 100, BepiPred-3.0 slightly outperformed CALIBER (AUC of 0.709 versus 0.697), for proteins in the 300–500 range, the AUC is equal for both methods and is lowest for all length ranges (AUC of 0.579). For the other length range groups, CALIBER outperformed BepiPred-3.0 (Figure 3E, Supp. Mat. Table S6).
Table 6.
Performance comparison of CALIBER and methods for Conformational epitopes: BepiPred-3.0, Epitope3D, Seppa-3.0, Discotope-2.0, and Ellipro, on the blind test set Epitope3D, on residues with RSA above 15%.
| Method | AUC | BAC | MCC |
|---|---|---|---|
| CALIBER-Boosting,ESM IF1 | 0.7 | 0.63 | 0.15 |
| BepiPred-3.0 | 0.67 | 0.63 | 0.16 |
| Epitope3D | 0.59 | 0.61 | 0.45 |
| Seppa-3.0 | 0.55 | 0.52 | 0.02 |
| Discotope-2.0 | 0.51 | 0.5 | -0.01 |
| Ellipro | 0.49 | 0.44 | -0.06 |
CALIBER website
CALIBER is accessible as a website. There are three valid input formats: protein sequences, PDB IDs and a zip of PDB files. The user can choose the desired model (BiLSTM/GCN/Boosting), the encoding (random initializing embedding/ESM-2/ESM-IF1), and the dataset that the model was trained on (not all the combinations are possible -only the ones reported here). Two output files are generated: 1) CSV file with four columns - protein name, AA letter, amino acid position, score by the model, 1/0 to predict epitope/non-epitope, 2) A FASTA file where the residue predicted as non-epitope are in lower case and those that are predicted as epitope in upper case. In addition, a graphical diagram is shown when each residue predicted to be part of an epitope is marked. The user can set the threshold (see default thresholds Supp. Mat. Table S4) and the 2 files will be regenerated according to the selected threshold, as well as the graphical diagram (Figure 2D).
DISCUSSION
One of the most important debates in machine learning is whether insight beyond the observed data improves the quality of predictions [49]. While often, the answer is positive, it is not always the case. In the case of B cell epitope prediction, we compared models for both linear and conformational epitopes. In both cases, the biological insight had a minimal contribution to the accuracy of the prediction. In conformational epitopes, including the 3D structure of the protein and the epitope in a GCN had practically no effect on the accuracy. The simple sequence-based classifier, the random initialization embedding-based BiLSTM model, was better than all current SOTA models for linear epitopes. In conformational epitopes, the GCN practically did not improve the sequence-based models.
While the reported accuracy of CALIBER is better than existing methods, it is far from being enough to replace experiments at this stage. There may be a few reasons for that. First, most epitope datasets are not curated and contain multiple errors that may affect the accuracy. Moreover, reported epitopes are a mixed bag of experimental methods and binding affinities, so it is unclear whether one can treat all reported epitopes similarly. This is clear for example from the fact that combining different origins of epitopes reduces the prediction accuracy.
The concept of epitope prediction contains an inherent limitation. An epitope is a part of the protein that an antigen can bind. However, this definition is inherently problematic, since it depends on the antibody tested, and given the appropriate antibody almost any external residue may be part of an epitope. Thus, a better definition of an epitope should be proposed to increase the prediction accuracy.
Epitope prediction can be used in different contexts in either testing or screening modes. In the testing model, one has a candidate epitope and is using prediction to test its probability. Screening can be important to validate targets for vaccines or interventions [50]. While the total accuracy of the current models is not high enough for screening, the top 1% results of CALIBER have an accuracy of 0.73 for conformational epitopes, suggesting that the vast majority of the top scores positions of CALIBER are in epitopes.
CONCLUSIONS
We have shown here that a similar prediction model can be developed for both linear and nonlinear B cell epitopes. This is based on three main elements that were each tested separately in the past: A) a learned representation of the AAs, B) a Recurrent Neural Network to learn the relation between following AA, and C) a prediction on each residue whether it belongs to an epitope, instead than a prediction on the entire epitope. These elements were combined to produce CALIBER a fast predictor for whether a given residue is part of an epitope.
Key Points
A BiLSTM with long-range interactions reaches better than the current SOTA prediction for linear and conformational epitopes.
The addition of biologically induced amino acid embeddings or distance between AA does not improve accuracy.
A first model is proposed that simultaneously predicts linear and conformational epitopes.
Supplementary Material
FUNDING
The work of Y.L. and S.I. was funded by ISF grant 870/20 and by a Vatat DSI grant.
Author Biographies
Sapir Israeli is a Ph.D. candidate in the Department of Mathematics at Bar Ilan University in Israel, earned dual bachelor's degrees in Computer Science and Neuroscience, and a master's degree in Computer Science. Her research integrates machine learning techniques with the study of Human Leukocyte Antigen (HLA) and its applications in Stem cell transplants.
Yoram Louzoun is a Professor of Mathematics at the Bar Ilan University in Israel. He has graduated from the Hebrew University in 2000 and continued to a post-doc in Princeton. In 2002, he started a position at Bar Ilan in the Mathematics department in 2002. He studies stochastic processes and machine learning, with a special focus on its application to immunology and microbiome. He has developed a set of algorithms to optimize Stem cell transplants, and machine learning algorithms to predict the host condition from his microbiome or from his T cell repertoire, as well as graph-based algorithms.
Contributor Information
Sapir Israeli, Department of Mathematics, Bar-Ilan University, Ramat Gan, Israel.
Yoram Louzoun, Department of Mathematics, Bar-Ilan University, Ramat Gan, Israel.
DATA AVAILABILITY STATEMENT
The original contributions presented in the study are publicly available. These data and CALIBER as a stand-alone code are available at https://github.com/louzounlab/epitope_b_cells_predictor and as a server at https://caliber.math.biu.ac.il.
References
- 1. Prechl J. A generalized quantitative antibody homeostasis model: regulation of b-cell development by bcr saturation and novel insights into bone marrow function. Clin Transl Immunol 2017;6(2):e130.1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Jespersen MC, Mahajan S, Peters B, et al.. Antibody specific b-cell epitope predictions: leveraging information from antibody-antigen protein complexes. Front Immunol 2019;10:298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Ratajczak W, Niedźwiedzka-Rystwej P, Tokarz-Deptuła B, Deptuła W. Immunological memory cells. Cent Eur J Immunol 2018;43(2):194–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Anthony Moody M, Haynes BF. Antigen-specific b cell detection reagents: use and quality control. Cytometry A 2008;73(11):1086–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Galanis KA, Nastou KC, Papandreou NC, et al.. Linear b-cell epitope prediction for in silico vaccine design: a performance review of methods available via command-line interface. Int J Mol Sci 2021;22(6):3210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Dudek NL, Perlmutter P, Aguilar I, et al.. Epitope discovery and their use in peptide based vaccines. Curr Pharm Des 2010;16(28):3149–57. [DOI] [PubMed] [Google Scholar]
- 7. Leinikki P, Lehtinen M, Hyöty H, et al.. Synthetic peptides as diagnostic tools in virology. Adv Virus Res 1993;42:149–86. [DOI] [PubMed] [Google Scholar]
- 8. Mucci J, Carmona SJ, Volcovich R, et al.. Next-generation elisa diagnostic assay for chagas disease based on the combination of short peptidic epitopes. PLoS Negl Trop Dis 2017;11(11) e0005972:1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Kozlova EEG, Cerf L, Schneider FS, et al.. Computational b-cell epitope identification and production of neutralizing murine antibodies against atroxlysin-i. Sci Rep 2018;8(1):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sanchez-Trincado JL, Gomez-Perosanz M, Reche PA, et al.. Fundamentals and methods for t-and b-cell epitope prediction. J Immunol Res 2017;2017:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Clifford JN, Høie MH, Deleuran S, et al.. Bepipred-3.0: improved b-cell epitope prediction using protein language models. Protein Sci 2022;31(12) e4497:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Kringelum JV, Lundegaard C, Lund O, Nielsen M. Reliable b cell epitope predictions: impacts of method development and improved benchmarking. PLoS Comput Biol 2012;8(12) e1002829:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Silva, Ascher DB, Pires DEV. epitope1d: accurate taxonomy-aware b-cell linear epitope prediction. Brief Bioinform 2023;24(3) bbad114:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Qi Y, Zheng P, Huang G. Deeplbcepred: a bi-lstm and multi-scale cnn-based deep learning method for predicting linear b-cell epitopes. Front Microbiol 2023;14(1117027):1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Alghamdi W, Attique M, Alzahrani E, et al.. Lbcepred: a machine learning model to predict linear b-cell epitopes. Brief Bioinform 2022;23(3) bbac035:1–11. [DOI] [PubMed] [Google Scholar]
- 16. Haodong X, Zhao Z. Netbce: an interpretable deep neural network for accurate prediction of linear b-cell epitopes. Genomics Proteomics Bioinformatics 2022;20(5):1002–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Pittala S, Bailey-Kellogg C. Learning context-aware structural representations to predict antigen and antibody binding interfaces. Bioinformatics 2020;36(13):3996–4003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Davila A, Zichang X, Li S, et al.. Abadapt: an adaptive approach to predicting antibody–antigen complex structures from sequence. Bioinformatics Advances 2022;2(1) vbac015:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Zichang X, Davila A, Wilamowski J, et al.. Improved antibody-specific epitope prediction using alphafold and abadapt. Chembiochem 2022;23(23) e202200303:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Tianyi Qiu L, Zhang ZC, Wang Y, et al.. Seppa-mab: spatial epitope prediction of protein antigens for mabs. Nucleic Acids Res 2023;51:W528–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Can H, Köseoğlu AE, Alak SE, et al.. In silico discovery of antigenic proteins and epitopes of sars-cov-2 for the development of a vaccine or a diagnostic approach for covid-19. Sci Rep 2020;10(1):22387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Zhang Shu, ZhengDequan, HuXinchen, YangMing. Bidirectional long short-term memory networks for relation classification. In Proceedings of the 29th Pacific Asia conference on language, information and computation. Institute of Linguistics, Academia Sinica, Taipei, Taiwan, R.O.C., 2015, pp. 73–78.
- 23. Jespersen MC, Peters B, Nielsen M, Marcatili P. Bepipred-2.0: improving sequence-based b-cell epitope prediction using conformational epitopes. Nucleic Acids Res 2017;45(W1):W24–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Zeng Y, Wei Z, Yuan Q, et al.. Identifying b-cell epitopes using alphafold2 predicted structures and pretrained language model. Bioinformatics 2023;39(4) btad187:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Collatz M, Mock F, Barth E, et al.. Epidope: a deep neural network for linear b-cell epitope prediction. Bioinformatics 2021;37(4):448–55. [DOI] [PubMed] [Google Scholar]
- 26. Lian Y, Ge M, Pan X-M. Epmlr: sequence-based linear b-cell epitope prediction method using multiple linear regression. BMC Bioinformatics 2014;15(1):1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Zhou C, Zikun Chen L, Zhang DY, et al.. Seppa 3.0–enhanced spatial epitope prediction enabling glycoprotein antigens. Nucleic Acids Res 2019;47(W1):W388–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Ponomarenko J, Bui H-H, Li W, et al.. Ellipro: a new structure-based tool for the prediction of antibody epitopes. BMC Bioinformatics 2008;9:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Liang S, Zheng D, Standley DM, et al.. Epsvr and epmeta: prediction of antigenic epitopes using support vector regression and multiple server results. BMC Bioinformatics 2010;11(1):1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rives A, Meier J, Sercu T, et al.. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc Natl Acad Sci 2021;118(15) e2016239118:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Jumper J, Evans R, Pritzel A et al.. Highly accurate protein structure prediction with alphafold. Nature, 596 (7873):583–9, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Gong L, Cheng Q. Exploiting edge features for graph neural networks. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. IEEE, Piscataway, NJ, 2019, pp. 9211–9.
- 33. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput 1997;9(8):1735–80. [DOI] [PubMed] [Google Scholar]
- 34. Vita R, Mahajan S, Overton JA, et al.. The immune epitope database (iedb): 2018 update. Nucleic Acids Res 2019;47(D1):D339–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Kringelum JV, Nielsen M, Padkjær SB, Lund O. Structural analysis of b-cell epitopes in antibody: protein complexes. Mol Immunol 2013;53(1–2):24–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Kidera A, Konishi Y, Oka M, et al.. Statistical analysis of the physical properties of the 20 naturally occurring amino acids. J Protein Chem 1985;4:23–55. [Google Scholar]
- 37. Reichmann ME, Rice SA, Thomas CA, Doty P. A further examination of the molecular weight and size of desoxypentose nucleic acid. J Am Chem Soc 1954;76(11):3047–53. [Google Scholar]
- 38. Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J Mol Biol 1982;157(1):105–32. [DOI] [PubMed] [Google Scholar]
-
39.
Chou PY, Fasman GD. Conformational parameters for amino acids in helical,
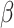 -sheet, and random coil regions calculated from proteins. Biochemistry 1974;13(2):211–22.
[DOI] [PubMed] [Google Scholar]
-sheet, and random coil regions calculated from proteins. Biochemistry 1974;13(2):211–22.
[DOI] [PubMed] [Google Scholar] - 40. Lobry JR, Gautier C. Hydrophobicity, expressivity and aromaticity are the major trends of amino-acid usage in 999 escherichia coli chromosome-encoded genes. Nucleic Acids Res 1994;22(15):3174–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Kunchur Guruprasad BV, Reddy B, Pandit MW. Correlation between stability of a protein and its dipeptide composition: a novel approach for predicting in vivo stability of a protein from its primary sequence. Protein Eng Des Sel 1990;4(2):155–61. [DOI] [PubMed] [Google Scholar]
- 42. Parks GA. Aqueous surface chemistry of oxides and complex oxide minerals: Isoelectric point and zero point of charge. ACS Publications, Washington, D.C, U.S, 1967. [Google Scholar]
- 43. Gill SC, Von Hippel PH. Calculation of protein extinction coefficients from amino acid sequence data. Anal Biochem 1989;182(2):319–26. [DOI] [PubMed] [Google Scholar]
- 44. Hsu C, Verkuil R, Liu J, et al.. Learning inverse folding from millions of predicted structures. In:International Conference on Machine Learning. PMLR, 2022, 8946–70. [Google Scholar]
- 45. Høie MH, Kiehl EN, Petersen B, et al.. Netsurfp-3.0: accurate and fast prediction of protein structural features by protein language models and deep learning. Nucleic Acids Res 2022;50(W1):W510–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Nair Vinod, HintonGeoffrey E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th international conference on machine learning (ICML-10). Omnipress, Madison, WI, US, 2010, pp. 807–814.
- 47. Klausen MS, Anderson MV, Jespersen MC, et al.. Lyra, a webserver for lymphocyte receptor structural modeling. Nucleic Acids Res 2015;43(W1):W349–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Moreira B, Silva YC, Myung DB, Ascher, and Douglas EV Pires.. epitope3d: a machine learning method for conformational b-cell epitope prediction. Brief Bioinform 2022;23(1, bbab423):1–8. [DOI] [PubMed] [Google Scholar]
- 49. Deng C, Ji X, Rainey C, et al.. Integrating machine learning with human knowledge. Iscience 2020;23(11):101656–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Rawal K, Sinha R, Abbasi BA, et al.. Identification of vaccine targets in pathogens and design of a vaccine using computational approaches. Sci Rep 2021;11(1):17626. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The original contributions presented in the study are publicly available. These data and CALIBER as a stand-alone code are available at https://github.com/louzounlab/epitope_b_cells_predictor and as a server at https://caliber.math.biu.ac.il.