Abstract
Dielectric constant is an important property which is widely utilized in many scientific fields and characterizes the degree of polarization of substances under the external electric field. In this work, a structure–property relationship of the dielectric constants (ε) for a diverse set of polymers was investigated. A transparent mechanistic model was developed with the application of a machine learning approach that combines genetic algorithm and multiple linear regression analysis, to obtain a mechanistically explainable and transparent model. Based on the evaluation conducted using various validation criteria, four- and eight-variable models were proposed. The best model showed a high predictive performance for training and test sets, with R2 values of 0.905 and 0.812, respectively. Obtained statistical performance results and selected descriptors in the best models were analyzed and discussed. With the validation procedures applied, the models were proven to have a good predictive ability and robustness for further applications in polymer permittivity prediction.
Keywords: dielectric permittivity, polarization, polymers, descriptors, models, machine learning
Introduction
Polymeric properties related to electrical conductivity are useful in many applications, such as cable insulation,1 capsules for electrical components, interlayer dielectrics, charge-storage capacitors,2,3 and printed circuit boards.4 Dielectric permittivity is an important value that is widely used and characterizes the degree of polarization of substances under the action of an external electric field. A larger dielectric constant means a larger polarization of the medium between the two charges. Therefore, the dielectric constant is the ability of a substance to separate the charge or orient its molecular dipoles in an external electric field. The dielectric constant is an important basic molecular property that can also be a useful predictor of other electrical properties of polymers.4–6 However, the exact experimental values of the dielectric constant for polymers are often unavailable. The prediction of dielectric constants computationally and by using theoretical approaches, such as machine learning predictive modeling, is important in the molecular design of new polymeric materials with the desired properties. The rapid and accurate implementation of predictions for a wide variety of chemical structures can significantly improve the performance and speed of phenomena investigation. However, the theoretical calculation of the property, such as dielectric constant of the polymer is not an easy problem, because this property is a nonlinear property and, therefore, a function of several factors, including polymer structure and composition, temperature, materials morphology, additives and plasticizers, impurities, and moisture in the volume of the polymer. A quantitative structure–activity/property relationship (QSAR/QSPR) is a subsection of machine learning (ML) modeling and chemical informatics for revealing relationships between chemical structures of molecules and their activity. QSAR modeling is a suitable approach for estimating the properties of polymers based on numerical features/descriptors derived from the molecular structure to fit the experimental data.7–9 The main idea of the QSAR approach is that the change in the desired property of a compound can be correlated with the structure-based properties that numerically expressed and called “molecular descriptors”.8–11 In cheminformatics, molecular descriptors are numbers that formally represent a molecule, obtained by a well-defined algorithm and applied to a well-defined experimental procedure. In other words, a molecular descriptor is the result of a mathematical expression that converts the chemical structure to a numerical value.12 Each molecular descriptor describes a molecular structure by encoding a part of the structure or a whole molecular structure. Molecular descriptors play a fundamental role in the development of QSPR models. One of the main features of the QSPR approach is that it requires only knowledge of the chemical structure and is independent of any experimental properties. Once a correlation is found, it can be applied to predict the properties of new compounds/materials that have not been synthesized previously or not found. Therefore, the QSPR approach can accelerate the development of new molecules and materials with the required properties. Using the QSPR approach, many different properties of polymers can be determined with a sufficient accuracy, in particular, this approach is already used to determine, such properties as a refractive index,4,13–21 glass transition temperature,14,22–33 cohesive energy,34 thermal decomposition temperature,35 solubility parameter,36 as well as fouling release properties.37 Several QSPR models for the dielectric constants of small organic molecules have also been reported in the literature.6,38–41 But the number of attempts to predict the dielectric constants of polymers was rather small.4,42 Liu et al.42 introduced a model with a correlation coefficient of (R2) 0.908 and a standard error (s) of 0.001 for 22 polyalkenes using three descriptors, but the values of ε in this case cover only the range from 2.154 to 2.165. Bicerano4 developed a QSPR model with (R2) 0.958 and (s) 0.087 to correlate ε with 32 topological and constitutional descriptors for 61 polymers. This model is good but contains too many descriptors. High correlation and randomness of correlations may be partly due to increased number of descriptors in the model and use a whole dataset as a trainig set. Moreover, the two models were not validated externally using a test set. In fact, validation is a crucial aspect of any QSPR/QSAR modeling.43
The purpose of this study was to develop a reliable predictive QSPR model that could effectively be used to predict dielectric constant values with mechanistically explainable descriptors for further design applications. The model is developed using a set of 71 polymers with a large structural diversity, with further model validation applying specific validation approaches and an external set.
Materials and Methods
Data Set
The experimental data (polymers 1–56) were taken from the source that published by Bicerano,4 the remaining data (polymers 57–71) from the source published by Ku and Liepins,5 at room temperature (298 K). In total, the data set for this study consists of 71 polymers with diverse structures (see Table 1). The data set contains polymers of the following types: polyvinyls, polyethylenes, polyoxides, polystyrenes, polyethers, polysulfones, polyacrylnitrile, polyamides, polyacrylates, poly siloxanes, polyxylylenes, and polycarbonates.
Table 1. Set of Experimental and Predicted Dielectric Constant Data for the Polymers Involved in the Experiment.
|
Equation 1. |
Equation 2. |
||||||
|---|---|---|---|---|---|---|---|
| no | name | data set status | Exp. | Pred. | residual | pred. | residual |
| 1 | poly(1,4-butadiene) | train. | 2.51 | 2.4104 | –0.0996 | 2.6006 | 0.0906 |
| 2 | poly[oxy(2,6-dimethyl-1,4-phenylene)] | train. | 2.6 | 2.9651 | 0.3651 | 2.7210 | 0.1210 |
| 3 | bisphenol-A polycarbonate | train. | 2.9 | 3.0325 | 0.1325 | 2.8725 | –0.0275 |
| 4 | poly(ether ketone) | train. | 3.2 | 3.0998 | –0.1002 | 3.0820 | –0.1180 |
| 5 | poly(ethylene terephthalate) | train. | 3.25 | 3.1291 | –0.1209 | 3.0958 | –0.1542 |
| 6 | poly(chloro-p-xylylene) | train. | 2.95 | 2.8054 | –0.1446 | 2.7932 | –0.1568 |
| 7 | polyacrylonitrile | train. | 4 | 3.6164 | –0.3836 | 3.9567 | –0.0433 |
| 8 | polystyrene | train. | 2.55 | 2.4631 | –0.0869 | 2.3794 | –0.1706 |
| 9 | polypropylene | train. | 2.2 | 2.3304 | 0.1304 | 2.3763 | 0.1763 |
| 10 | poly(p-xylylene) | train. | 2.65 | 2.4154 | –0.2346 | 2.3772 | –0.2728 |
| 11 | polyisobutylene | train. | 2.23 | 2.1490 | –0.0810 | 2.2123 | –0.0177 |
| 12 | poly(p-chloro styrene) | train. | 2.65 | 2.8016 | 0.1516 | 2.7449 | 0.0949 |
| 13 | poly(N-vinyl carbazole) | train. | 2.9 | 2.9390 | 0.0390 | 2.7868 | –0.1132 |
| 14 | poly(vinyl cyclohexane) | train. | 2.25 | 2.3931 | 0.1431 | 2.1312 | –0.1188 |
| 15 | polyisoprene | test | 2.37 | 2.2119 | –0.1581 | 2.4058 | 0.0358 |
| 16 | poly(p-hydroxybenzoate) | train. | 3.28 | 3.1280 | –0.1520 | 3.1413 | –0.1387 |
| 17 | poly(vinyl butyral) | train. | 2.69 | 2.9227 | 0.2327 | 3.0580 | 0.3680 |
| 18 | poly(cyclohexyl methacrylate) | train. | 2.58 | 2.9625 | 0.3825 | 2.7652 | 0.1852 |
| 19 | poly(vinyl acetate) | train. | 3.25 | 2.9128 | –0.3372 | 3.1751 | –0.0749 |
| 20 | poly(e-caprolactam) | train. | 3.5 | 3.5411 | 0.0411 | 3.4218 | –0.0782 |
| 21 | poly(3,4-dichlorostyrene) | test | 2.94 | 2.7643 | –0.1757 | 2.9000 | –0.0400 |
| 22 | poly(hexamethylene adipamide) | train. | 3.5 | 3.5852 | 0.0852 | 3.5226 | 0.0226 |
| 23 | poly(hexamethylene sebacamide) | test | 3.2 | 3.5443 | 0.3443 | 3.3880 | 0.1880 |
| 24 | poly(isobutyl methacrylate) | train. | 2.7 | 2.8675 | 0.1675 | 2.7456 | 0.0456 |
| 25 | poly(vinyl chloride) | train. | 2.95 | 3.1896 | 0.2396 | 2.9759 | 0.0259 |
| 26 | poly(m-chloro styrene) | train. | 2.8 | 2.6153 | –0.1847 | 2.8629 | 0.0629 |
| 27 | polychlorotrifluoroethylene | test | 2.6 | 2.1061 | –0.4939 | 2.2365 | –0.3635 |
| 28 | poly(ethyl methacrylate) | train. | 3 | 2.8124 | –0.1876 | 2.8927 | –0.1073 |
| 29 | poly(n-butyl methacrylate) | test | 2.82 | 2.9877 | 0.1677 | 2.9430 | 0.1230 |
| 30 | poly(methyl methacrylate) | train. | 3.1 | 2.8846 | –0.2154 | 2.8868 | –0.2132 |
| 31 | poly[2,2′-(m-phenylene)-5,5′-bibenzimidazole] | train. | 3.3 | 3.3864 | 0.0864 | 3.4484 | 0.1484 |
| 32 | polyethylene | test | 2.3 | 2.4908 | 0.1908 | 2.3596 | 0.0596 |
| 33 | poly(a-vinyl naphthalene) | test | 2.6 | 2.4277 | –0.1723 | 2.4579 | –0.1421 |
| 34 | poly(tetramethylene terephthalate) | train. | 3.1 | 3.2794 | 0.1794 | 3.1749 | 0.0749 |
| 35 | poly[thio(p-phenylene)] | train. | 3.1 | 3.4506 | 0.3506 | 3.2558 | 0.1558 |
| 36 | poly(4-methyl-1-pentene) | train. | 2.13 | 2.1958 | 0.0658 | 2.2527 | 0.1227 |
| 37 | poly(1-butene) | train. | 2.27 | 2.3378 | 0.0678 | 2.4632 | 0.1932 |
| 38 | poly(a,a,a′,a′-tetrafluoro-p-xylylene) | train. | 2.35 | 2.4386 | 0.0886 | 2.4448 | 0.0948 |
| 39 | poly(o-methylstyrene) | train. | 2.49 | 2.4046 | –0.0854 | 2.4385 | –0.0515 |
| 40 | poly(b-vinyl naphthalene) | train. | 2.51 | 2.4622 | –0.0478 | 2.5002 | –0.0098 |
| 41 | poly(a-methylstyrene) | test | 2.57 | 2.4189 | –0.1511 | 2.3614 | –0.2086 |
| 42 | poly[oxy(2,6-diphenyl-1,4-phenylene)] | train. | 2.8 | 2.8875 | 0.0875 | 2.9843 | 0.1843 |
| 43 | poly(vinylidene chloride) | train. | 2.85 | 2.9919 | 0.1419 | 2.7289 | –0.1211 |
| 44 | poly(p-methoxy-o-chloro styrene) | train. | 3.08 | 3.0777 | –0.0023 | 3.1591 | 0.0791 |
| 45 | poly(ethyl a-chloroacrylate) | test | 3.1 | 3.1639 | 0.0639 | 3.4555 | 0.3555 |
| 46 | poly(methyl a-chloroacrylate) | train. | 3.4 | 3.2357 | –0.1643 | 3.4685 | 0.0685 |
| 47 | poly(oxy-2,2-dichloromethyltrimethylene) | train. | 3 | 3.1478 | 0.1478 | 3.0166 | 0.0166 |
| 48 | Ultem 1000 | test | 3.15 | 3.4652 | 0.3152 | 3.3747 | 0.2247 |
| 49 | polyoxymethylene | train. | 3.1 | 2.9951 | –0.1049 | 3.0158 | –0.0842 |
| 50 | poly(1,4-cyclohexylidene dimethylene terephthalate) | train. | 3 | 3.1045 | 0.1045 | 3.0271 | 0.0271 |
| 51 | poly[N,N′-(p,p′-oxidiphenylene)pyromellitimide] | train. | 3.5 | 3.5482 | 0.0482 | 3.5032 | 0.0032 |
| 52 | poly[4,4′-diphenoxy di(4-phenylene)sulfone] | train. | 3.44 | 3.3943 | –0.0457 | 3.4010 | –0.0390 |
| 53 | poly[4,4′-isopropylidene diphenoxy di(4-phenylene)sulfone] | test | 3.18 | 3.3082 | 0.1282 | 3.4309 | 0.2509 |
| 54 | poly[4,4′-sulfone diphenoxy di(4-phenylene)sulfone] | train. | 3.8 | 3.5963 | –0.2037 | 3.6851 | –0.1149 |
| 55 | poly[1,1-cyclohexane bis(4-phenyl)carbonate] | test | 2.6 | 3.0918 | 0.4918 | 3.0117 | 0.4117 |
| 56 | poly[1,1-ethane bis(4-phenyl)carbonate] | train. | 2.9 | 3.0499 | 0.1499 | 2.9578 | 0.0578 |
| 57 | poly(cellulose propionate) | train. | 3.2 | 3.1174 | –0.0826 | 3.4035 | 0.2035 |
| 58 | poly(amide-imide) | train. | 3.32 | 3.4811 | 0.1611 | 3.3832 | 0.0632 |
| 59 | poly(diallyl phthalate) | train. | 3.57 | 3.2808 | –0.2892 | 3.3366 | –0.2334 |
| 60 | poly(diallyl phenyl phosphonate) | train. | 3.84 | 3.6409 | –0.1991 | 3.7696 | –0.0704 |
| 61 | poly(2,5-dichlorostyrene) | train. | 2.61 | 2.7786 | 0.1686 | 2.8859 | 0.2759 |
| 62 | polyfumaronitrile | excl. | 8.5 | ||||
| 63 | poly(methyl cellulose) | excl. | 6.8 | ||||
| 64 | Nylon-11 | train. | 3.3 | 3.3744 | 0.0744 | 3.3483 | 0.0483 |
| 65 | Nylon-12 | train. | 3.6 | 3.3392 | –0.2608 | 3.3367 | –0.2633 |
| 66 | poly(vinyl fluoride) | excl. | 8.5 | ||||
| 67 | poly(2-vinylpyridine) | excl. | 4.64 | ||||
| 68 | poly(vinyl toluene) | train. | 2.59 | 2.4524 | –0.1376 | 2.4418 | –0.1482 |
| 69 | poly(vinylidene fluoride) | excl. | 8.4 | ||||
| 70 | poly(dichloro-p-xylylene) | test | 2.82 | 2.9745 | 0.1545 | 2.8109 | –0.0091 |
| 71 | poly(methyl-p-xylylene) | train. | 2.48 | 2.3989 | –0.0811 | 2.4105 | –0.0695 |
Computational Details
In this work, the structures of all polymers were computationally optimized and used for generating structural properties/features/descriptors calculation. Because polymers are macromolecules with a large size and wide chain length distribution, the calculation of structural descriptors based on original structural formulas was not possible using current descriptor-generating software.23,30 Moreover, due to the high molecular weight of the polymers, the effect of the terminal groups on the overall structure of polymer is quite small, which allows us to neglect the contribution of the terminal structure contribution. In this regard, the structures of repeating monomer units of investigated polymers were used to calculate the structural features/descriptors (as shown in Figure 1).13,15,22–24,30 We assumed that the main contributing factor to the polymer property is the structure of monomer units and, therefore, the molecular descriptors are calculated based on the structure of repeating monomer units.44,45
Figure 1.
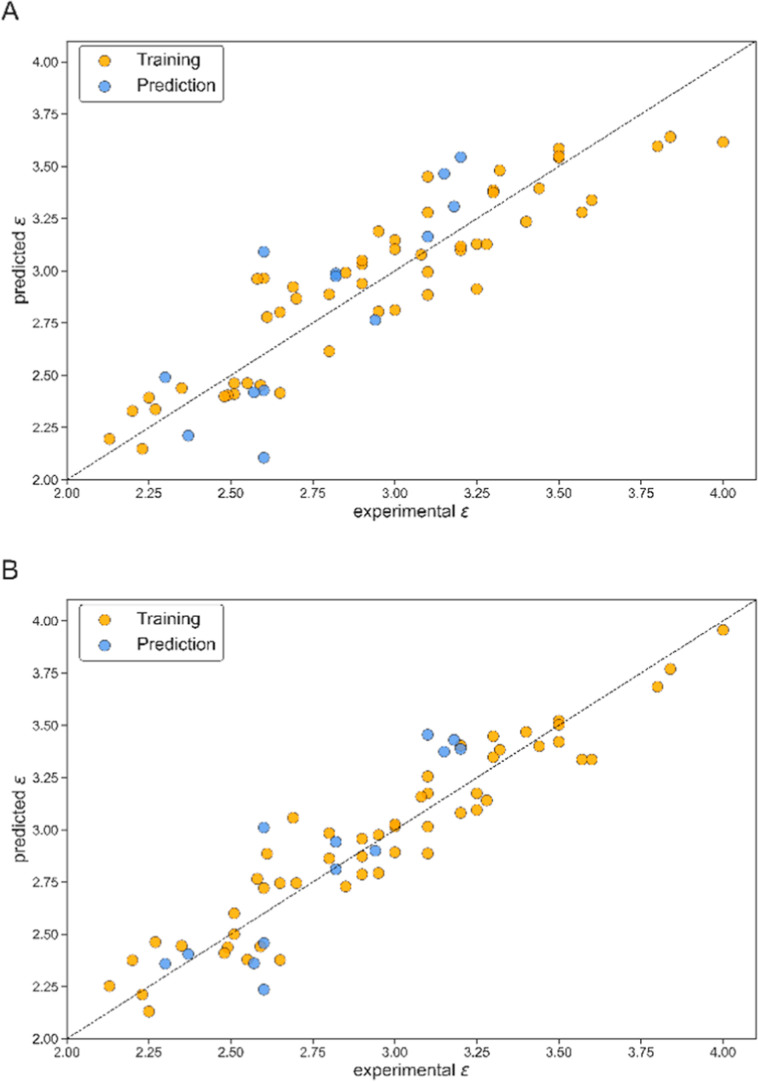
Plots of experimental and predicted values of the dielectric constants for the entire data set. Yellow dots are the training set, and blue dots are the test set (A—for eq 1.; B—for eq 2).
The molecular structures of each polymer were drawn in ChemSketch software.46 The optimization of monomeric units, i.e., geometry optimization and finding the minimal energy conformation, is an important step and provides a real conformation of the investigated structure for further QSAR modeling. Molecular modeling is often used for optimization and property assessment of various chemical systems.47–50 In this work, the geometry optimization was carried out using HyperChem software, applying molecular mechanics force-field MM+.51 The criterion for the energy optimization limit was chosen as the achieved gradient of 0.01 kcal/mol. The molecular descriptors for each polymer were calculated based on minimal energy conformation using DRAGON software.52 Dragon 6.0 allows one to generate about 5000 descriptors per structure.52 The generated descriptors include the following categories: constitutional indices, 2D and 3D matrix-based descriptors, 2D autocorrelations, topological descriptors, indicator descriptors, connectivity indexes, information indices, atom-centered fragments, charge-based descriptors, 0D, 2D, and 3D descriptors, molecular properties, and so on.12 Descriptors with high correlations, single variables, and noninformative information were discarded based on the constant value, near constant (R > 0.95), and pair correlation criteria (R > 0.7).
A total of 523 descriptors of different types were selected from about 5000 descriptors after the initial filter criteria applied. Each descriptor represents a molecular graph invariant, describes the particular property, and overall adds to chemical diversity of the monomeric unit.
The model development was performed by QSARINS software54,55 with the following setup to find the best model. For the genetic algorithm (GA)-based variable selection step, the number of generations was set to 2000 and a mutation rate of 35% was used. For the best models’ selection, the population size of the final models’ list was set to 20. For validation purposes, multiple methods were applied, including leave-one-out (LOO) cross validation, y-scrambling, as well as internal and external validation protocols. After validation techniques were applied, the best model was chosen based on multiple criteria: (1) high statistical performance of R2 and Q2 variables (including R2 – Q2 < 0.3);43 (2) a low number of variables in the model; (3) low cross-correlation between descriptors in the selected model; and (4) best performance of R2 for the external validation set (test set) to avoid model overfitting.43
Results and Discussion
In this work, a data set of 71 polymers was used to develop a quantitative structure–permittivity relationship model. For the model validation, the set was split into training and test sets consisting of 57 (80%) and 14 (20%) polymers, respectively. The splitting was performed with care to ensure that at least one compound of each structural class in the training set was represented in the test set. After genetic algorithm combined with multiple linear regression analysis (GA-MLRA) computation iterations, the best models were found. After a first round of GA-MLRA it was found that five compounds are outliers, with a high prediction value error. The outliers are 62, 63, 66, 67, and 69. After elimination of outliers, the GA-MLRA iteration was repeated. The set with a total of 66 components was split into training and test sets containing 53 (80%) and 13 (20%) polymers, respectively. In the process of finding the best model, several options were selected that best correlate with the dielectric constants of the selected polymers. Two models with four and eight variables are proposed, the statistical characteristics of which are given in Table 2.
Table 2. Statistical Characteristics of the Four- and Eight-Variable Models.
| model | no. of descriptors | Rtrain2 | Radj2 | s | F | Q2 | Rtest2 |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 0.842 | 0.829 | 0.187 | 64.124 | 0.813 | 0.715 |
| 2 | 8 | 0.905 | 0.888 | 0.151 | 52.542 | 0.865 | 0.812 |
The following equations represent the proposed models with four (1) and eight (2) variables
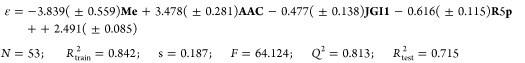 |
1 |
 |
2 |
The four-variable model shows a good performance, with Rtrain2 = 0.842 and Rtest2 = 0.715. A graphical representation of the model for the training and test sets is given in Figure 1A. Compared to the 4-variable model, the eight-variable model shows better Rtrain2 and Q2 performance values for the training set, smaller standard deviation s, and better predictive performance due to higher Rtest2 for the test set, 0.812. In comparison to the four-variable model, the 8-variable model has a larger number of variables, which can lead to some level of overfitting, but still very robust. A graphical representation of the model for the training and test sets is presented in Figure 1B.
Both equations: (1) and (2) show satisfactory statistical results that confirm the robustness of these models. However, considering the combined productivity for both training and test sets, the second model provides a better performance.
Descriptor selection was performed by applying a variable selection GA algorithm, followed by the MLRA approach together with a cross-validation LOO procedure. Based on the size of the data set and the correlation coefficients of the training and test sets (Rtrain2 and Rtest2), the significance criterion F and the standard errors, the number of descriptors in the final QSPR model was determined.
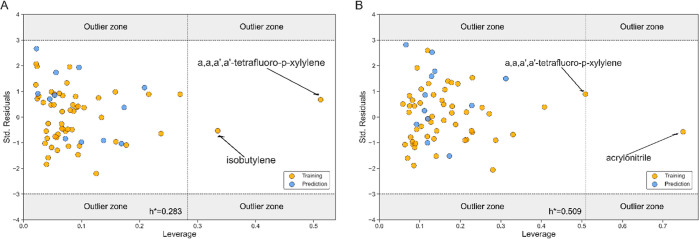
A very important step in the model's robustness is to check the applicability domain (AD). Predictions of compounds can be considered reliable only if the dataset’s chemical space of applicability is within the predictive chemical space of the developed model, before the model can be applied for further predictions. The AD check was performed by application of leverage approach, i.e., William’s plot evaluation for the final models. All data points were within the three standardized residues (±3σ) and within the HAT index, where h* is the critical value of leverage h. If the errors of estimation would exceed the values of the standardized residues, then the predicted values could go out of the AD and give inaccurate predictions as they go beyond reasonable extrapolation. If the value of h of the resulted data is higher than h*, then they are considered as structurally significant contributors to the model.53
As can be seen in the Williams plots (Figure 2) for both equations, in the first model (A) there are only two polymers, and in the second (B) only one polymer has values h higher than h*. However, these polymers have low residual values, which means that the model is stable enough to make reliable predictions for all polymers structurally similar to the ones in the data set.
Figure 2.
Williams plots for eq 1. (A) and eq 2. (B): yellow balls—training set; blue balls —test set.
The obtained models contain the following descriptors: Me—mean atomic Sanderson electronegativity (scaled on carbon atom); AAC—mean information index on atomic composition; R5p+—R maximal autocorrelation of lag 5/weighted by polarizability; JGI1—mean topological charge index of order 1; GATS 1p—Geary autocorrelation of lag 1 weighted by polarizability; Mor22v—signal 22/weighted by van der Waals volume; RARS—R matrix average row sum; ESpm11u—Spectral moment 11 from edge adj. matrix; R1v+—R maximal autocorrelation of lag 1/weighted by van der Waals volume; and nCt—number of total tertiary C(sp3).
More information about these descriptors can be found in the Dragon software user’s guide12,52 and the references therein.
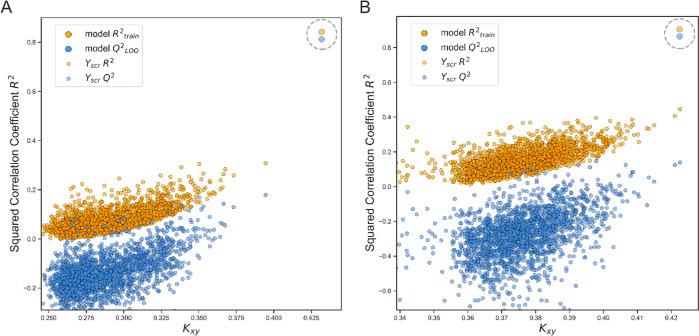
As a rule, the value of coefficient F indicates the ability of the model to predict the value of the properties in the training set. The large F ratio values in both eqs (64.124 and 52.542 for the first and second, respectively) indicate that both equations do an excellent job with predicting ε values. Each equation has an adjusted value of Radj2 0.829 and 0.888, which denotes a very good correspondence between correlation and data variation. The cross-validated correlation coefficient (Q2 for eq 1 is equal to 0.813 and Q2 for eq 2 is eqiual ro 0.865) demonstrates the robustness of the models. The model was further validated by using a y-randomization test. The obtained R2Yscr against the correlation coefficient between the original and shuffled data is shown in Figure 3. It can be seen from Figure 3 that the original models are not due to random correlations; since values of R2Yscr are significantly low. It is worth noting that model 1 (eq 1) showed much stronger robustness at the y-scrambling test than model 2 (eq 2), while both models are quite strong. The calculated results of the values of ε from eqs 1 and 2 for the training and test sets are shown in Table 1 and Figure 1.
Figure 3.
Y-scrambling plots of selected 4-descriptor eq 1 (A) and 8-descriptor eq 2 (B) models.
Based on the model selection procedure described earlier, the relative contribution of descriptors to the respective models was determined and shown in Figure 4. The descriptors involved in the model are having the reducing contribution to the model in the following order: for eq 1: Me > AAC > R5p+ > JGI1 and for eq 2: Me > AAC > RARS > R1v+ > GATS1p > ESpm11u > Mor22v > nCt.
Figure 4.
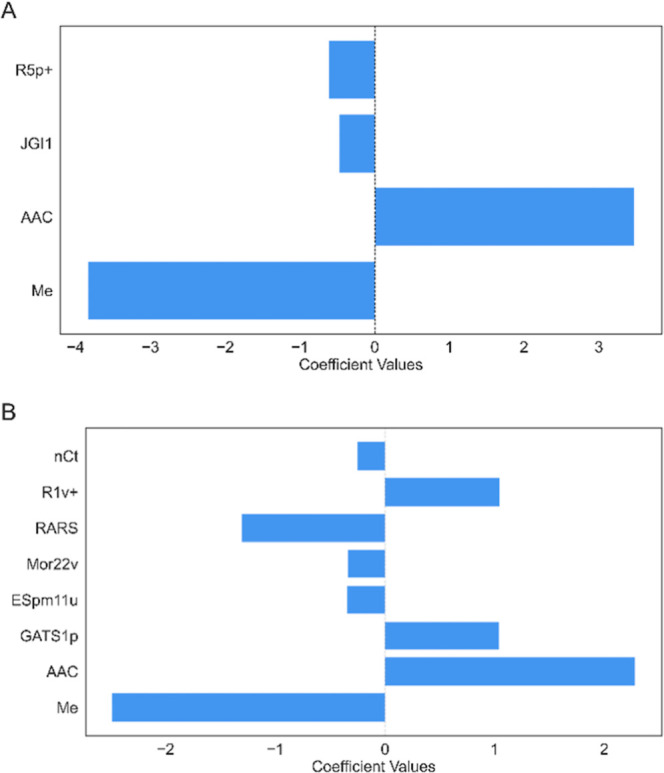
One of the most important descriptors involved in both equations is the AAC information index. This descriptor contains information about each atom in a molecule by its own atom type, its bond type, and the atom types of its first neighbors. AAC is a measure of atomic composition associated with molecular complexity. When a molecule is larger and its elemental composition is more complex, the value of the descriptor increases. The positive value of this descriptor indicates that polymers with a more complex structure and, accordingly, with a larger value for this descriptor would have larger values of ε. Another descriptor, ESpm11u, is based on the use of bond distances as weights in the diagonal entries of the edge matrix.
It is worth noting that the presented QSPR models can be a good simple way to predict the permittivity of homopolymers. These models can be improved further in future studies by improving the dataset size and variety of polymers. We believe that the results of this study will pave the way for future steps in investigating the electrical conductivity mechanism of polymeric materials.
Conclusions
In this work, a machine learning-based structure–property relationship model for dielectric constants (ε) based on a diverse set of polymers is developed. A transparent model was obtained with application of the GA-MLRA approach, to get a mechanistically explainable model. This work represents two QSPR models developed based on descriptors computed from monomeric polymer structures. The reliability of the models was validated using several verification methods. The best overall performance is achieved by a four- and eight-descriptor QSAR models, with R2 values of 0.842/0.715 and 0.905/0.812 for training/test sets, respectively, per each model. The models are suitable for further development of polymers with desired dielectric constants based on chemical structure information of monomers.
Acknowledgments
A.K. and B.R. thank the Department of Coatings and Polymeric Materials at North Dakota State University (NDSU) for providing the Lowell Wood funding. M.E. and B.R. acknowledge the support from the North Dakota Established Program to Stimulate Competitive Research (ND EPSCoR award #IIA-1355466) through the New Faculty Award. This work used resources of the Center for Computationally Assisted Science and Technology (CCAST) at North Dakota State University, which were made possible in part by National Science Foundation (NSF) MRI award no. 2019077. The authors thank Prof. Paola Gramatica for generously providing a free license for the QSARINS software. This work was financially supported by the National Science Centre under the NanoCARRIERS project (2021/40/Q/ST5/00117).
Author Contributions
CRediT: Yevhenii Zhuravskyi data curation, formal analysis, validation, writing-original draft; Anas Karuth data curation, formal analysis, writing-original draft; Maqsud N. Sayfiyev visualization, writing-review & editing; Dilshod A. Ziyaev resources, software, writing-review & editing; Zulayho Smanova writing-review & editing; Alicja Mikolajczyk conceptualization, methodology, visualization, writing-original draft, writing-review & editing.
The authors declare no competing financial interest.
Special Issue
Published as part of ACS Materials Auvirtual special issue “2023 Rising Stars”.
References
- Huang X.; Jiang P. Core-Shell Structured High-k Polymer Nanocomposites for Energy Storage and Dielectric Applications. Adv. Mater. 2015, 27 (3), 546–554. 10.1002/adma.201401310. [DOI] [PubMed] [Google Scholar]
- Rao Y.; Wong C. P. Material characterization of a high-dielectric-constant polymer–ceramic composite for embedded capacitor for RF applications. Appl. Polym. Sci. 2004, 92 (4), 2228–2231. 10.1002/app.13690. [DOI] [Google Scholar]
- Dang Z. M.; Yuan J. K.; Yao S. H.; Liao R.; Zhou T.; Li S. T.; Huang W.; Xie C.; Chen P.; Lin Y. Flexible Nanodielectric Materials with High Permittivity for Power Energy Storage. Adv. Mater. 2013, 25 (44), 6334–6365. 10.1002/adma.201301752. [DOI] [PubMed] [Google Scholar]
- Bicerano J.Prediction of Polymer Properties; Marcel Dekker: New York, 1996. [Google Scholar]
- Ku C. C.; Liepins R.. Electrical Properties of Polymers; Chemical Principles; Hanser: Munich, 1987. [Google Scholar]
- Hougham G.; Tesoro G.; Viehbeck A. Influence of Free Volume Change on the Relative Permittivity and Refractive Index in Fluoropolyimides. Macromolecules 1996, 29, 3453–3456. 10.1021/ma9503423. [DOI] [Google Scholar]
- Schweitzer R. C.; Morris J. B. Improved Quantitative Structure Property Relationships for the Prediction of Dielectric Constants for a Set of Diverse Compounds by Subsetting of the Data Set. J. Chem. Inf. Comput. Sci. 2000, 40, 1253–1261. 10.1021/ci0000070. [DOI] [PubMed] [Google Scholar]
- Devillers J.; Balaban A. T.. Topological Indices and Related Descriptors in QSAR and QSPR; Gordon & Breach: The Netherlands, 1999. [Google Scholar]
- Karelson M.Molecular Descriptors in QSAR/QSPR; Wiley Online Library: New York, 2000. [Google Scholar]
- Yao X. J.; Wang Y. W.; Zhang X. Y.; Zhang R. S.; Liu M. C.; Hu Z. D.; Fan B. T. Radial basis function neural network-based QSPR for the prediction of critical temperature. Chemom. Intell. Lab. Syst. 2002, 62, 217–225. 10.1016/S0169-7439(02)00017-5. [DOI] [Google Scholar]
- Xu J.; Guo B.; Chen B.; Zhang Q. A QSPR treatment for the thermal stabilities of second-order NLO chromophore molecules. J. Mol. Model. 2005, 12, 65–75. 10.1007/s00894-005-0006-x. [DOI] [PubMed] [Google Scholar]
- Todeschini R.; Consonni V.. Handbook of Molecular Descriptors; Wiley VCH: Weinheim, 2000. [Google Scholar]
- Katritzky A. R.; Sild S.; Karelson M. Correlation and Prediction of the Refractive Indices of Polymers by QSPR. J. Chem. Inf. Comput. Sci. 1998, 38, 1171–1176. 10.1021/ci980087w. [DOI] [Google Scholar]
- García-Domenech R.; de Julián-Ortiz J. V. Prediction of Indices of Refraction and Glass Transition Temperatures of Linear Polymers by Using Graph Theoretical Indices. J. Phys. Chem. B 2002, 106, 1501–1507. 10.1021/jp012360u. [DOI] [Google Scholar]
- Xu J.; Chen B.; Zhang Q.; Guo B. Prediction of refractive indices of linear polymers by a four-descriptor QSPR model. Polymer 2004, 45, 8651–8659. 10.1016/j.polymer.2004.10.057. [DOI] [Google Scholar]
- Yu X.; Yi B.; Wang X.; Zhang R. S.; Liu M. C.; Hu Z. D.; Fan B. T. Prediction of refractive index of vinyl polymers by using density functional theory. J. Comput. Chem. 2007, 28, 2336–2341. 10.1002/jcc.20752. [DOI] [PubMed] [Google Scholar]
- Gao J.; Xu J.; Chen B.; Zhang Q. A quantitative structure-property relationship study for refractive indices of conjugated polymers. J. Mol. Model. 2007, 13, 573–578. 10.1007/s00894-007-0180-0. [DOI] [PubMed] [Google Scholar]
- Xu J.; Liang H.; Chen B.; Xu W.; Shen X.; Liu H. Linear and nonlinear QSPR models to predict refractive indices of polymers from cyclic dimer structures. Chemom. Intell. Lab. Syst. 2008, 92, 152–156. 10.1016/j.chemolab.2008.02.006. [DOI] [Google Scholar]
- Jabeen F.; Chen M.; Rasulev B.; Ossowski M.; Boudjouk P. Refractive Indices of Diverse Data Set of Polymers: A Computational QSPR Based Study. Comput. Mater. Sci. 2017, 137, 215–224. 10.1016/j.commatsci.2017.05.022. [DOI] [Google Scholar]
- Erickson M. E.; Ngongang M.; Rasulev B. A Refractive Index Study of a Diverse Set of Polymeric Materials by QSPR with Quantum-Chemical and Additive Descriptors. Molecules 2020, 25 (17), 3772. 10.3390/molecules25173772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan M.; Rasulev B.; Roy K. QSPR Modeling of the Refractive Index for Diverse Polymers Using 2D Descriptors. ACS Omega 2018, 3 (10), 13374–13386. 10.1021/acsomega.8b01834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katritzky A. R.; Sild S.; Lobanov V. S.; Karelson M. Quantitative Structure–Property Relationship (QSPR) Correlation of Glass Transition Temperatures of High Molecular Weight Polymers. J. Chem. Inf. Comput. Sci. 1998, 38, 300–304. 10.1021/ci9700687. [DOI] [Google Scholar]
- Mattioni B. E.; Jurs P. C. Prediction of Glass Transition Temperatures from Monomer and Repeat Unit Structure Using Computational Neural Networks. J. Chem. Inf. Comput. Sci. 2002, 42, 232–240. 10.1021/ci010062o. [DOI] [PubMed] [Google Scholar]
- Cao C.; Lin Y. Correlation between the Glass Transition Temperatures and Repeating Unit Structure for High Molecular Weight Polymers. J. Chem. Inf. Comput. Sci. 2003, 43, 643–650. 10.1021/ci0202990. [DOI] [PubMed] [Google Scholar]
- Afantitis A.; Melagraki G.; Makridima K.; Alexandridis A.; Sarimveis H.; Iglessi-Markopoulou O. Prediction of high weight polymers glass transition temperature using RBF neural networks. J. Mol. Struct. 2005, 716, 193–198. 10.1016/j.theochem.2004.11.021. [DOI] [Google Scholar]
- Yu X.; Wang X.; Wang H.; Liu A.; Zhang C. Prediction of the glass transition temperatures of styrenic copolymers using a QSPR based on the DFT method. J. Mol. Struct. 2006, 766, 113–117. 10.1016/j.theochem.2006.04.018. [DOI] [Google Scholar]
- Yu X.; Yi B.; Wang X.; Xie Z. Correlation between the glass transition temperatures and multipole moments for polymers. Chem. Phys. 2007, 332, 115–118. 10.1016/j.chemphys.2006.11.029. [DOI] [Google Scholar]
- Bertinetto C.; Duce C.; Micheli A.; Solaro R.; Starita A.; Tiné M. R. Prediction of the glass transition temperature of (meth)acrylic polymers containing phenyl groups by recursive neural network. Polymer 2007, 48, 7121–7129. 10.1016/j.polymer.2007.09.043. [DOI] [Google Scholar]
- Duce C.; Micheli A.; Starita A.; Tiné M. R.; Solaro R. Prediction of the Glass Transition Temperature of Polymer Blends: A Quantitative Structure-property Relationship Approach. Macromol. Rapid Commun. 2006, 27, 711–715. 10.1002/marc.200600026. [DOI] [Google Scholar]
- Yu X. Support vector machine-based QSPR for the prediction of glass transition temperatures of polymers. Fibers Polym. 2010, 11, 757–766. 10.1007/s12221-010-0757-6. [DOI] [Google Scholar]
- Chen M.; Jabeen F.; Rasulev B.; Ossowski M.; Boudjouk P. A Computational Structure-property Relationship Study of Glass Transition Temperatures for a Diverse Set of Polymers. J. Polym. Sci., Part B: Polym. Phys. 2018, 56, 877–885. 10.1002/polb.24602. [DOI] [Google Scholar]
- Petrosyan L. S.; Sizochenko N.; Leszczynski J.; Rasulev B. Modeling of Glass Transition Temperatures for Polymeric Coating Materials: Application of QSPR Mixture-based Approach. Mol. Inf. 2019, 38 (8–9), 1800150. 10.1002/minf.201800150. [DOI] [PubMed] [Google Scholar]
- Karuth A.; Alesadi A.; Xia W.; Rasulev B. Predicting glass transition of amorphous polymers by application of cheminformatics and molecular dynamics simulations. Polymer 2021, 218, 123495. 10.1016/j.polymer.2021.123495. [DOI] [Google Scholar]
- Xu J.; Chen B.; Liang H.; Xu W.; Cui W. QSPR Models for the Prediction of Cohesive Energy of Alkanes. Polimery 2009, 54, 19. [Google Scholar]
- Ajloo D.; Sharifian A.; Behniafar H. Estimation of Thermal Decomposition Activation Energy for Important Organic Compounds Using QSPR Modeling. Bull. Korean Chem. Soc. 2008, 31, 2009. [Google Scholar]
- Yu X.; Wang X.; Wang H.; Li X.; Gao J. Prediction of Solubility Parameters for Polymers by a QSPR Model. QSAR Comb. Sci. 2006, 25, 156–161. 10.1002/qsar.200530138. [DOI] [Google Scholar]
- Rasulev B.; Jabeen F. J.; Stafslien S.; Chisholm B. J.; Bahr J.; Ossowski M.; Boudjouk P. Polymer Coating Materials and Their Fouling Release Activity: A Cheminformatics Approach to Predict Properties. ACS Appl. Mater. Interfaces 2017, 9 (2), 1781–1792. 10.1021/acsami.6b12766. [DOI] [PubMed] [Google Scholar]
- Cocchi M.; De Benedetti P. G.; Seeber R.; Tassi L.; Ulrici A. Modeling and Prediction by Principal Properties Indexes: 1. Calculation of Dielectric Constant. J. Chem. Inf. Comput. Sci. 1999, 39, 1190–1203. 10.1021/ci9903298. [DOI] [Google Scholar]
- Schweitzer R. C.; Morris J. B. The development of a quantitative structure property relationship (QSPR) for the prediction of dielectric constants using neural networks. Anal. Chim. Acta 1999, 384, 285–303. 10.1016/s0003-2670(98)00781-8. [DOI] [Google Scholar]
- Sild S.; Karelson M. A General QSPR Treatment for Dielectric Constants of Organic Compounds. J. Chem. Inf. Comput. Sci. 2002, 42, 360–367. 10.1021/ci010335f. [DOI] [PubMed] [Google Scholar]
- Liu J. P.; Wilding W. V.; Giles N. F.; Rowley R. L. A Quantitative Structure Property Relation Correlation of the Dielectric Constant for Organic Chemicals. J. Chem. Eng. Data 2010, 55, 41–45. 10.1021/je900518k. [DOI] [Google Scholar]
- Liu A.; Wang X.; Wang L.; Wang H.; Wang H. Prediction of dielectric constants and glass transition temperatures of polymers by quantitative structure property relationships. Eur. Polym. J. 2007, 43, 989–995. 10.1016/j.eurpolymj.2006.12.029. [DOI] [Google Scholar]
- Golbraikh A.; Tropsha A. Beware of q2!. J. Mol. Graph. Model. 2002, 20, 269–276. 10.1016/S1093-3263(01)00123-1. [DOI] [PubMed] [Google Scholar]
- Sun L.; Zhou L.; Yu Y.; Lan Y.; Li Z. QSPR Study of Polychlorinated Diphenyl Ethers by Molecular Electronegativity Distance Vector (MEDV-4). Chemosphere 2007, 66, 1039–1051. 10.1016/j.chemosphere.2006.07.013. [DOI] [PubMed] [Google Scholar]
- Marrero-Ponce Y. Total and Local (Atom and Atom Type) Molecular Quadratic Indices: Significance Interpretation, Comparison to Other Molecular Descriptors, and QSPR/QSAR Applications. Bioorg. Med. Chem. 2004, 12, 6351–6369. 10.1016/j.bmc.2004.09.034. [DOI] [PubMed] [Google Scholar]
- ACD . Advanced Chemistry Development; ChemSketch, 2014. [Google Scholar]
- Turabekova M. A.; Rasulev B. F.; Dzhakhangirov F. N.; Leszczynska D.; Leszczynski J. Aconitum and Delphinium Alkaloids of Curare-Like Activity. QSAR Analysis and Molecular Docking of Alkaloids into AChBP. Eur. J. Med. Chem. 2010, 45 (9), 3885–3894. 10.1016/j.ejmech.2010.05.042. [DOI] [PubMed] [Google Scholar]
- Juretic D.; Kusic H.; Dionysiou D. D.; Rasulev B.; Loncaric Bozic A. Modeling of Photooxidative Degradation of Aromatics in Water Matrix; Combination of Mechanistic and Structural-Relationship Approach. Chem. Eng. J. 2014, 257, 229–241. 10.1016/j.cej.2014.07.053. [DOI] [Google Scholar]
- Han Y.; Meng Q.; Rasulev B.; May P. S.; Berry M. T.; Kilin D. S. Photofragmentation of the Gas-Phase Lanthanum Isopropylcyclopentadienyl Complex: Computational Modeling vs Experiment. J. Phys. Chem. A 2015, 119 (44), 10838–10848. 10.1021/acs.jpca.5b07209. [DOI] [PubMed] [Google Scholar]
- Rasulev B. F.; Kušić H.; Leszczynska D.; Leszczynski J.; Koprivanac N. QSAR modeling of acute toxicity on mammals caused by aromatic compounds: the case study using oral LD50 for rats. J. Environ. Monit. 2010, 12 (5), 1037–1044. 10.1039/b919489d. [DOI] [PubMed] [Google Scholar]
- Hypercube . HyperChem for Windows. Release Version 8.0.7, 2014.
- Todeschini R.; Consonni V.; Mauri A.; Pavan M.. DRAGON-Software for the Calculation of Molecular Descriptors. Web Version 3; DRAGON, 2004.
- Gramatica P. Principles of QSAR Modeling: Comments and Suggestions from Personal Experience. Int. J. Quant. Struct. Relationships 2020, 5, 61–97. [Google Scholar]
- Gramatica P.; Cassani S.; Chirico N. QSARINS-Chem: Insubria datasets and new QSAR/QSPR models for environmental pollutants in QSARINS. J. Comput. Chem. 2014, 35, 1036–1044. [DOI] [PubMed] [Google Scholar]
- Gharagheizi F.; Eslamimanesh A.; Ilani-Kashkouli P.; Mohammadi A. H.; Richon D. QSPR molecular approach for representation/prediction of very large vapor pressure dataset. Chem. Eng. Sci. 2012, 76, 99–107. 10.1016/j.ces.2012.03.033. [DOI] [Google Scholar]