Abstract
This paper introduces a deconvolution-based method to enhance the elevation resolution of a linear array-based three-dimensional (3D) photoacoustic (PA) imaging system. PA imaging combines the high contrast of optical imaging with the deep, multi-centimeter spatial resolution of ultrasound (US) imaging, providing structural and functional information about biological tissues. Linear array-based 3D PA imaging is easily accessible and applicable for ex vivo studies, small animal research, and clinical applications in humans. However, its elevation resolution is limited by the acoustic lens geometry, which establishes a single elevation focus. Previous work used synthetic aperture focusing (SAF) to enhance elevation resolution, but the resolution achievable by SAF is constrained by the size of the elevation focus. Here, we introduce the application of Richardson-Lucy deconvolution, grounded in simulated point-spread-functions, to surpass the elevation resolution attainable with SAF alone. We validated this approach using both simulation and experimental data, demonstrating that the full-width-at-half-maximum of point targets on the elevation plane was reduced compared to using SAF only, suggesting resolution improvement. This method shows promise for improving 3D image quality of existing linear array-based PA imaging systems, offering potential benefits for disease diagnosis and monitoring.
1. Introduction
In recent decades, photoacoustic (PA) imaging has garnered increasing attention as a noninvasive hybrid imaging modality that combines the high contrast of optical properties and the high spatial resolution of ultrasound (US) imaging [1–3]. In PA imaging, a laser beam induces thermoelastic expansion in biological tissues, converting laser energy into ultrasonic waves that are recorded and used for image reconstruction [4]. Employing nonionizing radiation (both acoustic and optical), PA imaging is safe for animal and human use within regulatory laser energy limits, offering functional insights through chromophore detection like deoxy/oxy-hemoglobin. Various contrast agents have been developed for PA imaging, such as biocompatible dyes, plasmonic nanoparticles, carbon nanotubes, organic nanoparticles, and microbubbles [5–7], each with unique energy conversion mechanisms. For example, bio-compatible dyes convert light to acoustic energy through fluorescence. Plasmonic nanoparticles absorb light energy through the plasmon resonance effect, where free charges on the surface of plasmonic nanoparticles resonate with light. Disease-specific contrast agents, like prostate-specific membrane antigens (PSMA)-specific PA contrast agents [8–11], highlight PA imaging’s potential in targeted diagnostics. Compared to limited-depth optical imaging modalities, such as confocal microscopy and optical coherence tomography, PA imaging, particularly with near-infrared laser excitation, provides superior spatial resolution in multi-centimeter imaging depth due to ultrasonic wave’s weak scattering. Among many PA imaging system configurations, linear array-based PA imaging using commercially available handheld linear array US transducers is an economical option and makes PA imaging more readily available for clinical applications [12]. The only FDA-approved commercial PA system (Imagio, Seno Medical, USA) for clinical applications so far is equipped with a linear array transducer. However, the arbitrary orientation of 2D image acquisition complicates consistent region of interest (ROI) imaging, which is vital in monitoring. Also, volumetric ROI is visualized mentally based on continuously acquired 2D images. As a result, diagnosis relies heavily on clinician expertise [13]. Mechanically scanning the linear array US transducer in the elevation direction facilitates 3D PA imaging [14–15]. However, it was observed that the elevation resolution of the 3D PA image is worse than the resolution on the lateral plane since only fixed focusing was applied on the elevation plane due to the acoustic lens. It is worth mentioning that simply reducing the elevation motion step size will not improve the elevation resolution.
Several methods have been proposed to enhance the elevation resolution in linear array-based PA imaging systems [16]. Approaches involving multiple translation scans [17–21] exhibit substantial improvement in elevation resolution but are limited by slow scanning speeds. Modifying the transducer array presents another effective method [22], though it may incur additional costs and complicates the clinical approval process. An alternative strategy employs synthetic aperture focusing (SAF) in combination with various image reconstruction algorithms to enhance elevation resolution [23–27]. While these methods may not achieve the same level of resolution enhancement as those involving multiple scans or transducer modifications (as SAF's elevation resolution is constrained by the size of the elevation focus [16]), they offer the advantage of fast data acquisition and do not necessitate transducer modification, making them more suitable for clinical applications.
Deconvolution-based methods are widely used to enhance image resolution across various imaging modalities [28–30]. Among these, Richardson-Lucy (R-L) deconvolution is noteworthy for its iterative approach that leverages the known point spread function (PSF) of the imaging system to improve resolution [31–32]. Compared to other deconvolution techniques, such as Fourier transform-based deconvolution, R-L deconvolution is superior in image restoration. This method has been effectively employed to enhance in-plane resolution in ring-shape array-based PA tomography by precisely measuring PSFs across the imaging field of view [33]. While acquiring PSFs in some PA imaging systems presents challenges, the blind deconvolution (BD) method based on R-L deconvolution [34] has proven effective in enhancing resolution across various PA imaging modalities, including PA computed tomography [35–36] and PA microscopy [37], and super-resolution photoacoustic imaging [38–39]. However, as of yet, R-L deconvolution and its counterparts have not been applied in linear array-based 3D PA imaging systems to improve elevation resolution. Ideally, PSF of the linear array-based 3D PA imaging system would be obtained without experimentation, allowing for the direct application of R-L deconvolution for optimal results. Fortunately, the progress in PA imaging simulation technology now allows for the accurate computational determination of PSFs, paving the way for new applications of R-L deconvolution in enhancing 3D PA imaging.
In this paper, we simulated the linear array-based PA imaging system and used point targets to obtain PSFs based on SAF results. The R-L deconvolution method was subsequently applied to surpass the elevation resolution attainable with SAF alone. The proposed deconvolution-based method was first validated using simulation data, ensuing the method’s theoretical efficacy. Wethen extended our validation to experimental data. The experimental imaging subjects included a fishing wire phantom, chosen for its simplicity and suitability for resolution assessment, and ex vivo pork liver, selected to demonstrate the method’s applicability to biological tissues. The results show that the proposed method attains superior elevation resolution compared to the SAF method alone. This advancement promises to enhance the capabilities of linear array-based PA imaging systems, potentially leading to more accurate and detailed imaging in clinical settings.
2. Methods
2.1. Elevation synthetic aperture focusing
To overcome the challenge of poor elevation resolution in linear array-based 3D PA imaging system, the SAF technique was applied along the elevation direction [26]. For conventional linear array-based 3D PA imaging, the US transducer is linearly actuated with a fixed step size. A 3D volume is formed by stacking 2D images beamformed with respect to the lateral plane. SAF applies another stage on beamforming on the elevation plane to enhance both elevation resolution and signal-to-noise ratio (SNR). In SAF, the focal point of the acoustic lens in the ultrasound transducer is treated as a virtual source as shown in Fig. 1. SAF achieves the enlargement of the receive aperture by synthesizing the received RF data in relevant sub-apertures with appropriate delays. Considering as the beamformed RF data on the lateral plane at step n in the elevation motion, with a total of steps, slices of are synthesized on the elevation plane using delay-and-sum (DAS). The synthesized RF data, denoted as , is formulated in Eq. (1).
| (1) |
where and are physical locations of a particular pixel i in the axial direction and the elevation direction, respectively. The time delay between the location of pixel i and the virtual source in the elevation location is denoted as , being computed as
| (2) |
where F is the elevation focal depth, c is the speed of sound.
Fig. 1.
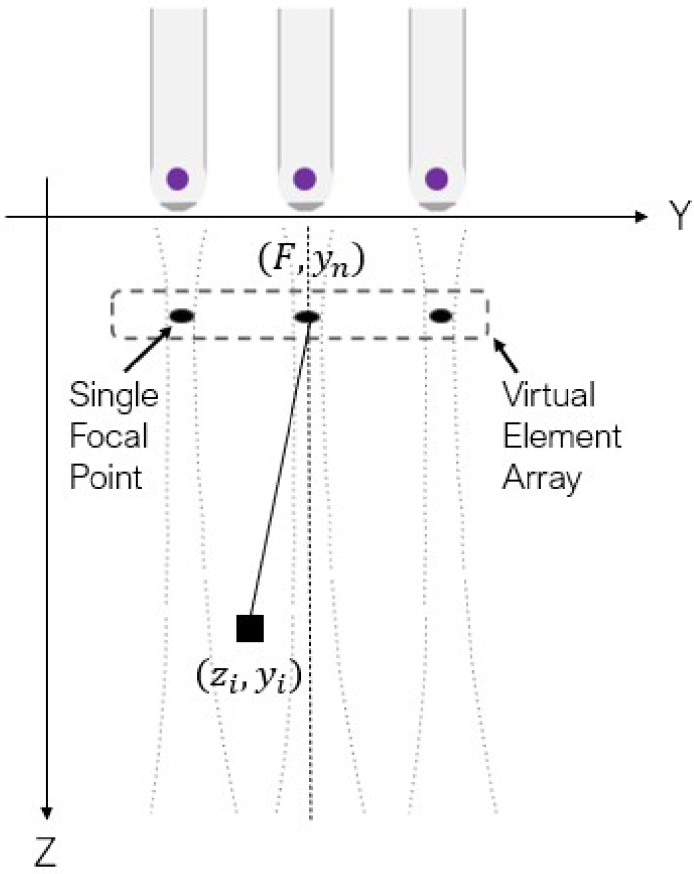
Synthetic aperture focusing on the elevation plane applied onto the linear array-based 3D photoacoustic imaging framework.
2.2. Richardson-Lucy (R-L) deconvolution
The probability that a pixel has a certain intensity can be modeled using a Poisson probability mass function,
| (3) |
where k is the pixel intensity, is the probability that a given pixel has an intensity of k. stands for the mean pixel intensity in the photoacoustic image. Then the statistics of the entire image can be modelled as
| (4) |
where is 2D image data on the elevation plane obtained by an imaging device, is the 2D image uncorrupted by noise and is the joint probabilities of all pixels. The objective of deconvolution is to find the which maximizes . Taking logarithms on both sides’ of (4) yields
| (5) |
In a linear, shift-invariant imaging system, the image without noise can be modeled as the convolution between the unblurred image without noise and of the imaging system.
| (6) |
where is two-dimensional convolution. The objective of R-L deconvolution is to maximize , which is essentially maximizing . A loss function can be derived by combining the above equations with the logarithmic of the total probability and adding a negative sign. Minimizing loss function is equivalent to maximizing ,
| (7) |
where is a convex function which guarantees to have a minimum (here the product and natural logarithm are elementwise). The optimization can be done using gradient descent, with the gradient of computed as
| (8) |
| (9) |
where is a matrix of ones. In Eq. (8) the division is elementwise. A minimum of can be found in an iterative way by updating O (and therefore ) in each iteration, where is the rate of gradient descent.
| (10) |
| (11) |
2.3. Linear array-based PA imaging system
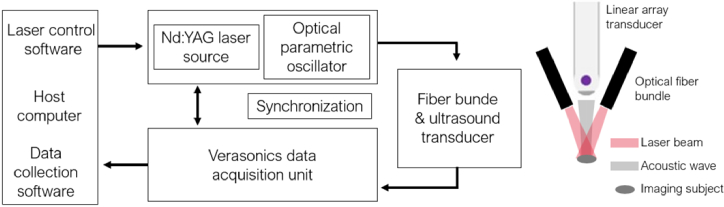
The linear array-based PA imaging system we implemented (Fig. 2) includes a linear array ultrasound transducer (L22_14vX LF, Verasonics, USA) with an 18 MHz central frequency, and a dual-head optical fiber bundle (01140-REVC, CeramOptec, USA) with a 22 mm length line output. A Q-switched Nd:YAG laser (Q-smart 450, Quantel, USA) outputted pulsed laser at 20 Hz, and an optical parametric oscillator (MagicPRISM, Opotek, USA) was used to modulate the laser wavelength. An US imaging research platform (Vantage 128, Verasonics, USA) was used to acquire PA signals with a maximum sampling frequency of 62.5 MHz. A linear actuator (VT-80, Physik Instrumente, Germany) was used for elevation linear motion with 0.8 µm unidirectional repeatability.
Fig. 2.
Schematic of linear array-based 3D photoacoustic imaging system.
2.4. Elevation PSF simulation and simulation validation
A simulation was carried out using the k-Wave MATLAB simulation package [40] to model the elevation PSF of the PA imaging system. A model of the L22_14vX LF transducer was set up, and its specifications are summarized in Table 1. The grid size was 1750 (axial) by 10 (lateral) by 500 (elevation) with a spatial step size of 20 µm in all directions, resulting in a maximum supported photoacoustic frequency of 37 MHz. Perfectly matched layers (PMLs) of 10 grid point thick were placed on edges along the lateral and axial directions, and 15 grid points thick were posed on edges along the elevation direction. Only one element is used to receive PA signals to minimize the grid size. Point targets were placed at five different depths in the center of elevation scan range. PA signals of 18 MHz were repeated for five cycles in each emission with a source strength of 5 MPa. The sampling frequency of the simulation was 248 MHz. The original simulation data was downsampled, and the sampling frequency became 62.5 MHz to match with the actual imaging system. A water medium is assumed for wave propagation whose physical properties [41] are summarized in Table 2. The step size of elevation movement is 0.1 mm, with a scanning range of 10 mm. The lab desktop used for simulation had an AMD Ryzen 3970x 32-core 64-thread processor, 128 GB RAM, and an Nvidia TITAN RTX GPU with 24 GB of memory. Computation in k-Wave was accelerated by the GPU and the entire simulation took 25 hours.
Table 1. L22_14vX LF transducer parameters.
| Central frequency [MHz] | 18 |
|---|---|
| Number of elements | 128 |
| Element width [mm] | 0.08 |
| Element length [mm] | 1.6 |
| Elevation focal depth [mm] | 20 |
Table 2. Assumed acoustic and optical properties of water.
| Sound speed [m/s] | 1480 |
|---|---|
| Density [kg/m3] | 1000 |
| [dB/(cmMHzb)] | 0.0021 |
| b | 2.0 |
| B/A | 4.98 |
Data were synthesized on the elevation plane using DAS-based SAF with an F-number of 2.0. After SAF, we sampled patches around five point targets as PSFs, and the elevation plane was divided into three regions: above the focal depth, at the focal depth, and below the focal depth. PSFs in each region are averaged to get a representative PSF. In R-L deconvolution, data were deconvoluted using PSFs from the corresponding regions. Results were evaluated using the full-width-at-half-maximum (FWHM) and signal-to-noise ratio (SNR).
2.5. Validation with experimental data
Experiments were carried out, including a fishing wire phantom and an ex vivo pork liver sample, to validate the proposed method. The black fishing wire has a diameter of 200 µm. Four wires were included in the phantom (arranged in a 2 by 2 grid) with an axial spacing of 5 mm and an elevation spacing of 10 mm. Pork liver was chosen for its hemoglobin richness, a common chromophore for PA imaging. The ex vivo pork liver sample was submerged in saline. In both experiments, subjects were imaged using the experimental setup with a 720 nm laser and an elevation motion step size of 0.1 mm. After stacking 2D images, PA data were firstly beamformed on the lateral plane using the beamforming function in k-Wave and then synthesized on the elevation plane using DAS-based SAF with a F-number of 2.0. Data were then deconvoluted using the simulated PSF below the focal depth. We employed 10 iterations in the R-L deconvolution process for both datasets. The computation time is approximately 0.2 seconds for each elevation frame. The wire phantom and the ex vivo dataset consist of 128 elevation frames to formulate a 3D volume, and thus the total computation time is approximately 26 seconds for each volumetric dataset. FWHM and SNR were used for image quality evaluation.
3. Results
3.1. Elevation PSF simulation
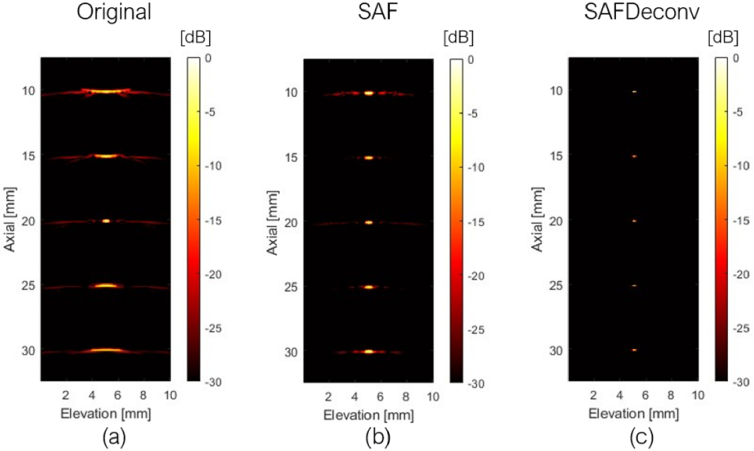
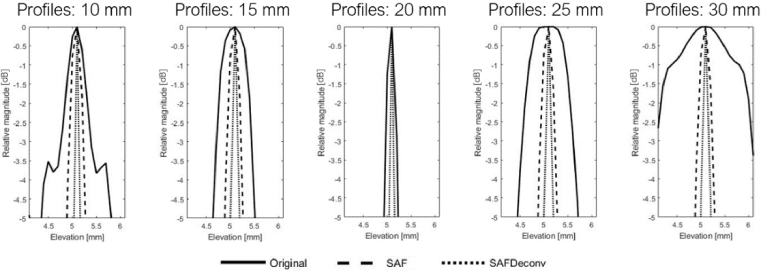
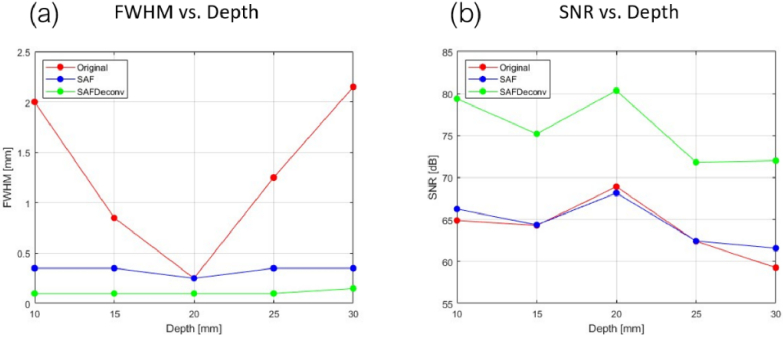
The original data on the elevation plane at the central lateral location of the linear array transducer are shown in Fig. 3 (a), data after applying SAF are shown in Fig. 3 (b), and results after applying R-L deconvolution to the SAF data (abbreviated as SAFDeconv) are shown in Fig. 3 (c). The corresponding PSF was used in R-L deconvolution at each depth, as shown in Fig. 4 (a-c). The beam profiles of five-point targets are plotted in Fig. 5. All point targets were used in the image quality evaluation. FWHM and SNR are computed, and the statistics are presented in Fig. 6. It was found that SAFDeconv achieved smaller FWHM values at all depths compared to SAF. It is worth noting that at 20 mm (the elevation focal depth), SAFDeconv brought improvement, while SAF did not make obvious changes to FWHM compared to the original data. In terms of SNR, SAFDeconv performed better than SAF at all depths.
Fig. 3.
Simulated images of point targets with linear motion along the elevation direction. (a) Data on the elevation plane at the central lateral location of the linear array transducer. (b) Data on the elevation plane focused with SAF. (c) Data on the elevation plane focused with SAF and enhanced with R-L deconvolution (SAFDeconv).
Fig. 4.
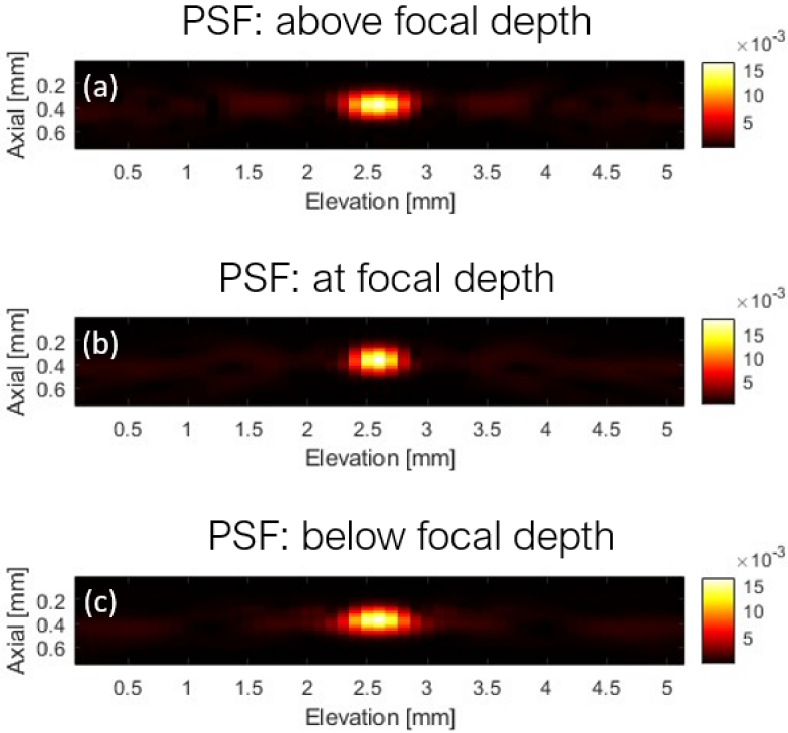
PSF sampled from Fig. 3 (b). (a) Averaged PSF of the region above the elevation focal depth. (b) Averaged PSF at the elevation focal depth. (c) Averaged PSF of the region below the elevation focal depth.
Fig. 5.
Beam profiles of point targets.
Fig. 6.
(a) FWHM variation versus depth. (b) SNR variation versus depth.
3.2. Wire phantom validation
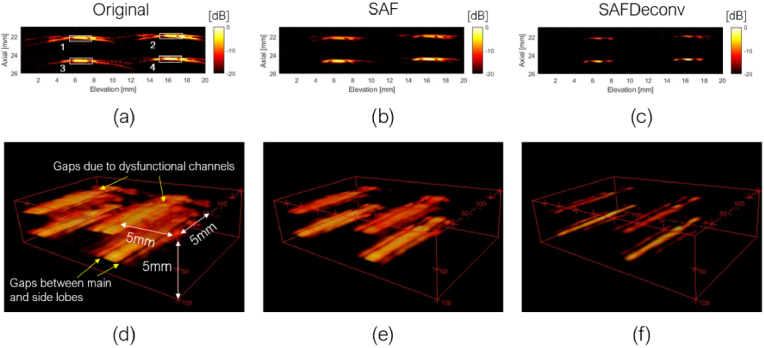
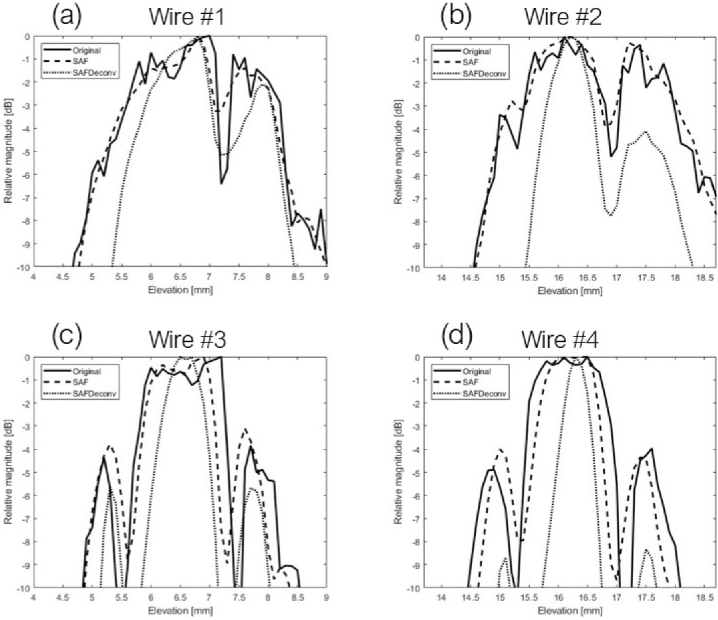
As the first part of the experimental validation of the proposed method, we collected data on a fishing wire phantom with wires oriented along the lateral direction of the linear array transducer. The original data on the elevation plane at the central lateral location of the linear array transducer are shown in Fig. 7 (a), data after applying SAF are shown in Fig. 7 (b), and SAFDeconv results are shown in Fig. 7 (c). The simulated PSF shown in Fig. 4(c) was used in R-L deconvolution. Figures 7 (d) - (f) show corresponding visualizations of volume data. Some gaps are visible in 3D visualization due to two reasons. First there were sidelobes apart from the main lobe in wire targets’ signal, as indicated by yellow arrows at the bottom of Fig. 7(d). Second there were some dysfunctional channels in our data acquisition platform, indicated by yellow arrows on the top of Fig. 7(d). The beam profiles of all wire targets (cross-section view) are plotted in Fig. 8. FWHM and SNR are presented in Table. 3. It is observed that SAFDeconv improved FWHM compared to SAF results. The SNR of SAFDeconv is also higher than SAF results.
Fig. 7.
3D photoacoustic image of fishing wire phantom. (a) Data on elevation plane at the central location of the linear array transducer. (b) Data on the elevation plane focused with SAF. (c) Data on the elevation plane with SAFDeconv. (d) – (e): 3D visualization of complete data corresponding to (a) – (c). (the dynamic range is [-20, 0] dB)
Fig. 8.
Beam profiles of wire phantoms (cross-sectional view).
Table 3. FWHM and SNR of all wire targets a .
| Mean (std) | Original | SAF | SAFDeconv |
|---|---|---|---|
| FWHM [mm] | 3.16 (±0.25) | 3.01 (±0.32) | 1.98 (±0.78) |
| SNR [dB] | 23.09 (±3.35) | 24.83 (±3.31) | 32.52 (±2.73) |
*Number out of parentheses is the mean value and the number in parentheses is the standard deviation.
3.3. Ex-vivo validation
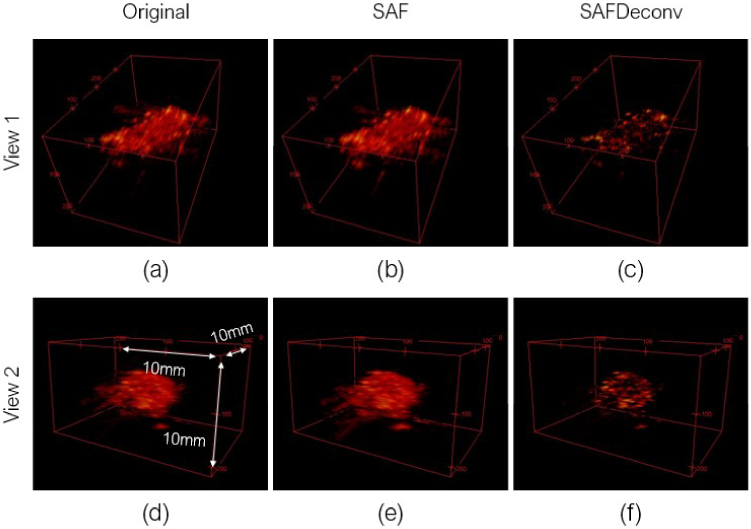
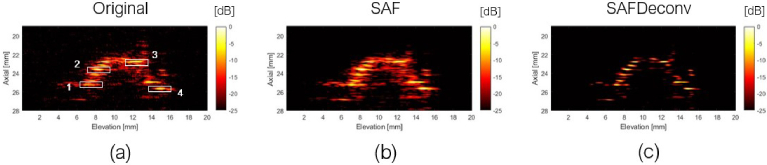
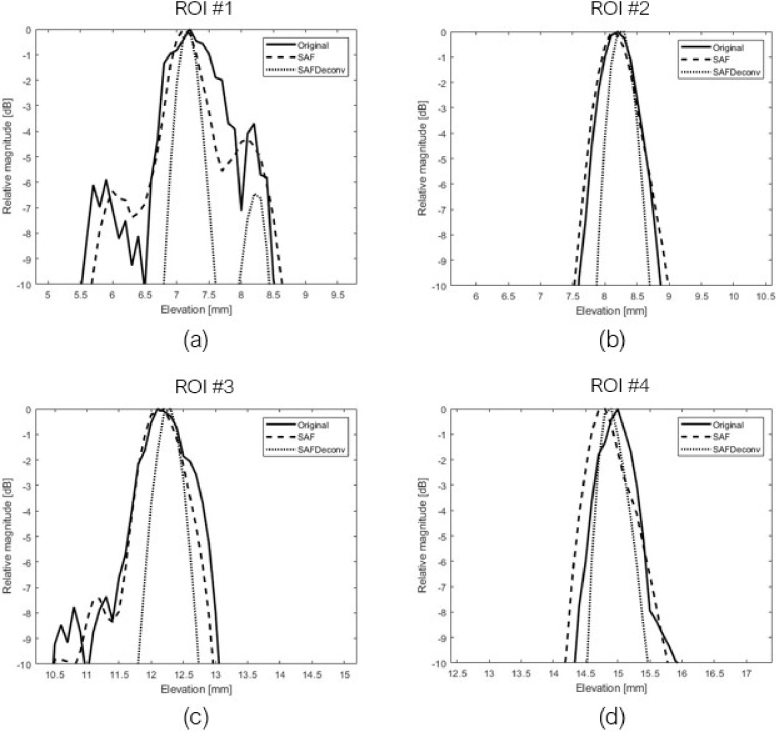
In the second part of experimental validation, a piece of pork liver was imaged, and data were used to validate the proposed deconvolution method. Two different views of 3D visualizations of the liver sample are shown in Fig. 9, and a cross-sectional view of the sample at the central lateral location of the linear array transducer was chosen for quantification, as shown in Fig. 10. The original data on the elevation plane on the central lateral location of the linear array transducer are shown in Fig. 10 (a), data after applying SAF are shown in Fig. 10 (b), and SAFDeconv results are shown in Fig. 10 (c). As with the wire phantom data, the simulated PSF in Fig. 4 (c) was used in R-L deconvolution. Four regions of interest (ROIs) with point-shape signals were selected for FWHM and SNR calculation, and their beam profiles are plotted in Fig. 11. FWHM and SNR of selected ROIs are presented in Table. 4. From the statistics, it is evident that SAFDeconv produced a smaller FWHM and a better SNR than SAF.
Fig. 9.
3D photoacoustic images of ex vivo pork liver sample in two visualization views. (a) Original photoacoustic data in view 1. (b) Data focused on elevation plane with SAF in view 1. (c) SAFDeconv results in view 1. (d) Original photoacoustic data in view 2. (e) Data focused on elevation plane with SAF in view 2. (f) SAFDeconv results in view 2. (the dynamic range is [-40, 0] dB)
Fig. 10.
Pork liver sample on elevation plane of central lateral location of the transducer and selected ROIs for quantification. (a) Original photoacoustic data. (b) Data focused on elevation plane with SAF. (c) SAFDeconv results.
Fig. 11.
Beam profiles of selected ROIs in pork liver data.
Table 4. FWHM and SNR of selected ROIs a .
| Mean (std) | Original | SAF | SAFDeconv |
|---|---|---|---|
| FWHM [mm] | 1.33 (±0.66) | 1.19 (±0.30) | 0.55 (±0.06) |
| SNR [dB] | 33.07 (2.66) | 38.61 (±1.73) | 42.95 (±2.06) |
*Number out of parentheses is the mean value and the number in parentheses is standard deviation.
4. Discussion
Our research confirms that the R-L deconvolution method using simulated PSFs improves image resolution on the elevation plane, surpassing the resolution limit of SAF method. The adaptability of this method to various PA imaging systems is facilitated by using simulated PSFs, allowing for straightforward translation to different types of linear array transducers by adjusting simulation parameters. The required simulation, which precedes application, is a one-time process that does not affect image acquisition time. Simulation in this work was completed in 25 hours, with time mainly relying on the grid size; ultrasound transducers with high central frequencies require larger grids and longer computation time. Given that the linear array transducer used in this work has a relatively high central frequency, simulations for transducers with lower central frequencies may be completed more quickly. Our method has potential applications beyond its current use, including enhancing the resolution of linear array-based 3D PA imaging system used in small animal studies [14], and optimizing handheld devices for human imaging [15]. Although using linear array-based 3D PA imaging for whole-body imaging of large animals or humans presents challenges, the principle of using a simulated PSF for R-L deconvolution can be extended to other PA imaging configurations, such as PA computed tomography and PA microscopy, to improve resolutions.
A limitation of our proposed method lies in the potential discrepancy between simulated and actual PA signals, affecting the efficacy of R-L deconvolution. In our study, applying R-L deconvolution to simulation data led to a 67% reduction in FWHM values compared to SAF data. However, for experimental data, the improvements were 34% and 54% for the wire phantom and the ex vivo pork liver samples, indicating a reduced effect. The discrepancy could be attributed to the differences between the simulated and actual PSF frequency spectra, influenced by factors by factors such as tissue and acoustic medium properties. Addressing this, collecting PA signals from various tissues, analyzing their frequency spectra, and incorporating them into simulations for case-specific PSFs could enhance accuracy. Another challenge is the using spatially-invariant PSFs for R-L deconvolution across the entire 3D volume. The limited number of transducer positions in practice can affect resolution of SAF results [25], particularly at the periphery of the elevation plane. With different PSFs in periphery regions, targets could suffer distortion after deconvolution. The PSF should be treated as a function of location rather than as a constant to eliminate any distortion from deconvolution results. Point targets should be more densely placed at edges of the elevation plane to capture PSF variation. Employing interpolation methods could then determine the optimal PSF for each location, especially at the edges. A more sophisticated method, such as establishing a model of the PSF as a function of location using principal component analysis [33,42], could offer further improvements by minimizing distortions in deconvolution results.
5. Conclusion
In this work, we introduced an elevation resolution enhancement method tailored for a linear array-based PA system, leveraging R-L deconvolution and simulated PSFs. Our method demonstrates superior resolution compared to the SAF method, as evidenced by both simulations and experimental validations. In the simulation results, we achieved a 67% improvement in FWHM over SAF results. Experimental validations further supported these findings, with FWHM enhancements of 34% in wire phantom results and 54% in ex vivo pork liver tests. These results indicate that our method could enhance elevation resolution beyond what is achievable with SAF alone. Such enhancements in resolution are expected to refine the localization and quantification of PA chromophores, offering benefits for disease diagnosis, follow-up evaluations, and the development of contrast agents.
Acknowledgement
This research work is supported by the National Institutes of Health under grants DP5OD028162, R01CA134675, R01DK133717, R01EB030539. Yixuan Wu is supported by the NIH Graduate Partnerships Program (GPP).
Funding
National Institutes of Health10.13039/100000002 (DP5OD028162, R01CA134675, R01DK133717, R01EB030539).
Disclosures
The authors declare no conflicts of interest.
Data Availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Xu M., Wang L. V., “Photoacoustic imaging in biomedicine,” Rev. Sci. Instrum. 77(4), 0411011-1 (2006). 10.1063/1.2195024 [DOI] [Google Scholar]
- 2.Baik J., Kim J., Cho S., et al. , “Super wide-field photoacoustic microscopy of animals and humans in vivo,” IEEE Trans. Med. Imaging 39(4), 975–984 (2020). 10.1109/TMI.2019.2938518 [DOI] [PubMed] [Google Scholar]
- 3.Wang L. V., Yao J., “A practical guide to photoacoustic tomography in life science,” Nat. Methods 13(8), 627–638 (2016). 10.1038/nmeth.3925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhou Y., Yao J., Wang L. V., “Tutorial on photoacoustic tomography,” J. Biomed. Opt. 21(6), 061007 (2016). 10.1117/1.JBO.21.6.061007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Luke G. P., Yeager D., Emelianov S. Y., “Biomedical applications of photoacoustic imaging with exogenous contrast agents,” Ann. Biomed. Eng. 40(2), 422–437 (2012). 10.1007/s10439-011-0449-4 [DOI] [PubMed] [Google Scholar]
- 6.Moon H., Kang J., Sim C., et al. , “Multifunctional theranostic contrast agent for photoacoustics- and ultrasound-based tumor diagnosis and ultrasound-stimulated local tumor therapy,” J. Controlled Release 218, 63–71 (2015). 10.1016/j.jconrel.2015.09.060 [DOI] [PubMed] [Google Scholar]
- 7.Ju K. Y., Kang J., Pyo J., et al. , “pH-Induced aggregated melanin nanoparticles for photoacoustic signal amplification,” Nanoscale 8(30), 14448–14456 (2016). 10.1039/C6NR02294D [DOI] [PubMed] [Google Scholar]
- 8.Zhang H. K., Chen Y., Kang J., et al. , “Prostate-specific membrane antigen-targeted photoacoustic imaging of prostate cancer in vivo,” J. Biophotonics 11(9), 1–6 (2018). 10.1002/jbio.201800021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lesniak W. G., Wu Y., Kang J., et al. , “Dual contrast agents for fluorescence and photoacoustic imaging: evaluation in murine model of prostate cancer,” Nanoscale 13(20), 9217–9228 (2021). 10.1039/D1NR00669J [DOI] [PubMed] [Google Scholar]
- 10.Wu Y., Kang J., Lesniak W. G., et al. , “Iterative fluence compensation and spectral unmixing for spectroscopic photoacoustic imaging,” Proc. IEEE Ultrason. Symp., Int. Symp. 1–4 (2021). [Google Scholar]
- 11.Wang Z., Tao W., Zhao H., “The optical inverse problem in quantitative photoacoustic tomography: a review,” Photonics 10(5), 487 (2023). 10.3390/photonics10050487 [DOI] [Google Scholar]
- 12.Beard P., “Biomedical photoacoustic imaging,” Interface Focus. 1(4), 602–631 (2011). 10.1098/rsfs.2011.0028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fenster A., Downey D. B., Cardinal H. N., “Three-dimensional ultrasound imaging,” Phys. Med. Biol. 46(5), R67–R99 (2001). 10.1088/0031-9155/46/5/201 [DOI] [PubMed] [Google Scholar]
- 14.Kim S., Chen Y., Luke G. P., et al. , “In vivo three-dimensional spectroscopic photoacoustic imaging for monitoring nanoparticle delivery,” Biomed. Opt. Express 2(9), 2540–2550 (2011). 10.1364/BOE.2.002540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee C., Choi W., Kim J., et al. , “Three-dimensional clinical handheld photoacoustic/ultrasound scanner,” Photoacoustic 18, 100173 (2020). 10.1016/j.pacs.2020.100173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang Y., Zhan Y., Tao M., et al. , “Review of methods to improve the performance of linear array-based photoacoustic tomography,” J. Innov. Opt. Health Sci. 13(02), 2030003 (2020). 10.1142/S1793545820300037 [DOI] [Google Scholar]
- 17.Gateau J., Caballero M. A., Dima A., et al. , “Three-dimensional optoacoustic tomography using a conventional ultrasound linear detector array: Whole-body tomographic system for small animals,” Med. Phys. 40(1), 013302 (2013). 10.1118/1.4770292 [DOI] [PubMed] [Google Scholar]
- 18.Gateau J., Gesnik M., Chassot J. M., et al. , “Single-sided access, isotropic resolution, and multispectral three-dimensional photoacoustic imaging with rotate-translate scanning of ultrasonic detector array,” J. Biomed. Opt. 20(05), 1 (2015). 10.1117/1.JBO.20.5.056004 [DOI] [PubMed] [Google Scholar]
- 19.Schwarz M., Buehler A., Ntziachristos V., “Isotropic high resolution optoacoustic imaging with linear detector arrays in bi-directional scanning,” J. Biophotonics 8(1-2), 60–70 (2015). 10.1002/jbio.201400021 [DOI] [PubMed] [Google Scholar]
- 20.Li G., Xia J., Li L., et al. , “Isotropic-resolution linear-array-based photoacoustic computed tomography through inverse Radon transform,” Proc. SPIE 9323, Photons Plus Ultrasound: Imaging and Sensing 2015, 93230I (2015). [Google Scholar]
- 21.Zhu L., Li L., Gao L., et al. , “Multiview optical resolution photoacoustic microscopy,” Optica 1(4), 217–222 (2014). 10.1364/OPTICA.1.000217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang Y., Wang D., Zhang Y., et al. , “Slit-enabled linear-array photoacoustic tomography with near isotropic spatial resolution in three dimensions,” Opt. Lett. 41(1), 127–130 (2016). 10.1364/OL.41.000127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang D., Wang Y., Zhou Y., et al. , “Coherent-weighted three-dimensional image reconstruction in linear-array-based photoacoustic tomography,” Biomed. Opt. Express 7(5), 1957–1965 (2016). 10.1364/BOE.7.001957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Alshaya A., Harput S., Cowell D. M. J., et al. , “Elevation resolution enhancement in 3D photoacoustic imaging using FDMAS beamforming,” 2017 IEEE International Ultrasonics Symposium (IUS), 1 (2017). [Google Scholar]
- 25.Nikolov S. I., Jensen J. A., “3D synthetic aperture imaging using a virtual source element in the elevation plane,” Proc. IEEE Ultrason. Symp., Int. Symp. 2, 1743–1747 (2000). 10.1109/ULTSYM.2000.921659 [DOI] [Google Scholar]
- 26.Yoon C., Kang J., Song T., et al. , “Elevational synthetic aperture focusing for three-dimensional photoacoustic imaging using a clinical one-dimensional array transducer,” IEEE Trans. Biomed. Eng. 69(9), 2817–2825 (2022). 10.1109/TBME.2022.3154754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Stepinski T., “Synthetic aperture focusing technique in ultrasound inspection of coarse grained materials,” Signals Syst., Uppsala Univ., Uppsala, Sweden, Swedish Nuclear Power Inspectorate Tech. Rep. 2008, 6 (2007).
- 28.Dey N., Blanc-Feraud L., Zimmer C., et al. , “3D microscopy deconvolution using Richardson-Lucy algorithm with total variation regularization,” INRIA, Research Report RR-5272 (2006). [DOI] [PubMed]
- 29.Jensen J. A., “Deconvolution of ultrasound images,” Ultrasonic Imaging 14(1), 1–15 (1992). 10.1177/016173469201400101 [DOI] [PubMed] [Google Scholar]
- 30.Dell’Acqua F., Rizzo G., Scifo P., et al. , “A model-based deconvolution approach to solve fiber crossing in diffusion-weighted MR imaging,” IEEE Trans. Biomed. Eng. 54(3), 462–472 (2007). 10.1109/TBME.2006.888830 [DOI] [PubMed] [Google Scholar]
- 31.Richardson W. H., “Bayesian-based iterative method of image restoration,” J. Opt. Soc. Am. 62(1), 55–59 (1972). 10.1364/JOSA.62.000055 [DOI] [Google Scholar]
- 32.Lucy L. B., “An iterative technique for the rectification of observed distributions,” Astron. J. 79, 745–754 (1974). 10.1086/111605 [DOI] [Google Scholar]
- 33.Xie D., Dong W., Zheng J., et al. , “Spatially-variant image deconvolution for photoacoustic tomography,” Opt. Express 31(13), 21641–21657 (2023). 10.1364/OE.486846 [DOI] [PubMed] [Google Scholar]
- 34.Fish D. A., Brinicombe A. M., Pike E. R., et al. , “Blind deconvolution by means of the Richardson-Lucy algorithm,” J. Opt. Soc. Am. A 12(1), 58–65 (1995). 10.1364/JOSAA.12.000058 [DOI] [Google Scholar]
- 35.Jetzfellner T., Ntziachristos V., “Performance of blind deconvolution in optoacoustic tomography,” J. Innov. Opt. Health Sci. 04(04), 385–393 (2011). 10.1142/S1793545811001691 [DOI] [Google Scholar]
- 36.Yang C., Jiao Y., Jian X., et al. , “Image deconvolution with hybrid reweighted adaptive total variation for optoacoustic tomography,” Photonics 8(2), 25 (2021). 10.3390/photonics8020025 [DOI] [Google Scholar]
- 37.Chen J., Lin R., Wang H., et al. , “Blind-deconvolution optical-resolution photoacoustic microscopy in vivo,” Opt. Express 21(6), 7316–7327 (2013). 10.1364/OE.21.007316 [DOI] [PubMed] [Google Scholar]
- 38.Yu J., Kang K., “Deconvolution-based approach for super-resolution photoacoustic imaging,” J. Acoust. Soc. Am. 140(4_Supplement), 2981 (2016). 10.1121/1.4969230 [DOI] [Google Scholar]
- 39.Amjadian M., Mostafavi S. M., Chen J., et al. , “Super-resolution photoacoustic microscopy using structured-illumination,” IEEE Trans. Med. Imaging 40(9), 2197–2207 (2021). 10.1109/TMI.2021.3073555 [DOI] [PubMed] [Google Scholar]
- 40.Treeby B. E., Cox B. T., “k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave-fields,” J. Biomed. Opt. 13(5), 021314-1 (2010). 10.1117/1.3360308 [DOI] [PubMed] [Google Scholar]
- 41.Martin E., Jaros J., Treeby B. E., “Experimental validation of k-Wave: nonlinear wave propagation in layered, absorbing fluid media,” IEEE Trans. Ultrason. Ferroelect. Freq. Control 67(1), 81–91 (2020). 10.1109/TUFFC.2019.2941795 [DOI] [PubMed] [Google Scholar]
- 42.Turcotte R., Sutu E., Schmidt C. C., et al. , “Deconvolution for multimode fiber imaging: modeling of spatially variant PSF,” Biomed. Opt. Express 11(8), 4759–4771 (2020). 10.1364/BOE.399983 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.