Abstract
A novel type of detachable precast concrete column-column joint (DPC) is proposed in this study to solve the problems in current column-column dry connections including complex load path, uncertainty of structural stiffness of beam-column joints and inconvenience for disassembly. The dry connection technology is applied by composing of steel plate and concrete. Finite element models of DPC were created to study its structural performance including hysteresis curve, skeleton curve, ductility, and energy dissipation capacity. The benchmark models are firstly established and validated against the test data and after that a small-scale parametric study is prepared. The effect of axial pressure ratio and eccentricity distance size on the seismic performance of DPC was studied. Results indict that the optimal value of axial pressure ratio ranges from 0.5 to 0.7. With increase of the axial pressure ratio, the ductility coefficient shows a decreasing trend in general. The eccentricity has little effect on the energy dissipation capacity of the joint.
Keywords: Precast concrete column-column joints, Seismic performance, Hysteresis curve, Skeleton curve
1. Introduction
Precast concrete column-column joint has a clear advantage in construction cost and energy consumption compared with the traditional construction of reinforced concrete structure [1,2]. However, the safety, structural performance and workability of the joint should be as reliable as cast-in-place concrete construction. The available precast concrete joint usually uses welding [[3], [4], [5]], prestressing [6], laminated beams [7,8] and profiled concrete [9,10] to connect different prefabricated members for the advantages of fast construction and less on-site casting operations. In addition, the seismic performance of traditional connection technology is unsatisfactory [11]. At present, there are two popular ways (dry connection and wet connection) available for precast concrete structure. Compared with wet connection structures, dry connection structures are easier for detachable operation. Hu et al. [12] proposed a dry joint based on precast concrete columns with flange plate connections and showed that columns with flange plate connection have similar seismic performance as conventional cast-in-place columns. Yamashita [13] et al. conducted an experimental study and finite element study of precast concrete columns and a shaking table test study of natural seismic waves on the test members of concrete columns. Shi et al. [14] proposed a fully precast steel frame connection consisting of cold-formed box columns, hot-rolled I-beams, end plate nodes, flexible supports and bolted precast plates, and conducted an experimental study of the structure consisting of this node connection and obtained the conclusion that the node has good cyclic performance, high horizontal bearing capacity and good ductility.
Kulkarni et al. [15] proposed a steel-concrete connection and studied the key parameters affecting the performance of the connection. Jiang et al. [16] proposed a recoverable steel beam-column connection and found that reasonable design of the connection parameters can make the beam-column exhibit good bearing capacity, seismic performance, and ductility. Nzabonimpa et al. [[17], [18], [19], [20], [21], [22]] conducted an experimental and nonlinear numerical study of mechanical connections between reinforced concrete laminated plates and concrete laminated slabs for transferring axial loads and bending moments and proposed a hybrid mechanical joint with laminated metal plates instead of the conventional grouted sleeve connection for shaped columns. Wei et al. [23] proposed a new type of assembled monolithic column with connection treatment in the form of outer steel plates welded with transverse reinforcement and investigated its seismic performance. Zhang et al. [24] proposed an improved assembled column joint with multiple slot connections. Hua et al. [[25], [26], [27]] proposed a new beam-column bolt-connection with plastically controllable hinges. Compared with frame connected with the cast-in-place joints, the frame connected with the new joints can improve the energy dissipation capacity and ductility. Al-Rousan [[28], [29], [30]] proposed to use carbon fiber and fiber-reinforced polymers to strengthen the connection for seismic performance of beam-column joints. The comparative analysis on compressive bearing capacity and corresponding strain, hysteretic curve, skeleton curve, ductility, energy dissipation capacity and stiffness degradation show that the ductility and energy dissipation capacity of beam-column joints using fiber-reinforced polymers are significantly improved. Jiang et al. [[31], [32], [33], [34], [35]] experimentally investigated the effect of fabrication technique on the seismic performance of the joint. Gao et al. [36] presents numerical findings of reinforced concrete interior beam-column joints under monotonic antisymmetric load.
In order to solve construction inconvenience of the existing column-column dry connection, this paper proposes a detachable precast concrete column-column joint (DPC) based on rigid connection technology. This joint has the characteristics of detachable and strong integrity. The main innovation of this article is to this DPC as dry connection. The influence of the geometrical design of DPC joint on the seismic performance is discussed and an optimal design scheme for the proposed DPC is given.
In this study, a detachable precast concrete column-column (DPC) joint was proposed with high-strength bolts, web connection plate, upper and lower connection plates, I-beam and studs, as shown in Fig. 1(a) and (b). The core part of DPC is the steel connection. In this part, the role of the cladding plate is to prevent stress concentration at the connection gap and to protect the concrete in contact with the cladding plate from being crushed. Steel studs can improve the performance of the connection of precast concrete beams. High-strength bolts and connecting plates are used to connect two steel I-heads for higher shear bearing capacity. Hence, a smaller number can be used to meet the design requirements of bearing capacity. The fewer number of holes reserved for the bolts on the I-beam connector makes higher integrity of the connecting plate and the I-beam connector. The precast concrete part and the steel connection part are prefabricated as a single unit, and the longitudinal reinforcement inside the concrete is welded to the steel connection, as shown in Fig. 2.
Fig. 1.
Detachable precast concrete column-column (DPC) joint.
Fig. 2.
Details of the DPC joint.
The DPC joint was proposed in this study to solve the problems in current column-column dry connections such as complex load path and inconvenience for disassembly. The dry connection technology is applied by composing of steel plate and concrete. Compared with the existing dry joints, another advantage of the DPC joint is that the design methods in the existing steel structure specifications can be used. Finite element models of DPC were created to study its structural performance including structural ductility and energy dissipation capacity. First, the FE modeling technique was validated by testing data. The seismic performance analysis of detachable precast concrete column-column joints (DPC) was then carried out.
2. Design philosophy of the DPC joint
2.1. The bearing capacity of the cast-in-situ concrete column
To study the structural performance of the DPC joint, a control joint, which is traditionally casted in site, is designed and proposed [37]. The size of cast-in-situ concrete column is 500*500*2500 mm and the protective layer thickness is 30 mm as shown in Fig. 3(a) and (b). Note that the concrete grade is C40 and the longitudinal reinforcement is 25 mm in diameter and the hoop reinforcement is φ10@100.
Fig. 3.
Geometry design.
First, the ultimate shear bearing capacity of the cast-in-situ concrete column is calculated according to Eqs. Eq. (1), Eq. (2), Eq. (3) from the Principles of Structural Design of Concrete [38].
| Eq. (1) |
| Eq. (2) |
| Eq. (3) |
Where, Vu is the shear bearing capacity of the column; λ is the shear-to-span ratio of the calculated section; ft is the design value of the concrete shear bearing capacity; b is the section width; h0 is the effective section height of the column; fyv is the design value of the tensile strength of the hoop reinforcement; Asv is the full cross-sectional area of each limb of the hoop reinforcement in the same section; S is the spacing of the hoop reinforcement along the length of the member; N is the design value of the axial tensile force; Hn is the net height of column; fc is the design value of axial compression strength of concrete; A is the total cross-sectional area of the column.
Second, the compressive bearing capacity of the cast-in-situ concrete column is calculated according to Eq. (4).
| Eq. (4) |
Considering the stochastic nature of earthquakes, symmetrical reinforcement was used to make the longitudinal and transverse bearing capacities of the columns the same. Hence, the relative compressive zone height of concrete is calculated by Eq. (5):
| Eq. (5) |
Since the relative compressive zone height x >εbh0, which belongs to the case of small eccentric pressure, recalculate x according to the case of eccentric load (Eq. (6)):
| Eq. (6) |
Where, Nu is the compressive bearing capacity of the cast-in-place columns; fc is the design value of the concrete compressive bearing capacity; A is the cross-sectional area of the member; fy is the design value of the compressive strength of the reinforcement; A's is the cross-sectional area of all longitudinal reinforcement; x is the height of the concrete compressive zone; α1 is the coefficient of the equivalent rectangular stress diagram of the concrete compressive zone, and takes the value of 1 when the concrete strength is less than C50; b section width; h0 is the effective height of the concrete; εb is the height of the relative boundary compressive zone.
Then, the eccentricity e and the bending bearing capacity Mu of the cast-in-situ concrete column are calculated by the following Eq. (7) and Eq. (8):
| Eq. (7) |
| Eq. (8) |
Finally, according to the size and reinforcement of the cast-in-situ concrete column, the compressive,the shear and the bending bearing capacity of the cast-in-situ concrete column are calculated, as Eq. (9):
| Eq. (9) |
2.2. Design of DPC joint
Based on the bending bearing capacity of the cast-in-situ concrete column Eq. (9), the dimension of the I-beam, the connecting plate and the number of high-strength studs are calculated according to design equations in Steel Connection Node Design Manual [39]. The dimension of the studs is determined according to test results [40]. According to the load-bearing capacity calculation result of the cast-in-situ concrete column, the size of the I-beam column can be initially selected as 420 × 440 × 28 × 20. According to Table 8.1.1 of the Steel Design Criteria [41], plastic development factor of the section γx = 1.05, γy=1.2 is used for strength calculation by substituting the following Eq. (10).
| Eq. (10) |
Table 8.
The ductility coefficient comparison.
| models | Loading direction | yield point |
Ultimate displacement (mm) | ||
|---|---|---|---|---|---|
| load capacity (kN) | displacement (vector) (mm) |
||||
| 0.3 | forward | 135.99 | 7.32 | 46.60 | 4.51 |
| negative direction | −129.41 | −6.63 | −47.70 | 6.61 | |
| 0.4 | forward | 137.52 | 6.91 | 48.96 | 4.17 |
| negative direction | −135.00 | −6.91 | −45.49 | 4.51 | |
| 0.5 | forward | 154.41 | 6.48 | 47.12 | 3.90 |
| negative direction | 142.49 | 5.43 | −48.51 | 5.23 | |
| 0.6 | forward | 162.86 | 6.70 | 43.59 | 3.63 |
| negative direction | 150.63 | 6.01 | −46.90 | 4.08 | |
| 0.7 | forward | 184.38 | 6.86 | 48.71 | 3.11 |
| negative direction | 176.80 | 5.92 | −48.31 | 3.31 | |
| 0.8 | negative direction | 173.84 | 6.34 | 46.34 | 2.88 |
| negative direction | 135.99 | 7.32 | −46.64 | 3.69 | |
Note that Q345 is used for I-beam, the connecting plate and 10.9 grade M30 high-strength bolts friction type double shear connection is used for studs. The number of high-strength bolts is determined according to Eq. (11) and Eq. (12):
| Eq. (11) |
| Eq. (12) |
Where, nFC is the number of high strength bolts required for single side flange; nWC is the number of high strength bolts required for single side web; Hc is the height of I-beam; tFC is the thickness of I-beam flange; NbHV is the design value of shear bearing capacity of high strength bolts, 238.5 for 10.9 grade high strength bolts; Bc is the width of I-beam flange; tWC is the thickness of I-beam web; hWC is the height of I-beam web.
Considering that the I-beam has two directions of strong axis (X direction) and weak axis (Y direction), the stiffness along two directions (X and Y) were calibrated separately in this paper. First, for the X direction, the net section moment of inertia of the I-beam is equal to the I-beam moment of inertia minus the I-beam bolt hole moment of inertia given by Eq. (13). The net section moment of inertia of the I-beam connecting plate is derived from Eq. (14). The net section modulus is obtained from the net section moment of inertia according to Eq. (15) and Eq. (16).
| Eq. (13) |
| Eq. (14) |
| Eq. (15) |
| Eq. (16) |
Where, Icox is the moment of inertia of I-steel in x direction; IcxR is the moment of inertia of the bolt hole section in the x-direction of the I-beam; Icnx is the net moment of inertia of the I-beam after deducting the bolt holes in the x-direction of the I-beam; Iplox is the gross section moment of inertia of the I-beam splice joint plate in the x-direction; IplxR is the moment of inertia of the bolt hole section in the x-direction of the I-beam splice joint plate;Iplnx is the moment of inertia of bolt hole section in the x direction of I-steel splicing connection plate;Wcnx is the net section modulus of the I-beam in the x-direction; Wplnx is the net section modulus in the x direction of I-steel splicing connection plate; Wooy is the net section modulus of the I-beam in the y-direction modulus; is the thickness of the outer flange joint plate; Hc is the height of I-steel; hc is the thickness of the outer connecting plate of the flange.
3. FE modelling analysis
3.1. Material constitutive model
To precisely model the joint behavior under low-reversed cyclic displacement loads, the plastic damage model (PDM) proposed by J. Lee and GL Fenves [42] was used to model the mechanical behavior of concrete structures. In this model, concrete is regarded as an isotropic material, and the reduction of the concrete elastic stiffness can effectively simulate the characteristics of concrete stiffness decreasing with loading and unloading.
The constitutive model of concrete material is provided in the ABAQUS material library. However, the corresponding relationship between concrete compressive stress and plastic compressive strain, concrete tensile stress and cracking tensile strain needs to be manually input for the plastic stage, since the full stress-strain curve of concrete is difficult obtained. In this study, the calculation method of the stress-strain relationship given by the design code for concrete structures [53] (GB50010-2002) is used. The nominal stress-strain curve is obtained from concrete structural design code as shown in Eqs. Eq. (17), Eq. (18), Eq. (19), Eq. (20).
When :
| Eq. (17) |
When :
| Eq. (18) |
| Eq. (19) |
During modelling process, the real stress and strain need to be input in the PDM model. Eq. (21) and Eq. (22) are used to convert the nominal stress-strain curve into the real nominal stress-strain curve.
| Eq. (20) |
| Eq. (21) |
| Eq. (22) |
Where, αa and αd are the values of the rising and falling segments of the uniaxial compressive stress-strain curves, respectively; σ, ε are the stress and strain of concrete, respectively; f*c are the uniaxial compressive strength of concrete; εc is the corresponding peak compressive strain of concrete; σc is compression stress inputted in the PDM model; εinc is the plastic strain to be input in the PDM model; and E is the modulus of elasticity of concrete.
For reinforcement and steel connection, the bilinear elastoplastic model is used. Table 1 and Table 2 gives concrete input parameters. The input parameters of reinforcement are given in Table 3 and the input parameters of steel are given in Table 4.
Table 1.
Stress-strain relationship of the concrete under uniaxial compression.
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1370 | 1470 | 1560 | 1640 | 1720 | 1790 | 1850 | 1920 | 1980 | 2030 | |
| 2.21 | 2.15 | 2.09 | 2.03 | 1.96 | 1.90 | 1.84 | 1.78 | 1.71 | 1.65 | |
| 0.41 | 0.74 | 1.06 | 1.36 | 1.65 | 1.94 | 2.21 | 2.48 | 2.74 | 3.00 | |
| 4.2 | 3.0 | 2.6 | 2.3 | 2.1 | 2.0 | 1.9 | 1.9 | 1.8 | 1.8 |
Note: is the compressive strain of concrete when the stress on the descending section of the stress-strain curve is equal to 0.5 .
Table 2.
Concrete input parameters.
| Expansion angle | Eccentricity |
Viscosity parameters | ||
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.667 | 0.00005 |
Notes. is the ratio of biaxial to uniaxial compressive ultimate strength. is the invariant stress ratio.
Table 3.
Rebar input parameters.
| column stressing bar yield strength (MPa) | column stressing bar yield strength (MPa) | hoop tendon yield strength (MPa) |
modulus of elasticity (MPa) | Poisson's ratio |
|---|---|---|---|---|
| 500 | 500 | 400 | 2 × 105 | 0.3 |
Table 4.
Steel input parameters.
| density (kg/mm3) | Modulus of elasticity (MPa) | Poisson's ratio | Yield stress (MPa) | plastic strain |
|---|---|---|---|---|
| 7.85E-009 | 200000 | 0.3 | 345 | 0 |
3.2. Analysis setting
Fig. 4 gives the loading and boundary condition used in modelling. The tangential behaviour of DPC model is based on the friction equation "penalty" by defining a friction coefficient of 0.45, while the normal behaviour is defined as a "hard contact" for pressure overload. The cladding plate and the column at the joints are connected by binding constraints. The four faces of the beams were set as master faces and the inner surfaces of the cladding slabs were set as slave faces; the longitudinal reinforcement and hoop bars were connected to the concrete through built-in areas and the geometric tolerance is set to the ABAQUS default value of 0.05. Table 5 lists the interactions between parts in modelling.
Fig. 4.

Loading and boundary condition setting.
Table 5.
Interaction between parts in modelling.
| Type of constraint | Part 1 | Part 2 |
|---|---|---|
| Binding constraints |  |
 |
| main surface | from the surface | |
| built-in area |  |
 |
| Embedded elements | Main elements | |
| Universal contact |  |
 |
| main surface | from the surface | |
| coupling |  |
 |
| coupling surface | coupling point | |
| built-in area |  |
 |
| Embedded elements | Main elements |
The symmetric modelling technique [43,44] introduced to simplify the modelling process and reduce the degrees of freedom and the computational cost. The steel bars of cast-in-situ joints and DPC joints are simulated by element type T3D2, while the concrete, steel plate and high-strength bolts are simulated by C3D8R.A finer mesh was used in the connection area between prefabricated members and steel connection, as shown in Fig. 5(b). Similar work can be found from Jiang's research group [31,45,46]. The seismic performance of dry-connection technique was experimentally and numerically studied and the modeling technology used was validated by the test data. Mesh sensitivity analysis was also organized that three mesh size of 12 mm, 6 mm and 2 mm were created (Fig. 5). In this study, The mesh sensitivity study results are summarized in Table 6. It is found that the ultimate bearing capacity does not change significantly for different mesh sizes. However, the mesh size gets smaller, the CPU time required for the analysis increases significantly. Hence, the optimal element size is selected to 5 mm and it is used for the following benchmark models and parametric studies.
Fig. 5.
Mesh sensitivity analysis.
Table 6.
The mesh sensitivity analysis.
| Mesh | Brick element size(mm) | Cost time (mins) | Ultimate capacity (kN) |
|---|---|---|---|
| Mesh I | 12 | 15 | 340 |
| Mesh II | 6 | 45 | 326 |
| Mesh III | 2 | 320 | 310 |
3.3. Validation of modelling results
An experimental study on the seismic performance of DPC beam-column joints was carried out and the modelling technique and results were validated by test data [31]. The geometrical parameters of the joints can be referred to the literature [31].
Fig. 6 shows the comparison between hysteresis curves from test and modelling. Note that the ultimate bearing capacity of the joint based on modelling is 203.6 kN, while the ultimate bearing capacity of the test joint is 219.2 kN. Hence, there is only a 7.6% difference between the modelling and test results. Hence, a precise result can be obtained by reasonable modelling technique used.
Fig. 6.
Validation of the modelling result.
3.4. Study of seismic performance of DPC joint
In order to study the seismic performance of DPC joint, two loading scenarios, cyclic displacement loading and monotonic displacement, were used in this study. The energy dissipation and the ductility of the joints were obtained and analysed.
3.4.1. Seismic performance analysis under cyclic displacement load
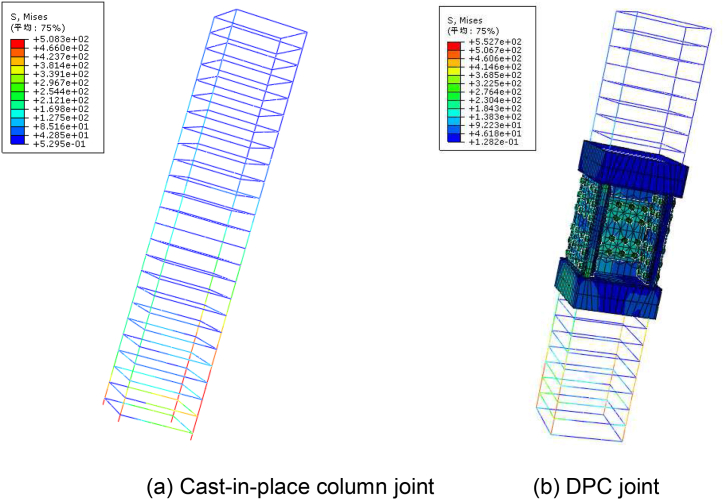
Fig. 7 gives the cyclic displacement loading applied on the top of the column. Fig. 8(a) and (b) show the equivalent cumulated compressive plastic strain of the joints under the applied load. Fig. 9, Fig. 10 show the hysteresis curves and skeleton curves of the cast-in-place joint and the DPC joint. It can be found that the maximum strain occurs mainly at the base of the column. The maximum strain in DPC joint is 0.017 and the maximum strain cast-in-place joint is 0.066. In other word, the maximum strain in DPC joint is reduced by 74.2% compared the cast-in-place joint. This is due to the inclusion of steel structure for DPC joint.
Fig. 7.
The cyclic displacement load.
Fig. 8.
Concrete strain contour.
Fig. 9.
Hysteresis curve comparison.
Fig. 10.
Skeleton curve comparison.
Fig. 9 shows that the hysteresis curves of the DPC joint and cast-in-place joint have the same trend. The hysteresis curves of the two joints almost overlap at the early stage of loading (when the loading displacement is 0–10 mm), indicating that the mechanical properties of the DPC joint at the elastic stage are consistent with those of the conventional cast-in-place column joint. In the middle and late loading stage (the loading displacement is 10–50 mm), both nodes enter the yield stage. The hysteresis curve of DPC node is slightly lower than that of cast-in-place node. Due to the steel structure used at the joints of DPC nodes, the hysteretic curves of DPC nodes are slightly fuller than those of cast-in-place nodes.
To evaluate the deformation capacity from yielding to the maximum bearing capacity for evaluating the seismic performance of the structure, the ductility coefficient can be evaluated according to Eq. (23).
| Eq. (23) |
Where μu refers to the displacement ductility coefficient; Δu refers to the ultimate displacement of the structure in millimetres (mm), which is generally taken as the displacement corresponding to the fall of the member to 0.85 Fmax after reaching the ultimate load; Δy refers to the yield displacement, which is in millimetres (mm).
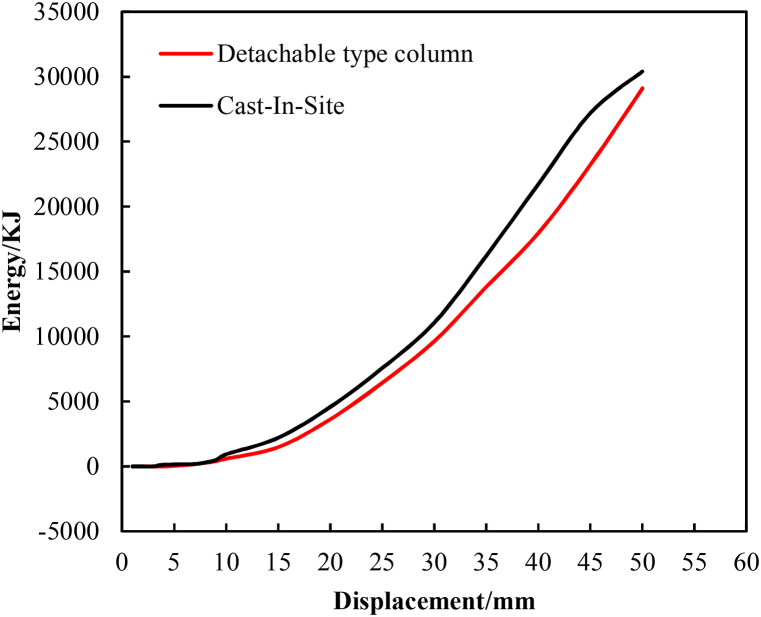
Table 7 lists the ductility coefficients of the DPC joint and cast-in-place joint. It can be found that the ductility coefficient difference between the two joints is 13.7% while the yield strengths of the two joints are very close. In fact, and the ductility coefficient of DPC joint is greater than that of the cast-in-place joints. A comparison of the joint energy dissipation under cyclic displacement loading is shown in Fig. 11. It can be seen that the energy dissipation capacity trend of the two joints is basically the same. When the loading displacement is 0 mm–10mm, the energy dissipation capacity of the two joint is relatively weak as the energy dissipation capacity of the joints is poor before yielding. When the loading displacement is 10 mm–50mm, the energy dissipation capacity of both joints is significantly increased. Overall, the energy dissipation capacity of the DPC joint is equivalent to that of cast-in-place joint.
Table 7.
the ductility coefficients of the DPC joint and cast-in-place joint.
| models | Loading direction | yield point |
Ultimate displacement (mm) | ||
|---|---|---|---|---|---|
| load capacity (kN) | displacement (vector) (mm) |
||||
| Cast-in-place nodes | forward | 138.13 | 7.77 | 43.18 | 3.93 |
| negative direction | −137.53 | −7.81 | −47.68 | 6.49 | |
| Loading and unloading nodes | forward | 138.95 | 7.46 | 48.96 | 4.47 |
| negative direction | −139.07 | −7.56 | −45.49 | 4.48 | |
Fig. 11.
Energy dissipation capacity comparison.
3.4.2. Seismic performance analysis under monotonic displacement load
Fig. 12(a) and Fig. 12(b) show stress contour of the two joints under monotonic displacement load of 0 mm–30mm applied to the top of the column. Fig. 13 shows the force-displacement curves. The stress concentration effect of the cast-in-place joint can be found on the column bottom reinforcement while the stress concentration phenomenon of the DPC joint is mainly located at the high-strength bolts and the column bottom reinforcement.
Fig. 12.
stress contour of the two joints.
Fig. 13.
The force-displacement curve comparison.
The initial stiffness is 28.8 kN/mm and 32.2 kN/mm for the cast-in-place joint and DPC joint, respectively. It means DPC joint has a 11.6% higher initial stiffness and 4.5% higher ultimate bearing capacity than the cast-in-place joint. In summary, it is shown that the seismic performance of the DPC is more or less equivalent to the cast-in-place joint.
4. Parametric study
4.1. Effect of axial pressure ratio
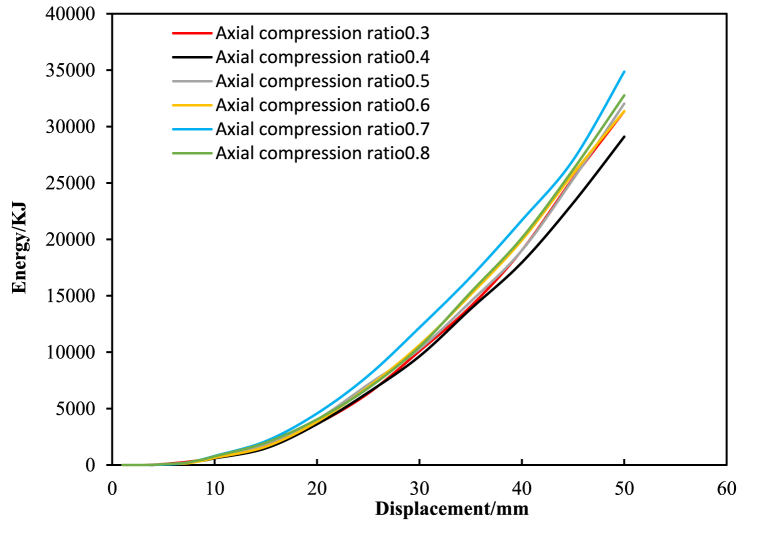
Six FE models with axial pressure ratios of 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 were created to study the effect of axial pressure ratio on seismic performance of the DPC joint. The hysteresis curve and skeleton curve comparisons are given in Fig. 14, Fig. 15. It can be observed that the axial pressure ratio has important influence on ultimate bearing capacity. However, the axial pressure ratio has no effect on the skeleton curve before yielding. Only on the stage of after yielding, the axial compression ratio has a important impact on ultimate bearing capacity. The energy dissipation energy comparison is shown in Fig. 16. The joint with axial pressure ratio of 0.7 has the best energy dissipation capacity and the joint with axial pressure ratio of 0.4 has the lowest energy dissipation capacity. The energy dissipation capacity of the joint with axial pressure ratio of 0.7 is 16.5% higher than that of the joint with axial pressure ratio of 0.4. The energy dissipation capacity for the joints with axial pressure ratio of 0.5–0.6 is higher than the joint with axial pressure ratio of 0.4 as well.
Fig. 14.
Hysteresis curve comparison.
Fig. 15.
Skeleton curve comparison.
Fig. 16.
The energy dissipation energy comparison.
The ductility coefficient comparison is shown in Table 8. With increase of the axial pressure ratio, the ductility coefficient shows a decreasing trend in general. The joint with axial pressure ratio of 0.3 has the largest ductility coefficient. When the axial pressure ratio is between 0.4 and 0.6, the ductility coefficient of the joint changes smoothly.
4.2. Effect of eccentricity
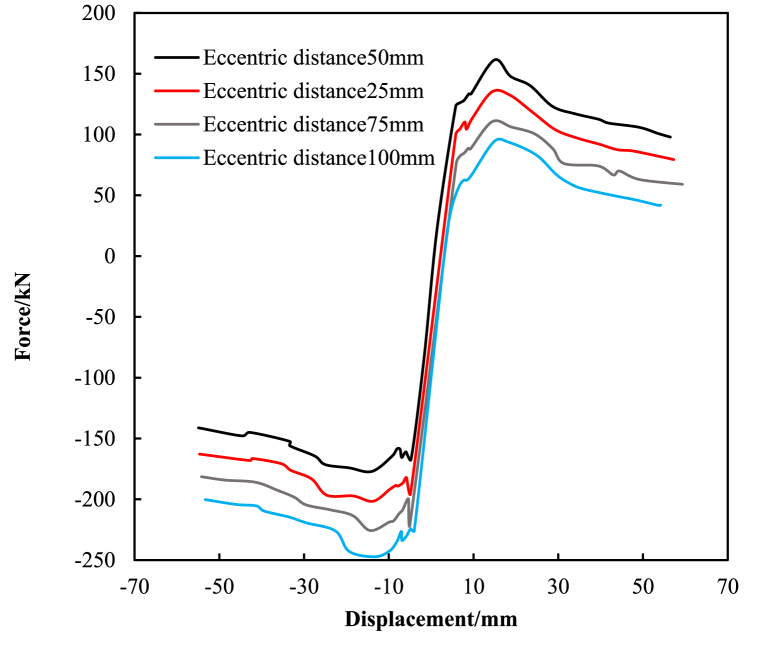
Four eccentric distances 25 mm, 50 mm, 75 mm, and 100 mm are selected to study the effect of eccentricity (Fig. 17). The comparisons the hysteresis curves and skeleton curves are shown in Fig. 18, Fig. 19. The overall trend of the hysteresis curves of the joints with different eccentric distances is the same. With increase of the eccentricity, the bearing capacity of positive load decreases and the bearing capacity of negative load increases. This phenomenon is due to the fact that the eccentric distance of the joint is relative to the positive X-axis. The ultimate load capacity of the joint decreases with the increase of the eccentricity. All joints reach the ultimate load at a displacement of about 14 mm.
Fig. 17.
Effect of eccentricity.
Fig. 18.
Hysteresis curve comparison.
Fig. 19.
Skeleton curve comparison.
The energy dissipation capacity comparison is shown in Fig. 20. It indicts that the axial pressure ratio almost has no effect on the energy dissipation capacity. The ductility parameter is listed in Table 9. The ductility coefficient of the joint in the positive direction decreases with the increase of eccentricity while the ductility coefficient of the joint in the negative direction increases with the increase of eccentricity. The ductility coefficient in the positive direction is 3.91 when the eccentricity is 25 mm, and it is reduced by 64.7% to 1.38 when the eccentricity is 100 mm. It shows that the larger the eccentricity of the joint, the smaller the ductility coefficient in the positive direction and the larger the ductility coefficient in the negative direction.
Fig. 20.
The energy dissipation capacity comparison.
Table 9.
The ductility parameter comparison.
| models | Loading direction | yield point |
Ultimate displacement (mm) | ||
|---|---|---|---|---|---|
| load capacity (kN) | displacement (vector) (mm) |
||||
| 25 mm | forward | 123.05 | 6.33 | 54.45 | 3.91 |
| negative direction | −164.10 | −4.89 | −54.91 | 7.34 | |
| 50 mm | forward | 111.28 | 9.17 | 57.25 | 2.76 |
| negative direction | −188.26 | −5.36 | −54.66 | 6.58 | |
| 75 mm | forward | 92.20 | 10.20 | 59.31 | 2.63 |
| negative direction | −205.47 | −5.46 | −54.19 | 6.77 | |
| 100 mm | forward | 59.55 | 27.86 | 54.16 | 1.38 |
| negative direction | −225.18 | −4.75 | −53.29 | 8.20 | |
5. Conclusion
A new type of detachable precast concrete column-column joint (DPC) is proposed in this study to solve the problems in current column-column dry connections. The dry connection technology is applied by composing of steel plate and concrete. The benchmark models are initially created and validated against the test data and after that a small-scale parametric study is organized. The effect of axial pressure ratio and eccentricity distance size on the seismic performance of DPC was studied. It is found that the DPC joint with axial pressure ratio of 0.7 has the best energy dissipation capacity and the joint with axial pressure ratio of 0.4 has the lowest energy dissipation capacity. With increase of the axial pressure ratio, the ductility coefficient shows a decreasing trend in general. The ductility coefficient of the joint in the positive direction decreases with the increase of eccentricity while the ductility coefficient of the joint in the negative direction increases with the increase of eccentricity.
Statements for conflicts of interest
The author of this paper with title of Structural performance of detachable precast concrete column-column joint receives research funding by the Scientific Research Start-up Funding of Shantou University (NTF22010) and Natural Science Foundation Funding of Guangdong Province (No. 2023A1515012502).
CRediT authorship contribution statement
H. Zhan: Investigation. M. Ye: Investigation, Data curation. J. Jiang: Supervision, Project administration, Methodology, Funding acquisition, Conceptualization. C.W. Zheng: Data curation. S.C. Duan: Data curation.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:Jiang Jin reports financial support was provided by Natural Science Foundation Funding of Guangdong Province (No. 2023A1515012502). If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.National Development and Reform Commission, Ministry of Housing and Urban-Rural Development. Green building action program [EB/OL]. http://www.gov.cn/zwgk/2013-01/06/content_2305793.htm..
- 2.General Office of the State Council. Guidance of the General Office of the State Council on vigorously developing assembly-type buildings [EB/OL]. http://www.gov.cn/zhengce/content/2016-09/30/content_5114118.htm..
- 3.Du Kecai. Harbin Institute of Technology; 2017. Research on Mechanical Properties of I-Beam Connections in Reinforced Concrete Precast Beam-Column Members. [Google Scholar]
- 4.Wang Yuanqing, Qiao Xueliang, Jia Lianguang, Zhang Tianxiong, Jiang Qinglin. Experimental study on the seismic performance of stainless steel beam-column nodes with different connection methods. J. Southeast Univ. (Nat. Sci. Ed.) 2018;48(2):316–322. [Google Scholar]
- 5.Zhao Zuozhou, Zhou Jian, Hou Jianqun, Ren Baoshuang. A review of horizontal joint shear mechanism and bearing capacity calculation methods for assembled concrete shear wall structures. Building Structure. 2015;45(12):39–47. [Google Scholar]
- 6.Wang Haishen, Edoardo M., Marino, Pan Peng. Engineering Structures; 2019. Design, Testing and Finite Element Analysis of an Improved Precast Prestressed Beam-To-Column Joint; p. 199. [Google Scholar]
- 7.Yan Weiming, Wang Wenming, Chen Shicai, Li Hongquan, Gao J. Experimental study on seismic performance of assembled precast concrete beam-column-stacked slab edge nodes. J. Civ. Eng. 2010;43(12):56–61. [Google Scholar]
- 8.Chen Shicai, Yan Weiming, Li Zhenbao, Wang Wenming, Gao J. Experimental study on the overall seismic performance of nodes in large precast concrete beam-column laminated slabs. Eng. Mech. 2012;29(2):135–141. [Google Scholar]
- 9.Sheikh T.M., Deierlein G.G., Yura J.A., et al. Beam-column moment connections for composite frames: part 2. J. Struct. Eng. 2016;115(11):2858–2876. [Google Scholar]
- 10.Yang Jianjiang, Zhijun Hao. Experimental study on the force performance of steel beam-reinforced concrete column nodes under low circumferential repeated loads. Building Structures. 2001;(7):35–38+42. [Google Scholar]
- 11.Shi Caihua. Beijing University of Architecture; 2017. Experimental Study of Assembled Concrete Beam-Column Nodes with Steel Plate Bolted Connections. [Google Scholar]
- 12.Hu Ju-Yun, Hong Won-Kee, Park Seon-Chee. Experimental investigation of precast concrete based dry mechanical column-column joints for precast concrete frames. Struct. Des. Tall Special Build. 2017;26(5) n/a-n/a. [Google Scholar]
- 13.Yamashita Ryo, David H.S. Ers. Seismic performance of precast Unbonded prestressed concrete columns. Structural Journal. 2009;106(6) [Google Scholar]
- 14.Shi Gang, Yin Hao, Hu Fangxin. Experimental study on seismic behavior of full-scale fully prefabricated steel frame: global response and composite action. Eng. Struct. 2018;169 [Google Scholar]
- 15.Kulkarni Sudhakar A., Li Bing, Yip Woon Kwong. Finite element analysis of precast hybrid-steel concrete connections under cyclic loading. Journal of Constructional Steel Research. 2007;64(2) [Google Scholar]
- 16.Jiang Z., Yang X., Dou C., et al. Seismic performance of prefabricated Corrugated web beam-column joint with replaceable cover plates. Adv. Struct. Eng. 2019;22(5):1161–1174. [Google Scholar]
- 17.Nzabonimpa J.D., Hong W.K. Experimental and nonlinear numerical analysis of precast concrete column splices with high-yield metal plates. Journal of structural engineering. 2019;145(2) 04018254.1-04018254.15. [Google Scholar]
- 18.Nzabonimpa J.D., Hong W.K. Structural performance of detachable precast composite column joints with mechanical metal plates. Eng. Struct. 2018;160:366–382. [Google Scholar]
- 19.Nzabonimpa J.D., Hong W.K., Kim J. Mechanical connections of the precast concrete columns with detachable metal plates. Struct. Des. Tall Special Build. 2017;26(17) [Google Scholar]
- 20.Nzabonimpa J.D., Hong W.K., Kim J. Nonlinear finite element model for the novel mechanical beam-column joints of precast concrete-based frames. Comput. Struct. 2017;189:31–48. [Google Scholar]
- 21.Nzabonimpa J.D., Hong W.K. Experimental investigation of hybrid mechanical joints for L-shaped columns replacing conventional grouted sleeve connections. Eng. Struct. 2019;185:243–277. [Google Scholar]
- 22.Nzabonimpa J.D., Hong W.K., Kim J. Composite Structures; 2018. Experimental and Non-linear Numerical Investigation of the Novel Detachable Mechanical Joints with Laminated Plates for Composite Precast Beam-Column Joint. S026382231733461X. [Google Scholar]
- 23.Biyang Wei. Xi'an University of Architecture and Technology; 2014. Research on the Seismic Performance of New Assembled Monolithic columns[D] [Google Scholar]
- 24.Zhang D.F., Gan H. Finite element analysis of multi-groove assembled column connection nodes. J. Changchun Univ. Technol. (Nat. Sci. Ed.) 2018;41(3):46–49+59. [Google Scholar]
- 25.Huang Hua, Li Ming, Yuan Yujie, Bai Hao. Experimental research on the seismic performance of precast concrete frame with replaceable artificial controllable plastic hinges. (ASCE) J. Struct. Eng. 2023;149(1) [Google Scholar]
- 26.Huang Hua, Li Ming, Yuan Yujie, Bai Hao. Theoretical analysis on the lateral drift of precast concrete frame with replaceable artificial controllable plastic hinges. J. Build. Eng. 2022;62 [Google Scholar]
- 27.Huang Hua, Li Ming, Zhang Wei, Yuan Yujie. Seismic behavior of a friction-type artificial plastic hinge for the precast beam-column connection. Arch. Civ. Mech. Eng. 2022;(22):201. [Google Scholar]
- 28.Alhassan M., Al-Rousan R.Z., Amaireh L.K., Barfed M.H. Nonlinear finite element analysis of BC connections: influence of the column axial load, jacket thickness, and fiber dosage. Structures. 2018, November;16:50–62. Elsevier. [Google Scholar]
- 29.Al-Rousan R.Z., Alhassan M.A., Al-omary R.J. Response of interior beam-column connections integrated with various schemes of CFRP composites. Case Stud. Constr. Mater. 2021;14 [Google Scholar]
- 30.Al-Rousan R.Z., Sharma A. Integration of FRP sheet as internal reinforcement in reinforced concrete beam-column joints exposed to sulfate damaged. Structures. 2021, June;31:891–908. Elsevier. [Google Scholar]
- 31.Jiang Jin, Dai Z.S., Wang Y.B., Ye M. Experimental study on fracture toughness of quenched and tempered and TMCP high strength steels. Journal of Constructional Steel Research. 2022;189 [Google Scholar]
- 32.Jin Jiang, Z.Y. Peng, W. Bao and M. Ye. Thermal effect of welding on mechanical behaviour of TMCP high strength steel, J. Mater. Civ. Eng., Volume 32 Issue 2, 04019364..
- 33.Jiang Jin, Peng Z.Y., Ye Z.J., Ye M. Behaviour of 690 MPa high strength steel built-up H-section columns under eccentric load scenarios. Eng. Struct. 2020;213 [Google Scholar]
- 34.Jiang Jin, Ye Z.J., Bao W., Wang Y.B., Wang X., Dai X.H. Flexural buckling behaviour of 690 MPa high strength steel H-section columns. Eng. Struct. 2019;200 [Google Scholar]
- 35.Jin Jiang, S.P. Chiew, C.K. Lee and P.L.Y. Tiong. Numerical investigation of high strength built-up box column, Proceedings of the Institution of Civil Engineers-Structures and Buildings..
- 36.Gao Fei, Tang Zhiqiang, Hu Biao, Chen Junbo, Zhu Hongping, Ma Jian. Investigation of the interior RC beam-column joints under monotonic antisymmetrical load. Front. Struct. Civ. Eng. 2019;13:pages1474–1494. [Google Scholar]
- 37.Fu Hao. Guangzhou University; 2019. Design and Research of New Prefabricated Loading Beam-Column Nodes [D] [Google Scholar]
- 38.Southeast University . China Construction Industry Press; 2008. Concrete Structures . Upper Volume, Principles of Concrete Structure Design. [Google Scholar]
- 39.Li X.R., Qin B. fourth ed. China Construction Industry Press; 2019. Handbook of Steel Structure Connection Node Design. [Google Scholar]
- 40.Li J.H., Wang F., Qiu D.L., et al. Study on the shear force transfer performance of steel-concrete sections with pinned joints. J. Civ. Eng. 2012;45(12):74–82. [Google Scholar]
- 41.The national standard of steel structure design gb50017-2017. China Building Metal Structure. 2018;(2):72. [Google Scholar]
- 42.Lee J., Fenves G.L. A plastic‐damage concrete model for earthquake analysis of dams. Earthquake engineering & structural dynamics. 1998;27(9):937–956. [Google Scholar]
- 43.Zhang C., An D., Zhu L. Axial compressive behavior of steel-damping-concrete composite wall. Appl. Sci. 2019;9(21):4679. [Google Scholar]
- 44.Ye M., Jiang J., Chen H.M., Zhou H.Y., Song D.D. Seismic behavior of an innovative hybrid beam-column connection for precast concrete structures. Eng. Struct. 2021;227 [Google Scholar]
- 45.Jiang J., Wu M., Ye M. Magazine of Concrete Research; 2023. Prediction of Fire Spalling Behaviour of Fibre-Reinforced Concrete; pp. 1–16. [Google Scholar]
- 46.Jiang J., Ye M., Chen L.Y., Zhu Z.W., Wu M. Study on static strength of Q690 built-up K-joints under axial loads. Structures. 2023;51:760–775. [Google Scholar]