Comparison of machine learning approaches for structure–function modeling in glaucoma

Abstract

To evaluate machine learning (ML) approaches for structure–function modeling to estimate visual field (VF) loss in glaucoma, models from different ML approaches were trained on optical coherence tomography thickness measurements to estimate global VF mean deviation (VF MD) and focal VF loss from 24‐2 standard automated perimetry. The models were compared using mean absolute errors (MAEs). Baseline MAEs were obtained from the VF values and their means. Data of 832 eyes from 569 participants were included, with 537 Asian eyes for training, and 148 Asian and 111 Caucasian eyes set aside as the respective test sets. All ML models performed significantly better than baseline. Gradient‐boosted trees (XGB) achieved the lowest MAE of 3.01 (95% CI: 2.57, 3.48) dB and 3.04 (95% CI: 2.59, 3.99) dB for VF MD estimation in the Asian and Caucasian test sets, although difference between models was not significant. In focal VF estimation, XGB achieved median MAEs of 4.44 [IQR 3.45–5.17] dB and 3.87 [IQR 3.64–4.22] dB across the 24‐2 VF for the Asian and Caucasian test sets and was comparable to VF estimates from support vector regression (SVR) models. VF estimates from both XGB and SVR were significantly better than the other models. These results show that XGB and SVR could potentially be used for both global and focal structure–function modeling in glaucoma.

Different machine learning models for global and focal visual field estimation were compared using independent internal and external test sets with different demographics. We compared several models and show that those based on gradient‐boosted trees generally performed well in both internal and external sets and thus may be a useful approach for future structure–function studies. We also found that all models had difficulties to varying degrees in more severe visual fields.

INTRODUCTION

Glaucoma, one of the leading causes of blindness worldwide, ¹ is a disease of the optic nerve in which there is progressive loss of ganglion nerve cells and their axons. While optical coherence tomography (OCT) imaging has now been widely adopted in clinical practice ² as a tool for observing objective, quantifiable structural changes in glaucoma, particularly in the retinal nerve fiber layer (RNFL), corresponding functional vision loss is assessed using standard automated perimetry (SAP), which remains the main outcome measure for treatments and trials. ³ , ⁴ Due to challenges in reliable visual field (VF) assessment, including test variability, ⁵ , ⁶ patient fatigue, ⁷ and learning effects, ⁸ there has been interest in developing models for the estimation of VF loss based on structural information, such as measurements of RNFL thickness.

Various modeling approaches have been reported for the estimation of VF loss from structural measurements using techniques based on linear and nonlinear regression, ⁹ support vector machines, ¹⁰ random forests, ¹¹ and, more recently, neural networks. ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ Instead of relying on structure–function maps based on sectoral groupings ¹⁶ or focal nerve fiber trajectories, ¹⁷ , ¹⁸ these models were developed using data‐driven associations in which estimations of either VF mean deviation (VF MD) or focal VF function were developed directly from structural measurements. While some of the previously reported approaches have compared the estimated values with results based on linear regression ⁹ , ¹¹ or averaged structural measurements, ¹³ there has yet to be comparison of predictive performance for both VF MD and focal VF loss between the different machine learning (ML) approaches on the same dataset. Further, although evaluation of such approaches is typically performed on test sets derived from the same study as the training data, evaluation of VF estimations on test sets with demographics not among the training data has not generally been shown.

In this study, we compare different ML models for both focal and global VF loss estimations using structural RNFL measurements in subjects with primary open angle glaucoma. Performance of the models applied to an external test set with a demographic and ethnic profile different from the training set is also evaluated.

METHODS

Data

Glaucoma participants from two centers, the Singapore National Eye Centre and the Carol Davila University of Medicine and Pharmacy in Bucharest, Romania were included in this study. Ethics approvals were obtained from the SingHealth Centralised Institutional Review Board and the Emergency University Hospital Bucharest Institutional Review Board, respectively. Methods adhered to the tenets of the Declaration of Helsinki and all participants provided written informed consent. Study protocols for both centers were identical and all subjects underwent standardized ophthalmic testing, including autorefraction keratometry (Canon RK‐5 Autorefractor Keratometer; Canon Inc., Tokyo, Japan), VF testing, and OCT. Refractive error was defined using the spherical equivalent (SE) as the sum of the spherical value with half of the cylindrical value. Eyes with high myopia, defined as SE worse than −6 dioptres, were excluded to avoid confounding variations in the RNFL thickness due to myopia. ¹⁹

VF testing was performed once in each eye using SAP with a Humphrey Field Analyzer II (Carl Zeiss Meditec, Inc, Jena, Germany), using a 24‐2 Swedish Interactive Testing Algorithm. Tests with fixation losses of more than 33%, false negative errors of more than 25%, or false positive errors of more than 25% were not considered reliable and excluded from the study. ¹⁰ VF MD and pointwise focal VF deviation data were extracted from the included tests. While other studies have used threshold sensitivities for the focal values, pointwise deviation values were used in our study to complement the estimates of global VF MDs, allowing us to report the modeling performance on VF deviations, both focally and globally.

All participants underwent spectral domain OCT imaging with Cirrus HD‐OCT (Carl Zeiss Meditec, Inc., Dublin, CA, USA) after pharmacological dilation. A 200 × 200 optic nerve head cube scan protocol was used. Circumpapillary RNFL measurements based on a 3.46 mm diameter ring centered on the optic nerve head center were extracted using the in‐built review software. Scans with signal strengths less than 6, with poor quality due to the presence of segmentation errors, or imaging artifacts as assessed by human graders were excluded.

Primary open angle glaucoma, based on clinical diagnosis, was defined by open angles on gonioscopy, glaucoma hemifield tests outside normal limits, and increased vertical cup‐to‐disc ratio with corresponding VF defects not due to secondary causes. Glaucoma severity was categorized based on the simplified Bascom Palmer Glaucoma Staging System, ²⁰ with mild glaucoma having VF MD better or equal to −6 dB, moderate glaucoma having VF MD better or equal to −12 dB, and worse than −6 dB, and advanced glaucoma with VF MD worse than −12 dB.

VF–OCT pairs were selected with a maximum interval of 12 months between VF and OCT tests for each eye. Training and internal test sets were based on the Asian data collected from the Singapore site and were split based on an 80/20 ratio for the training and internal test sets. Participants were split such that VF–OCT pairs from a subject were not allowed to be in different datasets. Stratified sampling based on glaucoma severities was used in the dataset construction so that the distribution of the severities was similar in both train and internal test sets. The dataset of Caucasian participants, collected from the Bucharest site, was used in its totality as the “external” test set.

Machine learning

ML models based on different paradigms were evaluated: standard multivariate linear regression and the more advanced extension elastic net regression, ²¹ which optimizes a weighted combination of both lasso and ridge regularization techniques to reduce model complexity and avoid overfitting; support vector regression (SVR) ²² machines, which operate based on the principle of support vectors by determining the optimal regression line through which the maximum number of points can be included within a margin; multi‐layer perceptrons (MLPs), a type of feed‐forward artificial neural network (ANN) containing layers of neuron‐like nodes with at least one hidden layer between the input and output layers ²³ and in which, nonlinear activation functions in each node allow the modeling of complex nonlinear relationships; convolutional neural networks (CNNs), like MLPs, are also a type of feed‐forward ANN but characterized by the presence of learnable convolutional filters that work as feature detectors and which model spatial relationships in data across different scales; ²⁴ and gradient‐boosted decision trees (XGB), a type of ensemble tree framework in which boosting by addition of regression trees in a sequential manner to minimize error is balanced by the use of regularization to improve generalization. ²⁵

Model development

Circumpapillary RNFL thickness measurements at 360 evenly spaced intervals were defined as inputs for all ML models, while outputs of the models were defined as either VF MD or focal VF deviation values. Although some ML models can generate multiple estimation outputs through parameter sharing, in our study, all models generated only single output. Specifically, for each ML approach, global VF estimates were obtained from one global model for estimation of VF MD, while focal VF estimates were obtained from 52 focal models, with each model trained to estimate the focal VF at a specific location in the 24‐2 SAP test pattern. For the CNN‐based models, we adopted the network architecture proposed by Mariottoni and coworkers. ¹² Briefly, two convolutional layers with one‐dimensional convolutional filters were defined, with the first and second layers having 32 and 64 kernels, respectively, both of size 3. The hidden layers were followed by a fully connected layer of 54 nodes and a final output layer with a single node. Nonlinear activation using rectified linear units (ReLU) followed each hidden layer, while linear activation was used for the final output layer. The MLP‐based models largely followed this architecture but with the convolutional layers excluded, and defined with a hidden fully connected layer of 54 notes followed by an output layer of a single node, with nonlinear activation using ReLU following the hidden layer, and linear activation following the output layer, as with the CNN models. Adam optimization was used with a learning rate set at 1 × 10⁻³ for both CNN and MLP approaches.

Grid search cross‐validation with five folds was performed for hyperparameter selection. This was done by stratified sampling of the training dataset such that five subsets were created with similar severity distribution profiles. The hyperparameters specific to each approach that resulted in the best performance during cross‐validation were selected. A final round of model optimization was done by retraining the model using the full training dataset with the selected hyperparameters, and these final models were evaluated using the internal and external test sets. For the CNN and MLP models, to avoid overtraining, the number of epochs that resulted in the lowest MAE during cross‐validation was noted and subsequently used to train the final models.

Statistical analysis

Demographic characteristics are presented as mean ± standard deviation, and differences in characteristics between datasets were evaluated using independent t‐testing for continuous variables and Fisher's exact test for categorical variables. Mean absolute error (MAE) between the estimated VF estimates and the actual values was used as the primary outcome. Pearson's correlation was also used to evaluate the association between the estimated and actual values. 95% confidence intervals were obtained using a clustered bootstrapping approach at the subject level to adjust for intrasubject correlations. Baseline MAEs were calculated with the differences between the actual values and the means of the datasets, and the extent by which the baseline MAEs were reduced with each of the models was also calculated. ¹⁴ For the global VF MD analysis, an additional linear regression (LR) model using global RNFL values was also developed. Model performance against baseline was evaluated using Wilcoxon's signed rank test. Differences between models were obtained using Friedman's test. If significant differences were found, post‐hoc multiple comparison testing using Nemenyi's test was performed. Focal MAE and correlations were presented as the median and interquartile range (IQR) of the results from the 52 VF locations in the 24‐2 VF. Focal reductions from baseline due to each model were first calculated pointwise at each VF location over baseline, before being summarized as median and IQR baseline reductions over all 52 locations. p Values less than 0.05 were considered statistically significant. CNN and MLP models were implemented using PyTorch, while XGB was implemented using the XGB library. ²⁵ All other models were implemented using the scikit‐learn library in the Python 3.6 platform. Post‐hoc testing for multiple comparisons was performed using the statsmodels library. ²⁶

RESULTS

VF–OCT pairs of 721 glaucoma eyes from 506 Asian Chinese participants from the Singapore site and 111 glaucoma eyes from 63 Caucasian participants from the Bucharest site were included in the study. The training set of 573 VF–OCT pairs (VF MD = −5.77 ± 5.32 dB) was constructed using the data from Singapore, which was split by an 80/20 ratio stratified based on VF severity, with the remaining 148 VF–OCT pairs (VF MD = −5.85 ± 5.05 dB) used as the Asian internal test set. All the data from the Bucharest site were used as the Caucasian external test set (VF MD = −4.79 ± 5.79). Characteristics of the datasets are summarized in Table 1. There were no significant differences (p = 0.118) in VF MD between the internal and external test sets, although there were differences in the focal VF distributions (p < 0.001). Subjects in the external test set were younger, had thicker RNFLs, and had more positive refractive errors (all p < 0.05).

TABLE 1.

Demographic characteristics of the datasets

Characteristics	Asian training set	Asian internal test set	Caucasian external test set	p Values*
Number of pairs	573	148	111	–
Number of participants	404	102	63	–
Age, years	66.2 ± 8.9	66.7 ± 8.1	63.6 ± 11.7	0.011
Male, n (%)	266 (66%)	62 (66%)	18 (29%)	<0.001
Ethnicity	Chinese	Chinese	Caucasian	–
Refractive error, D	−1.14 ± 2.25	−1.32 ± 2.22	0.38 ± 1.15	<0.001
Global RNFL thickness, μm	74.95 ± 12.23	76.06 ± 10.67	79.33 ± 13.34	0.030
Visual field mean deviation (VF MD), dB	−5.77 ± 5.32	−5.85 ± 5.05	−4.79 ± 5.79	0.118
Glaucoma severity a				–
Mild	368 (64.2%)	96 (64.9%)	78 (70.3%)	–
Moderate	137 (23.9%)	35 (23.6%)	22 (19.8%)	–
Advanced	68 (11.9%)	17 (11.5%)	11 (9.9%)	–

Note: Values presented as mean ± standard deviation, or number (%). Bold indicates significant difference.

Abbreviations: D, dioptres; RNFL, retinal nerve fiber layer.

^a Mild (VF MD ≥ −6 dB), moderate (−12 dB ≤ VF MD < −6), and advanced (VF MD < −12 dB).

*p Values represent significance values for t‐tests between the internal and external test sets.

The performance of the different approaches in estimating VF MD on the Asian internal and Caucasian external test sets is presented in Table 2, Table 3, and plotted against the corresponding measured VF MD in Figure 1. Baseline MAE of the internal test set for VF MD was −3.80 dB. The ML approaches (EN, SVR, MLP, and XGB) each performed significantly better (p < 0.05) than baseline MAE on the internal test set and each approach generated results significantly correlated with the measured VF MD (p < 0.05). However, only XGB and SVR showed significant improvements compared with LR. Among the ML approaches, XGB produced in a lower MAE and higher correlation than the other models; however, multiple comparison analysis showed that differences in MAE were not significant except between XGB and MLP. On the external test set with a baseline VF MD MAE of 4.09 dB, similar trends were observed, with all ML models performing significantly better than baseline and LR (p < 0.05). Although a lower MAE and a better correlation with VF MD was observed with XGB, differences between the models were again not significant. Table 3 shows the MAE performance stratified by glaucoma severities for the different approaches, with a higher MAE occurring in eyes with more severe glaucoma.

TABLE 2.

Comparison of machine learning approaches for global visual field mean deviation modeling

	Asian internal test set			Caucasian external test set
Approach	Pearson's correlation	Mean absolute error (MAE) a	Baseline MAE change (%) b	Pearson's correlation	Mean absolute error (MAE) a	Baseline MAE change (%) b
Baseline	–	3.80		–	4.09	–
Linear regression (LR)	0.43 [0.34, 0.57]	3.47 [2.97, 3.94]	−8.7 [−21.8, +3.7]	0.39 [0.24,0.50]	3.86 [3.54, 5.11]	−5.6 [−13.4, +24.9]
Elastic net regression (ENR)	0.51 [0.37, 0.59]	3.19 [2.74, 3.71]	−16.1 [−27.9, −2.7]	0.51 [0.36, 0.67]	3.45 [2.95, 4.51]	−15.6 [−27.9, +10.3]
Support vector regression (SVR)	0.54 [0.39, 0.64]	3.09 [2.58, 3.67]	−18.7 [−32.1, −3.4]	0.59 [0.35, 0.77]	3.15 [2.73, 4.39]	−23.0 [−33.3, +7.3]
Multi‐layer perceptron (MLP)	0.42 [0.21, 0.55]	3.35 [2.84, 3.96]	−11.4 [−25.3, +4.2]	0.61 [0.35, 0.76]	3.16 [2.87, 4.34]	−22.7 [−29.8, +6.1]
Convolutional neural net (CNN)	0.51 [0.35, 0.61]	3.25 [2.81, 3.79]	−14.5 [−26.1, −0.3]	0.62 [0.39, 0.79]	3.13 [2.70, 4.18]	−23.4 [−34.0, +2.2]
Gradient‐boosted trees (XGB)	0.59 [0.47, 0.66]	3.01 [2.57, 3.48]	−20.7 [−32.4, −8.4]	0.66 [0.46, 0.83]	3.04 [2.59, 3.99]	−25.5 [−36.7, −2.4]

Note: Values presented as means with 95% confidence intervals adjusted for intereye correlations using bootstrapping clustered by subject. Bolded values are significantly lower (p < 0.05) than baseline MAE within the corresponding test set using the Wilcoxon signed‐rank test.

^a MAE values presented in dB.

^b Represents % reduction of MAE from baseline MAE, where negative (−) values represent a reduction in MAE and positive (+) values represent an increase in MAE with respect to baseline values.

TABLE 3.

Mean absolute error (MAE) performance by glaucoma severity of machine learning approaches for global VF MD prediction

	Asian internal test set			Caucasian external test set
Model	Mild glaucoma	Moderate glaucoma	Advanced glaucoma	Mild glaucoma	Moderate glaucoma	Advanced glaucoma
Linear regression (LR)	2.61 [2.19, 2.84]	3.06 [2.37, 3.84]	9.05 [7.10, 11.32]	3.06 [2.60, 3.48]	2.14 [1.53, 2.95]	12.91 [11.62, 16.00]
Elastic net regression (ENR)	2.39 [1.94, 2.70]	2.88 [2.15, 3.54]	8.40 [6.55, 10.75]	2.48 [1.99, 2.77]	2.49 [1.80, 3.76]	12.18 [10.77, 15.95]
Support vector regression (SVR)	1.70 [1.37, 2.00]	3.76 [2.93, 4.49]	9.54 [7.87, 11.84]	1.87 [1.58, 2.14]	2.65 [2.05, 3.36]	13.22 [11.91, 17.31]
Multi‐layer perceptron (MLP)	2.37 [1.97, 2.87]	3.69 [2.84, 4.45]	8.17 [5.80, 11.18]	2.16 [1.99, 2.61]	2.81 [1.86, 3.34]	10.93 [9.11, 15.72]
Convolutional neural net (CNN)	2.39 [1.95, 2.87]	3.59 [2.80, 4.28]	7.37 [5.90, 9.88]	2.10 [1.76, 2.46]	3.25 [2.47, 4.06]	10.18 [7.86, 14.83]
Gradient‐boosted trees (XGB)	1.99 [1.60, 2.27]	3.47 [2.75, 4.13]	7.84 [5.88, 9.98]	2.08 [1.73, 2.36]	3.06 [2.65, 3.91]	9.77 [7.22, 14.36]

Note: Values are presented in dB, with 95% confidence levels. Glaucoma severity was categorized as mild (VF MD – 6 dB), moderate (−12 dB VF MD < −6), or advanced (VF MD < −12 dB).

FIGURE 1.

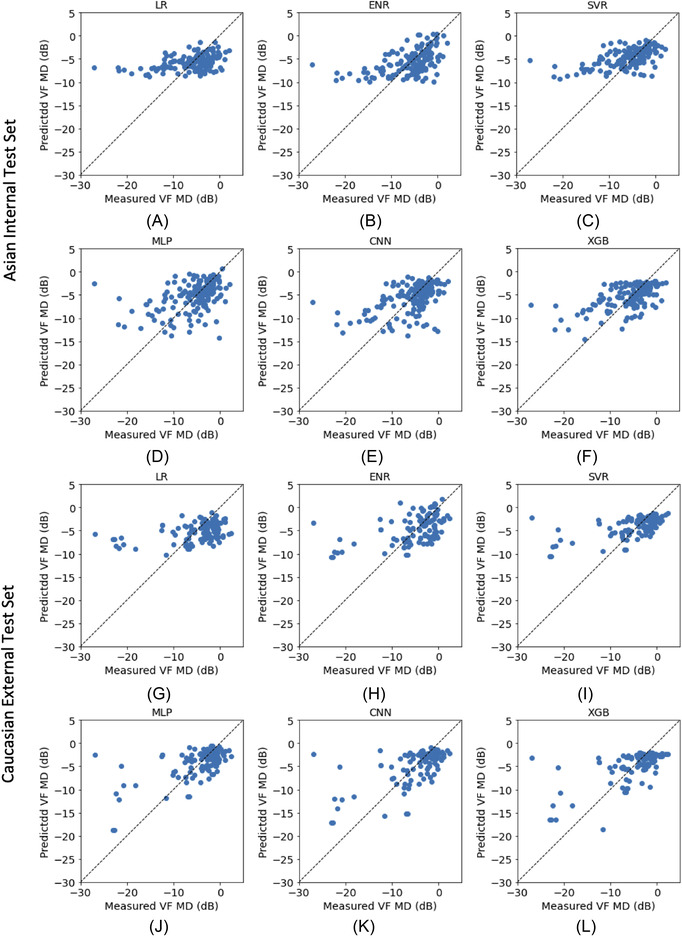
VF MD estimation performance of the different models on the (A–F) Asian internal test and (G–L) Caucasian external test sets. Abbreviations: CNN, convolutional neural net; ENR, elastic net regression; LR, linear regression; MLP, multi‐layer perceptron; SVR, support vector regression; XGB, gradient‐boosted trees

Focal estimation of point‐wise VF deviation values was developed using each ML model and the results of the Asian internal and Caucasian external test sets are summarized in Table 4 as the median and IQR across the VF. Scatter plots of the estimated values against the measured values are provided in the Supplementary Figures. All ML models performed significantly better than baseline on both test sets. Multiple comparison analysis showed that there were significant differences between the approaches (p < 0.001), with XGB and SVR achieving significantly better focal MAE than the other ML models (p < 0.05). XGB achieved a higher MAE on the internal test set (4.44 dB [IQR: 3.45–5.17]) but lower MAE on the external test set (3.87 dB [IQR: 3.64–4.22]) compared with SVR (internal test set: 4.30 dB [IQR: 3.38–5.21]; external test set: 3.89 dB [IQR: 3.62–4.30]). However, the differences between the two approaches were not statistically significant. Both XGB and SVR showed similar overall levels of error reduction in the internal and external test sets. The spatial distribution of focal VF severities and the performance of the XGB models is shown Figure 2. The focal results of the other models are shown in Figure 3 for the Asian test dataset and in Figure 4 for the Caucasian test dataset. Both test datasets have different spatial distributions (p < 0.001), with more VF locations in the superior hemifield having a greater severity in the internal test set, while the VF severities in the external test set are comparatively more distributed throughout the VF. Higher VF variability occurred at locations of higher VF severity. MAE reductions, which correspond to better VF estimations, tended to be better at focal locations of higher VF severity.

TABLE 4.

Comparison of machine learning models for focal visual field mean deviation modeling

	Asian internal test set			Caucasian external test set
Method	Pearson's correlation	Mean absolute error (MAE) a	Baseline MAE change (%) b	Pearson's correlation	Mean absolute error (MAE) a	Baseline MAE change (%) b
Baseline	–	5.16 [3.77–6.45]	–	–	4.66 [4.09–5.24]	–
Elastic net regression (ENR)	0.40 [0.35–0.45]	4.72 [3.65–5.65]	−8.76 [−12.03 to −3.27]	0.41 [0.36–0.45]	4.46 [3.80–4.98]	−5.57 [−11.28 to −0.81]
Support vector regression (SVR)	0.41 [0.36–0.47]	4.30 [3.38–5.21]	−15.35 [−18.52 to −10.17]	0.45 [0.39–0.52]	3.89 [3.62–4.30]	−14.52 [−18.13 to −10.79]
Multi‐layer perceptron (MLP)	0.35 [0.29–0.42]	4.96 [4.01–5.75]	−6.58 [−10.04 to +3.37]	0.44 [0.34–0.52]	4.23 [3.90–4.55]	−7.58 [−16.11 to −1.31]
Convolutional neural net (CNN)	0.38 [0.31–0.45]	4.58 [3.88–5.42]	−10.75 [−14.84 to +1.98]	0.48 [0.37–0.53]	4.03 [3.74–4.50]	−10.90 [−16.66 to −5.68]
Gradient‐boosted trees (XGB)	0.44 [0.30–0.51]	4.44 [3.45–5.17]	−14.40 [−18.85 to −9.36]	0.44 [0.35–0.49]	3.87 [3.64–4.22]	−14.12 [−19.67 to −9.96]

Note: Values presented as median and interquartile range over the 52 visual field test locations in the 24‐2 visual field. Bolded values are significantly lower (p < 0.05) than baseline MAE within the test set using Wilcoxon signed‐rank test.

^a MAE values presented in dB.

^b Represents % reduction of MAE from baseline MAE, where negative (−) values represent a reduction in MAE and positive (+) values represent an increase in MAE with respect to baseline values.

FIGURE 2.

Focal visual field severity and estimation performance for XGB. (Top row) (A) Mean focal severities (dB), (B) focal baselines (dB), (C) focal mean average errors (MAE, dB), and (D) focal MAE reduction (%) for the Asian internal test set; (bottom row) (E) mean focal severities (dB), (F) focal baselines (dB), (G) focal mean average errors (MAE, dB), and (H) focal MAE reduction (%) for Caucasian external test set. Focal MAE reductions were calculated against baselines at the same VF locations. Other models are shown in Figures 3 and 4

FIGURE 3.

Focal visual field (VF) estimation performance with respect to 24‐2 VF locations on the Asian internal test set, with left column showing focal mean absolute errors (MAEs) and right column showing MAE reduction against baseline in percentages. Abbreviations: CNN, convolutional neural net; ENR, elastic net regression; MLP, multi‐layer perceptron; SVR, support vector regression

FIGURE 4.

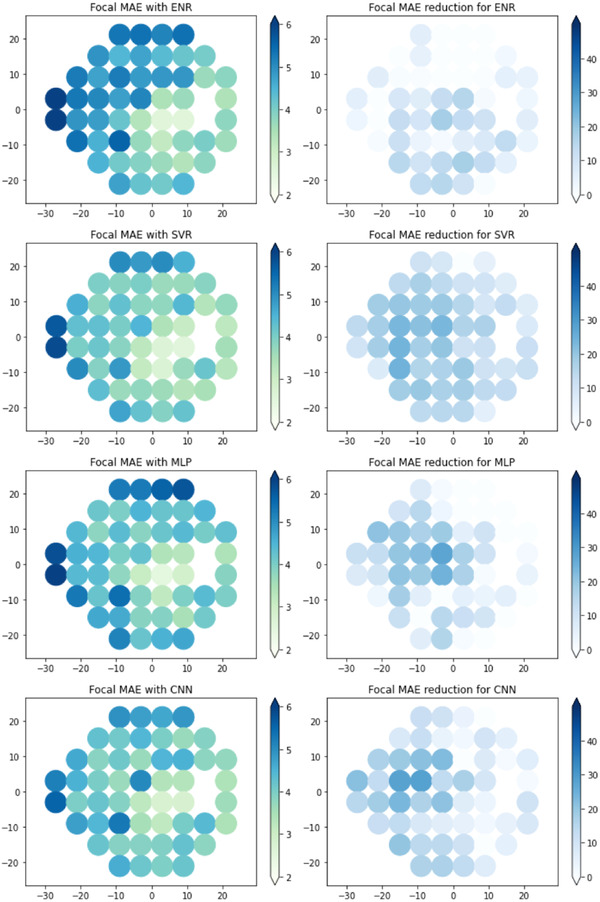
Focal visual field (VF) estimation performance with respect to 24‐2 VF locations on the Caucasian external test set, with left column showing focal mean absolute errors (MAEs) and right column showing MAE reduction against baseline in percentages. Abbreviations: CNN, convolutional neural net; ENR, elastic net regression; MLP, multi‐layer perceptron; SVR, support vector regression

DISCUSSION

In this study, we tested different current ML models for the estimation of VF loss using structural RNFL measurements. In addition to an internal test dataset composed of data from the primary study site (Asian), data from a secondary site comprised of participants with a different ethnicity (Caucasian) were used as an external test set. Results from both internal and external test sets showed that the ML models all performed significantly better than both baseline and standard linear regressions in estimating VF MD, but estimation accuracies were affected by underlying VF severities. Although XGB tended to perform better than the other ML approaches for the estimation of VF MD, differences between the approaches were largely not significant. In the modeling of focal VF losses, XGB and SVR were comparable, with post‐hoc analysis showing both performed significantly better than other approaches. We also observed that estimation performance in the external test set was better compared with the internal test set, which could be attributed to differences in the spatial distribution of focal severities in the two test sets. Strengths of our study include the use of a standardized, stratified approach for dataset construction, the use of a completely independent external test set, and the comparison of both global and focal VF estimations in the same study using representative approaches of current paradigms in ML.

There has been continued interest in the development and evaluation of models for the estimation VF loss in glaucoma from structural measurements of the retina ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ²⁷ , ²⁸ with reported MAEs in the range of 2–5 dB ¹¹ , ¹² , ¹³ , ¹⁴ for VF MD estimation. In most previous studies, comparisons with other approaches were largely limited to linear regression ⁹ , ¹¹ , ¹² , ²⁸ or SVMs. ¹¹ , ²⁸ As data‐driven ML models are highly susceptible to overfitting, the use of external test sets in addition to internal test sets is also increasingly becoming important for evaluating the generalizability of such models. A recent study by Huang and colleagues ¹¹ on VF MD estimation jointly compared several approaches with validation on several datasets; however, this was only for VF MD estimation. Further, it is challenging to compare the results of different ML models on different datasets from different studies owing to the inherent dependence of model performance on the underlying profiles of the datasets.

To address these limitations, we compared several models based on different ML paradigms on both internal and external test sets. The results we report are largely consistent with previous studies, which show that learning‐based methods, including ANNs ¹¹ or CNNs, ¹² can significantly improve VF MD estimations over linear regression. Among the different methods, XGB generally performed well in estimating both global and focal VF values, achieving MAEs of 3.01 and 3.04 dB, respectively, on the internal and external test sets for VF MD, with significantly better focal estimations than most other models. The results are supported by reports from Shwartz‐Ziv and Armon, ²⁹ who compared the performance of XGB against other deep networks, and from Olson and coworkers, ³⁰ who compared XGB against other ML networks. Their findings demonstrated that on heterogeneous tabular data for disparate tasks, ranging from the estimation of gestures to sales figures, ²⁹ to bioinformatics classification tasks, such as diagnosis and postoperative management, ³⁰ XGB was found to perform relatively well compared with other machine learning networks or against more advanced deep networks. Also, the close performance of SVR with XGB in our results is supported by other studies, which also found SVR to perform close to XGB ³⁰ or other decision tree‐based approaches. ³¹ Our findings also demonstrate the potentiality of these models in structure–function modeling for estimating VF estimates, not only globally but also focally. While global VF modeling allows an estimation of overall VF function, focal VF modeling could enable an earlier detection of developing focal VF defects, which can be useful when evaluating focal event‐based methods to complement global trend‐based methods for progression monitoring. ⁵

We found that model performance on the external test set was generally comparable to that of the internal test set, supporting the conclusion that the models were not overtrained on the training set. This is particularly important given that there were significant demographic differences between the internal and external test sets, including ethnicity. Although the differences in VF severity between the two test sets were not shown to be statistically significant, the reduced VF severity of eyes in the external test set, compared with the internal test set, likely contributed to the reduced MAE. These results are consistent with other studies ⁹ , ³² that have reported larger variabilities with more severe VF loss, which is also apparent from the focal VF maps in Figure 3, wherein locations of greater VF severity showing larger errors in the estimated VF can be observed.

While we found that XGB achieved an MAE 3 dB on both internal and external datasets, further improvements are needed before these models can be used clinically. In particular, the use of such models may be currently limited to earlier stages of disease, where lower MAEs have been shown. Our results (and data from other studies) using data‐driven ML methods show that higher VF severities remain challenging to estimate, where the MAE increases threefold or more. Characteristic of the structure–function relationship in glaucoma is the floor effect observed at higher VF severities, where progressive VF loss occurs without an observable thinning of the RNFL. ¹⁸ , ³³ , ³⁴ This describes the well‐known hockey‐stick shape of the structure–function relationship, ³⁵ in which a relatively linear relationship between structure and function in early glaucoma flattens at higher severities. This floor level, which has been reported to range from −8 to −12 dB in other studies, ¹⁸ , ³³ , ³⁴ , ³⁶ , ³⁷ can also be inferred from the flattening of the VF MD estimations at around the −10 dB level with the LR models in Figure 1. In our study and others using nonlinear approaches based on decision trees, support vectors, or neural networks, a pertinent question to ask is why these difficulties at higher severities remain?—even in nonlinear models trained with relatively larger datasets. The difficulty in modeling can be possibly attributed to several considerations.

Variability in the structure–function relationship, due to the presence of non‐neuronal components in the RNFL and individual differences, ³⁸ is increased in later stages of glaucoma due to residual floor effects, ³⁴ such that ganglion cell losses leading to worsening of visual function may not be adequately captured by changes in the RNFL. This variability acts as noise, which complicates model training by obscuring the structure–function relationship. Further, as we showed above (and others have noted), a large proportion of the data is composed of eyes with mild to moderate glaucoma (VF MD < −12 dB), which is within the floor effect reported in prior studies (−8 to −12 dB). The implication of this is that models are optimized to generate VF estimations based on the structure–function relationship at mild‐to‐moderate severities, leading to larger errors in estimating VF severities beyond the RNFL floor, where there is a flattening of the structure–function relationship. It may be challenging in practice, however, to obtain large enough datasets in which the severity distribution is uniform. While different models could be trained for different severities, this would ostensibly require predetermination of disease severities using an additional classification model, or the use of anatomical compensation ³⁹ to adjust RNFL measurements for interindividual demographic differences to better stratify disease severity. Inclusion of vascular information from OCT angiography, which we and others have shown to be less susceptible to floor effects, could also help to improve the structure–function association, ⁴⁰ , ⁴¹ , ⁴² , ⁴³ particularly in more advanced glaucoma. ³⁷ These and other strategies, such as the use of repeated VF data to reduce VF variability or a more precise determination of neuronal content in the RNFL, ⁴⁴ can be considered in future studies to further improve the VF estimation to allow these models to be used clinically.

Limitations of our study include the use of only circumpapillary RNFL thickness measurements from optic nerve head scans, which rely on segmentations provided by the review software. The RNFL measurements included both neuronal and non‐neuronal components, which could lead to an overestimation of the actual neuronal content with the RNFL. Wide‐field macula data can potentially provide additional information for VF locations within the central field of view but were not available for use in this study. We were also unable to determine the intertest variability of the VF tests, as only one test per eye was available. VF–OCT pairs were limited to an interval of 1 year and we were unable to determine if there were any progression or glaucomatous changes during the interval between the OCT scan and VF test for each participant, which could be a potential source of noise in the data. The MLP and CNN configurations were adapted from previous studies, and the findings associated with these approaches should not be generalized without a more exhaustive survey of all possible network configurations. In particular, more complicated CNN configurations trained on larger datasets could potentially improve performance, and further comparative studies on much larger datasets could provide more insight on relative performance at scale. In this study, we focused on evaluating VF estimates from segmented RNFL thickness measurements. However, recent studies using convolutional deep learning models based on unsegmented imaging data have shown promise in estimating VFs. ¹³ , ¹⁴ , ²⁷ , ⁴⁵ , ⁴⁶ Such approaches offer advantages by not relying on the accuracy of segmented RNFL measurements as well as potentially using intrinsic information beyond the RNFL layer, and studies will be needed to compare these approaches with methods using segmented data on the same datasets.

CONCLUSIONS

Different ML models for global and focal VF estimation were compared using independent internal and external test sets with different ethnicities and demographics. The results of our comparison of several models show that those based on XGB generally performed well in both internal and external test sets and thus may be a useful approach for future structure–function studies. We also found that all models had difficulties to varying degrees in more severe VFs. Future studies are needed to develop better models with more consistent performance across severities.

COMPETING INTERESTS

The authors declare no competing interests.

AUTHOR CONTRIBUTIONS

Conception and design: D.W., J.C., A.P.‐C., and L.S. Acquisition of data: I.B., E.N.V., R.H., A.P.‐C., and L.S. Analysis and interpretation of data: D.W., J.C., R.S.C., M.E.N., A.P.‐C., T.A, and L.S. Drafting of manuscript: D.W. and L.S. Revision of intellectual content of the manuscript: D.W., J.C., I.B., R.S.C., M.E.N., E.N.V., R.H., A.P.‐C., T.A., and L.S. Approval of final version of the manuscript: D.W., J.C., I.B., R.S.C., M.E.N., E.N.V., R.H., A.P.‐C., T.A, and L.S. Responsibility for the integrity of the data analysis: L.S.

PEER REVIEW

The peer review history for this article is available at: https://publons.com/publon/10.1111/nyas.14844.

Supporting information

Figure S1. Distribution of the focal visual field estimates for the Asian internal test data, stratified by severity of the measured focal visual field deviation, as box plots with interquartile limits represented by the box edges and medians by the lines within the boxes for (A) elastic net regression (ENR), (B) support vector regression (SVR), (C) multi‐layer perceptrons (MLP), (D) convolutional neural network (CNN), and (E) gradient‐boosted tress (XGB). The distribution at each severity is shown in (E). Note that the plots presented here are consolidated from the 52 individual models trained at each of the 52 VF locations.

Figure S2. Distribution of the focal visual field estimates for the Caucasian external test data, stratified by severity of the measured focal visual field deviation, as box plots with interquartile limits represented by the box edges and medians by the lines within the boxes for (A) elastic net regression (ENR), (B) support vector regression (SVR), (C) multi‐layer perceptrons (MLP), (D) convolutional neural network (CNN), and (E) gradient‐boosted tress (XGB). The distribution at each severity is shown in (E). Note that the plots presented here are consolidated from the 52 individual models trained at each of the 52 VF locations.

Wong, D. , Chua, J. , Bujor, I. , Chong, R. S. , Nongpiur, M. E. , Vithana, E. N. , Husain, R. , Aung, T. , Popa‐Cherecheanu, A. , & Schmetterer, L. (2022). Comparison of machine learning approaches for structure–function modeling in glaucoma. Ann NY Acad Sci., 1515, 237–248. 10.1111/nyas.14844