Socioeconomic status and depressive symptoms: An individual-participant data meta-analysis on range restriction and measurement in the United States

Abstract

Introduction:

The association between socioeconomic status (SES) and depressive symptoms is well documented, yet less attention has been paid to the methodological factors contributing to between-study variability. We examined the moderating role of range restriction and the depressive-symptom measurement instrument used in estimating the correlation between components of SES and depressive symptoms.

Methods:

We conducted an individual participant data meta-analysis of nationally-representative, public-access datasets in the United States. We identified 123 individual datasets with a total of 1,655,991 participants (56.8 % female, mean age = 40.33).

Results:

The presence of range restriction was associated with larger correlations between income and depressive symptoms and with smaller correlations between years of education and depressive symptoms. The measurement instrument of depressive symptoms moderated the association for income, years of education, and occupational status/prestige. The Center for Epidemiological Studies–Depression scale consistently produced larger correlations. Higher measurement reliability was also associated with larger correlations.

Limitations:

This study was not a comprehensive review of all measurement instruments of depressive symptoms, focused on datasets from the United States, and did not examine the moderating role of sample characteristics.

Discussion:

Methodological characteristics, including range restriction of SES and instrument of depressive symptoms, meaningfully influence the observed magnitude of association between SES and depressive symptoms. Clinicians and researchers designing future studies should consider which instrument of depressive symptoms is suitable for their purpose and population.

1. Introduction

A higher incidence of major depressive disorder and a negative association between socioeconomic status (SES) and depressive symptoms have consistently been reported among populations from lower-SES backgrounds (Elovainio et al., 2020; Lorant et al., 2003; Whitfield et al., 2021). Research syntheses, however, have documented substantial variation between effect sizes (Korous et al., 2018). Methodological characteristics such as measurement error likely contribute to the magnitude of the observed association (Brakenhoff et al., 2018). Given emerging research on the elevated risk of depressive symptoms at higher SES levels compared with national norms (Luthar et al., 2020) and variation in the indicators used to capture depression across different measurement instruments (Fried, 2017), the current study focused on two methodological factors: range restriction of SES and measurement of depressive symptoms (i.e., instrument type, measurement reliability).

Range restriction refers to when a subset of data values is included in an analysis instead of the full range of possible values. For instance, there would be a restricted range in grade point average (ranging from 0.0 to 4.0) if only values between 2.0 and 3.0 were included. This restriction of range, such as the use of a truncated range of values for a component of SES across a sample, can bias the magnitude of an effect size (Schmidt et al., 2019; Schmidt and Hunter, 2015). Range restriction is generally not a concern for regression coefficients when the relation between two variables is linear and homoscedastic; however, the magnitude of correlations (i.e., Pearson’s $r$) will be reduced when range is truncated (Cohen et al., 2003; Goodwin and Leech, 2006). Bland and Altman (2011) demonstrated this effect with body mass index (BMI), showing that when BMI values were restricted to 30–35 kg/m², the correlation between BMI and abdominal circumference was substantially reduced (r = − 0.09) compared to when the full range of BMI values were used (r = 0.85). Methods for estimating the true correlation in primary studies and meta-analyses (Hunter et al., 2006; Schmidt et al., 2019; Schmidt and Hunter, 2015) have not been extensively applied in studies of SES and depressive symptoms.

Range restriction can occur due to sampling methods (indirect; e.g., failure to recruit participants from both ends of the distribution) or due to measuring SES (direct; e.g., developing interval items with a bottom- or top-coded value that groups together participants with meaningful SES differences). Emerging research reveals that depression among individuals from the highest-income households is more common than previously understood (Luthar et al., 2020). Therefore, in some populations, the association between SES and depressive symptoms may be nonlinear. In the presence of range restriction, this nonlinear form is unlikely to be represented in a study; thus, the correlation between SES and depressive symptoms could be overestimated relative to a study that included, and distinguished, those from the highest ends of the distribution (Goodwin and Leech, 2006). Range restriction limits narrowing down the effect of SES on depressive symptoms and contributes to systematic noise between effect sizes.

Measuring depressive symptoms can also present a challenge to estimating an effect size. Instruments that measure depressive symptoms vary in the type of symptoms included, their reference time range (e.g., past 2 weeks, past month), and informant. A comparison of symptoms across 7 commonly used instruments (Fried, 2017), including the Beck Depression Inventory (BDI; Beck et al., 1996) and the Center for Epidemiological Studies–Depression scale (CES-D; Radloff, 1977), identified 52 distinct symptoms, 40 % of which were included in only one scale and 6 % of which were shared across all scales; the CES-D had the lowest overlap. Thus, one measurement instrument may not generalize to others, especially to the CES-D.

Measurement error or unreliability can also systematically bias the magnitude of an effect size (Schmidt et al., 2019). Instruments with lower internal reliability are likely to produce smaller-magnitude correlations than those with higher reliability. Despite this impact, measurement error has largely been overlooked in the epidemiological literature (Brakenhoff et al., 2018). Evidence of the role of measurement error in the association between SES and depressive symptoms is needed to encourage researchers to run sensitivity analyses to correct for this effect (Bartlett and Keogh, 2018; Campbell et al., 2021; Schmidt et al., 2019).

Prior meta-analyses have not provided conclusive evidence of the moderating role of SES range restriction and the depressive symptom instrument used. A meta-analysis of 51 studies (Lorant et al., 2003) found substantial heterogeneity between effect sizes, which was attributed in part to whether a symptom inventory (e.g., CES-D) or diagnostic instrument (e.g., the Composite International Diagnostic Interview [CIDI]; World Health Organization, 1997) was used. Another meta- analysis (Lemstra et al., 2008) found substantial heterogeneity between nine studies among youth but no evidence that the instrument explained the variability, although power was likely a limitation in this analysis. Two additional meta-analyses directed at youth did not test moderation of measurement; one reported a small effect size (Letourneau et al., 2011), the other a null effect size using the Child Depressive Inventory [CDI; Kovacs, 1985] (Twenge and Nolen-Hoeksema, 2002).

The aim of this study was to investigate the role of SES range restriction and the depressive symptom instrument used in estimating the correlation between components of SES and depressive symptoms. We operationalized SES using income, educational attainment, and occupational status/prestige because these components correlate with specific contexts and access to financial, social, and cultural capital (Bradley, 2016; Korous et al., 2018). Our research question was “Does range restriction in SES components and the depressive symptom instrument used, and these instruments’ measurement error, moderate the correlation between SES and depressive symptoms?”. We tested this question by conducting an individual participant data (IPD) meta-analysis using a combination of meta-analytic methods, multilevel modeling, and structural equation modeling.

2. Methods

We followed reporting standards for IPD meta-analyses (Stewart et al., 2015). Our reporting checklist is provided in Supplemental Table 1. This study was approved by the Institutional Review Board at Arizona State University. Study materials are available on Open Science Framework. Datasets can be requested from the Inter-university Consortium for Political and Social Research (ICPSR; University of Michigan, 2018). Additional details about the methods are available in supplemental material.

2.1. Study identification and screening

We identified IPD datasets from a pool of 127 public-access datasets deposited on ICPSR that focused on depressive symptoms in the United States. A detailed breakdown of study identification, systematic search, and eligibility is reported elsewhere (Causadias et al., 2018). Measurement instruments that had two or more items related to depressive symptoms were eligible for inclusion. Instruments that employed skip logic were excluded because they assess symptoms only after participants report feeling depressed or lost interest (e.g., CIDI). Additionally, datasets that did not include a codable measure for one of the three SES components (income, education, occupation) were excluded. Participants with missing data on depressive symptoms, SES components, age, gender/sex, or race/ethnicity were excluded during data extraction.

2.2. Data items

For each participant, we computed a mean score for depression symptoms. Income was defined as annual participant/household income. Education was defined as the number of completed years of formal education. For youth aged under 18 years, the highest level of parental education was included. Intervals were recoded at the midpoint (e.g., 9 to 12 years = 10.5). We used the Nam-Powers-Boyd Occupational Status Scale (Nam and Boyd, 2004) and the Nakao and Treas (1994) scale to compute occupational status and prestige scores, respectively. Both scales range from 0 (lowest) to 100 (highest). For youth aged under 18 years, the highest parental occupation status and prestige score was included. Range restriction was coded for each SES component by examining the minimum and maximum values across participants within each dataset. Table 1 displays the classification criteria for range restriction.

Table 1.

Range restriction classification.

Component of socioeconomic status	Did not include or distinguish participants with
	Lower-end	Upper-end
Income	<$20,000	>$120,000a
Years of education	<12 years	>16 years
Occupational statusb	<25	>75
Occupational prestigeb	<25	>75

^aAmerican Trends Panel reported that higher-income families had annual incomes of $120,400 or more in 2018 (Horowitz et al., 2020).

^b<25 = bottom-quartile, >75 = top-quartile.

Each instrument was dummy coded. The specific measurement instruments of depressive symptoms included in this study were based on the measurement instruments used in nationally-representative, public-access datasets that were available on ICPSR. These instruments included the Behavior Problem Index (BPI; Peterson and Zill, 1986), CES-D (Radloff, 1977), K6+ Self-Reporting Measure (K6; Kessler et al., 2003), Mental Health Inventory-5 (MHI-5; Stewart et al., 1988), Psychiatric Epidemiology Research Interview Demoralization Scale (PERID; Dohrenwend et al., 1980), Public Health Questionnaire-9 (PHQ-9; Kroenke et al., 2001), and Short Form-36 (SF-36; Ware and Sherbourne, 1992). A brief description of each measure and example symptoms are displayed in Supplemental Table 2. Measurement error was examined using two coefficients: alpha ($\alpha$; Cronbach, 1951) and omega ($\omega$; McDonald, 1999). The year of data collection for each dataset was coded as a potential confounding methodological characteristic.

2.3. Analysis plan

We used the metaSEM package (Cheung, 2015) in R Studio (RStudio Team, 2020) to conduct a multi-level mixed-effects meta-analysis. Correlations were transformed from $r$ to Fisher’s $z$ metric prior to analysis (Borenstein et al., 2021). A multi-level model was used because several correlations were extracted from the same dataset, making them conditionally dependent; clustering effect sizes more accurately estimates variance at different levels of analysis (Cheung, 2014). In our multi-level model, level-1 was defined as the sampling variability of the correlation, level-2 as the correlations ($r$), and level-3 as the dataset from which the correlations were extracted. We chose to cluster by dataset because some datasets, although from the same parent study, may have used different measurement instruments and reliability estimates.

Moderation analyses were conducted to examine the effect of range restriction, instrument used, measurement error, and year of data collection. Two moderation analyses were conducted for the instrument of depressive symptoms. First, an intercept-free model was specified to estimate the correlation and 95 % confidence interval (CI) for each instrument. Second, we dummy coded each instrument of depressive symptoms and specified the CES-D as the reference instrument (intercept) because it was the most frequently used and has the least amount of overlap with other instruments (Fried, 2017). Range restriction was tested as a dichotomized moderator, and measurement reliability and year of data collection were tested as continuous moderators (scaled and centered). As a post-hoc exploratory test, the number of items used for the CES-D instrument was also tested as a continuous moderator among datasets that included the CES-D.

3. Results

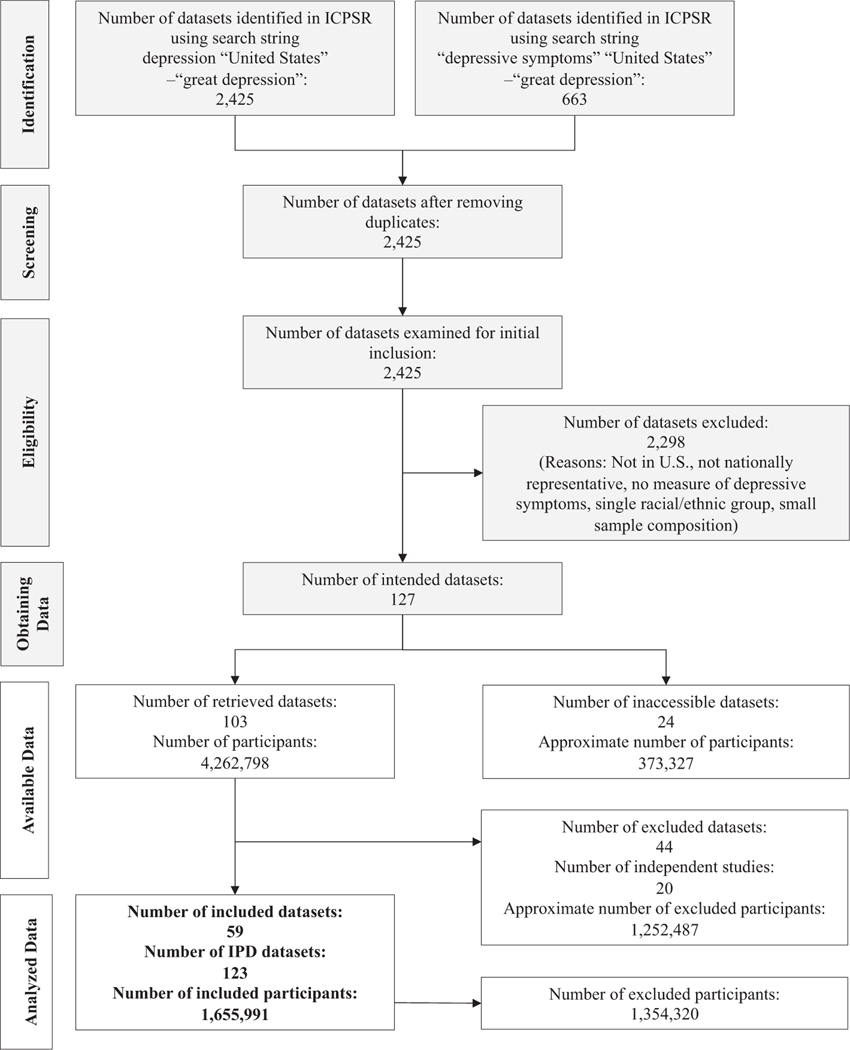
Fig. 1 shows our study selection process. We included 59 ICPSR datasets (out of 127) from 23 independent studies with a total of 1,655,991 participants. Because some of the 59 ICPSR datasets included more than one wave of data collection, different cohorts, or included respondent and spouse datasets separately, we extracted correlations from 123 IPD datasets.

Fig. 1.

Flow diagram of the inclusion and exclusion process.

The light grey boxes were part of the initially identified datasets (Causadias et al., 2018). The white boxes indicate the inclusion and exclusion process applied in the current study. ICPSR = Inter-university Consortium for Political and Social Research. IPD = individual participant data.

3.1. Descriptive characteristics

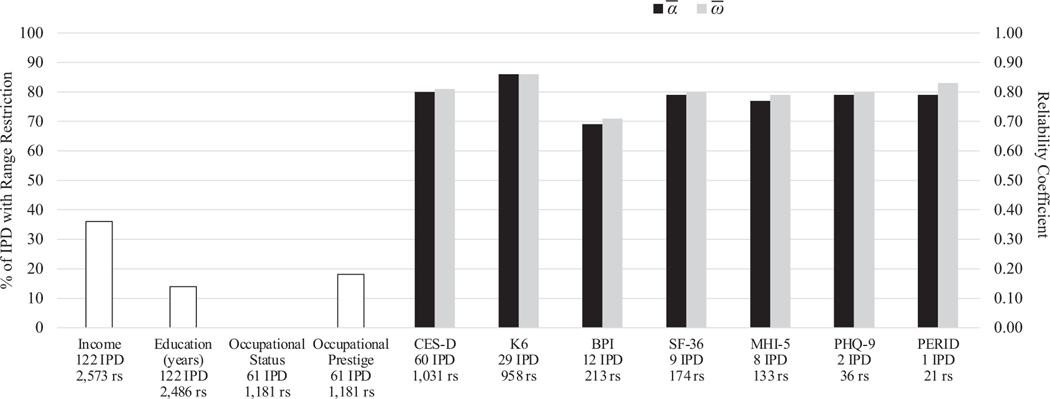
Supplemental Table 3 summarizes extracted data from the 59 ICPSR datasets. The average number of participants per IPD dataset was 13,463 (range 799–50,111). The average age across IPD datasets was 40.33 years (range of mean age 6.91–77.91). Female participants (56.8 %) outnumbered males. There were more non-Hispanic (NH) White (64.4 %) relative to NH Black (16.0 %), Hispanic/Latinx (14.9 %), NH Asian American (2.3 %), NH Native American (0.8 %) and NH multiracial (1.7 %) participants. Year of data collection ranged from 1985 to 2018. Fig. 2 displays the number of IPD datasets for each component of SES and for each instrument of depressive symptoms, the percent of IPD datasets that had evidence of range restriction, and the average reliability coefficient ($\overline{\alpha }$, $\overline{\omega }$) for each instrument of depressive symptoms. Additional characteristics are presented in supplemental material. For income and years of education, evidence of a restricted range was observed towards the upper-end, but not towards the lower-end. There was no evidence of a restricted range for occupational status or prestige.

Fig. 2.

Percentage of datasets (out of 123) with range restriction and average reliability coefficients for each measurement instrument of depressive symptoms. IPD = individual participant data. rs = number of correlations. $\overline{\alpha }$ = average alpha. $\overline{\omega }$ = average omega. BPI = Behavior Problem Index. CES-D = Center for Epidemiologic Studies Depression Scale. SF-36 = Short Form-36. K6 = K6+ Self-Reporting Measure. PERID = Psychiatric Epidemiology Research Interview Demoralization Scale. PHQ-9 = Public Health Questionnaire-5. MHI-5 = Mental Health Inventory-5.

3.2. Moderation by range restriction

We found evidence of moderation by range restriction for income (Table 2) and years of education (Table 3). For income, the correlation was larger for range-restricted than for non–range-restricted IPD datasets. For years of education, the correlation was smaller for range-restricted than for non–range-restricted datasets. We found no evidence of moderation by range restriction for occupational prestige (Table 5).

Table 2.

Moderation of the association between income and depressive symptoms.

Moderator	Est.	$p$	[95 % CI]	${\widehat{\tau }}_{(2)}^2$	${\widehat{\tau }}_{(3)}^2$	$R_{(2)}^2$	$R_{(3)}^2$
Range restriction				0.004	0.002	0.587	0.971
Not present (intercept)	−0.114	.000	[−0.125, −0.104]
Present (slope)	−0.027	.002	[−0.044, −0.010]
Measure				0.004	0.001	0.585	0.977
CES-D	−0.129	.000	[−0.140, −0.118]
BPI	−0.090**	.000	[−0.116, −0.064]
K6	−0.129	.000	[−0.144, −0.115]
MHI-5	−0.065***	.000	[−0.095, −0.035]
PERID	−0.150	.001	[−0.237, −0.064]
PHQ-9	−0.154	.000	[−0.212, −0.096]
SF-36	−0.163*	.000	[−0.192, −0.134]
Alpha ($\mathit{\alpha }$)				0.004	0.002	0.598	0.967
Intercept	−0.125	.000	[−0.133, −0.116]
Slope	−0.043	.000	[−0.050, −0.036]
Omega ($\mathit{\omega }$)				0.004	0.002	0.134	0.083
Intercept	−0.128	.000	[−0.136, −0.119]
Slope	−0.039	.000	[−0.046, −0.033]
Data collection year				0.004	0.002	0.586	0.970
Intercept	−0.125	.000	[−0.134, −0.117]
Slope	−0.010	.014	[−0.019, −0.002]
Multiple moderator model				0.004	0.001	0.599	0.983
Intercept	−0.130	.000	[−0.140, −0.120]
Range restriction	−0.047	.000	[−0.069, −0.024]
BPI	−0.024	.083	[−0.051, 0.003]
K6	0.074	.000	[0.048, 0.099]
MHI-5	0.059	.000	[0.030, 0.088]
PERID	−0.010	.802	[−0.092, 0.071]
PHQ-9	0.026	.361	[−0.030, 0.081]
SF-36	−0.039	.005	[−0.066, −0.012]
Omega ($\omega$)	−0.041	.000	[−0.047, −0.034]
Data collection year	−0.015	.000	[−0.023, −0.008]

Note. Alpha, omega, and data collection year were centered and standardized. Est. = intercept and slope coefficients, except for moderation by measure, which displays the estimated correlation (Fisher’s $z$) for each measure; asterisks indicate whether a particular measure is significantly different from the CES-D.

^*p < .05.

^**p < .01.

^***p < .001.

Table 3.

Moderation of the association between years of education and depressive symptoms.

Moderator	Est.	$p$	[95 % CI]	${\widehat{\tau }}_{(2)}^2$	${\widehat{\tau }}_{(3)}^2$	$R_{(2)}^2$	$R_{(3)}^2$
Range restriction				0.006	0.002	0.003	0.207
Not present (intercept)	−0.129	.000	[−0.139, −0.119]
Present (slope)	0.052	.000	[0.028, 0.076]
Measure				0.006	0.001	0.008	0.382
CES-D	−0.146	.000	[−0.159, −0.134]
BPI	−0.110	.000	[−0.157, −0.063]
K6	−0.087***	.000	[−0.102, −0.072]
MHI-5	−0.082***	.000	[−0.114, −0.050]
PERID	−0.095	.043	[−0.186, −0.003]
PHQ-9	−0.126	.000	[−0.188, −0.064]
SF-36	−0.138	.000	[−0.167, −0.108]
Alpha ($\mathit{\alpha }$)				0.006	0.002	0.008	0.000
Intercept	−0.120	.000	[−0.130, −0.110]
Slope	−0.009	.031	[−0.018, −0.001]
Omega ($\mathit{\omega }$)				0.006	0.002	0.010	0.000
Intercept	0.121	.000	[−0.131, −0.110]
Slope	−0.009	.026	[−0.017, −0.001]
Data collection year				0.006	0.002	0.001	0.028
Intercept	−0.120	.000	[−0.130, −0.110]
Slope	0.008	.108	[−0.002, 0.018]
Multiple moderator model				0.006	0.001	0.022	0.437
Intercept	−0.148	.000	[−0.160, −0.135]
Range restriction	0.037	.009	[0.009, 0.065]
BPI	0.018	.479	[−0.032, 0.068]
K6	0.052	.000	[0.029, 0.075]
MHI-5	0.055	.002	[0.021, 0.089]
PERID	0.011	.828	[−0.085, 0.107]
PHQ-9	−0.017	.628	[−0.084, 0.051]
SF-36	0.008	.611	[−0.023, 0.039]
Omega ($\omega$)	−0.013	.002	[−0.021, −0.005]

Note. Alpha, omega, and data collection year were centered and standardized. Est. = intercept and slope coefficients, except for moderation by measure, which displays the estimated correlation (Fisher’s $z$) for each measure; asterisks indicate whether a particular measure is significantly different from the CES-D.

^*p < .05.

^**p < .01.

^***p < .001.

Table 5.

Moderation of the association between occupational prestige and depressive symptoms.

Moderator	Est.	$p$	[95 % CI]	${\widehat{\tau }}_{(2)}^2$	${\widehat{\tau }}_{(3)}^2$	$R_{(2)}^2$	$R_{(3)}^2$
Range restriction				0.002	0.001	0.707	0.940
Not present (intercept)	−0.084	.000	[−0.095, −0.072]
Present (slope)	0.010	.416	[−0.014, 0.034]
Measure				0.002	0.001	0.712	0.956
CES-D	−0.097	.000	[−0.111, −0.083]
BPI	−0.062**	.000	[−0.084, −0.040]
K6	−0.080	.000	[−0.100, −0.060]
MHI-5	−0.058**	.000	[−0.081, −0.035]
PERID	−0.081	.017	[−0.147, −0.014]
Alpha ($\mathit{\alpha }$)				0.001	0.001	0.614	0.277
Intercept	−0.077	.000	[−0.086, −0.068]
Slope	−0.029	.000	[−0.038, −0.020]
Omega ($\mathit{\omega }$)				0.001	0.001	0.129	0.394
Intercept	−0.080	.000	[−0.089, −0.072]
Slope	−0.024	.000	[−0.033, −0.017]
Data collection year				0.001	0.001	0.708	0.939
Intercept	−0.081	.000	[−0.091, −0.071]
Slope	−0.001	.906	[−0.009, 0.011]
Multiple moderator model				0.001	0.000	0.134	0.632
Intercept	−0.092	.000	[−0.104, −0.081]
BPI	0.003	.794	[−0.021, 0.028]
K6	0.028	.006	[0.008, 0.047]
MHI-5	0.033	.003	[0.011, 0.055]
PERID	0.022	.435	[−0.034, 0.079]
Omega ($\omega$)	−0.027	.000	[−0.036, −0.019]

Note. Alpha, omega, and data collection year were centered and standardized. Est. = intercept and slope coefficients, except for moderation by measure, which displays the estimated correlation (Fisher’s $z$) for each measure; asterisks indicate whether a particular measure is significantly different from the CES-D.

^*p < .05.

^***p < .001.

^**p < .01.

3.3. Moderation by measurement of depressive symptoms & reliability

We found evidence of moderation by instrument of depressive symptoms for income (p < .001), years of education (p < .001), and occupational status (p = .010) and prestige (p = .026). We also found evidence of moderation when each instrument was compared with the CES-D (Tables 2–5). For income, the correlation was smaller for the BPI and MHI-5 and larger for the SF-36; for years of education, smaller for the K6 and MHI-5; and for occupational status and prestige, smaller for the BPI and MHI-5.

We found evidence of moderation by measures of reliability for income ($\alpha$: p < .001; $\omega$: p < .001), years of education ($\alpha$: p = .030; $\omega$: p = .026), and occupational status ($\alpha$: p < .001; $\omega$: p < .001) and prestige ($\alpha$: p < .001; $\omega$: p < .001). For income, years of education, and occupational status and prestige, an increase in $\alpha$ or $\omega$ was associated with an increase in the magnitude of association with depressive symptoms (Tables 2–5).

3.4. Multiple-moderator models

Significant moderators were included in a multiple-moderator model for each SES component (Tables 2–5). For income, range restriction, instrument of depressive symptoms, reliability, and year of data collection remained significant. This model explained 98.25 % of level-3 variability and 59.91 % of level-2 variability (p < .001). For years of education, range restriction, instrument of depressive symptoms, and reliability remained significant. This model explained 43.71 % of level-3 variability and 2.20 % of level-2 variability (p < .001). For occupational status, the instrument of depressive symptoms and reliability remained significant. This model explained 65.64 % of level-3 variability and 10.62 % of level-2 variability (p < .001). For occupational prestige, the instrument of depressive symptoms and reliability remained significant. This model explained 63.20 % of level-3 variability and 13.39 % of level- 2 variability (p < .001).

3.5. Post-hoc moderation analysis

The number of items used for the CES-D instrument ranged from 5 to 20 items. We found evidence of moderation by the number of items used for occupational status (slope = − 0.007, p = .013, 95 % CI [− 0.012, − 0.001]) and prestige (slope = −0.008, p = .006, 95 % CI [−0.013, −0.002]). For occupational status and prestige, an increase in the number of items used for the CES-D was associated with a decrease in the magnitude of association with depressive symptoms. There was no evidence of moderation for income (slope = −0.001, p = .765, 95 % CI [−0.006, 0.004]) or years of education (slope = − 0.001, p = .790, 95 % CI [−0.007, 0.005]).

4. Discussion

Our results advance understanding of the methodological factors that contribute to variability in estimating the association between SES and depressive symptoms. Our data suggest that the bivariate correlation between components of SES and depressive symptoms varies in magnitude based on coverage of the SES distribution and the measurement instrument used, as well as its reliability, even after adjusting for year of data collection. These findings have implications for the conduct of future research on SES and depressive symptoms and the clinical application of instruments used to measure depressive symptoms.

Our findings suggest a need for researchers to be more attuned to the range of values for income and years of education in their study sample. Among studies with a range-restricted sample, we found larger-magnitude correlations for income and smaller-magnitude correlations for years of education. The opposite effects of range restriction for income and years of education are likely due to nonlinearity. The increased risk of depressive symptoms among individuals from higher-SES backgrounds has focused on risk factors associated with excessive income rather than educational background (Luthar et al., 2020). For income, nonlinearity in non–range-restricted samples can reduce the linear correlation relative to range-restricted samples because a truncated range does not fully represent the plausible nonlinear pattern. For years of education, which is less likely to be influenced by nonlinearity, non–range-restricted samples can produce larger effect sizes because they have more within-sample variation than range-restricted samples (Goodwin and Leech, 2006). Overall, the presence of range restriction may overestimate the association between income and depressive symptoms and underestimate the association between years of education and depressive symptoms.

Given our findings, researchers should consider placing more emphasis on the design of survey items intended to assess SES and participant sampling. For example, some datasets may have included participants who reported incomes above $120,000, but the intervals used to assess income were top-coded (e.g., ≥$75,000). Alternatively, some datasets may not have captured higher-income individuals given response bias (Krieger et al., 1997) and the challenges associated with recruitment (Luthar and Sexton, 2004). By emphasizing participant recruitment from both ends of the income distribution, future studies can provide a more complete epidemiological understanding of depressive symptoms. For research syntheses, scholars should consider correcting effect sizes for range restriction (Schmidt et al., 2019), as well as using range restriction as a quality check or risk-of-bias item.

We also found consistent differences in the magnitude of association between instruments of depressive symptoms. Without adjusting for other moderators, the BPI produced a smaller correlation than the CES-D. The BPI was designed as a parent-report measure for youth, which may explain its smaller correlation, because parent-reported depressive symptoms are not always consistent with youth-reported symptoms (De Los Reyes and Kazdin, 2005). However, we did not test differences as a function of the informant. Understanding the impact of the informant and discrepancies between informant pairs (De Los Reyes and Kazdin, 2005) is a potential direction for future research. When adjusting for other moderators, the K6 and MHI-5 produced smaller correlations with SES than the CES-D while, for income, the SF-36 produced a larger correlation than the CES-D.

The reference timeframe and the type of items included in each instrument of depressive symptoms may explain the differences in the magnitude of the associations we observed. For example, the CES-D measures symptoms from the past week whereas the K6 and MHI-5 reference the past month. Additionally, the CES-D includes items related to appetite and sleep that are not included in the BPI, K6, or MHI- 5. While this lack of overlap across measures is not new (Fried, 2017), our findings nevertheless contribute to the discussion of depressive- symptom measurement because our data suggest that the CES-D produces larger effect sizes than some instruments, although smaller than the SF-36. Future studies should consider the generalizability of their findings to other instruments used to measure depressive symptoms.

A conceptual implication of the differences between instruments relates to whether variation between correlations is due to how instruments assess depressive symptoms or to how depressive symptoms manifest because of SES-associated factors. If these differences are truly attributable to measurement of depressive symptoms, variation across correlations may result from measurement error. Future studies should consider how depressive symptoms are defined and whether a particular instrument captures that definition. If symptom type is important in estimating the association with SES, future research should examine a subset of SES-associated environmental, cultural, or psychosocial factors that contribute to specific depressive symptoms such as whether a network of symptoms (Fried et al., 2016) are prevalent within each SES level. In effect, clinicians can better select the precise set of depressive symptoms to screen for in individuals. Future research may also consider using neuroimaging methods to assess biomarkers of depression (Li et al., 2022) and estimating their association with SES components.

Our study also reveals that measurement error influences the correlation between SES components and depressive symptoms. Higher reliability estimates were associated with larger correlations, which strengthens claims that measurement unreliability attenuates the magnitude of effect sizes (Schmidt et al., 2019). The role of measurement reliability has clinical and research implications. Clinicians should be aware of the evidence for reliability, validity, and suitability for the use of their chosen measure(s) in their situation, as defined by populations and contexts similar to their patient. Researchers should be similarly aware of reliability and should consider making effect size corrections as a sensitivity test (Bartlett and Keogh, 2018). For research syntheses, investigators can extract reliability coefficients to adjust effect sizes as a sensitivity test (Schmidt et al., 2019). Research syntheses can also include the reporting of reliability coefficients as a measure of methodological quality. These steps will aid consumers of epidemiological research on SES and depressive symptoms in evaluating the robustness of findings (Brakenhoff et al., 2018).

4.1. Limitations and future directions

The current study had some limitations. First, this study was not an exhaustive comparison across all instruments of depressive symptoms as the instruments included were identified from eligible nationally-representative, public-access datasets. Future inquiries should examine differences among other instruments (e.g., CDI, BDI). Based on our findings, we expect other instruments to vary, particularly compared with the CES-D. Next, we did not compare differences between specific types of depressive symptoms or assess the effect of repeated administrations for longitudinal associations (Twenge and Nolen-Hoeksema, 2002). We also focused on a subset of methodological characteristics and did not examine sample characteristics known to moderate the association between SES and depressive symptoms (Korous et al., 2018). Finally, we focused on IPD datasets from the United States, thus, our findings will need to be replicated with data from other countries to determine the extent of generalizability. Future research studies could examine moderation by country using metrics such as the human developmental index (HDI; Roser, 2014) or the Gini coefficient (OECD, 2018). Nevertheless, our rigorous study is one of the most comprehensive tests to date of the impact of range restriction and instrument of depressive symptoms on the association between SES and depressive symptoms.

5. Conclusion

Our findings suggest that methodological characteristics impact the observed magnitude of association between components of SES and depressive symptoms. Therefore, future research should emphasize the measurement of depressive symptoms, including increasing transparency in reporting measurement practices (Flake and Fried, 2020). Our study also informs research syntheses of SES by supporting methodological quality assessments, a preferred reporting item (Page et al., 2021; Stroup et al., 2000), and model-based artifact corrections (Campbell et al., 2021; Schmidt et al., 2019), both of which have been understudied in syntheses of SES and depressive symptoms (Lorant et al., 2003). Future studies must consider the full range of environmental circumstances that may contribute to depressive symptoms and decide which factors need to be controlled to determine the roles of income, education, and occupation. Accordingly, future research can obtain more-precise estimates of the association between SES and depressive symptoms, acknowledge variability between effect sizes, and identify symptoms of depression that are more common among specific populations.

Table 4.

Moderation of the association between occupational status and depressive symptoms.

Moderator	Est.	$p$	[95 % CI]	${\widehat{\tau }}_{(2)}^2$	${\widehat{\tau }}_{(3)}^2$	$R_{(2)}^2$	$R_{(3)}^2$
Measure				0.002	0.001	0.014	0.304
CES-D	−0.105	.000	[−0.119, −0.092]
BPI	−0.063**	.000	[−0.084, −0.041]
K6	−0.088	.000	[−0.108, −0.068]
MHI-5	−0.067**	.000	[−0.090, −0.044]
PERID	−0.093	.006	[−0.160, −0.026]
Alpha ($\mathit{\alpha }$)				0.002	0.001	0.104	0.431
Intercept	−0.085	.000	[−0.093, −0.076]
Slope	−0.027	.000	[−0.036, −0.018]
Omega ($\mathit{\omega }$)				0.002	0.001	0.102	0.440
Intercept	−0.088	.000	[−0.096, −0.079]
Slope	− 0.024	.000	[−0.032, −0.016]
Data collection year				0.002	0.001	0.000	0.000
Intercept	−0.089	.000	[−0.099, −0.079]
Slope	−0.001	.826	[−0.011, 0.009]
Multiple moderator model				0.002	0.000	0.106	0.656
Intercept	−0.101	.000	[−0.112, −0.089]
BPI	0.011	.358	[−0.129, 0.036]
K6	0.027	.006	[0.008, 0.047]
MHI-5	0.033	.004	[0.011, 0.055]
PERID	0.018	.532	[−0.039, 0.075]
Omega ($\omega$)	−0.026	.000	[−0.034, −0.017]

Note. Alpha, omega, and data collection year were centered and standardized. Est. = intercept and slope coefficients, except for moderation by measure, which displays the estimated correlation (Fisher’s $z$) for each measure; asterisks indicate whether a particular measure is significantly different from the CES-D.

^*p < .05.

^***p < .001.

^**p < .01.

Data availability statement

Individual participant data datasets can be requested from the Inter-university Consortium for Political and Social Research. Aggregate data and materials are available for review using a view-only link on Open Science Framework: https://osf.io/8xreq/.