Abstract
In this work, we develop a simple model to determine the upper bound of feed rates that do not cause jamming in material extrusion additive manufacturing, also known as fused deposition modeling (FDM)™ or fused-filament fabrication (FFF). We first derive a relation between the tube temperature and Péclet number for the solid portion of polymer filaments. We focus on the boundary between the solid and molten polymer in the heated portion of the tube. We find the Péclet number that corresponds to the point at which this boundary makes contact with the nozzle, and identify this as the upper bound of the feed rate. We compare our predictions to experimental results. We find good agreement for tube temperatures sufficiently above the glass-transition temperature, which is the temperature region of typical additive manufacturing.
Keywords: Material extrusion, Upper bound, Jamming, Feed rates, Thermal model, Temperature distribution, Fused-filament fabrication
1. Introduction
Traditional plastic manufacturing, such as injection molding [1], often involves extrusion of molten polymer through dies to produce, for example, tubes and sheets. In such cases, polymers are completely molten before they enter the dies and thus do not suffer from clogging. Recently, the extrusion of polymers has received renewed attention in an entirely different form, namely in material extrusion (MatEx) for 3-D plastic structures [2–7]. However, in MatEx there are significant differences with respect to thermal processing that can lead to insufficiently melted polymer, a major culprit in nozzle clogging. Consequently, thermal models in the traditional plastic manufacturing, which focus on melt flows inside cylindrical tubes [8–12], cannot be directly applied to the MatEx. As the low overall production rate is one major drawback to MatEx, it is critical to model and understand the upper bound of feed rates in the MatEx. Several models have been developed to determine temperature [3] and pressure distributions [5,6] in MatEx extruders. One of the pressure models was further applied to predict the minimum possible temperature that can be used to print a polymer [6]. In this work, to determine upper bounds of feed rates for the MatEx, we center on the temperature distribution in the solid portion of the filament.
2. Model
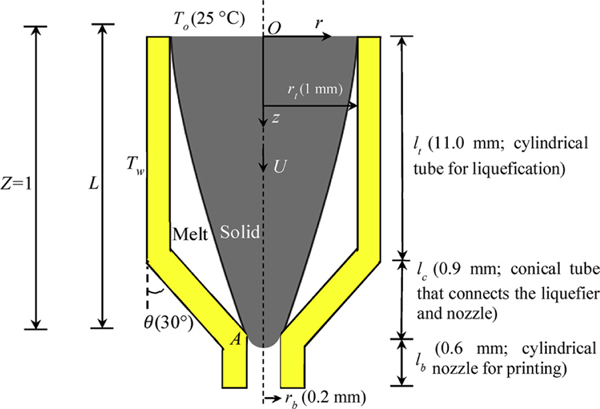
A typical extruder used in the MatEx includes three extrusion components (Fig. 1) [2]: a cylindrical liquefying tube with a length of and a radius of ; a conical connecting tube with a length of ; and a cylindrical print nozzle with a length of and a radius of . Since the cylindrical tube is much longer than the conical one, for simplicity, the conical tube is modelled as a cylindrical tube. Let . A feed force, , is applied to move the filament along the positive -direction in the cylindrical tube ( cylindrical coordinate system). In the region , the filament is assumed to maintain uniform temperature (), which is normally below melting temperature () or glass-transition temperature () of the polymer. At the plane , it passes into the heated tube, whose wall is maintained at constant temperature for all , where .
Fig. 1.
Cross-sectional (illustration) view of a polymer filament in a typical extruder used in fused-filament fabrication (not to scale). In this illustrative case, the front of the solid portion of a filament blocks the nozzle. Although a portion of the cylindrical tube is directly heated, the entire length of the extruder is considered to have a temperature of , since the extruder is all metal [6].
A few assumptions have been previously made to solve a so-called Graetz-Nusselt problem, which is a heat-transfer problem regarding Newtonian flows in cylindrical tubes (see [9], for example, for a summary of this problem). Four relevant assumptions are listed here: 1) temperature has reached a steady state; 2) heat conduction along is negligible in comparison with heat convection that occurs by overall filament motion along ; 3) (density), (heat capacity) and (thermal conductivity) are independent of position and temperature; and 4) gravitational forces are negligible. The second assumption is less straightforward. It will be justified later in Sub-section 4.4.
Based on the above four assumptions, the equation of energy for a flow inside a cylindrical tube is simplified as [8,9,13]:
| (1) |
where, , , and they are, respectively, the axial speed and flow temperature at location with and . The left- and right hand sides of Eq. (1) are convective and conductive terms, respectively. This equation has been solved by Graetz for two cases [8]: i) has a Poiseuillean distribution over a cross-section of the tube, and ii) is constant and uniform throughout the flow.
Let denote feed rate, whose unit is mm/s here. Using a line of reasoning similar to the one applied to derive Eq. (1) [13], the equation of energy for the solid portion of the filament inside a cylindrical tube is [6]
| (2) |
which is identical to the governing equation for Graetz’s second case.
In addition, let Pe denote the Péclet number. It provides a measure of the relative magnitude of heat transfer by convection in tube direction to heat transfer by conduction along the radial direction, with the following expression:
| (3) |
Set and . Both of them range from 0 to 1. Let
| (4) |
Subsequently, we obtain a nondimensionalized version of Eq. (2):
| (5) |
Moreover, there are three boundary conditions: 1) the filament has a temperature of , before it gets to the heated tube; 2) the filament has an axi-symmetric temperature distribution, and 3) the tube wall has a constant temperature of . Accordingly, we have
| (6) |
These three boundary conditions have been previously used for a flow inside a tube [8,9,13]. The first two boundary conditions still hold true for the solid portion of the polymer. However, as will be discussed in Sub-section 4.1, the third one is just an approximation.
Using the method of separation of variables, the solution to the set of Eqs. (5) and (6) is
| (7) |
In this equation, is the zero-order Bessel function of the first kind, represents the roots that satisfy (for instance, , , ), and is the first-order Bessel function of the first kind. Since the governing equation and boundary conditions of our considered problem are the same as those in Graetz’s second case, Eq. (7) is identical to what Graetz obtained [8]. Nevertheless, in our case, this solution only applies to the solid portion of the polymer.
In addition, with interpreted as time and also with replaced by , Eq. (2) is identical to the one in the case that a long cylinder, initially at a uniform temperature, is heated up in a large medium, which has a higher but constant temperature [14]. The solution to this heating problem is presented as a Heisler chart [14]. However, its boundary conditions are different from ours. For example, the heating of the cylinder is caused by the convective heat transfer between the body and its hot environment, while in our case it is due to the conduction between the heated tube and the polymer. Consequently, the solutions of the two problems are not the same.
We define a threshold temperature, . At or below this temperature, the polymer ceases to extrude through the nozzle due to a divergence in viscosity, conceptually the same as described by Mackay et.al [6]. In [6], has been predicted based on the entry pressure drop into the nozzle. The pressure drop was determined using a theoretical relation given in [15]. The assumption behind this theoretical relation was that the extruder was fully filled with polymer melt [15]. It is, however, not exactly the case for the MatEx, particularly when the clogging happens. Due to this concern, is determined experimentally in our case.
For glassy systems, such as the acrylonitrile butadiene styrene (ABS) studied, the viscosity increases exponentially as decreases towards . In the limit of a large but finite feed force and infinitesimally small feed rate, we would expect to approach . With set to be sufficiently low such that the system is isothermal (, is determined experimentally by measuring the resulting . Let denote the maximum force that the instrument can apply. We vary until we find the highest temperature where the feed force . This temperature is identified as . In our case, the current experiments with ABS, with , we set mm/s and find °C for ABS.
While there is some arbitrariness in the above definition of , it is nevertheless an important practical concept. As will be detailed in Sub-section 4.2, the viscosity and storage modulus of a typical ABS exhibit the expected strong temperature dependence over the temperature region just above . This dependence of the viscosity will dominate over the geometrical and variations that occur across different setups. Our value of is in-line with previous measurements [6], which are about 160 °C and 170 °C, respectively, for two extruders with different nozzle diameters (according to Fig. 3 of [6]).
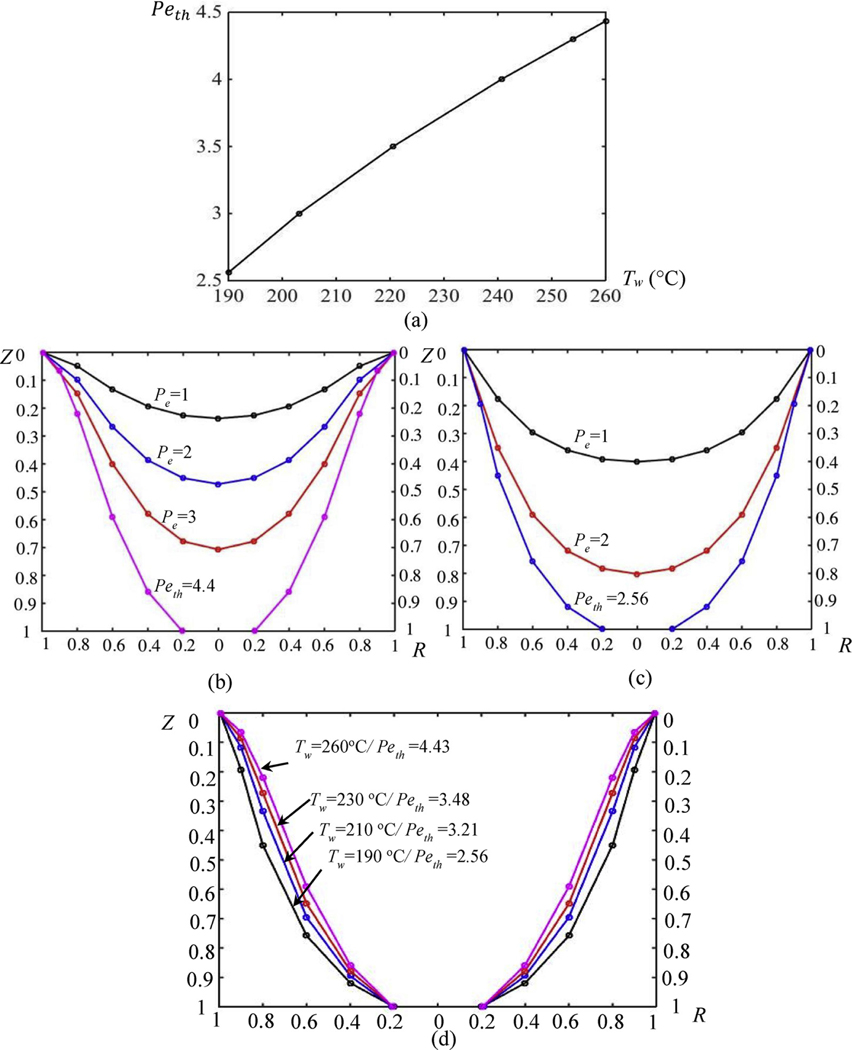
Fig. 3.
(a) relations obtained using Eq. (8). Isothermal lines of (164 °C), which are also interfaces between stiff and soft portions of the filament, determined using Eq. (7) for (b) °C, (c) °C, and (d) all considered at corresponding .
We use to predict the upper bound of the feed rate under typical MatEx conditions of finite Pe and . We again consider that, for a given , there is a transition between flow and no flow. However, since the conditions are non-isothermal and spatially inhomogeneous, we consider the temperature at the nozzle entrance, at and , as represented by the point marked A. This condition is schematically shown in Fig. 1. If the temperature at is , then the central portion of the filament should still be stiff enough to clog the nozzle. Thus, the upper bound of feed rate for a given is determined by a threshold value of Pe, denoted as , whereby at point . By Eqs. (7) and (4), at , we have
| (8) |
Subsequently, by Eq. (3), for a given , we find an upper bound for the feed rates:
| (9) |
where, denotes the upper bound that corresponds to .
3. Experimental setup
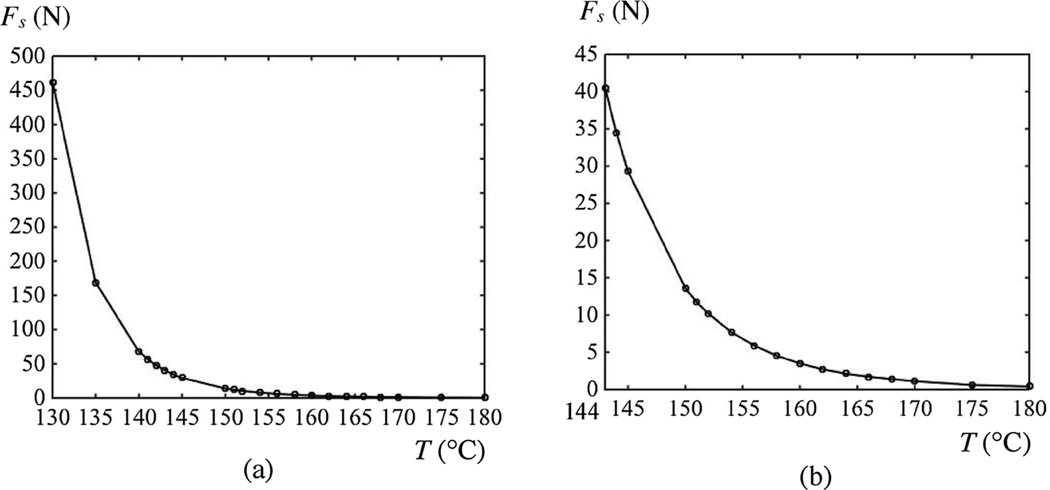
A photograph of the experimental setup is shown in Fig. 2(a). An extruder is fixed on a stage. The geometry and dimensions of the extruder are given in Fig. 1. The pinch rollers, which typically force the filament through the tube and nozzle, have been removed. The downward force on the filament is instead applied by an RSA3 Dynamic Mechanical Analyzer (DMA) (TA Instruments, New Castle, DC1) operating in constant displacement mode. The bottom end of the filament is inserted through a guiding tube to the end of the extruder, and its top end is clamped into a notch on the measurement head. The DMA applies a pre-determined velocity, , and measures the resulting up to . There are two control parameters in our setup: extrusion temperature and feed rate. The feed force required to trigger buckling decreases with the increase in the suspended length of a filament, as measured from the clamped end of the filament to the top of the guiding tube (Fig. 2(a)). As the suspended lengths were, respectively, 30 mm and 25 mm, the corresponding feed forces that caused buckling were 23.0 N and 32.5 N (Fig. 2(b)). To eliminate buckling, the maximum suspended length was set at 20 mm. This then set the amount of filament that could be inserted into the extruder in a given experiment.
Fig. 2.
(a) Experimental setup for extrusion, and (b) an example to show that buckling occurred when the suspended filament was 30 mm long, the extrusion temperature was 164 °C and feed rate was 0.1 mm/s.
4. Results and discussions
4.1. Comparison between theoretical and experimental results
The relation is found using Eq. (8) as follows: insert a value for in Eq. (8), calculate the summation, and determine the corresponding . This is shown in Fig. 3 (a) over the relevant range for MatEx of ABS, °C. We note that, since over this range, a sufficient condition for clogging is that convective heat flow dominates. Also, increases monotonically with . This relation demonstrates that, when more heat is conducted from the wall, the filament can move faster and still receive enough heat to become sufficiently softened by the time it reaches the nozzle. Fig. 3(b) and (c) show the isothermal lines of , when the wall temperatures are 260 °C and 190 °C, respectively. According to the pattern of these lines, the solid portion of a given filament increases with increasing Pe and decreasing . In addition, according to Fig. 3(d), the solid portions have roughly similar profiles at different across the range of .
Experimentally, we plot this threshold data in terms of and . The experimental relation is found using the same setup as for determination of . For a given , the value of was obtained by gradually increasing feed rate until it exceeded . The corresponding feed rate is plotted in Fig. 4. For the corresponding theoretical curve, we use the relation between and as given by Eq. (9). We set ρ and to be known values of solid ABS as 1226 kg/m3 and 1.189 kJ/(kg °C) [16], respectively, but the value of k is less straightforward.
Fig. 4.
Theoretical and experimental relations (the theoretical one is obtained using Eqs. (8) and (9). There is an error of 0.1 mm/s in the experimental value of for each temperature.
The issue with stems from a finite gap (≈ 0.13 mm) between the inner diameter of the tube and the edge of the filament, which facilitates its insertion and solid translation [2]. It leads to extra thermal resistance to heat transfer from wall to filament and thus some uncertainty about determination of its correct value. In our model, for simplicity, we did not consider this gap. We assumed that the filament diameter was equal to the tube diameter (Fig. 1). The gap may diminish with increasing z as the polymer becomes more molten. The polymer melt may fill this gap. In a cross-section of the filament, there may be both solid and molten ABS, which have different values of . The value of in Eq. (9) is thus fitted experimentally by matching the experimental and theoretical curves at the highest temperature ( °C), where the gap should have the least effect on .
Fig. 4 shows the theoretically predicted and experimentally measured curve of . As observed from this relation, increases with increasing . The measurement error is 0.1 mm/s. The fitted value of is 0.18 J/(m s °C) which is the same as the average of reported ABS solid and melt values of [16]. The difference between the theoretical and experimental values of is small when ranges from 210 °C to 260 °C, but increases with decreasing , reaching a maximum difference of 2.0 mm/s at 190 °C.
The third boundary condition, as given in the third relation of (6), is more suitable for a melt flow. The tube wall has a high temperature, the polymer located in its neighborhood should be molten. When this boundary condition is applied to the solid portion of the polymer, the assumption behind it is that the polymer melt, which surrounds the solid portion, also has a uniform speed of . In practice, this is not the case. The polymer melt has a zero speed at the tube wall, due to no-slip boundary condition. It has a speed of at its interface with the solid portion. Hence, this assumption should generate errors in the predicted temperature profiles, particularly when the solid portion just occupies a small part of the tube. On the other hand, our focus here is on the clogging issue. As illustrated in Fig. 1, the solid portion is large. The corresponding errors should be reduced. This point is justified by the small difference between the theoretical and experimental values of at higher extrusion temperatures (210 °C–260 °C). At a lower temperature, the error induced by the third boundary condition should be smaller, since the solid portion of polymer is larger. Therefore, this error should not be the main cause that the theoretical and experimental values of differ much at the lower temperatures.
We consider two possible origins for this discrepancy at the lower temperatures. The first concerns the filling of the gap between the tube and filament. As will be discussed in next sub-section, the viscosity at 190 °C is 4.4 times as much as that at 210 °C. This decrease of polymer mobility may hinder the filling of this gap and thus decrease the effective . Since in Eq. (9) is fitted to the highest temperature when the gap is filled, the difference between the theoretical and experimental values of can be expected to increase with decreasing .
As will also be discussed in next sub-section, a second possible origin relates to the fact that our model ignores wall shear force inside the cylindrical tube. This force increases with decreasing .
4.2. Change of viscosity with temperature, and forces required to drive a filament
In the case of an amorphous polymer, such as ABS, may be larger than . was measured to be 164 °C for ABS, much higher than reported of 104.5 °C [5] or 130 °C [17]. Viscosity, , changes with temperature. For a polymeric material, it is known that
| (10) |
where, is the consistency index at the reference temperature () and is horizontal shift factor at , with the following Williams-Landel-Ferry expression:
| (11) |
Where, for ABS similar to our tested one, , °C, and °C [5]. Set Pa-s [5]. Subsequently, relation is obtained using Eqs. (10) and (11). As observed from Fig. 5(a), decreases with increasing . is estimated to be 571 GPa-s near (104.5 °C) [5] and drops to 2.0 MPa-s at (164 °C) (Fig. 5(b)), a reduction of six orders in magnitude. In addition, as observed from Fig. 5(c), is 149 KPa-s at 190 °C and becomes 34 KPa-s at 210 °C, which is the lowest melt temperature suggested for injection molding of ABS [18]. at 190 °C is 4.4 times as much as that at 210 °C.
Fig. 5.
(a) relation for °C–180 °C, (b) the magnified relation for °C–180 °C, and (c) the relation for °C–260 °C.
In the proposed model (Fig. 1), at , the filament front is considered to be highly viscous. Consequently, filament motion becomes impractical in three possible locations, the conical tube, print nozzle, or the heated tube. Next, we explore these possibilities.
The force, , required to shear the molten polymer at a wall (print nozzle or cylindrical tube) is given by Eq. (7) of [6]:
| (12) |
where, and refer to and for the flow in the print nozzle and and for the flow in heated tube, is power-law index, and . Eq. (12) was derived based on the assumption that an extruder was fully filled with polymer melt. In our considered case, the polymer is just partially molten in the tube of the extruder, while it is fully molten in the nozzle. Therefore, Eq. (12) gives a good prediction of the shear force inside the nozzle, while just an estimate for the tube.
For ABS, [5]. Subsequently, relation is obtained using Eqs. (10)–(12) for the flow inside the print nozzle. As seen from Fig. 6, decreases with increasing . When °C, (Fig. 6(a)). Consequently, even if the filament could get into the nozzle, it could not be extruded through the nozzle using of our printer. Furthermore, at °C, (Fig. 6(b)), which is much smaller than , indicating that is not the main factor determining .
Fig. 6.
(a) relation for °C–180 °C, and (b) its magnification for °C–180 °C.
In addition, there is a difference of 2.0 mm/s between the theoretically predicted and experimentally measured values of at 190 °C. In practice, may be limited by . By Eq. (12), when is set to be the theoretically predicted , we have for °C. This force is much smaller than . Thus, inside the nozzle is also not the main factor that causes the discrepancy at 190 °C.
For the flow inside the heated tube, by Eq. (12), the corresponding driving forces are 28.2 N, 6.9 N, and 0.6 N, respectively, when the wall temperatures are 190 °C, 210 °C, and 260 °C. Their ratios relative to are approximately 0.8, 0.20 and 0.02. This result implies that, although could still be neglected with relatively small errors for °C, it is not negligible for °C. Consequently, for °C, our model should consider the shear force inside the heated tube. This may be one of the reasons why the theoretical and experimental values of differ much at °C.
Due to the high viscosity of the filament, the gap between the filament and the heated tube may not be filled at a lower temperature. As such, Eq. (12) may not be applicable to estimate the shear force inside the heated tube. For example, by Eq. (12), when the feed rate is 0.1 mm/s and wall temperature is 164 °C, we get . This result implies that the filament cannot be extruded at our , contradicting the experimental result.
During the extrusion, a filament encounters a resistance force in each component of the extruder. We have estimated such forces inside the heated tube and print nozzle, and also discussed their effects on extrusion at different wall temperatures. It is also interesting to know how the resistance force inside the conical tube varies with the wall temperature. We leave that to a future investigation.
4.3. Comparison of two theoretical relations
We consider first-order approximations to Eqs. (7) and (8) for the sake of simplicity and to facilitate order of magnitude estimates.
To the first-order approximation, keeping only the first term in the summation of Eq. (8), we get
| (13) |
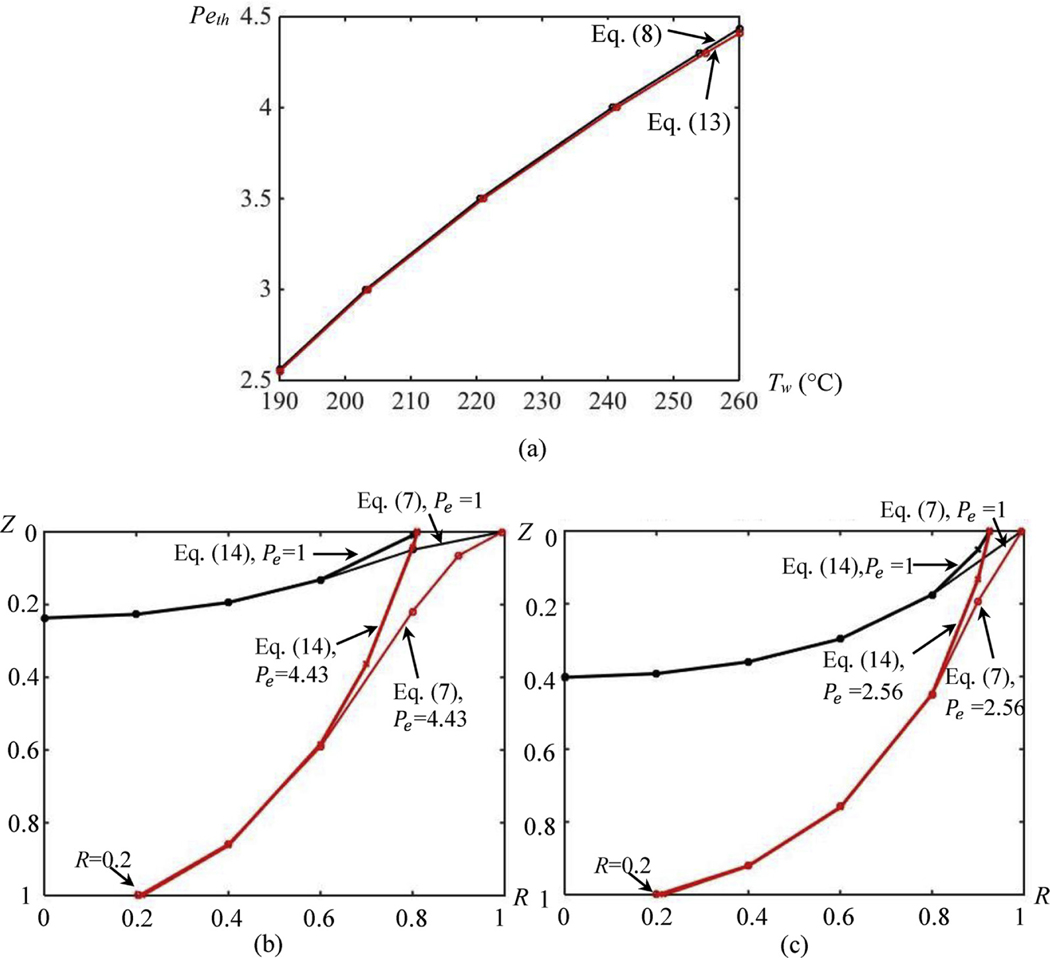
In comparison with Eq. (8) is simple to use. Fig. 7(a) gives relations obtained using Eqs. (8) and (13), respectively. The two relations match well. Their maximum difference in occurs at °C, which is only 0.15.
Fig. 7.
(a) relations obtained using Eqs. (8) and (13), respectively. Isothermal lines of (164 °C), determined, respectively, using Eqs. (7) and (14) for (b) °C and (c) °C.
To the first-order approximation, keeping only the first term in the summation of Eq. (7), we get
| (14) |
In comparison with Eq. (7) is also simple to use. Meanwhile, they may have much difference in predicting solid/melt interfaces, when Z/Pe < 0.2. For example, at °C, the isothermal lines of in the case of Pe = 4.43 found using Eqs. (7) and (14), respectively, are different when , while such a difference only appears for Z < 0.14 in the case of Pe = 1 (Fig. 7(b)). The same applies to the case of °C (Fig. 7(c)).
These results seem reasonable. increases with . As a result, due to the influence of the exponential function in each term of the summation in Eq. (7), for a relatively large Z/Pe, the other terms are negligible in comparison with the first term in the summation. Consequently, Eqs. (7) and (14) give similar results. On the other hand, the influence of the exponential function is reduced for a small Z/Pe, making the first term not the dominant one any more. Accordingly, the two equations may yield different results. The same also applies to Eqs. (8) and (13). The smallest value of 1/Peth in the case of Eq. (8) is 1/4.43, which corresponds to Z/Pe. This ratio is larger than 0.2. Thus, as in the case of Eqs. (7) and (14), Eqs. (8) and (13) gives about the same results (Fig. 7(a)).
4.4. Justification of an assumption
As mentioned in Section 2, in solving the Graetz-Nusselt problem, one of the assumptions is that the axial heat conduction, , is negligible in comparison with the axial heat convection, [8,9,13]. This assumption was adopted to derive Eq. (2). It was justified in [13] as follows: “heat conduction in the axial direction, will be omitted, since we know from experience that it is usually small in comparison with the heat convection in the axial direction.”
Next, using a scaling law, we also justify it for the case of ABS. Let Te denote the average temperature at the nozzle exit. Then, according to the length of our extruder (Fig. 1) and aforementioned material properties of ABS, we have
| (15) |
| (16) |
Subsequently, with the aid of the relations in (16), it follows from the two relations in (15) that
| (17) |
As observed from (17), is one order of magnitude higher than . Accordingly, it is reasonable to neglect in Eq. (2) for the case of ABS. If these two terms have the same order of magnitude, has to be added to the right-hand side of Eq. (2), and the resulting solution is different from the one given in Eq. (7).
4.5. Print speed and desired extrusion temperature
In MatEx, to obtain good bonding between stacked filaments, the print speed, which is the speed that the print head moves while printing, is suggested to equal extrusion speed [19]. The extrusion speed refers to the speed that an extrudate exits the nozzle. The print speed is limited by the capability of the controllers that are used to control the movement of the print head. In case the maximum allowed print speed is higher than the maximum allowed extrusion speed, which depends on the upper bound of the feed rate, the production rate is limited by this upper bound. The following gives an example. Set mm/s, which is the largest upper bound of feed rate measured in our tests, when the highest extrusion temperature was applied (260 °C). Our tested ABS filaments and nozzle have the diameters of 1.74 and 0.4 mm, respectively. By the law of conservation of mass, the corresponding extrusion speed is 123 mm/s. It is much lower than the maximum print speed of a fast 3D printer, which is 500 mm/s in the case of Delta WASP 20 × 40 Turbo 2 [20]. Hence, when a fast 3D printer, for example, is used to print ABS, the allowed feed rate, instead of the print speed, is the major factor to limit the production rate.
Jamming occurs, when the feed rate is higher than the corresponding . This problem may be resolved by raising the extrusion temperature. The threshold value of the needed extrusion temperature can be found from the pre-determined relation, by setting the preferred feed rate as .
4.6. Alternate way to determine upper bound
Instead of Eqs. (8) and (9), an order of magnitude upper bound can also be quickly found using a scaling law. When Pe =10, the convective heat is one order higher than the conductive heat. The left- and right-hand sides of Eq. (5) scale as and , respectively. The right-hand side is much smaller than the left-hand, and thus it can be neglected. Consequently, we have . By Eq. (4), this relation implies that approximately has a constant value of along the axial direction. The corresponding physical meaning is that the filament moves too fast, such that it receives little heat from the heated tube, resulting in the nozzle clogging. By Eq. (3), the resulting upper bound for feed rate is
| (18) |
In view of Eq. (18) and the fitted value of , we get mm/s. This gives a rough estimate of upper bound for all considered tube-wall temperatures. It is larger than the one obtained using Eqs. (8) and (9).
Finally, as observed from Eq. (9), to increase for a given filament, one approach is to elongate the liquefying tube. An alternate means is to have the polymer already pre-heated [21] or melted before it gets to the extruder. Consequently, jamming would diminish as a concern during the MatEx, as in the traditional plastic manufacturing.
5. Summary and conclusions
A simple model has been developed in this work to determine the upper bound of feed rates that do not cause jamming during the MatEx. Eq. (9), together with Eq. (13), gives a way to find the upper bounds for different tube-wall temperatures, while Eq. (18) may be applied to quickly determine a rough upper bound for all considered tube-wall temperatures.
Footnotes
Declaration of Competing Interest
All authors have participated in (a) conception and design, or analysis and interpretation of the data; (b) drafting the article or revising it critically for important intellectual content; and (c) approval of the final version.
This manuscript has not been submitted to, nor is under review at, another journal or other publishing venue.
The authors have no affiliation with any organization with a direct or indirect financial interest in the subject matter discussed in the manuscript
Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Insti-tute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
References
- [1].Malloy R, Plastic Part Design for Injection Molding: an Introduction, 2nd ed., Hanser Publishers, 2011. [Google Scholar]
- [2].Turner BN, Strong R, Gold SA, A review of melt extrusion additive manufacturing process: I. Process design and molding, Rapid Prototyping J 20 (3) (2014) 192–204. [Google Scholar]
- [3].Yardimci M, Hattori T, Guceri SI, Danforth SC, Thermal analysis of fused deposition, Proceedings of the Solid Freeform Fabrication Symposium (1997) 689–698. [Google Scholar]
- [4].Bellini A, Duceri S, Bertoldi M, Liquefier dynamics in fused deposition, J. Manuf. Sci. Eng. 126 (2004) 237–246. [Google Scholar]
- [5].Seppala JE, Han SH, Hillgartner KE, Davis CS, Migler KB, Weld formation during material extrusion additive manufacturing, Soft Matter 13 (2017) 6761–6769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Mackay ME, Swain ZR, Banbury CR, The performance of the hot end in a plasticating 3D printer, J. Rheol 61 (2017) 229–236. [Google Scholar]
- [7].Phan DD, Swain ZR, Mackay ME, Rheological and heat transfer effects in fused filament fabrication, J. Rheol 62 (2018) 1097–1107. [Google Scholar]
- [8].Drew TB, Mathematical attacks on forced convection problems, a review, Trans. Am. Inst. Chem. Eng. 26 (1931) 26–80. [Google Scholar]
- [9].Lychet BC, Bird RB. The Graetz-Nusselt problem for a power-law non-newtonian fluid, Chem. Eng. Sci 6 (1) (1956) 35–41. [Google Scholar]
- [10].Agur EE, Vlachopouos J, Heat transfer to molten polymer flow in tubes, J. Appl. Polym. Sci 26 (3) (1981) 765–773. [Google Scholar]
- [11].Wei D, Luo H, Finite element solutions of heat transfer in molten polymer flow in tubes with viscous dissipation, Int. J. Heat Mass Tran 46 (16) (2003) 3097–3108. [Google Scholar]
- [12].Luo C, Determination of constant viscosity for a power-law melt flow inside a circular tube, Chem. Eng. Sci 195 (23) (2019) 239–241. [Google Scholar]
- [13].Bird RB, Stewart WE, Lightfoot EN, Transport Phenomena, 2nd ed., John Wiley & Sons, 2002. [Google Scholar]
- [14].Çengel YA, Heat Transfer: a Practical Approach, 2nd ed., (2003), pp. 216–218. [Google Scholar]
- [15].Boles RL, Davis HL, Bogue DC, Entrance flows of polymeric materials: pressure drop and flow patterns, Polym. Eng. Sci 10 (1970) 24–31. [Google Scholar]
- [16].Tadmor Z, Gogos C, Principles of Polymer Processing, 2nd ed., (2006) (g A.3. [Google Scholar]
- [17].Jyoti J, Singh BP, Arya AK, Dhakate SR, Dynamic mechanical properties of multiwall carbon nanotube reinforced ABS composites and their correlation with entanglement density, adhesion, reinforcement and C factor, RSC Adv. 6 (5) (2016) 3997–4006. [Google Scholar]
- [18].Harper CA, Handbook of Plastics, Elastomers and Composites, 4th ed., (2004), p. 77. [Google Scholar]
- [19].Du J, Wei Z, Wang X, Wang J, Chen Z, An improved fused deposition modeling process for forming large-size thin-walled parts, J. Mater. Process. Technol 234 (2016) 332–341. [Google Scholar]
- [20].Datasheet of 3D printer Delta WASP 20×40 Turbo 2: https://www.personalfab.it/en/downloads-2/.
- [21].Go J, Hart AJ, Fast desktop-scale extrusion additive manufacturing, Addit. Manu 18 (2017) 276–284. [Google Scholar]