Detecting 3D Syndromic Faces as Outliers using Unsupervised Normalizing Flow Models

Abstract

Many genetic syndromes are associated with distinctive facial features. Several computer-assisted methods have been proposed that make use of facial features for syndrome diagnosis. Training supervised classifiers, the most common approach for this purpose, requires large, comprehensive, and difficult to collect databases of syndromic facial images. In this work, we use unsupervised, normalizing flow-based manifold and density estimation models trained entirely on unaffected subjects to detect syndromic 3D faces as statistical outliers. Furthermore, we demonstrate a general, user-friendly, gradient-based interpretability mechanism that enables clinicians and patients to understand model inferences. 3D facial surface scans of 2471 unaffected subjects and 1629 syndromic subjects representing 262 different genetic syndromes were used to train and evaluate the models. The flow-based models outperformed unsupervised comparison methods, with the best model achieving an ROC-AUC of 86.3% on a challenging, age and sex diverse data set. In addition to highlighting the viability of outlier-based syndrome screening tools, our methods generalize and extend previously proposed outlier scores for 3D face-based syndrome detection, resulting in improved performance for unsupervised syndrome detection.

Graphical Abstract

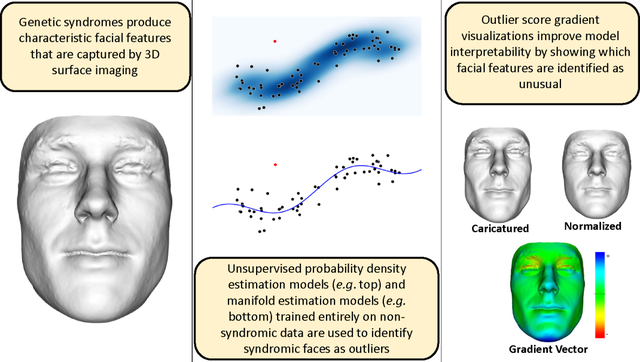
1. Introduction

The process for diagnosing a genetic syndrome can be complex. Many affected patients and families face prolonged periods of waiting and uncertainty before receiving a diagnosis [1]. Genetic testing is a powerful diagnostic tool. However, genetic experts and clinics are often scarce in less affluent countries, and genetic tests are often unavailable or do not produce a definitive diagnosis [2]. Patients may not even be referred to a genetics expert or receive a genetic test if the possibility of them having a syndrome is not recognized in the first place. Because many syndromes affect facial morphology [3], systems for computer-assisted diagnosis based on facial characteristics have been proposed as a low-cost and non-invasive option for genetic syndrome diagnosis.

State-of-the-art approaches typically use supervised learning to diagnose specific syndromes given a facial image [4, 5], training a multi-class model to map an input facial image to an output syndrome class (e.g., down syndrome) based on example input-output pairs (see [6, 7] for reviews of supervised learning). Although such approaches can achieve excellent performance for the task of syndrome diagnosis, supervised models require large databases of syndromic facial images to train. Such syndromic facial image databases are expensive, challenging to collect, and, due to the variety and rarity of genetic syndromes, often contain imbalances across syndrome classes and other demographic factors. For these reasons, most supervised multi-class syndrome diagnosis models support diagnosis of only those genetic syndrome classes that are well represented in the available training data, and exclude very rare disorders altogether [4, 5]. Other supervised approaches train binary classification models with only two output classes. These models typically have an unaffected class and a single generic syndrome class (see [4] for examples of these methods). Although these models may not be strictly limited to a subset of syndromes, they still require syndromic data to train.

In this work, we approach face-based syndrome detection as a statistical outlier detection problem, employing models that aim to capture typical facial morphological variation in an unaffected population. We use unsupervised normalizing flow models trained entirely on non-syndromic data to compute outlier scores that indicate unusual facial morphology. The primary advantage of an unsupervised outlier detection approach is the removal of any data requirement for labeled syndromic data [8]. Collecting diverse 3D facial scan data from syndromic patients is very challenging and expensive for a variety of reasons. While still challenging, collecting non-syndromic facial scans from diverse demographics is much easier than finding and imaging patients with numerous and rare diseases. Specifically, we explore two different approaches for modeling typical facial morphological variation using normalizing flows: probability density estimation and manifold estimation. A low dimensional example of both approaches is shown in the second column of the graphical abstract. Both, density and manifold estimation approaches, are often used for generative modeling as well as for outlier detection [9].

Instead of providing specific diagnostic suggestions based on syndrome-specific facial features, the outlier approach aims to identify unusual facial features in general. This approach is applicable to large scale, efficient genetic syndrome screening, where patients exhibiting unusual facial morphology for their demographic (e.g., age and sex) can be referred for genetic consultation and testing using more targeted approaches. In addition to greatly reduced data collection requirements, the outlier detection approach is also applicable in realistic clinical scenarios in which a patient may have an extremely rare or previously undocumented genetic disease that affects facial morphology.

1.1. Previous Work

1.1.1. Face-Based Syndrome Diagnosis

Many previously proposed face-based syndrome detection models [10, 11, 12, 4, 13, 14, 15] use 2D images of the subject’s face, as these can be easily acquired in a clinical setting. Less common are approaches that use 3D geometric information [5, 16] directly acquired via 3D facial scanning techniques. It is expected that 3D facial imaging will be become more common in the future, as consumer hardware and software products increasingly support 3D capture methods. For both 2D and 3D images, the most common modeling approaches involve training a supervised classification model. Binary classifiers, which discriminate between unaffected and syndromic subjects or between a single syndrome class and other syndromic or unaffected subjects, as well as multi-syndrome class models, have been developed for this purpose (see [4] for a survey). Both 2D and 3D classifier models can achieve excellent performance (above 90% sensitivity for the unaffected class [5, 4]). However, classification performance is typically highly variable across different syndrome classes and syndromes not represented in the training set cannot be classified at all.

Unsupervised approaches for face-based syndrome detection are rarely used. For example, Hammond et al. [16] proposed an outlier score, signature weight, as a ”relatively crude but useful estimate of the facial dysmorphism of an individual”. The signature weight corresponds to the magnitude of the face signature vector, which represents a normalized difference between a patient face and a demographic matched unaffected average face. The absolute difference between the two faces is normalized by the magnitude of typical facial variation for that demographic. Therefore, the face signature vector also identifies which particular regions of a patient face are abnormal relative to a demographic matched unaffected population. More recently, Matthews et al. [17] developed a series of 3D facial surface growth curves along with a set of demographic specific shape models that support the computation of face signature vectors and weights.

In this work, we generalize the signature weight score and develop more sophisticated unsupervised facial dysmorphism scoring methods. We also develop a general method of identifying which specific facial regions and features are abnormal (similar to the face signature vector) that is compatible with more complex facial dysmorphism scoring models. To accomplish this, we use flexible normalizing flow models for both probability density and manifold estimation.

1.1.2. Normalizing Flows

A normalizing flow (NF) is a type of machine learning model in which an invertible, bijective function is learned for some objective such as probability density estimation or manifold estimation (see [18, 19, 20] for comprehensive reviews). NF models differ from traditional neural network models primarily in that they have a tractable inverse and Jacobian determinant. These properties are highly desirable for many machine learning applications. For example, NF density estimators support efficient exact likelihood inference, unlike other generative models such as variational auto-encoders and generative adversarial models. NF manifold estimation models can be constructed using a single invertible function, unlike auto-encoders, which require training separate encoder and decoder functions that are not guaranteed to be consistent with one another. Another advantage of NF models is that the invertibility lends itself to interpretability. The ability to propagate information in both directions through a model has been used to develop visual interpretability mechanisms, such as counterfactual generation, that are highly effective at explaining model inferences to non-technical users [21, 22]. NFs have been applied to outlier detection tasks in other contexts [23, 24], but not for the task of face-based syndrome detection. Furthermore, by using conditional NFs for co-variate adjusted outlier detection, our methods account for patient demographic information when computing an outlier score.

1.2. Contributions

The main contribution of this work is the development of a flexible and mathematically sound framework for unsupervised 3D face-based outlier detection applied to genetic syndrome screening. This is achieved through the use of conditional normalizing flows models, which handle density- as well as manifold-based outlier detection in a unified framework. We show that the proposed methods generalize and extend previous approaches for unsupervised 3D face-based outlier detection applied to genetic syndrome screening resulting in improved syndrome detection performance. Furthermore, we demonstrate a general gradient-based interpretability mechanism, applicable to both density- and manifold-based NF models, that allows users to investigate which facial regions and features an outlier model identifies as unusual.

2. Materials and Methods

This section will first describe the 3D scan data used in our experiments as well as the 3D facial measurement process. The proposed methods for computing outlier scores using density and manifold estimation NF models as well as the outlier score gradient interpretability mechanism are then described in subsequent subsections.

2.1. Data Description

The 3D facial surface scans used to train and evaluate our models were acquired using 3DMD facial imaging systems¹ and are available through the FaceBase Consortium². Patients with syndromes were recruited through clinical geneticists at different sites across North America and have a clinical or molecular diagnosis. Ethics approval for this study was granted by the Conjoint Health Research Ethics Board (Id #: REB14-0340_REN4) at the University of Calgary.

The primary data used in this work consist of 1629 3D facial surface scans of syndromic patients representing 262 different genetic syndromes as well as 2471 scans of unaffected subjects. All subjects are between the ages of 5 and 40. Figure 1 shows the age and sex distribution of both syndromic and unaffected subjects. As is common among syndromic facial data sets, the data shows a prominent age imbalance between syndromic and unaffected subjects. Additionally, there is a prominent sex imbalance among unaffected subjects.

Figure 1:

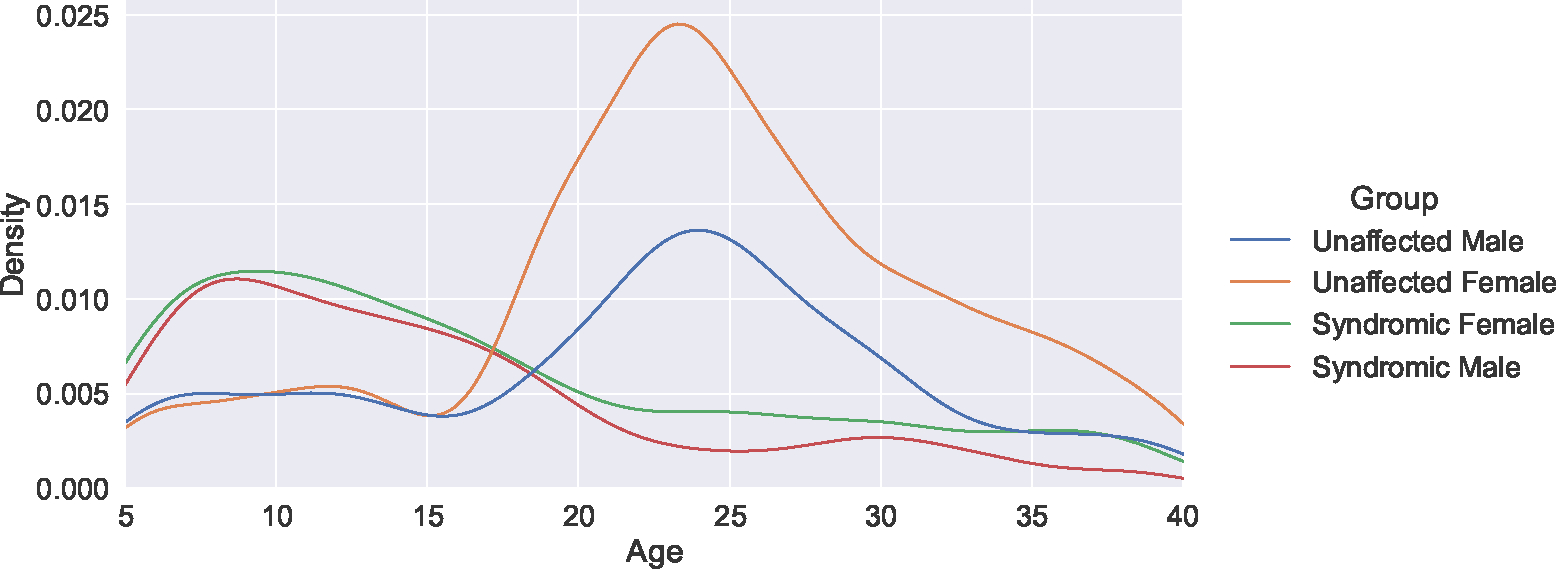
A kernel density plot of the subject demographic distribution. This data set shows a prominent age imbalance between syndromic and unaffected subjects, as well as a sex imbalance among unaffected subjects.

2.2. 3D Facial Measurement

3D facial surface scans are commonly represented in digital format using discrete polygonal meshes consisting of vertices connected by polygon faces. Generally, the mesh topology used to represent a 3D facial surface will not be the same across different facial scans. This means that there is no a priori correspondence between the vertices and polygons of different scans. Thus, as an initial data pre-processing step, we re-mesh all subject facial scans to a standardized mesh topology with a fixed number of vertices located at corresponding locations for each subject. Importantly, only the topology of the meshes is made uniform through this step. The vertex positions, which encode facial phenotype information like size and shape differences, are not the same across all subjects. Thus, our models are able to use facial size and shape information to detect outliers.

To achieve this, a template mesh is non-linearly registered to all subject meshes. The estimated transformations are then used to propagate the template vertices to all subject scans, which guarantees point-to-point correspondence and a uniform mesh topology across the population. A bilateral mapping between mesh vertices across the median plane of the template was also used to produce a flipped and symmetrized version of each face as a form of data augmentation. Irrelevant information associated with 3D facial position and rotation relative to the 3D scanner’s frame of reference was removed from each registration using rigid body transformations. At the end of this process, the 3D facial morphology of each subject $i$ is encoded as a vector ${\mathbf{x}}_i\in X={\mathbb{R}}^{3n_{\text{vert}}}$ where $n_{\text{vert}}$ is the number of vertices used to represent 3D facial morphology. We also combine each subject’s demographic information into a conditioning variable $y_i=\left\{{\mathrm{a}\mathrm{g}\mathrm{e}}_i\right.\left.,{\mathrm{s}\mathrm{e}\mathrm{x}}_i\right\}\in Y={\mathbb{R}}_{+}\times \{\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{e},\mathrm{f}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{e}\}$.

The objective of the methods presented below is to learn an outlier scoring function $s(\mathbf{x},y):X\times Y\mapsto \mathbb{R}$ that quantifies abnormal 3D facial morphology for specific unaffected demographic groups. The outlier scoring function is then used to discriminate between unaffected faces and syndromic faces. Given an outlier scoring function, outlier detection can be performed by thresholding outlier scores, or by presenting raw scores to users with appropriate context to support their decisions. In this work, we construct outlier scoring functions that rely on probability density estimation as well functions that rely on manifold estimation. Both approaches will be described in detail in the following sections.

2.3. Conditional Density Estimation

Intuitively, a density-based approach will identify a face as an outlier if it is improbable among unaffected subjects in the same demographic group. Therefore, the density-based outlier detection approach proposed in this work involves estimating a probability density $p_X(\mathbf{x}\mid y)$ over the space of 3D facial morphology $X$ for unaffected training subjects only. The conditional likelihood of test subject faces is then used as an outlier scoring function.

To model the complex and potentially non-Gaussian distribution $p_X(\mathbf{x}\mid y)$, we construct a trainable bijective function $h_{\theta }\left({\mathbf{z}}_{\mathrm{i}\mathrm{d}},y\right):Z_{\mathrm{i}\mathrm{d}}\times Y\mapsto X$ that maps points in $X$ to and from a Gaussian latent variable space $Z_{\text{id}}~\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}(0,\mathbf{I})$ conditional on demographic variable $y$. The potentially complex conditional likelihood $p_X(\mathbf{x}\mid y)$ can then be conveniently evaluated using the Gaussian prior via a change of variables formula:

$$p_X(\mathbf{x}\mid y)=p_{Z_{id}}\left(h_{\theta }^{-1}(\mathbf{x},y)\right)\cdot {\left|\mathrm{d}\mathrm{e}\mathrm{t}\left[J_{h_{\theta }}\left(h_{\theta }^{-1}(\mathbf{x},y),y\right)\right]\right|}^{-1}$$ (1)

Here, $J_{h_{\theta }}\left(z_{\mathrm{i}\mathrm{d}},y\right)$ represents the Jacobian of function $h_{\theta }\left(z_{\mathrm{i}\mathrm{d}},y\right)$ with respect to the variable $z_{\mathrm{i}\mathrm{d}}$. Given $n_{\mathit{pop}}$ unaffected training samples $\left\{{\mathbf{x}}_i,y_i\right\}$, parameters $\theta$ are then optimized to minimize a negative log likelihood loss:

$${ℒ}_{\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y}}(\theta )=\frac{-1}{n_{\mathrm{p}\mathrm{o}\mathrm{p}}}\sum _{i=1}^{n_{\mathrm{p}\mathrm{o}\mathrm{p}}}\mathrm{l}\mathrm{o}\mathrm{g}(p_X(x_i\mid y_i))$$ (2)

We use conditional density estimation models to leverage available demographic information (age and sex) as well as to account for demographic imbalance biases that may be present in facial image databases. This means that our models estimate probability densities specific to different demographic groups (e.g., females at 5 years of age) by making the bijection $h_{\theta }$ conditional on the demographic variable $y$. Thus, faces are identified as outliers if they are improbable with respect to their specific demographic group rather than with respect to unaffected faces in general.

2.4. Conditional Manifold Estimation

Intuitively, a manifold-based approach will identify a face as an outlier if it is far from a low-dimensional manifold representing the facial variation of unaffected subjects in the same demographic group. This approach assumes that 3D facial variation is well captured by low dimensional sub-manifolds of the input data space $X$, which has been shown to be a valid assumption in previous studies [25, 5]. Therefore, the manifold-based outlier detection approach proposed in this work estimates a low dimensional manifold of maximum data variation $ℳ(y)\subset X$ embedded within the data space $X$ conditional on demographic variable $y$ for unaffected training patients only.

Demographic-specific manifolds of maximum facial variation $ℳ(y)$ are defined by a coordinate chart $g_{\varphi }^{-1}(\mathbf{x},y):X\times Y\mapsto Z_{ℳ}$ and a corresponding inverse $g_{\varphi }\left({\mathbf{z}}_{ℳ},y\right):Z_{ℳ}\times Y\mapsto ℳ\subset X$, which map faces $\in X$ to and from the manifold coordinate space $Z_{ℳ}$. The reconstruction error $\parallel \mathbf{x}-g_{\varphi }(g_{\varphi }^{-1}(\mathbf{x},y),y){\parallel }^2$, which represents the squared distance between a face and its projection onto the demographically corresponding low dimensional manifold, is used as the outlier scoring function.

As described in [20], we construct $g_{\varphi }^{-1}$ and $g_{\varphi }$ using the forward and inverse directions of a shared bijective function $f_{\varphi }({\mathbf{z}}_{ℳ},{\mathbf{z}}_{\stackrel{-}{ℳ}},y):Z_{ℳ}\times Z_{\stackrel{-}{ℳ}}\times Y\mapsto X$, thus ensuring that $g_{\varphi }^{-1}$ and $g_{\varphi }$ are consistent with one another. Intuitively, bijection $f_{\varphi }$ maps between the data space $X$ and a latent space with the same dimensionality as $X$. Unlike density estimating NF models, where a base density is defined over the latent space, the latent space of manifold estimating NF models is divided into two complementary parts: $Z_{\stackrel{-}{ℳ}}$ and $Z_{ℳ}$. $Z_{ℳ}$ represents the coordinate space of the learned manifold, while $Z_{\stackrel{-}{ℳ}}$ is a null space. To project a face into the manifold coordinate space using $g_{\varphi }^{-1}(\mathbf{x},y)$, we apply the inverse of the bijective function $f_{\varphi }^{-1}(\mathbf{x},y)$ and discard $z_{\stackrel{-}{ℳ}}$ to get $z_{ℳ}$. To reconstruct a face from manifold coordinates $z_{ℳ}$ using $g_{\varphi }\left({\mathbf{z}}_{ℳ},y\right)$, we set $z_{\stackrel{-}{ℳ}}$ to zero and compute $f_{\varphi }\left({\mathbf{z}}_{ℳ},0,y\right)$. Parameters $\varphi$ are selected to minimize a reconstruction loss representing the magnitude of data variance not captured by the learned manifold given $n_{\mathit{pop}}$ unaffected training samples $\left\{{\mathbf{x}}_i,y_i\right\}$:

$${ℒ}_{\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{l}\mathrm{d}}(\varphi )=\frac{1}{n_{\mathrm{p}\mathrm{o}\mathrm{p}}}{\displaystyle \sum _{i=1}^{n_{\mathrm{p}\mathrm{o}\mathrm{p}}}{\Vert x_i-g_{\varphi }(g_{\varphi }^{-1}(x_i,y_i),y_i)\Vert }^2}$$ (3)

We use conditional manifold estimation models to leverage available demographic information (age and sex) as well as to account for demographic imbalances that are commonly present in facial image databases. This means that our models estimate manifolds of maximum data variation that are specific to different demographic groups (e.g., females at 5 years of age) by making the bijection $f_{\varphi }$ conditional on the demographic variable $y$. Thus, faces are identified as outliers if they are far from the manifold of maximum variation for their specific demographic group rather than the manifold of maximum variation for non-syndromic faces in general.

2.5. Normalizing Flow Layers

The manifold and density estimation approaches described above require the specification of a trainable bijective function ($h_{\theta }$ and $f_{\varphi }$ respectively) that we model using a NF. Just as in regular neural network models, a series of simple trainable functions called layers are composed to produce a complex trainable NF model. Unlike regular neural network models, bijective NF layers also support efficient evaluation of the inverse and Jacobian determinant of the layer. Furthermore, to construct conditional density and manifold estimation models, we use conditional NF layers that depend on variable $y$. The linear and non-linear conditional NF layers used in our experiments are described below. Section 2.6 then describes how the layers are composed to construct the models used in our experiments. The code for all NF layers and models is available on github³.

2.5.1. Translation

The linear translation layers used in our study represent the bijective function $l_{\text{translation}}(\mathbf{x},y)=\mathbf{x}+t_{\alpha }(y)$ where $t_{\alpha }(y):Y\mapsto {\mathbb{R}}^{3n_{\text{vert}}}$ is a dense neural network with trainable parameters $\alpha$. Function $l_{\text{translation}}$ is invertible and always has a Jacobian determinant of 1.

2.5.2. Scaling

The linear scaling layers used in our study represent the bijective function $l_{\text{scaling}}(\mathbf{x},y)=\mathbf{x}\odot \mathrm{e}\mathrm{x}\mathrm{p}\left(s{c}_{\beta }(y)\right)$ where $s{c}_{\beta }(y):Y\mapsto {\mathbb{R}}^{3n_{\text{vert}}}$ is a dense neural network with trainable parameters $\beta$. Function $l_{\text{scaling}}$ is invertible and has a tractable Jacobian determinant.

2.5.3. Rotation

The linear rotation layers used in our study represent the bijective function $l_{\text{rotation}}(\mathbf{x},y)=\mathbf{x}\cdot r_{\gamma }(y)$ where $r_{\gamma }(y):Y\mapsto \mathrm{S}\mathrm{O}\left(3n_{\text{vert}}\right)$ produces a rotation matrix from the special orthogonal group in $3n_{\text{vert}}$ dimensions $\mathrm{S}\mathrm{O}\left(3n_{\text{vert}}\right)$. Here, special techniques are required to produce a smooth paramaterization of $\mathrm{S}\mathrm{O}\left(3n_{\text{vert}}\right)$ (see [26] for a full discussion). The function $r_{\gamma }(y)$ is composed of a dense neural network with trainable parameters $\gamma$ that first produces a skew symmetric matrix $\in {\mathbb{R}}^{3n_{\text{vert}}\times 3n_{\text{vert}}}$. The Cayley transform is then applied to the skew symmetric matrix to produce a rotation matrix. The function $l_{\text{rotation}}$ is invertible and has a fixed Jacobian determinant of 1.

2.5.4. Affine Coupling

To learn non-Gaussian densities and non-linear manifolds, non-linear transformations must be included in our NF models. The non-linear layers used in our study are entropy preserving affine coupling layers as proposed in [27]. As coupling layers, function $l_{\text{coupling}}(\mathbf{x},y)$ splits the input $\mathbf{x}$ into two parts. Let ${\mathbf{u}}_1$ represent the first $3n_{\text{vert}}/2$ dimensions of $\mathbf{x}$ and ${\mathbf{u}}_2$ represent the remaining dimensions. The coupling layers used in our models represent the bijective function $l_{\text{coupling}}(\mathbf{x},y)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{e}\left[\mathrm{e}\mathrm{x}\mathrm{p}\left(s{c}_{\xi }\left({\mathbf{u}}_2,y\right)\right)\odot {\mathbf{u}}_1+t_{\xi }\left({\mathbf{u}}_2,y\right),{\mathbf{u}}_2\right]$ where $s{c}_{\xi }(\mathbf{x},y)$ and $t_{\xi }(\mathbf{x},y):{\mathbb{R}}^{3n_{\text{vert}}/2}\times Y\mapsto {\mathbb{R}}^{3n_{\text{vert}}/2}$ are dense neural networks with shared trainable parameters $\xi$. The function $l_{\text{coupling}}$ is invertible and the Jacobian determinant is fixed to 1 by imposing an additional constraint on function $s{c}_{\xi }(\mathbf{x},y)$ as proposed in [27].

Permuting or mixing the input dimensions between affine coupling layers is necessary because interactions between dimensions would be restricted otherwise. Therefore, we place random, fixed permutations after every affine coupling layer.

2.6. Normalizing Flow Models

In this section, the different NF model architectures used in our study are described in detail. Table 1 shows a high level summary of all models.

Table 1:

A summary of the NF model architectures used for probability density and manifold estimation.

NF Model	Architecture
Probability Density
Independent Gaussian	Scaling ↦ Translation
Gaussian	Scaling ↦ Rotation ↦ Translation
Non-Gaussian	Scaling ↦ Affine Coupling (×3)↦ Translation
Manifold
Linear	Rotation ↦ Translation
Non-Linear	Affine Coupling (×3)↦ Translation

2.6.1. Density Estimation Models

By composing different combinations of linear and non-linear NF layers, we construct three different density estimation models with different degrees of freedom. The simplest and most constrained model is only able to learn independent Gaussian densities. This independent Gaussian density model is also equivalent to the signature weight score (see Sec 2.7 for full details). Non-independent Gaussian, and non-Gaussian models are also explored to investigate if more complex models lead to improved syndrome detection performance. All models have the same, isotropic, unit variance Gaussian distribution for the latent variable space $Z_{\mathrm{i}\mathrm{d}}$.

The independent Gaussian NF model is composed of only translation and scaling layers. Therefore, the Gaussian distribution over the latent space $p_{Z_{\mathrm{i}\mathrm{d}}}\left({\mathbf{z}}_{\mathrm{i}\mathrm{d}}\right)$ is scaled along each dimension and translated according to variable $y$ producing the conditional distribution $p_X(\mathbf{x}\mid y)$. Because both NF layers are linear, and the latent distribution is Gaussian, distribution $p_X(\mathbf{x}\mid y)$ will also be Gaussian. Furthermore, translation and scaling layers alone are not able to produce a distribution $p_X(\mathbf{x}\mid y)$ where the dimensions of $X$ are not independent. The co-variance matrix of the Gaussian distribution $p_X(\mathbf{x}\mid y)$ is always diagonal because the scaling and translation layers are strictly diagonal. To construct a Gaussian NF model that allows for non-zero co-variance between different dimensions of $X$, we introduce an additional rotation layer into the model.

To transform a Gaussian latent distribution into a non-Gaussian conditional distribution $p_X(\mathbf{x}\mid y)$, non-linear layers must be introduced into the NF model. Thus, for our non-Gaussian density estimation model, we replace the linear rotation layer with a chain of three non-linear affine coupling layers interspersed with random permutations.

2.6.2. Manifold Estimation Models

We construct two different manifold estimation models: linear and nonlinear. The simpler and more constrained linear model is much like a conditional version of principal component analysis in that it also estimates linear manifolds of maximum data variation. Matthews et al. [17] accomplish a similar task using a sliding window approach to singular value decomposition. A non-linear NF model is also explored to investigate if more complex, non-linear manifold structures lead to improved syndrome detection performance. The linear model is composed of rotation and translation layers, which enable it to learn any linear sub-manifold of the input space. Like the non-Gaussian density estimation model, we replace the rotation layer with a chain of three non-linear affine coupling layers in order to learn non-linear manifolds.

2.7. Signature Weight Score

The independent Gaussian density estimation NF model described above differs from the signature weight score only in that it uses all three spatial components of point displacements, as opposed to the signature weight, which considers only the surface normal component. Although not described in a probabilistic way, the signature weight score proposed by Hammond et al. [16] is equivalent to a density-based outlier score in our framework. Computing a signature weight score involves first estimating expected faces as well as typical point displacement magnitudes for different patient demographics. These estimates effectively define the vertex mean and variance parameters for an independent Gaussian probability density conditioned on demographic variables. The signature weight score is then the square root of the sum of the squared normalized differences between a patient face and the corresponding demographic mean face. Importantly, this score is monotonically related to the negative likelihood of a patient face under a Gaussian density with corresponding demographic mean and variance parameters. Thus, if the signature weight score of patient A is larger than that of patient B, the negative conditional likelihood of patient A is also larger than that of patient B under a corresponding Gaussian density. This property makes the two scores equivalent as outlier scoring methods. Therefore, we use an independent Gaussian density estimator to emulate the signature weight score in our experiments.

2.8. Outlier Gradient Interpretability Mechanism

Clinicians are understandably hesitant to introduce black-box models into their medical decision making processes. Therefore, we propose a simple interpretability mechanism to visualize the 3D facial attributes that our unsupervised outlier detection models identify as unusual. For a manifold or density based outlier scoring function $s(\mathbf{x},y)$, we visualize the gradient of the score ${\nabla }_{x}s\left({\mathbf{x}}_i,y_i\right)$ for the 3D face ${\mathbf{x}}_i$ of interest using both color maps and counterfactual facial morphs. Caricature morphs show patient faces that are transformed along the outlier score gradient to exaggerate unusual facial characteristics. Normalized morphs show patient faces that are transformed along the outlier score gradient in the opposite direction to soften unusual facial characteristics. In this application, the gradient of the outlier score represents the most efficient transformation that would make a face more or less of an outlier according to the model.

Outlier score gradients are also a partial generalization of the face signature vector proposed by Hammond et al. [16] to identify which specific facial regions and features are unusual in a given subject’s face. Gradient vectors for the independent Gaussian density model (used in this work to emulate the signature weight score) also point in the same direction as the corresponding face signature vector.

3. Experiments and Results

All results presented below are cross validated using five Monte-Carlo 80%/20% train/test splits of the subjects. Syndromic subjects were excluded when training unsupervised models. Models were also trained using different numbers of vertices to represent 3D facial morphology. In order to accomplish this, sets of $n_{\mathit{vert}}$ vertices were selected uniformly at random from the full resolution mesh topology.

3.1. Supervised Baselines

To establish performance baselines for the task of syndrome detection, we first trained and evaluated linear and non-linear (multi-layer perceptron) binary logistic regression models. These models discriminate unaffected subjects from patients with any genetic syndrome and are trained on data that includes both unaffected and syndromic subjects. Age and sex information is not provided to the supervised models. Areas under receiver operating characteristic curves (ROC-AUC) results are shown in Table 2.

Table 2:

Areas under receiver operating characteristic curves (%) for different supervised multi-layer perceptron models trained using different syndromic facial data. Standard deviations across the cross validation folds are shown in parentheses.

Model	Syndrome Training Data	$n_{\mathrm{vert}}$
		100	1k	5k
Linear	100%	99.2 (0.3)	99.3 (0.2)	99.3 (0.2)
Non-Linear	100%	99.2 (0.2)	99.3 (0.2)	99.2 (0.2)
Linear	10%	98.9 (0.3)	98.8 (0.2)	96.4 (2.6)
Non-Linear	10%	96.6 (0.3)	96.3 (0.6)	95.6 (0.6)
Linear	Down Only	92.9 (0.8)	87.1 (2.3)	75.3 (20.8)
Non-Linear	Down Only	76.9 (1.4)	75.8 (1.7)	75.1 (1.1)

The first set of supervised experiments used 100% of the syndromic data available in each training set. All model configurations achieved excellent results (above 99% AUC-ROC). To investigate the impact of limited syndromic data, we conducted additional experiments where only 10% of the syndromic data from each training set was used. Performance for these models was slightly worse that that of models trained with complete data (98.9% AUC-ROC for the best performing model). Additionally, non-linear models and models using more vertices began to overfit and perform worse. Finally, we conducted experiments where data from a single syndrome (Down only) was available for model training, and the same syndrome was excluded from the test set. While these models produced even more over-fitting and worse performance than previous experiments, some configurations still performed well (92.9% AUC-ROC for the best performing model).

3.2. Density-Based Outlier Detection

All density and manifold estimation models used in this work were trained using only unaffected subjects (roughly 60% of the subjects used to train the supervised models). For the task of density-based outlier detection, we explored three different density estimation models. The first model (independent Gaussian) was designed to emulate the signature weight score as described in Section 2.7. The second model (Gaussian) relaxes the assumption of point independence through the addition of a rotation layer, but retains the Gaussian assumption. We found Gaussian model training to be intractable for large numbers of vertices due to the large computational cost of the conditional rotation layer. The third and most flexible model (non-Gaussian) completely relaxes the Gaussian assumption by introducing nonlinear transformations as described in section 2.5. The ROC-AUC results for density-based outlier scores are shown in Table 3.

Table 3:

Areas under the receiver operating characteristic curve (%) using conditional likelihood as an outlier score for the task of syndrome detection. Results are not shown for the full Gaussian model with large numbers of vertices due to intractable training. Standard deviations across the cross validation folds are shown in parentheses.

	$n_{\mathrm{vert}}$
	100	1k	5k
Independent Gaussian	81.6 (2.8)	84.1 (1.8)	83.5 (2.3)
Gaussian	84.3 (3.8)
non-Gaussian	84.6 (1.5)	86.3 (1.3)	85.7 (1.6)

Overall, density-based outlier detection performed well. The results do not fully reach the performance of supervised models, but this is not surprising given the valuable syndromic training data available to the supervised models. The independent Gaussian model performed surprisingly well given its simplicity. However, the non-Gaussian model achieved the highest ROC-AUC (86.3%) among the density-based outlier detection approaches. The Gaussian model also outperformed the independent Gaussian model when using a smaller number of vertices. Increasing vertex count from 100 to 1k improved results slightly, while the results from 1k and 5k are generally similar.

3.3. Manifold-Based Outlier Detection

Compared to NF density models, manifold estimation models have an additional hyper-parameter, which corresponds to the dimensionality of the sub-manifold to be estimated. In this work, we experiment with manifolds of dimension 1, 10, 50, and 100. Previous results from principal component analyses of 3D faces have shown that a 100-dimensional linear subspace is capable of capturing the overwhelming majority of data variance in neutral 3D facial data [5]. We further experiment with two different manifold estimation models, the simpler of which learns a linear sub-manifold. The more flexible, non-linear model uses non-linear layers as described in section 2.5. We found that training the linear manifold estimation model was intractable when using values of $n_{\text{vert}}\ge 1k$, again, due to the computational cost of the large matrices in the conditional rotation layer. The ROC-AUC results for manifold-based outlier scores are shown in Table 4.

Table 4:

Areas under receiver operating curves (%) using conditional manifold reconstruction error as an outlier score for the task of syndrome detection. Results are shown for linear and non-linear manifolds of different dimensionality. Results are not shown for the linear model with large numbers of vertices due to intractable training. Standard deviations across the cross validation folds are shown in parentheses.

Model	$n_{\mathrm{vert}}$	$\mathit{dim}(ℳ)$
		1	10	50	100
Linear	100	73.7 (1.4)	82.1 (2.4)	74.1 (0.9)	75.7 (1.3)
Non-Linear	100	74.9 (1.0)	81.2 (2.6)	82.9 (1.9)	83.8 (0.4)
Non-Linear	1k	76.5 (2.0)	84.7 (1.8)	82.6 (1.2)	82.2 (1.4)
Non-Linear	5k	78.2 (1.6)	85.5 (2.3)	82.2 (1.4)	81.5 (0.8)

Overall, manifold-based outlier detection also performed well, with ROC-AUC values reaching 85.5% for the best performing model. The results do not reach the performance of supervised models, but this is, again, not surprising given the additional syndromic training data available to the supervised models. The best manifold estimation results are similar to the density estimation results. However, some manifold estimation configurations (e.g., those with one dimensional manifolds) were reliably outperformed by density estimation models. For low vertex data, non-linear manifold estimation outperformed linear manifold estimation, especially for models with manifolds of dimension 50 and 100. Increasing vertex count improved performance for the two lowest dimensional manifold estimation models while the higher dimensional manifold results are quite similar.

3.4. Outlier Gradients

Figure 2 shows how outlier score gradients can be used to interpret outlier model inferences and identify specific facial features as unusual. Contrasting caricatured and normalized counterfactual facial morphs is a visually effective method to highlight facial features that contribute most to the outlier score. Another method is to visualize the surface normal component of the gradient using a colored map. The results shown in Figure 2 were produced using a non-Gaussian density estimation model with 1k vertex representations. The deformations were then mapped from the 1k representations to the full resolution mesh surface (shown in the figure) using a thin plate spline transform and an additional Laplacian smoothing step to remove noise associated with point sampling.

Figure 2:

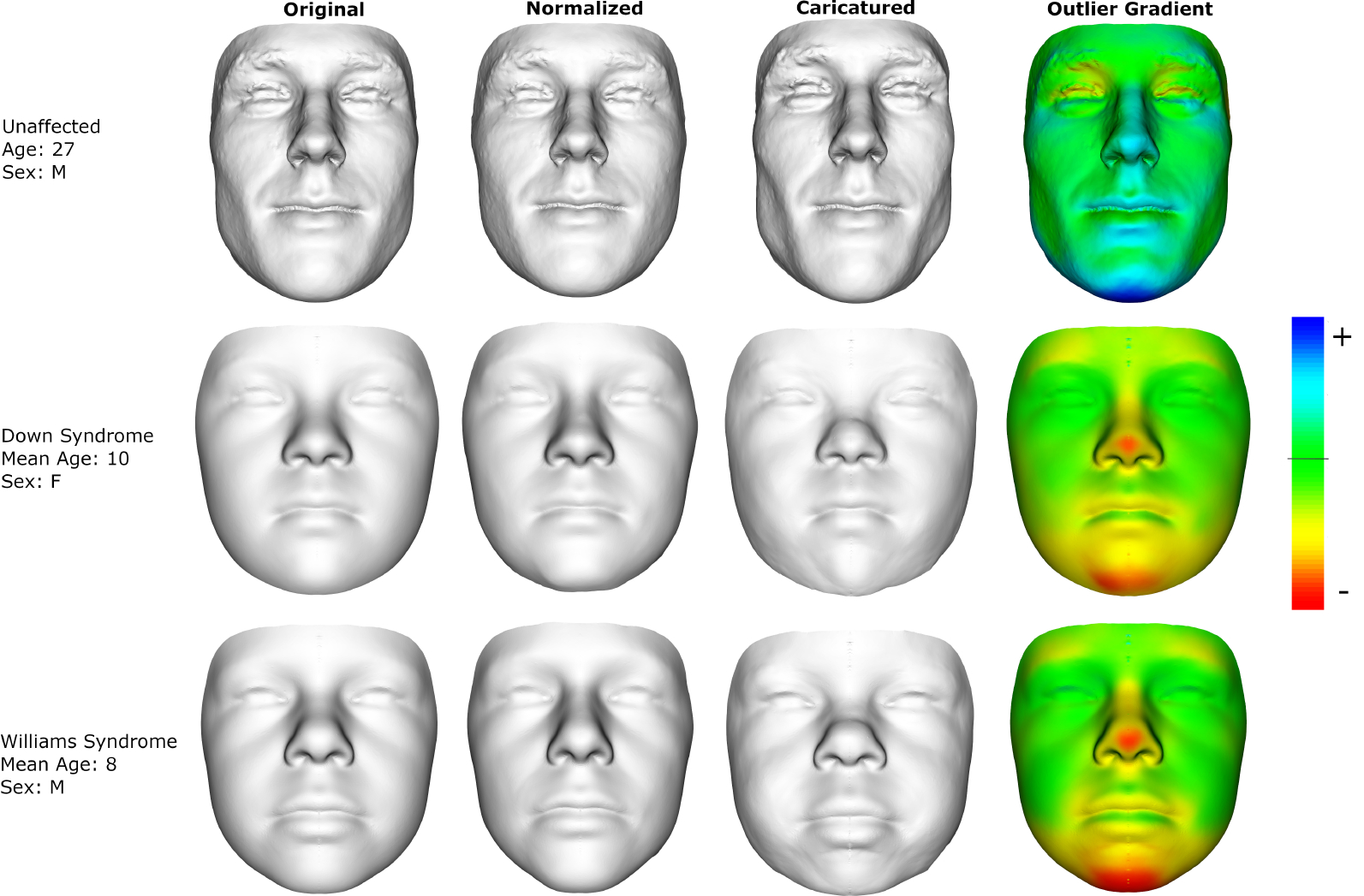
Faces (original column) that have been transformed along the outlier score gradient to look more normal (normalized) and more unusual (caricatured). The outlier gradient color map shows the surface normal component of the gradient with positive values indicating that the surface is pushed outwards compared to a normalized face and negative values indicating the opposite. The top row is a real example subject. The bottom two rows represent the average faces of Down or Williams syndrome subjects under the age of 15 years.

The example faces used in Figure 2 are a real unaffected subject as well as facial averages from patients with Down and Williams syndrome under the age of 15. The gradient figures show that the unaffected subject has a larger face and more prominent jaw and zygomatic bones compared to what the NF model expects for an unaffected person of their age and sex. The syndromic gradient morphs show that the NF model is able to identify characteristic facial features for both Down (flat nose and face, small chin) and Williams (puffy cheeks and lips, depressed nasal bridge) syndrome.

4. Discussion

Overall, our results demonstrate that outlier detection is a feasible method for population level genetic syndrome screening. Although unsupervised outlier scores did not reach the performance of supervised models trained using labeled syndromic subjects for the task of face-based syndrome detection, they did achieve a level of performance that would be clinically valuable in the context of population level syndrome screening. Furthermore, our results suggest that the use of non-linear layers (in non-Gaussian density estimation models and non-linear manifold-estimation models) improved performance over strictly linear models.

Previous work found that NF models can have poor out of distribution detection performance when applied to image data. The results of their experiments suggest that this is due to the inductive biases of coupling layers that encourage models to learn local pixel correlations rather than relevant semantic details of images [24]. In our experiments, we train and evaluate non-Gaussian and non-linear NF models with coupling layers as well as Gaussian and linear models without coupling layers (see Table 1 for full descriptions). The results, shown in Tables 3 and 4, demonstrate that models with coupling layers outperformed models without coupling layers. Thus, for the type of coupling layer used in our experiments, the inductive bias of coupling layers does not appear have a detrimental effect on outlier detection for this application.

Aside from the added ability to estimate non-Gaussian densities and nonlinear manifolds, the NF framework proposed in this work offers a mathematically elegant and unified approach to Gaussian and linear modelling of 3D facial morphology. The previously proposed signature weight score requires the creation of demographic bins to compute demographic-specific expected faces and point variances. In contrast, our equivalent independent Gaussian density estimating NF smoothly incorporates categorical and continuous demographic information in a single conditioning variable passed to a unified parametric model. Previous approaches for demographic-specific manifold estimation [17, 28] train multiple age and sex specific linear manifold estimation models. In contrast, our unified conditional linear manifold estimating NF model can smoothly account for age, sex, and other types of demographic information.

One important consideration is that the supervised models explored in this work do not incorporate or adjust for demographic information and may therefore exploit demographic biases present in the training and evaluation data. For example, the average age of syndromic subjects is less than that of unaffected subjects. A supervised discriminative model may spuriously associate youthful features with syndromic faces unless corrective measures are employed. One common way of controlling for demographic imbalances in training data is to model the demographic effects first and adjust all training data so as to remove the demographic effects. In fact, the conditional density estimation NF models used here could be used for exactly this purpose. Therefore, the development of good models of unaffected facial variation across different demographic groups is also highly valuable for correcting demographic biases in supervised syndrome diagnosis applications.

The direct comparison of various density and manifold estimation models in our evaluation also yielded some interesting insights. Generally speaking, density estimation can more completely capture a data distribution compared to a manifold estimation model (e.g., the toy 2D data shown in the graphical abstract). Somewhat surprisingly, our best performing manifold estimation model reached nearly the performance of the best density estimation model. This may be due to the fact that density estimation is also more challenging for high dimensional data. Another interesting observation from our results is the performance gap between linear and non-linear manifold estimation that emerges primarily for manifolds of dimension 50 and 100. It appears that lower dimensional manifolds of maximum 3D facial variation may be well approximated using linear manifolds, while higher dimensional manifolds have more non-linear structure.

Finally, comparing results between models trained and evaluated using different numbers of vertices to represent facial shape produced valuable insights. Generally, we saw improved performance using 1k vertices compared to 100 vertices. Using 5k vertices produced marginally increased or even decreased performance. This suggests that the models are primarily using low frequency information as opposed to fine surface details to detect outliers. This conclusion is also supported by the relatively smooth outlier score gradient visualizations shown in Fig 2.

4.1. Limitations

An important limitation of our approach is its dependence on 3D facial scanning technology. While 3D scanning devices are less expensive and more available than ever before, collecting a 3D facial scan is more complex and difficult compared with 2D color photography. Obtaining 3D facial scans from young patients is often more difficult than for older patients due to inability or unwillingness to cooperate and pose during image acquisition. Thus, a 3D approach may be sub-optimal for very young patients. For both, 2D and 3D image modalities, subjects with previous facial trauma or surgery are not good candidates for face-based syndrome diagnosis tools. An additional complexity of an outlier-based approach is that, in a clinical setting, an appropriate classification threshold would need to be selected and applied to the outlier scores to produce a binary classification.

Further limitations of our models are related to the data used in our experiments. Our data does not include children under the age of five years and, therefore, further data collection would be required to train and evaluate our model for very young children. Although this is a limitation of the current study, this is not a limitation of the proposed technical method. The proposed outlier detection approach can be easily extended to subjects below the age of 5 by retraining on an expanded data set. Our model does not consider ear morphology (which can be an important syndromic biomarker [5]). Additionally, we were unable to use facial texture information, which is also captured by some 3D facial scanners. Finally, ethnic variation was limited within our data. Generally, the data used to train an outlier detection model should include a large sample that is representative of the population on which the tool will be applied. Future work on conditional face models would ideally incorporate ethnicity into the conditioning variable y along with age and sex information.

We believe that combining NF-based manifold and density estimation (as in [20]) for outlier detection would be an challenging and interesting extension of this work. One specific challenge with combining manifold and density estimation is that likelihood values from such models are only defined for points on the manifold. Future work could investigate effective methods to combine the different outlier scores used for manifold and density NF models.

5. Conclusion

In this work, we presented a flexible and general framework for unsupervised 3D face-based outlier detection applied to genetic syndrome screening. This was achieved using normalizing flows models, which handle probability density- as well as manifold-based outlier detection in a unified framework. We showed that the proposed methods generalize and extend previous approaches for unsupervised 3D face-based outlier detection resulting in improved syndrome detection performance. Furthermore, we presented a general gradient-based interpretability mechanism, applicable to both density- and manifold-based NF models, that allows users to investigate which facial regions and features an outlier model identifies as unusual. Our results demonstrate that outlier detection is a feasible approach for face-based genetic syndrome screening that, unlike supervised approaches, does not require any syndromic facial data to train.

Highlights.

• A flexible framework for unsupervised 3D face-based outlier detection using conditional probability density and manifold estimation normalizing flow models is proposed.

• Outlier score gradient visualizations improve interpretability by showing users the specific facial regions and features the model identifies as unusual.

• Models are trained and evaluated using 3D surface scans of 2471 unaffected subjects and 1629 syndromic subjects representing 262 genetic syndromes.

• Both, density estimating and manifold estimating normalizing flow models, outperformed unsupervised baseline methods with the best model achieving an ROC-AUC of 86.3.